On Air-Cavity Formation during Water Entry of Flexible Wedges
Abstract
1. Introduction
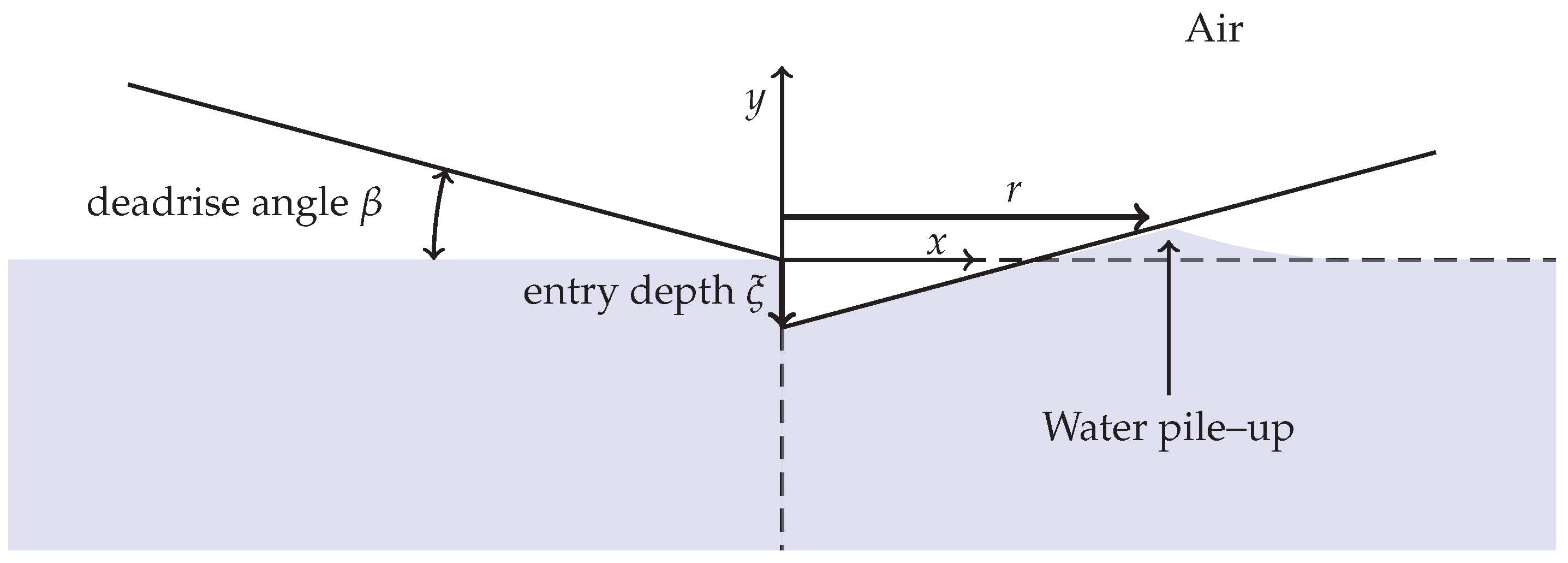
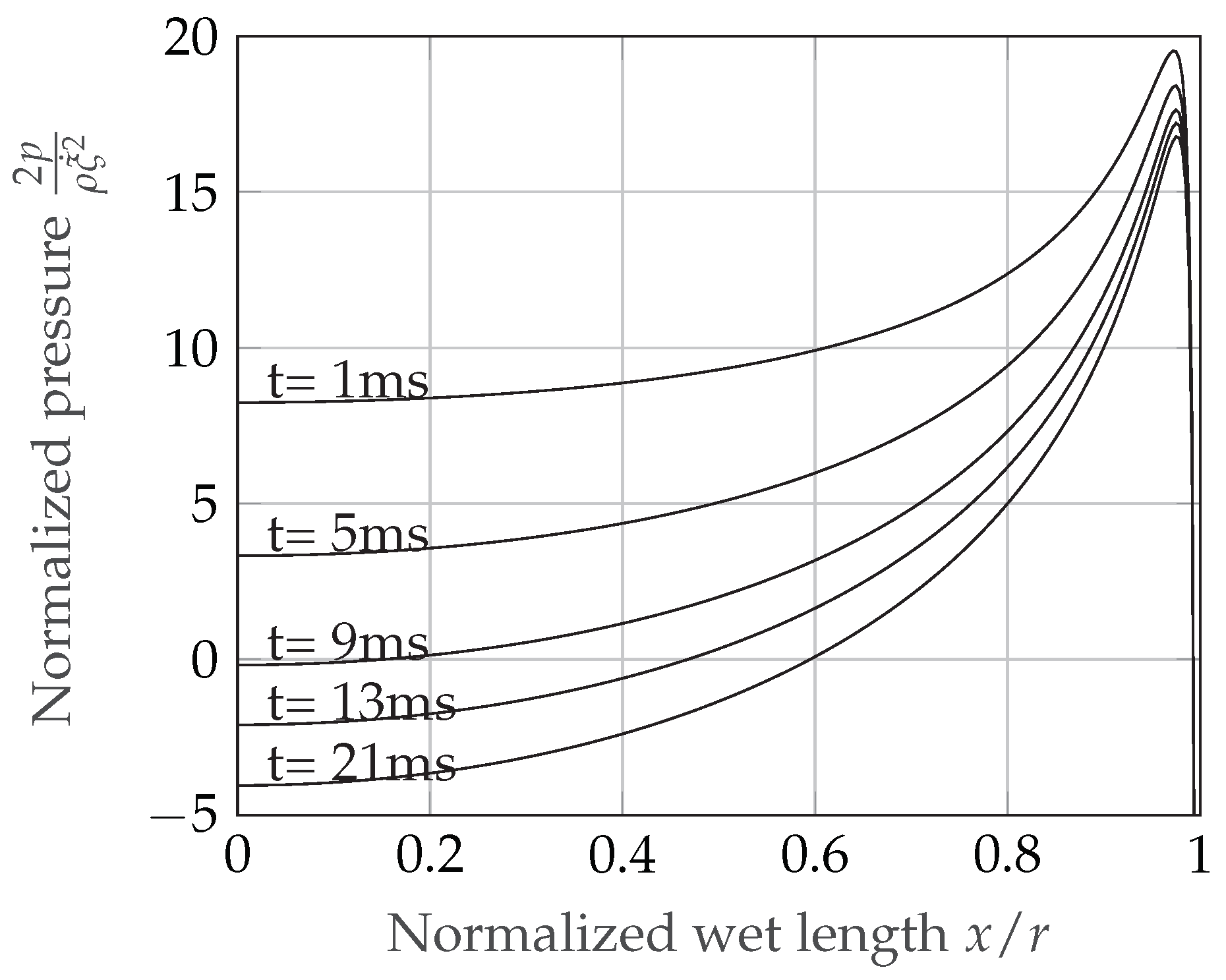
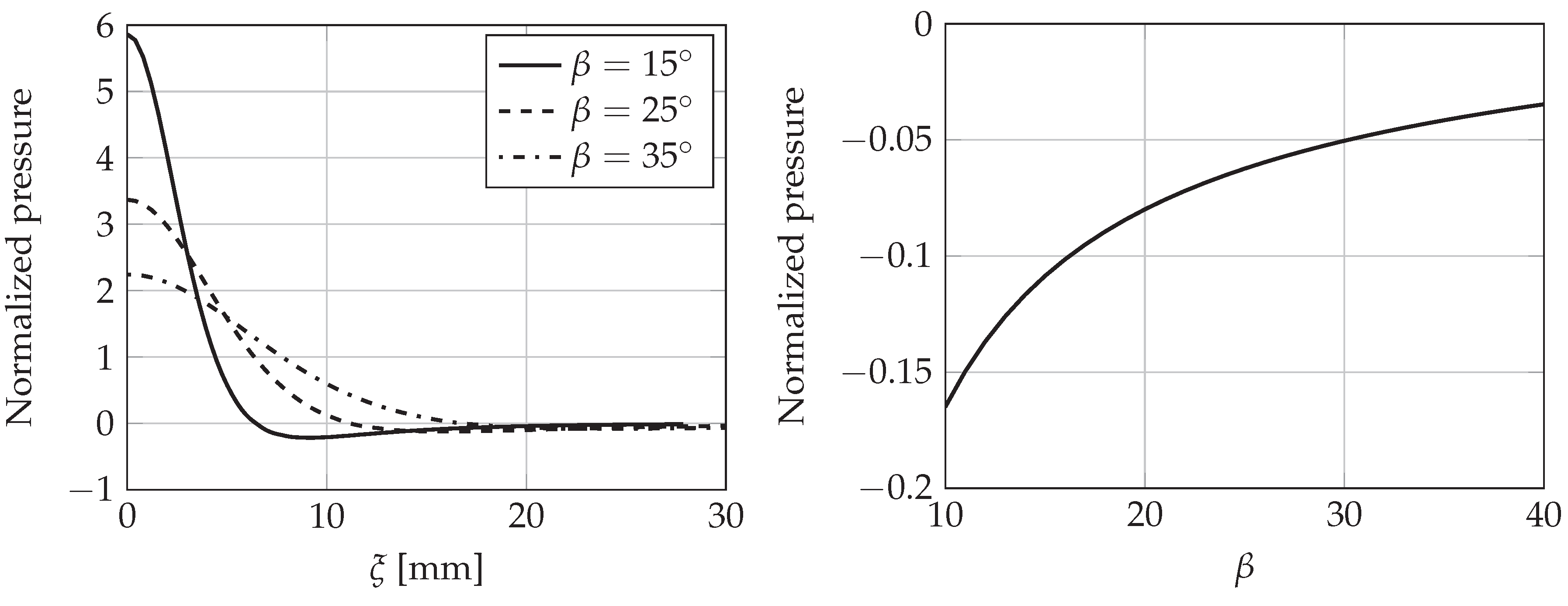
2. Cavitation Onset in Rigid Bodies’ Water Entry as Predicted by Analytical Formulations
3. Preliminary Experimental Evidences
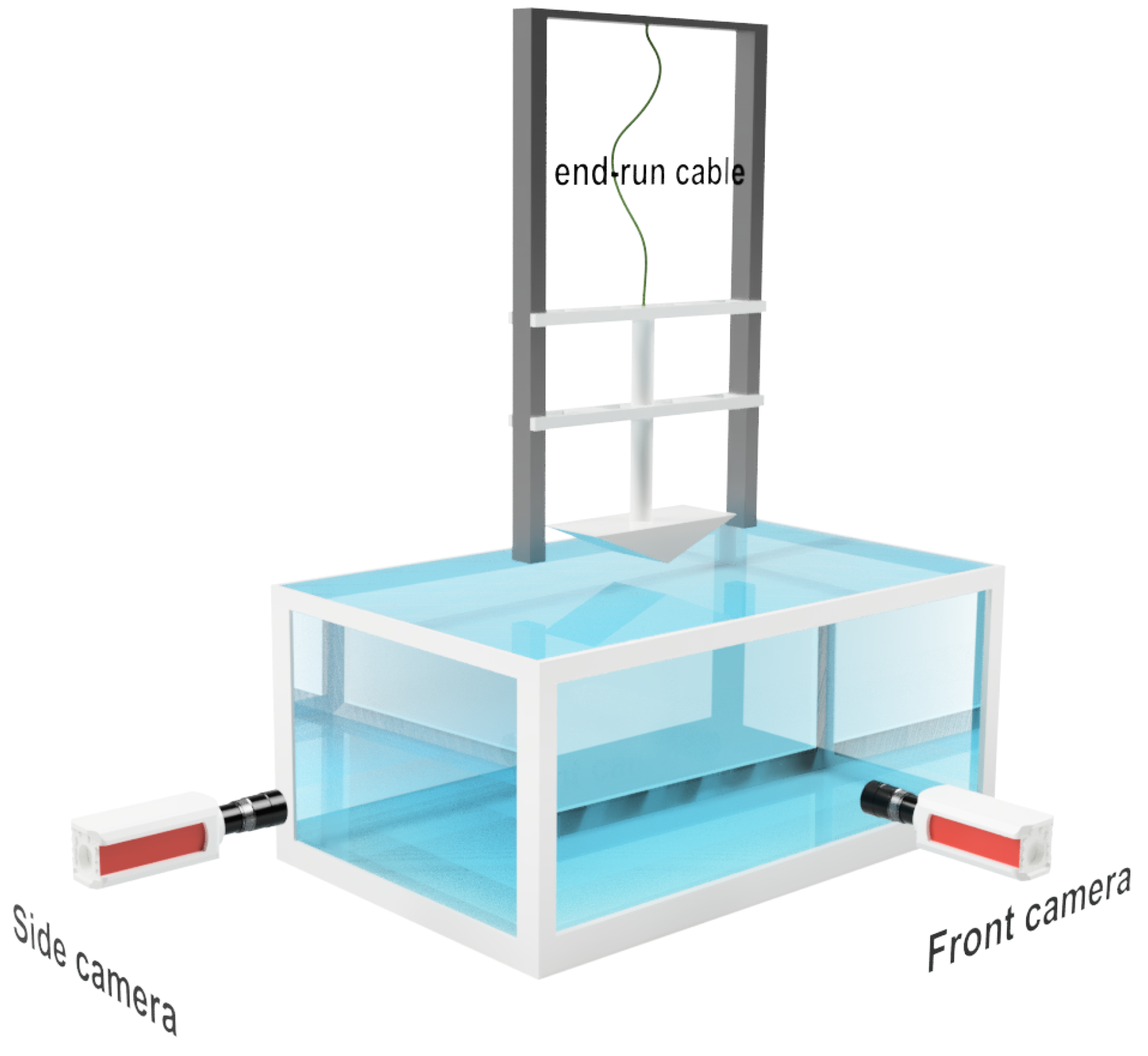
4. Experimental Setup
Specimens
5. Experimental Results
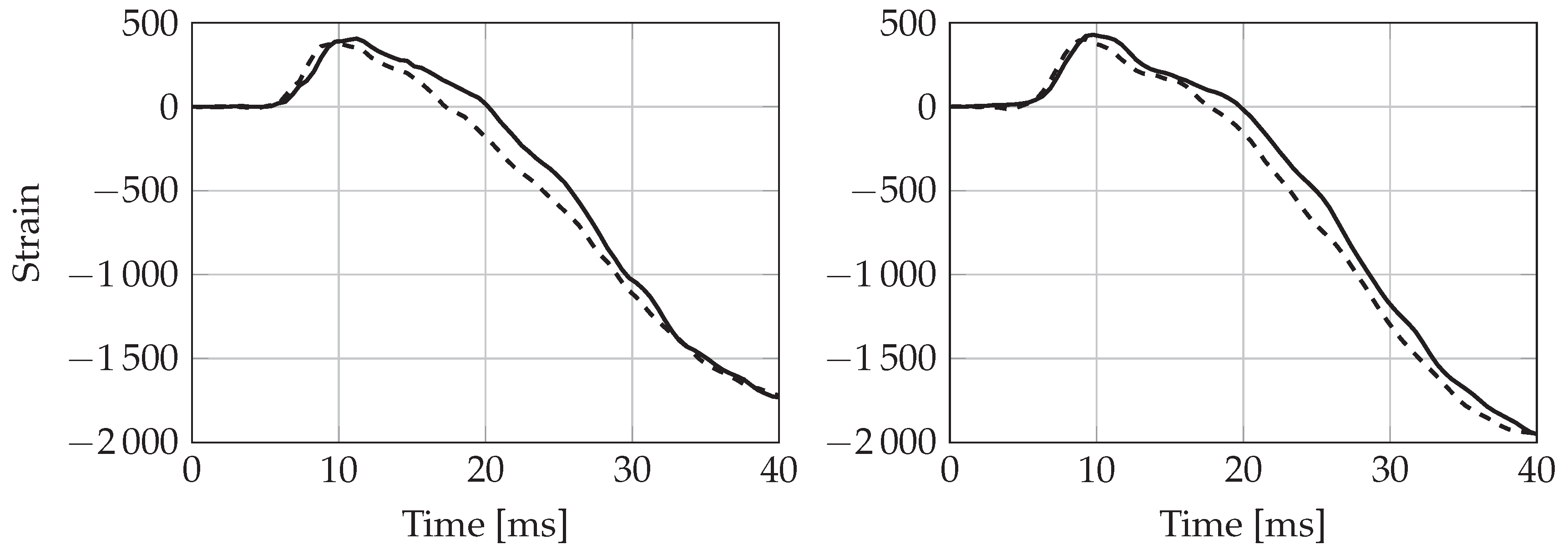
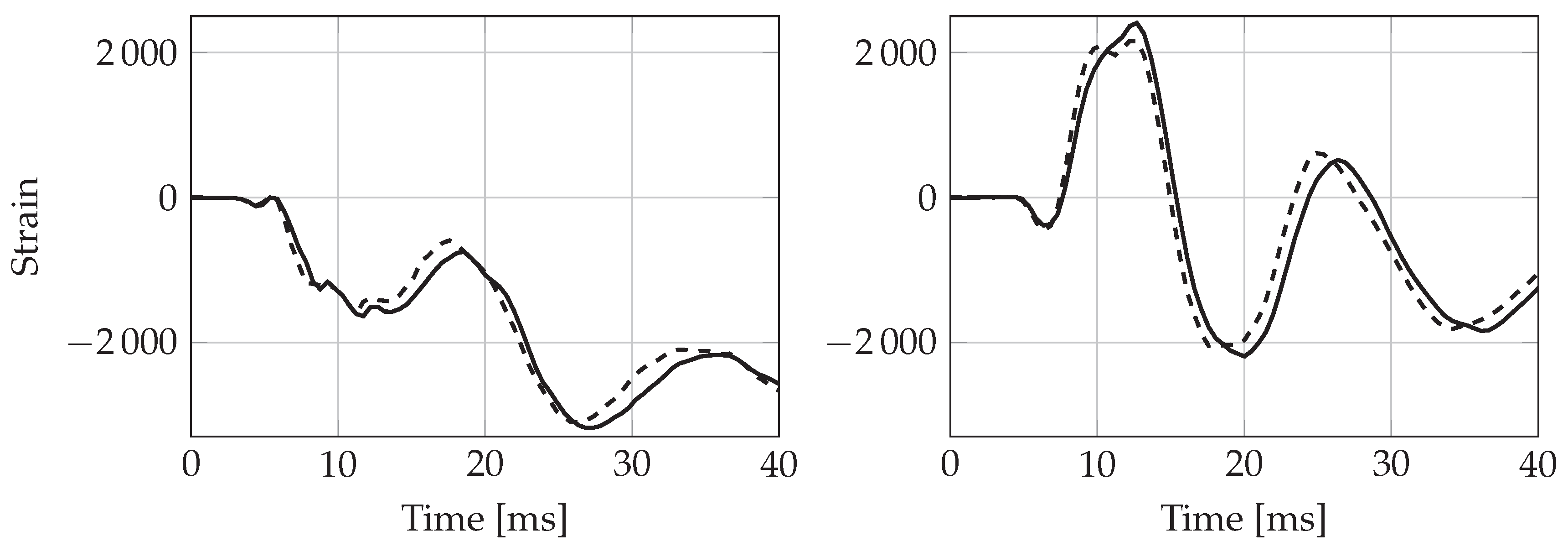
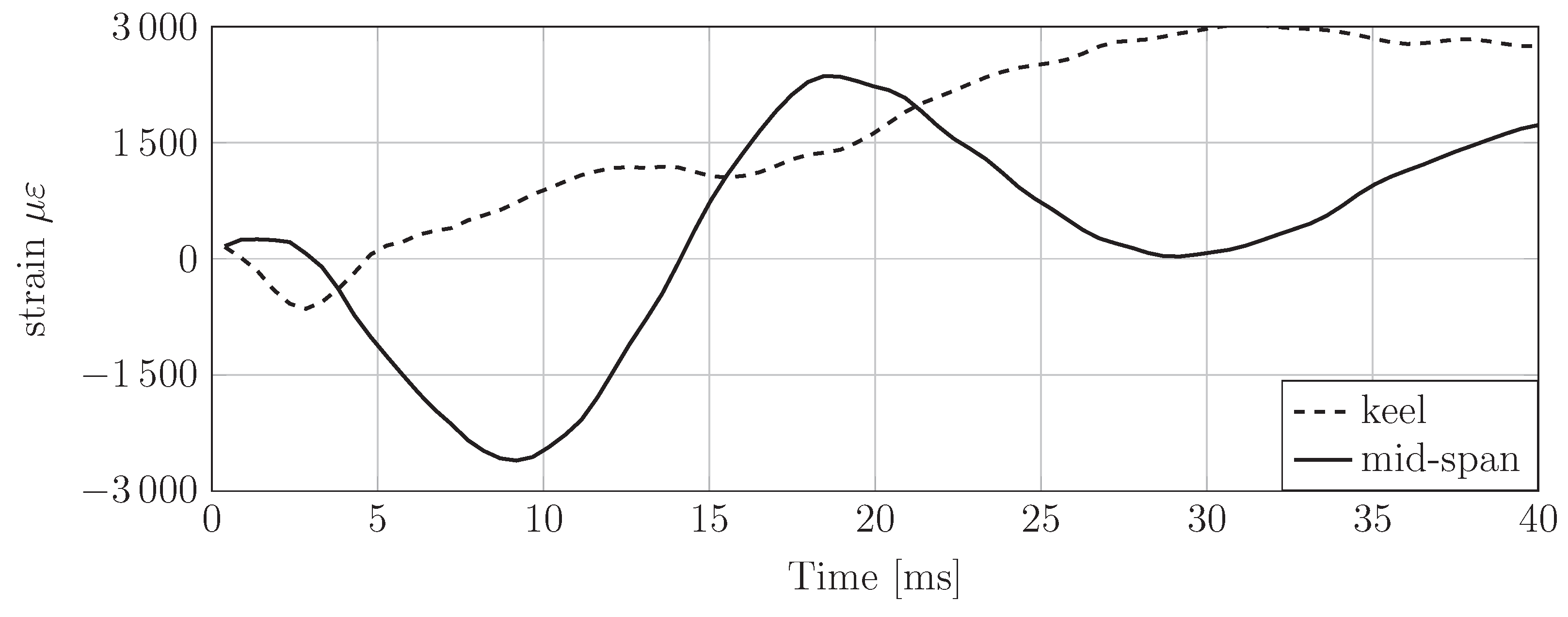
5.1. Wedge Deformation during Water Entry
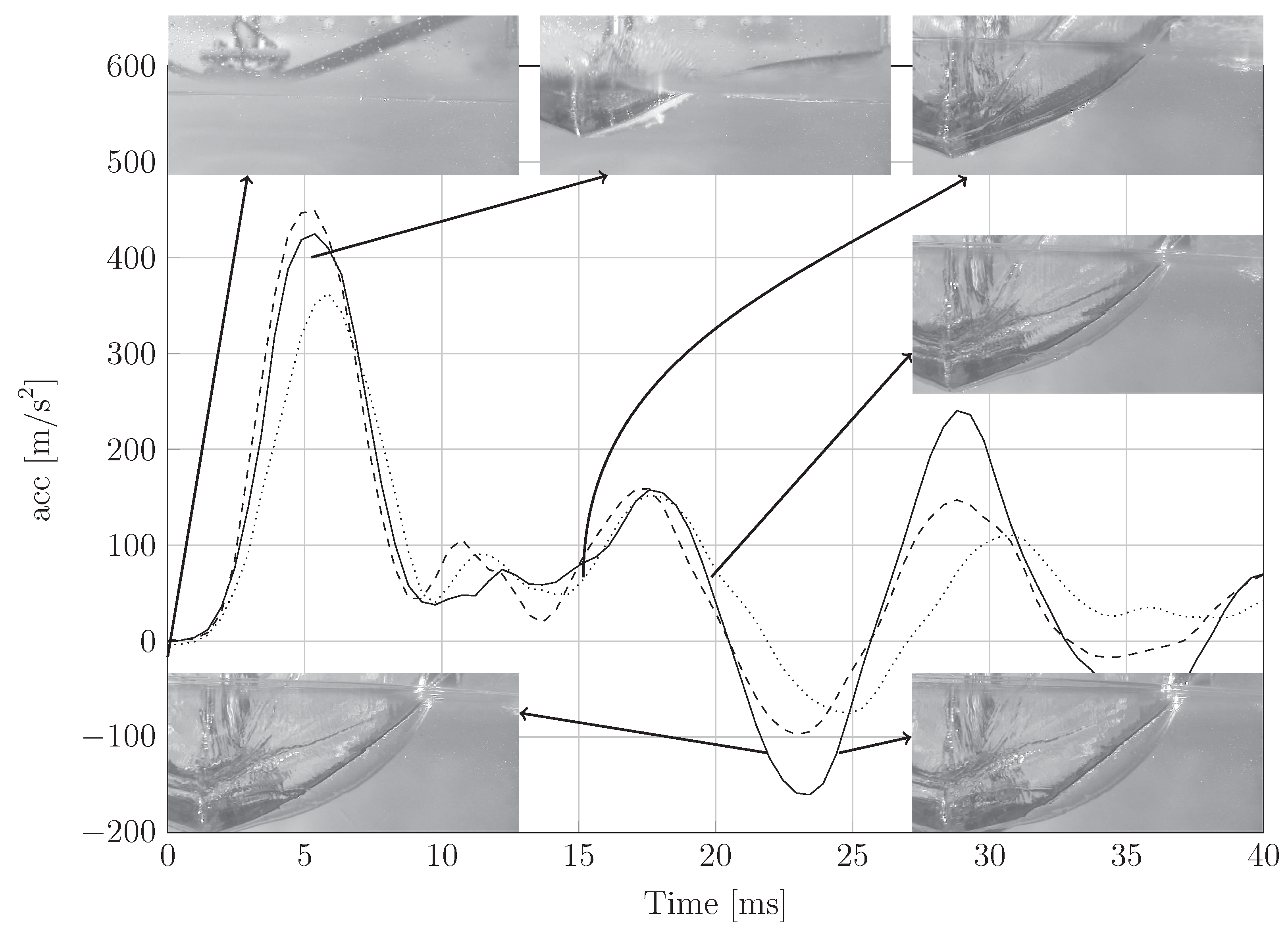
5.2. Evidence of Cavity Formation from High-Speed Images
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Qin, Z.; Batra, R.C. Local slamming impact of sandwich composite hulls. Int. J. Solids Struct. 2009, 46, 2011–2035. [Google Scholar] [CrossRef]
- Carcaterra, A.; Ciappi, E. Prediction of the Compressible Stage Slamming Force on Rigid and Elastic Systems Impacting on the Water Surface. Nonlinear Dyn. 2000, 21, 193–220. [Google Scholar] [CrossRef]
- Carcaterra, A.; Ciappi, E. Hydrodynamic shock of elastic structures impacting on the water: Theory and experiments. J. Sound Vib. 2004, 271, 411–439. [Google Scholar] [CrossRef]
- Panciroli, R.; Minak, G. Experimental evaluation of the air trapped during the water entry of flexible structures. Acta Imeko 2014, 3, 63–67. [Google Scholar] [CrossRef]
- Kapsenberg, G.K. Slamming of ships: where are we now? Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2011, 369, 2892–2919. [Google Scholar] [CrossRef] [PubMed]
- Faltinsen, O.M. Hydroelastic slamming. J. Mar. Sci. Technol. 2000, 5, 49–65. [Google Scholar] [CrossRef]
- Faltinsen, O.M.; Landrini, M.; Greco, M. Slamming in marine applications. J. Eng. Math. 2004, 48, 187–217. [Google Scholar] [CrossRef]
- Fragassa, C. Engineering Design Driven by Models and Measures: The Case of a Rigid Inflatable Boat. Preprints 2018. [Google Scholar] [CrossRef]
- Fragassa, C.; Minak, G. Measuring Deformations in a Rigid-Hulled Inflatable Boat. Key Eng. Mater. 2017, 754, 295–298. [Google Scholar] [CrossRef]
- Seddon, C.; Moatamedi, M. Review of water entry with applications to aerospace structures. Int. J. Impact Eng. 2006, 32, 1045–1067. [Google Scholar] [CrossRef]
- Campbell, J.C.; Vignjevic, R. Simulating structural response to water impact. Int. J. Impact Eng. 2012, 49, 1–10. [Google Scholar] [CrossRef]
- Hughes, K.; Vignjevic, R.; Campbell, J.; De Vuyst, T.; Djordjevic, N.; Papagiannis, L. From aerospace to offshore: Bridging the numerical simulation gaps–Simulation advancements for fluid structure interaction problems. Int. J. Impact Eng. 2013, 61, 48–63. [Google Scholar] [CrossRef]
- Wagner, H. {Ü}ber Sto{ß}- und Gleitvorg{ä}nge an der Oberfl{ä}che von Fl{ü}ssigkeiten. ZAMM Z. Angew. Math. Mech. 1932, 12, 193–215. [Google Scholar] [CrossRef]
- Chuang, S.L. Investigation of Impact of Rigid and Elastic Bodies with Water; NSRDC Report No. 3248; David Taylor Model Basin Reports; PN: Bethesheda, MA, USA, 1970. [Google Scholar]
- Panciroli, R.; Porfiri, M. Evaluation of the pressure field on a rigid body entering a quiescent fluid through particle image velocimetry. Exp. Fluids 2013, 54, 1630. [Google Scholar] [CrossRef]
- Korobkin, A.; Parau, E.I.; Vanden-Broeck, J.M. The mathematical challenges and modelling of hydroelasticity. Philos. Trans. Ser. A Math. Phys. Eng. Sci. 2011, 369, 2803–2812. [Google Scholar] [CrossRef] [PubMed]
- Korobkin, A.; Guéret, R.; Malenica, Š. Hydroelastic coupling of beam finite element model with Wagner theory of water impact. J. Fluids Struct. 2006, 22, 493–504. [Google Scholar] [CrossRef]
- Das, K.; Batra, R.C. Local water slamming impact on sandwich composite hulls. J. Fluids Struct. 2011, 27, 523–551. [Google Scholar] [CrossRef]
- Zhao, R.; Faltinsen, O.; Aarsnes, J. Water entry of Arbitrary Two-Dimensional sections with and without flow separation. In Twenty-First Symposium on Naval Hydrodynamics; The National Academies Press: Washington, DC, USA, 1997. [Google Scholar]
- Scolan, Y. Hydroelastic behaviour of a conical shell impacting on a quiescent-free surface of an incompressible liquid. J. Sound Vib. 2004, 277, 163–203. [Google Scholar] [CrossRef]
- Wu, G.X.; Sun, H.; He, Y.S. Numerical simulation and experimental study of water entry of a wedge in free fall motion. J. Fluids Struct. 2004, 19, 277–289. [Google Scholar] [CrossRef]
- Von Karman, T. The Impact on Seaplane Floats, during Landing; NACA-TN-321; National Advisory Committee for Aeronautics: Washington, DC, USA, 1929.
- Backer, G.D.; Vantorre, M.; Beels, C.; Pré, J.D.; Victor, S.; Rouck, J.D.; Blommaert, C.; De Backer, G.; Vantorre, M.; Beels, C.; et al. Experimental investigation of water impact on axisymmetric bodies. Appl. Ocean Res. 2009, 31, 143–156. [Google Scholar] [CrossRef]
- El Malki Alaoui, A.; Nême, A.; Tassin, A.; Jacques, N.; Alaoui, A.E.M.; Nême, A.; Tassin, A.; Jacques, N. Experimental study of coefficients during vertical water entry of axisymmetric rigid shapes at constant speeds. Appl. Ocean Res. 2012, 37, 183–197. [Google Scholar] [CrossRef]
- Chuang, S.L.; Milne, D.T. Drop Tests of Cone to Investigate the Three-Dimensional Effect Of Slamming; NRDC Report No. 3543; Naval Ship Research and Development Center: Washington, DC, USA, 1971. [Google Scholar]
- Jalalisendi, M.; Shams, A.; Panciroli, R.; Porfiri, M. Experimental reconstruction of three-dimensional hydrodynamic loading in water entry problems through particle image velocimetry. Exp. Fluids 2015, 56, 1–17. [Google Scholar] [CrossRef]
- Jalalisendi, M.; Osma, S.J.; Porfiri, M. Three-dimensional water entry of a solid body: A particle image velocimetry study. J. Fluids Struct. 2015, 59, 85–102. [Google Scholar] [CrossRef]
- Korobkin, A. Cavitation in liquid impact problems. In Proceedings of the Fifth International Symposium on Cavitation (CAV2003), Osaka, Japan, 1 January 2003; Volume 2, pp. 1–7. [Google Scholar]
- Faltinsen, O.M. The effect of hydroelasticity on ship slamming. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 1997, 355, 575–591. [Google Scholar] [CrossRef]
- Reinhard, M.; Korobkin, A.A.; Cooker, M.J. Cavity formation on the surface of a body entering water with deceleration. J. Eng. Math. 2015. [Google Scholar] [CrossRef]
- Bivin, Y.K.; Glukhov, Y.M.; Permyakov, Y.V. Vertical entry of solids into water. Fluid Dyn. 1986, 20, 835–841. [Google Scholar] [CrossRef]
- Yadong, W.; Xulong, Y.; Yuwen, Z. Natural Cavitation in High Speed Water Entry Process. In Proceedings of the 1st International Conference on Mechanical Engineering and Material Science, Shanghai, China, 28–30 December 2012; Atlantis Press: Paris, France, 2012; pp. 46–49. [Google Scholar] [CrossRef]
- Korobkin, A.A.; Khabakhpasheva, T.I.; Wu, G.X. Coupled hydrodynamic and structural analysis of compressible jet impact onto elastic panels. J. Fluids Struct. 2008, 24, 1021–1041. [Google Scholar] [CrossRef]
- Korobkin, A.; Ellis, A.S.; Smith, F.T. Trapping of air in impact between a body and shallow water. J. Fluid Mech. 2008, 611, 365–394. [Google Scholar] [CrossRef]
- Hicks, P.D.; Ermanyuk, E.V.; Gavrilov, N.V.; Purvis, R.; Mechanics, F. Air trapping at impact of a rigid sphere onto a liquid. J. Fluid Mech. 2012, 695, 310–320. [Google Scholar] [CrossRef]
- Cuomo, G.; Piscopia, R.; Allsop, W. Evaluation of wave impact loads on caisson breakwaters based on joint probability of impact maxima and rise times. Coast. Eng. 2011, 58, 9–27. [Google Scholar] [CrossRef]
- Ma, Z.H.; Causon, D.M.; Qian, L.; Mingham, C.G.; Mai, T.; Greaves, D.; Raby, A. Pure and aerated water entry of a flat plate. Phys. Fluids 2016, 28, 016104. [Google Scholar] [CrossRef]
- Panciroli, R.; Porfiri, M. Hydroelastic impact of piezoelectric structures. Int. J. Impact Eng. 2014, 66, 18–27. [Google Scholar] [CrossRef]
- Jalalisendi, M.; Porfiri, M. Water entry of compliant slender bodies: Theory and experiments. Int. J. Mech. Sci. 2018, 149, 514–529. [Google Scholar] [CrossRef]
- Panciroli, R.; Porfiri, M. Analysis of hydroelastic slamming through particle image velocimetry. J. Sound Vib. 2015, 347, 63–78. [Google Scholar] [CrossRef]
- Shams, A.; Zhao, S.; Porfiri, M. Water impact of syntactic foams. Materials 2017, 10. [Google Scholar] [CrossRef] [PubMed]
- Mei, R.; Luo, L.S.; Shyy, W. An Accurate Curved Boundary Treatment in the Lattice Boltzmann Method. J. Comput. Phys. 1999, 155, 307–330. [Google Scholar] [CrossRef]
- Panciroli, R.; Abrate, S.; Minak, G.; Zucchelli, A. Hydroelasticity in water-entry problems: Comparison between experimental and SPH results. Compos. Struct. 2012, 94, 532–539. [Google Scholar] [CrossRef]
- Panciroli, R.; Abrate, S.; Minak, G. Dynamic response of flexible wedges entering the water. Compos. Struct. 2013, 99, 163–171. [Google Scholar] [CrossRef]
- Panciroli, R. Hydroelastic Impacts of Deformable Wedges. Ph.D. Thesis, Alma Mater Studiorum Università di Bologna, Bologna, Italy, 2012. [Google Scholar] [CrossRef]
- Panciroli, R. Hydroelastic Impacts of Deformable Wedges. In Solid Mechanics and Its Applications; Abrate, S., Castanié, B., Rajapakse, Y.D.S., Eds.; Springer: Dordrecht, The Netherlands, 2013; Volume 192, pp. 1–45. [Google Scholar] [CrossRef]








| Material | Abbr. | Elastic Moduli | Poisson Ratio | Density |
|---|---|---|---|---|
| (kg/m) | ||||
| 6068 T6 | A | 68.0 GPa | 0.32 | 2700 |
| E-Glass/Vinylester | V | 20.4 GPa | 0.28 | 2050 |
| E-Glass/Epoxy | W | 30.3 GPa | 0.28 | 2015 |
| Abbr. | Material | Thickness | (Hz) | (Hz) | (Hz) |
|---|---|---|---|---|---|
| A2 | Aluminum | 2.0 mm | 18.0 | 112.8 | 316.1 |
| A4 | Aluminum | 4.0 mm | 36.0 | 225.7 | 632.2 |
| V2 | Fiberglass | 2.0 mm | 9.7 | 61.2 | 171.4 |
| V4 | Fiberglass | 4.0 mm | 19.7 | 123.6 | 346.2 |
| W2 | Fiberglass | 2.2 mm | 19.6 | 123.4 | 345.5 |
| W4 | Fiberglass | 4.4 mm | 37.8 | 236.9 | 663.4 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Panciroli, R.; Pagliaroli, T.; Minak, G. On Air-Cavity Formation during Water Entry of Flexible Wedges. J. Mar. Sci. Eng. 2018, 6, 155. https://doi.org/10.3390/jmse6040155
Panciroli R, Pagliaroli T, Minak G. On Air-Cavity Formation during Water Entry of Flexible Wedges. Journal of Marine Science and Engineering. 2018; 6(4):155. https://doi.org/10.3390/jmse6040155
Chicago/Turabian StylePanciroli, Riccardo, Tiziano Pagliaroli, and Giangiacomo Minak. 2018. "On Air-Cavity Formation during Water Entry of Flexible Wedges" Journal of Marine Science and Engineering 6, no. 4: 155. https://doi.org/10.3390/jmse6040155
APA StylePanciroli, R., Pagliaroli, T., & Minak, G. (2018). On Air-Cavity Formation during Water Entry of Flexible Wedges. Journal of Marine Science and Engineering, 6(4), 155. https://doi.org/10.3390/jmse6040155







