Hydrodynamic Zone of Influence Due to a Floating Structure in a Fjordal Estuary—Hood Canal Bridge Impact Assessment
Abstract
1. Introduction
2. Materials and Methods
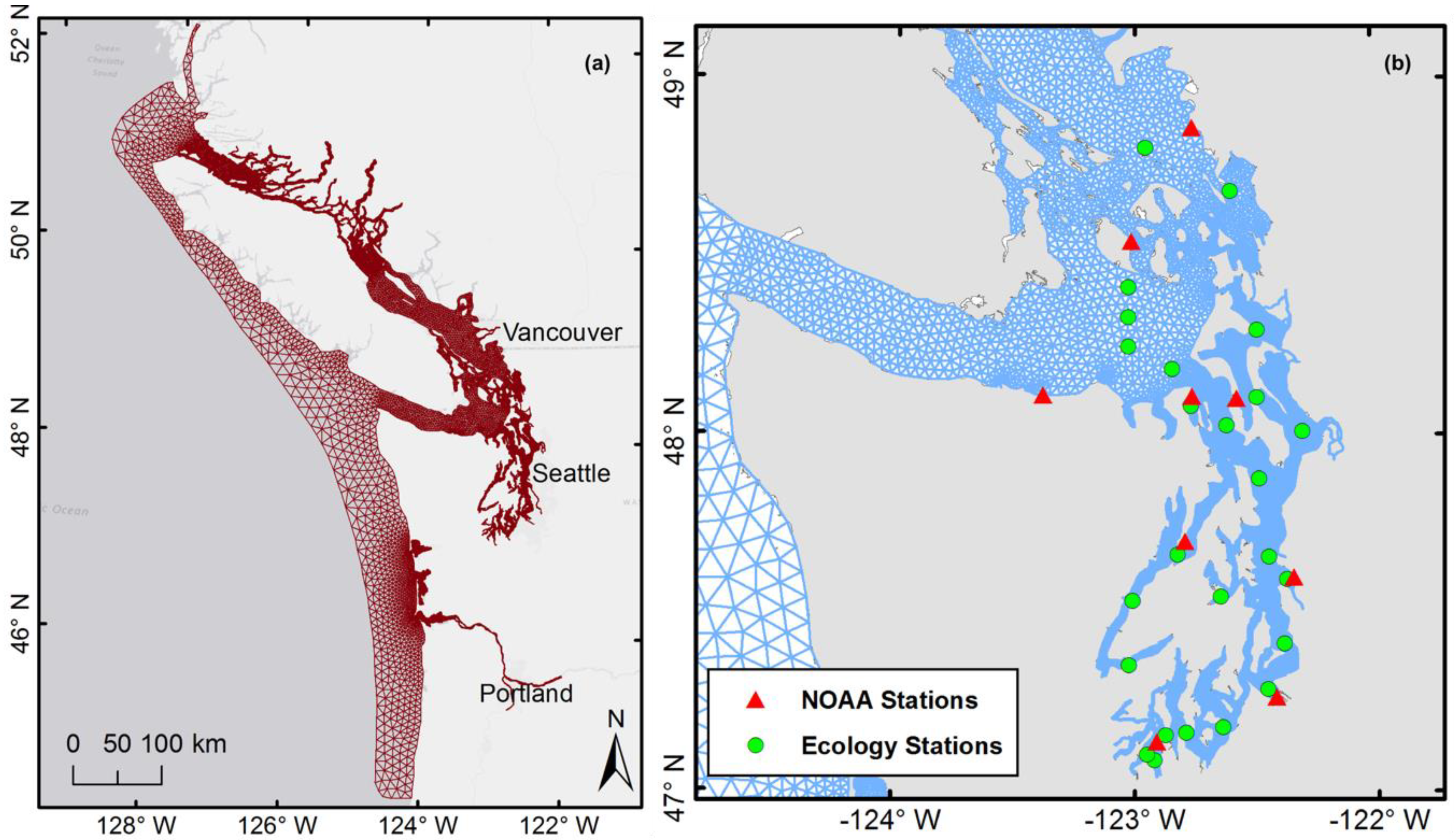
2.1. Oceanographic Data Collection
2.2. The Salish Sea Model Set-Up
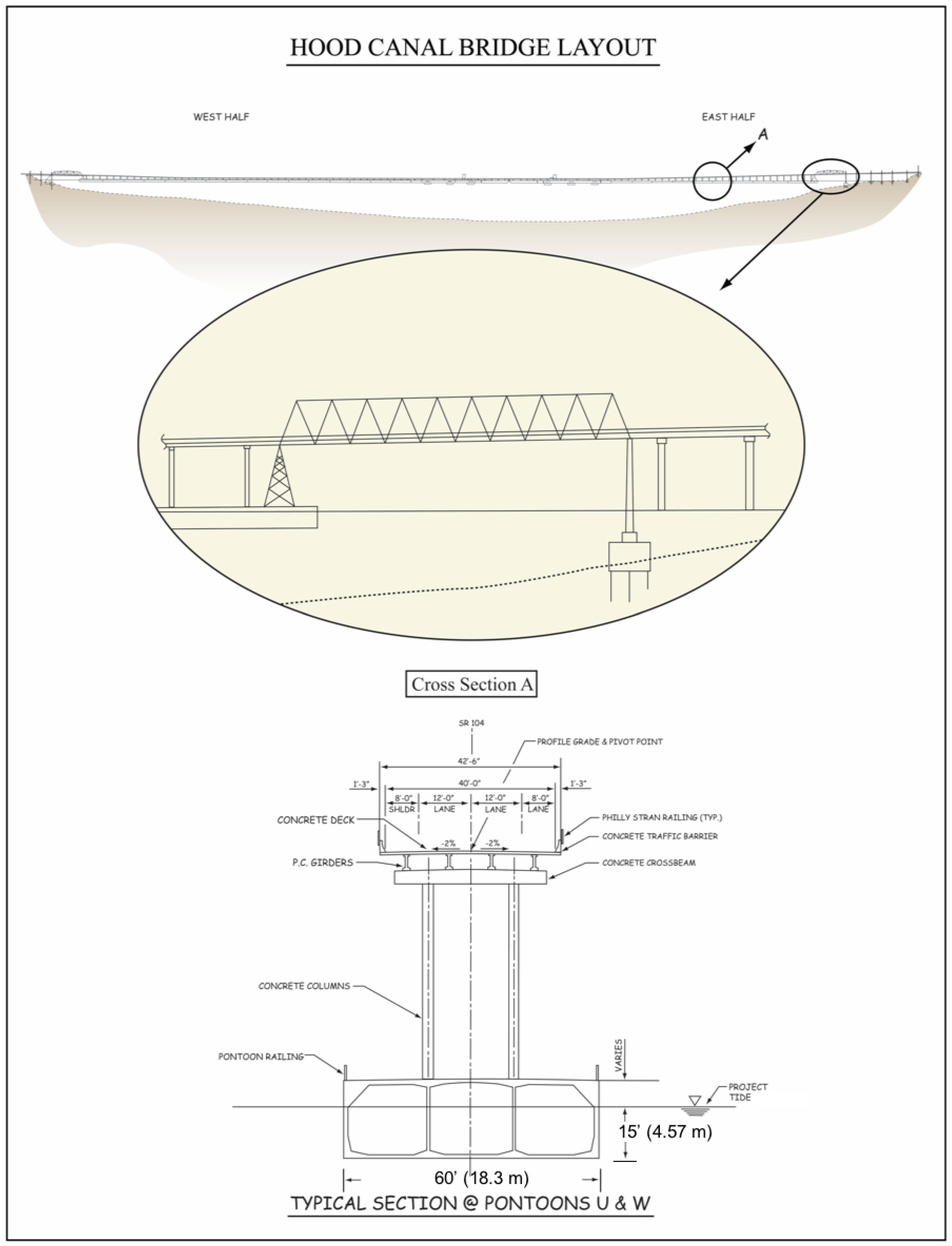
2.3. Hood Canal Bridge Module Implementation
- (a)
- Implementation of a velocity block: This approach is identical to that described by Khangaonkar and Wang (2013) [7] where the impermeable surface block was incorporated into FVCOM with modification of both external and internal modes of the solver. For the baroclinic internal mode, the horizontal velocities at the selected cells and surface layers were always specified as zero such that no horizontal flow was allowed to pass through. During the barotropic external mode calculations, the cross-sectional water column depth at selected cells occupied by the block was adjusted to a new reduced value by subtracting the blocked layer thickness from the total water depth. This modification accommodates the presence of the rigid structure but is an approximation, as non-hydrostatic components of the pressure term, which are likely to be strong in the near field, are neglected. Effects of the bridge on momentum terms are addressed, but are done so as an indirect effect of setting the surface boundary to zero velocity without affecting the pressure term.
- (b)
- Implementation of momentum sink at the bridge using form drag: In this approach, the cells occupying the bridge are populated with hypothetical cylinders similar to a densely packed kelp farm. The drag from the cylinders set to sufficiently high value results in blockage of nearly ~95% of surface currents. Although this represents a leaking bridge, the implementation allows effects on continuity, as well as momentum, terms of the governing equations. The implementation of form drag from suspended cylinders in the water column was described by Wang et al. (2013) [21]. This method also requires local modification of the bathymetry to a representative average depth under the bridge for representation of the rectangular shape of the bridge pontoons.
- (c)
- Free surface pressure modification with a bottom drag: This method relies on modification of the free surface pressure boundary condition; an increase in pressure equivalent of 4.57 m of head results in a model response of 4.57 m depression of the free surface. This method is an improvement over (a) and (b) in that bathymetry is unaltered. In addition to modifying the free surface, the method also employs drag formulation for the layer immediately under the bridge. This results in flow passing the bridge under modified pressure with suitable reduction in velocity induced by the form drag.
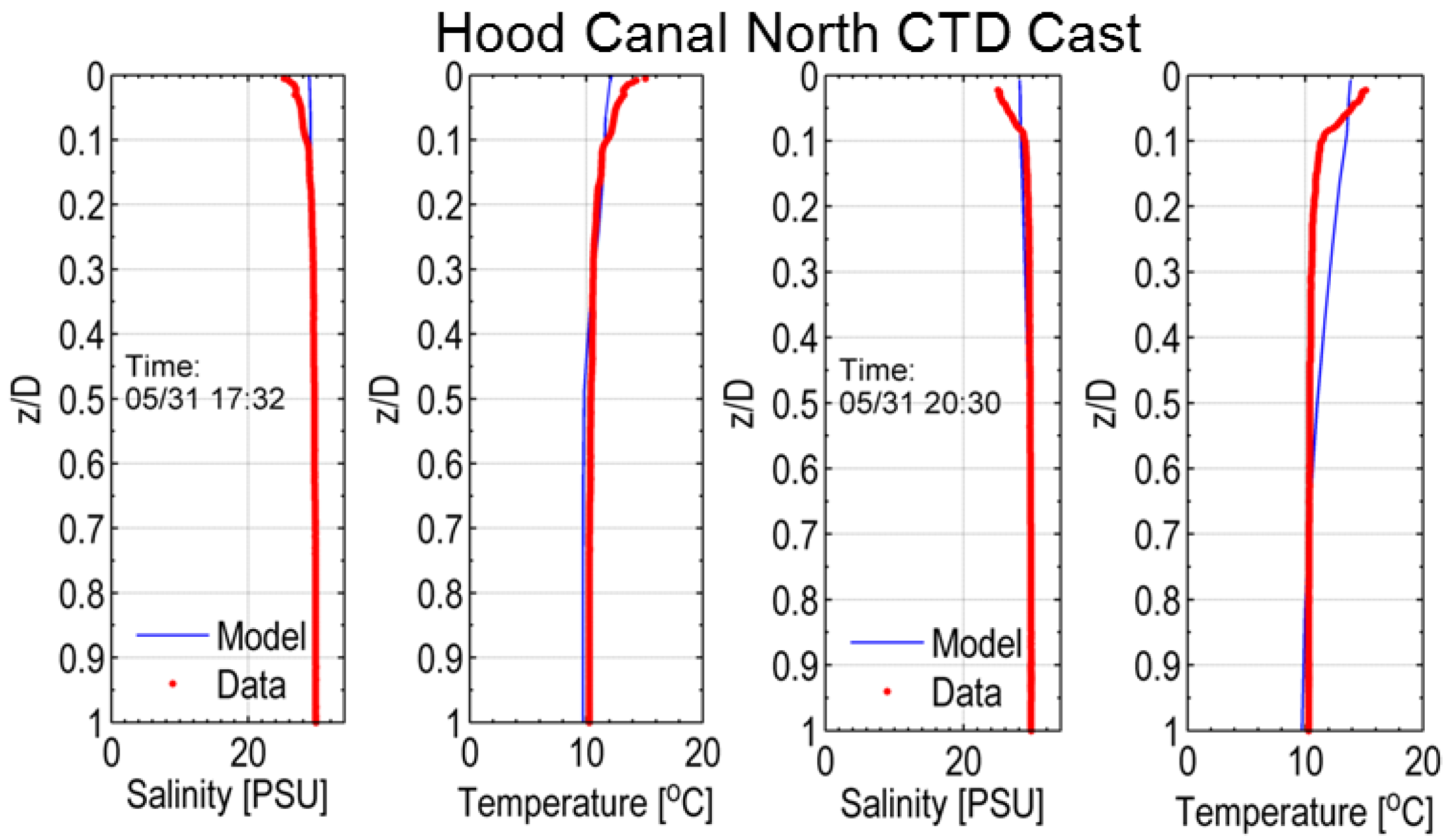
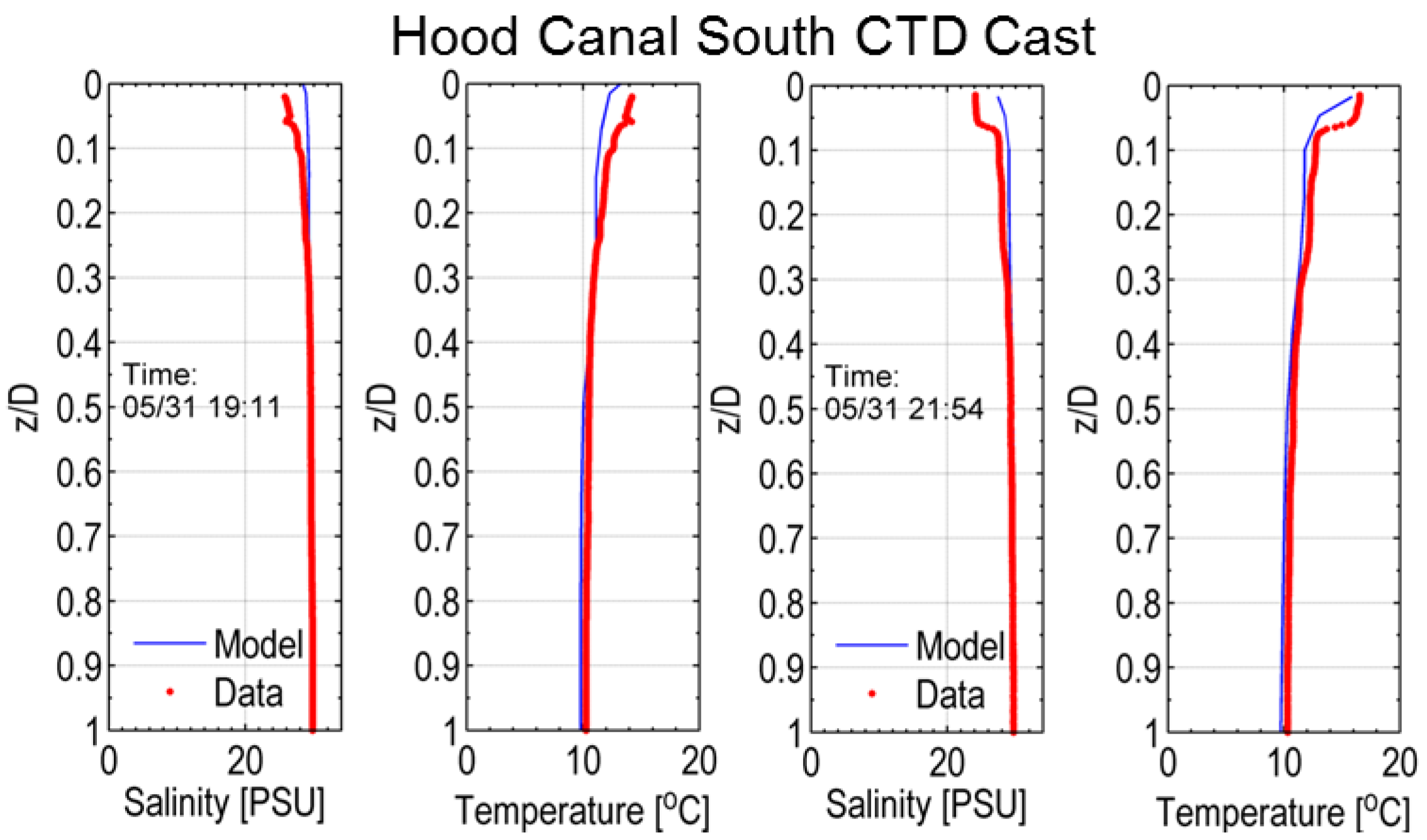
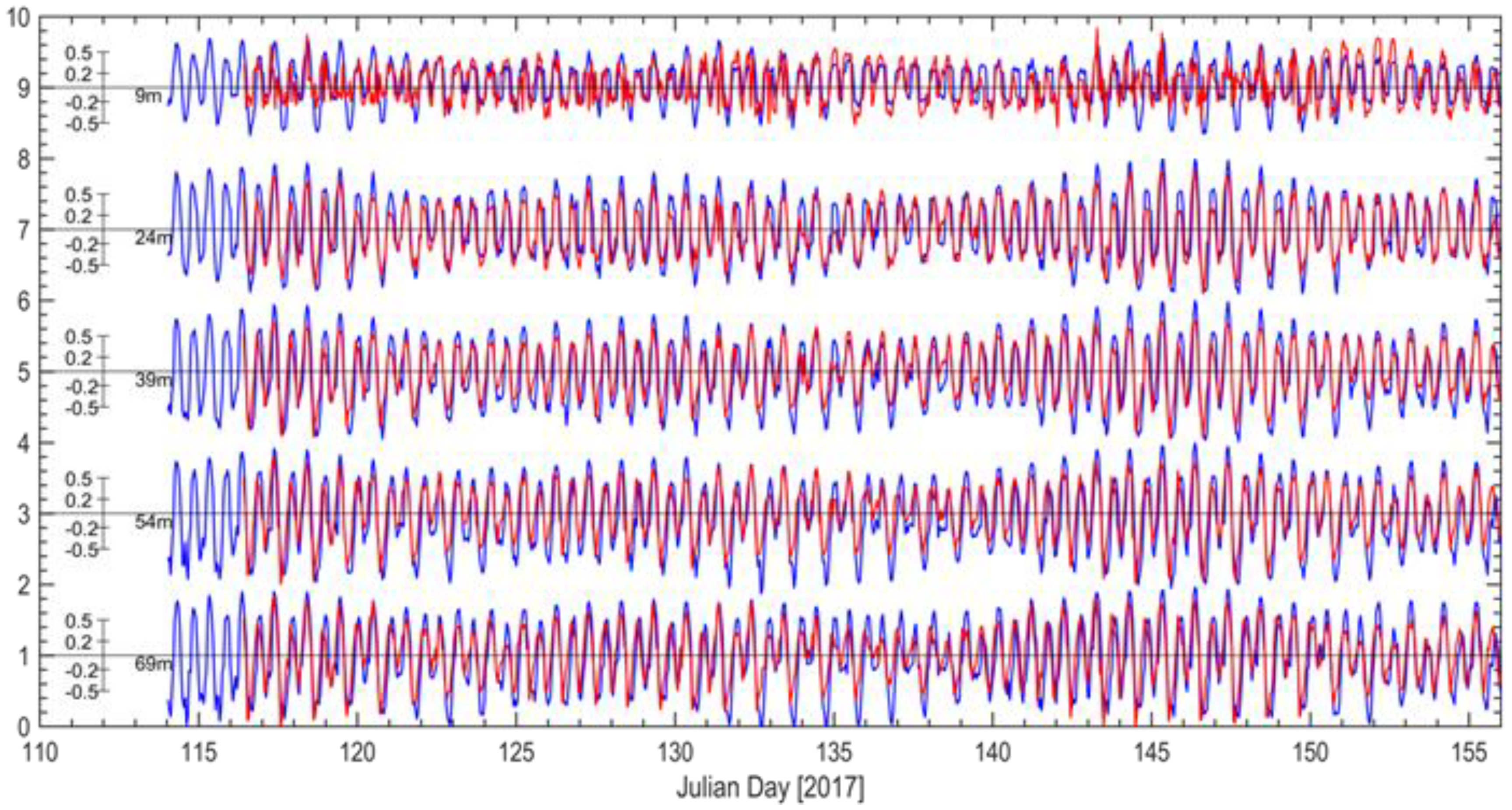
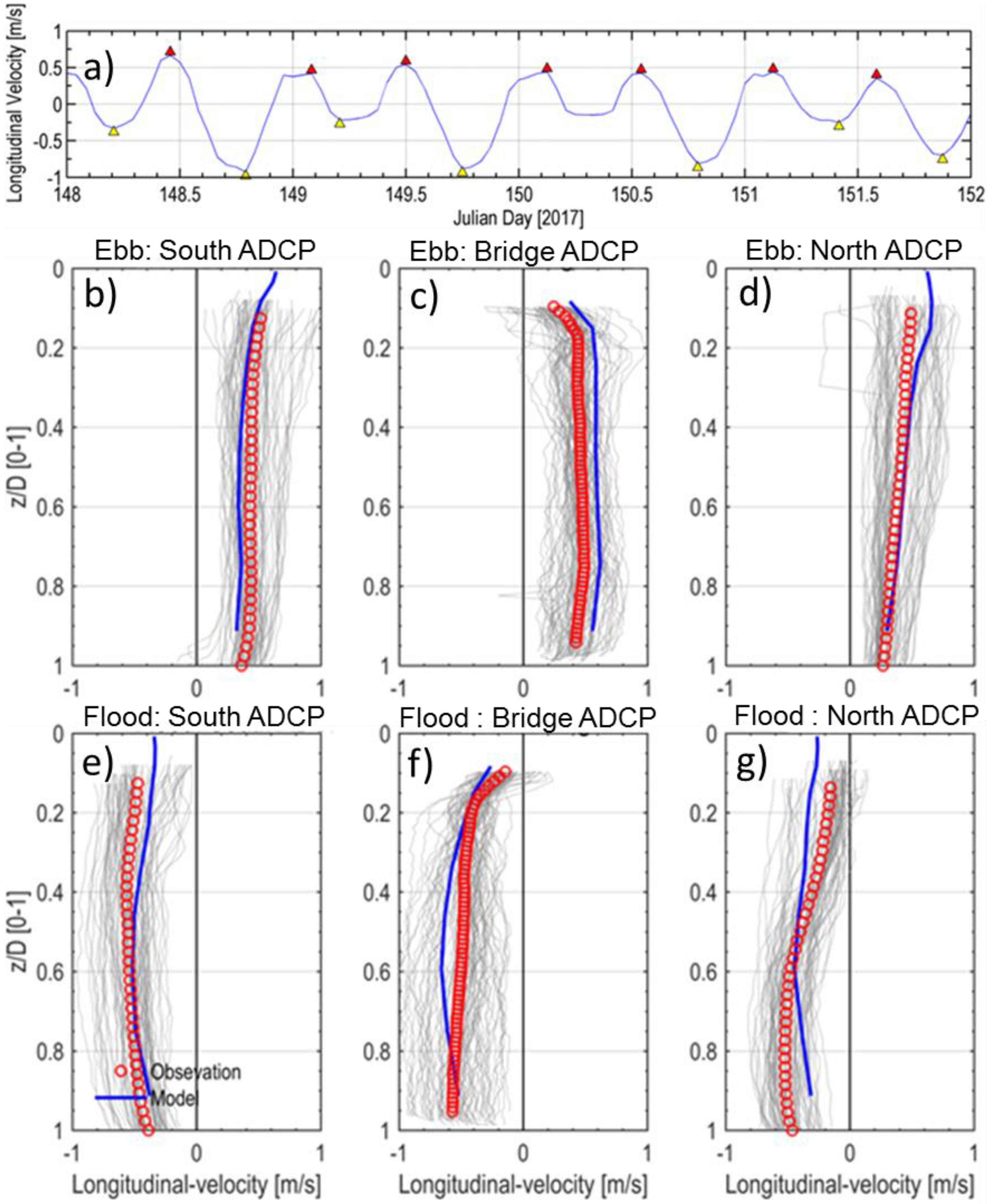
2.4. Near-Field Model Validation
3. Results
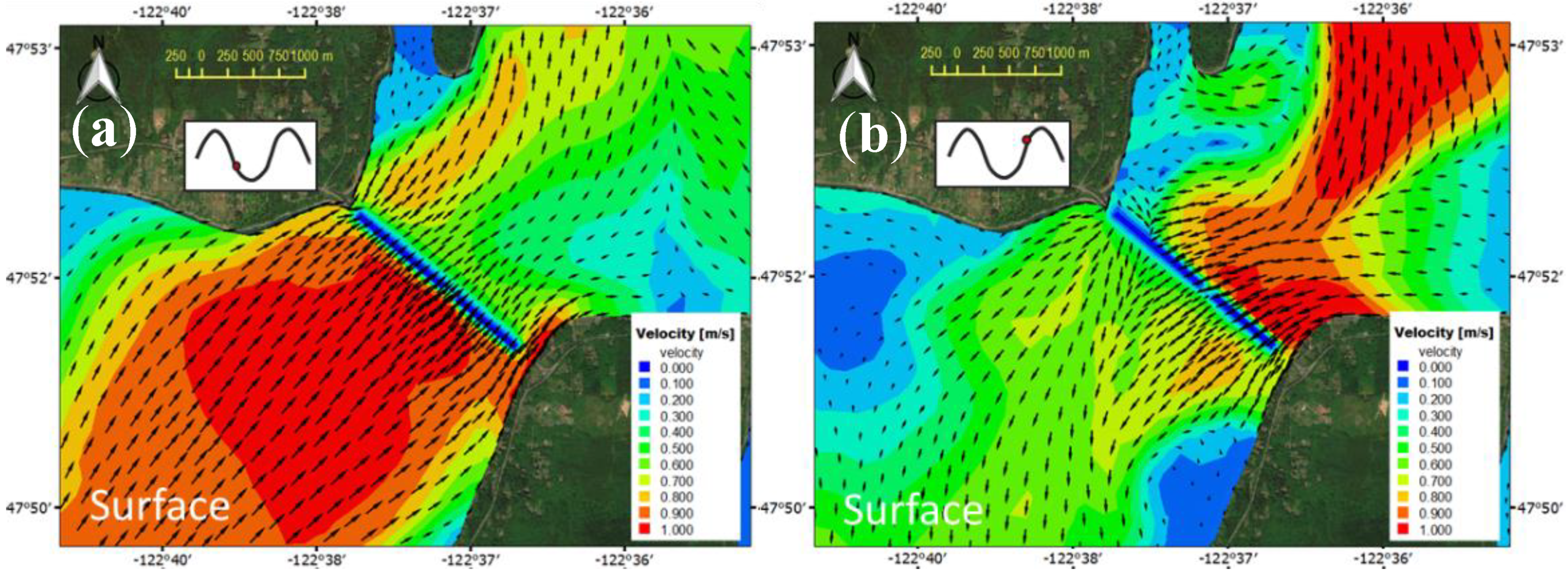
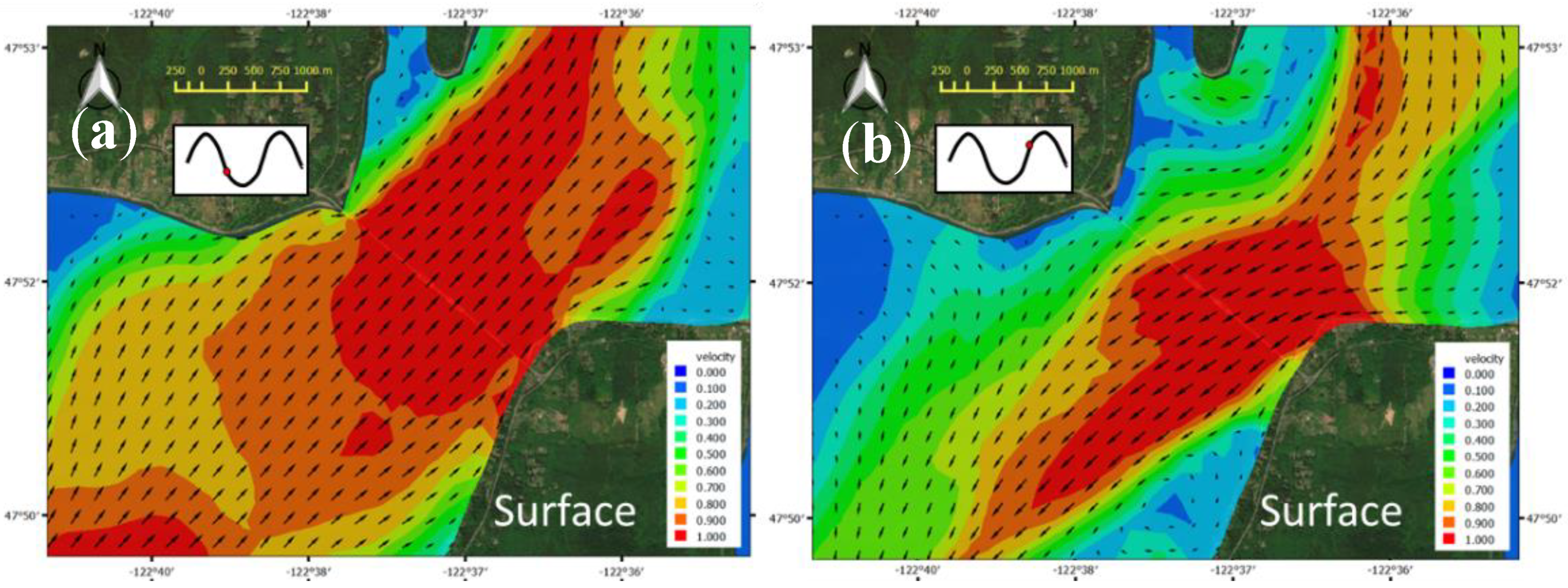
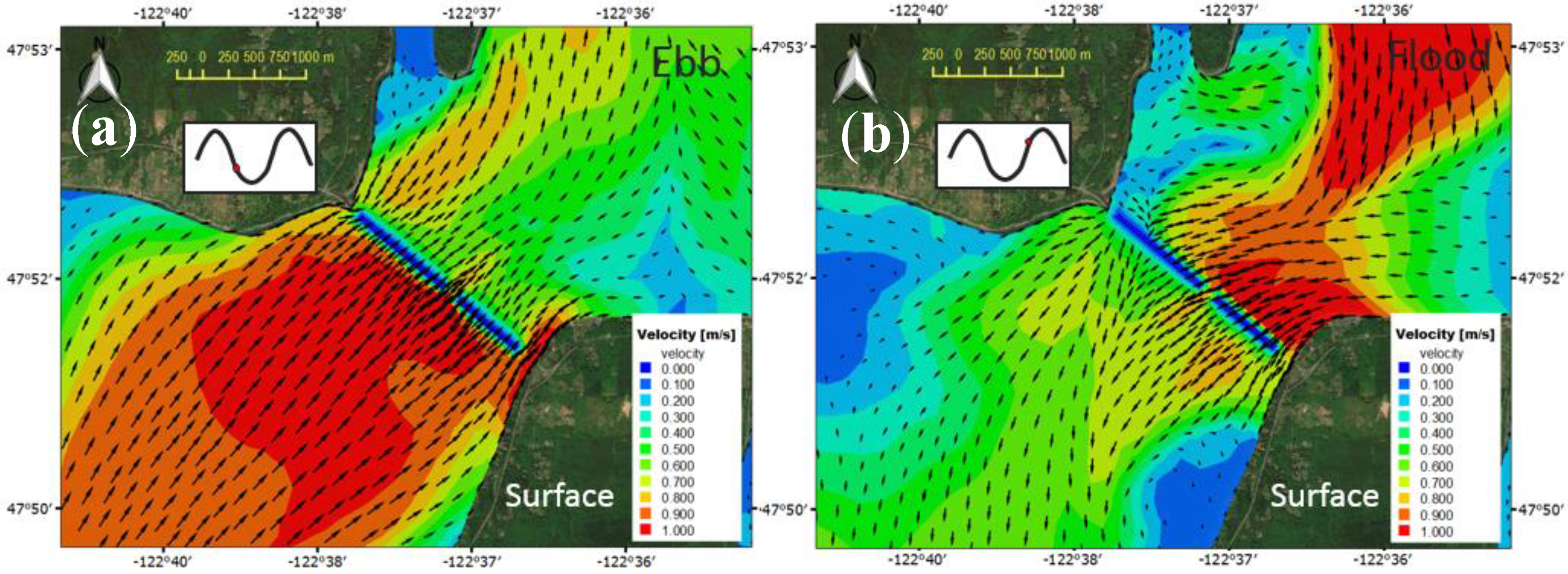
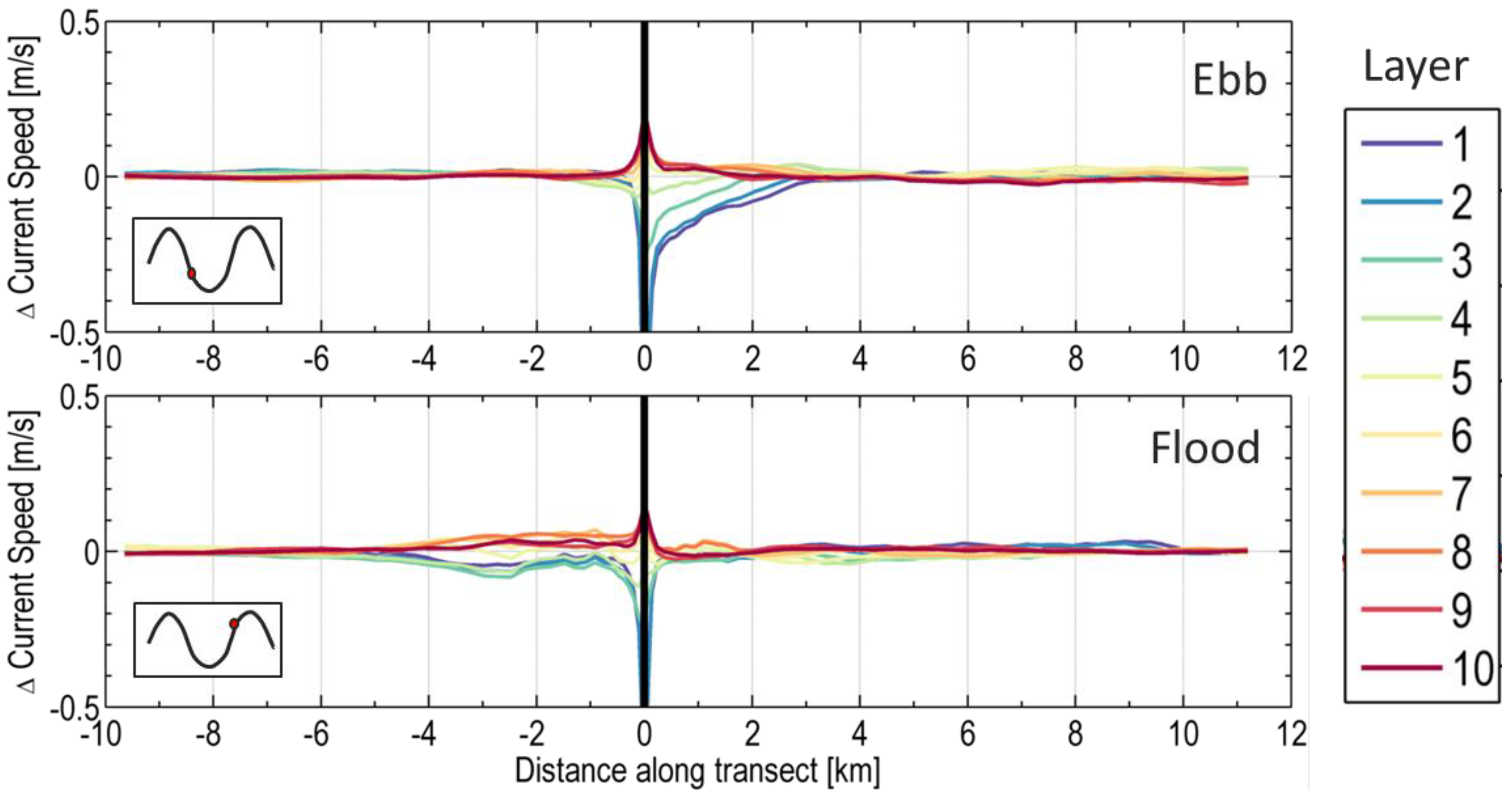
3.1. Zone of Impact—Surface Layer
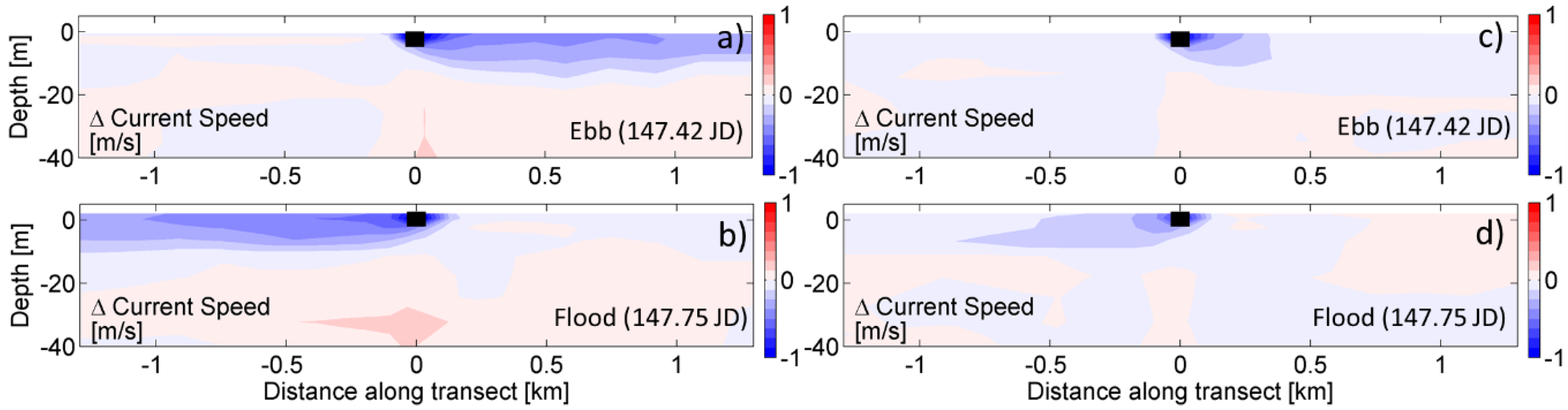
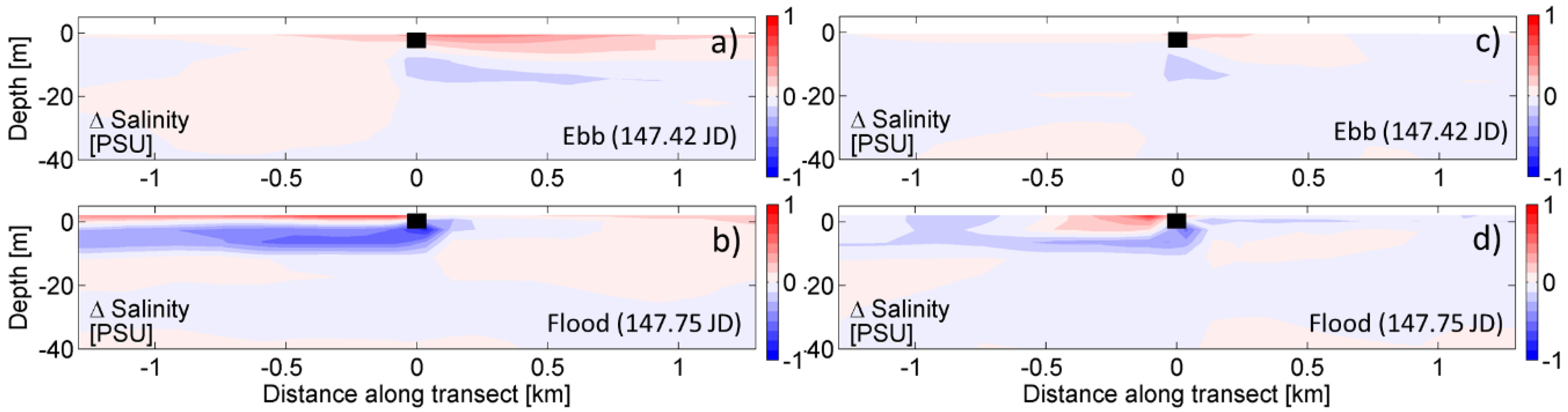
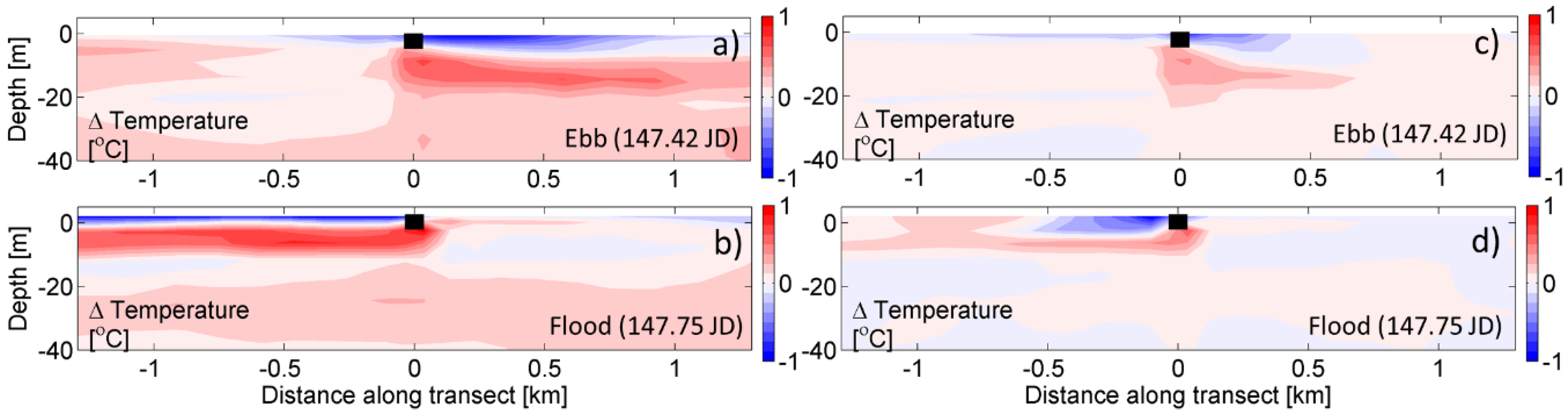
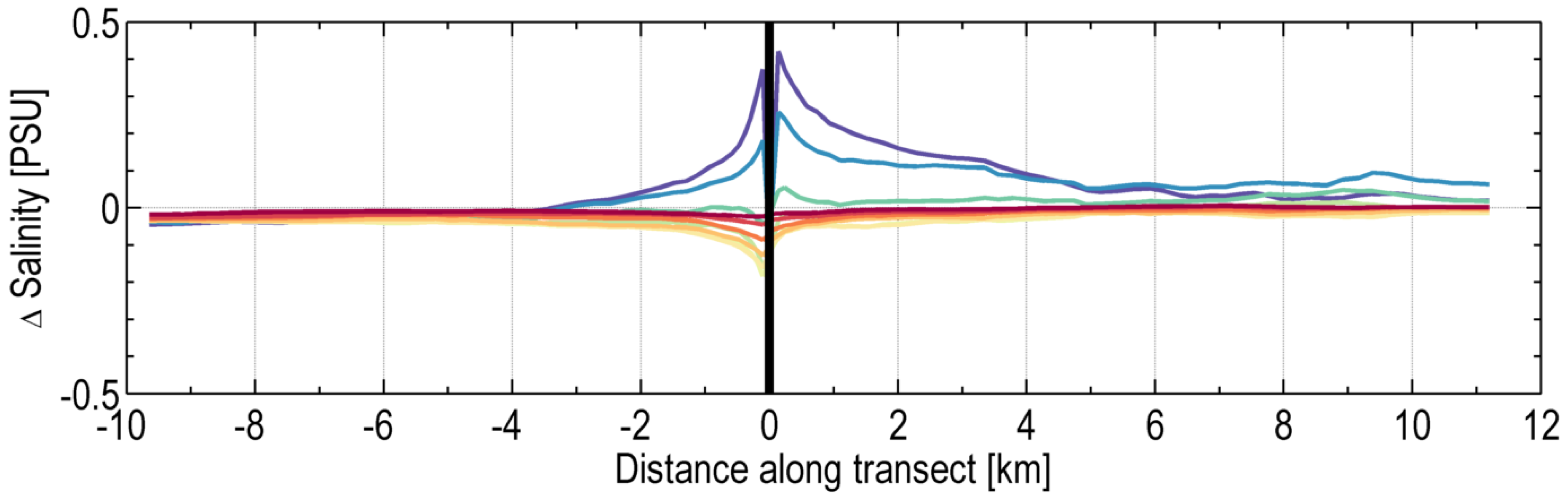
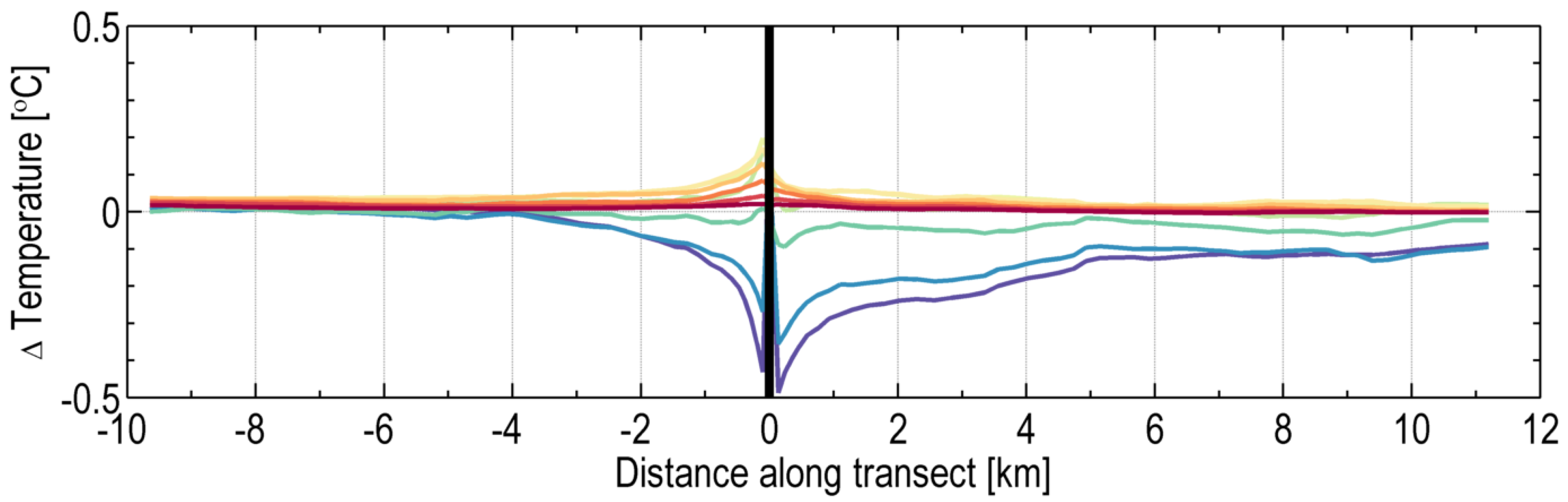
3.2. Zone of Impact—Vertical Transect
4. Discussion
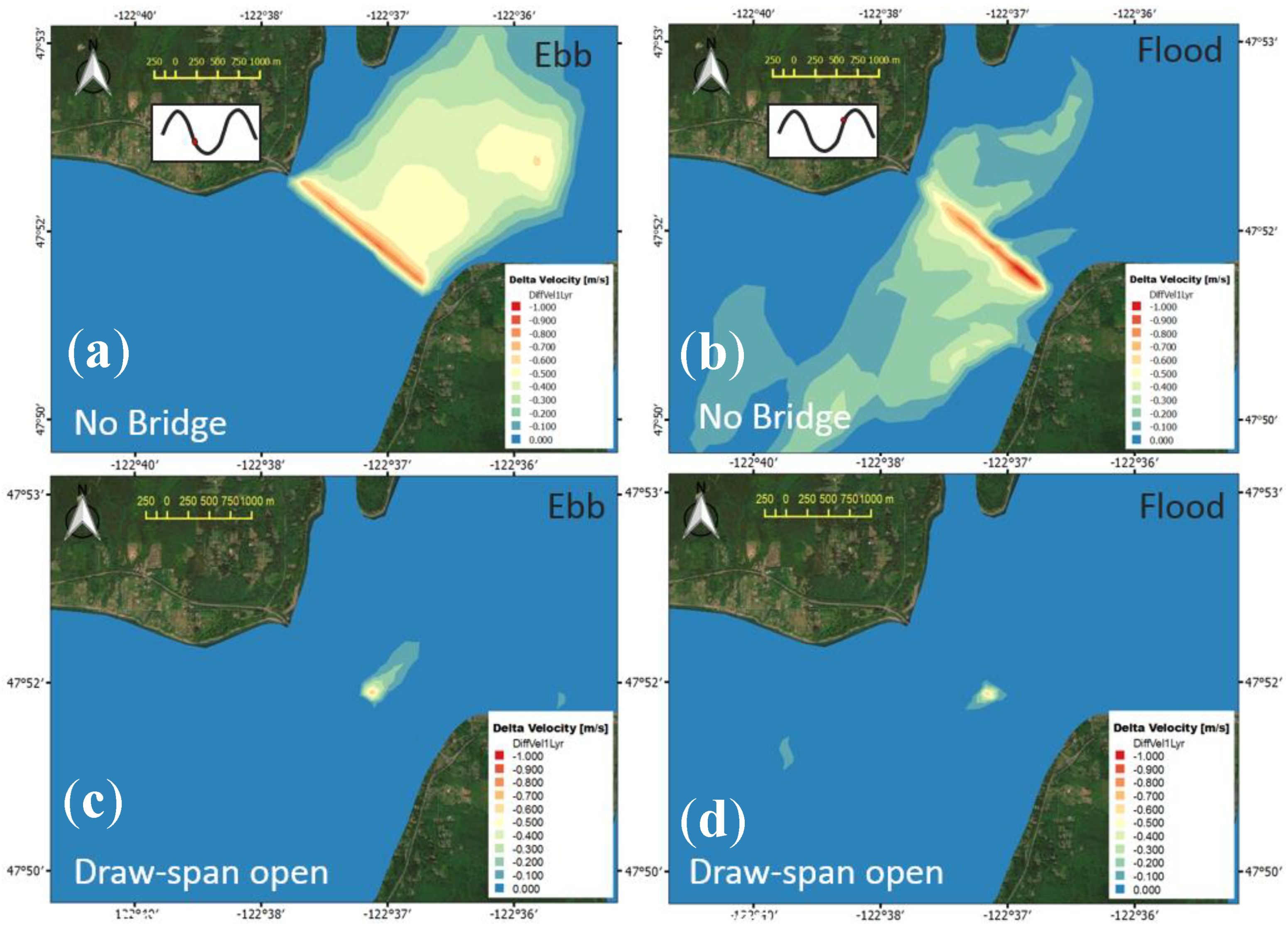
Zone of Influence—Quantitative Assessment
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Puget Sound Partnership. 2009 State of the Sound Report; No. PSP09-08; Puget Sound Partnership: Olympia, WA, USA, 2010. [Google Scholar]
- Khangaonkar, T.; Yang, Z.; Kim, T.; Roberts, M. Tidally Averaged Circulation in Puget Sound Sub-basins: Comparison of Historical Data, Analytical Model, and Numerical Model. J. Estuar. Coast. Shelf Sci. 2011, 93, 305–319. [Google Scholar] [CrossRef]
- Khangaonkar, T.; Sackmann, B.; Long, W.; Mohamedali, T.; Roberts, M. Simulation of annual biogeochemical cycles of nutrient balance, phytoplankton bloom(s), and DO in Puget Sound using an unstructured grid model. Ocean Dyn. 2012, 62, 1353–1379. [Google Scholar] [CrossRef]
- Khangaonkar, T.; Nugraha, A.; Xu, W.; Long, W.; Bianucci, L.; Ahmed, A.; Mohamedali, T.; Pelletier, G. Analysis of Hypoxia and Sensitivity to Nutrient Pollution in Salish Sea. J. Geophys. Res. Oceans 2018, 123, 4735–4761. [Google Scholar] [CrossRef]
- Newton, J.; Bassin, C.; Devol, A.; Richey, J.; Kawase, M.; Warner, M. Chapter 1: Overview and Results Synthesis. In Integrated Assessment and Modeling Report; Hood Canal Dissolved Oxygen Program; University of Washington: Washington, DC, USA, 2011; Available online: http://www.hoodcanal.washington.edu/documents/document.jsp?id=3019 (accessed on 10 December 2018).
- Cope, B.; Roberts, M. Review and Synthesis of Available Information to Estimate Human Impacts to Dissolved Oxygen in Hood Canal; Ecology Publication No. 13-03-016; EPA Publication No. 910-R-13-002; Washington State Department of Ecology and U.S. EPA: Washington, DC, USA, 2013. Available online: https://fortress.wa.gov/ecy/publications/documents/1303016.pdf (accessed on 10 December 2018).
- Khangaonkar, T.; Wang, T. Potential alteration of fjordal circulation due to a large floating structure—Numerical investigation with application to Hood Canal basin in Puget Sound. Appl. Ocean Res. 2013, 39, 146–157. [Google Scholar] [CrossRef]
- Moore, M.; Berejikian, B.A.; Tezak, E.P. A floating bridge disrupts seaward migration and increases mortality of steelhead smolts in Hood Canal, Washington State. PLoS ONE 2013, 8, e73427. [Google Scholar] [CrossRef] [PubMed]
- Hood Canal Bridge Assessment Team. Hood Canal Bridge Ecosystem Impact Assessment Plan: Framework and Phase 1 Details; Long Live the Kings: Seattle, WA, USA, 2016; Available online: https://lltk.org/wp-content/uploads/2016/08/Hood-Canal-Bridge-Impact-Assessment-Plan-FINAL-27September2016.pdf (accessed on 10 December 2018).
- RPS. Current Measurements in Hood Canal Data Report; Maya Whitmont and Kevin Redmond of RPS Group PLC: Seattle, WA, USA, 2017. [Google Scholar]
- Chen, C.; Liu, H.; Beardsley, R.C. An unstructured, finite-volume, three-dimensional, primitive equation ocean model: Application Tocoastal Ocean and estuaries. J. Atmos. Ocean. Technol. 2003, 20, 159–186. [Google Scholar] [CrossRef]
- Cerco, C.; Cole, T. Three-Dimensional Eutrophication Model of Chesapeake Bay; Tech. Rep. EL-94-4; U.S. Army Corps of Engineers: Vicksburg, MI, USA, 1994. [Google Scholar]
- Cerco, C.F.; Cole, T.M. User’s Guide to the CE-QUAL-ICM Three-Dimensional Eutrophication Model; Release Version 1.0; U.S. Army Corps of Engineers: Washington, DC, USA, 1995; p. 320. [Google Scholar]
- Khangaonkar, T.; Long, W.; Xu, W. Assessment of circulation and inter-basin transport in the Salish Sea including Johnstone Strait and Discovery Islands pathways. Ocean Model. 2017, 109, 11–32. [Google Scholar] [CrossRef]
- Bianucci, L.; Long, W.; Khangaonkar, T.; Pelletier, G.; Ahmed, A.; Mohamedali, T.; Roberts, M.; Figueroa-Kaminsky, C. Sensitivity of the regional ocean acidification and the carbonate system in Puget Sound to ocean and freshwater inputs. Elem. Sci. Anthropocene 2018, 6, 22. [Google Scholar] [CrossRef]
- Mohamedali, T.; Roberts, M.; Sackmann, B.S.; Kolosseus, A. Puget Sound Dissolved Oxygen Model: Nutrient Load Summary for 1999–2008; Publication No. 11-03-057; Washington State Department of Ecology: Olympia, WA, USA, 2011. [Google Scholar]
- Spargo, E.; Westerink, J.; Luettich, R.; Mark, D. Developing a Tidal Constituent Database for the Eastern North Pacific Ocean. In Proceedings of the 8th International Conference on Coastal Modeling, Mexico City, Mexico, 18–24 February 2007. [Google Scholar]
- Locarnini, R.A.; Mishonov, A.V.; Antonov, J.I.; Boyer, T.P.; Garcia, H.E.; Baranova, O.K.; Zweng, M.M.; Paver, C.R.; Reagan, J.R.; Johnson, D.R.; et al. World Ocean Atlas 2013; Volume 1: Temperature; NOAA Atlas NESDIS 73; Levitus, S., Mishonov, A., Eds.; National Oceanic and Atmospheric Administration: Silver Spring, MD, USA, 2013; p. 40. [Google Scholar]
- Zweng, M.M.; Reagan, J.R.; Antonov, J.I.; Locarnini, R.A.; Mishonov, A.V.; Boyer, T.P.; Garcia, H.E.; Baranova, O.K.; Johnson, D.R.; Seidov, D.; et al. World Ocean Atlas 2013; Volume 2: Salinity; NOAA Atlas NESDIS 74; Lev-itus, S., Mishonov, A., Eds.; National Oceanic and Atmospheric Administration: Silver Spring, MD, USA, 2013; p. 39. [Google Scholar]
- Willmott, C.J. Some comments on the evaluation of model performance. Bull. Am. Meteorol. Soc. 1982, 63, 1309–1313. [Google Scholar] [CrossRef]
- Wang, T.; Khangaonkar, T.; Long, W.; Gill, G. Development of a Kelp-Type Structure Module in a Coastal Ocean Model to Assess the Hydrodynamic Impact of Seawater Uranium Extraction Technology. J. Mar. Sci. Eng. 2014, 2, 81–92. [Google Scholar] [CrossRef]
- Wissmar, R.; Simenstad, C. Energetic Constraints of Juvenile Chum Salmon (Oncorhynchus keta) Migrating in Estuaries. Can. J. Fish. Aquat. Sci. 1988, 45, 1555–1560. [Google Scholar] [CrossRef]
- Greene, C.M.; Hall, J.; Small, D.; Smith, P. Effects of Intertidal Water Crossing Structures on Estuarine Fish and Their Habitat: A Literature Review and Synthesis. 2017. Available online: http://www.skagitclimatescience.org/wp-content/uploads/2018/07/Greene-et-al.-2017-review-on-intertidal-water-crossing-structures-and-fish-1.pdf (accessed on 10 December 2018).



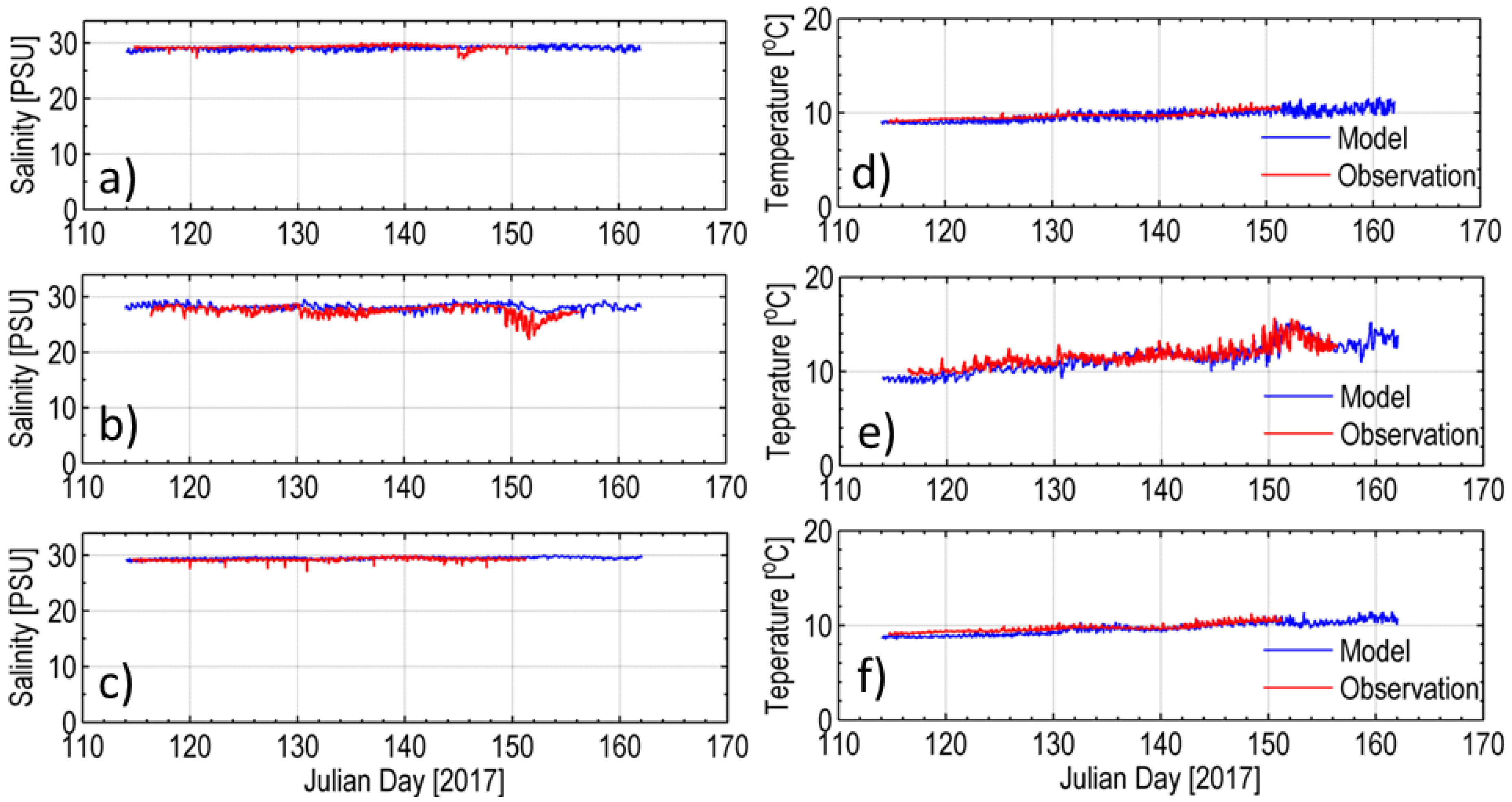


| Mean Error (Bias) | RMSE | WSS | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Max | Min | Ave | Max | Min | Ave | Max | Min | Ave | |
| T (°C) | 0.97 | −1.77 | −0.03 | 2.29 | 0.40 | 0.94 | 0.99 | 0.78 | 0.94 |
| S (PSU) | 0.09 | −0.93 | −0.24 | 2.27 | 0.39 | 0.96 | 0.90 | 0.60 | 0.80 |
| AME | RMSE | WSS | |
|---|---|---|---|
| Elevation (m) | 0.013 | 0.420 | 0.960 |
| Station | Temperature | Salinity | ||||
|---|---|---|---|---|---|---|
| AME | RMSE | WSS | AME | RMSE | WSS | |
| North ADCP | 0.22 | 0.56 | 0.74 | 0.21 | 0.57 | 0.30 |
| South ADCP | 0.08 | 0.40 | 0.85 | 0.12 | 0.36 | 0.41 |
| Bridge ADCP | 0.41 | 0.79 | 0.90 | 0.82 | 1.29 | 0.47 |
| North CTD | 0.47 | 0.91 | 0.80 | 0.33 | 0.86 | 0.68 |
| South CTD | 0.50 | 0.80 | 0.90 | 0.65 | 1.03 | 0.72 |
| Station | AME | RMSE | WSS |
|---|---|---|---|
| North ADCP | 0.00 | 0.14 | 0.94 |
| South ADCP | 0.02 | 0.21 | 0.89 |
| Bridge ADCP | 0.03 | 0.21 | 0.92 |
| Aquadopp | 0.02 | 0.33 | 0.36 |
| Variable | Max. (Δ) | South HCB | North HCB |
|---|---|---|---|
| ZOI (km) | ZOI (km) | ||
| Velocity (m/s) | −0.70 | 2.02 | 3.43 |
| Salinity (PSU) | 0.42 | 1.96 | 3.80–10 |
| Temperature (°C) | −0.49 | 2.23 | 4.51–10 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khangaonkar, T.; Nugraha, A.; Wang, T. Hydrodynamic Zone of Influence Due to a Floating Structure in a Fjordal Estuary—Hood Canal Bridge Impact Assessment. J. Mar. Sci. Eng. 2018, 6, 119. https://doi.org/10.3390/jmse6040119
Khangaonkar T, Nugraha A, Wang T. Hydrodynamic Zone of Influence Due to a Floating Structure in a Fjordal Estuary—Hood Canal Bridge Impact Assessment. Journal of Marine Science and Engineering. 2018; 6(4):119. https://doi.org/10.3390/jmse6040119
Chicago/Turabian StyleKhangaonkar, Tarang, Adi Nugraha, and Taiping Wang. 2018. "Hydrodynamic Zone of Influence Due to a Floating Structure in a Fjordal Estuary—Hood Canal Bridge Impact Assessment" Journal of Marine Science and Engineering 6, no. 4: 119. https://doi.org/10.3390/jmse6040119
APA StyleKhangaonkar, T., Nugraha, A., & Wang, T. (2018). Hydrodynamic Zone of Influence Due to a Floating Structure in a Fjordal Estuary—Hood Canal Bridge Impact Assessment. Journal of Marine Science and Engineering, 6(4), 119. https://doi.org/10.3390/jmse6040119






