A Hybrid Lagrangian–Eulerian Particle Model for Ecosystem Simulation
Abstract
1. Introduction
2. Methods
2.1. Property-Carrying Particle Model (PCPM)
- Read particle locations (x, y, z) and temperature. This step simply updates the location of each particle that is being used in the computation. Figure 2 is a conceptual representation of a PCPM computational cell, Particles (m1, m2, m3,…) move in and out of the cell at each PCPM time step based on their trajectories as computed from the hydrodynamic model. The total number of particles for a particular computation is assumed to be fixed for the duration of the computation, although some particles may enter or leave the PCPM domain during the computation. Water temperature or other physical properties from the hydrodynamic calculation can be stored along with the pre-computed particle trajectories and can be included as one of the properties (P1, P2, P3, …) carried by the particle.
- Determine the PCPM cell for each particle. In Figure 2, the PCPM cell is represented by the enclosing rectangle. The PCPM domain need not coincide with the domain that was used for the hydrodynamic simulation and computation of particle trajectories. It can be regular or irregular, as long as there is a prescribed method to calculate which PCPM cell contains a prescribed particle position (x, y, z). The PCPM cells are the volumes within which particle properties can interact, that is, during a single time step, all particles within a PCPM cell can influence the evolution of particle properties within that cell, but are independent of other cells.
- Apply boundary conditions to any particle-based properties that require them. If there is a property (e.g., concentration of a dissolved nutrient) that needs to be specified as a boundary condition, then particles within the cell where the boundary condition needs to be applied will have that property adjusted to meet the boundary condition. For example, in a cell that is associated with an inflow to the domain, the properties that are being carried into the domain through the inflow are adjusted to take account of the change in that property for particles within that cell. Alternatively, if particles from the hydrodynamic-based trajectory calculation are entering a PCPM cell, the values of the associated properties for each particle need to be specified.
- Calculate PCPM cell-based averages of each property. In this step, the averages of property for cell n are calculated as:where the summation includes all particles (m1, m2,...) currently within cell n. L is the number of particles within that cell. If no particles are present in a particular cell, PCPM uses the values of from the previous time step.
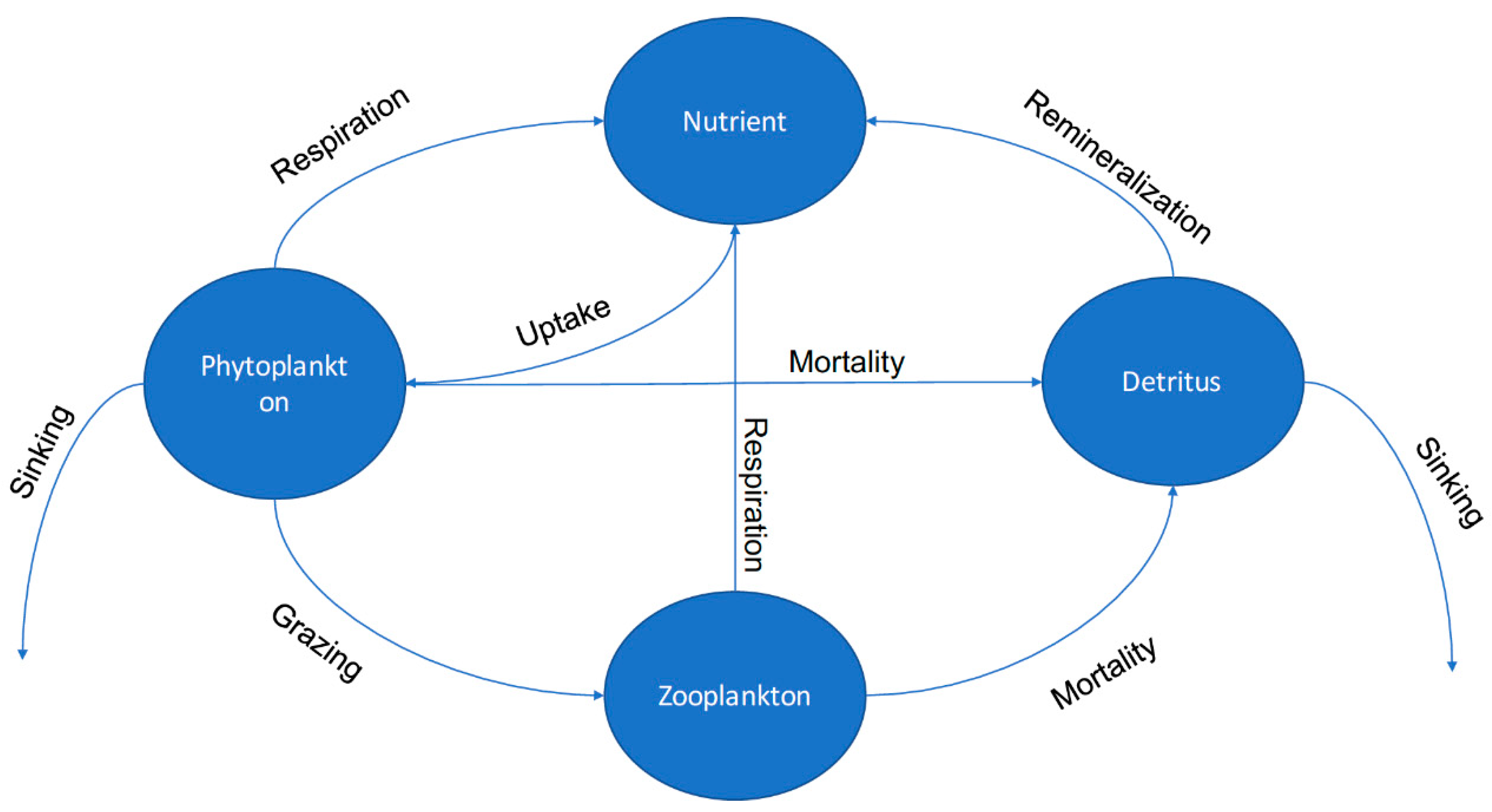
- Calculate the time evolution of the cell-based properties (and particle-based properties if necessary) using the process equation defined for that property. The process equations can incorporate terms which depend on either particle-based or cell-based properties, or both, i.e.,Note that M indicates m1, m2,.... The form of FN is completely general and depends on the problem being solved. For instance, in a NPZD model, the ) would be N, P, Z, D, and water temperature, and the FN would be the process equations relating these properties.Since the cell-based averages have already been computed, the right-hand side of Equation (4) is independent of the left-hand side, so the computation of the evolution equations can be carried out in parallel. This is another key design feature of PCPM allowing it to take full advantage of multiprocessing computer environments, both symmetric multi-processing (SMP) and massively parallel processing (MPP).
- Redistribute cell-based properties to particles within each cell by replacing the particle-based property with a weighted average of the cell-based property. After the evolution equations have been carried out (Step 5), particles within an individual cell most likely carry a range of different values of the various properties, which vary around the new cell-based average computed in Step 5, . PCPM provides an optional step to reduce the variance of the new particle-based properties within each cell. This optional step is applied as a ‘nudging’ term, i.e.,where 0 < < 1 is the redistribution weight (i.e., nudging) factor. If = 0, no adjustment is carried out and the particle-based property remains unchanged. If = 1, then all particles within a cell are assigned the cell-based average of that property. This step can be useful to smooth results when limited particle density results in excessive within-cell variability.
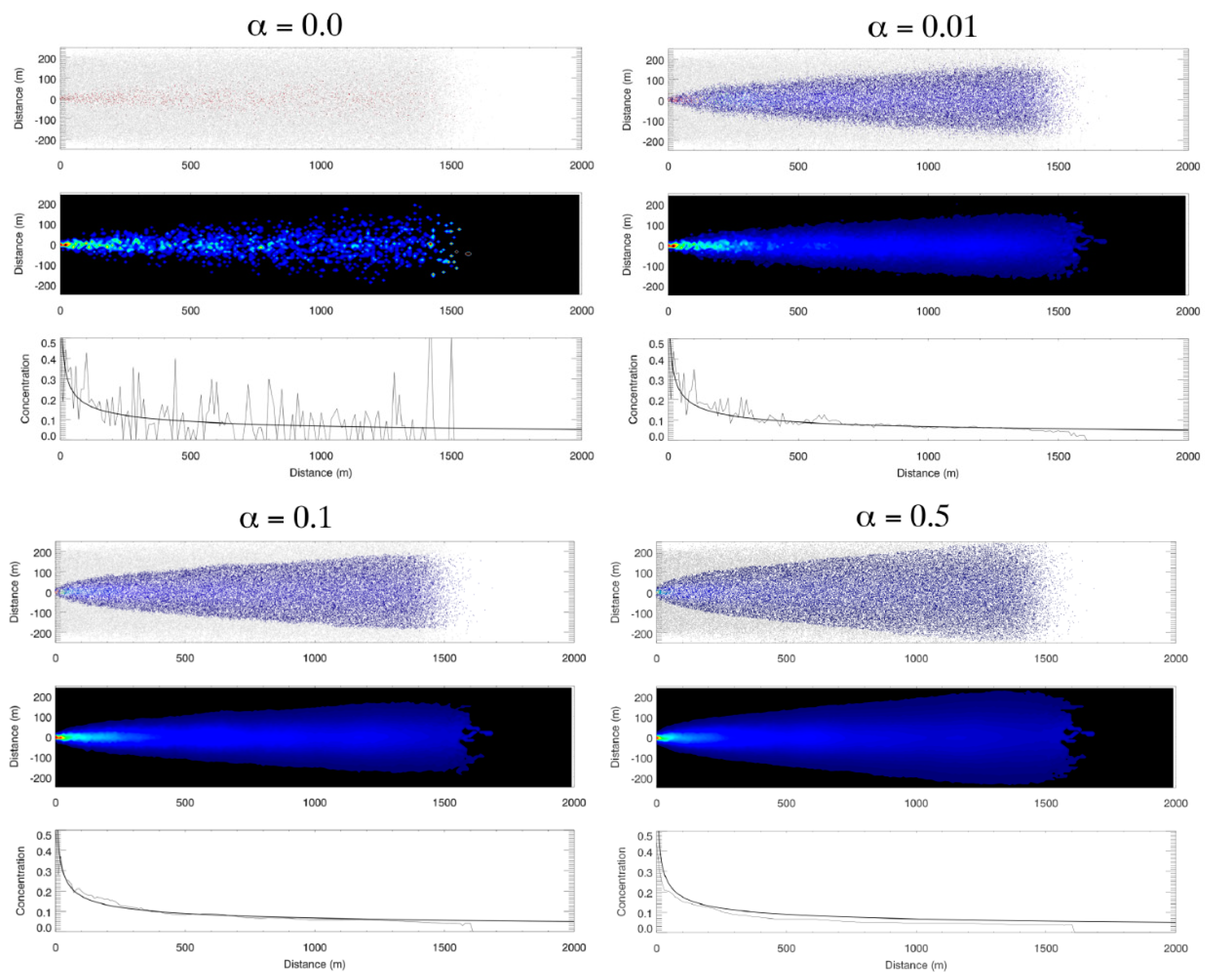
2.2. Idealized Case 1: Advection–Diffusion Plume
2.3. Idealized Case 2: Vertical Settling
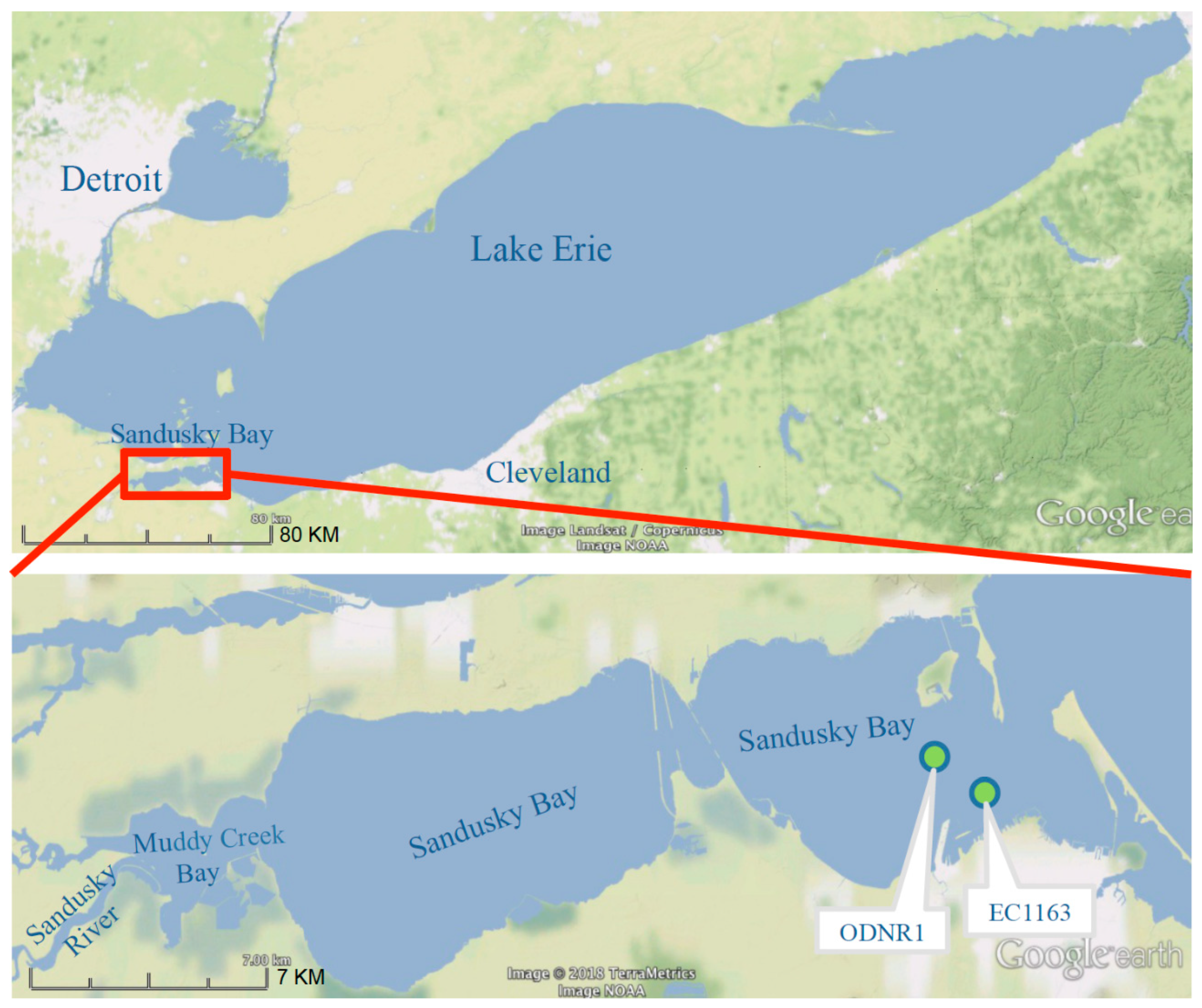
2.4. Sandusky Bay Model
2.5. Sandusky Bay Biological Model
3. Results
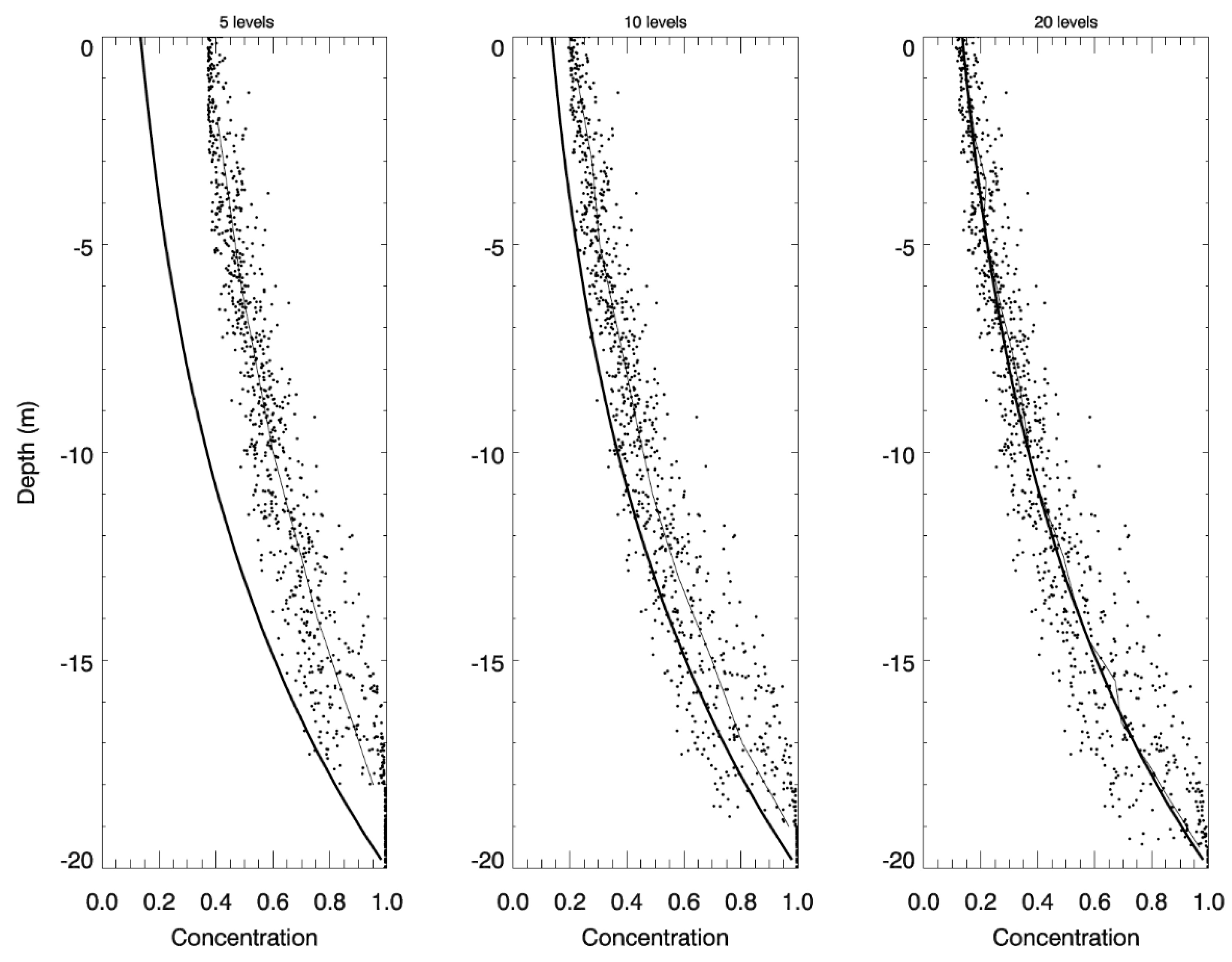
3.1. Idealized Case 1: Advection–Diffusion Plume
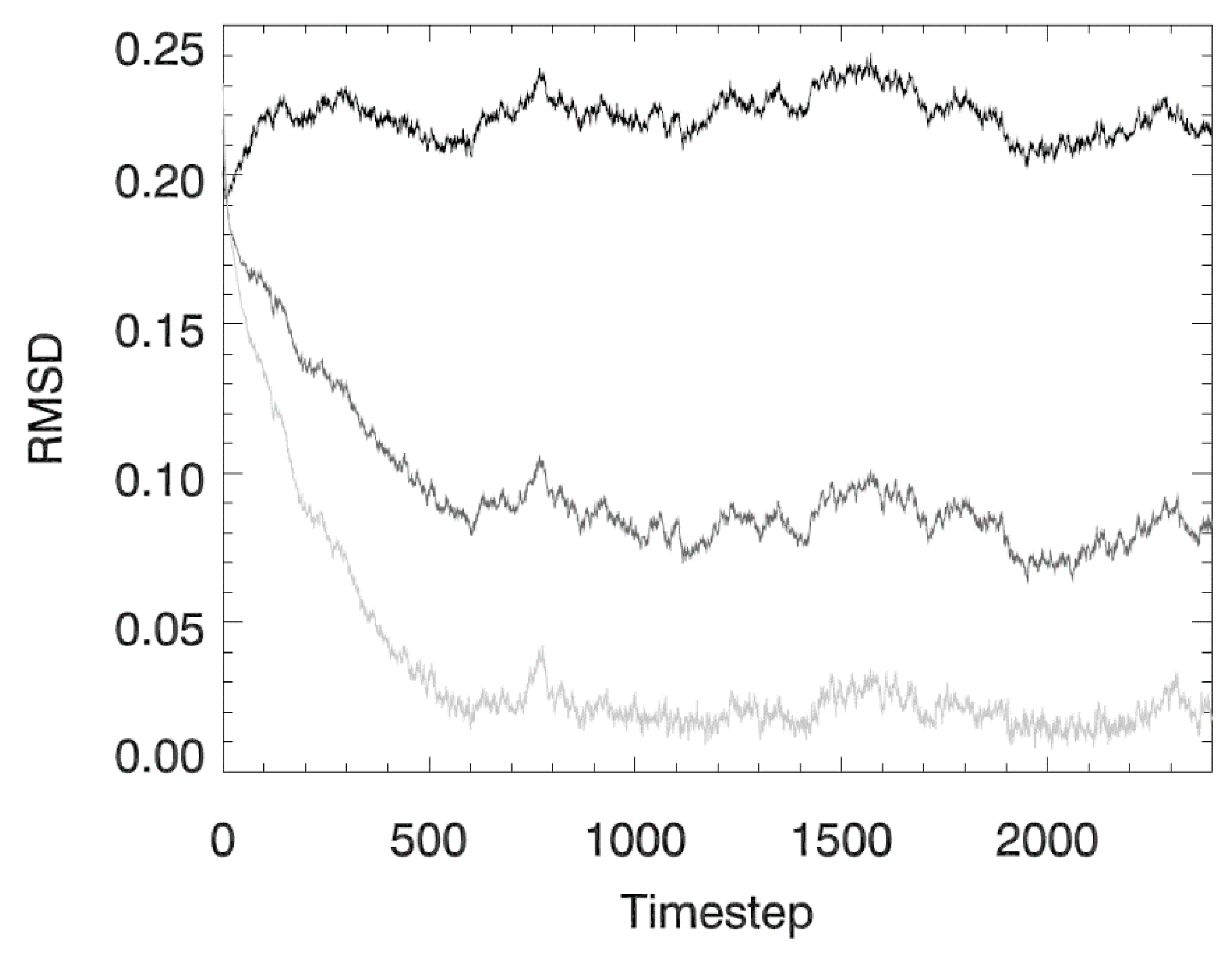
3.2. Idealized Case 2: Vertical Settling
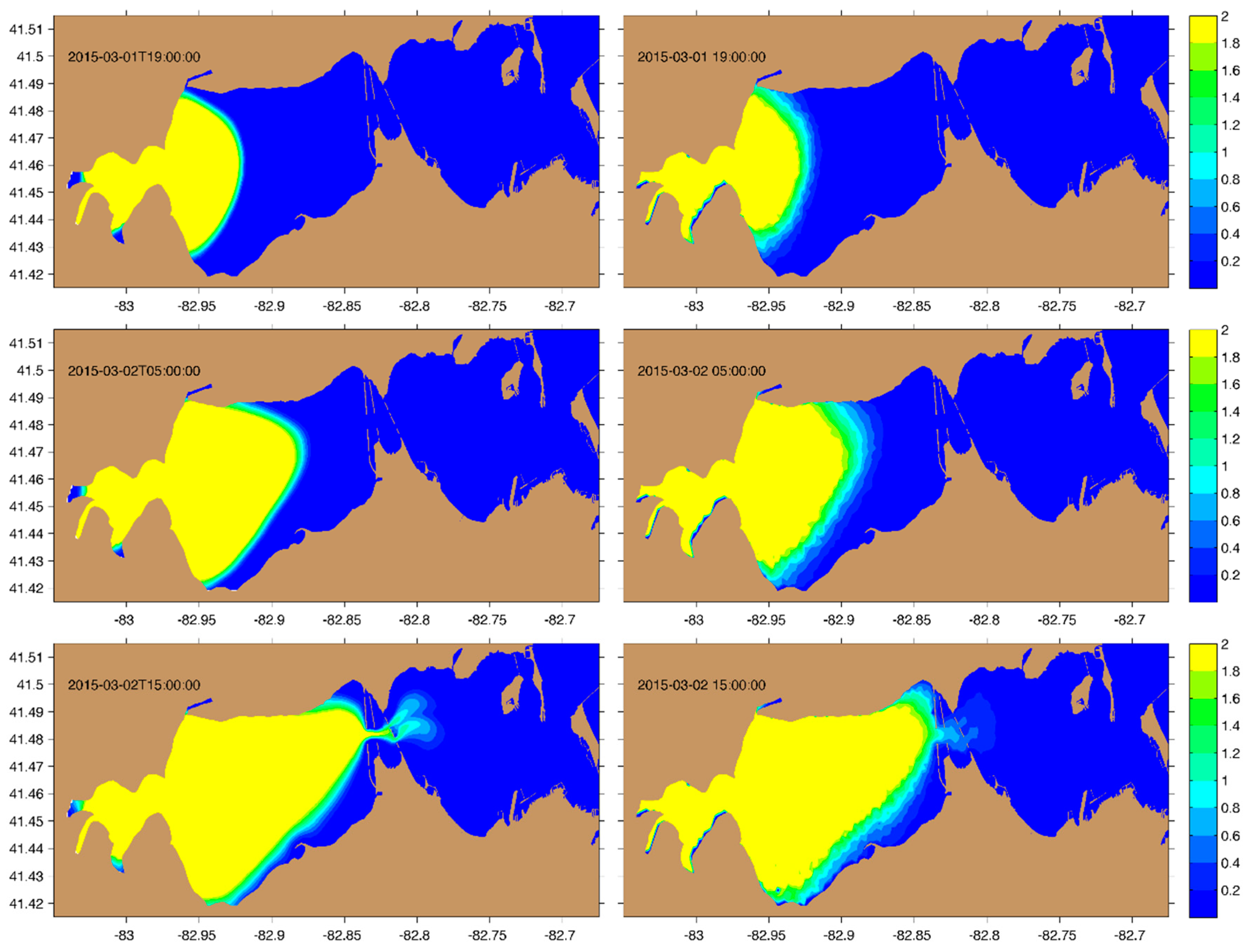
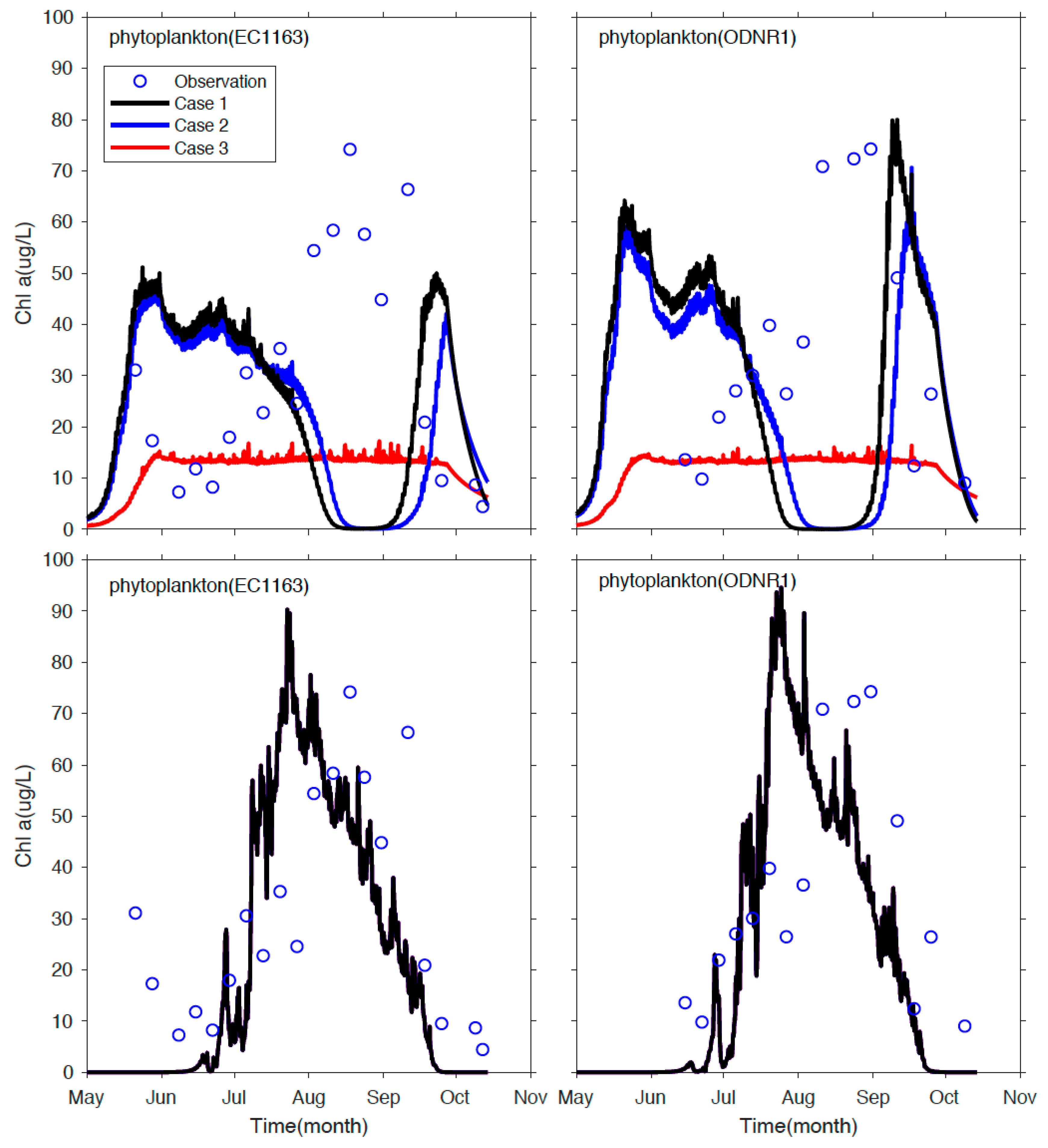
3.3. Application to Sandusky Bay
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Parameters | Description | Units | Value Used | References |
|---|---|---|---|---|
| Half-Saturation constant | µmol N/L | 3 (0.6) | [17] | |
| Nutrient threshold | µmol N/L | 0 (1.4) | [18] | |
| Initial linear slope at low irradiances | 7 | [18] | ||
| Negative slope at high irradiances | 0 | [43] | ||
| Maximum potential growth rate | 2.4 | [43] | ||
| Optimum temperature | °C | 27.2 | [42] | |
| Minimum temperature | °C | 5.5 | [42] | |
| Maximum growth rate for P | day−1 | 1.1 | ||
| Phytoplankton respiration coefficient | day−1 | 0.01 | [17] | |
| Exponential for Temperature forcing | dimensionless | 0.07 | [17] | |
| Remineralization rate of detritus | day−1 | 0.015 | [17] | |
| Maximum P grazing rate by Z | day−1 | 0.4 | [17] | |
| Preference coefficient of Z on P | 0.5 | [17] | ||
| Preference coefficient of Z on D | 0.1 | [17] | ||
| Mortality rate of P | day−1 | 0.005 (0.01) | [17] | |
| Mortality rate of Z | day−1 | 0.2 (0.01) | [17] | |
| Sink velocity of P | m/day | 0.6 | [17] | |
| Sink velocity of D | m/day | 0.6 | [17] | |
| Water attenuation coefficient | m−1 | 0.07 | [18] | |
| Phytoplankton attenuation coefficient | 0.03 | [18] | ||
| Detritus attenuation coefficient | 0.2 | [18] |
References
- Woods, J.D. The Lagrangian Ensemble metamodel for simulating plankton ecosystems. Prog. Oceanogr. 2005, 67, 84–159. [Google Scholar] [CrossRef]
- Hellweger, F.L.; Bucci, V. A bunch of tiny individuals—Individual-based modeling for microbes. Ecol. Model. 2009, 220, 8–22. [Google Scholar] [CrossRef]
- DeAngelis, D.L.; Grimm, V. Individual-based models in ecology after four decades. F1000prime Rep. 2014, 6, 39. [Google Scholar] [CrossRef] [PubMed]
- Chapra, S.C. Surface Water-Quality Modeling; McGraw-Hill: Boston, MA, USA, 1997. [Google Scholar]
- Franks, P.J. NPZ models of plankton dynamics: Their construction, coupling to physics, and application. J. Oceanogr. 2002, 58, 379–387. [Google Scholar] [CrossRef]
- Butenschön, M.; Clark, J.; Aldridge, J.N.; Allen, J.I.; Artioli, Y.; Blackford, J.; Lessin, G. ERSEM 15.06: A generic model for marine biogeochemistry and the ecosystem dynamics of the lower trophic levels. Geosci. Model Dev. 2016, 9, 1293–1339. [Google Scholar] [CrossRef]
- Hellweger, F.L.; Kianirad, E. Individual-based modeling of phytoplankton: Evaluating approaches for applying the cell quota model. J. Theor. Biol. 2007, 249, 554–565. [Google Scholar] [CrossRef] [PubMed]
- Hellweger, F.L.; Kravchuk, E.S.; Novotny, V.; Gladyshev, M.I. Agent-based modeling of the complex life cycle of a cyanobacterium (Anabaena) in a shallow reservoir. Limnol. Oceanogr. 2008, 53, 1227–1241. [Google Scholar] [CrossRef]
- Grimm, V.; Berger, U.; DeAngelis, D.L.; Polhill, J.G.; Giske, J.; Railsback, S.F. The ODD protocol: A review and first update. Ecol. Model. 2010, 221, 2760–2768. [Google Scholar] [CrossRef]
- Bruggeman, J.; Bolding, K. A general framework for aquatic biogeochemical models. Environ. Model. Softw. 2014, 61, 249–265. [Google Scholar] [CrossRef]
- Chai, F.; Dugdale, R.C.; Peng, T.H.; Wilkerson, F.P.; Barber, R.T. One-dimensional ecosystem model of the equatorial Pacific upwelling system. Part I: Model development and silicon and nitrogen cycle. Deep Sea Res. Part II Top. Stud. Oceanogr. 2002, 49, 2713–2745. [Google Scholar]
- Fennel, K.; Wilkin, J.; Levin, J.; Moisan, J.; O’Reilly, J.; Haidvogel, D. Nitrogen cycling in the Middle Atlantic Bight: Results from a three-dimensional model and implications for the North Atlantic nitrogen budget. Glob. Biogeochem. Cycles 2006, 20. [Google Scholar] [CrossRef]
- Edwards, K.P.; Barciela, R.; Butenschon, M. Validation of the NEMO-ERSEM operational ecosystem model for the North West European Continental Shelf. Ocean Sci. 2012, 8, 983–1000. [Google Scholar] [CrossRef]
- Rodrigues, M.; Oliveira, A.; Queiroga, H.; Fortunato, A.B.; Zhang, Y.J. Three-dimensional modeling of the lower trophic levels in the Ria de Aveiro (Portugal). Ecol. Model. 2009, 220, 1274–1290. [Google Scholar] [CrossRef]
- Xue, P.; Chen, C.; Qi, J.; Beardsley, R.C.; Tian, R.; Zhao, L.; Lin, H. Mechanism studies of seasonal variability of dissolved oxygen in Mass Bay: A multi-scale FVCOM/UG-RCA application. J. Mar. Syst. 2014, 131, 102–119. [Google Scholar] [CrossRef]
- Chao, X.; Jia, Y.; Shields Jr, F.D.; Wang, S.S.; Cooper, C.M. Three-dimensional numerical simulation of water quality and sediment-associated processes with application to a Mississippi Delta lake. J. Environ. Manag. 2010, 91, 1456–1466. [Google Scholar] [CrossRef] [PubMed]
- Luo, L.; Wang, J.; Schwab, D.J.; Vanderploeg, H.; Leshkevich, G.; Bai, X.; Wang, D. Simulating the 1998 spring bloom in Lake Michigan using a coupled physical-biological model. J. Geophys. Res. Oceans 2012, 117. [Google Scholar] [CrossRef]
- Rowe, M.D.; Anderson, E.J.; Vanderploeg, H.A.; Pothoven, S.A.; Elgin, A.K.; Wang, J.; Yousef, F. Influence of invasive quagga mussels, phosphorus loads, and climate on spatial and temporal patterns of productivity in Lake Michigan: A biophysical modeling study. Limnol. Oceanogr. 2017, 62, 2629–2649. [Google Scholar] [CrossRef]
- Wong, K.T.; Lee, J.H.; Choi, K.W. A deterministic Lagrangian particle separation-based method for advective-diffusion problems. Commun. Nonlinear Sci. Numer. Simul. 2008, 13, 2071–2090. [Google Scholar] [CrossRef]
- Dimou, K.N.; Adams, E.E. A random-walk, particle tracking model for well-mixed estuaries and coastal waters. Estuar. Coast. Shelf Sci. 1993, 37, 99–110. [Google Scholar] [CrossRef]
- Zhang, X.Y. Ocean Outfall Modeling—Interfacing Near and Far Field Models with Particle Tracking method. Ph.D. Thesis, MIT, Cambridge, MA, USA, 1995. [Google Scholar]
- Xue, P.; Schwab, D.J.; Sawtell, R.W.; Sayers, M.J.; Shuchman, R.A.; Fahnenstiel, G.L. A particle-tracking technique for spatial and temporal interpolation of satellite images applied to Lake Superior chlorophyll measurements. J. Great Lakes Res. 2017, 43, 1–13. [Google Scholar] [CrossRef]
- Harlow, F.H. The Particle-in-Cell Computing Method for Fluid Dynamics. Methods Comput. Phys. 1964, 3, 319–343. [Google Scholar]
- Tskhakaya, D. The Particle-in-Cell Method. In Computational Many-Particle Physics. Lecture Notes in Physics; Fehske, H., Schneider, R., Weiße, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 739. [Google Scholar]
- Hockney, R.W.; Eastwood, J.W. Computer Simulation Using Particles; McGraw-Hill: New York, NY, USA, 1981. [Google Scholar]
- Grigoryev, Y.N.; Vshivkov, V.A.; Fedoruk, M.P. Fedoruk Numerical “Particle-in-Cell” Methods: Theory and Applications; De Gruyter VSP: Utrecht, The Netherlands; Boston, MA, USA, 2002; 249p. [Google Scholar]
- Conroy, J.D.; Kane, D.D.; Quinlan, E.L.; Edwards, W.J.; Culver, D.A. Abiotic and biotic controls of phytoplankton biomass dynamics in a freshwater tributary, estuary, and large lake ecosystem: Sandusky Bay (Lake Erie) chemostat. Inland Waters 2017, 7, 473–492. [Google Scholar] [CrossRef]
- Salk, K.R.; Bullerjahn, G.S.; McKay, R.M.L.; Chaffin, J.D.; Ostrom, N.E. Nitrogen cycling in Sandusky Bay, Lake Erie: Oscillations between strong and weak export and implications for harmful algal blooms. Biogeosciences 2018, 15, 2891. [Google Scholar] [CrossRef]
- Stumpf, R.P.; Wynne, T.T.; Baker, D.B.; Fahnenstiel, G.L. Interannual variability of cyanobacterial blooms in Lake Erie. PLoS ONE 2012, 7, e42444. [Google Scholar] [CrossRef] [PubMed]
- Chaffin, J.D.; Bridgeman, T.B.; Bade, D.L. Nitrogen constrains the growth of late summer cyanobacterial blooms in Lake Erie. Adv. Microbiol. 2013, 3, 16. [Google Scholar] [CrossRef]
- U.S. EPA. U.S. Action Plan for Lake Erie. 10 August 2017. Available online: https://www.epa.gov/sites/production/files/2017/08/documents/us_dap_preliminary_draft_for_public_engagement_8-10-17.pdf (accessed on 15 May 2018).
- Davis, T.W.; Bullerjahn, G.S.; Tuttle, T.; McKay, R.M.; Watson, S.B. Effects of increasing nitrogen and phosphorus concentrations on phytoplankton community growth and toxicity during Planktothrix blooms in Sandusky Bay, Lake Erie. Environ. Sci. Technol. 2015, 49, 7197–7207. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Liu, H.; Beardsley, R.C. An unstructured grid, finite-volume, three-dimensional, primitive equations ocean model: Application to coastal ocean and estuaries. J. Atmosp. Ocean. Technol. 2003, 20, 159–186. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, T.; Copping, A.E. Modeling tidal stream energy extraction and its effects on transport processes in a tidal channel and bay system using a three-dimensional coastal ocean model. Renew. Energy 2013, 50, 605–613. [Google Scholar] [CrossRef]
- Xue, P.; Schwab, D.J.; Hu, S. An investigation of the thermal response to meteorological forcing in a hydrodynamic model of Lake Superior. J. Geophys. Res. Oceans 2015, 120, 5233–5253. [Google Scholar] [CrossRef]
- Anderson, E.J.; Bechle, A.J.; Wu, C.H.; Schwab, D.J.; Mann, G.E.; Lombardy, K.A. Reconstruction of a meteotsunami in Lake Erie on 27 May 2012: Roles of atmospheric conditions on hydrodynamic response in enclosed basins. J. Geophys. Res. Oceans 2015, 120, 8020–8038. [Google Scholar] [CrossRef]
- Xue, P.; Pal, J.S.; Ye, X.; Lenters, J.D.; Huang, C.; Chu, P.Y. Improving the Simulation of Large Lakes in Regional Climate Modeling: Two-Way Lake–Atmosphere Coupling with a 3D Hydrodynamic Model of the Great Lakes. J. Clim. 2017, 30, 1605–1627. [Google Scholar] [CrossRef]
- Khangaonkar, T.; Nugraha, A.; Xu, W.; Long, W.; Bianucci, L.; Ahmed, A.; Pelletier, G. Analysis of Hypoxia and Sensitivity to Nutrient Pollution in Salish Sea. J. Geophys. Res. Oceans 2018. [Google Scholar] [CrossRef]
- Ye, X.; Anderson, E.J.; Chu, P.Y.; Huang, C.; Xue, P. Impact of Water Mixing and Ice Formation on the Warming of Lake Superior: A Model-guided Mechanism Study. Limnol. Oceanogr. 2018. [Google Scholar] [CrossRef]
- Kelley, J.G.W.; Chen, Y.; Anderson, E.J.; Lang, G.A.; Xu, J. Upgrade of NOS Lake Erie Operational Forecast System (LEOFS) To FVCOM: Model Development and Hindcast Skill Assessment. NOAA Tech. Memo. NOS CS 2018, 40, 92. [Google Scholar]
- Platt, T.G.C.L.; Gallegos, C.L.; Harrison, W.G. Photoinhibition of photosynthesis in natural assemblages of marine phytoplankton. J. Mar. Res. 1981, 38, 687–701. [Google Scholar]
- Nicklisch, A.; Shatwell, T.; Köhler, J. Analysis and modelling of the interactive effects of temperature and light on phytoplankton growth and relevance for the spring bloom. J. Plankton Res. 2007, 30, 75–91. [Google Scholar] [CrossRef]
- Fahnenstiel, G.L.; Chandler, J.F.; Carrick, H.J.; Scavia, D. Photosynthetic characteristics of phytoplankton communities in Lakes Huron and Michigan: PI parameters and end-products. J. Great Lakes Res. 1989, 15, 394–407. [Google Scholar] [CrossRef]
- Stacey, M.T.; Cowen, E.A.; Powell, T.M.; Dobbins, E.; Monismith, S.G.; Koseff, J.R. Plume dispersion in a stratified, near-coastal flow: Measurements and modeling. Cont. Shelf Res. 2000, 20, 637–663. [Google Scholar] [CrossRef]
- Kim, T.; Khangaonkar, T. An offline unstructured biogeochemical model (UBM) for complex estuarine and coastal environments. Environ. Model. Softw. 2012, 31, 47–63. [Google Scholar] [CrossRef]
- Edwards, C.A.; Powell, T.A.; Batchelder, H.P. The stability of an NPZ model subject to realistic levels of vertical mixing. J. Mar. Res. 2000, 58, 37–60. [Google Scholar] [CrossRef]

| Month | Monthly Discharge (108 m3) | Particles (Number) |
|---|---|---|
| January | 0.364 | 10,405 |
| February | 2.27 | 64,980 |
| March | 7.19 | 205,367 |
| April | 1.53 | 43,741 |
| May | 0.443 | 12,640 |
| June | 3.00 | 85,754 |
| July | 1.97 | 56,347 |
| August | 0.129 | 3680 |
| September | 0.089 | 2544 |
| October | 0.093 | 2654 |
| November | 0.133 | 3798 |
| December | 1.15 | 32,951 |
| Simulation Period (day) | Number of Central Processing Units (CPUs) | Time Per Run (Hour) | Scenario 1 | Scenario 2 | |||
|---|---|---|---|---|---|---|---|
| Required Runs | Total Time | Required Runs | Total Time | ||||
| Hydrodynamic simulation (required for both methods) | 30 | 64 | 15 | 1 | 15 h | 1 | 15 h |
| Biological simulation | |||||||
| New Method | |||||||
| Particle trajectory model | 30 | 1 | 1.5 | 1 | 1.6 hrs (1 CPU) | 1 | 11.5 hrs (1 CPU) |
| PCPM-NPZD | 30 | 1 | 0.1 | 1 | 100 | ||
| Traditional Method | |||||||
| Eulerian, grid-based simulation | 30 | 32 | 5 | 1 | 5 hrs (32 CPUs) | 100 | 500 hrs (32 CPUs) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, P.; Schwab, D.J.; Zhou, X.; Huang, C.; Kibler, R.; Ye, X. A Hybrid Lagrangian–Eulerian Particle Model for Ecosystem Simulation. J. Mar. Sci. Eng. 2018, 6, 109. https://doi.org/10.3390/jmse6040109
Xue P, Schwab DJ, Zhou X, Huang C, Kibler R, Ye X. A Hybrid Lagrangian–Eulerian Particle Model for Ecosystem Simulation. Journal of Marine Science and Engineering. 2018; 6(4):109. https://doi.org/10.3390/jmse6040109
Chicago/Turabian StyleXue, Pengfei, David J Schwab, Xing Zhou, Chenfu Huang, Ryan Kibler, and Xinyu Ye. 2018. "A Hybrid Lagrangian–Eulerian Particle Model for Ecosystem Simulation" Journal of Marine Science and Engineering 6, no. 4: 109. https://doi.org/10.3390/jmse6040109
APA StyleXue, P., Schwab, D. J., Zhou, X., Huang, C., Kibler, R., & Ye, X. (2018). A Hybrid Lagrangian–Eulerian Particle Model for Ecosystem Simulation. Journal of Marine Science and Engineering, 6(4), 109. https://doi.org/10.3390/jmse6040109






