Next Article in Journal
Numerical Simulation and Uncertainty Analysis of an Axial-Flow Waterjet Pump
Next Article in Special Issue
Sensitivity of Offshore Tropical Cyclone Wave Simulations to Spatial Resolution in Wave Models
Previous Article in Journal
Ballast Water Management in the Black Sea’s Ports
Previous Article in Special Issue
Simulating Storm Surge Impacts with a Coupled Atmosphere-Inundation Model with Varying Meteorological Forcing
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
JMSE
Volume 6
Issue 2
10.3390/jmse6020070
jmse-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Frequency Analysis of Storm-Surge-Induced Flooding for the Huangpu River in Shanghai, China

by
Qian Ke
1,*,
Sebastiaan N. Jonkman
1,
Pieter H. A. J. M. Van Gelder
2 and
Jeremy D. Bricker
1
1
Section of Hydraulic Structures and Flood Risk, Department of Hydraulic Engineering, Faculty of Civil Engineering and Geosciences, Delft University of Technology, 2628 CN Delft, The Netherlands
2
Section of Safety and Security Science, Department of Values, Technology and Innovation, Faculty of Technology, Policy and Management, Delft University of Technology, 2628 BX Delft, The Netherlands
*
Author to whom correspondence should be addressed.
J. Mar. Sci. Eng. 2018, 6(2), 70; https://doi.org/10.3390/jmse6020070
Submission received: 14 May 2018 / Revised: 1 June 2018 / Accepted: 5 June 2018 / Published: 11 June 2018
(This article belongs to the Special Issue Coastal Hazards Related to Water)
Browse Figures
Versions Notes

Abstract

:
Shanghai, as a coastal city, is vulnerable to various types of flooding. The floodwalls along the Huangpu River provide protection against typhoon-induced flooding. However, there is limited insight into the actual safety level of the flood defences in Shanghai, and recent failures have highlighted their vulnerability. Therefore, the aims of this paper are to derive a series of new flood frequency curves for the Huangpu River, and to evaluate the level of protection of the floodwall system. This paper analysed over 100 years (1912–2013) of annual maximum water levels for three stations at near-sea, mid-stream and inland locations along the Huangpu River. Best-fit curves were determined for a number of selected probability distributions using statistical performance indicators. As a result, new flood frequency curves of the water levels for different storm surge return periods were produced. The results showed that generalised extreme value (GEV) was identified as the most suitable probability distribution for the datasets. Analysis showed that the current design water levels correspond to exceedance probabilities of 1/500 per year at the near-sea and mid-stream stations, and no more than 1/50 per year at the inland station of the Huangpu River, whereas the intended safety standard is 1/1000 per year. A comparison of the findings with a dataset of the crest heights of the floodwalls showed that the current protection level of the floodwalls along the Huangpu River is expected to be around 1/50 per year in terms of overtopping for the lowest sections. The results of this study can be utilized to provide future recommendations for flood risk management in Shanghai.

1. Introduction

In recent years, many cities worldwide have been severely affected by flooding. Examples of major flood disasters are the river floods in Thailand (2011), Hurricane Sandy in New York and New Jersey (2012) and flooding along the Elbe in Germany (2013). A large and rapidly growing part of the world’s population lives in low-lying coastal zones [1]. These areas have been threatened by extreme events, and in the future risks are expected to increase due to economic and population growth and the effects of climate change. Especially in Southeast Asia, cities such as Tokyo, Jakarta, Ho Chi Minh City, and Shanghai are located in coastal and delta areas and are threatened by potential flooding problems. Many of these cities have implemented flood defence systems to reduce flood risks. These systems have different safety standards, which are generally expressed as the allowed probability of exceeding a certain design water level as a required protection level. For example, the safety standards in The Netherlands are regarded as the most stringent in the world, with safety standards varying between 1/1250 per year and 1/10,000 per year. In the United States, a safety standard of 1/100 per year is often applied, e.g., for New Orleans. Cities such as a Tokyo, London, and Shanghai utilise safety standards of 1/1000 per year [2].
Shanghai (China), as a coastal city, is vulnerable to flooding due to its geographic location on flat and low-lying terrain in combination with land subsidence and climate change. In recent studies [3,4], Shanghai ranked as one of the top 20 cities in the world in terms of population exposure and property exposure to the floods. In a conservative estimate by Nicholls et al. [2] the expected annual risk is 2000 persons/year in terms of loss of life and US $73 million/year in terms of economic damage. Hallegatte et al. [4] estimated flood risk at US $63 million/year under an optimistic scenario of a maximum protection level of 1/1000 per year for Shanghai. Given the threat of flooding from typhoons and river floods, Shanghai has implemented a flood defence system consisting of sea dikes, floodwalls, and flood gates. Past studies have highlighted that the current system does not meet the standards, and that land subsidence could further reduce the level of protection [5,6].
Due to concerns about the level of flood protection and a high exposed value, it is necessary to evaluate protection level for Shanghai. This can be done by comparing the crest height of the current floodwall to the return period of water levels around the city by means of a flood frequency analysis. For the Huangpu River, the current design water levels (DWLs) of the floodwall were determined based on a calculation by a local water authority [7]. An additional analysis of the frequency of water levels in the Huangpu River was published in the year of 2004 [8]. A recent study by Xu and Huang [9] analysed the 100-year water levels at the mouth of the Huangpu River, but did not consider water levels at different locations along the river and other frequencies.
In recent years, the floodwalls along the Huangpu River have failed several times during typhoon seasons; for example in 1997, 2000, and 2005. The most recent failure of a floodwall along the Huangpu River occurred on 8 October 2013. During Typhoon Fitow in 2013, the water level at Mishidu in the inland area of the Huangpu River was recorded at WD (Wusong Datum is adopted as the reference) 4.61 m, which broke the records [10]. This observed water level corresponds to the 10,000-return period event, according to the previous flood frequency calculation from 1984 [7]. As a result, a breach occurred in the inland reach of the Huangpu River.
In the future, climate change and human activities might also have effects on the likelihood of storm surge and change hydrological patterns and exposure in the river catchment. Hence, an update of estimates of return periods of water levels in the Huangpu River is required. Local researchers [11] have calculated the 1/1000 per year water levels for the Huangpu River. They have compared the return periods of water levels to the crest heights of the floodwalls, in order to identify the weak points. But this study only considered one return period (i.e., 1000 years) and one probability distribution type. Moreover, as far as the authors could oversee, the studies on flood frequencies along the Huangpu River are available in the Chinese language but have not been published in international literature.
For a more complete assessment, it is desirable to have insight into the water levels for various return periods and the most appropriate statistical distribution. Therefore, the aims of this paper are to derive a series of new storm-surge-induced-flood frequency curves for the Huangpu River, and also to evaluate the protection level of the floodwalls. The results will provide new information that can be used for the evaluation of the existing system, the design of new interventions, as well as emergency planning.
Besides, considering the low terrain (around WD 3–4 m) and delta location, Shanghai is actually threatened by different types of flooding. The sea dikes can be overtopped by storm surges from the East China Sea; urban floods can be caused by insufficient drainage capacity during torrential rainfall and the failure of the floodwall system along the Huangpu River. Since large parts of the area along the Huangpu River are highly developed and densely populated, the focus of this research will be on storm-surge-induced river flooding. River flooding can potentially have large economic and social impacts as it could affect districts such as the city center and Pudong. Flooding due to rainfall and limited capacity of the drainage is not considered in this paper, but is a relevant topic for further research.
Moreover, as one of the additional scientific challenges, the paper addresses some of the complexities in deriving flood frequencies in areas with multiple flood sources (tide, surge). The study focuses on the area along the Huangpu River (not on the open coast, which is also prone to storm surge) and overflowing of the floodwall (although the relevance of other floodwall failure mechanisms is also discussed). The results and methods are expected to be relevant not only for Shanghai, but also for other (mega) cities in coastal areas that are exposed to various related flood hazards.
The outline of this paper is as follows: the second section introduces the study area and currently available information on water levels along the Huangpu River. The third section describes statistical methods and the hydraulic model applied to derive water levels along the Huangpu River. The fourth section provides results for probabilistic distributions and water level-frequency curves. The fifth section compares results with previous research and discusses implications for the protection level of Shanghai. The final section contains conclusions and recommendations.

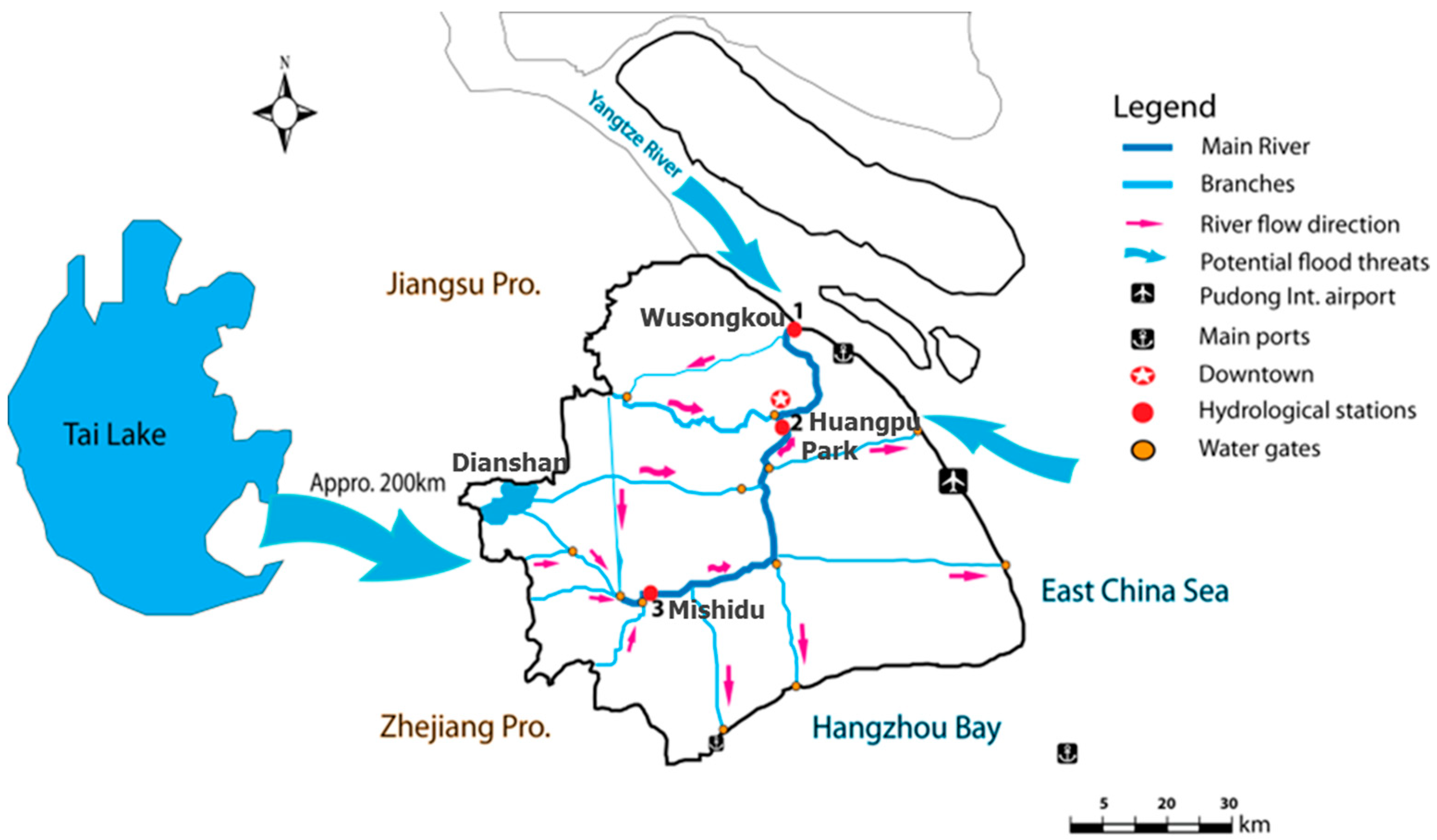
2. Study Area

Shanghai is located in eastern China. The whole city is situated on the eastern fringe of the Yangtze River Delta. This provincial-administration-level city is surrounded by water (see Figure 1). The estuary of the Yangtze River is situated to the north, the East China Sea to the east, Hangzhou Bay to the south, and Tai Lake to the west. The Huangpu River, which originates from Tai Lake and Dianshan Lake, meanders through the whole city from West to East in the inland region. It then changes its direction from South to North in mid-reach and near the sea. The Huangpu River is a tidal river that is also the last tributary of the Yangtze River. Three typical hydrological stations are located along the river, namely Wusongkou (‘1ߣ in Figure 1), Huangpu Park (‘2ߣ in Figure 1) and Mishidu (‘3ߣ in Figure 1). The downtown area is located near Huangpu Park station and the prosperous Pudong area is across the river from downtown. The width of the Huangpu River is around ~360 m on average and nearly ~800 m close to the Yangtze estuary. The annual average discharge in the inland reach (around 10 km down from Mishidu) is 439 m3/s with a standard deviation of ~67 m3/s for the period between 1998 and 2012.
Based on the Wusong Datum, the crest height of floodwalls, design water levels, warning levels and historical records at Wusongkou, Huangpu Park and Mishidu, respectively, are shown in Table 1. The crest height of the floodwalls is based on the design water level corresponding to the protection level, with an additional height to account for wind set-up and uncertainties in the freeboard. The historical records at Wusongkou (5.99 m) and Huangpu Park (5.72 m) were observed in August 1997 during Typhoon Winnie, while the historical record (4.61 m) at Mishidu was observed in October 2013 during Typhoon Fitow.
The current safety standards along the Huangpu River are 1/1000 per year in the near-sea and middle reaches, and 1/50 per year in the inland area as less economic development is present there. Flood protection mainly consists of concrete floodwalls, but also other types of flood defences are present, such as the wide ‘Bund Boulevard’ and several moveable flood gates at intersections with piers and ferry landings.
In 2013, parts of the floodwalls of the Huangpu River collapsed on 8 October during Typhoon Fitow [12]. A 15 m-wide breach occurred and this led to flooding of the adjacent farmland and residential areas. Besides, at several other points in the inland area, floodwalls were also overtopped. The maximum inundation depth was estimated at more than 2.5 m near the Qianbujing breach in Songjiang District. More than 300 soldiers were involved in rescue and emergency response, and no casualties were reported [12]. A temporary flood defence system was built in 8 h after the breach to prevent further flooding. It was also reported that one industry lost US $10 million during the flooding and needed 45 days to completely recover production [13]. Moreover, Shanghai insurance administration reported that the direct damage to the farmland reached approximately US $10 million during Typhoon Fitow in Shanghai [14]. In 1997, Typhoon Winnie led to US $100 million of economic damage. The water level at Huangpu Park (city center) rose to 5.72 m, which was almost equivalent to the water level with a 500-year return period [8]. These events further demonstrated the vulnerability of the flood protection system and the need for further analysis of flood frequencies in Shanghai.

3. Methods

3.1. Data

In this paper, annual maximum water levels at three hydrological stations (refer to Figure 1) were used for frequency analysis. The information about the datasets is shown in Table 2. Land subsidence has occurred in Shanghai for a long time, especially due to large-scale groundwater extraction from 1921 to 1965 [5]. After 1965, the local government took measures (e.g., groundwater recharging) to decrease the subsidence rate and control the extraction. Since land subsidence and other effects of interventions could affect the observed water levels, they have been revised to reach consistency. Water levels have been corrected to account for the affected factors mentioned before (see [15] for further details). The average annual maximum water levels at Wusongkou, Huangpu Park, and Mishidu are 5.02 m, 4.75 m, and 4.15 m, respectively. Note, that the extreme water levels at Wusongkou and Huangpu Park are dominated by the combination of tides and storm surge, whereas extreme water levels at Mishidu reflect the combination of tides, storm surge, and precipitation-driven river discharge.

3.2. Statistical Methods

Probabilistic distribution functions can be used to characterise stochastic variables, such as water level and river discharges. Different regions and countries use different probability distributions to characterize hydrological phenomena. For instance, the log Pearson type III distribution is commonly used in the United States [16], the general extreme value (GEV) distribution is recommended by the United Kingdom [17], while the Pearson type III (P-III) distribution with a curve fitting method is widely applied in China [18]. Five probability distributions, which are most commonly used, were selected as potential probability distributions for the datasets, namely (1) generalized extreme value (GEV), (2) Pearson type III (P-III), (3) Gumbel Max, (4) Log-Pearson3 and (5) Weibull (with three parameters). In this study, the GEV and P-III were further analysed. First, the P-III distribution is recommended to be used for frequency distributions for hydrological stochastic variables in China, according to the ‘Chinese standards of design flood calculation in hydraulic engineering’ [19]. Second, the GEV distribution is generally used as an approximation to model the maxima of long sequences of random variables, such as the annual maximum water levels for the Huangpu River analysed in this study. More details about P-III and GEV distributions are shown in Appendix A.
Three approaches for estimating the best values of the parameters of P-III and GEV distributions are chosen, namely least-square estimation (LSE), maximum likelihood estimation (MLE), and the linear moments method (LMM). First, LSE assumes the best-fit curve of a given type; it is the curve that has the minimal sum of the deviations squared (least square error) from a given set of data. This method is one of the most frequently used parameter estimation methods in hydrology [20]. Second, MLE is an indispensable tool for many statistical modelling techniques and is a preferred method of parameter estimation in statistics, in particular in non-linear modelling with non-normal data [21]. MLE is a typical statistical principle for fitting a mathematical model to the observed data, which is famous for its sufficiency, consistency, efficiency, and parameterization invariance [21]. Last, for LMM, it contains linear combinations of probability weighted moments [22]. LMM is regarded as desirable because of its notable advantages e.g., fast, small biases, and easy to understand. LMM can often be used when MLE is unavailable or is difficult to compute. LMM sometimes yields more efficient parameter estimates than MLE [22]. The best method for parameter estimation will not be further discussed since the aim of this paper is to derive frequency curves for the Huangpu River rather than to compare these methods.
However, in order to specify the distribution for the datasets, three statistics performance indicators—Chi-square test (χ2), Kolmogorov-Smirnov (K-S) test, and mean square deviation (MSD), are employed to decide which parameter estimation method calculates best value of the parameters for probability distribution (see details in Appendix B). MSD has been employed as a performance indicator in wide applications [23,24]. More details of the selection of statistical performance indicators are referred to [25]. It should be noted that the Chi-square test is conducted in the probability density function (PDF) domain after the data is binned into categories, whereas the K-S test is conducted in the cumulative distribution function (CDF) domain, assigning empirical probabilities to each individual observation [26]. Binning the data takes away information, which would favor a K-S test. However, for a K-S test, the distribution should be fully specified. If the location, scale, and shape parameters of the distribution are estimated from the data, the critical region of the K-S test is no longer valid. Furthermore, the K-S test is more sensitive near the center of the distribution than at the tails, although correcting weight functions have been developed by Chicheportiche and Bouchaud [27] to account for the tails in a Weighted K-S test.

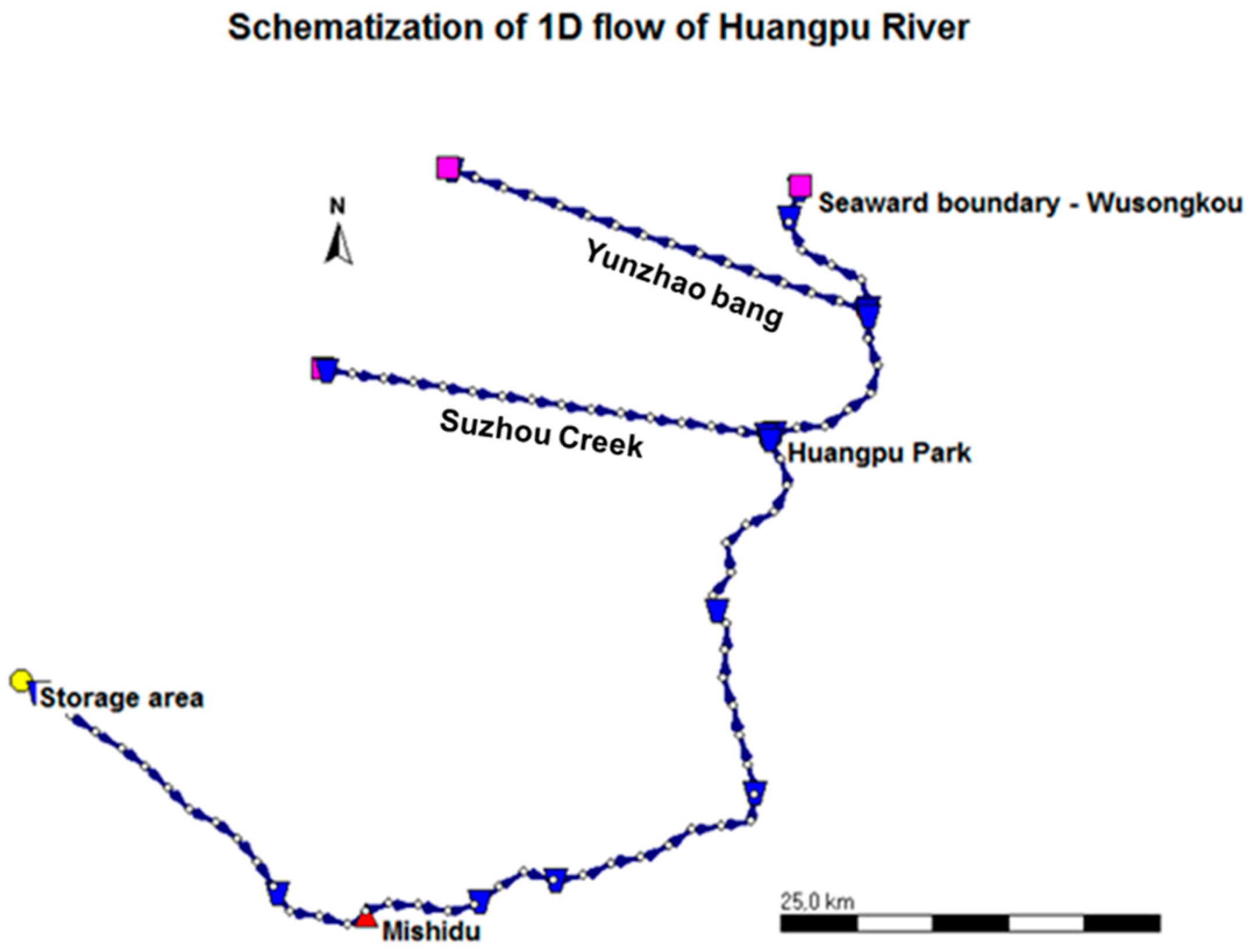
3.3. Hydraulic Model

SOBEK 1D-Flow [28] solves the continuity and St. Venant equations numerically using a finite difference method. Based on this, a Huangpu River 1D model was set up in order to simulate the water levels at different return periods in each cross section. The model schematization is presented in Figure 2. In reality, the water network is fairly complicated, with many creeks and small drainage canals. However, only the macro water management system is considered here. This consists of the Huangpu River and the branches of Suzhou Creek, Yunzhao Bang, and Dianshan Lake (as a storage area).
Model boundary conditions are defined at the inland and seaward extents of the model, which is shown as follows:
  • Seaward boundary (Wusongkou): time series of measured water levels, which represents the effects of storm surge and tide fluctuation.
  • Boundary at Suzhou creek and Yunzhao bang: they are narrow (average width 58.6 m) and shallow (average depth 3.4 m) rivers with an annual average discharge of 10–30 m3/s each [29]; the discharge is not significant and mainly depends on the downstream tide level. Hence, a constant discharge of 20 m3/s for each river is assumed.
  • Storage area: Dianshan Lake, with an area of 62 km2, is the biggest lake in Shanghai. In the SOBEK 1D model, the storage area was set as 1.5 times the area of Dianshan Lake, which represents the additional storage area of related creeks and canals in the inland reach of the Huangpu River. This boundary condition enables a realistic simulation of the tides and storm surge response in the upper reaches of the model domain, but does not account for precipitation-driven river discharge associated with a storm event. A sensitivity analysis (see Appendix C) shows that a 50% change of the size of the storage area does not largely affect water levels in the Huangpu River (only a few centimeters at most) at Wusongkou and Mishidu.
Cross sections of river channel were estimated to be trapezoidal. In the procedure of calibration and validation of the model, the simulated water levels computed by the 1D model were compared to measured water levels during different typhoon periods. The measured water levels in the year of 1997 were recorded hourly, while in 2012 and 2013 the measured water levels were recorded every 5 min. Two gauge stations were selected for the calibration and validation: Huangpu Park and Mishidu (see Figure 2). During calibration, the uniform Manning’s n value for the river channels was adjusted to minimize the root mean square error (RMSE) in water level at these two stations. The resulting Manning’s n was 0.05 s/m1/3. The calibration results during Typhoon Winnie on 15–22 August 1997 are shown in Figure 3a,b, with RMSE of 19 cm and 23 cm, at Huangpu Park and Mishidu, respectively. In Figure 3c,d, the water level results were calibrated during Typhoon Haikui on 3–10 August 2012, with RMSE of 17 cm and 28 cm at Huangpu Park and Mishidu, respectively. In Figure 3e,f, the water level results were validated during Typhoon Fitow on 27 September–9 October 2013, at Huangpu Park and Mishidu with RMSE of 22 cm and 38 cm, respectively. In general, the model appears to over-predict the water level response due to the tide and possibly the storm surge at Mishidu, although peak water levels at Mishidu were under-predicted in 2013, presumably due to the omission of precipitation-driven river discharge during this event.

4. Results

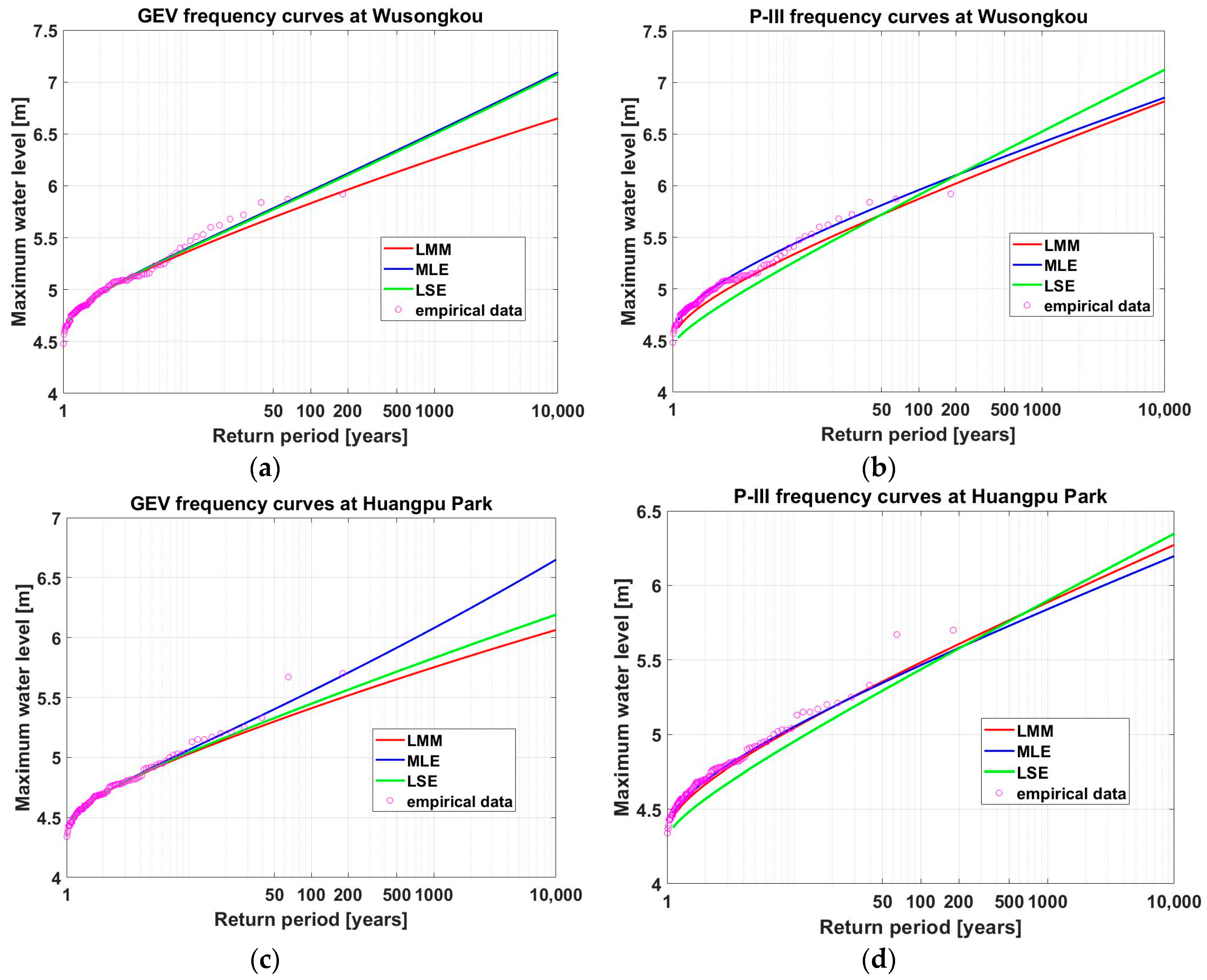
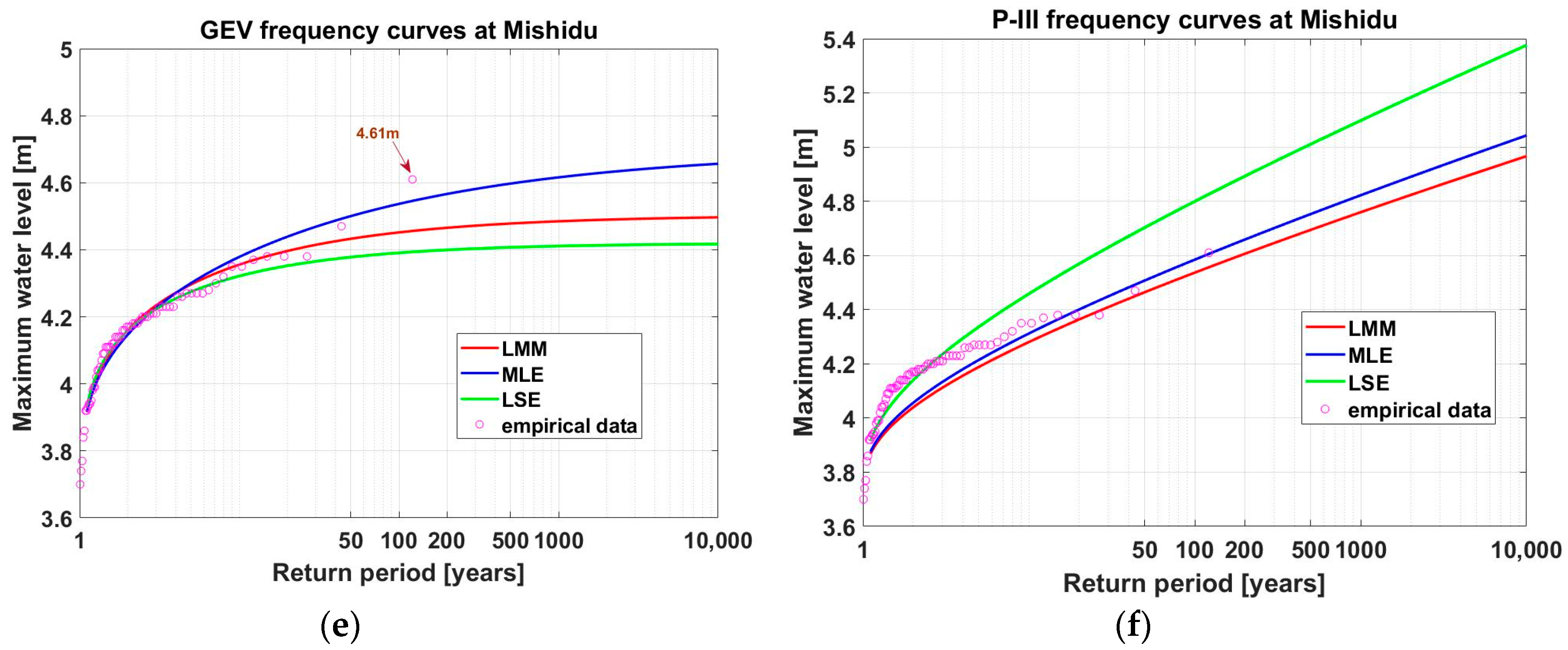
4.1. Comparison of Distributions

The smaller the values of Chi-Square test, K-S test and MSD are, the better the fit of the probability distributions is. Table 3 shows the overall results of the statistical performance indicators are more or less same. For the three locations along the Huangpu River, GEV provided the better fit since the values of statistical performance indicator for P-III are generally larger than the ones for GEV.
Overall, it appears that the values of the Chi-Square test and K-S test for GEV (at three stations by three estimation methods) were smaller than the critical values (see Appendix B and Table 3), which proved the goodness-of-fit for GEV distribution.
Moreover, for the P-III distribution, it was found that the values of Chi-Square test were generally larger; and the values of the K-S and MSD indicators for P-III were also larger than the values for GEV. According to the critical values of the K-S test, the values of K-S for P-III were rejected, except one result (0.0709) calculated by MLE at Huangpu Park (see Table 3).
In addition, the value of the MSD indicator for GEV was a factor of 100 smaller than for P-III. Based on these test statistics, GEV was recommended as the probability distribution for the Huangpu River. Besides, the values of statistical performance indicators at Wusongkou and Huangpu Park showed MLE resulted in best statistical performance, which represented as 6.45, 0.0527 and 0.345 for Chi-squared test, K-S test, and MSD at Wusongkou, respectively; and 1.36, 0.0506 and 0.0257 at Huangpu Park, respectively (see the highlighted grey in Table 3).
At Mishidu, LMM and LSE showed a better statistical performance since the values of Chi-Square test (5.12), K-S test (0.1106) and MSD (0.0304) for MLE were higher than the other two parameter estimation methods (LMM and LSE). However, at this station, the GEV results by LMM and LSE showed fairly flat curves at this location (see Figure 4e), which means that the water levels hardly increases for return periods larger than 100 years. For example, the water level for a 10,000-year return period would be no larger than WD 4.5 m, especially based on the parameters estimation methods of LMM and LSE. The maximum water level at Mishidu was observed at WD 4.61 m during Typhoon Fitow in October 2013 (see Figure 4e). This new record directly rejected the two results produced by LMM and LSE for GEV. Hence, in this case, only GEV result by MLE (which is highlighted in grey in Table 3) was suggested at Mishidu. The test statistics of fitting curves by LSE, MLE and LMM under GEV and P-III at Wusongkou, Huangpu Park and Mishidu are shown in Figure 4 and Figure 5.

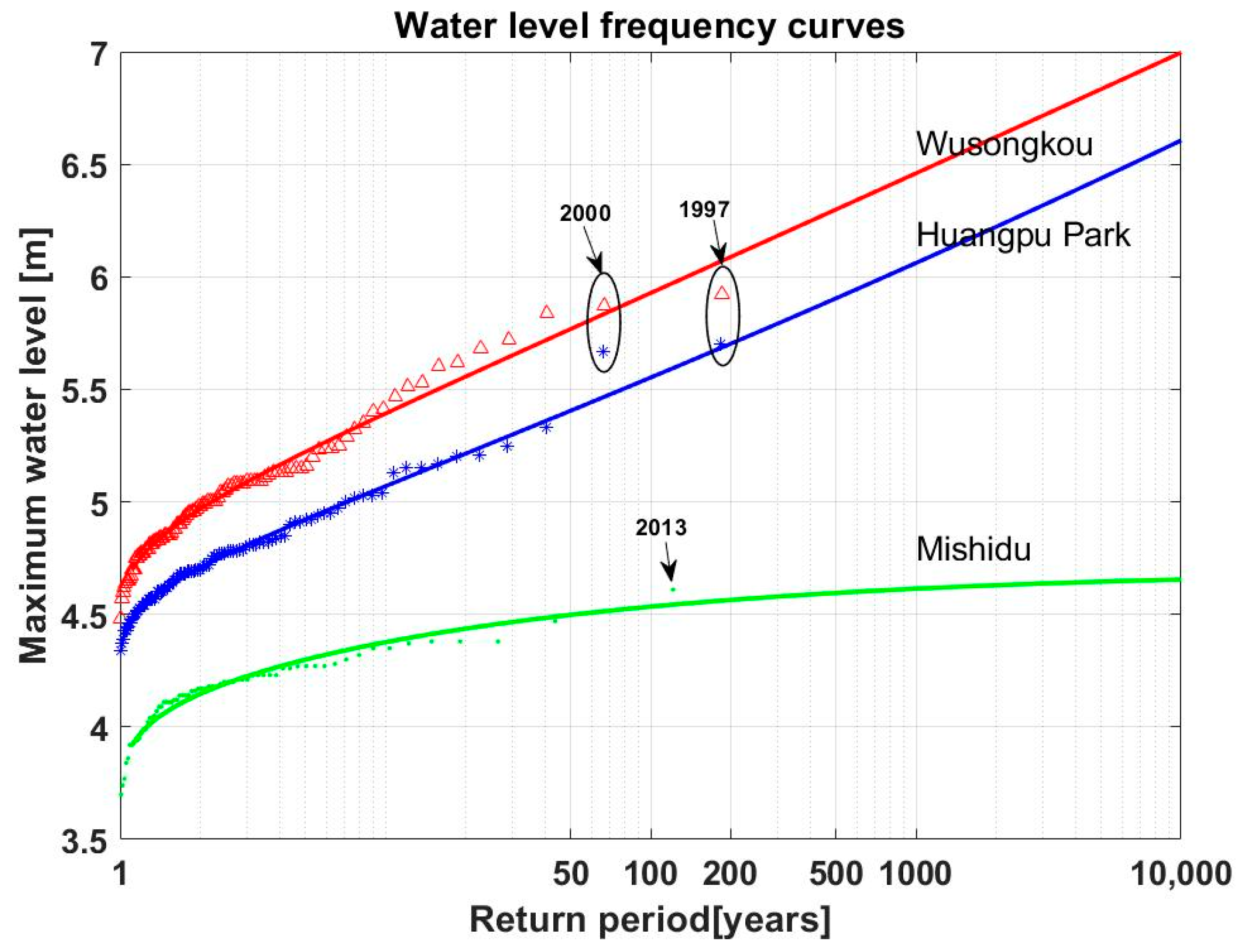
4.2. Water-Level Frequency Curves

In summary, the GEV distribution is the most suitable probability distribution for the datasets of annual maximum water levels at the three locations along the Huangpu River. Consequently, the selected frequency curves of water level as a function of return periods were derived (for Wusongkou, Huangpu Park and Mishidu), and are shown in Figure 5. Table 4 provides the water levels corresponding to the frequencies of 1/50, 1/100, 1/200, 1/500, 1/1000 and 1/10,000 at each hydrological station, with 95% confidence interval. The uncertainty bounds could provide indications for practical purposes further (e.g., design of crest height of the floodwall). The difference in water levels between return periods with intervals of a factor of 10 (e.g., 1000 years and 100 years) at Wusongkou and Huangpu Park were 55 cm and 53 cm, respectively, while only an 8 cm difference was observed at Mishidu. The relatively small difference at Mishidu was also reflected by the low gradient of frequency curve (also see in Figure 5).
Moreover, these results showed that the statistical water-level pattern is similar at Wusongkou (near sea) and at Huangpu Park (~26 km from the river mouth) as they are relatively close to the river mouth and greatly affected by typhoon surge. The identical pattern is also shown by the two ellipses in Figure 5, which indicate the highest water level and the second highest one occurred in 1997 and in 2000, respectively. The location of Mishidu is further away from the river mouth (~79.8 km) and thus less impacted by the surge propagation.

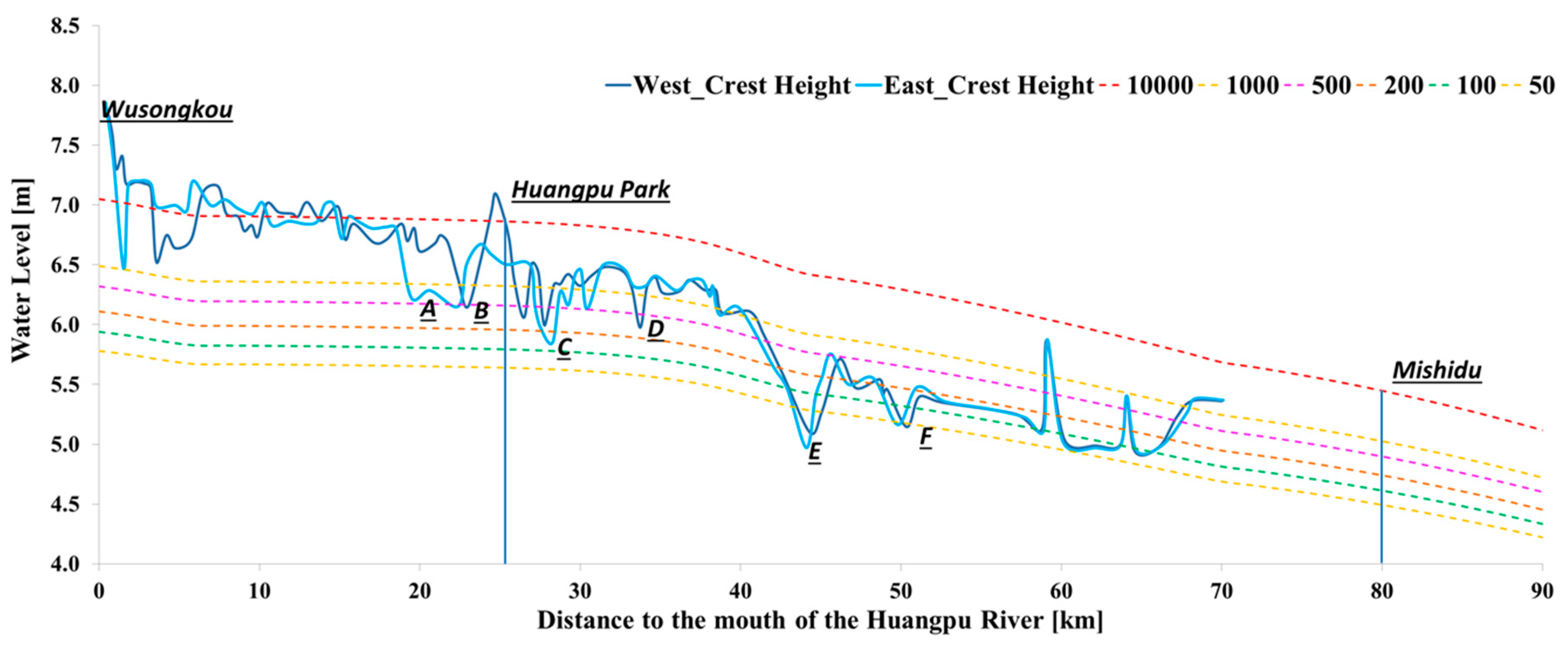
4.3. Protection Levels of Floodwall

High water levels during Typhoon Winnie in 1997 were employed as a typical hydrological process to represent a flood period in the Huangpu River, since the historical highest water levels at Wusongkou (5.99 m) and at Huangpu Park (5.72 m) both occurred in August 1997 due to the coincidence of a high astronomical tide and a storm surge. The near-sea boundary water levels were up-scaled and down-scaled based on a factor of the calculated water levels as a function of return period (see Table 4) to the highest water level in 1997. Therefore, typhoon-induced water levels were modelled for various cross-sections for higher (200, 500, 1000 and 10,000 year) and lower return periods (50 and 100 years). Finally, a series of water levels as a function of return period were derived by the SOBEK 1D flow model along the Huangpu River.
This information was compared with data on crest heights of the floodwalls on both sides of the Huangpu River—data from [10]. In comparing water levels with floodwall heights, effects of wave run-up have not been included, as fetch lengths are limited. The information of crest height was obtained in 2008 and may therefore not be fully accurate for the current system. The results are included in Figure 6, which shows the return periods of water levels and floodwall elevations. As seen from Figure 6, the crest heights of the floodwalls on the east side of the river (light blue curve) are lower than those on the west side (dark blue curve), since economic exposure in the downtown area of Shanghai (west side) is higher than in the newly developing area on the east side of the Huangpu River. It is thus observed that, according to this study, the current protection level of the floodwalls is expected to be less than the safety standard of 1/1000 per year. Lower floodwall sections are indicated by letters (A to F). The figure shows that two lowest sections of the current floodwall (point E at ~45 km from the mouth of the river; point F at ~50 km from the mouth of the river) have protection levels less than 1/50 per year. The floodwall in the seaward reaches of Huangpu River maintains the required safety standards of 1/1000 per year between Wusongkou and Huangpu Park, except section A-B; the safety standard between Huangpu Park and Mishidu is no more than 1/50 per year, see point E and F in Figure 6. Note that the model validation (Figure 3e,f) indicated that the neglect of rainfall in the model caused an underestimation of water levels in the inland reach of the river near Mishidu, so the 1/50 per year protection level assessed here might in actuality be even weaker in light of a combined rainfall and storm surge flood analysis. Besides, other potential overtopping points were identified for return periods of 200 years (C) and 500 years (D). Finally, it is expected that the floodwall will be overtopped almost completely under a storm surge return period of 10,000 years.
The results can be used for an analysis of the probability of failure due to overtopping of the floodwalls. In addition to this failure mechanism, the occurrence of geotechnical and structural failure of the floodwalls has to also be considered, as well as the failure or non-closure of several movable gates in the system. Finally, the statistics on hydraulic conditions could be combined with probabilistic information on the strength of the floodwalls to perform a complete reliability analysis, see e.g., [30]. To come to a flood risk analysis, not only the probability of failure but also the consequences have to be considered [31]. That would imply that also flood simulations—resulting in flood maps—and impact assessments for economic damage and loss of life would have to be included. These results can be used to quantify flood risk and inform decision making on (prioritization of) flood management interventions.

5. Discussion

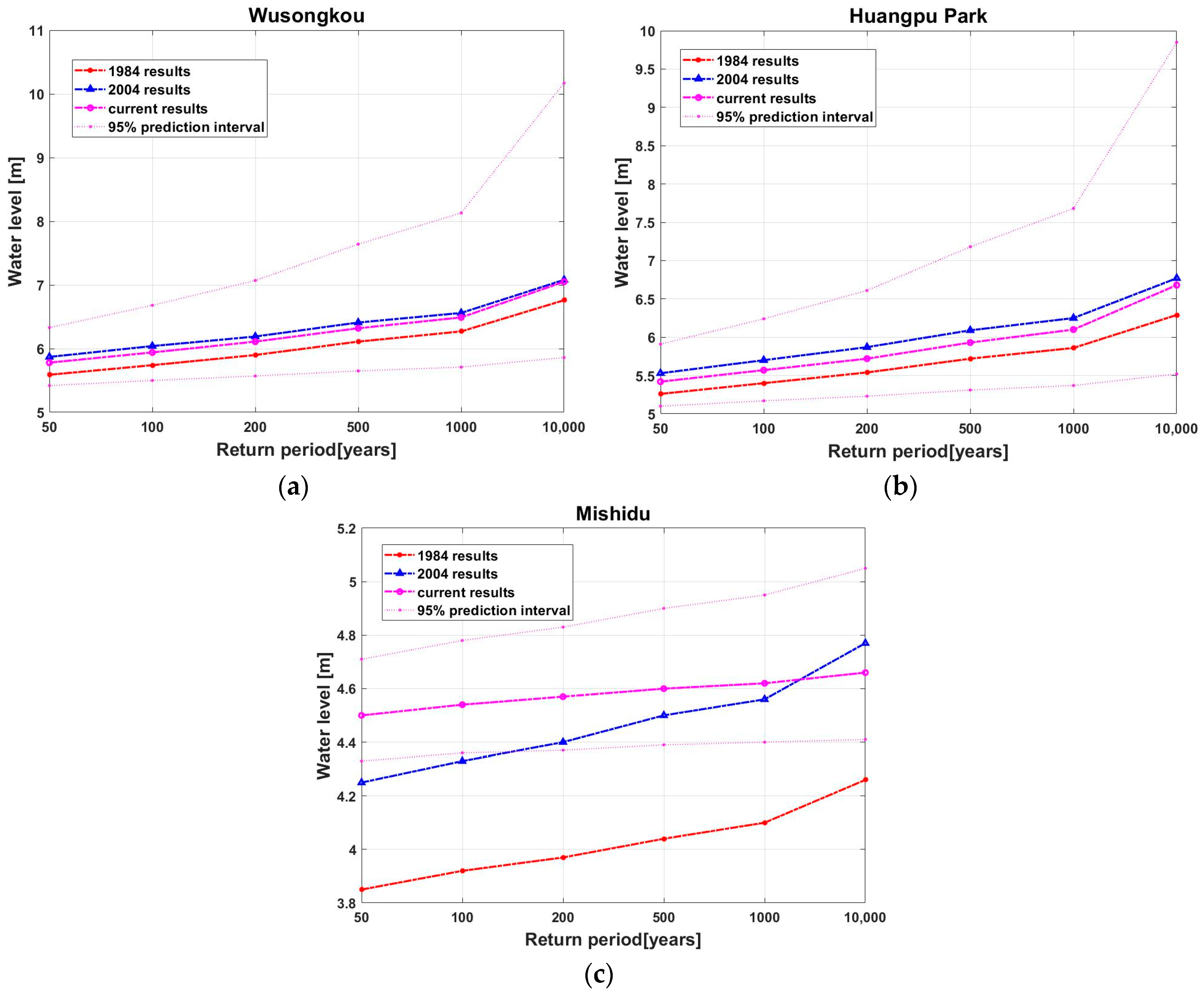
5.1. Comparison of the Historical Frequency Curves

From the results, it can be seen that the water levels at Huangpu Park are significantly influenced by storm surge as it has a similar shape to the frequency curve at Wusongkou in Figure 5. The frequency curve at Huangpu Park is lower than the one at Wusongkou, since the full effect of the storm surge cannot propagate to Huangpu Park. The frequency curve at Mishidu has a lower gradient than the other two. There is less influence of the storm surge because the location of Mishidu is around 80 km away from the mouth of the river.
A comparison with previous studies in 1984 and in 2004 is shown in Figure 7. The current study produced higher water levels at Wusongkou and Huangpu Park (on average ~24 cm higher) under different return periods than the study in 1984, while lower results (on average ~15 cm lower) were found compared to the study in 2004. Although, at Wusongkou and Huangpu Park (Figure 7a,b), the results from 1984 and 2004 fall well within the prediction interval of the current analysis.
As seen from Figure 7c, the current results at Mishidu are ~56 cm and ~16 cm higher than the 1984 and 2004 results, respectively, except that the water level for a 10,000-year return period in the current study was lower than the result of the 2004 study. Moreover, the 1984 results are well outside of the 95% prediction intervals of the current analysis (see Figure 7c), which suggests a quantitative difference. The main reason for this difference can be attributed to, firstly, the difference in the original datasets. The current study employed the most updated data (until 2013) for annual maxima of water levels at each station. This also includes the latest highest event at Mishidu (in 2013), leading to an increase in water levels for this location. For the other two locations (Huangpu Park and Wusongkou) the annual maximum water levels for the additional data considered in this study (2002–2013) are somewhat lower than the observations before 2002. Secondly, P-III was widely adopted as the probability distribution in China, also presented in the previous studies for the Huangpu River [14]. In this study, the GEV distribution was found to be the most appropriate for the extrapolation of water levels for the Huangpu River. Thirdly, the original data in the report of 1984 did not reflect the current anthropogenic changes in the system, which causes the modern water level to be higher than the historical ones [14], apparently leading to the lower results than the other two studies.

5.2. Water Level at Each Cross Section along the Huangpu River

The water levels at Huangpu Park and Mishidu as a function of return period in Figure 6 do not exactly correspond to the statistical results in Table 4, which were calculated based on a series of historical maximum water levels. The water levels for the landward locations, such as Mishidu, were ‘over-estimated’ with 16.9%, 8.8%, 6.5%, 3.7%, 1.6% and 0% at the return periods of 10,000 years, 1000 years, 500 years, 200 years, 100 years, and 50 years, respectively, compares to the statistical results. This is because the extreme events used for calibrating and validating the hydraulic model fit better by the P-III analysis of Figure 4f at Mishidu (more extreme data fits in P-III than in GEV), although the GEV was chosen because it has the best statistical fit to most of the data (except an extreme value in 2013). Comparing the hydraulic model’s water levels in Figure 6 at Mishidu with the fitted measured water level frequency curve of Figure 6f (MLE fitting curve), the agreement is relatively better (with 7.9%, 4.7%, 3.1%, 1.5%, 0.5%, −0.6% discrepancy at the return periods of 10,000 years, 1000 years, 500 years, 200 years, 100 years, and 50 years, respectively). These model over-predictions occur despite the omission of precipitation-drive river discharge, which is expected to be most important for extreme events.
Therefore, at Mishidu, it is necessary to study further the influence of the high water levels from torrential rainfall and high runoff from the inland area, since the results shows that Mishidu has different patterns than the other stations, which are apparently dominated by storm tide. It is thus recommended to conduct further validation of both GEV and P-III distribution by means of further data collection. Hence, the results in this paper are regarded as preliminary but indicative results for flood frequency analysis.

6. Conclusions and Recommendations

This paper analysed over 100 years (1912–2013) of annual maximum water levels for hydrological stations at Wusongkou, Huangpu Park, and Mishidu along the Huangpu River in Shanghai. It has derived a series of new water level frequency curves for the Huangpu River and evaluated the level of protection level of floodwalls.
  • The flood frequency analysis showed that the GEV distribution provides the best characterization of flood frequencies for datasets at three hydrological locations of the Huangpu River.
  • The derived water level frequency curves at Wusongkou and Huangpu Park were in line with the previous results of the 2004, but significantly higher than the results of a study from 1984—which still forms the basis for the design of floodwalls. A comparison of flood frequencies due to combined tides and storm surge with a floodwall elevation dataset shows that the weakest sections are expected to have a flood frequency higher than 1/50 per year, which is far higher than the safety standard of 1/1000 per year. Several other locations are also expected to have overflow/overtopping frequencies higher than the safety standard.
  • In addition, it is also found that the current design water levels correspond to the exceedance probabilities of 1/500 per year in the near-sea and middle reaches, and no more than 1/50 per year in the inland area of the Huangpu River. Since this study neglects rainfall, the actual protection offered by floodwalls in the inland area of the river might be even weaker than the values determined here.
Based on the limitations of this study, a number of recommendations are provided for further study and work. Firstly, in this study, only annual maximum water levels in the Huangpu River were considered for the flood frequency analysis. River discharge and precipitation during the typhoon season should be used as additional information in the hydraulic model for future analysis. Especially, information on the rating curve of Mishidu could provide additional insights that help to explain why the water-level frequency curve at this location is more flat than for the other two stations. In this context, it is also important to take into account the hydrological interactions between Tai Lake and from the branches of the Huangpu River. Secondly, since the assumption of deterministic correspondence among water levels in the three stations provides limited indication for practitioners, a study of the multivariate analysis about water levels and discharge among three stations is recommended further. Thirdly, the dataset only included information on floodwall crest heights from 2008. It is recommended to update this information, and to add more data on the geometry of the floodwall and soil characteristics. Lastly, it is recommended to perform a more complete reliability analysis for the floodwall system (taking into account various failure modes) and a more complete flood risk analysis for the city of Shanghai, such as coastal flood risk analysis. This will provide a basis for effective decision-making on future flood risk management in this rapidly growing mega-city.

Author Contributions

S.N.J. and P.H.A.J.M.V.G. initiated and designed the study. Q.K. conducted the statistical analysis and hydraulic modelling. Q.K., S.N.J., P.H.A.J.M.V.G. and J.D.B. analyzed and interpreted the hydraulic model results. Q.K. wrote the paper with substantial input from all co-authors.

Funding

This research was funded by Nederlandse Organisatie voor Wetenschappelijk Onderzoek grant number ALWSD.2016.007.

Acknowledgments

We are grateful for the floodwall information provided by IWHR and for language improvement by Claire Taylor. We thank two anonymous reviewers and the editor for their valuable comments and suggestions to improving the quality of the paper.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.

Appendix A. Probability Distribution Functions

The P-III distribution is called a three-parameter gamma distribution, since it can be obtained from the two-parameter gamma distribution by introducing the location parameter a o . The probability density function of the P-III distribution of random variable x is shown below:
f ( x | μ , α , β ) = α β ( x − μ ) β − 1 e − α ( x − μ ) Γ ( α )
where μ is the location parameter, α is the scale parameter, β is the shape parameter.
The generalized extreme value distribution combines three distributions into a single form, allowing a continuous range of possible shapes that includes all three of the underlying distributions. Types I (k = 0), II (k > 0), and III (k < 0) are sometimes also referred to as the Gumbel, Frechet, and Weibull distributions, although this terminology is not consistently used. For the GEV distribution, the probability density function is formulated as follows:
f ( x | k , μ , σ ) = ( 1 σ ) e x p [ − ( 1 + k ( x − μ ) σ ) 1 k ] ( 1 + k ( x − μ ) σ ) − 1 − 1 k f o r   ( 1 + k ( x − μ ) σ ) > 0
where k is the shape parameter, μ is the location parameter and σ is the scale parameter.

Appendix B. Statistical Performance Indicators

Appendix B.1. Chi-Square Test

The Chi-Square test [32] is used to test if a sample of data came from a population with a specific distribution. An attractive feature of the chi-square test is that it can be applied to any univariate distribution for which cumulative distribution function can be calculated.
If the computed test statistic is large, then the observed and expected values are not close and the model is a poor fit to the data. The model of chi-square test is shown as below:
χ 2 = ∑ ( x i − y i ) 2 y i
where χ2—Chi-Square test statistic; xi is the observed frequency for bin i and y i is the expected frequency for bin i .
The critical value of the Chi-Square test is calculated under the significance level and the degrees of freedom, which depend on the number of bins and the number of the estimated parameters for the distribution. In this paper, the critical values, under the significance level of 0.05, are produced as 7.8 m for Wusongkou and Huangpu Park stations, and 5.99 m for Mishidu station. If the test statistic is greater than the critical value, the distribution is rejected.

Appendix B.2. K-S Test

The K-S test performs a Kolmogorov-Smirnov test to compare the expected frequency to theoretic frequency.
D = s u p | P ( x ) − S ( x ) |
where D —K-S test statistic; P( x ) is the empirical cumulative frequency and S( x ) is the prediction cumulative frequency. Dagnelie [33] indicated that the critical value can be approximated numerically. The critical value C = ( N , α ) can be obtained as a function of level of significance α and the sample size N with an expression of the form:
C ( N , α ) = a ( α ) N + 1.5
where C ( N , α ) is the critical value of the K-S test; a ( α ) is a function of   α ; for the usual alpha levels of a ( 0.05 ) = 0.886 [34].
The hypothesis regarding the type of probabilistic distribution will be rejected if the test statistic is greater than the critical value. The critical values of the K-S test at Wusongkou, Huangpu Park, and Mishidu are calculated as 0.0873, 0.0877 and 0.108, respectively.

Appendix B.3. MSD (Mean-Square Deviation)

The mean-square deviation (MSD) of an estimator is a way to quantify the difference between values implied by the density estimator and the empirical estimates. The MSD of an estimator with respect to the estimated parameter is usually defined as:
MSD = E [ ( x i − x i ^ ) 2 ] = ∑ i = 1 N ( ( x i − x i ^ ) 2 ) N − 1
where x i is the theoretical frequency for the observation, x i ^ is the corresponding empirical frequency, N is the sample size.

Appendix C. Sensitivity Analysis of the Storage Area in the 1D Model

In order to examine to what extent the size of the storage area could affect the water levels in the Huangpu River in the 1D Flow model, three sizes of storage area (the size of Dianshan Lake—62 km2, 1.5 time larger size of Dianshan lake—91 km2 and double size of the Dianshan Lake—124 km2) were modelled in the 1D Flow SOBEK, while keeping other variables same as the input. Two stations, Huangpu Park and Mishidu, were selected to represent the water levels 1997, 2012, and 2013. The sensitivity value was defined as the RMSE of the modelled water levels results at stations. Table A1 shows the size of the storage area (with 50% changes) has no more than 1 cm effect at Huangpu Park and only a few centimeters effect at Mishidu.
Table
Table A1. Results of sensitivity analysis of the size of the storage area in 1D Flow model.
Table A1. Results of sensitivity analysis of the size of the storage area in 1D Flow model.
YearStationStorage AreaStorage Area
62 km291 km291 km2124 km2
RMSE [cm]RMSE [cm]
1997Huangpu Park0.40.28
Mishidu3.21.9
2012Huangpu Park0.70.4
Mishidu2.71.5
2013Huangpu Park0.40.3
Mishidu3.22.4

References

  1. Small, C.; Nicholls, R.J. A global analysis of human settlement in coastal zones. J. Coast. Res. 2003, 19, 584–599. [Google Scholar]
  2. Nicholls, R.J.; Hanson, S.; Herweijer, C.; Patmore, N.; Hallegatte, S.; Corfee-Morlot, J.; Chateau, J. Muir-Wood, Ranking of the World’s Cities Most Exposed to Coastal Flooding Today and in the Future—Executive Summary; OECD Project; OECD Publishing: Paris, France, 2007. [Google Scholar]
  3. Nicholls, R.J.; Hanson, S.; Herweijer, C.; Patmore, N.; Hallegatte, S.; Corfee-Morlot, J.; Chateau, J.; Muir-Wood, R.; Classification, J. Ranking Port Cities with High Exposure and Vulnerability to Climate Extremes: Exposure Estimates; OECD Environment Working Papers No.1; OECD Publishing: Paris, France, 2007. [Google Scholar]
  4. Hallegate, S.; Green, C.; Nicholls, R.J.; Corfee-Morlot, J. Future flood losses in major coastal cities. Nat. Clim. Chang. 2013, 3, 802–806. [Google Scholar] [CrossRef]
  5. Gong, S. Impact of land subsidence on urban flood defence of Shanghai city. Yangtze River 2008, 39, 1–4. (In Chinese) [Google Scholar]
  6. Shen, H.; Wei, Z.; Wu, J.; Cheng, W.; Zou, D. Subsidence features of Huangpu River floodwall and the analysis on its effects on flood control ability. Shanghai Geol. 2005, 4, 21–24. (In Chinese) [Google Scholar]
  7. Jia, R.H. Water level frequency analysis for the main hydrological stations in the Huangpu River. Shanghai Hydraul. Eng. 1984, 1, 1–10. (In Chinese) [Google Scholar]
  8. Hohai University. Tide Analysis for the Huangpu River; Hohai University: Nanjing, China, 2004. (In Chinese) [Google Scholar]
  9. Xu, S.; Huang, W. Estimating extreme water levels with long-term data by GEV distribution at Wusong station near Shanghai city in Yangtze Estuary. Ocean Eng. 2011, 38, 468–478. [Google Scholar] [CrossRef]
  10. SWA—Shanghai Water Authority. Public Report of Water Resources Information for Shanghai. 2013. Available online: http://222.66.79.122/BMXX/default.htm?GroupName=%CB%AE%D7%CA%D4%B4%B9%AB%B1%A8 (accessed on 3 February 2014). (In Chinese).
  11. Li, N.; Wang, J.; Wang, Y.Y. Flood Risk Mapping of Pudong Distrcit in Shanghai City; China Institute of Water Resources and Hydropower Research: Beijing, China, 2011. (In Chinese) [Google Scholar]
  12. Li, R. Floodwall Breach along the Huangpu River in Shanghai Suburb. 2013. Available online: http://news.xinhuanet.com/local/2013-10/08/c_117625658.htm (accessed on 9 October 2013). (In Chinese).
  13. Liu, X.L. Shanghai Laishi Lost 60 Million RMB during Typhoon Fitow. 2013. Available online: http://stock.sohu.com/20131011/n387995427.shtml (accessed on 11 October 2013). (In Chinese).
  14. NetEase. Fitow Led to 60 Million RMB Loss for Agriculture in Shanghai. 2013. Available online: http://news.163.com/13/1021/04/9BMBP3JB00014AEE.html (accessed on 21 October 2013). (In Chinese).
  15. Hohai University. Shanghai City Huangpu River Final Report on Flood Protection and Water Level Analysis, Huangpu River Storm Surge Barrier Study Volume 1; Hohai University: Nanjing, China, 2001. (In Chinese) [Google Scholar]
  16. NERC—Natural Environment Research Council. Flood Studies Reports; Natural Environmental Research Council: London, UK, 1975. [Google Scholar]
  17. WRC—Water Resources Council. Guidelines for Determining Floods Flow Frequency; Bulletin 17B of the Hydrology Subcommittee; Water Resources Council: Washington, DC, USA, 1981.
  18. MWR—Ministry of Water Resources. Standard Methods for Flood Quantile Estimation Procedure; SDJ 22-79; Water Resources Publishing House: Beijing, China, 1980. (In Chinese) [Google Scholar]
  19. MWR—Ministry of Water Resources. Regulation for Hydrological Computation of Water Resources and Hydropower Project; SL278-2002; The Ministry of Water Resources of the People’s Republic of China: Beijing, China, 2002. (In Chinese)
  20. Singh, V.P. Methods of Parameter Estimation. In Entropy-Based Parameter Estimation in Hydrology; Water Science and Technology Library; Springer: Dordrecht, The Netherlands, 1998; Volume 30, pp. 12–44. [Google Scholar]
  21. Myung, J. Tutorial on maximum likelihood estimation. J. Math. Psychol. 2003, 47, 90–100. [Google Scholar] [CrossRef]
  22. Hosking, J.R.M. L-moments: Analysis and Estimation of Distribution using Linear Combinations of Order Statistics. J. R. Stat. Soc. Ser. 1990, 52, 105–124. [Google Scholar]
  23. Di Salvo, F.; Ruggieri, M.; Plaia, A.; Agro, G. EOFs for gap filling in multivariate air quality data: A FDA approach. In Proceedings of the 19th International Conference on Computational Statistics, Paris, France, 22–27 August 2010. [Google Scholar]
  24. Yang, H.; Wu, Z.; Liu, S.; Sun, H. Research on Optimal Sensor Placement Based on Reverberation Matrix for Structural Health Monitoring. Int. J. Distrib. Sens. Netw. 2012, 8, 1–7. [Google Scholar] [CrossRef]
  25. Van Gelder, P.H.A.J.M. Statistical Methods for the Risk-Based Design of Civil Structures. Ph.D. Thesis, Dept of Hydraulic Engineering, TU Delft, Delft, The Netherlands, 2000. [Google Scholar]
  26. Gailmard, S. Statistical Modeling and Inference for Social Science; Cambridge University Press: Cambridge, UK, 2014; ISBN 978-1-107-00314-9. [Google Scholar]
  27. Chicheportiche, R.; Bouchaud, J.-P. Weighted Kolmogorov-Smirnov test: Accounting for the tails. Phys. Rev. 2012, 86, 1115. [Google Scholar] [CrossRef] [PubMed]
  28. Deltares, SOBEK—User Manual. Hydrodynamics, Rainfall Runoff and Real Time Control; Deltares: Delft, The Netherlands, 2015. [Google Scholar]
  29. Cui, Y.; Wu, Y.; Shao, L.; Zhang, G. Seasonal variations of organic matter and nutrients in Suzhou river and Huangpu River and its environmental effect. Environ. Chem. 2011, 30, 645–651. (In Chinese) [Google Scholar]
  30. Jongejan, R.B.; Maaskant, B. Quantifying flood risks in The Netherlands. Risk Anal. 2015, 35, 252–264. [Google Scholar] [CrossRef] [PubMed]
  31. Jonkman, S.N.; Vrijling, J.K.; Kok, M. Flood risk assessment in The Netherlands: A case study for dike ring South Holland. Risk Anal. 2008, 28, 1357–1373. [Google Scholar] [CrossRef] [PubMed]
  32. Snedecor, G.W.; Cochran, W.G. Statistical Methods, 8th ed.; Iowa State University Press: Ames, IA, USA, 1989. [Google Scholar]
  33. Dagnelie, P. A propos de l’emploi du test de Kolmgorov-Smirnov comme test de de normalite. Biom. Praxim. 1968, 1, 3–13. [Google Scholar]
  34. Molin, P.; Abdi, H. New Table and Numerical Approximations for Kolmogorov-Smirnov/Lilliefors/van Soest Normality Test; Technical Report; University of Texas at Dallas: Dallas, TX, USA, 1998. [Google Scholar]
Jmse 06 00070 g001 550
Figure 1. Water system of Shanghai.
Figure 1. Water system of Shanghai.
Jmse 06 00070 g001
Jmse 06 00070 g002 550
Figure 2. Schematization of 1D Flow of macro water system of Huangpu River.
Figure 2. Schematization of 1D Flow of macro water system of Huangpu River.
Jmse 06 00070 g002
Jmse 06 00070 g003 550
Figure 3. Calibration results of water levels at Huangpu Park and Mishidu, (a,b) in 1997 and (c,d) in 2012; validation results of water levels at Huangpu Park (e) and Mishidu (f) in 2013. In each plot, red line is model result, and blue dots are gauge measurements.
Figure 3. Calibration results of water levels at Huangpu Park and Mishidu, (a,b) in 1997 and (c,d) in 2012; validation results of water levels at Huangpu Park (e) and Mishidu (f) in 2013. In each plot, red line is model result, and blue dots are gauge measurements.
Jmse 06 00070 g003
Jmse 06 00070 g004a 550Jmse 06 00070 g004b 550
Figure 4. Best-fit curves for three parameter estimation methods (LMM, MLE and LSE) for the three locations, for the GEV and P-III distributions. (a) best-fits curves for GEV at Wusongkou; (b) best-fits curves for P-III at Wusongkou; (c) best-fits curves for GEV at Huangpu Park; (d) best-fits curves for P-III at Huangpu Park; (e) best-fits curves for GEV at Mishidu; (f) best-fits curves for P-III at Mishidu.
Figure 4. Best-fit curves for three parameter estimation methods (LMM, MLE and LSE) for the three locations, for the GEV and P-III distributions. (a) best-fits curves for GEV at Wusongkou; (b) best-fits curves for P-III at Wusongkou; (c) best-fits curves for GEV at Huangpu Park; (d) best-fits curves for P-III at Huangpu Park; (e) best-fits curves for GEV at Mishidu; (f) best-fits curves for P-III at Mishidu.
Jmse 06 00070 g004aJmse 06 00070 g004b
Jmse 06 00070 g005 550
Figure 5. Water level-frequency curves for three hydrological stations: Wusongkou, Huangpu Park and Mishidu, along the Huangpu River (the highest and second highest records and the recorded year at Wusongkou and Huangpu Park are shown by means of ellipse).
Figure 5. Water level-frequency curves for three hydrological stations: Wusongkou, Huangpu Park and Mishidu, along the Huangpu River (the highest and second highest records and the recorded year at Wusongkou and Huangpu Park are shown by means of ellipse).
Jmse 06 00070 g005
Jmse 06 00070 g006 550
Figure 6. A comparison of crest height of the floodwall with the water level for various return periods for the Huangpu River in Shanghai.
Figure 6. A comparison of crest height of the floodwall with the water level for various return periods for the Huangpu River in Shanghai.
Jmse 06 00070 g006
Jmse 06 00070 g007 550
Figure 7. Comparison of water levels in the current research as a function of return periods at Wusongkou (a), Huangpu Park (b) and Mishidu (c), to the previous studies [7,8] (with 95% prediction interval).
Figure 7. Comparison of water levels in the current research as a function of return periods at Wusongkou (a), Huangpu Park (b) and Mishidu (c), to the previous studies [7,8] (with 95% prediction interval).
Jmse 06 00070 g007
Table
Table 1. Crest height, design water level, warning water level, and historical records at hydrological stations (Wusongkou, Huangpu Park and Mishidu) for Huangpu River.
Table 1. Crest height, design water level, warning water level, and historical records at hydrological stations (Wusongkou, Huangpu Park and Mishidu) for Huangpu River.
Water Level/Crest HeightHydrological Station
WusongkouHuangpu ParkMishidu
Current height of flood wall [m]7.36.94.7
Design water level [m]6.275.864.1
Highest water level ever-recorded [m]5.995.724.61
Warning level [m]4.84.553.5
Table
Table 2. Description of datasets for flood frequency analysis in the Huangpu River.
Table 2. Description of datasets for flood frequency analysis in the Huangpu River.
Hydrological StationObservation Periods [Year]Length [Years]Distance to the Mouth of the River [km]
Wusongkou (1)1912–2013102 0
Huangpu Park (2)1913–2013101 25.6
Mishidu (3)1948–201366 79.8
Table
Table 3. Results of the statistical performance indicator (Chi-Square test, K-S test and MSD) with three parameter estimation methods (LMM, MLE, LSE) for GEV and P-III distributions at the locations of Wusongkou, Huangpu Park and Mishidu (the selected results are highlighted in grey).
Table 3. Results of the statistical performance indicator (Chi-Square test, K-S test and MSD) with three parameter estimation methods (LMM, MLE, LSE) for GEV and P-III distributions at the locations of Wusongkou, Huangpu Park and Mishidu (the selected results are highlighted in grey).
Probability DistributionGEVP-IIICritical Value
StationsMethodsχ2K-SMSDχ2K-SMSDChi-Square TestK-S Test
WusongkouLMM7.660.05530.043816.740.154.50737.8
MLE6.450.05270.03457.280.0924.41580.0873
LSE6.430.04930.035459.080.344.6079
Huangpu ParkLMM1.590.05250.04544.40.11204.33457.8
MLE1.360.05060.02571.690.07094.31560.0877
LSE1.540.05020.038734.870.28164.4223
MishiduLMM3.360.080.027634.130.35673.73255.99
MLE5.120.11060.030425.200.31473.71410.108
LSE1.810.07050.035614.330.13663.6246
Table
Table 4. Results of the parameter estimation for GEV and water levels as a function of return periods at three hydrological stations, with 95% confidence interval.
Table 4. Results of the parameter estimation for GEV and water levels as a function of return periods at three hydrological stations, with 95% confidence interval.
Water level [m]Hydrological StationNo.Parameters in GEVReturn Period [Years]
kσμ50100200500100010,000
WusongkouLower bound−0.13270.19304.83405.425.505.575.655.715.86
Mean0.00830.22604.88335.785.946.116.326.497.05
Upper bound0.14930.26464.93256.336.687.077.648.1310.17
Huangpu ParkLower bound−0.10620.15794.59465.105.175.235.315.375.52
Mean0.03740.18564.63545.425.575.725.936.106.68
Upper bound0.18100.21814.67615.916.246.617.187.689.85
MishiduLower bound−0.38850.14954.03844.334.364.374.394.404.41
Mean−0.28910.17784.08454.504.544.574.604.624.66
Upper bound−0.18960.21164.13074.714.784.834.94.955.05
k—shape parameter; σ—scale parameter; μ—location parameter.

Share and Cite

MDPI and ACS Style

Ke, Q.; Jonkman, S.N.; Van Gelder, P.H.A.J.M.; Bricker, J.D. Frequency Analysis of Storm-Surge-Induced Flooding for the Huangpu River in Shanghai, China. J. Mar. Sci. Eng. 2018, 6, 70. https://doi.org/10.3390/jmse6020070

AMA Style

Ke Q, Jonkman SN, Van Gelder PHAJM, Bricker JD. Frequency Analysis of Storm-Surge-Induced Flooding for the Huangpu River in Shanghai, China. Journal of Marine Science and Engineering. 2018; 6(2):70. https://doi.org/10.3390/jmse6020070

Chicago/Turabian Style

Ke, Qian, Sebastiaan N. Jonkman, Pieter H. A. J. M. Van Gelder, and Jeremy D. Bricker. 2018. "Frequency Analysis of Storm-Surge-Induced Flooding for the Huangpu River in Shanghai, China" Journal of Marine Science and Engineering 6, no. 2: 70. https://doi.org/10.3390/jmse6020070

APA Style

Ke, Q., Jonkman, S. N., Van Gelder, P. H. A. J. M., & Bricker, J. D. (2018). Frequency Analysis of Storm-Surge-Induced Flooding for the Huangpu River in Shanghai, China. Journal of Marine Science and Engineering, 6(2), 70. https://doi.org/10.3390/jmse6020070

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop