Regime Changes in Global Sea Surface Salinity Trend
Abstract
1. Introduction
2. Data and Methods
2.1. Long-Term Global Salinity Data
2.2. SMOS Satellite Data
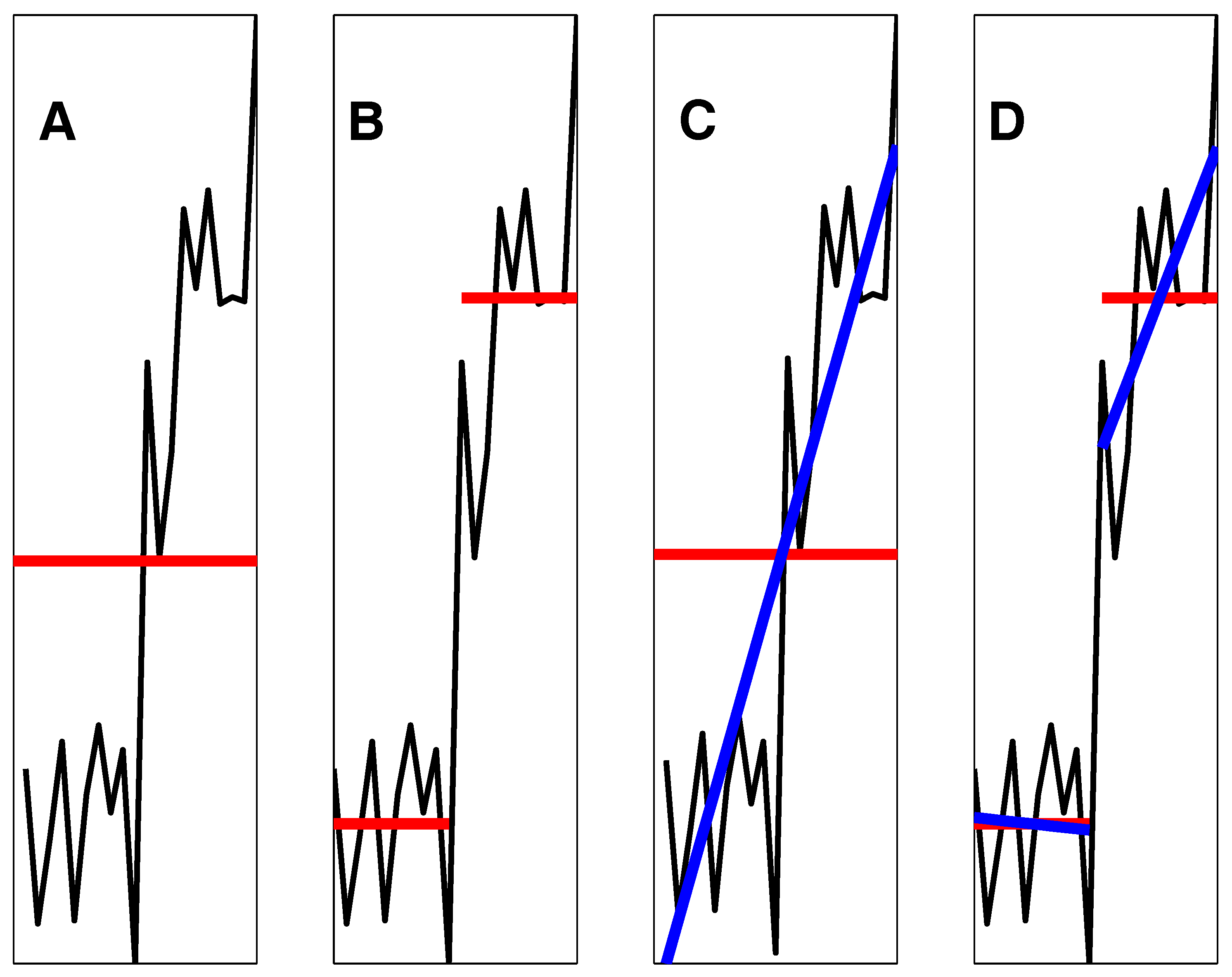
2.3. Gaussian Mixture Models and Expectation-Maximization
- Expectation step: For each time point, t, in the dataset, the expected value for component k of the likelihood function, , is calculated under the current estimate of the parameters (mean), (trend), and (covariance):Then, the likelihoods are normalized,
- Maximization step: The optimal parameters that maximize the current estimate given the data are calculated. Note that , , , and may all be maximized independently of each other since they appear in separate linear terms. The frequency of the k-th component distribution, , is computed and normalized,where is the length of the time series.
2.4. Non-Subjective Choice of Number of Regimes: Bayesian Information Criterion
3. Results
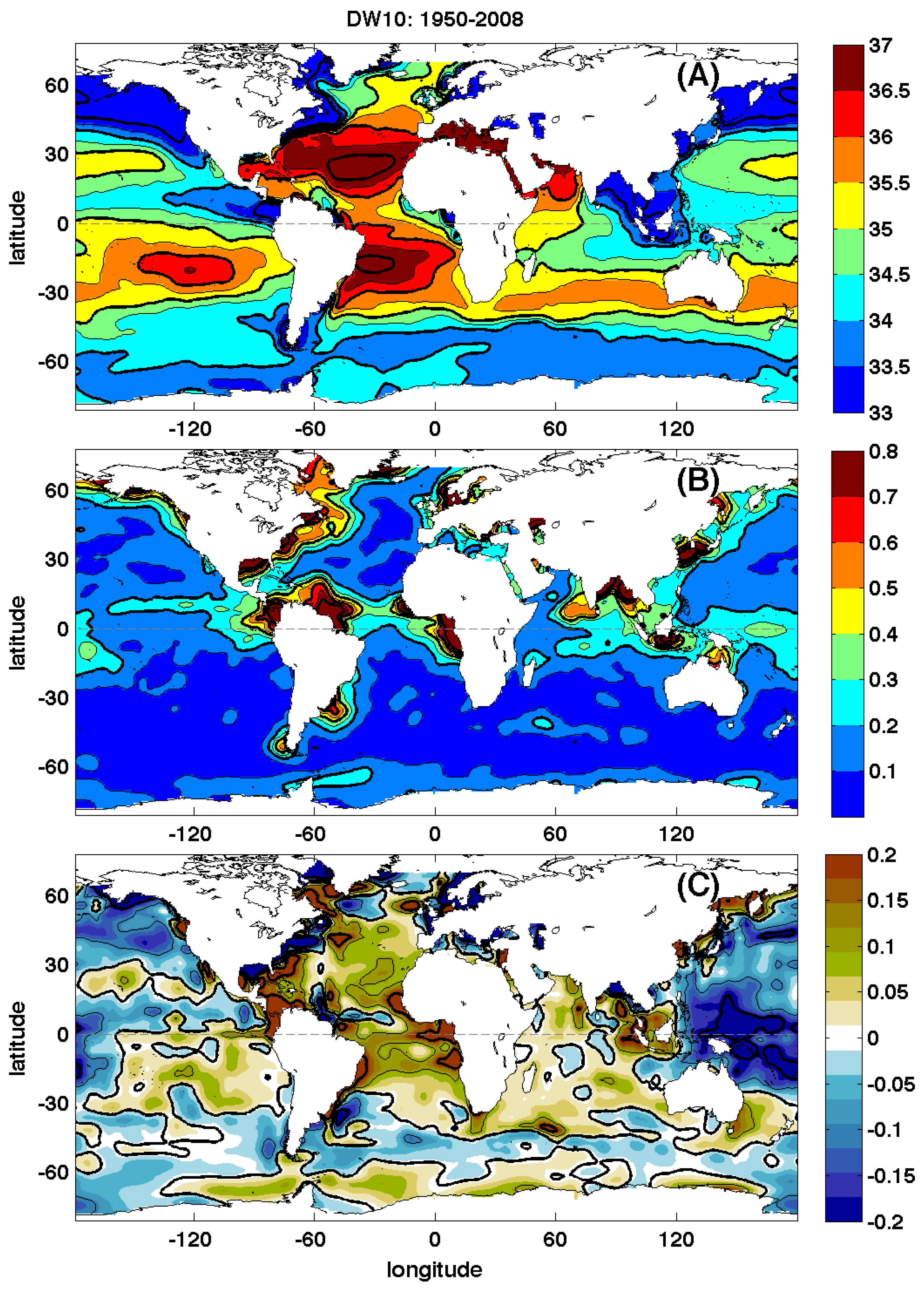
3.1. Comparison with DW10
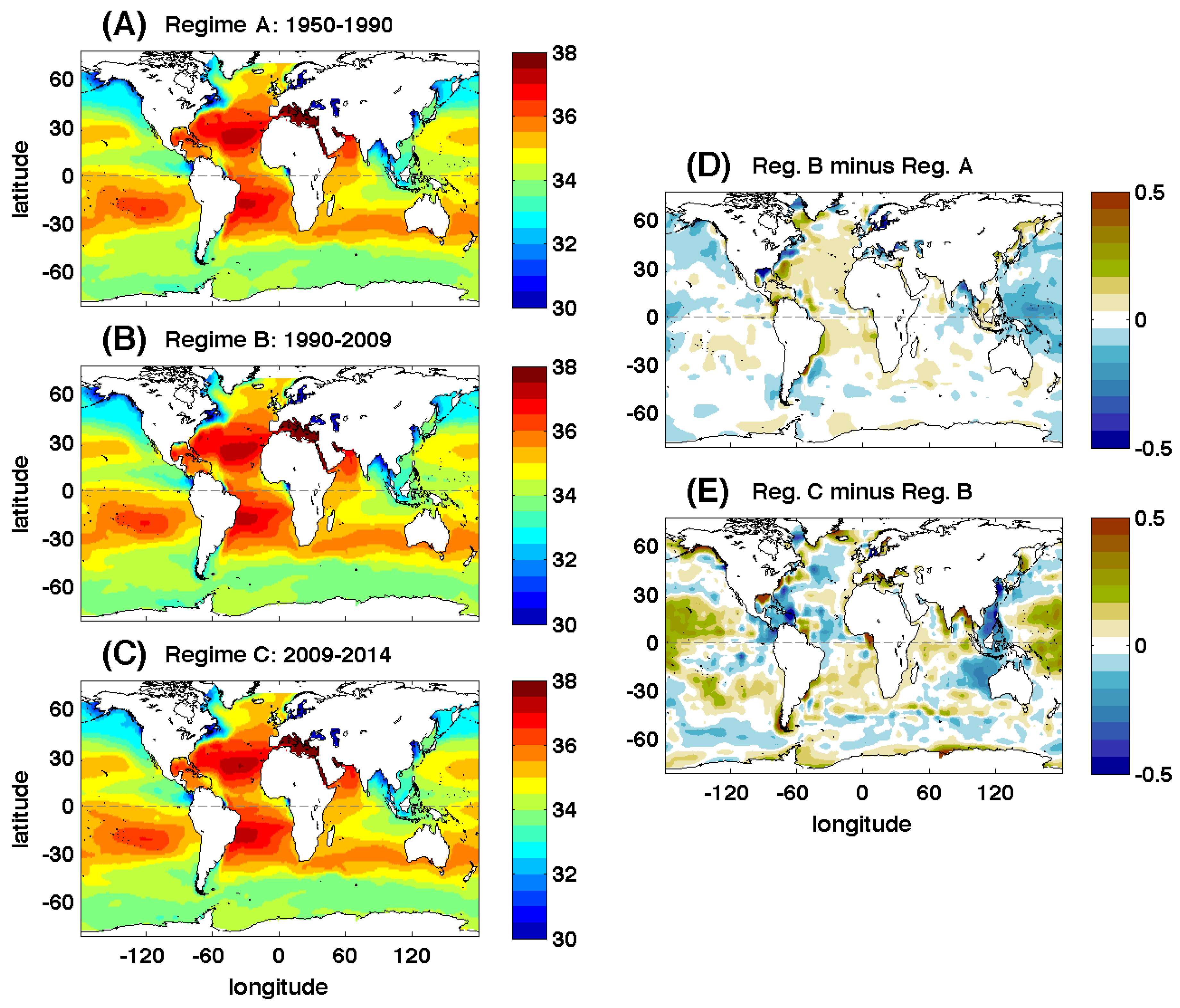
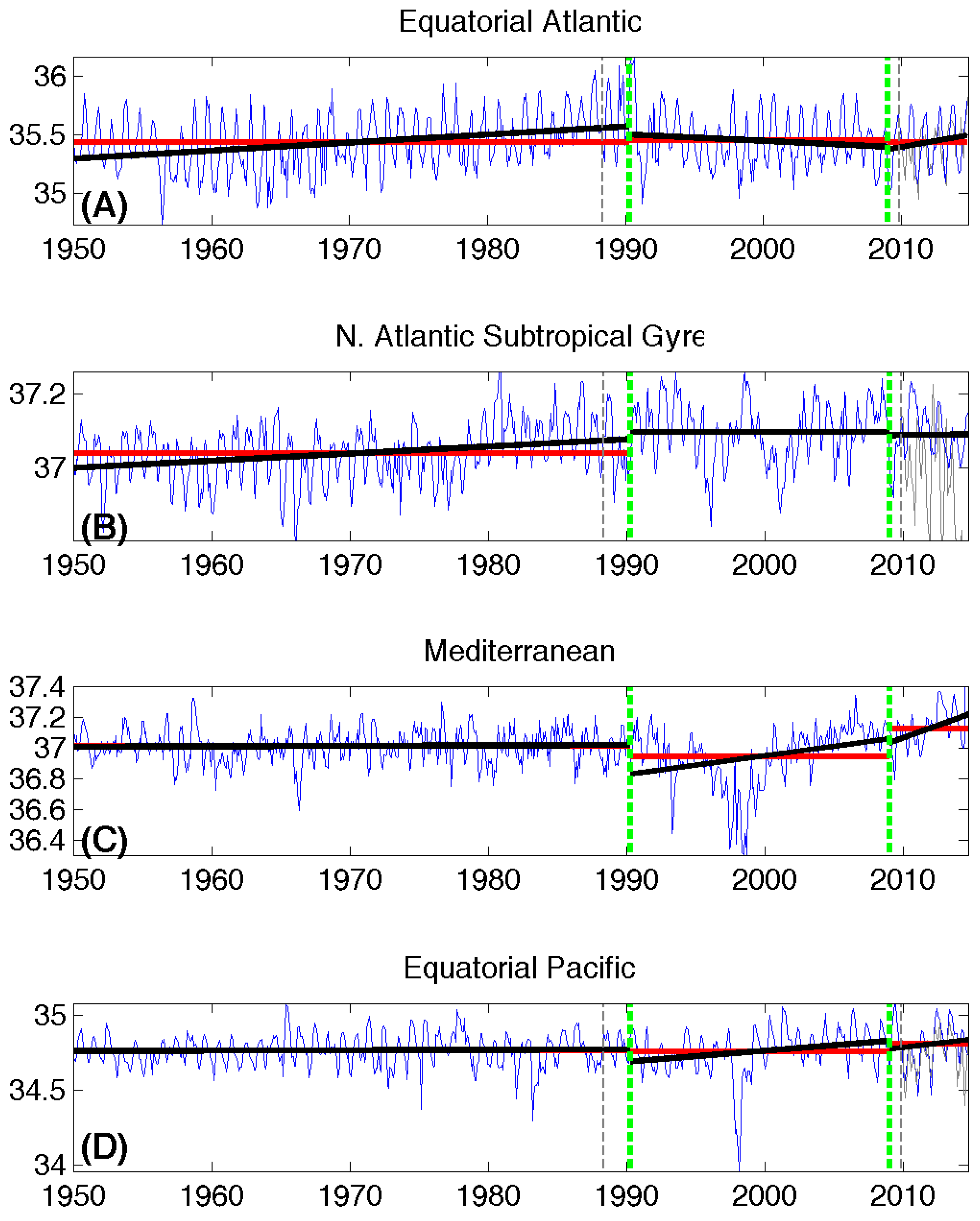
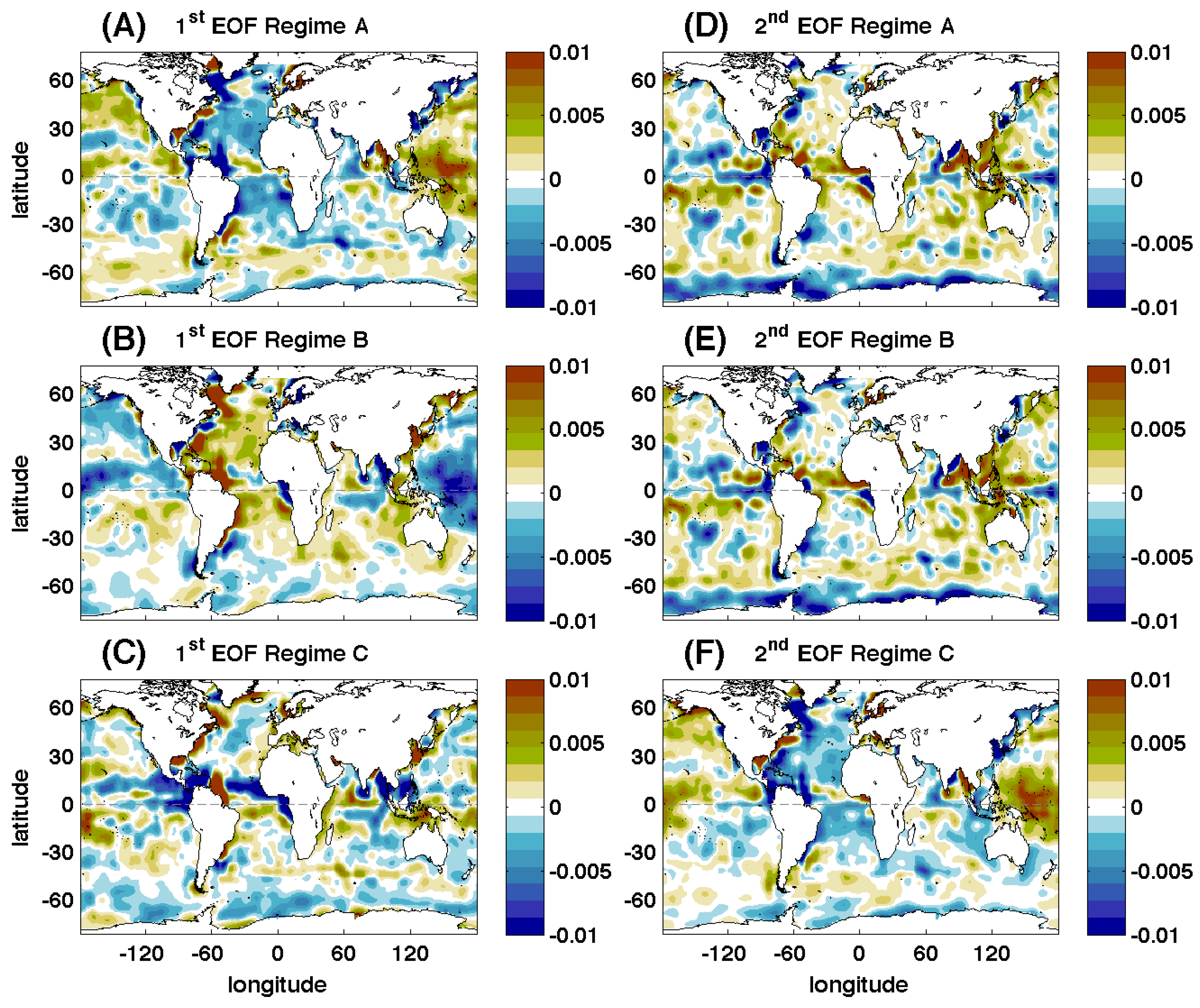
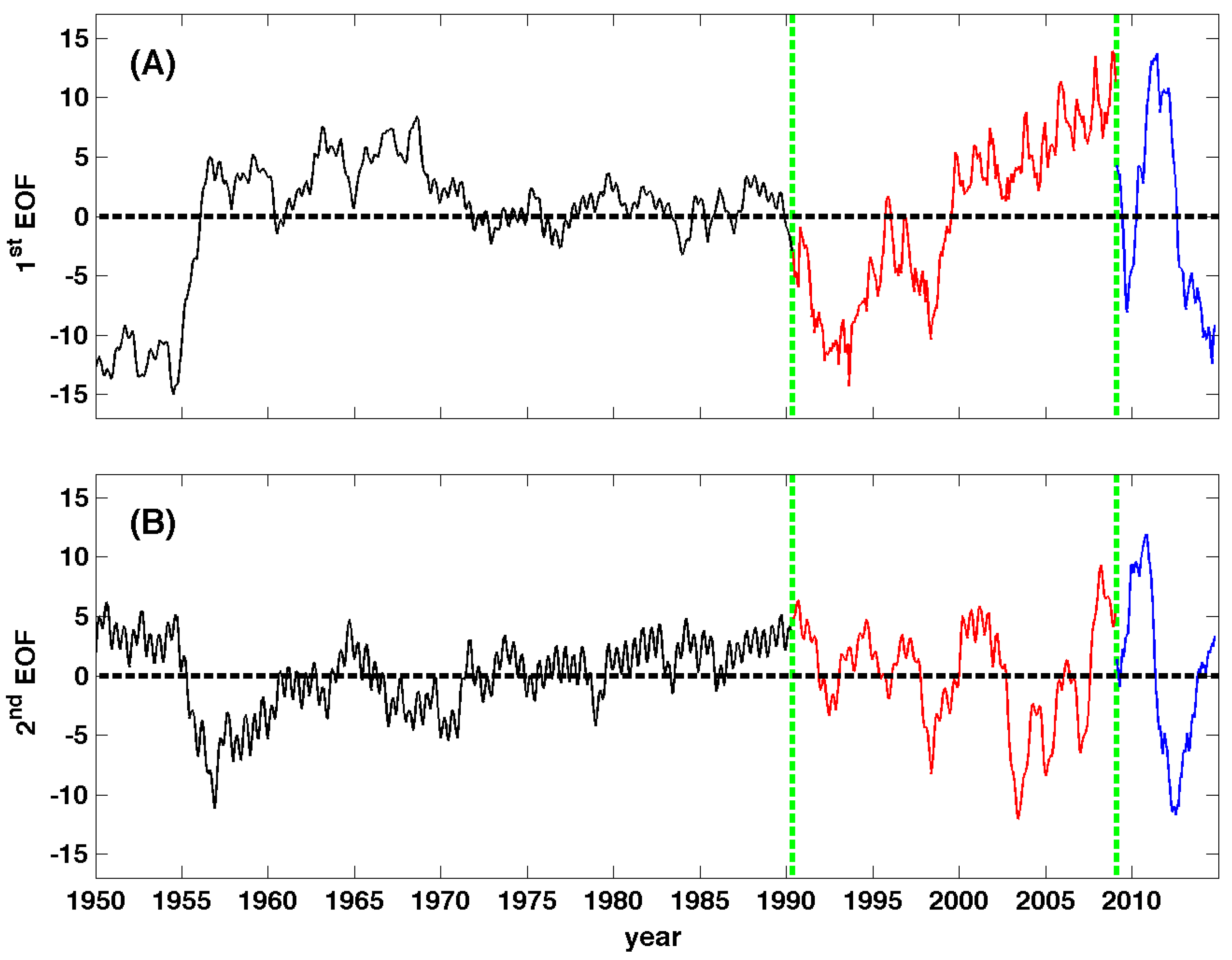
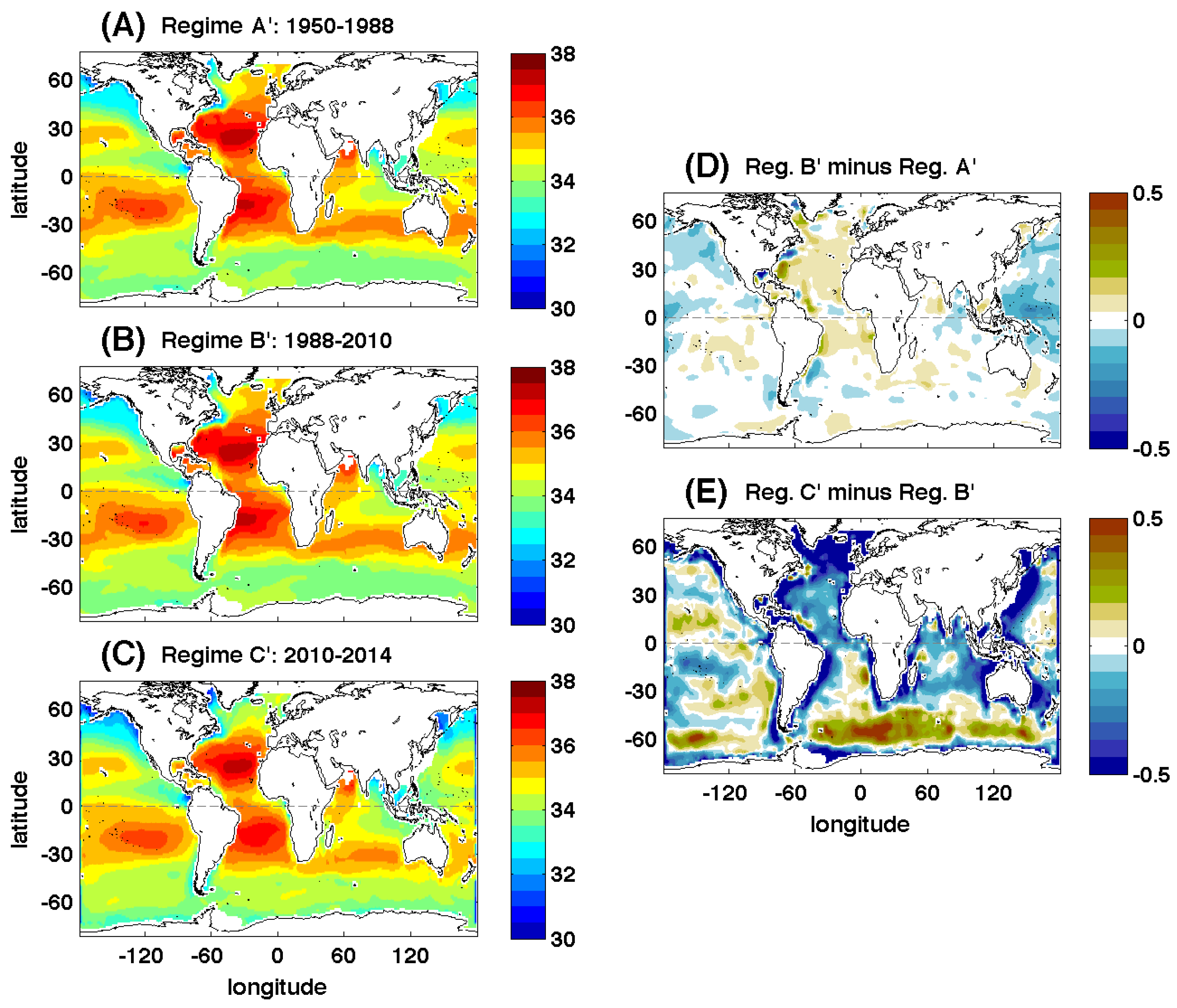
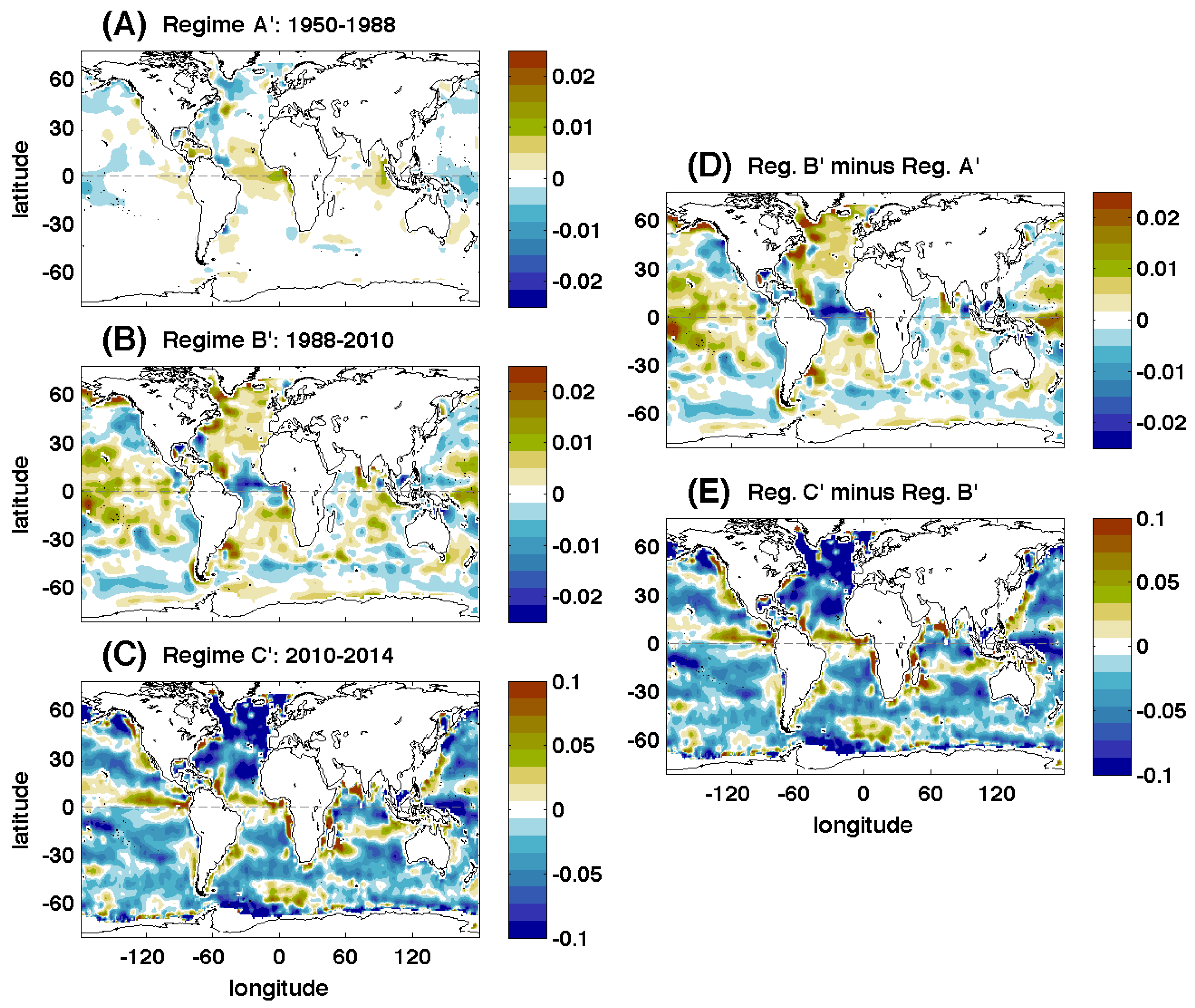
3.2. Regime Separation Using Hadley Centre EN4 1950–2014 Fields
3.3. Regime Separation with Updated SMOS Fields 2010–2014
4. Discussion
5. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Antonov, J.I.; Levitus, S.; Boyer, T.P. Steric sea level variations during 1957–1994: Importance of salinity. J. Geophys. Res. 2002, 107. [Google Scholar] [CrossRef]
- Boyer, T.P.; Levitus, S.; Antonov, J.I.; Locarnini, R.A.; Garcia, H.E. Linear trends in salinity for the World Ocean, 1955–1998. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Held, I.M.; Soden, B.J. Robust responses of the hydrological cycle to global warming. J. Clim. 2006, 19, 5686–5699. [Google Scholar]
- Durack, P.J.; Wijffels, S.E.; Matear, R.J. Ocean Salinities Reveal Strong Global Water Cycle Intensification During 1950 to 2000. Science 2012, 336, 455–458. [Google Scholar] [CrossRef] [PubMed]
- Ponte, R.; Vinogradova, N. An assessment of basic processes controlling mean surface salinity over the global ocean. Geophys. Res. Lett. 2016, 43, 7052–7058. [Google Scholar] [CrossRef]
- Vinogradova, N.T.; Ponte, R.M. In Search of Fingerprints of the Recent Intensification of the Ocean Water Cycle. J. Clim. 2017, 30, 5513–5528. [Google Scholar] [CrossRef]
- Curry, R.; Dickson, R.R.; Yashayaev, I. A change in the fresh-water balance of the Atlantic Ocean over the past four decades. Nature 2003, 426, 826–829. [Google Scholar] [CrossRef] [PubMed]
- Cravatte, S.; Delcroix, T.; Zhang, D.; McPhaden, M.; Leloup, J. Observed freshening and warming of the western Pacific warm pool. Clim. Dyn. 2009, 33, 565–589. [Google Scholar] [CrossRef]
- Hosoda, S.; Sugo, T.; Shikama, N.; Mizuno, K. Global surface layer salinity change detected by Argo and its implication for hydrological cycle intensification. J. Oceanogr. 2009, 65, 579–586. [Google Scholar] [CrossRef]
- Friedman, A.R.; Reverdin, G.; Khodri, M.; Gastineau, G. A new record of Atlantic sea surface salinity from 1896 to 2013 reveals the signatures of climate variability and long-term trends. Geophys. Res. Lett. 2017, 44, 1866–1876. [Google Scholar] [CrossRef]
- Hurrell, J.W.; Kushnir, Y.; Ottersen, G.; Visbeck, M. An overview of the North Atlantic oscillation. In The North Atlantic Oscillation: Climatic Significance and Environmental Impact; Wiley Online Library: Hoboken, NJ, USA, 2003; pp. 1–35. [Google Scholar]
- Kerr, R.A. A North Atlantic climate pacemaker for the centuries. Science 2000, 288, 1984–1985. [Google Scholar] [CrossRef] [PubMed]
- Durack, P.J.; Wijffels, S.E. Fifty-year trends in global ocean salinities and their relationship to broad-scale warming. J. Clim. 2010, 23, 4342–4362. [Google Scholar] [CrossRef]
- Chou, C.; Neelin, J.D.; Chen, C.A.; Tu, J.Y. Evaluating the “rich-get-richer” mechanism in tropical precipitation change under global warming. J. Clim. 2009, 22, 1982–2005. [Google Scholar] [CrossRef]
- Schmitt, R.W. Salinity and the Global Water Cycle. Oceanography 2008, 21, 12. [Google Scholar] [CrossRef]
- Helm, K.P.; Bindoff, N.L.; Church, J.A. Changes in the global hydrological-cycle inferred from ocean salinity. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Durack, P.J. Ocean salinity and the global water cycle. Oceanography 2015, 28, 20–31. [Google Scholar] [CrossRef]
- Skliris, N.; Marsh, R.; Josey, S.A.; Good, S.A.; Liu, C.; Allan, R.P. Salinity changes in the World Ocean since 1950 in relation to changing surface freshwater fluxes. Clim. Dyn. 2014, 43, 709–736. [Google Scholar] [CrossRef]
- Church, J.A.; White, N.J. A 20th century acceleration in global sea-level rise. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Ezer, T. Sea level rise, spatially uneven and temporally unsteady: Why the US East Coast, the global tide gauge record, and the global altimeter data show different trends. Geophys. Res. Lett. 2013, 40, 5439–5444. [Google Scholar] [CrossRef]
- Durack, P.J.; Wijffels, S.E.; Gleckler, P.J. Long-term sea-level change revisited: The role of salinity. Environ. Res. Lett. 2014, 9, 114017. [Google Scholar] [CrossRef]
- Good, S.A.; Martin, M.J.; Rayner, N.A. EN4: Quality controlled ocean temperature and salinity profiles and monthly objective analyses with uncertainty estimates. J. Geophys. Res. Oceans 2013, 118, 6704–6716. [Google Scholar] [CrossRef]
- Ingleby, B.; Huddleston, M. Quality control of ocean temperature and salinity profiles—Historical and real-time data. J. Mar. Syst. 2007, 65, 158–175. [Google Scholar] [CrossRef]
- Lorenc, A.; Bell, R.; Macpherson, B. The Meteorological Office analysis correction data assimilation scheme. Q. J. R. Meteorol. Soc. 1991, 117, 59–89. [Google Scholar] [CrossRef]
- Font, J.; Camps, A.; Borges, A.; Martín-Neira, M.; Boutin, J.; Reul, N.; Kerr, Y.; Hahne, A.; Mecklenburg, S. SMOS: The Challenging Sea Surface Salinity Measurement From Space. Proc. IEEE 2010, 98, 649–665. [Google Scholar] [CrossRef]
- Font, J.; Ballabrera-Poy, J.; Camps, A.; Corbella, I.; Duffo, N.; Duran, I.; Emelianov, M.; Enrique, L.; Fernández, P.; Gabarró, C.; et al. A new space technology for ocean observation: The SMOS mission. Sci. Mar. 2012, 76, 249–259. [Google Scholar]
- Xie, P.; Boyer, T.; Bayler, E.; Xue, Y.; Byrne, D.; Reagan, J.; Locarnini, R.; Sun, F.; Joyce, R.; Kumar, A. An in situ-satellite blended analysis of global sea surface salinity. J. Geophys. Res. Oceans 2014, 119, 6140–6160. [Google Scholar] [CrossRef]
- Aretxabaleta, A.L.; Smith, K.W. Multi-regime non-Gaussian data filling for incomplete ocean datasets. J. Mar. Syst. 2013, 119, 11–18. [Google Scholar] [CrossRef]
- Hernandez, O.; Boutin, J.; Kolodziejczyk, N.; Reverdin, G.; Martin, N.; Gaillard, F.; Reul, N.; Vergely, J. SMOS salinity in the subtropical north Atlantic salinity maximum: 1. Comparison with Aquarius and in situ salinity. J. Geophys. Res. 2014, 119, 8878–8896. [Google Scholar] [CrossRef]
- Kolodziejczyk, N.; Hernandez, O.; Boutin, J.; Reverdin, G. SMOS salinity in the subtropical North Atlantic salinity maximum: 2. Two-dimensional horizontal thermohaline variability. J. Geophys. Res. Oceans 2015, 120. [Google Scholar] [CrossRef]
- Reul, N.; Chapron, B.; Lee, T.; Donlon, C.; Boutin, J.; Alory, G. Sea surface salinity structure of the meandering Gulf Stream revealed by SMOS sensor. Geophys. Res. Lett. 2014, 41, 3141–3148. [Google Scholar] [CrossRef]
- Köhler, J.; Sena Martins, M.; Serra, N.; Stammer, D. Quality assessment of spaceborne sea surface salinity observations over the northern North Atlantic. J. Geophys. Res. Oceans 2015, 120, 94–112. [Google Scholar] [CrossRef]
- Tzortzi, E.; Josey, S.A.; Srokosz, M.; Gommenginger, C. Tropical Atlantic salinity variability: New insights from SMOS. Geophys. Res. Lett. 2013, 40, 2143–2147. [Google Scholar] [CrossRef]
- Hasson, A.; Delcroix, T.; Boutin, J.; Dussin, R.; Ballabrera-Poy, J. Analyzing the 2010Ð2011 La Niña signature in the tropical Pacific sea surface salinity using in situ data, SMOS observations, and a numerical simulation. J. Geophys. Res. 2014, 119, 3855–3867. [Google Scholar] [CrossRef]
- Sabia, R.; Klockmann, M.; Fernandez-Prieto, D.; Donlon, C. A first estimation of SMOS-based ocean surface T-S diagrams. J. Geophys. Res. Oceans 2014, 119, 7357–7371. [Google Scholar] [CrossRef]
- Olmedo, E.; Martínez, J.; Turiel, A.; Ballabrera-Poy, J.; Portabella, M. Debiased non-Bayesian retrieval: A novel approach to SMOS Sea Surface Salinity. Remote Sens. Environ. 2017, 193, 103–126. [Google Scholar] [CrossRef]
- Guimbard, S.; Gourrion, J.; Portabella, M.; Turiel, A.; Gabarro, C.; Font, J. SMOS semi-empirical ocean forward model adjustment. IEEE T. Geosci. Remote 2012, 50, 1676–1687. [Google Scholar] [CrossRef]
- Yin, X.; Boutin, J.; Martin, N.; Spurgeon, P.; Vergely, J.L.; Gaillard, F. Errors in SMOS sea surface salinity and their dependency on a priori wind speed. Remote Sens. Environ. 2014, 146, 159–171. [Google Scholar] [CrossRef][Green Version]
- Smith, K.W.; Aretxabaleta, A.L. Expecation-Maximization analysis of spatial time series. Nonlinear Process. Geophys. 2007, 14, 73–77. [Google Scholar] [CrossRef]
- Aretxabaleta, A.L.; Smith, K.W. Analyzing state-dependent model-data comparison in multi-regime systems. Comput. Geosci. 2011, 15, 627–636. [Google Scholar] [CrossRef]
- Houseago-Stokes, R.E.; Challenor, P.G. Using PPCA to Estimate EOFs in the Presence of Missing Values. J. Atmos. Ocean. Technol. 2004, 21, 1471–1480. [Google Scholar] [CrossRef]
- Kondrashov, D.; Ghil, M. Spatio-temporal filling of missing points in geophysical data sets. Nonlinear Process. Geophys. 2006, 13, 151–159. [Google Scholar] [CrossRef]
- Tipping, M.E.; Bishop, C.M. Probabilistic principal component analysis. J. R. Stat. Soc. B 1999, 61, 611–622. [Google Scholar] [CrossRef]
- Friedman, J.H. Multivariate Adaptive Regression Splines. Ann. Stat. 1991, 1, 1–67. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Schanze, J.J.; Schmitt, R.W.; Yu, L. The global oceanic freshwater cycle: A state-of-the-art quantification. J. Mar. Res. 2010, 68, 569–595. [Google Scholar] [CrossRef]
- Yu, L. A global relationship between the ocean water cycle and near-surface salinity. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Meehl, G.A.; Covey, C.; Taylor, K.E.; Delworth, T.; Stouffer, R.J.; Latif, M.; McAvaney, B.; Mitchell, J.F. The WCRP CMIP3 multimodel dataset: A new era in climate change research. Bull. Am. Meteorol. Soc. 2007, 88, 1383–1394. [Google Scholar] [CrossRef]
- Corbett, C.M.; Subrahmanyam, B.; Giese, B.S. A comparison of sea surface salinity in the equatorial Pacific Ocean during the 1997–1998, 2012–2013, and 2014–2015 ENSO events. Clim. Dyn. 2017, 49, 1–14. [Google Scholar] [CrossRef]
- Hoareau, N.; Umbert, M.; Martínez, J.; Turiel, A.; Ballabrera-Poy, J. On the potential of data assimilation to generate SMOS-Level 4 maps of sea surface salinity. Remote Sens. Environ. 2014, 146, 188–200. [Google Scholar] [CrossRef]
- Droghei, R.; Nardelli, B.B.; Santoleri, R. Combining In Situ and Satellite Observations to Retrieve Salinity and Density at the Ocean Surface. J. Atmos. Ocean. Technol. 2016, 33, 1211–1223. [Google Scholar] [CrossRef]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aretxabaleta, A.L.; Smith, K.W.; Kalra, T.S. Regime Changes in Global Sea Surface Salinity Trend. J. Mar. Sci. Eng. 2017, 5, 57. https://doi.org/10.3390/jmse5040057
Aretxabaleta AL, Smith KW, Kalra TS. Regime Changes in Global Sea Surface Salinity Trend. Journal of Marine Science and Engineering. 2017; 5(4):57. https://doi.org/10.3390/jmse5040057
Chicago/Turabian StyleAretxabaleta, Alfredo L., Keston W. Smith, and Tarandeep S. Kalra. 2017. "Regime Changes in Global Sea Surface Salinity Trend" Journal of Marine Science and Engineering 5, no. 4: 57. https://doi.org/10.3390/jmse5040057
APA StyleAretxabaleta, A. L., Smith, K. W., & Kalra, T. S. (2017). Regime Changes in Global Sea Surface Salinity Trend. Journal of Marine Science and Engineering, 5(4), 57. https://doi.org/10.3390/jmse5040057





