1. Introduction
The topic of low-frequency acoustic waves transmitting in seawater piping systems in ocean surface ships and under-water vehicles, of which their outlets are underneath the water surface, etc., is of special interest [
1,
2]. The seawater pipe is an excellent medium that can carry acoustic waves, especially the low-frequency sounds, to a distance far way and almost without energy loss. Therefore, a lot of researchers have committed themselves to controlling the noise transmission in piping systems [
3,
4].
It can be seen from the open public literature that there has been a considerable number of noise reduction methods available for the piping systems, e.g., (i) arrangement of elastic joints, corrugated pipe/bellows, or other components to the piping systems [
5,
6,
7,
8]; (ii) installation of a muffler elbow and micro-perforated plates [
9,
10]; (iii) avoidance of short-radius elbow, sharp bends, and branch pipes in pipeline [
11]; (iv) laying damping materials [
9]; (v) active control technologies [
12,
13,
14,
15]; and installation of pipe mufflers [
16,
17,
18,
19], etc. Particularly, installation of a pipe muffler is the most widely used means among these methods. Research has shown that installing a muffler at the broadside inlet of a seawater pipe can effectively suppress or isolate the noise radiating from ship piping system to the outboard field. Nevertheless, existing problems that may beset the current silencers may be ascribed to the limitation in low-frequency noise control capacity. Take the Helmholtz resonator (HR) as an example. Although it can achieve a suppression effect in the low-frequency range, its effective silencing band is always too narrow [
4,
18,
19,
20]. In contrast, the expansion-type silencer can achieve a broadband character of noise reduction, yet its silencing frequency is often too high [
21,
22].
Recently, the propagation of elastic or acoustic waves in artificial materials/structures called acoustic metamaterials (AMs) has received considerable attention [
23,
24,
25]. The most important characteristic of AMs is their periodic structure or array of substructures. The initial attraction of using periodic structures may be due to their unusual dynamical characteristics, e.g., the existence of wave bands within which the propagation of elastic waves is forbidden over some selected frequency ranges. Bradley has examined the propagation of linear, dissipative, time-harmonic waves in a broad class of periodic waveguides and confirmed the peculiar dispersion characteristics marked by the phenomenon of stop bands or band gaps in a frequency domain [
26]. Following on Bradley’s work, Sugimoto and Horioka investigated dispersion characteristics of sound waves propagating in a tunnel with an array of Helmholtz resonators connected axially, as well as the effects of wall friction and the thermoviscous diffusivity of sound [
27]. Advantage of the array of resonators is to increase the effective silencing frequency range for the piping system and a downshifting effect on the central of anechoic bands, rendering the bandwidth of noise elimination broadened and the location moved toward the low frequency domain. The introduction of visco-thermal losses tend to increase the damping effects on non-dispersive sound waves such that noise transmitting in the pipe system will be quickly damped spatially. However, in a plausible case, the wall friction and the diffusive effect of sound are very small as compared to that of the stopping bands. More recent studies have been on the nonlinear acoustic behavior of dispersion relation for the air-filled waveguide tube with an array of axially distributed resonators installed [
28,
29,
30]. These works showed that the usually observed band gaps for the wave transmission coefficient through the system are found to be amplitude-dependent.
In the present work, a metamaterial-based periodic system, consisting of a seawater pipe upon which are mounted axially an array of HRs, is constructed. The difference between the current and foregoing works lies in the improvements of HR design. Here, the HR cavity is designed to be a gas-liquid hybrid chamber, such that the bandwidth may be notably expanded. A transfer matrix (TM) method is utilized to conduct the investigation, and an acoustic-structure interaction model is constructed to give an estimation for the sound transmission loss in a quasi-experimental case. Further, the effects of high pressure on the properties of acoustic band gaps are considered, and comparisons between the liquid-filled chamber and the gas-liquid hybrid chamber are carried out.
2. Acoustic Equations and Calculation Method
The essential model of an HR could be viewed as a spring-mass dynamical absorber with mass
MH =
ρwSnlne and spring stiffness
KH =
κwSn2/
Vc, or could be analogous to an inductor-capacitor circuit, whose acoustic impedance
LH and capacitance
CH are
LH =
ρwlne/S
n and
CH =
Vc/
κw, respectively, for the HR and the pipe, which are filled with liquid (e.g., water) only [
29]. Symbol
lne is the effective length of the neck, which can be calculated by
lne =
ln + 1.4
rn [
31,
32].
ln,
rn, and
Sn represent the length, the radius, and the cross-sectional area of HR neck, respectively.
ρw and
κw are, respectively, the fluid density and the bulk modulus. Subscripts “w” and “a” indicate the fluid “water” and “air,” respectively. Such an equivalent physical model is sufficiently accurate if the frequency range concerned was low enough. The dimension of HR will be smaller than the corresponding wavelength. In this sense, the HR can be defined as the local resonator according to the AMs theory. When the HR cavity is composed of a liquid chamber and a gas chamber, e.g., a water and air hybrid chamber, the acoustic impedance
LH and capacitance
CH should be changed to
LH =
ρwln/S
n and
CH = (
Vcw/
κw2 +
Vca/
κa2), respectively. Mounting this HR periodically into the seawater piping system with a fixed lattice space
la that is much smaller than the acoustic wavelength
λ (
la ~
λ/5), the periodic system will behave as a homogenized effective medium where the acoustic band gaps may be expected [
32]. Numerical validation will be addressed in next section. Construction of the periodic seawater piping system is sketched in
Figure 1. Wave equation of the acoustic medium inside the seawater pipe can be given by the following formula [
4,
17,
28]:
wherein
p is the acoustic pressure. Volumes of the liquid- and gas- chambers are respectively expressed as
Vcw and
Vca;
Sp is the cross-sectional area of the pipe; bulk modulus
κ is calculated by
ρc2, in which
ρ and
c denote the density and the acoustic speed of fluid inside the pipe and the HR, respectively. Based on the time-harmonic assumption, the above acoustic equations can be simplified to be the following form:
of which the term exp (−j
ωt) has been suppressed throughout.
ω is the radian frequency, and
k is the wave number that formulated by
ω/
c. Hence, the acoustic pressure within the tube can be expressed as
and acoustic speed
v as [
1]
wherein
At and
Ar indicate the amplitude coefficients of transmitted and reflected waves, respectively. Acoustic speed
v is derived from pressure
p through the relation between the sound pressure and the acoustic velocity:
v = −
ρ0−1∫
∂p/
∂xd
t. Volume speed
Q is the product of acoustic speed
v and cross-sectional area of pipe
Sp. Thus, acoustic states at the two ends of a uniform pipe section with length of
la (e.g., the uniform pipe section between the (
n−1)th and the
nth periodic pipe cells as sketched in
Figure 1) has the following transfer matrix relation [
1,
17]:
Letter “
n” indicates the relevant variables for the
nth periodic cell. When a HR is mounted to the pipe section, the corresponding transfer matrix relation in terms of the classical state variables has to modify to the following form:
wherein
ZH is the acoustic impedance of HR. It can be formulated by
ZH = j
ωLH + (j
ωCH)
−1. Introducing the state vector Γ = {
p,
Q}’ into the above equation, Equation (6) can be rewritten into the following abbreviated form:
in which T
c is the corresponding transfer matrix relating to the state vectors at the two ends of a periodic cell. Moreover, the two state vectors at the left and the right sides of periodic cell should also satisfy the following restriction due to the periodic boundary condition [
33]:
Combining Equations (7) with (8) gives rise to
Solving the values of
μ in Equation (9), as functions of
ω, one can easily obtain the dispersive relation to describe the state of acoustic waves propagating in the infinite periodic pipe, that is, the well-known acoustic band structure. Such a band structure comprises two parts: the real and the imaginary parts. The real part is the so-called phase constant, and the imaginary part is referred to as attenuation constant. In this sense, the symbol
μ can be referred as the effective wavenumber inside the metamaterial. Wave propagation is possible within frequency bands where
μ is real (pass bands), whereas attenuation occurs for the frequency values that provide an imaginary part to
μ, referred to as band gap. It describes the attenuation degree of amplitude coefficient of waves transmitting from one side of a periodic cell to the other side [
33].
For a finite periodic pipe consisting of
N Helmholtz resonators mounted equidistantly in a uniform pipe, the transmitting relationship for the acoustic states at the inlet and the outlet can be given by
It can be further simplified to
if the inlet and the outlet of the finite periodic pipe are perfectly impedance matched and
τp = exp (±j
kla). Accordingly, the sound transmission loss
TL can be given by 10lg(
tp−1). Up to now, propagation characteristics of acoustic waves in the infinite and the finite periodic pipes can be examined by the calculation of
TL and band structure, respectively, upon which relative analysis for the periodic system could be carried out.
3. Results and Discussion
In what follows, numerical examples are addressed to illuminate the acoustic characteristics of low-frequency wave transmission in the metamaterial-type periodic pipe designed in the current work. The cavity shape of Helmholtz resonance can be spherical, cylindrical, or even an irregular cavity. Also, the cross section of the neck tube can be a regular shape, such as circular, square, oval, or other shape. In fact, the most important geometric factors that affect the performance of HR are the volume of Helmholtz chamber, the cross-sectional area, and the length of Helmholtz tube, etc. In the low frequency range, the effects of geometric shape of the neck tube and chamber on the performance of muffler may be neglected. Without loss of generality, this paper chooses the shape for the HR chamber and neck tube to be cylindrical. Radii for the pipe, HR chamber, and neck are respectively employed as rp = 5 cm, rc = 2rp, and rn = 0.8rp; lengths for the periodic cell, HR chamber, and neck are chosen to be la = 0.96 m, lcw = 4.5rp, and ln = 1.5rp, respectively.
In the first place, the periodic seawater pipe system is assumed to be filled with water; acoustic speed and density for water are respectively 1500 m/s and 1000 kg/m
3.
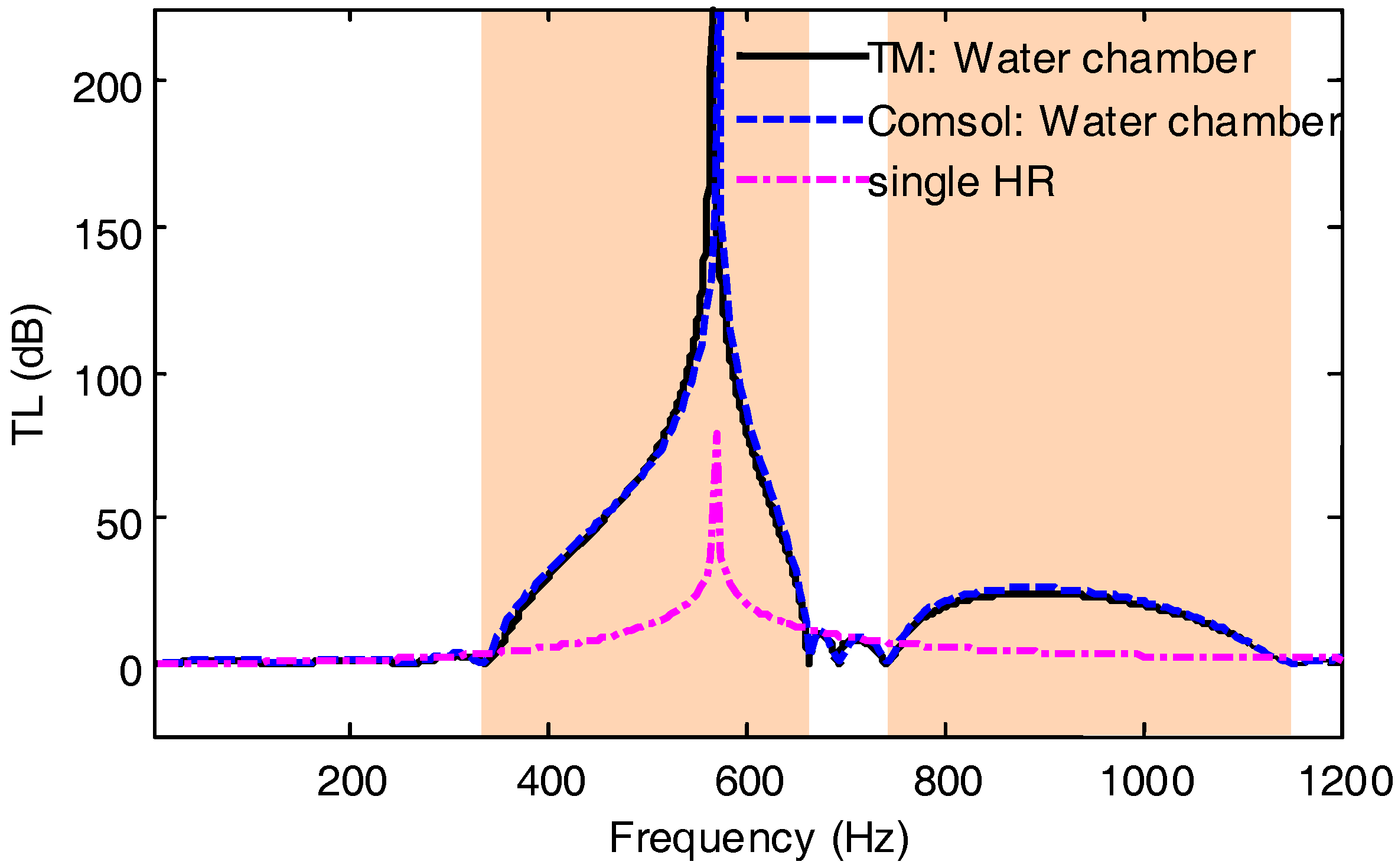
Figure 2 exhibits the corresponding numerical results for a seawater pipe system with four HRs installed equidistantly, as shown by the solid line; the dashed line corresponds to the simulation of Comsol commercial software for the same periodic system. The good agreement of solid line with dashed line validates the accuracy of the numerical algorithm developed in this paper. Comparing the sound transmission loss of the periodic pipe system with that of a same pipe system with a single HR mounted, as illustrated by the dash-dotted line, one can see that there are two attenuation ranges of sound transmission in the former case. They are 356.5–645.5 Hz and 781–1094 Hz. Within these two frequency zones, acoustic wave propagation in the periodic system is attenuated evidently; in contrast, sound transmitting in the latter one, i.e., the pipe system with one HR attached, is damped only in a very narrow frequency range near the resonant frequency peak
fH of HR that determined by
fH = (2
π)
−1(
CHLH)
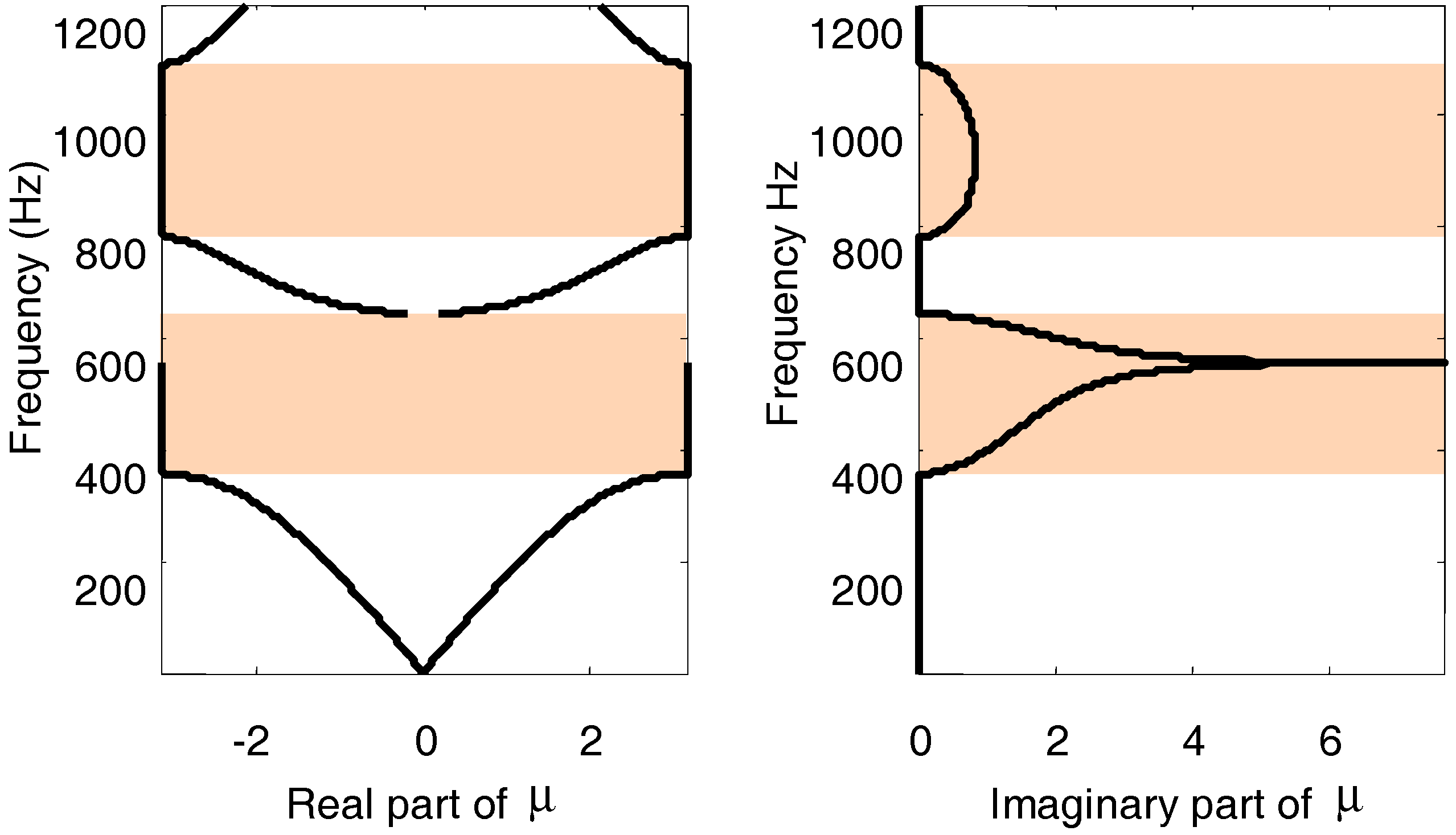
−1/2. With regard to the infinite periodic pipe system, the acoustic propagation characteristics are captured by the band structure, as shown in
Figure 3, of which the lattice constant
la and other geometric parameters involved in the calculation are the same as those in
Figure 2. On examination of
Figure 3, it can be seen that the location and bandwidths of these two BGs are exactly the same as that of the sound suppression zones in the finite periodic structure, as well as the attenuation effects, as revealed by the imaginary part of
μ in
Figure 3 and the TL in
Figure 2. In fact, both the sound transmission loss and the band structure are equivalent in describing acoustic characteristics for periodic systems. The difference of these two approaches lies in that the former is used for finite periodic systems and the latter is for ideal periodic structures, i.e., the infinite periodic systems. The damping in the band gap has nothing to do with energy loss transformed into heat, so it can occur in the lossless cases. Introduction of visco-thermal losses into the metamaterial-type seawater pipe system may strengthen the damping effects in both the stop and the pass bands, yet it tends to smooth out the sharply cusped features that occur at the boundaries of the Bragg gaps and at scatterer resonance gaps [
27]. Moreover, the diffusive effect of sound in a plausible case is very small except for the stopping bands, thus the dissipation is not taken into account in the current work.
Next, we consider the water-filled chamber of HR to be replaced by an air-water hybrid chamber and investigate the acoustic characteristics of the periodic pipe. As mentioned above, if the HR chamber is filled by air and water, then the acoustic capacitance
CH will be changed from
CH =
Vcw/
κw2 to
CH = (
Vcw/
κw2 +
Vca/
κa2), such that the location of the first BG will be notably lowered, as the resonant frequency of HR
fH is decreased with the increase of
CH.
Figure 4 validates such a conclusion. Lengths for the water and the air chambers employed in the calculation are
lcw = 0.4
rp and
lca = 0.5
rp, respectively. Other parameters are kept the same with those in
Figure 3. Density and sound speed of air are 1.225 kg/m
3 and 342 m/s, respectively.
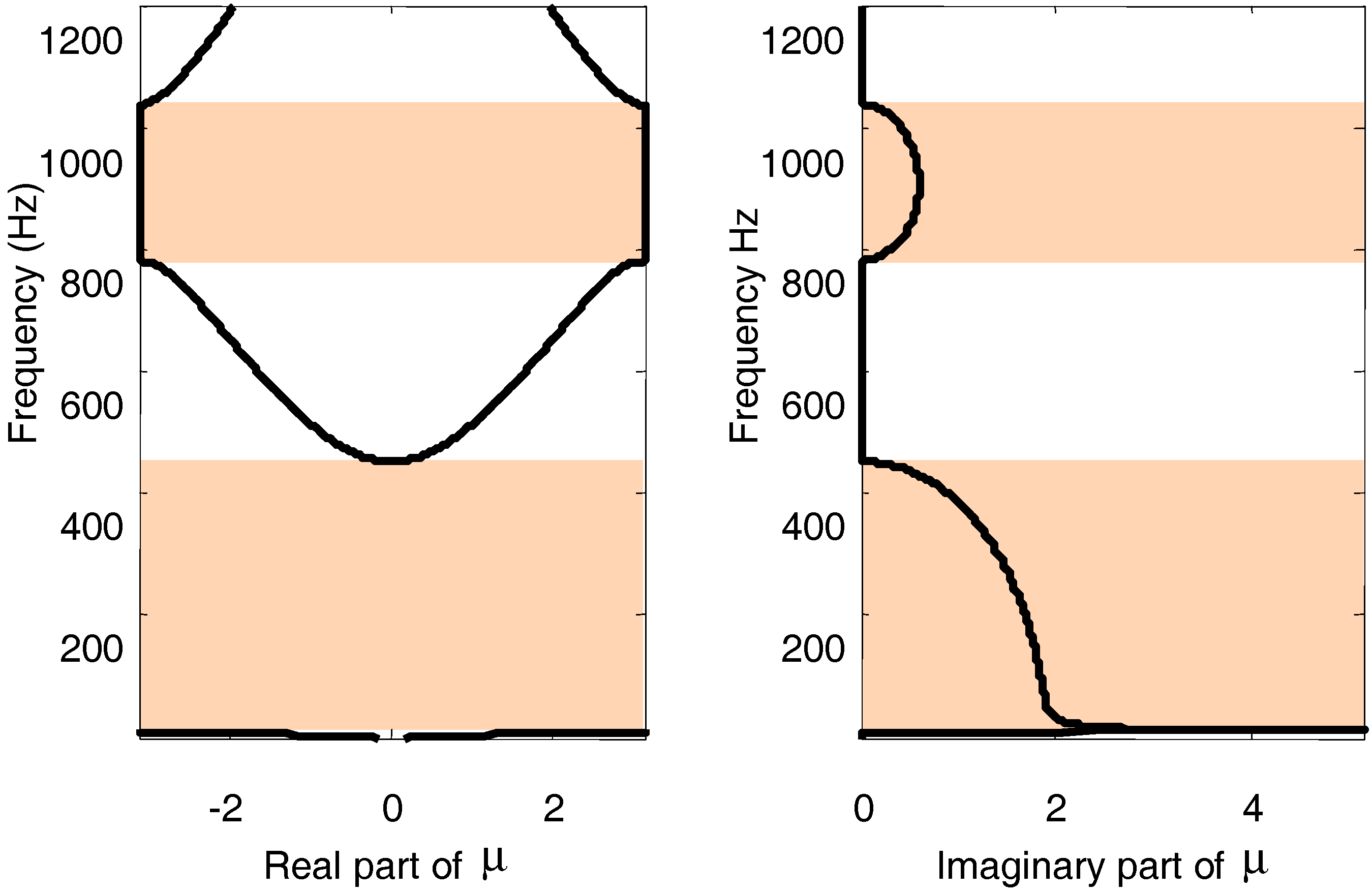
On observation of
Figure 4, it is easy to see that band edge of the first band gap can be decreased as low as 9 Hz. Moreover, the bandwidth is broadened to be 444 Hz. This change in the first band gap is, of course, good for the low-frequency noise control for the seawater piping system. Probing into the formation mechanism of the first band gap, it may be ascribed to the co-resonance of HR array (scattering resonances) in the periodic system. The resonant peak with maximum attenuation coefficient in the band gap exactly corresponds to the resonant frequency
fH of HR, i.e., 13.3 Hz under the aforementioned parameters. Consequently, this band gap is categorized as resonant gap (RG). As for the second band gap in
Figure 4, namely the frequency range 781–1036 Hz, one can see that it is almost unchanged as compared to that in
Figure 3. Tracing it to its causation, we know that the behavior of the second band gap is dominated by the Bragg scattering mechanism. In other words, the generation of the second gap could be ascribed to the effects of interference between the incident, reflected, and transmitted acoustic waves in the system cells. Thereupon, one of the band edge
fB, is determined by
mc/2
la, i.e., the Bragg condition;
m = 1, 2, 3, …, denotes the
mth band gap induced by this Bragg scattering mechanism. In this sense, the second band gap is defined as Bragg-type gap (BG). From the Bragg condition, it can be known that the adoption of air-water hybrid chamber in the HR medium in fact has little influence on the Bragg condition, hence the BG would experience no change in its band gap features, such as bandwidth, location, etc.
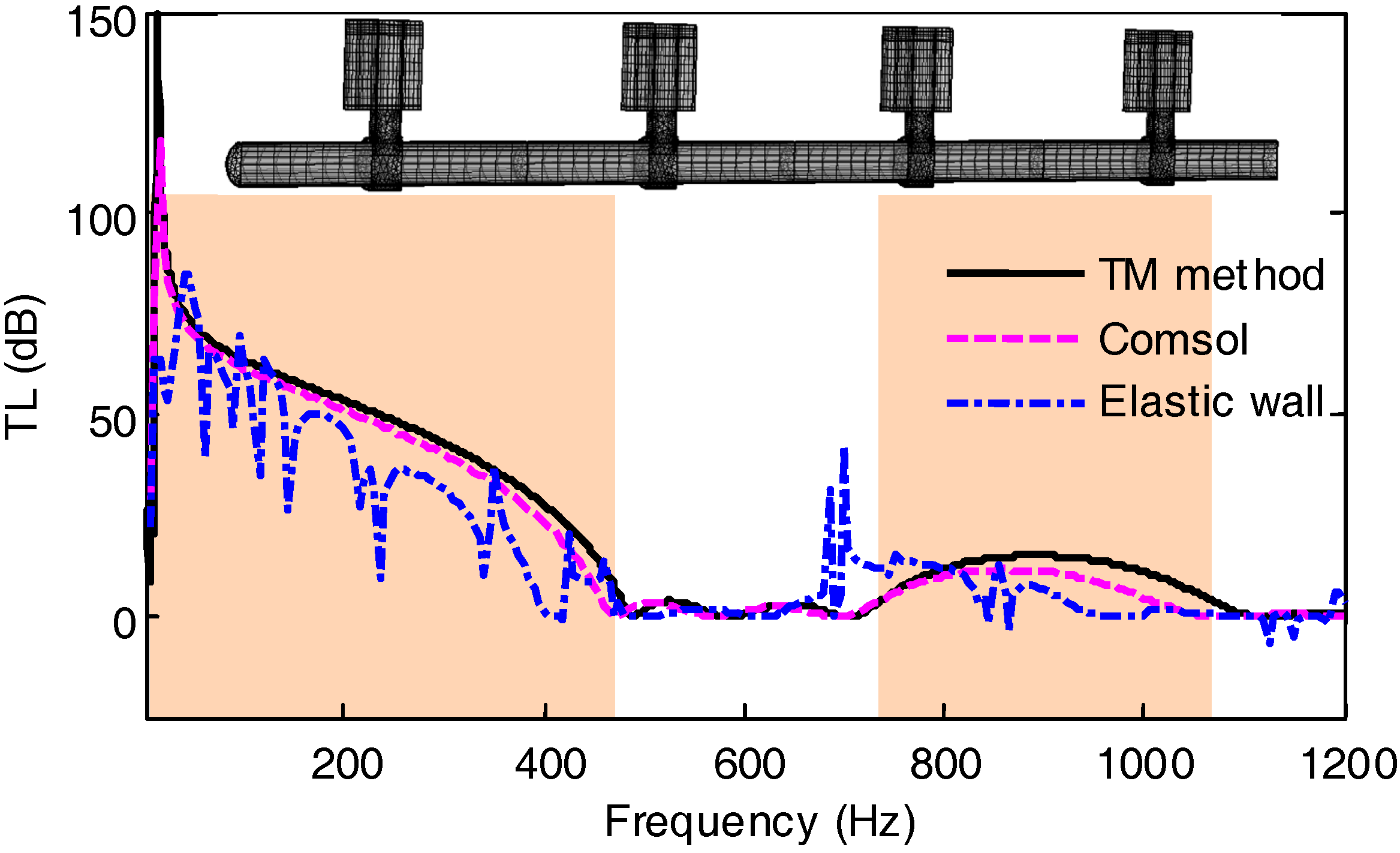
Figure 5 shows the corresponding sound transmission loss for the same model as studied in
Figure 4, except that the seawater pipe now is assumed to be a finite structure. The seawater pipe system discussed at this stage is loaded by four identical water-air chamber HRs in an axial array of lattice
la. Material and geometric parameters involved in the calculation are kept the same as those applied in
Figure 4. The solid and the dashed lines correspond to the simulation of TM method and Comsol commercial software, respectively. The TL curves predicted by these two different numerical methods agree in the low frequency range, while only small differences can be observed near the Bragg gap between the TM method and the Comsol simulation. This may due to a nonlinear conversion of propagative waves toward evanescent waves and due to the hypothesis used in the TM algorithm that the HR neck connected to pipe wall is viewed as a point such that its neck geometric dimension is neglected. The attenuation zones in this plot agree well with the two gaps shown in
Figure 4, thus the effectiveness of low-frequency noise suppression capacity by changing the cavity of a water-filled HR by a mix between the liquid and gas cavity (water and air) is validated once again.
Toward the practical consideration for engineering piping systems, there are some experimental constraints that should be discussed. One key factor is that acoustic waves will propagate not only in water, but also in the material of the pipe wall, e.g., steel, due to the low impedance contrast between media. This effect will be presented in any experiment, so here, an acoustic-structure interaction model is constructed to give an estimation for the sound transmission loss in a plausible case. The evaluation model, i.e., a finite element model (FEM), used in the investigation is presented in the inset of
Figure 5. The thicknesses for the elastic pipe and, the HR cavity, and neck walls are chosen as 4 mm, 9.5 mm, and 3.5 mm, respectively; other geometric parameters are kept unchanged. Numerical results of such an acoustic-structure model under the aforementioned parameters are shown by the dash-dotted line in
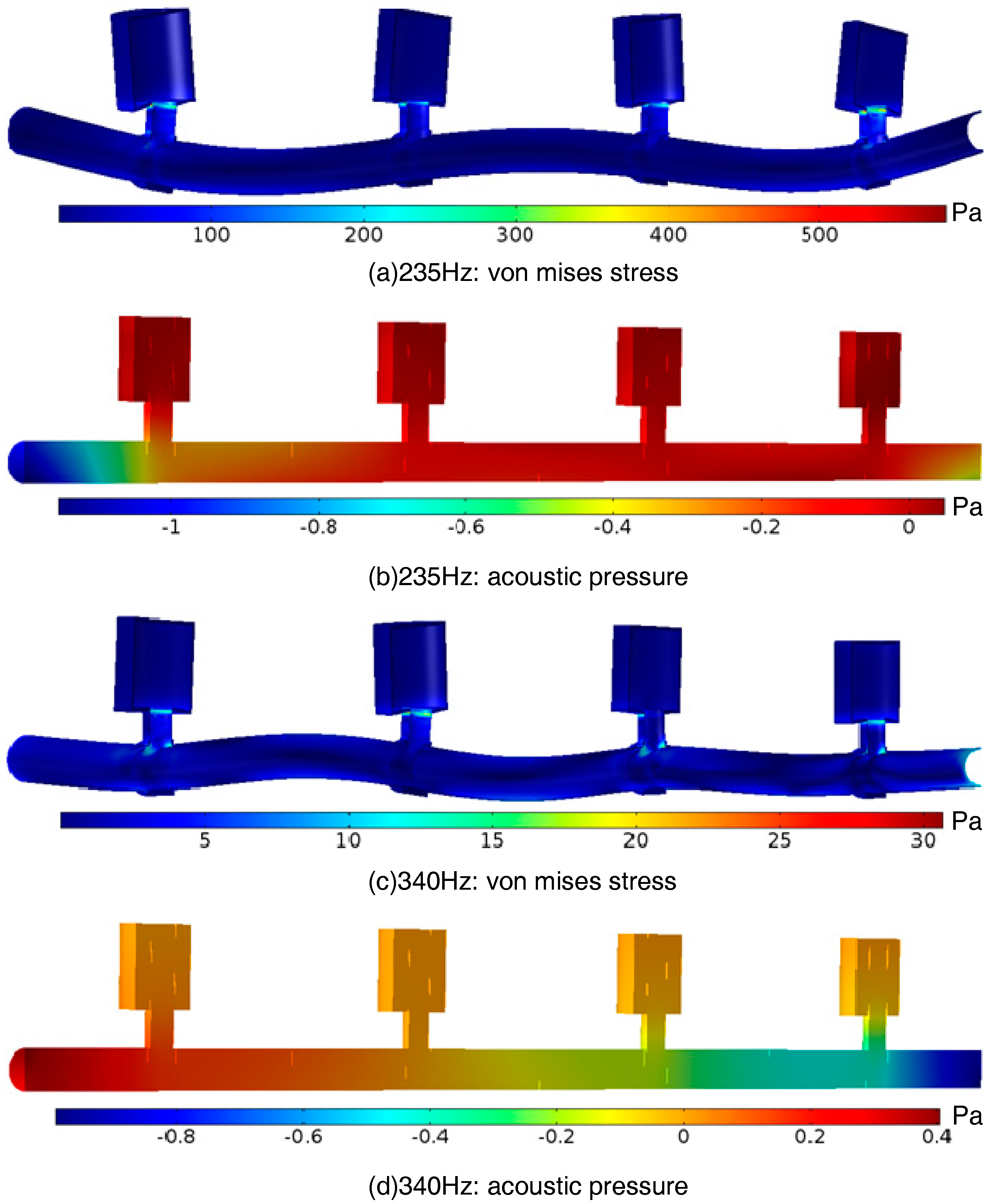
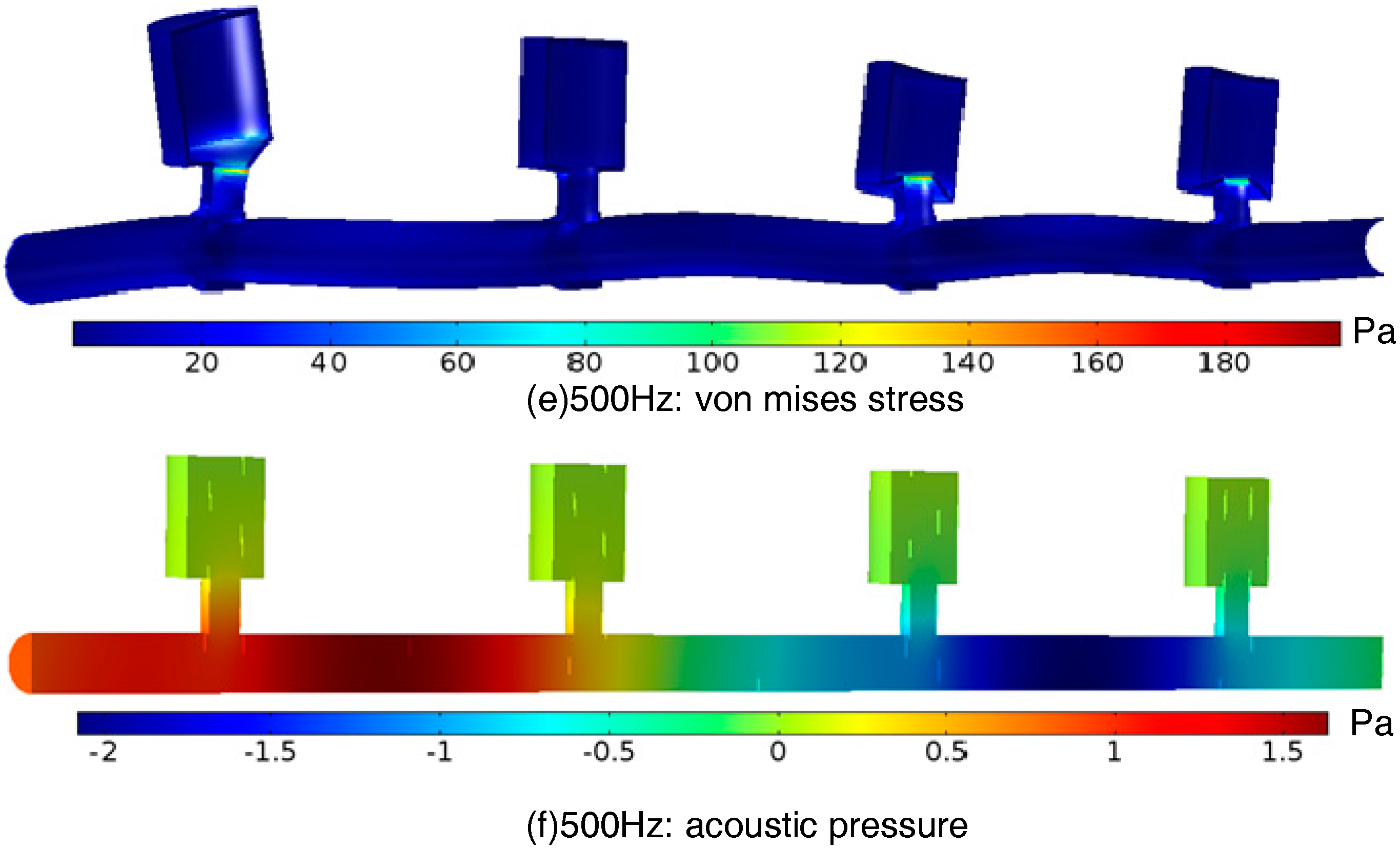
Figure 5. It is seen that total amount of noise elimination in this case experiences a bit of a decrease over most of the band gap ranges. Moreover, there are numerous “resonant peaks” in the previously smooth TL curve, rendering the noise damping effects in the band gaps deteriorated at these frequencies. In fact, acoustic waves transmission in this FEM experiences a small amount of energy loss due to the sound radiation through the pipe wall and also motivates the structure vibration modes that occurred because of the acoustic-structure interaction effects, as demonstrated by the subsequent
Figure 6a,c for the von misses stress at frequencies 235 Hz and 340 Hz, respectively. Thereupon, structure-borne sound is induced, as shown by the acoustic pressure fields in
Figure 6b,d, respectively corresponding to these two frequency locations. The pressure excitation is loaded at the inlet (the left end) of the pipe, and signals are picked up in the outlet (the right end). For better comparison, the von misses stress distribution and the acoustic pressure field that located outside the band gap (for example, at frequency 500 Hz) are given in
Figure 6e,f. Apparently, sound transmission in the pass band could propagate freely through the pipe system without any attenuation, whereas in the stop gap, wave propagation is blocked forward, even in a worse case wherein the structure-borne sound is excited.
In what follows, some key factors that may modulate the band gap features will be discussed. As revealed in the foregoing, the design technology of using an air cavity could greatly increase the acoustic capacitance of HR
CH, therein resulting in a low-frequency and broad RG. Hence, it should be noted that the filling ratio of air chamber plays an important part in generating this low-frequency and wide RG. RG with broader width and lower central frequency may be achieved if the volume of HR air cavity is increased.
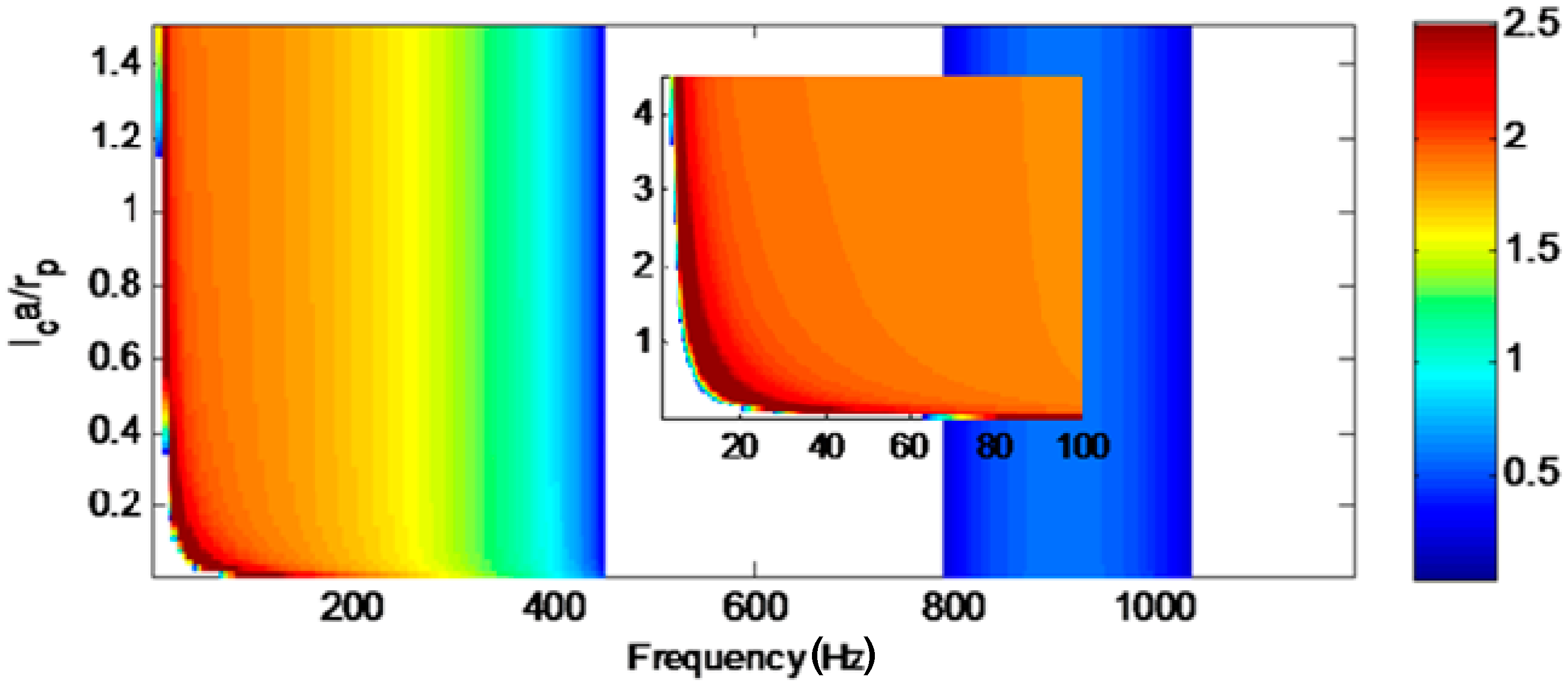
Figure 7 presents a complete surface of imaginary parts of
μ, as functions of frequency and volume of air chamber (i.e., length of the air chamber
lca), through which detailed information on the behavior of the band gap location, width, and attenuation coefficient can be roundly known. According to the planform view of this attenuation constant surface, a conclusion can be reached as follows: a little bit of air chamber added to the water chamber of HR will lead to a sharply decrease in the central frequency of the resonant gap, as well as an extension in the bandwidth; however, a further increase of air volume cannot bring in such a remarkable change in the RG as that in the beginning. Still, it does broaden the bandwidth and lower the band gap location to some extent. Anyway, revelation of the RG and BG behavior against these key parameters will eventually prove to be useful in obtaining a broad, low-frequency band gap for noise transmitting suppression, mainly to form experience for reference.
In terms of practical application, especially for under-water vehicles with outlets of seawater piping systems that are underneath the water surface, the influence of high pressure on the transmission of seawater pipe noise to the outlets might attract much more attention. Hence, at this stage, focus is put on the effects of high pressure on the band gaps of the periodic seawater pipe constructed in the current work. The most directly influence of high pressure on the seawater pipe system is the variation of acoustic characteristics of the media inside both of the HR chamber and the tube. That is to say the external pressure on the piping system would lead to a change to either the acoustic speed or the density, or both, for the filled water and air. The gas density
ρ relating with pressure
p could be written as
ρ =
pM/
RT, which is deduced from the classical ideal gas law that may be given by
pV =
nRT, wherein
V and
n correspond to volume and number of moles of a substance, respectively;
T,
M, and
R are respectively corresponding to absolute temperature, molar mass, and ideal gas constant, approximately 8.3144621 J/(mol·K). For air, the average molar mass
M is approximately 0.029 kg/mol. Sound speed in an ideal gas depends only on its temperature and composition. The speed has a weak dependence on frequency and pressure in ordinary air, deviating slightly from ideal behavior. In general, the speed of sound
c is given by the Newton-Laplace equation:
c = (
Kf/
ρ)
1/2, in which the bulk modulus
Kf is simply the gas pressure
p multiplied by the dimensionless adiabatic index
γ, which is about 1.4 for air. Effects of external pressure on the sound transmission properties of the seawater pipe system with air-water chamber HRs attached periodically are illustrated in
Figure 8. Geometric parameters are chosen to be the same as those in
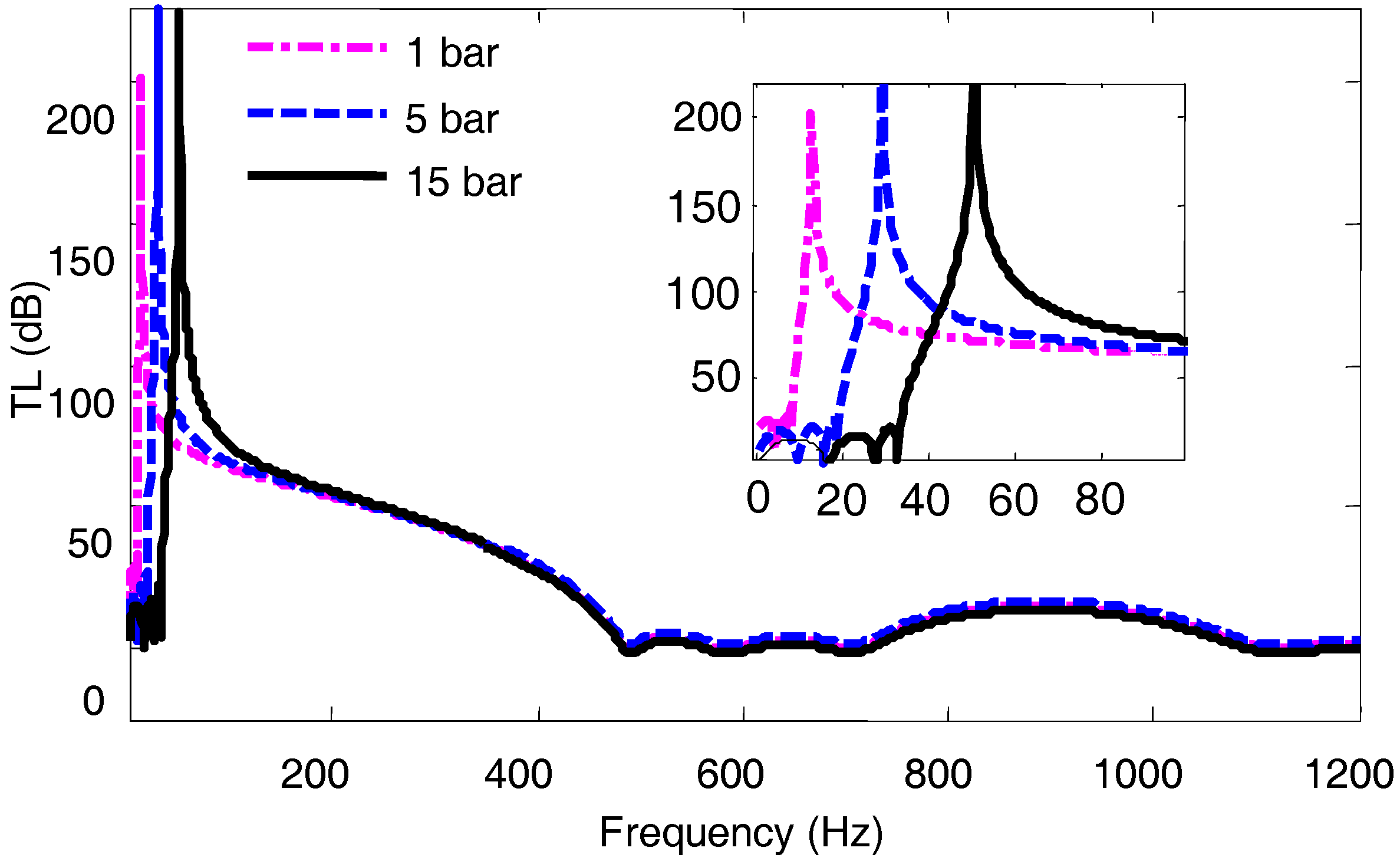
Figure 4. Temperature of the surroundings and the internal media of the pipe system is assumed to be 25 degrees Celsius. The dash-dotted, the dashed, and the solid lines correspond to pressure values of 1 bar, 5 bars, and 15 bars, respectively.
On examination of
Figure 8, some useful information can be obtained: (i) the augment of external pressure on the periodic system will bring in an increase in the lower band edge of the RG, yet has no change in the higher band edge, thus causing a reduction to the RG bandwidth. (ii) The variation of pressure does not change the second band gap induced by the Bragg scattering mechanism. This is expectable, since such a gap is generated by the interference of reflected waves by the periodic geometric cells of the system. (iii) The features of broad band gaps of the periodic system are still unchanged, although high pressure is loaded on the pipe system. The good news is that such a noise control strategy of periodic design may be applicable in the area of noise control for underwater vehicles where high pressure may be subjected. It is important to mention that the acoustic nonlinearities due to the intrinsic air behavior in the HR cavity and due to the high amplitude waves were not taken into account here. The presence of nonlinearities may introduce an interplay between nonlinear effects and spatial periodicity. As a consequence, the HR band gap width tends to increase with the acoustic amplitude in some extent, as revealed in Ref. [
28]. In this study, our analytical model is simplified (i.e., based on a linear model). However, this simplification allowed us to provide a full understand of the band gap characteristics of the metamaterial-type pipe and to guide the structure design for a seawater pipe system to avoid the low-frequency noise control problem as mentioned in the introduction. A further consideration of the present work may be the nonlinear effects, so as to capture more detailed behavior of the acoustic waves in the periodic system subjected to high pressure loadings. Nevertheless, as a first step toward the study of nonlinear effects, the investigation of linear system is reasonable.