1. Introduction
Climate change is predicted to have far reaching physical, social, environmental and economic impacts [
1,
2,
3,
4,
5]. The capacity for mankind to adapt will (in part) be governed by the pace at which impacts will manifest and the success of global adaptation endeavours which might offset (or delay) the inevitability of impacts from longer term commitments such as sea level rise.
Sea level rise is one of the more insidious (or irreversible) of the postulated climate change impacts, due in part to the fact that thermal expansion (as one of the key elements of the sea level rise budget) will continue for centuries after stabilization of radiative forcing owing to the thermal inertia of the ocean water mass and the long response time scale of the deep ocean [
6] and ice sheets [
7]. The continued trend for coastal global population migration [
4] fuels the increasing projected risks associated with sea level rise.
The Intergovernmental Panel on Climate Change (IPCC) Fifth Assessment Report (AR5) [
8] provides the most authoritative and up-to-date global assessment of the state of climate science, including sea level change, past, present and future [
9,
10]. The Coupled Model Intercomparison Project—Phase 5 (CMIP5), developed in conjunction with AR5, provides the means by which to assess the differences in future model projections of dynamical sea level changes at fine resolution scale for the benefit of climate research, policy setting and adaptation planning [
11,
12].
This paper provides a methodology for improved comparison and integration of long tide gauge record data with CMIP5 model outputs at a specific location using New York as a case study. The analysis uses state-of-the-art techniques for resolving the mean sea level signal and associated kinematic properties from the long tide gauge record at Battery Park, New York with improved temporal resolution [
13,
14]. These techniques have been extended to the ensemble model outputs for total sea level rise from CMIP5 at the nearest ocean model grid point to New York with complete model data coverage and normalized to the tide gauge record.
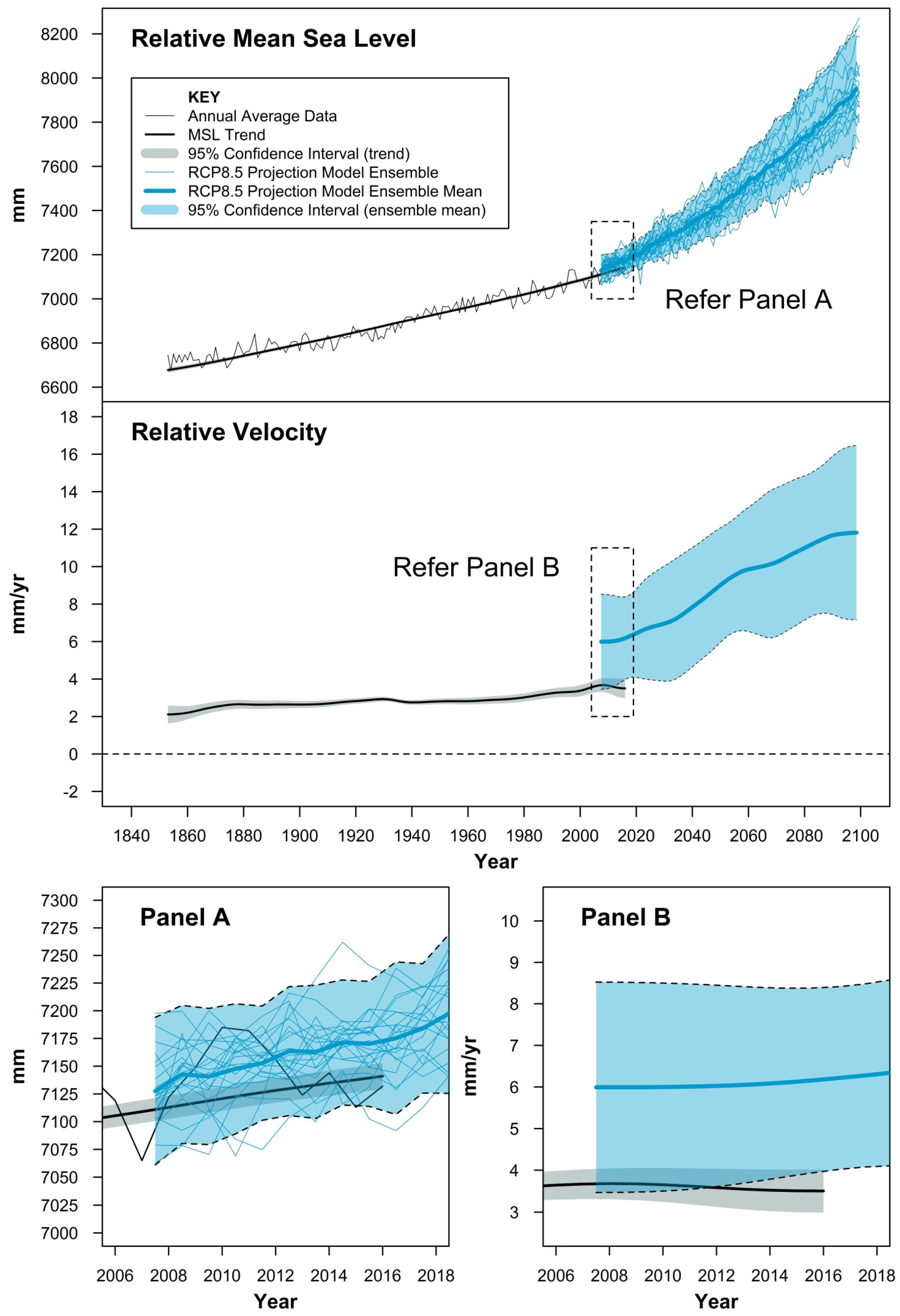
From the analysis undertaken, it is of particular interest to note that associated error margins from the ensemble model outputs for sea level rise for all Representative Concentration Pathway (RCP) experiments [
15], are ≈5–10 times that of the mean sea level trend analysis from the long New York tide gauge record over the period of overlapping coverage (2007 to 2016). When considering key kinematic properties of mean sea level (such as velocity) over the projection timescale to 2100, the error margins highlight the comparatively wide spread in the model ensemble outputs.
It is also noted that at the 95% confidence level, the initial mean relative velocity of the projected mean sea level ensemble (i.e., at 2007) is estimated at 6.3 (3.6 to 9.0) mm/year for RCP2.6, 6.0 (3.0 to 9.0) mm/year for RCP4.5 and 6.0 (3.5 to 8.5) mm/year for RCP8.5 compared to 3.7 (3.5 to 3.9) mm/year estimated from the tide gauge record at New York. If such analyses in other ocean basins of the world reveal similar artefacts, then this might be something requiring attention in the model evaluation processes of the CMIP6 design [
16] for improved utility in the development of associated projection modelling outputs for AR6 [
17].
2. Data and Methods
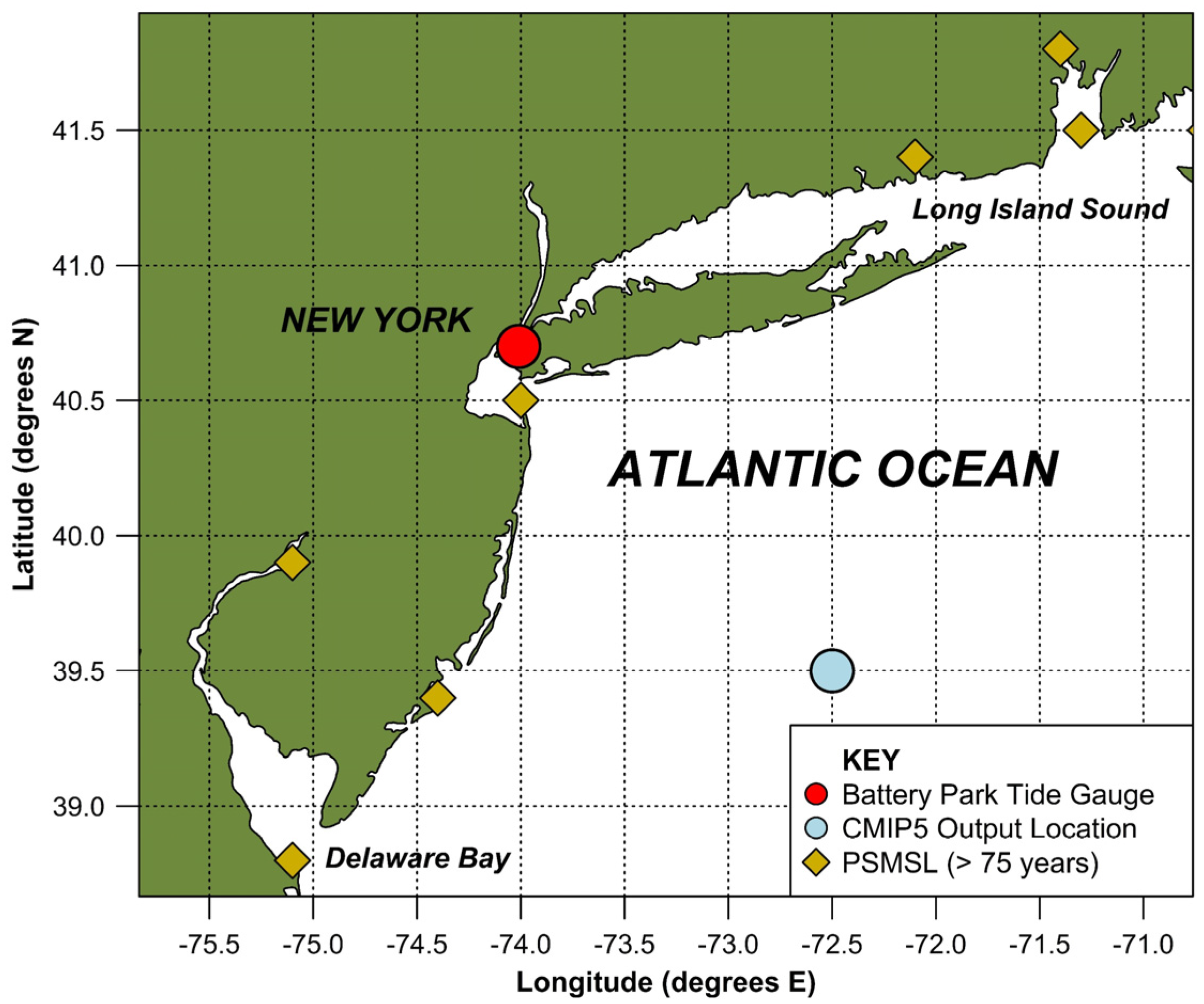
The Battery Park, New York tide gauge used in this study is the longest publicly available ocean water level record along the east coast of the USA.
Figure 1 also identifies seven additional quality tide gauge records from the PSMSL extending back prior to 1940 within proximity of the Battery Park record. The selection of the Battery Park record for the task at hand is based on the fact the key temporal regional characteristics evident in each of these time series records are also captured adequately by this much longer record. In addition, the longer record has improved utility for Singular Spectrum Analysis (SSA) to isolate the trend component.
CMIP5 regional sea level data from IPCC AR5 [
9] has been used to extract model ensemble outputs for total projected relative sea level rise for each of the respective RCP2.6, 4.5 and 8.5 experiments. The RCPs were developed for the climate modeling community as a basis for long-term and near-term modeling experiments, based on together spanning the range of year 2100 radiative forcing values found in the open literature, i.e., from 2.6 to 8.5 W/m
2 [
18].
Time series data for each of the respective RCP experiments have been extracted at the nearest grid point to the Battery Park tide gauge record, for which there is complete ensemble model coverage (refer
Figure 1).
It is important to note that no allowance for vertical land motion has been applied to the tide gauge analysis. The reason for this is that the CMIP5 outputs for which we are comparing the tide gauge results too, have already been corrected for glacial isostatic adjustment to project sea surface height “relative” to the land.
All analysis and graphical outputs have been developed by the author from customized scripting code within the framework of the R Project for Statistical Computing [
19] and are available upon request. The applied methodology can be appropriately partitioned into analysis of the historical tide gauge record and that of the CMIP5 ensemble projection model outputs.
2.1. Historical Tide Gauge Analysis
Annual average time series data for the Battery Park, New York tide gauge have been analysed for the period spanning the timeframe 1853–2016, which are available from the public archives of the Permanent Service for Mean Sea Level (PSMSL) [
20,
21]. This record contains 18 missing years of data which have been filled from the extensive composite time series work by Hogarth using near neighbour tide gauge records [
22].
Analysis of the observational tide gauge record at Battery Park, New York is based upon the use of the “msltrend” extension package in R [
23]. This package has been specifically built as a state-of-the-art analysis tool for decomposing annual average ocean water level records to estimate mean sea level with improved temporal resolution [
13,
14]. The package development has been underpinned by time series analysis testing and parameter optimisation using all records in the PSMSL exceeding 100 years in length [
24] that are a minimum of 85% complete. Details of the methodology underpinning “msltrend” and the analysis of the Battery Park record can be broadly summarised in the following three steps:
Step 1: Estimation of mean sea level. The time series is decomposed using a one dimensional Singular Spectrum Analysis (SSA). The method decomposes the original record into a series of components of slowly varying trend, oscillatory components with variable amplitude, and a structure-less noise [
25]. The trend (or in this case mean sea level) can be isolated by reconstructing only the components that possess distinctly “trend-like” characteristics. Trend components are automatically detected and reconstructed based on the singular value having a relative contribution threshold ≥75% contained within the low frequency bin ≤0.01.
Step 2: Estimation of mean sea level velocity. The approach adopted to estimating the time varying velocity is based on the first derivative of a fitted cubic smoothing spline. This approach provides a realistic representation of a smoothly varying trend, so long as the cubic smoothing spline model fit can accurately describe the reconstructed trend-like components of the SSA decomposition.
Trial and error on a wide variety of long records in PSMSL indicates that by fitting a cubic smoothing spline to the trend (determined in Step 1) with approximately 1 degree of freedom per every eight years of record length, optimises the fit whilst removing the extraneous effects of the “sawtoothing”. This so-called “sawtoothing” effect can occur because the isolated trend components from the SSA decomposition are portions of linearly additive components that reconstruct the original time series and thus are not precisely smooth or curvilinear at point to point scale.
For the numerous records tested, the coefficient of determination (R2) of the fitted spline to the estimated mean sea level (trend) exceeds 0.99 in all cases, providing a high degree of confidence in this form of model to estimate the associated time varying velocity.
Step 3: Estimation of errors. The estimation of errors in the trend and associated velocity is one of the more significant features of the “msltrend” package and is based on bootstrapping techniques. This process initially involves fitting an autoregressive time series model to remove the serial correlation in the residuals between the SSA derived trend and the original annual average time series [
26]. The uncorrelated residuals are then tested to identify change points in the statistical variance along the time series.
Where a change point is detected, bootstrapping processes to randomly sample uncorrelated residuals are quarantined between identified variance change points (otherwise known as “block” bootstrapping). The randomly sampled uncorrelated residuals are then added to the SSA derived trend and the process repeated 10,000 times (Steps 1 and 2). From the extensive pool of outputted trends and associated velocities, standard deviations are readily calculated to derive robust confidence intervals.
2.2. CMIP5 Projection Model Output Analysis
The CMIP5 models used in AR5 provide projection outputs of sea surface height at each grid point for model experiments that meet requisite evaluation protocols [
27]. These data are publicly available in netCDF format from the Integrated Climate Data Center (ICDC) [
28] with yearly outputs spanning the period 2007 to 2100 on a spatial resolution grid of 1° × 1° for RCP2.6, 4.5 and 8.5 experiments. The CMIP5 multi-model ensemble contains only 16 models for the RCP2.6 experiment however, the RCP4.5 and 8.5 experiments are based on all 21 models (Dr Mark Carson, Institute of Oceanography, ICDC, University of Hamburg, 2017, pers.comm., 19 June). These outputs are based upon modelled responses to dynamic ocean responses, atmospheric loading, land ice, terrestrial water sources and glacial isostatic adjustment in order to estimate sea surface height “relative” to the land. These time series are extracted from the respective RCP2.6, 4.5 and 8.5 netCDF format files available from the ICDC [
28] using customised R scripting code at the point of interest (refer
Figure 1). The following methodology has then been applied to these data products in order to both assimilate and compare them to the observational tide gauge data:
Step 1: Normalise ensemble model outputs to tide gauge datum. The ensemble model sea surface height output products are based on a 20 year moving average with the modelling start point set at 1986–2005 (i.e., centred around 1995). The annual time series output products from the ICDC for AR5 start at 2007 and have therefore been normalized to the Battery Park tide gauge record by using the estimate of mean sea level derived from the SSA decomposition in 1995.
Step 2: Estimation of projected mean sea level velocity. The approach adopted is similar to that described for the tide gauge record analysis above, whereby a cubic smoothing spline has been fitted to each of the respective ensemble sea surface height time series from 2007 to 2100 to estimate the associated time varying velocity. The only difference is that less degrees of freedom are necessary for the smoothing spline (1 degree of freedom per 15 years) in order to achieve the same quality of model fit (R2) owing to the very different characteristics of the sea surface height time series from the model projections. The selection of the optimum spline stiffness for the model outputs is somewhat arbitrary based on trial and error.
Step 3: Estimation of means and errors. The pool of outputted sea surface height time series and associated velocities for each of the respective RCP experiments enables provision to calculate simple arithmetic means and standard deviations from which to estimate robust confidence intervals.
3. Results
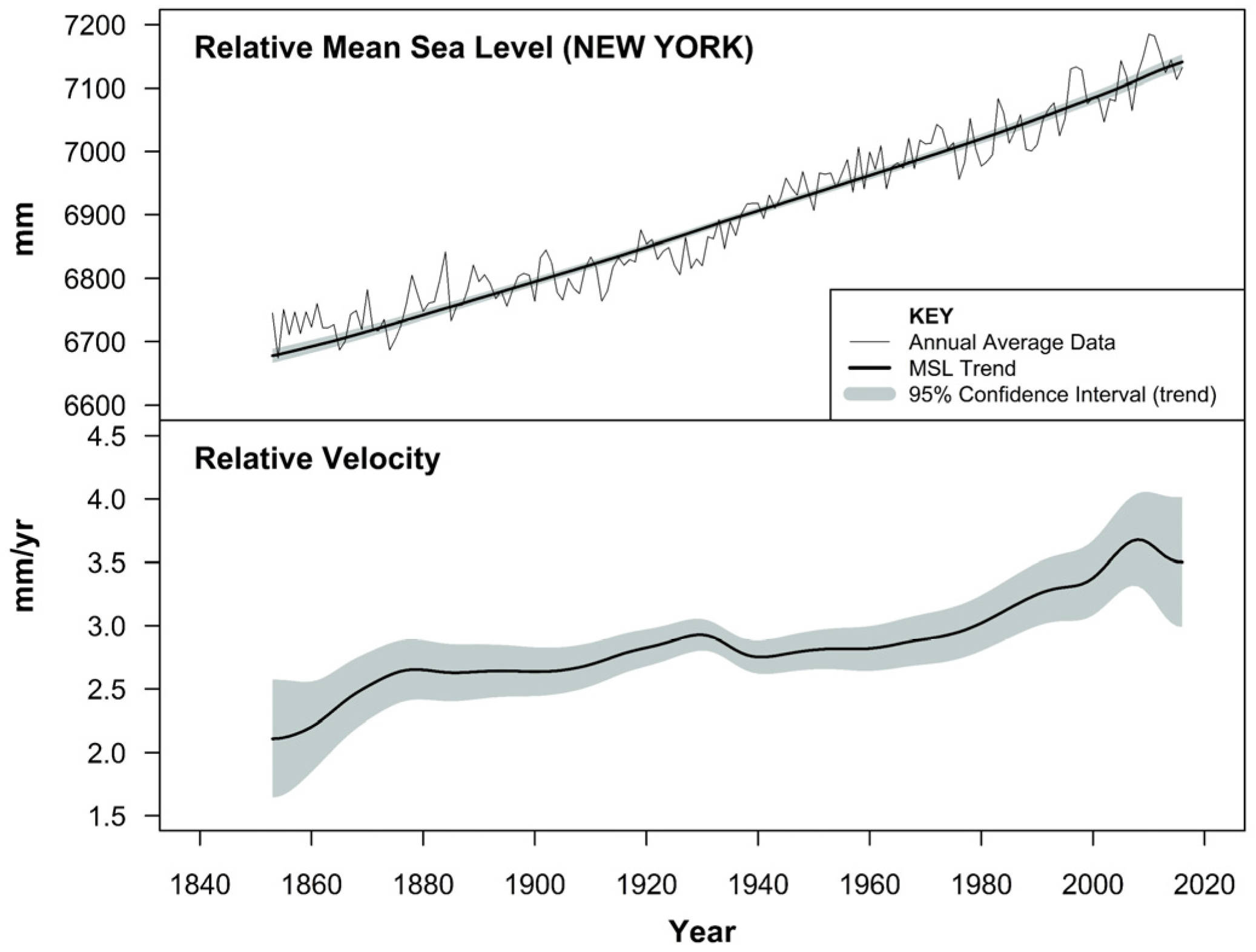
The results from the decomposition of the Battery Park tide gauge record are diagrammatically summarised in
Figure 2. The decomposition of the annual time series in the top panel highlights the nature of the internal climate variability influence on mean sea level at this location, with an amplitude in the range of ≈50–60 mm. The removal of such influences reveals the mean sea level signal which can be assumed to approximate the climate change signal resulting from external forcings. The higher resolution of the kinematic properties of the mean sea level signal provide more instruction on the how relative mean sea level (that is “relative” to the land) has been changing from 1853 to present at this gauge location. Points to note include:
The relative mean sea level has been rising continuously at this location over the 163 year record (≈465 mm)
The relative velocity has continued to increase steadily over the course of the record peaking at around 3.7 (3.3 to 4.1) mm/year (95% CI) in 2008;
At the 95% confidence level, the relative velocity in 2016 at 3.5 (3.0 to 4.0) mm/year is higher than the velocity at the start of the record in 1853; and
Time varying relative velocity increasing over time suggests the presence of a positive acceleration.
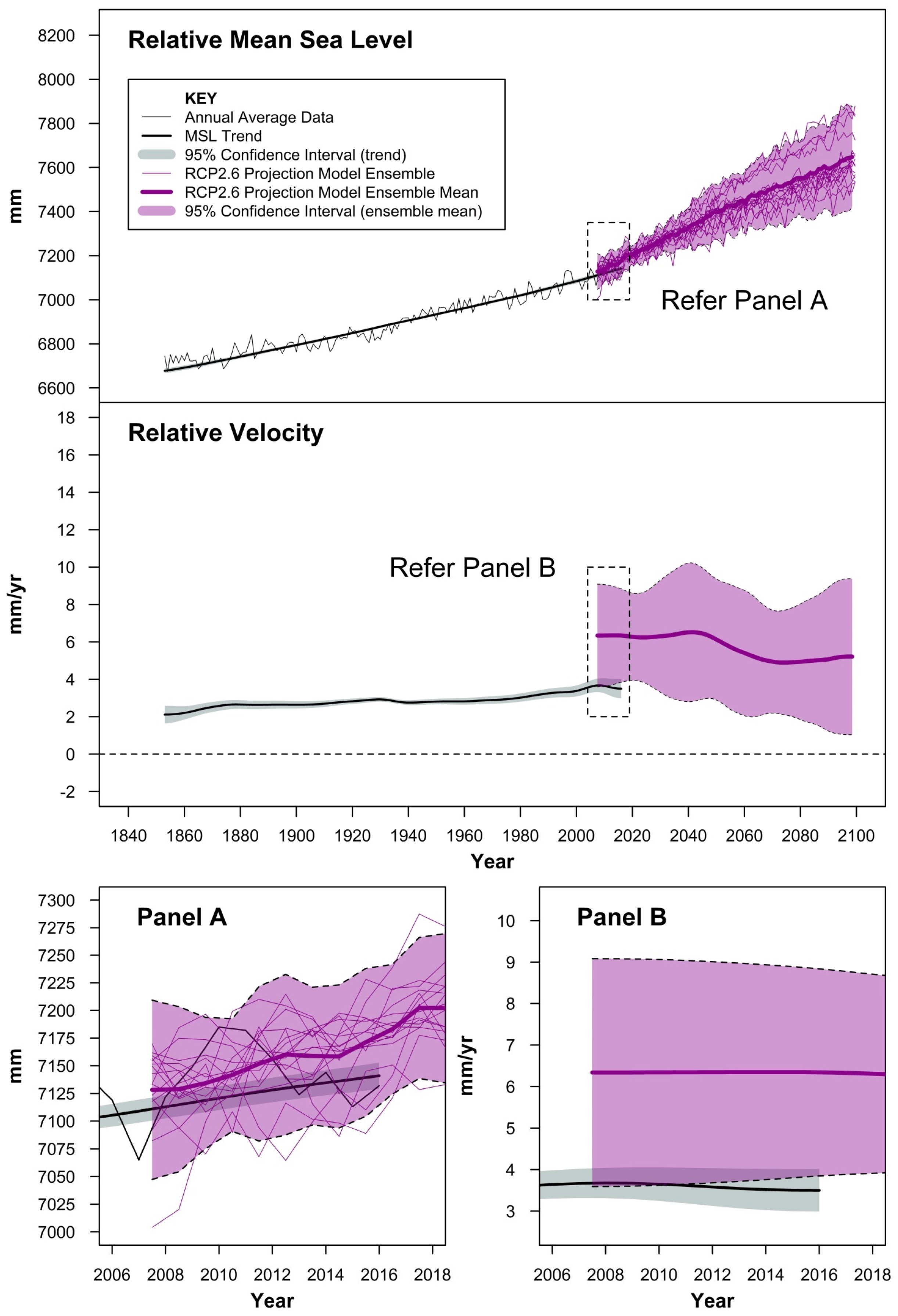
Figure 3,
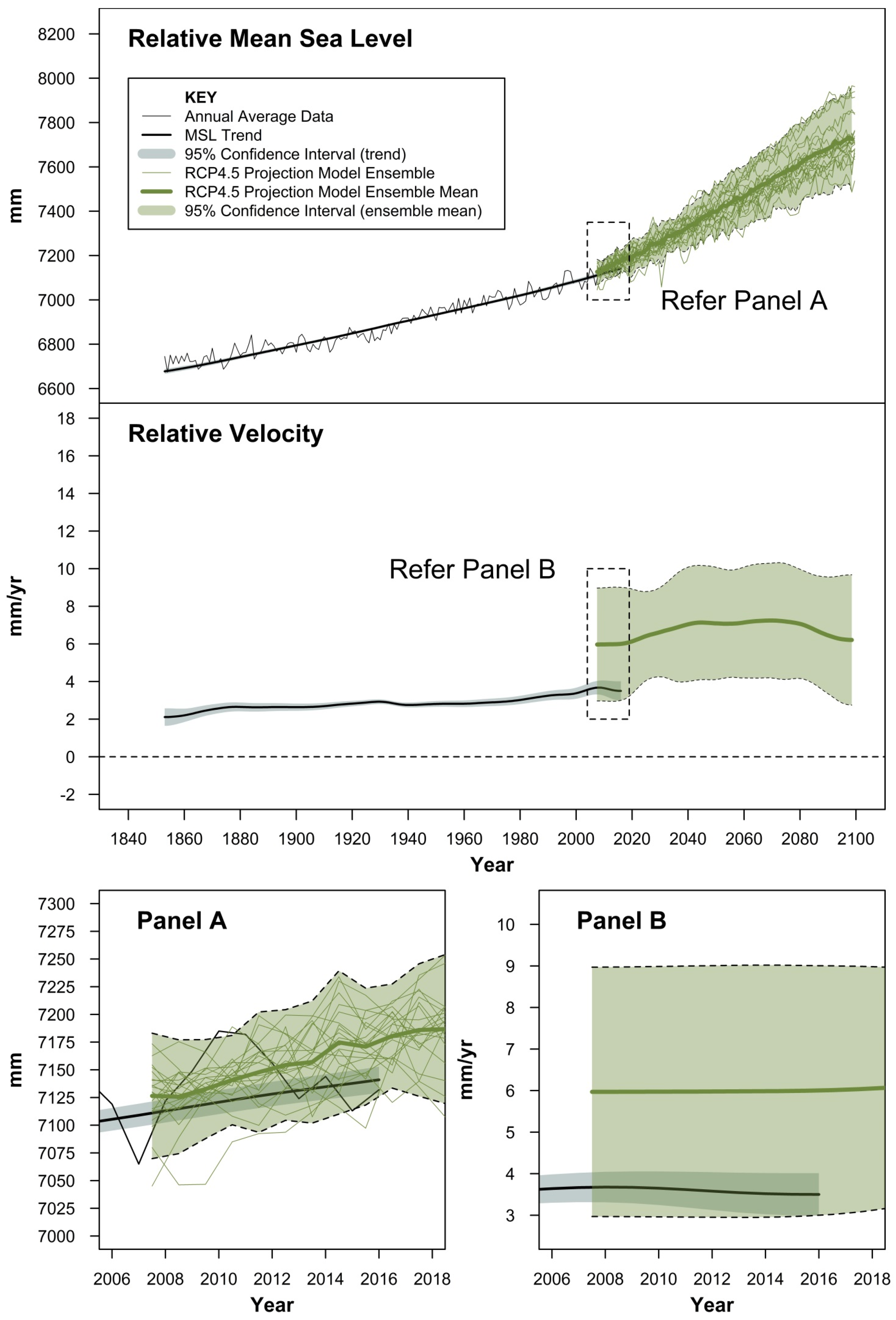
Figure 4 and
Figure 5 summarise the analysis of the ensemble outputs corresponding to the RCP2.6, 4.5 and 8.5 experiments, respectively, integrated with the observational tide gauge analysis (
Figure 2). The top panel in each figure integrates the tide gauge time series with the ensemble projection outputs. The middle panel provides an estimate of relative velocity in mean sea level from both data sets while the bottom 2 panels provide zoomed in versions of the analysis for the period of common coverage (2007–2016) of both the observational record and CMIP5 ensemble projection modelling products at the 1° × 1° grid resolution. All three figures use the same scales for ready comparison between RCP’s.
It is evident that internal modes of climate variability built into the projection modelling products (to replicate ENSO, PDO, etc.) would appear visually to be of comparable scale and amplitude to that evident over the course of the observational record at this location.
As anticipated, the mean velocity of the projection model ensembles increase in line with the increased radiative forcing associated with the respective RCP experiments. Further, the mean velocity stabilises mid-century before declining slightly to 2100 under the RCP2.6 experiment, increases slightly to mid-century remaining relatively steady to 2100 under RCP4.5 and increases steadily to 2100 under the RCP8.5 experiment. These temporal characteristics mirror those of the global mean sea level projections for the respective RCP experiments advised in AR5 [
9], though the scale of the initial velocities are considerably higher at this grid location.
The mean of the ensemble for all RCP experiments at this location exhibit a higher gradient (and therefore rate of rise) over the period of common coverage than for the tide gauge record.
Specifically, at the 95% confidence level, the mean velocity of the projection model ensembles estimated in 2016 for RCP2.6, 4.5 and 8.5 are 6.3 (3.8 to 8.8), 6.0 (3.0 to 9.0) and 6.2 (4.0 to 8.4) mm/year, respectively compared to 3.5 (3.0 to 4.0) mm/year for the tide gauge record. In 2016, the mean relative velocity of the model projection products is of the order of 2.5–2.8 mm/year higher than the estimate observed from the tide gauge record.
4. Discussion
The techniques espoused in this case study provide improved means by which to test the veracity of the CMIP5 (and future CMIP6) sea level projections to replicate observational data at increasingly localized scales, using long quality tide gauge records.
The differing nature of the respective data sets present challenges in aligning analysis products to be directly comparable. For example, with the tide gauge analysis, it is a relatively straightforward task to remove the internal modes of climate variability (and other cyclical dynamic influences) from the time series record using SSA as described. The resulting mean sea level (or trend) is assumed to be principally attributable to external (or climate change) forcings. However, the CMIP5 projection model ensembles are designed to encompass a wide range of possible climate outcomes embedded with randomly phased internal modes of climate variability over the future projection horizon. The larger the pool of ensemble model outputs, the better the chance that internal climate variability can be accommodated (or averaged out) to reveal the more consistent sustained response to the external (or climate change) forcing.
However, there are only 16 CMIP5 ensemble sea surface height model projection products available for RCP2.6 and 21 for the RCP4.5 and 8.5 experiments. Thus, owing to the intrinsic nature of the projection modelling products, the ensemble mean sea level and associated velocity will be associated with much larger error margins than the analysis of a singular tide gauge time series which is clearly evident in
Figure 3,
Figure 4 and
Figure 5. By virtue of these large error margins, at least from a statistical perspective at the 95% confidence level, the projected mean sea level and associated velocity over the period of common coverage for all RCP experiments are comparable to that of the tide gauge record for this location. Unless the CMIP6 framework [
16] results in a substantial increase in the available number of sea surface height model projections, then the spread of the ensemble products is likely to remain similar for AR6, irrespective of increased performance and improved resolution of the models.
To tease out whether the CMIP5 projection outputs at this case study site are indeed aligned with the observational record, we perhaps need to look a bit deeper with additional resources available. As advised in
Section 3, the mean relative velocity of the projection modelled outputs for 2016 are of the order of 2.5–2.8 mm/year higher than that from the Battery Park tide gauge analysis. The CMIP5 ensemble outputs provided by the ICDC have the Glacial Isostatic Adjustment (GIA) correction inverted so the projection outputs provide continuity of the picture relative to the land (Dr Mark Carson, Institute of Oceanography, ICDC, University of Hamburg, 2017, pers.comm., 31 March). For the CMIP5 grid point considered (refer
Figure 1), the GIA estimate is approximately −1.4 mm/year, whereas the total vertical land motion (VLM) which includes GIA, measured from a GPS station collocated at the Battery Park tide gauge site is approximately −2.12 ± 0.62 mm/year (1σ) [
29,
30]. Thus if the relative tide gauge record were corrected to incorporate GIA only (and not all VLM sources) in order to be more directly comparable to the CMIP5 ensemble model outputs, then the actual gap between the relative tide gauge velocity and the projection modelled outputs over the common period would be wider again. It is noted that there are other GPS stations within 20 km of the Battery Park tide gauge with measured VLM ranging from −1.02 ± 0.30 (Willets Point) to −2.65 ± 0.27 mm/year (Sandy Hook) [
29,
30]. Whilst it is acknowledged that estimates of GIA and VLM are sources of uncertainty, measured VLM will play an increasingly important role for augmenting mean sea level records from tide gauges, particularly as the GPS measurements lengthen.
It is also worth noting that this paper attempts to compare the characteristics of the overlapping parts of the tide gauge record and projection modelling products for a comparatively small time window (10 years) at the end and start of the respective records. Although every effort has been made to take advantage of state-of-the-art analytical techniques to improve the resolution of the mean sea level signal from the tide gauge record, in reality time series analysis techniques are inherently limited by the ubiquity of end effects. Extensive time series analysis testing and optimization for sea level research [
24,
31] has limited these influences, but, notwithstanding, the broadened error margins at the ends of the respective records take some account of the uncertainties of the respective mean estimates (mean sea level and velocity) near the ends of such records. The utility of such analyses will therefore continue to improve as the length of the overlapping records increase into the future.
One element not examined during the course of this case study is whether there would be any particular physical or oceanographic reason why the rise in mean sea level at a point ≈200–230 km offshore (projection modelling grid point) would necessarily be occurring at a faster rate to that observed at the land/sea interface by a tide gauge. This issue might be a worth investigating on a more global scale within the context of the ensemble sea surface height model projection products available, but is beyond the scope of this study.
5. Conclusions
The analysis of the long Battery Park record enables a more temporally resolved and accurate estimate of mean sea level through the identification and removal of contaminating influences of decadal to multi-decadal timescale (e.g., [
32,
33,
34,
35,
36,
37]). This presents an opportunity to improve evaluation of climate models to the rate of mean sea level rise at increasingly finer resolution. Similarly, these processes present an opportunity to augment the broader, global Archiving, Validation and Interpretation of Satellite Oceanographic (AVISO) data products [
38] currently used to evaluate CMIP5 dynamic sea surface heights [
27], that are only 20–25 years in length. The longer decadal and multi-decadal influences are not able to be removed from these satellite data products at this point in time.
The higher mean relative velocity of the CMIP5 model projection products compared to that observed from the tide gauge record over the common time frame (2007–2016) from this case study might prove to be site specific. However, if this proves to be a more common phenomenon across other ocean basins in key locations, then this might raise the necessity to improve the evaluation of the ocean component of the climate models for CMIP6 using a key set of long PSMSL gauge records and the techniques espoused in this paper as a guide. In addition to integrating more advanced oceanographic phenomena at increasingly finer resolution into the ocean model components, e.g., [
39], the techniques espoused in this paper might also be considered part of the evolutionary process by which to improve the robustness and veracity of these critical projection modelling tools at increasingly finer resolution over the course of CMIP6 and AR6 and beyond.