CaMEL and ADCIRC Storm Surge Models—A Comparative Study
Abstract
:1. Introduction
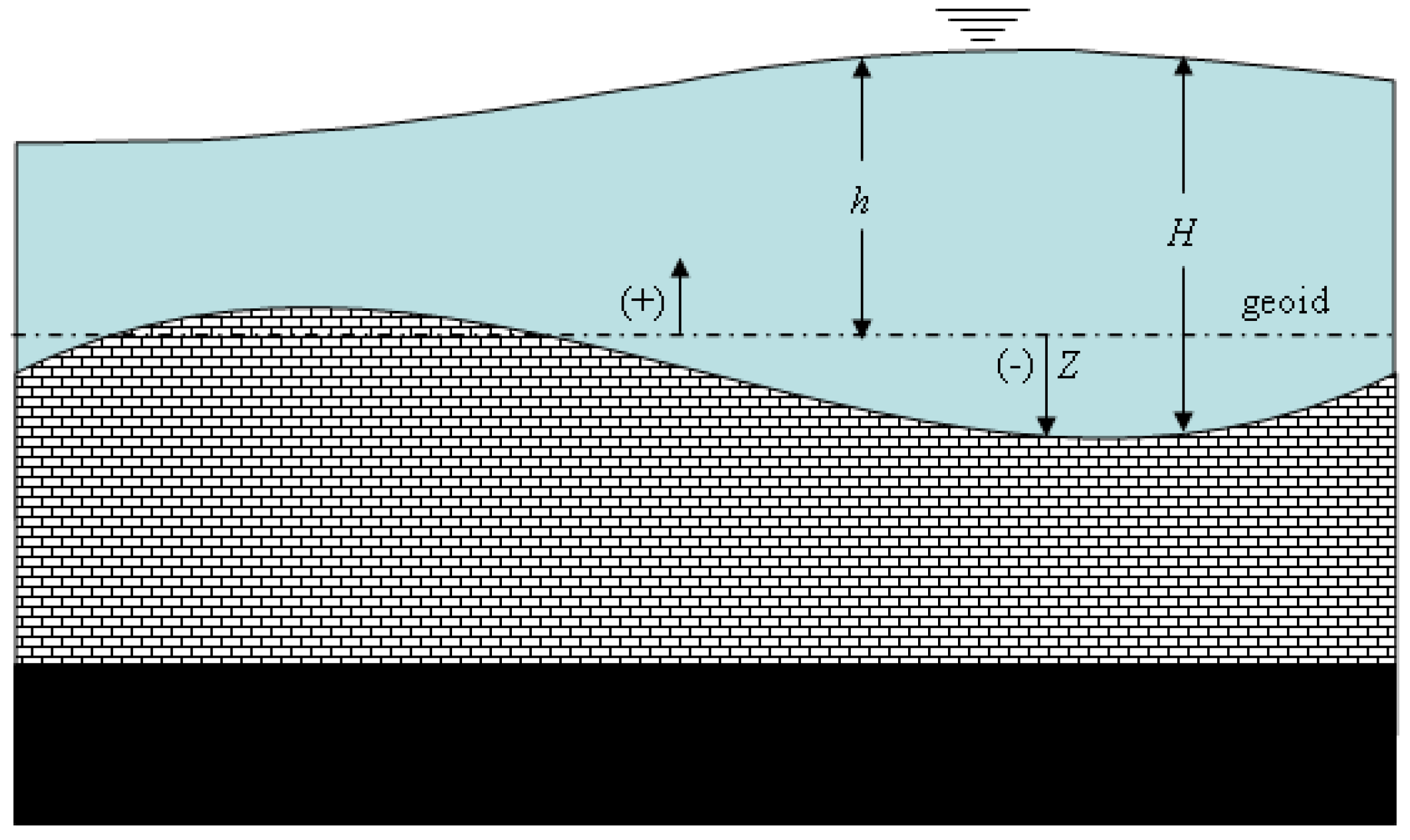
2. Governing Equations
3. CaMEL Model Approach
3.1. Predictor
3.2. Corrector
3.3. CaMEL Finite Volume Method for Momentum Equation
3.4. CaMEL Finite Element Formulation
3.5. CaMEL Solution Strategy
4. ADCIRC Model Approach
5. CaMEL Parallel Implementation
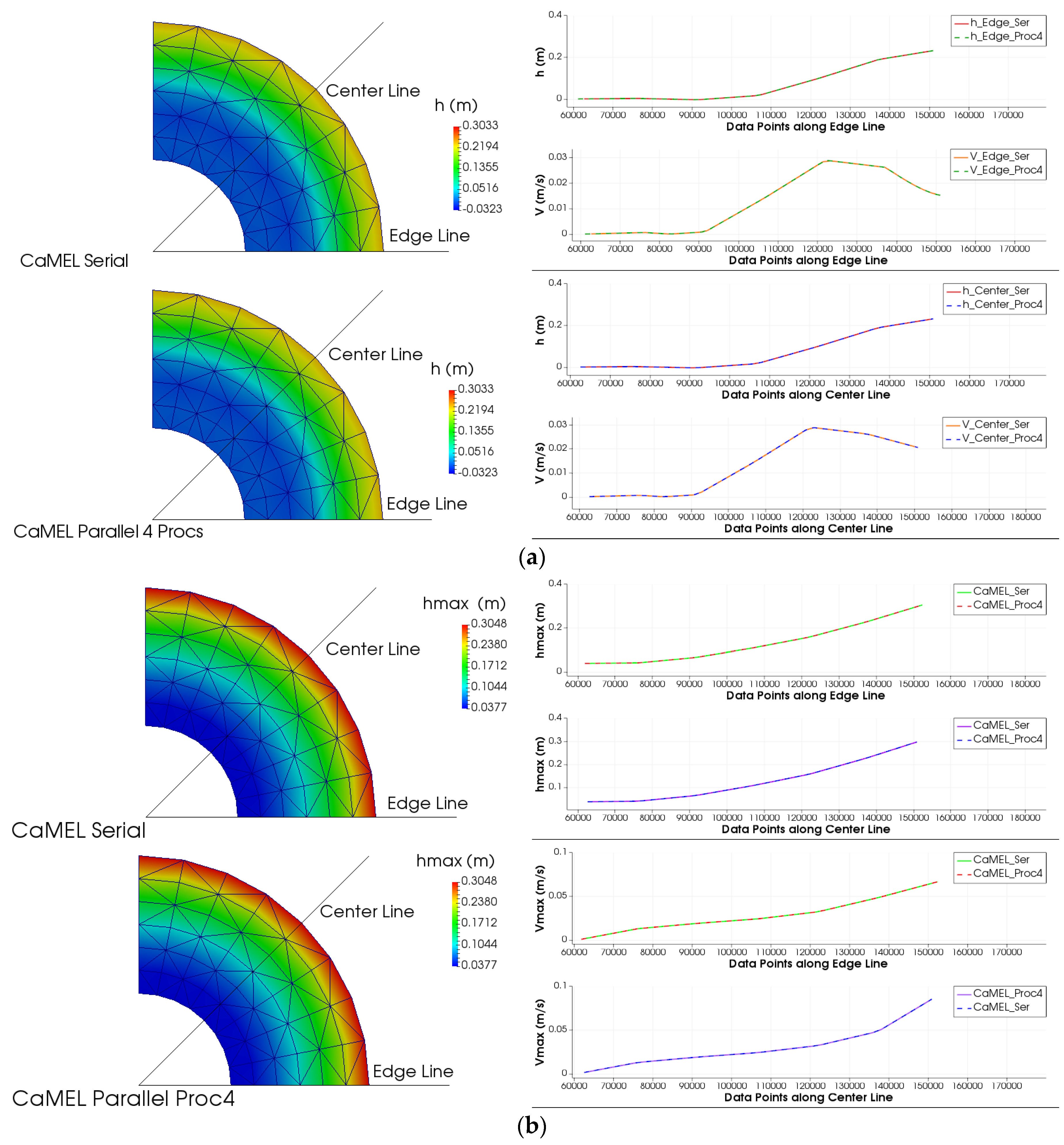
6. Benchmarking of Parallel CaMEL Model
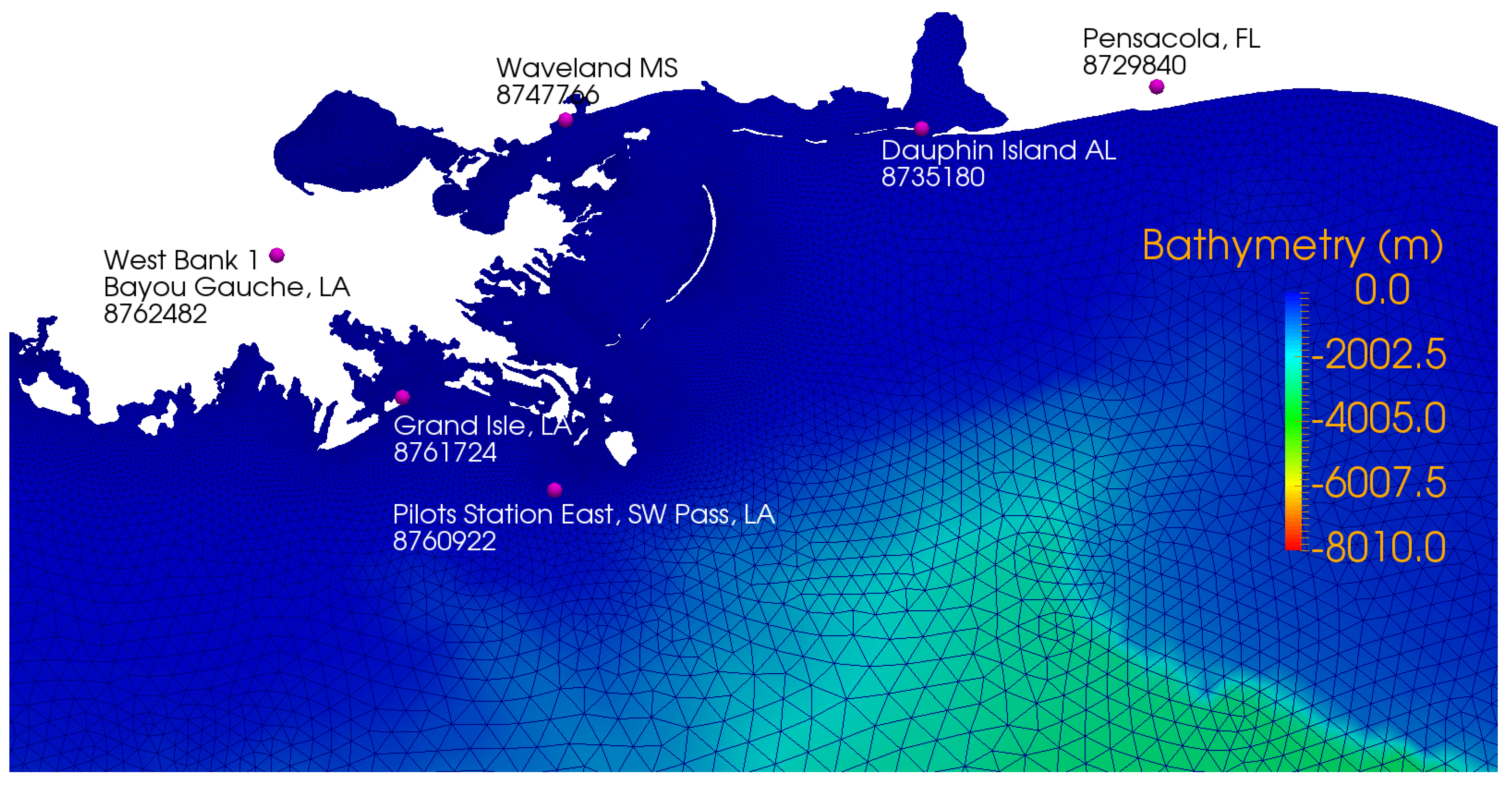
7. Model Comparison Using Katrina Storm Surge Hindcast
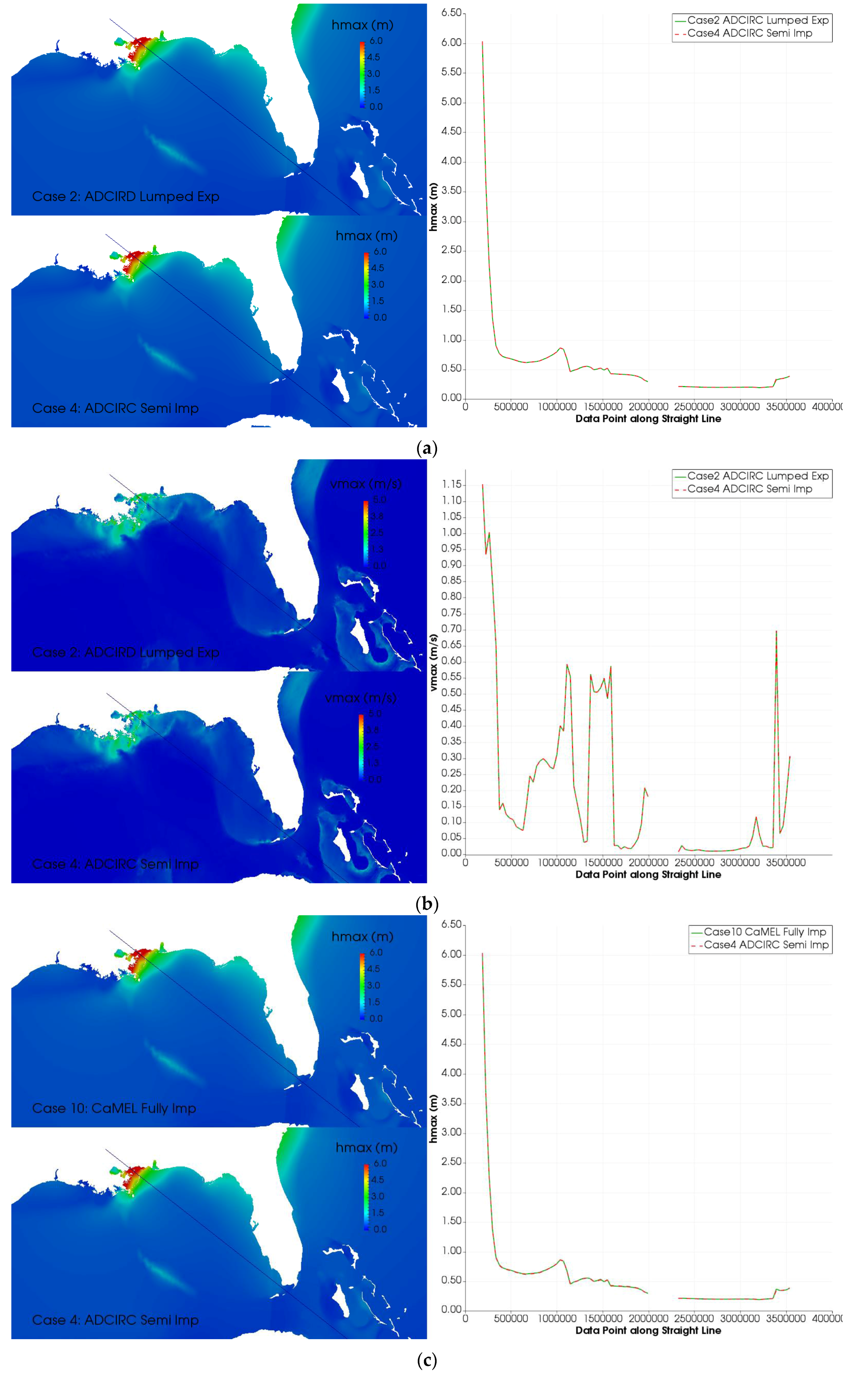
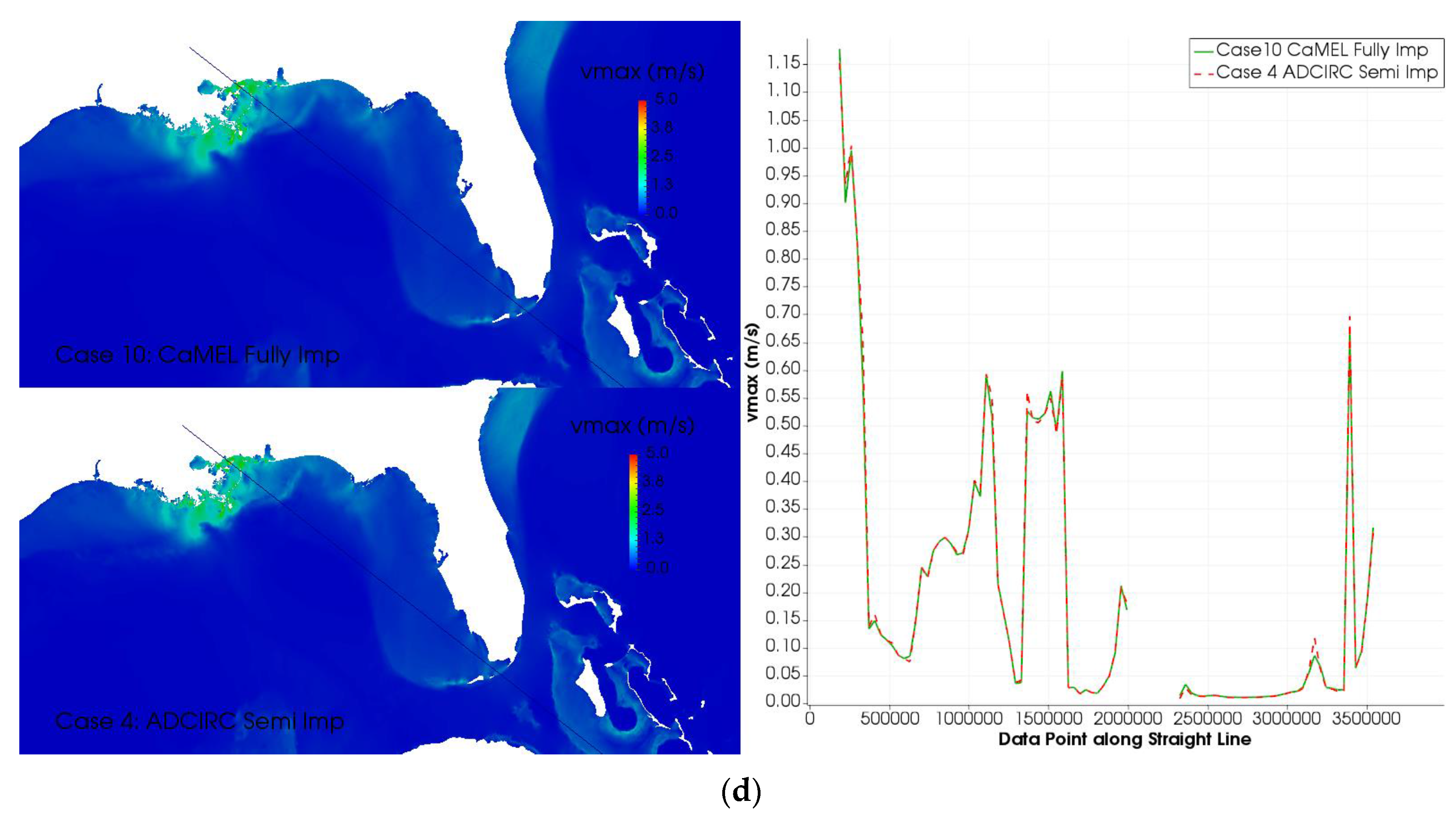
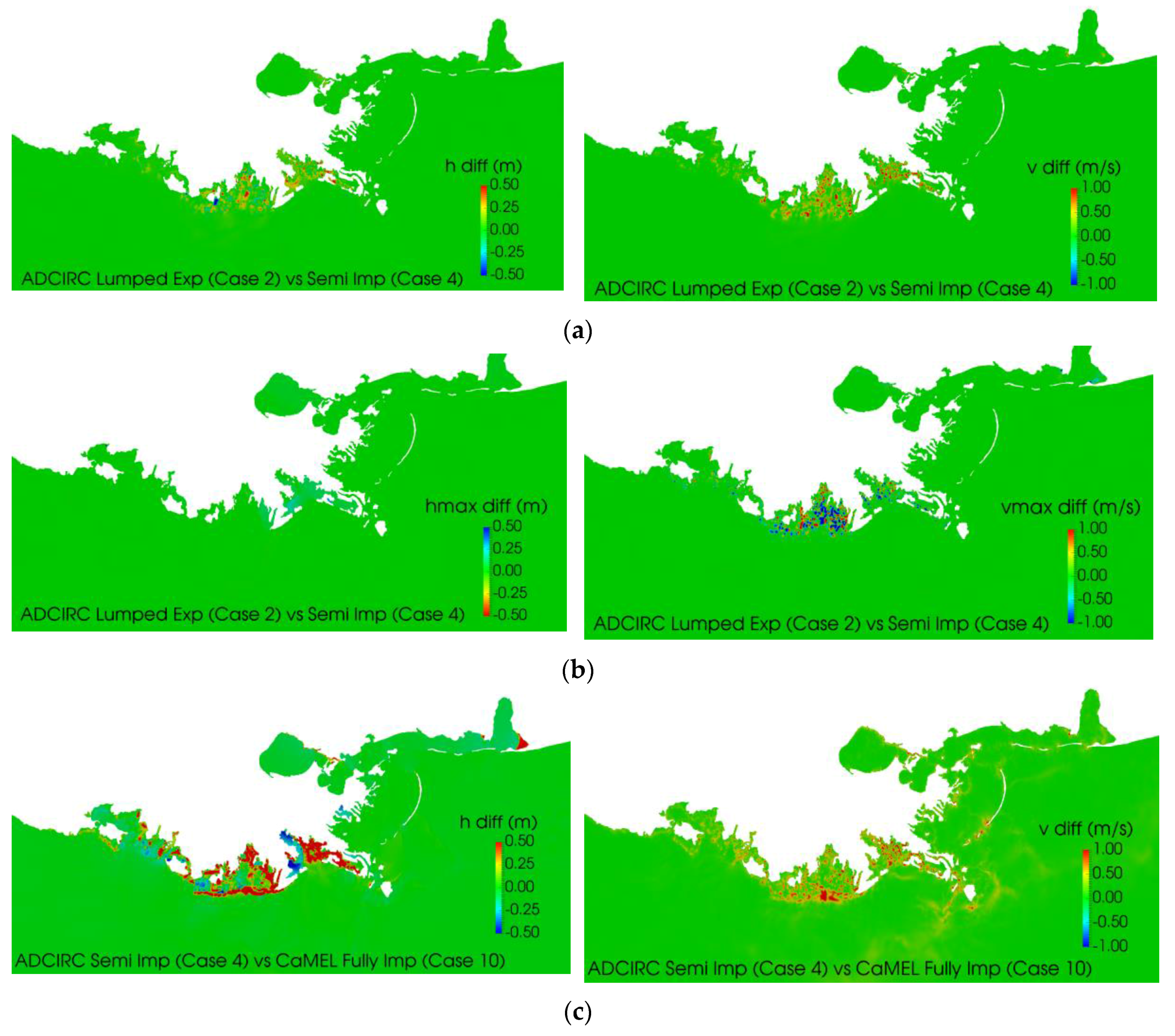
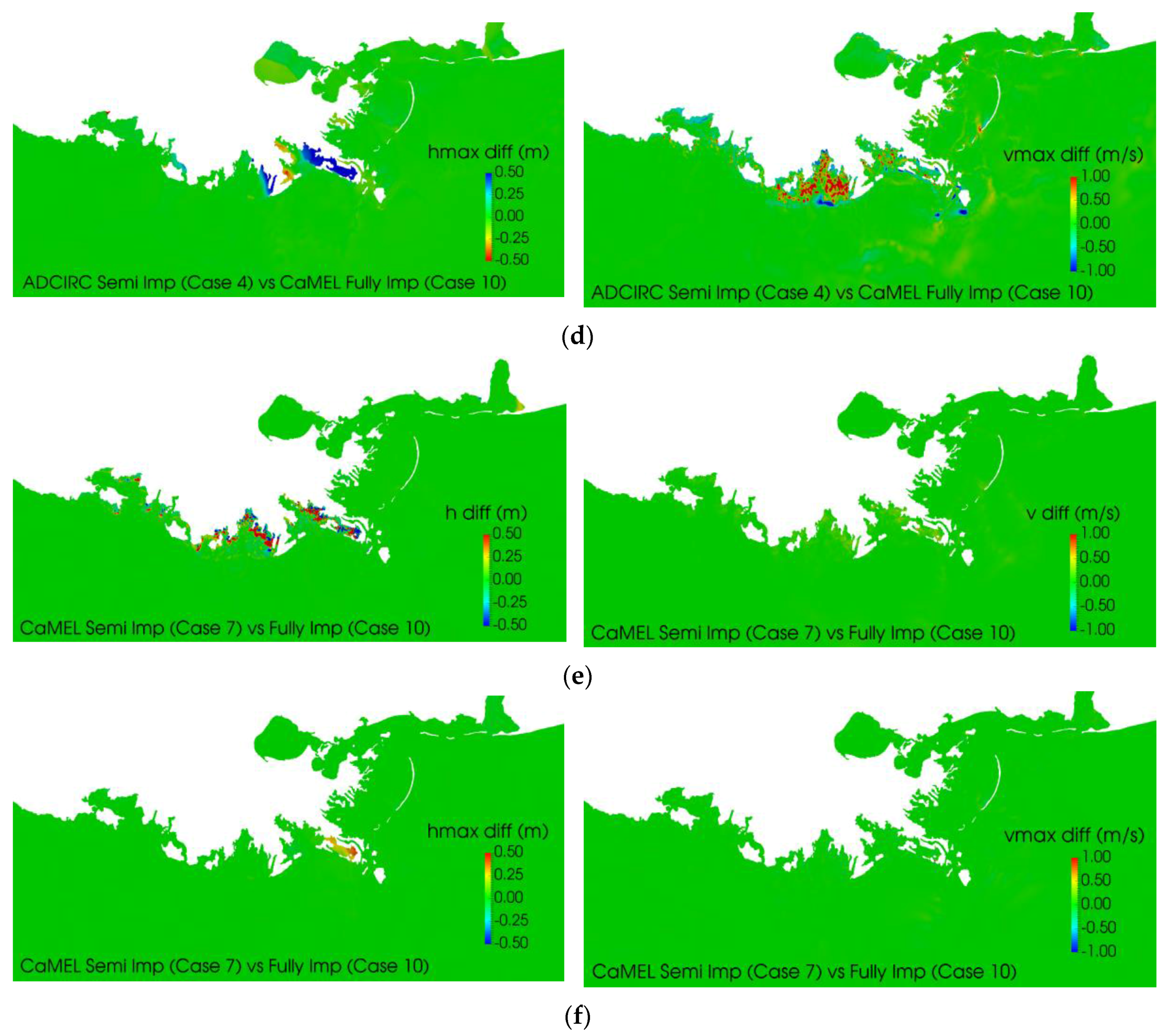
7.1. Solver Effects
7.2. Time Step Effects
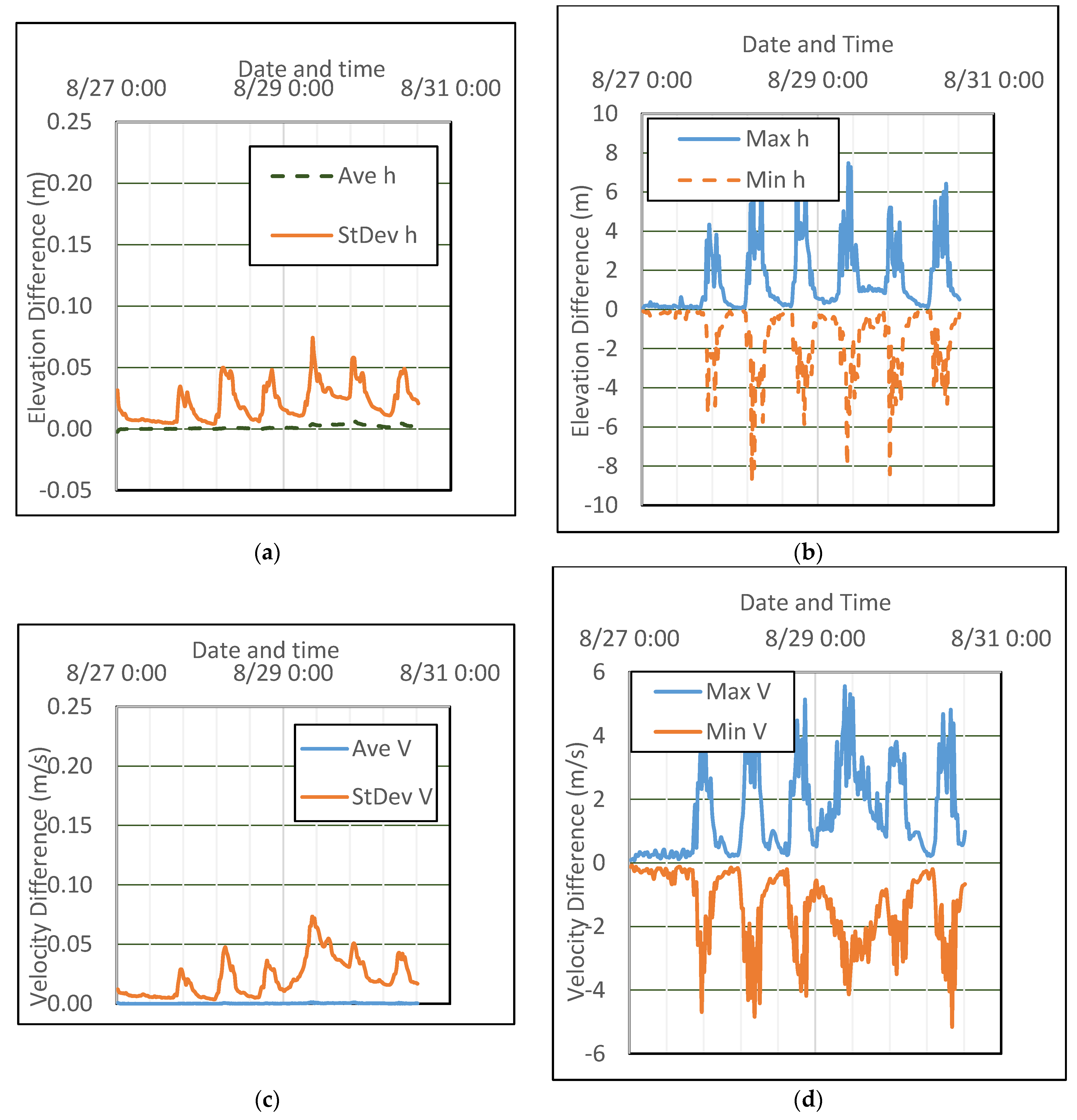
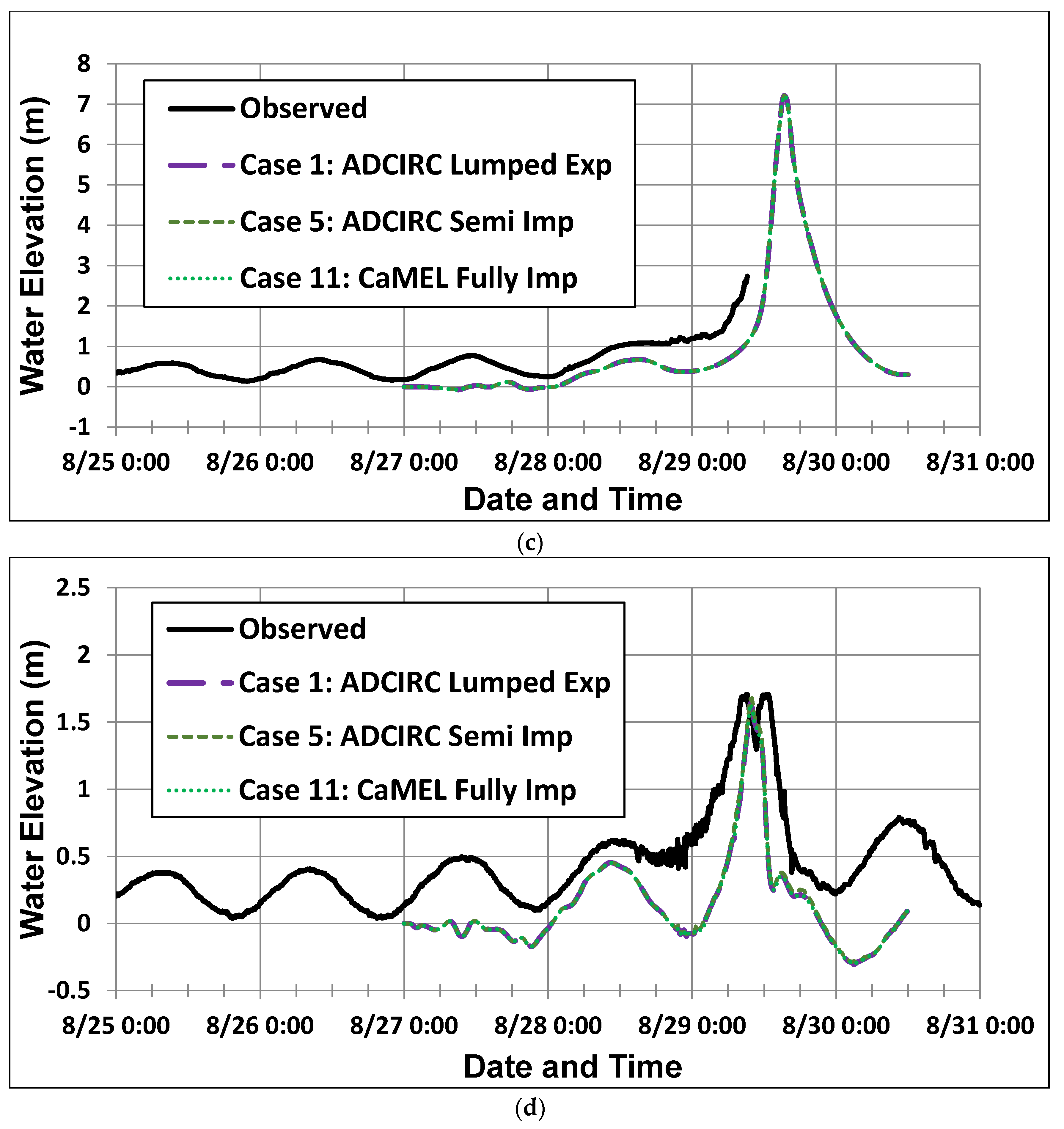
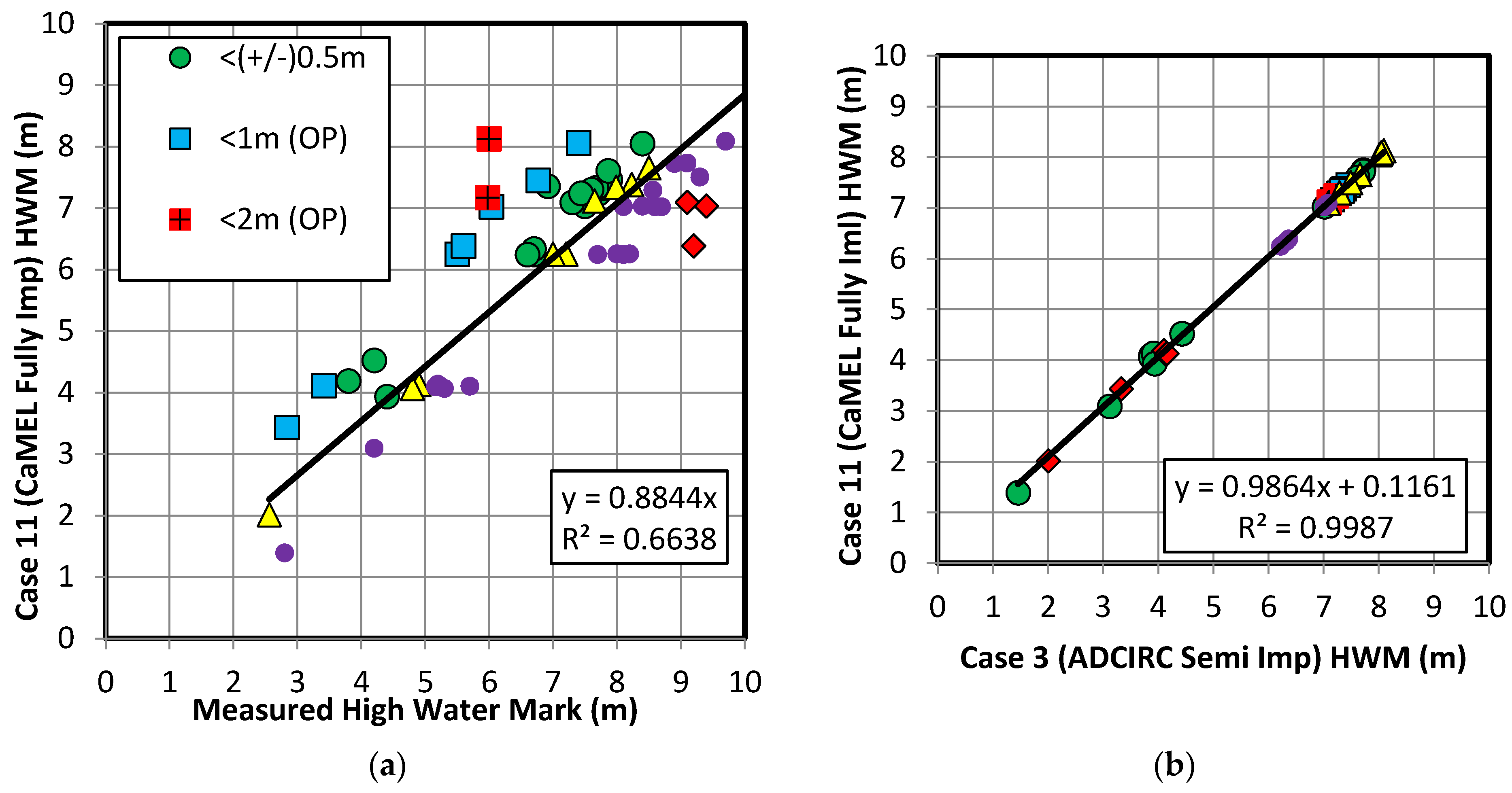
7.3. Buoy Time Series and High Water Mark Comparison
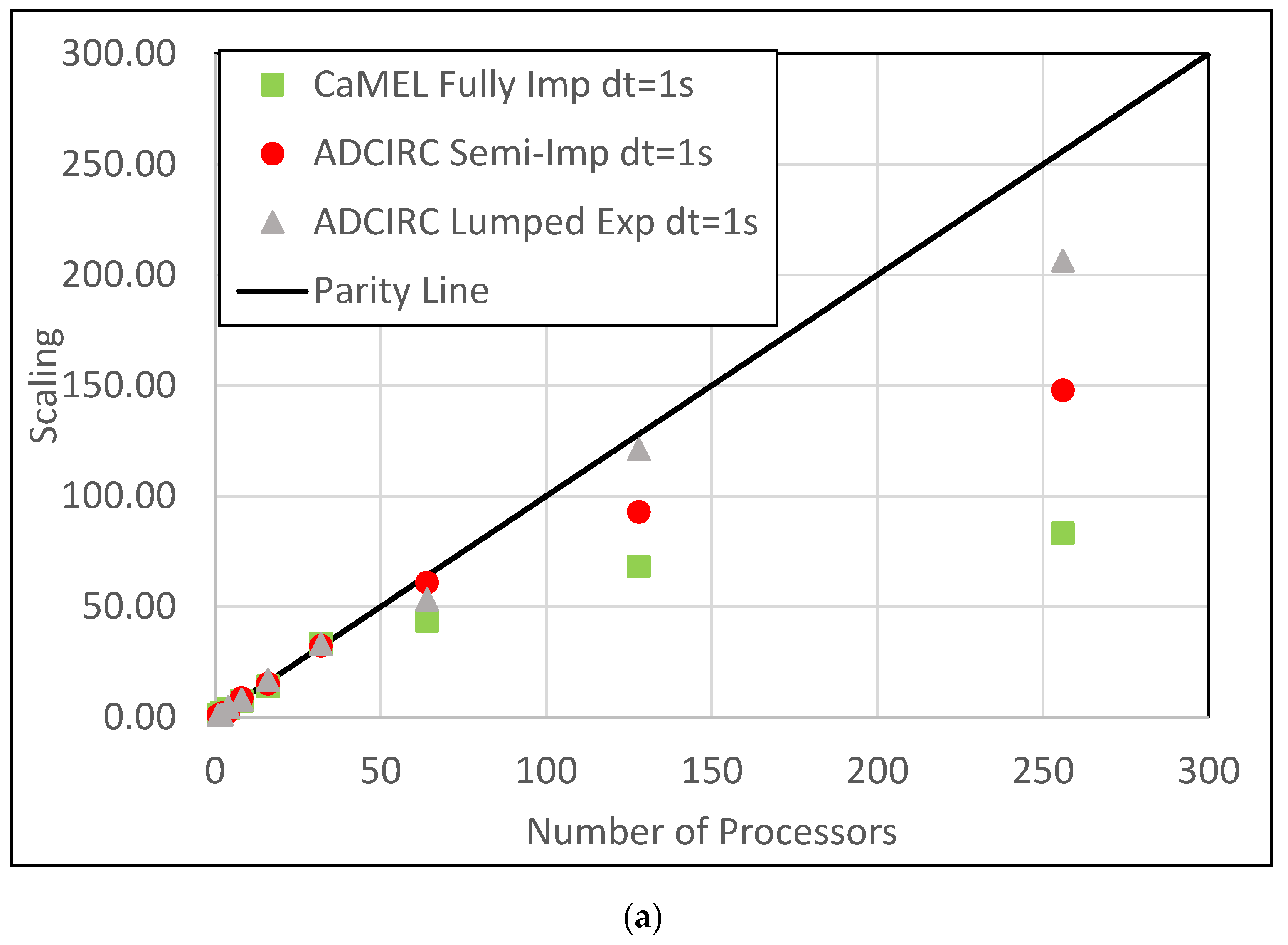
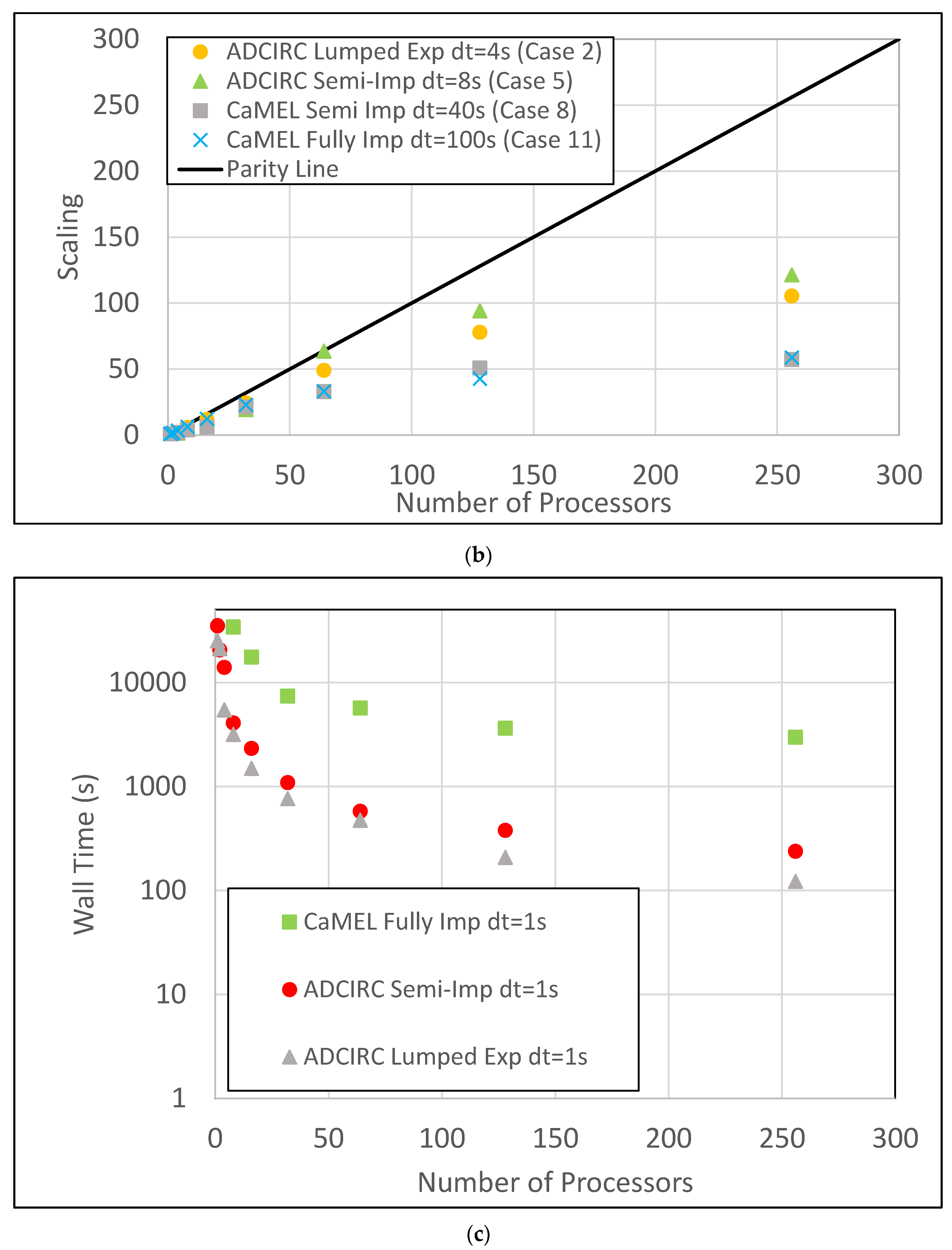
8. Model Execution Time and Parallel Scalability
9. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Resio, D.T.; Westerink, J.J. Modeling the physics of storm surges. Phys. Today 2008, 61, 33–38. [Google Scholar] [CrossRef]
- Luettich, R.A.; Westerink, J.J.; Scheffner, N.W. ADCIRC: An Advanced Three-Dimensional Circulation Model for Shelves, Coasts and Estuaries. Report 1: Theory and Methodology of ADCIRC-2DDI and ADCIRC-3DL; Technical Report DRP-92-6; Department of the Army, USACE: Washington, DC, USA, 1991.
- Westerink, J.J.; Luettich, R.A.; Blain, C.A.; Scheffner, N.W. An Advanced Three-Dimensional Circulation Model for Shelves, Coasts and Estuaries. Report 2: Users’ Manual for ADCIRC-2DDI; Department of the Army, USACE: Washington, DC, USA, 1992.
- Kolar, R.L.; Gray, W.G.; Westerink, J.J.; Luettich, R.A., Jr. Shallow water modeling in spherical coordinates: Equation formulation, numerical implementation, and application. J. Hydraul. Res. 1994, 32, 3–24. [Google Scholar] [CrossRef]
- Kolar, R.L.; Westerink, J.J.; Cantekin, M.E.; Blain, C.A. Aspects of nonlinear simulations using shallow water models based on the wave continuity equation. Comput. Fluids 1994, 23, 523–538. [Google Scholar] [CrossRef]
- Blain, C.A.; Rogers, W.E. Coastal Tide Prediction Using the ADCIRC-2DDI Hydrodynamic Finite Element Model: Model Validation and Sensitivity Analyses in the Southern North Sea/English Channel; Technical Report-NRL/FR/7322-98-9682; Naval Research Lab Stennis Space Center MS Coastal and Semi-Enclosed Seas Section: Washington, DC, USA, 1998. [Google Scholar]
- Luettich, R.A.; Westerink, J.J. Formulation and Numerical Implementation of the 2D/3D ADCIRC Finite Element Model Version 44.XX. 8 December 2004. Available online: http://www.unc.edu/ims/adcirc-/adcirc_theory_2004_12_08.pdf (accessed on 5 August 2017 ).
- Akbar, M.K.; Aliabadi, S. Hybrid numerical methods to solve shallow water equations for hurricane induced storm surge modeling. Environ. Model. Softw. 2013, 46, 118–128. [Google Scholar] [CrossRef]
- Atkinson, J.H.; Westerink, J.J.; Hervouet, J.M. Similarities between the Wave Equation and the Quasi-Bubble Solutions to the Shallow Water Equations. Int. J. Numer. Methods Fluids 2004, 45, 689–714. [Google Scholar] [CrossRef]
- Atkinson, J.H.; Westerink, J.J.; Luettich, R.A. Two-Dimensional Dispersion Analysis of Finite Element Approximations to the Shallow Water Equations. Int. J. Numer. Methods Fluids 2004, 45, 715–749. [Google Scholar] [CrossRef]
- Dawson, C.N.; Westerink, J.J.; Feyen, J.C.; Pothina, D. Continuous, Discontinuous and Coupled Discontinuous-Continuous Galerkin Finite Element Methods for the Shallow Water Equations. Int. J. Numer. Methods Fluids 2006, 52, 63–88. [Google Scholar] [CrossRef]
- Westerink, J.J.; Luettich, R.A., Jr.; Feyen, J.C.; Atkinson, J.H.; Dawson, C.; Powell, M.D.; Dunion, J.P.; Roberts, H.J.; Kubatko, E.J.; Pourtaheri, H. A Basin to Channel Scale Unstructured Grid Hurricane Storm Surge Model as Implemented for Southern Louisiana. Mon. Weather Rev. 2008, 136, 833–864. [Google Scholar] [CrossRef]
- Dietrich., J.C.; Zijlema, M.; Westerink, J.J.; Holthuijsen, L.H.; Dawson, C.; Luettich, R.A.; Jensen, R.; Smith, J.M.; Stelling, G.S.; Stone, G.W. Modeling Hurricane Waves and Storm Surge using Integrally-Coupled, Scalable Computations. Coast. Eng. 2011, 58, 45–65. [Google Scholar] [CrossRef]
- Bunya, S.; Dietrich, J.C.; Westerink, J.J.; Ebersole, B.A.; Smith, J.M.; Atkinson, J.H.; Jensen, R.; Resio, D.T.; Luettich, R.A.; Dawson, C.; et al. A High-Resolution Coupled Riverine Flow, Tide, Wind, Wind Wave, and Storm Surge Model for Southern Louisiana and Mississippi. Part I: Model Development and Validation. Mon. Weather Rev. 2000, 138, 345–377. [Google Scholar] [CrossRef]
- Tanaka, S.; Bunya, S.; Westerink, J.J.; Dawson, C.; Luettich, R.A. Scalability of an Unstructured Grid Continuous Galerkin Based Hurricane Storm Surge Model. J. Sci. Comput. 2011, 46, 329–358. [Google Scholar] [CrossRef]
- Aliabadi, S.; Akbar, M.K.; Patel, R. Hybrid Finite Element/Volume Method for Shallow Water Equations. Int. J. Numer. Methods Fluids 2010, 83, 1719–1738. [Google Scholar] [CrossRef]
- Dresback, K.M.; Kolar, R.L.; Dietrich, J.C. A 2D implicit time-marching algorithm for shallow water models based on the generalized wave continuity equation. Int. J. Numer. Methods Fluids 2004, 45, 253–274. [Google Scholar] [CrossRef]
- Tu, S.; Aliabadi, S.; Patel, R.; Watts, M. An Implementation of the Spalart-Allmaras DES Model in an Implicit Unstructured Hybrid Finite Volume/Element Solver for Incompressible Turbulent Flow. Int. J. Numer. Methods Fluids 2009, 59, 1051–1062. [Google Scholar] [CrossRef]
- Tu, S.; Aliabadi, S. Development of a Hybrid Finite Volume/Element Solver for Incompressible Flows. Int. J. Numer. Methods Fluids 2007, 55, 177–203. [Google Scholar] [CrossRef]
- Timmermans, L.J.P.; Minev, P.D.; Van De Vosse, F.N. An approximate projection scheme for incompressible flow using spectral elements. Int. J. Numer. Methods Fluids 1996, 22, 673–688. [Google Scholar] [CrossRef]
- Aliabadi, S. Parallel Finite Element Computations in Aerospace Applications. Ph.D. Thesis, University of Minnesota, Minneapolis, MN, USA, 1994. [Google Scholar]
- Hageman, L.A.; Young, D.M. Applied Iterative Methods; Courier Corporation, Dover Publications, Inc.: Mineola, NY, USA, 2012. [Google Scholar]
- Dresback, K.M. Algorithmic Improvements and Analyses of the Generalized Wave Continuity Equation Based Model, ADCIRC. Ph.D. Thesis, University of Oklahoma, Norman, OK, USA, 2005. [Google Scholar]
- Karypis, G.; Kumar, V. Parallel Multilevel k-Way Partitioning Scheme for Irregular Graphs. SIAM Rev. 1999, 41, 278–300. [Google Scholar] [CrossRef]
- Aliabadi, S.; Johnson, A.; Zellars, B.; Abatan, A.; Berger, C. Parallel simulation of flows in open channels. Future Gener. Comput. Syst. 2002, 18, 627–637. [Google Scholar] [CrossRef]
- Lynch, D.R.; Gray, W.G. A wave equation model for finite element tidal computations. Comput. Fluids 1979, 7, 207–228. [Google Scholar] [CrossRef]
- Lynch, D.R.; Gray, W.G. Analytical solutions for computer flow model testing. ASCE J. Hydraul. Div. 1948, 104, 1409–1428. [Google Scholar]
- Lynch, D.R.; Officer, C.B. Analytic test cases for three-dimensional hydrodynamic models. Int. J. Numer. Methods Fluids 1958, 5, 529–543. [Google Scholar] [CrossRef]
- Mukai, A.Y.; Westerink, J.J.; Luettich, R.A., Jr. Guidelines for Using the Eastcoast 2001 Database of Tidal Constituents within the Western North Atlantic Ocean, Gulf of Mexico and Caribbean Sea, Coastal and Hydraulic Engineering Technical Note (IV-XX). 2002. Available online: http://www.unc.edu/ims/adcirc/publications/2002/2002_Mukai02.pdf (accessed on 9 August 2017).
- Chow, S.H. A Study of the Wind Field in the Planetary Boundary Layer of a Moving Tropical Cyclone. Master’s Thesis, School of Engineering and Science, New York University, New York, NY, USA, 1970. [Google Scholar]
- Cardone, V.J.; Young, J.D.; Pierson, W.J.; Moore, R.K.; Greenwood, J.A.; Greenwood, C.; Chan, H.L.; Fung, A.K.; Mcclain, E.P.; Salfi, R.; et al. The Measurement of the Winds near the Ocean Surface with a Radiometer-Scatterometer on Skylab; Final Report on EPN550, Cont. No. NAS-9-13642; City Univ. of New York: New York, NY, USA, 1976. [Google Scholar]
- Shapiro, L.J. The asymmetric boundary layer flow under a translating hurricane. J. Atmos. Sci. 1983, 40, 1984–1998. [Google Scholar] [CrossRef]
- Thompson, E.F.; Cardone, V.J. Practical modeling of hurricane surface wind fields. J. Waterw. Port Coast. Ocean Eng. 1996, 122, 195–205. [Google Scholar] [CrossRef]
- Vickery, P.J.; Skerlj, P.F.; Steckley, A.C.; Twisdale, L.A. Hurricane wind field model for use in hurricane simulations. J. Struct. Eng. 2000, 126, 1203–1221. [Google Scholar] [CrossRef]
- NOAA. National Oceanic and Atmospheric Administration. Available online: http://www.noaa.gov/ (accessed on 5 August 2017).
- Blain, C.A.; Massey, T.C.; Dykes, J.D.; Posey, P.G.; Naval Research Lab Stennis Space Center MS Oceanography Div. Advanced Surge and Inundation Modeling: A Case Study from Hurricane Katrina; Stennis Space Center: Hancock County, MS, USA, 2007. [Google Scholar]
- FEMA. High Water Mark Collection for Hurricane Katrina in Louisiana; FEMA-1603-DR-LA, Task Orders 412 and 419; Federal Emergency Management Agency: Denton, TX, USA, 2006.
- FEMA. Final Coastal and Riverine High Water Mark Collection for Hurricane Katrina in Mississippi; FEMA-1604-DR-MS, Task Orders 413 and 420; Federal Emergency Management Agency: Atlanta, GA, USA, 2006.
- FEMA. High Water Mark Collection for Hurricane Katrina in Alabama; FEMA-1605-DR-AL, Task Orders 414 and 421; Federal Emergency Management Agency: Atlanta, GA, USA, 2006.
- Kerr, P.C.; Donahue, A.S.; Westerink, J.J.; Luettich, R.A.; Zheng, L.Y.; Weisberg, R.H.; Huang, Y.; Wang, H.V.; Teng, Y.; Forrest, D.R.; et al. US IOOS coastal and ocean modeling testbed: Inter-model evaluation of tides, waves, and hurricane surge in the Gulf of Mexico. J. Geophys. Res. Oceans 2013, 118, 5129–5172. [Google Scholar] [CrossRef]
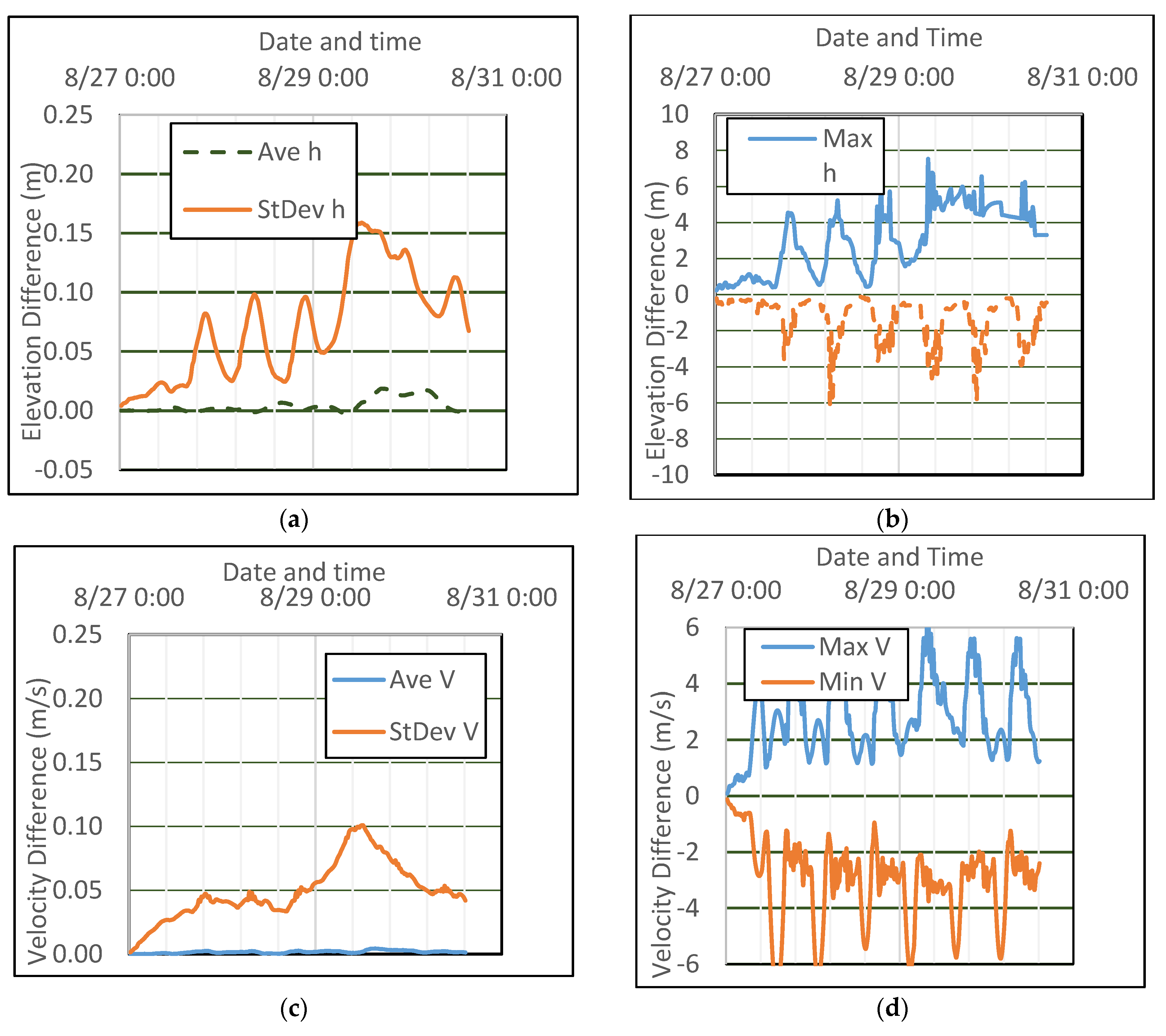
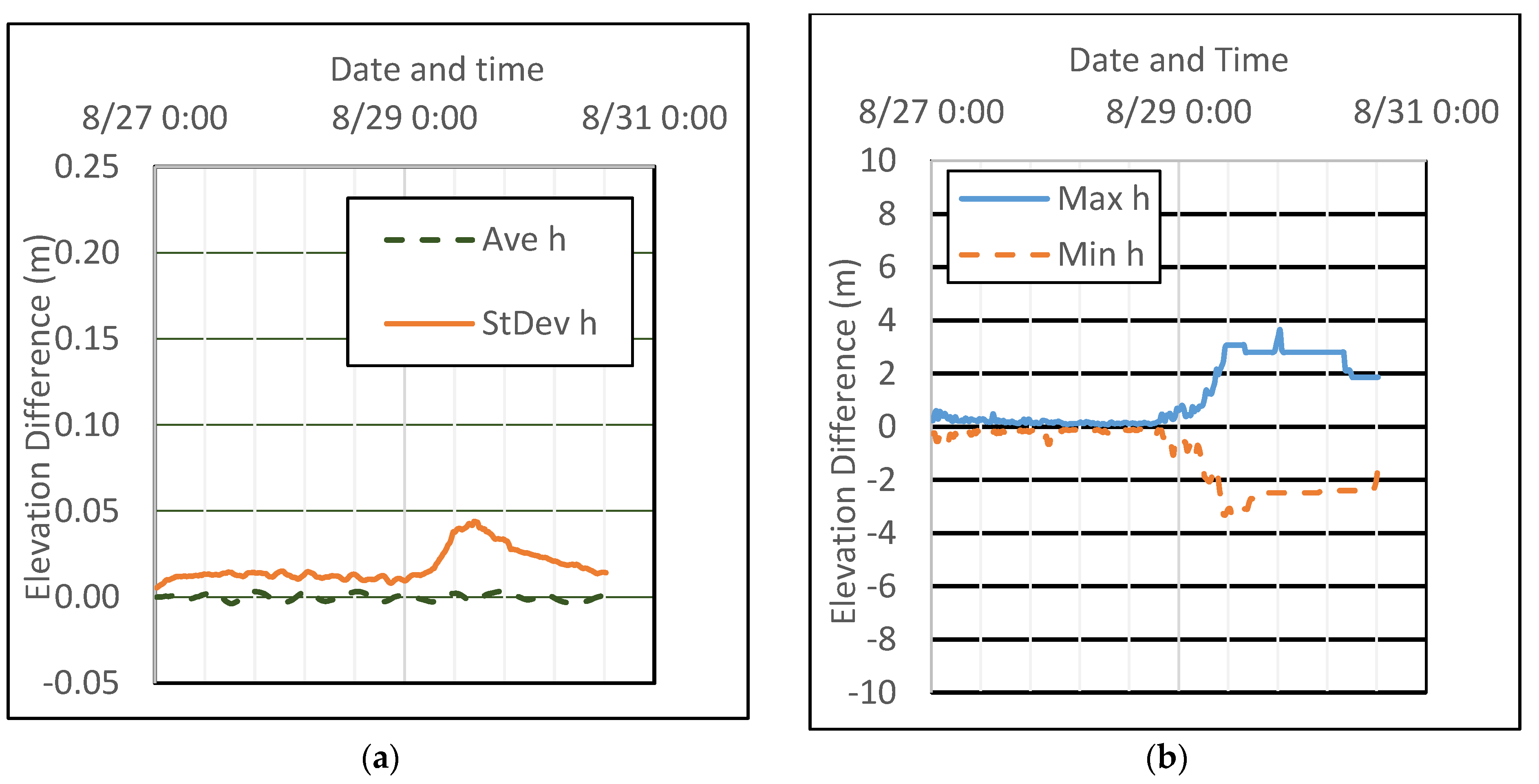
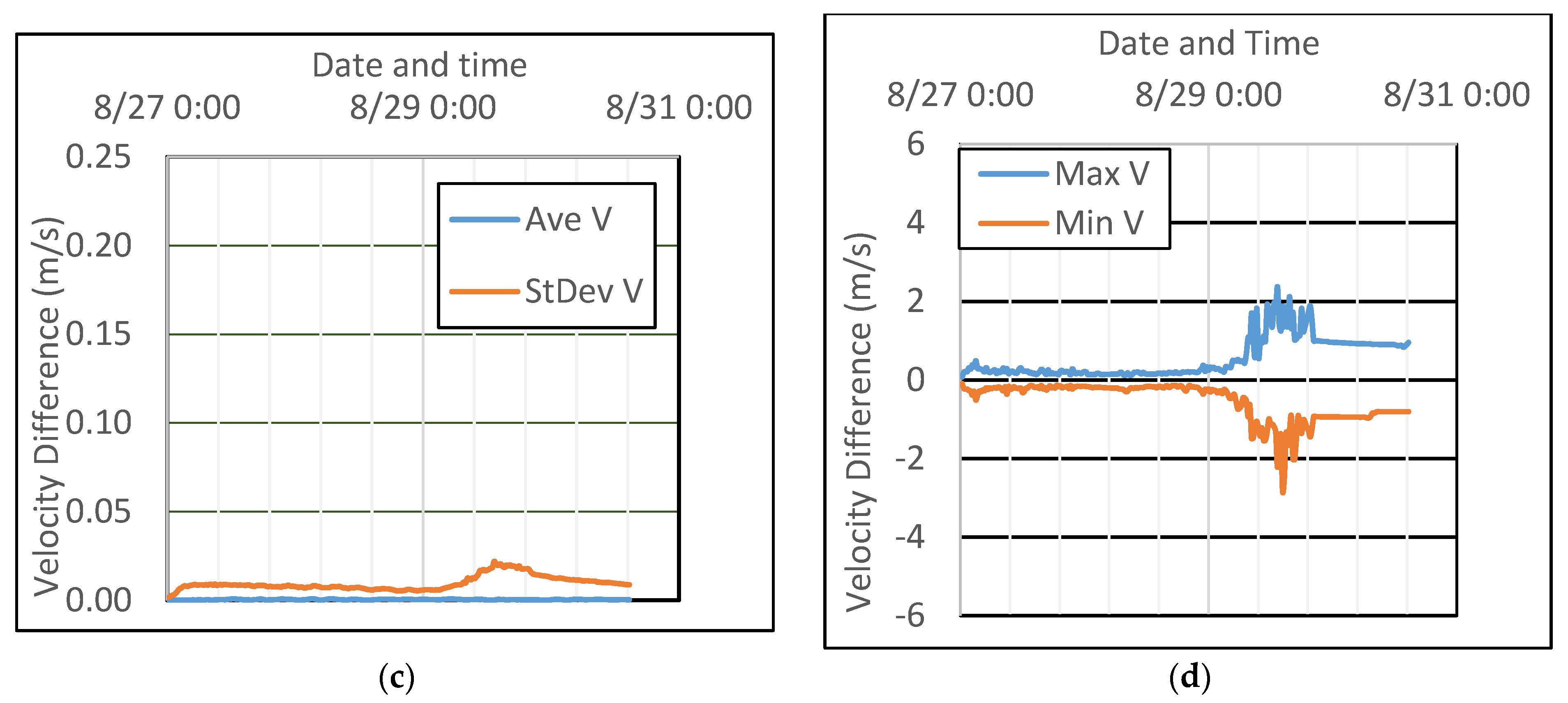
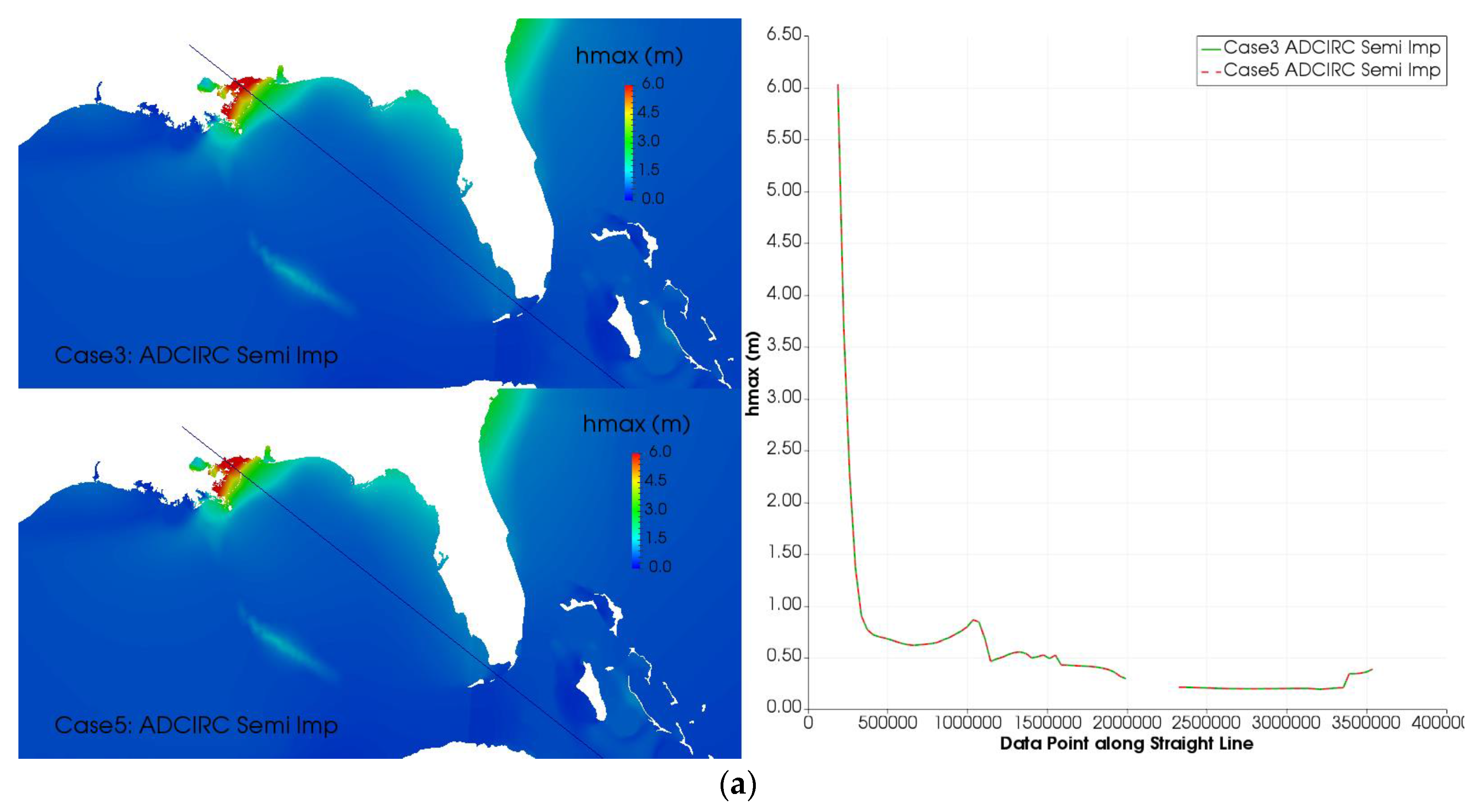
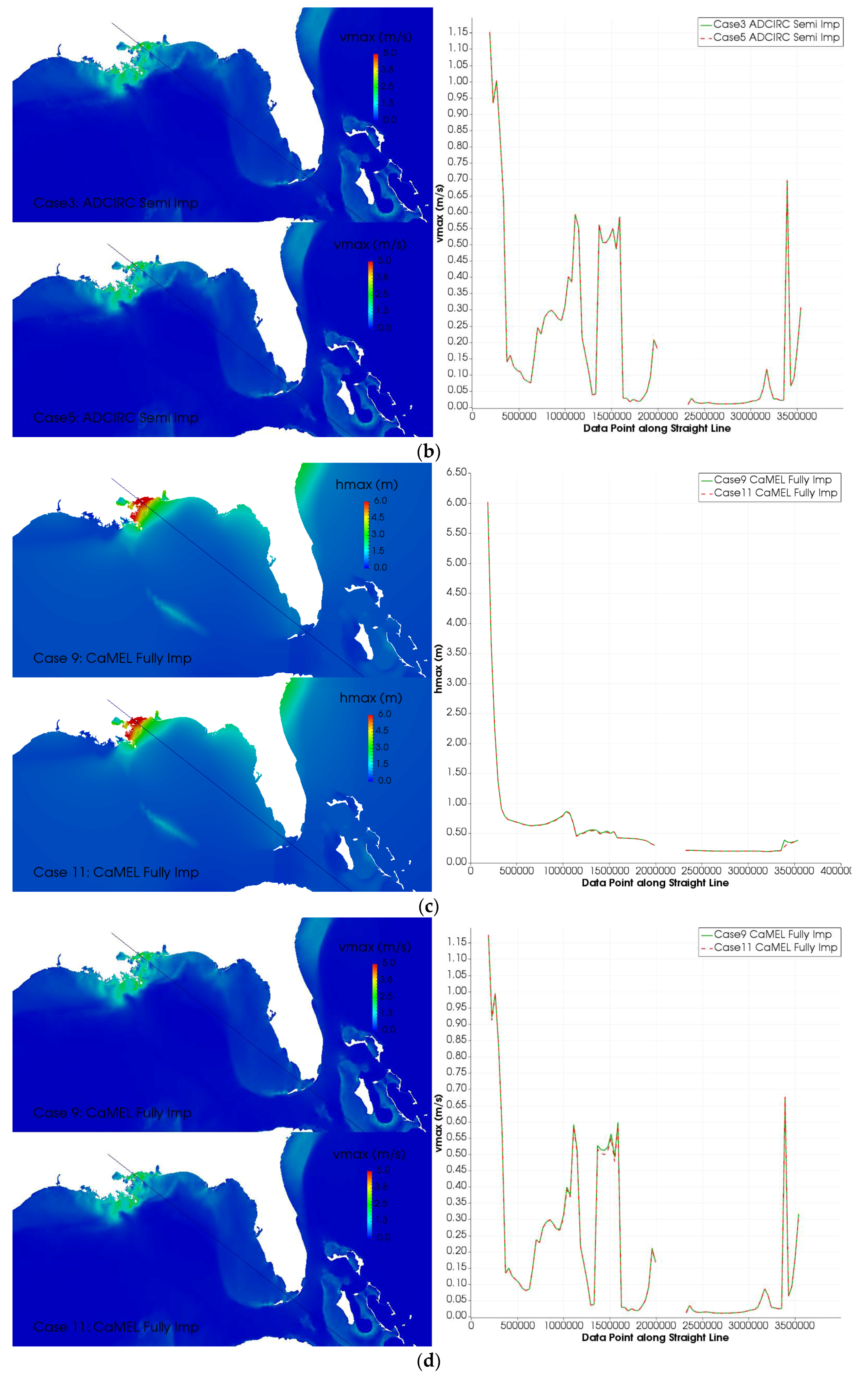

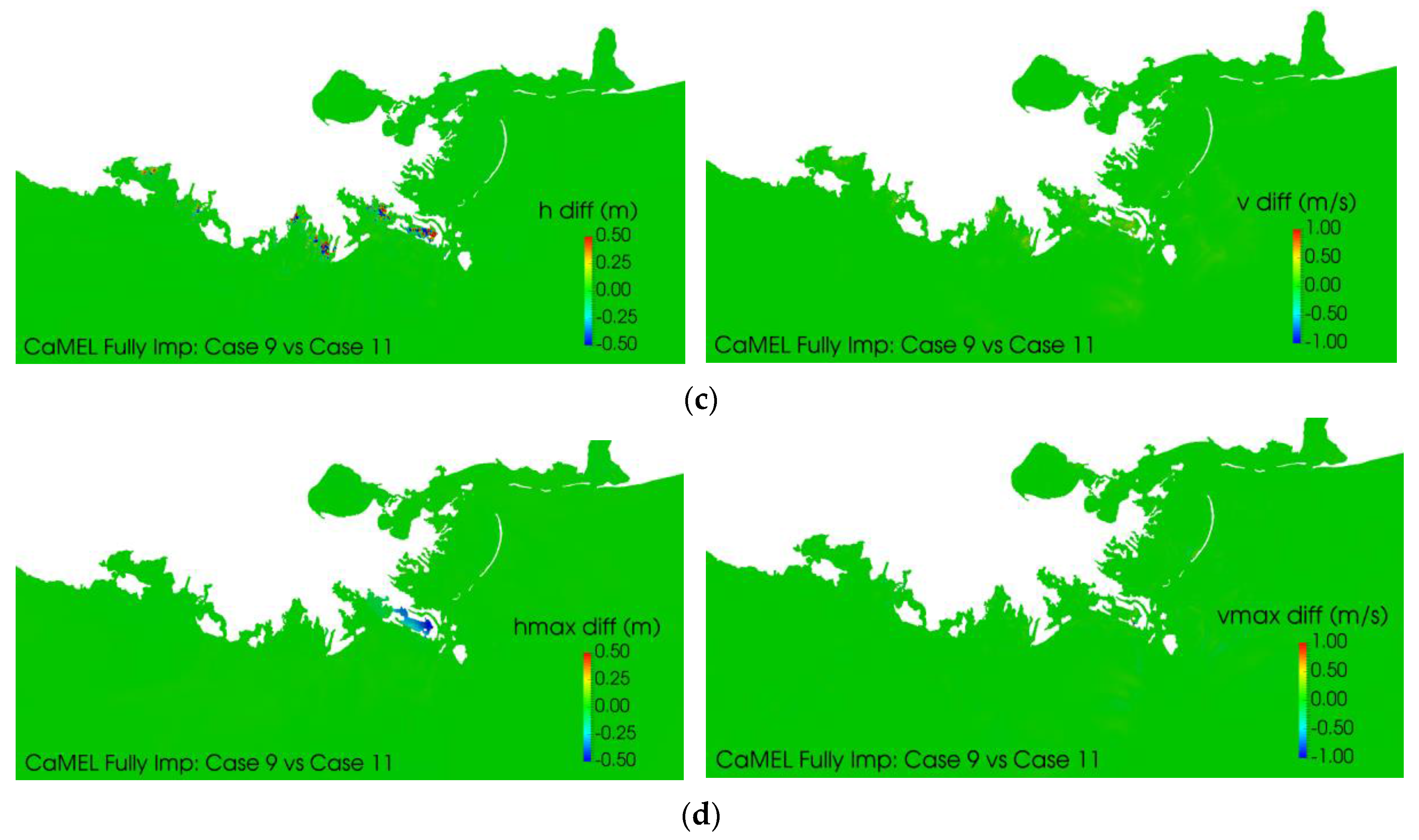
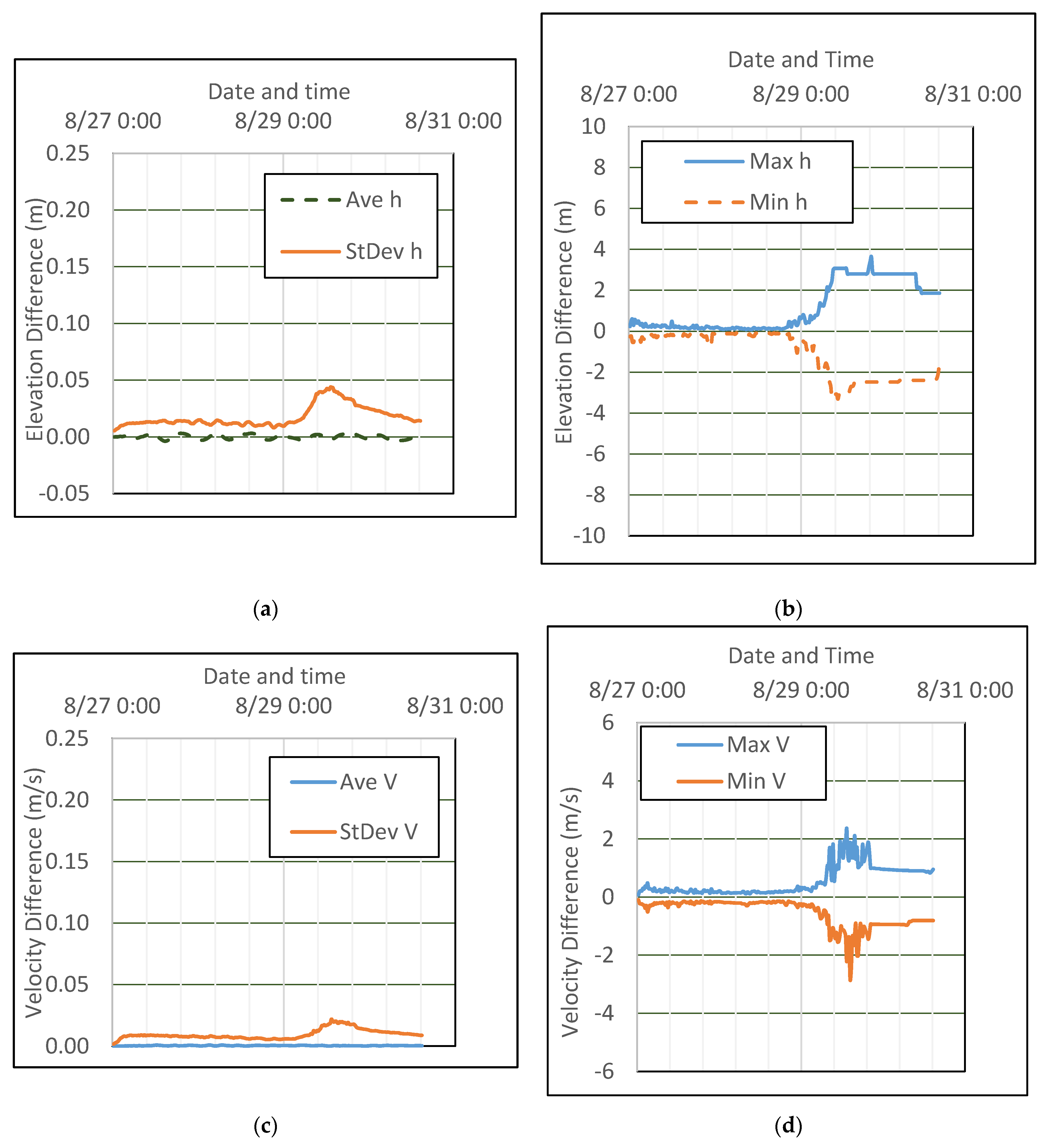
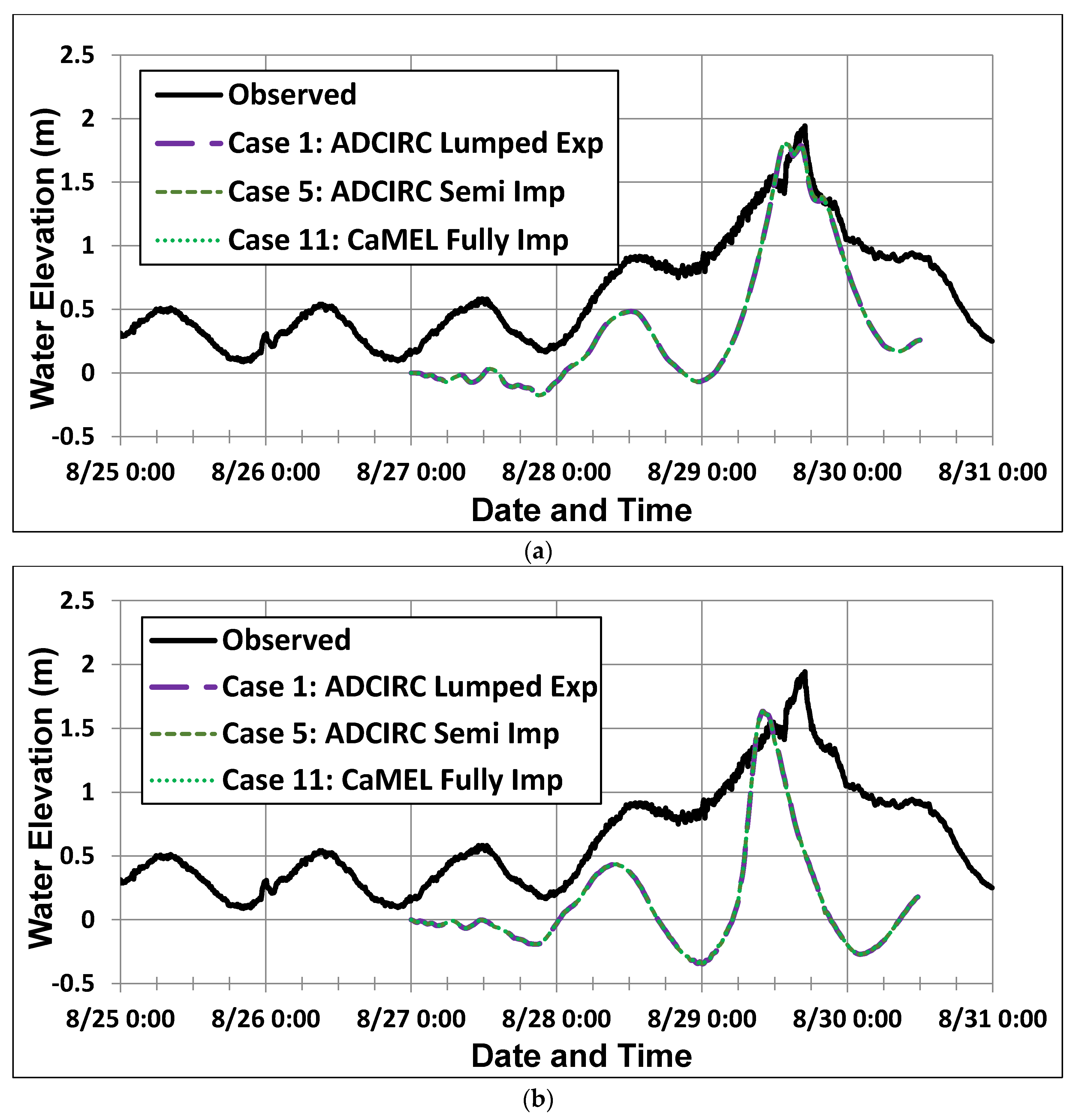

| Case # | Time Step (s) | Wall Time (s) | Solver | Comments |
|---|---|---|---|---|
| 1 | 2.0 | 773 | ADCIRC Lumped Exp | Ran Successful |
| 2 | 4.0 | 672 | ADCIRC Lumped Exp | Ran Successful |
| 3 | 2.0 | 1150 | ADCIRC Semi-Imp | Ran Successful |
| 4 | 4.0 | 738 | ADCIRC Semi-Imp | Ran Successful |
| 5 | 8.0 | 547 | ADCIRC Semi-Imp | Ran Successful |
| 6 | 2.0 | 30,881 | CaMEL Semi-Imp | Ran Successful |
| 7 | 4.0 | 10,846 | CaMEL Semi-Imp | Ran Successful |
| 8 | 40.0 | 2125 | CaMEL Semi-Imp | Ran Successful |
| 9 | 2.0 | 33,852 | CaMEL Fully-Imp | Ran Successful |
| 10 | 4.0 | 10,283 | CaMEL Fully-Imp | Ran Successful |
| 11 | 100.0 | 1655 | CaMEL Fully-Imp | Ran Successful |
| 12 | 8.0 | N/A | ADCIRC Lumped Exp | Did not Run |
| 13 | 16.0 | N/A | ADCIRC Semi-Imp | Did not Run |
| 14 | 80.0 | N/A | CaMEL Semi-Imp | Did not Run |
| 15 | 120.0 | N/A | CaMEL Fully-Imp | Did not Run |
| Case # | R2 | Slope |
|---|---|---|
| 1 (ADCIRC Lumped Exp) | 0.6706 | 0.8802 |
| 3 (ADCIRC Semi-Imp) | 0.6686 | 0.8808 |
| 6 (CaMEL Semi-Imp) | 0.6624 | 0.8844 |
| 8 (CaMEL Semi-Imp) | 0.6623 | 0.8843 |
| 9 (CaMEL Fully-Imp) | 0.6635 | 0.8838 |
| 11 (CaMEL Fully-Imp) | 0.6638 | 0.8844 |
| Computing Units | CaMEL Fully Implicit | ADCIRC Semi Implicit | ADCIRC Lumped Explicit | |||
|---|---|---|---|---|---|---|
| Procs. (x) | Scaling (y) | Wall Time (s) | Scaling (y) | Wall Time (s) | Scaling (y) | Wall Time (s) |
| 1 | 1.00 | 247,747 | 1.00 | 35,176 | 1.00 | 25,188 |
| 2 | 2.03 | 122,157 | 1.71 | 20,559 | 1.19 | 21,195 |
| 4 | 3.83 | 64,604 | 2.51 | 14,009 | 4.62 | 5451 |
| 8 | 7.25 | 34,162 | 8.60 | 4,090 | 7.95 | 3168 |
| 16 | 14.06 | 17,622 | 15.14 | 2324 | 16.86 | 1494 |
| 32 | 33.45 | 7407 | 32.27 | 1090 | 32.93 | 765 |
| 64 | 43.47 | 5699 | 60.86 | 578 | 53.25 | 473 |
| 128 | 68.12 | 3637 | 92.81 | 379 | 121.10 | 208 |
| 256 | 83.11 | 2981 | 147.80 | 238 | 206.46 | 122 |
| Computing Units | ADCIRC Lumped Explicit (Case 2) | ADCIRC Semi Implicit (Case 5) | CaMEL Semi Implicit (Case 8) | CaMEL Fully Implicit (Case 11) | ||||
|---|---|---|---|---|---|---|---|---|
| Procs. (x) | Scaling (y) | Wall Time (s) | Scaling (y) | Wall Time (s) | Scaling (y) | Wall Time (s) | Scaling (y) | Wall Time (s) |
| 1 | 1.00 | 23,817 | 1.00 | 24,282 | 1.00 | 112,418 | 1.00 | 70,894 |
| 0.91 | 26,101 | 1.11 | 21,917 | 0.97 | 116,225 | 1.86 | 38,159 | |
| 4 | 1.43 | 16,704 | 1.49 | 16,331 | 1.89 | 59,423 | 3.51 | 20,203 |
| 8 | 5.71 | 4168 | 4.02 | 6035 | 3.93 | 28,616 | 6.43 | 11,019 |
| 16 | 11.87 | 2007 | 7.11 | 3415 | 6.15 | 18,282 | 12.38 | 5728 |
| 32 | 24.38 | 977 | 19.30 | 1258 | 21.34 | 5267 | 23.05 | 3076 |
| 64 | 49.01 | 486 | 63.57 | 382 | 32.95 | 3412 | 33.19 | 2136 |
| 128 | 77.83 | 306 | 94.12 | 258 | 50.84 | 2211 | 42.76 | 1658 |
| 256 | 105.38 | 226 | 121.41 | 200 | 57.18 | 1966 | 58.83 | 1205 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akbar, M.K.; Luettich, R.A.; Fleming, J.G.; Aliabadi, S.K. CaMEL and ADCIRC Storm Surge Models—A Comparative Study. J. Mar. Sci. Eng. 2017, 5, 35. https://doi.org/10.3390/jmse5030035
Akbar MK, Luettich RA, Fleming JG, Aliabadi SK. CaMEL and ADCIRC Storm Surge Models—A Comparative Study. Journal of Marine Science and Engineering. 2017; 5(3):35. https://doi.org/10.3390/jmse5030035
Chicago/Turabian StyleAkbar, Muhammad K., Richard A. Luettich, Jason G. Fleming, and Shahrouz K. Aliabadi. 2017. "CaMEL and ADCIRC Storm Surge Models—A Comparative Study" Journal of Marine Science and Engineering 5, no. 3: 35. https://doi.org/10.3390/jmse5030035
APA StyleAkbar, M. K., Luettich, R. A., Fleming, J. G., & Aliabadi, S. K. (2017). CaMEL and ADCIRC Storm Surge Models—A Comparative Study. Journal of Marine Science and Engineering, 5(3), 35. https://doi.org/10.3390/jmse5030035





