Development of a Model for Increasing the Capacity of Small and Medium-Sized Ports Using the Principles of Probability Theory
Abstract
1. Introduction
- -
- Up to 50,000 passengers per year (small ports);
- -
- From 50,000 to 100,000 passengers per year (medium-sized);
- -
- More than 100,000 passengers per year (large ports).
- -
- Small ports (with an annual turnover of up to 1 million tons);
- -
- Medium-sized ports (with an annual turnover of 1 million tons to 10 million tons);
- -
- Large ports (with an annual turnover exceeding 10 million tons).
2. Small and Medium-Sized Ports and Literature Review
3. Methodology for Assessing the Possibilities of Small and Medium-Sized Ports and Ship Mooring at Quays Using the Principles of Probability Theory
3.1. Steps of Research Methodology
3.2. Mathematical Assessment of Small and Medium-Sized Port Activities and Ship Mooring Opportunities at Quays, Applying the Principles of Probability Theory
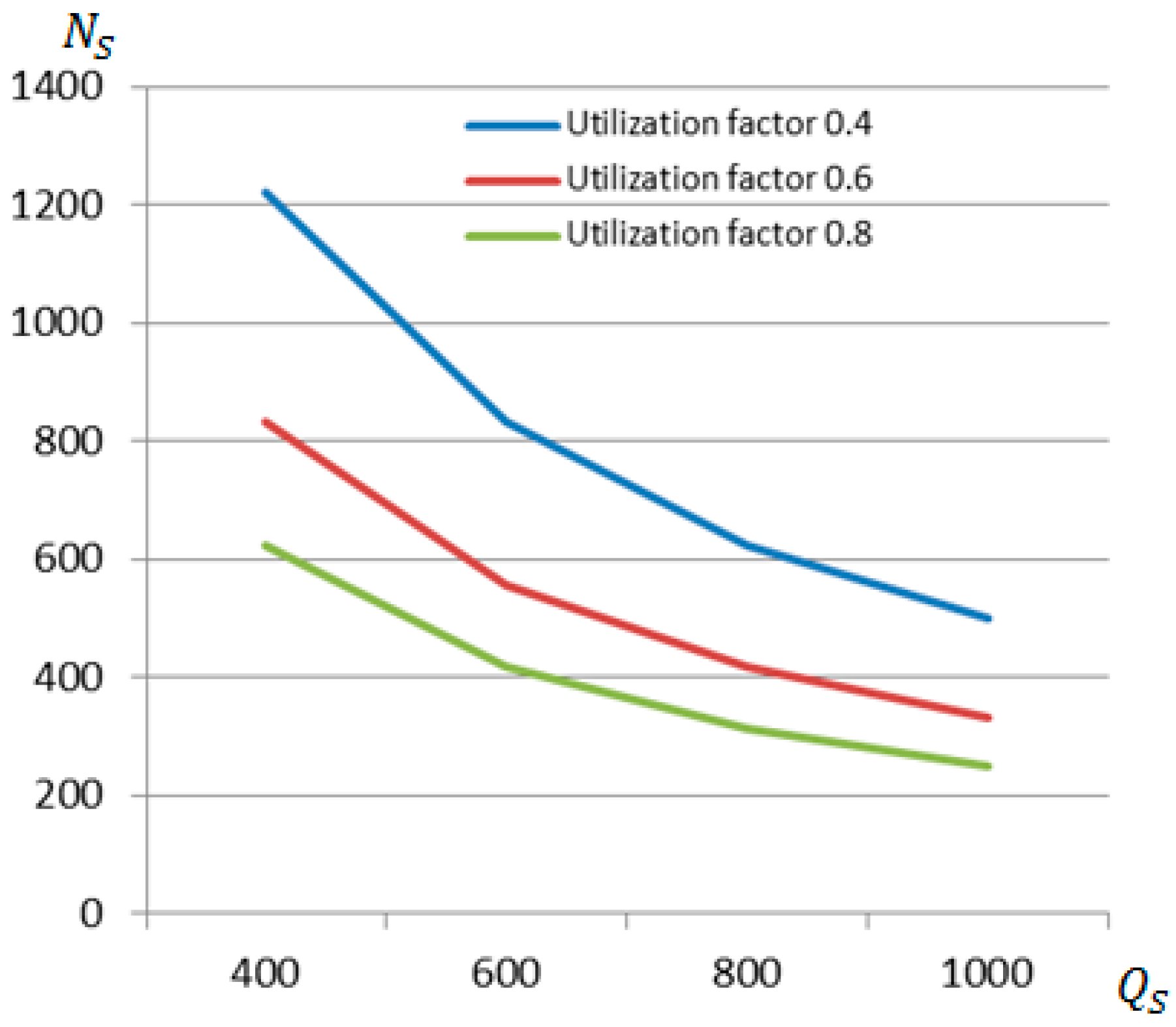
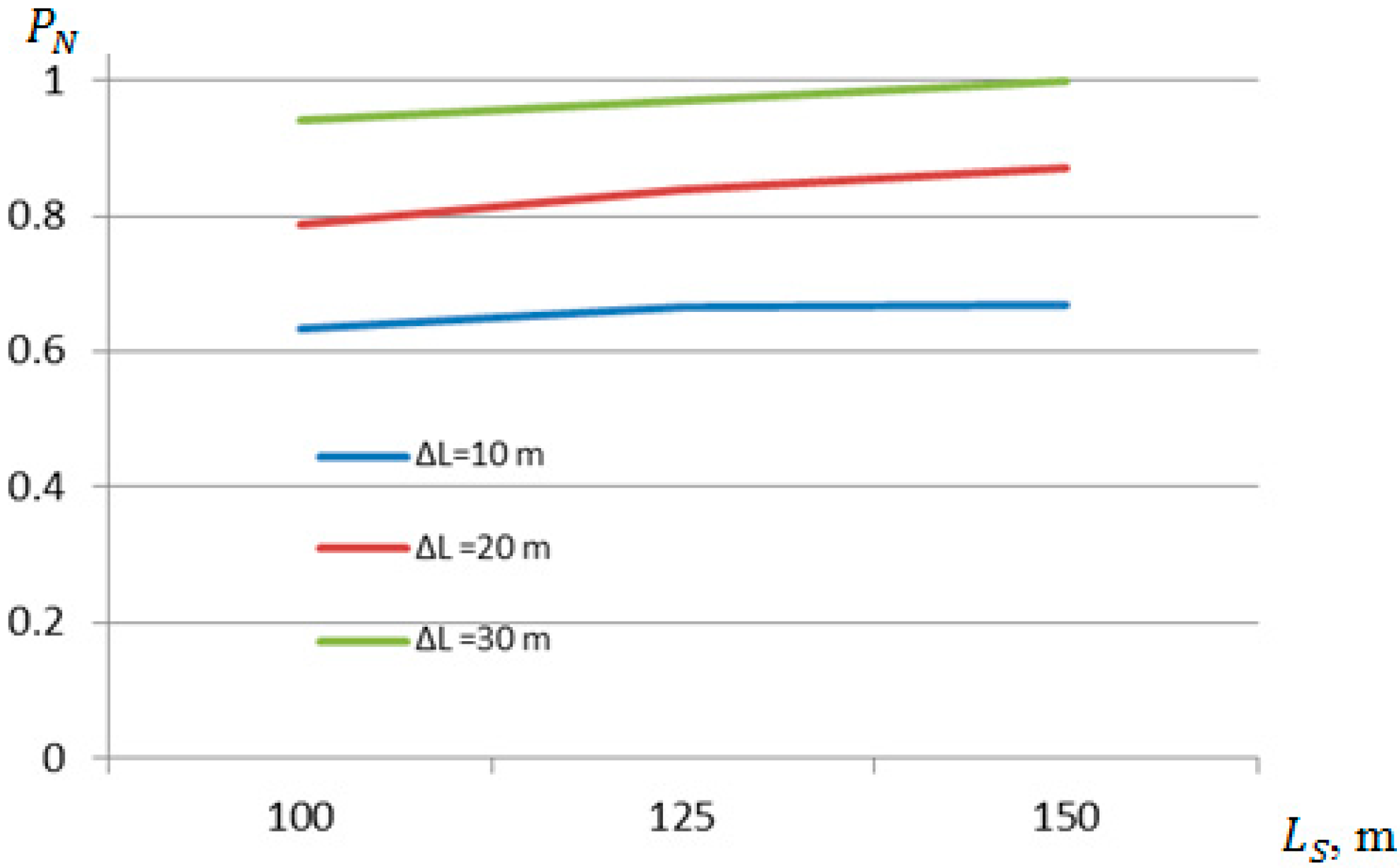
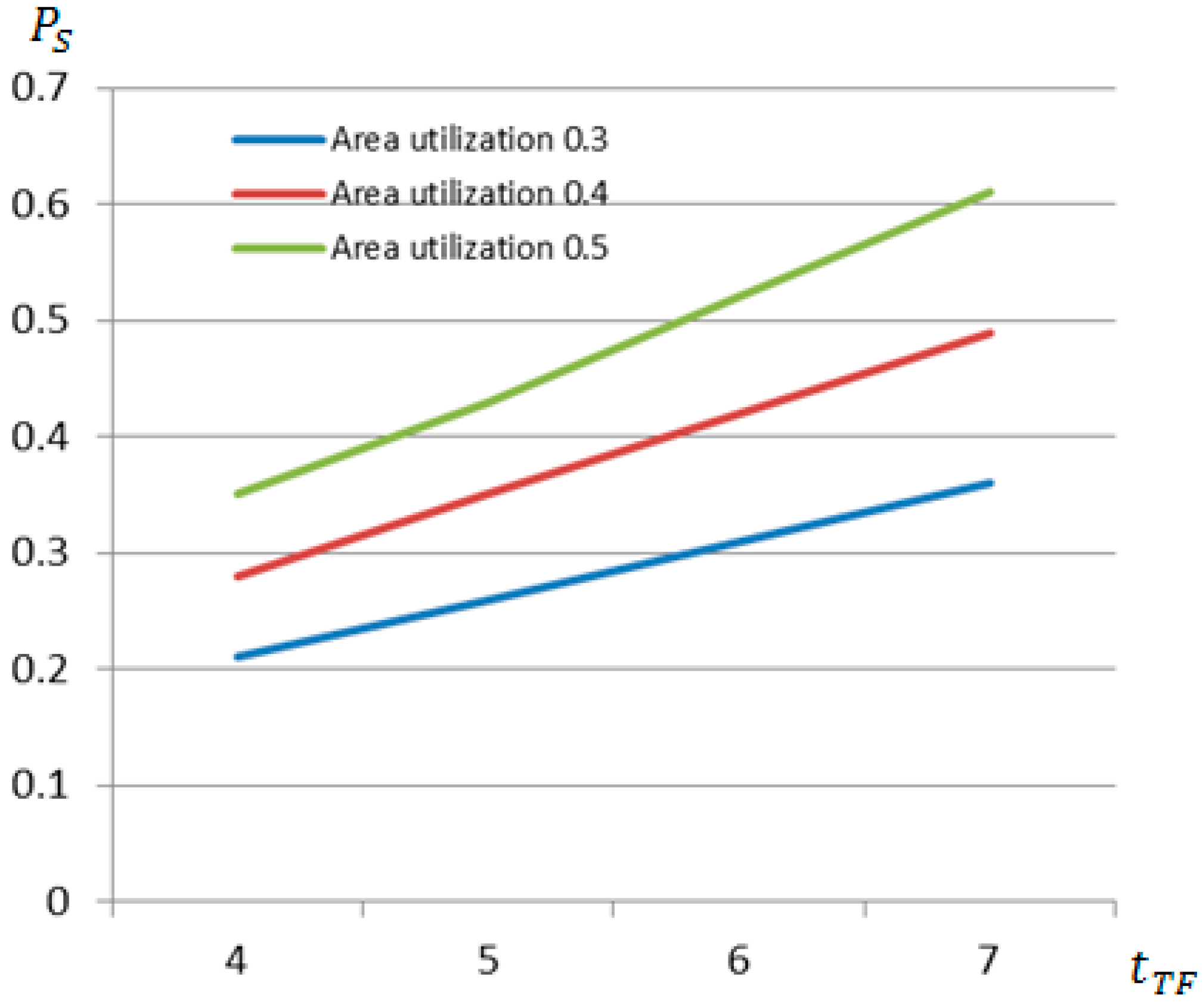
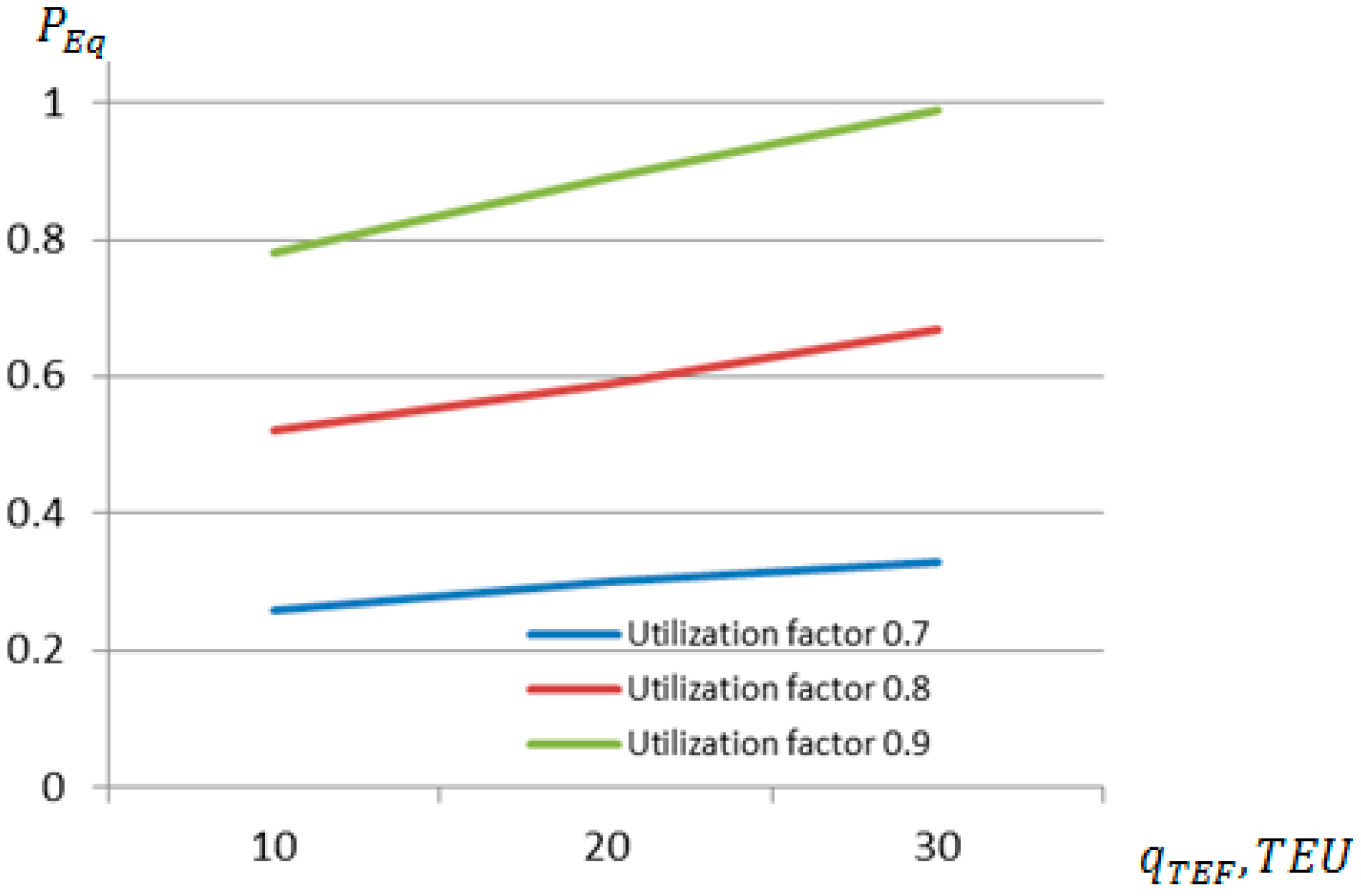
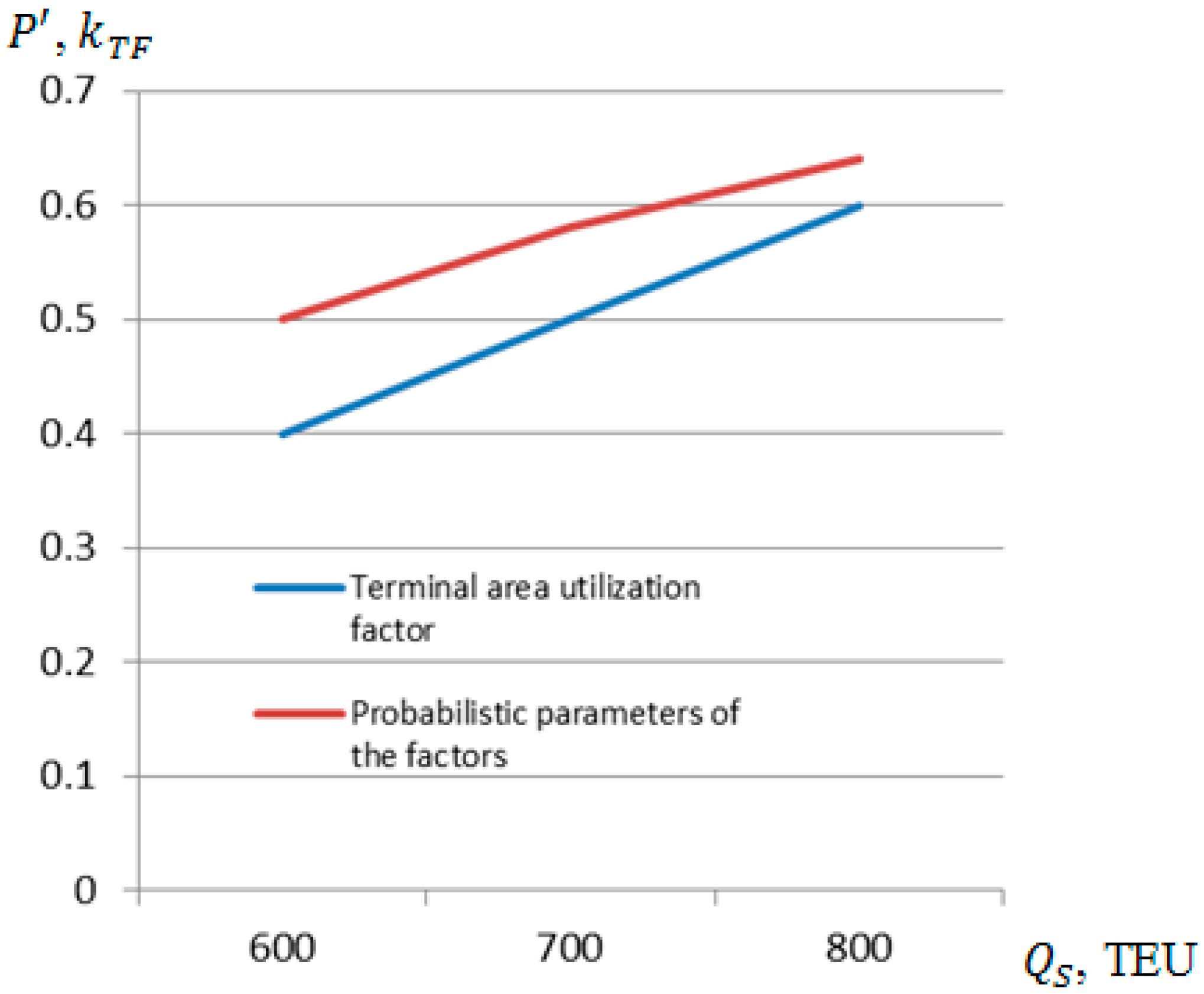
4. Case Study of Probabilistic Assessment of Port Activities and Ship Moorings at Port Quays
5. Discussions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pereira, M.T.; Rocha, N.; Silva, F.G.; Moreira, M.Â.L.; Altinkaya, Y.O.; Pereira, M.J. Process Optimization in Sea Ports: Integrating Sustainability and Efficiency Through a Novel Mathematical Model. J. Mar. Sci. Eng. 2025, 13, 119. [Google Scholar] [CrossRef]
- Danladi, C.; Tuck, S.; Tziogkidis, P.; Tang, L.; Okorie, C. Efficiency analysis and benchmarking of container ports operating in lower-middle-income countries: A DEA approach. J. Shipp. Trd. 2024, 9, 7. [Google Scholar] [CrossRef]
- Gerlitz, L.; Meyer, C. Small and Medium-Sized Ports in the TEN-T Network and Nexus of Europe’s Twin Transition: The Way towards Sustainable and Digital Port Service Ecosystems. Sustainability 2021, 13, 4386. [Google Scholar] [CrossRef]
- Karimah, I.D.; Yudhistira, M.H. Does small-scale port investment affect local economic activity? Evidence from small-port development in Indonesia. Econ. Transp. 2020, 23, 100–180. [Google Scholar] [CrossRef]
- Merk, O.; Notteboom, T. The Competitiveness of Global Port-Cities; OECD Publishing: Paris, France, 2014. [Google Scholar] [CrossRef]
- Krivokapic, R. Perspectives for the Development of Small Seaports, with Reference to the Adriatic Seaports. Transform. Bus. Econ. 2022, 21, 21–33. [Google Scholar]
- Park, J.S.; Seo, Y.-J. The impact of seaports on the regional economies in South Korea: Panel evidence from the augmented Solow model. Transp. Res. Part E Logist. Transp. Rev. 2016, 85, 107–119. [Google Scholar] [CrossRef]
- Paulauskas, V.; Filina-Dawidowicz, L.; Paulauskas, D. Ports Digitalization Level Evaluation. Sensors 2021, 21, 6134. [Google Scholar] [CrossRef] [PubMed]
- Knill, O. Probability Theory and Stochastic Processes with Applications; Overseas Press: New York, NY, USA, 2009; 382p. [Google Scholar]
- Cao, B.; Shahraki, A.A. Planning of Transportation Infrastructure Networks for Sustainable Development with Case Studies in Chabahar. Sustainability 2023, 15, 5154. [Google Scholar] [CrossRef]
- Notteboom, T.; Pallis, A.; Rodrigue, J.-P. Port Economics, Management and Policy; Routledge: New York, NY, USA, 2021; Available online: https://porteconomicsmanagement.org (accessed on 10 August 2025).
- Ettorre, B.; Daldanise, G.; Giovene di Girasole, E.; Clemente, M. Co-Planning Port–City 2030: The InterACT Approach as a Booster for Port–City Sustainable Development. Sustainability 2023, 15, 15641. [Google Scholar] [CrossRef]
- Gerlitz, L.; Meyer, C.; Henesey, L. Sourcing Sustainability Transition in Small and Medium-Sized Ports of the Baltic Sea Region: A Case of Sustainable Futuring with Living Labs. Sustainability 2024, 16, 4667. [Google Scholar] [CrossRef]
- Meyer, C. Integration of Baltic Small and Medium-Sized Ports in Regional Innovation Strategies on Smart Specialisation (RIS3). J. Open Innov. Technol. Mark. Complex. 2021, 7, 184. [Google Scholar] [CrossRef]
- Kawasaki, T.; Hanaoka, S.; Saito, Y.; Hoshi Tagawa, H. Port choice problem in a linear city: Application to Manila and Batangas ports in the Philippines. Marit. Transp. Res. 2021, 2, 100010. [Google Scholar] [CrossRef]
- Wagner, N.; Kotowska, I.; Pluciński, M. The Impact of Improving the Quality of the Port’s Infrastructure on the Shippers’ Decisions. Sustainability 2022, 14, 6255. [Google Scholar] [CrossRef]
- Tijan, E.; Jović, M.; Žgaljić, D.; Aksentijević, S. Factors Affecting Container Seaport Competitiveness: Case Study on Port of Rijeka. J. Mar. Sci. Eng. 2022, 10, 1346. [Google Scholar] [CrossRef]
- Wu, B.; Yip, T.L.; Yan, X.; Guedes Soares, C. Review of Techniques and Challenges of Human and Organizational Factors Analysis in Maritime Transportation. Reliab. Eng. Syst. Saf. 2022, 219, 108249. [Google Scholar] [CrossRef]
- Weerasinghe, B.A.; Perera, H.N.; Bai, X. Optimizing container terminal operations: A systematic review of operations research applications. Marit. Econ. Logist. 2023, 26, 307–341. [Google Scholar] [CrossRef]
- Chu, L.; Zhang, J.; Chen, X.; Yu, Q. Optimization of Integrated Tugboat–Berth–Quay Crane Scheduling in Container Ports Considering Uncertainty in Vessel Arrival Times and Berthing Preferences. J. Mar. Sci. Eng. 2024, 12, 1541. [Google Scholar] [CrossRef]
- Meyer, C.; Gerlitz, L.; Henesey, L. Cross-Border Capacity-Building for Port Ecosystems in Small and Medium-Sized Baltic Ports. Baltic J. Eur. Stud. 2021, 11, 113–132. [Google Scholar] [CrossRef]
- Argyriou, I.; Nisiforou, O.; Tsoutsos, T. Setting Sail for a Sustainable Growth in Small/Medium Ports. Sustainability 2025, 17, 3330. [Google Scholar] [CrossRef]
- Kong, Y.; Liu, J. Sustainable Port Cities with Coupling Coordination and Environmental Efficiency. Ocean. Coast. Manag. 2021, 205, 105534. [Google Scholar] [CrossRef]
- Bottasso, A.; Conti, M.; Ferrari, C.; Tei, A. Ports and regional development: A spatial analysis on a panel of European regions. Transp. Res. A Policy Pract. 2014, 65, 44–55. [Google Scholar] [CrossRef]
- Li, T.; Dong, Q.; Sun, X. Integrated Scheduling of Handling Equipment in Automated Container Terminal Considering Quay Crane Faults. Systems 2024, 12, 450. [Google Scholar] [CrossRef]
- Zheng, S.; Sha, J.; Wang, A. An improved storage-space selection model and algorithm for outbound shipping containers: Considering the synchronous operation of multiple gantry cranes in port terminals worldwide. J. Coast. Resour. 2019, 35, 1120–1130. [Google Scholar]
- Tierney, K.; Pacino, D.; Jensen, R.M. On the complexity of container stowage planning problems. Discret. Appl. Math. 2014, 169, 225–230. [Google Scholar] [CrossRef]
- Kaliszewski, A. Fifth and Sixth Generation Ports (5gp, 6gp)—Evolution of Economic and Social Roles of Ports. Stud. Mater. Inst. Marit. Transp. Trade 2017, 14, 93–123. [Google Scholar] [CrossRef]
- Bronshtein, I.N.; Semendyayev, K.A.; Musiol, G.; Muehlig, H. Probability Theory and Mathematical Statistics. In Handbook of Mathematics; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar] [CrossRef]
- Chauhan, S.; Patil, C.; Sinha, M.; Halder, A. Fuzzy state noise-driven Kalman filter for sensor fusion. Proc. Inst. Mech. Eng. Part G. J. Aerosp. Eng. 2009, 223, 1091–1097. [Google Scholar] [CrossRef]
- Paulauskas, V.; Paulauskas, D.; Simutis, M. Estimation of Tug Pulling Power (Bollard Pull) and Number of Tugs Require During Ship Mooring Operations. J. Mar. Sci. Eng. 2024, 12, 1959. [Google Scholar] [CrossRef]
- Jin, H.; Peng, S. Optimal unbiased estimation for maximal distribution. Am. Inst. Math. Sci. 2021, 6, 189–198. [Google Scholar] [CrossRef]
- Zheng, H.; Wang, Z.; Liu, H. The Integrated Rescheduling Problem of Berth Allocation and Quay Crane Assignment with Uncertainty. Processes 2023, 11, 522. [Google Scholar] [CrossRef]
- Luo, M.; Liu, L.; Gao, F. Post-entry container port capacity expansion. Transp. Res. Part B Methodol. 2012, 46, 120–138. [Google Scholar] [CrossRef]
- Jurjević, M.; Hess, S. The operational planning model of transshipment processes in the port. Promet-Trafic Transp. 2016, 28, 81–89. [Google Scholar] [CrossRef]
- A Systematic Analysis of Port Capacity Literature: Trends and Future Research Avenues. Available online: https://www.researchgate.net/publication/350754695_A_systematic_Analysis_of_Port_Capacity_Literature_Trends_and_Future_Research_Avenues (accessed on 24 August 2025).
- Han, D.; Cheng, X.; Chen, H.; Xiao, C.; Wen, Y.; Sui, Z. Simulation Modeling for Ships Entering and Leaving Port in Qiongzhou Strait Waters: A Multi-Agent Information Interaction Method. J. Mar. Sci. Eng. 2024, 12, 1560. [Google Scholar] [CrossRef]
- Burdett, R.L. Optimisation models for expanding a railway′s theoretical capacity. Eur. J. Oper. Res. 2016, 251, 783–797. [Google Scholar] [CrossRef]
- Jensen, L.W.; Schmidt, M.; Nielsen, O.A. Determination of infrastructure capacity in railway networks without the need for a fixed timetable. Transp. Res. Part C Emerg. Technol. 2020, 119, 102751. [Google Scholar] [CrossRef]
- Ding, Z.-Y.; Jo, G.-S.; Wang, Y.; Yeo, G.-T. The relative efficiency of container terminals in small and me-dium—Sized ports in China. Asian J. Shipp. Logist. 2015, 31, 231–251. [Google Scholar] [CrossRef]
- Rusu, M. Smart specialization a possible solution to the new global challenges. Procedia Econ. Financ. 2013, 6, 128–136. [Google Scholar] [CrossRef]
- New Technologies in Small and Medium-Sized Ports: Its Impacts on the Future of Work. Available online: https://www.researchgate.net/publication/387645114_New_Technologies_in_Small_and_Medium-sized_Ports_Its_Impacts_on_the_Future_of_Work (accessed on 24 August 2025).
- Chowdhury, P.; Paul Sanjoy, K. Applications of MCDM methods in research on corporate sustainability: A systematic literature review. Manag. Environ. Qual. Int. J. 2020, 31, 385–405. [Google Scholar] [CrossRef]
- Bottasso, A.; Conti, M.; Ferrari, C.; Merk, O.; Tei, A. The impact of port throughput on local employment: Evidence from a panel of European regions. Transp. Policy 2013, 27, 32–38. [Google Scholar] [CrossRef]



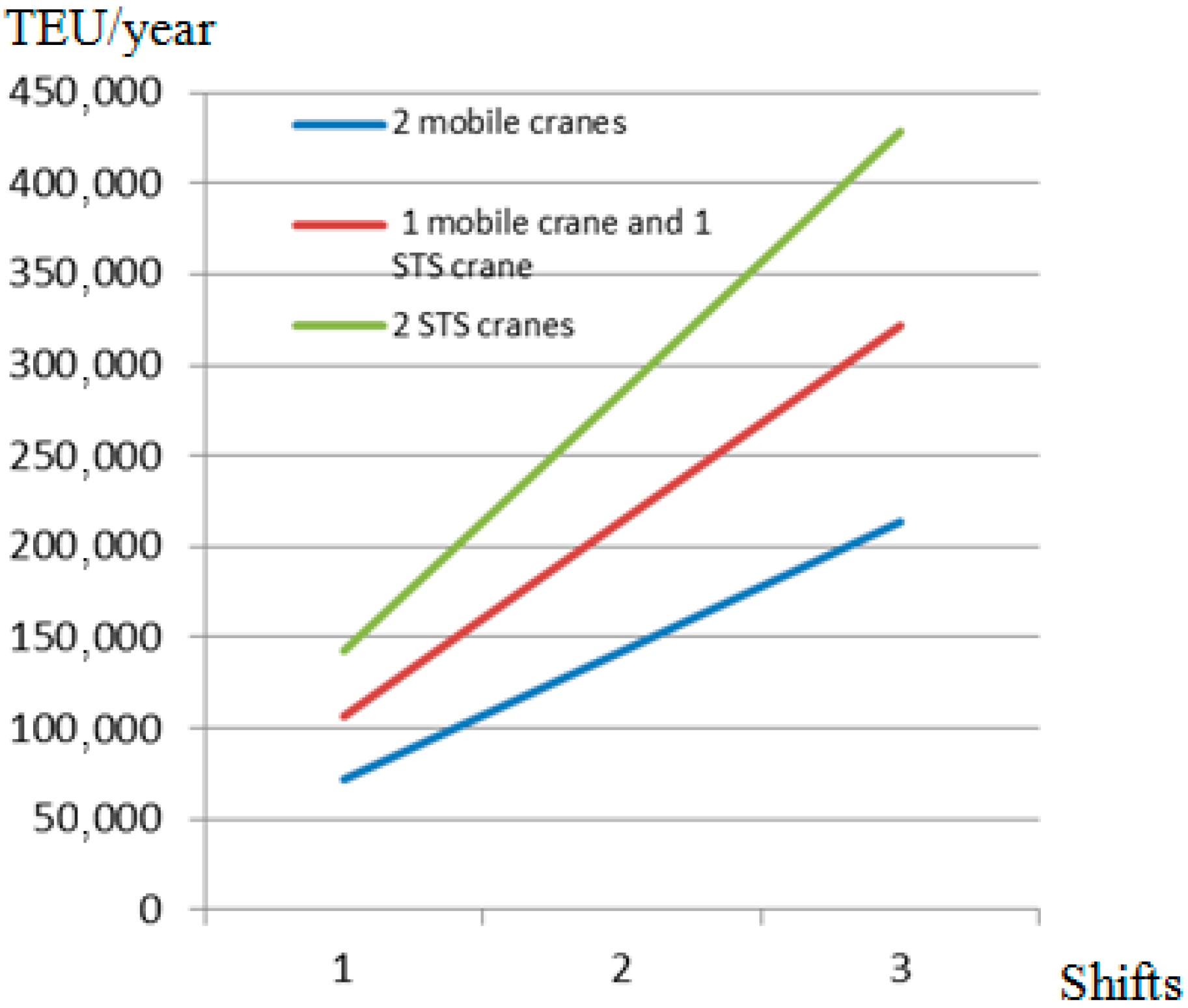
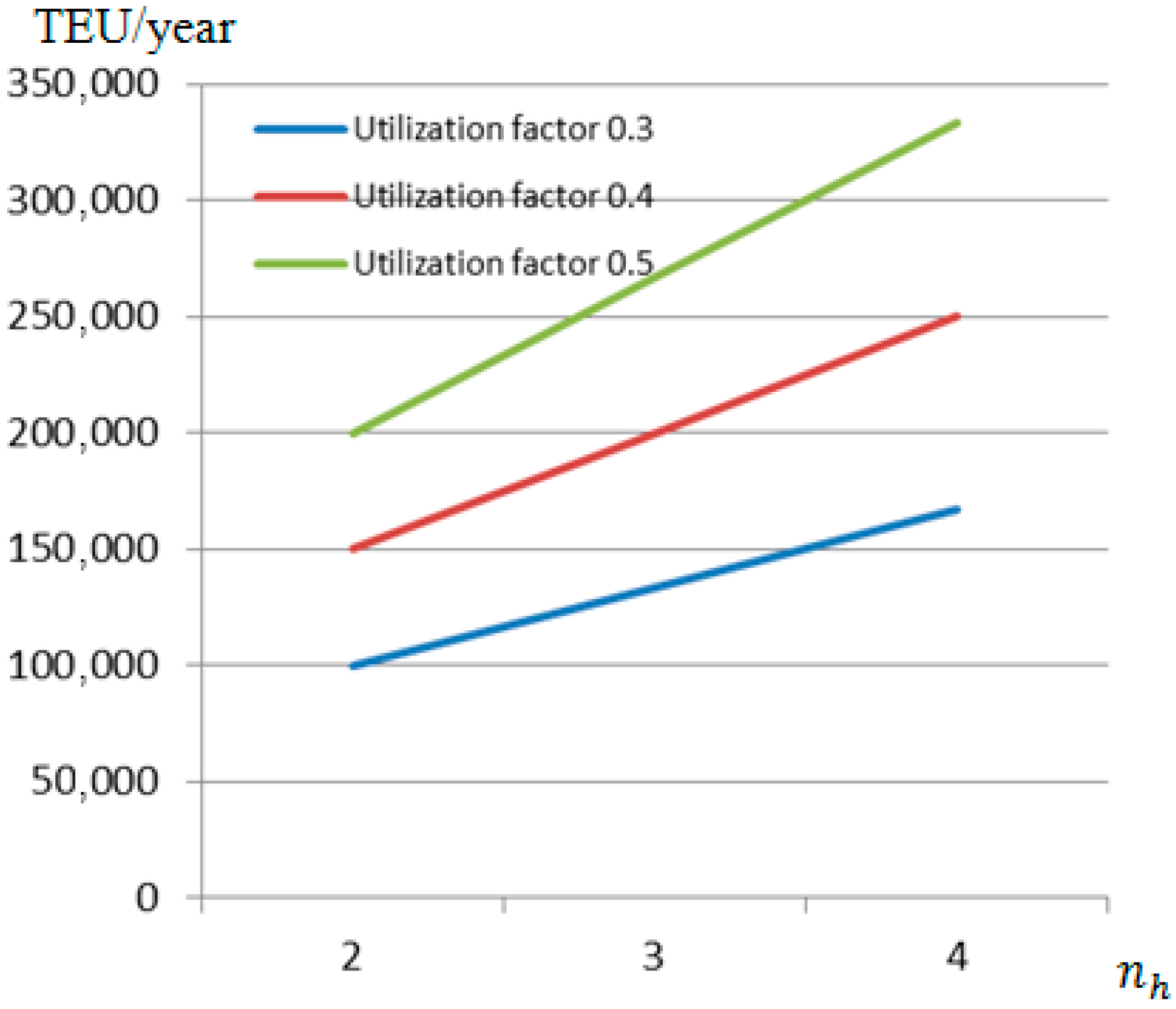
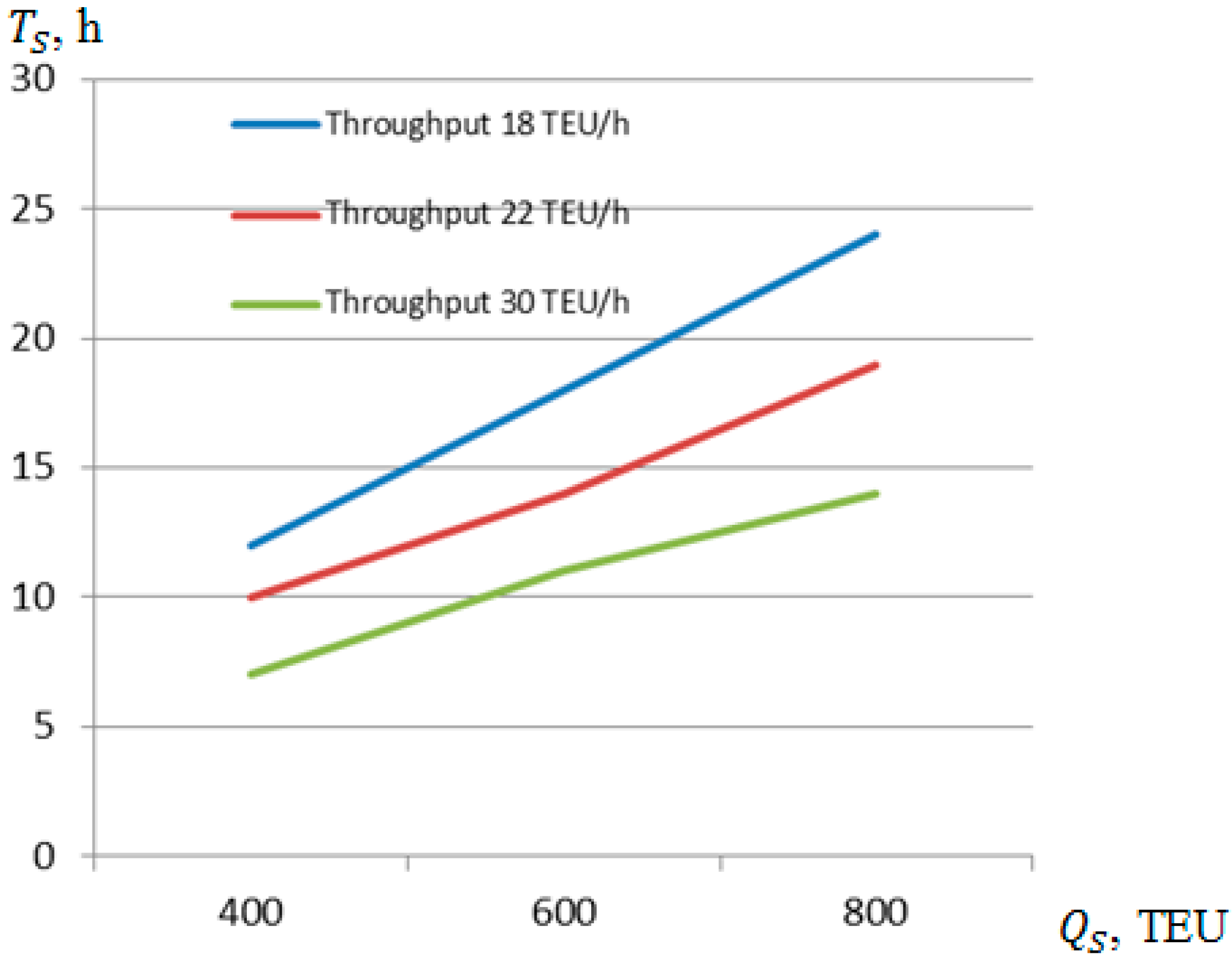
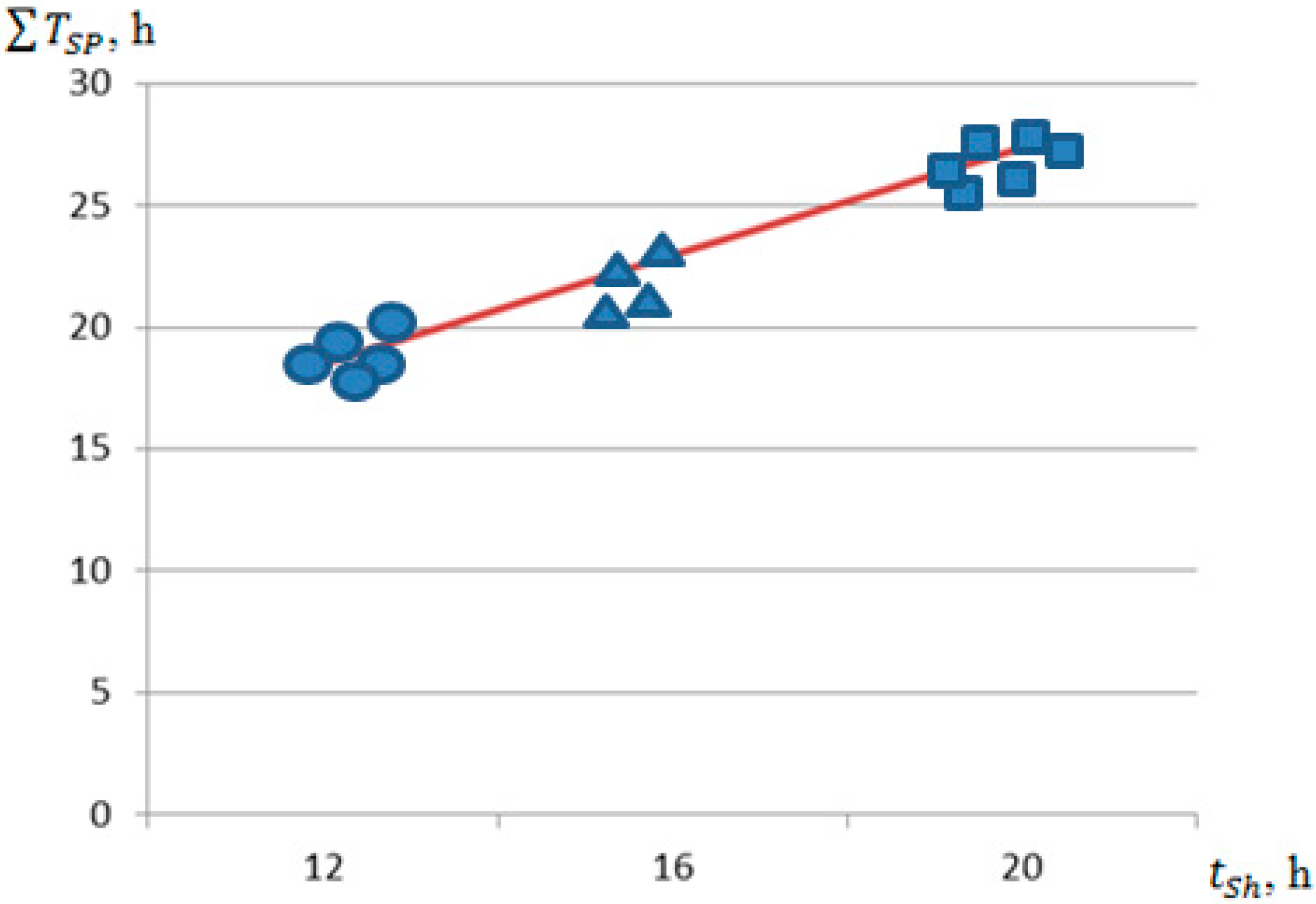


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paulauskas, V.; Paulauskas, D.; Paulauskas, V. Development of a Model for Increasing the Capacity of Small and Medium-Sized Ports Using the Principles of Probability Theory. J. Mar. Sci. Eng. 2025, 13, 1833. https://doi.org/10.3390/jmse13091833
Paulauskas V, Paulauskas D, Paulauskas V. Development of a Model for Increasing the Capacity of Small and Medium-Sized Ports Using the Principles of Probability Theory. Journal of Marine Science and Engineering. 2025; 13(9):1833. https://doi.org/10.3390/jmse13091833
Chicago/Turabian StylePaulauskas, Vytautas, Donatas Paulauskas, and Vytas Paulauskas. 2025. "Development of a Model for Increasing the Capacity of Small and Medium-Sized Ports Using the Principles of Probability Theory" Journal of Marine Science and Engineering 13, no. 9: 1833. https://doi.org/10.3390/jmse13091833
APA StylePaulauskas, V., Paulauskas, D., & Paulauskas, V. (2025). Development of a Model for Increasing the Capacity of Small and Medium-Sized Ports Using the Principles of Probability Theory. Journal of Marine Science and Engineering, 13(9), 1833. https://doi.org/10.3390/jmse13091833






