A Novel Displacement Prediction Model for Inclined Anchor Bolt Based on Mindlin’s Solution
Abstract
1. Introduction
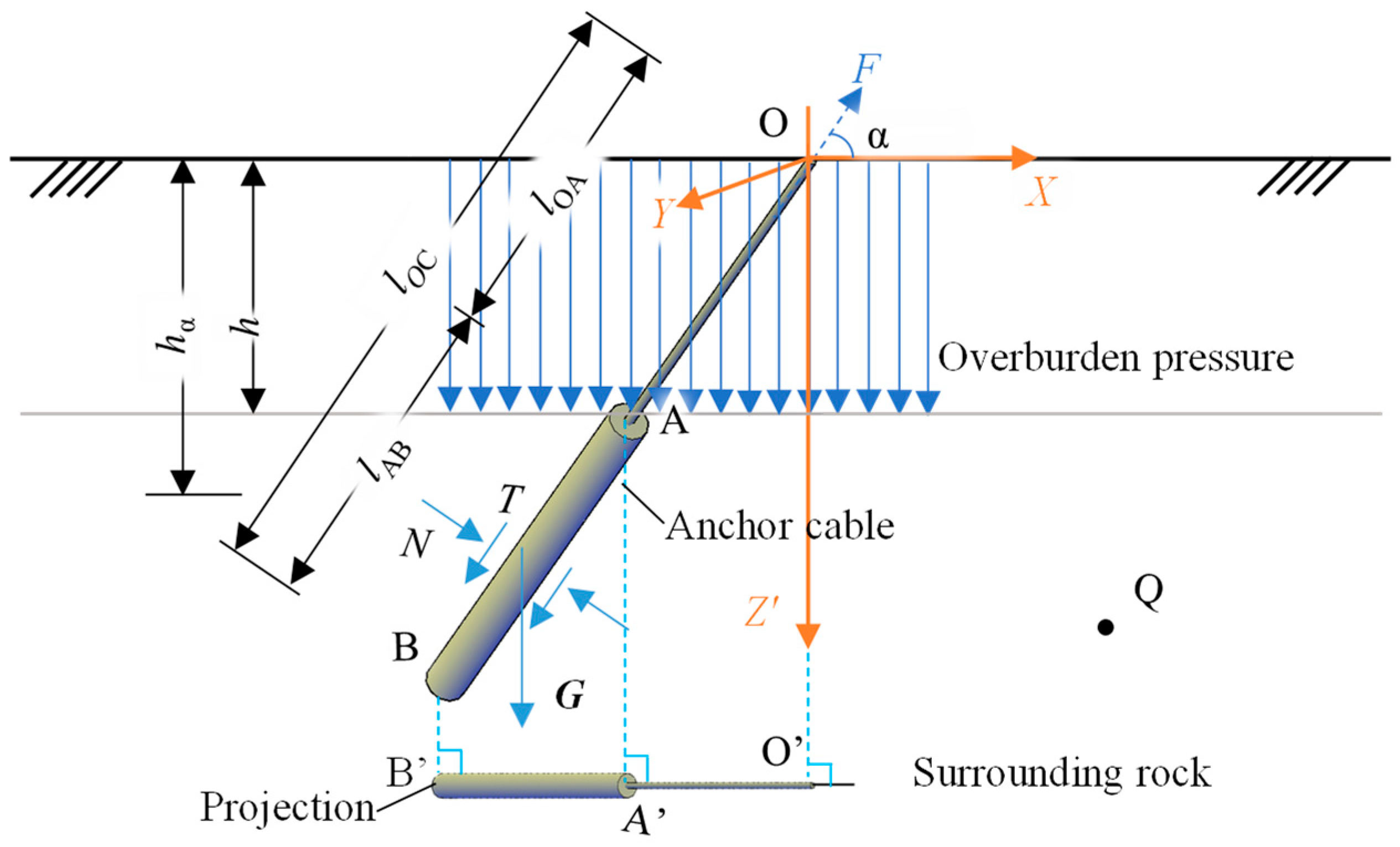
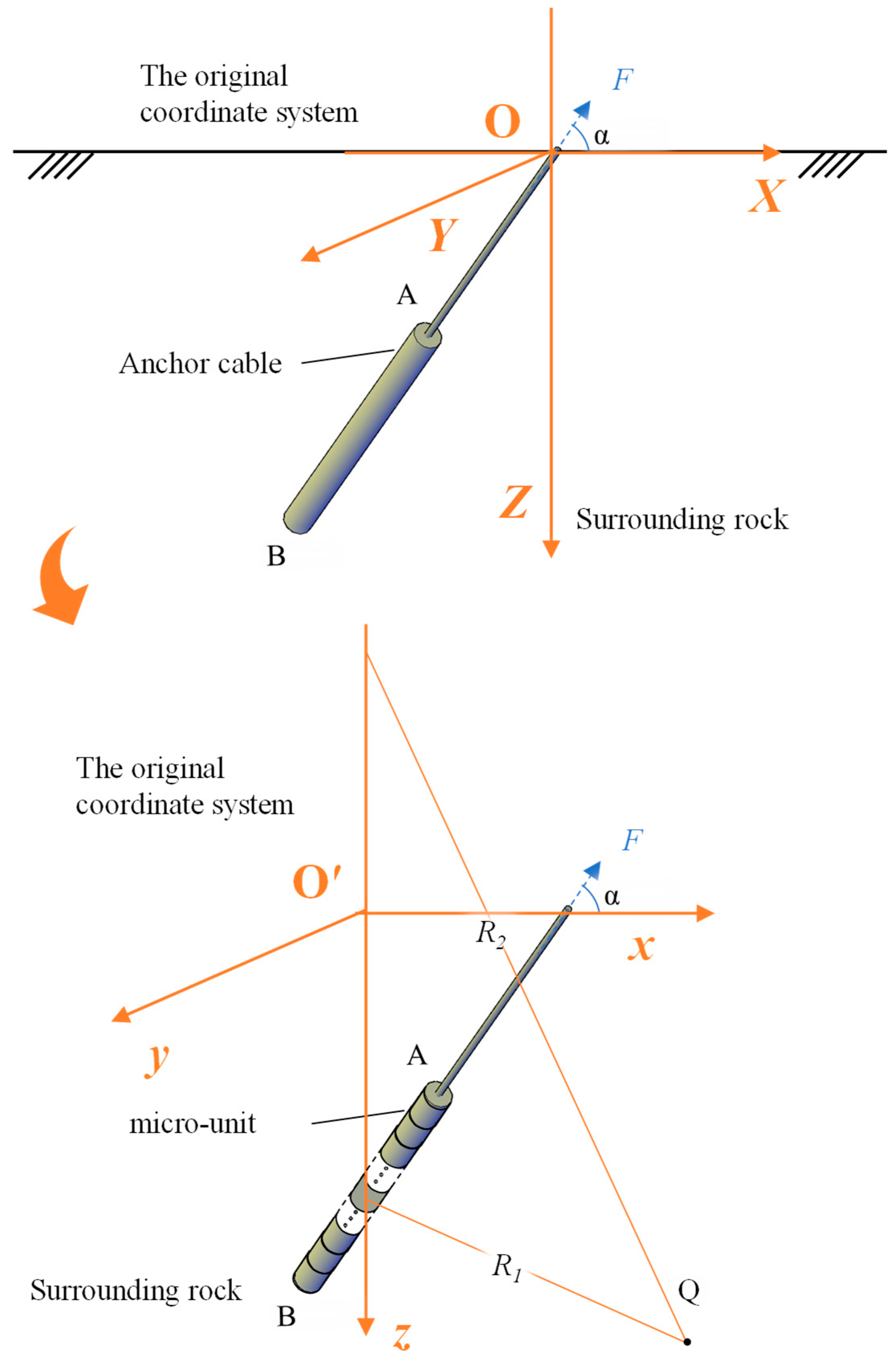
2. Theoretical Model for Calculating the Displacement of the Anchor Bolt
2.1. Axial Force Distribution of Inclined Anchor Bolt
2.2. Displacement Solution for Anchor Bolts Under Pulling Force
3. Experimental Validation
4. Discussion
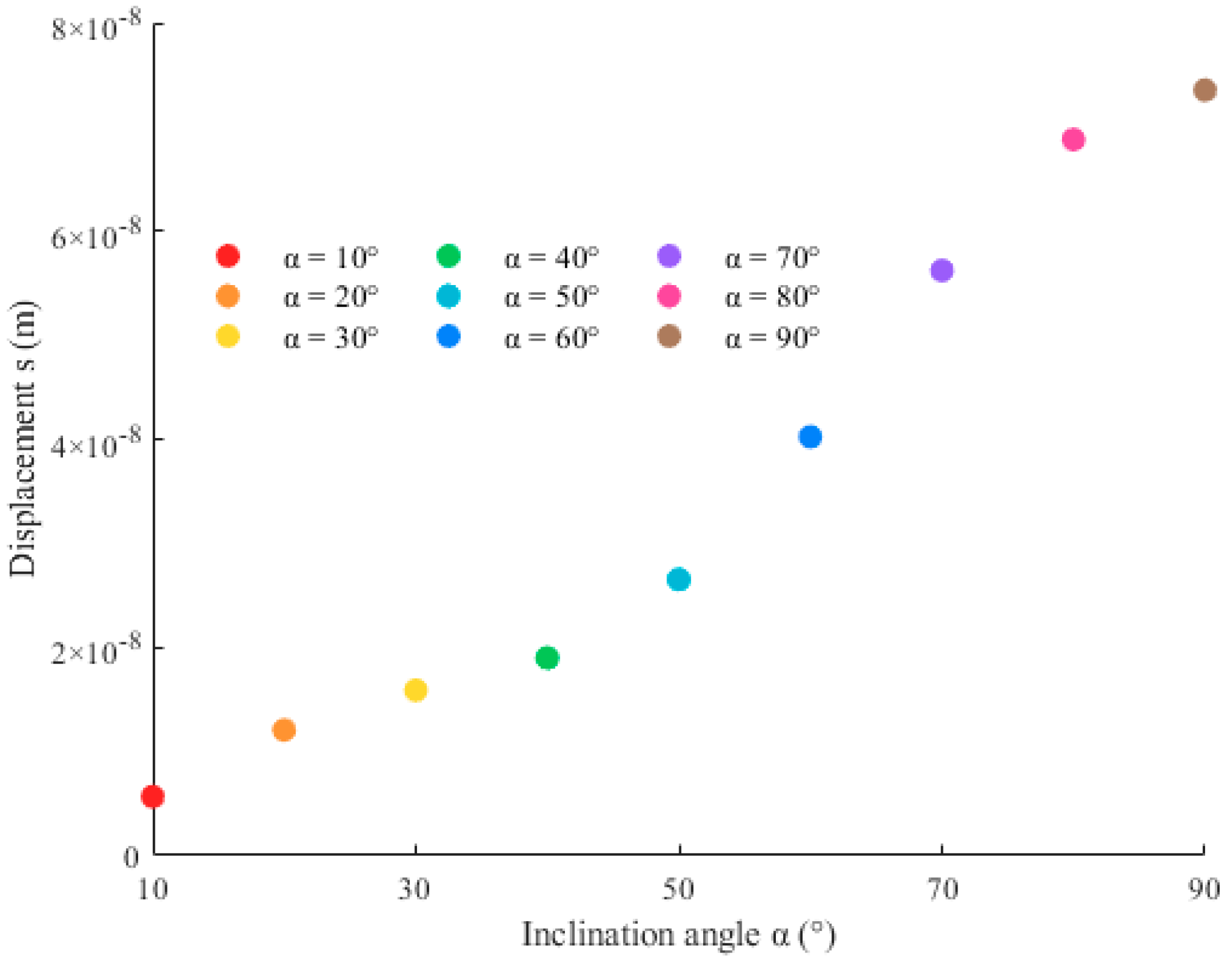
4.1. Effect of Inclination Angle on Anchor Bolt Displacement
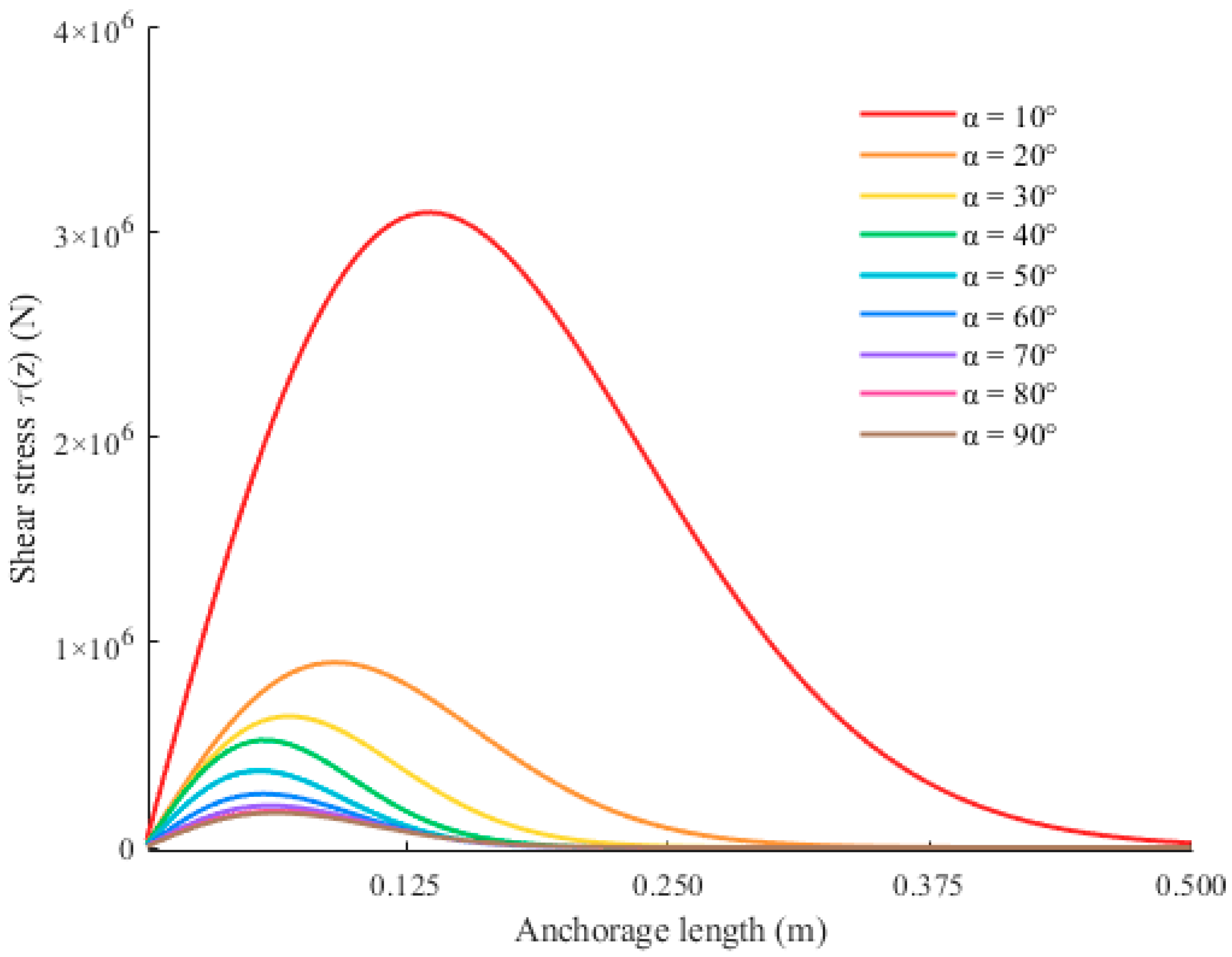
4.2. The Shear Distribution of the Anchor Bolt
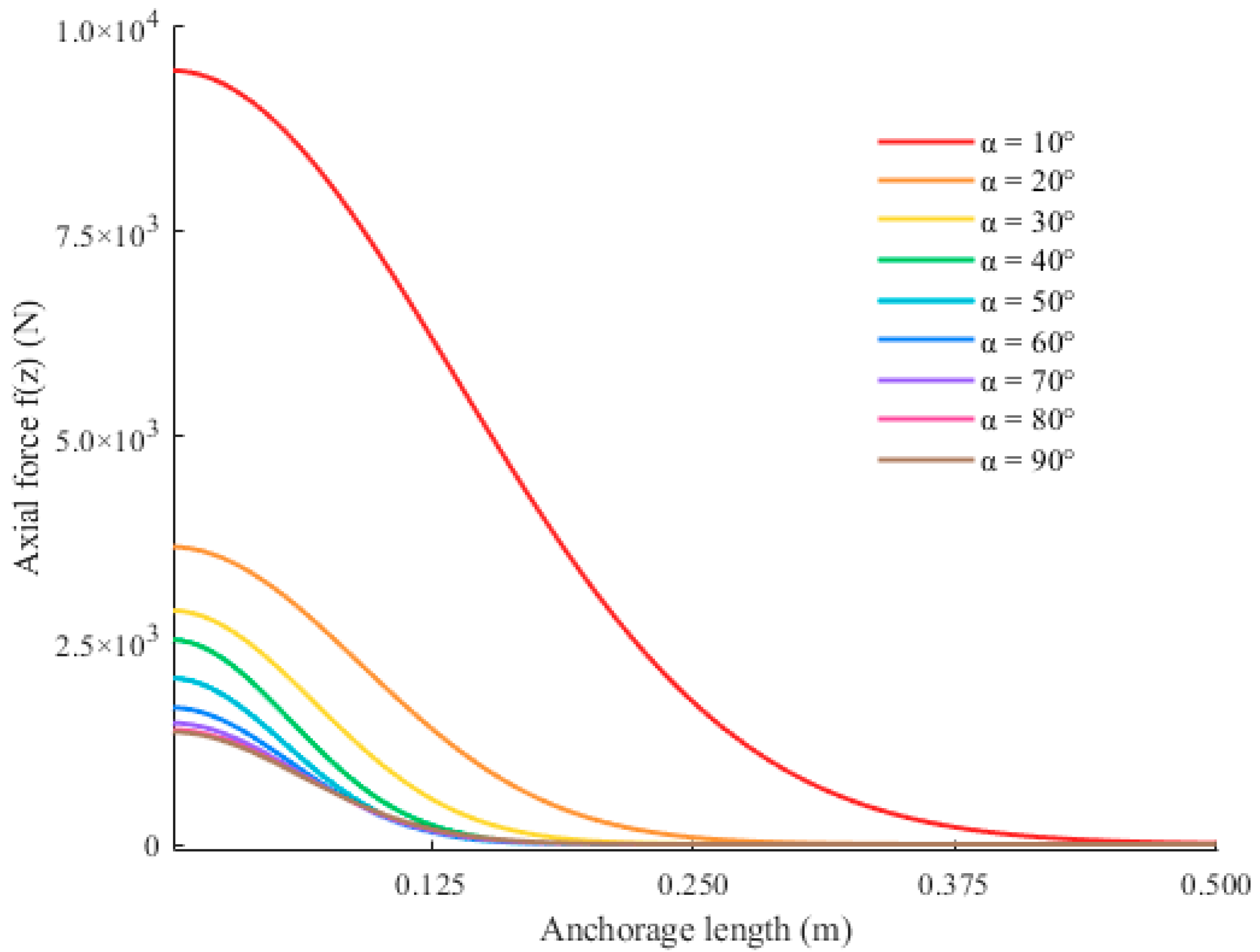
4.3. The Axial Force Distribution of the Anchor Bolt
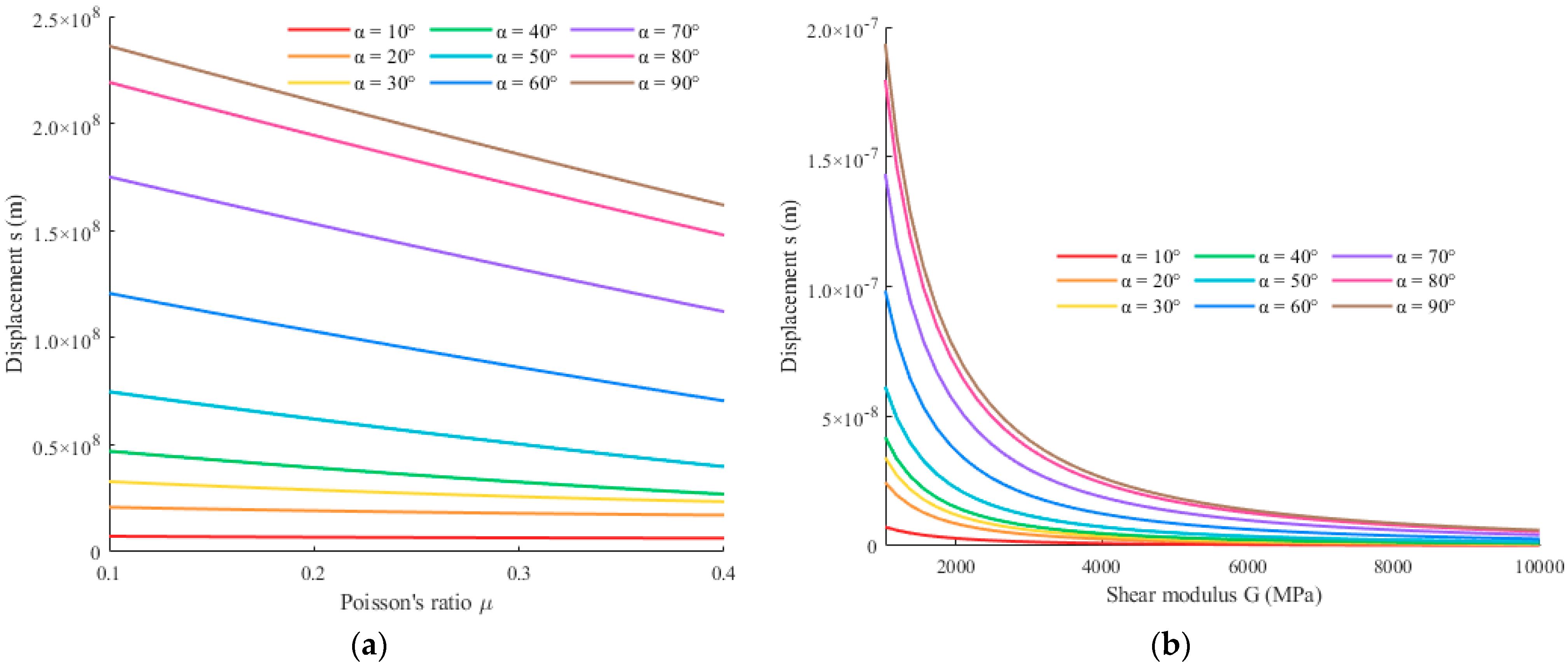
4.4. Influence of Poisson’s Ratio and Shear Modulus of Surrounding Rock on the Anchor Bolt Displacement
4.5. Comparison with Engineering Standards
5. Conclusions
- (1).
- A novel displacement prediction model for inclined anchor bolts was derived based on Mindlin’s solution, explicitly incorporating inclination angle (0° < α < 90°) into force decomposition and displacement superposition.
- (2).
- The inclination angle of the anchor bolt exerts a significant influence on its displacement. The displacement of the anchor bolt increases with inclination angle, with a sharp growth in the 50–70° range. And both peak shear stress and initial axial force decrease with increasing inclination angle.
- (3).
- Validation with three experimental datasets [8,23,31] shows that the model’s relative errors are within 5%. Even if minor measurement uncertainties of input parameters exist in practical engineering scenarios, the calculated displacement results will not undergo significant deviations, confirming its reliability.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Grindheim, B.; Li, C.C.; Høien, A.H. Full-scale pullout tests of rock anchors in a limestone quarry focusing on bond failure at the anchor-grout and grout-rock interfaces. J. Rock Mech. Geotech. Eng. 2023, 15, 2264–2279. [Google Scholar] [CrossRef]
- Ouyang, J.; Shi, X.; Qiu, X.; Zhang, Z.; Li, Z. Bond length and interface failure mechanism of anchor bolt under continuous radial pressure conditions. Int. J. Min. Sci. Technol. 2025, 35, 231–247. [Google Scholar] [CrossRef]
- Chen, W.Q.; Jia, L.Y. Analytical model of bolt shear resistance considering progressive yield of surrounding material. SN Appl. Sci. 2022, 4, 42. [Google Scholar] [CrossRef]
- Brown, E.T. Rock engineering design of post-tensioned anchors for dams—A review. J. Rock Mech. Geotech. Eng. 2015, 7, 1–13. [Google Scholar] [CrossRef]
- Fu, M.; Huang, S.; Fan, K.; Liu, S.; He, D.; Jia, H. Study on the relationship between the maximum anchoring force and anchoring length of resin-anchored bolts of hard surrounding rocks based on the main slip interface. Constr. Build. Mater. 2023, 409, 134000. [Google Scholar] [CrossRef]
- Xu, X.; Tian, S. Load transfer mechanism and critical length of anchorage zone for anchor bolt. PLoS ONE 2020, 15, e0227539. [Google Scholar] [CrossRef] [PubMed]
- Zhou, C.; Hu, Y.; Xiao, T.; Ou, Q.; Wang, L. Analytical model for reinforcement effect and load transfer of pre-stressed anchor bolt with bore deviation. Constr. Build. Mater. 2023, 379, 131219. [Google Scholar] [CrossRef]
- Nourizadeh, H.; Mirzaghorbanali, A.; McDougall, K. Exploring the axial performance of protective sheathed rock bolts through large-scale testing. Tunn. Undergr. Space Technol. 2025, 155, 106157. [Google Scholar] [CrossRef]
- Fang, G.W.; Zhu, Y.P.; Ye, S.H.; Huang, A.P. Analysis of force and displacement of anchor systems under the non-limit active state. Sci. Rep. 2022, 12, 1306. [Google Scholar] [CrossRef]
- Ye, S.; Chen, J. Reliability analysis of slope reinforced by frame anchors considering multi-anchor failure. Arab. J. Geosci. 2022, 15, 37. [Google Scholar] [CrossRef]
- Zhu, B.; Zhou, C.; Jiang, N. Dynamic characteristics and safety control of mortar bolts under tunnel blasting vibration loads. Tunn. Undergr. Space Technol. 2023, 135, 105005. [Google Scholar] [CrossRef]
- Zheng, Y.; Wang, R.; Chen, C.; Sun, C.; Ren, Z.; Zhang, W. Dynamic analysis of anti-dip bedding rock slopes reinforced by pre-stressed bolts using discrete element method. Eng. Anal. Bound. Elem. 2021, 130, 79–93. [Google Scholar] [CrossRef]
- Li, X.; Si, G.; Oh, J.; Corbett, P.; O’Sullivan, T.; Xiang, Z.; Aziz, N.; Mirzaghorbanali, A. Effect of pretension on the performance of bolt bolts and its optimisation in underground coal mines with various geological conditions. Int. J. Rock Mech. Min. Sci. 2022, 154, 105076. [Google Scholar] [CrossRef]
- Ma, H.; Chen, L.; Tan, X.; Qian, J.; Lu, Z. Theoretical dynamic displacement analysis for rock bolt with surrounding rock-soil body. Int. J. Rock Mech. Min. Sci. 2021, 141, 104698. [Google Scholar] [CrossRef]
- Yue, Z.; Li, A.; Wang, P.; Wang, P. An analytical analysis for the mechanical performance of fully-grouted roc bolts based on the exponential softening model. Int. J. Rock Mech. Min. Sci. Technol. 2022, 32, 981–995. [Google Scholar] [CrossRef]
- Li, D.; Cai, M.; Masoumi, H. A constitutive model for modified bolt bolts exhibiting cone-shaped failure mode. Int. J. Rock Mech. Min. Sci. 2021, 145, 104855–104864. [Google Scholar] [CrossRef]
- Martín, L.; Tijani, M.; Hadj-Hassen, F.; Noiret, A. Assessment of the bolt-grout interface behaviour of fully grouted rockbolts from laboratory experiments under axial loads. Int. J. Rock Mech. Min. Sci. 2013, 63, 50–61. [Google Scholar] [CrossRef]
- Chen, J.; Li, D. Numerical simulation of fully encapsulated rock bolts with a tri-linear constitutive relation. Tunn. Undergr. Space Technol. 2022, 120, 104265. [Google Scholar] [CrossRef]
- Liang, L.; Zou, X.; Liu, J. Approximate analytical algorithm for pull-out resistance-displacement relationship of combined anchor system. Eng. Fail. Anal. 2024, 166, 13. [Google Scholar] [CrossRef]
- Jia, H.; Wang, Y.; Liu, S.; Li, Y.; Shao, R.; Wang, G.; Guo, Z.; Wang, L. Experimental study on double cuneiform reamed anchorages for bolt bolt boreholes in soft rock. Int. J. Rock Mech. Min. Sci. 2022, 158, 105198. [Google Scholar] [CrossRef]
- Lin, H.; Zhong, W.W.; Xiong, W.; Tang, W.Y.; Cao, P. Effect of bolt length and slope rate on optimum anchorage angle. Chin. J. Geotech. Eng. 2014, 36, 7–11. [Google Scholar] [CrossRef]
- Sun, C.; Chen, C.; Zheng, Y.; Yuan, J. Assessing the stability of bolt-reinforced high bedding rock slopes against rotational bi-planar failure. Rock Mech. Rock Eng. 2023, 56, 1697–1715. [Google Scholar] [CrossRef]
- Cheng, Y.; Xu, Y.; Wang, L.; Wang, L. Stability of expansive soil slopes reinforced with anchor bolts based on rotational-translational mechanisms. Comput. Geotech. 2022, 146, 104747. [Google Scholar] [CrossRef]
- Zhang, J.; Niu, J.; Fu, X.; Cao, L.; Xie, Q. Shaking table test of seismic responses of anchor bolt and lattice beam reinforced slope. J. Mt. Sci. 2020, 17, 1251–1268. [Google Scholar] [CrossRef]
- Al-Shayea, N.A. Displacement of rods during pullout failure of rock anchors: A case study. Geotech. Geol. Eng. 2024, 42, 5117–5141. [Google Scholar] [CrossRef]
- Mindlin, R.D. Force at a Point in the Interior of a Semi-Infinite Solid. Physics 1936, 7, 195–202. [Google Scholar] [CrossRef]
- Zheng, B.; Bayat, M.; Shi, Y.; Cao, M.; Jiang, Y.; Qian, X.; Sumarac, D. A prognostic model of side friction of rock bolt anchoring section based on associated flow law. Kuwait J. Sci. 2025, 52, 100374. [Google Scholar] [CrossRef]
- Nourizadeh, H.; Mirzaghorbanali, A.; Serati, M.; Mutaz, E.; McDougall, K.; Aziz, N. Failure characterization of fully grouted rock bolts under triaxial testing. J. Rock Mech. Geotech. Eng. 2024, 16, 778–789. [Google Scholar] [CrossRef]
- Zhang, N.; Lu, F.; Li, C.; Guo, H.; Yin, S.; Liu, Y.; Li, Q. Shear stress distribution of fully grouted rockbolts under tensile loads. Int. J. Geomech. 2025, 25, 04025022. [Google Scholar] [CrossRef]
- Fu, X.; Li, Q.; Liu, H.; Wang, L.; Liu, X. Bearing capacity characteristic analysis of anti-floating bolts in unsaturated soil based on mindlin solution. Indian Geotech. J. 2025, 55, 1044–1053. [Google Scholar] [CrossRef]
- You, C.A. Study on static load test of group anchors. Rock Soil. Mech. 2004, 25, 383–385. [Google Scholar] [CrossRef]
- EN 1997-1:2004; European Committee for Standardization. Eurocode 7: Geotechnical Design—Part 1: General Rules. CEN: Brussels, Belgium, 2004.
- GB 50330-2013; Ministry of Housing and Urban—Rural Development of the People’s Republic of China. Technical Code for Building Slope Engineering. China Architecture & Building Press: Beijing, China, 2013.
| Symbol | Physical Quantity | Unit |
|---|---|---|
| α | Inclination angle | ° |
| Gρ | Shear modulus of surrounding rock | GPa |
| E | Elastic modulus of surrounding rock | GPa |
| μ | Poisson’s ratio of the surrounding rock | / |
| Eα | Elastic modulus of the anchor bolt | GPa |
| f | Resultant force of the micro-unit | N |
| fx | x-axis force component of micro-unit | N |
| fz | z-axis force component of the micro-unit | N |
| F | Pulling force of the anchor bolt | N |
| lAB | Anchorage segment length | m |
| l | Coordinate of the micro-unit along the z-axis. | / |
| uO | Displacements of the point O along the x-axis | m |
| vO | Displacements of the point O along the y-axis | m |
| wO | Displacements of the point O along the z-axis | m |
| ux | Displacement of point Q caused by fx along the x-axis | m |
| vx | Displacement of point Q caused by fx along the y-axis | m |
| wx | Displacement of point Q caused by fx along the z-axis | m |
| uz | Displacement of point Q caused by fz along the x-axis | m |
| vz | Displacement of point Q caused by fz along the y-axis | m |
| wz | Displacement of point Q caused by fz along the z-axis | m |
| uf | Displacements of the point Q along the x-axis caused by the i-th micro-unit | m |
| vf | Displacements of the point Q along the y-axis caused by the i-th micro-unit | m |
| wf | Displacements of the point Q along the z-axis caused by the i-th micro-unit | m |
| τ | Shear stress | / |
| r | Grouting hole radius | m |
| AS | Cross-sectional area of anchor bolt | m2 |
| δf | Total displacements of the micro-unit | m |
| u | Displacements of the anchor bolt along the x-axis | |
| v | Displacements of the anchor bolt along the y-axis | |
| w | Displacements of the anchor bolt along the z-axis | |
| h | Distance from the boundary between the anchorage segment and the free segment to the ground surface | |
| s | Total displacement of the anchor bolt |
| Reference | Inclination Angle of Centerline α (°) | Elastic Modulus of Surrounding Rock E (GPa) | Elastic Modulus of the Bolt Ea (GPa) | Anchorage Length lAB (m) | Poisson’s Ratio μ | Pulling Force F (MN) | Displacement of Anchor Bolt (mm) | Relative Error (%) | |
|---|---|---|---|---|---|---|---|---|---|
| Experimental Value | Theoretical Value | ||||||||
| You (2004) [31] | 88 | 1.2 | 210 | 6 | 0.3 | 13.9 | 1.48 | 1.47 | 0.6 |
| Cheng et al. (2022) [23] | 15 | 0.8 | 205 | 8 | 0.35 | 8.5 | 2.12 | 2.17 | 2.4 |
| Cheng et al. (2022) [23] | 20 | 0.8 | 205 | 8 | 0.35 | 8.5 | 2.35 | 2.44 | 2.1 |
| Nourizadeh et al. (2025) [8] | 30 | 1.5 | 210 | 5 | 0.28 | 10.2 | 1.86 | 1.91 | 2.7 |
| Parameter | Variation | Calculated Displacement (mm) | Displacement Change (%) | |
|---|---|---|---|---|
| Name | Value | |||
| Elastic modulus of surrounding rock E | 1.2 GPa | +5% (1.26 GPa) | 1.41 | −4.1 |
| −5% (1.14 GPa) | 1.53 | +4.1 | ||
| Poisson’s ratio of the surrounding rock μ | 0.3 | +5% (0.315) | 1.45 | −1.4 |
| −5% (0.285) | 1.49 | +1.4 | ||
| Anchorage length lAB | 6 m | +5% (6.3 m) | 1.43 | −2.7 |
| −5% (5.7 m) | 1.51 | +2.7 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Xu, G.; Xi, B. A Novel Displacement Prediction Model for Inclined Anchor Bolt Based on Mindlin’s Solution. J. Mar. Sci. Eng. 2025, 13, 1828. https://doi.org/10.3390/jmse13091828
Zhang Z, Xu G, Xi B. A Novel Displacement Prediction Model for Inclined Anchor Bolt Based on Mindlin’s Solution. Journal of Marine Science and Engineering. 2025; 13(9):1828. https://doi.org/10.3390/jmse13091828
Chicago/Turabian StyleZhang, Zhenhua, Guojuan Xu, and Banglu Xi. 2025. "A Novel Displacement Prediction Model for Inclined Anchor Bolt Based on Mindlin’s Solution" Journal of Marine Science and Engineering 13, no. 9: 1828. https://doi.org/10.3390/jmse13091828
APA StyleZhang, Z., Xu, G., & Xi, B. (2025). A Novel Displacement Prediction Model for Inclined Anchor Bolt Based on Mindlin’s Solution. Journal of Marine Science and Engineering, 13(9), 1828. https://doi.org/10.3390/jmse13091828




