A Hierarchical Slip-Compensated Control Strategy for Trajectory Tracking of Wheeled ROVs on Complex Deep-Sea Terrains

Abstract

With the rapid development of deep-sea resource exploration and marine scientific research, wheeled remotely operated vehicles (ROVs) have become crucial for seabed operations. However, under complex seabed conditions, traditional ROV control systems suffer from insufficient trajectory tracking accuracy, poor disturbance rejection capability, and low dynamic torque distribution efficiency. These issues lead to poor motion stability and high energy consumption on sloped terrains and soft substrates, which limits the effectiveness of deep-sea engineering. To address this, we proposed a comprehensive motion control solution for deep-sea wheeled ROVs. To improve modeling accuracy, a coupled kinematic and dynamic model was developed, together with a body-to-terrain coordinate frame transformation. Based on rigid-body kinematics, three-degree-of-freedom kinematic equations incorporating the slip ratio and sideslip angle were derived. By integrating hydrodynamic effects, seabed reaction forces, the Janosi soil model, and the impact of subsidence depth, a dynamic model that reflects nonlinear wheel–seabed interactions was established. For optimizing disturbance rejection and trajectory tracking, a hierarchical control method was designed. At the kinematic level, an improved model predictive control framework with terminal constraints and quadratic programming was adopted. At the dynamic level, non-singular fast terminal sliding mode control combined with a fixed-time nonlinear observer enabled rapid disturbance estimation. Additionally, a dynamic torque distribution algorithm enhanced traction performance and trajectory tracking accuracy.

1. Introduction

With the increasing depletion of terrestrial resources and the surging global demand for energy and minerals, the deep sea—rich in polymetallic nodules, hydrothermal sulfides, gas hydrates, and bioactive substances—has emerged as a critical strategic frontier for sustaining societal development [1]. However, its extreme environmental conditions, characterized by high pressure, low temperature, and perpetual darkness, impose stringent challenges on exploration and operational equipment, driving intensive advancements in deep-sea technologies worldwide. Among various robotic platforms, wheeled ROVs have gained prominence due to their superior mobility efficiency and cost-effectiveness in specific operational scenarios.

Significant progress has been achieved in the development of deep-sea robotic systems. For instance, ROVs deployed by the Woods Hole Oceanographic Institution integrate high-resolution sonar and multispectral imaging to map seabed mineral distributions with high precision, providing foundational data for geological research. Meanwhile, the robotic platforms developed by the Japan Agency for Marine-Earth Science and Technology (JAMSTEC) utilize advanced control algorithms to achieve high-precision trajectory tracking under strong currents, ensuring reliable execution of tasks such as pipeline inspection [2]. Complementary advancements include the deep-sea wheeled ROV developed by the Shenyang Institute of Automation, which is equipped with a high-performance power system and has demonstrated excellent performance in biological sampling missions [3]; additionally, Shanghai Jiao Tong University has optimized wheel designs based on insights into wheel-seabed interactions, significantly reducing energy consumption during locomotion [4].

In deep-sea exploration, wheeled ROVs excel on flat or gently sloped terrains. Their low ground contact pressure minimizes subsidence in soft sediments while maintaining high mobility, outperforming legged or tracked systems. The number of wheels is critical to operational stability: two-wheeled setups slip easily on soft seabeds and are thus only suitable for laboratory environments; three-wheeled designs enhance stability via triangular support but face rollover/slippage risks on slopes due to uneven steering forces; six-wheeled models adapt to complex terrains yet encounter control issues caused by drive redundancy. Four-wheeled configurations, by contrast, balance stability and controllability, exhibiting lower average slippage than six-wheeled counterparts on irregular terrains.

For drive systems: synchronous drive ensures steady straight-line movement but induces slippage during frequent turns due to response lag; omnidirectional drive—achieved via Mecanum wheels—enables free translation but increases sealing difficulty and energy consumption under high pressure; differential drive, a method that adjusts the speeds of left and right wheels to realize steering, pairs well with four-wheeled setups, responds quickly to changes in soft seabeds, and avoids obvious slippage. Overall, four-wheeled ROVs with differential drive optimize slippage control, making them the preferred choice for complex deep-sea environments.

Three mainstream wheel types are used for deep-sea wheeled ROVs, each with distinct trade-offs. Rigid metal wheels offer strong pressure resistance and wear durability, but their smooth surfaces result in low dynamic friction at the wheel-seabed interface, limiting their use in scenarios requiring precise slippage control. Inflatable rubber wheels enhance contact with soft sediments but deform easily under extreme deep-sea pressure, rendering them unsuitable for areas with large water depth fluctuations. Solid rubber wheels with anti-slip treads combine structural stability and high friction: the rubber conforms to the contours of soft seabeds to expand the contact area, while anti-slip treads strengthen interlocking with sediment particles—with no risk of pressure-induced deformation.

In the domain of wheeled robot modeling, diverse methodologies have been proposed to address terrain-specific challenges. Bhattacharya et al. developed a three-dimensional (3D) kinematic model incorporating circular wheel assumptions and passive joint mechanisms, which effectively resolves lateral degree-of-freedom constraints on irregular terrains [5]. Jazayeri’s dynamic model for heavy-duty differential steering robots highlighted the critical role of tire–ground contact dynamics under high-load and high-speed conditions, refining the limitations of traditional kinematic models [6]. For amphibious applications, the paddle-footed robot developed by Harbin Engineering University enables intelligent motion mode switching between beach and underwater environments, overcoming mobility limitations in shallow coastal areas [7]. Additionally, studies integrating the Janosi-Hanamoto soil model have quantified the impacts of subsidence and slippage on soft terrains, advancing dynamic modeling capabilities in unstructured environments [8].

Control strategies for wheeled robots have evolved to enhance operational robustness. Schjølberg et al. proposed a three-tier classification system (direct, shared, and automatic control) that delineates the transition from manual operation to autonomous systems [9]. Sliding Mode Control (SMC), as formulated by Utkin V, reduces system order through sliding surface design, offering strong robustness against nonlinear uncertainties and external disturbances [10]. Model Predictive Control (MPC), centered on receding horizon optimization, has become a staple for trajectory tracking under constrained conditions; however, Fontes’ nonlinear MPC framework, while ensuring stability, faces challenges related to computational complexity [11]. Complementary efforts include Peng’s neural network-based torque compensation method to improve tracking accuracy in nonholonomic robots [12], Zhu’s fuzzy rule-optimized Artificial Potential Field Method for path planning, and anti-disturbance controllers that combine SMC with disturbance observers to mitigate slippage-induced instability [13].

Despite these advancements, wheeled ROVs still encounter critical challenges in unstructured seabeds, particularly in loose sediment environments. Key issues include dynamic subsidence resulting from tire–sediment interactions, nonlinear responses arising from fluid–structure coupling, and motion instability under high slip ratios. Existing research predominantly focuses on compensating for individual factors, lacking systematic solutions that address the coupled effects of multiple physical fields. To address these limitations, this study focuses on motion control modeling and trajectory tracking optimization for wheeled ROVs in complex seabed environments. The research encompasses three core components:

(1)

Developing a coupled kinematic-dynamic model that integrates hydrodynamic effects, seabed reaction forces, and dynamic friction characteristics to enhance modeling accuracy;

(2)

Proposing a hierarchical control strategy, where MPC optimizes trajectory tracking at the kinematic level, and non-singular fast terminal sliding mode control (NFTSMC) combined with a fixed-time nonlinear observer improves disturbance rejection at the dynamic level;

(3)

Designing a dynamic torque distribution algorithm to optimize drive force allocation, thereby enhancing adaptability and robustness.

This work aims to provide a technical foundation for reliable deep-sea resource exploration, advance independent innovation in China’s deep-sea equipment sector, and support maritime development strategies. The findings are expected to extend to related fields such as polar expeditions and underwater rescue, offering both scientific significance and engineering application value.

2. Slope Motion Characteristics and Dynamic Analysis of Wheeled ROVs

2.1. Kinematic Modeling of Slope Motion Considering Slip Characteristics

To accurately construct the kinematic and dynamic models of the wheeled ROV on deep-sea sloped seabeds, the ROV used in this study is equipped with solid rubber driving wheels with diamond-shaped anti-slip treads and adopts a four-wheel differential drive configuration. Based on this wheel configuration, a dual-coordinate-frame modeling method was employed for kinematic analysis: the full 3D spatial pose of the wheeled ROV is described by establishing the transformation between the world inertial coordinate frame and the ROV’s body-fixed coordinate frame, using Euler angle attitude representations and homogeneous transformation matrices.

The world inertial coordinate frame $\left\{{\mathrm{O}}_{\mathrm{I}}{\mathrm{X}}_{\mathrm{I}}{\mathrm{Y}}_{\mathrm{I}}{\mathrm{Z}}_{\mathrm{I}}\right\}$ serves as the global reference for determining the ROV’s absolute position and heading on a deep-sea slope. The body-fixed coordinate frame $\left\{{\mathrm{O}}_{\mathrm{B}}{\mathrm{X}}_{\mathrm{B}}{\mathrm{Y}}_{\mathrm{B}}{\mathrm{Z}}_{\mathrm{B}}\right\}$, rigidly attached to the ROV, is used to accurately characterize the ROV’s relative attitude changes and motion states via roll-pitch-yaw angles [14]. The specific representation of the wheeled ROV under the dual-coordinate-frame system is shown in Figure 1.

The pose coordinate frame of the ROV is represented as follows:

$$\mathit{q}={[\begin{array}{ccc}{x}_I& y_I& {\theta }_I\end{array}]}^T$$

(1)

The velocity of the ROV’s center of mass, when transformed into the global coordinate frame, is expressed as [15]

$$\left[\begin{array}{c}{\dot{x}}_I\\ {\dot{y}}_I\\ \dot{\theta }\end{array}\right]=\left[\begin{array}{ccc}\cos \theta & -\sin \theta & 0\\ \sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{v}_x\\ v_y\\ w_c\end{array}\right]$$

(2)

Assuming the ROV’s center of mass coincides with its geometric center at 0 s, the v_x values of the left and right wheels are identical, and the front and rear wheels share the same v_y [16]. The following relationship holds:

$$\left\{\begin{array}{l}{v}_x=v\cos \beta =v_1\cos {\beta }_1+w_{c}L=v_2\cos {\beta }_2-w_{c}L=v_3\cos {\beta }_3-w_{c}L=v_4\cos {\beta }_4+w_{c}L\\ v_y=v\sin \beta =v_1\sin {\beta }_1-w_{c}d=v_2\sin {\beta }_2-w_{c}d=v_3\sin {\beta }_3+w_{c}d=v_4\sin {\beta }_4+w_{c}d\end{array}\right.$$

(3)

The sideslip angle of each wheel is given by

$$\begin{array}{l}{\beta }_1={\tan }^{-1}({\displaystyle \frac{v\sin \beta +w_{c}d}{v\cos \beta -w_{c}L}})\\ {\beta }_2={\tan }^{-1}({\displaystyle \frac{v\sin \beta +w_{c}d}{v\cos \beta +w_{c}L}})\\ {\beta }_3={\tan }^{-1}({\displaystyle \frac{v\sin \beta -w_{c}d}{v\cos \beta +w_{c}L}})\\ {\beta }_4={\tan }^{-1}({\displaystyle \frac{v\sin \beta -w_{c}d}{v\cos \beta -w_{c}L}})\end{array}$$

(4)

Considering sideslip during ROV motion, the expressions for longitudinal velocity, lateral velocity, and angular velocity can be derived as

$$\left\{\begin{array}{l}{v}_x={\displaystyle \frac{v_1\cos {\beta }_1+v_2\cos {\beta }_2+v_3\cos {\beta }_3+v_4\cos {\beta }_4}{4}}\hfill \\ v_y={\displaystyle \frac{v_1\sin {\beta }_1+v_2\sin {\beta }_2+v_3\sin {\beta }_3+v_4\sin {\beta }_4}{4}}\hfill \\ w_c={\displaystyle \frac{v_1\cos {\beta }_1-v_2\cos {\beta }_2-v_3\cos {\beta }_3+v_4\cos {\beta }_4}{4L}}\hfill \end{array}\right.$$

(5)

It is further simplified to obtain

$$\left[\begin{array}{c}{\dot{x}}_I\\ {\dot{y}}_I\\ \dot{\theta }\end{array}\right]={\displaystyle \frac{1}{4}}\left[\begin{array}{cccc}\cos (\theta +{\beta }_1)& \cos (\theta +{\beta }_2)& \cos (\theta +{\beta }_3)& \cos (\theta +{\beta }_4)\\ \sin (\theta +{\beta }_1)& \sin (\theta +{\beta }_2)& \sin (\theta +{\beta }_3)& \sin (\theta +{\beta }_4)\\ {\displaystyle \frac{\cos {\beta }_1}{L}}& -{\displaystyle \frac{\cos {\beta }_2}{L}}& -{\displaystyle \frac{\cos {\beta }_3}{L}}& {\displaystyle \frac{\cos {\beta }_4}{L}}\end{array}\right]\left[\begin{array}{c}{v}_1\\ v_2\\ v_3\\ v_4\end{array}\right]$$

(6)

When considering the longitudinal slip effect during the ROV’s motion, the actual longitudinal velocity v_x of the center of mass is much smaller than the theoretical longitudinal velocity V_x,theory due to relative sliding between the tire and the seabed. To describe this phenomenon accurately, independent slip ratios s₁, s₂, s₃, s₄ for the four driving wheels are introduced, where s_i represents the slip ratio of the i-th tire and is defined as $s_i=(v_{theory}-v_{actual})/v_{theory}$. The longitudinal velocity v_x of the center of mass is the product of the theoretical velocity and the slip compensation term; the lateral velocity v_y is affected by the sideslip angle β; and the angular velocity ω_c of the center of mass must incorporate disturbances caused by differences in the slip ratios and offset angles of the individual wheels. Based on this, the formulas for correcting the longitudinal and lateral velocities, as well as the angular velocity, of the ROV’s center of mass can be derived:

$$\left\{\begin{array}{l}{v}_x={\displaystyle \frac{v_1(1-s_1)\cos {\beta }_1+v_2(1-s_2)\cos {\beta }_2+v_3(1-s_3)\cos {\beta }_3+v_4(1-s_4)\cos {\beta }_4}{4}}\hfill \\ v_y={\displaystyle \frac{v_1(1-s_1)\sin {\beta }_1+v_2(1-s_2)\sin {\beta }_2+v_3(1-s_3)\sin {\beta }_3+v_4(1-s_4)\sin {\beta }_4}{4}}\hfill \\ w_c={\displaystyle \frac{v_1(1-s_1)\cos {\beta }_1-v_2(1-s_2)\cos {\beta }_2-v_3(1-s_3)\cos {\beta }_3+v_4(1-s_4)\cos {\beta }_4}{4L}}\hfill \end{array}\right.$$

(7)

Substitute v_x, v_y, and ω_c into Equation (2), and rearrange the substituted terms into a linear combination of the inputs ${\left[\begin{array}{cccc}{v}_1& v_2& v_3& v_4\end{array}\right]}^T$ as follows:

$$\dot{\mathit{q}}=\left[\begin{array}{cccc}{\displaystyle \frac{(1-s_1)\cos (\theta +{\beta }_1)}{4}}& {\displaystyle \frac{(1-s_2)\cos (\theta +{\beta }_2)}{4}}& {\displaystyle \frac{(1-s_3)\cos (\theta +{\beta }_3)}{4}}& {\displaystyle \frac{(1-s_4)\cos (\theta +{\beta }_4)}{4}}\\ {\displaystyle \frac{(1-s_1)\sin (\theta +{\beta }_1)}{4}}& {\displaystyle \frac{(1-s_2)\sin (\theta +{\beta }_2)}{4}}& {\displaystyle \frac{(1-s_3)\sin (\theta +{\beta }_3)}{4}}& {\displaystyle \frac{(1-s_4)\sin (\theta +{\beta }_4)}{4}}\\ {\displaystyle \frac{(1-s_1)\cos {\beta }_1}{4L}}& -{\displaystyle \frac{(1-s_2)\cos {\beta }_2}{4L}}& -{\displaystyle \frac{(1-s_3)\cos {\beta }_3}{4L}}& {\displaystyle \frac{(1-s_4)\cos {\beta }_4}{4L}}\end{array}\right]\left[\begin{array}{c}{v}_1\\ v_2\\ v_3\\ v_4\end{array}\right]$$

(8)

When the ROV operates on a slope with both longitudinal and lateral inclinations, its motion is illustrated in Figure 2. To clarify the ROV’s structural basis for supporting this motion, its overall structure is shown in Figure 3. On such a slope, the gravitational acceleration g can be decomposed into three components along the axes of the body-fixed frame: longitudinal, lateral, and vertical. These components significantly influence the ROV’s dynamic behavior. When describing the ROV’s pose, pitch motion about the X-axis, roll motion about the Y-axis, and yaw motion about the Z-axis must be considered. Its kinematic model must consider the coupled effects between the slope geometry and the ROV’s body attitude. By establishing a transformation between the slope coordinate frame and the ROV’s body-fixed frame, an improved kinematic equation incorporating terrain inclination parameters can be derived. This equation accurately characterizes the velocity constraints at the contact points between the driving wheels and the slope surface [17].

The rotation matrices of the world inertial coordinate frame about the X, Y, and Z axes $R_X\left(\gamma \right)$, $R_Y\left(\phi \right)$,$R_Z\left(\theta \right)$ are given by

$$R_X(\gamma )=\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos \gamma & -\sin \gamma \\ 0& \sin \gamma & \cos \gamma \end{array}\right], R_Y(\phi )=\left[\begin{array}{ccc}\cos \phi & 0& \sin \phi \\ 0& 1& 0\\ -\sin \phi & 0& \cos \phi \end{array}\right], R_Z(\theta )=\left[\begin{array}{ccc}\cos \theta & -\sin \theta & 0\\ \sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right]$$

(9)

To compute the 3D rotation matrix, the inertial coordinate frame of the ROV on the slope is rotated sequentially: first around the X-axis by $\gamma$, then around the Y-axis by $\phi$, and finally around the Z-axis by $\theta$:

$$\begin{array}{l}{R}_{ZYX}(\theta ,\phi ,\gamma )=R_Z(\theta )R_Y(\phi )R_X(\gamma )\\ =\left[\begin{array}{ccc}\cos \theta \cos \phi & \cos \theta \sin \phi \sin \gamma -\sin \theta \cos \gamma & \cos \theta \sin \phi \cos \gamma +\sin \theta \sin \gamma \\ \sin \theta \cos \phi & \sin \theta \sin \phi \sin \gamma +\cos \theta \cos \gamma & \sin \theta \sin \phi \cos \gamma -\cos \theta \sin \gamma \\ -\sin \phi & \cos \phi \sin \gamma & \cos \phi \cos \gamma \end{array}\right]\end{array}$$

(10)

$$\mathit{q}=R_{ZYX}(\theta ,\phi ,\gamma ){\mathit{q}}_B$$

(11)

The motion state of the ROV is affected by the inclined plane. When its state parameters change, the expressions for correcting the longitudinal effective velocity ${v^{\prime }}_y$, lateral effective velocity ${v^{\prime }}_x$, effective wheel speed $v_{i,\mathrm{eff}}$, and side slip angle ${{\beta }^{\prime }}_i$ are as follows:

$$\left\{\begin{array}{l}{v^{\prime }}_y=v_i\cos \gamma \cos \phi \\ {v^{\prime }}_x=v_i\sin \gamma \sin \phi \\ v_{i,\mathrm{eff}}=v_i\cos \gamma \cos \phi (1-s_i)\\ {{\beta }^{\prime }}_i={\beta }_i+\arctan \left(\tan \gamma \sin \phi \right)\end{array}\right.$$

(12)

After accounting for the slope’s inclination angle, the ROV’s center of mass velocity and angular velocity are as follows:

$$\left\{\begin{array}{l}{v}_x={\displaystyle \frac{{\displaystyle \sum _{i=1}^4{v}_i}\cos \gamma \cos \phi (1-s_i)\cos {{\beta }^{\prime }}_i}{4}}\hfill \\ v_y={\displaystyle \frac{{\displaystyle \sum _{i=1}^4{v}_i}\cos \gamma \cos \phi (1-s_i)\sin {{\beta }^{\prime }}_i}{4}}\hfill \\ w_c=\cos \gamma \cos \phi \cdot {\displaystyle \frac{v_1(1-s_1)\cos {{\beta }^{\prime }}_1-v_2(1-s_2)\cos {{\beta }^{\prime }}_2-v_3(1-s_3)\cos {{\beta }^{\prime }}_3+v_4(1-s_4)\cos {{\beta }^{\prime }}_4}{4L}}\hfill \end{array}\right.$$

(13)

The ROV velocity after coupling with the slope is transformed into the global coordinate frame as

$$S(\mathit{q})=\cos \gamma \cos \phi \left[\begin{array}{cccc}{\displaystyle \frac{(1-s_1)\cos (\theta +{{\beta }^{\prime }}_1)}{4}}& {\displaystyle \frac{(1-s_2)\cos (\theta +{{\beta }^{\prime }}_2)}{4}}& {\displaystyle \frac{(1-s_3)\cos (\theta +{{\beta }^{\prime }}_3)}{4}}& {\displaystyle \frac{(1-s_4)\cos (\theta +{{\beta }^{\prime }}_4)}{4}}\\ {\displaystyle \frac{(1-s_1)\sin (\theta +{{\beta }^{\prime }}_1)}{4}}& {\displaystyle \frac{(1-s_2)\sin (\theta +{{\beta }^{\prime }}_2)}{4}}& {\displaystyle \frac{(1-s_3)\sin (\theta +{{\beta }^{\prime }}_3)}{4}}& {\displaystyle \frac{(1-s_4)\sin (\theta +{{\beta }^{\prime }}_4)}{4}}\\ {\displaystyle \frac{(1-s_1)\cos {{\beta }^{\prime }}_1}{4L}}& -{\displaystyle \frac{(1-s_2)\cos {{\beta }^{\prime }}_2}{4L}}& -{\displaystyle \frac{(1-s_3)\cos {{\beta }^{\prime }}_3}{4L}}& {\displaystyle \frac{(1-s_4)\cos {{\beta }^{\prime }}_4}{4L}}\end{array}\right]$$

(14)

where

$$\mathit{v}={\left[\begin{array}{cccc}{v}_1& v_2& v_3& v_4\end{array}\right]}^T,\mathit{G}(\mathit{q})=\left[\begin{array}{c}-g\sin \phi \cos \theta +g\sin \gamma \sin \theta \\ -g\sin \phi \sin \theta -g\sin \gamma \cos \theta \\ 0\end{array}\right]$$

(15)

To meet the design requirements of the wheeled ROV, the robot’s structural parameters and terrain parameters are specified herein, providing a basis for subsequent controller design and simulation verification. The kinematic parameters are presented in

Table 1. Kinematic parameters.

Parameter	Numerical Value
Distance d from front and rear wheel axles to the robot’s transverse axis (m)	0.6
Distance L from the wheel’s central axis to the robot’s longitudinal axis (m)	0.5
Height of center of mass h (m)	0.35
Tire radius r (m)	0.2
Tire width b (m)	0.15

.

2.2. Dynamics Modeling Based on Seabed Sand Environment

2.2.1. Water Resistance Analysis

We considered only the straight-line resistance exerted by the current on the ROV, as the ROV’s steering angular velocity is relatively low during actual seabed operations. The hydrodynamic characteristics of the ROV during straight-line motion were analyzed via numerical simulations in Ansys 2022 R1 software. The ROV’s 3D model was first simplified to a reasonable extent to retain its main structural frame and key hydrodynamic features. A hybrid meshing technique was adopted to generate a high-quality computational mesh for the domain.

In the numerical simulation, the Reynolds-averaged Navier–Stokes (RANS) equations were solved using the standard k-ω turbulence model, which effectively handles boundary layer flows and moderately separated flows. The computational domain was configured as a cuboid-shaped basin. A velocity inlet boundary condition was applied at the inlet, a pressure outlet boundary condition at the outlet, and the ROV surface was treated as a no-slip wall boundary. To simulate the flow field characteristics at different operating velocities, the incoming flow velocity was set to range from 0 to 1 m/s, with an increment of 0.1 m/s. The SIMPLE algorithm was used to solve the pressure-velocity coupling problem. Spatial discretization was implemented with a second-order upwind scheme, and time discretization with an implicit method. The convergence of the resistance coefficient was monitored during the entire simulation to ensure result reliability. Finally, water resistance data for the ROV were obtained at 11 operating velocities. Figure 4 and

Table 2. Numerical values for the relationship between water resistance and flow rate.

v (m/s)	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1
F (N)	0	3.54	12.24	24.22	40.68	63.05	89.55	121.14	157.45	205.69	246.57

present the water resistance curves and corresponding resistance values at different velocities.

2.2.2. Analysis of Wheel–Seabed Interaction Forces

The motion characteristics of wheeled ROVs in the soft seabed sand environment are significantly different from those on hard and flat ground. The deformable nature of sandy soil leads to complex nonlinear characteristics in the wheel–ground interaction, which are mainly manifested in the increase in the longitudinal slip ratio and lateral slip displacement—directly affecting the trajectory tracking accuracy of the robot. The wheel subsidence caused by soil plastic deformation significantly changes the mechanical characteristics of wheel–ground contact, increases motion resistance, and intensifies energy consumption. This dynamically changing wheel–ground interaction mechanism introduces additional motion uncertainties, posing challenges to operational efficiency and system stability. To address the special working conditions of soft seabed terrain, it is necessary to establish a wheel–ground interaction model incorporating multiple parameters such as subsidence depth and slip ratio. Figure 5 illustrates the mechanical interaction model of the driving wheel on deformable ground.

When a wheeled robot operates in a loose sandy environment, the wheel dynamics are influenced by multiple factors, and the mechanism through which these factors act is centrally reflected in the wheel-terrain interaction. From a mechanical perspective, the primary forces acting on the wheels include: tangential motion resistance, normal load, motor driving torque, and the shear and normal stresses exerted by the soil. Key parameters characterizing the wheel’s motion state include: slip ratio s, sideslip angle β, angular velocity ω, and the wheel–seabed contact angle θ_k [18]. Among them, the sideslip angle β represents the angle between the actual travel direction of the wheel and the longitudinal axis of the vehicle body, indicating the degree of lateral deviation of the wheel. The wheel–seabed contact angle θ_k comprises three key components: the entry angle θ_e, defined as the angle between the wheel’s vertical center plane and the radial direction at the initial contact point; the departure angle θ_l, representing the angle between the vertical center plane and the radial direction at the final contact point; and the maximum stress angle θ_m, corresponding to the direction of maximum radial stress. As a core motion parameter, the slip ratio s quantitatively characterizes the difference between the actual moving velocity v_s of the wheel and its theoretical rolling velocity. Its mathematical expression is given by [19]

$$v_s=r\omega -v\cos {\theta }_k=r\omega \left[1-(1-s)\cos {\theta }_k\right]$$

(16)

The longitudinal shear displacement between the wheel and the soil can be obtained by integration.

$$j({\theta }_k)={\displaystyle {\int }_0^t{v}_s}dt=r[{\theta }_e-{\theta }_k-(1-s)(\sin {\theta }_e-\sin {\theta }_k)]$$

(17)

Maximum stress angle θ_m:

$${\theta }_m=(c_1+c_2|s|){\theta }_e$$

(18)

In the environment of soft seabed sand, pore water pressure significantly offsets the normal load of the soil and reduces its shear strength. Based on Terzaghi’s principle of effective stress, the calculation formulas for the longitudinal shear force and vertical stress at any point in the contact area between the wheel and the ground can be derived.

$$\left\{\begin{array}{l}\sigma ({\theta }_k)=({\displaystyle \frac{k_c}{b}}+k_{\phi })r^n{({\cos \theta }_k-{\cos \theta }_e)}^n-u_w\\ \tau ({\theta }_k)=(c+\sigma ({\theta }_k)\tan \phi )(1-e^{-j({\theta }_k)/k_s})\end{array}\right.$$

(19)

In the formula, c is the soil cohesion parameter (Pa), φ is the soil internal friction angle (°), k_s is the soil shear deformation parameter (m), k_c is the cohesion deformation modulus (m), k_φ is the friction deformation modulus (m), and n is the sinkage index. u_w is the pore water pressure. In this study, a simplified calculation model is adopted: u_w = γ_w⋅z, where γ_w is the seawater density and z is the sinkage. Among them, z = r (1 − cosθ_k).

In the wheel–ground contact mechanics analysis, the maximum vertical stress σ_m in the contact area occurs at the contact center. Its stress distribution can be characteristically decomposed into two key regions: the stress σ₁ in the front contact region and the stress σ₂ in the rear contact region, which are asymmetrically distributed on both sides of σ_m. This dichotomous characterization reveals the basic mechanical characteristics of tire–ground interaction.

$$\left\{\begin{array}{cc}{\sigma }_1({\theta }_k)=({\displaystyle \frac{k_c}{b}}+k_{\phi })r^n{({\cos \theta }_k-{\cos \theta }_e)}^n\hfill & \hfill ({\theta }_m\le {\theta }_k\le {\theta }_e)\\ {\sigma }_m=\sigma ({\theta }_m)=({\displaystyle \frac{k_c}{b}}+k_{\phi })r^n{({\cos \theta }_m-{\cos \theta }_e)}^n\hfill & \\ {\sigma }_2({\theta }_k)=({\displaystyle \frac{k_c}{b}}+k_{\phi })r^n[\cos ({\theta }_e-{\displaystyle \frac{{\theta }_k-{\theta }_l}{{\theta }_m-{\theta }_l}})\times ({\theta }_e-{\theta }_m)-{\cos \theta }_e{]}^n\hfill & \hfill ({\theta }_l\le {\theta }_k\le {\theta }_m)\end{array}\right.$$

(20)

When a wheeled ROV passes through a loose soil environment, the tangential shear strength of the soil directly determines the maximum traction the wheels can generate. Therefore, the soil’s shear characteristics are a decisive factor affecting vehicle trafficability. Based on the classical Janosi–Hanamoto soil model, the relationship between soil shear stress and shear displacement assumes the following nonlinear form [20]:

$$\left\{\begin{array}{l}{\tau }_1({\theta }_k)=(c+{\sigma }_1({\theta }_k)\tan \phi )(1-e^{-{\displaystyle \frac{-j({\theta }_k)}{k_s}}})\begin{array}{ccc}& & \end{array}({\theta }_m\le {\theta }_k\le {\theta }_e)\\ {\tau }_m=\tau ({\theta }_m)=(c+{\sigma }_m\tan \phi )(1-e^{-r\left[({\theta }_e-{\theta }_m)-(1-s)(\sin {\theta }_e-\sin {\theta }_m)\right]/k_s})\\ {\tau }_2({\theta }_k)=(c+{\sigma }_2({\theta }_k)\tan \phi )(1-e^{-{\displaystyle \frac{-j({\theta }_k)}{k_s}}})\begin{array}{ccc}& & \end{array}({\theta }_l\le {\theta }_k\le {\theta }_m)\end{array}\right.$$

(21)

In the deep-sea environment, the partial subsidence of the ROV will cause the height of the center of buoyancy to rise. At this time, the effective buoyancy F_b′ is less than the theoretical buoyancy F_b, and the buoyancy reduction effect can be quantified by the following formula, F_b′ = F_b⋅(1 − α⋅z), where α is the buoyancy reduction coefficient and z is the subsidence-related parameter.

The normal load, traction force, and rotational torque are given as

$$\left\{\begin{array}{l}{W}_i=rb\left\{{\displaystyle {\int }_{{\theta }_{\mathrm{l}}}^{{\theta }_m}\left[{\sigma }_2({\theta }_k)\cos {\theta }_k+{\tau }_2({\theta }_k)\sin {\theta }_k\right]}d\theta +{\displaystyle {\int }_{{\theta }_m}^{{\theta }_e}\left[{\sigma }_1({\theta }_k)\cos {\theta }_k+{\tau }_1({\theta }_k)\sin {\theta }_k\right]}d{\theta }_k\right\}\\ F_{D{P}_i}=rb\left\{{\displaystyle {\int }_{{\theta }_l}^{{\theta }_m}\left[{\tau }_2({\theta }_k)\cos {\theta }_k-{\sigma }_2({\theta }_k)\sin {\theta }_k\right]}d{\theta }_k+{\displaystyle {\int }_{{\theta }_m}^{{\theta }_e}\left[{\tau }_1({\theta }_k)\cos {\theta }_k-{\sigma }_1({\theta }_k)\sin {\theta }_k\right]}d{\theta }_k\right\}\\ T_i=r^{2}b\left[{\displaystyle {\int }_{{\theta }_2}^{{\theta }_m}{\tau }_2}({\theta }_k)d{\theta }_k+{\displaystyle {\int }_{{\theta }_m}^{{\theta }_1}{\tau }_1}({\theta }_k)d{\theta }_k\right]\end{array}\right.$$

(22)

Under the working condition where the robot as a whole bears a vertical normal load of 600 N and the ground slope ranges from 0° to 10°, the wheel pressures of each driving wheel show a dynamic distribution of 100–200 N. Based on the established wheel–ground contact mechanics model, when the slip ratio variation range of the wheels is set to 0–0.5, curves of wheel–ground interaction with respect to the slip ratio as shown in Figure 6 are obtained through numerical simulation.

In Figure 6a, the Sinkage Curve shows that the sinkage increases with the rise in the slip ratio under a fixed wheel pressure. In Figure 6b, the Traction Curve indicates that the traction force increases as the slip ratio goes up, but tends to stabilize after reaching a critical value, and increasing the wheel pressure can raise the critical slip ratio. These results provide important mechanical basis for slope motion control. When the wheeled ROV moves on a slope, the vehicle as a whole is subjected to a vertically downward normal load W(N) (the resultant of gravity, vertical thrust, and buoyancy) and water resistance F_water(N) acting opposite to the direction of linear velocity. Each wheel experiences the slope support force N_i(N), traction F_DPi(N), seabed resistance F_ri(N), and lateral force F_yi(N). The forces on the ROV on the sloped seabed are shown in Figure 7.

To enhance the trafficability of mobile robots in soft ground and slope environments, this study proposes a driving torque optimal distribution method based on the difference in wheel normal loads. When the robot operates on a slope with different postures, the normal loads on each wheel exhibit a non-uniform distribution characteristic. Based on this mechanical property, a load distribution calculation model considering the slope inclination angle and wheel position is established. By accurately calculating the normal load of each wheel, a reasonable distribution of driving torque is achieved, thereby maximizing the traction output. When the robot is on a slope at different angles, the normal load of each wheel varies, and its calculation formula is

$$\left\{\begin{array}{l}{N}_1={\displaystyle \frac{G_z}{4}}-{\displaystyle \frac{G_{x}h}{4d}}-{\displaystyle \frac{G_{y}h}{4L}}\begin{array}{ccc}& & N_2={\displaystyle \frac{G_z}{4}}-{\displaystyle \frac{G_{x}h}{4d}}+{\displaystyle \frac{G_{y}h}{4L}}\end{array}\\ N_3={\displaystyle \frac{G_z}{4}}+{\displaystyle \frac{G_{x}h}{4d}}+{\displaystyle \frac{G_{y}h}{4L}}\begin{array}{ccc}& & N_4={\displaystyle \frac{G_z}{4}}+{\displaystyle \frac{G_{x}h}{4d}}-{\displaystyle \frac{G_{y}h}{4L}}\end{array}\end{array}\right.$$

(23)

Substituting G_x = Gsinφ, G_y = Gsinγcosφ, and G_z = Gcosγcosφ into Equation (23), we can obtain

$$\left\{\begin{array}{l}{N}_1={\displaystyle \frac{G}{2}}\cos (\phi )({\displaystyle \frac{1}{2d}}(d\cos (\gamma )-h\tan (\phi ))+{\displaystyle \frac{h}{2L}}\sin (\gamma ))\\ N_2={\displaystyle \frac{G}{2}}\cos (\phi )({\displaystyle \frac{1}{2d}}(d\cos (\gamma )-h\tan (\phi ))-{\displaystyle \frac{h}{2L}}\sin (\gamma ))\\ N_3={\displaystyle \frac{G}{2}}\cos (\phi )({\displaystyle \frac{1}{2d}}(d\cos (\gamma )+h\tan (\phi ))-{\displaystyle \frac{h}{2L}}\sin (\gamma ))\\ N_4={\displaystyle \frac{G}{2}}\cos (\phi )({\displaystyle \frac{1}{2d}}(d\cos (\gamma )+h\tan (\phi ))+{\displaystyle \frac{h}{2L}}\sin (\gamma ))\end{array}\right.$$

(24)

The lateral force of a wheel is related to both the wheel slip angle and the wheel normal load, and their relationship curves are illustrated in Figure 8.

It can be seen from Figure 8 that the variation law of the wheel lateral force exhibits a typical dual-parameter coupling characteristic. Under the condition of constant normal load, when the slip angle is within a reasonable range, there is an approximately linear increasing relationship between the lateral force and the slip angle; if the slip angle is kept constant, a phenomenon that the lateral force increases monotonically with the increase in the normal load can be observed. This mechanical characteristic is consistent with the experimental results on deep-sea soft sand. Based on the analysis of this mechanical characteristic, to simplify the complexity of controller design, this paper adopts a linearization method to establish a wheel cornering force calculation model under slope conditions [21]. This model simplifies the complex ground mechanical relationship into a linear functional relationship between the slip angle and the normal load, as follows:

$$\left\{\begin{array}{l}{F}_{y1}=c_1{\beta }_1=-c_{\beta }{N}_1{\beta }_1=-c{N}_1{\displaystyle \frac{v_y+d{\omega }_c}{v_x-L{\omega }_c}}\\ F_{y2}=c_2{\beta }_2=-c_{\beta }{N}_2{\beta }_2=-c{N}_2{\displaystyle \frac{v_y+d{\omega }_c}{v_x+L{\omega }_c}}\\ F_{y3}=c_3{\beta }_3=-c_{\beta }{N}_3{\beta }_3=-c{N}_3{\displaystyle \frac{v_y-d{\omega }_c}{v_x+L{\omega }_c}}\\ F_{y4}=c_4{\beta }_4=-c_{\beta }{N}_4{\beta }_4=-c{N}_4{\displaystyle \frac{v_y-d{\omega }_c}{v_x-L{\omega }_c}}\end{array}\right.$$

(25)

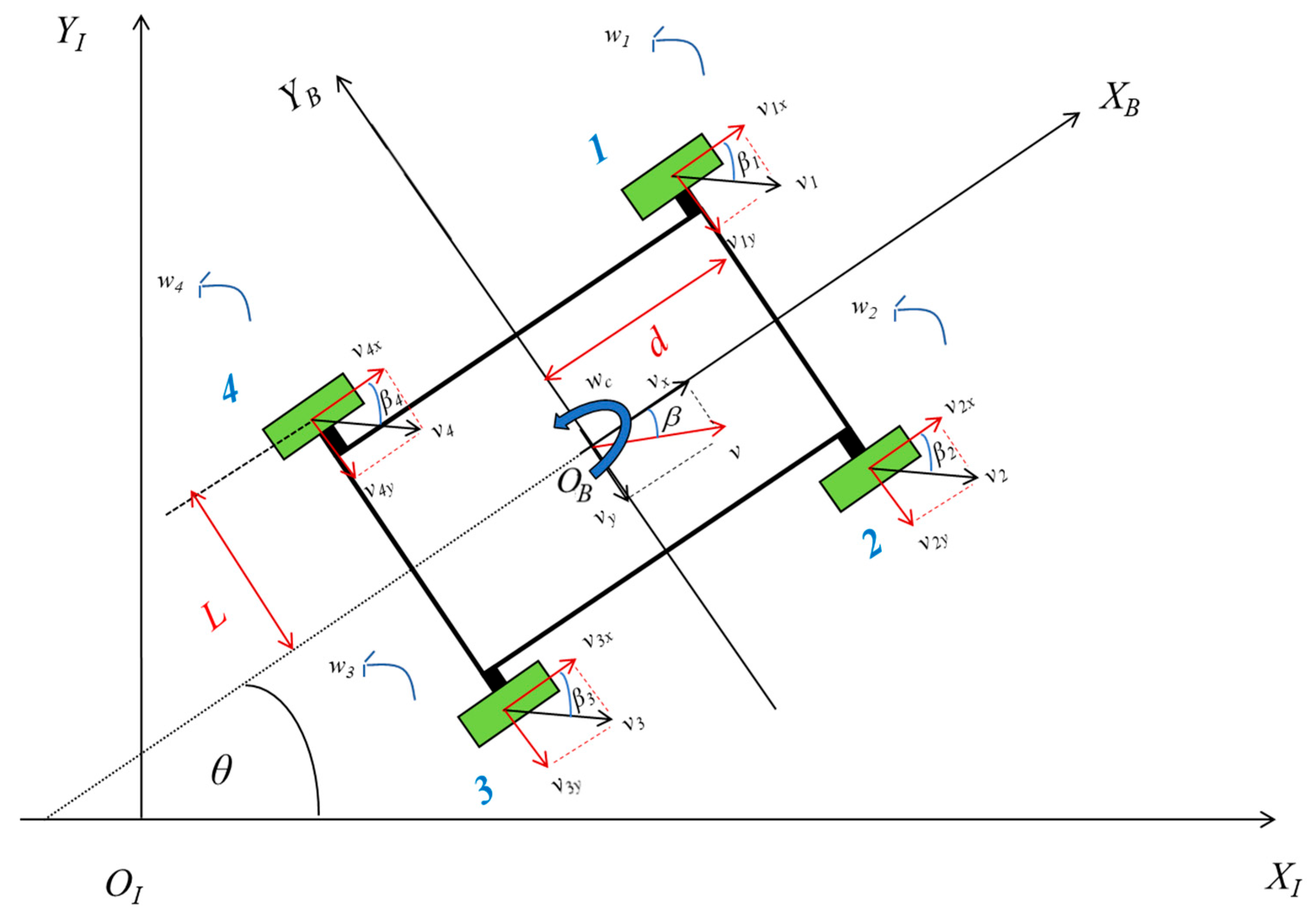
In the formula, c_i is the cornering stiffness of the i-th wheel (KN/rad), c_β is the relative cornering stiffness (KN/(kN/(rad·kN))), and the parameter values are selected from the test values obtained in the deep-sea sandy soil environment in reference [21]. To establish a complete dynamic closed-loop system, it is essential to supplement the coupling relationship between wheel rotation and vehicle body movement. To clarify the physical meaning and ensure coordinate system consistency, the velocity components in the body-fixed coordinate system {O_B X_B Y_B Z_B} are explicitly defined as follows: X′ Longitudinal velocity component along the X_B-axis at the robot’s center of mass; Y′: Lateral velocity component along the Y_B-axis at the robot’s center of mass. On this basis, the three-degree-of-freedom dynamic equilibrium equations for the ROV operating on a loose sloped seabed are formulated.

$$\left\{\begin{array}{l}m\ddot{X}-m\dot{Y}{\omega }_c-(G-F_b)\sin \gamma \cos \phi ={\displaystyle \sum _{i=1}^4{F}_{DPi}}-F_{water,xB}\\ m\ddot{Y}+m\dot{X}{\omega }_c-(G-F_b)\sin \phi ={\displaystyle \sum _{i=1}^4{F}_{yi}-F_{water,yB}}\\ I_z{\dot{\omega }}_c=L(F_{DP2}+F_{DP3}-F_{DP1}-F_{DP4})+d(F_{y1}+F_{y2}-F_{y3}-F_{y4})\\ T_i-r{F}_{DPi}-T_{r,i}=J_w{\dot{\omega }}_i\end{array}\right.$$

(26)

Among them, J_w represents the moment of inertia of the wheel, and $J_w={\displaystyle \frac{1}{2}}m{r}^2$. T_f,i is the rolling resistance moment of the wheel, which satisfies T_f,i = rF_f,i. Here, F_f,i is the rolling friction force, and its expression is F_fi = μW_i, μ is the ground friction coefficient, and T_i is the input torque of the motor. I_z represents the moment of inertia of the robot. The simplified hydrodynamic drag formula is as follows:

$$F_W={\displaystyle \frac{1}{2}}{\gamma }_{\mathrm{w}}{C}_{d}A{v}_{\mathrm{w}}^2$$

(27)

where C_d is the drag coefficient; A is the projected area of the robot perpendicular to the direction of motion; and v_w is the speed of the robot relative to the water flow. The seabed soil parameters are provided in

Table 3. Seabed soil parameters.

Soil Parameter	Numerical Value
Maximum stress angle factor c1	0.325
Maximum stress angle factor c2	0.425
Subsidence deformation index n	0.5
Soil shear modulus ks/m	0.006
Cone index CI/kPa	20
Cohesive deformation modulus kc/kNn+1	1.84
Frictional deformation modulus kφ/kNn+2	103.27
Cohesion c/kPa	4.9
Internal friction angle φ/deg	32
Buoyancy reduction coefficient α	0.3
Seawater Density γw/kg/m3	1400
Lateral Stiffness Coefficient ci/N/rad	1.2
Relative Lateral Stiffness cβ/kN/(rad·KN)	0.8

.

Slip and sideslip phenomena occurring during wheeled ROV operation significantly impact wheel velocity. Thus, it is difficult to maintain precise motion control with position tracking alone. Therefore, a complete dynamic model based on the inertial coordinate frame is required. This model should describe both the overall motion of the vehicle and the dynamic behavior of the wheels. By introducing the effects of longitudinal slippage and sideslip into the model, precise control of wheel velocity $\widehat{v}={[v_1,v_2,v_3,v_4]}^T$ can be achieved, enhancing the system’s trajectory tracking performance under non-ideal seabed conditions. An integrated dynamic analysis yields the following system model:

$$\mathit{M}(\mathit{q})\ddot{\mathit{q}}+\mathit{V}(\mathit{q},\dot{\mathit{q}})\dot{\mathit{q}}+\mathit{F}(\dot{\mathit{q}})+\mathit{G}(\mathit{q})+\mathit{f}(\dot{q})+{\tau }_d+A^T(q)\lambda =B(q)\tau$$

(28)

where $M(q)$ denotes the inertial force matrix, $V(q,\dot{q})$ $\mathrm{is}$ the Coriolis and centrifugal force matrix, $F(\dot{q})$ denotes the water resistance term, $G(q)$ the gravity term, $f(\dot{q})$ the friction force term, ${\tau }_d$ the unknown disturbance term, $A^T(q)$ the system constraint, $\lambda$ the constraint force, $B(q)$ the input transfer matrix, and $\mathit{\tau }$ the motor driving torque.

$$\begin{gathered} M(q)=\left[\begin{array}{ccc}m& 0& 0\\ 0& m& 0\\ 0& 0& I_c\end{array}\right],A^T(q)=\left[\begin{array}{c}\sin \theta \\ -\cos \theta \\ 0\end{array}\right], \\ \lambda =-m({\dot{x}}_c\cos \theta +{\dot{y}}_c\sin \theta )\dot{\theta },B(q)={\displaystyle \frac{1}{r}}\left[\begin{array}{cc}\cos \theta & \cos \theta \\ \sin \theta & \sin \theta \\ L^{\prime }& -L^{\prime }\end{array}\right] \end{gathered}$$

Differentiating $\dot{q}$ yields:

$$\ddot{q}=\dot{S}(q)v+S(q)\dot{v}$$

(29)

Substituting Equations (6), (11), and (17) into Equation (16) yields Equation (18):

$$\left\{\begin{array}{l}M(q)(\dot{S}(q)v+S(q)\dot{v})+V(q,\dot{q})S(q)v+F(\dot{q})+G(q)+f(\dot{q})+{\tau }_d+A^T(q)\lambda =B(q)\tau \\ M(q)\dot{S}(q)v+M(q)S(q)\dot{v}+V(q,\dot{q})S(q)v+F(\dot{q})+G(q)+f(\dot{q})+{\tau }_d+A^T(q)\lambda =B(q)\tau \end{array}\right.$$

(30)

Given $S^T(q)A^T(q)=0$, an explicit mathematical relationship between the wheel angular velocity and the body dynamics of the vehicle can be established. By left-multiplying both sides of the equation by the transpose matrix $S^T(q)$, the system dynamics equations can be transformed into the body-fixed coordinate frame of the vehicle, yielding a complete dynamic model that includes wheel–seabed interaction forces:

$$\begin{array}{l}{S}^T(q)M(q)\dot{S}(q)v+S^T(q)M(q)S(q)\dot{v}+S^T(q)V(q,\dot{q})S(q)v+S^T(q)F(\dot{q})\\ +S^T(q)G(q)+S^T(q)f(\dot{q})+S^T(q){\tau }_d+S^T(q)A^T(q)\lambda =S^T(q)B(q)\tau \end{array}$$

(31)

After organizing and combining terms,

$$\begin{array}{l}{S}^{T}M(q)S(q)\dot{v}+(S^{T}M(q)\dot{S}(q)+S^{T}V(q,\dot{q})S(q))v+S^{T}F(\dot{q})\\ +S^{T}G(q)+S^{T}f(\dot{q})+S^T{\tau }_d+S^T{A}^T(q)\lambda =S^{T}B(q)\tau \end{array}$$

(32)

Let $\overline{M}(q)=S^{T}M(q)S(q)$, $\overline{V}(q,\dot{q})=S^{T}M(q)\dot{S}(q)+S^{T}V(q,\dot{q})S(q)$, $\overline{F}(\dot{q})=S^{T}F(\dot{q})$, $\overline{G}(q)=S^{T}G(q)$, $\overline{f}(\dot{q})=S^{T}f(\dot{q})$, ${\overline{\tau }}_d=S^T{\tau }_d$, $\overline{B}(q)=S^{T}B(q)$.

Simplification gives

$$\overline{M}(q)\dot{v}+\overline{V}(q,\dot{q})v+\overline{F}(\dot{q})+\overline{G}(q)+\overline{f}(\dot{q})+{\overline{\tau }}_d=\overline{B}(q)\tau$$

(33)

The dynamic equations for operation on a sloped seabed are expressed as

$$\left\{\begin{array}{l}\widehat{v}={[v_1,v_2,v_3,v_4]}^T\\ \ddot{q}=\stackrel{·}{\widehat{S}}(q)\widehat{v}+\widehat{S}(q)\stackrel{·}{\widehat{v}}\end{array}\right.$$

(34)

Similarly, substituting and multiplying both sides by $\widehat{S}(q)$ results in

$$\widehat{M}(q)\dot{\widehat{v}}+\widehat{V}(q,\dot{q})\widehat{v}+\widehat{F}(\dot{q})+\widehat{G}(q)+\widehat{f}(\dot{q})+{\widehat{\tau }}_d=\widehat{B}(q)\tau$$

(35)

where $\widehat{M}(q)={\widehat{S}}^{T}M(q)\widehat{S}(q)$, $\widehat{V}(q,\dot{q})={\widehat{S}}^{T}M(q)\dot{\widehat{S}}(q)+{\widehat{S}}^{T}V(q,\dot{q})\widehat{S}(q)$, $\widehat{F}(\dot{q})={\widehat{S}}^{T}F(\dot{q})$, $\widehat{G}(q)={\widehat{S}}^{T}G(q)$, $\widehat{f}(\dot{q})={\widehat{S}}^{T}f(\dot{q})$, ${\widehat{\tau }}_d={\widehat{S}}^T{\tau }_d$, $\widehat{B}(q)={\widehat{S}}^{T}B(q)$.

3. Wheeled ROV Trajectory Tracking Controller Design and Implementation

Accurate trajectory tracking control of wheeled ROVs in complex seabed environments faces multiple technical challenges: coupled effects from pitch and roll attitude changes induced by 3D terrains, tire slippage and slip ratios caused by soft seabed substrates, hydrodynamic disturbances, and nonlinear characteristics of the propulsion system. All these factors significantly constrain the performance of traditional control methods. To address these challenges, we propose a comprehensive hierarchical control architecture. The upper layer tackles the trajectory tracking problem at the kinematic level using a Terminal Constraint MPC (TC-MPC) framework. By employing a discretized linear model and quadratic programming optimization, optimal control over a finite time horizon is achieved. The middle layer implements a dynamic controller using NFTSMC, integrated with a fixed-time nonlinear observer to estimate and compensate for unknown disturbances in real time. The lower layer innovatively introduces a dynamic torque distribution algorithm based on real-time slip ratio feedback to optimize the driving torques of the four wheels, thereby significantly reducing energy consumption on soft seabeds. The structure of the trajectory tracking controller is shown in Figure 9.

3.1. Design of MPC Motion Controller Based on Terminal Constraints

Based on the kinematic model of a four-wheeled vehicle operating on a slope as established, the nonlinear model of the wheeled ROV is defined as

$$\dot{q}(t)=f[q(t),u(t)]$$

(36)

where $q=\left[\begin{array}{ccc}{x}_I& y_I& {\theta }_I\end{array}\right]$ denotes the state variable; $u=[\begin{array}{cccc}{v}_1& v_2& v_3& v_4\end{array}]$ denotes the system input variable.

Based on the MPC prediction model and the linearized model, the terminal region Ω is defined as a subset of the state space [22]:

$$\mathsf{\Omega }:=\left\{\widehat{q}(k)\in R^n\mid \widehat{q}{(k)}^{T}P\widehat{q}(k)\le \alpha \right\}$$

(37)

where P represents the terminal penalty matrix (positive definite and symmetric); $\alpha >0$ is the boundary parameter of the terminal region. A linear feedback control law is applied:

$$\mu (k)=K\widehat{q}(k)$$

(38)

The gain matrix K is determined using either the linear quadratic regulator (LQR) approach or pole placement to ensure that the eigenvalues of the closed-loop system matrix $\mu (k)=K\widehat{q}(k)$ have negative real parts. With the inclusion of terminal constraints, the prediction equation is modified as

$$\left[\begin{array}{c}Y(t)\\ P\widehat{q}(k+N_p|t)\end{array}\right]=\left[\begin{array}{cc}{\psi }_t& {\Theta }_t\\ {\displaystyle \mathbf{0}}& P{\Phi }_{N_p}\end{array}\right]\left[\begin{array}{c}\xi (k|t)\\ \mathsf{\Delta }U(t)\end{array}\right]$$

(39)

A terminal penalty term is added to the objective function, yielding

$$J(\eta (t),\mathsf{\Delta }u(t),\epsilon )={\displaystyle \sum _{i=1}^{N_P}\Vert \eta (k+i|t)-{\eta }_t(k+i|t){\Vert }_Q^2}+{\displaystyle \sum _{i=1}^{N_c-1}\Vert \mathsf{\Delta }u(}k+i|t){\Vert }_R^2+\Vert \widehat{q}(k+N_p){\Vert }_P^2+\rho {\epsilon }^2$$

(40)

The quadratic programming problem is further modified by introducing new terminal constraints:

$$\left\{\begin{array}{l}\widehat{q}(k+N_p|t)={\widehat{A}}_t{N}^p\widehat{q}(k|t)+{\displaystyle \sum _{i=0}^{N_p-1}{\widehat{A}}_t}{\widehat{B}}_t\mathsf{\Delta }u(k+i|t)\\ \widehat{q}{(k+N_p|t)}^{T}P\widehat{q}(k+N_p|t)\le \alpha \end{array}\right.$$

(41)

This results in the standard formulation of the quadratic programming problem:

$$\Phi (t)={\displaystyle \frac{1}{2}}\mathsf{\Delta }{U}^T(t)H(t)\mathsf{\Delta }U(t)+f^T(t)\mathsf{\Delta }U(t)+\widehat{q}{(k+N_p)}^{T}P\widehat{q}(k+N_p)+d(t)$$

(42)

For the TC-MPC system, the following candidate Lyapunov function is constructed to analyze closed-loop stability:

$$V(\widehat{q}(k))=\widehat{q}{(k)}^{T}P\widehat{q}(k)$$

(43)

Its discrete-time form is given by

$$\mathsf{\Delta }V=V(\widehat{q}(k+1))-V(\widehat{q}(k))$$

(44)

By solving the algebraic Riccati equation:

$$A_K^{T}P{A}_K-P=-Q^{*}$$

(45)

where $Q^{*}=Q+K^{T}RK$ ensures the positive definiteness of P. When $\widehat{q}(k)\in \mathsf{\Omega }$, the terminal controller guarantees

$$\mathsf{\Delta }V\le -\widehat{q}{(k)}^T{Q}^{*}\widehat{q}(k)\le 0$$

(46)

By constraining the optimization problem with $\widehat{q}(k+N_p|t)\in \mathsf{\Omega }$, it is ensured that the system states converge to the terminal region within the finite prediction horizon. With this, the design of the MPC motion controller with terminal constraints is completed.

3.2. Design of the Disturbance-Rejection Dynamics Controller

3.2.1. Design of the Fixed-Time Nonlinear Observer

As shown in Equation (22), the ROV dynamic model includes uncertainties and bounded disturbances, including a partially known term ${\tilde{\tau }}_d$ and an unknown term $d\left(t\right)$ [23]. That is, ${\widehat{\tau }}_d={\tilde{\tau }}_d+d(t)$. Equation (22) is reformulated to include an unknown disturbance term:

$$\left\{\begin{array}{l}\dot{\widehat{v}}=\widehat{M}{(q)}^{-1}\widehat{B}(q)\tau -\widehat{M}{(q)}^{-1}(\widehat{V}(q,\dot{q})\widehat{v}+\widehat{F}(\dot{q})+\widehat{G}(q)+\widehat{f}(\dot{q})+{\tilde{\tau }}_d)+\widehat{M}{(q)}^{-1}d(t)\\ \dot{\widehat{v}}=U(\widehat{v})\tau +C(\widehat{v})+D(t)\end{array}\right.$$

(47)

where $U(\widehat{v})=\widehat{M}{(q)}^{-1}\widehat{B}(q)$ is the input term; $D(t)=\widehat{M}{(q)}^{-1}d(t)$ is the unknown disturbance. $C(\widehat{v})=\widehat{M}{(q)}^{-1}(\widehat{V}(q,\dot{q})\widehat{v}+\widehat{F}(\dot{q})+\widehat{G}(q)+\widehat{f}(\dot{q})+{\tilde{\tau }}_d)$ is the known term;

The observer equations are given as

$$\left\{\begin{array}{l}\dot{\tilde{v}}=\tilde{U}(\widehat{v})+\tilde{C}(\widehat{v})+\tilde{D}(t)+{\gamma }_{1}sgn{(e_{x_1})}^{{\lambda }_1}+{\beta }_{1}sgn{(e_{x_1})}^{{\delta }_1}\\ \dot{\tilde{D}}(t)={\gamma }_{2}sgn{(e_{x_2})}^{{\lambda }_2}+{\beta }_{2}sgn{(e_{x_2})}^{{\delta }_2}\end{array}\right.$$

(48)

where $\tilde{\mathit{v}}$ and $\tilde{\mathit{D}}\left(t\right)$ represent the estimates of $\widehat{\mathit{v}}$ and $\mathit{D}\left(t\right)$, respectively. The estimation errors are denoted as $e_{x_1}=\widehat{v}-\tilde{v}$ and $e_{x_2}=D(t)-\tilde{D}(t)$, and ${\gamma }_1,{\gamma }_2,{\beta }_1,{\beta }_2>0$ represents the observer gain [24].

From ${\lambda }_1\in (0.5,1), {\delta }_1\in (1,1.5), {\lambda }_2=2{\lambda }_1-1, {\delta }_2=2{\delta }_1-1$, the following is derived:

An upper bound $\dot{D}(t)\le L$ can be obtained, where L is a constant. Considering system Equation (34), the fixed-time extended state observer is designed as in Equation (35). If the error system is described by Equation (36), the estimation errors ${\mathit{e}}_{{\mathit{x}}_1}$ and ${\mathit{e}}_{{\mathit{x}}_2}$ of the fixed-time extended state observer converge to a neighborhood of the origin within a fixed time. According to [25], the observation errors ${\mathit{e}}_{{\mathit{x}}_1}$ and ${\mathit{e}}_{{\mathit{x}}_2}$ are uniformly ultimately bounded in fixed time, and the convergence time satisfies:

$$\left\{\begin{array}{l}{T}_1\le {\displaystyle \frac{1}{b}}{\displaystyle \frac{2{\delta }_1}{{\delta }_1-1}}{\mathsf{\Gamma }}^{-{\displaystyle \frac{\delta -1}{2{\delta }_1}}},if{\displaystyle \frac{2b_{\mathsf{\Delta }}L}{b}}\ge 1\\ T_2\le {\displaystyle \frac{1}{b}}({\displaystyle \frac{2{\lambda }_1}{1-{\lambda }_1}}+{\displaystyle \frac{2{\delta }_1}{{\delta }_1-1}}),if{\displaystyle \frac{2b_{\mathsf{\Delta }}L}{b}}\le 1,\mathsf{\Gamma }={({\displaystyle \frac{2b_{\mathsf{\Delta }}L}{b}})}^{{\displaystyle \frac{2{\lambda }_1}{2{\lambda }_1-1}}}\end{array}\right.$$

(49)

where $T_i$ (i = 1, 2) represents the convergence times for the respective states. $b,b_{\mathsf{\Delta }}>0$ satisfies the corresponding lemma in the cited literature.

3.2.2. Design of the NFTSMC Law

Traditional terminal sliding mode controllers exhibit slower convergence rates near equilibrium compared to linear sliding mode controllers. Therefore, a new fast terminal sliding mode surface was proposed by integrating linear and fast terminal sliding modes [26]:

$$s=X_1+\mu X_1^{f/g}+\chi X_2^{p/q}$$

(50)

where $\mu ,f,g$ denote the sliding surface parameter matrix; $\mu$ is a positive definite matrix; $f, g$ is a positive odd matrix, satisfying the condition p/q < f/g.

In dynamics-based vehicle motion control, control inputs are expressed as the torque outputs of the drive wheels. By establishing the dynamic relationship between bounded control inputs and trajectory tracking performance, the vehicle can be enabled to accurately follow the desired trajectory. The kinematic controller computes the required rotational velocities of the left and right wheels for tracking the target trajectory, which are then converted into the desired body motion velocity through the wheel-to-vehicle velocity mapping. This control architecture seamlessly integrates trajectory planning at the kinematic level with torque control at the dynamic level, forming a closed-loop control system. The desired values are specified as follows:

$$\left\{\begin{array}{c}{\tilde{v}}_c={\displaystyle \frac{v_r(1-s_r)+v_l(1-s_l)}{2}}\\ {\tilde{\omega }}_c={\displaystyle \frac{v_r(1-s_r)-v_l(1-s_l)}{2L^{\prime }}}\end{array}\right.$$

(51)

Let the velocity tracking error between the actual velocity of the vehicle and the desired velocity from the position controller be defined as

$$\left\{\begin{array}{l}{e}_1=\widehat{v}-{\stackrel{⌢}{v}}_c=[\begin{array}{l}{\widehat{v}}_c-{\tilde{v}}_c\\ {\widehat{\omega }}_c-{\tilde{\omega }}_c\end{array}]\\ s=e_1+\mu e_1^{f/g}+\chi e_2^{p/q}\end{array}\right.$$

(52)

where

$$s=[\begin{array}{c}{s}_1\\ s_2\end{array}], \mu =[\begin{array}{cc}{\mu }_1& 0\\ 0& {\mu }_2\end{array}], \chi =[\begin{array}{cc}{\chi }_1& 0\\ 0& {\chi }_2\end{array}], f=[\begin{array}{cc}{f}_1& 0\\ 0& f_2\end{array}], \mathrm{g}=[\begin{array}{cc}{g}_1& 0\\ 0& g_2\end{array}], p=[\begin{array}{cc}{p}_1& 0\\ 0& p_2\end{array}],q=[\begin{array}{cc}{q}_1& 0\\ 0& q_2\end{array}].$$

The driving torque control laws for both sides of the ROV are defined as

$$\tau ={(\widehat{M}{(q)}^{-1}\widehat{B}(q))}^{-1}[{\dot{\stackrel{⌢}{\mathit{v}}}}_c+\widehat{M}{(q)}^{-1}(\widehat{V}(q,\dot{q})\widehat{v}+\widehat{F}(\dot{q})+\widehat{G}(q)+\widehat{f}(\dot{q})+{\tilde{\tau }}_d)+\eta sgn(s)]$$

(53)

where $\eta >0$. To analyze the convergence time, let $s=e_1+\mu e_1^{f/g}+\chi e_2^{p/q}$, and take the derivative of the sliding surface $s$:

$$\dot{s}={\dot{e}}_1+\mu {\displaystyle \frac{f}{g}}{e}_1^{{\displaystyle \frac{f}{g}}-1}{\dot{e}}_1+\chi {\displaystyle \frac{p}{q}}{e}_2^{{\displaystyle \frac{p}{q}}-1}{\dot{e}}_2$$

(54)

Substituting ${\dot{e}}_1=e_2$ and ${\dot{e}}_2=\dot{U^{\prime }}\tau +\dot{C^{\prime }}+\dot{D^{\prime }}$ yields:

$$\dot{s}=e_2+\mu {\displaystyle \frac{f}{g}}{e}_1^{{\displaystyle \frac{f}{g}}-1}{e}_2+\chi {\displaystyle \frac{p}{q}}{e}_2^{{\displaystyle \frac{p}{q}}-1}(\dot{U^{\prime }}\tau +\dot{C^{\prime }}+\dot{D^{\prime }})$$

(55)

3.3. Design of Dynamic Slip-Based Torque Distribution

To achieve precise torque distribution between the front and rear wheels, it is necessary to consider the ROV’s dynamic model, real-time motion states, and the external forces acting on the vehicle. Real-time data on the ROV’s velocity, acceleration, and attitude were obtained via sensors. Combined with the pre-established dynamic model, these data were used to compute the optimal torque required for the front and rear wheels. The drive system was then adjusted in real time to achieve accurate torque distribution. From Section 3.2, the normal loads on the ROV’s four wheels on soft seabed were obtained, allowing the calculation of the load ratio for each wheel.

$$k_i={\displaystyle \frac{N_i}{{\displaystyle \sum _{j=1}^4{N}_j}}},\hspace{1em}i\in \{1,2,3,4\}$$

(56)

The conventional torque distribution method can be expressed as

$$T_i=\tau \cdot k_i,\hspace{1em}i\in \{1,2,3,4\}$$

(57)

Although this approach of load distribution statically allocates torque based on theoretical mechanical models, its performance is highly dependent on accurate dynamic parameters and the assumption of a homogeneous seabed. In contrast, the proposed dynamic slip-based torque distribution method introduces a closed-loop feedback mechanism based on real-time slip ratio and a weight normalization scheme, achieving multiple levels of optimization. In terms of dynamic adaptability, online slip ratio monitoring allows the system to automatically compensate for substrate variability and model errors, forming a hybrid control architecture of “model initialization and feedback correction.” In terms of robustness, this approach preserves the core physical principles of load distribution while utilizing closed-loop data feedback to suppress uncertainties. This significantly improves computational efficiency, environmental adaptability, and system fault tolerance [27].

To achieve adaptive distribution of dynamic slip-load torque, a piecewise function for torque weights w_i is designed for three operating conditions: positive slip (drive slippage), negative slip (brake skidding), and normal driving. The function is as follows:

$$w_i=\left\{\begin{array}{cc}\begin{array}{c}1-{\displaystyle \frac{s_i-s_{threshold}}{s_{\max }-s_{threshold}}}\\ 1+{\displaystyle \frac{\left|s_i\right|-s_{brake}}{s_{\max }-s_{brake}}}\\ 1\end{array}& \begin{array}{c}{s}_i\ge s_{threshold}\\ s_i\le -s_{brake}\\ -s_{brake}\le s_i\le s_{threshold}\end{array}\end{array}\right.$$

(58)

Among them, s_threshold denotes the positive slip threshold, s_brake denotes the negative slip threshold, and s_max denotes the maximum allowable slip ratio, with the relationship s_brake = 0.5 s_threshold satisfied. Based on the Janosi-Hanamoto model, by analyzing the saturation characteristics of the sinkage-slip ratio curve and the traction-slip ratio curve, the formula for the slip ratio threshold is defined as follows:

$$s_{threshold}=0.2\left({\displaystyle \frac{{\tau }_m}{c+({\sigma }_m-{\gamma }_{w}z)\tan \phi }}\right)e^{-{\displaystyle \frac{z}{r}}}$$

(59)

After re-normalizing the torque weights, the torque distribution expressions for the four wheels are obtained as

$$T_i=\tau \cdot {\displaystyle \frac{w_i{k}_i}{{\displaystyle \sum _{j=1}^4{w}_j}{k}_j}},\hspace{1em}i\in \{1,2,3,4\}$$

(60)

The above distribution method minimizes energy losses in the ROV’s driving wheels and prevents wheel slippage. It also ensures that the output torque of all four wheels remains within the allowable maximum torque range, satisfying the condition $T_i\le T_{\max }$.

3.4. Comparative Analysis of Trajectory Tracking Performance

This section presents simulation-based comparisons of the performance of MPC and TC-MPC trajectory tracking controllers across a variety of classical trajectory tracking tasks. The parameters of the MPC are configured as shown in

Table 4. Configuration of MPC Controller Parameters.

Parameters	Definition	Value/(Unit)
NP	Prediction horizon	10
NC	Control horizon	3
Q	State error weight	$diag[5,8,3]$
R	Control input weight	$diag[1,1,1,1]$
P	Terminal Penalty Matrix	$diag[10,12,6]$
Ts	Sampling time	0.05/(s)
$\tilde{v}$	Angular velocity constraint range	[0, 0.4]/(m/s)
$\tilde{\omega }$	Linear velocity constraint range	[−2, 2]/(rad/s)
$\mathsf{\Delta }\tilde{v}$	Linear velocity control increment constraint	2/(m/s)
$\mathsf{\Delta }\tilde{\omega }$	Angular velocity control increment constraint	2/(rad/s)

below.

$diag[5,8,3]$$diag[1,1,1,1]$$diag[10,12,6]$$\tilde{v}$$\tilde{\omega }$$\mathsf{\Delta }\tilde{v}$$\mathsf{\Delta }\tilde{\omega }$

3.4.1. Linear Trajectory Simulation Analysis

The initial pose of the wheeled ROV is set as follows: displacement in the X direction is $x=0\mathrm{m}$, displacement in the Y direction is $y=0\mathrm{m}$, and the heading angle is $\theta =0\mathrm{rad}$. The desired trajectory is a straight line parallel to the X-axis $y=5\mathrm{m}$, with an expected ROV travel velocity of $\tilde{v}=1\mathrm{m}/\mathrm{s}$. Based on these parameters, the desired trajectory in the two-dimensional plane is defined as

$$\left\{\begin{array}{l}{x}_I(t)=\tilde{v}t\cos (\theta )\\ y_I(t)=5+\tilde{v}t\sin (\theta )\\ {\theta }_I(t)=\theta \end{array}\right.$$

(61)

For linear motion on a slope, motion parameters, such as sideslip velocity and longitudinal slip ratio are defined based on physical characteristics:

$$\left\{\begin{array}{l}{v}_y=-0.1\\ s_1=s_2=s_3=s_4=0.2\end{array}\right.$$

(62)

The simulation results for the linear trajectory are shown in Figure 10.

Table 5. Comparison of linear trajectory performance.

Performance Metric	TC-MPC	MPC	Effectiveness Enhancement
Root-mean-square lateral error (m)	0.36821	0.42792	13.95%
Root-mean-square longitudinal error (m)	1.6723	1.6826	0.61%
Root-mean-square heading angle error (°)	0.52422	0.55209	5.04%
Sideslip angle (rad)	0.63033	0.6637	5.03%
Root-mean-square linear velocity error (m/s)	0.45998	0.48691	5.53%
Root-mean-square angular velocity error (rad/s)	0.42711	0.45536	6.20%
Accommodation time (s)	4.55	5.05	9.90%

compares the results of the two algorithms in terms of linear trajectory performance.

$e_X$ denotes the root-mean-square (RMS) error of X-direction displacement; $e_Y$ the RMS error of Y-direction displacement; $e_{\theta }$ the RMS error of the heading angle; $e_{\beta }$ the RMS error of the sideslip angle; $e_v$ the RMS error of the linear velocity; $e_{\omega }$ the RMS error of the angular velocity; and $t$ the regulation time.

As shown in Figure 10a, the linear motion trajectory demonstrates that the TC-MPC achieves faster and smoother convergence to the reference trajectory within a finite time domain, with a 9.9% reduction in convergence time compared to the traditional method. Figure 10b depicts the variation in the sideslip angle. The simulation results show that without terminal constraints, the sideslip angle exhibits greater fluctuations, around 5%, and persists for a longer duration. Figure 10c,d present the displacement and heading angle trajectories along with their respective error plots in the X and Y directions. The introduction of terminal constraints enhances position tracking accuracy by 13.95%. Figure 10e,f illustrate the simulated variations and corresponding errors in linear and angular velocities. Under sloped conditions and with initial deviations present, the TC-MPC enables the ROV to track the desired linear and angular velocities more quickly and stably, with accuracy improvements of 5.53% and 6.20%, respectively. Figure 10h shows that the motor torque output is continuous and free from abrupt changes, indicating high actuator response efficiency. Additionally, the driving torque of each wheel stays within the allowable maximum torque range. Simulation results indicate that the proposed TC-MPC controller can effectively track the vehicle trajectory even under external disturbances caused by slippage. Compared with traditional control methods, this controller exhibits stronger disturbance rejection capability, significantly boosting the linear tracking accuracy of vehicle trajectories in complex environments.

3.4.2. Circular Trajectory Simulation Analysis

The initial pose of the wheeled ROV is set as follows: displacement in the X direction is $x=0\mathrm{m}$, displacement in the Y direction is $y=0\mathrm{m}$, and the heading angle is $\theta =0\mathrm{rad}$. The desired circular trajectory has a radius of $R=5\mathrm{m}$. The ROV’s desired linear velocity and rotational angular velocity are $\tilde{v}=1\mathrm{m}/\mathrm{s}$ and $\tilde{\omega }=0.2\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}$, respectively. Based on these parameters, the equation of the desired circular trajectory is derived as follows:

$$\left\{\begin{array}{l}{x}_I(t)=R\sin (\tilde{w}t)\\ y_I(t)=-R\cos (\tilde{w}t)\\ {\theta }_I(t)=\tilde{w}t\end{array}\right.$$

(63)

In the circular trajectory simulation, the sideslip and longitudinal slip are set to vary as

$$\left\{\begin{array}{l}{v}_y=-0.1\sin (0.3t)\\ s_1=s_2=s_3=s_4=0.2\sin t+0.2\cos t\end{array}\right.$$

(64)

The simulation results for the circular trajectory are shown in Figure 11.

Table 6. Comparison of circular trajectory performance.

Performance Metric	TC-MPC	MPC	Effectiveness Enhancement
Root-mean-square lateral error (m)	0.81067	0.94352	14.08%
Root-mean-square longitudinal error (m)	1.3734	1.4927	7.99%
Root-mean-square heading angle error (°)	0.64943	0.70934	8.45%
Sideslip angle (rad)	0.36085	0.40073	9.95%
Root-mean-square linear velocity error (m/s)	0.52789	0.57352	7.96%
Root-mean-square angular velocity error (rad/s)	0.37185	0.38656	3.81%
Accommodation time (s)	6.25	7.55	17.22%

compares the results of the two algorithms in terms of circular trajectory performance.

Figure 11 illustrates the simulation results for circular trajectory tracking. Each subplot presents key data, including the ROV’s actual trajectory versus the reference trajectory, tracking error analysis, and variation curves of control inputs. As shown in Figure 11a, the traditional method exhibited overshoot and a longer convergence time (7.55 s), while the improved control strategy reduced the response time to 6.25 s, representing a 17.22% improvement. From the sideslip angle plot (Figure 11b), with terminal constraints, the fluctuation of the sideslip angle was reduced, and stability was achieved more rapidly. As shown in Figure 11c,d, the displacement tracking errors in the X and Y directions were smaller than those under the traditional method, with a 14.08% improvement. Although heading angle tracking errors were larger at the initial stage, they achieved higher accuracy once stabilized, with an 8.45% error reduction compared to the traditional MPC. Figure 11e,f depict the tracking of linear and angular velocities. While the improved controller introduced more oscillation at the initial stage, the system stabilized more quickly after adding terminal constraints. The tracking accuracy of linear and angular velocities improved moderately by 7.96% and 3.81%, respectively. As shown in Figure 11h, motor torque output was continuous and free of sudden fluctuations, and the driving torques of all wheels remained within the allowable range of maximum driving torque. Overall, the proposed control algorithm enabled high-precision tracking of circular trajectories.

3.4.3. Figure-of-Eight Trajectory Simulation Analysis

The initial pose of the wheeled ROV is set as follows: displacement in the X direction is $x=0\mathrm{m}$, displacement in the Y direction is $y=0\mathrm{m}$, and the heading angle is $\theta =0\mathrm{rad}$. The desired figure-of-eight trajectory has a radius of $R=2.5\mathrm{m}$. The desired linear velocity and rotational angular velocity of the ROV are $\tilde{v}=1\mathrm{m}/\mathrm{s}$ and $\tilde{\omega }=0.2\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}$, respectively. Based on these conditions, the desired trajectory can be formulated as follows:

$$\left\{\begin{array}{l}{x}_I(t)=R\sin (0.2t)\\ y_I(t)=R\sin (0.2t)\cos (0.2t)\\ {\theta }_I(t)=a\tan 2(\cos (0.4t),\cos (0.2t))\end{array}\right.$$

(65)

In the figure-of-eight trajectory simulation, the variations in sideslip and longitudinal slip are set as

$$\left\{\begin{array}{l}{v}_y=-0.1\sin (0.3t)\\ s_1=s_2=s_3=s_4=0.2\sin t+0.2\cos t\end{array}\right.$$

(66)

The simulation results for the Figure-of-Eight trajectory are shown in Figure 12.

Table 7. Performance comparison of figure-of-eight trajectories.

Performance Metric	TC-MPC	MPC	Effectiveness Enhancement
Root-mean-square lateral error (m)	0.07246	0.084782	14.53%
Root-mean-square longitudinal error (m)	0.062561	0.083614	25.18%
Root-mean-square heading angle error (°)	0.089177	0.098799	9.74%
Sideslip angle (rad)	0.11569	0.14591	20.71%
Root-mean-square linear velocity error (m/s)	0.24973	0.25588	2.40%
Root-mean-square angular velocity error (rad/s)	0.17738	0.20063	11.59%
Accommodation time (s)	3.45	4.2	17.86%

compares the results of the two algorithms in terms of Figure-of-Eight trajectory performance.

Figure 12 shows that the MPC strategy with terminal constraints enables faster tracking of the reference trajectory, achieves a shorter convergence time, and results in a smoother convergence process. As presented in Figure 12a, the trajectory tracking controller without terminal constraints only began to approximate the trajectory at the first turn; in contrast, the controller with terminal constraints nearly achieved full tracking at the first turn. Figure 12b illustrates the variation in the ROV’s sideslip angle, and the proposed method improves this metric by 20.71%. The simulation results in Figure 12c,d indicate that on a 10° slope, the ROV—after heading angle compensation—can still converge rapidly to the reference trajectory even with initial pose deviation, with the tracking response time reduced by 17.86%. Figure 12e,f further confirm that the reference commands for linear and angular velocities, dynamically generated based on real-time slip conditions, allow the ROV to achieve more agile trajectory tracking. Figure 12h shows continuous and smooth motor torque output, which indicates high actuator responsiveness, and the driving torque of each wheel remains within the range of the maximum allowable torque. The experimental results verify that the TC-MPC controller designed in this study exhibits strong resistance to slip-induced disturbances and delivers superior control performance in figure-of-eight trajectory tracking tasks.

To intuitively demonstrate the performance advantages of the proposed TC—MPC over MPC under different trajectory types,

Table 8. Performance Comparison for Summarized Different Trajectories.

Performance Metric	Linear Trajectory		Circular Trajectory		Figure-of-Eight Trajectory		Average Effectiveness Enhancement
	TC-MPC	MPC	TC-MPC	MPC	TC-MPC	MPC
RMS error of lateral (m)	0.36821	0.42792	0.81067	0.94352	0.07246	0.084782	14.85%
RMS error of longitudinal (m)	1.6723	1.6826	1.3734	1.4927	0.062561	0.083614	13.44%
RMS error of heading angle (rad)	0.52422	0.55209	0.64943	0.70934	0.089177	0.098799	7.74%
RMS error of sideslip angle (rad)	0.63033	0.6637	0.36085	0.40073	0.11569	0.14591	11.90%
RMS error of linear velocity (m/s)	0.45998	0.48691	0.52789	0.57352	0.24973	0.25588	5.30%
RMS error of angular velocity (rad/s)	0.42711	0.45536	0.37185	0.38656	0.17738	0.20063	7.20%
Accommodation time (s)	4.55	5.05	6.25	7.55	3.45	4.2	15.00%

summarizes the key performance metrics for linear, circular, and figure-of-eight trajectories. As can be seen from the table, TC—MPC yields remarkable outcomes in reducing tracking errors and shortening accommodation time: the RMS error in the lateral direction is decreased by an average of 14.85%, and that in the longitudinal direction by an average of 13.44%; the RMS error of the heading angle is reduced by an average of 7.74%, and the RMS error of the sideslip angle by an average of 11.90%; the RMS error of linear velocity is cut down by an average of 5.30%, and the RMS error of angular velocity by an average of 7.20%; meanwhile, the accommodation time is shortened by an average of 15.00%. These results fully illustrate that TC—MPC excels in trajectory tracking accuracy, dynamic response speed, and motion stability. This superiority is particularly notable in complex trajectory scenarios like the figure-of-eight trajectory, which is of great significance for the operation of wheeled ROVs in deep-sea sloped terrain.

4. Conclusions

For the control system of a wheeled ROV for deep-sea exploration, we focused on achieving precise trajectory tracking in complex deep-sea environments and made notable theoretical and practical progress. A coupled kinematic and dynamic model was developed, integrating sloped terrain and soft seabed features to overcome the limitations of traditional models in complex seabed conditions. At the kinematic level, a body-to-terrain coordinate transformation model described pose changes on slopes, with slip ratio and sideslip angle introduced to quantify tire slippage on soft seabeds. At the dynamic level, a 3-degree-of-freedom model incorporated hydrodynamic effects, seabed reaction forces, and dynamic friction, and combined with the Janosi soil model to reveal how slip ratio affects traction and subsidence depth, effectively reflecting the ROV’s motion in complex environments.

We also proposed a hierarchical control strategy to tackle trajectory tracking challenges, integrating TC-MPC, NFTSMC, a fixed-time nonlinear observer, and dynamic torque distribution. At the kinematic control level, finite-time domain optimization is achieved through discretization, quadratic programming, and a terminal penalty matrix. For dynamic control, a fixed-time observer is employed to estimate disturbances, and a nonsingular fast terminal sliding mode controller is constructed based on a novel sliding mode surface—effectively suppressing the impacts caused by hydrodynamic disturbances and wheel–terrain slippage. Furthermore, a dynamic torque distribution algorithm integrated with real-time slip ratio feedback is adopted to reduce the average total slip ratio.

This strategy delivers notable improvements in trajectory tracking performance across linear, circular, and figure-of-eight trajectories: specifically, the RMS error in the lateral direction is reduced by an average of 14.85%, the RMS error in the longitudinal direction by 13.44%, the RMS error of the heading angle by 7.74%, and the RMS error of the sideslip angle by 11.90%; meanwhile, the RMS error of linear velocity is cut down by 5.30%, the RMS error of angular velocity by 7.20%, and the accommodation time is shortened by 15.00%.Simulation results verify the excellent performance of this strategy, confirming that it can enhance the motion stability and tracking accuracy of deep-sea wheeled ROVs. Ultimately, this work provides a comprehensive motion control solution for wheeled ROVs operating in complex deep-sea terrains.

This study mainly focuses on the simulation-based validation of the TC-MPC strategy for wheeled ROVs operating in deep-sea sloped terrains. Nevertheless, there are several limitations that need to be addressed. First, the simulation environment is built on the assumption of ideal deep-sea conditions, such as constant current velocity and homogeneous seabed substrate. In contrast, real-world deep-sea environments are much more complex–dynamic currents, uneven soft sediments, and pressure variations in actual scenarios may all have an impact on the control performance of the strategy. Second, the evaluation of the strategy’s performance only depends on numerical simulations. No experimental validation has been conducted using physical ROV prototypes, which makes it challenging to fully confirm the robustness of the strategy when it is applied in practical hardware-operation scenarios. Third, the current TC-MPC algorithm does not take energy consumption optimization into account. Energy consumption is a crucial factor for long-duration deep-sea missions, like polymetallic nodule exploration, where the battery life of ROVs is usually limited.

To address the aforementioned limitations and further improve the proposed TC-MPC algorithm, future research will focus on advancing four key aspects: first, conduct experimental validation under near-realistic environments by using a physical prototype of the wheeled ROV to test the strategy in a laboratory water tank equipped with a current simulation device and a sloped sediment bed, reproducing the characteristics of the deep-sea environment, acquiring key data, and verifying the accuracy and robustness of the algorithm in physical scenarios; second, promote the hardware implementation and real-time optimization of the strategy by integrating the TC-MPC algorithm into the ROV’s on-board control system in a modular manner, selecting a hardware platform suitable for deep-sea requirements, ensuring the control delay meets the standards, and realizing the transition of the strategy from simulation to hardware implementation; third, achieve the integration of the algorithm with environmental perception by linking environmental perception modules such as sonar terrain detection and visual image recognition with the TC-MPC logic to build a “perception–decision–control” closed-loop system, where the ROV dynamically adjusts the strategy’s constraint boundaries based on real-time seabed data to enhance its adaptability to complex environments and operational safety.