Analysis on Phase Polarity of Mandrel Fiber-Optic Vector Hydrophones Based on Phase Generated Carrier Technique
Abstract
1. Introduction
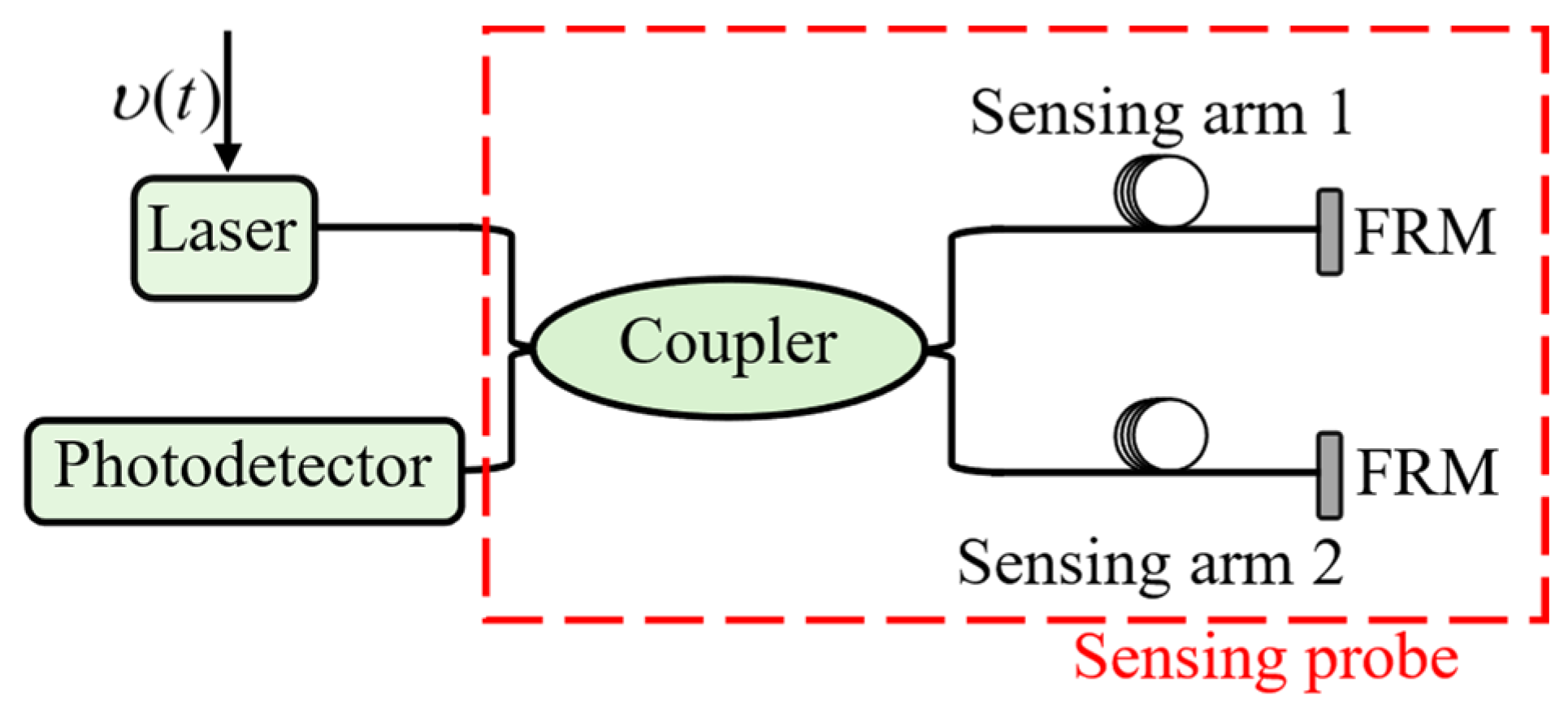
2. Theoretical Framework
2.1. Phase Relationship Between Sound Pressure and Particle Acceleration
2.2. Phase Characteristics of PGC Demodulation Signals
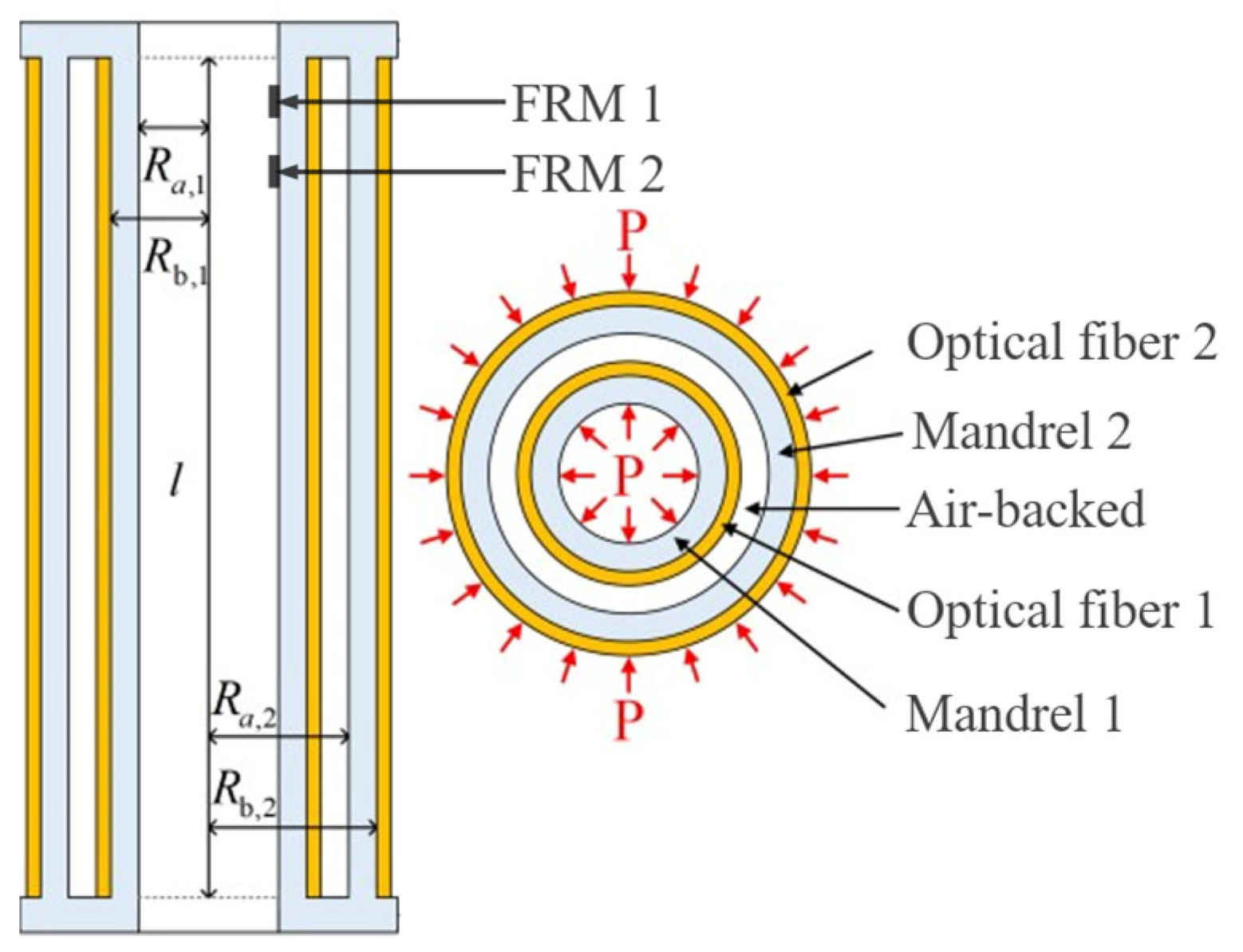
2.3. Elastic Mechanics Characteristics of Pressure Sensor
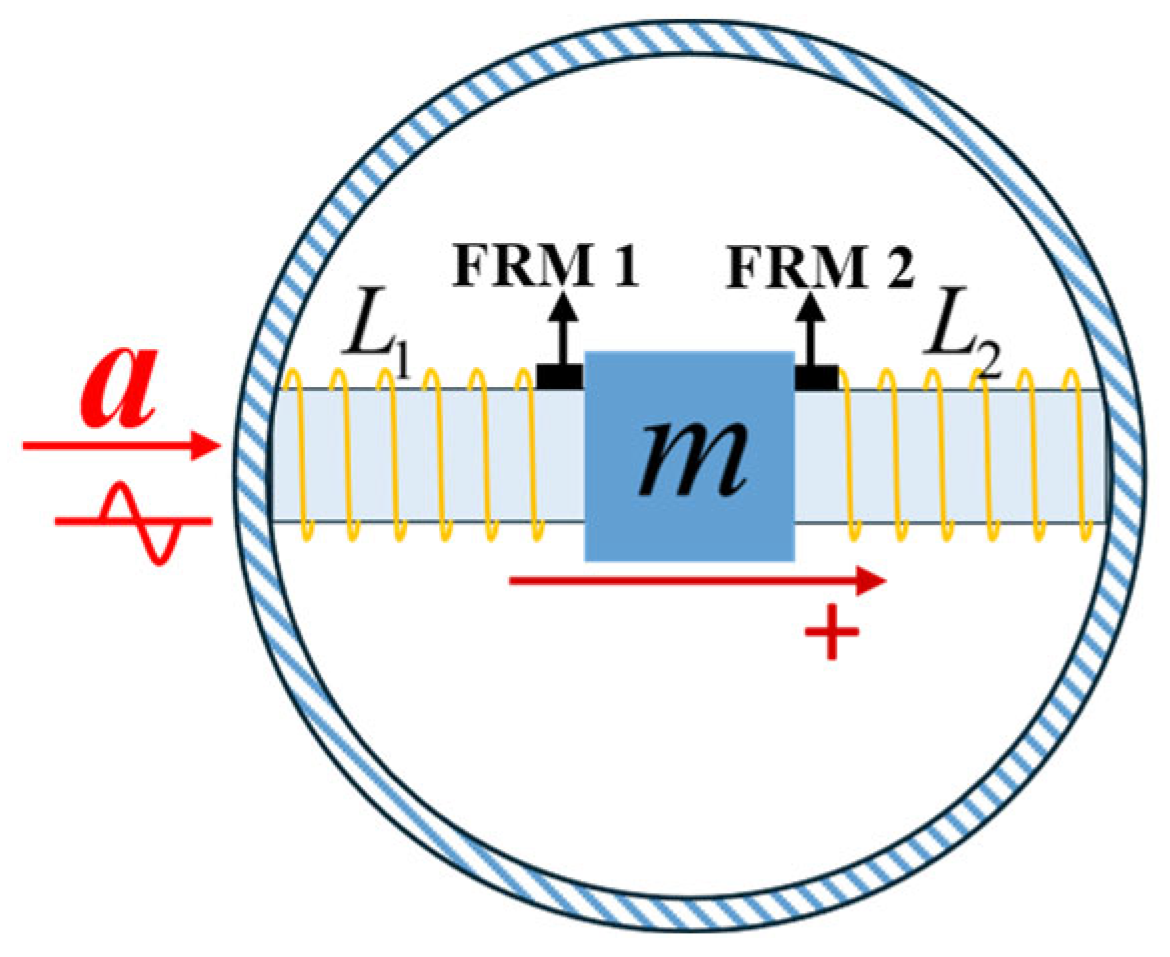
2.4. Elastic Mechanics Characteristics of Accelerometer
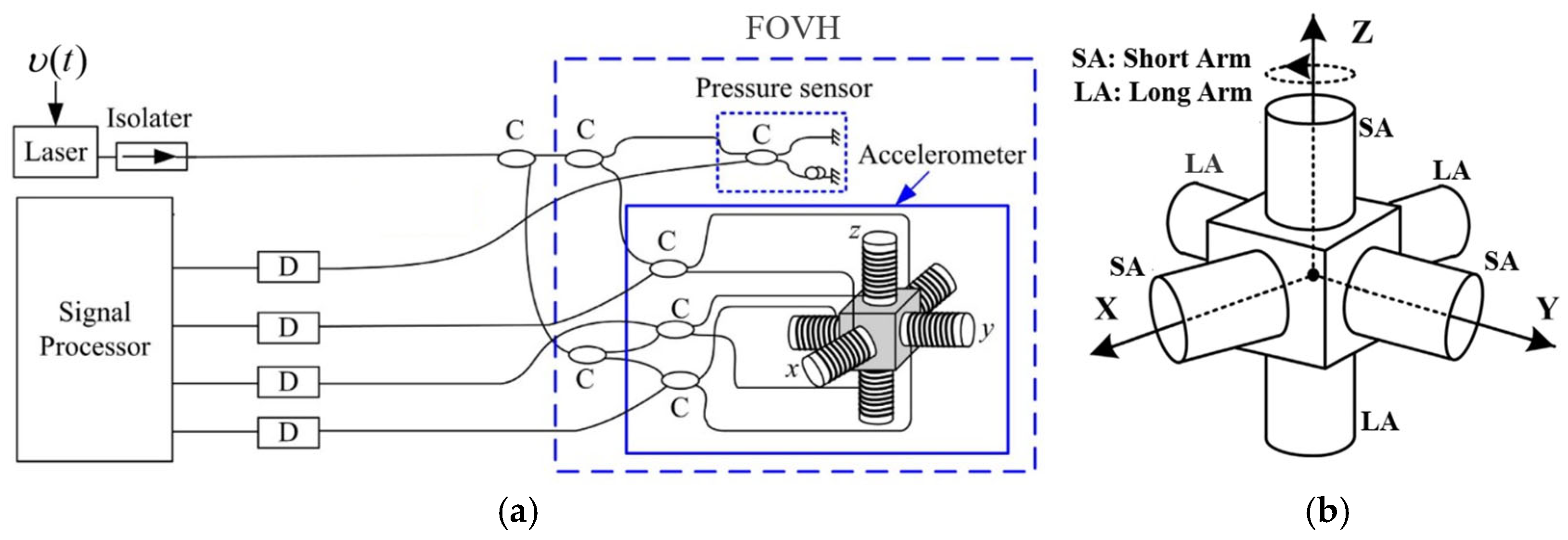
2.5. Three-Dimensional FOVH Polarity Configuration
3. Experiments and Results
3.1. Sensors Fabrication
3.2. Experiments in a Standing Wave Tube
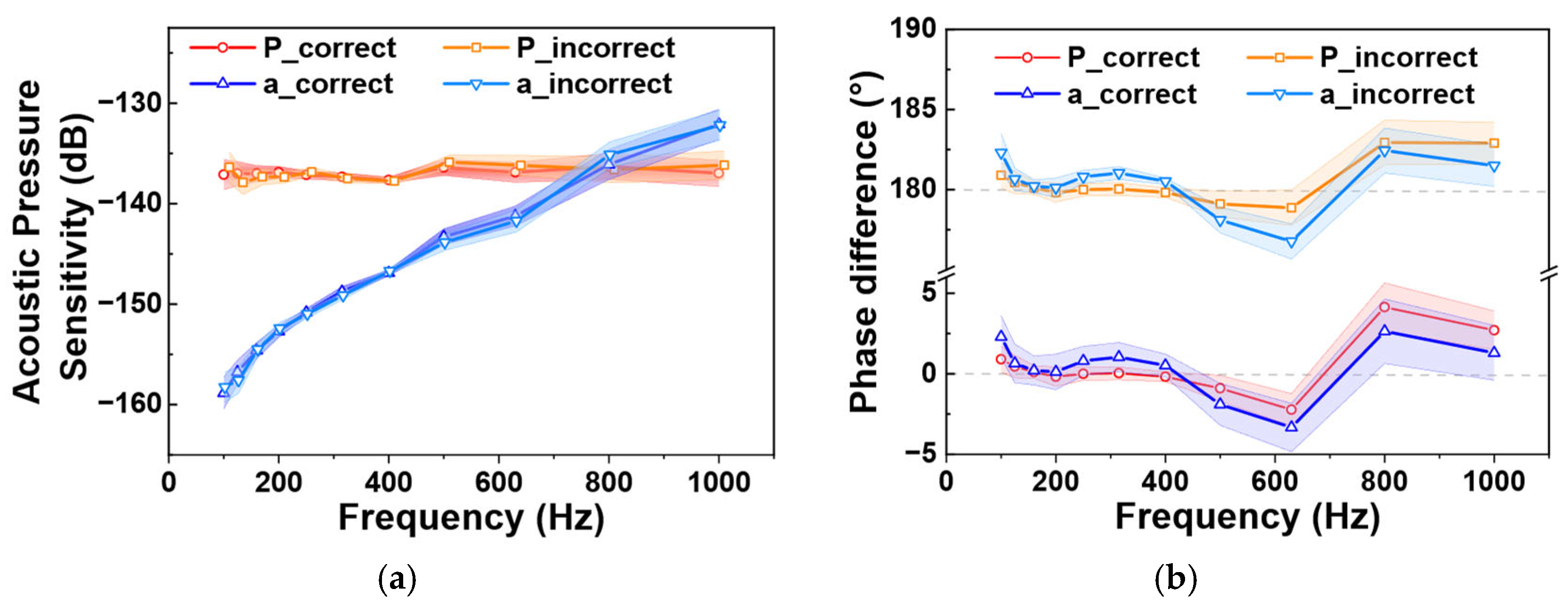
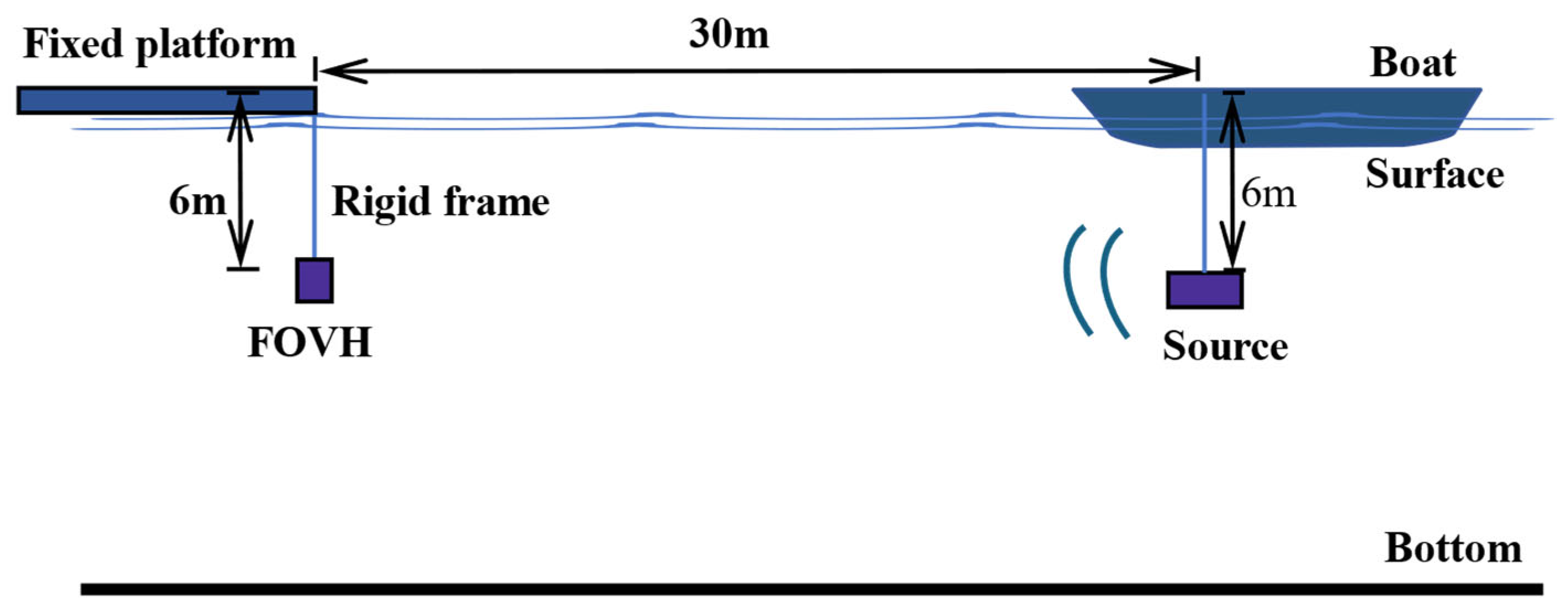
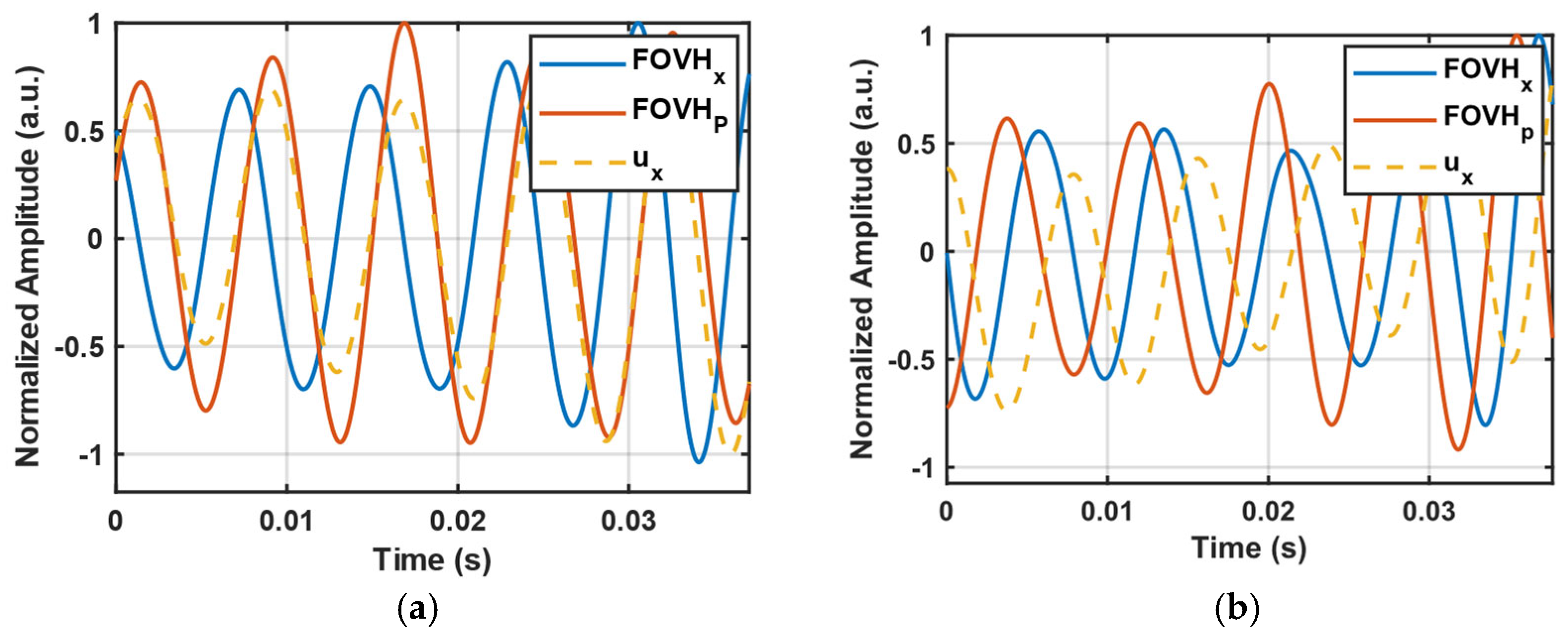
3.3. Tests in a Lake
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FOVH | Fiber-optic vector hydrophone |
| PH | Piezoelectric hydrophone |
| PGC | Phase-generated carrier |
| FRM | Faraday rotation mirrors |
| MI | Michelson interferometer |
| LA | Long sensing arm of the MI |
| SA | Short sensing arm of the MI |
| OPD | optical phase difference |
| PD | Photodetector |
| SD | Standard deviation |
References
- Wang, J.; Luo, H.; Meng, Z.; Hu, Y. Experimental Research of an All-Polarization-Maintaining Optical Fiber Vector Hydrophone. J. Light. Technol. 2012, 30, 1178–1184. [Google Scholar] [CrossRef]
- Meng, Z.; Chen, W.; Wang, J.; Hu, X.; Chen, M.; Zhang, Y. Recent Progress in Fiber-Optic Hydrophones. Photonic Sens. 2021, 11, 109–122. [Google Scholar] [CrossRef]
- Yu, Z.; Cai, Y.; Mo, D. Comparative Study on Noise Reduction Effect of Fiber Optic Hydrophone Based on LMS and NLMS Algorithm. Sensors 2020, 20, 301. [Google Scholar] [CrossRef] [PubMed]
- Sun, G.; Yang, D.; Zhang, L. Research on the Method for Measuring Radiated Noise by an Underwater Target in Low Frequency Band Based on the Vector Hydrophone. Acta Acust. 2002, 27, 429–434. [Google Scholar] [CrossRef]
- Fan, H.; Nie, W.; Yao, S.; An, L.; Yu, F.; Zhang, Y.; Wu, Q. A High-Order Time-Delay Difference Estimation Method for Signal Enhancement in the Distorted Towed Hydrophone Array. J. Acoust. Soc. Am. 2024, 156, 1996–2008. [Google Scholar] [CrossRef]
- Ashry, I.; Mao, Y.; Wang, B.; Hveding, F.; Bukhamsin, A.Y.; Ng, T.K.; Ooi, B.S. A Review of Distributed Fiber–Optic Sensing in the Oil and Gas Industry. J. Light. Technol. 2022, 40, 1407–1431. [Google Scholar] [CrossRef]
- Janneh, M.; Bruno, F.A.; Guardato, S.; Donnarumma, G.P.; Iannaccone, G.; Gruca, G.; Werzinger, S.; Gunda, A.; Rijnveld, N.; Cutolo, A.; et al. Field Demonstration of an Optical Fiber Hydrophone for Seismic Monitoring at Campi-Flegrei Caldera. Opt. Laser Technol. 2023, 158, 108920. [Google Scholar] [CrossRef]
- Guang, D.; Sun, X.; Shi, J.; Wu, X.; Zhang, G.; Zuo, C.; Zhu, P.; Yu, B. Sensitivity Improvement of Fiber Optic Interferometric Hydrophone Based on Composite Structure. Opt. Express 2024, 32, 47721–47734. [Google Scholar] [CrossRef]
- Liu, Z.; Gao, K.; Sun, Y.; Huang, F.; Ye, Q.; Cai, H. High-Performance Compact Fiber Optic Interferometric Accelerometer Based on a Novel Push–Pull Structure. IEEE Trans. Instrum. Meas. 2024, 73, 9508208. [Google Scholar] [CrossRef]
- Yang, Y.; Luo, Z.; Wang, Z.; Zhang, Y.; Chang, T.; Yu, M.; Cheng, L.; Wu, C.; Cui, H.-L. High-Performance Fiber Optic Interferometric Hydrophone Based on Push–Pull Structure. IEEE Trans. Instrum. Meas. 2021, 70, 9511313. [Google Scholar] [CrossRef]
- Bozzi, F.D.A.; Jesus, S.M. Vector Sensor Beam Steering for Underwater Acoustic Communications. Proc. Mtgs. Acoust. 2020, 42, 070002. [Google Scholar]
- Zhu, J.; Wang, J.; Wang, X.; Wu, Y.; Hu, Z.; Hu, Y. Influence Analysis of an Asymmetrical Suspension System on Triaxial Signals’ Phase Differences of Fiber Optic Vector Hydrophones. In Proceedings of the SPIE Proceedings; Wang, L., Zhou, Z., Eds.; SPIE: Beijing, China, 2016; Volume 10152, p. 1015208. [Google Scholar]
- Wang, C.; Ma, S.; Meng, Z.; Wang, J.; Chen, Y. Analysis of Phase Difference of Acceleration Fiber Optic Vector Hydrophone Based on Signal-to-Noise Ratio. In Proceedings of the 2019 18th International Conference on Optical Communications and Networks (ICOCN), Huangshan, China, 5–8 August 2019; pp. 1–3. [Google Scholar]
- Peter, H.D.; Julien, B.; David, R.D. On the Equivalence of Scalar-Pressure and Vector-Based Acoustic Dosage Measures as Derived from Time-Limited Signal Waveforms. J. Acoust. Soc. Am. 2024, 155, 3291–3301. [Google Scholar]
- Oppeneer, V.O.; de Jong, C.A.F.; Binnerts, B.; Wood, M.A.; Ainslie, M.A. Modelling Sound Particle Motion in Shallow Water. J. Acoust. Soc. Am. 2023, 154, 4004–4015. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, J.; Luo, H.; Meng, Z. Research of the Polarity Characteristic for an Optical Fiber Accelerometer Demodulated by Phase Generated Carrier Technology. Optik 2014, 125, 3748–3751. [Google Scholar] [CrossRef]
- Li, Y.; Wang, J.; Chen, M.; Liang, R.; Chen, Y.; Meng, Z.; Hu, X.; Lu, Y. Analysis of Photoelectric Detection Phase Polarity of Fiber-Optic Hydrophones Based on 3 × 3 Coupler Demodulation Technique. Photonics 2025, 12, 535. [Google Scholar] [CrossRef]
- Malarkodi, A.; Latha, G.; Sridhar, P.; Bøgholm, N.V. Design Considerations and Establishment of a Low Frequency Hydrophone Calibration Setup Using the Principle of Vibrating Water Column. Int. J. Acoust. Vib. 2018, 23, 44–48. [Google Scholar] [CrossRef]
- Li, Z.; Wang, C.; Gui, X.; Fu, X.; Wang, Y.; Wang, Z.; Wang, Y. A High-Performance Fiber-Optic Hydrophone for Large Scale Arrays. J. Light. Technol. 2023, 41, 4201–4210. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, H.; Zhang, H.; Wang, P. Sensitivity Correction of Co-Vibrating Vector Hydrophone in Standing Wave Tube by Numerical Calculation. Acta Acust. 2023, 48, 532–540. [Google Scholar] [CrossRef]
- Hu, L.; Liu, Q.; Zhang, H.; Wang, J.; Lu, Y.; Chen, D.; Chen, J. A Very Low-Frequency 3-D Vector Hydrophone Based on an Electrochemical Vibration Sensor. IEEE Sens. J. 2025, 25, 14709–14716. [Google Scholar] [CrossRef]
- Jiao, J.; He, Y.; Leong, T.; Kentish, S.E.; Ashokkumar, M.; Manasseh, R.; Lee, J. Experimental and Theoretical Studies on the Movements of Two Bubbles in an Acoustic Standing Wave Field. J. Phys. Chem. B 2013, 117, 12549–12555. [Google Scholar] [CrossRef]
- Chen, M.-H.; Lin, W.-W.; Shih, S.-T. Analysis of Fibre Optic Michelson Interferometric Sensor Distortion Caused by the Imperfect Properties of Its 3 × 3 Coupler. IEE Proc. Optoelectron. 1997, 144, 377–382. [Google Scholar] [CrossRef]




| Symbol | Indicator | Values | Units |
|---|---|---|---|
| Young’s modulus of the mandrel of pressure sensor | 70 | GPa | |
| Young’s modulus of the mandrel of accelerometer | 3.25 | GPa | |
| Poisson’s ratio of the mandrel of pressure sensor | 0.33 | - | |
| Poisson’s ratio of the mandrel of accelerometer | 0.22 | - | |
| refractive index of the fiber | 1.457 | - | |
| center wavelength of Laser | 1550 | nm | |
| inner radius of inner mandrel of pressure sensor | 7.5 | mm | |
| inner radius of outer mandrel of pressure sensor | 8.1 | mm | |
| outer radius of inner mandrel of pressure sensor | 9 | mm | |
| outer radius of outer mandrel of pressure sensor | 9.6 | mm | |
| radius of the mandrel of accelerometer | 10.0 | mm | |
| the length of the LA in pressure sensors and accelerometers | 68.52 | m | |
| the length of the SA in pressure sensors and accelerometers | 68.00 | m | |
| fiber strain-optic coefficient | 0.116 | - | |
| fiber strain-optic coefficient | 0.255 | - | |
| Poisson’s ratio of the fiber | 0.17 | - |
| Sensing Arm | Pressure Sensor Configurations | Accelerometer Configurations | ||
|---|---|---|---|---|
| P_Correct | P_Incorrect | A_Correct | A_Incorrect | |
| LA | Inner mandrel | Outer mandrel | Near-source | Far-source |
| SA | Outer mandrel | Inner mandrel | Far-source | Near-source |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Wang, J.; Liang, R.; Feng, J.; Chen, M.; Zhao, J.; Meng, Z. Analysis on Phase Polarity of Mandrel Fiber-Optic Vector Hydrophones Based on Phase Generated Carrier Technique. J. Mar. Sci. Eng. 2025, 13, 1825. https://doi.org/10.3390/jmse13091825
Li Y, Wang J, Liang R, Feng J, Chen M, Zhao J, Meng Z. Analysis on Phase Polarity of Mandrel Fiber-Optic Vector Hydrophones Based on Phase Generated Carrier Technique. Journal of Marine Science and Engineering. 2025; 13(9):1825. https://doi.org/10.3390/jmse13091825
Chicago/Turabian StyleLi, Yatao, Jianfei Wang, Rui Liang, Jingjing Feng, Mo Chen, Jiaze Zhao, and Zhou Meng. 2025. "Analysis on Phase Polarity of Mandrel Fiber-Optic Vector Hydrophones Based on Phase Generated Carrier Technique" Journal of Marine Science and Engineering 13, no. 9: 1825. https://doi.org/10.3390/jmse13091825
APA StyleLi, Y., Wang, J., Liang, R., Feng, J., Chen, M., Zhao, J., & Meng, Z. (2025). Analysis on Phase Polarity of Mandrel Fiber-Optic Vector Hydrophones Based on Phase Generated Carrier Technique. Journal of Marine Science and Engineering, 13(9), 1825. https://doi.org/10.3390/jmse13091825







