Dynamic Spatio-Temporal Modeling for Vessel Traffic Flow Prediction with FSTformer
Abstract
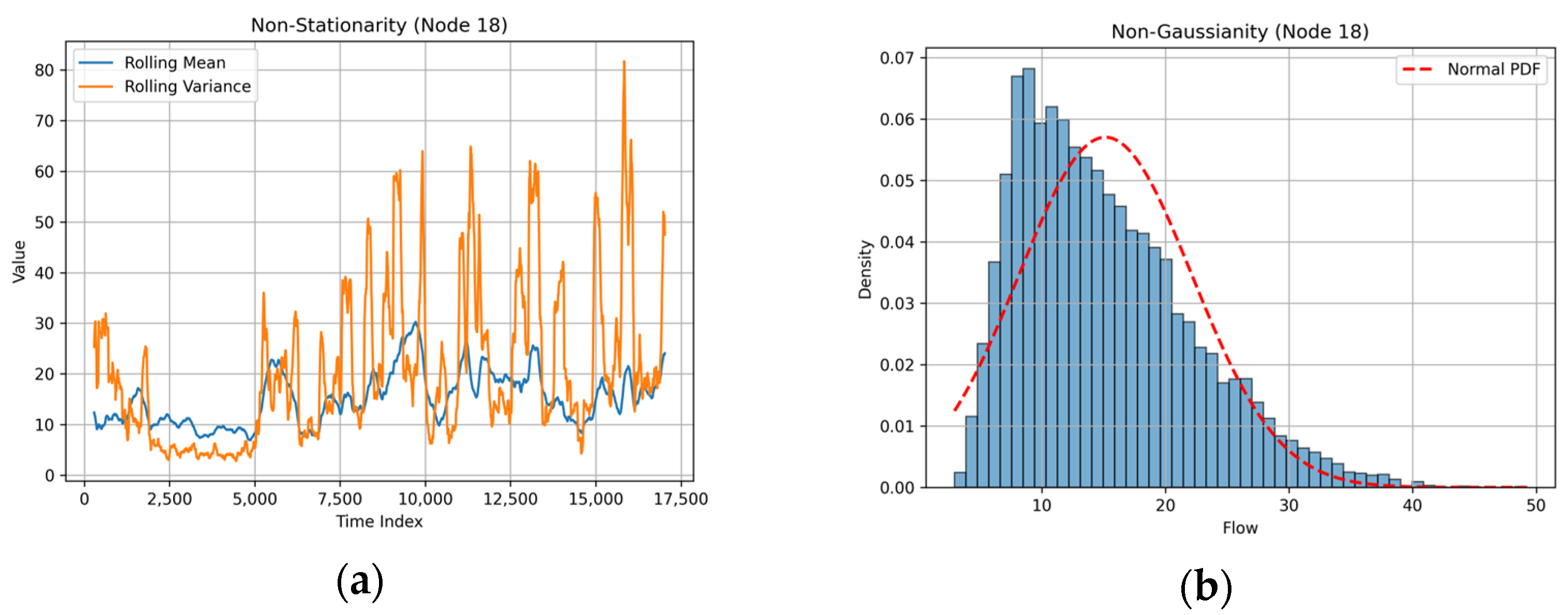
1. Introduction
- A VTF prediction model, Fusion Spatio-Temporal Transformer (FSTformer), is proposed, integrating distribution transformation, spatiotemporal attention modeling, and an expert structure enhancement mechanism. This model effectively adapts to the non-Gaussianity, non-stationarity, and spatiotemporal heterogeneity inherent in VTF data, and demonstrates excellent accuracy and robustness in multi-step prediction tasks.
- The Weibull–Gaussian Transform (WGT) is introduced to map VTF data into a near-Gaussian distribution, reducing data volatility and enhancing model stability and performance.
- A Fusion Spatio-Temporal Transfomer Encoder layer is designed, which embeds dynamic graph structure information into the spatial attention mechanism and incorporates a Heterogeneous Mixture-of-Experts (HMoE) module composed of MLP and TCN components, thereby enhancing the capability to capture complex spatiotemporal heterogeneity within traffic networks.
- The Kernel MSE loss function is employed to improve long-term prediction performance, providing greater robustness to outliers and enhancing the stability of model training, which leads to more accurate multi-step VTF forecasting.
2. Related Work
3. Methodology
3.1. Problem Definition
3.2. Weibull–Gaussian Transform
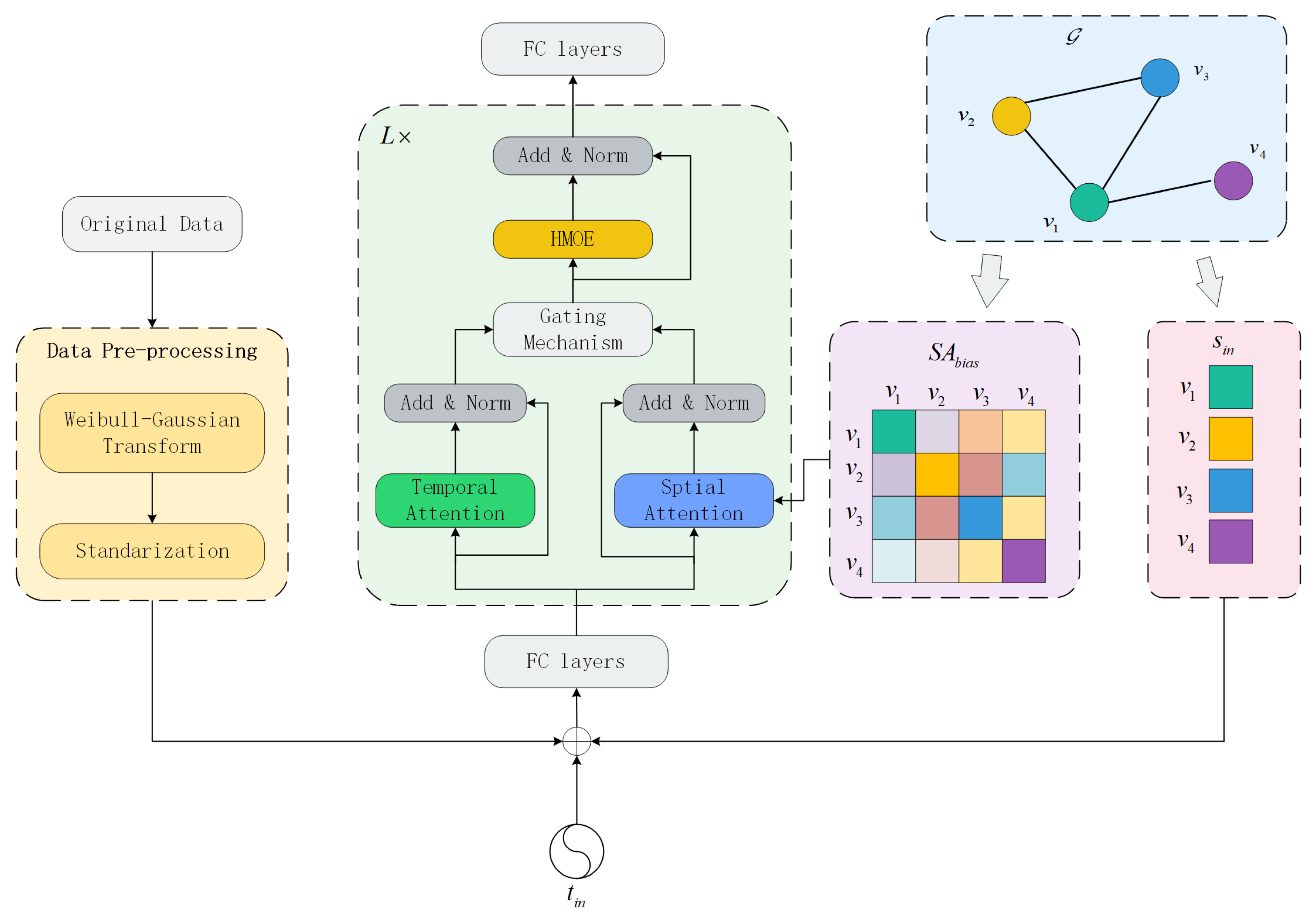
3.3. FSTformer
3.3.1. Spatio-Temporal Position Embedding Layer
3.3.2. Fusion Spatio-Temporal Attention Mechanism
3.3.3. Heterogeneous Mixture-of-Experts
3.3.4. Output Layer
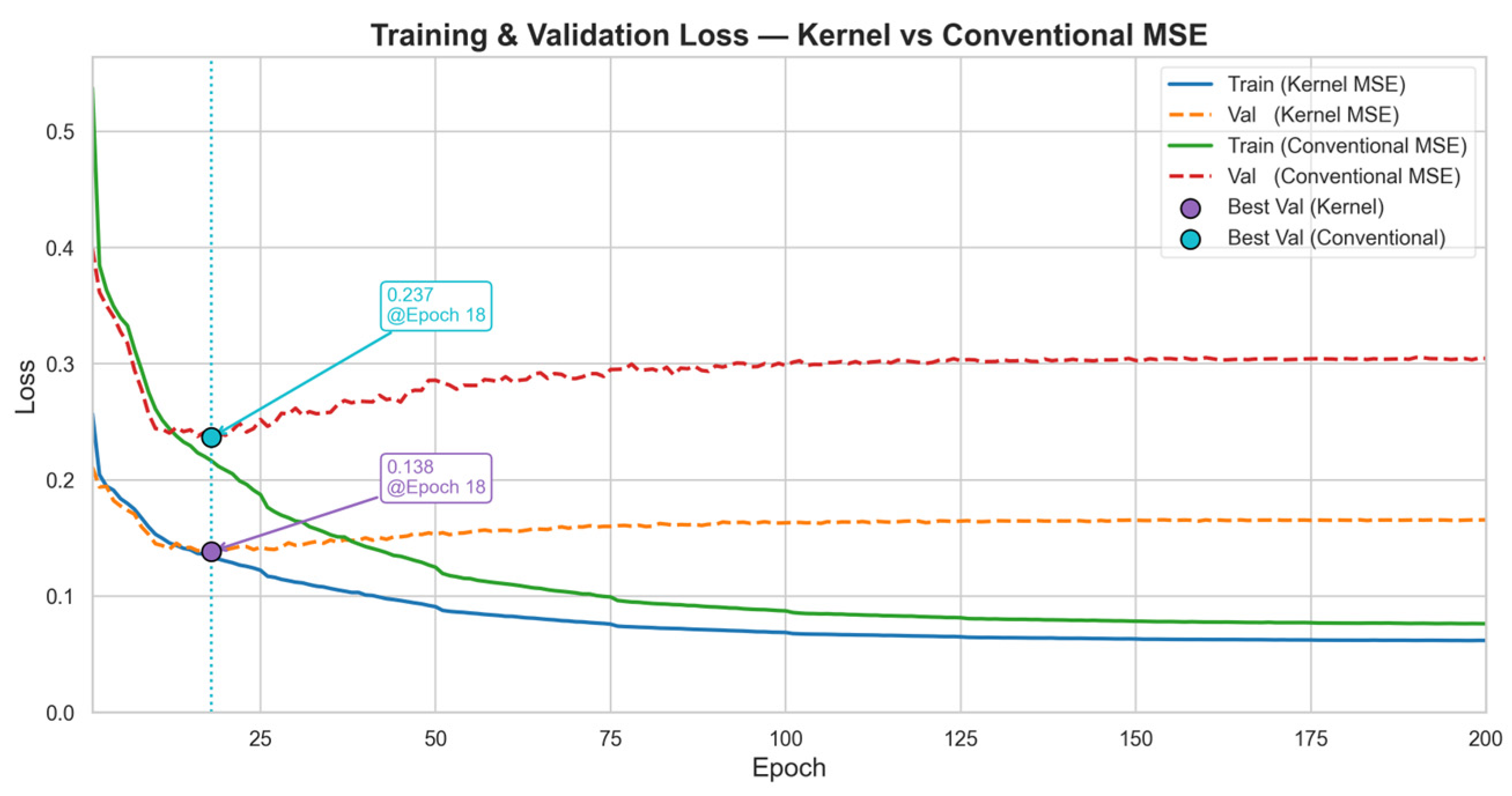
3.4. Loss Function
- Its first-order derivative remains positive, thereby maintaining a gradient direction similar to that of the MSE loss function.
- Its second-order derivative is negative, indicating that as the error increases, the growth rate of the loss slows down, thereby reducing the impact of outliers on the training process.
- Compared with the traditional MSE loss function, the Kernel MSE loss function better preserves the details of small errors and exhibits greater robustness to large errors.
4. Experiment
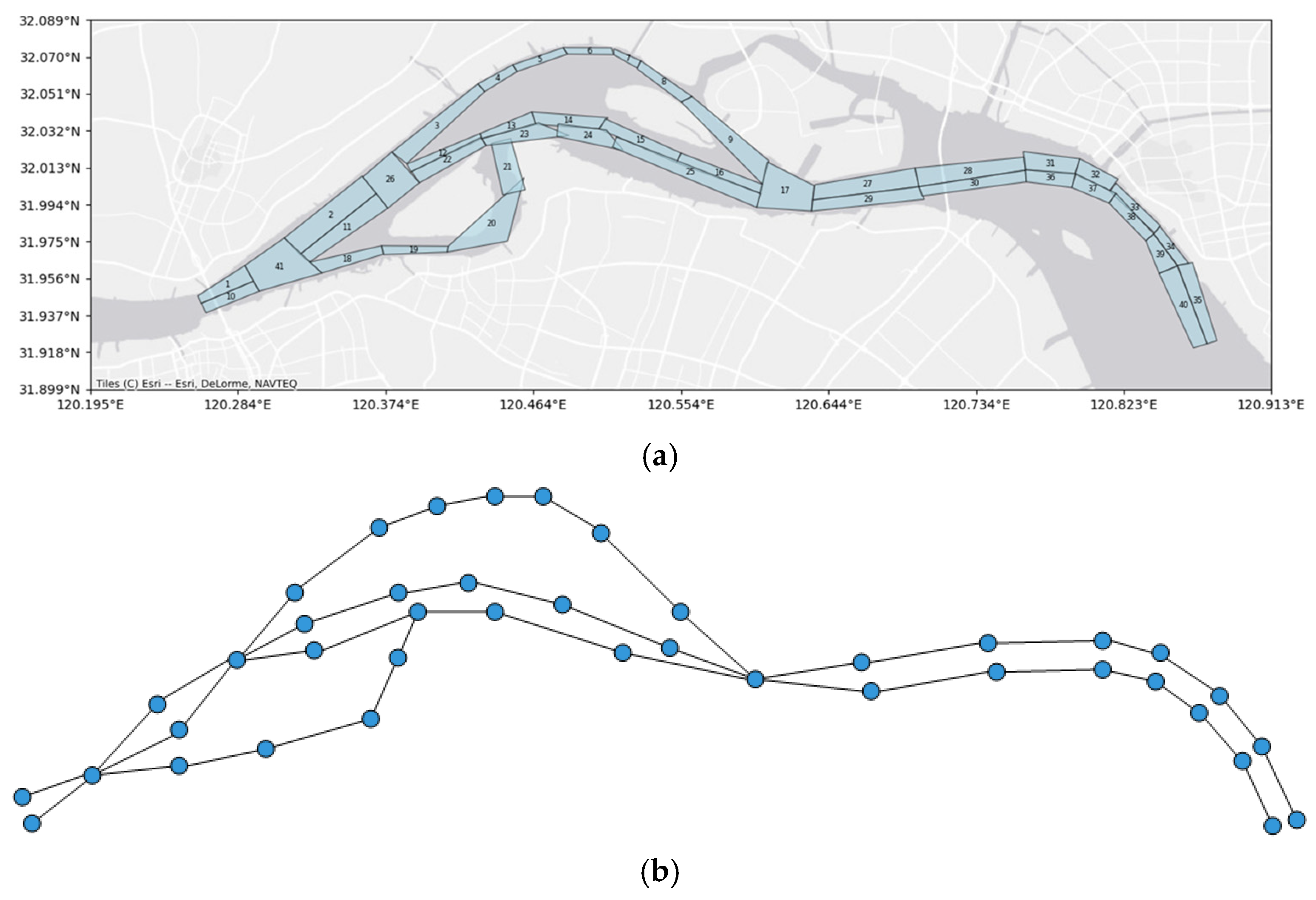
4.1. Data Description
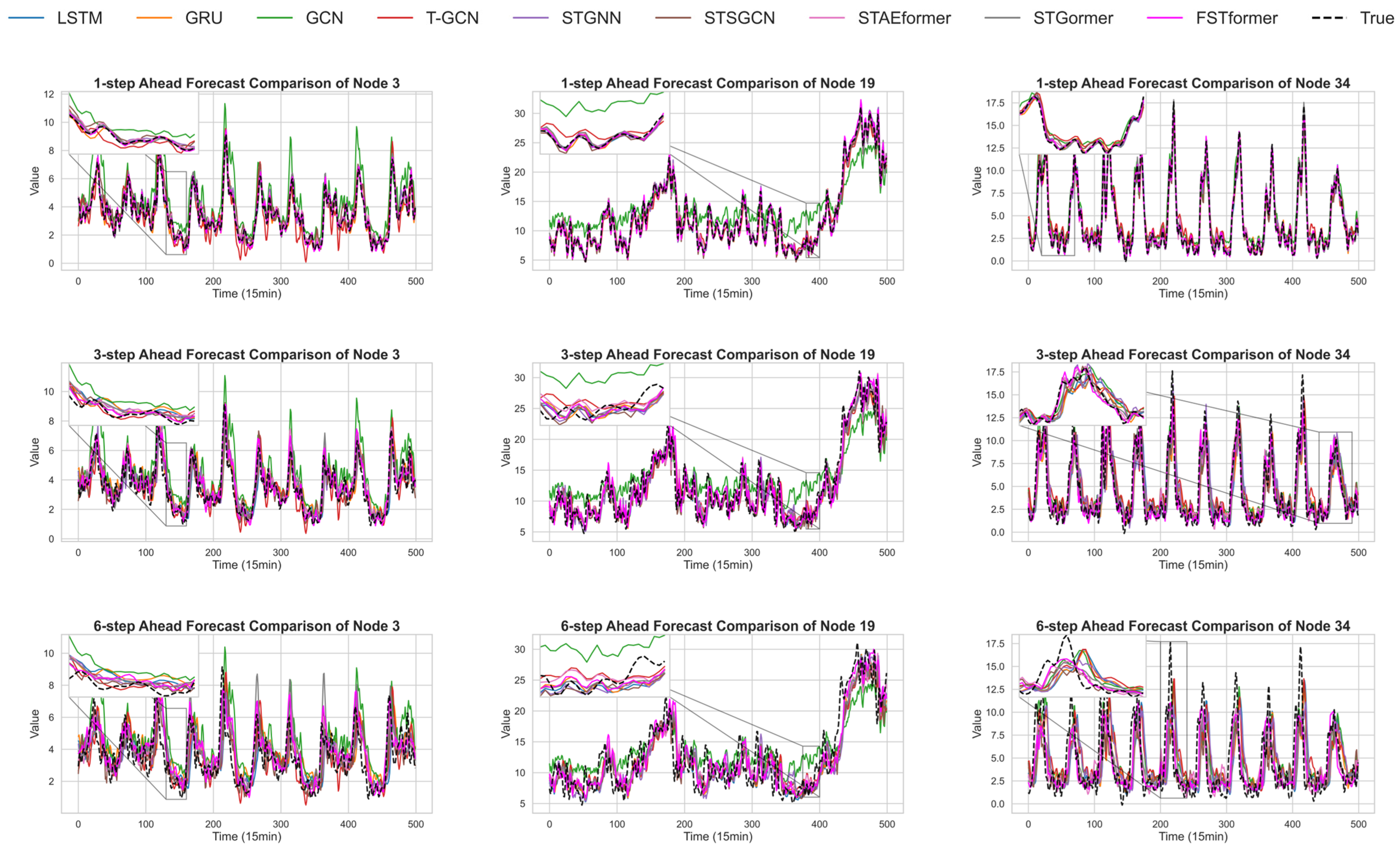
4.2. Comparative Model
- LSTM: The Long Short-Term Memory (LSTM) network, a variant of the Recurrent Neural Network (RNN), retains information through a gating mechanism comprising forget, input, and output gates. The output gate regulates the information used for predicting future time steps.
- GRU: The Gated Recurrent Unit (GRU) is a variant of the LSTM network that simplifies the architecture by combining the forget gate and the input gate into a single update gate.
- GCN: The Graph Convolutional Network (GCN) is a graph neural network model that captures spatial dependencies between nodes through graph convolution operations.
- T-GCN: The Temporal Graph Convolutional Network (T-GCN) extends GCN by integrating time series modeling capabilities, enabling simultaneous spatial and temporal feature extraction.
- STGNN: The Spatio-Temporal Graph Neural Network (STGNN) combines graph convolution and time series models to capture both spatial topological structures and temporal dynamics, making it suitable for prediction tasks involving spatiotemporal coupling characteristics.
- STSGCN: The Spatio-Temporal Synchronous Graph Convolutional Network (STSGCN) proposes a novel convolutional operation that simultaneously captures temporal and spatial correlations.
- STAEformer: The Spatio-Temporal AutoEncoder Transformer (STAEformer) integrates the Transformer self-attention mechanism with an autoencoder architecture, enabling efficient extraction of deep features and long-range dependencies from spatiotemporal data.
- STGormer: The Spatio-Temporal Graph Transformer (STGormer) embeds attribute gating and MoE modules into the multi-head self-attention mechanism, enhancing the model’s ability to capture complex spatiotemporal heterogeneity in vessel traffic data.
4.3. Experiment Setting
4.4. Experiment Analysis
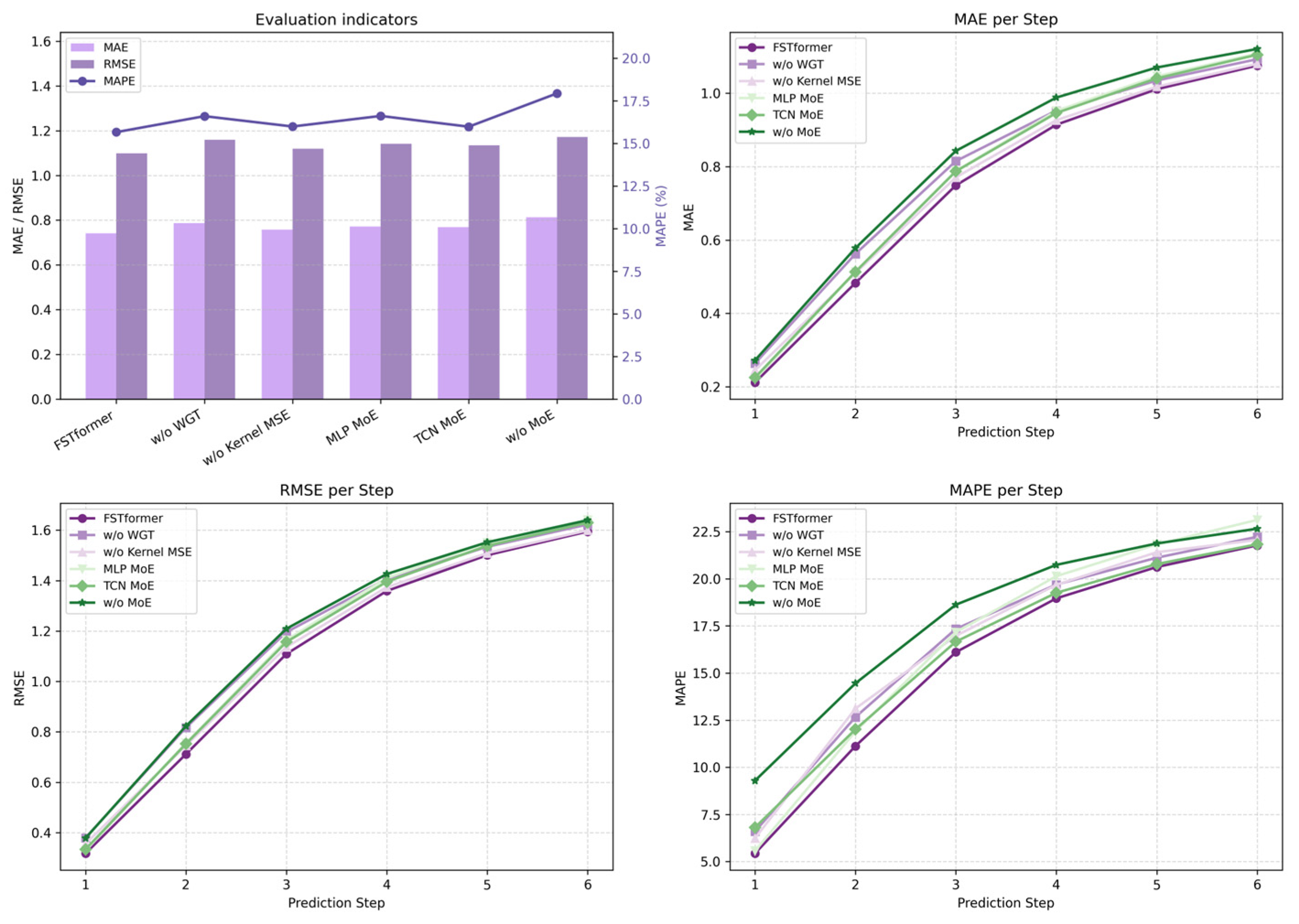
4.5. Ablation Experiment
- w/o WGT: In this model, the WGT transformation module is omitted and the commonly used Standard method is used to process the data to verify the impact of non-Gaussian data on the model.
- w/o Kernel MSE: In this model, the Kernel MSE loss function is omitted and replaced with the traditional MSE loss function.
- Full MLP MoE: In this variant, only MLP experts are used within the MoE structure to assess the contribution of TCN experts for time series modeling.
- Full TCN MoE: In this variant, only TCN experts are used within the MoE structure to evaluate the modeling capability of MLP experts for static features.
- w/o MoE: This model replaces the MoE structure with a standard feedforward neural network (FFN) in the Transformer to evaluate the overall effectiveness of the heterogeneous expert structure.
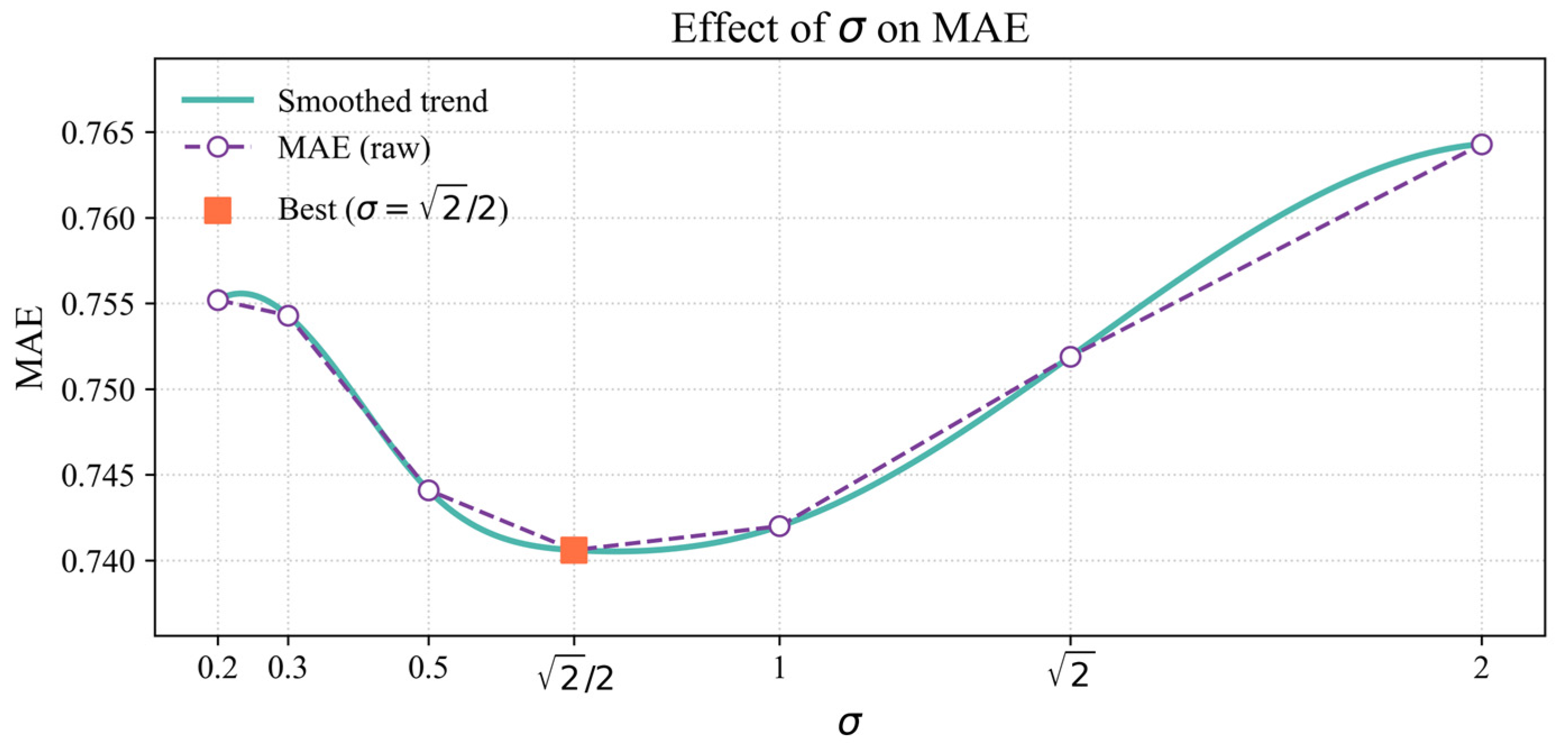
4.6. The Sensitivity Analysis of σ in Kernel MSE Loss Function
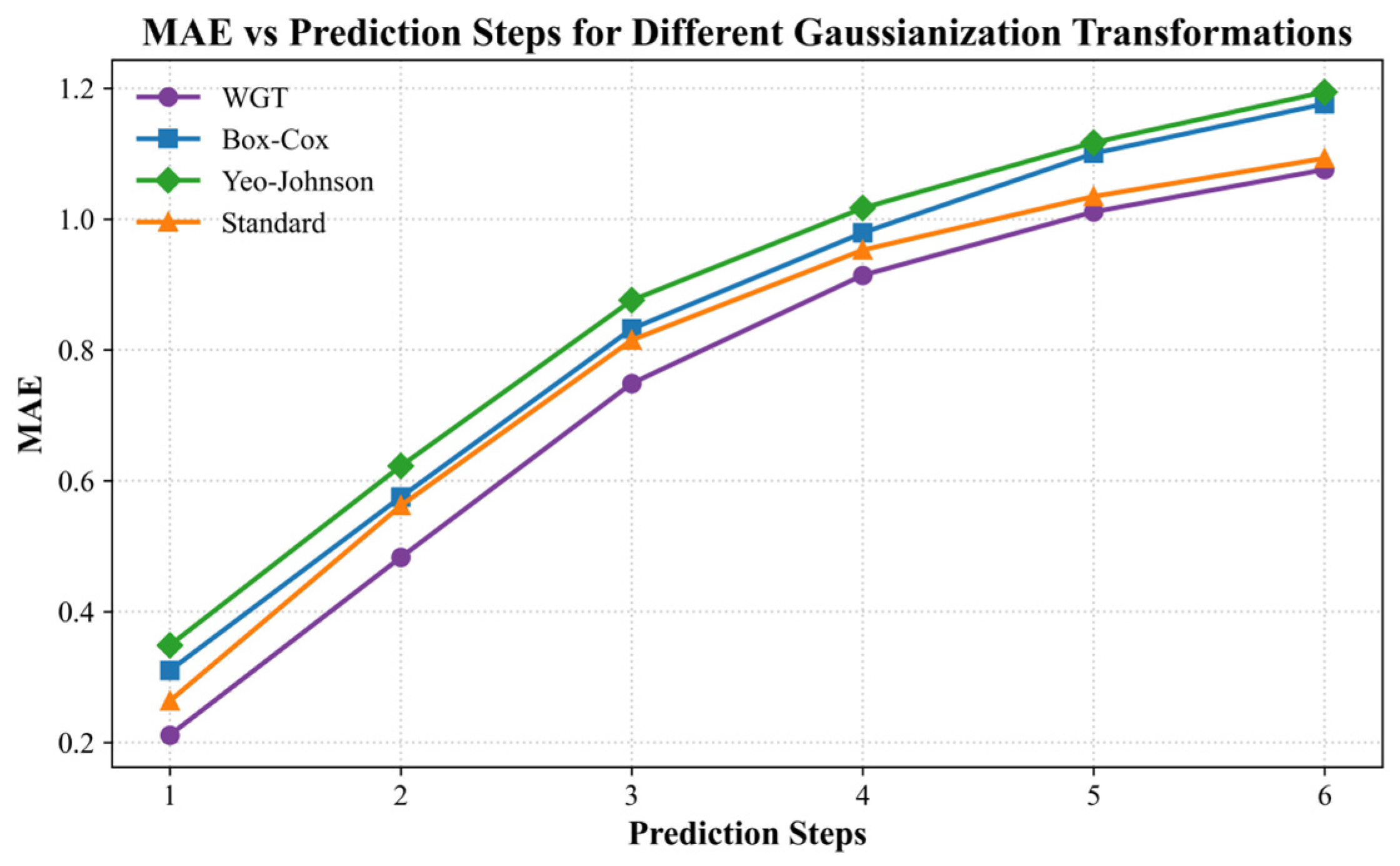
4.7. Comparison of Gaussianization Functions in Prediction Performance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FSTformer | Fusion Spatio-Temporal Transformer |
| MoE | Mixture-of-Experts |
| HMoE | Heterogeneous Mixture-of-Experts |
| VTF | Vessel Traffic Flow |
| AIS | Automatic Identification System |
| LSTM | Long Short-Term Memory |
| GRU | Gated Recurrent Unit |
| ITS | Intelligent Traffic Systems |
| ARIMA | Autoregressive Integrated Moving Average |
| ELM | Extreme Learning Machine |
| SVR | Support Vector Regression |
| STGNN | Spatio-Temporal Graph Neural Network |
| TCN | Temporal Convolutional Network |
| MSE | Mean Squared Error |
| WGT | Weibull–Gaussian Transform |
| VAR | Vector Auto-Regression |
| CNN | Convolutional Neural Network |
| RNN | Recurrent Neural Network |
| GNN | Graph Neural Network |
| PG-STGNN | Physics-Guided Spatio-Temporal Graph Neural Network |
| MRA-BGCN | Multi-Range Attentive Bicomponent Graph Convolutional Network |
| ST-MGCN | Spatio-Temporal Multi-Graph Convolution Network |
| MSSTGNN | Multi-Scaled Spatio-Temporal Graph Neural Network |
| STSGCN | Spatial-Temporal Synchronous Graph Convolutional Network |
| STMGCN | Spatio-Temporal Multi-Graph Convolutional Network |
| GAT | Graph Attention Network |
| ASTGNN | Attention-based Spatial-Temporal Graph Neural Network |
| ASTGCN | Attention-Based Spatial-Temporal Graph Convolutional Network |
| SDSTGNN | Semi-Dynamic Spatial–Temporal Graph Neural Network |
| SPD | Shortest Path Distance |
| FFN | Feed-Forward Network |
| MLP | Multi-Layer Perceptron |
| Q-Q plot | Quantile-Quantile Plot |
| STAEformer | Spatio-Temporal Adaptive Embedding Transformer |
| STGormer | Spatio-Temporal Graph Transformer |
| MAE | Mean Absolute Error |
| RMSE | Root Mean Squared Error |
| MAPE | Mean Absolute Percentage Error |
References
- Zhang, G.P. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Lu, Z.; Zhou, C.; Wu, J.; Jiang, H.; Cui, S.Y. Integrating granger causality and vector auto-regression for traffic prediction of large-scale WLANs. KSII Trans. Internet Inf. Syst. 2016, 10, 136–151. [Google Scholar]
- Wu, C.H.; Ho, J.M.; Lee, D.T. Travel-time prediction with support vector regression. IEEE Trans. Intell. Transp. Syst. 2004, 5, 276–281. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: A new learning scheme of feedforward neural networks. In Proceedings of the 2004 IEEE International Joint Conference on Neural Networks (IEEE Cat. No. 04CH37541), Budapest, Hungary, 25–29 July 2004; IEEE: New York, NY, USA, 2004; Volume 2, pp. 985–990. [Google Scholar]
- Li, Y.; Liang, M.; Li, H.; Yang, Z.L.; Du, L.; Chen, Z.S. Deep learning-powered vessel traffic flow prediction with spatial-temporal attributes and similarity grouping. Eng. Appl. Artif. Intell. 2023, 126, 107012. [Google Scholar] [CrossRef]
- Wang, J.; Wang, X.; Zhou, J. Model selection for predicting marine traffic flow in coastal waterways using deep learning methods. Ocean. Eng. 2025, 329, 121151. [Google Scholar] [CrossRef]
- Yu, B.; Yin, H.; Zhu, Z. Spatio-temporal graph convolutional networks: A deep learning framework for traffic forecasting. arXiv 2017, arXiv:1709.04875. [Google Scholar]
- Zhao, L.; Song, Y.; Zhang, C.; Liu, Y.; Wang, P.; Lin, T.; Deng, M.; Li, H.F. T-GCN: A temporal graph convolutional network for traffic prediction. IEEE Trans. Intell. Transp. Syst. 2019, 21, 3848–3858. [Google Scholar] [CrossRef]
- Wang, D.; Meng, Y.R.; Chen, S.Z.; Xie, C.; Liu, Z. A hybrid model for vessel traffic flow prediction based on wavelet and prophet. J. Mar. Sci. Eng. 2021, 9, 1231. [Google Scholar] [CrossRef]
- Xing, W.; Wang, J.B.; Zhou, K.W.; Li, H.H.; Li, Y.; Yang, Z.L. A hierarchical methodology for vessel traffic flow prediction using Bayesian tensor decomposition and similarity grouping. Ocean Eng. 2023, 286, 115687. [Google Scholar] [CrossRef]
- Huan, Y.; Kang, X.Y.; Zhang, Z.J.; Zhang, Q.; Wang, Y.J.; Wang, Y.F. AIS-based vessel traffic flow prediction using combined EMD-LSTM method. In Proceedings of the 4th International Conference on Advanced Information Science and System, Sanya, China, 25–27 November 2022; pp. 1–8. [Google Scholar]
- Shi, Z.; Li, J.; Jiang, Z.Y.; Li, H.; Yu, C.Q.; Mi, X.W. WGformer: A Weibull-Gaussian Informer based model for wind speed prediction. Eng. Appl. Artif. Intell. 2024, 131, 107891. [Google Scholar] [CrossRef]
- Chen, X.; Yu, R.; Ullah, S.; Wu, D.M.; Li, Z.Q.; Li, Q.L.; Qi, H.G.; Liu, J.H.; Liu, M.; Zhang, Y.D. A novel loss function of deep learning in wind speed forecasting. Energy 2022, 238, 121808. [Google Scholar] [CrossRef]
- Sadeghi Gargari, N.; Akbari, H.; Panahi, R. Forecasting short-term container vessel traffic volume using hybrid ARIMA-NN model. Int. J. Coast. Offshore Environ. Eng. 2019, 4, 47–52. [Google Scholar] [CrossRef]
- Zhang, Q.; Jian, D.; Xu, R.; Dai, W.; Liu, Y. Integrating heterogeneous data sources for traffic flow prediction through extreme learning machine. In Proceedings of the 2017 IEEE International Conference on Big Data (Big Data), Boston, MA, USA, 11–14 December 2017; IEEE: New York, NY, USA, 2017; pp. 4189–4194. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.H.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar] [CrossRef]
- Ji, Z.; Wang, L.; Zhang, X.; Wang, F. 2022 Ship traffic flow forecast of Qingdao port based on, L.S.T.M. In Proceedings of the Sixth International Conference on Electromechanical Control Technology and Transportation, Chongqing, China, 14–16 May 2021; SPIE: Bellingham, WA, USA, 2021; Volume 12081, pp. 587–595. [Google Scholar]
- Xu, X.; Bai, X.; Xiao, Y.; He, J.; Xu, Y.; Ren, H. A port ship flow prediction model based on the automatic identification system gated recurrent units. J. Mar. Sci. Appl. 2021, 20, 572–580. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 84–90. [Google Scholar] [CrossRef]
- Bai, S.; Kolter, J.Z.; Koltun, V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar] [CrossRef]
- Zhang, D.; Zhao, L.N.; Liu, Z.Y.; Pan, M.Y.; Li, L. Temporal-TimesNet: A novel hybrid model for vessel traffic flow multi-step prediction. Ships Offshore Struct. 2025, 1–14. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Q. Adaptive genetic algorithm-optimized temporal convolutional networks for high-precision ship traffic flow prediction. Evol. Syst. 2025, 16, 4. [Google Scholar] [CrossRef]
- Wu, Y.Y.; Zhao, L.N.; Yuan, Z.X.; Zhang, C. CNN-GRU ship traffic flow prediction model based on attention mechanism. J. Dalian Marit. Univ. 2023, 49, 75–84. [Google Scholar]
- Chang, Y.; Ma, J.; Sun, L.; Ma, Z.Q.; Zhou, Y. Vessel Traffic Flow Prediction in Port Waterways Based on POA-CNN-BiGRU Model. J. Mar. Sci. Eng. 2024, 12, 2091. [Google Scholar] [CrossRef]
- Narmadha, S.; Vijayakumar, V. Spatio-Temporal vehicle traffic flow prediction using multivariate CNN and LSTM model. Mater. Today Proc. 2023, 81, 826–833. [Google Scholar] [CrossRef]
- Scarselli, F.; Gori, M.; Tsoi, A.C.; Hagenbuchner, M.; Monfardini, G. The graph neural network model. IEEE Trans. Neural Netw. 2008, 20, 61–80. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Kipf, T.N.; Welling, M. Variational graph auto-encoders. arXiv 2016, arXiv:1611.07308. [Google Scholar] [CrossRef]
- Pan, Y.A.; Li, F.L.; Li, A.R.; Niu, Z.Q.; Liu, Z. Urban intersection traffic flow prediction: A physics-guided stepwise framework utilizing spatio-temporal graph neural network algorithms. Multimodal Transp. 2025, 4, 100207. [Google Scholar] [CrossRef]
- Chen, W.; Chen, L.; Xie, Y.; Cao, W.; Gao, Y.S.; Feng, X.J. Multi-range attentive bicomponent graph convolutional network for traffic forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 3529–3536. [Google Scholar]
- Geng, X.; Li, Y.G.; Wang, L.Y.; Zhang, L.Y.; Yang, Q.; Ye, J.P.; Liu, Y. Spatiotemporal multi-graph convolution network for ride-hailing demand forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 3656–3663. [Google Scholar]
- Qu, Y.; Jia, X.L.; Guo, J.H.; Zhu, H.R.; Wu, W.B. MSSTGNN: Multi-scaled Spatio-temporal graph neural networks for short-and long-term traffic prediction. Knowl.-Based Syst. 2024, 306, 112716. [Google Scholar] [CrossRef]
- Song, C.; Lin, Y.F.; Guo, S.N.; Wan, H.Y. Spatial-temporal synchronous graph convolutional networks: A new framework for spatial-temporal network data forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 914–921. [Google Scholar]
- Liang, M.; Liu, R.W.; Zhan, Y.; Li, H.H.; Zhu, F.H.; Wang, F.Y. Fine-grained vessel traffic flow prediction with a spatio-temporal multigraph convolutional network. IEEE Trans. Intell. Transp. Syst. 2022, 23, 23694–23707. [Google Scholar] [CrossRef]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Li`o, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Li, Y.; Li, Z.X.; Mei, Q.; Wang, P.; Hu, W.L.; Wang, Z.S.; Xie, W.X.; Yang, Y.; Chen, Y.R. Research on multi-port ship traffic prediction method based on spatiotemporal graph neural networks. J. Mar. Sci. Eng. 2023, 11, 1379. [Google Scholar] [CrossRef]
- Guo, S.N.; Lin, Y.F.; Feng, N.; Song, C.; Wang, H.Y. Attention based spatial-temporal graph convolutional networks for traffic flow forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 922–929. [Google Scholar]
- Wang, Y.; Jing, C.F.; Xu, S.S.; Guo, T. Attention based spatiotemporal graph attention networks for traffic flow forecasting. Inf. Sci. 2022, 607, 869–883. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2017; p. 30. [Google Scholar]
- Li, L.; Pan, M.Y.; Liu, Z.Y.; Sun, H.; Zhang, R.L. Semi-dynamic spatial–temporal graph neural network for traffic state prediction in waterways. Ocean Eng. 2024, 293, 116685. [Google Scholar]
- Guo, S.; Lin, Y.F.; Wan, H.Y.; Li, X.C.; Cong, G. Learning dynamics and heterogeneity of spatial-temporal graph data for traffic forecasting. IEEE Trans. Knowl. Data Eng. 2021, 34, 5415–5428. [Google Scholar] [CrossRef]
- Zhou, J.; Liu, E.D.; Chen, W.; Zhang, S.R.; Liang, Y.X. Navigating Spatio-Temporal Heterogeneity: A Graph Transformer Approach for Traffic Forecasting. arXiv 2024, arXiv:2408.10822. [Google Scholar] [CrossRef]
- Brown, B.G.; Katz, R.W.; Murphy, A.H. Time series models to simulate and forecast wind speed and wind power. J. Appl. Meteorol. Climatol. 1984, 23, 1184–1195. [Google Scholar] [CrossRef]
- Dubey, S.Y.D. Normal and Weibull distributions. Nav. Res. Logist. Q. 1967, 14, 69–79. [Google Scholar] [CrossRef]
- Ying, C.; Cai, T.L.; Luo, S.J.; Zheng, S.X.; Ke, G.L.; He, D.; Shen, Y.M.; Liu, T.Y. Do transformers really perform badly for graph representation? Adv. Neural Inf. Process. Syst. 2021, 34, 28877–28888. [Google Scholar]
- Krishnan, S.R.; Seelamantula, C.S. On the selection of optimum Savitzky-Golay filters. IEEE Trans. Signal Process. 2012, 61, 380–391. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, X.H.; Pan, M.Y.; Loo, C.K.; Li, S.X. Weighted error-output recurrent echo kernel state network for multi-step water level prediction. Appl. Soft Comput. 2023, 137, 110131. [Google Scholar] [CrossRef]
- Box, G.E.P.; Cox, D.R. An analysis of transformations. J. R. Stat. Soc. Ser. B Stat. Methodol. 1964, 26, 211–243. [Google Scholar] [CrossRef]
- Yeo, I.K.; Johnson, R.A. A new family of power transformations to improve normality or symmetry. Biometrika 2000, 87, 954–959. [Google Scholar] [CrossRef]


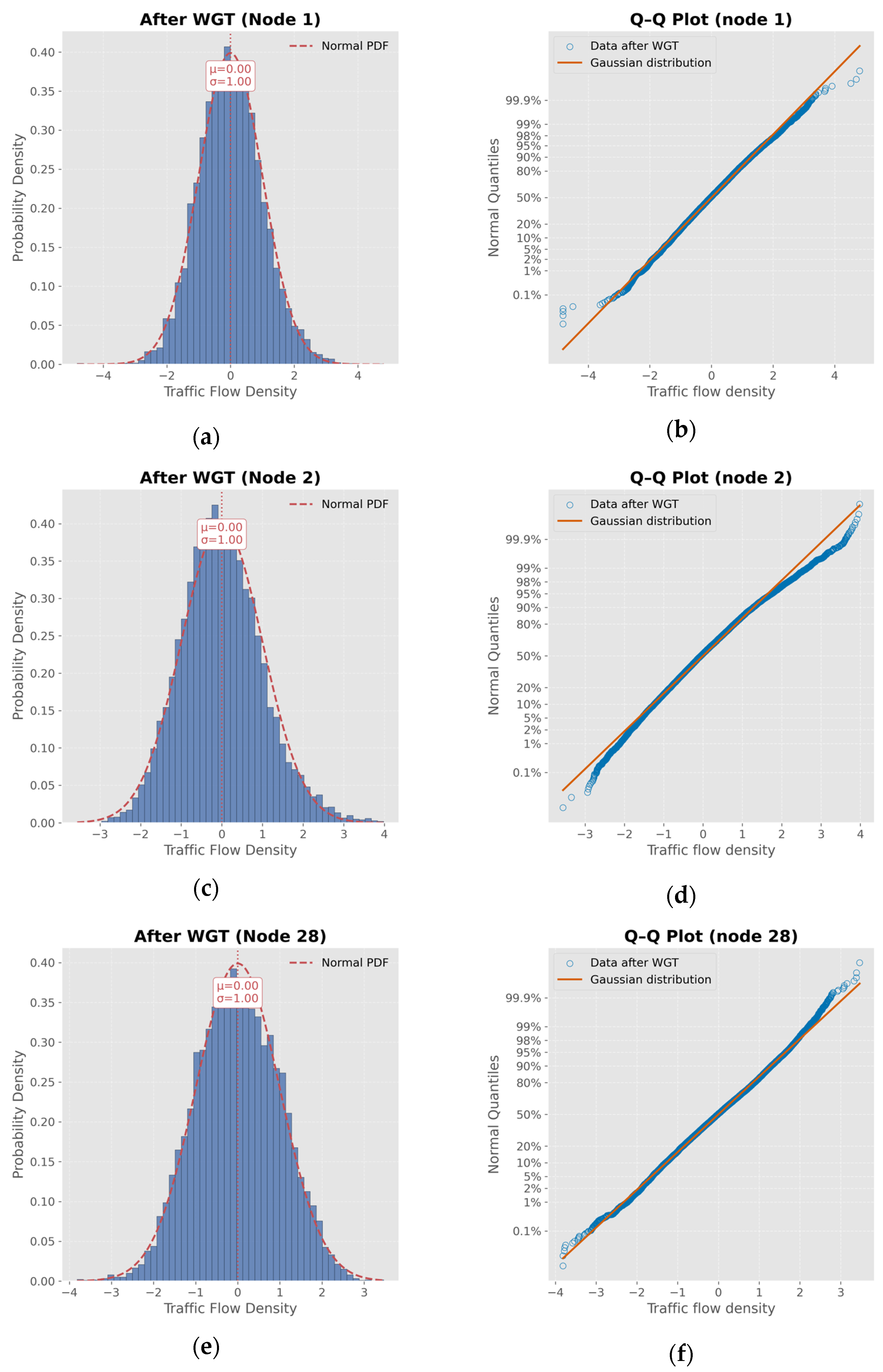
| Node | Raw p-Value | WGT p-Value | Raw Skewness | WGT Skewness | Raw Kurtosis | WGT Kurtosis |
|---|---|---|---|---|---|---|
| 1 | 7.3 × 10−35 | 3.3 × 10−7 | 8.6 × 10−1 | 1.4 × 10−1 | 1.2 × 100 | 2.7 × 10−1 |
| 2 | 1.2 × 10−33 | 2.3 × 10−16 | 8.7 × 10−1 | 3.4 × 10−1 | 1.2 × 100 | 3.2 × 10−1 |
| 3 | 4.7 × 10−26 | 5.8 × 10−4 | 7.0 × 10−1 | 3.0 × 10−2 | 7.5 × 10−1 | 9.1 × 10−2 |
| 4 | 1.1 × 10−30 | 6.6 × 10−9 | 8.2 × 10−1 | −1.4 × 10−1 | 1.2 × 100 | 2.8 × 10−1 |
| 5 | 1.5 × 10−37 | 2.0 × 10−7 | 8.9 × 10−1 | 1.3 × 10−3 | 1.3 × 100 | 3.8 × 10−1 |
| 6 | 9.8 × 10−43 | 5.4 × 10−10 | 9.1 × 10−1 | −3.7 × 10−2 | 9.4 × 10−1 | 6.2 × 10−2 |
| 7 | 3.0 × 10−33 | 3.8 × 10−7 | 8.1 × 10−1 | −1.3 × 10−1 | 8.2 × 10−1 | 3.1 × 10−1 |
| 8 | 4.7 × 10−29 | 2.2 × 10−5 | 9.7 × 10−1 | −1.0 × 10−1 | 2.5 × 100 | 8.0 × 10−1 |
| 9 | 2.8 × 10−23 | 5.9 × 10−5 | 8.2 × 10−1 | −8.9 × 10−2 | 2.2 × 100 | 8.3 × 10−1 |
| 10 | 2.0 × 10−17 | 3.5 × 10−5 | 5.7 × 10−1 | 1.2 × 10−1 | 3.3 × 10−1 | −2.6 × 10−2 |
| Model | Indicators | 1 | 2 | 3 | 4 | 5 | 6 | 1–6 |
|---|---|---|---|---|---|---|---|---|
| LSTM | MAE | 0.2599 | 0.6966 | 1.0401 | 1.2462 | 1.3538 | 1.4275 | 1.0040 |
| RMSE | 0.3765 | 1.0129 | 1.5188 | 1.8264 | 1.9901 | 2.1021 | 1.4711 | |
| MAPE | 7.2912% | 15.6889% | 22.3178% | 26.0726% | 28.0435% | 29.4130% | 21.4712% | |
| GRU | MAE | 0.3825 | 0.7630 | 1.0575 | 1.2275 | 1.3203 | 1.3870 | 1.0230 |
| RMSE | 0.5256 | 1.0884 | 1.5282 | 1.7838 | 1.9276 | 2.0268 | 1.4801 | |
| MAPE | 12.9086% | 19.1043% | 24.5740% | 27.0930% | 29.0452% | 29.0179% | 23.6238% | |
| GCN | MAE | 1.3272 | 1.3818 | 1.5324 | 1.6785 | 1.7831 | 1.8587 | 1.5936 |
| RMSE | 2.1148 | 2.1638 | 2.3208 | 2.4894 | 2.6149 | 2.7105 | 2.4024 | |
| MAPE | 21.6285% | 22.8631% | 25.8879% | 28.6359% | 30.5907% | 31.9998% | 26.9343% | |
| T-GCN | MAE | 0.7154 | 0.9407 | 1.1422 | 1.2765 | 1.3578 | 1.4223 | 1.1425 |
| RMSE | 1.0123 | 1.3313 | 1.6289 | 1.8321 | 1.9573 | 2.0567 | 1.6365 | |
| MAPE | 20.0820% | 29.5519% | 25.9278% | 28.0734% | 30.5356% | 30.5711% | 27.4570% | |
| STGNN | MAE | 0.4353 | 0.7749 | 1.0610 | 1.2264 | 1.3143 | 1.3837 | 1.0326 |
| RMSE | 0.6046 | 1.1248 | 1.5501 | 1.7952 | 1.9363 | 2.0450 | 1.5093 | |
| MAPE | 11.5941% | 19.2110% | 22.6423% | 27.0294% | 27.5967% | 28.5792% | 22.7755% | |
| STGormer | MAE | 0.2977 | 0.6466 | 0.9016 | 1.0347 | 1.1075 | 1.1596 | 0.8580 |
| RMSE | 0.4254 | 0.9363 | 1.3152 | 1.5177 | 1.6319 | 1.7157 | 1.2571 | |
| MAPE | 13.7863% | 16.3553% | 21.2535% | 23.5637% | 24.9357% | 25.7361% | 20.9384% | |
| STEAformer | MAE | 0.2343 | 0.5258 | 0.8031 | 0.9515 | 1.0298 | 1.0873 | 0.7720 |
| RMSE | 0.3286 | 0.7495 | 1.1556 | 1.3869 | 1.5105 | 1.6015 | 1.1221 | |
| MAPE | 6.0228% | 11.7809% | 16.6266% | 22.3207% | 20.8708% | 22.8488% | 16.7451% | |
| FSTformer | MAE | 0.2113 | 0.4829 | 0.7489 | 0.9142 | 1.0111 | 1.0756 | 0.7406 |
| RMSE | 0.3175 | 0.7113 | 1.1086 | 1.3589 | 1.5009 | 1.5948 | 1.0987 | |
| MAPE | 5.4267% | 11.1221% | 16.1063% | 18.9628% | 20.6251% | 21.7744% | 15.6696% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.; Xu, H.; Guo, Y.; Li, S.; Lu, Y.; Pan, M. Dynamic Spatio-Temporal Modeling for Vessel Traffic Flow Prediction with FSTformer. J. Mar. Sci. Eng. 2025, 13, 1822. https://doi.org/10.3390/jmse13091822
Zhang D, Xu H, Guo Y, Li S, Lu Y, Pan M. Dynamic Spatio-Temporal Modeling for Vessel Traffic Flow Prediction with FSTformer. Journal of Marine Science and Engineering. 2025; 13(9):1822. https://doi.org/10.3390/jmse13091822
Chicago/Turabian StyleZhang, Dong, Haichao Xu, Yongfeng Guo, Shaoxi Li, Yinyin Lu, and Mingyang Pan. 2025. "Dynamic Spatio-Temporal Modeling for Vessel Traffic Flow Prediction with FSTformer" Journal of Marine Science and Engineering 13, no. 9: 1822. https://doi.org/10.3390/jmse13091822
APA StyleZhang, D., Xu, H., Guo, Y., Li, S., Lu, Y., & Pan, M. (2025). Dynamic Spatio-Temporal Modeling for Vessel Traffic Flow Prediction with FSTformer. Journal of Marine Science and Engineering, 13(9), 1822. https://doi.org/10.3390/jmse13091822






