Developing a Framework for Assessing Boat Collision Risks Using Fuzzy Multi-Criteria Decision-Making Methodology

Abstract

Boat collisions pose severe threats to maritime safety, economic activity, and environmental sustainability. Conventional risk assessment methods—such as Failure Mode and Effects Analysis, and Fault Tree Analysis—are widely applied but remain inadequate for addressing the uncertainty, subjectivity, and interdependency of risk factors in complex maritime environments. This study proposes a fuzzy Multi-Criteria Decision-Making framework for the risk assessment of boat collisions. The model integrates fuzzy logic with Analytic Hierarchy Process for criterion weighting and the Technique for Order Preference by Similarity to the Ideal Solution for risk ranking. Fuzzy logic is employed to capture linguistic expert judgments and to manage vague or incomplete data, which are common challenges in marine operations. Key collision risk factors—human error, boat engine system failure, environmental conditions, and intentional threats—are identified through literature review, incident data analysis, and expert consultation. A comparative analysis with a baseline non-fuzzy model demonstrates the added value of the fuzzy-integrated framework, showing improved capacity to handle imprecision and uncertainty. The model outputs not only prioritise risk rankings but also support the identification of critical control actions and effective safety measures. A case study of Nigerian waters illustrates the practicality of the framework in guiding risk mitigation strategies and informing policy decisions under uncertainty.

1. Introduction

Marine transportation plays an important role in the movement of goods and people, particularly for riverine and coastal nations. It represents one of humanity’s oldest and most efficient modes of transporting goods and passengers across the world. However, with the growing density of maritime traffic and increasingly complex navigational environments, the risks of boat collisions have become a pressing concern. Such incidents pose serious threats to human life and property while also causing significant environmental harm, particularly in ecologically sensitive waters. The consequences of these accidents include vessel sinking, extensive vessel damage, pollution (e.g., chemical and oil spills), long-term ecological degradation, and the tragic loss of crew and passengers’ lives. They also generate considerable economic repercussions, such as supply chain disruptions, exorbitant repair costs, significant legal fees, costly clean-up operations, and severe disruptions to port operations and shipping lanes. Furthermore, companies involved in such accidents often experience profound and enduring reputational damage, undermining business continuity and eroding stakeholder trust. The pervasive nature of these risks underscores a fundamental challenge: maritime risk is not a static phenomenon but rather a highly dynamic interplay of numerous factors, many of which exhibit non-linear relationships or are characterised by inherent uncertainty. Consequently, simplistic linear risk models are invariably inadequate for comprehensive assessment. A truly robust risk assessment framework must therefore demonstrate the capacity to adapt to evolving operational conditions and accurately capture the intricate, and often non-obvious, interdependencies among diverse risk elements.

Traditional risk assessment methodologies, notably Failure Mode and Effects Analysis (FMEA) and Fault Tree Analysis (FTA), have long served as foundational tools for identifying and evaluating hazards, and are widely adopted across various industries for reliability, safety, and quality control in engineering design. FMEA, for instance, is valued for its proactive approach in anticipating potential issues and addressing them prior to occurrence by systematically identifying failure modes, their consequences, and their causes [1]. Conversely, FTA is employed for fault finding, comprehensive risk analysis, and root cause identification, particularly in complex systems with multiple interacting elements [2]. Other common applied risk assessment techniques in the maritime industry include Hazard Identification (HAZID) and Hazard Operability Study (HAZOP). HAZID identifies hazards and associated events that could result in significant impacts. HAZOP, by contrast, is a systematic and structured examination of a planned system or procedure, focusing on design variance and assessing their potential causes and consequences [3].

Despite their usefulness, these conventional methods often prove inadequate in the intricate and dynamic maritime environment, as they are inherently limited in their ability to manage the pervasive uncertainty, subjectivity, and complex interdependencies that characterise maritime risk factors. Moreover, they typically rely on crisp values and linear relationships, which can oversimplify real-world scenarios where expert judgement and incomplete data play a critical role [4,5]. FMEA, while comprehensive, is time-consuming, has a limited capacity for identifying unforeseen threats, and may be overly dependent on subjective expert assessments, thereby introducing bias. Its effectiveness is further compromised if analysts lack sufficient expertise or if the procedure is conducted hastily. Conversely, FTA is marked by rigidity, operating on a binary (yes/no) framework that renders it poorly suited for determining probabilities or considering an asset’s entire lifecycle [4]. This highlights a critical gap: traditional quantitative methods frequently struggle to accommodate the impression, subjective, and data-sparse realities of complex operational environments. The fundamental limitation lies in their inability to systematically process linguistic or vague expert inputs, which are essential for understanding and anticipating risks [5]. This methodological shortcoming underscores the need for the development and adoption of a framework capable of effectively bridging qualitative expert judgement with rigorous quantitative analysis.

To address these limitations, this study proposes a robust risk assessment framework grounded in a fuzzy Multi-Criteria Decision-Making (MCDM) technique. This innovative framework integrates fuzzy logic with the Analytic Hierarchy Process (AHP) for rigorous criteria weighting and the Technique for Order Preference by Similarity to the Ideal Solution (TOPSIS) for comprehensive risk ranking. Fuzzy logic is specifically employed to capture nuanced linguistic expert judgments and to manage imprecise, uncertain, or vague input data—challenges that are particularly prevalent in real-world marine operations. The framework systematically identifies key collision risk factors through an extensive process involving a thorough literature review, past incident data analysis, and expert consultation. The critical factors considered include human error, boat engine system failure, prevailing environmental conditions, and intentional threats.

A comparative analysis with a non-fuzzy model is undertaken to quantitatively evaluate the proposed approach’s added value and enhanced performance. The model’s outputs extend beyond risk ranking and prioritisation; they also provide decision support for identifying critical control actions and formulating effective safety measures.

2. Literature Review

Multi-Criteria Decision-Making (MCDM) is a decision-making tool fundamentally designed to explicitly articulate the decision-maker’s preferences within complex environments characterised by multiple, often conflicting, criteria. MCDM methodologies systematically evaluate a set of alternatives against these diverse criteria, incorporating scores that reflect each alternative’s expected performance and weights that represent each criterion’s relative importance, typically derived through pairwise comparisons. Traditional MCDM techniques include the Analytical Hierarchy Process (AHP), Stepwise Weight Assessment Ratio Analysis (SWARA), the Technique for Order Preference by Similarity to the Ideal Solution (TOPSIS), Weighted Aggregate Sum Product Assessment (WASPAS), amongst others. However, some of these classical techniques are limited in their ability to adequately address the uncertainty inherent in decision-making. To overcome this limitation, modifications through hybridisation with complementary techniques are often required, for example, the SWARA-WASPAS method [6]. As decision-making frequently involves subjective judgement, fuzzy logic has been integrated with traditional MCDM methods by employing fuzzy numbers to represent imprecise or uncertain assessments. This has led to the development of fuzzy logic-based MCDM techniques, such as fuzzy SWARA (FSWARA), fuzzy TOPSIS (FTOPSIS), and hybrid approaches including the FSWARA-FTOPSIS technique.

Fuzzy MCDM is specifically tailored to model vagueness and effectively address real-world systems that inherently involve imprecise and incomplete information. It enables decision-makers to provide meaningful evaluations of alternatives with respect to various criteria, even in situations where establishing traditional, precise numerical ratings is challenging or impossible. Zadeh [7] conceptualised fuzzy logic as a significant extension of traditional binary logic, designed to facilitate reasoning under uncertainty. Unlike traditional binary logic, where variables take rigid values of either 0 or 1, fuzzy logic allows variables to assume degrees of truth that range continuously between 0 and 1. This fundamental characteristic provides a robust framework for handling inherently imprecise information. Fuzzy logic operates on fuzzy sets. A fuzzy set is characterised by a membership function which map each element in a set to a membership degree between 0 and 1. This approach enables experts to employ linguistic variables (e.g., “medium,” “very high”) when evaluating critical risk factors. The relationship between fuzzy linguistic terms and fuzzy numbers is grounded on the fuzzy set theory [7] and practices of modelling uncertainty and vagueness. Linguistic terms are commonly represented mathematically by triangular fuzzy numbers (TFNs) or trapezoidal fuzzy numbers (TrFNs) due to their intuitive interpretations [8]. A TFN is defined by three parameters (a, b, c) representing the minimum value, modal value, and maximum value, respectively. Conversely, a TrFN is represented by four parameters (a, b, c, and d), forming a trapezoidal shape. For example, the linguistic term “moderate” might be presented in TRN as B = (2, 3, 4), where 2 denotes the minimum value, 3 the modal value, and 4 the maximum value of “moderate”. In practice, the appropriate selection of fuzzy numbers for linguistic terms depends on expert input and established methodologies [9,10]. In summary, the principal strength of fuzzy MCDM lies in its transformative capacity to convert qualitative, subjective, linguistically expressed expert knowledge into a quantifiable, actionable, and robust analytical decision-making framework.

Marine accidents arise from diverse causes, and numerous studies have examined these accidents from different perspectives in order to identify, develop and implement effective risk control strategies. Four primary causative factors—human, environment, management and vessel-related have been attributed to accidents, with the relative importance of each factor varying according to situational contexts [11]. Among these, human error has consistently been identified as the predominant cause of most marine accidents [12,13]. The United Kingdom Marine Accident Investigation Branch (MAIB) has similarly reported human error as the principal cause of majority of waterborne accidents [14]. Other contributory factors include management deficiencies [15,16], with Bhardwaj [12] highlighting management problems as frequently underlying the root causes of accidents; ship-related issues [17,18,19] with the International Maritime Organization (IMO) reporting that approximately one-quarter of maritime accidents stem from mechanical failures, which also contribute significantly to collision incidents [20]; and environmental factors [21,22,23] with Bye [24] emphasising that poor visibility markedly increases the likelihood of accidents.

To address these challenges, scholars have developed a variety of tools for root cause analysis and risk assessment of marine accidents, employing methodologies such as fuzzy logic and Multi-Criteria Decision-Making (MCDM). Using a fuzzy SWOT-AHP approach, Kececi et al. [25] developed the Ship Accident Root Cause Evaluation (SHARE) technique to assist in investigating causal factors and implementing corrective actions. This framework facilitated the standardisation of accident investigation reports, enabling root causes to be examined quantitatively through the integration of a decision-support system. Similarly, Sur and Kim [26] formulated a multi-criteria decision-making problem incorporating frequency, fatalities, and injuries, and ranked high-risk accident types using the Ordinal Priority Approach (OPA) for weighting and Grey Relational Analysis (GRA) for ranking. Their study addressed the lack of effective risk management strategies in maritime contexts and concluded that collisions and safety-related accidents represent the most hazardous categories. Hu et al. [27] proposed a quantitative, real-time multi-ship collision risk analysis and collision-avoidance decision-making model based on five key influencing factors of collision risk. Fuzzy logic was employed to calculate collision risks, and avoidance decisions were derived by altering vessel course or speed. Their results indicated that the proposed model offers an effective solution to ship collision-avoidance decision problems.

While MCDM methods have previously been applied to accident analysis, this paper distinguishes itself by presenting a fuzzy-integrated framework for risk assessment of boat collisions, specifically within the Nigerian coastal context, and provides a direct comparative analysis to demonstrate the added value of fuzzy logic in managing the inherent uncertainties of such complex scenarios. The strength of the proposed framework lies not only in the comparative results but also in its capacity to accommodate vagueness and uncertainty in maritime accident analysis. Unlike traditional crisp models, fuzzy logic enables the mathematical representation of linguistic expert judgements, thereby enhancing the reliability of risk assessments in contexts such as Nigeria, where data are often imprecise or sparse. The direct comparative analysis highlights the practical benefits of this structural advantage. By comparing the outputs of the fuzzy model with those of a non-fuzzy model, the study demonstrates that the fuzzy approach yields a more realistic and nuanced assessment. For instance, whereas a crisp model might classify a scenario simply as “medium risk,” a fuzzy model can generate a risk score that indicates the degree to which the scenario belongs to the” medium risk” category. This refined output provides a more informative and actionable basis for risk assessment.

3. Methodology

This paper proposes a hybrid fuzzy AHP-TOPSIS technique to assess the risk of boat collisions by incorporating uncertainty and expert judgement within a multi-criteria decision-making environment. The methodology comprises three major stages: (1) identification of risk criteria, (2) application of fuzzy AHP to determine criteria weights, and (3) application of fuzzy TOPSIS to rank collision risk scenarios. A comparative analysis is also conducted using a baseline model without fuzzy logic in order to evaluate the added value of the fuzzy-integrated approach.

3.1. Identification of Risk Criteria

Through a review of the literature, analysis of past incident data, and consultation with experts, a comprehensive set of criteria contributing to collision risk was identified and categorised into four main groups: human error, boat engine system failure, environmental conditions, and intentional threats. Each of these criteria is subsequently evaluated using expert judgement in the FAHP phase. Understanding these contributing elements is essential for conducting a comprehensive risk assessment.

(a)

Human Error: Human error is widely recognised as the predominant contributory factor in boat collisions, with several studies attributing over 70% of incidents to human-related causes. Examples include negligence, overloading, speeding on the waterways and disregarding safety limits, reckless behaviour, failure to maintain a proper lookout, and operating under the influence of alcohol or drugs. Additional causes include distractions such as mobile phone use, navigational errors (e.g., misjudgements in crowded waterways or misinterpretation of navigational aids), inadequate training, operator inexperience, crew fatigue, critical communication failures (both between boats and with port authorities), and disregard for boating regulations.

(b)

Boat Engine System Failure: Failures in engine system failures are a big significant cause of maritime accidents, including collision, grounding, capsizing, fires, and explosions. Examples of such failures include main engine malfunctions, electrical failure, and dangerous gas leaks, especially within the highly critical engine room area. Poor or inadequate maintenance practices are consistently cited as major contributors to engine system failure.

(c)

Environmental Conditions: Adverse environmental conditions substantially increase the collision risk, reducing visibility and impairing manoeuvrability. Contributing factors include dense fog, severe storms, high winds, night-time travel, turbulent seas, wreck collisions, and the presence of surface or underwater obstacles such as tree stumps.

(d)

Intentional Threats: Intentional threats arise from deliberate acts, such as ramming another vessel or intentionally creating hazardous situations. These may involve aggressive behaviour by boaters (“boat rage”), piracy, kidnapping attempts, and acts of terrorism.

3.2. Fuzzy AHP (Criteria Weighting)

FAHP is employed to determine the relative weights of the identified criteria. It extends the traditional AHP, a structured decision-making methodology originally introduced by Thomas Saaty [27], which has been widely applied in MCDM for solving complex decision-making problems through pairwise comparison. AHP structures the decision problem into a hierarchical model comprising three levels: the goal, the criteria, and the alternatives. The goal represents the overall objective, the criteria are the factors used to evaluate the alternatives, and the alternatives are the potential solutions. The next step involves developing pairwise comparisons, whereby decision-makers assess the importance of one criterion relative to another at each level of the hierarchy using a numerical scale. In this study, Saaty’s 1–5 scale [28], as presented in

Table 1. The 5-point triangular fuzzy scale.

Crisp Number	Linguistic Term	TFN
1	Equally important	(1, 1, 1)
2	Slightly more important	(1, 2, 3)
3	Moderately more important	(2, 3, 4)
4	Strongly more important	(3, 4, 5)
5	Very strongly more important	(4, 5, 5)

, is applied.

The n × n pairwise comparison matrix, X^k, is formed from the n criteria relative importance pairwise comparison, resulting from expert judgments. The resulting matrix is shown below [29]:

$${\mathrm{X}}^k={[x_{i\dot{J}}^{\kappa }]}_{n\times n}=\left[\begin{array}{cccc}{x}_{11}^{\kappa }& x_{12}^{\kappa }& \dots & x_{1n}^{\kappa }\\ x_{21}^{\kappa }& x_{22}^{\kappa }& \dots & x_{2n}^{\kappa }\\ ⋮& ⋮& \ddots & ⋮\\ x_{n1}^{\kappa }& x_{n2}^{\kappa }& \dots & x_{nn}^{\kappa }\end{array}\right]$$

(1)

After developing the pairwise comparison matrix, weights are assigned to the criteria C₁, C₂, …, C_n. Each criterion weight is evaluated as follows:

$$w_i^k={\displaystyle \frac{1}{n}}{{\displaystyle \sum }}_j{\displaystyle \frac{x_{ij}^k}{{\Sigma }_i{x}_{ij}^k}}$$

(2)

where $w_i^k$ is the criterion C_i weight.

The FAHP incorporates fuzzy logic to deal with the inherent uncertainty and imprecision present in pairwise comparisons. Traditional AHP relies on precise numerical values for pairwise comparisons, but human judgement is often imprecise or subjective in real world situations. FAHP uses fuzzy numbers to represent these uncertainties. The resulting criteria weights derived from FAHP are more robust because they explicitly reflect the intrinsic uncertainty present in subjective evaluations, ultimately rendering the overall risk assessment more reliable and trustworthy. The following steps are followed in applying FAHP:

3.2.1. Risk Criteria

The four main groups of collision risk criteria identified in Section 3.1 are used for the analysis. These include human error, boat engine system failure, environmental conditions, and intentional threats.

3.2.2. Fuzzy Pairwise Comparison Matrix

The subject matter experts (SMEs) used linguistics terms (e.g., “equally Importance”) to express each criterion relative importance, which were then converted into TFNs as presented in Table 1. The fuzzy comparison values from all experts were aggregated to construct the fuzzy pairwise decision matrix.

3.2.3. Matrix Normalisation and Fuzzy Weights

The decision matrix is normalised and fuzzy weights are derived.

3.2.4. Defuzzification

The fuzzy weights from Section 3.2.3 are converted to crisp numbers using the averaging technique for easier interpretation and ranking.

3.3. Fuzzy TOPSIS (Alternative Ranking)

Fuzzy TOPSIS allows for the representation of vague and ambiguous information in decision-making problems, and is used in evaluating and ranking of alternatives on how close or distant the alternatives are to an imaginary ideal solution. The best ranked alternative is closer to an ideal positive solution and farther from an ideal negative solution. The following steps are followed in applying FTOPSIS:

3.3.1. Linguistic Expressions by SMEs

SMEs rated how much each criterion contributes to the risk level of each alternative, which in this case are collision scenarios using linguistics terms such as “very low contribution”, “high contribution”, etc. The linguistic terms are converted to crisp values presented in

Table 2. Alternative Rating Scale.

Crisp Number	Linguistic Term	TFN
1	Very Low Contribution	(0, 0, 0.2)
2	Low Contribution	(0.1, 0.3, 0.5)
3	Medium Contribution	(0.3, 0.5, 0.7)
4	High Contribution	(0.5, 0.7, 0.9)
5	Very High Contribution	(0.8, 1.0, 1.0)

.

3.3.2. Construction of the Decision Matrix

Using the averaging method, the decision matrix is constructed by converting the fuzzy values of the matrix to crisp numbers.

3.3.3. Decision Matrix Normalisation

Then, the decision matrix is normalised by applying the vector normalisation technique for the $r_{ji}$ element as follows:

$$r_{ji}={\displaystyle \frac{x_{ji}}{\sqrt{{\sum }_{j=1}^N{x}_{ji}^2}}}$$

(3)

where j = 1, 2…, N; i = 1, 2…, k and $x_{ji}$ = alternative j value with respect to attribute i.

3.3.4. Weighted Normalised Decision Matrix

The weighted normalised fuzzy decision matrix, $u_{ji}$, is then calculated by multiplying the normalised fuzzy numbers obtained in Section 3.3.3 with the weight values of the criteria calculated from Section 3.2.4.

$$u_{ji}=w_i{r}_{ji}$$

(4)

3.3.5. Determination of Positive-Ideal (A⁺) and Negative-Ideal (A⁻) Solutions

The fuzzy $A^{+}$ and $A^{-}$ values are used to evaluate alternatives against criteria with $A^{+}$ representing the imaginary optimal value and $A^{-}$ representing the least desired value, for each criterion. They are defined as follows:

$$A^{+}=\left\{v_1^{+},v_2^{+},\dots ,v_i^{+},\dots ,v_k^{+}\right\}$$

(5)

$$A^{-}=\left\{v_1^{-},v_2^{-},\dots ,v_i^{-},\dots ,v_k^{-}\right\}$$

(6)

where $v_j^{+}$ and $v_j^{-}$ represent $A^{+}$ and $A^{-}$ values for each criterion j, respectively. They are calculated based on whether the criterion is benefit- or cost-oriented.

The positive-ideal solution for a benefit criterion (jϵI) represents the criteria where higher values are preferred (e.g., efficiency). The numerical value is the maximum across all alternatives ($\underset{i}{max}$ v_ij)

$$v_j^{+}=(\underset{i}{max} v_{ij} |jϵI)$$

(7)

where I is set of benefit criteria

The positive-ideal solution for a cost criterion (jϵI′) represents the criteria where lower values are preferred (e.g., cost). The numerical value is the minimum across all alternatives ($\underset{i}{min}$ v_ij).

$$v_1^{+}=(\underset{i}{min} v_{ij} |jϵI^{\prime })$$

(8)

where I′ is set of cost criteria

The negative-ideal solution for a benefit criterion (jϵI) represents the criteria where higher values are preferred. The numerical value is the minimum across all alternatives ($\underset{i}{min}$ v_ij)

$$v_j^{-}=(\underset{i}{min} v_{ij} |jϵI)$$

(9)

The negative-ideal solution for cost criterion (jϵI′) represents the criteria where lower values are preferred. The numerical value is the maximum across all alternatives ($\underset{i}{max}$ v_ij)

$$v_1^{+}=(\underset{i}{max} v_{ij} |jϵI^{\prime })$$

(10)

3.3.6. Calculating the Distance

The distance of the alternative from $A^{+}$ and $A^{-}$ determines the final ranking of each alternative. The distances from the positive and negative ideal solutions, $S_i^{+}$ and $S_i^{-}$, respectively, are obtained from the equation

$$S_i^{+}=\sqrt{{{\displaystyle \sum }}_{i=1}^K{\left(v_{ji}-v_i^{+}\right)}^2}$$

(11)

where $v_{ji}$ is the i-th alternative for the j-th criterion value

$$S_i^{-}=\sqrt{{{\displaystyle \sum }}_{i=1}^K{\left(v_{ji}-v_i^{-}\right)}^2}$$

(12)

where j = 1, 2…, n.

3.3.7. Closeness Coefficient (CC) and Alternatives Ranking

The distance of each alternative A_j from $A^{+}$ is estimated as follows:

$$\mathrm{CC}={\displaystyle \frac{s_j^{-}}{s_j^{+}+s_j^{-}}}$$

(13)

3.4. Case Study

Nigeria possesses a vast water transportation network that facilitates relatively easy and cost-effective movement between urban and rural areas. With an extensive system, Nigeria has the second-longest waterways in Africa [30,31]. A wide range of vessels, including cargo boats, passenger ferries, fishing boats and trawlers, operate across these waterways. According to the National Inland Waterways Authority (NIWA), over 60% of Nigeria’s 36 states utilise water as a means of transportation [32]. The inadequacy of road infrastructure has compelled farmers, traders, and other Nigerians to adopt boats as a viable alternative, particularly during the rainy season. Many also prefer water travel as a means of reducing exposure to armed banditry and abductions along rural and urban highways. Despite these advantages, frequent accidents on Nigeria’s waterways have resulted in considerable loss of life and property. Boats have historically been regarded as a safe mode of transport; however, accidents have become increasingly prevalent due to growing reliance on water transportation [33]. These incidents have led to fatalities, injuries, and economic disruptions. The Marine Crafts Builders Association of Nigeria (MCBAN) reports that more than 3000 boat accidents occurred between 2015 and 2025, with a marked rise in recent years [34]. These figures likely understate the true scale of the problem, as many accidents remain unreported or underreported.

According to the International Centre for Investigating Reporting (ICIR), Nigeria recorded 1204 deaths from boat accidents between January 2018 and October 2023, averaging approximately 17 fatalities per month. These incidents occurred across 25 states and the Federal Capital Territory, with Niger State having the highest number of deaths. Overloading, poorly maintained boats, and a lack of safety equipment were identified as the primary causes [35]. In 2024 alone, 326 fatalities were recorded from boat accidents—an 8.67% increase from 2023. Causes included collisions with surface and underwater objects (such as high-tension poles and submerged snags), inter-boat collisions, strong waves, overloading, engine-explosions, and fires [36]. In one recent incident, on 25 July 2025, an overloaded boat capsized in Niger state while enroute to a market, resulting in at least 25 confirmed deaths and dozens missing [37].

The economic implications of these accidents are also significant. The World Bank estimates that Nigeria’s inland waterways transport sector could contribute up to 10% of the country’s GDP if fully optimised [38]. However, the frequency of accidents undermines investor confidence and constrains growth potential in the sector.

A study by Akpudo [39] found that human-related factors constitute the leading causes of boat accidents and collisions in Nigeria, followed by natural factors. Human-related factors include poor operator experience, overloading, reckless navigation, night travel, and inadequate boat maintenance. Natural factors comprise turbulent weather, submerged debris, and seasonal water hyacinth. Additional causes include operational inefficiencies, insufficient safety measures, and weak regulatory oversight. The study further revealed that cargo and passenger boats account for majority of accidents.

These factors highlight the urgent need for comprehensive measures to restore public confidence in waterway transport and enhance safety. Addressing the root causes of accidents is essential for improving the sector’s performance. Effective risk assessment and analysis can assist in identifying high-risk factors, thereby enabling targeted interventions. The framework proposed in this paper provides a structured approach to guide maritime authorities in prioritising risk mitigation strategies, while also informing policy interventions and safety measures.

4. Results

4.1. Baseline Model (AHP + TOPSIS)

4.1.1. Criteria Weighting (AHP)

Criteria Pairwise Comparison

As mentioned in Section 3.1, four criteria will be considered in this study. These include human error, boat engine system failure, environmental conditions, and intentional threats. Six SMEs working in the maritime accident investigation unit of a Nigerian government marine regulatory agency quantified the relative importance of each criterion using linguistic terms such as “equally important”, and “strongly more important”. The terms are converted to crisp values in Table 1. The results are presented in

Table 3. Criteria Pairwise Comparison (AHP).

	Human Error	Boat Engine System Failure	Environmental Conditions	Intentional Threats
SME 1
Human Error	1	4	3	5
Boat Engine System Failure	1/4	1	1/2	2
Environmental Conditions	1/3	2	1	2
Intentional Threats	1/5	1/2	1/2	1
SME 2
Human Error	1	3	4	4
Boat Engine Failure	1/3	1	1/2	3
Environmental Conditions	1/4	2	1	2
Intentional Threats	1/4	1/3	1/2	1
SME 3
Human Error	1	4	2	5
Boat Engine Failure	1/4	1	1/2	2
Environmental Conditions	1/2	2	1	3
Intentional Threats	1/5	1/2	1/3	1
SME 4
Human Error	1	4	2	5
Boat Engine Failure	1/4	1	1/2	3
Environmental Conditions	1/2	2	1	2
Intentional Threats	1/5	1/3	1/2	1
SME 5
Human Error	1	4	3	5
Boat Engine Failure	1/4	1	1/2	2
Environmental Conditions	1/3	2	1	2
Intentional Threats	1/5	1/2	1/2	1
SME 6
Human Error	1	4	4	5
Boat Engine Failure	1/4	1	1/2	2
Environmental Conditions	1/4	2	1	2
Intentional Threats	1/5	1/2	1/2	1

.

Construction of the Decision Matrix

The comparison values from all SMEs in Table 3 are aggregated using the average method to form the decision matrix, as presented in

Table 4. Criteria Decision Matix (AHP).

	Human Error	Boat Engine System Failure	Environmental Conditions	Intentional Threats
Human Error	1	3.83	3	4.83
Boat Engine System Failure	0.26	1	0.5	2.33
Environmental Conditions	0.36	2	1	2.17
Intentional Threats	0.21	0.44	0.47	1

.

Matrix Normalisation and Weighting of Criteria

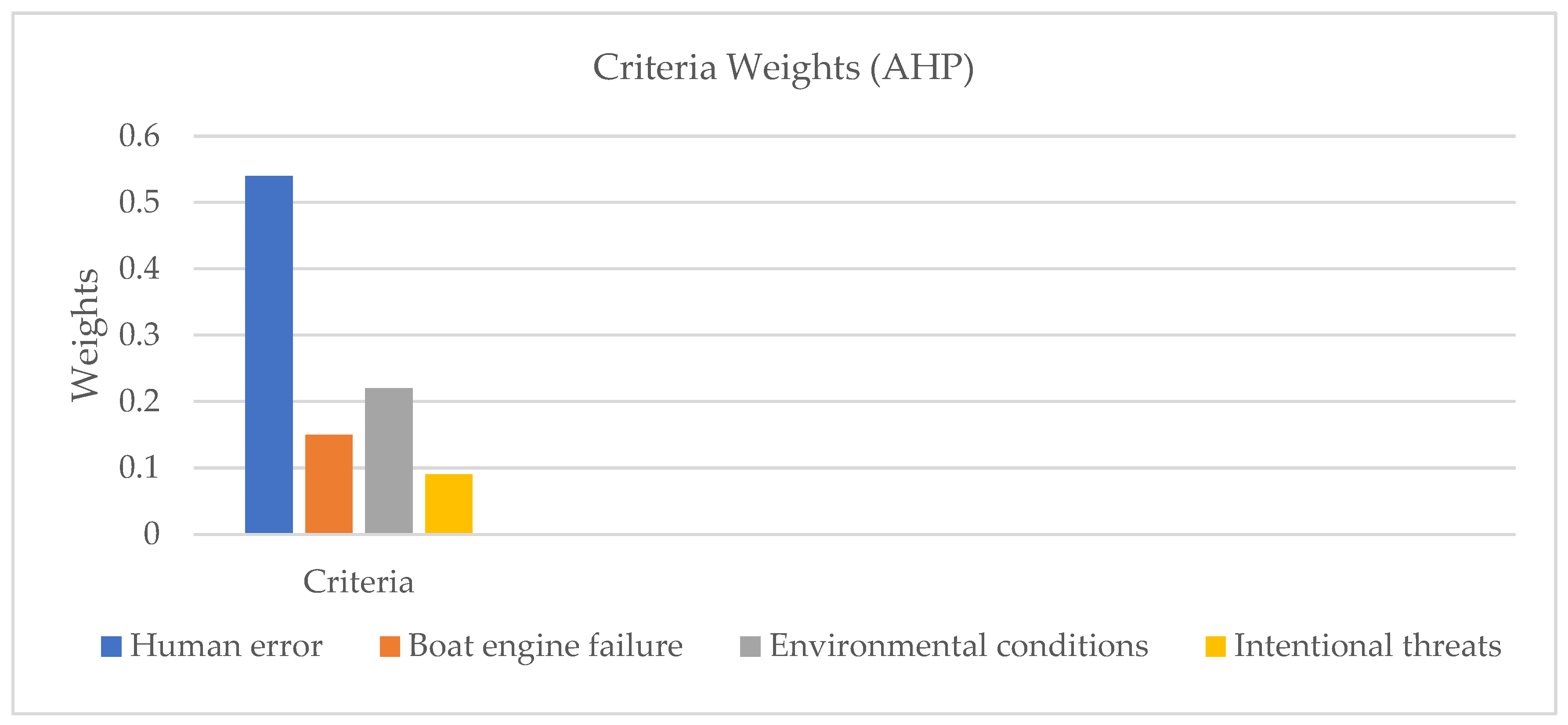
The pairwise comparison matrix is then normalised. Using Equation (2), the weight of each criterion is calculated and the results are presented in

Table 5. Normalised Pairwise Comparison and AHP Criteria Weights.

	Human Error (C1)	Boat Engine System Failure (C2)	Environmental Conditions (C3)	Intentional Threats (C4)	Criteria Weight
Human Error (C1)	0.55	0.53	0.60	0.47	0.54
Boat Engine Failure (C2)	0.14	0.14	0.10	0.22	0.15
Environmental Conditions (C3)	0.20	0.27	0.20	0.21	0.22
Intentional Threats (C4)	0.11	0.06	0.10	0.10	0.09

and graphically in Figure 1.

Consistency Check (CR)

The reliability of the pairwise comparison is determined by the consistency of the decision-maker’s judgements which is evaluated using the consistency ratio, CR. A consistency ratio of less than 0.1 is acceptable. However, if CR is greater than 0.1, the decision-maker is advised to revise their initial assessment [28].

CR = CI/RI

(14)

where CI represents the Consistency Index; RI is the Random Index.

$$\mathrm{CI}={\lambda }_m-n/n-1$$

(15)

where ${\lambda }_m$ is the maximum eigenvalue of the pairwise comparison matrix, and RI is the corresponding n × n matrix average random CI value. The RI values are presented in

Table 6. Matrix orders RI values.

n	1	2	3	4	5	6	7
RI	0	0	0.52	0.90	1.11	1.25	1.35

.

From (15), CI = ${\lambda }_m$ − n/n − 1 = 4.0860 − 4/4 − 1 = 0.0287

Where ${\lambda }_m$ (from pairwise comparison matrix) − calculated by MATLAB Online (basic) software (version R2024a) = 4.0860, n = 4 (matrix order)

From (14), Consistency Ratio, CR = 0.0287/0.90 = 0.0319

Where RI is obtained from Table 6 (n = 4).

Since CR is less than 0.10, the matrix can be considered reasonably consistent. Thus, these criteria weights can be used for ranking.

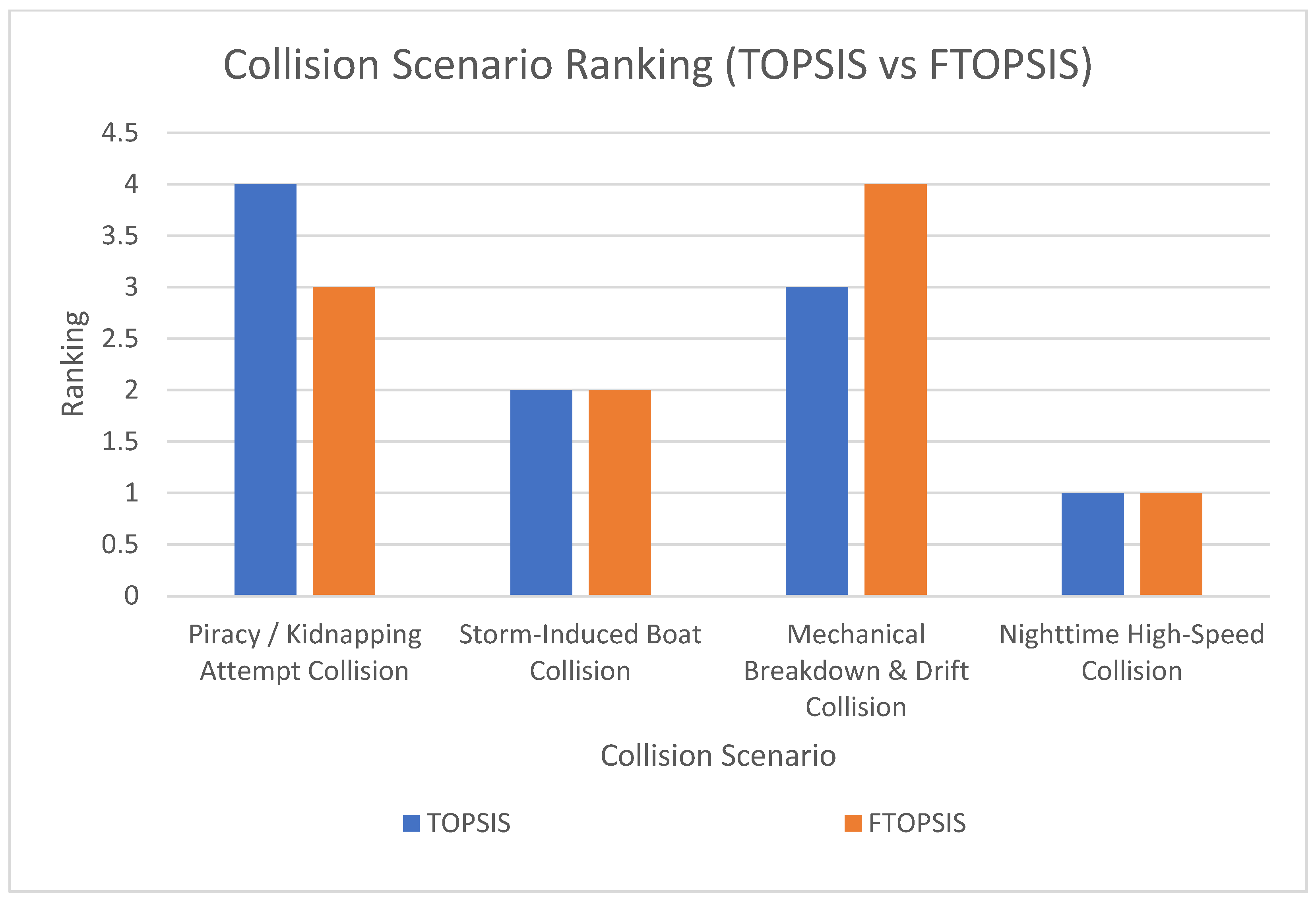
4.1.2. TOPSIS (Collision Scenario Risk Ranking)

The TOPSIS technique is used for alternative ranking. Different boat collision scenarios in Nigeria’s coastal areas, known for high traffic and past incidents, are used as alternatives. The risk level of each scenario is assessed. The scenarios are as follows:

• Scenario 1 (A1): Piracy/Kidnapping Attempt Collision—this is an intentional collision orchestrated by criminal elements as part of a piracy or kidnapping attempt.
• Scenario 2 (A2): Storm-Induced Boat Collision—this involves collision between two or more boats during severe stormy weather, leading to reduced visibility, rough seas, and loss of control.
• Scenario 3 (A3): Mechanical Breakdown and Drift Collision—this involves a collision where a boat experiences engine failure and drifts into another vessel or fixed obstacle, like a wreck. This is often caused by improper engine boat maintenance, and the presence of wrecks and underwater debris.
• Scenario 4 (A4): Nighttime High-Speed Collision—this involves a collision of two or more boats at night, often due to limited visibility and over speeding. This is exacerbated by inexperienced operators or alcohol consumption.

The six SMEs rated how much each criterion contributed to the risk level of each specific collision scenario using linguistics terms like “very low contribution”, and “high contribution”. The terms are changed to crisp values in Table 2. The crisp values are aggregated using the average method to form the decision matrix, as presented in

Table 7. Alternatives Decision Matrix (TOPSIS).

Collison Scenarios	C1 (Human Error)	C2 (Boat Engine System Failure	C3 (Environmental Conditions)	C4 (Intentional Threats)
A1 (Piracy/Kidnapping Attempt Collision)	5	2	4	1
A2 (Storm-Induced Boat Collison)	3	5	3	1
A3 (Mechanical Breakdown & Drift Collison)	4	3	5	1
A4 (Nighttime High-Speed Collision)	3	1	2	5

.

As presented in Table 7, the SMEs aggregated ratings provide important insights into the relative contributions of each criterion across the collision scenarios. They consider human error (C1) to be a major contributing factor in piracy/kidnapping attempt collision scenarios (A1). While intentional threats (C4) define the nature of piracy/kidnapping attempt collision scenario, the SMEs stress that the collision risk is often heightened by human responses to such threats. Thus, over-speeding to evade the threat, panic, and loss of concentration can increase the likelihood of collision. Intentional acts act as triggers, but the boat operator reactions determine the collision outcome. The SMEs also highlighted that boat engine failure (C2) is a significant contributor in storm-induced collision scenarios (A2), even though the scenario’s defining characteristics are formed by environmental conditions (C3). The reasoning adduced is that while storms introduce poor navigational conditions, the boat’s mechanical resilience determines the effectiveness of operator’s response. During a storm, a loss of propulsion increases the likelihood of collisions. Therefore, the SMEs’ assessments show the interdependence between environmental challenges and engine reliability. Failures in boat engines increases the impact of poor weather conditions. Furthermore, the SMEs assigned environmental conditions (C3) as the dominant contributor in mechanical breakdown and drift collision (A3). Drifting vessels are vulnerable to collisions in strong current or poor visibility, and the operators may not have sufficient space and time to take evasive action. Finally, the SMEs considered intentional threats (C4) as a major contributor to night-time high-speed collision (A4), in addition to human error. The high score for intentional threats is a reflection of the increased risks associated with hostile behaviours in night-time travel, especially when compounded by high speed and poor visibility. In summary, the interactive nature of risk factors is emphasised by the SMEs’ aggregated judgements, while each scenario has a defining criterion, for example, environmental conditions in storm-induced collision. The likelihood of collision often depends on the interplay between various factors, rather than a single dominant factor.

The matrix is normalised, and the results are presented in

Table 8. Normalised Decision Matrix (TOPSIS).

Collison Scenarios	C1 (Human Error)	C2 (Boat Engine System Failure	C3 (Environmental Conditions)	C4 (Intentional Threats)
A1 (Piracy/Kidnapping Attempt Collision)	0.33	0.18	0.29	0.13
A2 (Storm-Induced Boat Collison)	0.20	0.45	0.21	0.13
A3 (Mechanical Breakdown & Drift Collison)	0.27	0.27	0.36	0.13
A4 (Nighttime High-Speed Collision)	0.20	0.10	0.14	0.61

.

Weighted Normalised Matrix

Using Equation (4) and criteria weights from Table 5, the weighted normalised matrix is obtained and presented in

Table 9. Weighted Alternatives Decision Matrix (TOPSIS).

Collison Scenarios	C1 (Human Error)	C2 (Boat Engine System Failure	C3 (Environmental Conditions)	C4 (Intentional Threats)
A1 (Piracy/Kidnapping Attempt Collision)	0.178	0.027	0.064	0.012
A2 (Storm-Induced Boat Collison)	0.108	0.068	0.046	0.012
A3 (Mechanical Breakdown & Drift Collison)	0.146	0.041	0.079	0.012
A4 (Nighttime High-Speed Collision)	0.108	0.015	0.031	0.055

.

Positive Ideal Solution (A⁺) and Negative Ideal Solution (A⁻) Determination

Using Equations (5) and (6), the imaginary $A^{+}$ and $A^{-}$ reference points are determined, results are presented in

Table 10. Positive-Ideal and Negative-Ideal Values.

	Category	A+	A−
C1	Cost	0.108	0.178
C2	Cost	0.015	0.068
C3	Cost	0.031	0.079
C4	Cost	0.012	0.055

.

Distance Calculation

Using Equations (11) and (12), the distances of each collision scenario alternative from $A^{+}$ and $A^{-}$ with respect to each criterion are calculated and results presented in

Table 11. TOPSIS Analysis Summary.

	A+	A−	CC	Ranking
A1 (Piracy/Kidnapping Attempt Collision)	0.0784	0.0611	0.4380	4
A2 (Storm-Induced Boat Collison)	0.0550	0.0883	0.6162	2
A3 (Mechanical Breakdown & Drift Collison)	0.0662	0.0594	0.4729	3
A4 (Nighttime High-Speed Collision)	0.0430	0.1000	0.6993	1

.

Closeness Coefficient (CC) and Alternatives Ranking

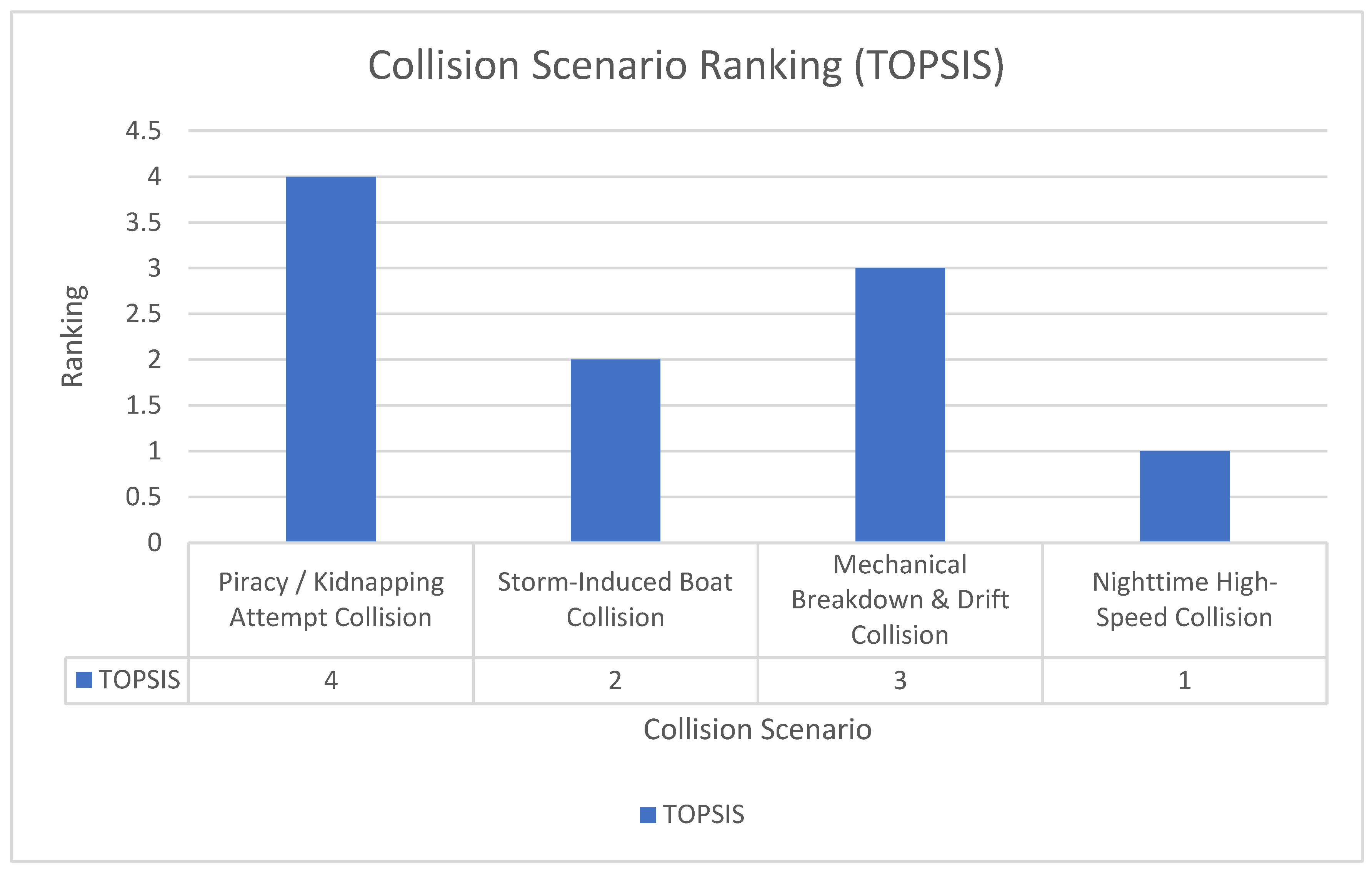
From the results obtained in Section “Distance Calculation”, the closeness coefficient (CC) of each alternative can be calculated using Equation (13), and the alternatives subsequently ranked. The closeness coefficients represent the overall risk level for each scenario. The results are presented in Table 11 and the ranking is shown graphically in Figure 2.

The closer an alternative is to PIS and further from the NIS, the higher its closeness coefficient.

4.2. Fuzzy-Integrated Model (Fuzzy AHP + Fuzzy TOPSIS)

4.2.1. Fuzzy AHP (Criteria Weighting)

Decision Matrix

The linguistic terms used by SMEs in the criteria pairwise comparison are changed to triangular fuzzy numbers (TFNs) as presented in Table 1, reflecting uncertainty in judgements. The fuzzy comparison values from all SMEs are aggregated using the average method to form the decision matrix, as presented in

Table 12. Fuzzy Decision Matrix.

	Human Error	Boat Engine System Failure	Environmental Conditions	Intentional Threats
Human Error	1, 1, 1	2.83, 3.83, 4.83	2, 3, 4	3.83, 4.83, 5
Boat Engine System Failure	0.21, 0.26, 0.36	1, 1, 1	0.33, 0.5, 1	1.33, 2.33, 3.33
Environmental Conditions	0.26, 0.36, 0.61	1, 2, 3	1, 1, 1	1.17, 2.17, 3.17
Intentional Threats	0.20, 0.21, 0.26	0.30, 0.44, 0.83	0.32, 0.47, 0.92	1, 1, 1

.

Fuzzy Decision Matrix (Crisp Values)

The fuzzy numbers in Table 12 are transformed into crisp values, and the results are presented in

Table 13. Fuzzy Decision Matrix (Crisp Values).

	Human Error	Boat Engine System Failure	Environmental Conditions	Intentional Threats
Human Error	1	3.83	3	4.55
Boat Engine System Failure	0.28	1	0.61	2.33
Environmental Conditions	0.41	2	1	2.17
Intentional Threats	0.22	0.52	0.57	1

.

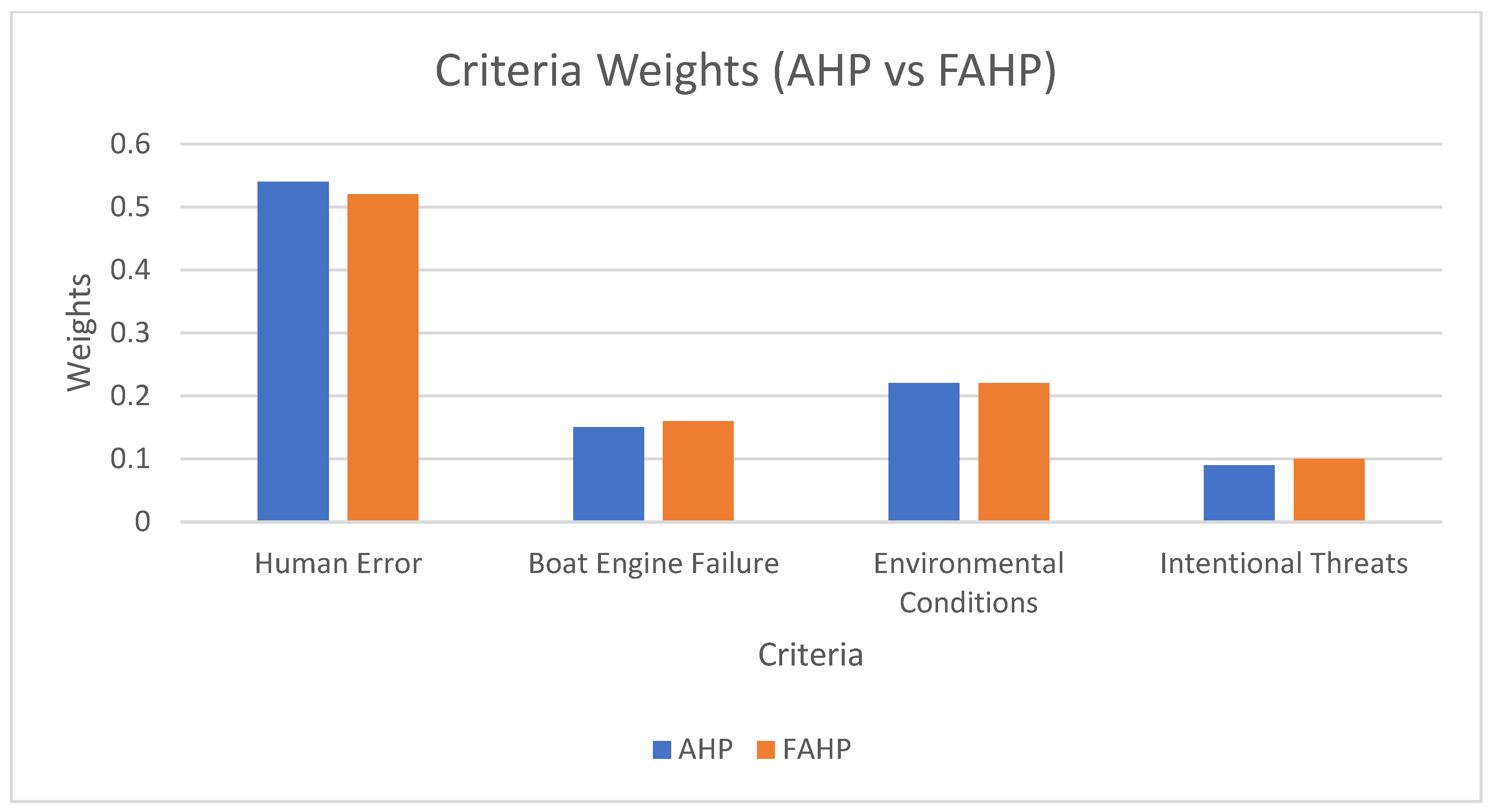
Matrix Normalisation and Criteria Weighting

The pairwise comparison matrix (Table 13) is normalised, and the results presented in

Table 14. Normalised Fuzzy Pairwise Comparison and Criteria Weights.

	Human Error (C1)	Boat Engine System Failure (C2)	Environmental Conditions (C3)	Intentional Threats (C4)	Criteria Weight
Human Error (C1)	0.52	0.52	0.58	0.45	0.52
Boat Engine System Failure (C2)	0.15	0.14	0.12	0.23	0.16
Environmental Conditions (C3)	0.21	0.27	0.19	0.22	0.22
Intentional Threats (C4)	0.12	0.07	0.11	0.10	0.10

, and also graphically in Figure 3.

4.2.2. Fuzzy TOPSIS (Collision Scenario Risk Ranking)

The six SMEs rated how much each criterion contributes to the risk level of each specific collision scenario using linguistics terms such as “very low contribution”, “high contribution”, etc. The terms are changed to fuzzy numbers presented in Table 2. The fuzzy ratings of all SMEs are aggregated using the average method to form the decision matrix, and presented in

Table 15. Alternatives Fuzzy Decision Matrix.

Collison Scenarios	C1 (Human Error)	C2 (Boat Engine System Failure	C3 (Environmental Conditions)	C4 (Intentional Threats)
A1 (Piracy/Kidnapping Attempt Collision)	0.8, 1.0, 1.0	0.1, 0.3, 0.5	0.5, 0.7, 0.9	0, 0, 0.2
A2 (Storm-Induced Boat Collison)	0.3, 0.5, 0.7	0.8, 1.0, 1.0	0.3, 0.5, 0.7	0, 0, 0.2
A3 (Mechanical Breakdown & Drift Collison)	0.5, 0.7, 0.9	0.3, 0.5, 0.7	0.8, 1.0, 1.0	0, 0, 0.2
A4 (Nighttime High-Speed Collision)	0.3, 0.5, 0.7	0, 0, 0.2	0.1, 0.3, 0.5	0.8, 1.0, 1.0

.

Fuzzy Decision Matrix (Crisp Values)

The fuzzy numbers in Table 15 are transformed into crisp values, and the results are presented in

Table 16. Alternatives Fuzzy Decision Matrix (Crisp Values).

Collison Scenarios	C1 (Human Error)	C2 (Boat Engine System Failure	C3 (Environmental Conditions)	C4 (Intentional Threats)
A1 (Piracy/Kidnapping Attempt Collision)	0.93	0.3	0.7	0.07
A2 (Storm-Induced Boat Collison)	0.5	0.93	0.5	0.07
A3 (Mechanical Breakdown & Drift Collison)	0.7	0.5	0.93	0.07
A4 (Nighttime High-Speed Collision)	0.5	0.07	0.3	0.93

.

The fuzzy decision matrix is normalised and results presented in

Table 17. Normalised Alternatives Fuzzy Decision Matrix.

Collison Scenarios	C1 (Human Error)	C2 (Boat Engine System Failure)	C3 (Environmental Conditions)	C4 (Intentional Threats)
A1 (Piracy/Kidnapping Attempt Collision)	0.35	0.17	0.29	0.06
A2 (Storm-Induced Boat Collison)	0.19	0.51	0.21	0.06
A3 (Mechanical Breakdown & Drift Collison)	0.27	0.28	0.38	0.06
A4 (Nighttime High-Speed Collision)	0.19	0.04	0.12	0.82

.

Weighted Normalised Matrix

The weighted normalised matrix is obtained by using Equation (4) and the criteria weights from Table 14. Results are as presented in

Table 18. Weighted Alternatives Decision Matrix (FTOPSIS).

Collison Scenarios	C1 (Human Error)	C2 (Boat Engine System Failure)	C3 (Environmental Conditions)	C4 (Intentional Threats)
A1 (Piracy/Kidnapping Attempt Collision)	0.182	0.027	0.064	0.006
A2 (Storm-Induced Boat Collison)	0.099	0.082	0.046	0.006
A3 (Mechanical Breakdown & Drift Collison)	0.140	0.045	0.084	0.006
A4 (Nighttime High-Speed Collision)	0.099	0.0064	0.026	0.082

.

Fuzzy Positive Ideal Solution (A⁺) and Fuzzy Negative Ideal Solution (A⁻) Determination

The $A^{+}$ and $A^{-}$ points are determined using Equations (5) and (6). The results are as presented in

Table 19. FPIS and FNIS Values (FTOPSIS).

	Category	A+	A−
C1	Cost	0.099	0.182
C2	Cost	0.0064	0.082
C3	Cost	0.026	0.084
C4	Cost	0.006	0.082

.

Distance Calculation

Using Equations (11) and (12), the distances of each collision scenario alternative from $A^{+}$ and $A^{-}$ with respect to each criterion are calculated, and the results are as presented in

Table 20. Fuzzy TOPSIS Analysis Summary.

	A+	A−	CC	Ranking
A1 (Piracy/Kidnapping Attempt Collision)	0.0934	0.0959	0.4345	3
A2 (Storm-Induced Boat Collison)	0.0781	0.1187	0.6188	2
A3 (Mechanical Breakdown & Drift Collison)	0.0812	0.0949	0.4341	4
A4 (Nighttime High-Speed Collision)	0.0762	0.1265	0.7088	1

.

Closeness Coefficient (CC) and Alternatives Ranking

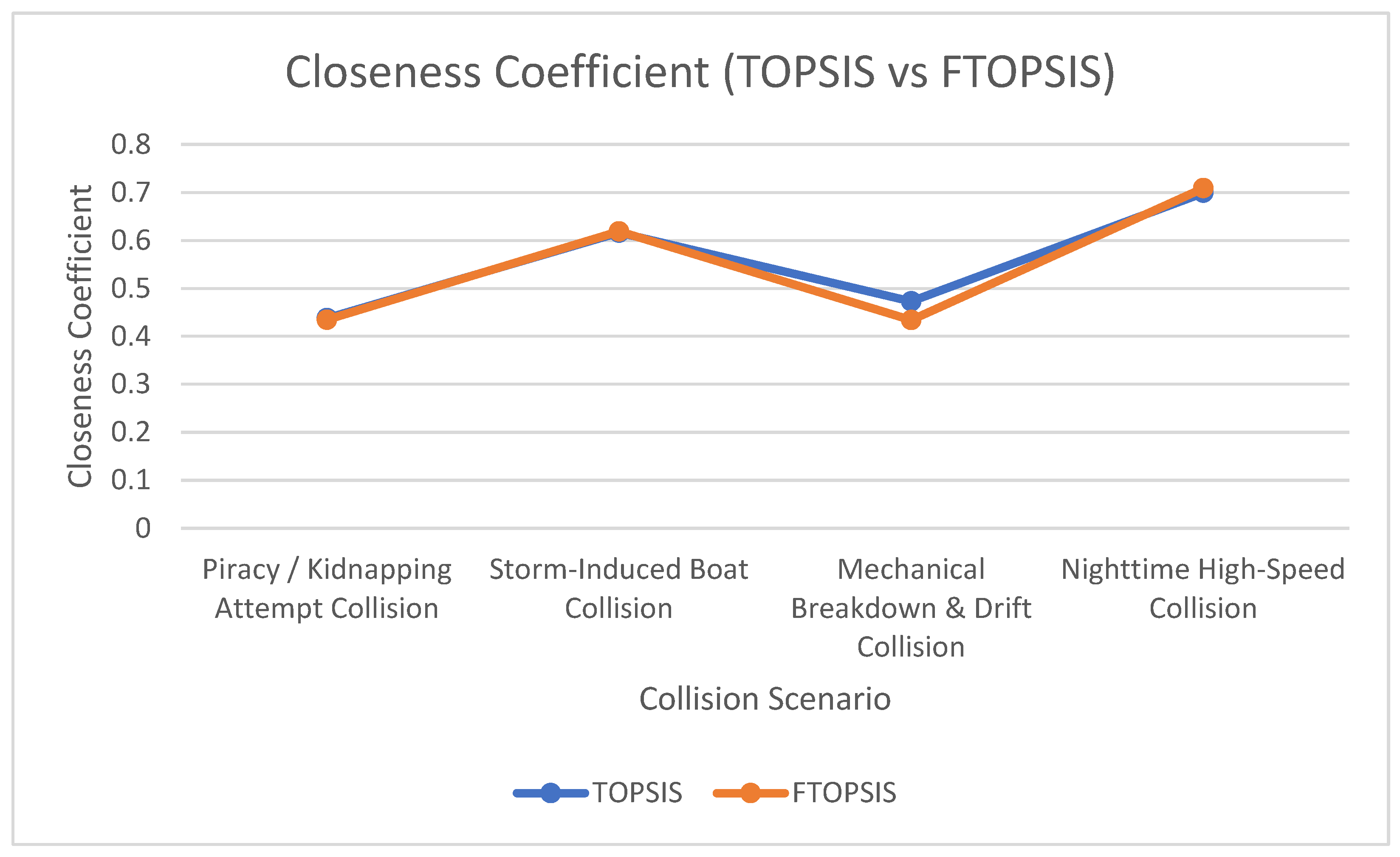
From the results obtained in Section “Distance Calculation”, the closeness coefficient of each alternative is calculated, and results are as presented in Table 20, and Figure 4 and Figure 5, respectively.

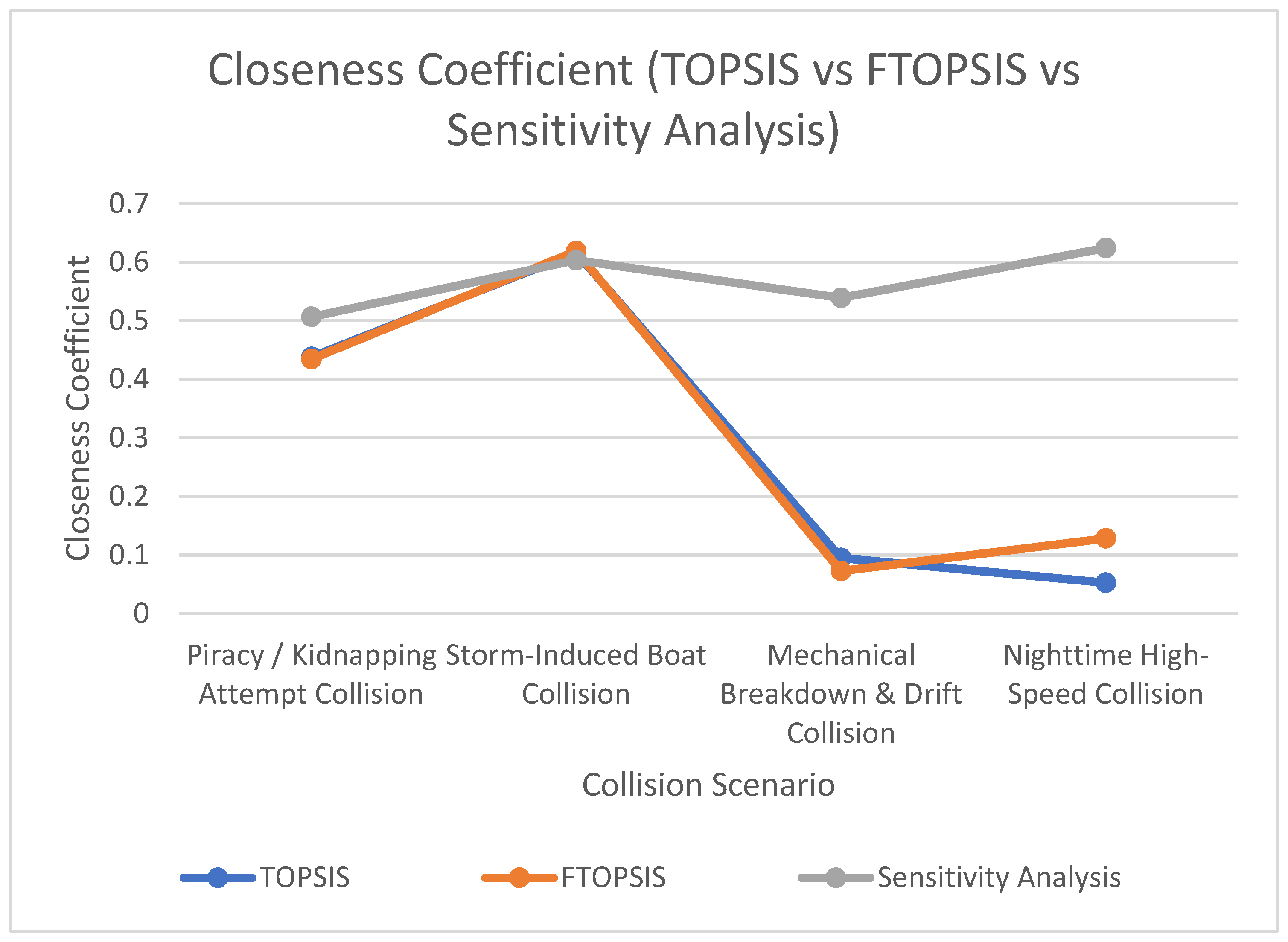
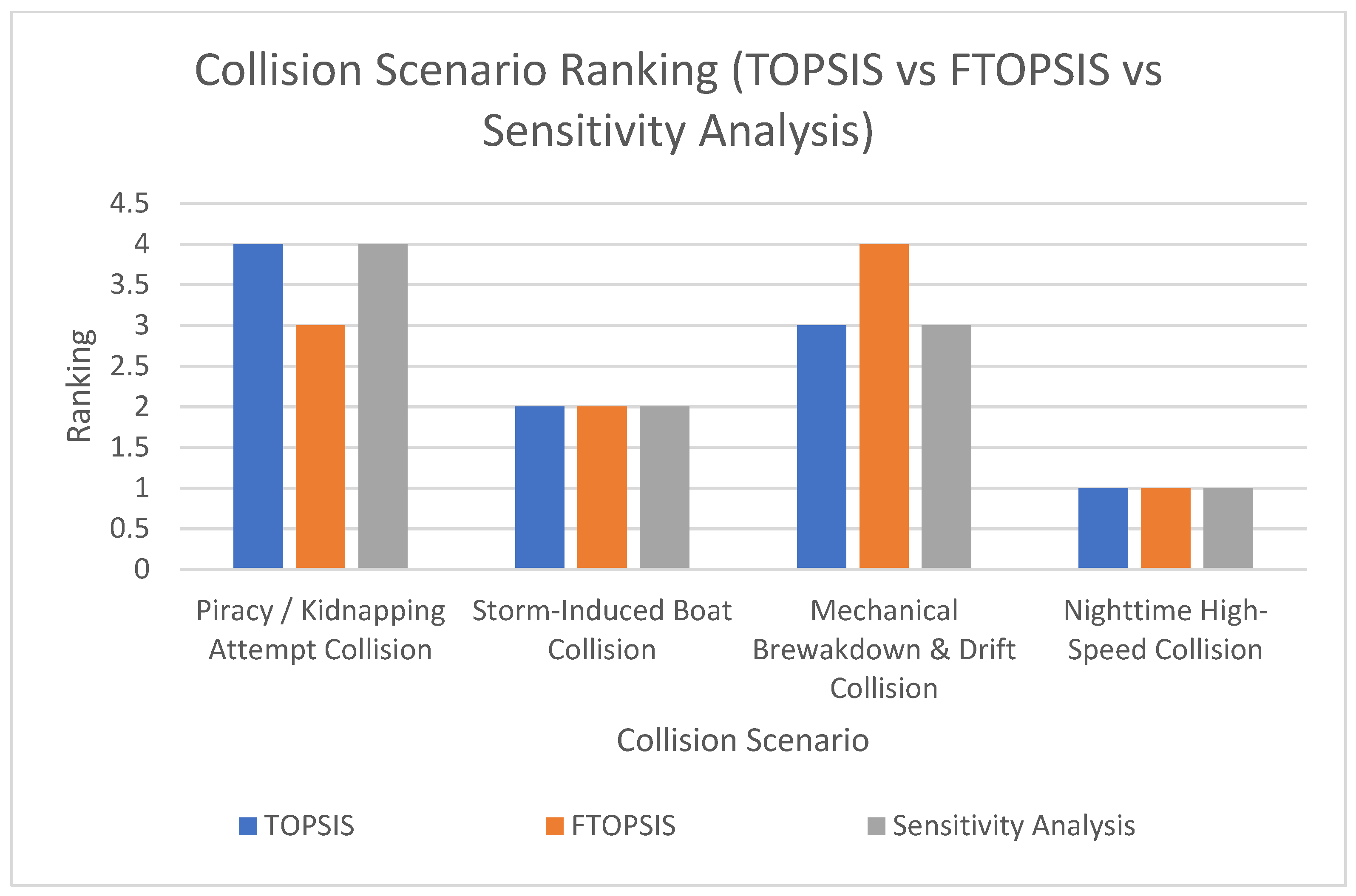
5. Sensitivity Analysis

To assess the impact of weight changes to collision scenarios, a sensitivity analysis was conducted. Environmental conditions (C3) weight from Table 14 was increased by 40%, from 0.22 to 0.31. Other weight changes are as follows: C1—0.49, C2—0.13, and C4—0.07. The sensitivity analysis results are presented in

Table 21. Sensitivity Analysis Summary.

	A+	A−	CC	Ranking
A1 (Piracy/Kidnapping Attempt Collision)	0.0963	0.0740	0.5066	4
A2 (Storm-Induced Boat Collison)	0.0669	0.1086	0.6032	2
A3 (Mechanical Breakdown & Drift Collison)	0.0949	0.0728	0.5389	3
A4 (Nighttime High-Speed Collision)	0.0528	0.1285	0.6241	1

. The results are also presented in a graphical manner in Figure 6 and Figure 7, respectively.

6. Discussion

This study evaluates boat collision risks by applying both a traditional crisp AHP-TOPSIS approach and an integrated fuzzy AHP-TOPSIS (FAHP-FTOPSIS) model. Four criteria were considered in the assessment: human error (C1), boat engine failure (C2), environmental conditions (C3), and intentional threats (C4). These criteria were used to evaluate four collision scenarios within Nigerian coastal waters: piracy/kidnapping attempt collision (A1), storm-induced boat collision (A2), mechanical breakdown and drift collision (A3), and nighttime high-speed collision (A4).

In relation to criteria weighting, the results derived from the traditional AHP technique indicate that human error (C1) is the most important factor contributing to boat collision risks, with a relative weight of 0.54. Environmental conditions (C3) emerge as the second most influential factor (0.22), followed by boat engine failure (C2) at 0.15, and intentional threats (C4) at 0.09. The fuzzy approach (FAHP) produces slightly different, though largely consistent, results. Human error (C1) remains the most dominant (0.52), followed by environmental conditions (C3) (0.22). Boat engine failure (C2) records a marginal increase (0.16), as does intentional threats (C4) (0.10). Despite these variations, the relative importance of the criteria remains unchanged.

The TOPSIS/FTOPSIS methodologies were subsequently employed to rank the collision scenarios. These techniques calculate the distance of each alternative from both positive-ideal and negative-ideal solutions, before deriving a closeness coefficient to establish the ranking. A higher closeness coefficient denotes a greater overall risk. Both the AHP-TOPSIS and FAHP-FTOPSIS models yielded an identical ranking of collision scenarios: A4 > A2 > A3 > A1. This indicates that nighttime high-speed collision (A4) is consistently identified as the highest-risk scenario, whereas piracy/kidnapping attempt collision (A1) is consistently ranked as the lowest. The incorporation of fuzzy logic enhances the robustness of the analysis by more effectively capturing real-world uncertainty in both the weighting of criteria and the evaluation of alternatives.

A sensitivity analysis was conducted by increasing the weight of environmental conditions (C3) by 40%, resulting in revised weights: C1 = 0.49, C2 = 0.13, C3 = 0.31, and C4 = 0.07. This adjustment led to a change in the ranking of the third (A3) and fourth (A1) alternatives. While A4 (nighttime high-speed collision) and A2 (storm-induced boat collision) retained their top positions, A3 (mechanical breakdown and drift collision) dropped from third to fourth, whereas A1 (piracy/kidnapping attempt collision) moved up from fourth to third. This outcome demonstrates that the model’s ranking is sensitive to substantial changes in criterion weights, particularly when the relative importance of a single criterion, such as C3, is markedly increased.

Although both the crisp and fuzzy approaches produced the same final ranking of the alternatives in the primary analysis, the added value of the fuzzy-integrated approach lies in its capacity to enhance decision reliability. Fuzzy logic enables experts to articulate their preferences using linguistic terms (e.g., “equal,” “strongly more important”), which are subsequently converted into fuzzy numbers. This process more accurately reflects human cognition, reduces cognitive bias and improves weighting precision under uncertainty. The fuzzy approach also provides more realistic outcomes, even when the resulting ranking remains unchanged. For instance, the range of FTOPSIS closeness coefficient values in this study (0.5066–0.6241) is narrower and higher than that observed in TOPSIS (0.4380–6993). This suggests that the fuzzy model yields a more robust measure of closeness, thereby providing a more confident assessment of the alternatives’ proximity to the ideal solution.

The framework developed in this study directly identifies and prioritises the collision events that pose the greatest risk in Nigerian coastal waters, thereby enabling authorities to allocate resources towards the most critical threats. The findings offer valuable insights for maritime regulators and policymakers in Nigeria in formulating targeted risk mitigation strategies. In particular, prioritising interventions to address nighttime high-speed collisions and storm-induced boat collisions is essential, with a strong emphasis on reducing human error as the primary contributing factor.

In contrast to conventional approaches such as Failure Mode Effect Analysis (FMEA), which rely on precise data and a fixed scoring scale, the fuzzy multi-criteria decision-making (MCDM) framework explicitly accounts for vagueness and uncertainty in expert judgements. For instance, risk priority numbers (RPNs) are derived from crisp, single-point scales, which presents challenges in capturing subjectivity and uncertainty in risk assessment. Assigning a single numerical value to the “severity” of a boat collision is often a matter of expert judgement, which may not fully capture the complexity of the situation. The fuzzy-integrated approach addresses this limitation by employing linguistic variables (e.g., “high,” “medium”) and fuzzy numbers, thereby enabling a more nuanced representation of expert opinions. While FMEA is effective for analysing single-component failures, it is less suited to modelling interdependencies between different risk factors. For example, a “human error” may be influenced by “environmental conditions,” which in turn could be exacerbated by “engine system failure.” The proposed fuzzy MCDM framework explicitly models and weighs such interdependencies through the AHP component, which systematically evaluates the relative importance of each criterion, ensuring that the final ranking reflects a more holistic understanding of system complexities. Furthermore, FMEA’s reliance on RPNs can result in identical scores for different failure modes, thereby complicating prioritisation. By contrast, the TOPSIS component of the proposed fuzzy MCDM framework provides a transparent and rigorous method for ranking alternatives according to their distance from both the positive and negative ideal solutions. This produces a clear and unambiguous prioritisation of risks, directly supporting the identification and implementation of appropriate safety measures.

The study’s results, which ranked the risk factors based on their weighted importance, provide a quantitative foundation for recommendations aimed at addressing the most critical factors contributing to boat collisions in Nigeria’s waterways. Since human error was identified as the most influential risk factor in both AHP (0.54) and FAHP (0.52), and nighttime speed collision as the highest risk scenario, interventions should prioritise operators and passengers embarking on nighttime journeys. Regular public awareness campaigns targeting both groups should highlight the dangers of night travel, speeding, overloading, operator distraction during navigation, and substance use. To reduce casualties when boat collisions occur, regulatory authorities should ensure that boats are equipped with essential safety equipment, and passengers are required to wear life jackets at all times. A strict “No Life Jacket, No Boarding” policy should be enforced. Environmental conditions, which emerged as the second most influential risk factor with a weighting of 0.22 in both AHP and FAHP, and storm-induced collision as the second-highest risk scenario, also require mitigation. Restrictions on boat travel during storms and periods of poor visibility should be strictly enforced. Furthermore, waterways should be regularly dredged, and hazards such as debris, wrecks, underwater tree stumps, and water hyacinth should be systematically removed. Boat engine failure, with weights of 0.15 (AHP) and 0.16 (FAHP), was identified as a contributor to collision risk, while mechanical breakdown and drift collision ranked third among the scenarios. To address this, regulatory inspectors should conduct routine technical inspections of boat engines prior to departure. Operators should be encouraged, and where necessary compelled, to establish and adhere to strict maintenance ensure seaworthiness. Training programmes should also be implemented to enable operators to recognise early signs of mechanical faults. Although intentional threats received the lowest weighting (AHP 0.09, FAHP 0.10) and piracy/kidnapping attempt collisions ranked lowest among the scenarios, their potential impact can be catastrophic, particularly in piracy-prone areas of the Niger Delta. Accordingly, security agencies should intensify patrols, strengthen surveillance, and enforce restrictions on night-time navigation to reduce vulnerability to such threats.

In addition, the government should consider legislation mandating the installation of basic technological devices and electronic equipment on all commercial boats. Examples include automatic identification systems, collision-warning systems, night-vision cameras, and VHF radios for communication. However, given the current level of technological development and infrastructure in the country, implementation challenges must be anticipated, and phased or context-appropriate adoption strategies may be required.

7. Conclusions

This study developed a fuzzy MCDM-based framework integrating FAHP and FTOPSIS for assessing boat collision risks in Nigeria’s coastal waters. The approach prioritised high-speed nighttime collisions and storm-induced incidents as the most critical scenarios. Comparative analysis against a crisp AHP-TOPSIS model demonstrated that the fuzzy model provides greater expressiveness, improves handling of uncertainty, and offers more reliable prioritisation. The model was further validated through sensitivity analysis, confirming its robustness to changes in criteria importance, particularly with environmental conditions.

The findings of this paper offer valuable insights for maritime authorities and policymakers in Nigeria to formulate targeted risk mitigation strategies, particularly with respect to human factors, which were identified as the primary contributor to boat collisions. Addressing these underlying causes is crucial to improving safety on Nigeria’s waterways, and several recommendations have been proposed.

Proposed directions for future research include the expansion of criteria and alternatives, the exploration of other hybrid fuzzy MCDM approaches, stakeholder perception analysis, and cost–benefit evaluations of mitigation strategies. Further studies could also undertake cross-regional comparisons, incorporate dynamic risk factors such as traffic density, and engage a broader range of domain experts. Additionally, future research may consider other risk scenarios, such as port congestion or navigation through narrow waterways, and validate the proposed framework using actual accident data or independent third-party records.