Comparison of Numerical Simulations of Propeller Open-Water Performance with Cavitation for High-Speed Planing Hulls
Abstract
1. Introduction
2. Computational Methods and Setup
2.1. Mathematical Model and Numerical Method
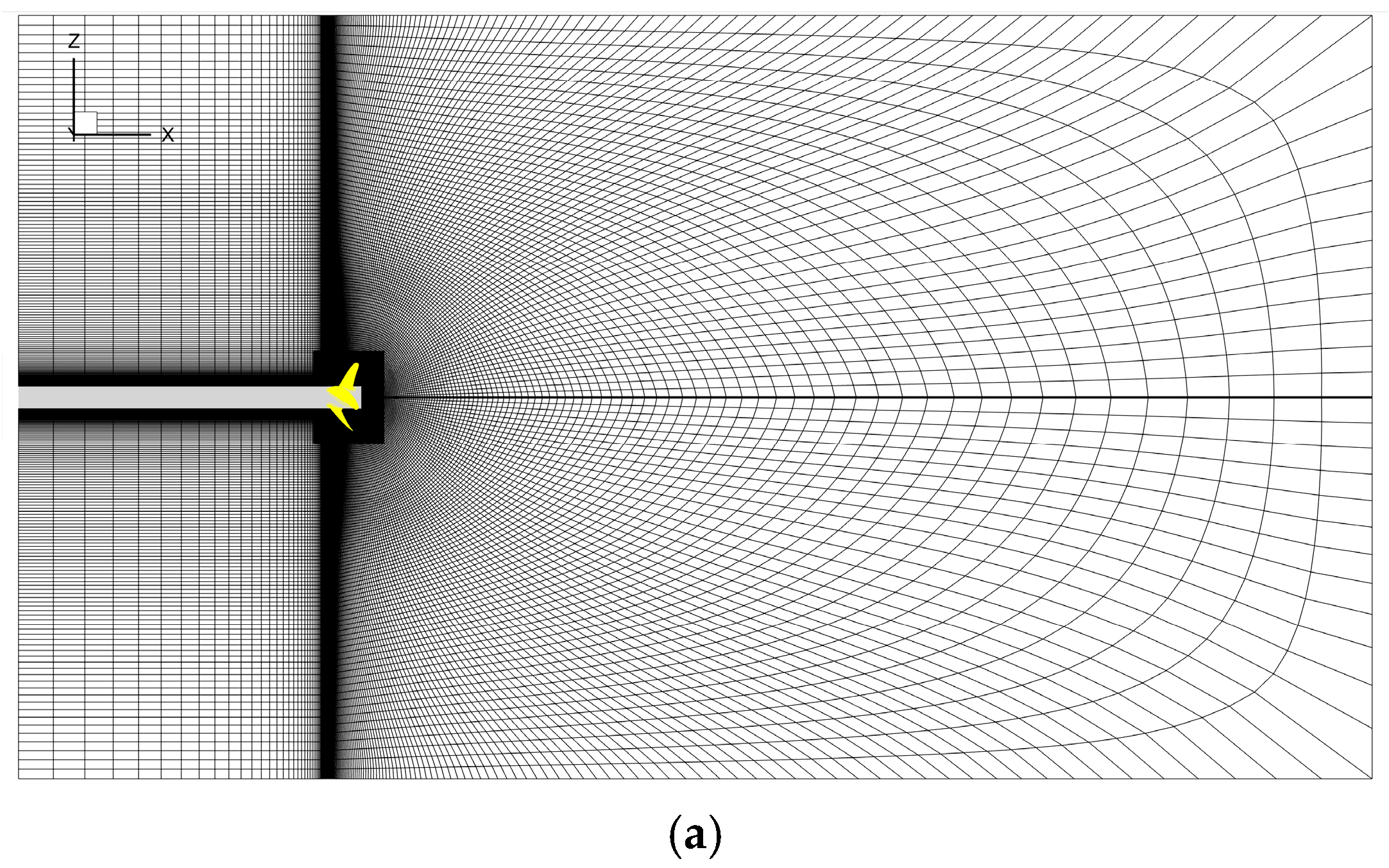
2.2. Computational Setup
3. Results
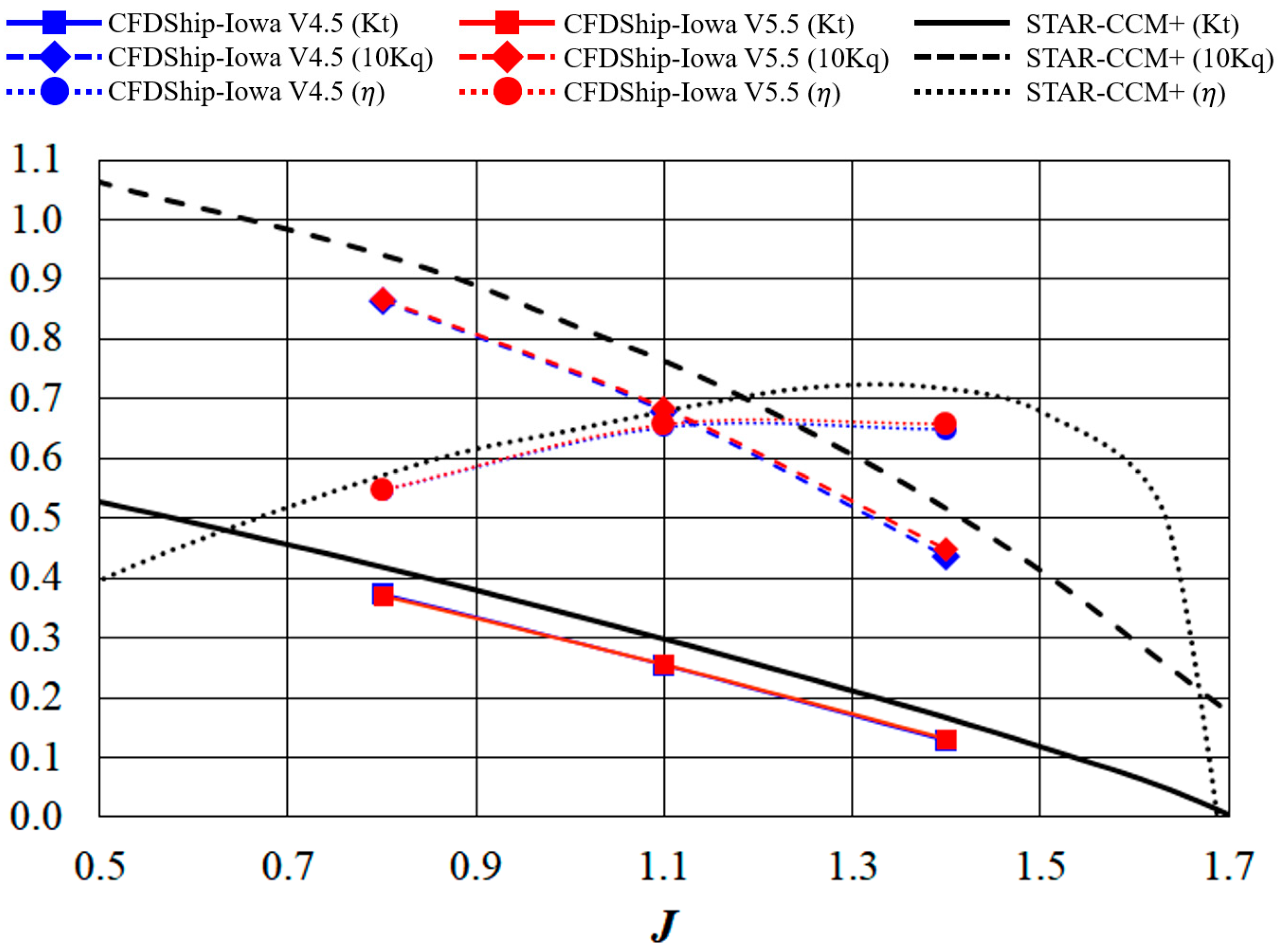
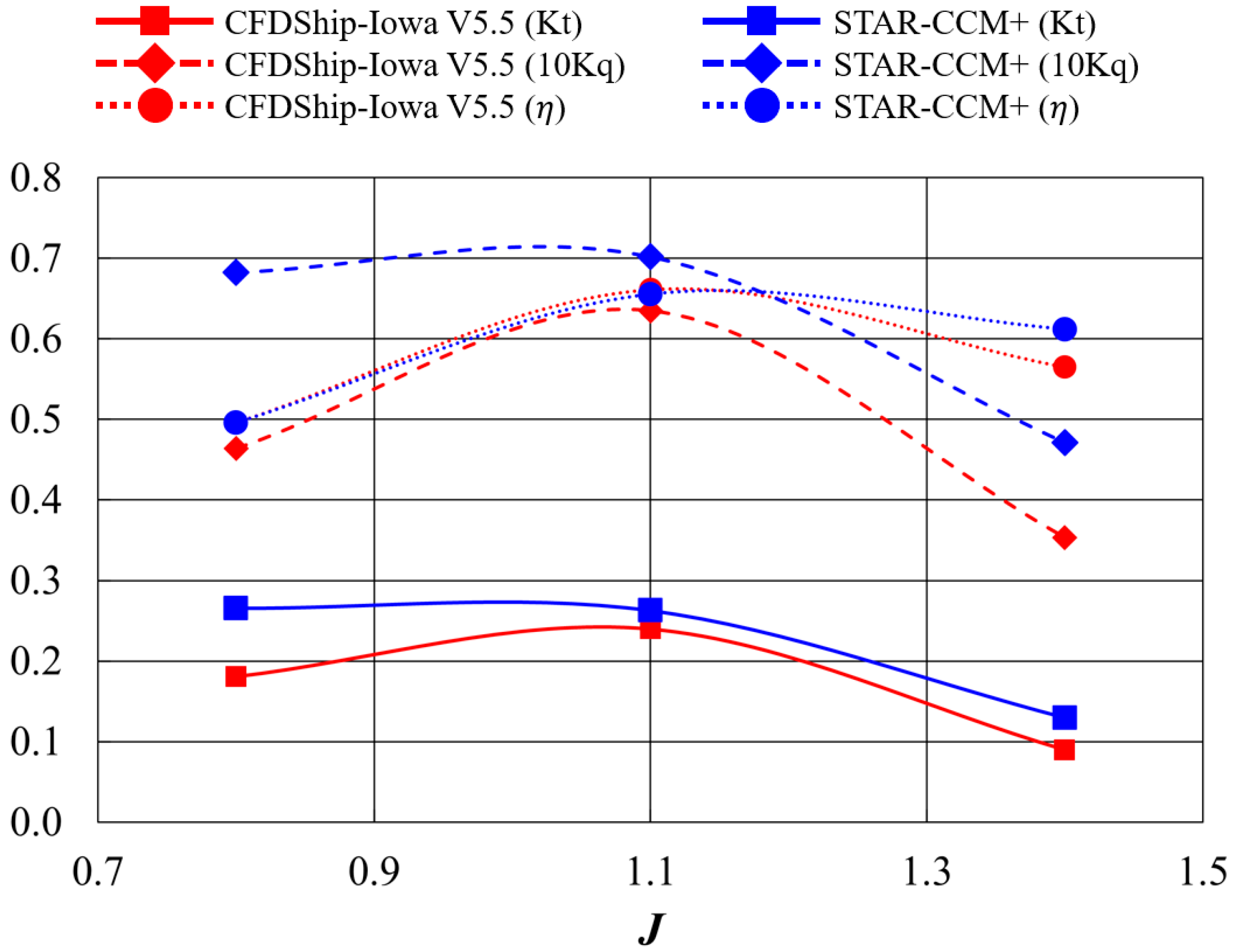
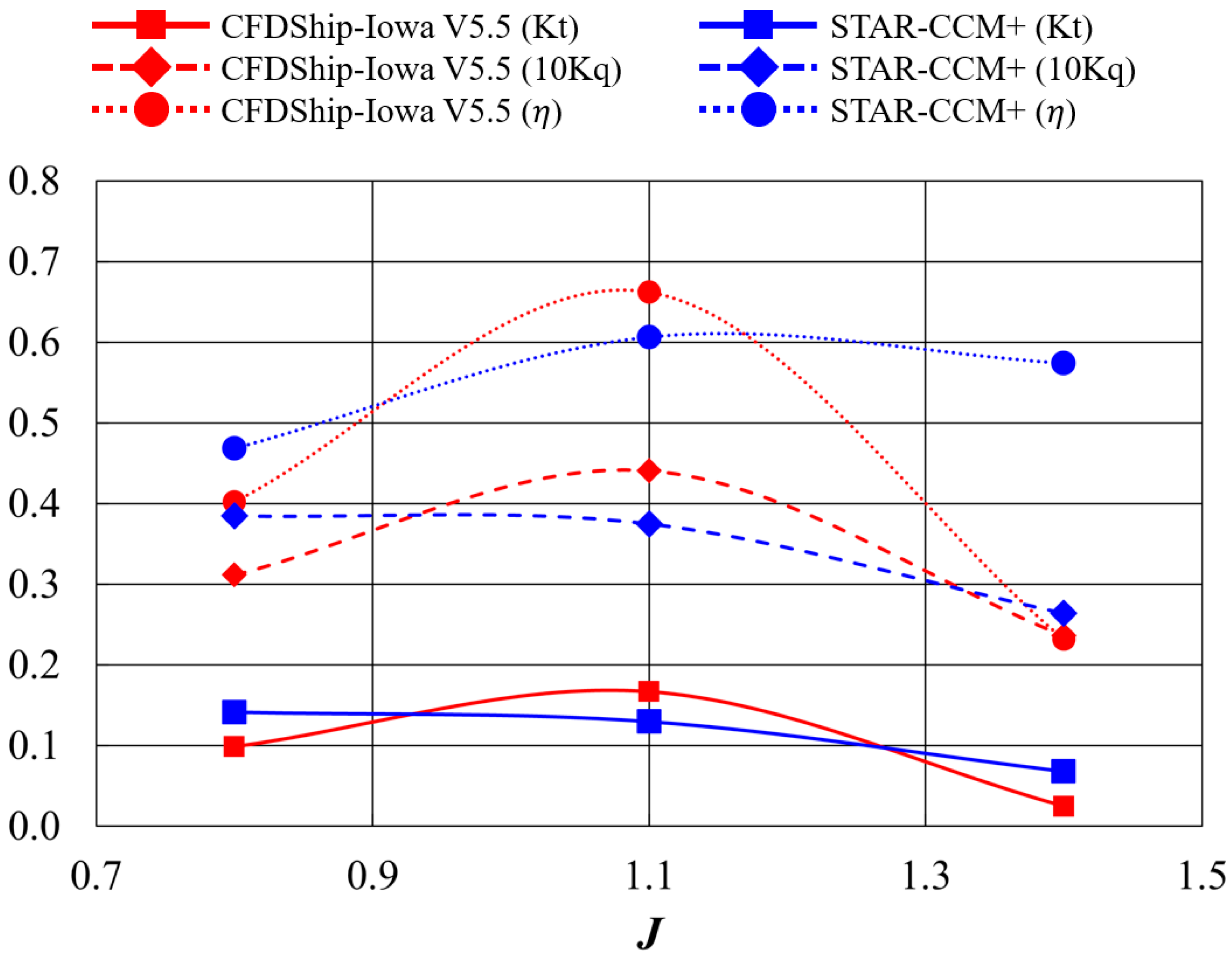
3.1. Thrust and Torque Coefficients and Propeller Efficiency
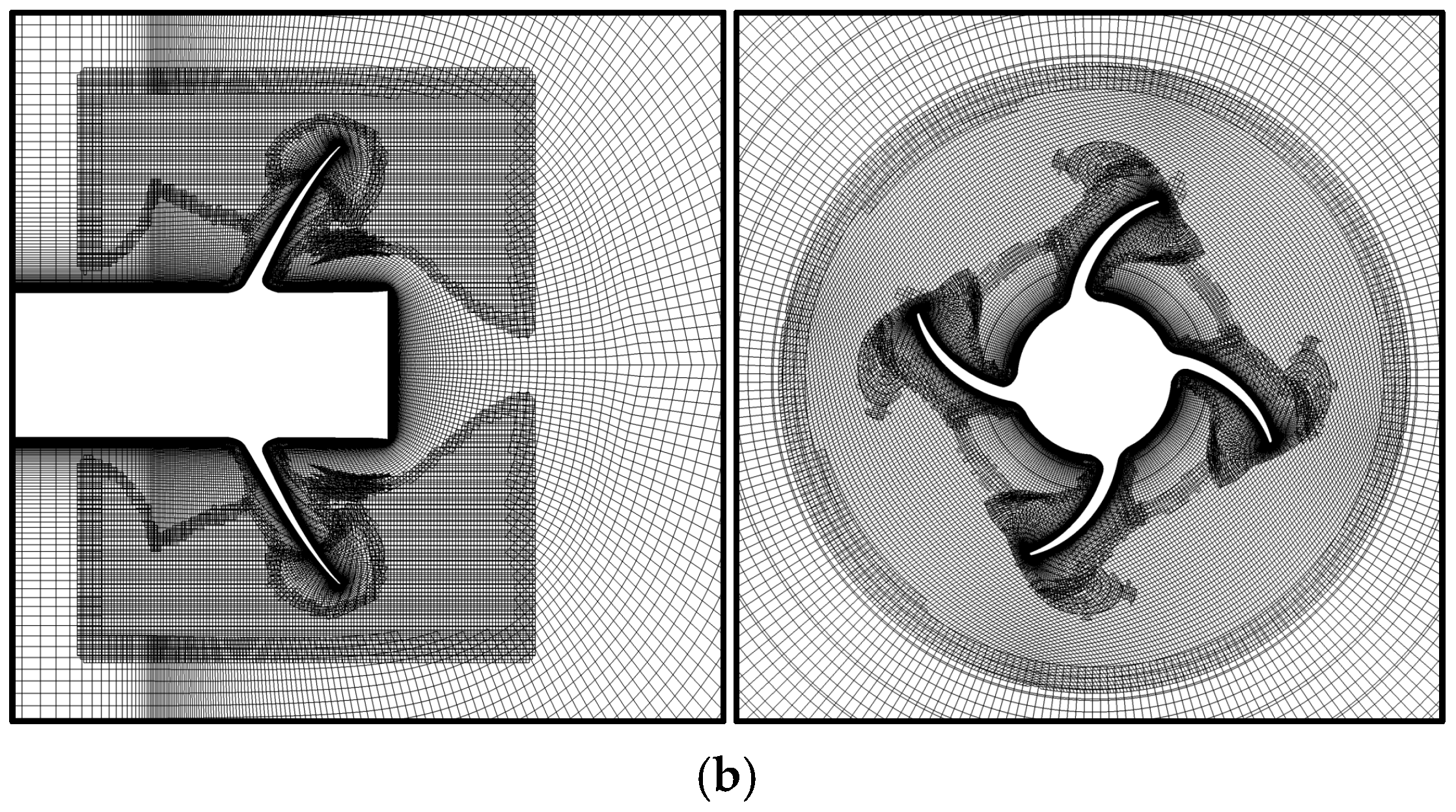
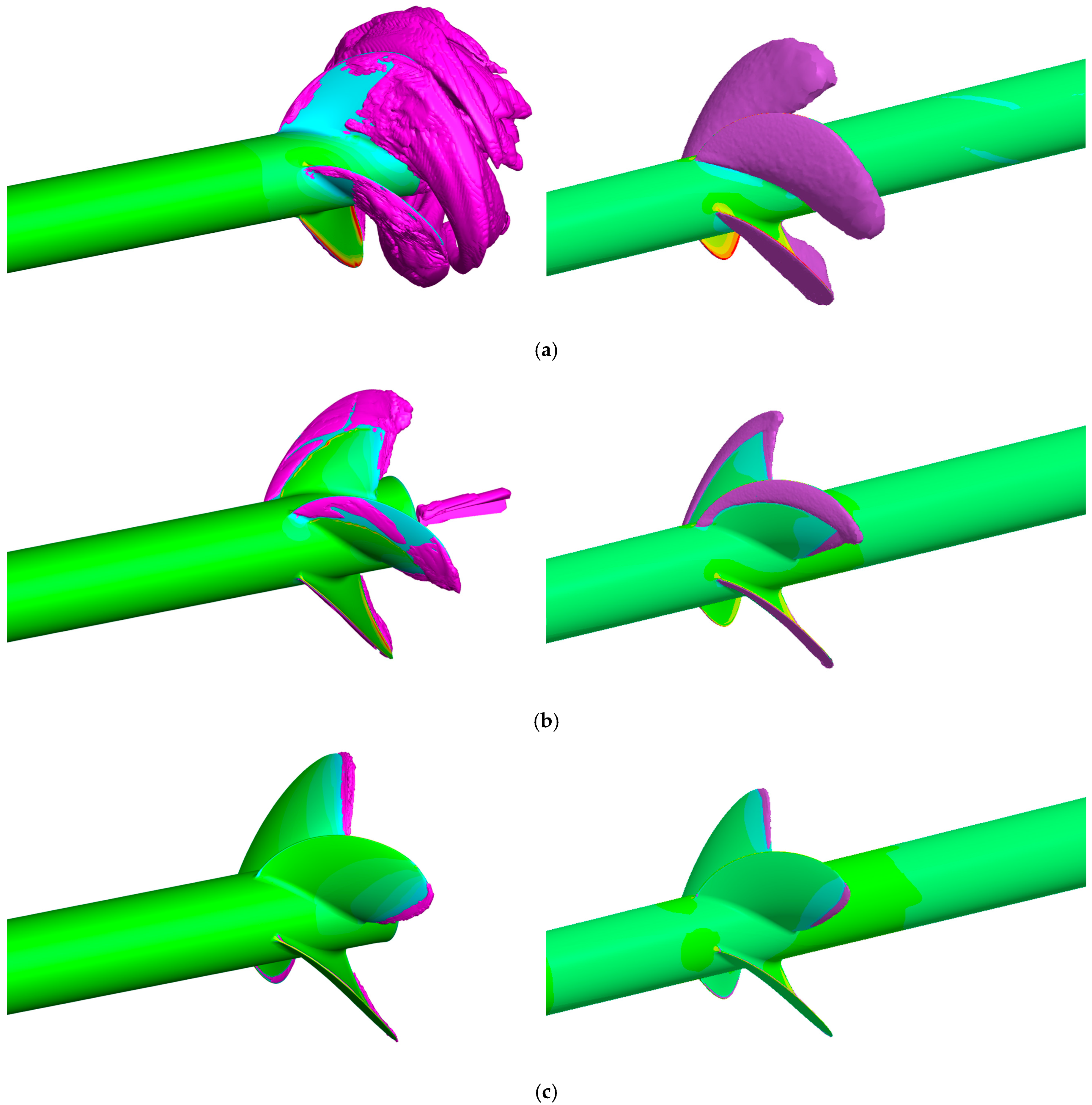
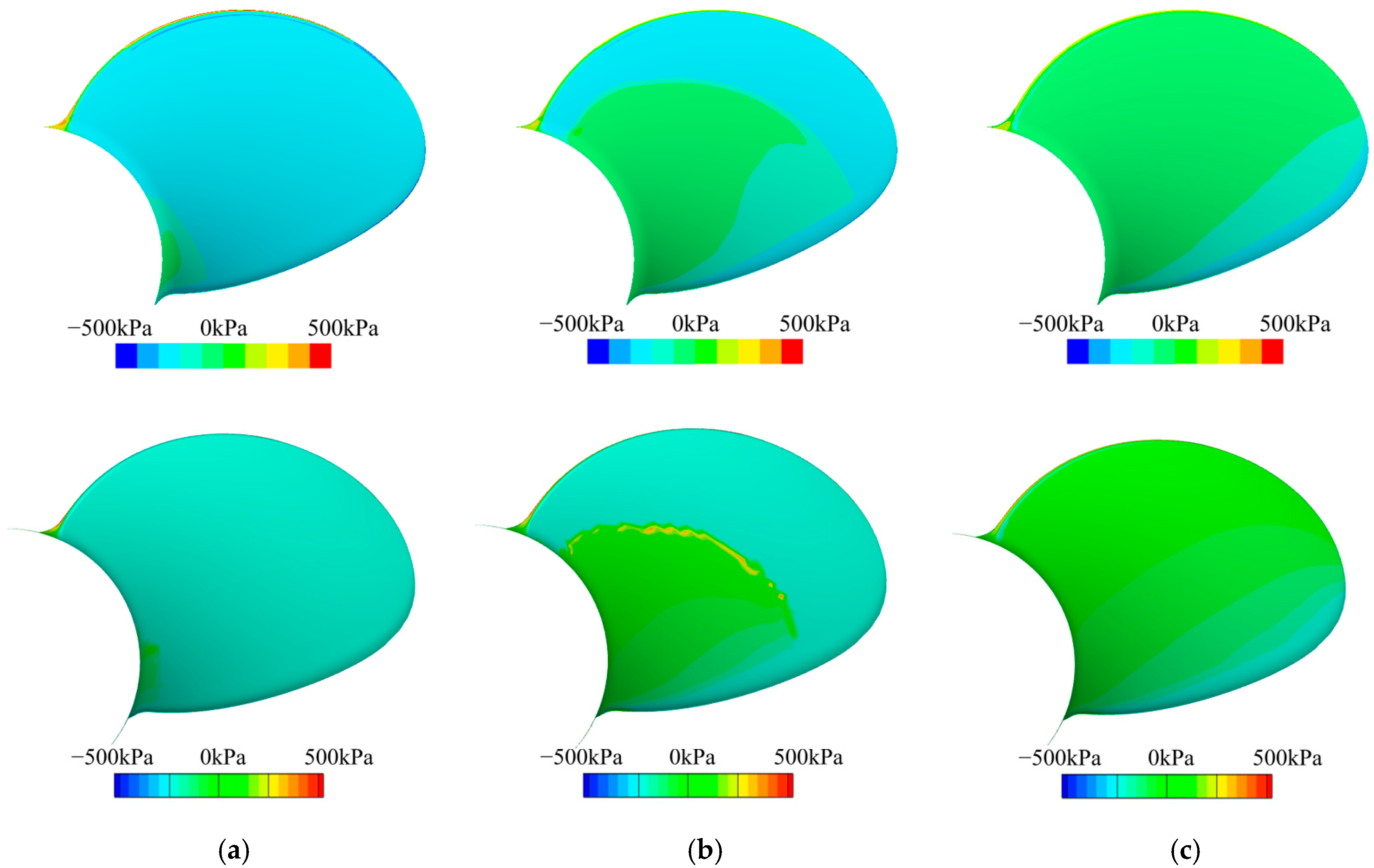
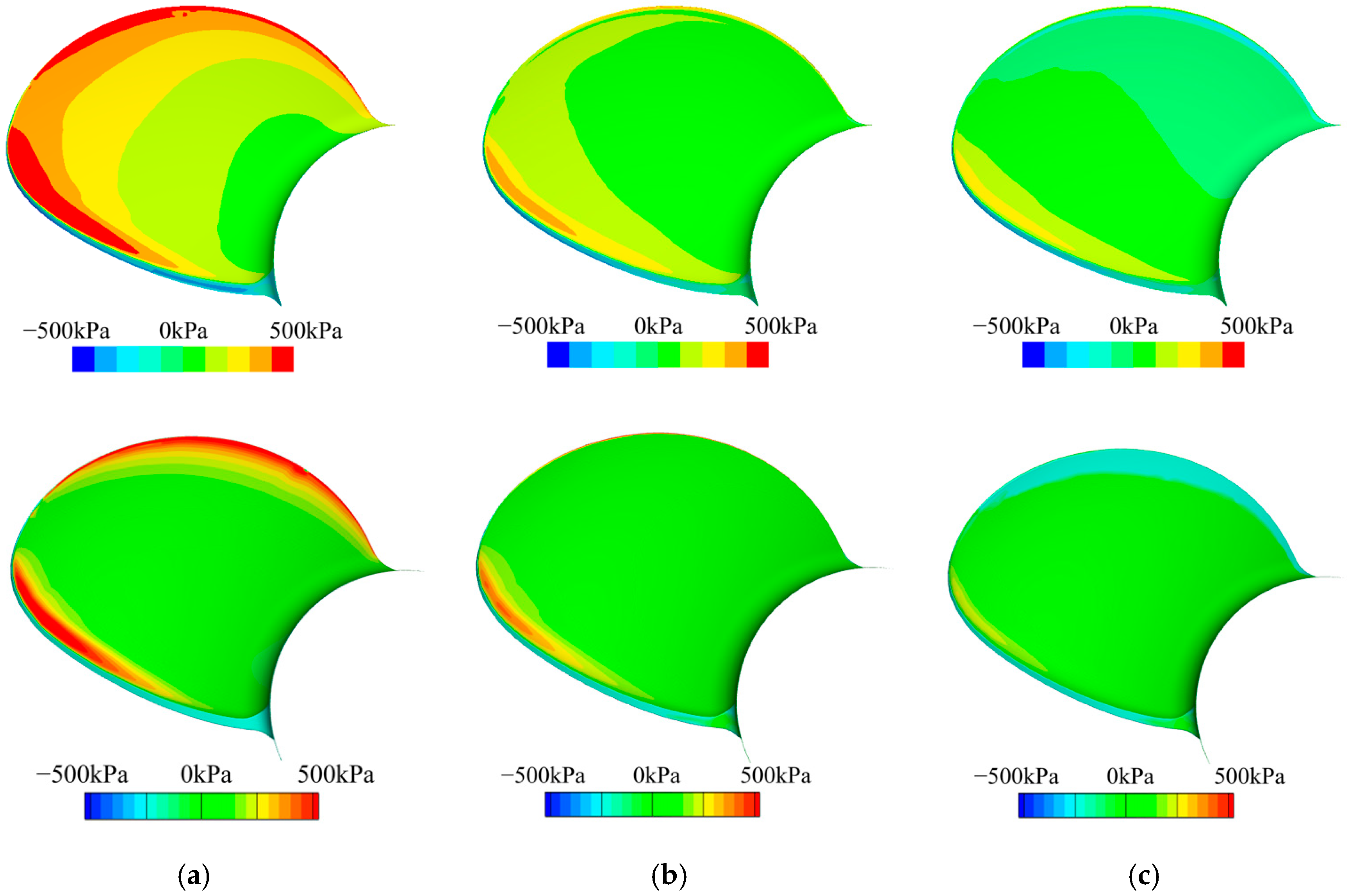
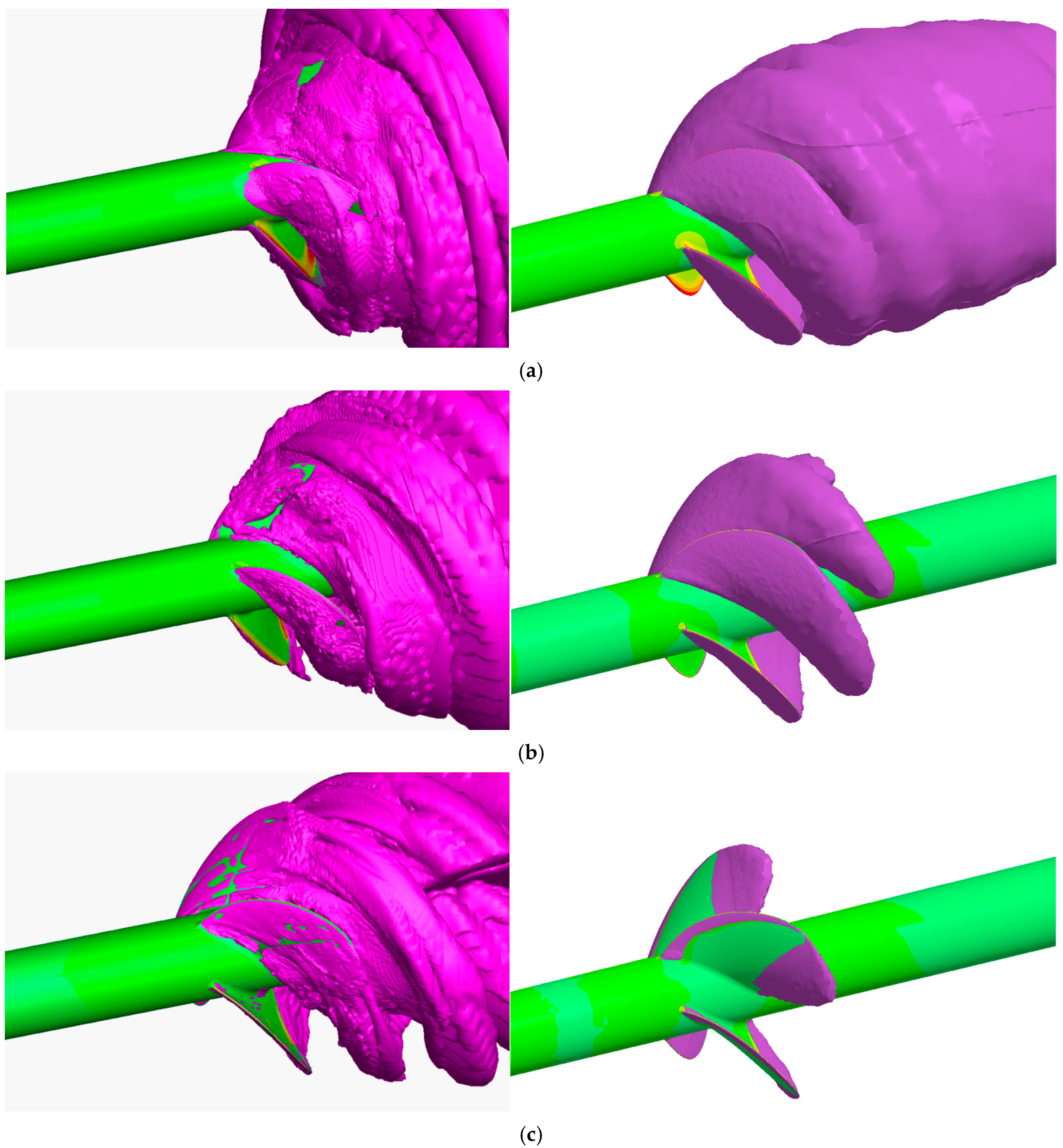
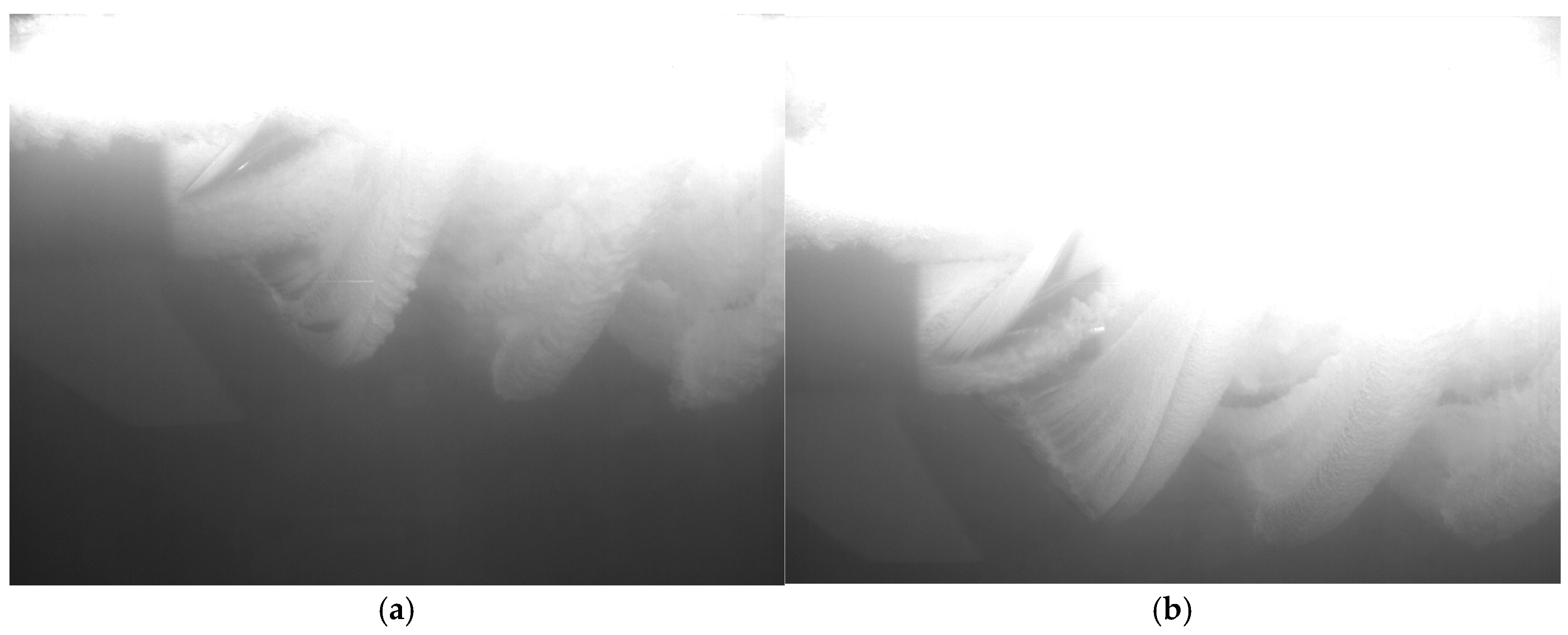
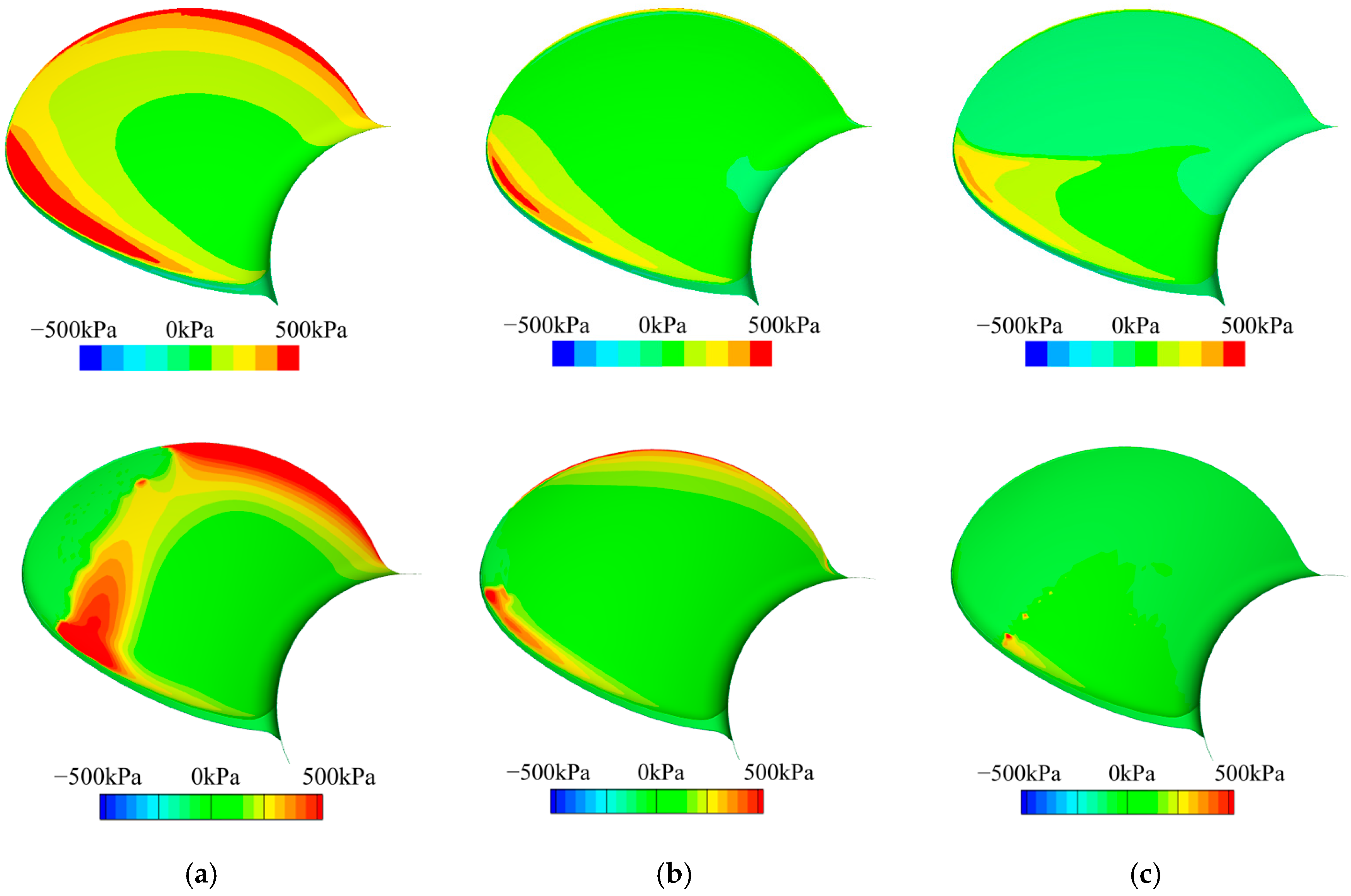
3.2. Cavitation Profiles and Pressure Distributions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Olofsson, N. Force and Flow Characteristics of a Partially Submerged Propeller. Ph.D. Thesis, Chalmers University of Technology, Göteborg, Sweden, 1996. [Google Scholar]
- Young, Y.L.; Kinnas, S.A. Fluid and Structural Modeling of Cavitating Propeller Flows. In Proceedings of the 5th International Symposium on Cavitation, Osaka, Japan, 1–4 November 2003. [Google Scholar]
- Nouroozi, H.; Zeraatgar, H. A reliable simulation for hydrodynamic performance prediction of surface-piercing propellers using URANS method. Appl. Ocean Res. 2019, 92, 101939. [Google Scholar] [CrossRef]
- Yari, E.; Moghadam, A.B. BEM applied to the cup effect on the partially submerged propeller performance prediction and ventilation pattern. J. Mar. Eng. Technol. 2020, 21, 159–177. [Google Scholar] [CrossRef]
- Yilmaz, N.; Atlar, M.; Khorasanchi, M. An improved Mesh Adaption and Refinement approach to Cavitation Simulation (MARCS) of propellers. Ocean Eng. 2019, 171, 139–150. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Q.; Zhang, M.; Xie, Z. Numerical Prediction of Cavitation Fatigue Life and Hydrodynamic Performance of Marine Propellers. J. Mar. Sci. Eng. 2023, 12, 74. [Google Scholar] [CrossRef]
- Vázquez-Santos, A.; Camacho-Zamora, M.; Hernández-Hernández, J.; Herrera-May, A.L.; Santos-Cortes, L.D.C.; Tejeda-del-Cueto, M.E. Numerical Analysis and Validation of an Optimized B-Series Marine Propeller Based on NSGA-II Constrained by Cavitation. J. Mar. Sci. Eng. 2024, 12, 105. [Google Scholar] [CrossRef]
- Zhang, B.; Zheng, C.S.; Shao, X.M.; Deng, J. Multiscale modeling of propeller cavitation flows in open water. J. Hydrodyn. 2025, 37, 1–13. [Google Scholar] [CrossRef]
- Ristea, M.; Popa, A.; Volintiru, O.-N. CFD Design Performance Analysis for a High-Speed Propeller. Appl. Sci. 2025, 15, 8754. [Google Scholar] [CrossRef]
- Ghoniem, A.M.; Elazm, A.S.A.; Benaya, M.I.; Mohamed, S.A. Effect of salinity on marine propeller performance. J. Phys. Conf. Ser. 2023, 2616, 012016. [Google Scholar] [CrossRef]
- Irannezhad, M.; Kjellberg, M.; Bensow, R.E.; Eslamdoost, A. Experimental and numerical investigations of propeller open water characteristics in calm water and regular head waves. Ocean Eng. 2024, 302, 117703. [Google Scholar] [CrossRef]
- Oloan, A.F.N.; Ariana, I.M.; Baidowi, A. Open Water and Performance Analysis of Marine Propeller with PBCF Based CFD Method. In Proceedings of the 6th International Conference on Marine Technology, Surabaya, Indonesia, 27 November 2021. [Google Scholar]
- Grlj, C.G.; Degiuli, N.; Farkas, A.; Martić, I. Numerical Study of Scale Effects on Open Water Propeller Performance. J. Mar. Sci. Eng. 2022, 10, 1132. [Google Scholar] [CrossRef]
- Ali, M.A.; Peng, H.; Qiu, W. Propeller-hull interaction simulation for self-propulsion with sinkage and trim. Phys. Fluids 2024, 36, 025159. [Google Scholar] [CrossRef]
- Stern, F.; Wang, Z.; Park, S.; Milano, C.; Gunderson, A.; Scherer, J.; Yasukawa, H.; Diez, M. Multi-Fidelity Full Throttle Acceleration from Rest for High-Speed Planing-Hulls with Engine Curves. In Proceedings of the 36th Symposium on Naval Hydrodynamics, Busan, Republic of Korea, 14–19 June 2026. [Google Scholar]
- Wang, Z.; Stern, F. Volume-of-fluid based two-phase flow methods on structured multiblock and overset grids. Int. J. Numer. Methods Fluids 2022, 94, 557–582. [Google Scholar] [CrossRef]
- Wang, Z.; Park, S.; Stern, F. Cavitation Implementation Algorithms Based on Pressure Projection Method for Incompressible Flows with Three-Phase Interactions. Int. J. Numer. Methods Fluids 2025, 97, 1057–1072. [Google Scholar] [CrossRef]
- Zwart, P.J.; Gerber, A.G.; Belamri, T. A Two-Phase Flow Model for Predicting Cavitation Dynamics. In Proceedings of the International Conference on Multiphase Flow, Yokohama, Japan, 30 May–3 June 2004. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Noack, R. SUGGAR: A general capability for moving body overset grid assembly. In Proceedings of the 17th AIAA Computational Fluid Dynamics Conference, Toronto, ON, Canada, 6–9 June 2005; p. 5117. [Google Scholar]
- Schnerr, G.H.; Sauer, J. Physical and Numerical Modeling of Unsteady Cavitation Dynamics. In Proceedings of the 4th International Conference on Multiphase Flow, New Orleans, LA, USA, 27 May–1 June 2001. [Google Scholar]





| Number of Blades | Propeller Diameter | Hub Diameter | Pitch Distance |
|---|---|---|---|
| 4 | 0.71 m | 0.2282 m | 1.065 m |
| Skew | Tip rake | Skew-induced rake | Disc area |
| 11.77 deg | 0.1739 m | 0.0348 m | 0.3959 m2 |
| Kt | CFDShip-Iowa V5.5 | STAR-CCM+ | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| σ | No-Cav | 1.095 | Diff (%) | 0.274 | Diff (%) | No-Cav | 1.095 | Diff (%) | 0.274 | Diff (%) |
| J = 0.8 | 0.372 | 0.181 | −51.4 | 0.098 | −73.5 | 0.418 | 0.266 | −36.5 | 0.142 | −66.2 |
| J = 1.1 | 0.257 | 0.240 | −6.7 | 0.167 | −35.1 | 0.298 | 0.263 | −11.7 | 0.130 | −56.4 |
| J = 1.4 | 0.133 | 0.090 | −32.4 | 0.025 | −81.4 | 0.166 | 0.129 | −21.9 | 0.068 | −58.9 |
| Average | −30.2 | −63.4 | −23.4 | −60.5 | ||||||
| 10Kq | CFDShip-Iowa V5.5 | STAR-CCM+ | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| σ | No-Cav | 1.095 | Diff (%) | 0.274 | Diff (%) | No-Cav | 1.095 | Diff (%) | 0.274 | Diff (%) |
| J = 0.8 | 0.867 | 0.464 | −46.5 | 0.312 | −64.1 | 0.939 | 0.683 | −27.3 | 0.385 | −59.0 |
| J = 1.1 | 0.685 | 0.635 | −7.3 | 0.441 | −35.6 | 0.761 | 0.702 | −7.8 | 0.375 | −50.8 |
| J = 1.4 | 0.449 | 0.353 | −21.3 | 0.236 | −47.4 | 0.515 | 0.471 | −8.4 | 0.264 | −48.6 |
| Average | −25.0 | −49.0 | −14.5 | −52.8 | ||||||
| CFDShip-Iowa V5.5 | STAR-CCM+ | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| σ | No-Cav | 1.095 | Diff (%) | 0.274 | Diff (%) | No-Cav | 1.095 | Diff (%) | 0.274 | Diff (%) |
| J = 0.8 | 0.546 | 0.496 | −9.2 | 0.402 | −26.4 | 0.571 | 0.496 | −13.2 | 0.469 | −18.0 |
| J = 1.1 | 0.657 | 0.661 | 0.7 | 0.662 | 0.8 | 0.680 | 0.655 | −3.5 | 0.606 | −10.8 |
| J = 1.4 | 0.658 | 0.565 | −14.1 | 0.232 | −64.8 | 0.714 | 0.612 | −14.3 | 0.574 | −19.6 |
| Average | −7.6 | −30.1 | −10.4 | −16.1 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, S.; Wang, Z.; Stern, F.; Gunderson, A.; Scherer, J. Comparison of Numerical Simulations of Propeller Open-Water Performance with Cavitation for High-Speed Planing Hulls. J. Mar. Sci. Eng. 2025, 13, 1804. https://doi.org/10.3390/jmse13091804
Park S, Wang Z, Stern F, Gunderson A, Scherer J. Comparison of Numerical Simulations of Propeller Open-Water Performance with Cavitation for High-Speed Planing Hulls. Journal of Marine Science and Engineering. 2025; 13(9):1804. https://doi.org/10.3390/jmse13091804
Chicago/Turabian StylePark, Sungtek, Zhaoyuan Wang, Frederick Stern, Andrew Gunderson, and John Scherer. 2025. "Comparison of Numerical Simulations of Propeller Open-Water Performance with Cavitation for High-Speed Planing Hulls" Journal of Marine Science and Engineering 13, no. 9: 1804. https://doi.org/10.3390/jmse13091804
APA StylePark, S., Wang, Z., Stern, F., Gunderson, A., & Scherer, J. (2025). Comparison of Numerical Simulations of Propeller Open-Water Performance with Cavitation for High-Speed Planing Hulls. Journal of Marine Science and Engineering, 13(9), 1804. https://doi.org/10.3390/jmse13091804








