Coupled Simulation Study on the High-Pressure Air Expulsion from Submarine Ballast Tanks and Emergency Surfacing Dynamics
Abstract
1. Introduction
2. Simulation Model
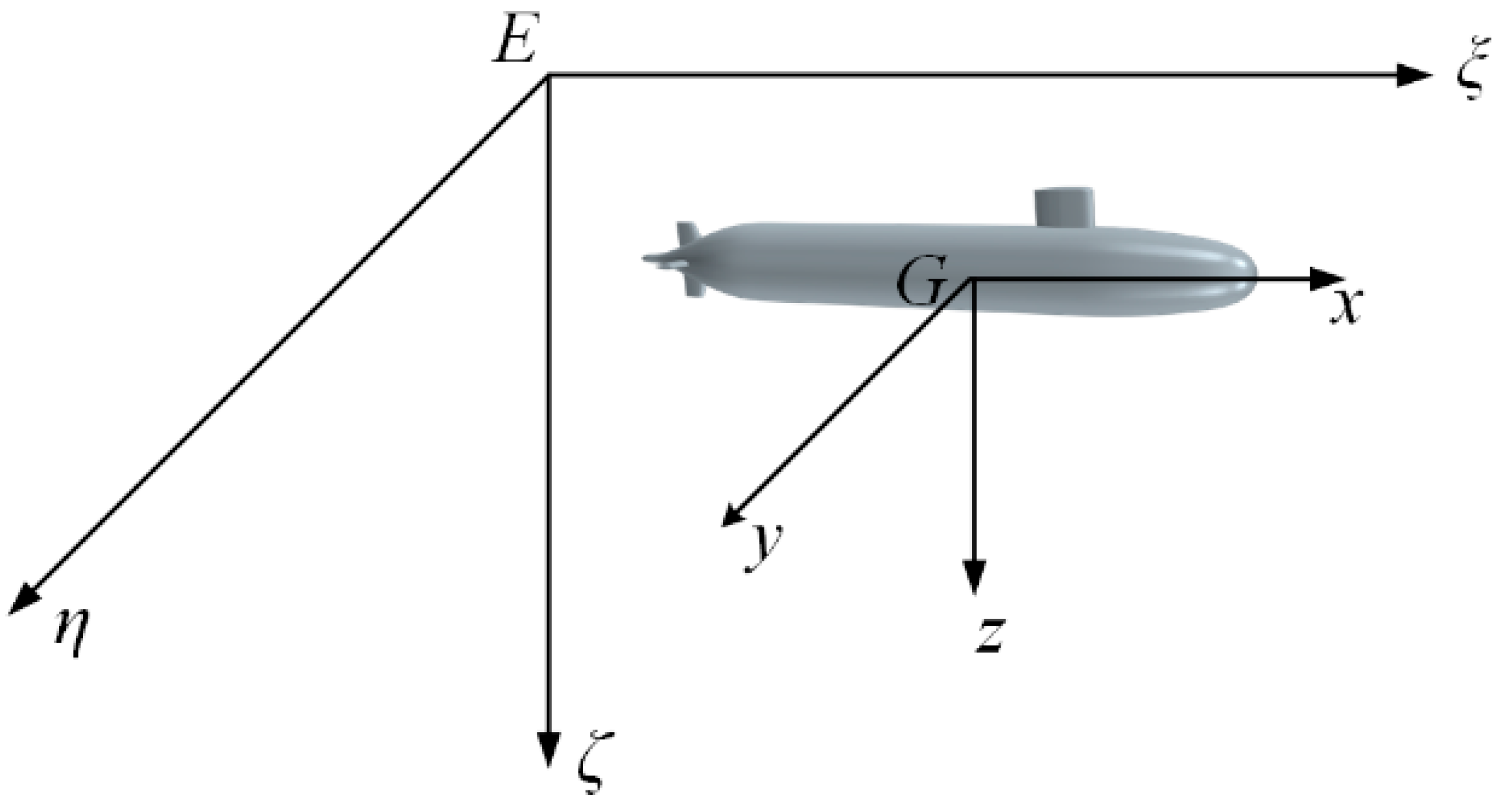
2.1. Research Subject
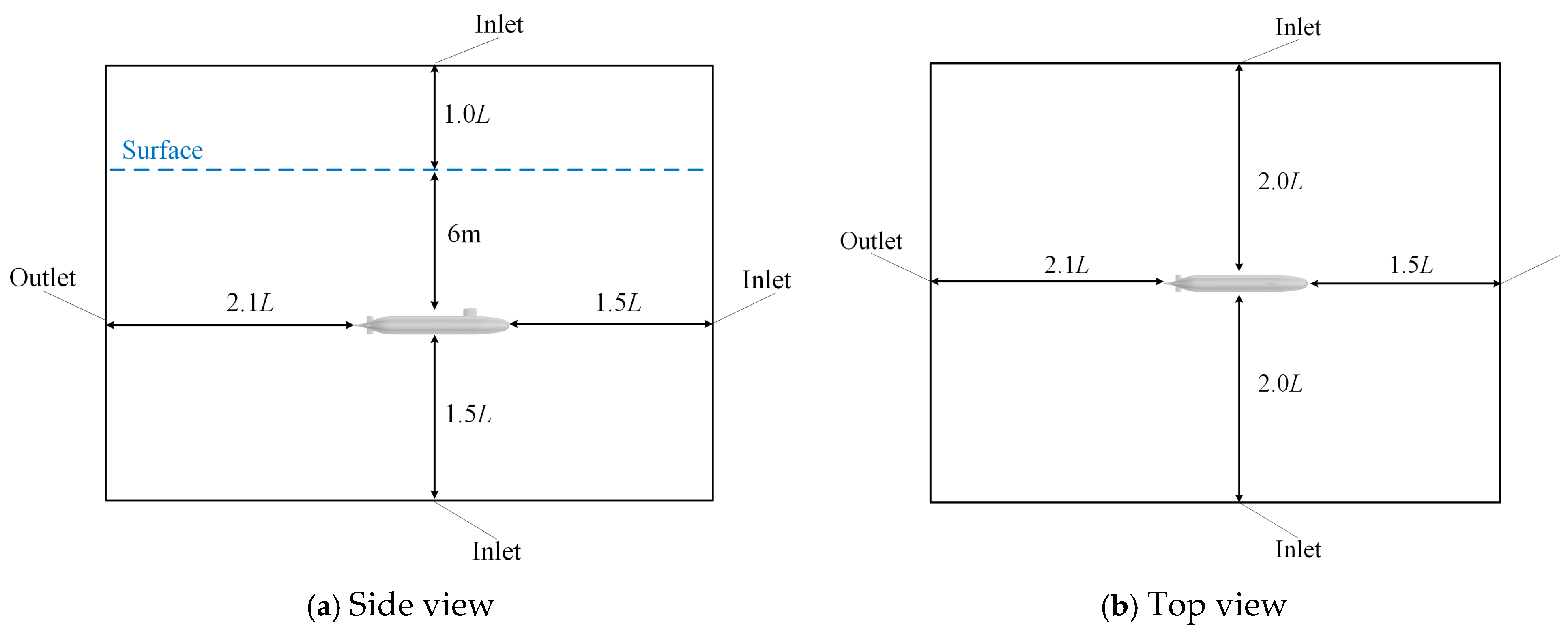
2.2. Computational Domain Setup
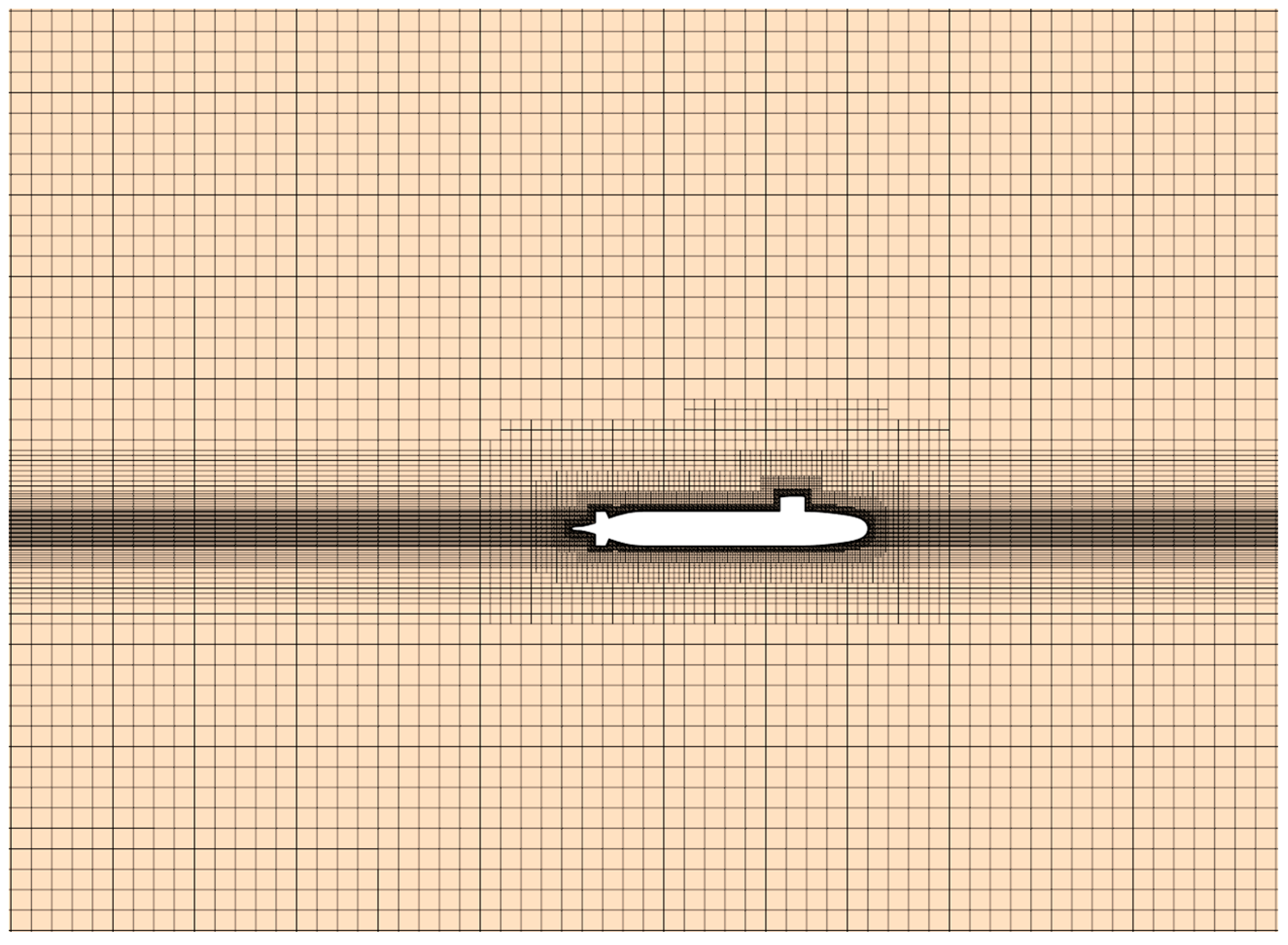
2.3. Mesh Partitioning
3. Numerical Simulation
3.1. Governing Equations
3.2. Turbulence Model
4. Validation of Results’ Effectiveness
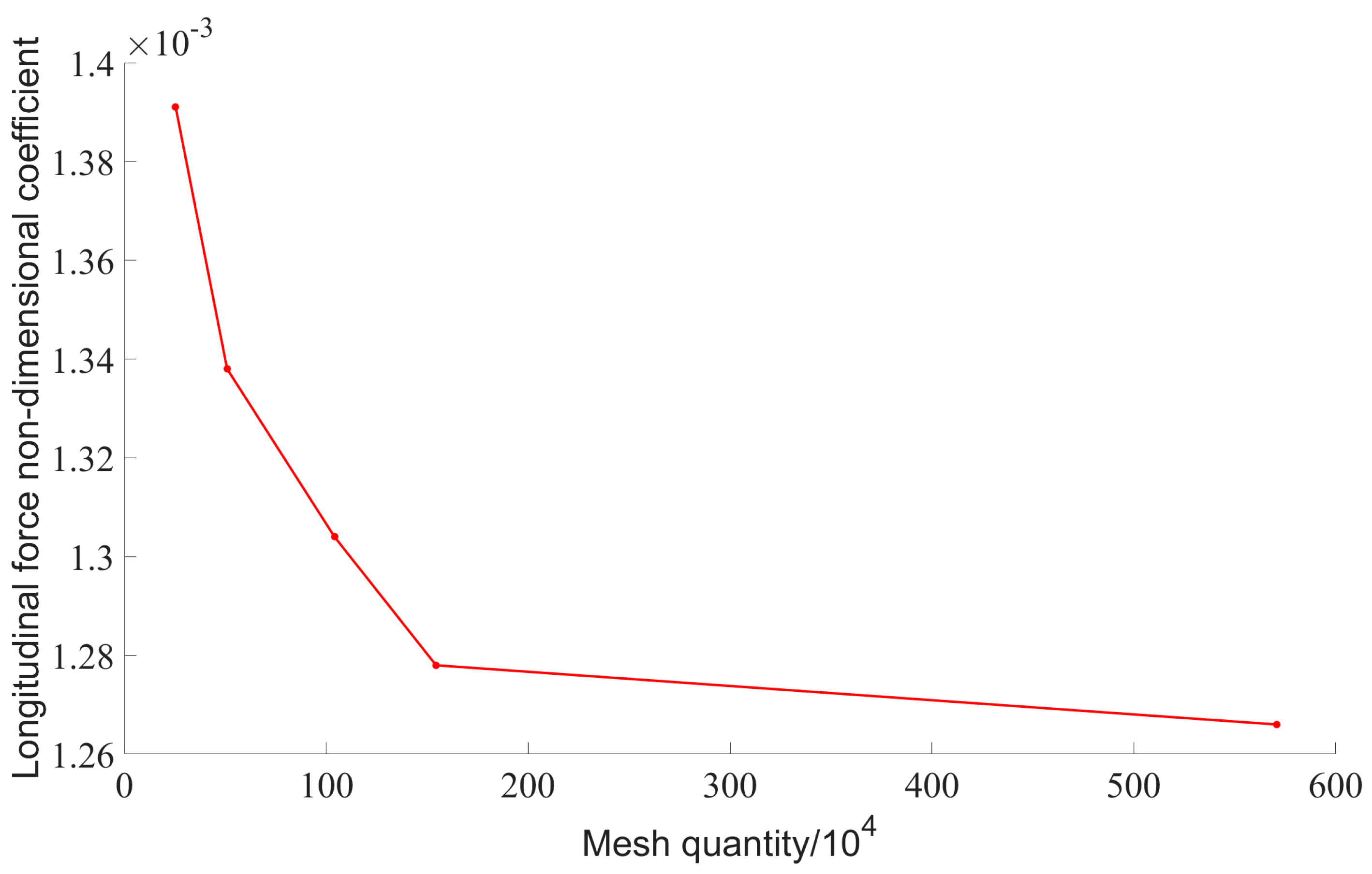
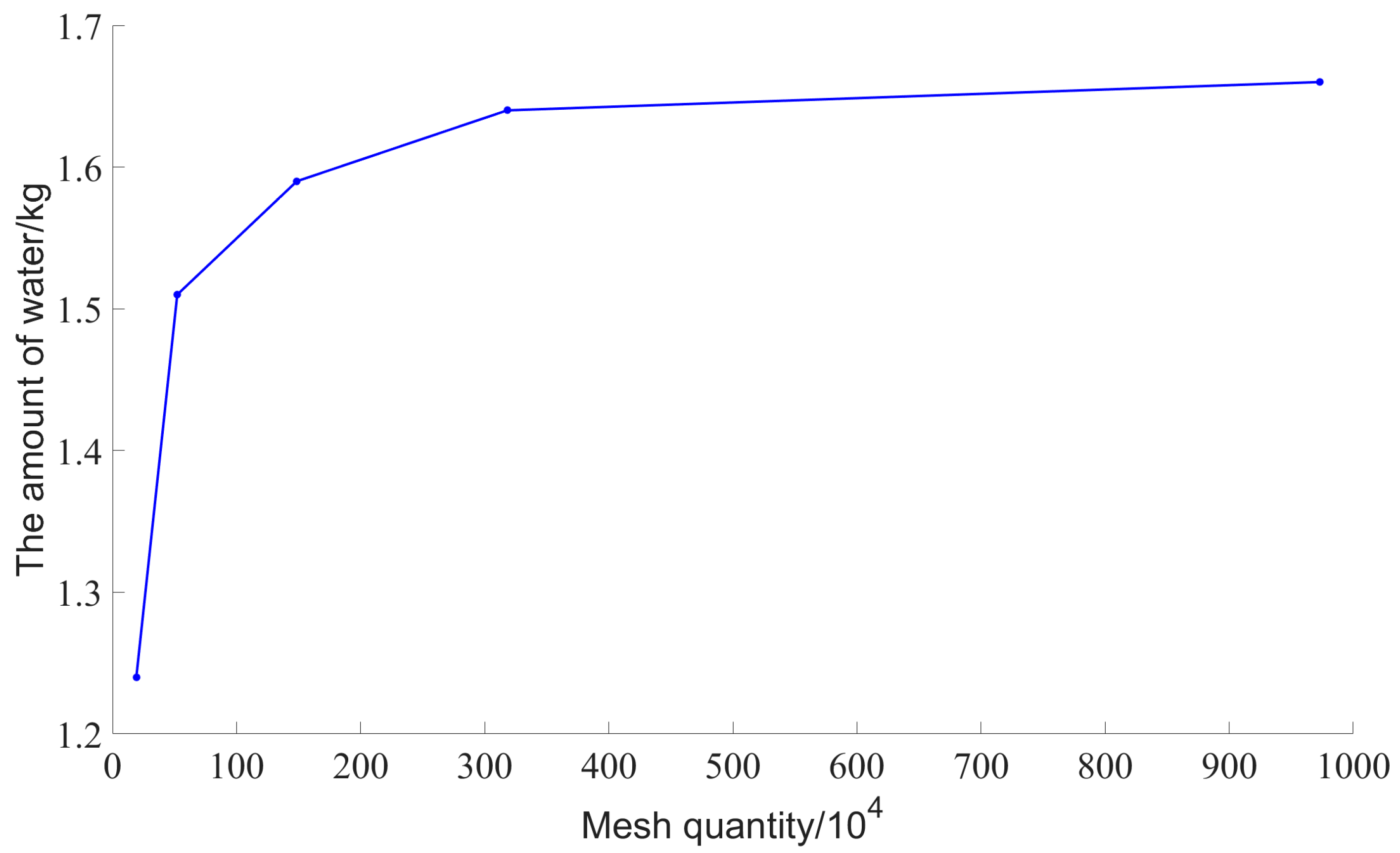
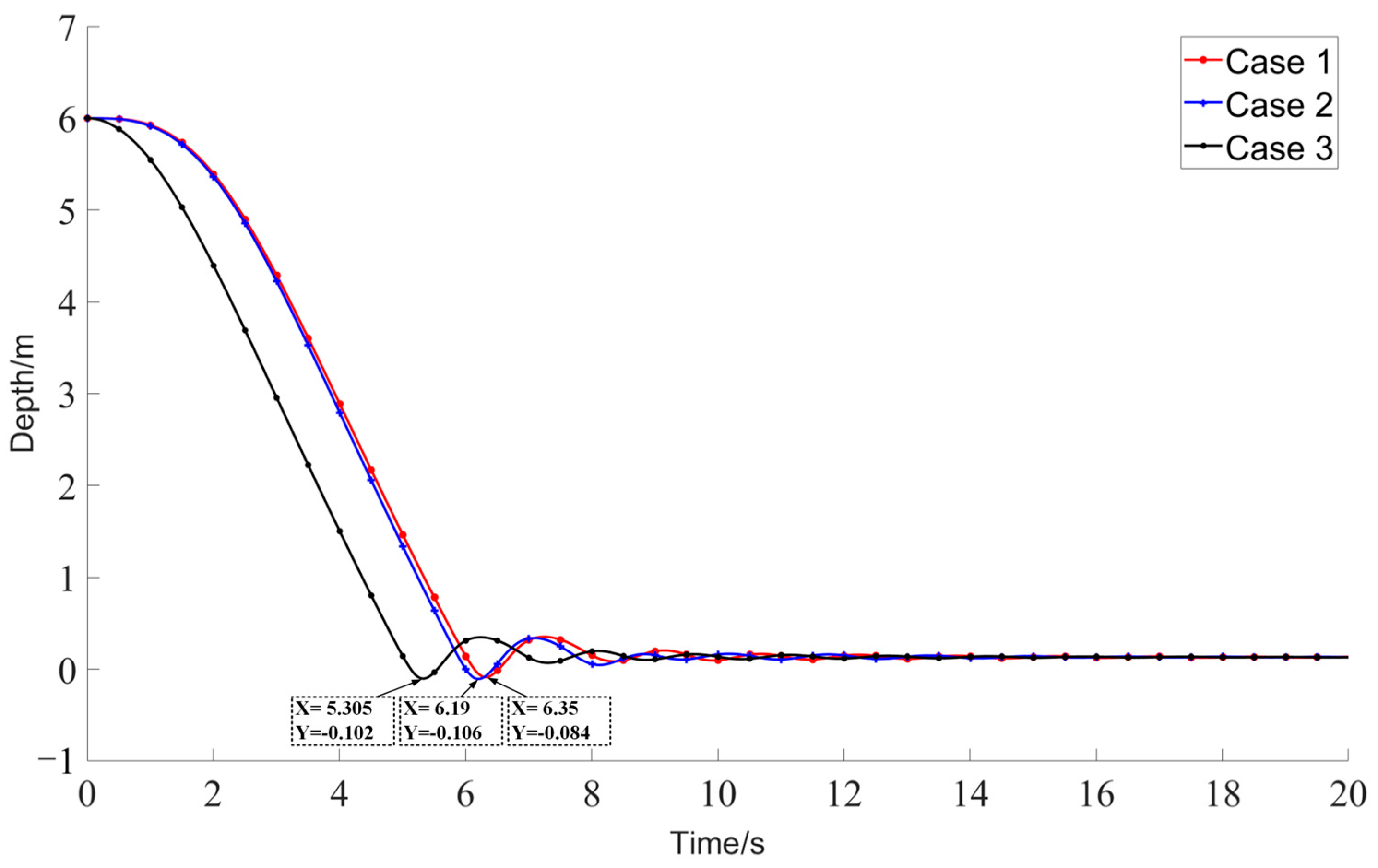
4.1. Mesh-Independence Analysis
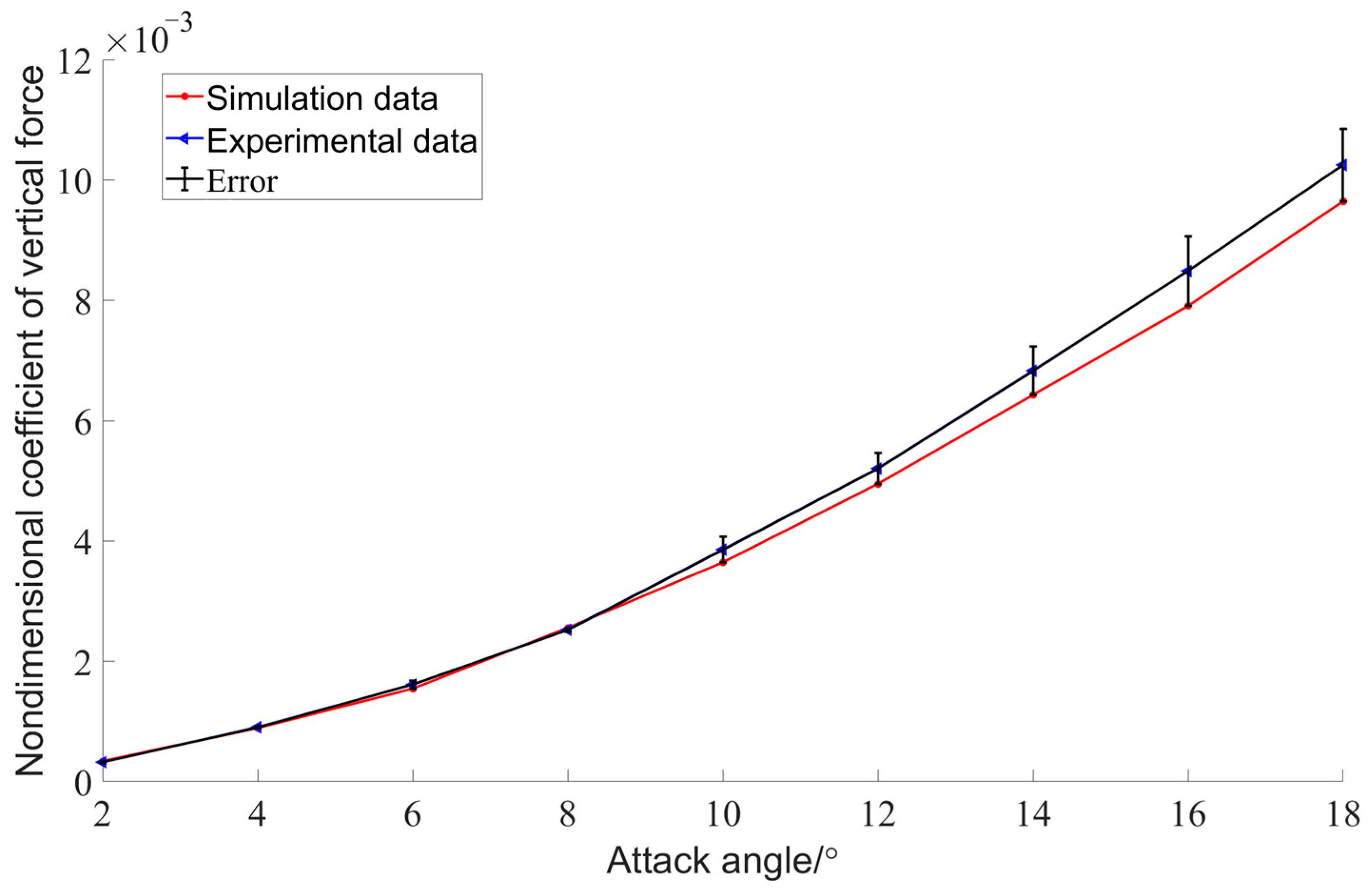
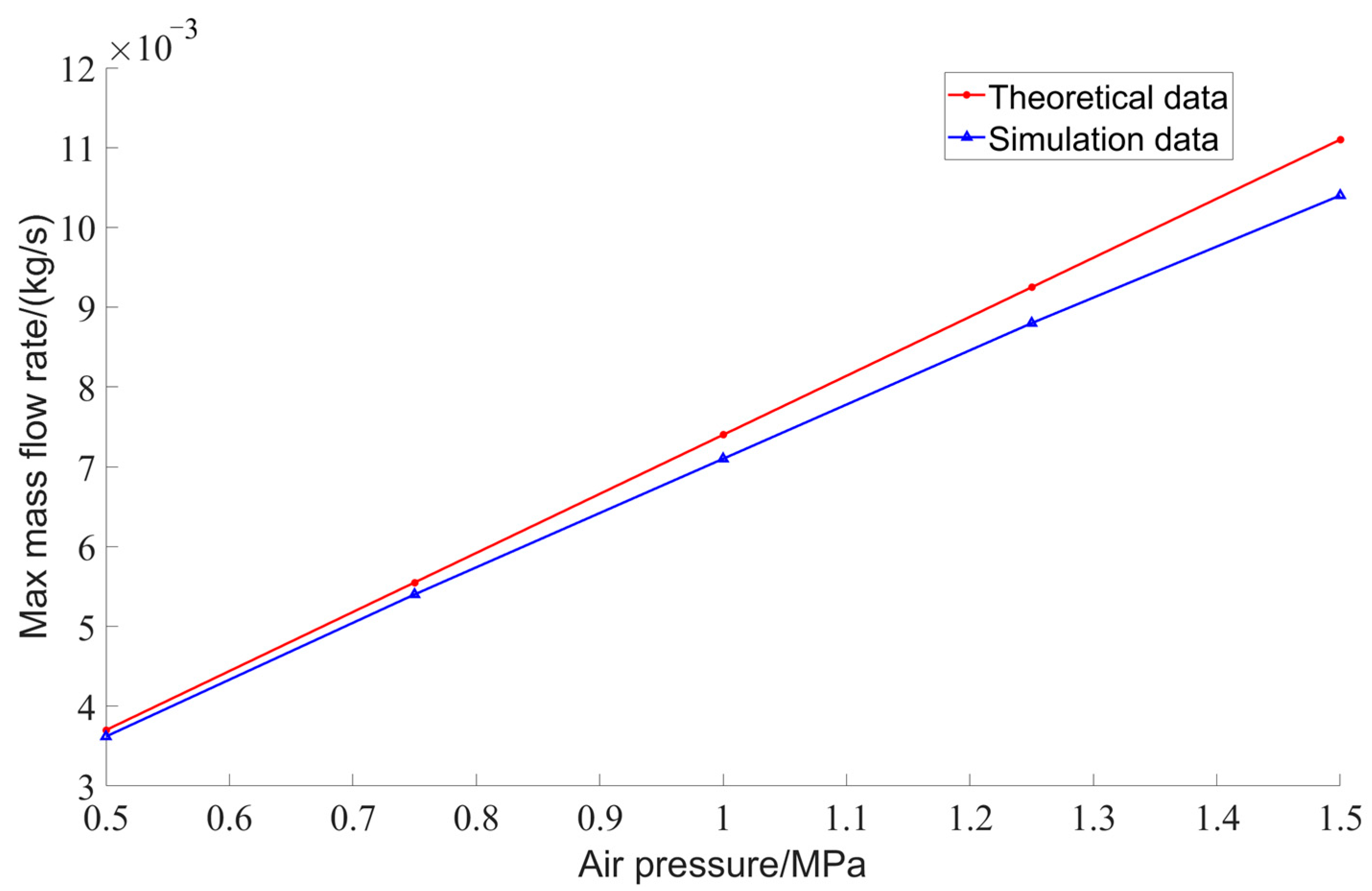
4.2. Validation of Simulation Accuracy
5. Simulation Scenarios and Results Analysis
5.1. Scenario Configuration
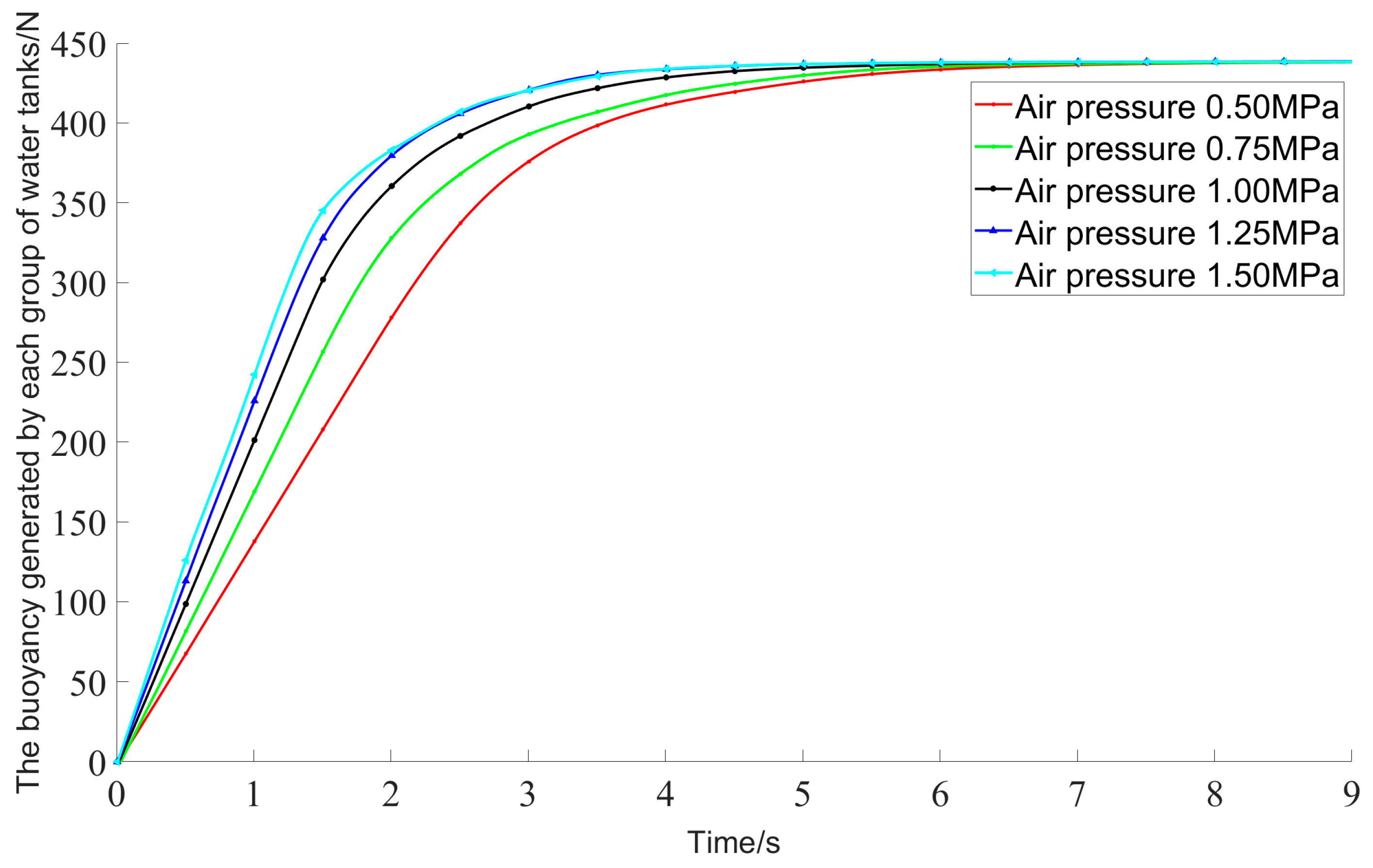
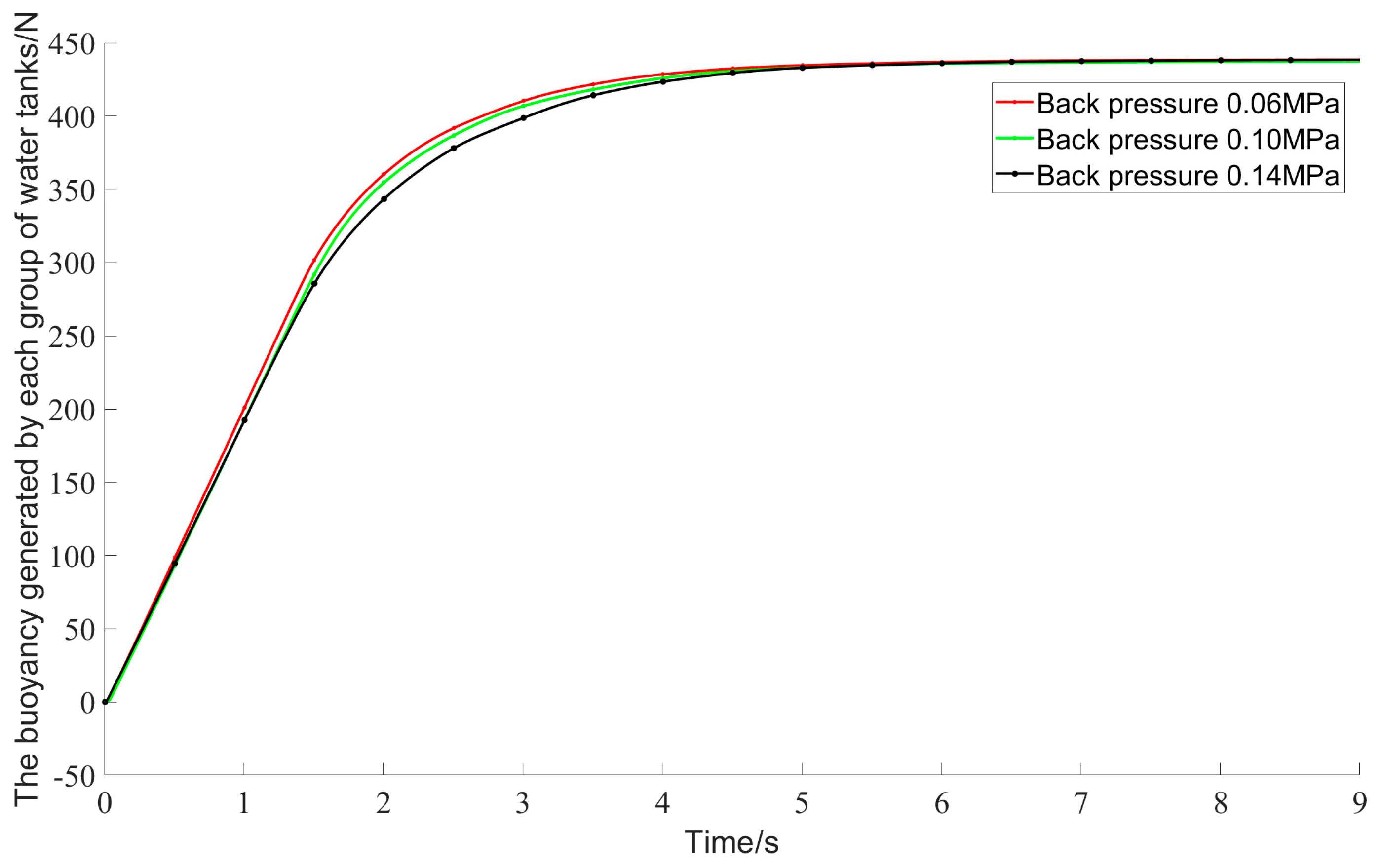
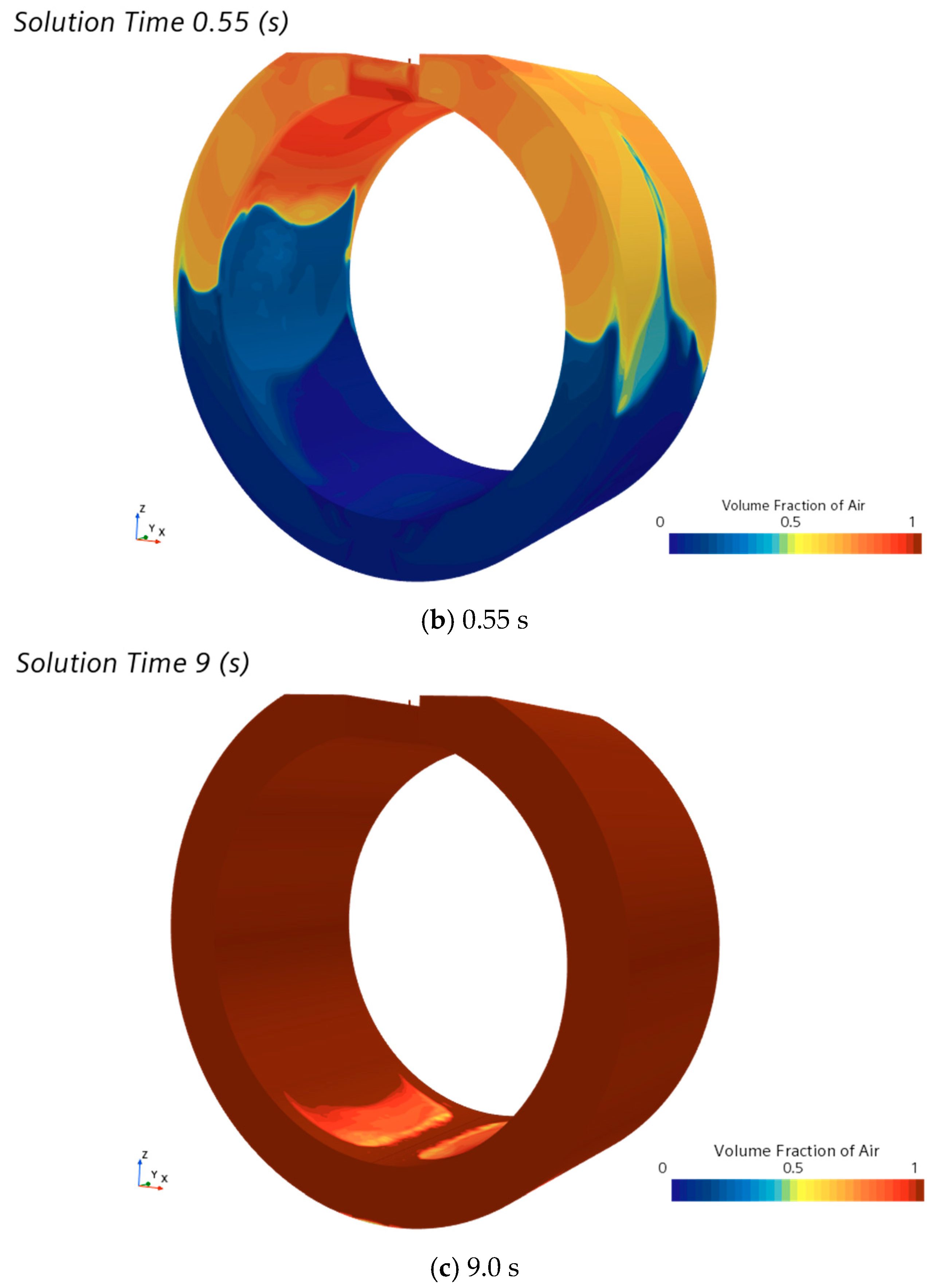
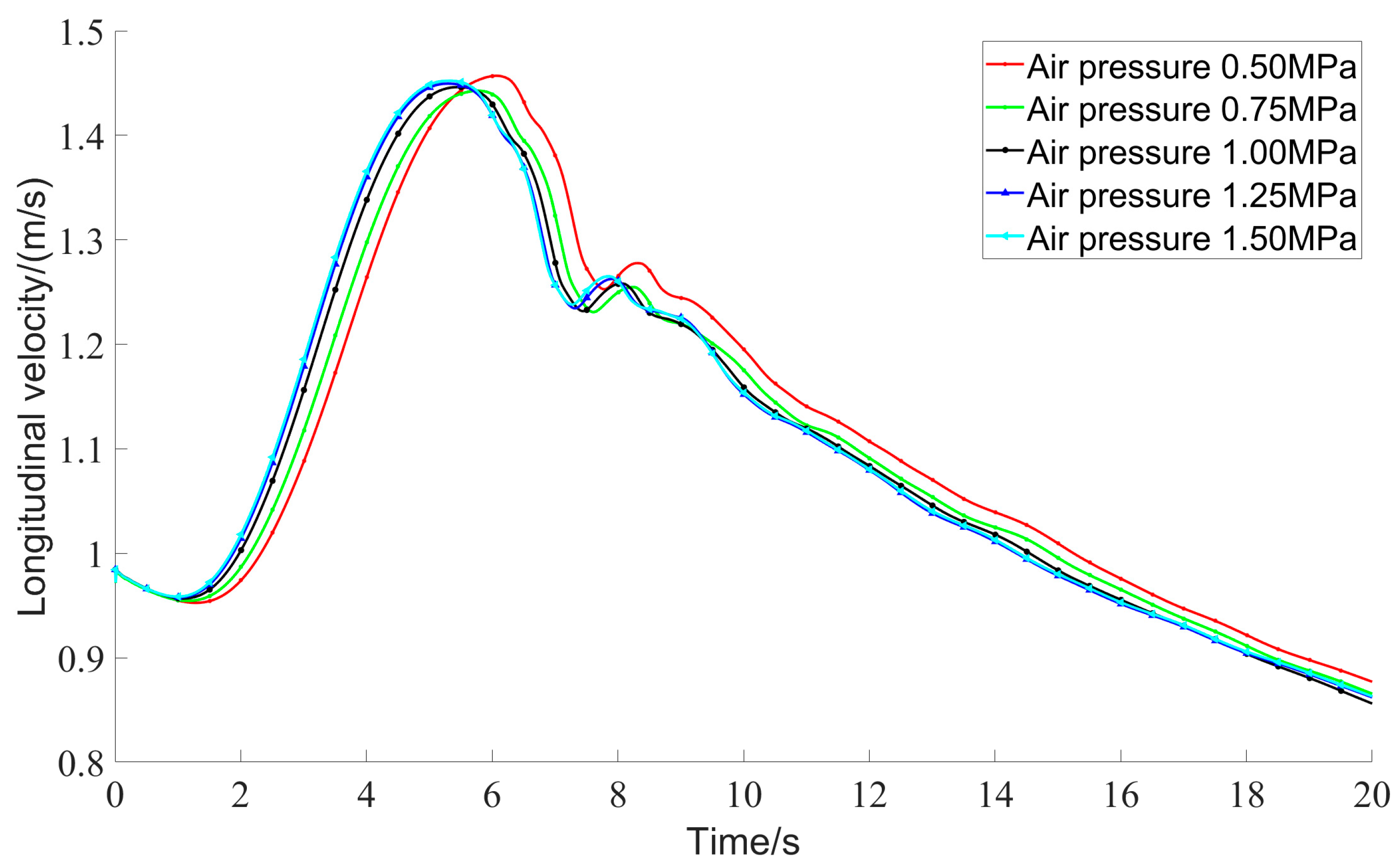
5.2. Simulation Results and Analysis of High-Pressure Air Blowing
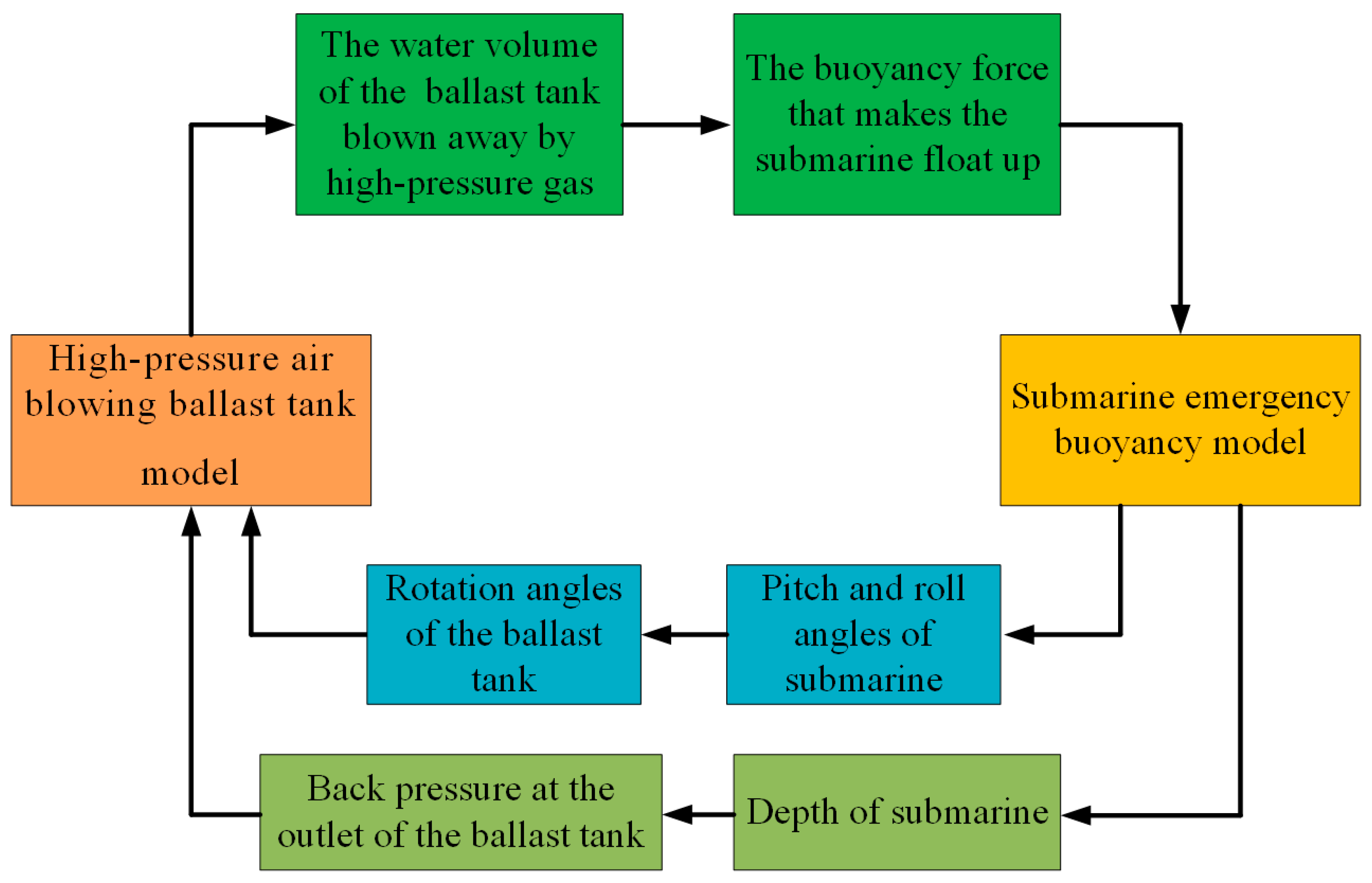
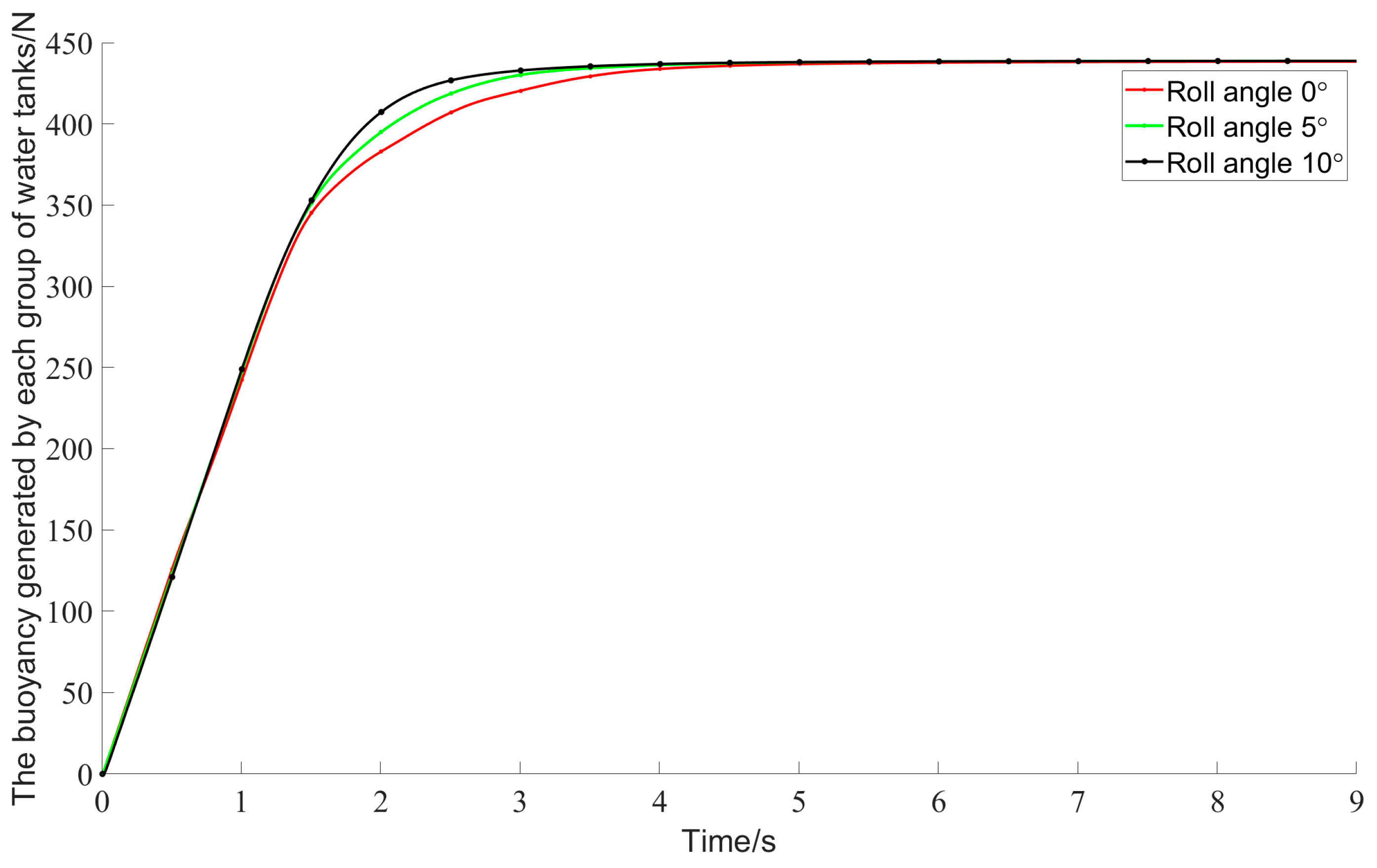
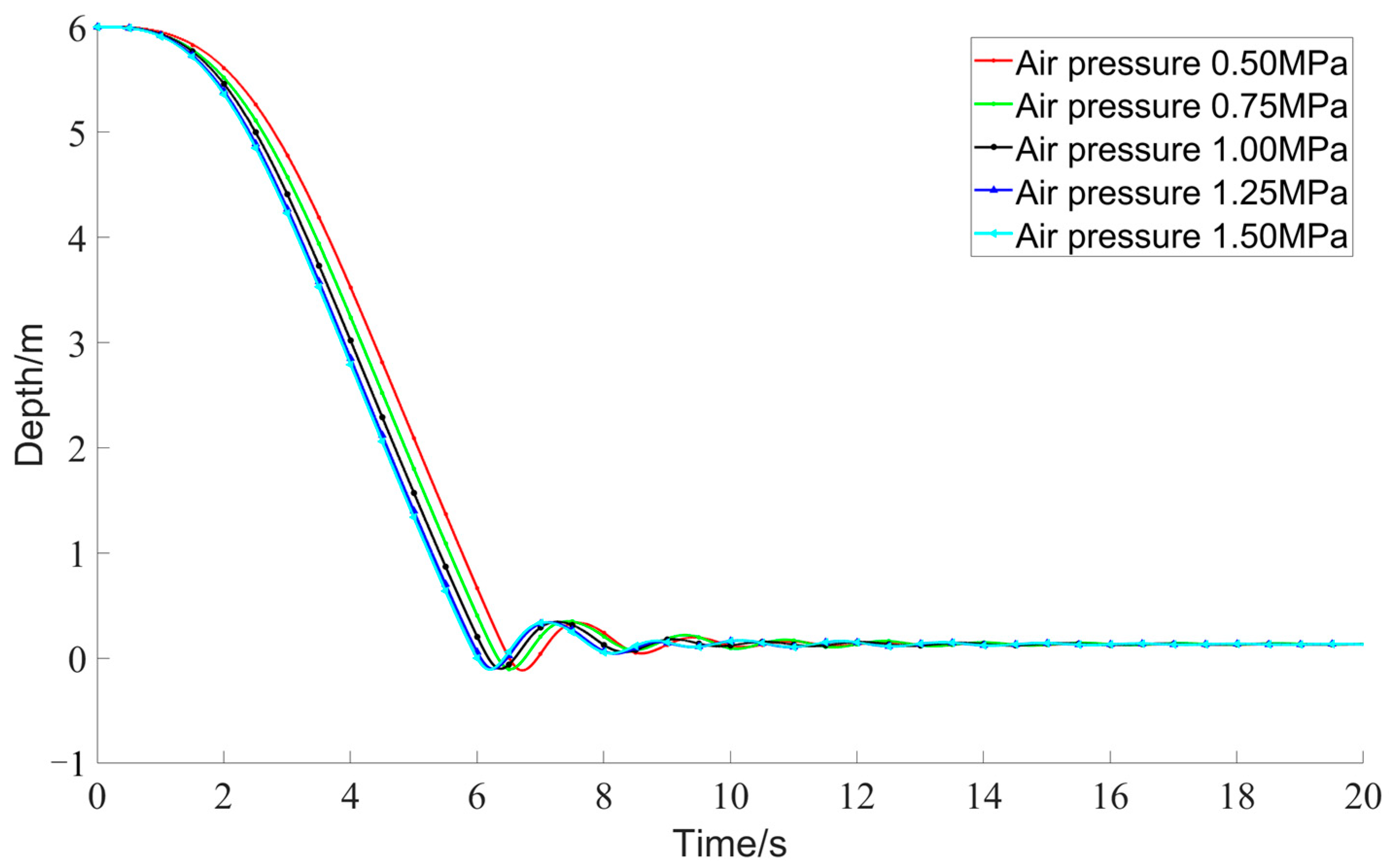
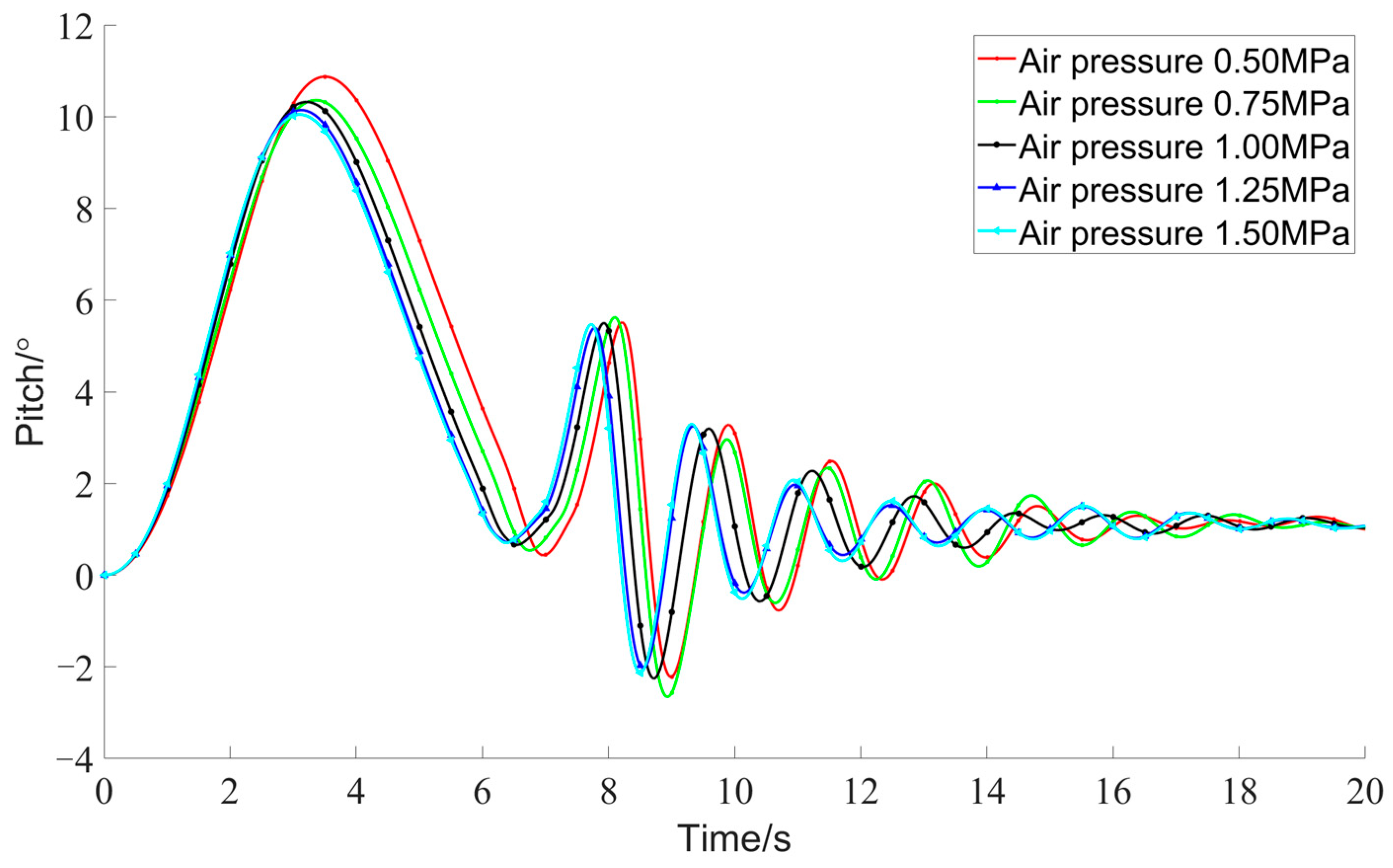
5.3. Coupled Simulation Results and Analysis
6. Discussion and Conclusions
- The hull emerges slightly earlier and reaches a marginally higher point when coupling effects are accounted for compared to scenarios where these effects are neglected.
- At constant expulsion pressures, larger pitch and roll angles, coupled with lower back pressures, accelerate the expulsion rate from the ballast tanks.
- Higher expulsion pressures facilitate quicker surfacing of the hull, reduce the amplitude of pitch angles, and increase the amplitude of roll angles.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pan, W.; Wang, Y.; Song, F.; Peng, L.; Zhang, X. UUV-Assisted Icebreaking Application in Polar Environments Using GA-SPSO. J. Mar. Sci. Eng. 2024, 12, 1845. [Google Scholar] [CrossRef]
- Lin, Y.-H.; Tseng, S.-H.; Chen, Y.-H. The experimental study on maneuvering derivatives of a submerged body SUBOFF by implementing the Planar Motion Mechanism tests. Ocean Eng. 2018, 170, 120–135. [Google Scholar] [CrossRef]
- Xiang, G.; Ou, Y.; Chen, J.; Wang, W.; Wu, H. Identification of Hydrodynamic Coefficients of the SUBOFF Submarine Using the Bayesian Ridge Regression Model. Appl. Sci. 2023, 13, 12342. [Google Scholar] [CrossRef]
- Park, J.-Y.; Kim, N.; Shin, Y.-K. Experimental study on hydrodynamic coefficients for high-incidence-angle maneuver of a submarine. Int. J. Nav. Archit. Ocean Eng. 2016, 8, 735–754. [Google Scholar] [CrossRef]
- Kim, D.J.; Kwon, C.S.; Lee, Y.Y.; Kim, Y.G.; Yun, K. Practical 6-dof manoeuvring simulation of a bb2 submarine near the free surface. Ocean Eng. 2024, 312, 23. [Google Scholar] [CrossRef]
- Watson, K.P.; Webster, J.S. Prediction of submersible maneuvering performance at high incidence angles. In Proceedings of the OCEANS’93, Victoria, BC, Canada, 18–21 October 1993; pp. 289–294. [Google Scholar]
- Font, R.; García-Peláez, J.; Murillo, J.A.; Periago, F. Modelling and control of blowing-venting operations in manned submarines. Ocean Eng. 2011, 38, 1627–1636. [Google Scholar]
- Gertler, M.; Hagen, G.R. Standard Equations of Motion for Submarine Simulation, NSRDC Report 2510. Available online: https://apps.dtic.mil/sti/pdfs/AD0653861.pdf (accessed on 25 November 2020).
- Liu, R.; Xiao, C.; Liu, Y. The experiment research of high-pressure air blowing ballast tanks. Appl. Mech. Mater. 2013, 411, 3010–3015. [Google Scholar] [CrossRef]
- Zhang, S.; Li, H.; Pang, Y.; Chen, Q.; Yan, P. Experimental investigation on roll stability of blunt-nose submarine in buoyantly rising maneuvers. Appl. Ocean Res. 2018, 81, 34–46. [Google Scholar] [CrossRef]
- Jung, J.S.; Lee, S.W.; Shin, J.H. A Model Experimental Study on Water flows out from the Ballast Tank for Emergency Rising of Submarines. J. Ocean Eng. Technol. 2024, 38, 370–383. [Google Scholar] [CrossRef]
- Wang, Z.; Dong, Z.; He, R.; Wang, X. Numerical simulation of submarine surfacing with 6 DOF model in the ocean current effect. In Proceedings of the 12th Pacific-Asia Offshore Mechanics Symposium, Gold Coast, Australia, 4–7 October 2016; pp. 137–143. [Google Scholar]
- Zhang, Z.; Guo, L.; Wei, P.; Wang, X.; Feng, D. Numerical simulation of submarine surfacing motion in regular waves. Iran. J. Sci. Technol. Trans. Mech. Eng. 2018, 44, 359–372. [Google Scholar] [CrossRef]
- Chen, Q.; Li, H.; Pang, Y.; Zhang, S.; Chang, W. Investigation of the excess roll problem of an emergent buoyantly rising submarine. J. Fluids Struct. 2019, 91, 102720. [Google Scholar] [CrossRef]
- Chen, Q.; Li, H.; Zhang, S.; Wang, J.; Pang, Y. Effect of waves on the behavior of emergent buoyantly rising submarines using CFD. Appl. Sci. 2020, 10, 8403. [Google Scholar] [CrossRef]
- Zhang, S.; Li, H.; Zhang, T.; Pang, Y.; Chen, Q. Numerical simulation study on the effects of course keeping on the roll stability of submarine emergency rising. Appl. Sci. 2019, 9, 3285. [Google Scholar] [CrossRef]
- Wei, K.; Gao, X.; Liu, D.; Wei, F.; Luo, P. Numerical calculation of six degree of freedom floating motion of submarine with flow holes. J. Mar. Sci. Technol. 2022, 27, 916–934. [Google Scholar] [CrossRef]
- Wei, K.; Gao, X.; Liu, D.; Wei, F.; Luo, P. Research on the submarine floating movement in waves involving the water holes. Ocean Eng. 2023, 272, 111326. [Google Scholar] [CrossRef]
- Guo, X.; Ou, Y.; Chen, J.; Wang, W.; Wu, H. A study on the influence of unsteady forces on the roll characteristics of a submarine during free ascent from great depth. J. Mar. Sci. Eng. 2024, 12, 757. [Google Scholar] [CrossRef]
- Xiang, G.; Ou, Y.; Chen, J.; Wang, W.; Wu, H. Numerical Study on the Flow Characteristics of High Attack Angle around the Submarine’s Vertical Plane. Appl. Sci. 2024, 14, 395. [Google Scholar] [CrossRef]
- Chen, X.; Yao, J. Rans analysis of manoeuvring hydrodynamic performance for a submarine in six degree of freedom motion. Ocean Eng. 2024, 294, 116781. [Google Scholar] [CrossRef]
- Lin, Y.; Li, X. The investigation of a sliding mesh model for hydrodynamic analysis of a suboff model in turbulent flow fields. J. Mar. Sci. Eng. 2020, 8, 744. [Google Scholar] [CrossRef]
- ITTC. ITTC—Recommended Procedures and Guidelines 7.5-03-01-04 CFD. In General CFD Verification; ITTC: Singapore, 2011. [Google Scholar]
- Roddy, R.F. Investigation of the stability and control characteristics of several configurations of the DARPA Suboff model (DTRC Model 5470) from captive-model experiments. In David Taylor Research Center Report; Ship Hydromechanics Dept, David Taylor Research Center: Bethesda, MD, USA, 1990. [Google Scholar]




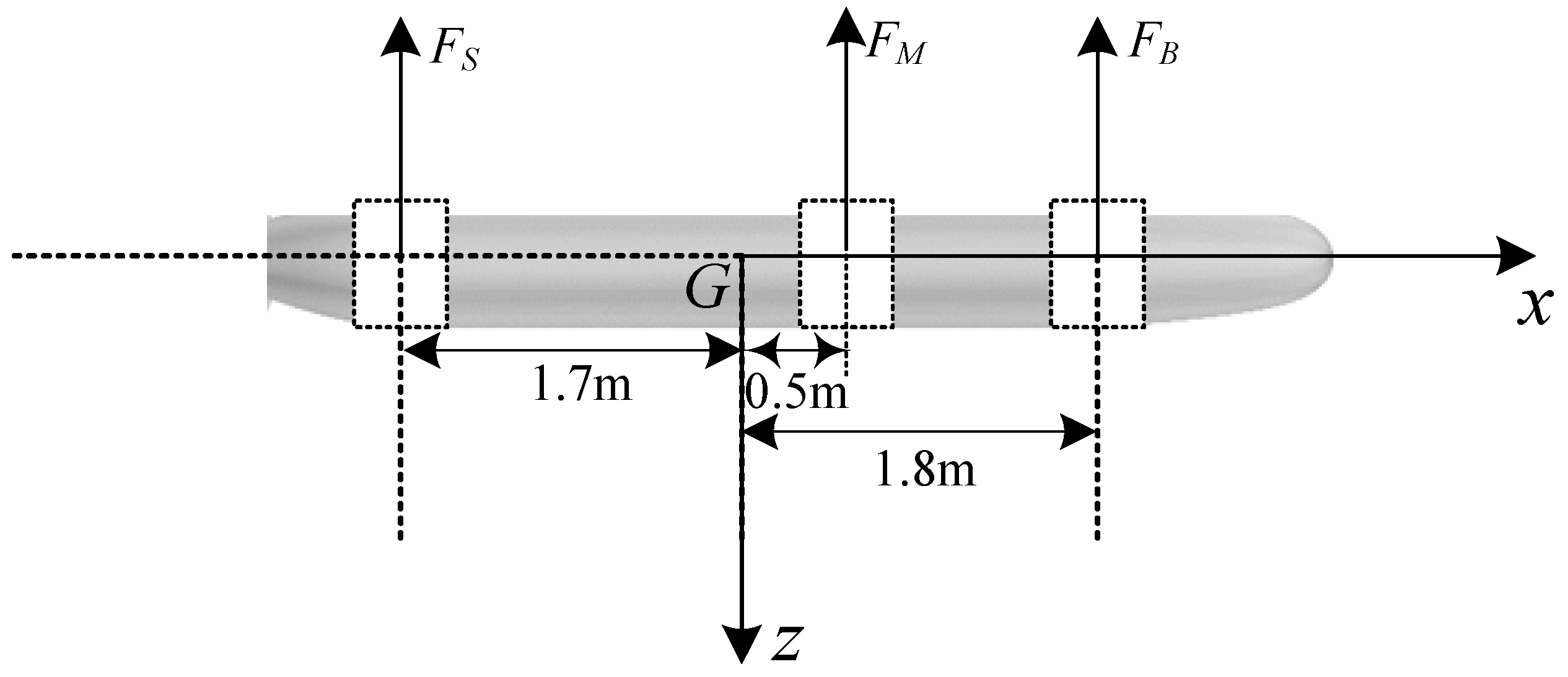








| Parameters | Value |
|---|---|
| Length L (m) | 4.356 |
| Beam B (m) | 0.508 |
| Submerged Displacement Mass M (kg) | 704 kg |
| Center of Gravity Position (m) | (2.002, 0.0, 0.02) |
| Moment of Inertia (kg·m−2) | (27.65, 834.15, 834.15) |
| Submarine emergency buoyancy model | Mesh size/m | 0.141 | 0.1 | 0.07 | 0.05 | 0.035 |
| Mesh quantity/104 | 25.4 | 50.9 | 104.1 | 154.4 | 570.8 | |
| High-pressure air blowing ballast tank model | Mesh size/m | 0.004 | 0.0028 | 0.002 | 0.0014 | 0.001 |
| Mesh quantity/104 | 19.2 | 52.2 | 148.6 | 318.1 | 973.1 |
| Attack Angle (°) | (10−3) | (10−3) | Relative Error |
|---|---|---|---|
| 2 | 0.3422 | 0.3237 | 5.7% |
| 4 | 0.8907 | 0.9034 | −1.4% |
| 6 | 1.545 | 1.612 | −4.2% |
| 8 | 2.556 | 2.525 | 1.2% |
| 10 | 3.644 | 3.856 | −5.5% |
| 12 | 4.949 | 5.205 | −4.9% |
| 14 | 6.427 | 6.829 | −5.9% |
| 16 | 7.905 | 8.486 | −6.8% |
| 18 | 9.645 | 10.25 | −5.9% |
| Attack Angle (°) | (10−3) | (10−3) | Relative Error |
|---|---|---|---|
| 2 | 0.4424 | 0.4761 | −7.1% |
| 4 | 0.7908 | 0.8326 | −5.0% |
| 6 | 1.110 | 1.105 | 0.5% |
| 8 | 1.341 | 1.315 | 2.0% |
| 10 | 1.491 | 1.462 | 2.0% |
| 12 | 1.585 | 1.543 | 2.7% |
| 14 | 1.689 | 1.621 | 4.2% |
| 16 | 1.807 | 1.704 | 6.1% |
| 18 | 1.909 | 1.762 | 8.3% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Peng, L.; Lv, B.; Pan, W.; Wang, Y. Coupled Simulation Study on the High-Pressure Air Expulsion from Submarine Ballast Tanks and Emergency Surfacing Dynamics. J. Mar. Sci. Eng. 2025, 13, 1769. https://doi.org/10.3390/jmse13091769
Chen J, Peng L, Lv B, Pan W, Wang Y. Coupled Simulation Study on the High-Pressure Air Expulsion from Submarine Ballast Tanks and Emergency Surfacing Dynamics. Journal of Marine Science and Engineering. 2025; 13(9):1769. https://doi.org/10.3390/jmse13091769
Chicago/Turabian StyleChen, Jiabao, Likun Peng, Bangjun Lv, Wei Pan, and Yong Wang. 2025. "Coupled Simulation Study on the High-Pressure Air Expulsion from Submarine Ballast Tanks and Emergency Surfacing Dynamics" Journal of Marine Science and Engineering 13, no. 9: 1769. https://doi.org/10.3390/jmse13091769
APA StyleChen, J., Peng, L., Lv, B., Pan, W., & Wang, Y. (2025). Coupled Simulation Study on the High-Pressure Air Expulsion from Submarine Ballast Tanks and Emergency Surfacing Dynamics. Journal of Marine Science and Engineering, 13(9), 1769. https://doi.org/10.3390/jmse13091769






