Full Waveform Inversion of Irregularly Sampled Passive Seismic Data Based on Robust Multi-Dimensional Deconvolution
Abstract
1. Introduction
2. Methods
2.1. Robust Multi-Dimensional Deconvolution (RMDD) Seismic Interferometry Based on Multi-Domain Stepwise Interpolation
2.1.1. Traditional Seismic Interferometry
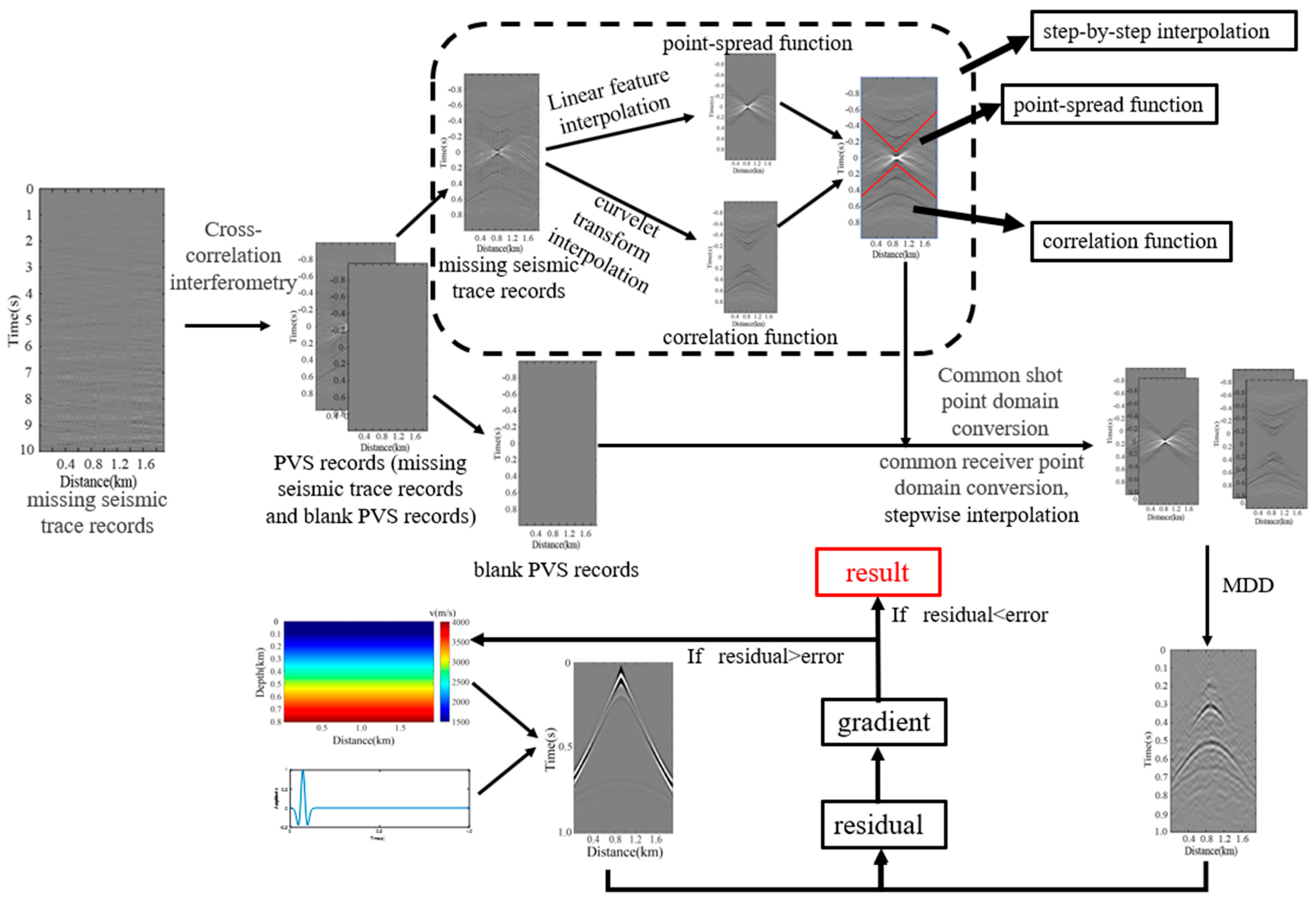
2.1.2. RMDD Based on Multi-Domain Stepwise Interpolation
2.2. PSFWI Based on RMDD
2.2.1. Source-Independent Time-Domain PSFWI
2.2.2. Normalized Correlation PSFWI Based on RMDD (RMDD-NCPSFWI)
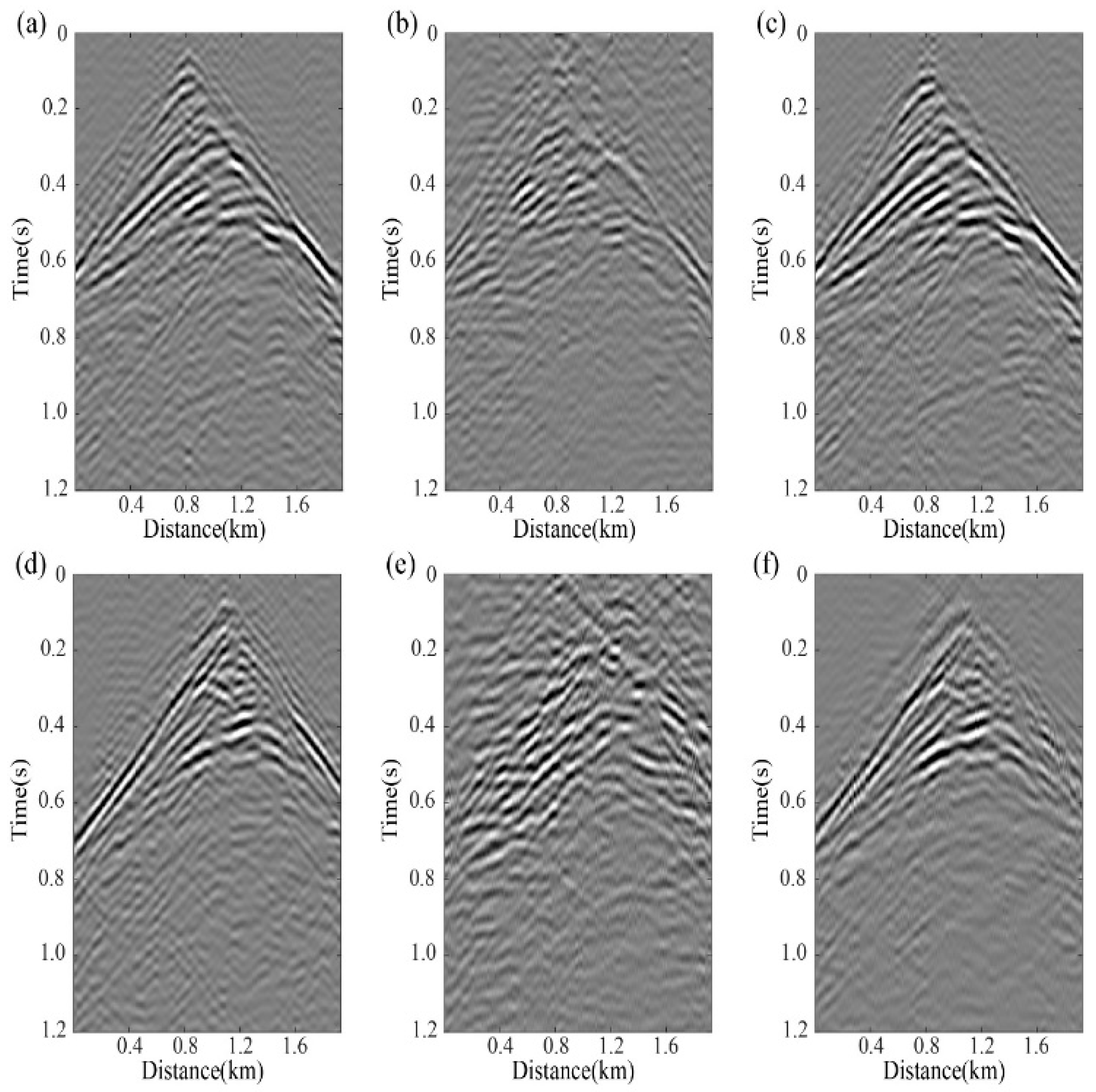
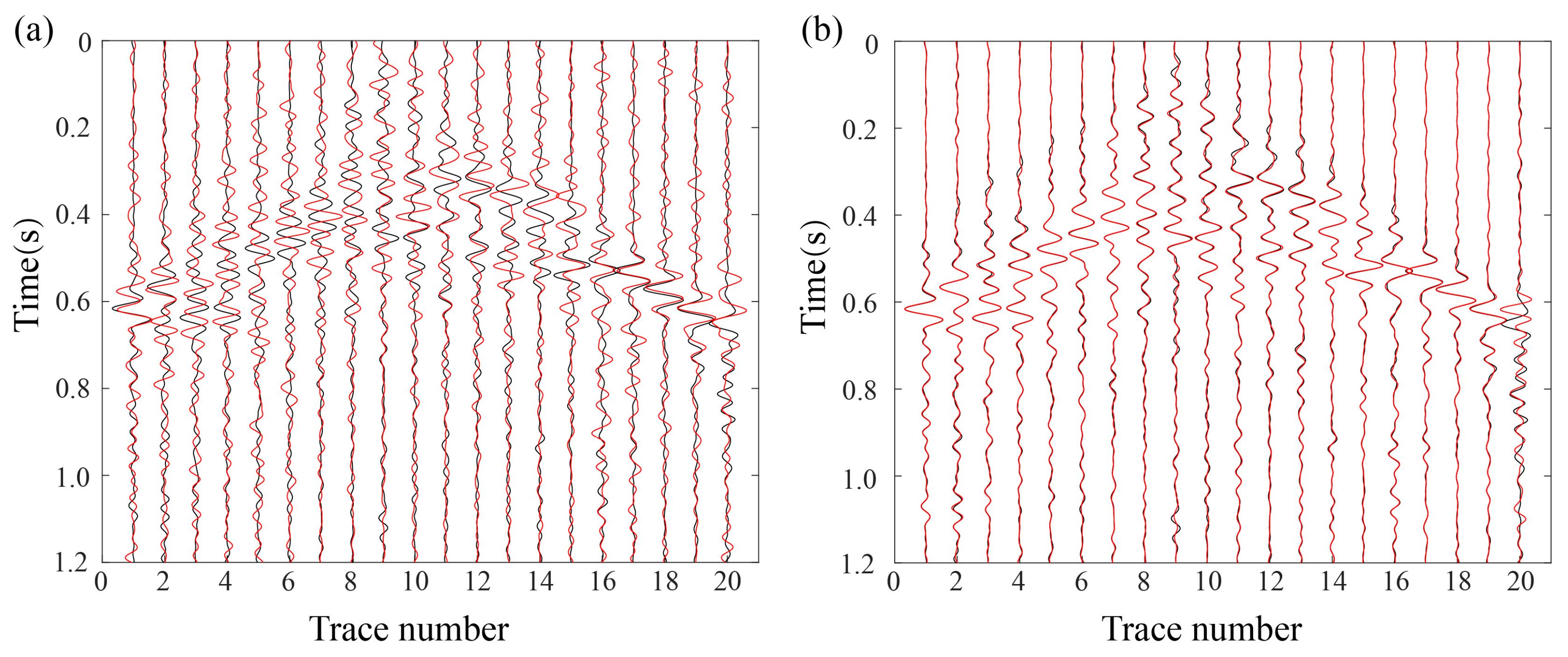
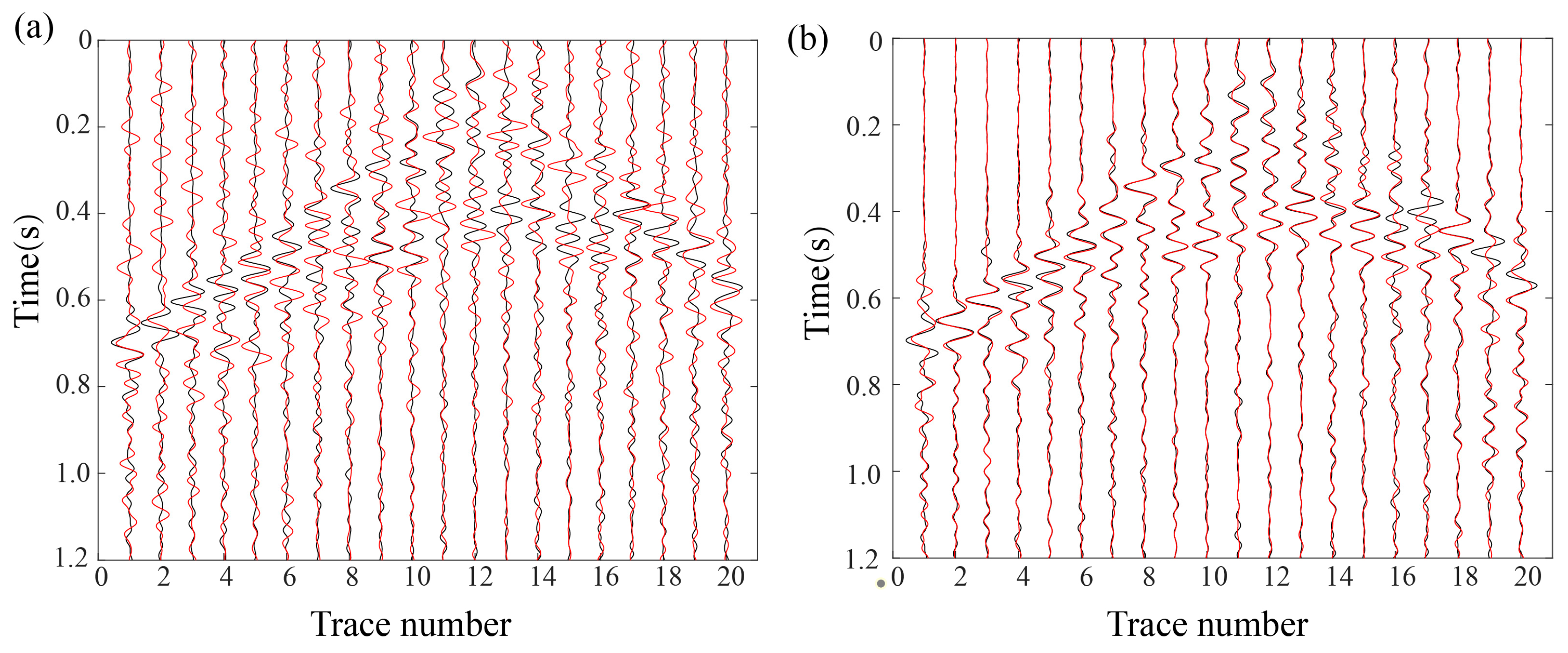
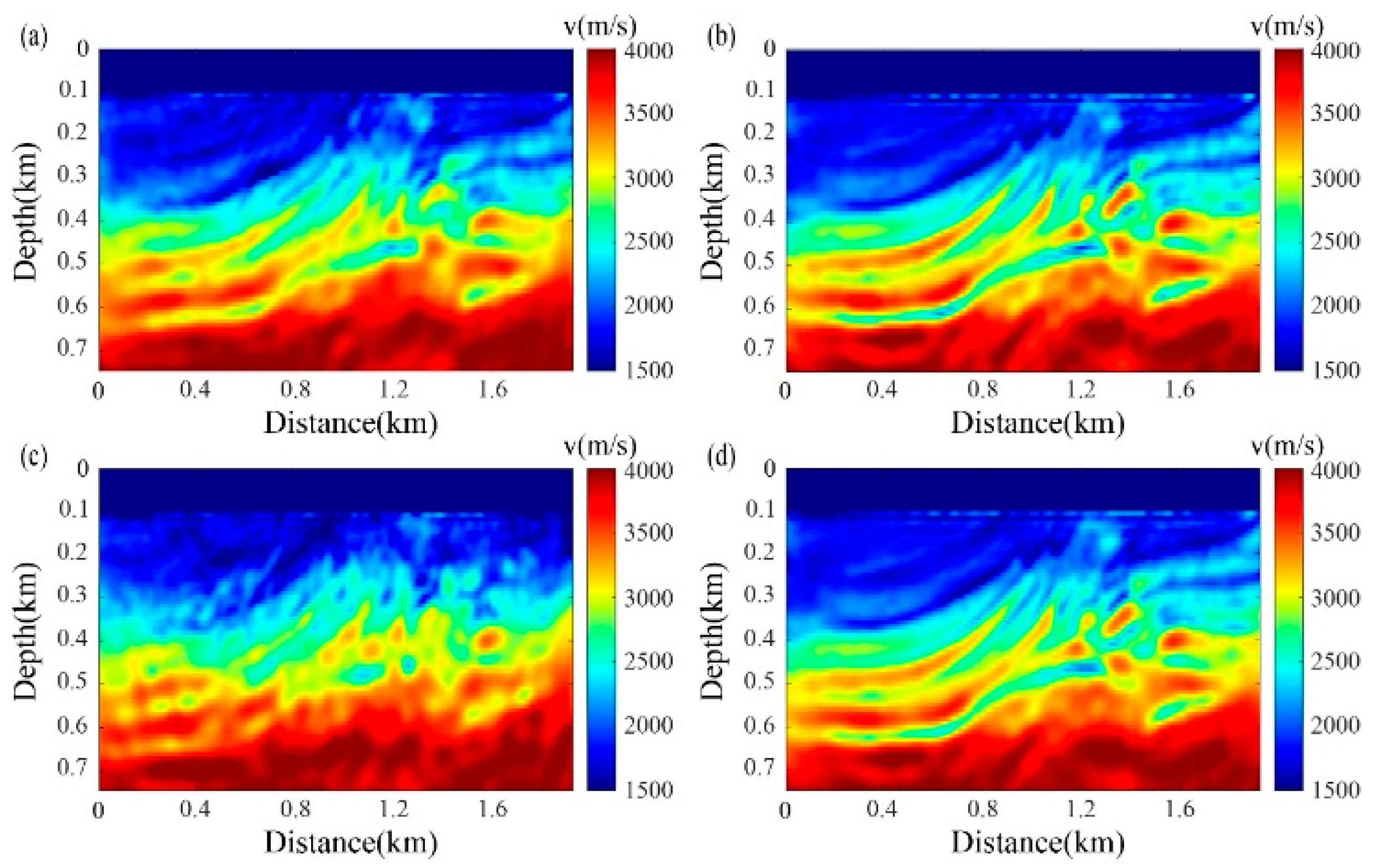
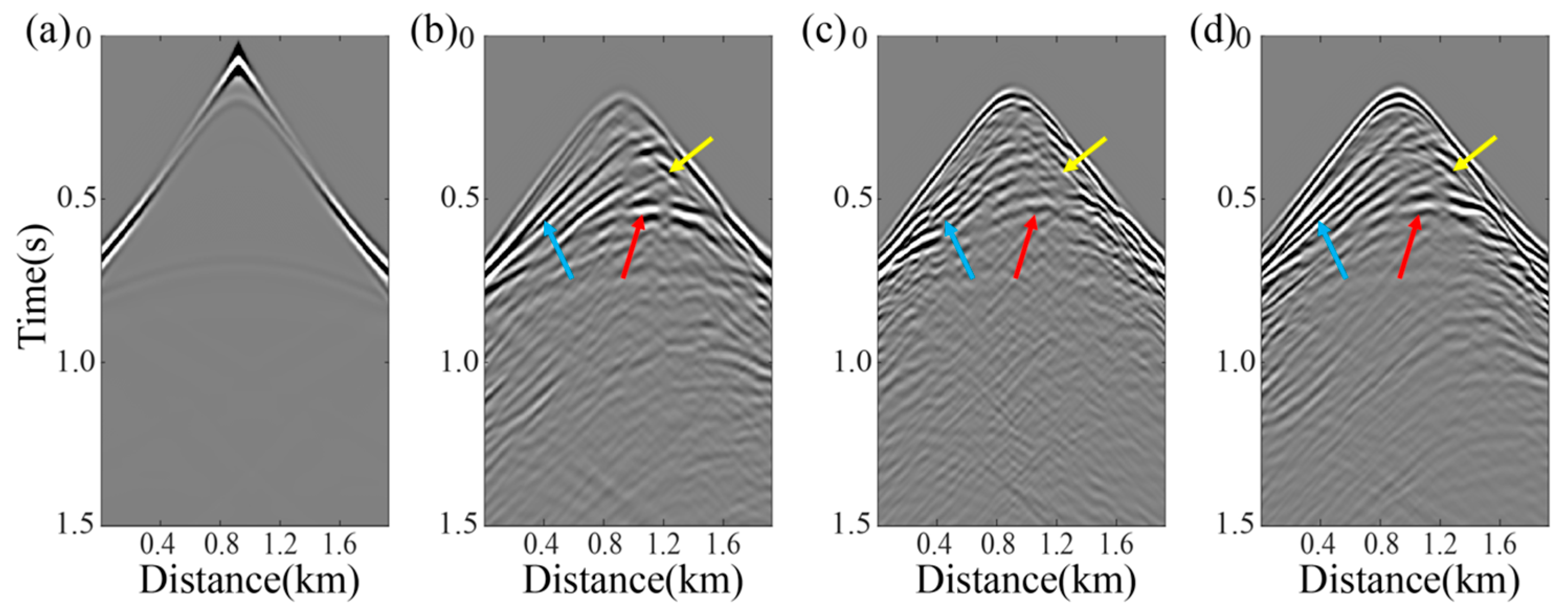
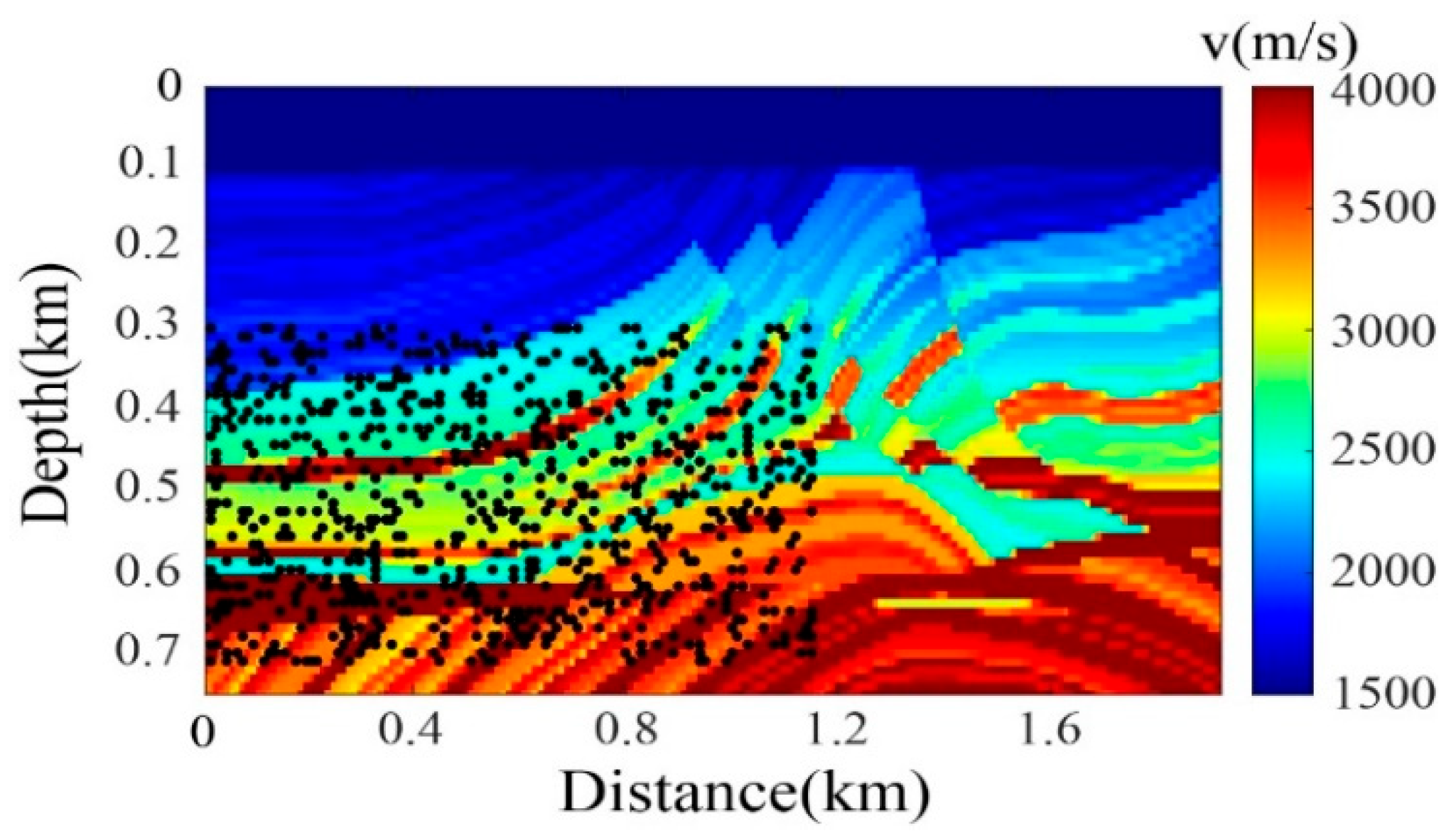
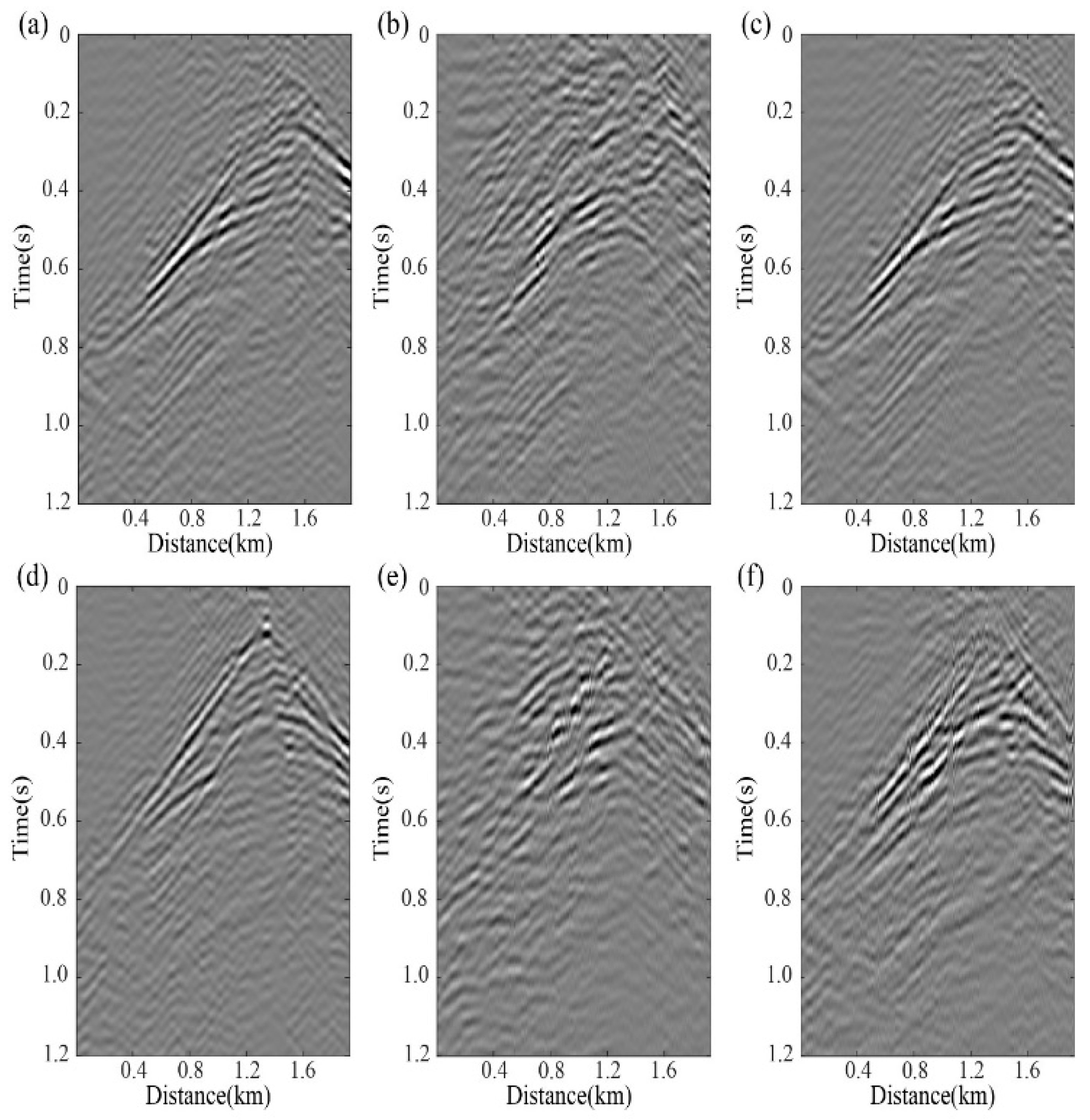
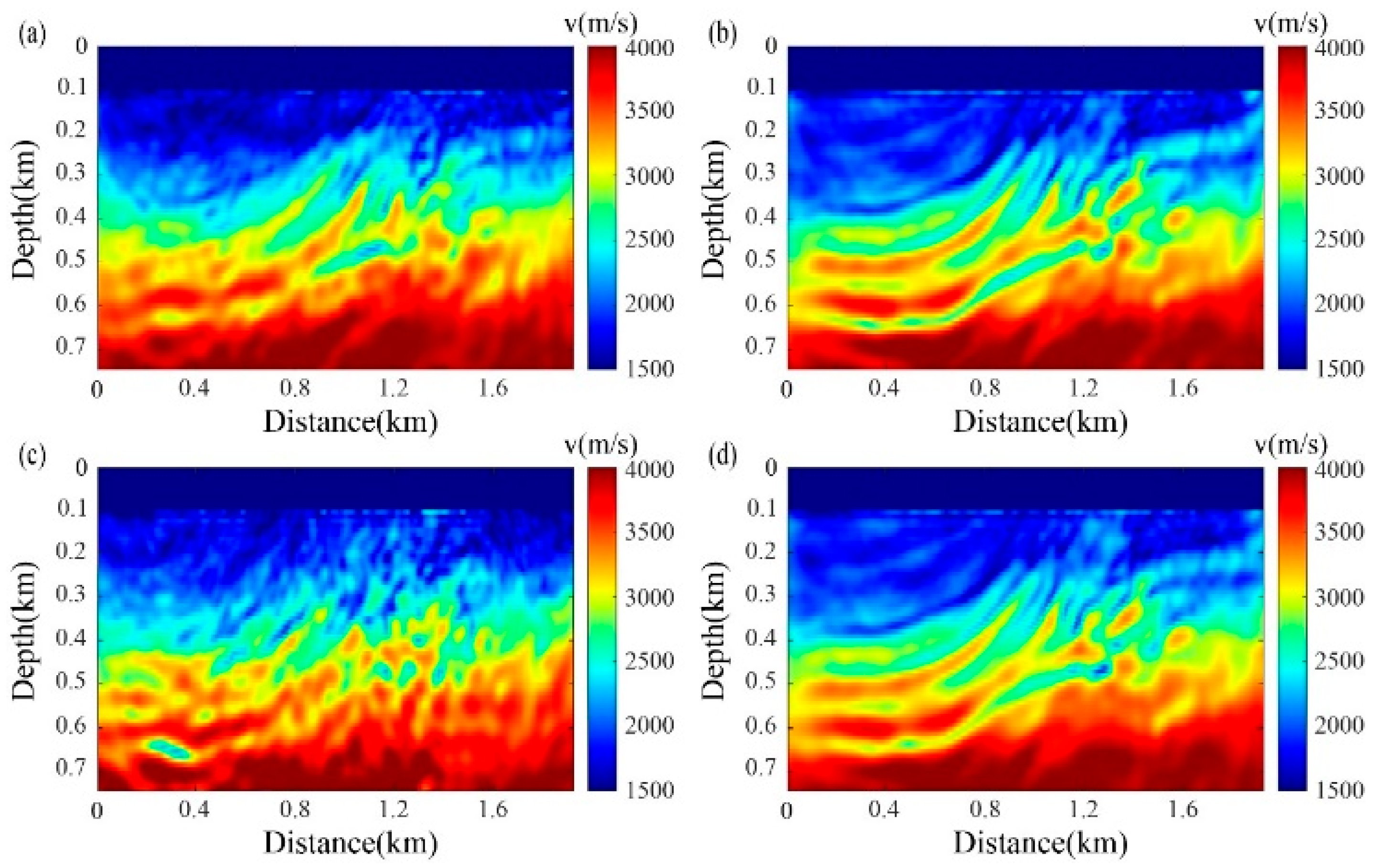
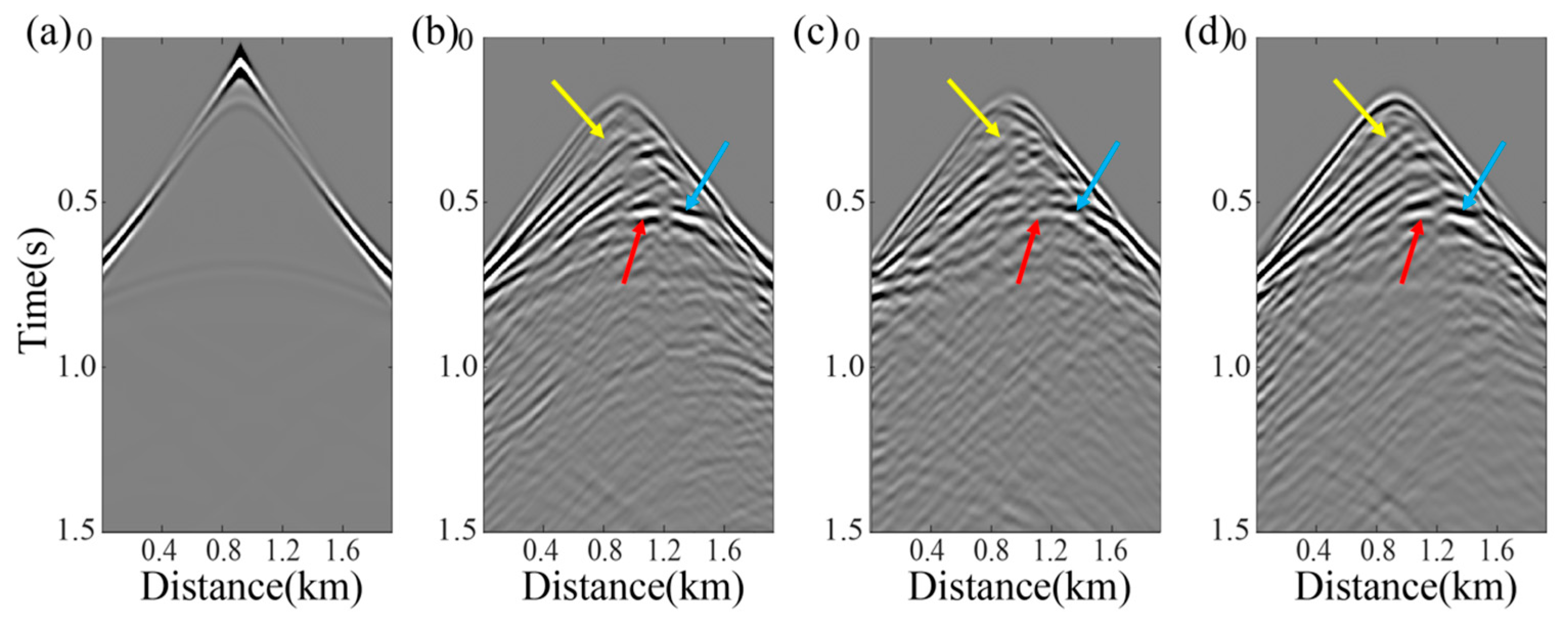
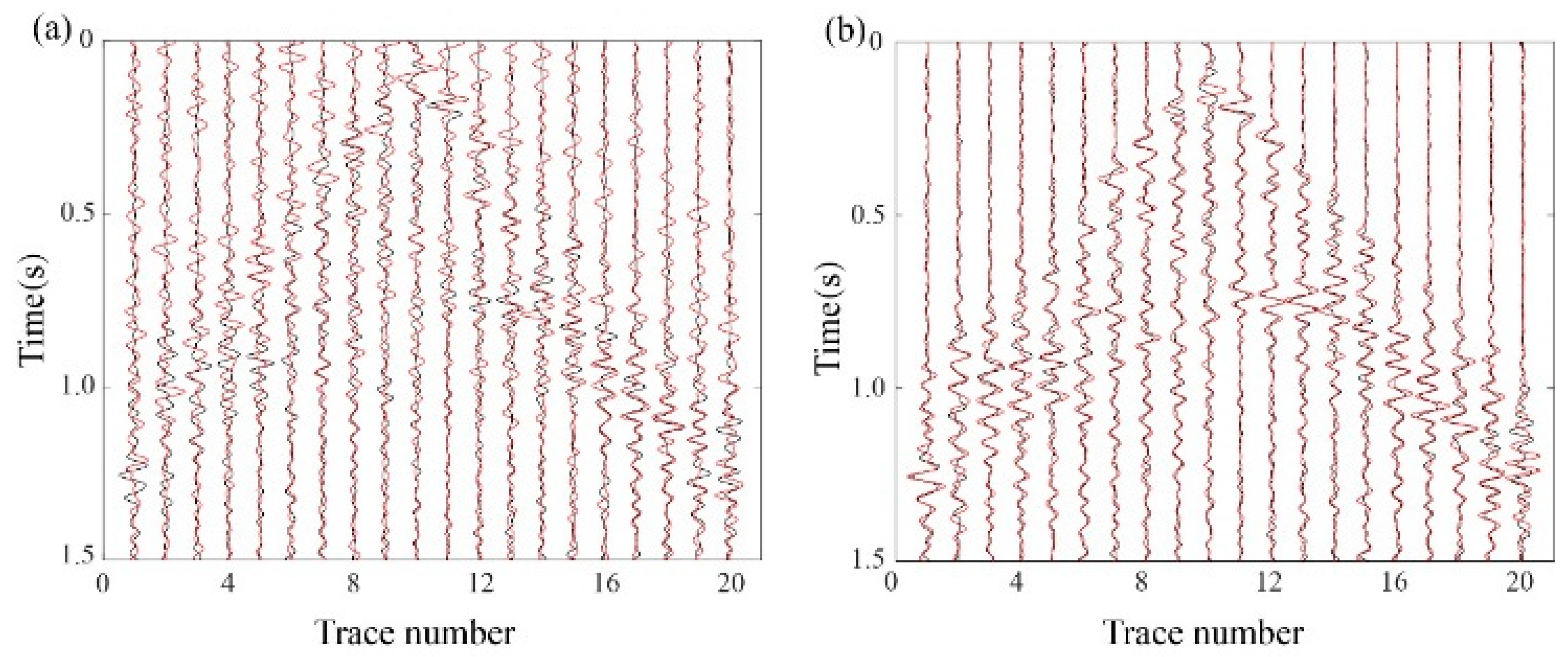
3. Results
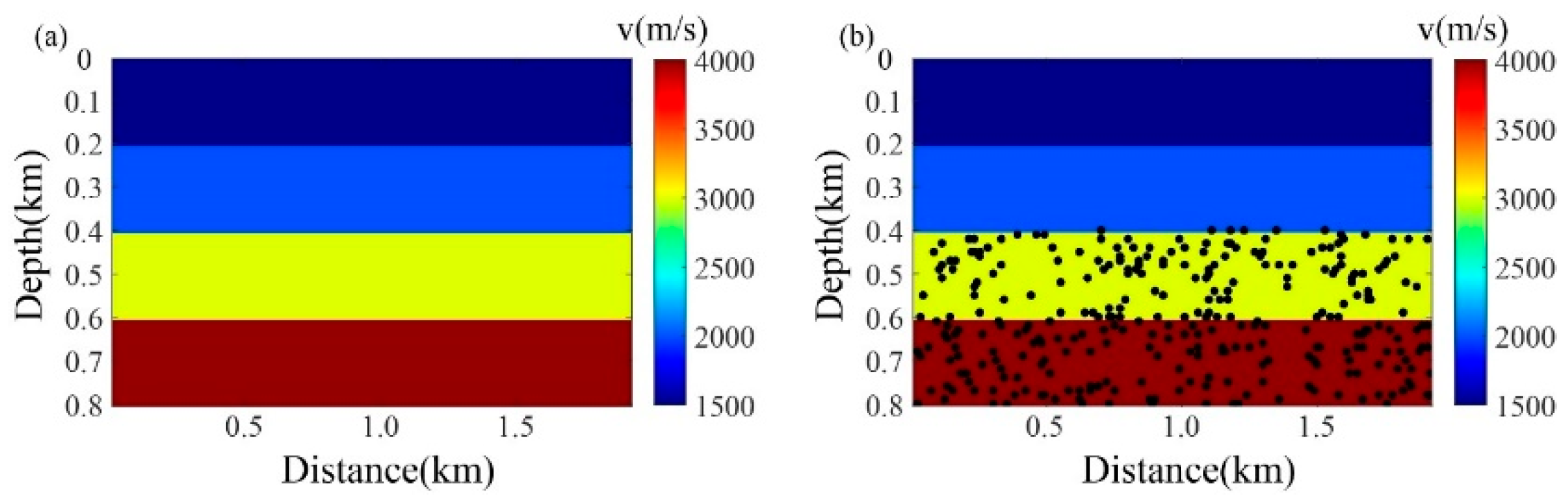
3.1. Idealized Passive-Source Distribution Testing
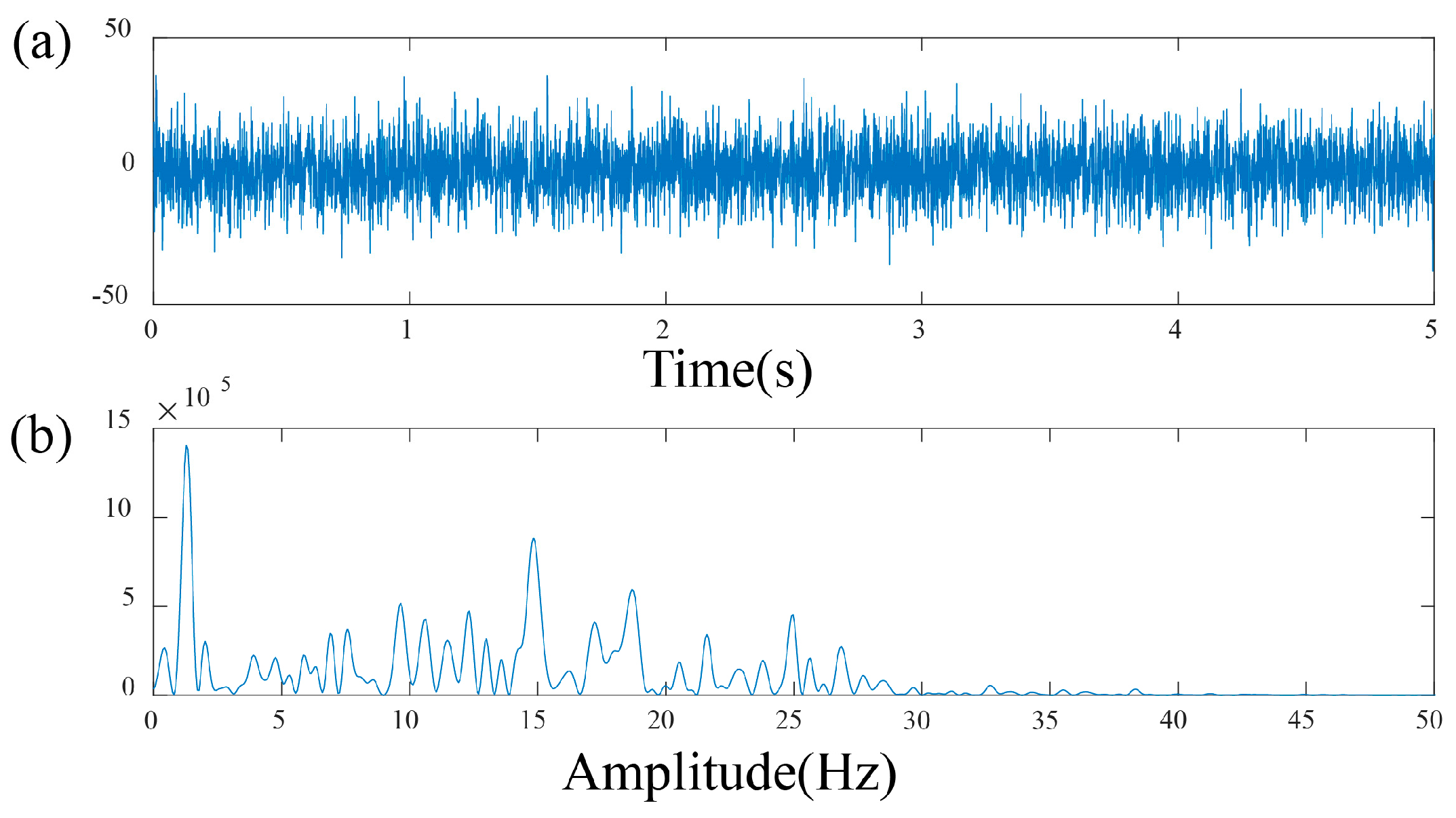
3.2. Non-Idealized Passive-Source Distribution Testing
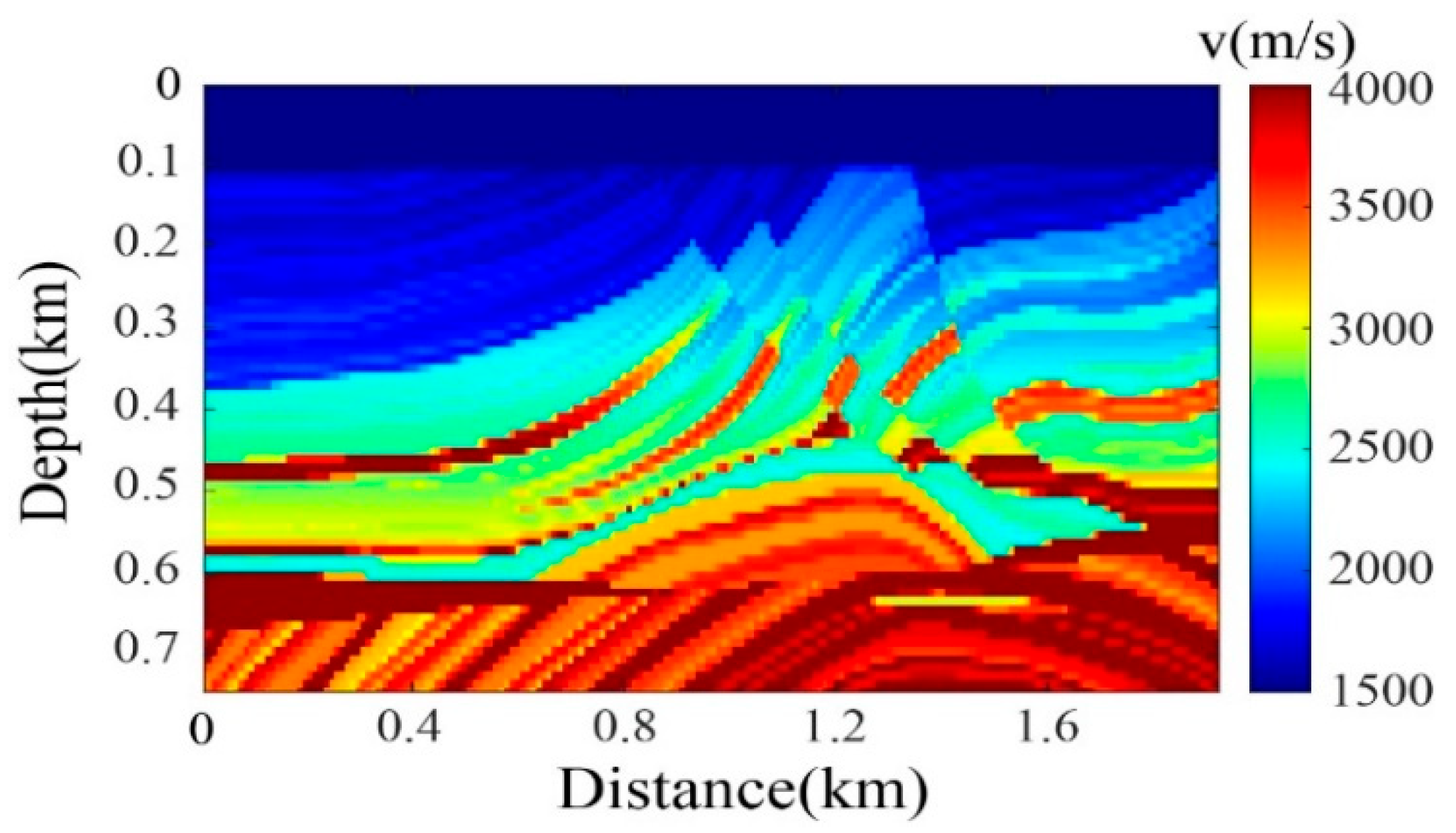
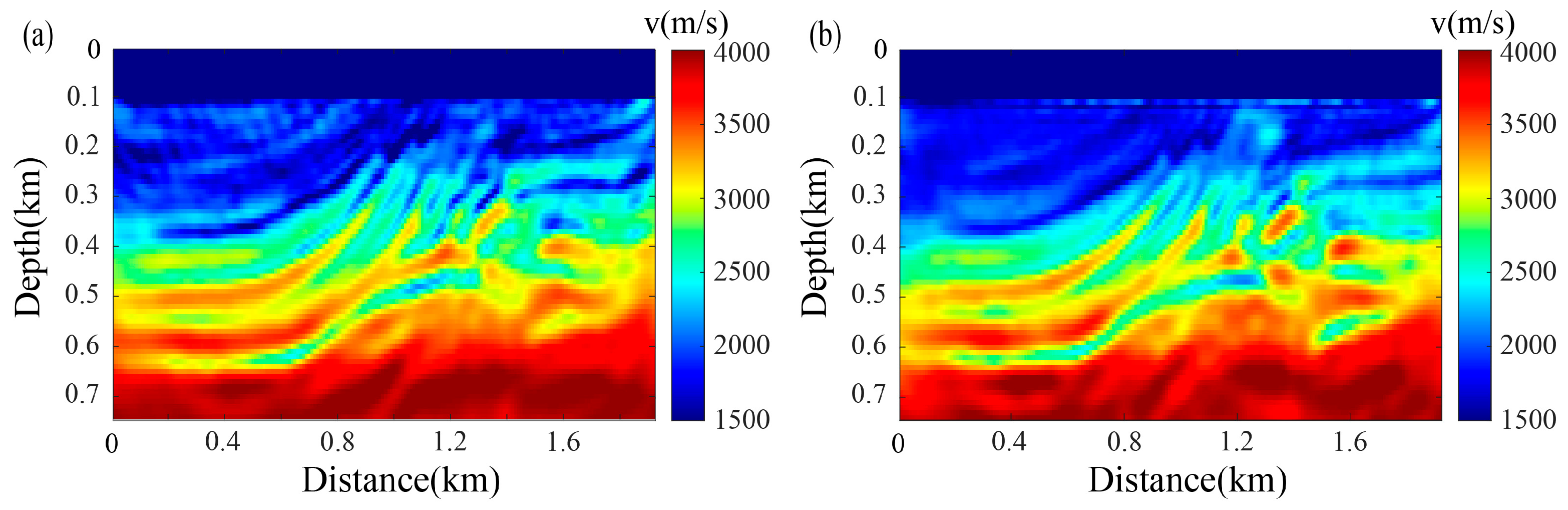
3.3. Complex Strong-Scattering Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FWI | Full waveform inversion |
| PSFWI | Passive-source full waveform inversion |
| MDD | Multi-dimensional deconvolution |
| RMDD | Robust multi-dimensional deconvolution |
| PVS | Passive virtual source |
References
- Claerbout, J.F. Synthesis of a layered medium from its acoustic transmission response. Geophysics 1968, 33, 264–269. [Google Scholar] [CrossRef]
- Schuster, G.T. Theory of Daylight/Interferometric Imaging: Tutorial. In Seismic Interferometry: History and Present Status; Wapenaar, K., Draganov, D., Robertsson, J.O.A., Pelissier, M.A., Eds.; Society of Exploration Geophysicists: Houston, TX, USA, 2008; Volume 26, ISBN 978-1-56080-150-4. [Google Scholar]
- Wapenaar, K.; Draganov, D.; Thorbecke, J.; Fokkema, J. Theory of Acoustic Daylight Imaging Revisited. In SEG Technical Program Expanded Abstracts 2002; Society of Exploration Geophysicists: Houston, TX, USA, 2002; pp. 2269–2272. [Google Scholar]
- Wapenaar, K.; Van Der Neut, J.; Ruigrok, E. Passive Seismic Interferometry by Multidimensional Deconvolution. Geophysics 2008, 73, A51–A56. [Google Scholar] [CrossRef][Green Version]
- Wapenaar, K.; Van Der Neut, J.; Ruigrok, E.; Draganov, D.; Hunziker, J.; Slob, E.; Thorbecke, J.; Snieder, R. Seismic Interferometry by Crosscorrelation and by Multidimensional Deconvolution: A Systematic Comparison: Seismic Interferometry. Geophys. J. Int. 2011, 185, 1335–1364. [Google Scholar] [CrossRef]
- Wapenaar, K.; Ruigrok, E.; Van Der Neut, J.; Draganov, D. Improved Surface-Wave Retrieval from Ambient Seismic Noise by Multi-Dimensional Deconvolution: Surface-wave retrieval by deconvolution. Geophys. Res. Lett. 2011, 38, 1–5. [Google Scholar] [CrossRef]
- Bakulin, A.; Calvert, R. Virtual Source: New Method for Imaging and 4D below Complex Overburden. In SEG Technical Program Expanded Abstracts 2004; Society of Exploration Geophysicists: Houston, TX, USA, 2004; pp. 2477–2480. [Google Scholar]
- Vasconcelos, I.; Snieder, R. Interferometric Imaging by Deconvolution: Theory and Numerical Examples. In SEG Technical Program Expanded Abstracts 2006; Society of Exploration Geophysicists: Houston, TX, USA, 2006; pp. 2416–2420. [Google Scholar]
- Gaiser, J.E.; Vasconcelos, I.; Calderón-Macias, C. Elastic Interferometry for OBC Data: Theory and Examples. In the SEG Technical Program Expanded Abstracts 2008; Society of Exploration Geophysicists: Houston, TX, USA, 2008; pp. 1073–1077. [Google Scholar]
- Bellezza, C.; Poletto, F. Multidimensional Deconvolution and Processing of Seismic-Interferometry Arctic Data. Geophysics 2014, 79, WA25–WA38. [Google Scholar] [CrossRef]
- Van Dalen, K.N.; Wapenaar, K.; Halliday, D.F. Surface Wave Retrieval in Layered Media Using Seismic Interferometry by Multidimensional Deconvolution. Geophys. J. Int. 2014, 196, 230–242. [Google Scholar] [CrossRef][Green Version]
- Ravasi, M.; Meles, G.; Curtis, A.; Rawlinson, Z.; Yikuo, L. Seismic Interferometry by Multidimensional Deconvolution without Wavefield Separation. Geophys. J. Int. 2015, 202, 1–16. [Google Scholar] [CrossRef]
- Luiken, N.; Van Leeuwen, T. Seismic Wavefield Redatuming with Regularized Multi-Dimensional Deconvolution. Inverse Probl. 2020, 36, 095010. [Google Scholar] [CrossRef]
- Vargas, D.; Vasconcelos, I.; Ravasi, M.; Luiken, N. Time-Domain Multidimensional Deconvolution: A Physically Reliable and Stable Preconditioned Implementation. Remote Sens. 2021, 13, 3683. [Google Scholar] [CrossRef]
- Herrmann, F.J.; Hennenfent, G. Non-Parametric Seismic Data Recovery with Curvelet Frames. Geophys. J. Int. 2008, 173, 233–248. [Google Scholar] [CrossRef]
- Hennenfent, G.; Fenelon, L.; Herrmann, F.J. Nonequispaced Curvelet Transform for Seismic Data Reconstruction: A Sparsity-Promoting Approach. Geophysics 2010, 75, WB203–WB210. [Google Scholar] [CrossRef]
- Naghizadeh, M.; Sacchi, M.D. Beyond Alias Hierarchical Scale Curvelet Interpolation of Regularly and Irregularly Sampled Seismic Data. Geophysics 2010, 75, WB189–WB202. [Google Scholar] [CrossRef]
- Yang, P.; Gao, J.; Chen, W. Curvelet-Based POCS Interpolation of Nonuniformly Sampled Seismic Records. J. Appl. Geophys. 2012, 79, 90–99. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, X.-H.; Zhang, L.-Y. 3D Simultaneous Seismic Data Reconstruction and Noise Suppression Based on the Curvelet Transform. Appl. Geophys. 2017, 14, 87–95. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, H.; Zhang, J.; Hao, Y.; Wang, B. An Anti-Aliasing POCS Interpolation Method for Regularly Undersampled Seismic Data Using Curvelet Transform. J. Appl. Geophys. 2020, 172, 103894. [Google Scholar] [CrossRef]
- Wang, C.; Gu, Z.; Zhu, Z. Seismic Data Reconstruction and Denoising by Enhanced Hankel Low-Rank Matrix Estimation. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5908113. [Google Scholar] [CrossRef]
- Tarantola, A. Inversion of Seismic Reflection Data in the Acoustic Approximation. Geophysics 1984, 49, 1259–1266. [Google Scholar] [CrossRef]
- Wang, X.; Tan, H.; Xu, Z. The application of CPU/GPU collaborative computing in the frequency domain 2D full waveform inversion. CT Theory Appl. 2016, 25, 23–32. (In Chinese) [Google Scholar] [CrossRef]
- Bunks, C.; Saleck, F.M.; Zaleski, S.; Chavent, G. Multiscale Seismic Waveform Inversion. Geophysics 1995, 60, 1457–1473. [Google Scholar] [CrossRef]
- Han, G.; Li, Y.; Huang, J. Hierarchical Joint Elastic Full Waveform Inversion Based on Wavefield Separation for Marine Seismic Data. J. Mar. Sci. Eng. 2025, 13, 1430. [Google Scholar] [CrossRef]
- Liu, X.; Beroza, G.C.; Li, H. Ambient Noise Differential Adjoint Tomography Reveals Fluid-Bearing Rocks near Active Faults in Los Angeles. Nat. Commun. 2023, 14, 6873. [Google Scholar] [CrossRef]
- Yan, M.; Yao, H.; Lei, T.; Luo, S.; Feng, J. Linear Array Double Difference Adjoint Ambient Noise Tomography of the Central Tanlu Fault Zone, Eastern China. J. Geophys. Res. Solid. Earth 2024, 129, e2024JB028791. [Google Scholar] [CrossRef]
- Dong, X.; Yang, D. Positions of Large Earthquakes Revealed from Velocity Heterogeneities and Radial Anisotropy in the Eastern Tibetan Plateau. Sci. Bull. 2022, 67, 2026–2029. [Google Scholar] [CrossRef]
- Zhu, W.; Xu, K.; Darve, E.; Biondi, B.; Beroza, G.C. Integrating Deep Neural Networks with Full-Waveform Inversion: Reparameterization, Regularization, and Uncertainty Quantification. Geophysics 2022, 87, R93–R109. [Google Scholar] [CrossRef]
- Sun, P.; Yang, F.; Liang, H.; Ma, J. Full-Waveform Inversion Using a Learned Regularization. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5920715. [Google Scholar] [CrossRef]
- Yang, F.; Ma, J. FWIGAN: Full-Waveform Inversion via a Physics-Informed Generative Adversarial Network. J. Geophys. Res. Solid. Earth 2023, 128, e2022JB025493. [Google Scholar] [CrossRef]
- Colombo, D.; Turkoglu, E.; Sandoval-Curiel, E.; Alyousuf, T. Active Learning Full-Waveform Inversion. In Proceedings of the Seventh International Conference on Engineering Geophysics, Al Ain, UAE, 16–19 October 2023; Society of Exploration Geophysicists: Houston, TX, USA, 2024; pp. 37–41. [Google Scholar]
- Zhang, Y.; Singh, S.; Thanoon, D.; Devarakota, P.; Jin, L.; Tsvankin, I. Physics-guided unsupervised deep-learning seismic inversion with uncertainty quantification. J. Seism. Explor. 2023, 32, 257–270. [Google Scholar]
- Gu, Z.; Chai, X.; Yang, T. Deep-Learning-Based Low-Frequency Reconstruction in Full-Waveform Inversion. Remote Sens. 2023, 15, 1387. [Google Scholar] [CrossRef]
- Zheng, Q.; Li, M.; Wu, B. Physics-Guided Self-Supervised Learning Full Waveform Inversion with Pretraining on Simultaneous Source. J. Mar. Sci. Eng. 2025, 13, 1193. [Google Scholar] [CrossRef]
- Choi, Y.; Alkhalifah, T. Source-Independent Time-Domain Waveform Inversion Using Convolved Wavefields: Application to the Encoded Multisource Waveform Inversion. Geophysics 2011, 76, R125–R134. [Google Scholar] [CrossRef]
- Choi, Y.; Alkhalifah, T. Application of Multi-source Waveform Inversion to Marine Streamer Data Using the Global Correlation Norm. Geophys. Prospect. 2012, 60, 748–758. [Google Scholar] [CrossRef]
- Sun, J.; Xue, Z.; Zhu, T.; Fomel, S.; Nakata, N. Full-Waveform Inversion of Passive Seismic Data for Sources and Velocities. In SEG Technical Program Expanded Abstracts 2016; Society of Exploration Geophysicists: Dallas, TX, USA, 2016; pp. 1405–1410. [Google Scholar]
- Wang, H.; Guo, Q.; Alkhalifah, T.; Wu, Z. Regularized Elastic Passive Equivalent Source Inversion with Full-Waveform Inversion: Application to a Field Monitoring Microseismic Data Set. Geophysics 2020, 85, KS207–KS219. [Google Scholar] [CrossRef]
- Lyu, B.; Nakata, N. Iterative Passive-Source Location Estimation and Velocity Inversion Using Geometric-Mean Reverse-Time Migration and Full-Waveform Inversion. Geophys. J. Int. 2020, 223, 1935–1947. [Google Scholar] [CrossRef]
- Zhang, P.; Han, L.G.; Jin, Z.Y.; Zhang, F.J. Passive Source Illumination Compensation Based Full Waveform Inversion. In Proceedings of the 78th EAGE Conference and Exhibition 2016, Online, 30 May–2 June 2016; European Association of Geoscientists & Engineers: Bunnik, The Netherlands, 2016; Volume 2016, pp. 1–3. [Google Scholar] [CrossRef]
- Zhang, P.; Han, L.; Yin, Y.; Feng, Q. Passive Seismic Full Waveform Inversion Using Reconstructed Body-Waves for Subsurface Velocity Construction. Explor. Geophys. 2019, 50, 124–135. [Google Scholar] [CrossRef]
- Shang, X.; Zhang, P.; Han, L.; Yang, Y.; Zhou, Y. Joint FWI of Active Source Data and Passive Virtual Source Data Reconstructed Using an Improved Multidimensional Deconvolution. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5905614. [Google Scholar] [CrossRef]









Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.; Zhang, P.; Huang, W.; Shang, X.; Han, L. Full Waveform Inversion of Irregularly Sampled Passive Seismic Data Based on Robust Multi-Dimensional Deconvolution. J. Mar. Sci. Eng. 2025, 13, 1725. https://doi.org/10.3390/jmse13091725
Zhang D, Zhang P, Huang W, Shang X, Han L. Full Waveform Inversion of Irregularly Sampled Passive Seismic Data Based on Robust Multi-Dimensional Deconvolution. Journal of Marine Science and Engineering. 2025; 13(9):1725. https://doi.org/10.3390/jmse13091725
Chicago/Turabian StyleZhang, Donghao, Pan Zhang, Wensha Huang, Xujia Shang, and Liguo Han. 2025. "Full Waveform Inversion of Irregularly Sampled Passive Seismic Data Based on Robust Multi-Dimensional Deconvolution" Journal of Marine Science and Engineering 13, no. 9: 1725. https://doi.org/10.3390/jmse13091725
APA StyleZhang, D., Zhang, P., Huang, W., Shang, X., & Han, L. (2025). Full Waveform Inversion of Irregularly Sampled Passive Seismic Data Based on Robust Multi-Dimensional Deconvolution. Journal of Marine Science and Engineering, 13(9), 1725. https://doi.org/10.3390/jmse13091725





