Spatial and Seasonal Characteristics of the Submesoscale Energetics in the Northwest Pacific Subtropical Ocean
Abstract
1. Introduction
2. Method
2.1. Model Configuration
2.2. Multiscale Energetic Diagnostic Methods
3. Spatiotemporal Variations in Submesoscale Energetics
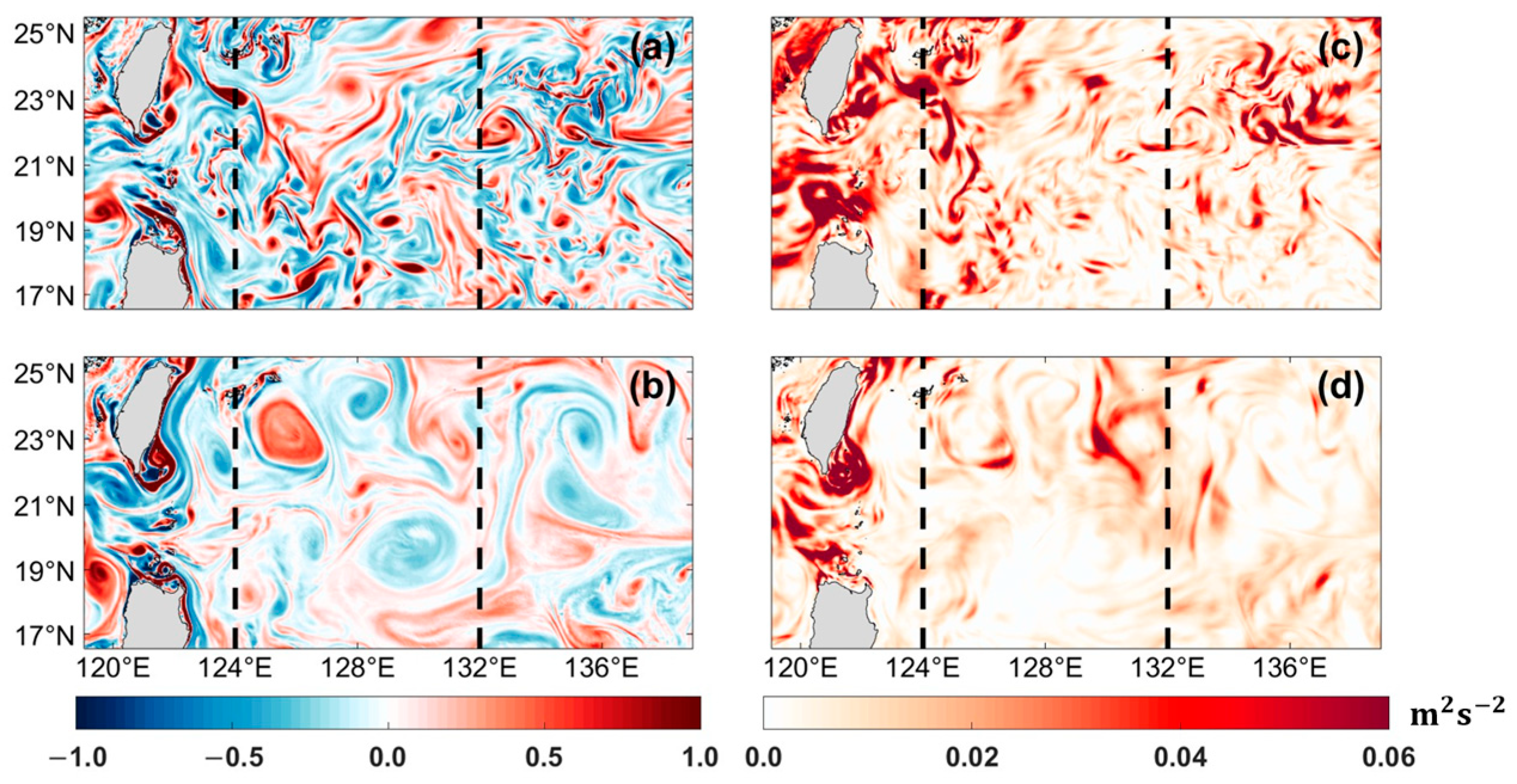
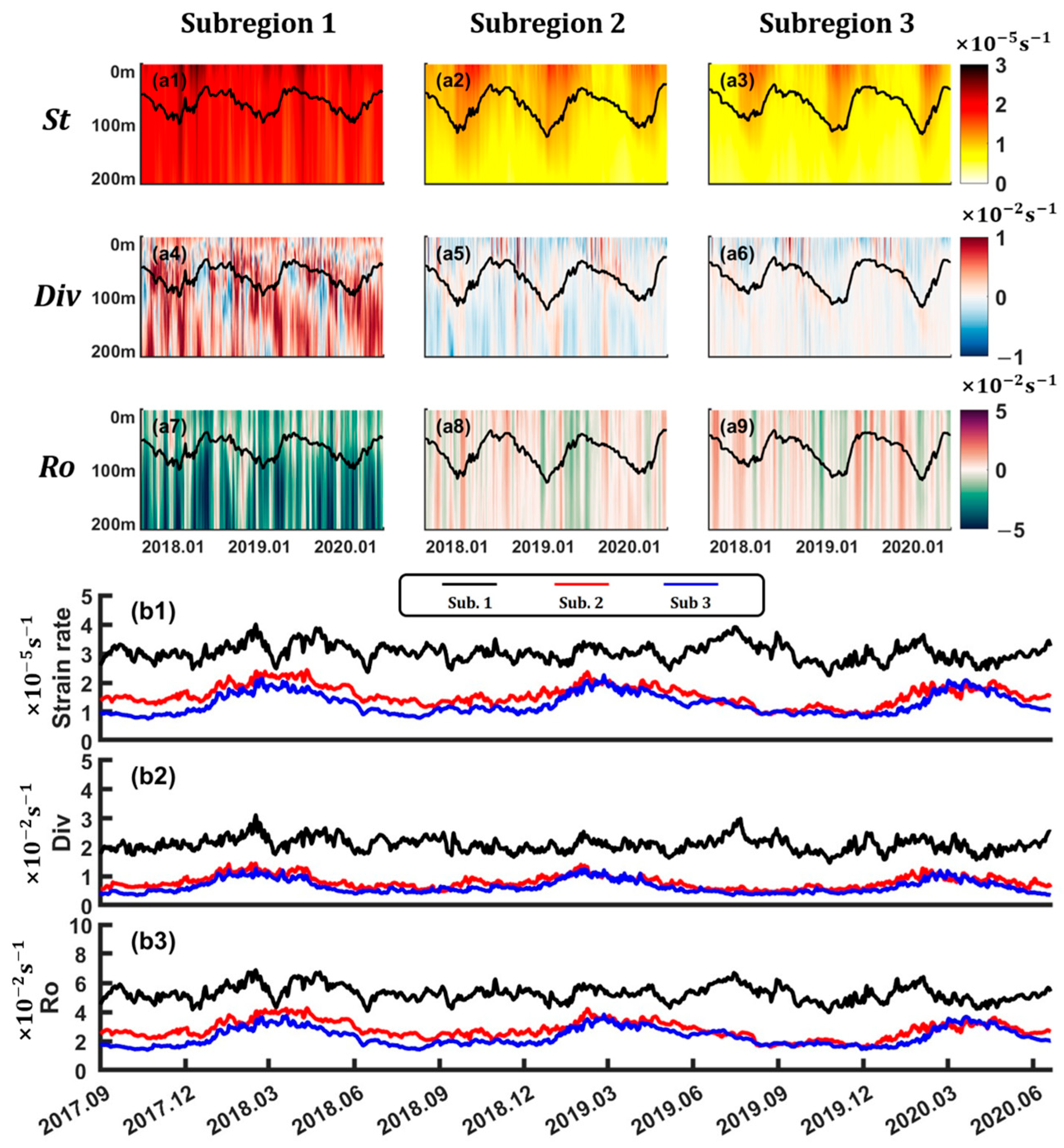
3.1. Spatiotemporal Characteristics of Submesoscales in the Northwest Pacific Subtropical Ocean
3.2. Spatial and Seasonal Characteristics of Submesoscale APE
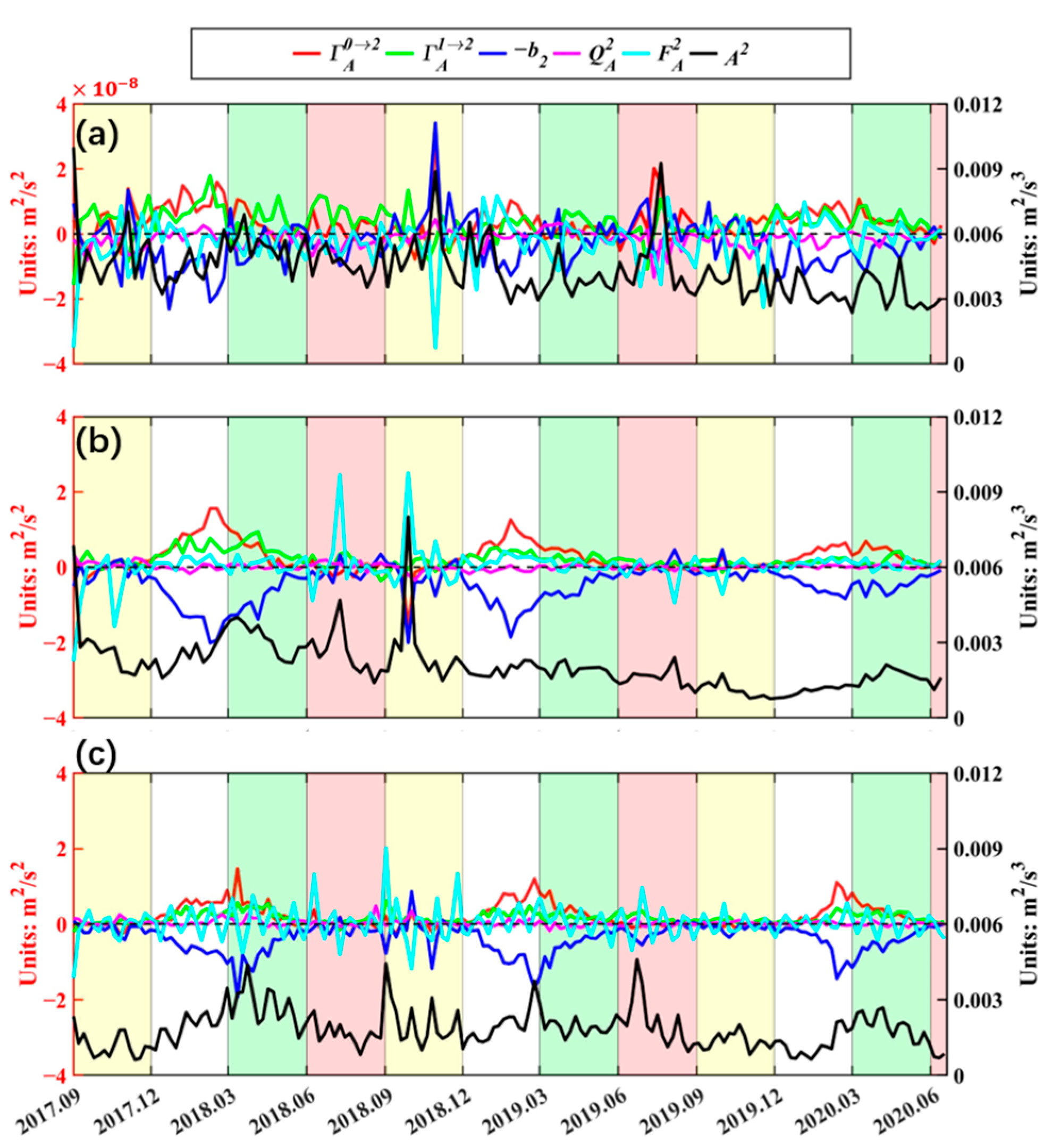
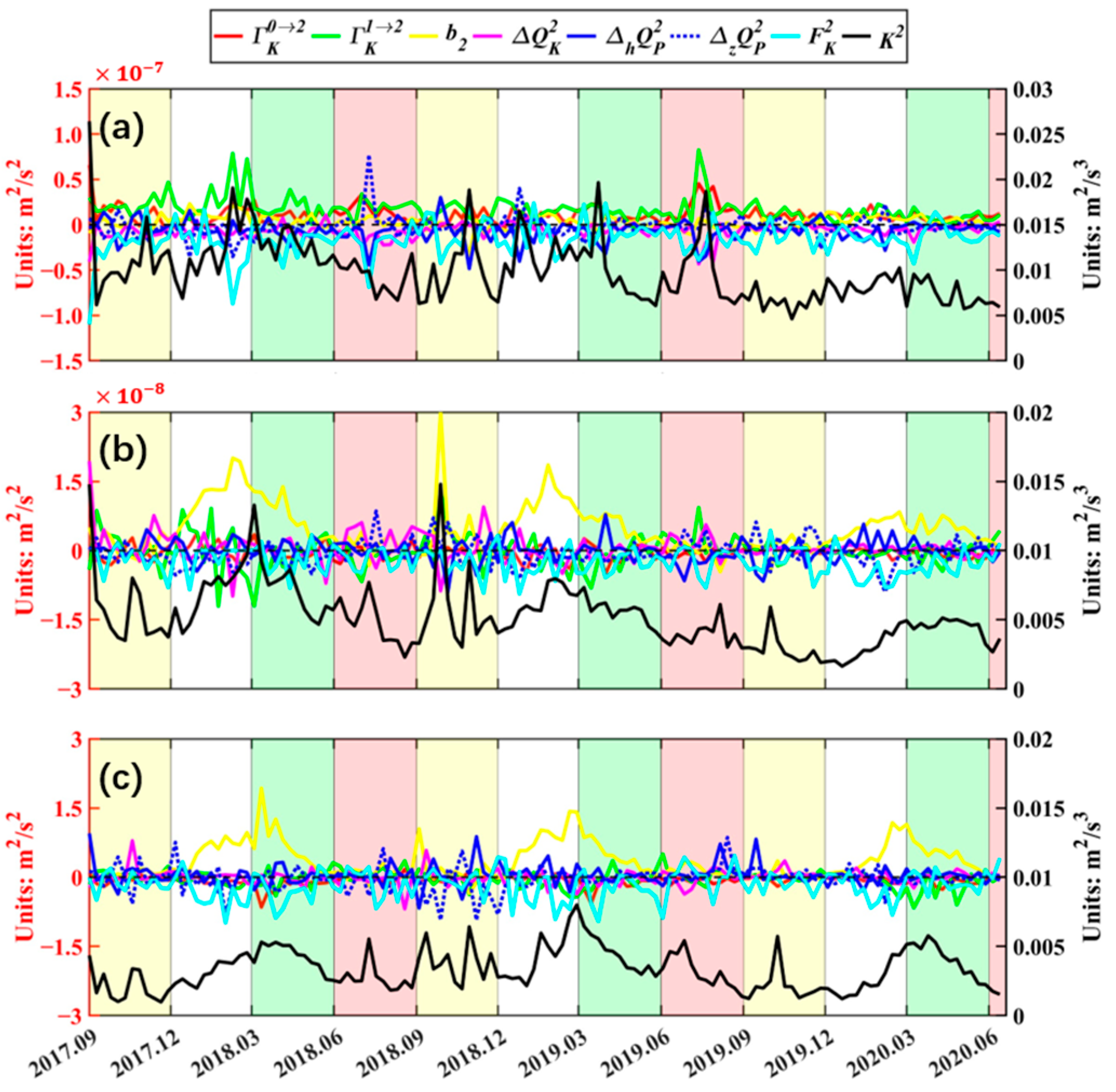
3.3. Spatial and Seasonal Characteristics of Submesoscale KE
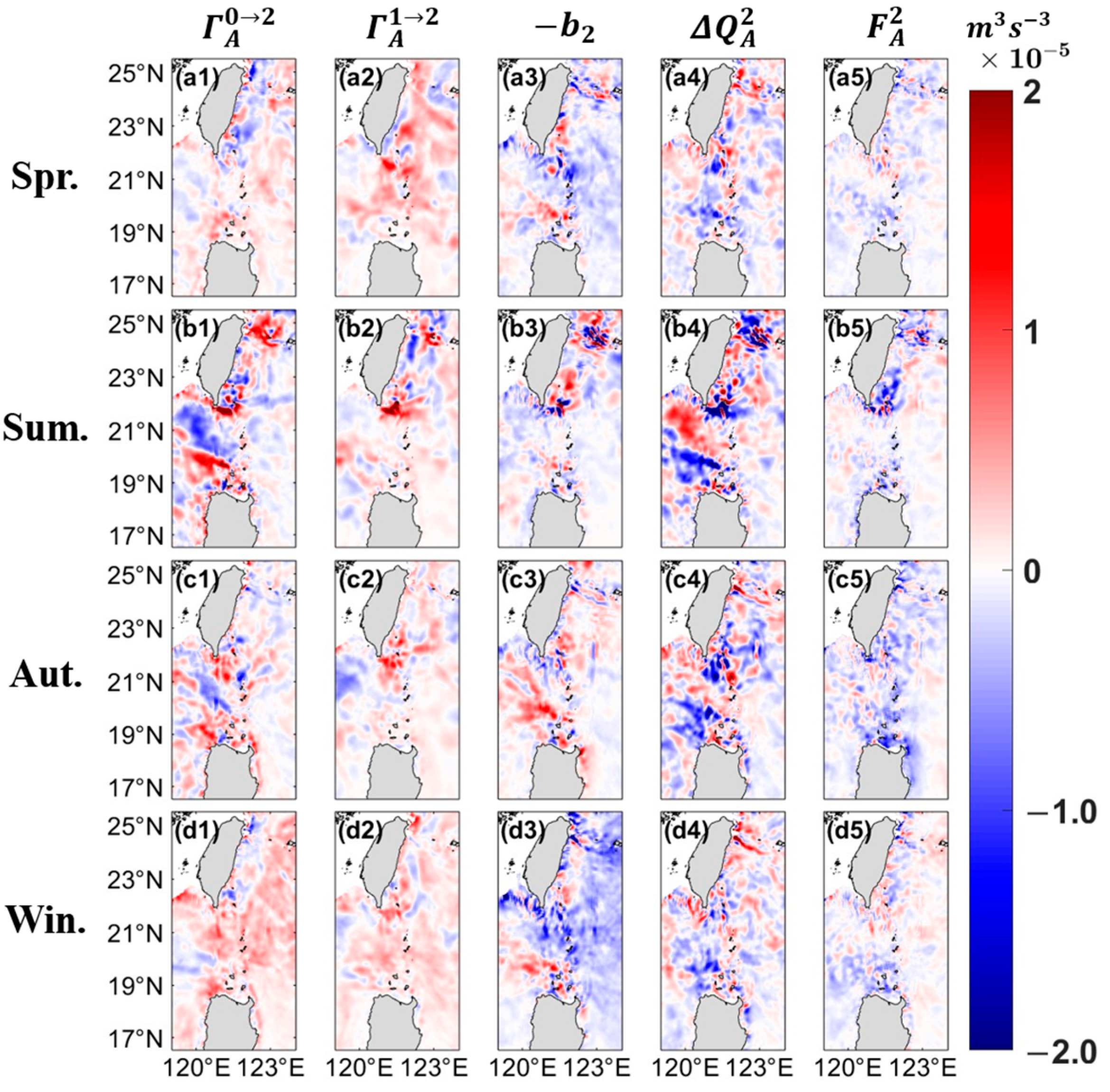
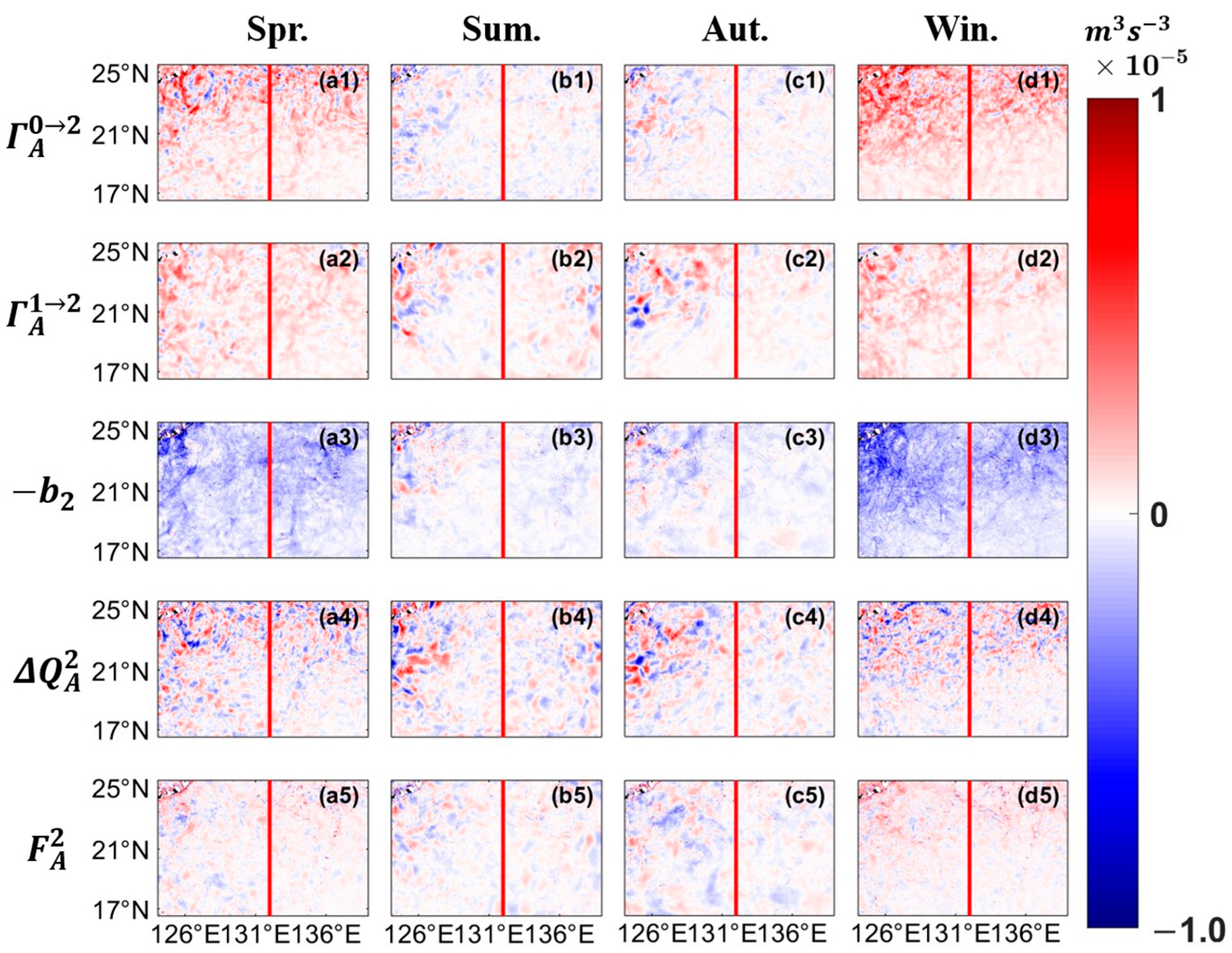
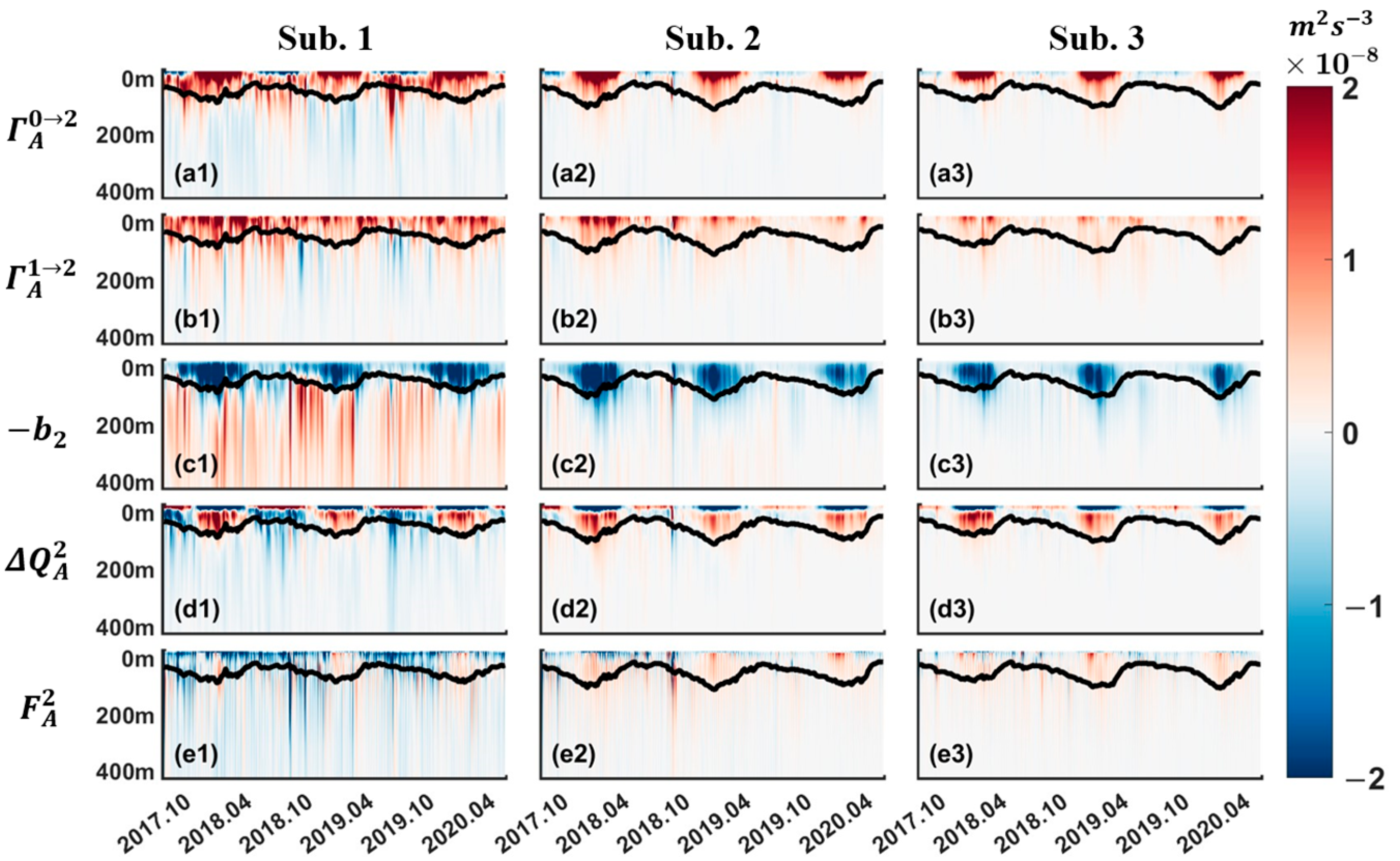
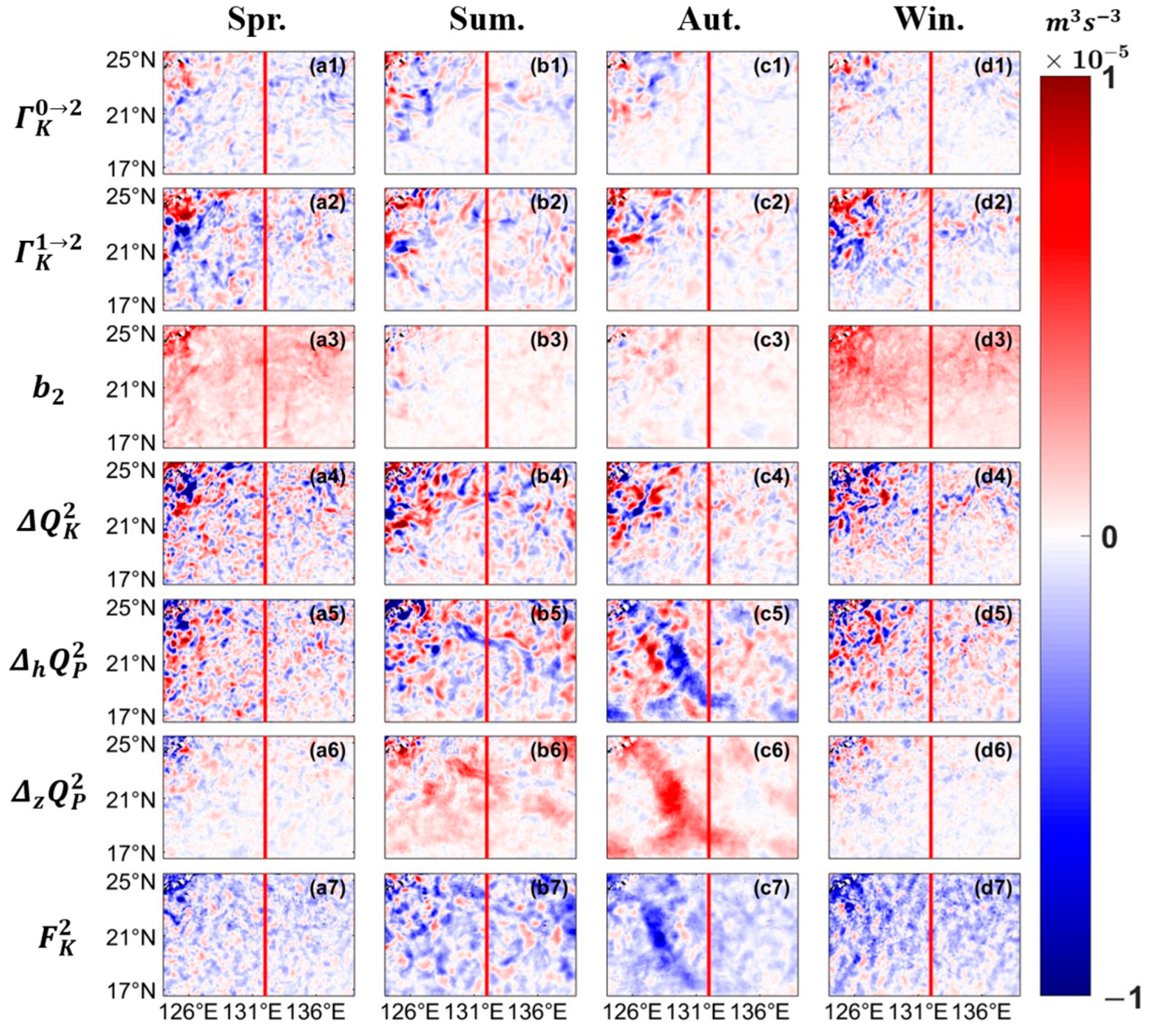
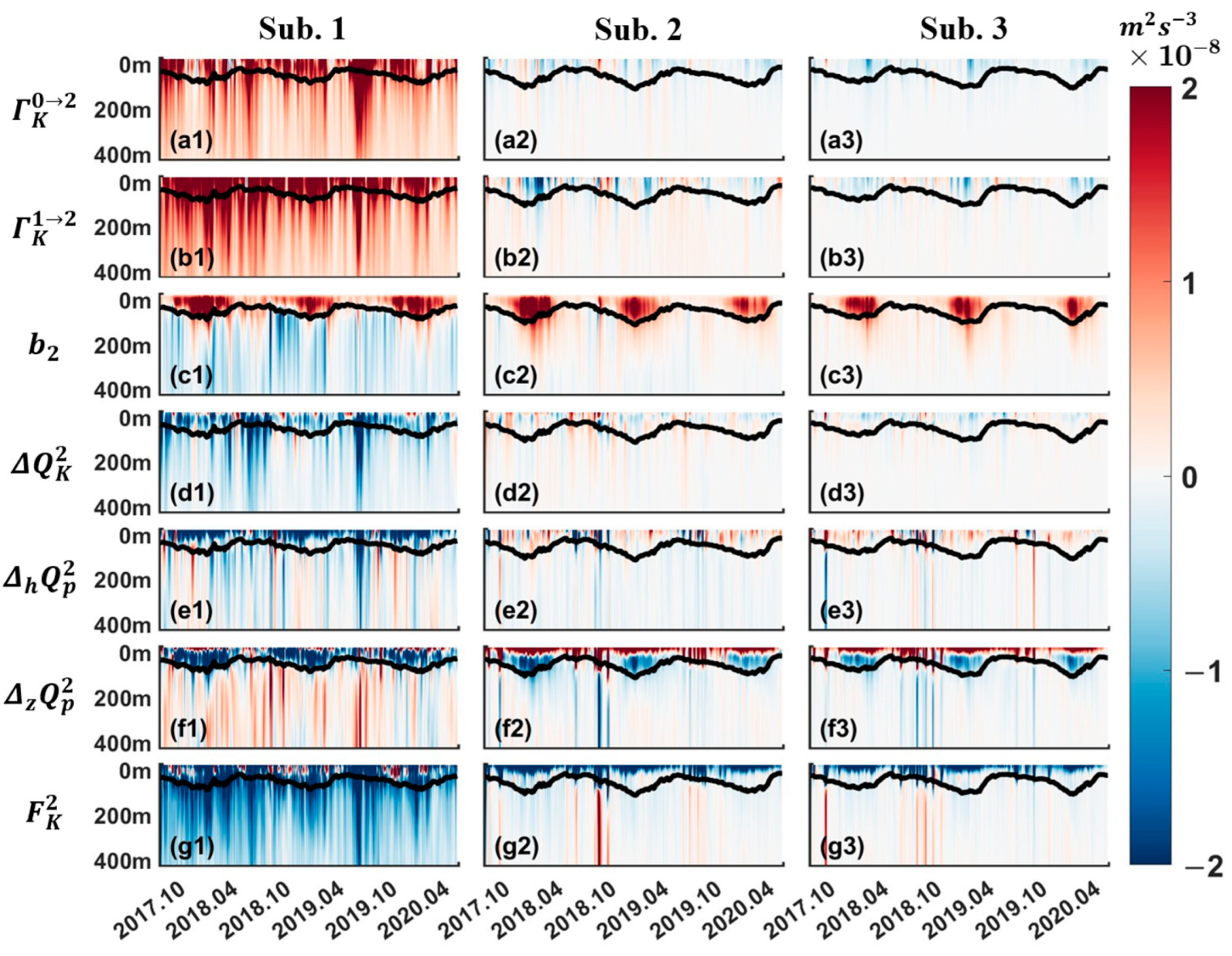
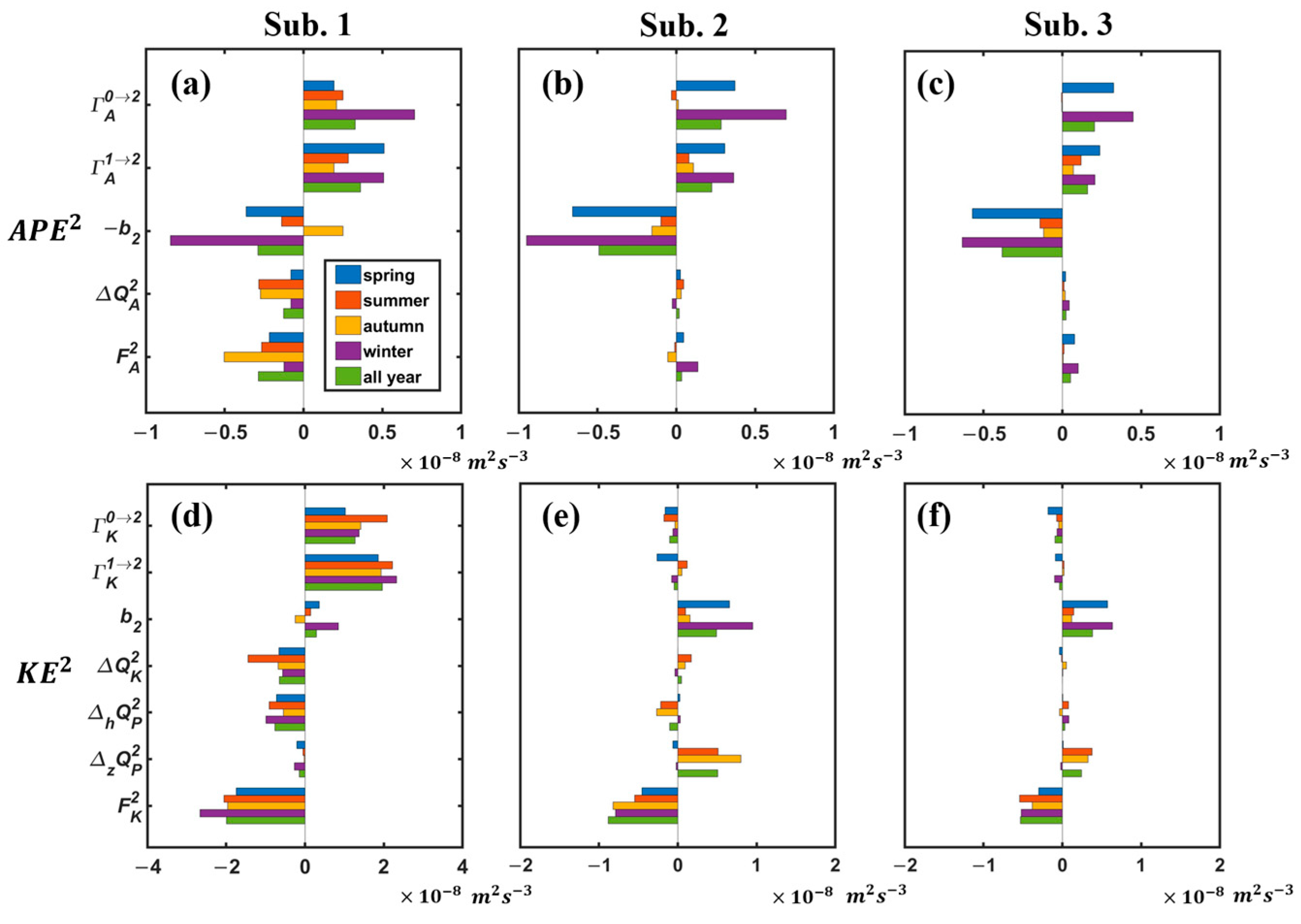
3.4. Spatial and Seasonal Characteristics of Submesoscale Energy Budget
4. Summary and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Buckingham, C.E.; Naveira Garabato, A.C.; Thompson, A.F.; Brannigan, L.; Lazar, A.; Marshall, D.P.; George Nurser, A.J.; Damerell, G.; Heywood, K.J.; Belcher, S.E. Seasonality of submesoscale flows in the ocean surface boundary layer. Geophys. Res. Lett. 2016, 43, 2118–2126. [Google Scholar] [CrossRef]
- Callies, J.; Flierl, G.; Ferrari, R.; Fox-Kemper, B. The role of mixed-layer instabilities in submesoscale turbulence. J. Fluid Mech. 2016, 788, 5–41. [Google Scholar] [CrossRef]
- McWilliams, J.C. Submesoscale currents in the ocean. Proc. R. Soc. A 2016, 472, 20160117. [Google Scholar] [CrossRef]
- Thomas, L.N.; Taylor, J.R.; Ferrari, R.; Joyce, T.M. Symmetric instability in the Gulf stream. Deep. Sea Res. Part II 2013, 91, 96–110. [Google Scholar] [CrossRef]
- Boccaletti, G.; Ferrari, R.; Fox-Kemper, B. Mixed layer instabilities and restratification. J. Phys. Oceanogr. 2007, 37, 2228–2250. [Google Scholar] [CrossRef]
- Capet, X.; Roullet, G.; Klein, P.; Maze, G. Intensification of upper-ocean submesoscale turbulence through Charney baroclinic instability. J. Phys. Oceanogr. 2016, 46, 3365–3384. [Google Scholar] [CrossRef]
- Fox-Kemper, B.; Ferrari, R.; Hallberg, R. Parameterization of mixed layer eddies. Part I: Theory and diagnosis. J. Phys. Oceanogr. 2008, 38, 1145–1165. [Google Scholar] [CrossRef]
- Thompson, A.F.; Lazar, A.; Buckingham, C.; Naveira Garabato, A.C.; Damerell, G.M.; Heywood, K.J. Open-Ocean submesoscale motions: A full seasonal cycle of mixed layer instabilities from gliders. J. Phys. Oceanogr. 2016, 46, 1285–1307. [Google Scholar] [CrossRef]
- Capet, X.; McWilliams, J.C.; Molemaker, M.J.; Shchepetkin, A.F. Mesoscale to submesoscale transition in the California current system. Part II: Frontal processes. J. Phys. Oceanogr. 2008, 38, 44–64. [Google Scholar] [CrossRef]
- McWilliams, J.C. Submesoscale surface fronts and filaments: Secondary circulation, buoyancy flux, and frontogenesis. J. Fluid Mech. 2017, 823, 391–432. [Google Scholar] [CrossRef]
- Gula, J.; Molemaker, M.J.; McWilliams, J.C. Submesoscale dynamics of a Gulf Stream frontal eddy in the South Atlantic Bight. J. Phys. Oceanogr. 2016, 46, 305–325. [Google Scholar] [CrossRef]
- Srinivasan, K.; McWilliams, J.C.; Renault, L.; Hristova, H.G.; Molemaker, J.; Kessler, W.S. Topographic and mixed layer submesoscale currents in the near-surface southwestern tropical Pacific. J. Phys. Oceanogr. 2017, 47, 1221–1242. [Google Scholar] [CrossRef]
- Qiu, B.; Nakano, T.; Chen, S.; Klein, P. Submesoscale transition from geostrophic flows to internal waves in the northwestern Pacific upper ocean. Nat. Commun. 2017, 8, 14055. [Google Scholar] [CrossRef] [PubMed]
- Rocha, C.B.; Gille, S.T.; Chereskin, T.K.; Menemenlis, D. Seasonality of submesoscale dynamics in the Kuroshio Extension. Geophys. Res. Lett. 2016, 43, 11–304. [Google Scholar] [CrossRef]
- Torres, H.S.; Klein, P.; Menemenlis, D.; Qiu, B.; Su, Z.; Wang, J.; Chen, S.; Fu, L. Partitioning ocean motions into balanced motions and internal gravity waves: A modeling study in anticipation of future space missions. J. Geophys. Res. Ocean. 2018, 123, 8084–8105. [Google Scholar] [CrossRef]
- Klein, P.; Hua, B.L.; Lapeyre, G.; Capet, X.; Gentil, S.L.; Sasaki, H. Upper ocean turbulence from high-resolution 3D simulations. J. Phys. Oceanogr. 2008, 38, 1748–1763. [Google Scholar] [CrossRef]
- Mahadevan, A.; Pascual, A.; Rudnick, D.L.; Ruiz, S.; Tintoré, J.; D’Asaro, E. Coherent pathways for vertical transport from the surface ocean to interior. Bull. Amer. Meteor. Soc. 2020, 101, E1996–E2004. [Google Scholar] [CrossRef]
- Su, Z.; Wang, J.; Klein, P.; Thompson, A.F.; Menemenlis, D. Ocean submesoscales as a key component of the global heat budget. Nat. Commun. 2018, 9, 775. [Google Scholar] [CrossRef]
- Wang, S.; Song, Z.; Ma, W.; Shu, Q.; Qiao, F. Mesoscale and submesoscale turbulence in the Northwest Pacific Ocean revealed by numerical simulations. Deep. Sea Res. Part II 2022, 206, 105221. [Google Scholar] [CrossRef]
- Bachman, S.D.; Fox-Kemper, B.; Taylor, J.R.; Thomas, L.N. Parameterization of frontal symmetric instabilities. I: Theory for resolved fronts. Ocean. Model. 2017, 109, 72–95. [Google Scholar] [CrossRef]
- D’Asaro, E.; Lee, C.; Rainville, L.; Harcourt, R.; Thomas, L. Enhanced turbulence and energy dissipation at ocean fronts. Science 2011, 332, 318–322. [Google Scholar] [CrossRef]
- Srinivasan, K.; Barkan, R.; McWilliams, J.C. A forward energy flux at submesoscales driven by frontogenesis. J. Phys. Oceanogr. 2022, 53, 287–305. [Google Scholar] [CrossRef]
- Schubert, R.; Gula, J.; Greatbatch, R.J.; Baschek, B.; Biastoch, A. The submesoscale kinetic energy cascade: Mesoscale absorption of submesoscale mixed layer eddies and frontal downscale fluxes. J. Phys. Oceanogr. 2020, 50, 2573–2589. [Google Scholar] [CrossRef]
- Yang, Y.; McWilliams, J.C.; Liang, X.; Zhang, H.; Weisberg, R.H.; Liu, Y.; Menemenlis, D. Spatial and temporal characteristics of the submesoscale energetics in the Gulf of Mexico. J. Phys. Oceanogr. 2021, 47, 1243–1489. [Google Scholar] [CrossRef]
- Jing, Z.; Fox-Kemper, B.; Cao, H.; Rui, Z.; Du, Y. Submesoscale fronts and their dynamical processes associated with symmetric instability in the northwest Pacific subtropical ocean. J. Phys. Oceanogr. 2021, 51, 83–100. [Google Scholar] [CrossRef]
- Sasaki, H.; Klein, P.; Sasai, Y.; Qiu, B. Regionality and seasonality of submesoscale and mesoscale turbulence in the North Pacific Ocean. Ocean Dyn. 2017, 67, 1195–1216. [Google Scholar] [CrossRef]
- Zhao, W.; Zhou, C.; Zhang, Z.; Huang, X.; Guan, S.; Yang, Q.; Sun, Z.; Qin, C.; Guan, Y.; Tian, J. The South China Sea Mooring Array and its applications in exploring oceanic multiscale dynamics. Sci. Bull. 2024, 70, 609–623. [Google Scholar] [CrossRef]
- Jia, Y.; Chassignet, E.P. Seasonal variation of eddy shedding from the Kuroshio intrusion in the Luzon Strait. J. Phys. Oceanogr. 2011, 67, 601–611. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, Z.; Qiu, B.; Zhang, X.; Tian, J. Three-dimensional structure and interannual variability of the Kuroshio loop current in the northeastern South China Sea. J. Phys. Oceanogr. 2020, 50, 2437–2455. [Google Scholar] [CrossRef]
- Duda, T.F.; Lynch, J.F.; Irish, J.D.; Beardsley, R.C.; Ramp, S.R.; Chiu, C.S.; Tang, T.Y.; Yang, Y.-J. Internal tide and nonlinear internal wave behavior at the continental slope in the northern South China Sea. IEEE J. Oceanic. Eng. 2005, 29, 1105–1130. [Google Scholar] [CrossRef]
- Ramp, S.R.; Tang, T.Y.; Duda, T.F.; Lynch, J.F.; Liu, A.K.; Chiu, C.S.; Bahr, F.L.; Kim, H.R.; Yang, Y.J. Internal solitons in the northeastern South China Sea. Part I: Sources and deepwater propagation. IEEE J. Oceanic. Eng. 2004, 29, 1157–1181. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Y.; Qiu, B.; Sasaki, H.; Sun, Z.; Zhang, X.; Zhao, W.; Tian, J. Spatiotemporal characteristics and generation mechanisms of submesoscale currents in the northeastern South China Sea revealed by numerical simulations. J. Geophys. Res. Ocean. 2020, 125, e2019JC015404. [Google Scholar] [CrossRef]
- Zheng, R.; Jing, Z. Submesoscale-Enhanced Filaments and Frontogenetic Mechanism within Mesoscale Eddies of the South China Sea. Acta Oceanol. Sin. 2022, 41, 42–53. [Google Scholar] [CrossRef]
- Tang, T.; Zhang, Z.; Zhang, J.; Zhang, X.; Sun, Z.; Feng, Z. Submesoscale processes in the Kuroshio Loop Current: Roles in energy cascade and salt and heat transports. J. Geophys. Res. Ocean. 2024, 129, e2023JC020226. [Google Scholar] [CrossRef]
- Qiu, B. Seasonal eddy field modulation of the North Pacific subtropical countercurrent: TOPEX/Poseidon observations and theory. J. Phys. Oceanogr. 1999, 29, 2471–2486. [Google Scholar] [CrossRef]
- Qiu, B.; Chen, S.; Klein, P.; Sasaki, H. Seasonal mesoscale and submesoscale eddy variability along the North Pacific Subtropical Countercurrent. J. Phys. Oceanogr. 2014, 44, 3079–3098. [Google Scholar] [CrossRef]
- Jan, S.; Yang, Y.J.; Wang, J.; Mensah, V.; Kuo, T.H.; Chiou, M.D.; Chern, C.S.; Chang, M.H.; Chien, H. Large variability of the Kuroshio at 23.75°N east of Taiwan. J. Geophys. Res. Ocean. 2015, 120, 1825–1840. [Google Scholar] [CrossRef]
- Tsai, C.J.; Andres, M.; Jan, S.; Mensah, V.; Sanford, T.B.; Lien, R.C.; Lee, C.M. Eddy-Kuroshio interaction processes revealed by mooring observations off Taiwan and Luzon. Geophys. Res. Lett. 2015, 42, 8098–8105. [Google Scholar] [CrossRef]
- Yan, X.M.; Kang, D.J.; Pang, C.G. Energetics Analysis of the Eddy-Kuroshio Interaction East of Taiwan. J. Phys. Oceanogr. 2022, 52, 647–664. [Google Scholar] [CrossRef]
- Wu, B.; Gan, J. Seasonal Modulation of the Eddy Kinetic Energy and Subtropical Countercurrent Near the Western North Pacific Boundary. J. Geophys. Res. Ocean. 2022, 128, e2022JC019160. [Google Scholar] [CrossRef]
- Shchepetkin, A.F.; McWilliams, J.C. The regional oceanic modeling system (ROMS): A split-explicit, free-surface, topography-following-coordinate oceanic model. Ocean Model. 2005, 9, 347–404. [Google Scholar] [CrossRef]
- Large, W.G.; McWilliams, J.C.; Doney, S.C. Oceanic with vertical mixing: A review layer and a model with a nonlocal boundary. Rev. Geophys. 1994, 32, 363–403. [Google Scholar] [CrossRef]
- Beckmann, A.; Haidvogel, D.B. Numerical simulation of flow around a tall isolated seamount. Part I: Problem formulation and model accuracy. J. Phys. Oceanogr. 1993, 23, 1736–1753. [Google Scholar] [CrossRef]
- Dong, J.; Kemper, F.B.; Zhang, H.; Dong, C. The scale of submesoscale baroclinic instability globally. J. Phys. Oceanogr. 2020, 50, 2649–2667. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, W.; Wang, H.; Zhang, X. Assessing the spatio-temporal features and mechanisms of symmetric instability activity probability in the central part of the South China Sea based on a regional ocean model. J. Mar. Sci. Eng. 2023, 11, 431–450. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Y.; Qiu, B.; Luo, Y.; Cai, W.; Yuan, Q.; Zhang, H.; Liu, H.; Miao, M. Submesoscale inverse energy cascade enhances Southern Ocean eddy heat transport. Nat. Commun. 2023, 14, 1335. [Google Scholar] [CrossRef]
- Liang, X.S. Canonical transfer and multiscale energetics for primitive and quasigeostrophic atmospheres. J. Atmos Sci. 2016, 73, 4439–4468. [Google Scholar] [CrossRef]
- Ma, J.; Liang, X.S. Multiscale dynamical processes underlying the wintertime Atlantic blockings. J. Atmos Sci. 2017, 74, 3815–3831. [Google Scholar] [CrossRef]
- Quan, Q.; Liu, Z.; Sun, S.; Cai, Z.; Yang, Y.; Jin, G.; Li, Z.; Liang, X.S. Influence of the Kuroshio intrusion on deep flow intraseasonal variability in the Northern South China Sea. J. Geophys. Res. Ocean. 2021, 126, e2021JC017429. [Google Scholar] [CrossRef]
- Quan, Q.; Xue, H.; Yang, Y.; Cai, Z.; Zhang, H.; Liu, X. Characterization of intraseasonal fluctuations in the abyssal South China Sea: An insight into the energy pathway. Prog Oceanogr. 2022, 206, 102829. [Google Scholar] [CrossRef]
- Yang, Y.; Liang, X.S. The instabilities and multiscale energetics underlying the mean-interannual-eddy interactions in the Kuroshio Extension region. J. Phys. Oceanogr. 2016, 46, 1477–1494. [Google Scholar] [CrossRef]
- Yang, Y.; Liang, X.S. On the seasonal eddy variability in the Kuroshio Extension. J. Phys. Oceanogr. 2018, 48, 1675–1689. [Google Scholar] [CrossRef]
- Li, M.; Pang, C.; Yan, X.; Zhang, L.; Liu, Z. Energetics of multiscale interactions in the Agulhas retroflection current system. J. Phys. Oceanogr. 2023, 53, 457–476. [Google Scholar] [CrossRef]
- Liang, X.S.; Robinson, A.R. Localized multi-scale energy and vorticity analysis: II. Finite-amplitude instability theory and validation. Dynam. Atmos. Oceans. 2007, 44, 51–76. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Z.; Qiu, B.; Zhang, X.; Sasaki, H.; Zhao, W.; Tian, J. Seasonal modulation of submesoscale kinetic energy in the upper ocean of the northeastern South China Sea. J. Geophys. Res. Ocean. 2021, 126, e2021JC017695. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, Y.; Mao, L.; Zhang, Y. On the Genesis of the South China Sea Mesoscale Eddies. J. Mar. Sci. Eng. 2022, 10, 188. [Google Scholar] [CrossRef]
- Xiu, P.; Chai, F.; Shi, L.; Xue, H.; Chao, Y. A Census of Eddy Activities in the South China Sea during 1993–2007. J. Geophys. Res. 2010, 115, C03012. [Google Scholar] [CrossRef]
- Zhang, M.; von Storch, H.; Chen, X.; Wang, D.; Li, D. Temporal and Spatial Statistics of Travelling Eddy Variability in the South China Sea. Ocean Dyn. 2019, 69, 879–898. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, Y.; Liang, X.S.; Zhang, Y. Different Mechanisms for the Seasonal Variations of the Mesoscale Eddy Energy in the South China Sea. Deep. Sea Res. Part II 2021, 179, 103677. [Google Scholar] [CrossRef]
- Charney, J.G. Geostrophic turbulence. J. Atmos. Sci. 1971, 28, 1087–1095. [Google Scholar] [CrossRef]
- Lapeyre, G.; Klein, P. Dynamics of the upper oceanic layers in terms of surface quasigeostrophy theory. J. Phys. Oceanogr. 2006, 36, 165–176. [Google Scholar] [CrossRef]
- Boyd, J.P. The energy spectrum of fronts: Time evolution of shocks in Burger’s equation. J. Atmos. Sci. 1992, 49, 128–139. [Google Scholar] [CrossRef]
- Callies, J.; Ferrari, R. Interpreting energy and tracer spectra of upper-ocean turbulence in the submesoscale range (1–200km). J. Phys. Oceanogr. 2013, 43, 2456–2474. [Google Scholar] [CrossRef]
- Nan, F.; Xue, H.; Chai, F.; Shi, L.; Shi, M.; Guo, P. Identification of different types of Kuroshio intrusion into the south china sea. Ocean Dyn. 2011, 61, 1291–1304. [Google Scholar] [CrossRef]
- Caruso, M.J.; Gawwarkiewicz, G.G.; Beardsley, R.C. Interannual variability of the Kuroshio intrusion in the South China Sea. J. Phys. Oceanogr. 2006, 62, 559–575. [Google Scholar] [CrossRef]
- Molemaker, J.; McWilliams, J.C.; Capet, X. Balanced and unbalanced routes to dissipation in an equilibrated Eady flow. J. Fluid Mech. 2010, 654, 35–63. [Google Scholar] [CrossRef]
- von Storch, J.S.; Eden, C.; Fast, I.; Haak, H.; Hernández Deckers, D.; Maier-Reimer, E.; Marotzke, J.; Stammer, D. An estimate of the Lorenz energy cycle for the World Ocean based on the STORM/NCEP simulation. J. Phys. Oceanogr. 2012, 42, 2185–2205. [Google Scholar] [CrossRef]
- Mensa, J.A.; Garraffo, Z.; Griffa, A.; Özgökmen, T.M.; Haza, A.; Veneziani, M. Seasonality of the submesoscale dynamics in the Gulf Stream region. Ocean Dyn. 2013, 63, 923–941. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, X.; Sun, Z.; Zhang, Z.; Sasaki, H.; Zhao, W.; Tian, J. Region-dependent eddy kinetic energy budget in the northeastern South China Sea revealed by submesoscale-permitting simulations. J. Marine. Syst. 2022, 235, 103797. [Google Scholar] [CrossRef]
- Cao, H.; Meng, X.; Jing, Z.; Yang, X. High-Resolution Simulation of Upper-Ocean Submesoscale Variability in the South China Sea: Spatial and Seasonal Dynamical Regimes. Acta Oceanol. Sin. 2022, 41, 26–41. [Google Scholar] [CrossRef]
- Zhang, Z.; Tian, J.; Qiu, B.; Zhao, W.; Chang, P.; Wu, D.; Wan, X. Observed 3D structure, generation, and dissipation of oceanic mesoscale eddies in the South China Sea. Sci. Rep. 2016, 6, 24349. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Zhao, W.; Qiu, B.; Tian, J. Anticyclonic eddy sheddings from Kuroshio loop and the accompanying cyclonic eddy in the northeastern South China Sea. J. Phys. Oceanogr. 2017, 47, 1243–1259. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fei, Y.; Zhang, S.; Wang, K.; Yu, Y.; Gao, Y.; Cui, T. Spatial and Seasonal Characteristics of the Submesoscale Energetics in the Northwest Pacific Subtropical Ocean. J. Mar. Sci. Eng. 2025, 13, 1691. https://doi.org/10.3390/jmse13091691
Fei Y, Zhang S, Wang K, Yu Y, Gao Y, Cui T. Spatial and Seasonal Characteristics of the Submesoscale Energetics in the Northwest Pacific Subtropical Ocean. Journal of Marine Science and Engineering. 2025; 13(9):1691. https://doi.org/10.3390/jmse13091691
Chicago/Turabian StyleFei, Yunlong, Shaoqing Zhang, Kaidi Wang, Yangyang Yu, Yang Gao, and Tong Cui. 2025. "Spatial and Seasonal Characteristics of the Submesoscale Energetics in the Northwest Pacific Subtropical Ocean" Journal of Marine Science and Engineering 13, no. 9: 1691. https://doi.org/10.3390/jmse13091691
APA StyleFei, Y., Zhang, S., Wang, K., Yu, Y., Gao, Y., & Cui, T. (2025). Spatial and Seasonal Characteristics of the Submesoscale Energetics in the Northwest Pacific Subtropical Ocean. Journal of Marine Science and Engineering, 13(9), 1691. https://doi.org/10.3390/jmse13091691






