1. Introduction
Ro-Ro (Roll-on/Roll-off) ships are designed to rapidly and efficiently load or unload self-propelled cargo such as vehicles, heavy equipment, and railway cars. Because these cargos can move under their own power, large volumes can be loaded in a short time without dedicated loading machinery, greatly reducing transport time and labor costs. Consequently, Ro-Ro vessels have become essential in various maritime logistics sectors including the import/export of automobiles and the transport of military and industrial equipment [
1]. Ro-Ro ships originated from late 19th-century rail ferries and were adapted as military landing ships for mass transport of troops and supplies during World War I [
2]. After the war, the technology transferred to civilian shipping, leading to the development of commercial Ro-Ro vessels in the 1950s. With the growth of the automotive industry, specialized types such as Pure Car Carriers (PCC) and Pure Car and Truck Carriers (PCTC) were introduced [
3]. Today, Ro-Ro ships continue to evolve alongside port automation, smart loading systems, and eco-friendly designs, and multi-level car deck structures for efficient use of internal space are regarded as a core technology [
4]. A Ro-Ro ship’s car deck must be height-adjustable to load vehicles of varying heights, and applying a variable deck structure is required for efficient space allocation and hull form optimization [
5]. Past research on car decks has mainly focused on improving structural performance—such as predicting fatigue life, minimizing welding deformation, weight reduction with high-strength materials, and introducing flame-retardant composites (e.g., FRP, GFRP) [
6,
7,
8,
9,
10,
11,
12]. However, relatively few studies have addressed modular design, ease of installation, or improved maintainability from an operational perspective, highlighting the need for structural designs that emphasize efficiency, flexibility, and safety in real operating environments [
13,
14,
15,
16].
Most current Ro-Ro ships use decks constructed by connecting very large single plate panels (over 10 m in width and length each). To allow height adjustment of these decks, two main systems are typically used, as shown in
Figure 1. The overall arrangement of the car decks within a Ro-Ro vessel is presented in
Figure 1a. The hoistable car deck system
Figure 1b uses ropes and hydraulic devices to lift deck panels, which allows convenient operation; however, all panels on the same level move together, so individual panel heights on a deck level cannot be adjusted independently. Additionally, the complex combination of wire ropes and hydraulic components makes maintenance difficult [
17,
18,
19]. The liftable car deck system in
Figure 1c has no built-in drive and instead uses external equipment (mobile scissor lifts) to raise or lower the deck panels. This approach is structurally simple and allows high space utilization, but the lift equipment must move to each deck panel for height adjustment. Moreover, exhaust gas and noise from the lift’s operation degrade air quality inside the ship and reduce working efficiency, negatively impacting crew health and onboard environmental safety [
20,
21]. Besides these operational issues, the use of a single large deck plate per level leads to structural limitations and low operational efficiency; in particular, disassembly and reassembly of such car decks are difficult, and maintainability is poor.
To address the structural limitations and operational inefficiencies of existing car deck systems, this study proposes a new hoistable car deck system incorporating a hinge-based mechanism as shown in
Figure 2. The design introduces modular hinge connections so that deck panels can be easily assembled and disassembled, greatly improving maintainability. The hinge drive also allows a more compact system compared to existing designs and provides structural flexibility to fit various ship layouts. In the proposed hoistable deck, even individual panels on the same level can have their height adjusted independently, enabling flexible accommodation of different cargo heights, and the deck operates solely via an integrated drive system without the need for external lifting equipment. Overall, the hinge-based hoistable car deck effectively addresses the limitations of current hoistable/liftable systems—such as the inability to adjust panels individually, the inconvenience of moving heavy equipment, and environmental side-effects—while improving both space utilization and operational efficiency in actual ship operations.
To validate the reliability of the proposed hinge-based hoistable car deck, a simulation-based verification procedure was carried out. First, a static structural analysis was performed using ANSYS Mechanical 2024 R2 Mechanical on the hinge-type car deck structure under static load conditions defined by classification society rules (DNV “Rules for Classification of Ships”). Allowable stress criteria were established based on these rules, and the analysis evaluated whether each component could maintain structural integrity under the design loads. Second, to simulate actual operating conditions, a multibody dynamics (MBD) analysis was conducted using MSC Adams 2023.1 to examine the effects of the deck’s lifting motion. Reaction forces at the hinge and support connections during raising and lowering were obtained as time-history data and then applied as time-dependent loads in a transient FEA in ANSYS Mechanical. This evaluated the deck structure’s ability to operate stably under repeated dynamic loads and reaction forces. In the finite element analyses, boundary conditions were defined to realistically simulate the operating environment of the hoistable car deck. The hinge connections were modeled as rotationally free but translationally constrained to represent their actual mechanical behavior. The supporting edges of the deck panels were constrained against displacement in the vertical and horizontal directions to ensure structural stability. For static structural analysis, design loads specified in the DNV “Rules for Classification of Ships” were applied as uniformly distributed pressures on the deck surface. For dynamic analysis, time-history reaction forces at the hinge and support connections, obtained from the multibody dynamics (MSC Adams) simulation of the deck lifting motion, were applied as time-dependent loads in the transient FEA. These boundary conditions ensured that both static and dynamic operating scenarios were appropriately represented in the numerical simulations. Using this integrated static–dynamic analysis approach, we examined the feasibility of applying the proposed hinge-based car deck structure to a real Ro-Ro vessel [
22].
Although previous studies have addressed various aspects of hoistable or liftable car decks—such as enhancing structural strength, predicting fatigue life, reducing weight using high-strength steels, or applying composite materials—relatively few works have focused on modular design concepts, maintainability, or integrated verification under both static and dynamic loading conditions. This lack of attention to modularity and operational reliability highlights a critical research gap. To address this gap, the present study proposes a hinge-based modular hoistable car deck system and comprehensively validates its performance through finite element and multibody dynamic analyses. By bridging the identified gap, this study contributes to improving the flexibility, maintainability, and structural safety of next-generation Ro-Ro vessels.
2. Design Validation of a Hinged Car Deck Using Finite Element Analysis: Static Loads
2.1. Finite Element Model Setup for Static Analysis
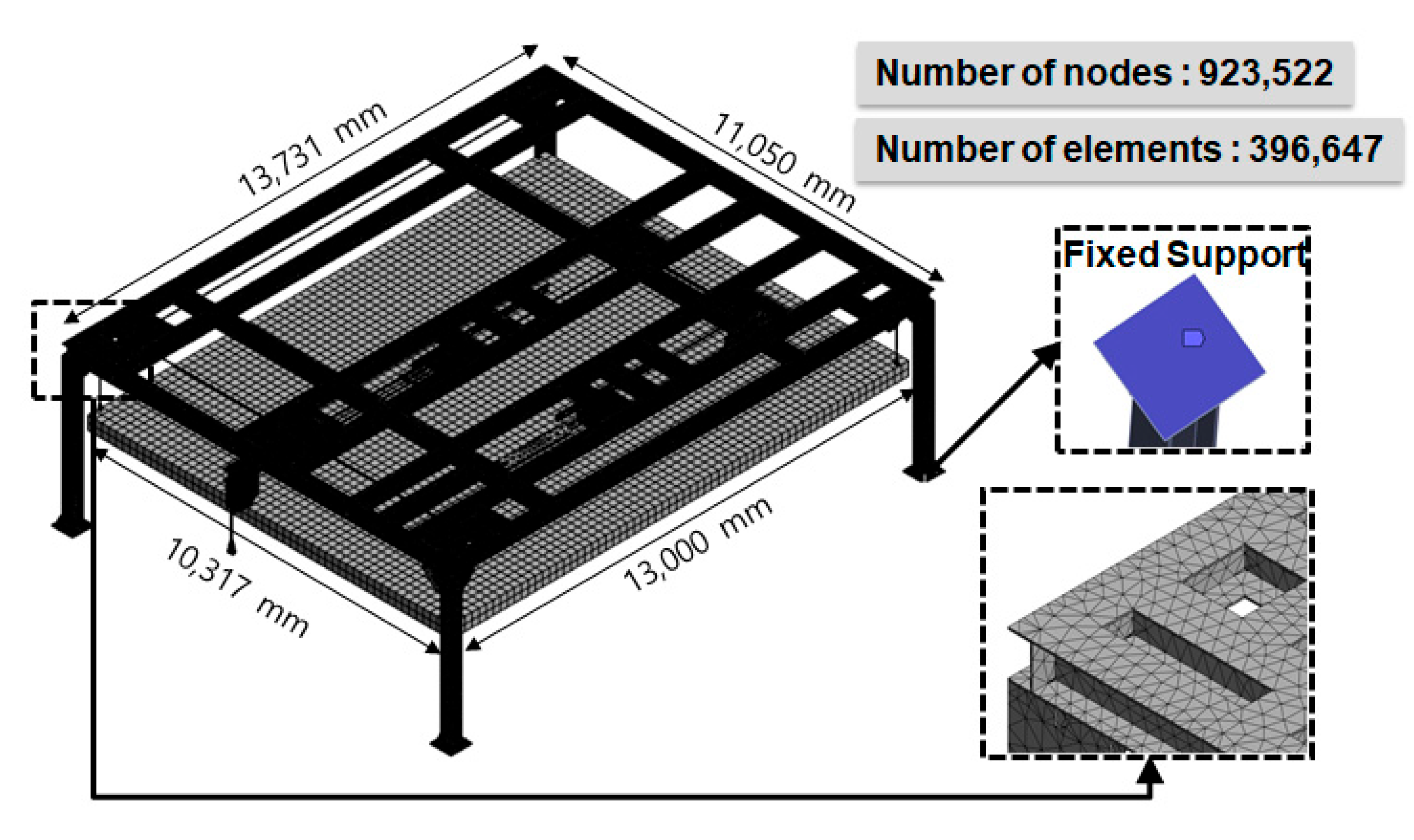
The hinge-based hoistable car deck was modeled as a large flat deck structure measuring a width of L
w = 10,317 mm and a length of L
l = 13,000 mm, with a total of eight hinge mechanisms evenly distributed along the deck’s mid-span as shown in
Figure 3.
Each hinge assembly consists of a fixed base, a rotating pin, and a moving bracket, and provides a mechanical pivot allowing the deck to fold or unfold at a certain angle (as illustrated earlier in
Figure 2). In the finite element model, the car deck plating was represented by four-node quadrilateral shell elements (SHELL181), while the hinge components were modeled using 20-node quadratic hexahedral solid elements (SOLID186). This combination was chosen to improve computational efficiency, as the quadratic formulation and second-order shape functions of SOLID186 provide improved accuracy in capturing bending and nonlinear stress fields, while reduced integration with 8 Gauss points minimized shear locking and ensured numerical stability. No mixed-element merging was applied; instead, shell–solid coupling was used at the deck–hinge interface to maintain both accuracy and efficiency.
Meshing of the entire structure was performed as shown in
Figure 4. The mesh consists of 101,229 nodes and 69,752 elements in total. A mesh convergence study was conducted by gradually refining the element size from 150 mm down to 80 mm. Convergence was achieved when the element size reached approximately 100 mm, at which point further refinement changed the maximum von Mises stress and deflection by less than 3%. This element size corresponds to less than one-tenth of the hinge thickness and less than one-eightieth of the deck span, satisfying standard FEA modeling guidelines. Although the car deck shows geometric regularity, no symmetry reduction was applied in the modeling. The full deck was analyzed to conservatively capture possible asymmetric loading scenarios. The material grades were selected according to DNV ship rules (Pt.3 Ch.1 Sec.2 Materials). AH36 high-tensile steel was used for the deck plate, and SS275 structural steel for the stiffeners. A linear elastic isotropic material model was adopted for both steels. The properties were: Young’s modulus (E = 210 GPa), Poisson’s ratio (ν = 0.3), density (ρ = 7850 kg/m
3), with yield strengths of (σ
y, AH36 = 355 MPa) and (σ
y, SS275 = 275 MPa). This assumption is sufficient since all loading scenarios remained within the elastic range. Allowable stresses for tension and shear were calculated using the class rule formulas (Equations (1) and (2)) based on yield strength, and these values were used as structural safety criteria, as shown in
Table 1.
Here, σ denotes normal (tensile/compressive) stress, τ denotes shear stress, and f1 is a material-specific factor: f1 = 1.39 for AH36 material and f1 = 1.09 for SS275.
2.2. Loading and Boundary
The static loading conditions for the car deck were determined based on DNV rules for car carriers (Pt.5 Ch.2 Sec.7, Car Carriers). A distributed cargo load of q = 250 kg/m
2 was applied to represent vehicle loading, consistent with previous FEM-based studies on Ro-Ro car decks [
23]. In addition, a vertical inertia load corresponding to a = 1.5 g = 14.715 m/s
2 was included. The self-weight of the deck plate (W = 15,124 kg) was also incorporated in the analysis as a gravity load. For boundary conditions, all six degrees of freedom were fixed at four support points on the deck’s base (corners of the deck structure). All connections between components were defined with bonded contact, assuming fully rigid attachment. The specific arrangement of the applied loads and supports is shown in
Figure 5 [
24,
25]. The use of 1.5G follows the requirement in the DNV “Rules for Classification of Ships” as a conservative design factor, ensuring that the structural assessment covers potential extreme dynamic conditions. In particular, the bonded contact condition was applied to the interfaces between the deck plate (shell elements) and the hinge components (solid elements), ensuring continuity of displacement and stress transfer across the connection. This modeling approach appropriately represents welded joints in practical ship structures. In the present analysis, the vehicle weight was modeled as a uniformly distributed load to represent the average effect of multiple vehicles on the deck surface. This approach is commonly adopted in preliminary design stages for Ro-Ro vessels and provides a conservative estimation of structural response. However, it is recognized that in practice the load is transmitted through individual wheel contacts. Therefore, the application of localized wheel loads will be considered in future studies to further refine the assessment of deck performance under realistic loading conditions.
2.3. Topology Optimization of Hinge Component
The hinge component of the car deck structure (in its initial design form) was redesigned using topology optimization to remove unnecessary material while maintaining structural stiffness. We utilized the ANSYS topology optimization module, targeting two levels of mass reduction (75% and 50% of the hinge component’s mass) as the objective. The design space for optimization included the entire hinge component except bolt attachment regions. The positions of the eight hinges on the deck are indicated in
Figure 6, and the resulting optimized material layouts for the hinge component are shown in
Figure 7a,b for the 75% and 50% mass reduction cases. For the topology optimization, the following details were applied: the hinge component was modeled using a linear elastic isotropic material (E = 210 GPa, ν = 0.3). Loads and boundary conditions from the static FEA were directly transferred to the optimization model. The full hinge volume, excluding the bolt attachment regions, was clearly defined as the design space. Mass reduction constraints of 75% and 50% were carefully applied to evaluate the effects of weight reduction while preserving adequate structural stiffness. Symmetry constraints were also introduced to ensure reliable manufacturability and balanced stress distribution. The optimization process was continued until numerical convergence was successfully achieved, defined as less than 1% change in the compliance between successive iterations. The software automatically generated detailed iteration histories, convergence plots, and final density distributions, which removed non-load-bearing material while still ensuring uniform stress distribution.
The topology optimization identified regions outside the primary load paths (marked by black dotted circles in the results) as removable material. These regions (located on the side block of the hinge base and the lower part of the central fixed bracket) were found to have negligible effects on load-bearing capacity. Using the optimization results, we created four redesigned hinge configurations, labeled Case 1 through Case 4, as shown in
Figure 8. Case 1 is the baseline hinge shape with the topology optimization applied directly to the initial design. Cases 2–4 are modified designs where additional reinforcements were added to the hinge block in areas expected to experience stress concentration. Each of these four hinge designs was incorporated into the car deck FEA model, and a static load analysis was performed for comparison of their structural performance.
3. Finite Element Analysis Results: Static Loads
Finite element analyses under static load conditions were performed for the four design cases (Cases 1–4) of the hinge-based hoistable car deck to quantitatively evaluate structural safety. The simulations, conducted in ANSYS Mechanical, focused on the stress distribution and deflection behavior of the deck structure in each case. Because the cases differ in hinge shape and reinforcement, comparing their results reveals the effects of the design modifications.
Figure 9,
Figure 10 and
Figure 11 show the distributions of normal stress in the deck plate for each case in the X direction, Z direction, and shear (XZ) direction, respectively, and
Figure 12 shows the vertical deflection of the deck plate for each case.
In Case 1 (baseline hinge with topology optimization only), the maximum stress was σt = 209.6 MPa, which is clearly well within the allowable tensile stress σt,allow = 222.4 MPa. However, the compressive stress was σc = −307.7 MPa, significantly exceeding the allowable compressive stress σc,allow = −222.4 MPa, thereby indicating the presence of an excessive local compressive hotspot. The XZ-plane shear stress was τ = 224.9 MPa, which was more than 80% higher than the allowable limit τ,allow = 125.1 MPa. In Case 2 (hinge with a reinforced central block extended in the Z-direction), the maximum tensile stress was σt = 118.4 MPa and the minimum compressive stress σc = −210.1 MPa, both very clearly satisfying the allowable criteria. However, the shear stress was τ = 205.2 MPa, still remaining above the allowable limit τ,allow = 125.1 MPa, thereby indicating that local stress concentrations were not completely eliminated. Even so, compared to Case 1, the peak stresses in Case 2 were considerably and significantly lower, and the overall compression stability was greatly (q = 250 kg/m2) improved.
Case 3 (hinge with reinforcement extended in the X-direction) showed a maximum tensile stress σt = 229.3 MPa, slightly exceeding the allowable σy,allow = 222.4 MPa, and a compressive stress σc = −221.8 MPa, very close to the allowable σc,allow = −222.4 MPa. The shear stress was τ = 169.2 MPa, also above the allowable τ,allow = 125.1 MPa, indicating a structural imbalance. This outcome suggests that the reinforcement in Case 3 did not align with the primary load path, and therefore failed to sufficiently disperse the stress.
Case 4 (hinge with an added triangular reinforcement at the base) satisfied all stress criteria. The maximum tensile stress was σt = 104.15 MPa and the maximum compressive stress σc = −130.2 MPa; the shear stress was τ = 120.5 MPa, which is below the allowable τ,allow = 125.1 MPa. Notably, the stress distribution in Case 4 was much more uniform than in the other cases, and stable stress levels were observed in both shear and compression regions. Additionally, the stresses in the reinforcement members (angle and channel sections) were well within the allowable limits for SS275 steel (σν,allow = 172.8 MPa, τ,allow = 97.2 MPa). In Case 4, the maximum stress in the reinforcements was the lowest among all cases, indicating that the triangular gusset effectively distributed load away from the hinge center and minimized stress transfer into the reinforcements.
In terms of deformation, Cases 1–3 exhibited a maximum deflection of δ
max ≈ 40 mm at the mid-span of the deck, whereas Case 4 showed δ
max = 35.25 mm, which is approximately 12% lower than the others. This reduction indicates that Case 4 achieved the highest stiffness and the most balanced structural behavior. Moreover, the maximum deflection of 35.25 mm in Case 4 satisfies both the allowable deflection limits defined in the DNV Rules for Classification of Ships, Part 3: Hull—Structural Design Principles (Deflection Criteria, L/200–L/250) and the maximum edge deflection criterion, which specifies that the lowest point of the panel (δ) should not exceed 50 mm to ensure safe vehicle passage between adjacent car decks [
26,
27]. This confirms that the proposed structure’s deflection remains within the acceptable range, ensuring structural safety. It should be noted that in
Figure 9,
Figure 10 and
Figure 11, the color legends were set based on the allowable stress values defined by DNV rules (222.4 MPa for AH36 normal stress, 125.1 MPa for AH36 shear stress, etc.), while the maximum values reported in the text represent the actual finite element analysis results. In addition, although the figures mainly present the stress distribution of the deck plate (AH36), the reinforcement members (SS275) were also verified. The maximum stresses in the stiffeners (σ
t = 104 MPa, τ = 82 MPa) were found to be within the allowable limits (σ
,allow = 172.8 MPa, τ
,allow = 97.2 MPa), confirming that both plate and stiffeners remain structurally safe.
Overall, the static analysis identified Case 4 as the optimal design, with lower stress, smaller deflection, and a more uniform stress distribution. To approximate dynamic effects, a quasi-dynamic analysis was conducted by applying an equivalent 1.5 g inertia load to the static model. This resulted in slightly higher local stresses and about 1.7 mm additional deflection compared to the static case. Nevertheless, the hinge system effectively constrained deformation, and the overall deformation and stress patterns remained consistent. Thus, the static analysis provides a conservative estimate, while the quasi-dynamic check further confirms the robustness of Case 4 under accelerated loading.
4. Integration of Multibody Dynamics and Finite Element Analysis: Dynamic Loads
After validating the static performance of the hinge-based deck, we analyzed its behavior under dynamic operation. The hoistable car deck (with the optimized hinge design from the static analysis) functions as a liftable platform for vehicle loading and unloading, meaning the entire deck moves over time when the lifting mechanism operates. Thus, the deck structure is subjected not only to static loads but also to time-varying reaction forces and inertial loads during operation, which can induce complex dynamic stresses throughout the structure. To accurately account for these effects, a multibody dynamics (MBD) simulation of the hoisting system was carried out and coupled with the FEA.
4.1. Multibody Dynamics Model Configuration
The MBD model was developed using the commercial code MSC Adams to include the main components and mechanisms of the hoistable car deck system. As shown in
Figure 13, the model consists of the deck structure itself, a fixed support frame, a cylinder-piston actuator for lifting, and a wire-and-pulley system acting at four points (front-left, front-right, rear-left, rear-right) to raise and lower the deck. The pulleys and wire ropes serve as the key load-transmitting elements, so their physical properties (mass m, diameter d, density ρ, and tension behavior) were carefully calibrated to represent real operating characteristics. The total mass of the deck in the model was set to m = 15,124 kg (matching the FE model). The wire system was modeled with diameters d_c = 36 mm for the central hoisting cables and d_s = 18 mm for the four corner support cables. The hydraulic piston-cylinder actuator was specified to operate at a maximum lifting speed v = 400 mm/min. Reaction forces F
i were transmitted from the deck through the wire-pulley system, and in the Adams model these reaction forces were measured at 20 defined points (i = 1…20), including pulley supports and connection points in the mechanism. In the model, the abbreviations RL, RR, CEN, FR, and FL denote the Rear Left, Rear Right, Center, Front Right, and Front Left connection points, respectively.
Figure 14 shows the complete Adams simulation model, including the deck in raised and lowered positions (and a plan view), with the applied loads and connection conditions visualized.
4.2. Multibody Dynamics Analysis Results: Reaction Force According to Time History
The MBD simulation was run to obtain the time-history of reaction forces at each connection point during a full lifting cycle of the deck. In the analysis, the force components in the X, Y, and Z directions (denoted Fx, Fy, Fz) at each of the 20 monitored points were recorded at 0.01 s intervals. These time-history results capture the real-time variation in dynamic loads transmitted through the structure, providing crucial information for assessing potential stress concentrations or overloads. To make the subsequent finite element analysis tractable, the 0.01 s interval data were linearly interpolated to a coarser time step of 1 s. A comparison of structural responses using the interpolated 1 s data versus the original 0.01 s data confirmed that the overall force variation trends and peak magnitudes were preserved, validating the interpolation approach.
Table 2 presents the maximum reaction force values in each axis (Fx, Fy, Fz) obtained from the MBD simulation at representative points in the hoisting mechanism.
The interpolated reaction force time-histories were then applied in ANSYS Mechanical as time-dependent external loads in a transient structural FEA. Each of the 20 load application points from the MBD model was assigned a corresponding time-varying force in the FEA model. This MBD–FEA coupled analysis approach allows a dynamic examination of how the structure responds under realistic operating conditions, overcoming the limitations of a purely static analysis. The coupled simulation procedure provides practical, quantitative evidence that can be used in the future for actual ship design, class approval testing, and commissioning of the new deck system.
5. Finite Element Analysis Results Considering Dynamic Loads During Operation of Hoistable Car Deck
To evaluate the deck’s performance under dynamic loads, we applied the time-history reaction forces from the MBD simulation to the finite element model of the hoistable car deck. The transient FEA reflects the actual operating environment by subjecting the structure to the lifting-induced forces varying over time at multiple points.
5.1. Finite Element Model for Dynamic Analysis
The transient structural FEA model included all major structural components of the hoistable deck (with the optimized hinge design) and was meshed similarly to the static model. The boundary conditions remained the same: the four base corner supports of the deck were fixed in all degrees of freedom, and all structural contacts were bonded (fully fixed). The overall model size, mesh details, and supports for the dynamic analysis are depicted in
Figure 15.
The loading condition was defined by the 20-point reaction force time-histories obtained from the Adams MBD simulation, using the interpolated 1 s interval data. These time-dependent forces were input as external loads in the transient FEA model.
5.2. Finite Element Analysis Results: Dynamic Loads
As shown in
Figure 16, the maximum von Mises stress in the deck structure during the lifting operation was approximately 93.7 MPa, occurring at the bottom of the leg members that support the deck. This region corresponds to the path through which the lifting reaction forces are transmitted to the ship structure, making it a likely point for load concentration. However, the peak stress (93.7 MPa) is well below the allowable stress for the deck material (222.4 MPa for AH36), and the high-stress area is confined to a localized region at the leg base. The overall stress distribution indicates no widespread or critical overstressing of the structure.
The maximum deflection of the deck during dynamic operation was on the order of 1 mm or less in the vertical (Y-axis) direction as shown in
Figure 17, which occurred at the deck’s mid-span. Given the scale of the structure and the magnitude of the loads, this deflection is very small and would not impair the deck’s function. These results indicate that under realistic time-varying loads, the structure’s response remains well within safe limits.
In comparison with the static analysis, it can be observed that both stress levels and deformation patterns under dynamic loads follow a similar trend, with the dynamic response remaining slightly lower due to load redistribution over time. This indicates that the static analysis provides a conservative approximation of the structural performance, while the dynamic analysis offers further validation by capturing the transient effects of time-dependent forces. Consequently, the combined evaluation confirms that the deck maintains structural integrity and serviceability under both static and dynamic operating conditions
Furthermore, the analysis showed that stress concentrations under dynamic loading followed a similar pattern to the static case, demonstrating effective load distribution through the hinge components and deck structure as intended by the design. The combination of topology-optimized hinges and strategic reinforcements achieved a balanced stress distribution, and the deck maintained a stable response (both in terms of stress and deflection) throughout the lifting motion.
It should be noted that the stress scale in
Figure 16 was set to 250 MPa to maintain consistency with the yield strength (σ
y) of structural steels (e.g., SS275 ≈ 250 MPa). Although the actual maximum von Mises stress (σ
v, max) was only 93.7 MPa, the wider legend range was adopted to provide a conservative reference, allowing direct comparison with material strength across all figures and confirming that stresses remain well below allowable limits, thereby verifying structural adequacy.
The dynamic analysis confirms that the hinge-based hoistable car deck can withstand the actual operational loads associated with raising and lowering, without experiencing excessive stress or deformation. The combined MBD and FEA approach provided a comprehensive evaluation of the deck’s structural stability at the full-system level (rather than just individual components), offering essential data for design validation and class approval of the system. Even under the applied time-history loading, the deck exhibited sufficient strength, stiffness, and load distribution capacity, demonstrating its viability for real application.
6. Conclusions
In this study, we designed a new hoistable car deck system with a hinge-based folding mechanism as an alternative to conventional Ro-Ro ship car decks, and we comprehensively validated its structural performance through simulations.
The proposed design aims to resolve the structural inefficiencies and operational constraints of existing car deck systems (such as fixed decks or costly hydraulic lift decks) by using modular hinge connections to create a foldable deck, thereby achieving both practicality and structural soundness. During the design process, standard high-tensile shipbuilding steels (AH36 for the deck plate and SS275 for stiffeners) were used to ensure compliance with actual Ro-Ro ship structural requirements and class rules. A topology optimization technique was applied to the hinge component to remove material not contributing to load support, achieving both weight reduction and improved stress distribution. The optimization resulted in approximately 24.9 kg of weight savings per hinge, contributing to the overall weight reduction in the system. Four hinge design cases were then analyzed, and the case with an added triangular reinforcement (Case 4) was identified as the optimal design, as it met all stress criteria and exhibited the most uniform stress distribution and smallest deformation under load. The structural analysis included not only static loading scenarios but also a coupled multibody dynamics (MBD) and transient FEA to simulate time-varying operational loads. By incorporating reaction force data from an Adams MBD simulation (covering 20 key points over time) into an ANSYS transient analysis, we overcame the limitations of static analysis and examined the deck’s behavior under realistic dynamic conditions. This integrated approach demonstrated that even during lifting operations, the deck structure remained stable without any excessive stress or deflection. The combined system analysis showed a maximum von Mises stress of about 93.7 MPa, providing ample safety margin relative to the material’s yield strength, and a maximum vertical deflection of about 1 mm, indicating a very stable response. These analysis results suggest that the hinge-type hoistable car deck is an effective alternative to overcome the limitations of existing Ro-Ro deck structures. The design offers structural advantages in terms of weight reduction, ease of maintenance, modular construction, and stress distribution. Moreover, by proving its structural safety under actual operating conditions, we have established a solid engineering basis supporting its feasibility for real-world ship applications. The hinge-based hoistable car deck thus represents a promising solution for next-generation Ro-Ro vessels, enhancing both operational flexibility and structural efficiency. In future research, extended fatigue life evaluations and long-term performance assessments under diverse sea states and loading conditions will be conducted to further validate the proposed design. Optimization studies on hinge geometry and modular deck connections will also be explored to enhance durability and manufacturability. Furthermore, experimental validation through scaled model tests or full-scale prototype measurements will be carried out to complement the numerical simulations and ensure reliability under real operational conditions. From an engineering and industrial perspective, the proposed hinge-based hoistable car deck can be applied to next-generation Ro-Ro vessel designs to improve cargo handling flexibility and reduce maintenance costs. In addition, it offers potential for retrofitting existing vessels with more efficient deck systems, thereby extending their operational lifespan. Beyond Ro-Ro applications, the methodology may also be adapted for offshore platforms and modular floating structures that require adjustable deck solutions, thus broadening the applicability of the proposed system to wider marine and offshore engineering domains.
Author Contributions
Conceptualization, S.K. and J.H.K.; methodology, S.K.; software, H.S.K., M.G.C., B.K. and K.C.; validation, H.S.K., B.K. and S.K.; formal analysis, H.S.K.; investigation, S.K.; resources, H.S.K.; data curation, H.S.K. and K.C.; writing—original draft preparation, S.K.; writing—review and editing, S.K. and J.H.K.; visualization, M.G.C.; supervision, S.K. and J.H.K.; project administration, S.K. and J.-I.P.; funding acquisition, S.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Technology development Program (S3273332) funded by the Ministry of SMEs and Startups (MSS, Republic of Korea).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
Jang-Ik Park was employed by the company Dae Lyun Engineering Co. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Nomenclature
| CEN | Center (hoisting mechanism point) |
| DNV | Det Norske Veritas (Classification Society) |
| E | Young’s modulus [GPa] |
| F | Force [N] |
| FEA | Finite element analysis |
| FL | Front left (hoisting mechanism point) |
| FR | Front right (hoisting mechanism point) |
| FRP | Fiber-reinforced plastic |
| GFRP | Glass fiber reinforced plastic |
| IMO | International Maritime Organization |
| L | Span length [m] |
| M | Bending moment |
| MBD | Multibody dynamics |
| P | Applied load/Force |
| PCC | Pure Car Carrier |
| PCTC | Pure Car and Truck Carrier |
| RL | Rear left (hoisting mechanism point) |
| RR | Rear right (hoisting mechanism point) |
| Ro-Ro | Roll-on/Roll-off |
| Δ | Displacement/Change |
| δ | Deflection [mm] |
| ν | Poisson’s ratio [−] |
| ρ | Density [kg/m3] |
| σ | Normal stress [MPa] |
| τ | Shear stress [MPa] |
References
- Martynas, J. RO-RO Transportation Management in the Southern Baltic. Master’s Thesis, Wold Maritime University, Malmö, Sweden, 21 August 2000. [Google Scholar]
- Joel, H. The Logistics Considerations of the Landing Ship Tank and Its Evolution as an Auxiliary Repair Ship in World War II. Master’s Thesis, University of New Orleans, New Orleans, LA, USA, 2021. [Google Scholar]
- Alyona, L.; Oleksij, F.; V’aclav, P.; Pavel, K. Dynamic Load and Strength Determination of Carrying Structure of Wagons Transported by Ferries. J. Mar. Sci. Eng. 2020, 8, 902. [Google Scholar] [CrossRef]
- Apostolos, P.; George, Z.; Zaraphonitis, S.S.; Evangelos, B. An Integrated Methodology for the Design of Ro-Ro Passenger Ships. Ship Technol. Res. 2010, 57, 26–39. [Google Scholar] [CrossRef]
- Jerolim, A.; Stanislav, K.; Vito, R.; Pero, P. Structural analysis and design of a car carrier with composite sandwich deck panels. Ship Offshore Struct. 2019, 14 (Suppl. 1), 83–90. [Google Scholar]
- Vittorio, A. When the road controls the sea: A case study of Ro-Ro transport in the Mediterranean. Marit. Policy Manag. 2000, 27, 375–389. [Google Scholar] [CrossRef]
- Bernt, O.V.; Lars, M.H.; Kjetil, F. Optimization of Stowage Plans for Ro-Ro Ships. Comput. Oper. Res. 2011, 38, 1425–1434. [Google Scholar]
- Alamsyah, A.; Mapangandro, A.B.; Amalia, I.W.; Pawara, M.U. Fatigue Life Analysis of Ramp Door Ferry Ro-Ro Gt 1500 Using Finite Element Method. Maj. Ilm. Pengkaj. Ind. 2021, 15, 42–49. [Google Scholar] [CrossRef]
- Report of the marine safety investigation into a fatality of a crew member on a roll-on, roll-off passenger ferry. In GRYF-Marine Safety Investigation Report; IMO Number: 8818300 Official Number: 8000862; Bahamas Maritime Authority: London, UK, 2019.
- Alamsyah; Samsu, D.; Suardi; Pawarah, M.U.; Jumalia. The Strength and fatigue Life analysis of Sedan car Ramp of The Ferry Ro-Ro 5000GT Using Finite Element Method. Kapal J. Ilmu Pengetah. Teknol. Kelaut. 2021, 18, 101–111. [Google Scholar] [CrossRef]
- Andersson, E.; Guhren, A. Alternative Design of Steel/Aluminium Car Deck. Master’s Thesis, Chalmers University of Technology, Göteborg, Sweden, 2014. [Google Scholar]
- Junbo, J.; Anders, U. Dynamic analysis of vehicle-deck interactions. Elsevier Ocean Eng. 2006, 33, 1765–1795. [Google Scholar]
- Pack, H.; Lee, Y. A Study on the Standardization of ASET on Deck of Ro-Ro Passenger Ship through Simulation Analysis of the SEWOL Ship Turnover Accident. J. Korean Soc. Hazard Mitig. 2016, 16, 495–503. [Google Scholar]
- Nguyen, H.; Chu, Q.; Kim, S. Dynamic response of steel–concrete composite structures under impact and explosive loads. J. Constr. Steel Res. 2011, 67, 647–655. [Google Scholar] [CrossRef]
- Karatug, C.; Durmusoglu, Y. Design of a solar photovoltaic system for a Ro-Ro ship and estimation of performance analysis: A case study. Elsevier Sol. Energy 2020, 207, 1259–1268. [Google Scholar] [CrossRef]
- Ammar, N.; Seddiek, I. Eco-environmental analysis of ship emission control methods: Case study RO-RO cargo vessel. Elsevier Ocean Eng. 2017, 137, 166–173. [Google Scholar] [CrossRef]
- Korkut, E.; Atlar, M.; Incecik, A. An experimental study of global loads acting on an intact and damaged Ro–Ro ship model. Elsevier Ocean Eng. 2005, 32, 1370–1403. [Google Scholar] [CrossRef]
- Jia, J.; Ulfvarson, A. A parametric study for the structural behavior of a lightweight deck. Elsevier Eng. Struct. 2004, 26, 963–977. [Google Scholar] [CrossRef]
- TTS Group ASA. Car Decks and Ramps; Brochure; TTS Group ASA: Bergen, Norway; Available online: https://www.macgregor.com/globalassets/tts/product-sheets/car-decks-and-ramps.pdf (accessed on 31 July 2025).
- Yusuke, T.; Sherif, R.; Yasuhisa, O.; Yasuo, K.; Hidekazu, M. Prediction of Welding Distortion and Panel Buckling of Car Carrier Decks Using Database Generated by FEA. Trans. JWRI 2007, 36, 65. [Google Scholar]
- Yongmoon, N.; Wooki, C. Study for Structure of Liftable Car Deck on PCTC. Spec. Issue Soc. Nav. Archit. Korea 2013, 60–65. [Google Scholar]
- Tuswan; Achmad, Z.; Bambang, P.; Abdi, I. Dynamic Characteristic of partially debonded sandwich of ferry ro-ro’s car deck: A numerical modeling. Open Eng. 2020, 10, 424–433. [Google Scholar]
- Amalia, I.W.; Nindi, W.D.R.; Luh, P.A.; Alamsyah; Rodlian, J.I. Fatigue Analysis of 5000 GT Ferry Ro-Ro’ s Car Deck Using Finite Element Method. Kapal J. Ilmu Pengetah. Teknol. Kelaut. 2021, 18, 160–170. [Google Scholar]
- Baris, A.; Hamed, S. Parametric Design and Optimization of Steel Car Deck Panel Structures. Master’s Thesis, Chalmers University of Technology, Gothenburg, Sweden, 2012. [Google Scholar]
- Romanas, P. Optimal stowage on Ro-Ro decks for efficiency and safety. J. Mar. Eng. Technol. 2018, 20, 17–33. [Google Scholar] [CrossRef]
- Tuswan; Achmad, Z.; Agung, B.; Sujiatanti, S.H. Comparative Study on Ferry Ro-Ro’s car Deck Structural Strength by means of the Application of Sandwich Materials. In Proceedings of the 3rd International Conference on Marine Technology (SENTA2018), Surabaya, Indonesia, 5–6 December 2018; pp. 87–96. [Google Scholar]
- Yi, M.-S.; Park, J.-S. Nonlinear analysis and weight optimization of living quarters for offshore jack-up rigs: A sustainable engineering approach. Appl. Ocean Res. 2025, 158, 104515. [Google Scholar] [CrossRef]
Figure 1.
Ro-Ro ship car deck systems: (a) schematic placement of car decks in a Ro-Ro vessel; (b) hoistable car deck; (c) liftable car deck.
Figure 1.
Ro-Ro ship car deck systems: (a) schematic placement of car decks in a Ro-Ro vessel; (b) hoistable car deck; (c) liftable car deck.
Figure 2.
Schematic of the proposed hinge-based hoistable car deck structure.
Figure 2.
Schematic of the proposed hinge-based hoistable car deck structure.
Figure 3.
Dimensions of the initial hinge design and its placement on the car deck.
Figure 3.
Dimensions of the initial hinge design and its placement on the car deck.
Figure 4.
Finite element mesh of the hinge-type car deck structure.
Figure 4.
Finite element mesh of the hinge-type car deck structure.
Figure 5.
Applied static load and boundary conditions for the hinge-based car deck model (distributed deck load, gravitational acceleration, fixed supports).
Figure 5.
Applied static load and boundary conditions for the hinge-based car deck model (distributed deck load, gravitational acceleration, fixed supports).
Figure 6.
Numbering of hinge positions on the car deck (red circles indicate hinge locations).
Figure 6.
Numbering of hinge positions on the car deck (red circles indicate hinge locations).
Figure 7.
Topology optimization results for the hinge component: (a) 75% mass reduced; (b) 50% mass reduced (red circles indicate removable material regions).
Figure 7.
Topology optimization results for the hinge component: (a) 75% mass reduced; (b) 50% mass reduced (red circles indicate removable material regions).
Figure 8.
Four redesigned hinge shapes based on topology optimization (Case 1: optimized base design; Cases 2–4: designs with various added reinforcements).
Figure 8.
Four redesigned hinge shapes based on topology optimization (Case 1: optimized base design; Cases 2–4: designs with various added reinforcements).
Figure 9.
X-direction normal stress distribution in the car deck plate under static load: (a) Case 1; (b) Case 2; (c) Case 3; (d) Case 4.
Figure 9.
X-direction normal stress distribution in the car deck plate under static load: (a) Case 1; (b) Case 2; (c) Case 3; (d) Case 4.
Figure 10.
Z-direction normal stress distribution in the car deck plate under static load: (a) Case 1; (b) Case 2; (c) Case 3; (d) Case 4.
Figure 10.
Z-direction normal stress distribution in the car deck plate under static load: (a) Case 1; (b) Case 2; (c) Case 3; (d) Case 4.
Figure 11.
XZ-direction shear stress distribution in the car deck plate under static load: (a) Case 1; (b) Case 2; (c) Case 3; (d) Case 4.
Figure 11.
XZ-direction shear stress distribution in the car deck plate under static load: (a) Case 1; (b) Case 2; (c) Case 3; (d) Case 4.
Figure 12.
Vertical (Y-direction) deflection of the car deck plate under static load: (a) Case 1; (b) Case 2; (c) Case 3; (d) Case 4.
Figure 12.
Vertical (Y-direction) deflection of the car deck plate under static load: (a) Case 1; (b) Case 2; (c) Case 3; (d) Case 4.
Figure 13.
Operating mechanism of the hinge-based hoistable car deck system (MSC Adams model): (a) perspective view; (b) top view.
Figure 13.
Operating mechanism of the hinge-based hoistable car deck system (MSC Adams model): (a) perspective view; (b) top view.
Figure 14.
Adams multibody model of the hoistable car deck (MSC Adams model): (a) Top view showing the wire/pulley system and load application points; (b) deck in the raised state (plate up); (c) deck in the lowered state (plate down).
Figure 14.
Adams multibody model of the hoistable car deck (MSC Adams model): (a) Top view showing the wire/pulley system and load application points; (b) deck in the raised state (plate up); (c) deck in the lowered state (plate down).
Figure 15.
Finite element model for transient analysis, showing the overall structure, mesh, and boundary conditions for the hoistable car deck.
Figure 15.
Finite element model for transient analysis, showing the overall structure, mesh, and boundary conditions for the hoistable car deck.
Figure 16.
Maximum von Mises stress distribution in the hoistable car deck during lifting operation (transient analysis).
Figure 16.
Maximum von Mises stress distribution in the hoistable car deck during lifting operation (transient analysis).
Figure 17.
Maximum vertical (Y-direction) displacement of the hoistable car deck during lifting operation (transient analysis).
Figure 17.
Maximum vertical (Y-direction) displacement of the hoistable car deck during lifting operation (transient analysis).
Table 1.
Material properties and allowable stress criteria for deck plate and stiffener.
Table 1.
Material properties and allowable stress criteria for deck plate and stiffener.
| | Materials | Thickness
t [mm] | Yield Strength σy [MPa] | Tensile Strength σu [MPa] | Allowable Stress σa11 [MPa] | E [GPa] | ν [−] |
|---|
| Plate | AH36 | - | 355.0 | 490.0 | Normal 222.4
Shear 125.1 | 210 | 0.3 |
| Stiffener | SS275 | t ≤ 15 | 275.0 | 410.0 | Normal 172.8
Shear 97.2 | 210 | 0.3 |
Table 2.
Maximum reaction forces in each direction at joint parts of the hoisting mechanism (from MBD simulation).
Table 2.
Maximum reaction forces in each direction at joint parts of the hoisting mechanism (from MBD simulation).
| Wire | Points | Fx [N] | Fy [N] | Fz [N] |
|---|
| Main Wire Center | Sheave_1 | 343,164.3 | 1128.3 | 1128.3 |
| Sheave_2 | −171,582.1 | 171,982.5 | 1035.1 |
| Sheave_3 | −171,505.5 | −171,793.1 | 1142.6 |
| Sheave_4 | 1412.6 | 0.0 | 2649.4 |
| End_Mount | 10.7 | 0.0 | −1154.8 |
| Main Wire FL | Sheave_1 | 42,377.8 | −42,356.3 | 451.2 |
| Sheave_2 | −59.7 | 42,306.0 | 42,515.6 |
| End_Mount | 52.4 | 47.0 | −42,317.6 |
| Main Wire FR | Sheave_1 | 42,398.8 | 42,378.6 | 423.2 |
| Sheave_2 | −59.7 | −42,328.4 | 42,537.9 |
| End_Mount | 52.5 | −47.0 | −42,339.9 |
| Main Wire RL | Sheave_1 | 42,651.8 | −42,587.1 | 287.8 |
| Sheave_2 | 42,572.3 | 42,590.3 | 521.0 |
| Sheave_3 | −42,495.5 | 6.8 | 42,893.8 |
| End_Mount | −58.2 | −2.6 | −42,516.1 |
| Main Wire RR | Sheave_1 | 42,627.6 | 42,598.9 | 287.8 |
| Sheave_2 | 42,584.2 | −42,602.2 | 521.0 |
| Sheave_3 | −42,507.3 | −6.9 | 42,906.2 |
| End_Mount | −58.2 | −3.2 | −42,577.9 |
| Sheave Block | CG | 169,934.8 | 39.8 | 5187.8 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).