Deep-Sea Convergence Zone Parameter Prediction with Non-Uniform Mixed-Layer Sound Speed Profiles

Abstract

The deep-sea convergence zone (CZ) is a critical phenomenon for long-range underwater acoustic propagation. Accurate prediction of its distance, width, and gain is essential for enhancing sonar detection performance. However, conventional ray-tracing models, which assume vertically stratified sound speed profiles (SSPs), fail to account for horizontal sound speed gradients in the mixed layer, leading to significant prediction errors. To address this, we propose a novel ray-tracing model that incorporates horizontally inhomogeneous SSPs in the mixed layer. Our approach combines empirical orthogonal function (EOF) decomposition with the Del Grosso sound speed formula to construct a continuous 3D sound speed field. We further derive a modified ray equation including horizontal gradient terms and solve it using a fourth-order Runge–Kutta method. Simulation and experimental validation in the South China Sea demonstrate that our model reduces the prediction error for the first CZ distance by 2.26%, width by 2.66%, and gain deviation by 5.85% compared to the Bellhop model. These results confirm the effectiveness of our method in improving CZ parameter prediction accuracy.

1. Introduction

The convergence zone (CZ) is a periodic region of acoustic energy focusing formed due to the propagation characteristics of sound waves in the deep-sea sound channel. Its essence originates from the refraction and reflection effects of sound waves in the oceanic waveguide. In a vertically stratified sound speed profile (SSP), the sound speed gradient causes the ray trajectories to bend. When the rays traverse a certain horizontal distance and reconverge, they form a high-intensity acoustic focusing region. The convergence zone represents a distinctive acoustic propagation phenomenon within the deep-sea environment. This phenomenon is characterized by a periodically focused acoustic energy structure, which facilitates the transmission of acoustic signals over extended distances with reduced attenuation, thereby significantly augmenting the operational efficacy of sonar detection systems [1]. Predicting the characteristic parameters of the deep-sea convergence zone necessitates an examination of its distance, width, and gain. Investigating these parameters enables underwater combat units to precisely understand the influence of convergence zone characteristics on equipment performance. This understanding provides a supplementary basis for decision-making in the formulation of detection maneuver strategies during deep-sea operations.

In contemporary research, the primary approach for predicting the characteristic parameters of convergence zones involves analyzing the propagation paths of acoustic rays through the development of acoustic field models [2,3,4,5,6]. Notably, the Bellhop ray acoustic field model, introduced by Porter and Bueker, serves as a prominent method for modeling acoustic fields in horizontally inhomogeneous environments [7]. This model has gained widespread application in recent years for examining acoustic propagation characteristics. For instance, Weishuai et al. utilized the Douglas–Peucker algorithm to extract oceanographic factors from a database and employed the BELLHOP ray-tracing model to derive acoustic propagation characteristics, thereby offering a predictive tool for studying underwater acoustic propagation in oceanic front environments [8]. Similarly, Liu et al. utilized a three-dimensional ocean acoustic framework, integrating the MITgcm and BELLHOP ray model, to investigate the coupling effects of the Luzon cold vortex and tidal waves [9]. Additionally, Ma et al. applied the BELLHOP ray theory model to explore the acoustic field characteristics associated with a pair of cyclonic vortices and a typical anticyclonic vortex [10]. Chen et al. present an efficient sound-speed estimation technique for turning rays, which leverages the reliable acoustic path boundary to separate turning direct arrivals and builds a ray-tracing model for range correction [11]. Ray equations for BELLHOP 2D, as well as general 3D, environments are classical and appear in several textbooks [12,13]. However, the response mechanisms of existing coupled models to small-scale perturbations within the mixed layer remain incompletely understood, resulting in insufficient modeling resolution of the horizontal sound speed gradient and limiting their ability to capture the rapid spatiotemporal evolution of the mixed-layer sound speed profile.

Moreover, there is still a significant discrepancy between predictions using ray models and acoustic experimental observations [14,15]. Therefore, data-driven prediction methods have been widely applied. Yang et al. designed an intelligent convergence zone recognition algorithm based on convolutional neural networks [16]. By inputting sound speed profiles and acoustic propagation loss data, the algorithm automatically extracts the spatiotemporal characteristics of caustic zones, and it achieved synchronous prediction of convergence zone distance and width in an East China Sea experiment, significantly improving efficiency compared to traditional physical models. Xu et al. developed a convergence zone prediction model based on high-resolution ocean fronts and tested 24 machine learning algorithms using k-fold cross-validation [17]. Li et al. constructed a convergence zone parameter prediction model under the influence of mesoscale eddies by integrating numerical simulations and measured data in multiple dimensions [18]. Ibebuchi and Richman used an autoencoder neural network to encode nonlinear sea surface temperature patterns in the tropical Pacific to predict the Nino 3.4 index [19]. Xu et al. utilized physics-informed machine learning methods to identify and predict acoustic convergence zone characteristics of mesoscale eddies under limited data conditions [20]. However, data-driven prediction methods struggle to cover multi-spatiotemporal scale acoustic–ocean joint datasets and face dual challenges of data quality and model interpretability due to their opaque physical mechanisms. The non-uniformity of sound speed in the mixed layer originates from the spatial heterogeneity of temperature and salinity and their dynamic coupling effects. Existing models often rely on local temperature and salinity profile interpolation or empirical formulas, which fail to characterize the small-scale fluctuations in sound speed caused by mesoscale eddies and internal wave disturbances. Moreover, the accuracy of existing sound field characteristic parameter forecasting algorithms is jointly influenced by multiple factors, including sound speed profile modeling, sound ray-tracing algorithms, and environmental dynamics. The horizontal non-uniformity of sound speed in the mixed layer has not been adequately characterized, leading to cumulative deviations in sound ray trajectories, which directly affect the prediction accuracy of the distance and width of convergence zones.

Empirical orthogonal function (EOF) analysis was employed to isolate the dominant modes of spatial and temporal variability in ocean mixed-layer temperature and salinity. This technique decomposes the covariance structure of the anomaly fields into orthogonal spatial patterns (EOFs) and their associated principal component (PC) time series. The leading modes, which account for the largest fraction of total variance, effectively highlight the key large-scale patterns and their temporal evolution, revealing influential processes such as seasonal forcing, interannual climate oscillations, and regional trends. This article specifically addresses the following problem: based on the Bellhop model, focusing on the influence of the horizontal sound speed gradient within the mixed layer on the parameters of the convergence zone, we propose a core algorithm to construct a parametric model of the sound speed profile with a continuous horizontal gradient and then establish a ray-tracing equation under non-uniform sound speed conditions. On this basis, we investigate the numerical solution algorithm of the model to achieve the calculation of the characteristic parameters of the convergence zone.

The actual marine environment is highly spatially heterogeneous and dynamically complex. Sound speed profiles are not uniformly distributed but are influenced by factors such as temperature and salinity, exhibiting significant horizontal gradient characteristics [21]. Particularly in the upper ocean (mixed layer), due to the effects of solar radiation, seasonal temperature differences, and ocean current shearing, sound speed profiles often show strong inhomogeneity [22]. Neither ray models nor data-driven prediction methods have fully considered the horizontal inhomogeneity of sound speed in the deep-sea mixed layer, resulting in cumulative offsets in ray trajectories and directly affecting the prediction accuracy of convergence zone distance and width. To address this gap, this article proposes a horizontally inhomogeneous sound speed profile model for the mixed layer. Our main contributions are as follows:

• A method for constructing horizontally inhomogeneous sound speed profiles in the deep-sea mixed layer is proposed. By using EOF decomposition technology to extract the spatial model characteristics of temperature and salinity fields and combining them with the Del Grosso formula, a three-dimensional continuous sound speed field is generated.
• A ray-tracing algorithm based on non-uniformly distributed sound speed profiles is developed. By introducing the horizontal sound speed gradient term into the ray equation and designing a fourth-order Runge–Kutta numerical solution algorithm, the bottleneck of traditional ray models in representing the influence of horizontal sound speed gradients is overcome, thereby improving the prediction accuracy of convergence zone ray trajectories.
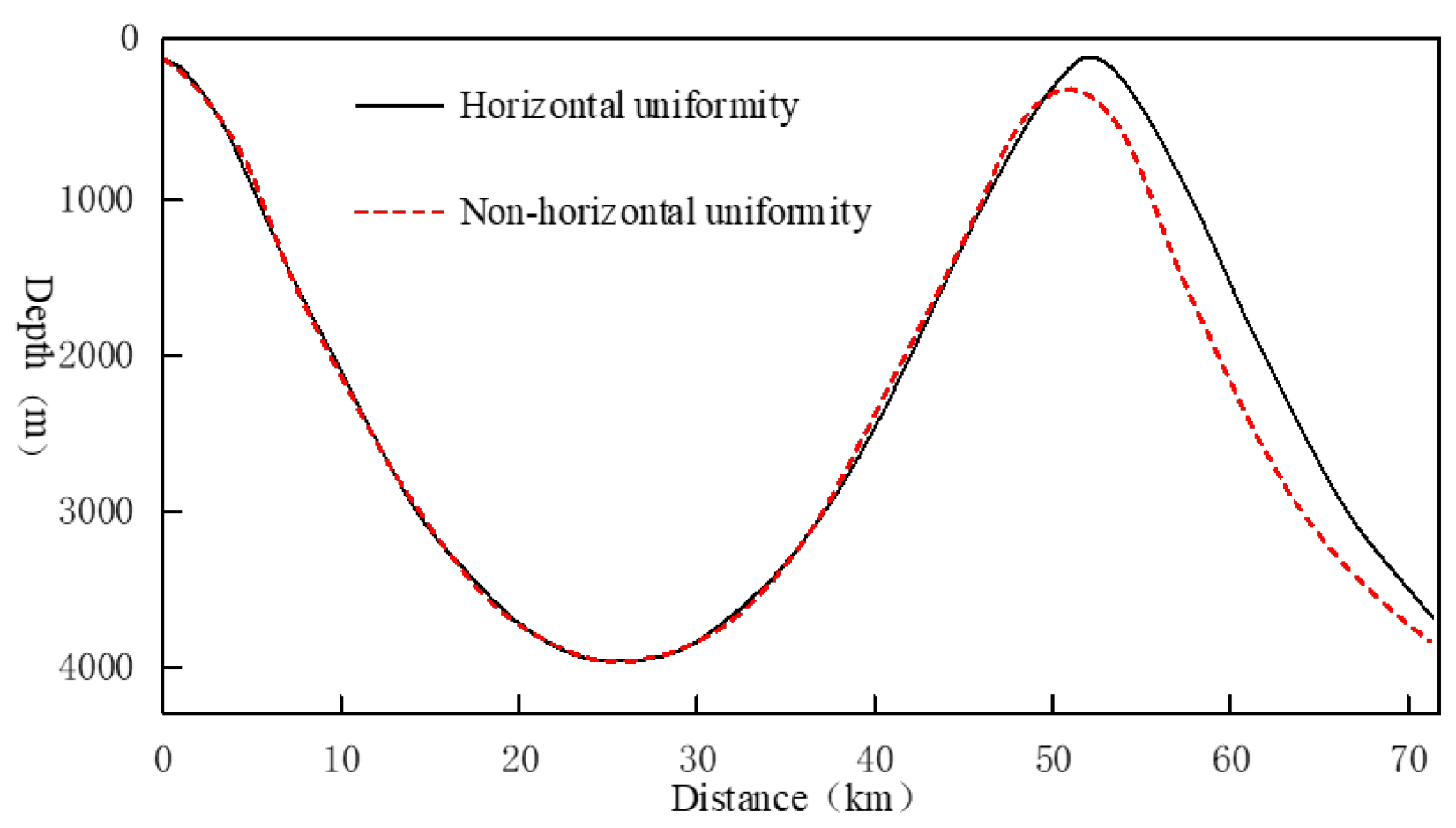
• The algorithm for forecasting convergence zone characteristic parameters is validated using environmental parameters from a representative marine area. The findings indicate that the algorithm successfully accounts for the forward displacement of the convergence zone induced by the horizontal gradient of sound speed within the mixed layer, thereby enhancing the forecast’s accuracy.

The rest of this article is organized as follows. Section 2 is the analysis of the non-uniform sound speed profile in the deep-sea mixed layer. Section 3 is the prediction of characteristic parameters of the deep-sea convergence zone. Section 4 is the simulation. Section 5 is the conclusion.

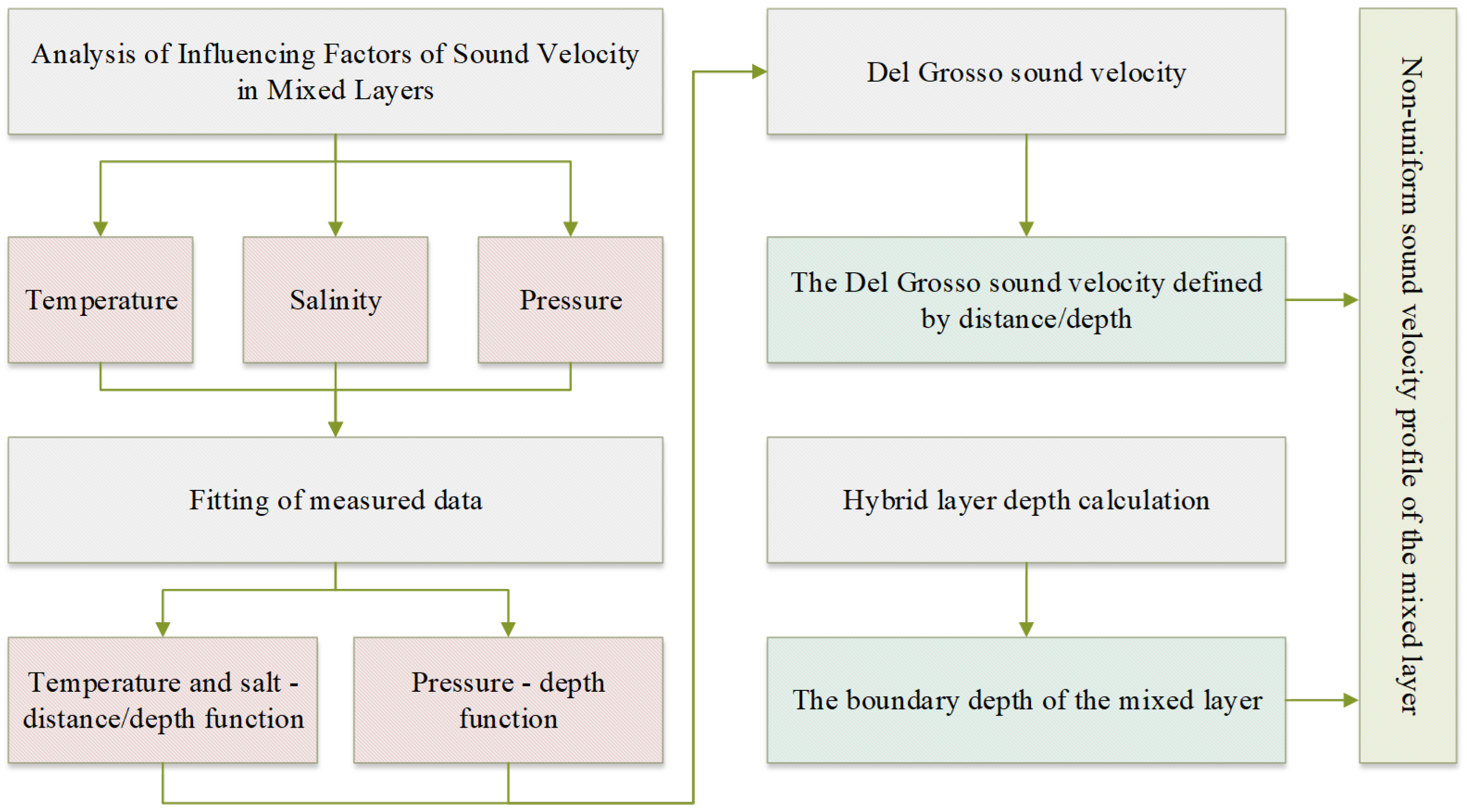
2. Analysis of the Non-Uniform Sound Speed Profile in the Deep-Sea Mixed Layer

This article constructs a non-uniform sound speed profile model for the mixed layer by measuring temperature, salinity, and pressure data and substituting them into empirical formulas [23,24]. Firstly, the driving factors of sound speed in the mixed layer are analyzed from the perspective of physical mechanisms. It is clarified that the horizontal gradients of the temperature and salinity fields are the main sources of spatial heterogeneity of sound speed, while the pressure field dominates the vertical stratification structure through the hydrostatic effect. Secondly, within the framework of the classical Del Grosso sound speed formula [25], the temperature and salinity parameters are decomposed into coupled functions of horizontal distance and vertical depth using gridded measured temperature, salinity, and pressure data, thereby establishing the non-uniform distribution relationship of sound speed with horizontal distance and vertical depth within the mixed layer of the sea area. Finally, the mixed-layer depth is introduced as a boundary threshold to construct a piecewise continuous sound speed profile model. The steps are shown in Figure 1.

2.1. Analysis of Factors Affecting Sound Speed in the Mixed Layer

This section reviews the established empirical formulas for sound speed calculation [25,26,27], which form the basis of our horizontally varying SSP model. The following equations are derived from prior work and are used in our model to compute sound speed based on temperature, salinity, and pressure, as shown in Equations (1)–(3):

$$\begin{array}{cc}\hfill C& =1449.2+4.6T-0.055T^2+0.000029T^3\hfill \\ \hfill & +\left(1.34-0.01T\right)\left(S-35\right)+0.016Z.\hfill \end{array}$$

(1)

$$\left\{\begin{array}{c}V=1449.14+V_T+V_P+V_S+V_{STP},\hfill \\ V_T=4.5721T-4.4532\times {10}^{-2}{T}^2\hfill \\ -2.604\times {10}^{-4}{T}^3+7.9851\times {10}^{-6}{T}^4,\hfill \\ V_P=1.60272\times {10}^{-1}P+1.0268\times {10}^{-5}{P}^2\hfill \\ +3.5216\times {10}^{-9}{P}^3-3.3603\times {10}^{-12}{P}^4,\hfill \\ V_S=1.39799(S-35)+1.69202\times {10}^{-3}{(S-35)}^2,\hfill \\ V_{STP}=(S-35)(-1.1244\times {10}^{-2}T\hfill \\ +7.7711\times {10}^{-7}{T}^2+7.7016\times {10}^{-5}P\hfill \\ -1.2943\times {10}^{-7}{P}^2+3.1580\times {10}^{-8}PT\hfill \\ +1.5790\times {10}^{-9}P{T}^2)+\mathrm{P}(-1.8607\times {10}^{-4}T\hfill \\ +7.4812\times {10}^{-6}T+4.5283\times {10}^{-8}{T}^3)\hfill \\ +P^2(-2.5294\times {10}^{-7}T+1.8563\times {10}^{-9}{T}^2)\hfill \\ +P^3(-1.9646\times {10}^{-10}T).\hfill \end{array}\right.$$

(2)

$$\begin{array}{cc}\hfill & C=(1.389-1.262\times {10}^{-2}t+7.164\times {10}^{-5}{t}^2\hfill \\ \hfill & +2.006\times {10}^{-6}{t}^3-3.21\times {10}^{-6}{t}^4)S\left(s_0\right)\hfill \\ \hfill & +(-1.922\times {10}^{-2}-4.42\times {10}^{-5}t)S{\left(s_0\right)}^{3/2}\hfill \\ \hfill & +1.727\times {10}^{-3}S{\left(s_0\right)}^2,\hfill \end{array}$$

(3)

where C represents the speed of sound in seawater when the temperature is constant, while V represents the speed of sound in seawater when the temperature varies. T is the temperature of the sea, t is the instantaneous temperature, S is the salinity of the sea, $S_0$ is the standard value of salinity, Z is depth, P is pressure, and p is the instantaneous pressure.

While Equation (3) stands as the modern international standard, Equation (1) represents a critical historical advancement in precision. Derived from meticulous laboratory measurements, its high-order polynomial structure provided a new benchmark for accuracy, bridging the gap between earlier models like Equation (2) and contemporary standards. Its rigorous foundation on the sound speed in pure water, with robust corrections for salinity and pressure, established a physically meaningful and highly reliable reference that remains widely cited and utilized. These empirical relationships are integrated into our horizontally varying sound speed model through the Del Grosso formula, enabling the construction of a continuous 3D sound speed field.

According to the theory of the wave equation, sound speed refers to the phase velocity of a plane wave, which is a longitudinal wave and is related to density and compressibility. It can be expressed as

$$C={\displaystyle \frac{1}{\sqrt{\rho \beta }}},$$

(4)

where $\rho$ and $\beta$ represent the density and adiabatic compressibility of seawater.

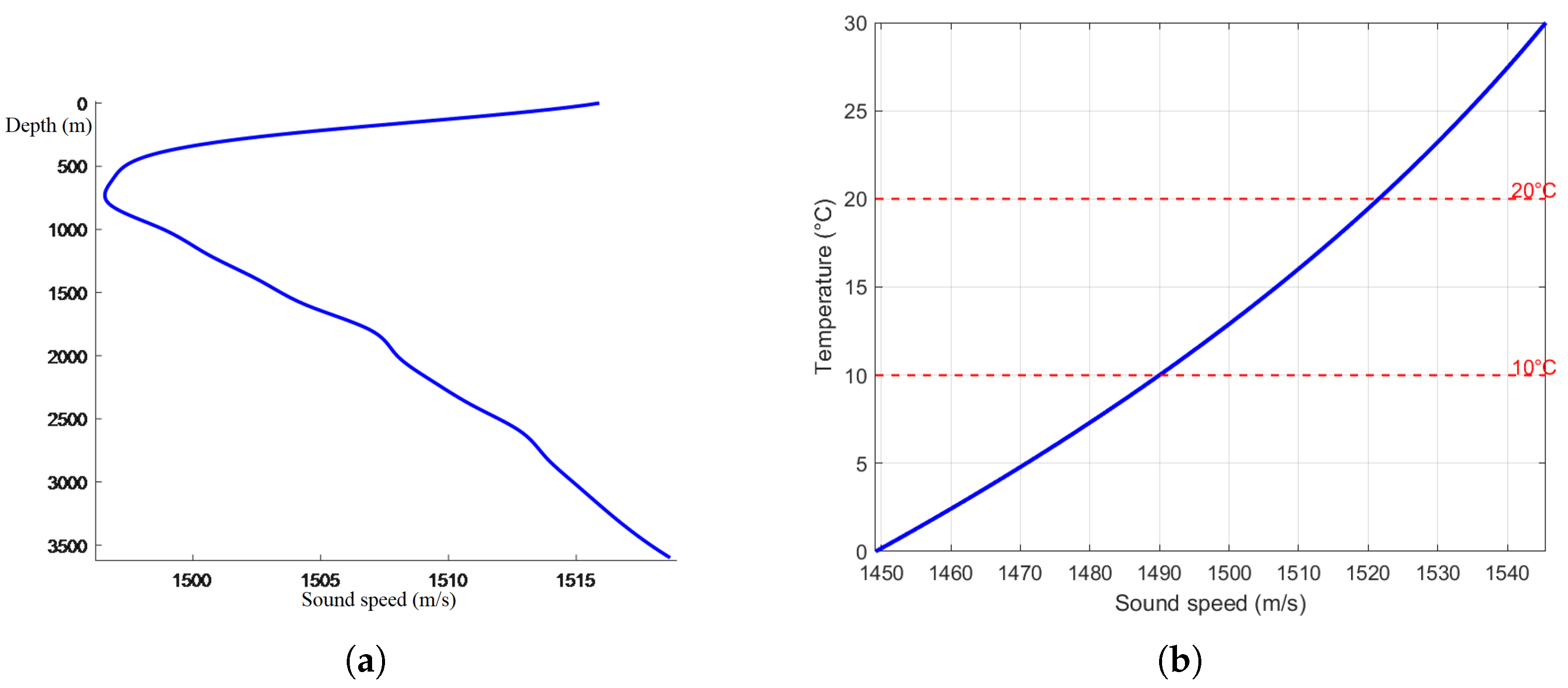
2.1.1. The Effect of Temperature on Sound Speed

Based on the functional relationship between the compressibility of seawater and the temperature field, an empirical relationship model was established using marine observational data [26,27,28]:

$$\beta =481\times {10}^{-13}(1-0.00707T).$$

(5)

Let ${\beta }_0=481\times {10}^{-13}$, $S_0=0.00707$, then we have

$$\beta ={\beta }_0(1-S_{0}T).$$

(6)

Within the typical fluctuation range of conventional marine environmental parameters, the variation in density is minimal. By adopting the assumption of approximate constancy, we have

$$C_e={\displaystyle \frac{1}{\sqrt{\rho {\beta }_0(1-S_{0}T)}}}={\displaystyle \frac{C_0}{\sqrt{(1-S_{0}T)}}},$$

(7)

where $C_0$ represents the sound speed at a temperature of 0 °C.

By applying the Taylor series expansion method to linearize the above equation and retaining the first- and second-order terms to construct a simplified model, we then have

$$C_e=C_0\left(1+{\displaystyle \frac{1}{2}}{S}_{0}T\right).$$

(8)

The expression for the change in sound speed derived through this model is

$$\mathsf{\Delta }\mathrm{C}=C_e-C_0={\displaystyle \frac{1}{2}}{S}_{0}T=C_0\times 0.00354T.$$

(9)

Equation (9) indicates that when the temperature changes by 1 °C, the relative increase in sound speed is approximately 0.354% of the original value.

2.1.2. The Effect of Salinity on Sound Speed

According to the empirical formula between seawater density and salinity [28], we have

$$\rho ={\rho }_0(1+0.0008S)={\rho }_0(1+{\alpha }_{p}S),$$

(10)

where S represents salinity and ${\alpha }_p=0.0008$ represents the density compressibility coefficient. The relationship between the compressibility coefficient of seawater and salinity can be expressed as

$$\beta ={\beta }_0(1-0.0024S)={\beta }_0(1-{\alpha }_{k}S),$$

(11)

where ${\alpha }_k=0.0024$ represents the salinity compressibility coefficient, $\beta$ denotes the compressibility coefficient, and ${\beta }_0$ is the initial value of the compressibility coefficient.

From Equations (10) and (11), it can be seen that when the salinity increases by 1, the compressibility decreases by 0.24%, and the sound speed increases. When the density increases by 0.08%, the sound speed decreases. Substituting Equations (10) and (11) into Equation (4), we have

$$C={\displaystyle \frac{C_0}{\sqrt{(1+{\alpha }_{p}S)(1-{\alpha }_{k}S)}}}\cong C_0+{\displaystyle \frac{1}{2}}{C}_0({\alpha }_k-{\alpha }_p)S.$$

(12)

Substituting ${\alpha }_k=0.0024$ and ${\alpha }_p=0.0008$ into Equation (12), we have

$$\mathsf{\Delta }C=C-C_0=C_0\times 0.000825S.$$

(13)

From Equation (13), it can be concluded that when salinity increases by 1, the relative increase in sound speed is approximately 0.0825% of the original value.

2.1.3. The Effect of Pressure on the Speed of Sound

The change in sound speed due to pressure mainly depends on the variation in the compressibility coefficient $\beta$. For seawater, the greater the pressure, the more difficult it is to compress, and the smaller the compressibility coefficient becomes, which ultimately leads to an increase in sound speed. Therefore, pressure is positively correlated with sound speed. The following is the expression for the relationship between the static pressure of seawater and the compressibility coefficient:

$$\beta ={\beta }_0(1-0.00044P)={\beta }_0(1-{\mu }_{k}P),$$

(14)

where the pressure is measured in units of one standard atmosphere (101,325 Pa). Substituting Equation (14) into Equation (4), the change in sound speed is finally obtained as

$$\mathsf{\Delta }C={\displaystyle \frac{C_0}{2}}{\mu }_{k}P=0.00022C_{0}P.$$

(15)

As can be seen from Equation (15), when the pressure increases by 1 Pa, the relative increase rate of sound speed is approximately 0.022% of its original value.

2.2. Construction of Non-Uniform Sound Speed Profiles

This section elaborates on the data-driven method for constructing non-uniform sound speed profiles, including data acquisition and processing, modeling of the horizontal–vertical distribution of temperature and salinity, and Del Grosso sound speed coupling analysis.

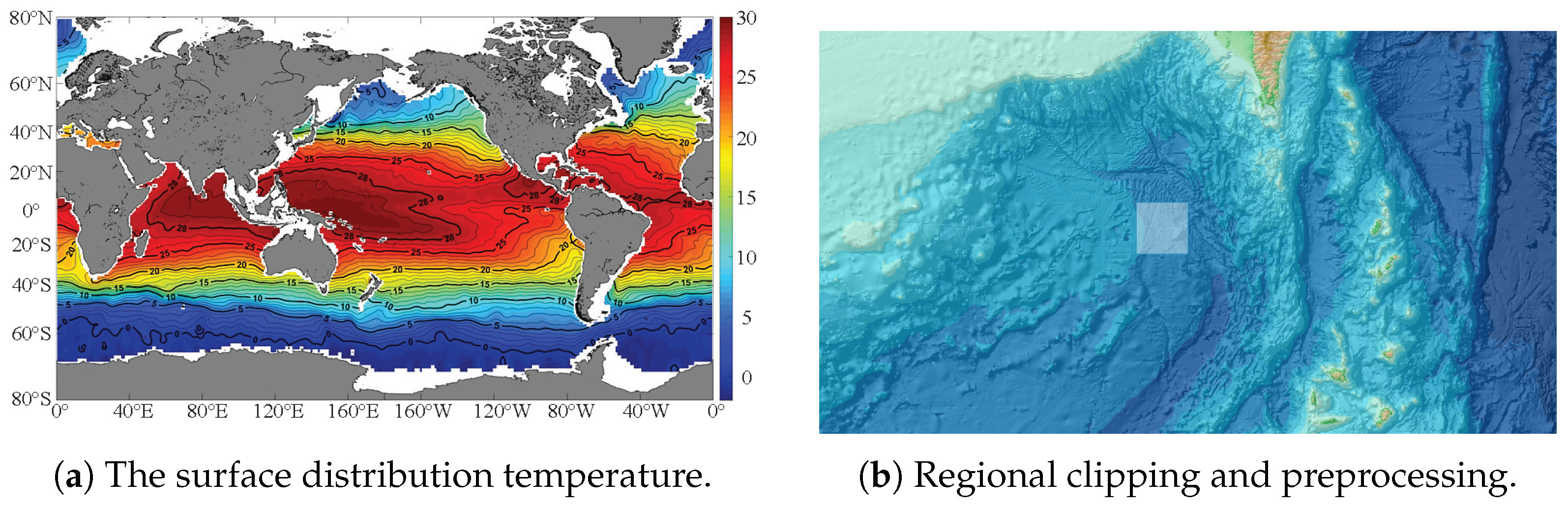
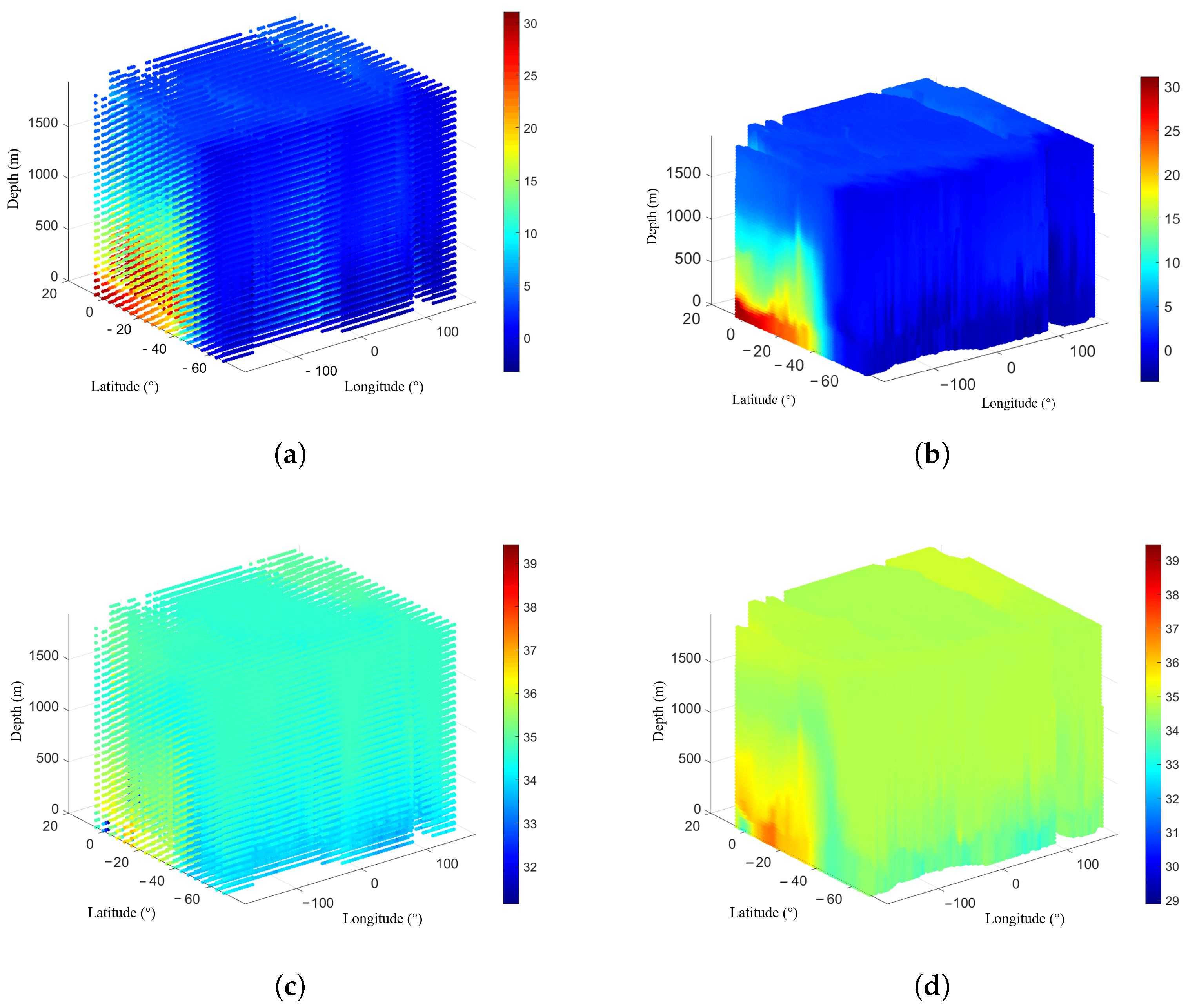
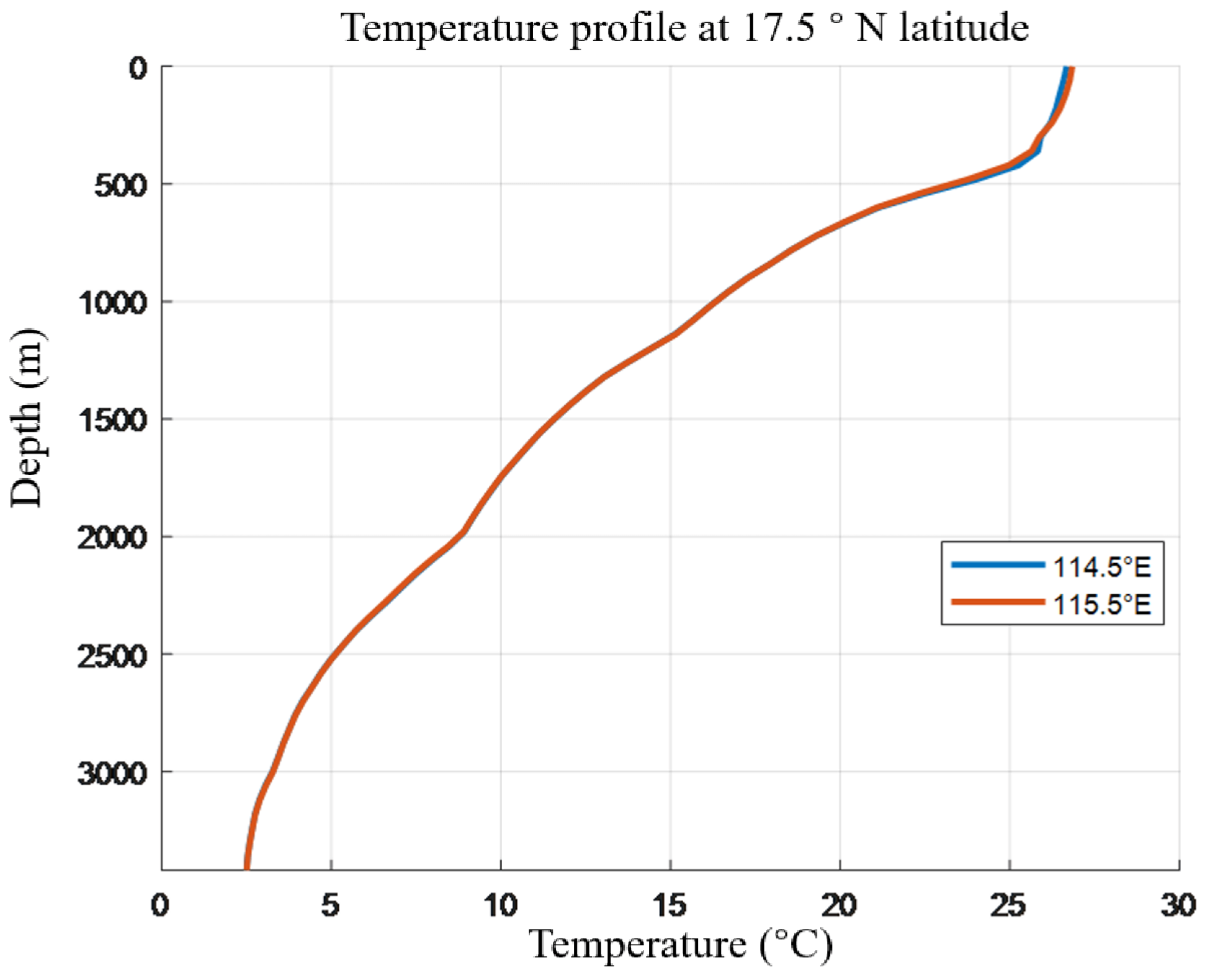
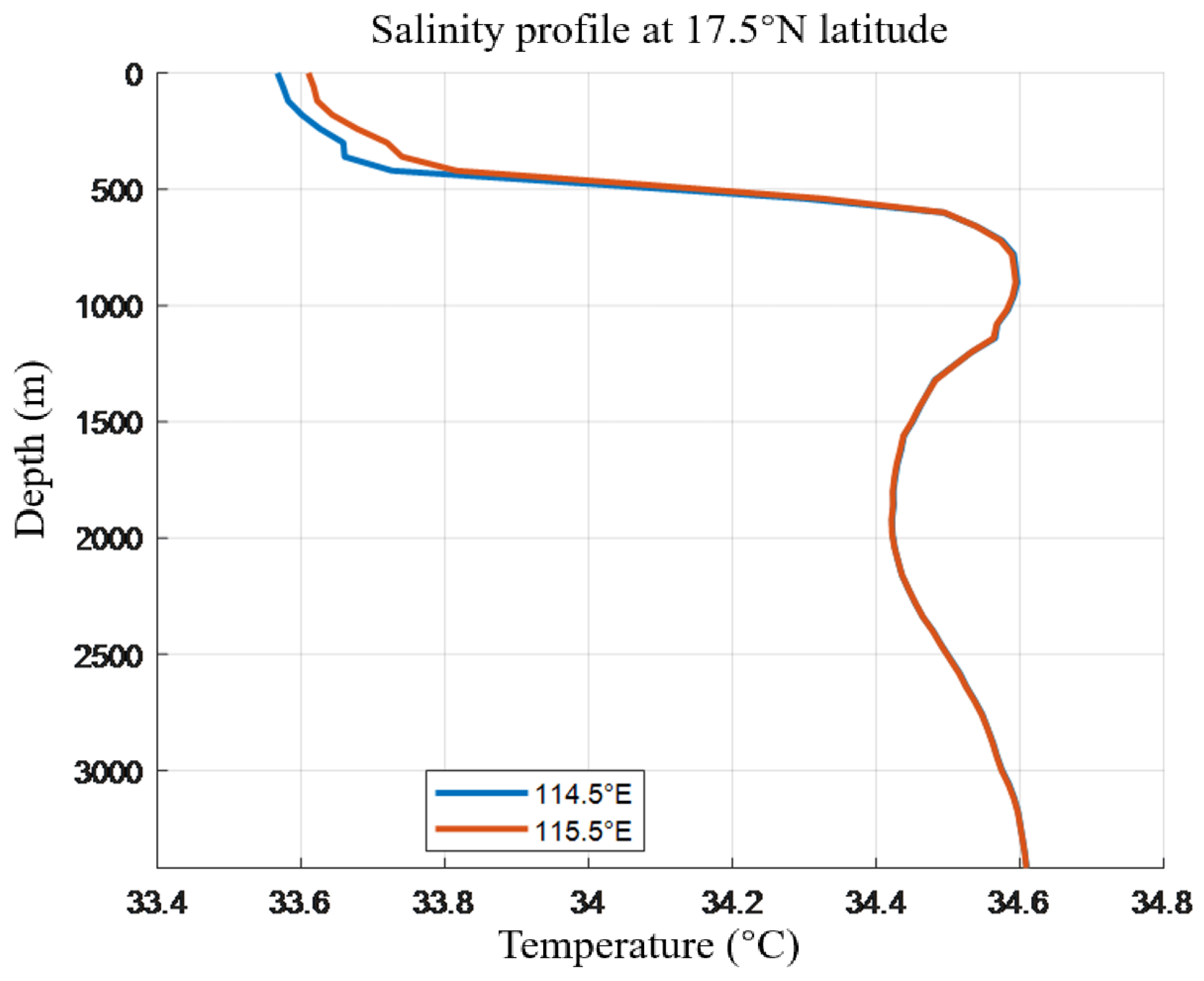
2.2.1. Data Acquisition and Preprocessing

The data source used in this article is the ocean space temperature, salinity, and pressure data, which is derived from the global ocean Argo gridded dataset (BOA_Argo) provided by the Argo Real-Time Data Center [29]. The data applied include longitude, latitude, pressure, salinity, temperature, and mixed-layer depth. Taking temperature as an example, its surface distribution is shown in Figure 2a. After obtaining the measured data, the data are preprocessed by regional clipping according to the research sea area. The index corresponding to longitude $i_0$ is obtained through the following minimization formula, and the same applies to latitude j. The final longitude and latitude index ranges are determined as $i\in \left[i_{min},i_{max}\right]$ and $j\in \left[j_{min},j_{max}\right]$, and the clipped sea area is shown in Figure 2b.

2.2.2. Modeling the Horizontal and Vertical Distribution of Temperature and Salinity

To accurately characterize the continuous spatial distribution of temperature, salinity, and pressure, this article employs a two-dimensional empirical orthogonal function (EOF) decomposition method, combined with measured data and function interpolation techniques, to construct a temperature field parameterization model [30]. The EOF decomposition retained the top k modes in the temperature and salinity fields. This threshold was determined by analyzing the cumulative contribution rate of eigenvalues, ensuring the reconstructed fields balance accuracy and computational efficiency. The original temperature and salinity data have a horizontal resolution of $1^{\circ }\times 1^{\circ }$ and are vertically divided at 10 m intervals within the mixed layer. The data are preprocessed to eliminate the dimensional differences in the vertical stratification and to highlight the spatial characteristics of the temperature and salinity fields. Each depth layer of the temperature and salinity fields is normalized.

Based on the BOA_Argo data, the horizontal–vertical distribution model of temperature and salinity established using EOF and the comparison with the original data are shown in Figure 3.

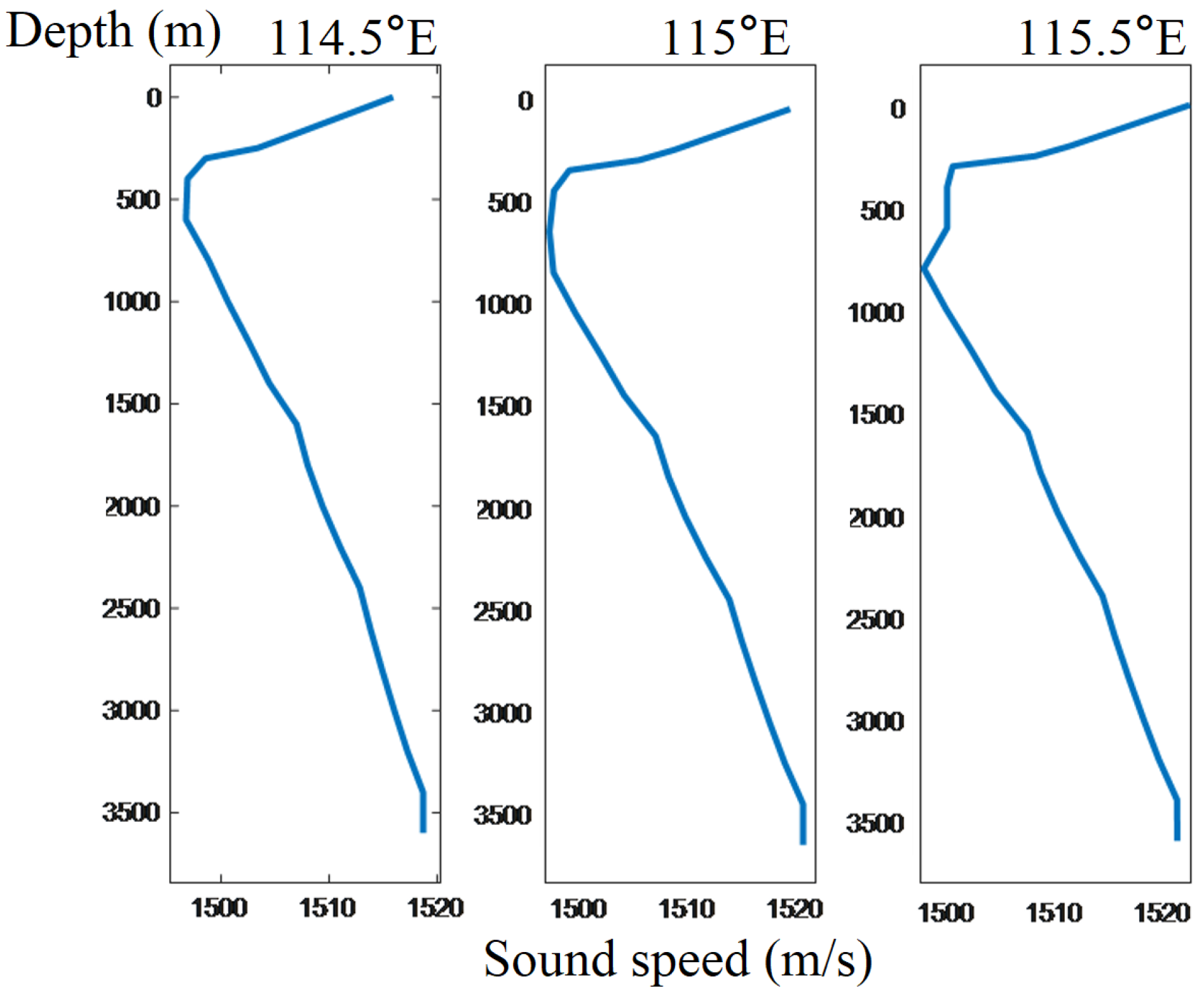
2.2.3. Del Grosso Acoustic Velocity Coupling

While the Del Grosso formula is well-established, our contribution lies in its coupling with the EOF-derived continuous temperature and salinity fields to generate a horizontally varying SSP. Additionally, we introduce a transition function $\eta \left(z\right)$ to ensure smooth continuity at the mixed-layer base, which is novel in this context. Considering the horizontal inhomogeneity of the sound speed profile in the deep-sea mixed layer, the sound speed profile is described in segments. The entire sound speed profile can be represented by the following equation:

$$C(r,z)=\left\{\begin{array}{cc}C(r,z),& 0<z<z_M,\\ C\left(z\right),& z_M<z<H,\end{array}\right.$$

(16)

where r represents the horizontal distance, z represents the vertical depth, $z_M$ represents the depth of the mixed layer, and H represents the sea depth. When $0<z<z_M$, the sound speed profile will fluctuate with changes in horizontal distance and vertical depth, exhibiting non-uniform distribution characteristics. When $z_M<z<H$, the sound speed is located below the mixed layer and varies only with depth. The schematic diagram of the sound speed profile is shown in Figure 4, with the mixed layer above the stratification line. The solid line represents the simplified equivalent sound speed profile that ignores the non-uniform changes in the marine environment, and the black area represents the fluctuation range caused by the non-uniform distribution of sound speed.

The Del Grosso algorithm is shown in Equation (1). To ensure the continuity of the sound speed profile at $z_M$, the function C in Equation (16) must satisfy $C\in C^1$.

The temperature and salinity at the base of the mixed layer must smoothly transition to the deep-layer constant values, which is specifically realized by introducing the transition function $\eta \left(z\right)$:

$$\begin{array}{cc}\hfill T^{\prime }(r,z)=& \eta \left(z\right)T(r,z)+(1-\eta (z\left)\right)T,\hfill \\ \hfill & {\mathrm{z}}_M-\mathsf{\Delta }z\le z\le {\mathrm{z}}_M+\mathsf{\Delta }z.\hfill \end{array}$$

(17)

where $\eta \left(z\right)$ is a cubic polynomial weighting function:

$$\eta \left(z\right)=\left\{\begin{array}{cc}& 1,z\le {\mathrm{z}}_M-\mathsf{\Delta }z,\\ & 2{\left({\displaystyle \frac{{\mathrm{z}}_M+\mathsf{\Delta }z-z}{2\mathsf{\Delta }z}}\right)}^3-3{\left({\displaystyle \frac{{\mathrm{z}}_M+\mathsf{\Delta }z-z}{2\mathsf{\Delta }z}}\right)}^2+1,\\ & {\mathrm{z}}_M-\mathsf{\Delta }z<z\le {\mathrm{z}}_M+\mathsf{\Delta }z,\\ & 0,z>{\mathrm{z}}_M+\mathsf{\Delta }z.\end{array}\right.$$

(18)

To avoid a significant impact on the sound speed, the thickness of the transition layer, $\mathsf{\Delta }z$, is set to only 2–5 m to ensure the continuity of the first-order derivative of the sound speed. The $\mathsf{\Delta }z$ range was selected to satisfy physical constraints: oceanographic observations confirm that mixed-layer base gradients decay rapidly below 5 m depth [22,27]. A thicker $\mathsf{\Delta }z$ would artificially dilute thermohaline gradients. In this case, the temperature gradient at the base of the mixed layer, ${\displaystyle \frac{\partial T}{\partial z}}$, and the salinity gradient, ${\displaystyle \frac{\partial S}{\partial z}}$, will smoothly decay to zero, avoiding the occurrence of a sawtooth discontinuity in the sound speed at the boundary point.

3. Prediction of Characteristic Parameters of the Deep-Sea Convergence Zone

3.1. Ray Equations Considering the Mixed-Layer Sound Speed Profile

Bellhop is a model for predicting acoustic pressure fields in marine environments using ray and Gaussian beam tracing. It calculates sound fields in horizontally non-uniform environments by associating each ray within a beam with a Gaussian intensity profile orthogonal to its path. Crucially, the central ray of a Gaussian beam can penetrate shadow zones and traverse caustics smoothly. This method requires integrating only two additional differential equations (determining beam width and curvature) alongside the standard ray equations to compute the near-central-ray field. Consequently, it overcomes key limitations of traditional ray models, such as zero intensity in shadow zones and infinite intensity at caustics. These attributes make the technique particularly valuable for high-frequency applications in certain range-dependent scenarios. However, Bellhop, as a deterministic model, possesses inherent limitations. These include difficulties handling horizontally varying sound speeds and representing the time-varying characteristics of the ocean environment [31].

Within the framework of a ray equation, the tracing of ray trajectories is based on the horizontally stratified assumption, where the sound speed varies only with depth. However, the horizontal inhomogeneity of the sound speed profile in the mixed layer will cause lateral deviations in the ray propagation paths and alter the characteristics of energy focusing. This section derives the ray-tracing equations for inhomogeneous media and designs a numerical solution algorithm.

According to the eikonal equation, the ray direction is defined as the normal direction of the wavefront, where the wavefront is the set of points with the same acoustic pressure vibration phase. The normal direction at any point on the wavefront is the direction of the phase gradient at that point, representing the direction of sound-wave propagation, that is,

$${\displaystyle \frac{d\mathbf{x}}{ds}}={\displaystyle \frac{\nabla \tau }{|\nabla \tau |}}=C\nabla \tau .$$

(19)

Combining the eikonal equation $|\nabla \tau |=1/C$, we have

$${\displaystyle \frac{d\mathbf{x}}{ds}}=C\nabla \tau \Rightarrow \nabla \tau ={\displaystyle \frac{1}{C}}{\displaystyle \frac{d\mathbf{x}}{ds}}.$$

(20)

We differentiate with respect to s, using the chain rule, and we have

$${\displaystyle \frac{d}{ds}}\left({\displaystyle \frac{1}{C}}{\displaystyle \frac{d\mathbf{x}}{ds}}\right)=\nabla \left({\displaystyle \frac{1}{C}}\right),$$

(21)

and after expanding Equation (20), we obtain that

$${\displaystyle \frac{d^2\mathbf{x}}{d{s}^2}}={\displaystyle \frac{1}{C}}\nabla C-{\displaystyle \frac{2}{C^2}}\left({\displaystyle \frac{d\mathbf{x}}{ds}}·\nabla C\right){\displaystyle \frac{d\mathbf{x}}{ds}}.$$

(22)

In the two-dimensional vertical plane (horizontal x, vertical z), let the angle between the sound ray and the horizontal plane be $\theta$, then we have

$${\displaystyle \frac{dx}{ds}}=sin\theta {\displaystyle \frac{dz}{ds}}=cos\theta .$$

(23)

We differentiate with respect to $\theta$, using the geometric relationship, and we have

$${\displaystyle \frac{d\theta }{ds}}=-{\displaystyle \frac{1}{C}}{\displaystyle \frac{dC}{dz}}cos\theta .$$

(24)

Finally, we obtain the differential equation system describing the sound ray trajectory in the ray model by Equations (19)–(24):

$$\left\{\begin{array}{c}{\displaystyle \frac{dr}{ds}}=sin\theta ,\hfill \\ {\displaystyle \frac{dz}{ds}}=cos\theta ,\hfill \\ {\displaystyle \frac{d\theta }{ds}}=-{\displaystyle \frac{1}{C\left(z\right)}}{\displaystyle \frac{dc}{dz}}cos\theta .\hfill \end{array}\right.$$

(25)

In Equation (25), s is the arc length of the sound ray, $\theta$ is the angle between the sound ray and the horizontal plane, and $C\left(z\right)$ is the vertically stratified sound speed. This equation does not consider the effect of the horizontal gradient term of the sound speed ${\displaystyle \frac{\partial C}{\partial r}}$.

Considering the non-uniform sound speed profile $C(r,z)$ that depends on both the horizontal position r and depth z, the equation includes the horizontal gradient term ${\displaystyle \frac{\partial C}{\partial r}}$. The propagation of sound waves can be regarded as particles moving along ray trajectories. Therefore, starting from the Hamiltonian mechanics framework, the  ray-tracing problem is transformed into a particle trajectory problem in classical mechanics. The position coordinates are defined as $mathbfq=(r,z)$ and the momentum as $\mathbf{p}=\nabla \tau$, with the Hamiltonian [32]

$$H={\displaystyle \frac{1}{2}}\left(p_r^2+p_z^2-{\displaystyle \frac{1}{C^2(r,z)}}\right).$$

(26)

The equations of motion in Hamiltonian mechanics are

$${\displaystyle \frac{dq}{ds}}={\displaystyle \frac{\partial H}{\partial p}}{\displaystyle \frac{dp}{ds}}=-{\displaystyle \frac{\partial H}{\partial q}}.$$

(27)

After expanding Equation (27) and using Equation (26), the canonical equation that the ray trajectory satisfies is as follows:

$$\left\{\begin{array}{c}{\displaystyle \frac{dr}{ds}}={\displaystyle \frac{\partial H}{\partial p_r}}=p_r,\hfill \\ {\displaystyle \frac{dz}{ds}}={\displaystyle \frac{\partial H}{\partial p_z}}=p_z,\hfill \\ {\displaystyle \frac{d{p}_r}{ds}}=-{\displaystyle \frac{\partial H}{\partial r}}={\displaystyle \frac{1}{C^3}}{\displaystyle \frac{\partial C}{\partial r}},\hfill \\ {\displaystyle \frac{d{p}_z}{ds}}=-{\displaystyle \frac{\partial H}{\partial z}}={\displaystyle \frac{1}{C^3}}{\displaystyle \frac{\partial C}{\partial z}}.\hfill \end{array}\right.$$

(28)

From the eikonal equation $|\nabla \tau |={\displaystyle \frac{1}{C}}$, the physical meaning of the momentum $\mathbf{p}=\nabla \tau$ is the direction of the wave vector. Combining this with the sound ray direction angle $\theta$, we can write $p_r={\displaystyle \frac{sin\theta }{C}}$ and $p_z={\displaystyle \frac{cos\theta }{C}}$. Through variable substitution, we obtain the ray equation as follows:

$$\left\{\begin{array}{c}{\displaystyle \frac{dr}{ds}}={\displaystyle \frac{sin\theta }{C(r,z)}},\hfill \\ {\displaystyle \frac{dz}{ds}}={\displaystyle \frac{cos\theta }{C(r,z)}},\hfill \\ {\displaystyle \frac{d\theta }{ds}}=-{\displaystyle \frac{1}{C(r,z)}}\left({\displaystyle \frac{\partial C}{\partial z}}cos\theta -{\displaystyle \frac{\partial C}{\partial r}}sin\theta \right).\hfill \end{array}\right.$$

(29)

Compared with Equation (25), the added term $\left({\displaystyle \frac{\partial C}{\partial r}}\right)sin\theta$ in Equation (29) quantifies the contribution of the horizontal gradient to the curvature of the sound ray. When ${\displaystyle \frac{\partial C}{\partial r}}\ne 0$, the sound ray will deflect towards the direction of increasing sound speed, resulting in a lateral displacement of the propagation path, as shown in Figure 5.

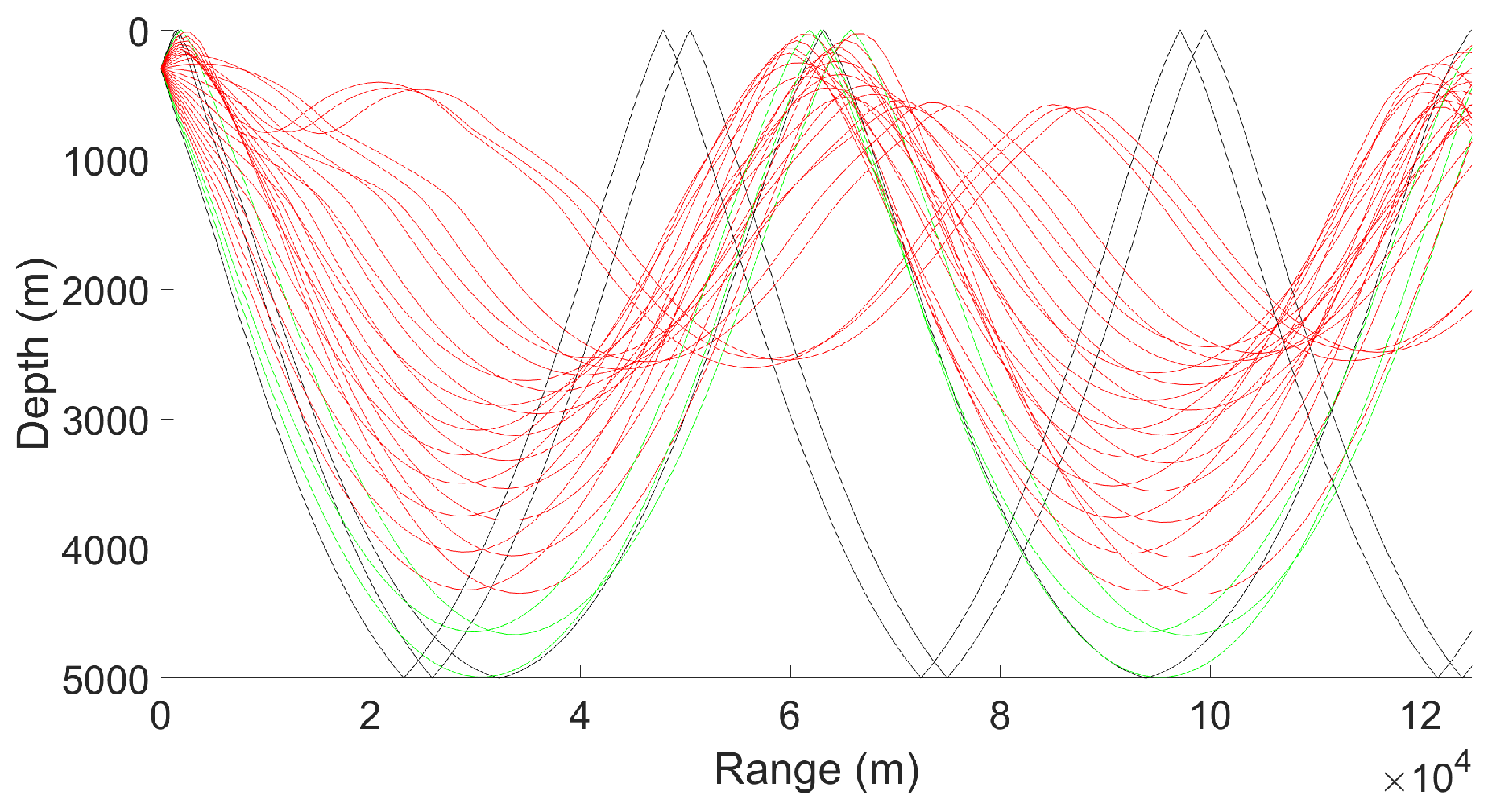
3.2. Forecast of Convergence Zone Characteristic Parameters

Bellhop is suitable for high-frequency acoustic signals, has a more intuitive physical meaning, and offers relatively fast computational speed. The parabolic equation model is suitable for low-frequency, far-field conditions with horizontal variations, but its errors accumulate with increasing distance. The complexity of the ray-tracing algorithm makes the equations analytically intractable, necessitating the use of numerical methods. This article employs the fourth-order Runge–Kutta method (RK4) to numerically integrate the ray equations. The RK4 method is a high-accuracy numerical integrator for initial-value problems of ordinary differential equations. In underwater ray tracing, RK4 outperforms single-slope schemes such as Euler’s method because its multi-stage corrections effectively suppress errors induced by strong spatial gradients in sound speed. Consequently, RK4 provides more accurate and stable ray-path predictions in horizontally variable environments. The pseudocode for its algorithm implementation is shown as Algorithm 1.

Algorithm 1 Improved sound ray-tracing algorithm for the ray model.
Input: Marine temperature dataset S, Marine salinity dataset T
Output: Sound ray position dataset $\left(r_n,z_n\right)$
	Set the source location $(r_0,z_0)$, the initial grazing angle ${\theta }_0$, the maximum propagation distance $R_{\max }$, the initial step size $\mathsf{\Delta }s$
	while $r<R_{max}$ do
		Read the temperature $T(r,z)$ and salinity $S(r,z)$ at the current point
		Calculate the sound speed value: $$\begin{array}{cc}\hfill C(T,S,z)=& 1449.2+4.6T-0.055T^2+0.000029T^3\hfill \\ & +\left(1.34-0.01T\right)\left(S-35\right)+0.016Z\hfill \end{array}$$
		Calculate the sound speed gradients ${\displaystyle \frac{\partial C}{\partial r}}$ and ${\displaystyle \frac{\partial C}{\partial z}}$
		for $k=1$ to 4 do
			Calculate the first slope $k1=\left(k{1}_r,k{1}_z,k{1}_{\theta }\right)$ based on the current sound ray position $\left(r_n,z_n,{\theta }_n\right)$
			Using $\left(r_n,z_n,{\theta }_n\right)$, half-step length ${\displaystyle \frac{\mathsf{\Delta }s}{2}}$ and $k1$, calculate the second slope $k2=\left(k{2}_r,k{2}_z,k{2}_{\theta }\right)$
			Using $\left(r_n,z_n,{\theta }_n\right)$, half-step length ${\displaystyle \frac{\mathsf{\Delta }s}{2}}$ and $k2$, calculate the third slope $k3=\left(k{3}_r,k{3}_z,k{3}_{\theta }\right)$
			Using $\left(r_n,z_n,{\theta }_n\right)$, step length $\mathsf{\Delta }s$ and $k3$, calculate the fourth slope $k4=\left(k{4}_r,k{4}_z,k{4}_{\theta }\right)$
			Update the sound ray position $\left(r_{n+1},z_{n+1}\right)$: $$\begin{array}{c}{r}_{n+1}=r_n+{\displaystyle \frac{\mathsf{\Delta }s}{6}}(k{1}_r+2k{2}_r+2k{3}_r+k{4}_r)\\ z_{n+1}=z_n+{\displaystyle \frac{\mathsf{\Delta }s}{6}}(k{1}_z+2k{2}_z+2k{3}_z+k{4}_z)\end{array}$$
			Calculate the updated grazing angle ${\theta }_{n+1}$: $${\theta }_{n+1}={\theta }_n+{\displaystyle \frac{\mathsf{\Delta }s}{6}}(k{1}_{\theta }+2k{2}_{\theta }+2k{3}_{\theta }+k{4}_{\theta })$$
		end for
		Accumulate the propagation distance $r=r+\mathsf{\Delta }s$
		Store the new position of the sound ray $\left(r_{n+1},z_{n+1}\right)$
	end while
	return Outputs

The construction of sound rays in the acoustic field is achieved using the Bellhop acoustic toolbox in Matlab, which further enables the calculation of the distance, width, and gain of the first convergence zone. The subsequent rows contain the actual sound speed values, in meters per second, with each row corresponding to a fixed depth. The actual depths used are taken from the depth data below the fifth line in the environmental file.

When analyzing specific sea areas, bathymetric data can be obtained from the General Bathymetric Chart of the Oceans (GEBCO) database [33]. The plotssp2d command is used to draw the horizontal inhomogeneous distribution of sound speed profiles in the mixed layer. The resulting sound speed profile curves associated with horizontal distance and vertical depth, as well as the color-mapped sound speed profile images, are shown in Figure 6 and Figure 7, respectively. The plotray command is used to track sound rays and generate the sound field model of the convergence zone, as shown in Figure 8. It can be seen that the sound rays in the convergence zone, considering the horizontally inhomogeneous sound speed profile, exhibit significant fluctuations compared to those under the typical Munk profile during propagation. The overall shape of the sound rays is more complex and clearly conforms more closely to the actual sound signal propagation patterns. Based on this, the prediction of the distance and width of the first convergence zone is consistent with the method under the typical Munk profile and can be easily calculated by measuring the upper bending point of the sound ray with a $0^{\circ }$ launch angle and the critical depth bending sound ray. The prediction of the gain in the first convergence zone is also calculated by constructing a transmission loss model, as shown in Figure 9.

3.3. Computational Complexity Analysis

The computational complexity of the proposed ray-tracing algorithm is primarily determined by the number of rays N, the number of integration steps per ray M, and the cost of evaluating sound speed and its gradients at each step. Let $C_{eval}$ denote the cost of evaluating $C(r,z)$, ${\displaystyle \frac{\partial C}{\partial r}}$, and ${\displaystyle \frac{\partial C}{\partial z}}$ at a point. The Runge–Kutta method requires four function evaluations per step. Thus, the total cost is approximately $O\left(4·N·M·C_{eval}\right)$.

In comparison, the standard Bellhop model assumes a vertically stratified SSP, so $C_{eval}$ is cheaper and no horizontal gradients are computed. However, it does not account for horizontal variability. Although our method incurs higher computational cost due to the horizontal gradient term and RK4 integration, the improvement in prediction accuracy justifies the additional expense for applications requiring high precision, such as military sonar or oceanographic research. Future work will focus on optimizing the algorithm through parallelization or adaptive step-size control.

4. Simulation

In this section, an acoustic propagation characteristic experiment conducted in the South China Sea in 2018 is selected as the benchmark case data.

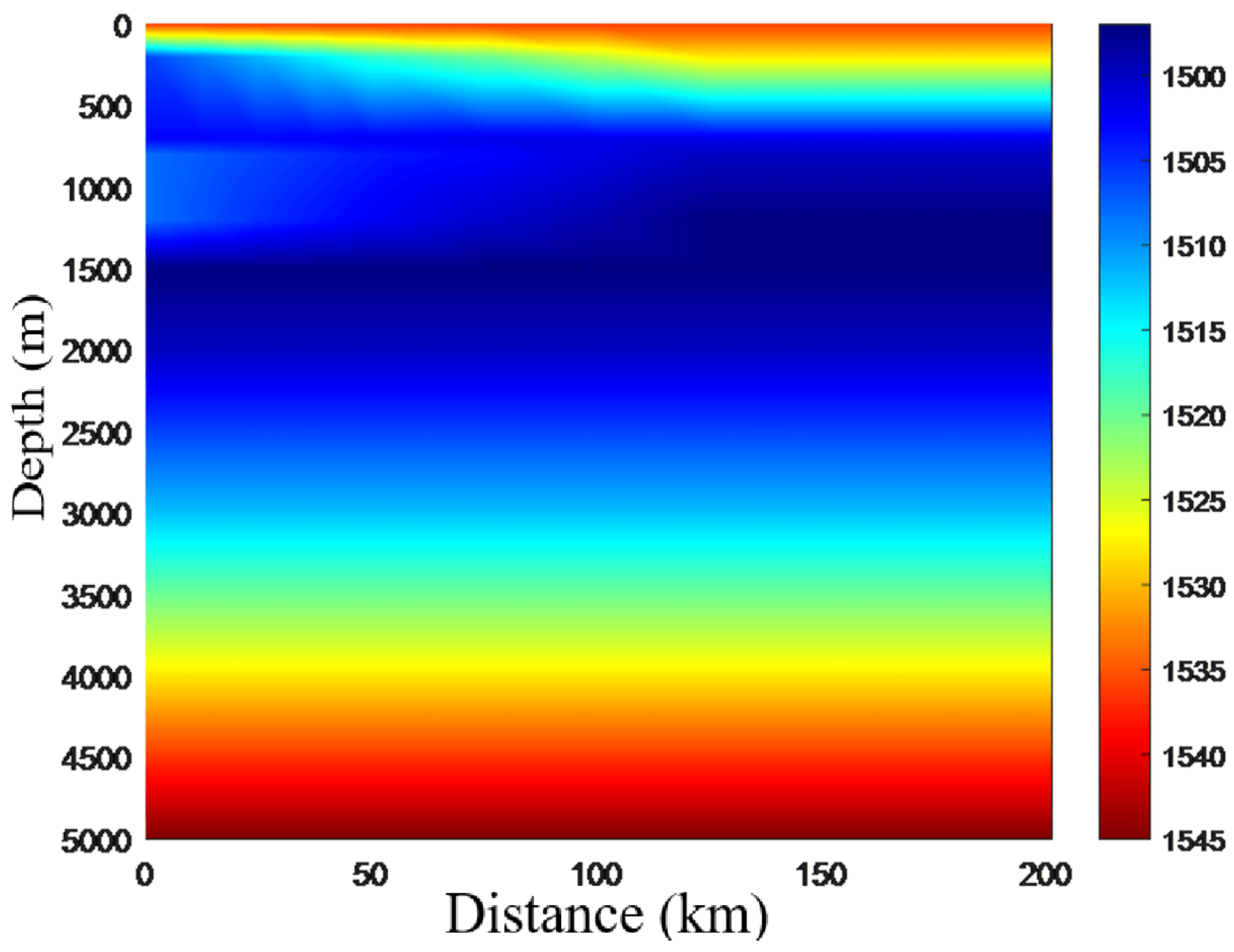
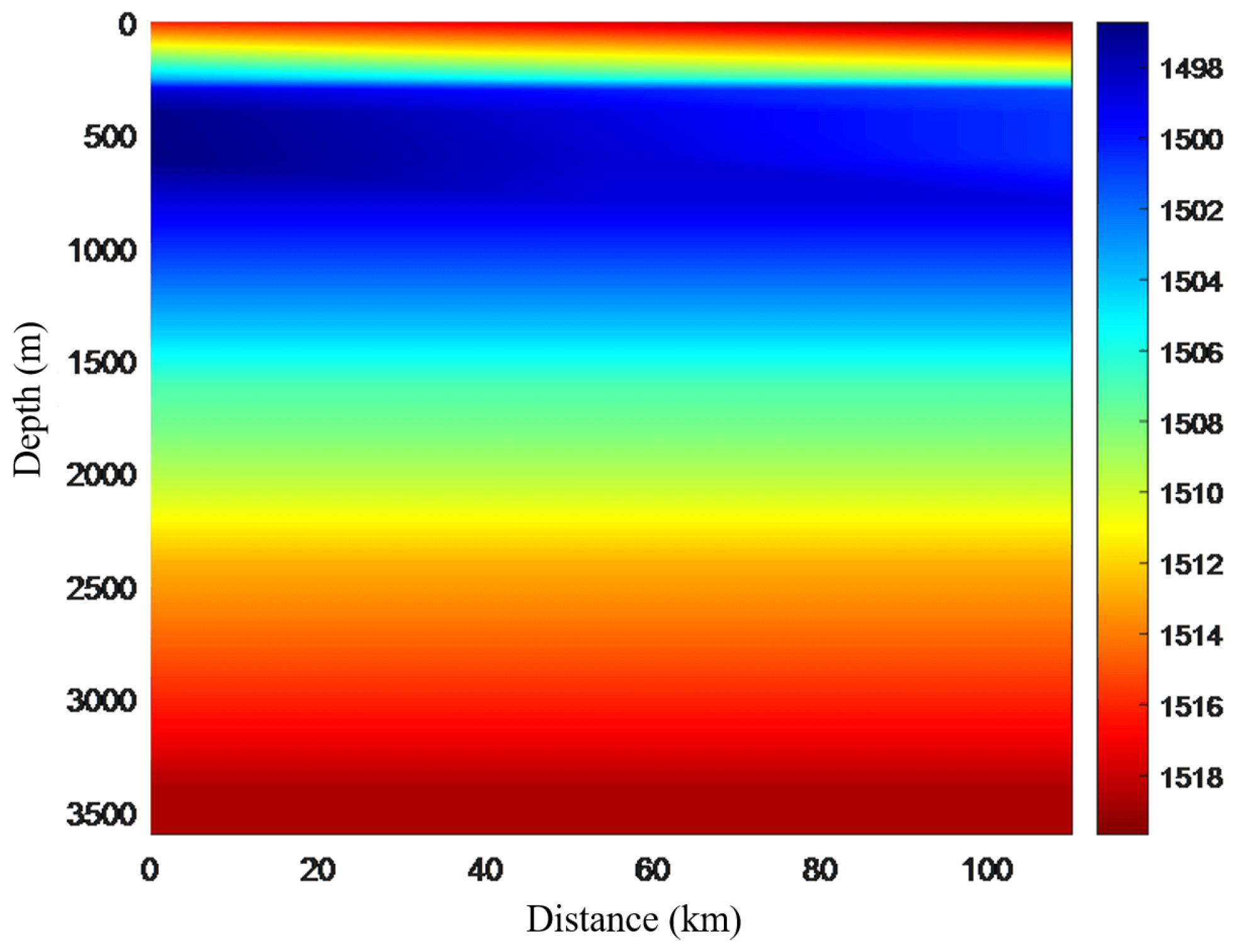
4.1. Characteristic Features of Typical Marine Environment and Data Preparation

The typical sea area selected for the simulation experiment of the convergence zone characteristic parameter forecasting algorithm is covered by the sea area of the 2018 spring South China Sea acoustic propagation experiment. The selected area is located at $17.5^{\circ }$ N latitude and $114.5^{\circ }$ E–$115.5^{\circ }$ E longitude in the South China Sea, with a depth of approximately 3500 m and a horizontal distance of about 110 km. The environmental characteristic data include temperature, salinity, pressure, and mixed-layer depth. The temperature and salinity profiles are shown in Figure 10 and Figure 11.

In the South China Sea experiment, the source depth was 80 m and the source frequency was 300 Hz. The convergence zone characteristic parameters obtained using the first-order internal wave normal mode basis function model are shown in

Table 1. The characteristic parameters of the convergence zone predicted in the South China Sea experiment.

Distance (km)	Width (km)	Gain (dB)
61.5	21.4	13.5

, which are used to verify the accuracy of the Bellhop ray model and the improved ray model in predicting convergence zone characteristics.

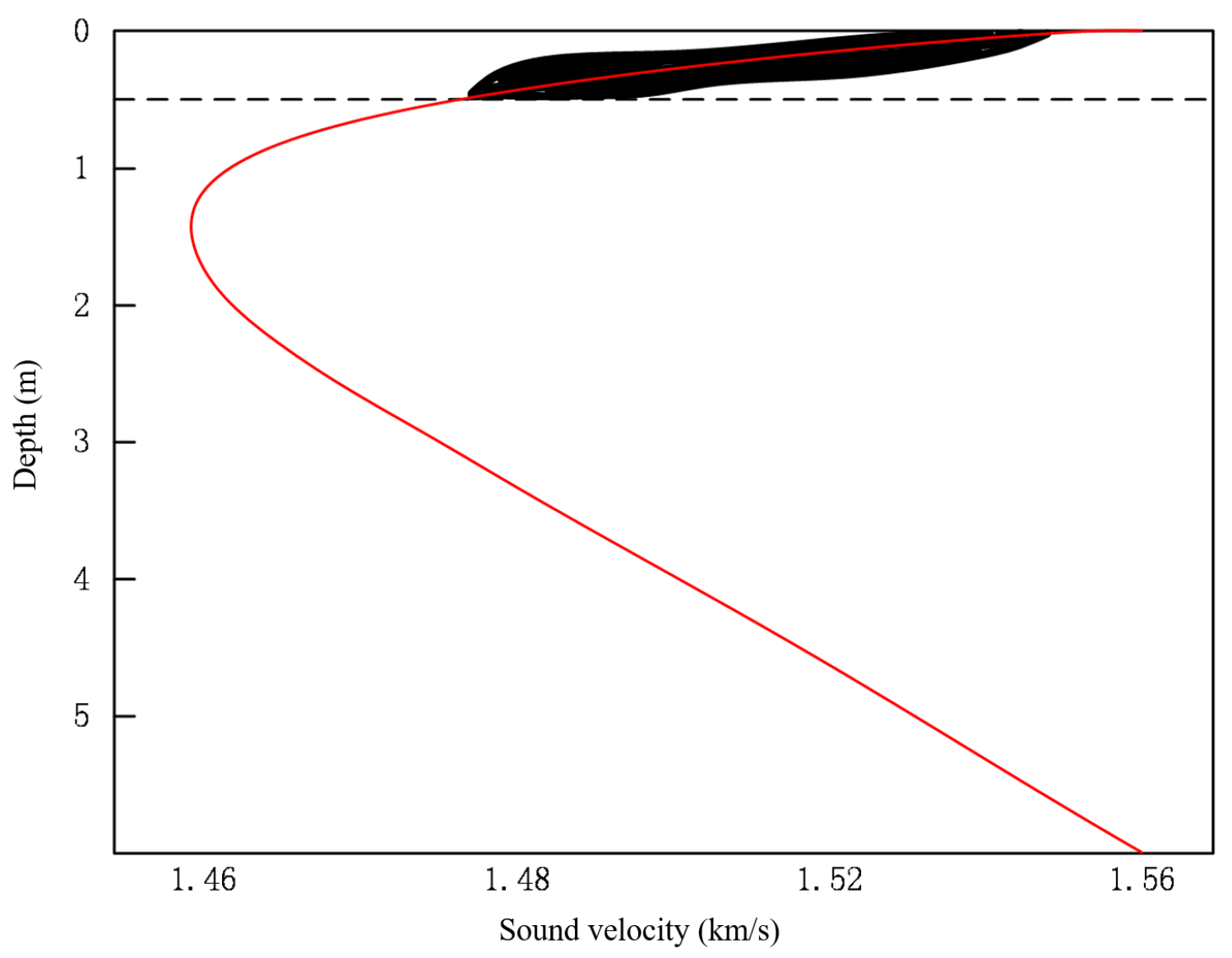
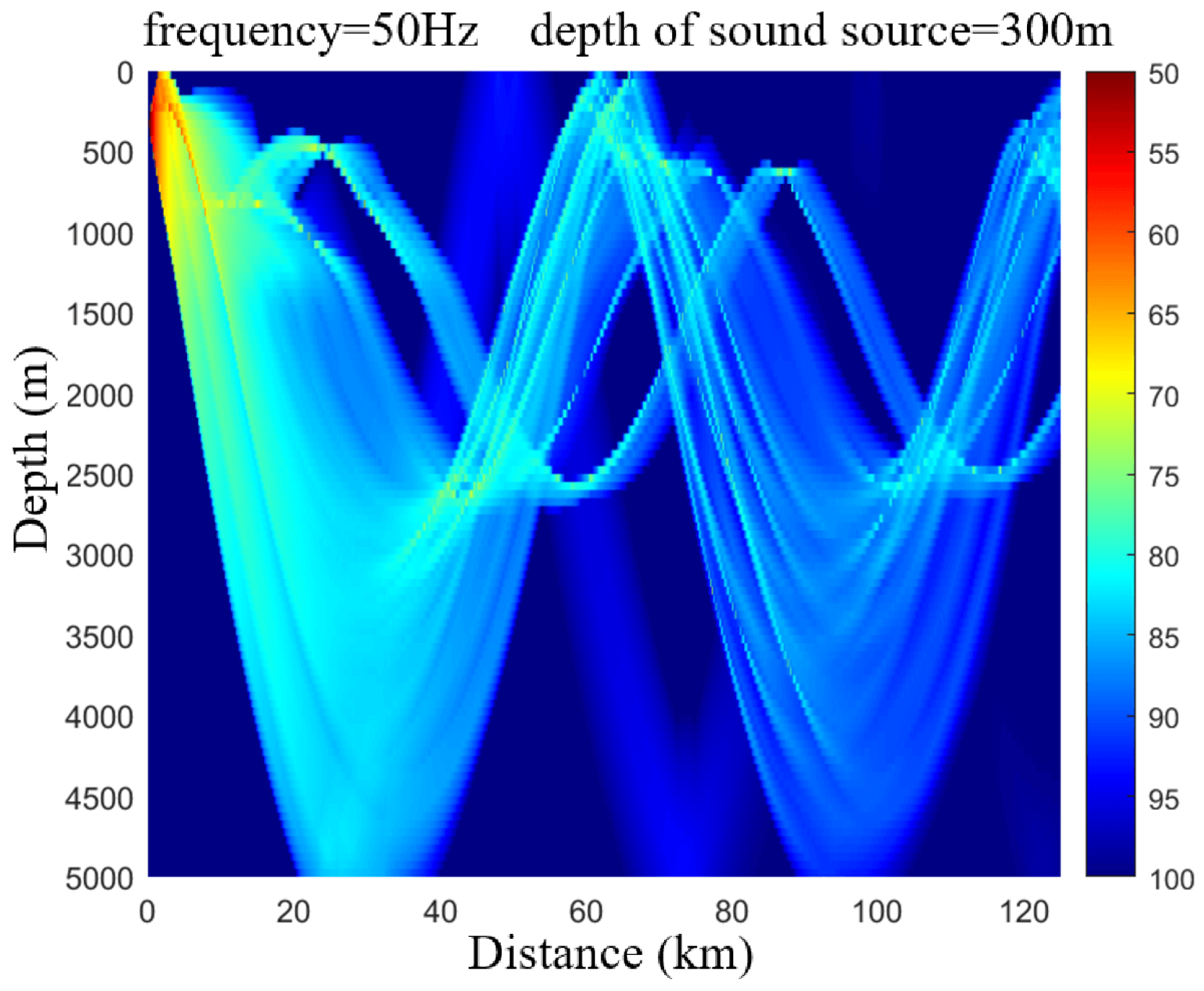
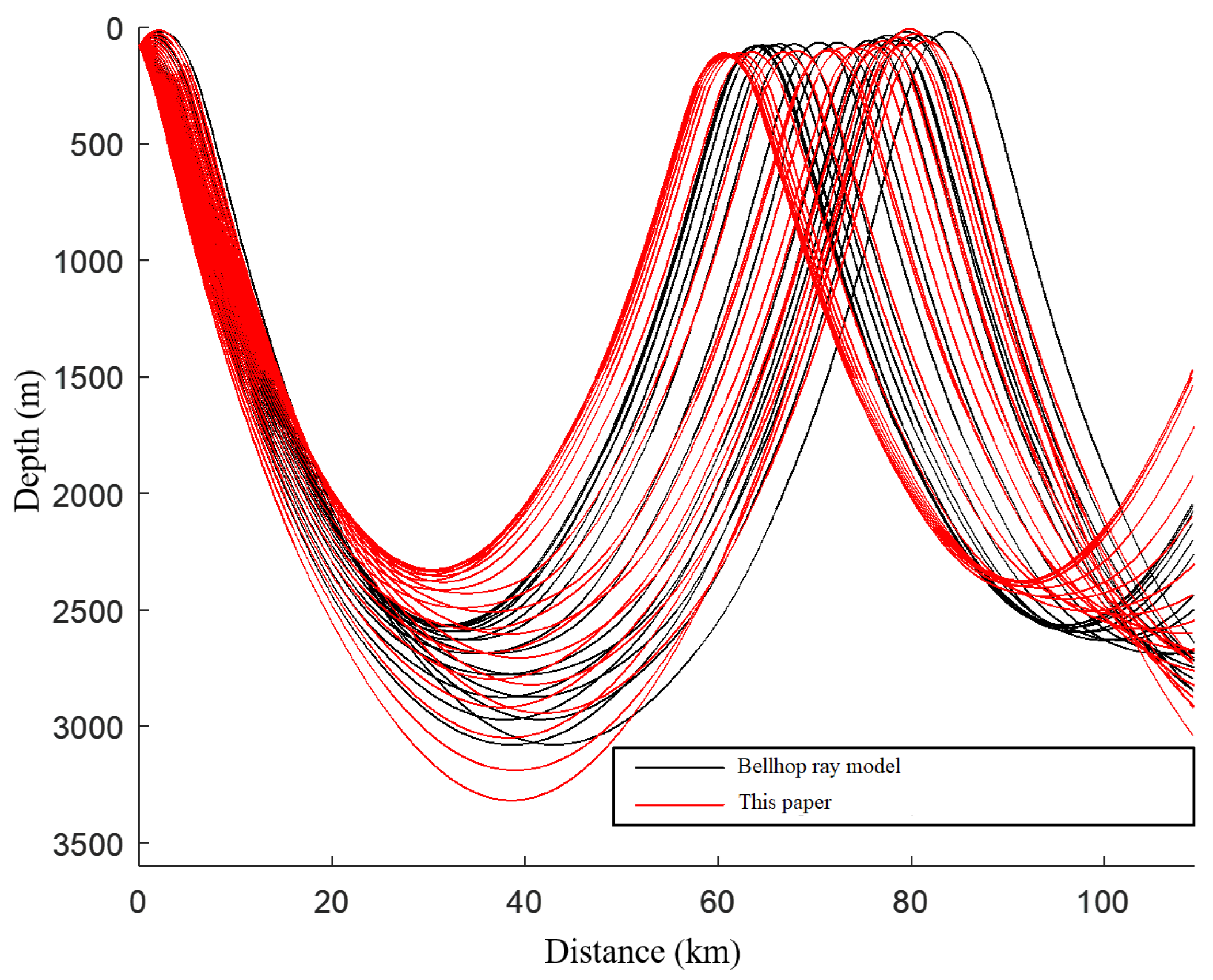
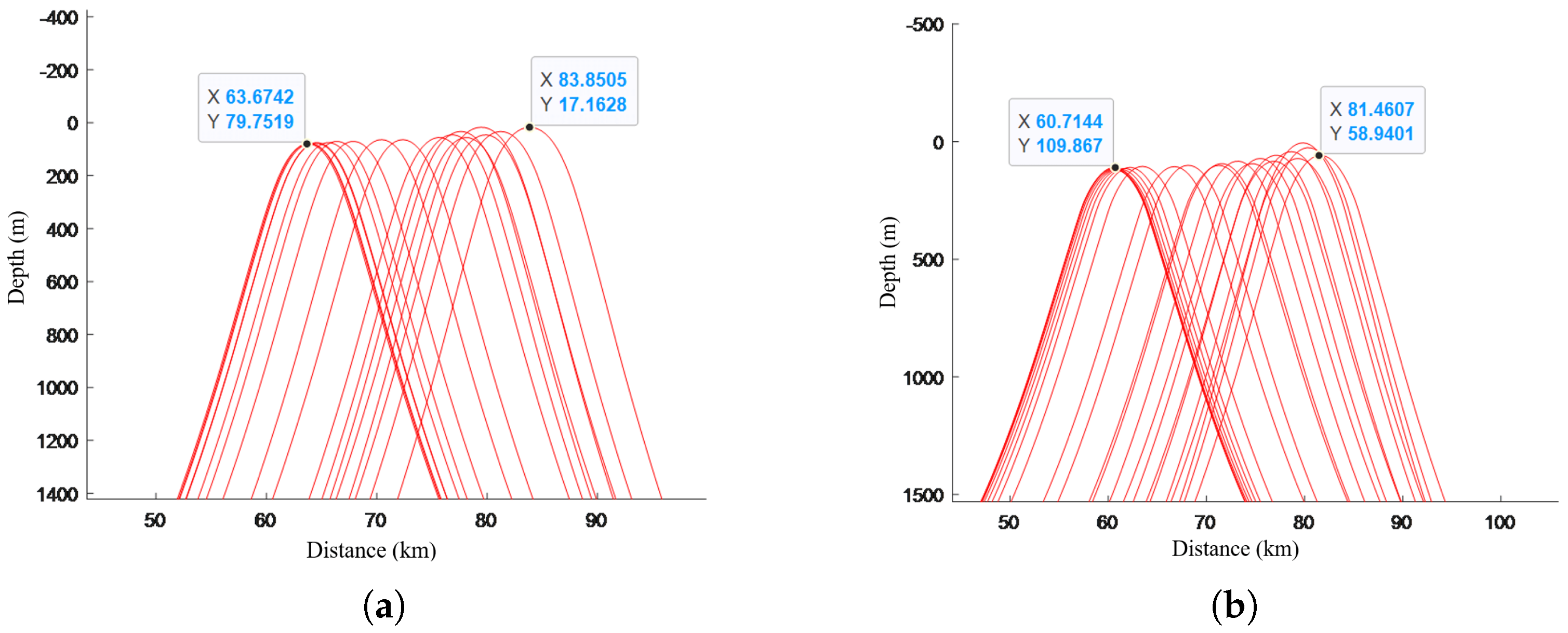
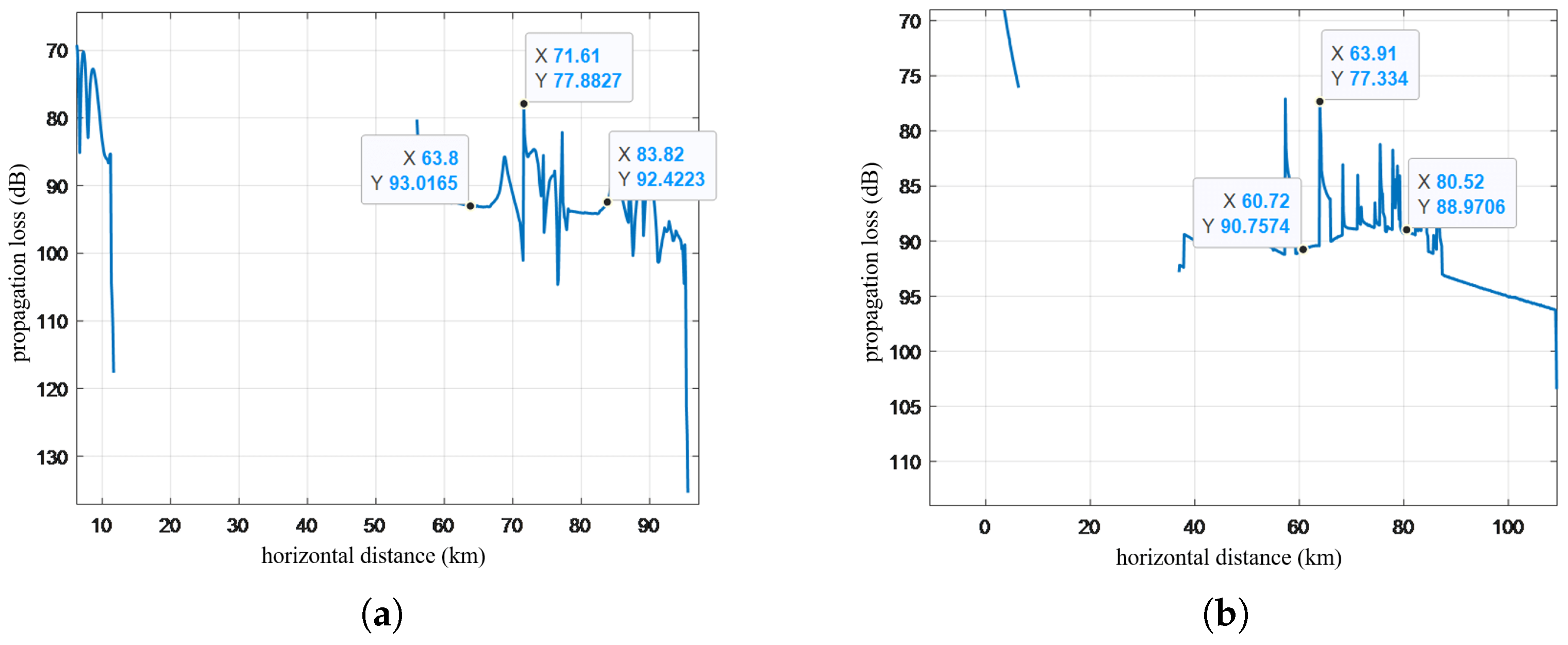
4.2. Simulation of Convergence Zone Characteristic Parameter Forecasting and Comparative Analysis of Results

The temperature, salinity, and depth data of the typical sea area are substituted into the empirical sound speed formula of Del Grosso. The sound speed profile is then written into the environmental file to generate a simplified equivalent sound speed profile for the entire sea area, as shown in Figure 12.

Under the Bellhop ray model, the simple equivalent sound speed profile is relatively smooth. The mixed layer does not take into account the horizontal distance. The sound channel axis is located at a depth of about 800 m. The minimum sound speed is 1496.74 m/s, the sea surface sound speed is 1515.9 m/s, and the sea bottom sound speed is 1518.67 m/s. Under this sound speed profile, there is a convergence zone effect.

Combining the temperature, salinity, and depth data with the latitude and longitude data of typical sea areas, a horizontal–vertical distribution model of the temperature–salinity field was constructed using the two-dimensional empirical orthogonal functions. By coupling the Del Grosso empirical formula for sound speed, the horizontally non-uniform sound speed profiles in the mixed layer were obtained, as shown in Figure 13 and Figure 14.

Figure 13 shows that the sound speed profile changes with horizontal distance due to the mixed layer’s temperature and salinity inhomogeneity. At the sea surface, sound speed is 1515.86 m/s at $114.5^{\circ }$ E, 1517.65 m/s at ${115}^{\circ }$ E, and 1519.67 m/s at $115.5^{\circ }$ E, while it is nearly constant below the mixed layer. This is because the mixed layer’s temperature and salinity increase with distance but remain constant below it. The color mapping of sound speed also shows that the mixed layer’s sound speed rises with distance. Although the sound speed considering the mixed layer’s non-uniformity differs from the simple equivalent sound speed, their overall trends are similar, with the sound channel axis depth around 800 m. This confirms the effectiveness of the improved sound speed profile.

Based on the construction of the sound speed profile, the acoustic propagation paths under the Bellhop ray model and the improved ray model are simulated. According to the experimental scenario, the source depth is set to 80 m, the source frequency is set to 300 Hz, and the emission angle range is set to $\pm {10}^{\circ }$. The sound rays of the sound field drawn by the Bellhop ray model and the method proposed in this article are shown in Figure 15.

The proposed method exhibits a notable forward shift in the acoustic field compared to the Bellhop ray model when predicting ray propagation paths. This shift arises from the consideration of horizontally inhomogeneous sound speed profiles, which alter the turning points of the rays. Specifically, rays with smaller emission angles have shallower turning point depths, while those with larger emission angles have deeper turning point depths. This phenomenon can be explained by Snell’s law: the increased sound speed due to horizontal variations in the mixed layer maintains a constant ratio between sound speed and ray angle, thereby amplifying the change in ray turning angles and causing the convergence zone to shift forward.

The upper turning points of the $0^{\circ }$ emission angle ray and the critical depth bending ray are shown in Figure 16. It can be seen that according to the Bellhop ray model, the distance to the first convergence zone is 63.6742 km, and the width of the first convergence zone is 20.1763 km; according to the improved ray model, the distance to the first convergence zone is 60.7144 km, and the width of the first convergence zone is 20.7463 km.

The first convergence zone gain is obtained by plotting the propagation loss model. The magnitude of the propagation loss varies with the receiver location. Therefore, according to the experimental setup, the receiver is placed at a depth of 200 m within the convergence zone distance to measure the magnitude of the convergence zone gain [15]. The propagation loss models of the Bellhop ray model and the proposed prediction method in this article are shown in Figure 17.

The Bellhop ray model shows a propagation loss of about 93 dB outside the convergence zone and a minimum loss of 77.8827 dB inside it, giving a convergence zone gain of around 15.12 dB. The proposed prediction method in this article has a propagation loss of about 90 dB outside the convergence zone and a minimum loss of 77.334 dB inside, resulting in a gain of about 12.67 dB. Thus, the convergence zone gain from the Bellhop model is slightly higher than that from the proposed prediction method in this article. Compare the prediction results of the characteristics parameters of the first convergence zone by the Bellhop ray model and the proposed prediction method in this article with the experimental results, as shown in

Table 2. Comparison of forecast results.

Method	Distance (km)	Width (km)	Gain (dB)
Measured	61.5	21.4	13.5
Bellhop	63.6742	20.1763	15.12
This article	60.7144	20.7463	12.67

. The gain is calculated as follows: $\mathrm{Gain}=T{L}_{\mathrm{out}}-T{L}_{\mathrm{in}}+10{log}_{10}\left({\displaystyle \frac{{\mathrm{Noise}}_{\mathrm{out}}}{{\mathrm{Noise}}_{\mathrm{in}}}}\right)$, where ${TL}_{out}$ and ${TL}_{in}$ are propagation losses outside/inside the convergence zone, and noise ratios account for directionality.

The comparison shows that the proposed prediction method in this article has enhanced the accuracy of the first convergence zone distance prediction by 2.26%, the first convergence zone width prediction by 2.66%, and the first convergence zone gain prediction by approximately 5.85% compared with the Bellhop ray model, which demonstrates the effectiveness of the proposed prediction method in this article.

5. Conclusions

The deep-sea convergence zone, as a key area for long-range propagation of underwater acoustic signals, has significant implications for the accurate forecasting of its characteristic parameters to enhance the detection capabilities of underwater equipment. This paper combines measured ocean environmental data to construct a sound speed profile model with horizontal gradient correction and verifies the effectiveness of the prediction model through numerical simulation and experimental validation. The main research work and achievements of this paper are as follows:

• A modeling method for the horizontal non-uniform sound speed profile in the mixed layer is proposed. The spatial variation characteristics of the temperature and salinity fields are extracted by stratified empirical orthogonal functions and combined with the Del Grosso sound speed formula to generate a three-dimensional sound speed field. This method breaks through the limitation of the vertical stratification assumption and constructs a continuous sound speed profile model associated with horizontal distance and vertical depth.
• The construction of a ray model with horizontal gradient correction and the implementation of ray tracing are realized. A correction term for the horizontal gradient of sound speed is introduced into the classical ray equation, and the ray-tracing equation under non-uniform media is derived. A fourth-order Runge–Kutta numerical integration algorithm is designed to quantify the effect of the horizontal gradient on the curvature of the ray, achieving high-precision tracking of the ray trajectory and analysis of the energy-focusing characteristics, and significantly improving the ability to characterize the sound field in complex sea areas.
• The convergence zone characteristic parameter forecasting algorithm is applied and its effectiveness is verified in a typical sea area environment. Taking the South China Sea acoustic propagation experiment as the benchmark case, the forecasting performance of the Bellhop model, the method in this paper, and the measured data are compared. The experimental results show that when the sound source depth is 80 m, the frequency is 300 Hz, and the launch angle is ±10°, the first convergence zone distance forecasting error of the improved model is reduced by 2.26%, the width error is reduced by 2.66%, and the gain prediction deviation is improved by 5.85%.