Performance Enhancement of Autonomous Sailboats via CFD-Optimized Wing–Tail Sail Configurations
Abstract
1. Introduction
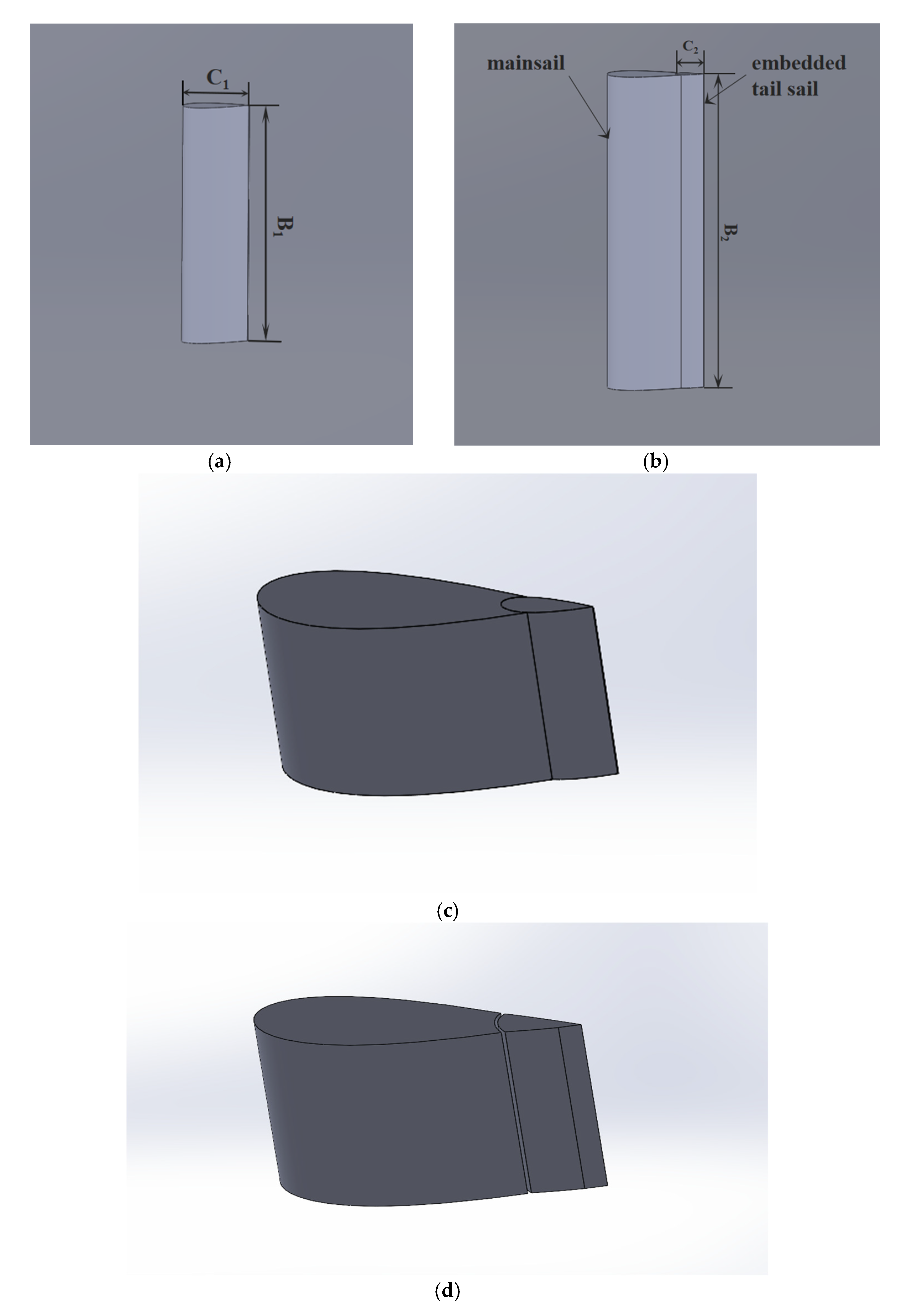
2. Modeling of Main Wing Sail
2.1. Simulation Model Establishment
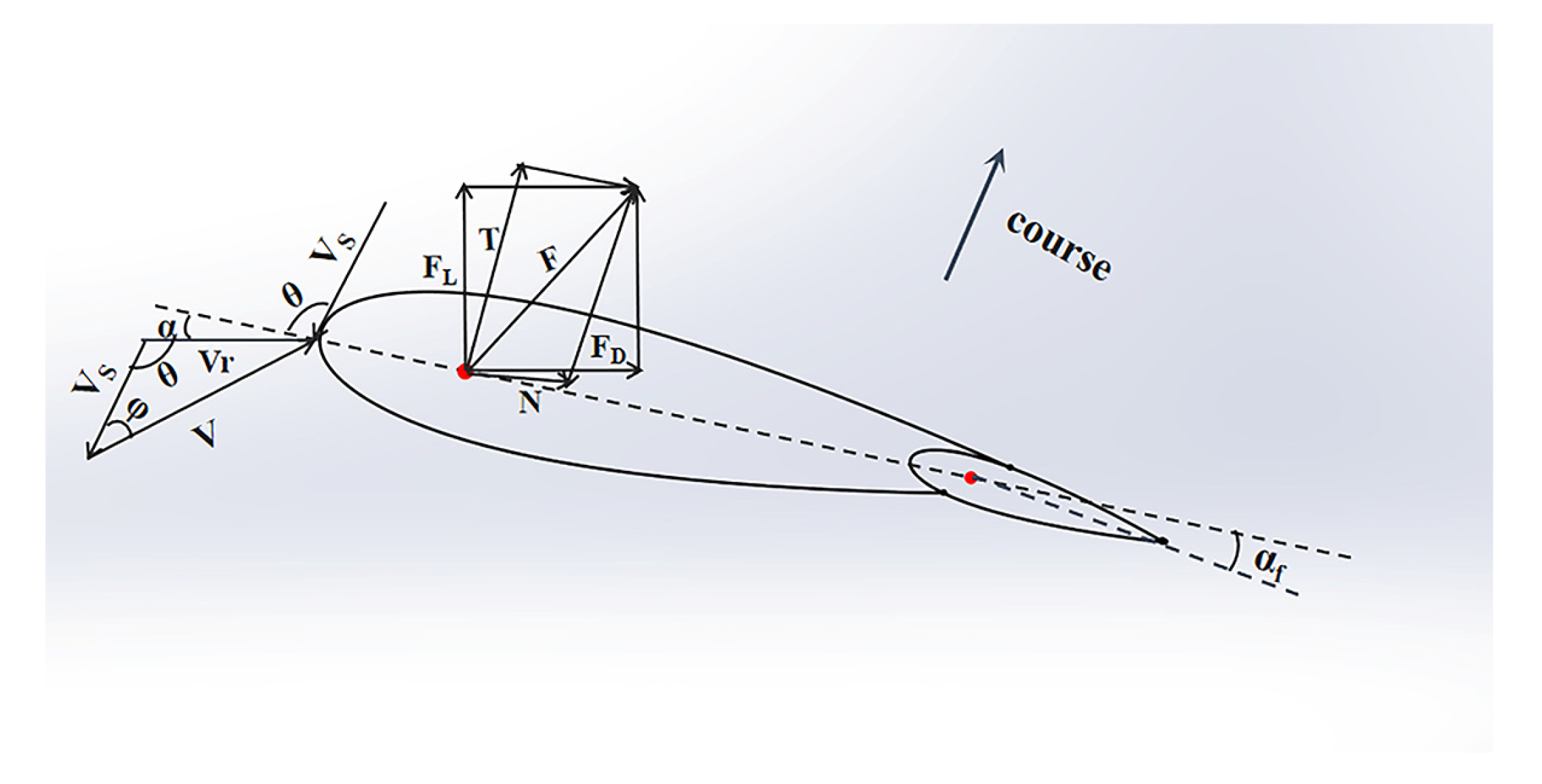
2.2. Force Analysis of the Main Wing Sail
3. The Aerodynamic Study of the Main Wing Sail
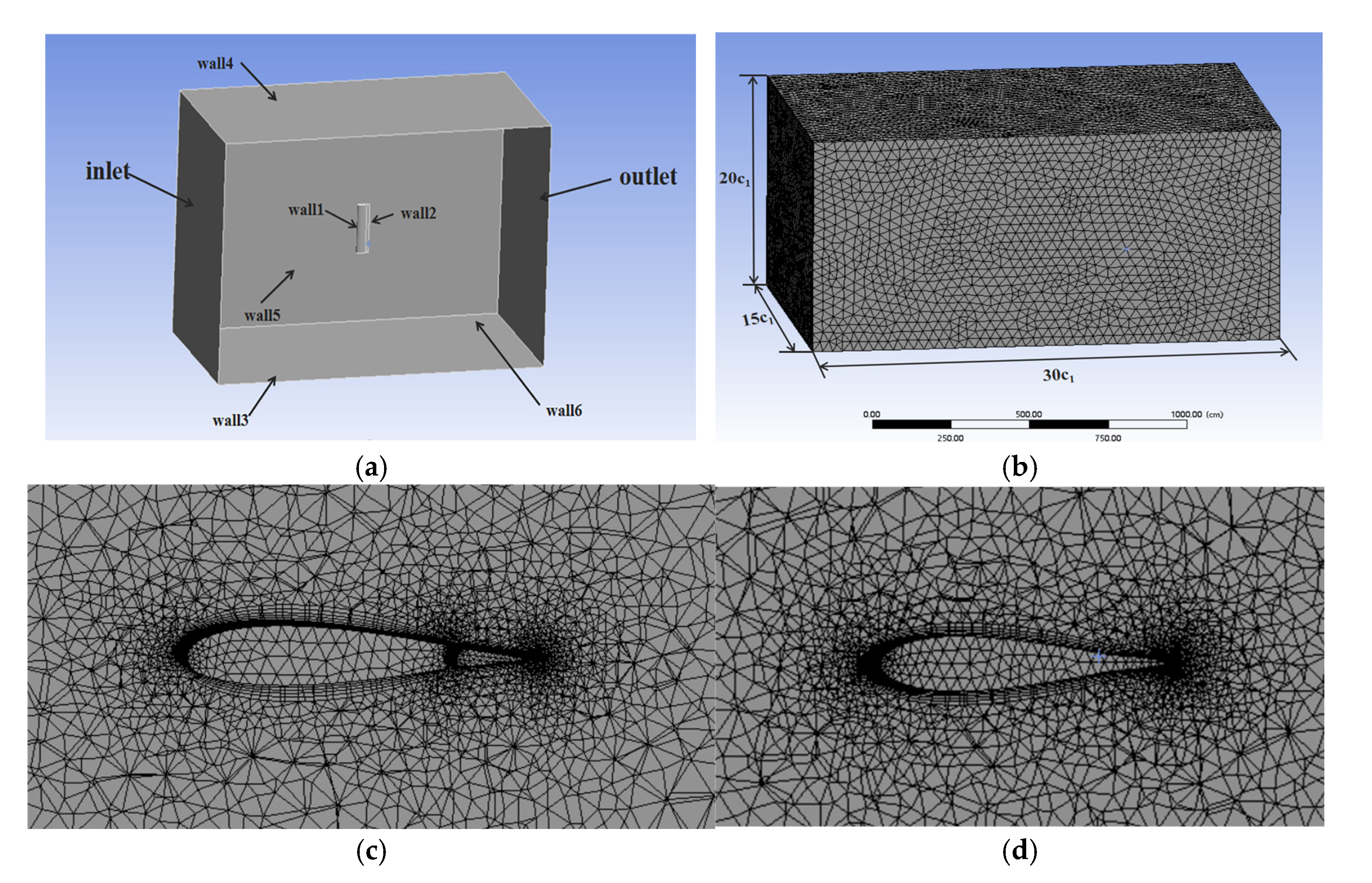
3.1. Mesh Generation
3.2. Calculation Method
3.3. Relevant Parameter Settings
3.4. Reliability Validation of the Computational Method
4. The Analysis of Simulation Results
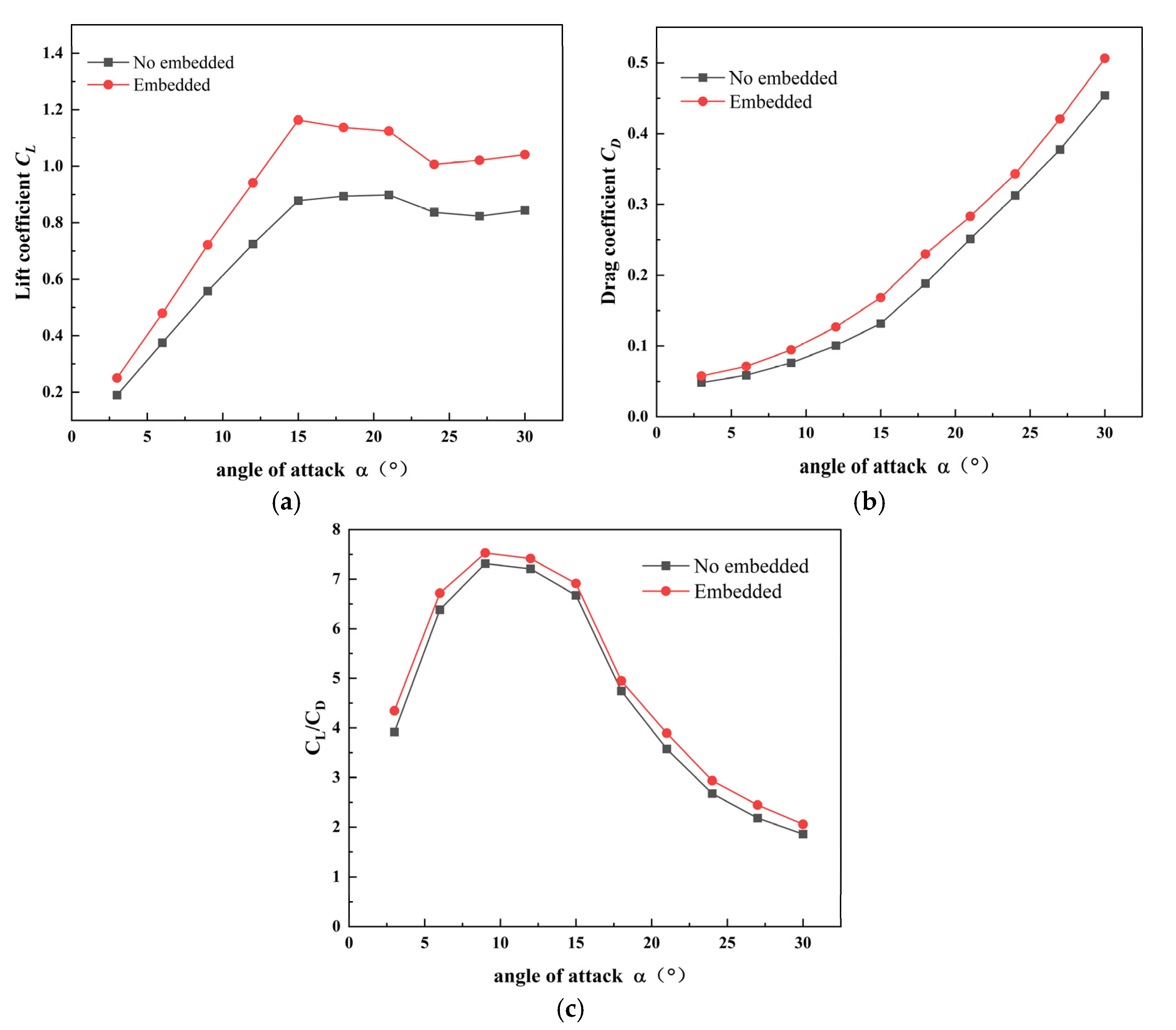
4.1. Impact of Embedded Tail Sail on the Aerodynamic Performance of the Main Sail
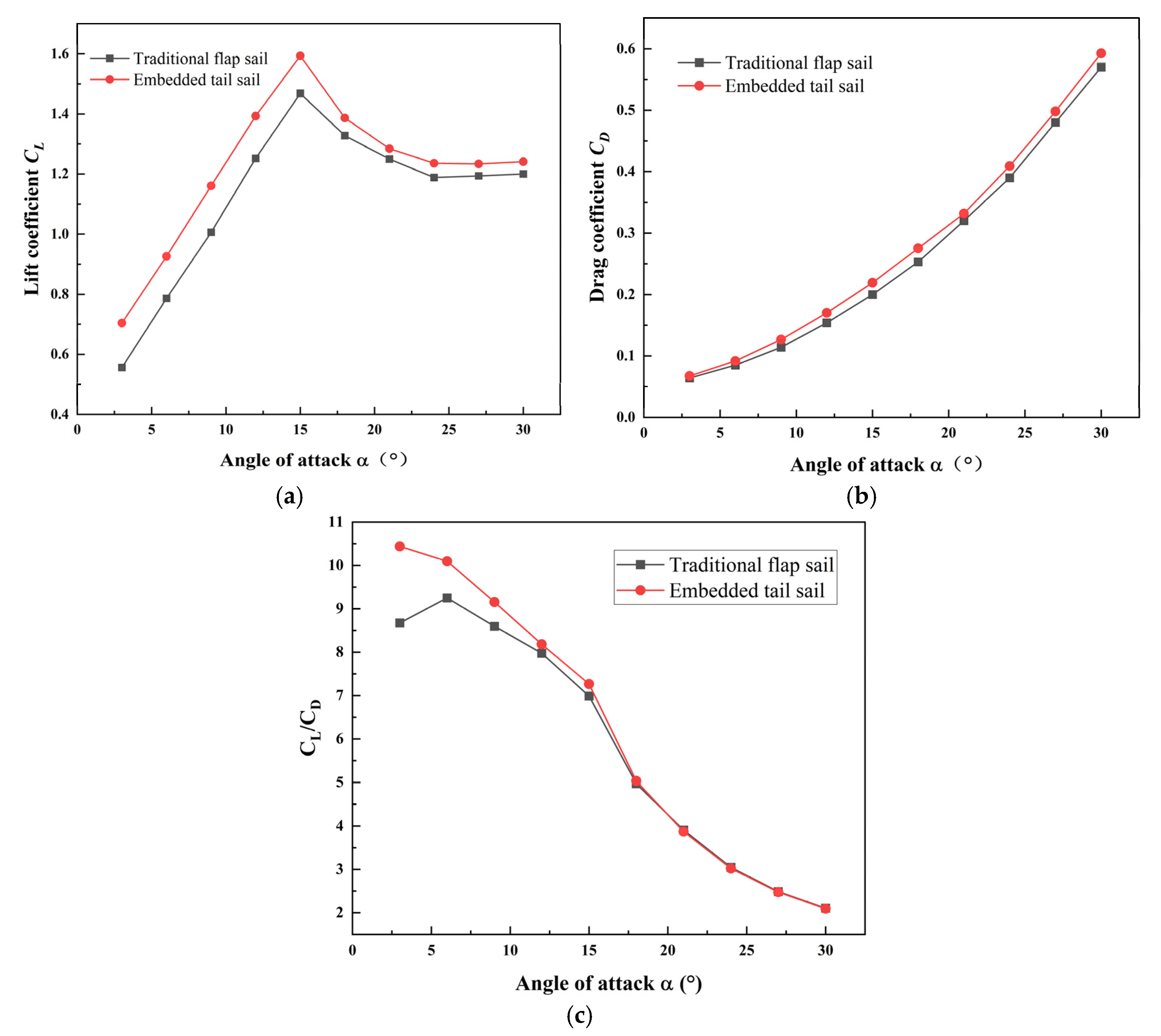
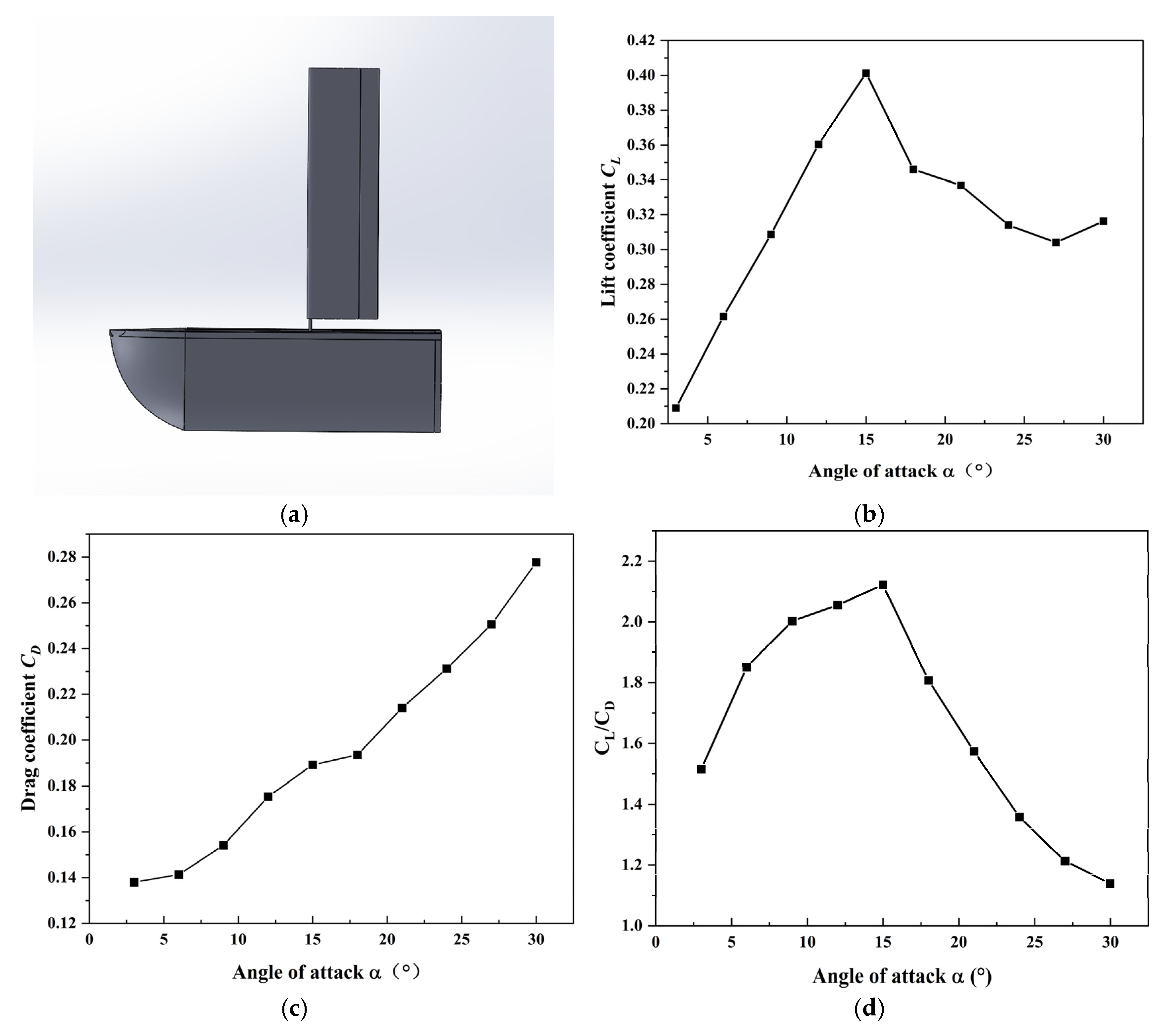
4.2. Comparative Aerodynamic Analysis of Traditional Flap Sails and Embedded Tail Sails
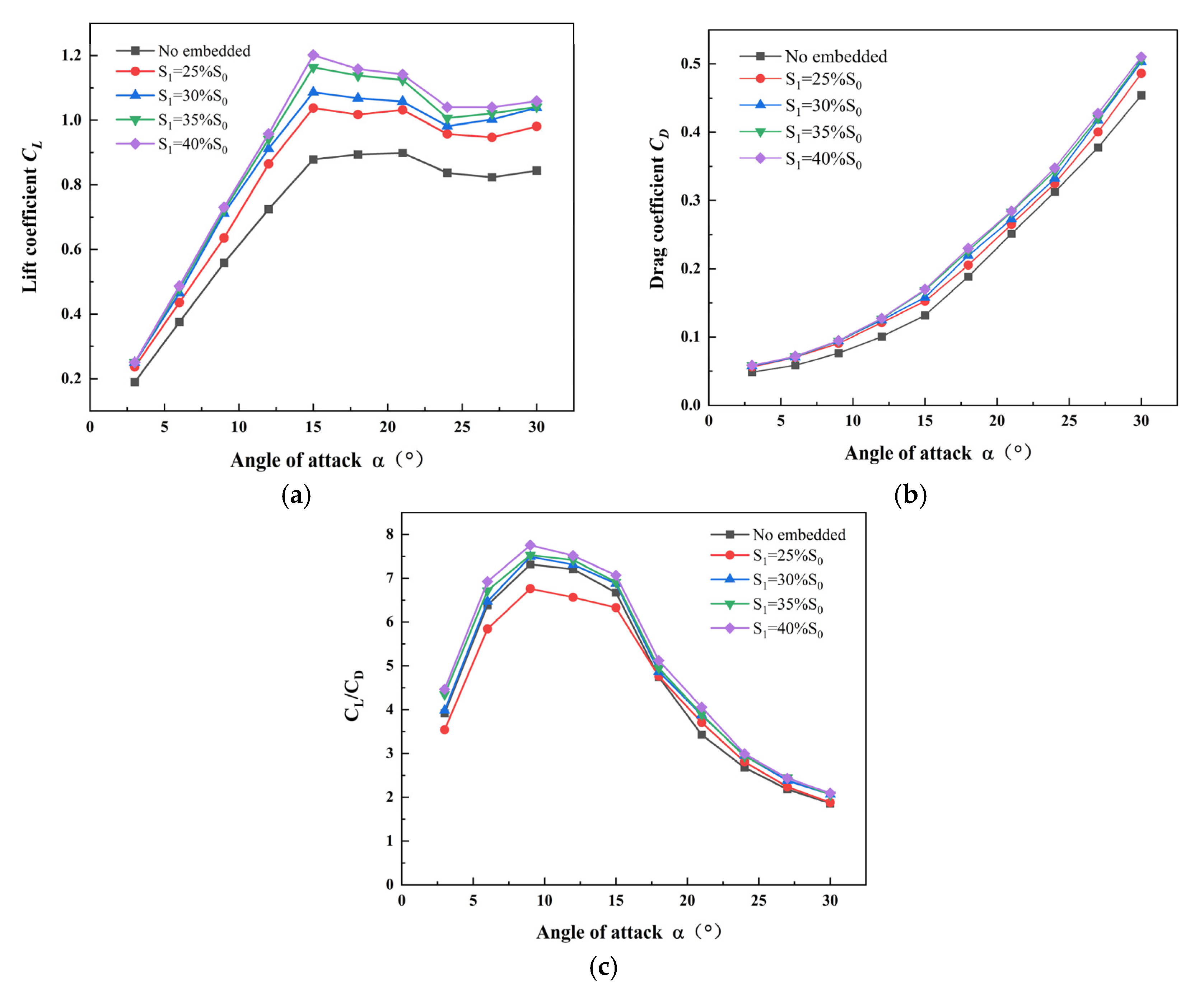
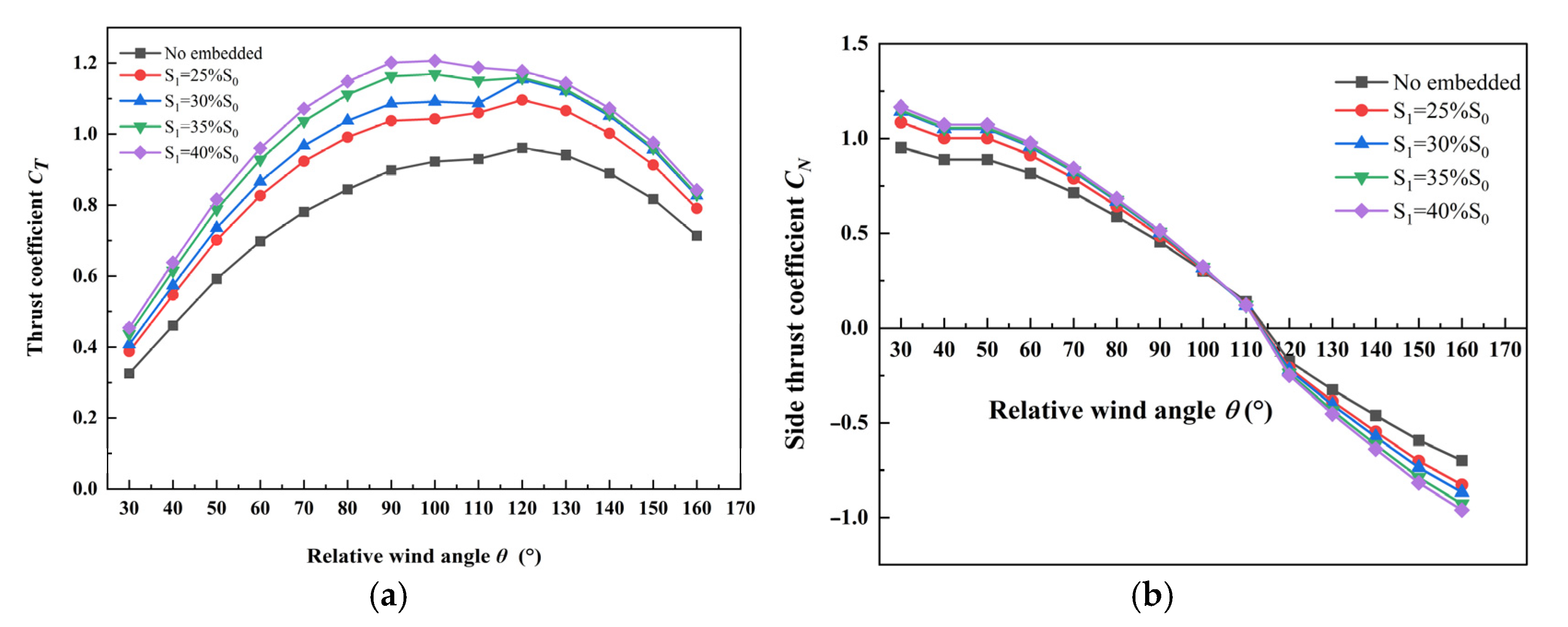
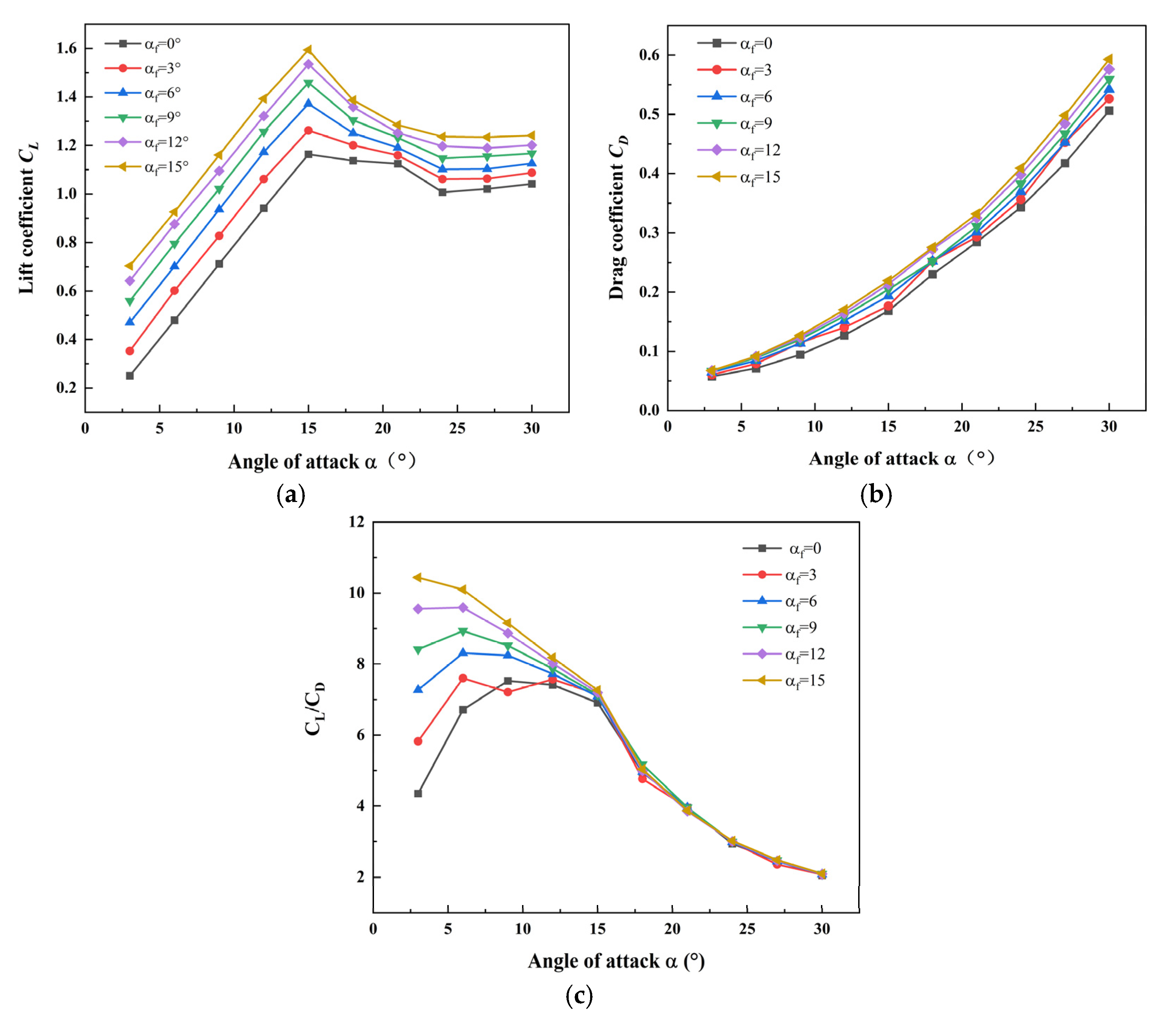
4.3. Influence of Embedded Tail Sail Area Size on the Aerodynamic Performance of the Main Sail
4.4. Impact of Deflection Angle for the Tail Sail on the Aerodynamic Performance of the Main Sail
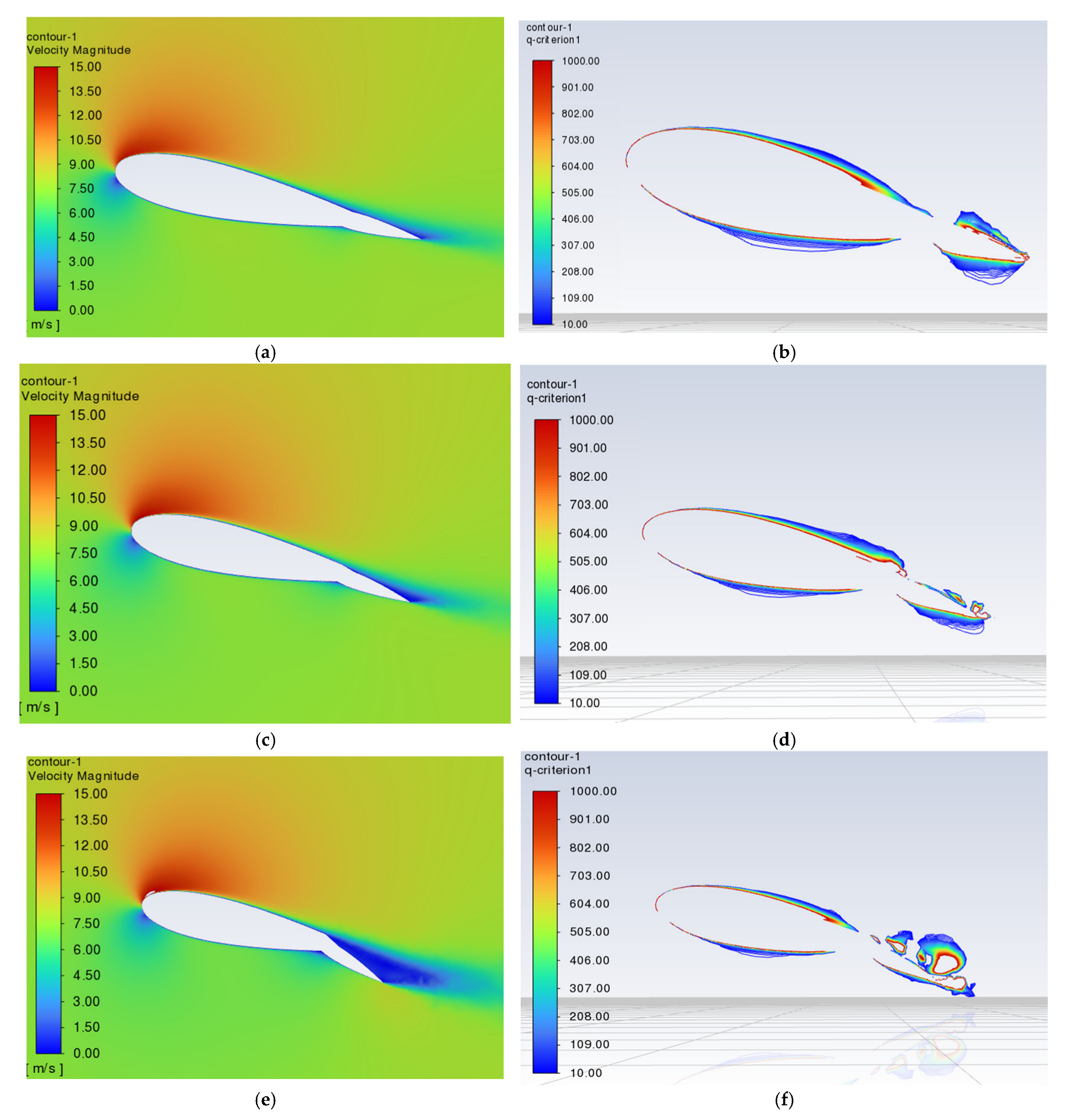
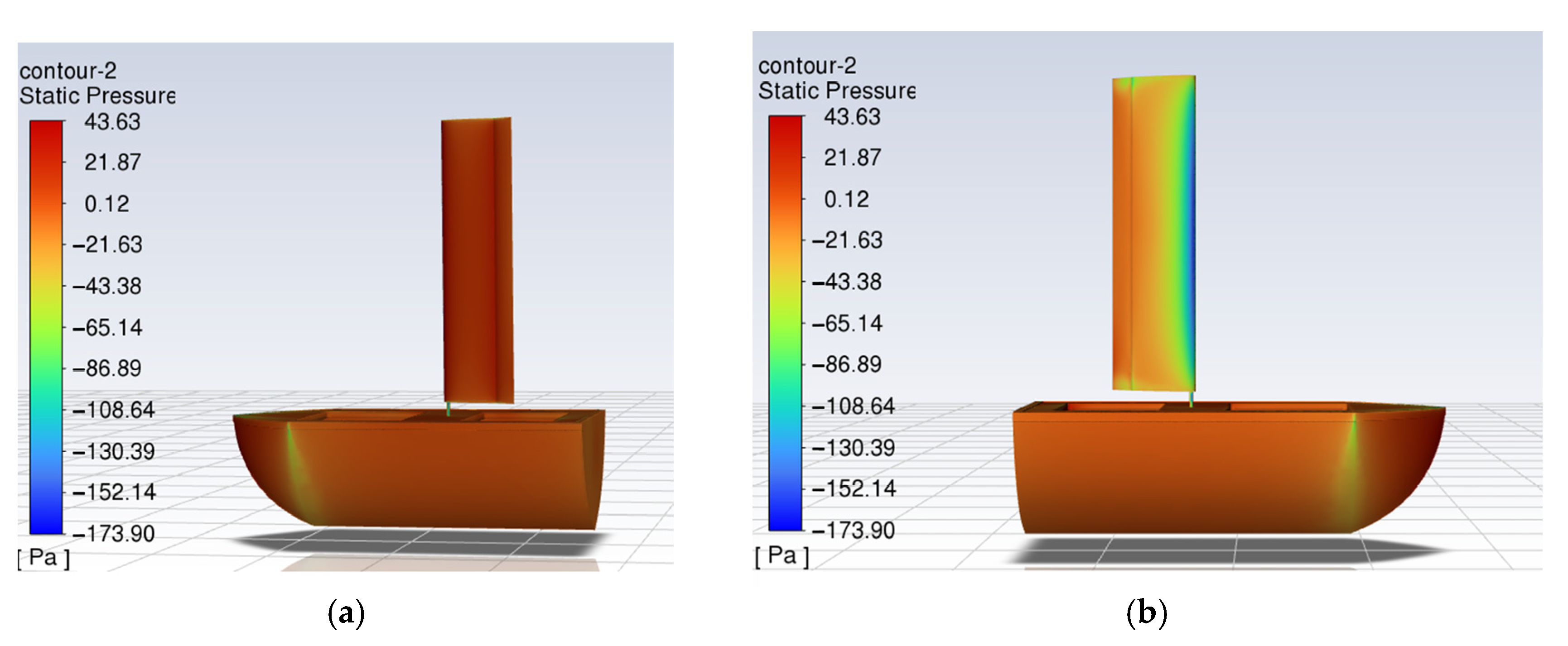
4.5. Computational Fluid Dynamics (CFD) Analysis of Hull–Sail Interaction Effects
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| α | angle of attack |
| θ | relative wind angle |
| φ | wind angle |
| αf | deflection angle |
| FD | drag force |
| FL | lift force |
| T | thrust force |
| N | side thrust force |
| CL | lift coefficient |
| CD | drag coefficient |
| CT | thrust coefficient |
| CN | side thrust coefficient |
| ρ | air density |
| S0 | projected area of the main wing sail |
| N-S | Navier–Stokes |
| RANS | Reynolds-averaged Navier–Stokes |
| P | pressure |
| μ | hydrodynamic viscous coefficient |
| gi | mass force |
| SST | Shear-Stress Transport |
| k | turbulent kinetic energy |
| ω | specific dissipation rate |
| Pk | generating term of turbulent kinetic energy k |
| μt | eddy viscosity |
| Re | Reynolds number |
| Ma | Mach number |
References
- Yodyium, T.; Peerayot, S.; Nattakit, T. Overview and control strategies of autonomous sailboats—A survey. Ocean Eng. 2023, 281, 114879. [Google Scholar] [CrossRef]
- Sun, Z.; Feng, A.; Yu, J.; Zhao, W.; Huang, Y. Development of autonomous sailboat sails and future perspectives: A review. Renew. Sustain. Energy Rev. 2025, 207, 114918. [Google Scholar] [CrossRef]
- Meinig, C.; Burger, E.F.; Cohen, N.; Cokelet, E.D.; Cronin, M.F.; Cross, J.N.; de Halleux, S.; Jenkins, R.; Jessup, A.T.; Mordy, C.W.; et al. Public–Private Partnerships to Advance Regional Ocean-Observing Capabilities: A Saildrone and NOAA-PMEL Case Study and Future Considerations to Expand to Global Scale Observing. Front. Mar. Sci. 2019, 6, 448. [Google Scholar] [CrossRef]
- Meng, X.; Yang, Y.; Yin, S.; Wang, X. Unmanned sailboat with self-balancing rotating sail based on elastic rope: Modeling, optimization, and sea trials. Appl. Energy 2024, 363, 123045. [Google Scholar] [CrossRef]
- Domínguez-Brito, A.C.; Valle-Fernández, B.; Cabrera-Gámez, J.; Ramos-de-Miguel, A.; García, J.C. A-TIRMA G2: An oceanic autonomous sailboat. In Proceedings of the World Robotic Sailing Championship and International Robotic Sailing Conference, Mariehamn, Finland, 31 August–4 September 2015; pp. 3–13. [Google Scholar]
- Stelzer, R.; Jafarmadar, K. THE ROBOTIC SAILING BOAT ASV ROBOAT AS A MARITIME RESEARCH PLATFORM. Environ. Sci. Eng. 2012. [Google Scholar]
- Miller, P.; Sauzé, C.; Neal, M. Development of ARRTOO: A Long-Endurance, Hybrid-Powered, Oceanographic Research Vessel. In Robotic Sailing 2013; Springer: Cham, Switzerland, 2013. [Google Scholar] [CrossRef]
- Kuang, L.; Li, H.; Su, X.; Song, X.; Wang, Z.; Zhang, Y.; Ma, W. Effect of chord length ratio on aerodynamic performance of two-element wing sail. Ocean Eng. 2023, 287, 115946. [Google Scholar] [CrossRef]
- Li, D.; Zheng, X.; Li, J.; Dai, J.; Li, G. Design and Performance of Contractible Twin-Tail Flap Sails. J. Jiangsu Univ. Sci. Technol. Nat. Sci. Ed. 2017, 31, 707–713. [Google Scholar]
- Li, S.; Guan, D.; Xia, T.; Ji, J. CFD-based aerodynamic study of unmanned sailboat flap sails. J. Nav. Archit. 2022, 44, 67–72+144. [Google Scholar] [CrossRef]
- Abdolahipour, S. Review on flow separation control: Effects of excitation frequency and momentum coefficient. Front. Mech. Eng. 2024, 10, 1380675. [Google Scholar] [CrossRef]
- Taleghani, A.S.; Torabi, F. Editorial: Recent developments in aerodynamics. Front. Mech. Eng. 2025, 10, 1537383. [Google Scholar] [CrossRef]
- Soheila, A. Effects of low and high frequency actuation on aerodynamic performance of a supercritical airfoil. Front. Mech. Eng. 2023, 9, 1290074. [Google Scholar] [CrossRef]
- Mi, B.; Yu, J. A New Grid-Slat Fusion Device to Improve the Take-Off and Landing Performance of Amphibious Seaplanes. J. Mar. Sci. Eng. 2024, 12, 2303. [Google Scholar] [CrossRef]
- Zhang, X.; Yao, W.; Ding, L.; Huang, B. Multi-Objective Optimization Design of Dynamic Performance of Hydrofoil with Gurney Flap. J. Mar. Sci. Eng. 2024, 12, 1147. [Google Scholar] [CrossRef]
- Chinnappa, V.; Srinivas, G. Numerical investigation of aerodynamic characteristics of naca 23112 using passive flow control technique—Gurney flaps. Cogent Eng. 2023, 10, 2222566. [Google Scholar] [CrossRef]
- Xie, Y.H.; Jiang, W.; Lu, K.; Zhang, D. Numerical investigation into energy extraction of flapping airfoil with Gurney flaps. Energy 2016, 109, 694–702. [Google Scholar] [CrossRef]
- Li, H.; Zhao, N.; Zhou, J.; Chen, X.; Wang, C. Uncertainty Analysis and Maneuver Simulation of Standard Ship Model. J. Mar. Sci. Eng. 2024, 12, 1230. [Google Scholar] [CrossRef]
- Zheng, Z.; Chen, L.; Melani, P.F.; Nayeri, C.; Bangga, G. Aerodynamic performance and wake development of NACA 0018 airfoil with serrated gurney flaps. Front. Energy Res. 2024, 12, 1363402. [Google Scholar] [CrossRef]
- Sun, Z.Y.; Yu, J.C.; Zhang, A.Q.; Jin, Q.L. Analysis of Influencing Factors on Lift Coefficients of Autonomous Sailboat Double Sail Propulsion System Based on Vortex Panel Method. J. Ocean Univ. China 2019, 33, 7. [Google Scholar] [CrossRef]
- Vuong, T.H.N.; Nguyen, H.V.; Le, T.L. Numerical study on thin cambered-plate airfoil profiles operating in micro Unmanned Aerial Vehicles. Results Eng. 2025, 25, 104364. [Google Scholar] [CrossRef]
- Sun, Z.; Hu, F.; Yu, J.; Zhao, W.; Zhang, A. Influence of Autonomous Sailboat Dual-Wing Sail Interaction on Lift Coefficients. J. Ocean Univ. China 2022, 21, 656–668. [Google Scholar] [CrossRef]
- Yang, M.y.; Shao, H.; Zhao, X.; Cheng, G.; Dai, S.; Wang, L.; Mao, X.z. Spatiotemporal distribution, evolution, and complementarity of wind and waves in China’s offshore waters and its implications for the development of green energy. Energy Convers. Manag. 2024, 312, 118567. [Google Scholar] [CrossRef]
- Kallath, H.; Lee, J.S.; Kholi, F.K.; Ha, M.Y.; Min, J.K. A multi-objective airfoil shape optimization study using mesh morphing and response surface method. J. Mech. Sci. Technol. 2021, 35, 1075–1086. [Google Scholar] [CrossRef]
- Hakan, A.H.; Melike, T.; Serdar, G.M.; Kemal, K. Numerical investigation on NACA0012 airfoil with tubercular structure. EPJ Web Conf. 2022, 269, 01001. [Google Scholar] [CrossRef]
- Seeni, A.; Rajendran, P.; Mamat, H. A CFD mesh independent solution technique for low Reynolds number propeller. CFD Lett. 2021, 11, 10. [Google Scholar]
- Chen, L.; Hongming, W.; Peiting, S. Study on the Influence of Gradient Wind on the Aerodynamic Characteristics of a Two-Element Wingsail for Ship-Assisted Propulsion. J. Mar. Sci. Eng. 2023, 11, 134. [Google Scholar] [CrossRef]
- Riesner, M.; Sigmund, S.; Moctar, O.e. Comparative study of nonlinear wave-induced global loads on a container ship in regular head waves predicted with numerical methods based on weakly nonlinear potential theory and Reynolds-averaged Navier-Stokes equations. Ship Technol. Res. 2024, 71, 239–262. [Google Scholar] [CrossRef]
- He, X.; Luo, L.-S. Lattice Boltzmann Model for the Incompressible Navier–Stokes Equation. J. Stat. Phys. 1997, 88, 927–944. [Google Scholar] [CrossRef]
- Moshfeghi, M.; Song, Y.J.; Xie, Y.H. Effects of near-wall grid spacing on SST-K-ω model using NREL Phase VI horizontal axis wind turbine. J. Wind Eng. Ind. Aerodyn. 2012, 107–108, 94–105. [Google Scholar] [CrossRef]
- Atkins, D.W. The CFD Assisted Design and Experimental Testing of a Wing-Sail with High Lift Devices; University of Salford: Salford, UK, 1996. [Google Scholar]



| Number of Meshes | Main Sail Lift Coefficient CL | Main Sail Drag Coefficient CD |
|---|---|---|
| 8.0 × 105 | 0.909 | 0.128 |
| 9.1 × 105 | 0.925 | 0.126 |
| 1.2 × 106 | 0.934 | 0.127 |
| 2.2 × 106 | 0.942 | 0.127 |
| 4.5 × 106 | 0.943 | 0.126 |
| 6.6 × 106 | 0.944 | 0.127 |
| 9.3 × 106 | 0.943 | 0.127 |
| 1.4 × 107 | 0.945 | 0.127 |
| Flow field velocity | 8 m/s |
| Angle of attack α | 0°, 3°, 6°, 9°, 12°, 15°, 18°, 21°, 24°, 27°, 30° |
| Viscous equation | SST k-ω |
| Calculate reference area | The projected area of the main sail in the Y direction |
| Calculate reference length | 0.5 m |
| Reporting definitions | Lift, drag, lift coefficient, drag coefficient |
| Number of iterations | 103 |
| Angle of Attack | Lift Coefficient of Slotted-Flap Sails | Drag Coefficient of Slotted-Flap Sails | Lift Coefficient of the Structure of This Paper | Drag Coefficient of the Structure of This Paper |
|---|---|---|---|---|
| 3° | 0.24 | 0.042 | 0.25 | 0.049 |
| 6° | 0.43 | 0.059 | 0.48 | 0.069 |
| 9° | 0.66 | 0.085 | 0.72 | 0.101 |
| 12° | 0.81 | 0.111 | 0.94 | 0.143 |
| 15° | 0.90 | 0.136 | 1.16 | 0.195 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, T.; Tian, C.; Wang, H.; Xu, C.; Ye, J.; Gong, A.; Liu, M.; Xia, T. Performance Enhancement of Autonomous Sailboats via CFD-Optimized Wing–Tail Sail Configurations. J. Mar. Sci. Eng. 2025, 13, 1640. https://doi.org/10.3390/jmse13091640
Ding T, Tian C, Wang H, Xu C, Ye J, Gong A, Liu M, Xia T. Performance Enhancement of Autonomous Sailboats via CFD-Optimized Wing–Tail Sail Configurations. Journal of Marine Science and Engineering. 2025; 13(9):1640. https://doi.org/10.3390/jmse13091640
Chicago/Turabian StyleDing, Tianci, Cunwei Tian, Huimin Wang, Changbin Xu, Jiaqi Ye, Aijiao Gong, Mingfei Liu, and Tao Xia. 2025. "Performance Enhancement of Autonomous Sailboats via CFD-Optimized Wing–Tail Sail Configurations" Journal of Marine Science and Engineering 13, no. 9: 1640. https://doi.org/10.3390/jmse13091640
APA StyleDing, T., Tian, C., Wang, H., Xu, C., Ye, J., Gong, A., Liu, M., & Xia, T. (2025). Performance Enhancement of Autonomous Sailboats via CFD-Optimized Wing–Tail Sail Configurations. Journal of Marine Science and Engineering, 13(9), 1640. https://doi.org/10.3390/jmse13091640





