Attentive Neural Processes for Few-Shot Learning Anomaly-Based Vessel Localization Using Magnetic Sensor Data
Abstract
1. Introduction
2. Related Work
2.1. Magnetic-Anomaly Localization and Tracking
2.2. Acoustic and Hybrid Underwater Positioning
2.3. Domain Randomization and Simulation-to-Real Transfer
2.4. Meta-Learning for Rapid Adaptation
2.5. Stochastic-Process Families
2.6. Uncertainty-Aware Localization and Calibration
3. Data and Benchmark Design
3.1. Dataset Generation and Task Definition
- From AMPERES Output to Trajectory CSVs:
- Magnetic-field transform:
- Sensor configuration:
- Trajectory set:
3.2. Task Taxonomy
- Depth tasks (): To define this task, we decided to fix the hull size at m, and the number of available sensors to , then we took the corresponding datasets with depths of m which define our in-distribution (ID) for the task; a 30 m depth constitutes the out-of-distribution (OOD) probe.
- Size tasks (): In this second task, we fixed the depth as 20 m, and the number of sensors as sensors, taking the corresponding datasets of hull sizes m for the ID data; m is the OOD probe.
- Sensor-drop tasks (): For the last task we tested, we fixed the vessel size as m and depth as 20 m; our sensor subsets were four, five, and six sensors, and the extreme three-sensor case is our OOD data for this task. The order of sensor dropping wasas follows: first drop sensor 1, then sensor 3, and lastly sensor 5. It was carried out this way to retain as much triangulation capabilities as possible (see Figure A1).
- Train/validation partition:
4. Methods
4.1. Task-Specific MLP Baselines
- Multilayer Perceptron Basics.
- Our baseline architecture.
- Specialisation strategy.
- (a)
- Depth MLPs: fixed hull of m and sensors, with one model per depth in m.
- (b)
- Size MLPs: fixed depth of 20 m and sensors, with one model per hull size in m.
- (c)
- Sensor MLPs: fixed hull of m at 20 m depth, with one model per active-sensor count in .
- Inference use cases.
- 1.
- Upper-bound oracle: Within their own scenario, they approximate the best MAE attainable with a lightweight feed-forward regressor (no uncertainty; no meta-adaptation).
- 2.
- Cross-scenario stress test: When evaluated outside their training regime, they expose the brittleness of deterministic, over-specialised models, providing a stringent foil for the ANP’s meta-generalisation (Section 5).
- Limitations of the MLP baseline and how the ANP addresses them.
4.2. Domain-Randomized MLP Baselines (DRS)
- Task-aggregated DRS models. Three models each aggregate the in-distribution (ID) trajectories for a single factor:
- DRS_depth: depths m; hull m; sensors.
- DRS_size: hulls m; depth 20 m; .
- DRS_sensors: sensor counts ; hull m; depth 20 m.
Each sees 300 trajectories (the union of the three specialised datasets in its group as seen in Table 2). - Global DRS-general model. One model ingests the entire ID corpus spanning all nine scenario combinations defined in Section 3.2: depths m × hulls m × sensor counts channels. This totals 2700 trajectories ( input–target pairs), an order of magnitude more data than any single specialised model.
- Architecture.
- Training protocol.
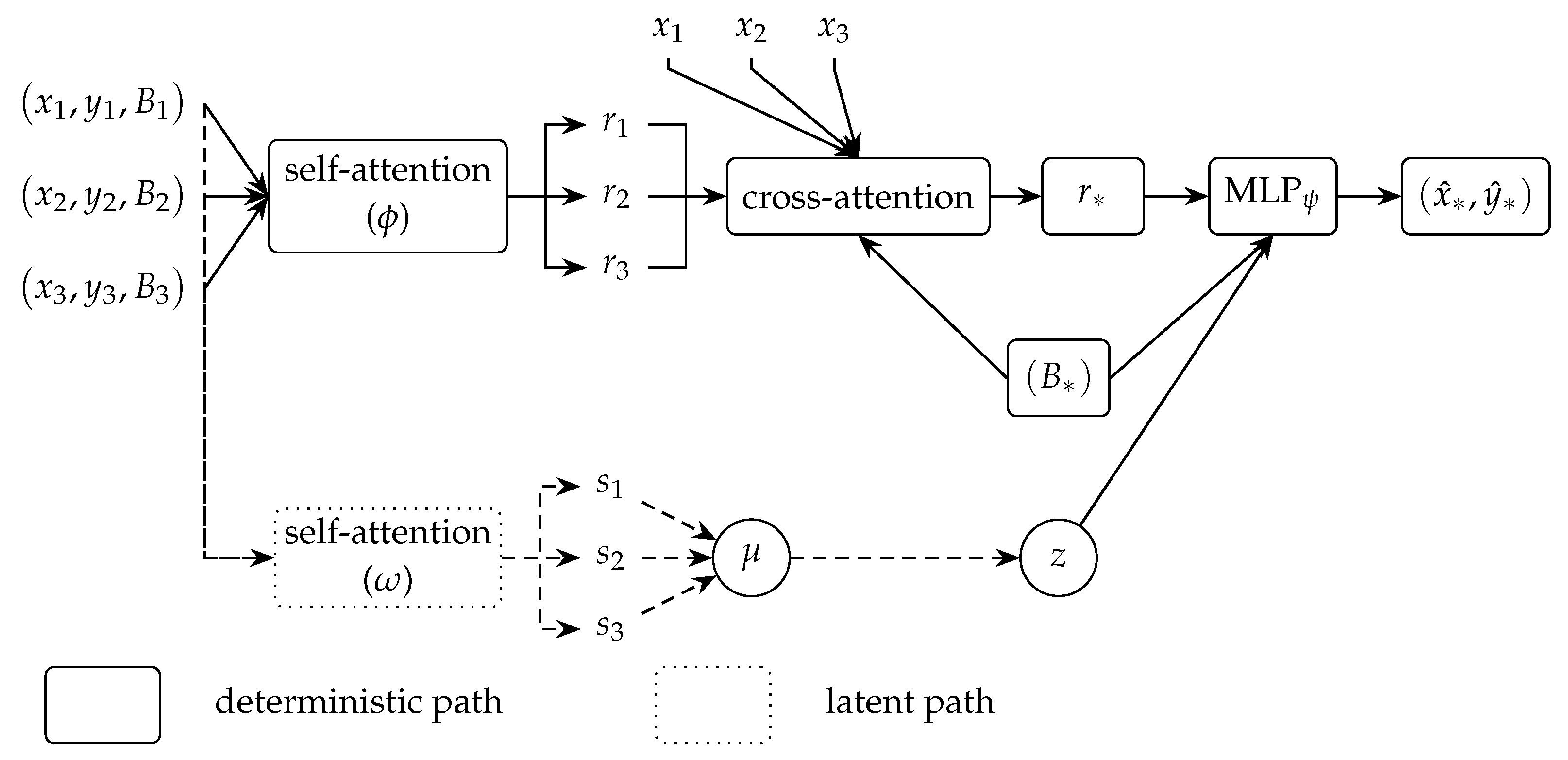
4.3. Attentive Neural Process
- (i)
- Deterministic encoder
- (ii)
- Latent encoder
- (iii)
- Decoder
- (iv)
- Training objective-evidence lower bound.
- (v)
- Context-target sampling and batching.
5. Results
5.1. Statistical Analysis
- Step 1—omnibus test.
- Step 2—pairwise follow-up.
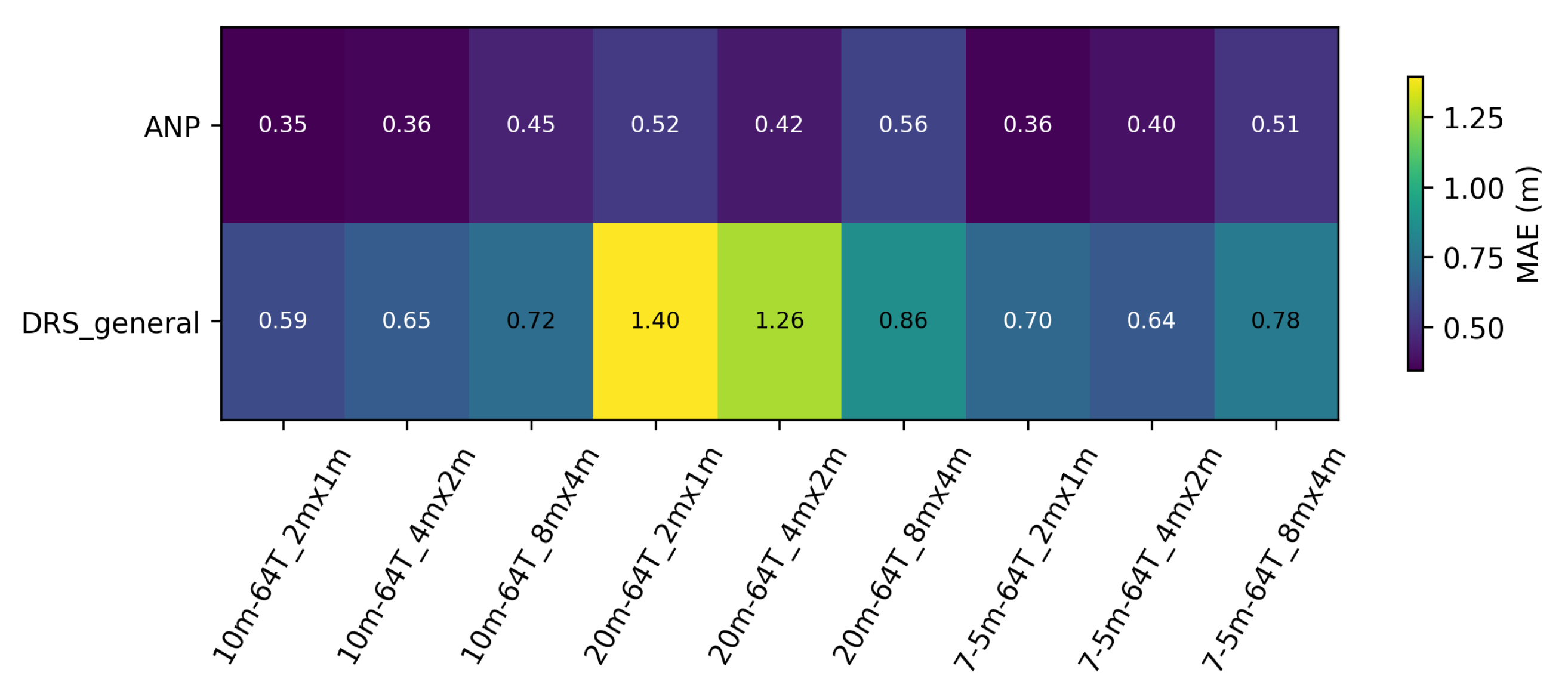
5.2. ANP vs. DRS-General on ID and OOD Tasks
- Quantitative results
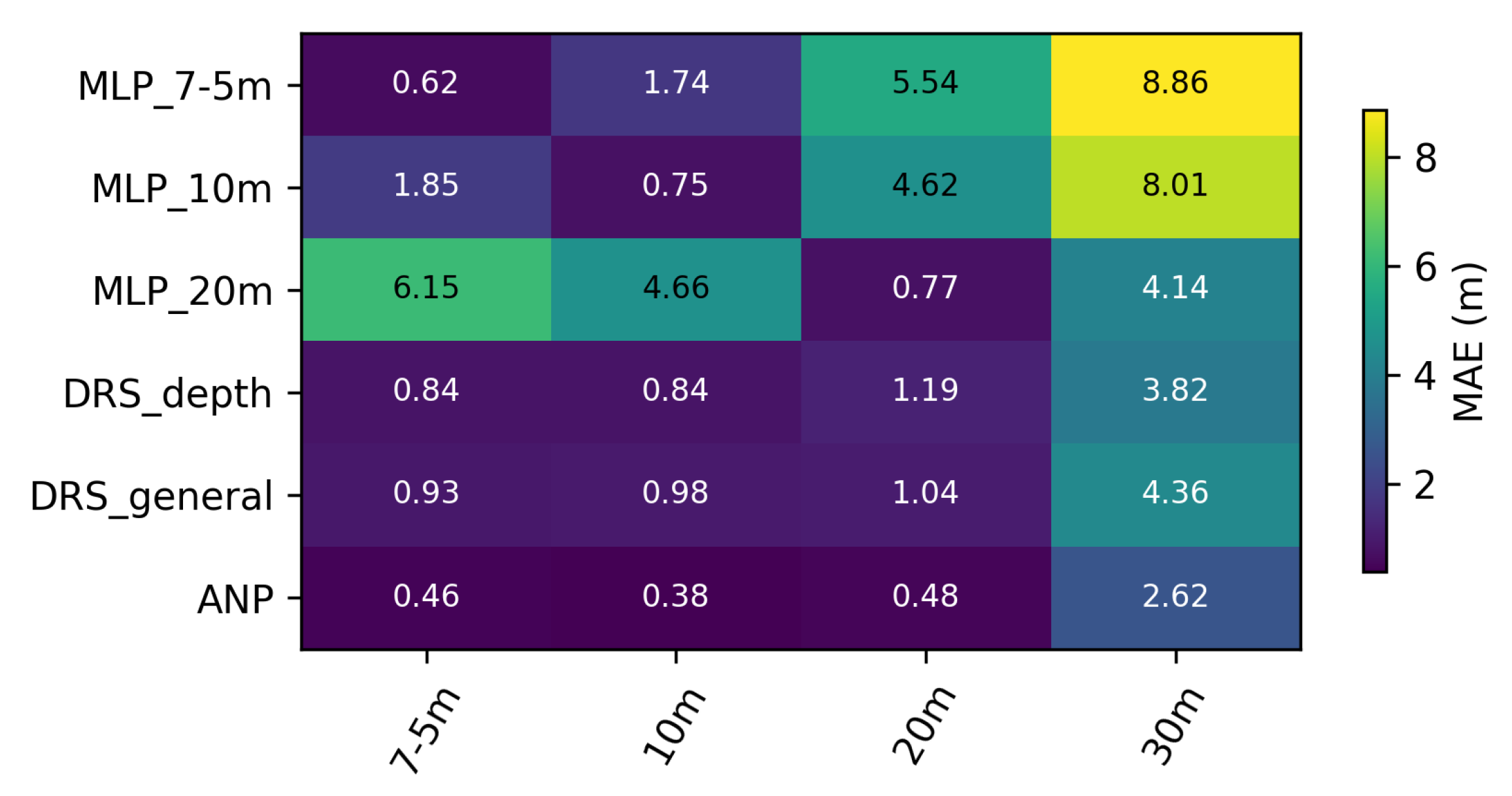
5.3. Depth Ablation
- 7.5 m, 10 m, 20 m in-distribution: depths seen during training.
- 30 m → out-of-distribution: an extrapolation stress-test never shown to the models.
- Models under test
- Quantitative results
5.4. Hull-Size Ablation
- 2 m × 1 m (small), 4 m × 2 m (medium), 8 m × 4 m (large),
- Models under test
- Quantitative results
5.5. Sensor Count Ablation
- 6 s, 5 s, 4 s—three in-distribution subsets in which zero, one, or two sensors are disabled at the same time;
- 3 s—an out-of-distribution subset that removes a third channel, emulating a more severe hardware failure.
- Models under test
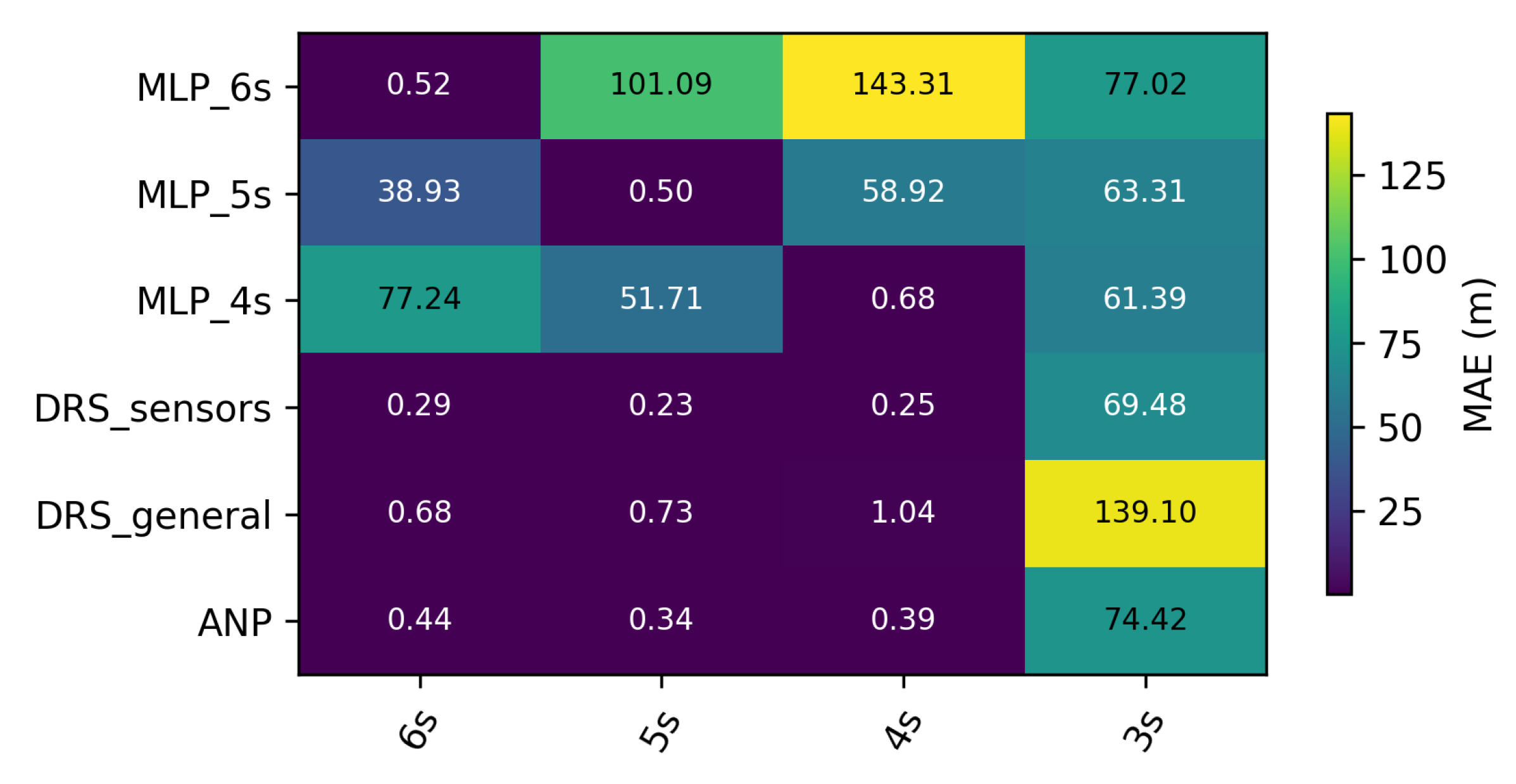
- Quantitative results
5.6. Unified Cross-Task Benchmark
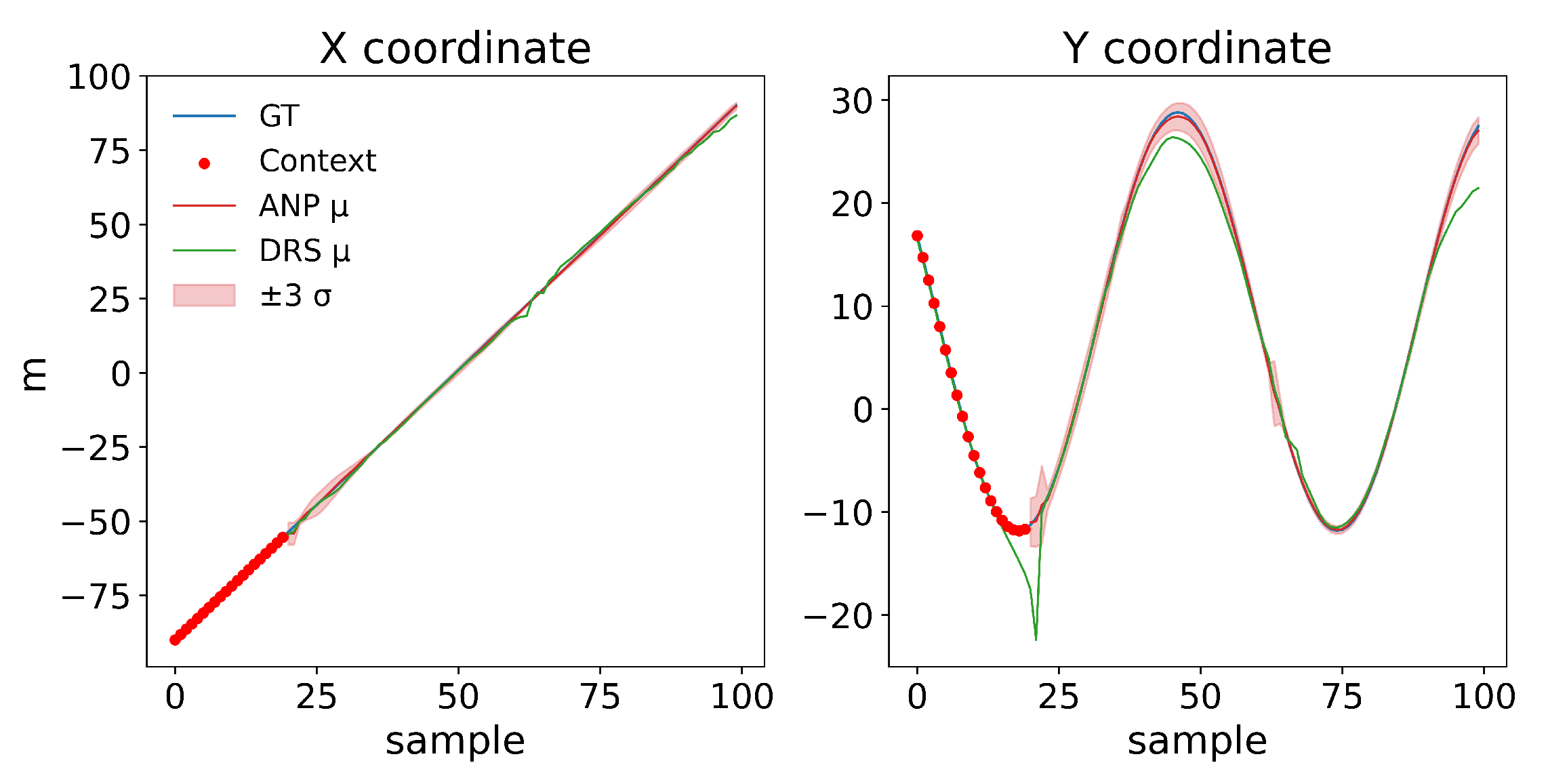
5.7. Trajectory-Level Extrapolation: ANP vs. DRS-General
5.8. Results Discussion
- (a)
- ANP consistently achieves the lowest MAE across all settings. In every in-distribution scenario (Table 3), the ANP improves over the deterministic baseline DRS-general by nearly 50% on average (0.43 m vs. 0.84 m MAE). It also retains a clear advantage in all out-of-distribution tests. The difference of the ANP against all other methods is statistically very significative, as seen in Table 11. Also, the fact that this approach provides uncertainty values, gives us the important advantage of having an interval to perform our localization.
- (b)
- Task-specific MLPs excel only in their training domain. As shown in the depth, size, and sensor ablation studies (Table 5, Table 6, Table 7, Table 8 and Table 9), each specialized MLP performs well on its target dataset but fails to generalize, often showing errors one to two orders of magnitude higher in other settings (e.g., hull-size extrapolation).
- (c)
- Domain randomization is not sufficient. While DRS-general is more robust than single-task MLPs, it still lags behind ANP by roughly in some ID scenarios and over in some OOD scenarios. Conditioning on a small, trajectory-specific context at test time, as ANP does, proves to be substantially more effective than a global set of weights alone.
- (i)
- Few-shot adaptability: The ANP matches and even surpasses the accuracy of oracle-like MLPs with only a handful of labelled samples, avoiding costly retraining cycles.
- (ii)
- Robustness to sensor failure: In the three-sensor OOD test, the ANP maintains errors around 70 m MAE (Table 9), comparable to specialized single-task MLP and DRS_sensors.
- (iii)
- Low inference latency: A single forward pass of the ANP (20 context points + 80 targets, ) takes approximately 3.8 ms on an RTX 2080 Ti (FP32). Scaled estimates suggest about 38 ms in FP32 or 9 ms in FP16/TensorRT on Jetson Xavier NX, and 110 ms in FP32 on Jetson Nano Appendix D), which means that our procedure could be implemented in real-time estimation applications with low-cost hardware.
6. Conclusions and Future Work
Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Dataset Construction
Appendix A.1. Sensor Geometry
Appendix A.2. Trajectory Generator
Appendix A.3. Measurement Transform
Appendix A.4. Sensor Configuration
Appendix A.5. Absolute ΔB Ranges
| Depth (m) | Hull (m) | N | ||||||
|---|---|---|---|---|---|---|---|---|
| 7.5 | 20 × 10 | 6328 | −277.10 | 277.10 | 0.0482 | 0.5022 | 147.20 | 277.10 |
| 7.5 | 2 × 1 | 6328 | −169.00 | 169.00 | 0.0113 | 0.1005 | 56.892 | 169.00 |
| 7.5 | 4 × 2 | 6328 | −246.70 | 246.70 | 0.0174 | 0.1550 | 87.140 | 246.70 |
| 7.5 | 8 × 4 | 6328 | −1015.0 | 1015.0 | 0.0780 | 0.6977 | 398.89 | 1015.0 |
| 10.0 | 20 × 10 | 6328 | −156.10 | 156.10 | 0.0683 | 0.6481 | 101.32 | 156.10 |
| 10.0 | 2 × 1 | 6328 | −72.920 | 72.920 | 0.0149 | 0.1303 | 37.363 | 72.920 |
| 10.0 | 4 × 2 | 6328 | −109.50 | 109.50 | 0.0230 | 0.2010 | 56.766 | 109.50 |
| 10.0 | 8 × 4 | 6328 | −468.70 | 468.70 | 0.1031 | 0.9022 | 255.42 | 468.70 |
| 20.0 | 20 × 10 | 6328 | −32.320 | 32.320 | 0.1095 | 1.032 | 27.710 | 32.320 |
| 20.0 | 2 × 1 | 6328 | −2.528 | 2.528 | 7.055 × | 0.0582 | 2.081 | 2.528 |
| 20.0 | 4 × 2 | 6328 | −14.240 | 14.240 | 0.0388 | 0.3293 | 11.764 | 14.240 |
| 20.0 | 8 × 4 | 6328 | −63.110 | 63.110 | 0.1753 | 1.484 | 52.232 | 63.110 |
| 30.0 | 20 × 10 | 6328 | −11.290 | 11.290 | 0.1082 | 1.109 | 10.442 | 11.290 |
| 30.0 | 2 × 1 | 6328 | −0.7535 | 0.7535 | 6.885 × | 0.0638 | 0.6910 | 0.7535 |
| 30.0 | 4 × 2 | 6328 | −4.256 | 4.256 | 0.0382 | 0.3604 | 3.906 | 4.256 |
| 30.0 | 8 × 4 | 6328 | −18.980 | 18.980 | 0.1724 | 1.620 | 17.446 | 18.980 |
Appendix B. Baseline MLP Architecture
Appendix B.1. Forward Mapping
Appendix B.2. Loss and Optimization
Appendix B.3. MLP Baseline Hyper-Parameters
- Architecture: 6-128-128-2 with GELU activations; He uniform initialization.
- optimizer: Adam, , .
- Batch size: 500 samples.
- Early stopping: patience 1000 on validation MAE; max 10,000 epochs.
- Base MLPs: one model per scenario (100 samples each).
- DRS MLP: same capacity, trained on concatenated 300 samples.
Appendix C. Evaluation Results
Appendix C.1. Heatmaps ANP vs. DRS-General
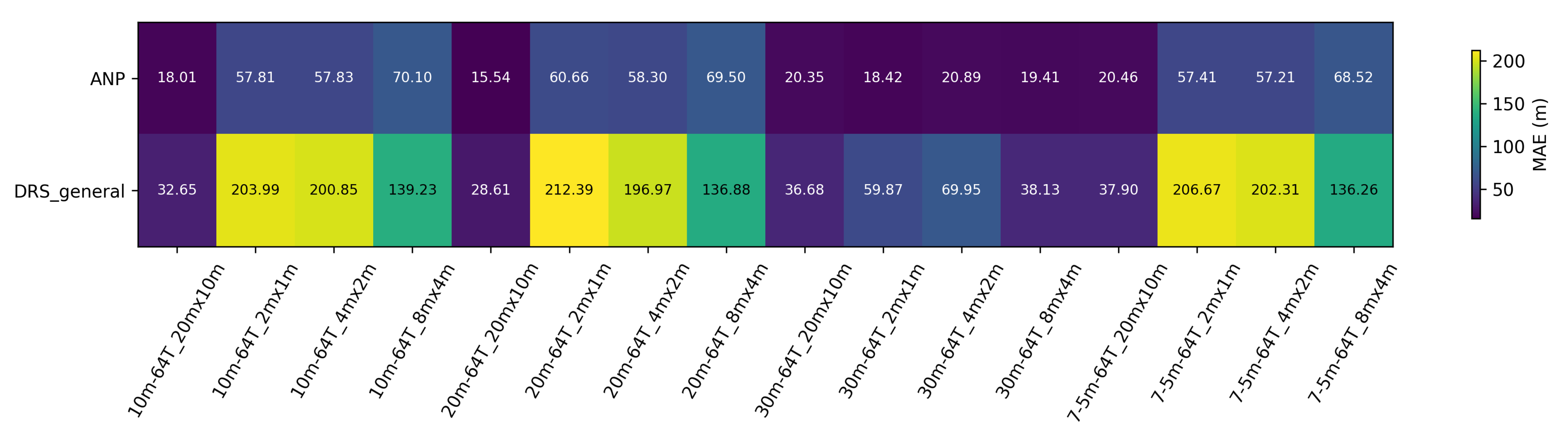
Appendix C.2. Heatmaps Task: Depth
Appendix C.3. Heatmaps Task: Size
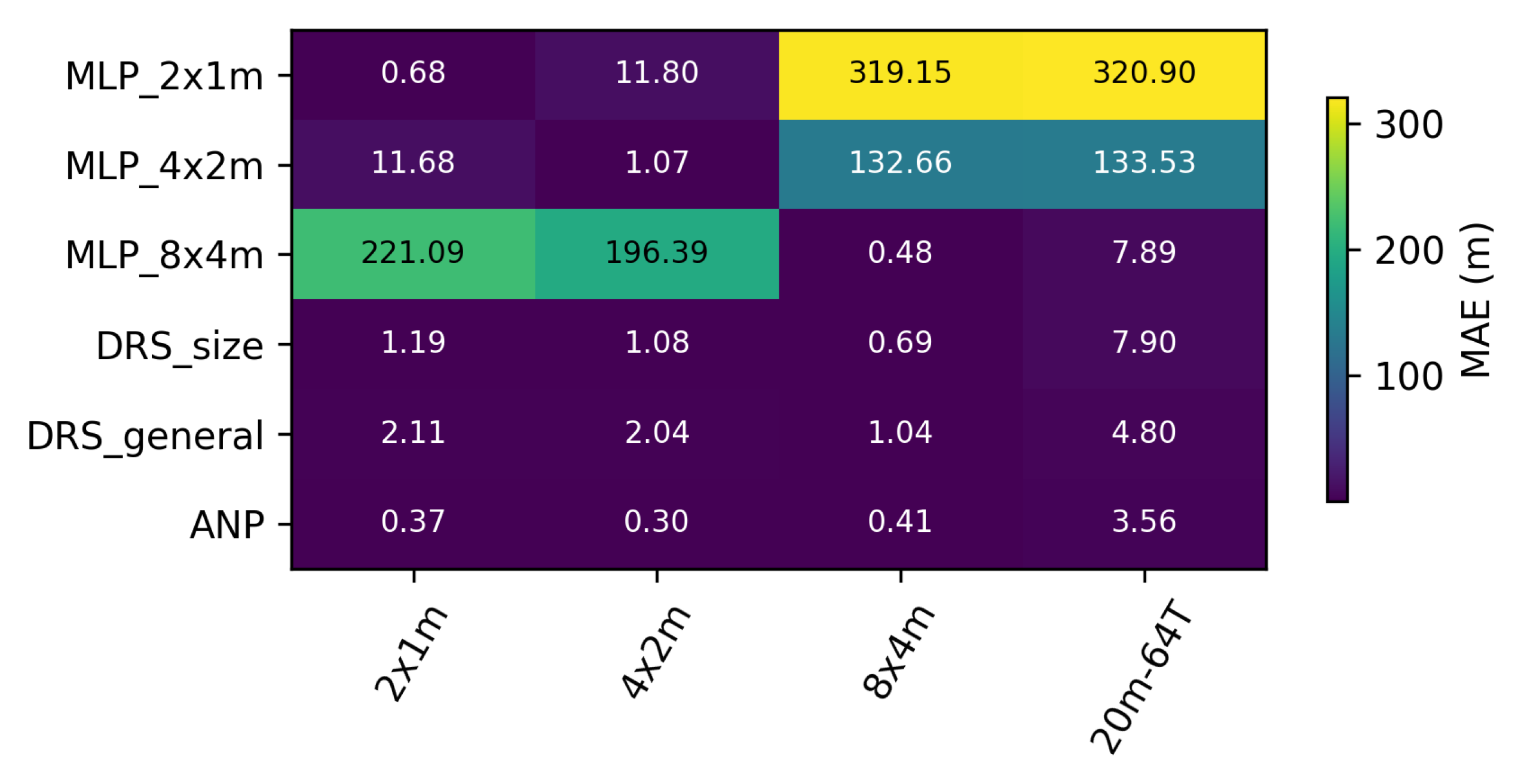
Appendix C.4. Heatmaps Task: Sensors
Appendix C.5. Complete MAE Matrix for the Unified Benchmark
| Depth-7–5 m | depth-10 m | depth-20 m | depth-30 m | size-2 × 1 m | size-4 × 2 m | size-8 × 4 m | size-20 × 10 m | sens-6 s | sens-5 s | sens-4 s | sens-3 s | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ANP | 0.42 | 0.34 | 0.38 | 2.67 | 0.33 | 0.24 | 0.38 | 3.91 | 0.35 | 0.34 | 0.38 | 69.66 |
| DRS-general | 0.93 | 0.98 | 1.04 | 4.36 | 2.11 | 2.04 | 1.04 | 4.80 | 0.68 | 0.73 | 1.04 | 139.10 |
| MLP-7–5 m | 0.74 | 1.67 | 5.21 | 8.34 | 199.64 | 188.71 | 5.21 | 6.68 | 67.58 | 34.01 | 5.21 | 109.34 |
| MLP-10 m | 1.61 | 0.66 | 4.40 | 8.06 | 958.86 | 840.54 | 4.40 | 7.60 | 124.86 | 45.66 | 4.40 | 433.72 |
| MLP-20 m | 6.45 | 4.81 | 0.67 | 3.94 | 135.73 | 128.30 | 0.67 | 5.30 | 100.06 | 67.64 | 0.67 | 126.07 |
| DRS-depth | 0.88 | 0.83 | 1.51 | 4.11 | 687.02 | 641.54 | 1.51 | 5.46 | 132.48 | 145.68 | 1.51 | 53.03 |
| MLP-2 × 1 m | 328.56 | 325.96 | 319.15 | 317.11 | 0.68 | 11.80 | 319.15 | 320.90 | 390.72 | 395.22 | 319.15 | 425.03 |
| MLP-4 × 2 m | 135.91 | 135.38 | 132.66 | 129.93 | 11.68 | 1.07 | 132.66 | 133.53 | 141.52 | 181.26 | 132.66 | 346.08 |
| MLP-8 × 4 m | 6.84 | 4.99 | 0.48 | 3.59 | 221.09 | 196.39 | 0.48 | 7.89 | 267.76 | 81.66 | 0.48 | 93.91 |
| DRS-size | 6.57 | 4.69 | 0.69 | 3.91 | 1.19 | 1.08 | 0.69 | 7.90 | 149.91 | 140.70 | 0.69 | 72.53 |
| MLP-6 s | 144.38 | 143.49 | 143.31 | 145.16 | 206.65 | 194.01 | 143.31 | 143.16 | 0.52 | 101.09 | 143.31 | 77.02 |
| MLP-5 s | 60.06 | 59.94 | 58.92 | 59.29 | 287.17 | 253.58 | 58.92 | 60.41 | 38.93 | 0.50 | 58.92 | 63.31 |
| MLP-4 s | 6.56 | 4.92 | 0.68 | 4.08 | 243.44 | 218.31 | 0.68 | 5.71 | 77.24 | 51.71 | 0.68 | 61.39 |
| DRS-sensors | 8.86 | 6.36 | 0.25 | 4.03 | 345.17 | 320.20 | 0.25 | 7.57 | 0.29 | 0.23 | 0.25 | 69.48 |
Appendix D. Latency Estimation on Embedded Devices
Appendix D.1. Reference Measurement on Our Server Desktop
- Hardware & Software: NVIDIA RTX 2080 Ti (13.45 TFLOPS FP32) running PyTorch 2.2.
- Script: test_latency.py scritp that performs timed iterations after ten warm-up passes.
- Result: per batch ( points, , FP32).
Appendix D.2. Computational Scaling Model
Appendix D.3. Device Specifications
| Device | Architecture | TFLOPS FP32 | TFLOPS FP16 |
|---|---|---|---|
| RTX 2080 Ti | Turing TU102 | 13.45 | 27.0 |
| Jetson Xavier NX | Volta (384 CUDA) | 1.30 | 6.0 |
| Jetson Nano | Maxwell (128 CUDA) | 0.47 | — |
Appendix D.4. Resulting Latency Estimates
| Device | Mode | Scale Factor | Latency |
|---|---|---|---|
| Jetson Xavier NX | FP32 | ~38 ms | |
| Jetson Xavier NX | FP16 (TensorRT) | ~9 ms | |
| Jetson Nano | FP32 | ~110 ms |
Appendix D.5. Limitations
- (i)
- Throttling on the Nano under passively cooled cases can add ∼20 % latency.
- (ii)
- Host ↔ device transfers are excluded.
References
- Zhang, S.; Yang, Y.; Xu, T.; Qin, X.; Liu, Y. Long-range LBL underwater acoustic navigation considering Earth curvature and Doppler effect. Measurement 2025, 240, 115524. [Google Scholar] [CrossRef]
- Alimi, R.; Fisher, E.; Nahir, K. In Situ Underwater Localization of Magnetic Sensors Using Natural Computing Algorithms. Sensors 2023, 23, 1797. [Google Scholar] [CrossRef]
- Gidugu, A.; Vandavasi, B.N.J.; Narayanaswamy, V. Bio-inspired machine-learning aided geo-magnetic field based AUV navigation system. Sci. Rep. 2024, 14, 17912. [Google Scholar] [CrossRef]
- Chen, X.; Hu, J.; Jin, C.; Li, L.; Wang, L. Understanding Domain Randomization for Sim-to-real Transfer. arXiv 2022, arXiv:2110.03239. [Google Scholar] [CrossRef]
- Muratore, F.; Ramos, F.; Turk, G.; Yu, W.; Gienger, M.; Peters, J. Robot Learning from Randomized Simulations: A Review. arXiv 2022, arXiv:2111.00956. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Mnih, A.; Schwarz, J.; Garnelo, M.; Eslami, A.; Rosenbaum, D.; Vinyals, O.; Teh, Y.W. Attentive Neural Processes. arXiv 2019, arXiv:1901.05761. [Google Scholar] [CrossRef]
- Tobin, J.; Fong, R.; Ray, A.; Schneider, J.; Zaremba, W.; Abbeel, P. Domain Randomization for Transferring Deep Neural Networks from Simulation to the Real World. arXiv 2017, arXiv:1703.06907. [Google Scholar] [CrossRef]
- Heshmat, M.; Saoud, L.S.; Abujabal, M.; Sultan, A.; Elmezain, M.; Seneviratne, L.; Hussain, I. Underwater SLAM Meets Deep Learning: Challenges, Multi-Sensor Integration, and Future Directions. Sensors 2025, 25, 3258. [Google Scholar] [CrossRef]
- Cohen, K.M.; Park, S.; Simeone, O.; Shamai, S. Bayesian Active Meta-Learning for Reliable and Efficient AI-Based Demodulation. IEEE Trans. Signal Process. 2022, 70, 5366–5380. [Google Scholar] [CrossRef]
- Etiabi, Y.; Eldeeb, E.; Shehab, M.; Njima, W.; Alves, H.; Alouini, M.S.; Amhoud, E.M. MetaGraphLoc: A Graph-based Meta-learning Scheme for Indoor Localization via Sensor Fusion. arXiv 2024, arXiv:2411.17781. [Google Scholar] [CrossRef]
- Garnelo, M.; Schwarz, J.; Rosenbaum, D.; Viola, F.; Rezende, D.J.; Eslami, S.M.A.; Teh, Y.W. Neural Processes. arXiv 2018, arXiv:1807.01622. [Google Scholar] [CrossRef]
- Gordon, J.; Bruinsma, W.P.; Foong, A.Y.K.; Requeima, J.; Dubois, Y.; Turner, R.E. Convolutional Conditional Neural Processes. arXiv 2020, arXiv:1910.13556. [Google Scholar] [CrossRef]
- Song, J.; Bagoren, O.; Skinner, K.A. Uncertainty-Aware Acoustic Localization and Mapping for Underwater Robots. arXiv 2023, arXiv:2307.08647. [Google Scholar] [CrossRef]
- Wang, C. Calibration in Deep Learning: A Survey of the State-of-the-Art. arXiv 2024, arXiv:2308.01222. [Google Scholar] [CrossRef]
- Song, J.; Jo, H.; Jin, Y.; Lee, S.J. Uncertainty-Aware Depth Network for Visual Inertial Odometry of Mobile Robots. Sensors 2024, 24, 6665. [Google Scholar] [CrossRef]
- Pérez, M.; Parras, J.; Zazo, S.; Pérez-Álvarez, I.A.; Sanz Lluch, M.M. Using a Deep Learning Algorithm to Improve the Results Obtained in the Recognition of Vessels Size and Trajectory Patterns in Shallow Areas Based on Magnetic Field Measurements Using Fluxgate Sensors. IEEE Trans. Intell. Transp. Syst. 2022, 23, 3472–3481. [Google Scholar] [CrossRef]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65 6, 386–408. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. arXiv 2015, arXiv:1502.01852. [Google Scholar] [CrossRef]
- Hendrycks, D.; Gimpel, K. Gaussian Error Linear Units (GELUs). arXiv 2023, arXiv:1606.08415. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar] [CrossRef]
- Viet, P.Q.; Romero, D. Spatial Transformers for Radio Map Estimation. arXiv 2024, arXiv:2411.01211. [Google Scholar] [CrossRef]
- Garnelo, M.; Rosenbaum, D.; Maddison, C.J.; Ramalho, T.; Saxton, D.; Shanahan, M.; Teh, Y.W.; Rezende, D.J.; Eslami, S.M.A. Conditional Neural Processes. arXiv 2018, arXiv:1807.01613. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. arXiv 2022, arXiv:1312.6114. [Google Scholar] [CrossRef]
- Demšar, J. Statistical Comparisons of Classifiers over Multiple Data Sets. J. Mach. Learn. Res. 2006, 7, 1–30. [Google Scholar]
- Rainio, O.; Teuho, J.; Klén, R. Evaluation metrics and statistical tests for machine learning. Sci. Rep. 2024, 14, 6086. [Google Scholar] [CrossRef]
- Chulliat, A.; Brown, W.; Beggan, C.; Nair, M.; Young, L.; Boneh, N.; Watson, C.; Perez, N.G.; Meyer, B.; Paniccia, M. The US/UK World Magnetic Model for 2025–2030: Technical Report; Institution of National Centers for Environmental Information, NOAA: Boulder, CO, USA, 2025. [Google Scholar] [CrossRef]
- Ganin, Y.; Ustinova, E.; Ajakan, H.; Germain, P.; Larochelle, H.; Laviolette, F.; Marchand, M.; Lempitsky, V. Domain-Adversarial Training of Neural Networks. arXiv 2016, arXiv:1505.07818. [Google Scholar] [CrossRef]
- Khirodkar, R.; Kitani, K.M. Adversarial Domain Randomization. arXiv 2021, arXiv:1812.00491. [Google Scholar] [CrossRef]
- Kim, D.; Cho, S.; Lee, W.; Hong, S. Multi-Task Neural Processes. arXiv 2022, arXiv:2110.14953. [Google Scholar] [CrossRef]
- Wu, D.; Chinazzi, M.; Vespignani, A.; Ma, Y.A.; Yu, R. Multi-fidelity Hierarchical Neural Processes. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining. ACM, KDD ’22, Washington, DC, USA, 14–18 August 2022; pp. 2029–2038. [Google Scholar] [CrossRef]
- Williams, S.; Waterman, A.; Patterson, D. Roofline: An insightful visual performance model for multicore architectures. Commun. ACM 2009, 52, 65–76. [Google Scholar] [CrossRef]

| Group | Model Name | Depth [m] | Hull [m] | Sensors [#] | #Traj |
|---|---|---|---|---|---|
| Depth | MLP_7–5 m | 7.5 | 8 × 4 | 4 s | 100 |
| MLP_10 m | 10 | 8 × 4 | 4 s | 100 | |
| MLP_20 m | 20 | 8 × 4 | 4 s | 100 | |
| Size | MLP_2 × 1m | 20 | 2 × 1 | 4 s | 100 |
| MLP_4 × 2 m | 20 | 4 × 2 | 4 s | 100 | |
| MLP_8 × 4 m | 20 | 8 × 4 | 4 s | 100 | |
| Sensors | MLP_6 s | 20 | 8 × 4 | 6 s | 100 |
| MLP_5 s | 20 | 8 × 4 | 5 s | 100 | |
| MLP_4 s | 20 | 8 × 4 | 4 s | 100 |
| Model Name | Depth [m] | Hull [m] | Sensors [#] | #Traj |
|---|---|---|---|---|
| DRS-depth | {7.5, 10, 20} | 8 × 4 | 4 s | 300 |
| DRS-size | 20 | {2 × 1, 4×2, 8 × 4} | 4 s | 300 |
| DRS-sensors | 20 | 8 × 4 | {6 s, 5 s, 4 s} | 300 |
| DRS-general | {7.5, 10, 20} | {2 × 1, 4 × 2, 8 × 4} | {6 s, 5 s, 4 s} | 2700 |
| Validation Scenario | ANP | DRS-General |
|---|---|---|
| 10 m–2 m × 1 m | 0.35 | 0.59 |
| 10 m–4 m × 2 m | 0.36 | 0.65 |
| 10 m–8 m × 4 m | 0.45 | 0.72 |
| 20 m–2 m × 1 m | 0.52 | 1.40 |
| 20 m–4 m × 2 m | 0.42 | 1.26 |
| 20 m–8 m × 4 m | 0.56 | 0.86 |
| 7.5 m–2 m × 1 m | 0.36 | 0.70 |
| 7.5 m–4 m × 2 m | 0.40 | 0.64 |
| 7.5 m–8 m × 4 m | 0.51 | 0.78 |
| Method | Wilcoxon | Friedman | Mean MAE (m) |
|---|---|---|---|
| ANP | 1 | 0.5 | 0.435 |
| DRS-general | 0.0039 | 0.0027 | 0.844 |
| Model | 7.5 m | 10 m | 20 m | 30 m (OOD) |
|---|---|---|---|---|
| MLP_7-5m | 0.62 | 1.74 | 5.54 | 8.86 |
| MLP_10m | 1.85 | 0.75 | 4.62 | 8.01 |
| MLP_20m | 6.15 | 4.66 | 0.77 | 4.14 |
| DRS_depth | 0.84 | 0.84 | 1.19 | 3.82 |
| DRS_general | 0.93 | 0.98 | 1.04 | 4.36 |
| ANP | 0.46 | 0.38 | 0.48 | 2.62 |
| Model | Mean MAE (m) | Wilcoxon | Friedman |
|---|---|---|---|
| MLP_7-5m | 3.99 | 0.375 | 0.0138 * |
| MLP_10m | 3.68 | 0.375 | 0.0350 * |
| MLP_20m | 3.97 | 0.375 | 0.0467 * |
| DRS_depth | 1.83 | 0.375 | 0.0890 |
| DRS_general | 1.83 | 0.375 | 0.0565 |
| ANP | 0.99 | 1.000 | 0.500 |
| Model | 2 × 1 m | 4 × 2 m | 8 × 4 m | 20 × 10 m (OOD) |
|---|---|---|---|---|
| MLP_2x1m | 0.68 | 11.80 | 319.15 | 320.90 |
| MLP_4x2m | 11.68 | 1.07 | 132.66 | 133.53 |
| MLP_8x4m | 221.09 | 196.39 | 0.48 | 7.89 |
| DRS_size | 1.19 | 1.08 | 0.69 | 7.90 |
| DRS_general | 2.11 | 2.04 | 1.04 | 4.80 |
| ANP | 0.37 | 0.30 | 0.41 | 3.56 |
| Model | Mean MAE (m) | Wilcoxon | Friedman |
|---|---|---|---|
| MLP_2x1m | 163.13 | 0.375 | 0.0138 * |
| MLP_4x2m | 69.74 | 0.375 | 0.0350 * |
| MLP_8x4m | 106.46 | 0.375 | 0.0350 * |
| DRS_size | 2.72 | 0.375 | 0.0890 |
| DRS_general | 2.50 | 0.375 | 0.0882 |
| ANP | 1.16 | 1.000 | 0.500 |
| Model | 6 s | 5 s | 4 s | 3 s (OOD) |
|---|---|---|---|---|
| MLP_6s | 0.52 | 101.09 | 143.31 | 77.02 |
| MLP_5s | 38.93 | 0.50 | 58.92 | 63.31 |
| MLP_4s | 77.24 | 51.71 | 0.68 | 61.39 |
| DRS_sensors | 0.29 | 0.23 | 0.25 | 69.48 |
| DRS_general | 0.68 | 0.73 | 1.04 | 139.10 |
| ANP | 0.44 | 0.34 | 0.39 | 72.42 |
| Model | Mean MAE (m) | Wilcoxon | Friedman |
|---|---|---|---|
| MLP_6s | 80.48 | 0.375 | 0.0245 * |
| MLP_5s | 40.41 | 0.5625 | 0.1779 |
| MLP_4s | 47.76 | 0.5625 | 0.1779 |
| DRS_sensors | 17.56 | 1.000 | 0.500 |
| DRS_general | 35.39 | 0.375 | 0.0584 |
| ANP | 18.90 | 0.375 | 0.4497 |
| Method | Mean MAE (m) | Wilcoxon | Friedman |
|---|---|---|---|
| ANP | 6.58 | 1.00 | 0.50 |
| DRS_general | 13.24 | 0.0034 | 0.0327 |
| DRS_depth | 139.63 | 0.0244 | 0.0029 |
| DRS_size | 32.55 | 0.0034 | 0.0102 |
| DRS_sensors | 63.58 | 0.0244 | 0.0327 |
| MLP_7-5m | 52.69 | 0.0034 | 0.0043 |
| MLP_10m | 202.90 | 0.0034 | 0.0001 |
| MLP_20m | 48.36 | 0.0034 | 0.0294 |
| MLP_2x1m | 289.45 | 0.0034 | <0.0001 |
| MLP_4x2m | 134.53 | 0.0034 | <0.0001 |
| MLP_8x4m | 73.80 | 0.0034 | 0.0053 |
| MLP_6s | 132.12 | 0.0034 | <0.0001 |
| MLP_5s | 88.33 | 0.0037 | 0.0001 |
| MLP_4s | 56.28 | 0.0244 | 0.0135 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernández-Salvador, L.F.; Vilallonga Tejela, B.; Almodóvar, A.; Parras, J.; Zazo, S. Attentive Neural Processes for Few-Shot Learning Anomaly-Based Vessel Localization Using Magnetic Sensor Data. J. Mar. Sci. Eng. 2025, 13, 1627. https://doi.org/10.3390/jmse13091627
Fernández-Salvador LF, Vilallonga Tejela B, Almodóvar A, Parras J, Zazo S. Attentive Neural Processes for Few-Shot Learning Anomaly-Based Vessel Localization Using Magnetic Sensor Data. Journal of Marine Science and Engineering. 2025; 13(9):1627. https://doi.org/10.3390/jmse13091627
Chicago/Turabian StyleFernández-Salvador, Luis Fernando, Borja Vilallonga Tejela, Alejandro Almodóvar, Juan Parras, and Santiago Zazo. 2025. "Attentive Neural Processes for Few-Shot Learning Anomaly-Based Vessel Localization Using Magnetic Sensor Data" Journal of Marine Science and Engineering 13, no. 9: 1627. https://doi.org/10.3390/jmse13091627
APA StyleFernández-Salvador, L. F., Vilallonga Tejela, B., Almodóvar, A., Parras, J., & Zazo, S. (2025). Attentive Neural Processes for Few-Shot Learning Anomaly-Based Vessel Localization Using Magnetic Sensor Data. Journal of Marine Science and Engineering, 13(9), 1627. https://doi.org/10.3390/jmse13091627






