An Adaptive Dual-Channel Underwater Target Detection Method Based on a Vector Cross-Trispectrum Diagonal Slice
Abstract
1. Introduction
2. Theoretical Background
2.1. Target Detection via Pressure–Velocity Correlation
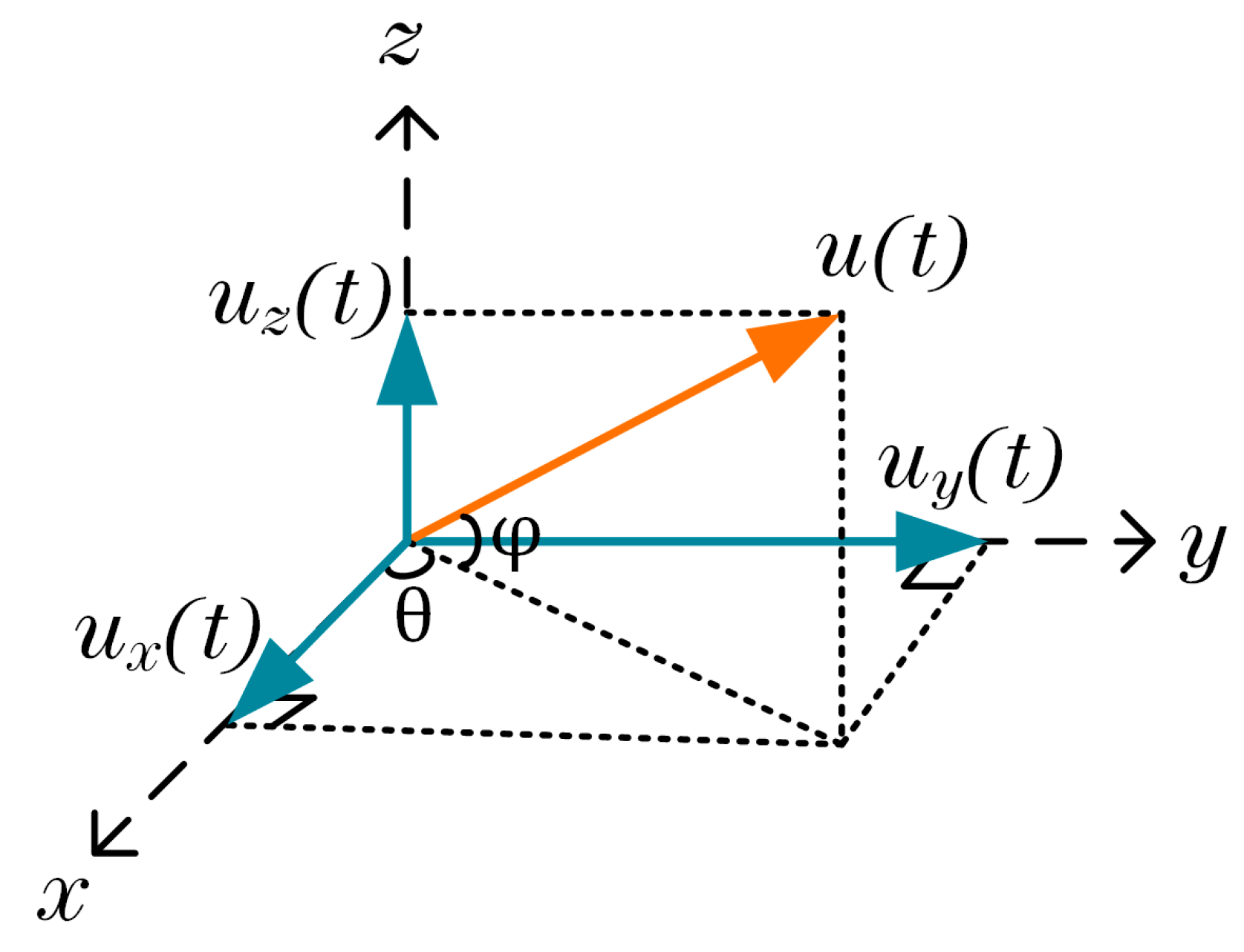
2.1.1. Signal Model for a Single Vector Hydrophone
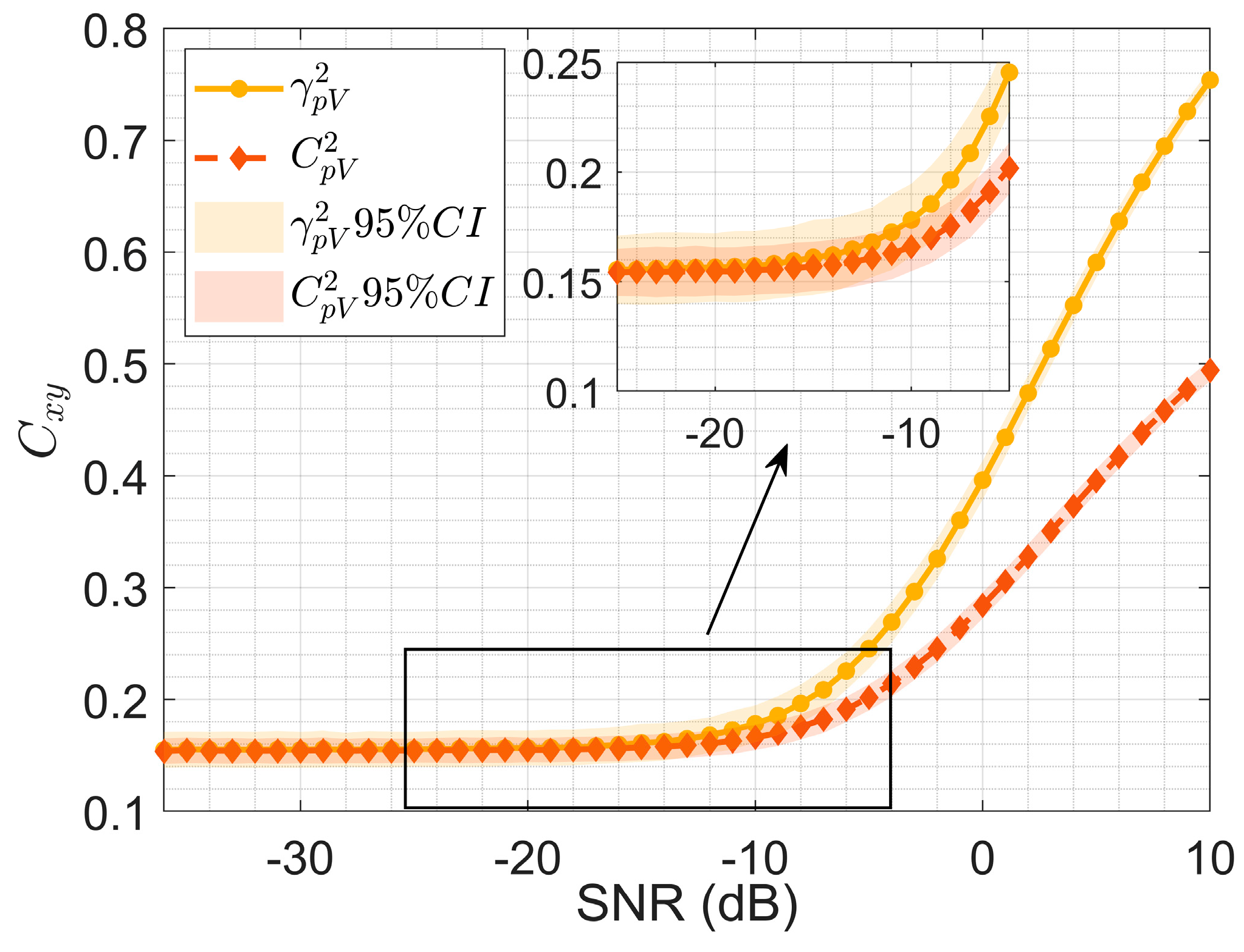
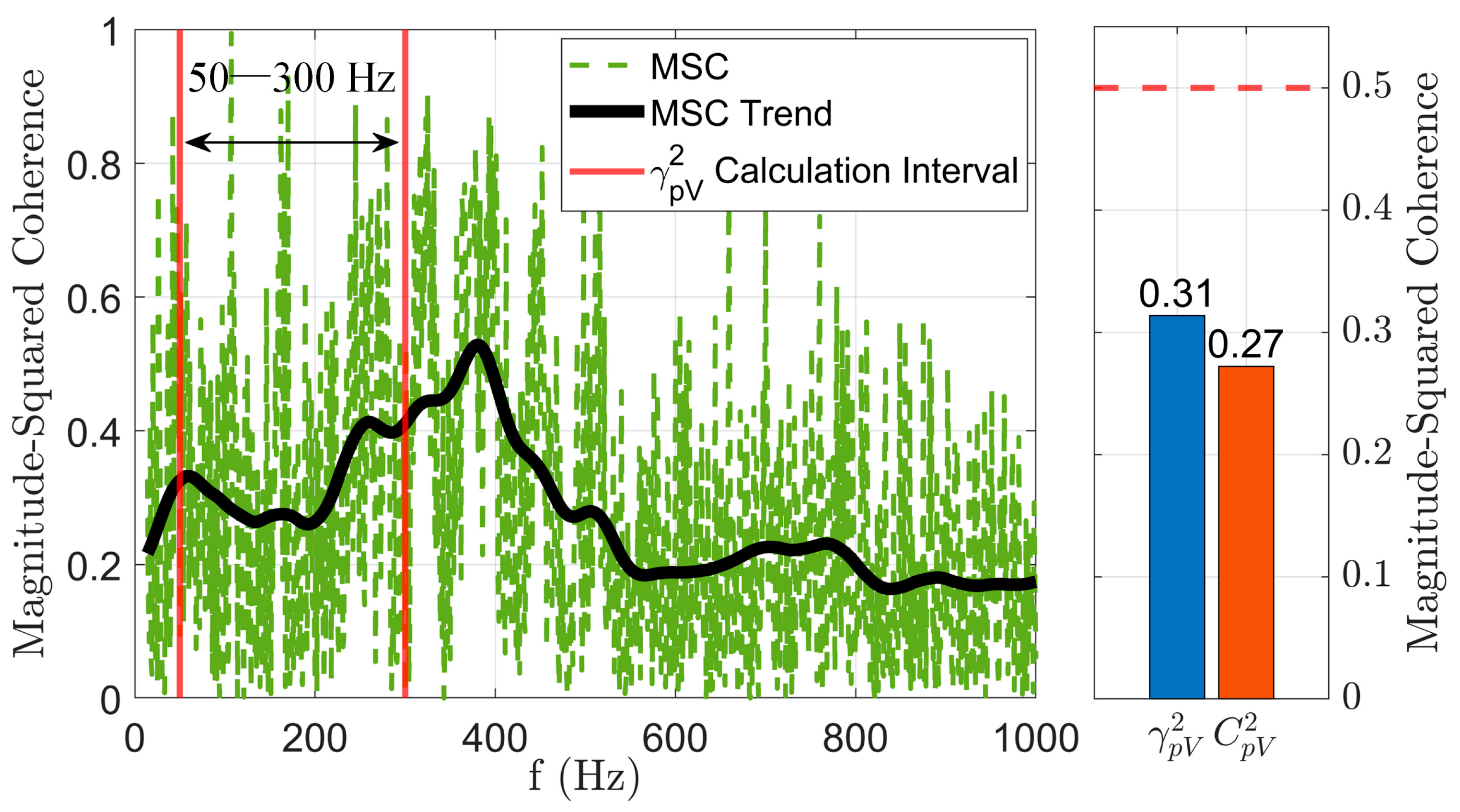
2.1.2. Coherence of Sound Pressure and Particle Velocity
2.2. Vector Cross-Trispectrum Diagonal Slice Detection
2.2.1. Definition of the Vector Cross-Trispectrum Diagonal Slice
2.2.2. The Vector Cross-Trispectrum Diagonal Slice of Gaussian Signals
2.3. Line Spectrum Detection
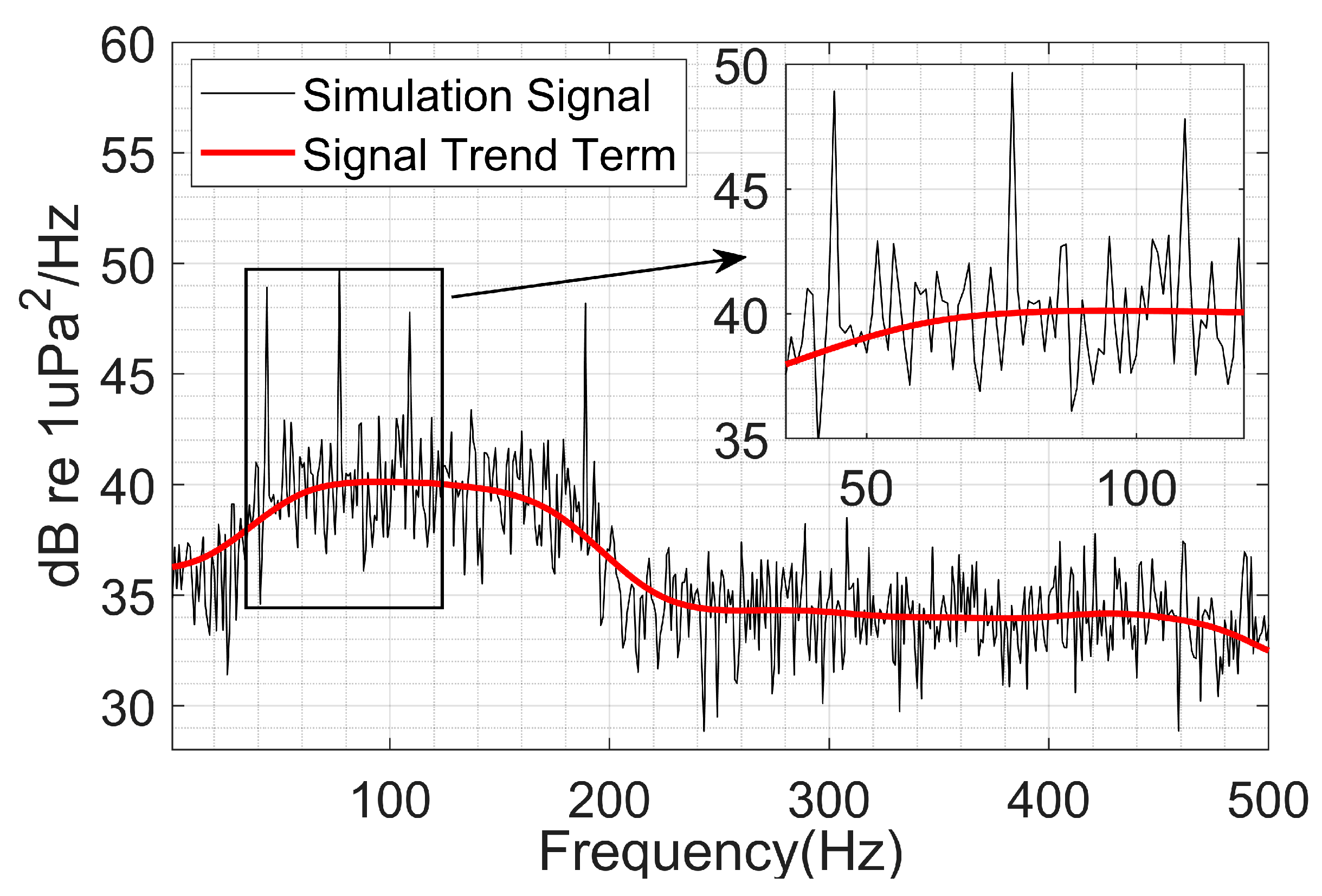
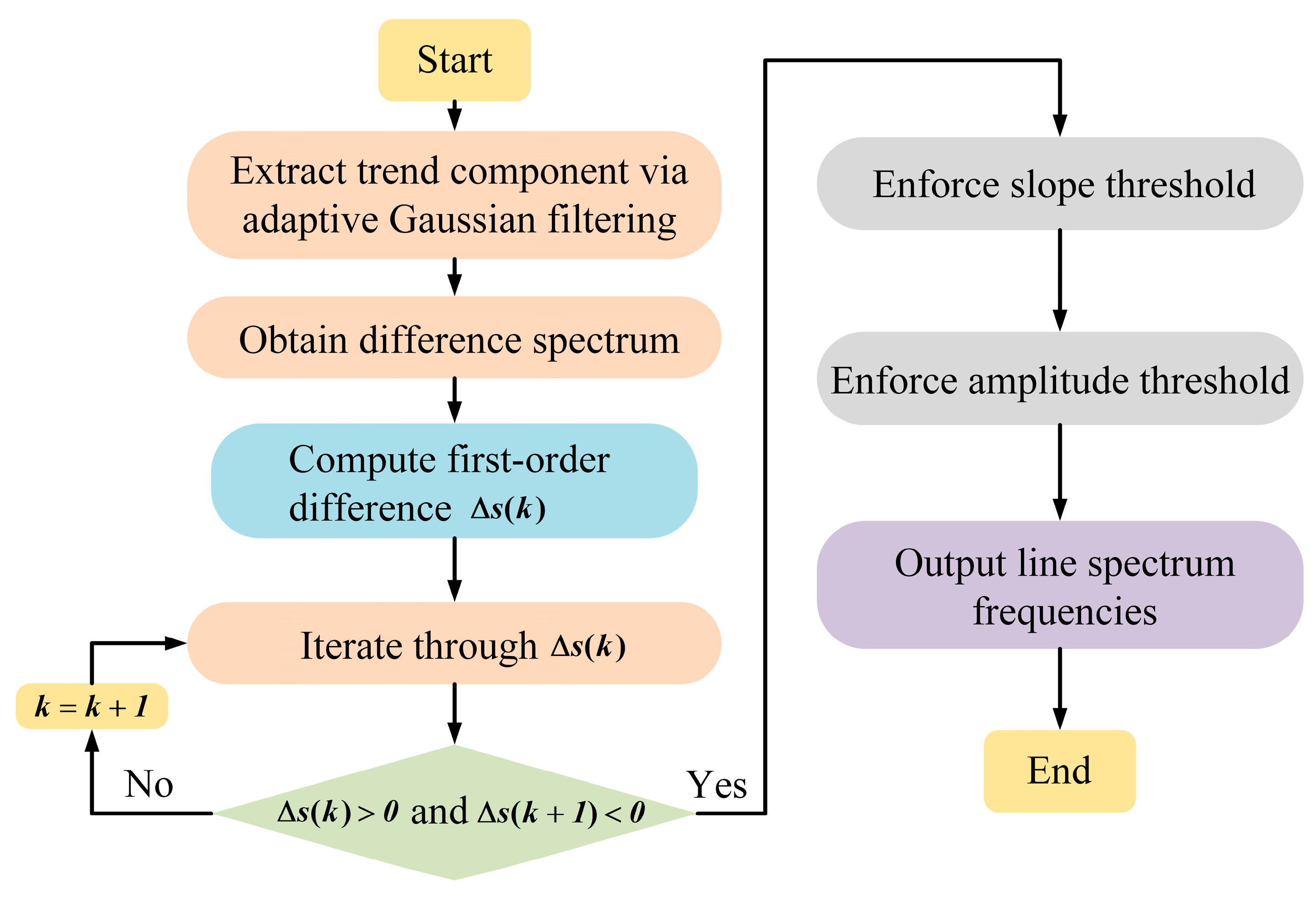
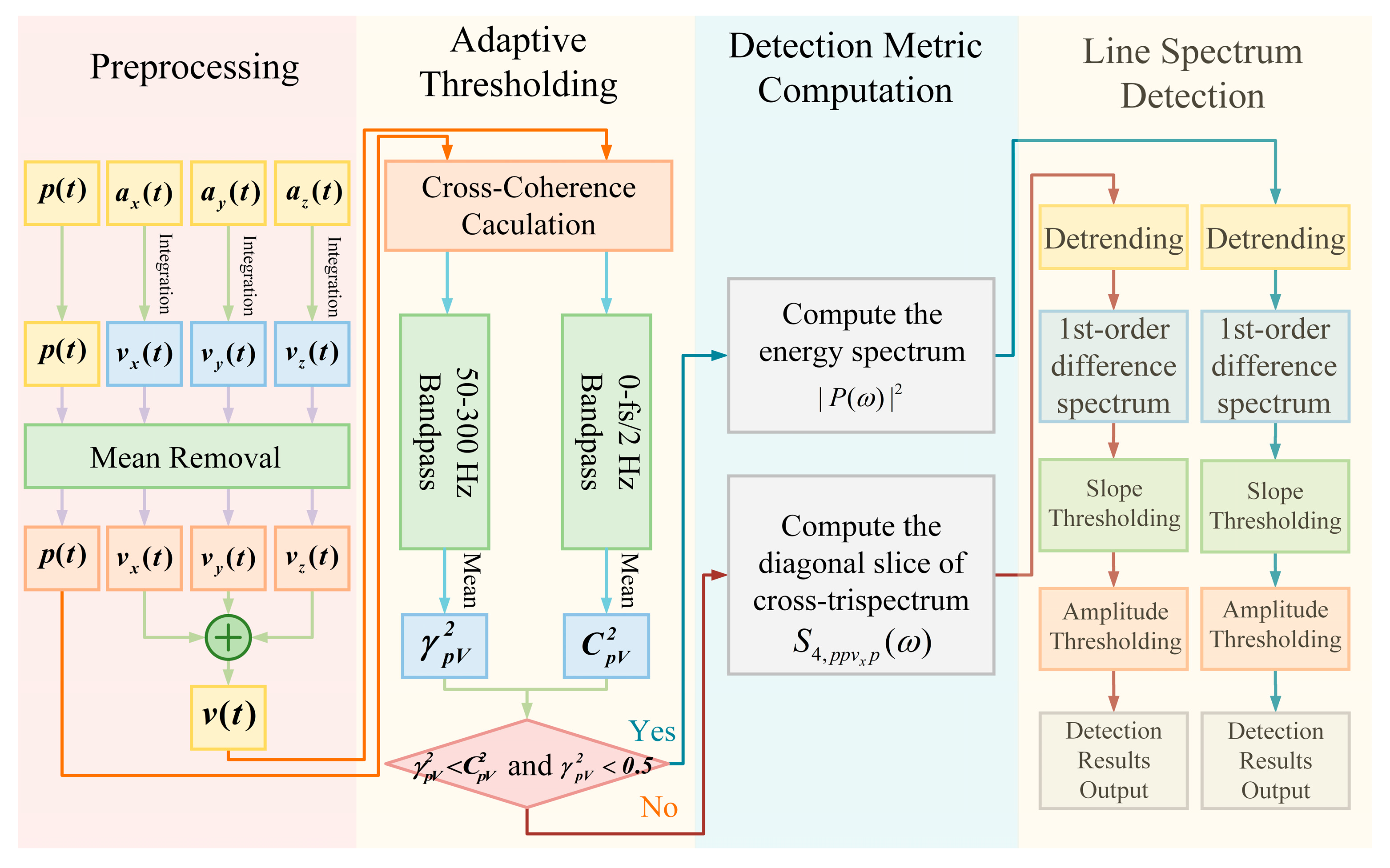
2.3.1. Preprocessing for Line Spectrum Detection
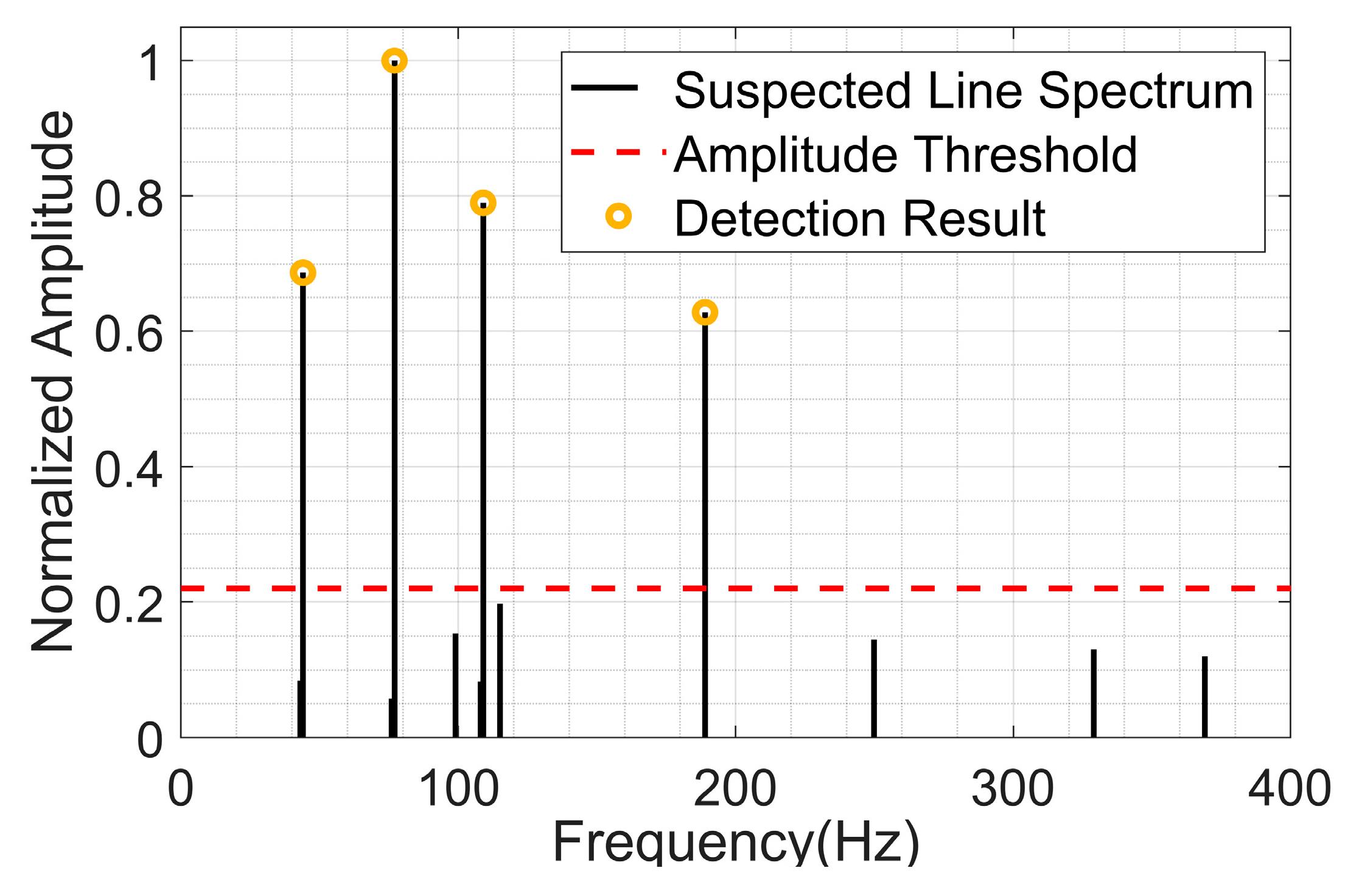
2.3.2. Principles of Line Spectrum Detection
3. Proposed Detection Method
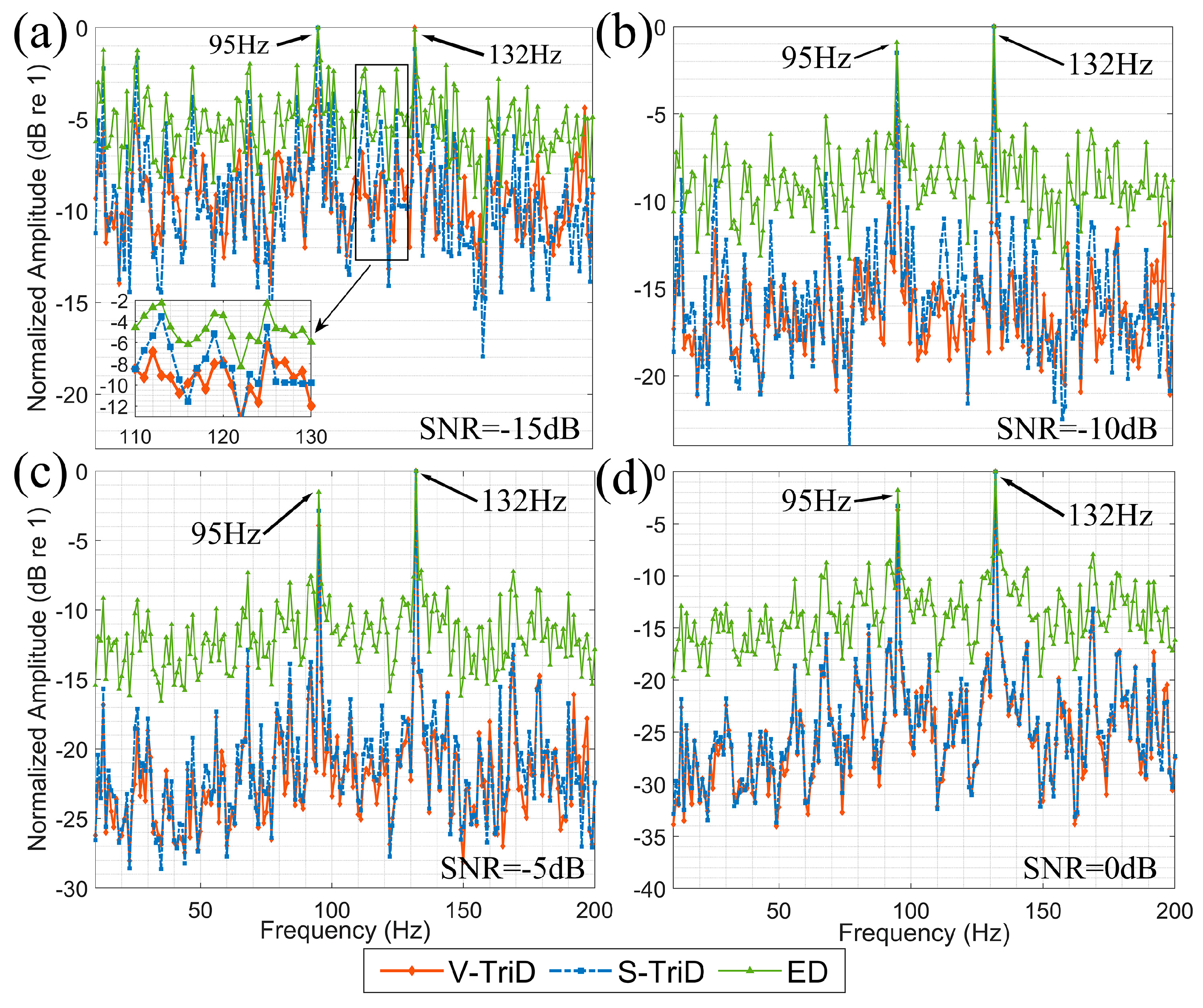
4. Simulation Experiments
- (a)
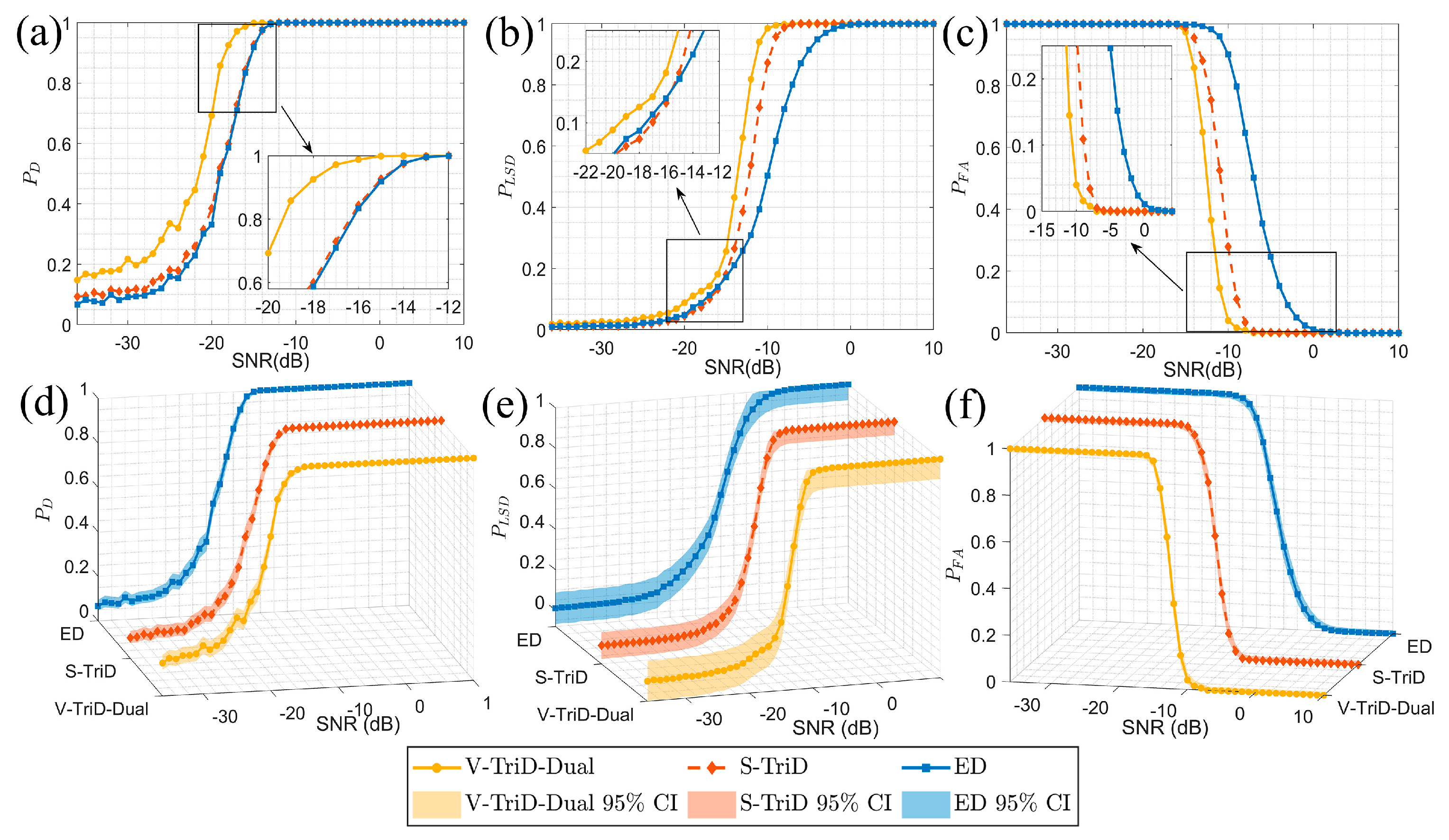
- Probability of Detection (): The ratio of trials in which the target frequency components are correctly detected to the total number of Monte Carlo trials.
- (b)
- Effective Detection Rate of Target Line Spectra (): This metric assesses the purity of the detection results. For a single trial , it is the ratio of the number of detected target line spectra to the total number of detected line spectra. The final is the average over all trials: .
- (c)
- Probability of False Alarm (): The ratio of trials containing one or more erroneously detected non-target frequency components to the total number of Monte Carlo trials.
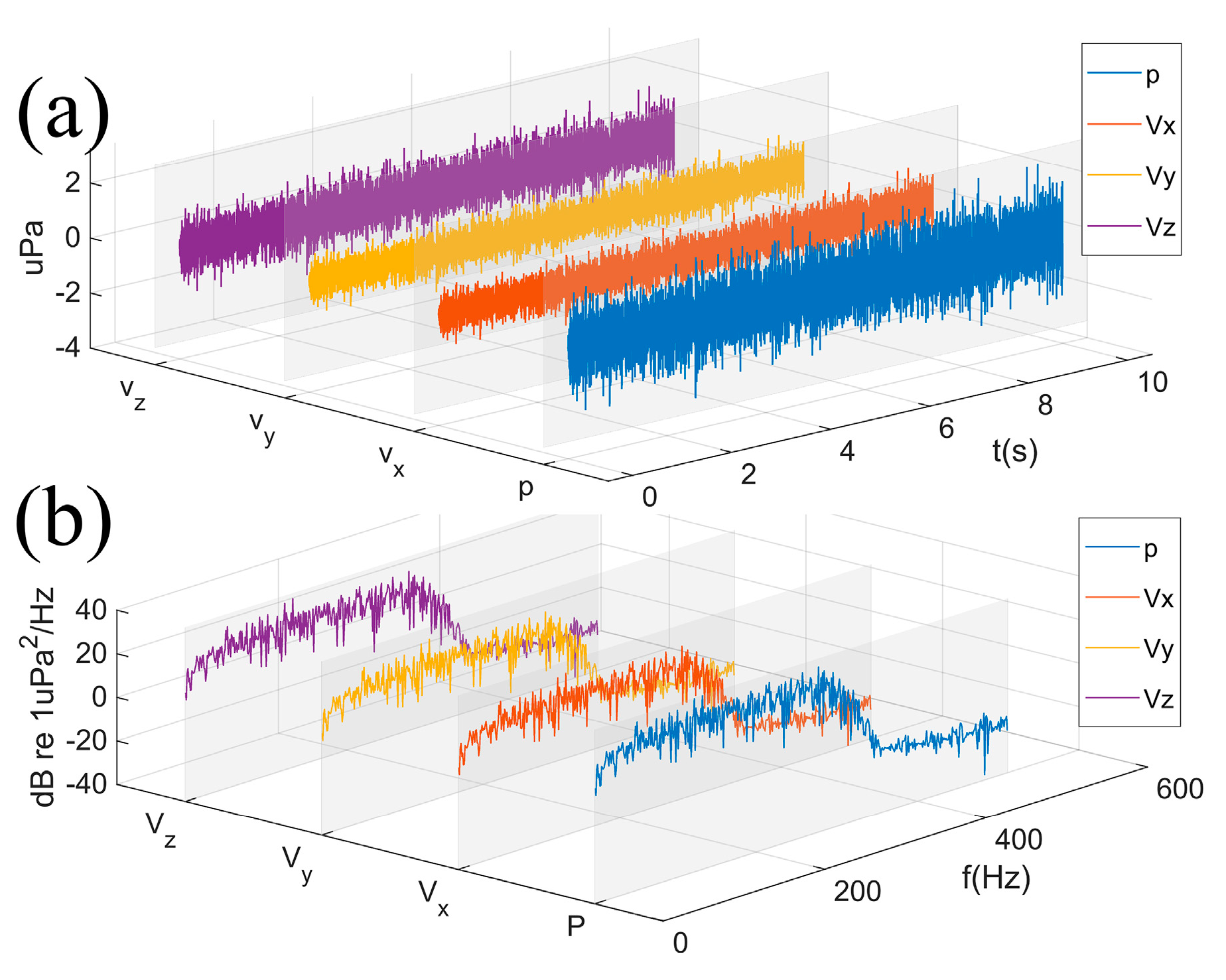
5. Experimental Analysis
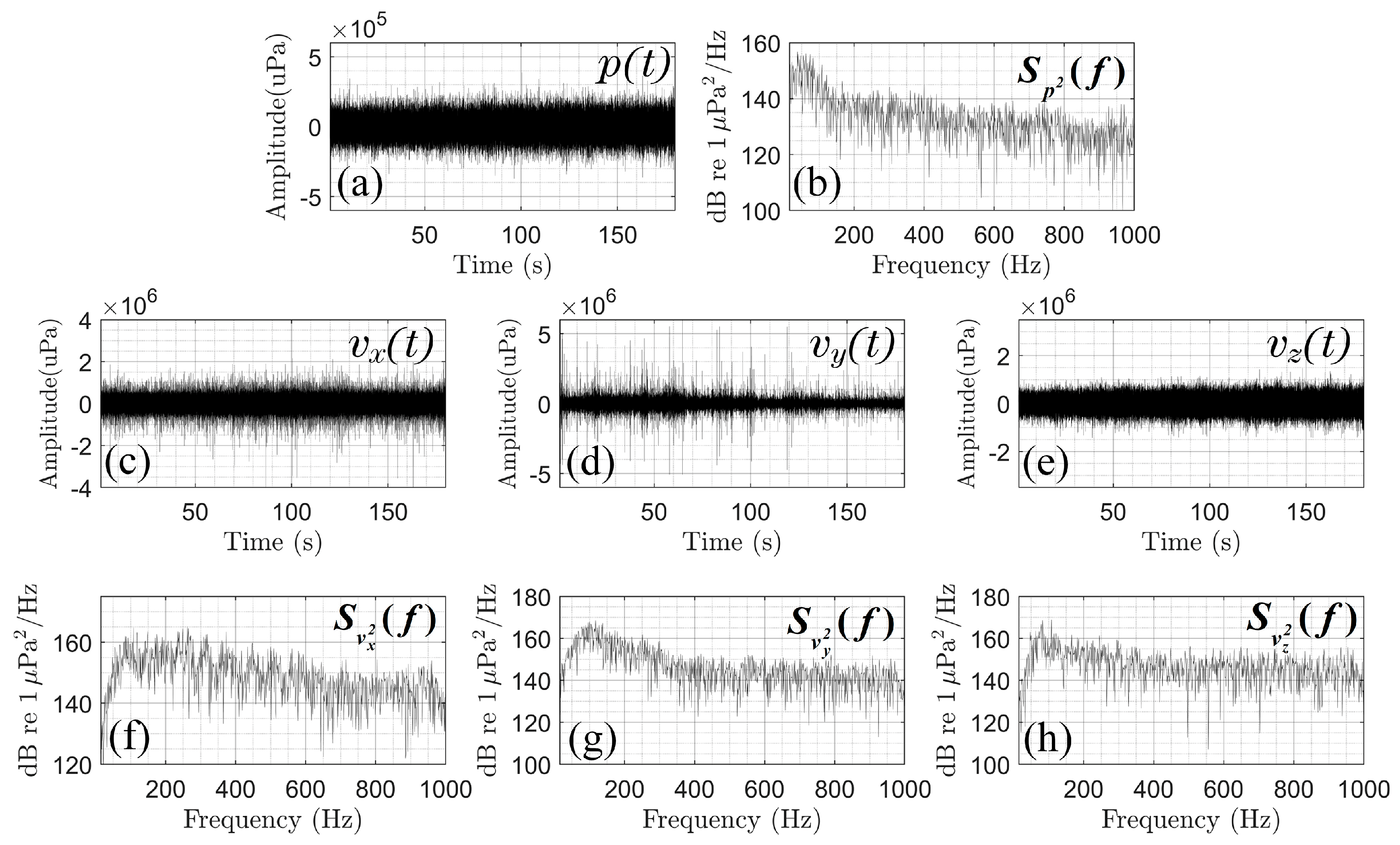
5.1. Basic Experimental Settings
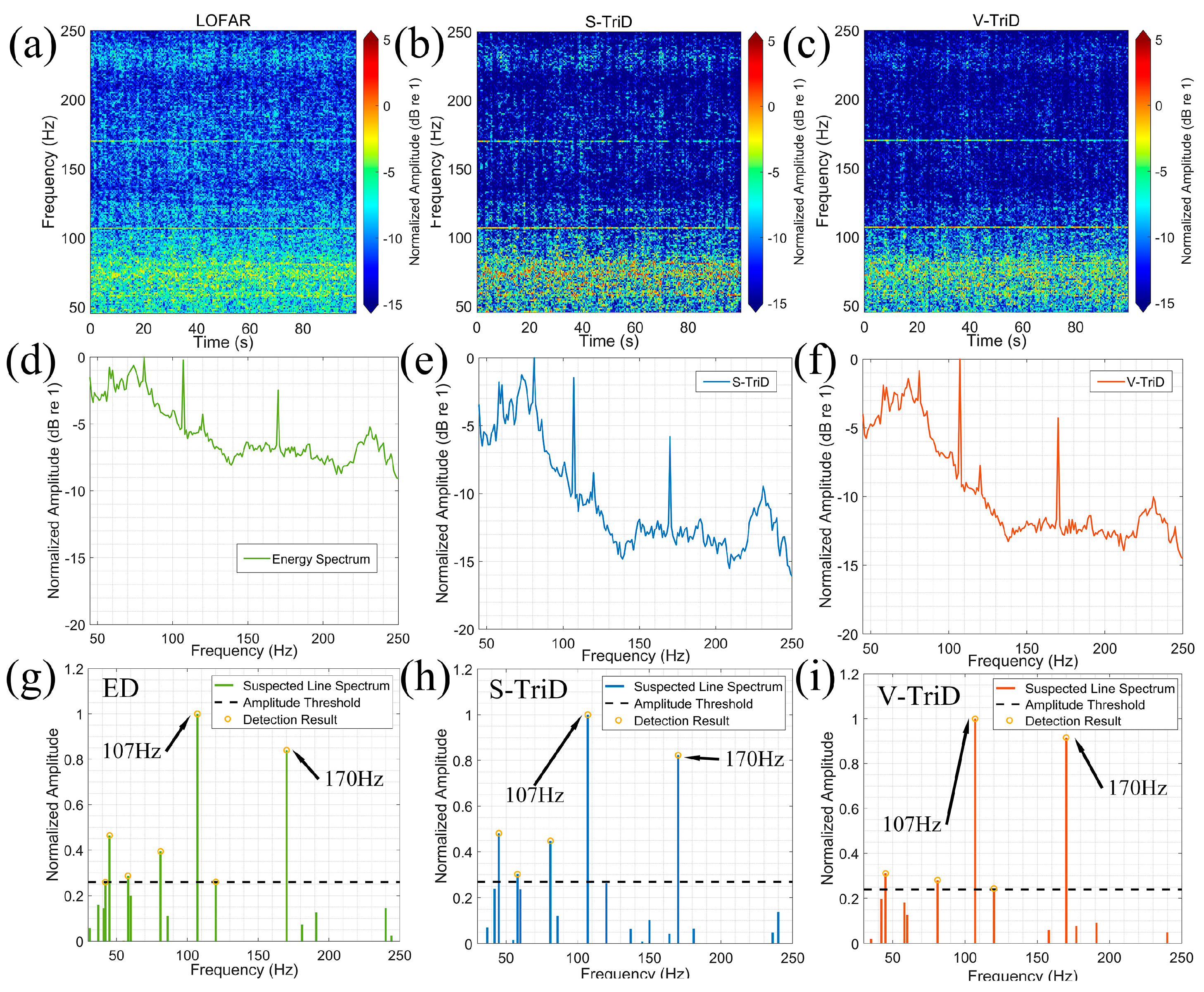
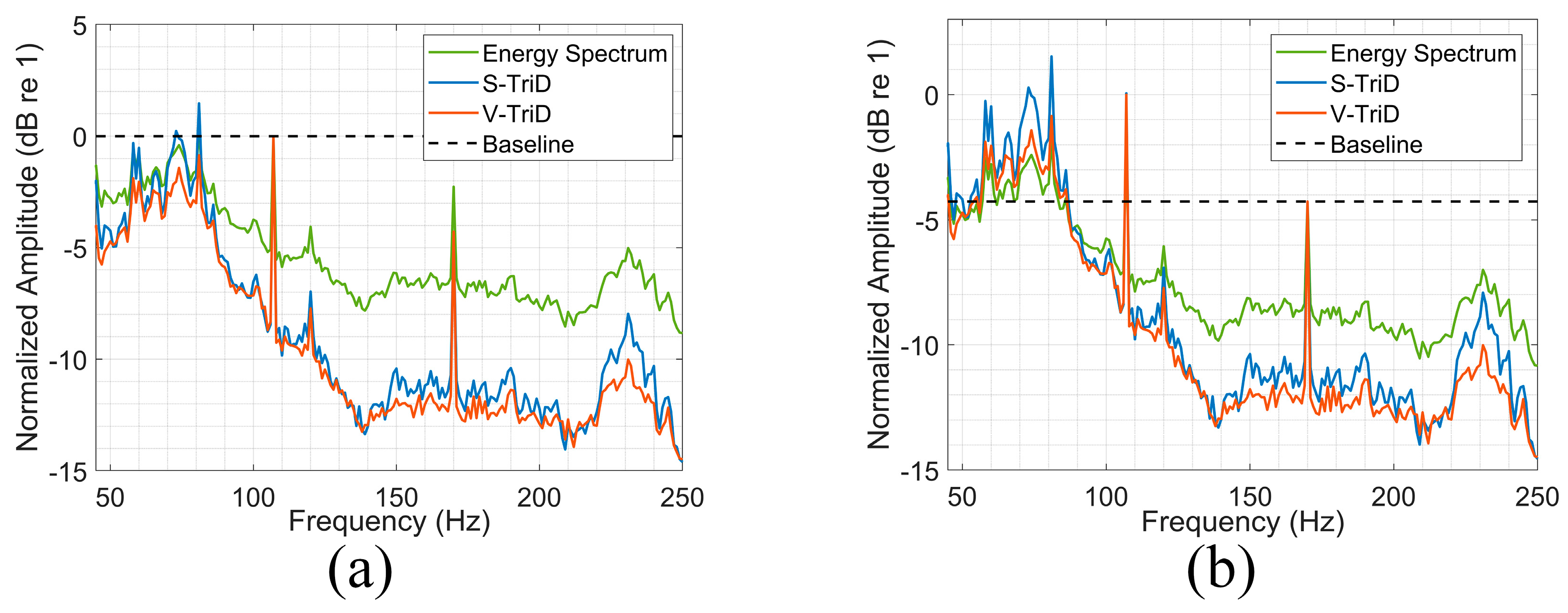
5.2. Processing Results
6. Discussion
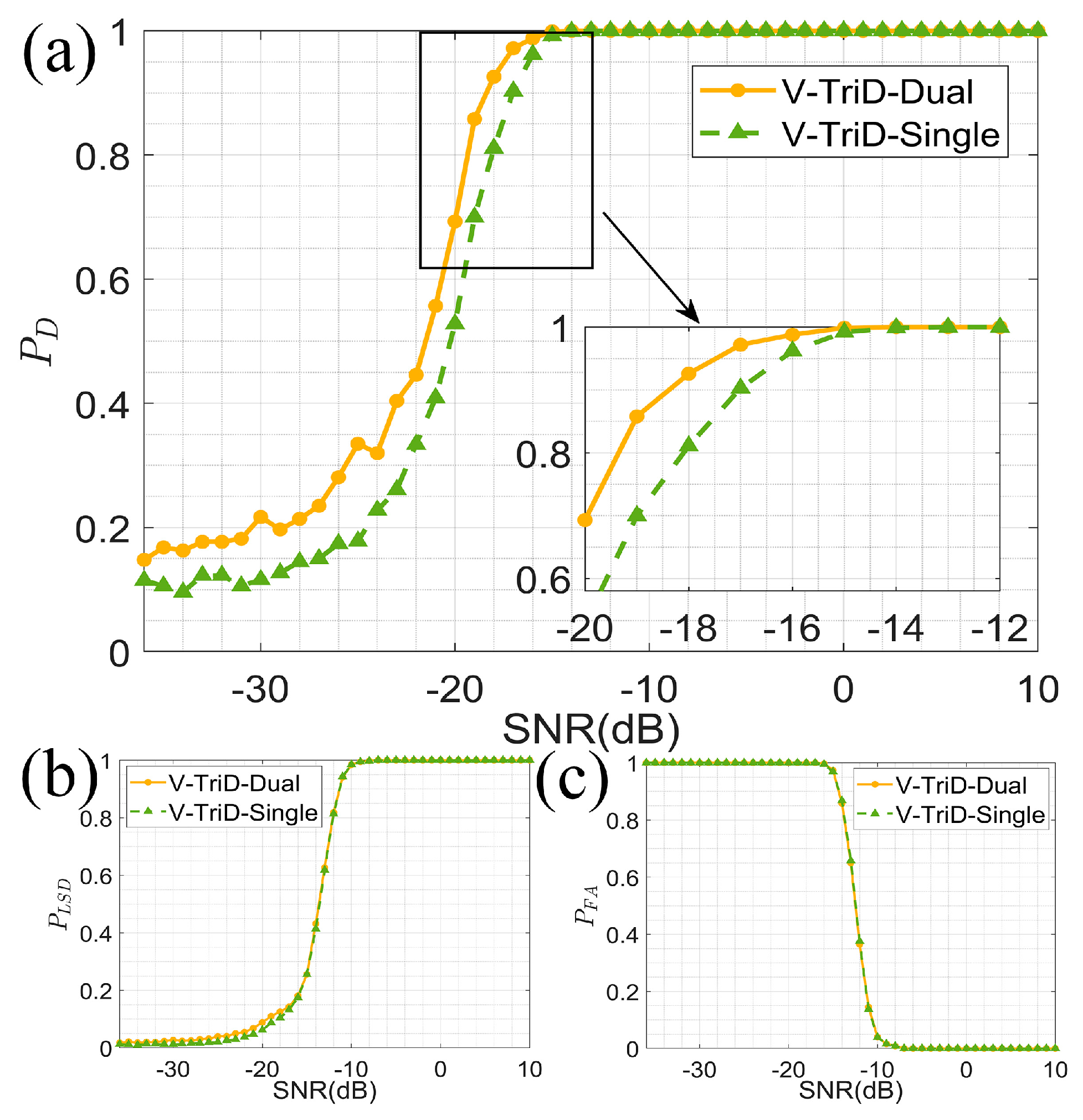
6.1. Performance Analysis
6.2. Limitations and Future Work
7. Conclusions
- (1)
- A metric, termed the vector cross-trispectrum diagonal slice (V-TriD), was formulated and theoretically derived. This metric is constructed by jointly processing the acoustic pressure and composite particle velocity signals from a vector hydrophone. Its formulation utilizes the mutual coherence between these components to enhance the discrimination between signal and noise.
- (2)
- An adaptive dual-channel detection framework, V-TriD-Dual, was developed. It incorporates a channel selection discriminator that employs a dynamic threshold based on signal coherence. This allows the system to automatically select the more suitable processing path (V-TriD or energy detection) for the given conditions without manual intervention. The computational efficiency of the proposed method is comparable to that of a traditional single-channel technique, as only one processing path is active at any given moment. This characteristic makes the algorithm well suited for applications that require real-time detection capabilities.
- (3)
- The performance of the V-TriD-Dual method was evaluated through both simulation and sea trial analysis. Its effectiveness is rooted in an adaptive framework that leverages the V-TriD channel’s noise suppression capabilities in high-coherence scenarios while switching to the robust ED channel when coherence is low. This adaptability yields quantifiable performance gains across key metrics. Simulation results demonstrate that at an SNR of −18 dB, the detection probability (PD) increased by 57.8% over the ED method. Concurrently, the method provides superior false alarm suppression: its false alarm rate (PFA) was 0.040 at an SNR of −10 dB (a reduction of 0.861 and 0.239 relative to the ED and S-TriD methods, respectively) and reached zero by −5 dB, a level of reliability not matched by the competing detectors. The practical viability of this adaptive approach was subsequently confirmed through the analysis of the sea trial data.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DOA | Direction of Arrival |
| SNR | Signal-to-Noise Ratio |
| ED | Energy Spectrum Detection |
| S-TriD | Scalar Cross-Trispectrum Diagonal Slice Detection |
| V-TriD | Vector Cross-Trispectrum Diagonal Slice Detection |
| V-TriD-Single | Vector Cross-Trispectrum Diagonal Slice Single-Channel Detection |
| V-TriD-Dual | Vector Cross-Trispectrum Diagonal Slice Dual-Channel Detection |
| CI | Confidence Interval |
References
- Luo, J.; Han, Y.; Fan, L. Underwater Acoustic Target Tracking: A Review. Sensors 2018, 18, 112. [Google Scholar] [CrossRef]
- Sahoo, S.; Mohanta, R.K.; Pani, P.P.; Mohapatra, S.K.; Chakravarty, S. A Multi-Faceted Approach for Underwater Sonar Rock vs Mine Classification Using Machine Techniques. In Proceedings of the 2024 1st International Conference on Cognitive, Green and Ubiquitous Computing (IC-CGU), Bhubaneswar, India, 1–2 March 2024; pp. 1–5. [Google Scholar]
- Jin, A.; Zeng, X. A Novel Deep Learning Method for Underwater Target Recognition Based on Res-Dense Convolutional Neural Network with Attention Mechanism. JMSE 2023, 11, 69. [Google Scholar] [CrossRef]
- Ji, Y.; Xie, L.; Xu, G.; Zhu, Z.; Gu, Y.; Fei, J.; Li, Y.; Chen, Y.; Cai, K. Sonar image denoising based on Noise2Void self-supervised learning. Remote Sens. Lett. 2025, 16, 560–571. [Google Scholar] [CrossRef]
- Yu, T.; Xie, Y.; Luo, J.; Zhu, W.; Liu, J. Research on underwater disease target detection method of inland waterway based on deep learning. Sci. Rep. 2025, 15, 14072. [Google Scholar] [CrossRef] [PubMed]
- Dong, H.; Ma, S.; Suo, J.; Zhu, Z. Matched Stochastic Resonance Enhanced Underwater Passive Sonar Detection under Non-Gaussian Impulsive Background Noise. Sensors 2024, 24, 2943. [Google Scholar] [CrossRef] [PubMed]
- Mendel, J.M. Tutorial on higher-order statistics (spectra) in signal processing and system theory: Theoretical results and some applications. Proc. IEEE 1991, 79, 278–305. [Google Scholar] [CrossRef]
- Petropulu, A.P. Higher-Order Spectral Analysis; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Li, Z.; Cheng, Y.; Qiu, J. Adaptive Line Enhancer for Passive Sonars Based on Frequency-Domain Sparsity, Shannon Entropy Criterion and Mixed-Weighted Error. Arab. J. Sci. Eng. 2025, 50, 5899–5920. [Google Scholar] [CrossRef]
- Tufts, D.W.; Griffiths, L.J.; Widrow, B.; Glover, J.; McCool, J.; Treichler, J. Adaptive line enhancement and spectrum analysis. Proc. IEEE 1977, 65, 169–173. [Google Scholar] [CrossRef]
- Widrow, B.; Glover, J.R.; McCool, J.M.; Kaunitz, J.; Williams, C.S.; Hearn, R.H.; Zeidler, J.R.; Eugene, D., Jr.; Goodlin, R.C. Adaptive noise cancelling: Principles and applications. Proc. IEEE 1975, 63, 1692–1716. [Google Scholar] [CrossRef]
- Kazemi, R.; Farsi, A.; Ghaed, M.H.; Karimi-Ghartemani, M. Detection and extraction of periodic noises in audio and biomedical signals using Kalman filter. Signal Process. 2008, 88, 2114–2121. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Y.; Ali, W.; Liu, L. Line Spectrum Enhancement of Underwater Acoustic Signals Using Kalman Filter. J. Mar. Sci. Appl. 2020, 19, 148–154. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, Q.; Xia, Z.; Shang, D. A Single-Hydrophone Coherent-Processing Method for Line-Spectrum Enhancement. Remote Sens. 2023, 15, 659. [Google Scholar] [CrossRef]
- Li, G.; Liu, F.; Yang, H. A new detection model of ship-radiated noise signal. Ocean. Eng. 2024, 297, 117081. [Google Scholar] [CrossRef]
- Li, H.; Liu, Y.; Ye, Z.; Zhang, Q.; Yang, S.; Xu, M. Underwater target detection using hybrid carbon nanotube self-adhesive sensors. Device 2024, 2, 100223. [Google Scholar] [CrossRef]
- Santos, P.; Felisberto, P.; Jesus, S.M. Vector Sensor Arrays in Underwater Acoustic Applications. In Emerging Trends in Technological Innovation; Camarinha-Matos, L.M., Pereira, P., Ribeiro, L., Eds.; IFIP Advances in Information and Communication Technology; Springer: Berlin/Heidelberg, Germany, 2010; Volume 314, pp. 316–323. ISBN 978-3-642-11627-8. [Google Scholar]
- Nehorai, A.; Paldi, E. Acoustic vector-sensor array processing. IEEE Trans. Signal Process. 1994, 42, 2481–2491. [Google Scholar] [CrossRef]
- Dahl, P.H.; Dall’Osto, D.R. Range-Dependent Inversion for Seabed Parameters Using Vector Acoustic Measurements of Underwater Ship Noise. IEEE J. Oceanic Eng. 2022, 47, 680–689. [Google Scholar] [CrossRef]
- Dahl, P.H.; Dall’Osto, D.R. Vector Acoustic Analysis of Time-Separated Modal Arrivals From Explosive Sound Sources During the 2017 Seabed Characterization Experiment. IEEE J. Oceanic Eng. 2020, 45, 131–143. [Google Scholar] [CrossRef]
- Dahl, P.H.; Bonnel, J. Vector acoustic and polarization properties of underwater ship noise. J. Acoust. Soc. Am. 2022, 151, 3818–3827. [Google Scholar] [CrossRef] [PubMed]
- D’Spain, G.L.; Luby, J.C.; Wilson, G.R.; Gramann, R.A. Vector sensors and vector sensor line arrays: Comments on optimal array gain and detection. J. Acoust. Soc. Am. 2006, 120, 171–185. [Google Scholar] [CrossRef]
- Li, H.; Wang, T.; Guo, X.; Su, L.; Mo, Y. Application research on vector coherent frequency-domain batch adaptive line enhancement in deep water. IET Radar Sonar Navi. 2024, 18, 1859–1873. [Google Scholar] [CrossRef]
- Nikias, C.L.; Raghuveer, M.R. Bispectrum estimation: A digital signal processing framework. Proc. IEEE 1987, 75, 869–891. [Google Scholar] [CrossRef]
- Fan, Y.; Shang, J.; Sun, J.; Li, P.; Xu, J. Feature extraction of ship-radiated noise using higher-order spectrum. Chin. J. Acoust. 2000, 24, 159–165. [Google Scholar] [CrossRef]
- Jiang, H.; Xia, Y.; Wang, X. Rolling bearing fault detection using an adaptive lifting multiwavelet packet with a dimension spectrum. Meas. Sci. Technol. 2013, 24, 125002. [Google Scholar] [CrossRef]
- Shen, X.; Bao, M.; Chen, Z.; Zhao, J.; Gao, Y. Fourth-Order Cumulant-Based Acoustic Imaging via Small-Aperture Acoustic Vector-Sensor Array. IEEE Trans. Instrum. Meas. 2024, 73, 1–12. [Google Scholar] [CrossRef]
- Hinich, M.J.; Marandino, D.; Sullivan, E.J. Bispectrum of Ship-Radiated Noise. J. Acoust. Soc. Am. 1988, 85, 127. [Google Scholar] [CrossRef]
- Bian, J.; Chang, Q.H.; Jing, J.Y. Fault Feature Detection of Rolling Bearing Based on LMD and Third-Order Cumulant Diagonal Slice Spectrum. AMM 2016, 851, 333–339. [Google Scholar] [CrossRef]
- Fan, Y.; Tao, B.; Xiong, K. A study of information included in FOC of harmonic signal. J. Astronaut. 2002, 23, 46–50. [Google Scholar]
- Bao, Z.; Gong, S.; Wu, Z.; Li, J. Line spectrum extraction of harmonic signals by using fourth-order cumulant slice spectrum. J. Nav. Univ. Eng. 2010, 53, 31–34. [Google Scholar]
- Chen, H.; Zhang, J.; Jiang, B.; Cui, X.; Zhou, R.; Zhang, Y. Multi-source underwater DOA estimation using PSO-BP neural network based on high-order cumulant optimization. China Commun. 2023, 20, 212–229. [Google Scholar] [CrossRef]
- Xing, C.; Dong, S.; Wan, Z. Direction-of-Arrival Estimation Based on Sparse Representation of Fourth-Order Cumulants. IEEE Access 2023, 11, 128736–128744. [Google Scholar] [CrossRef]
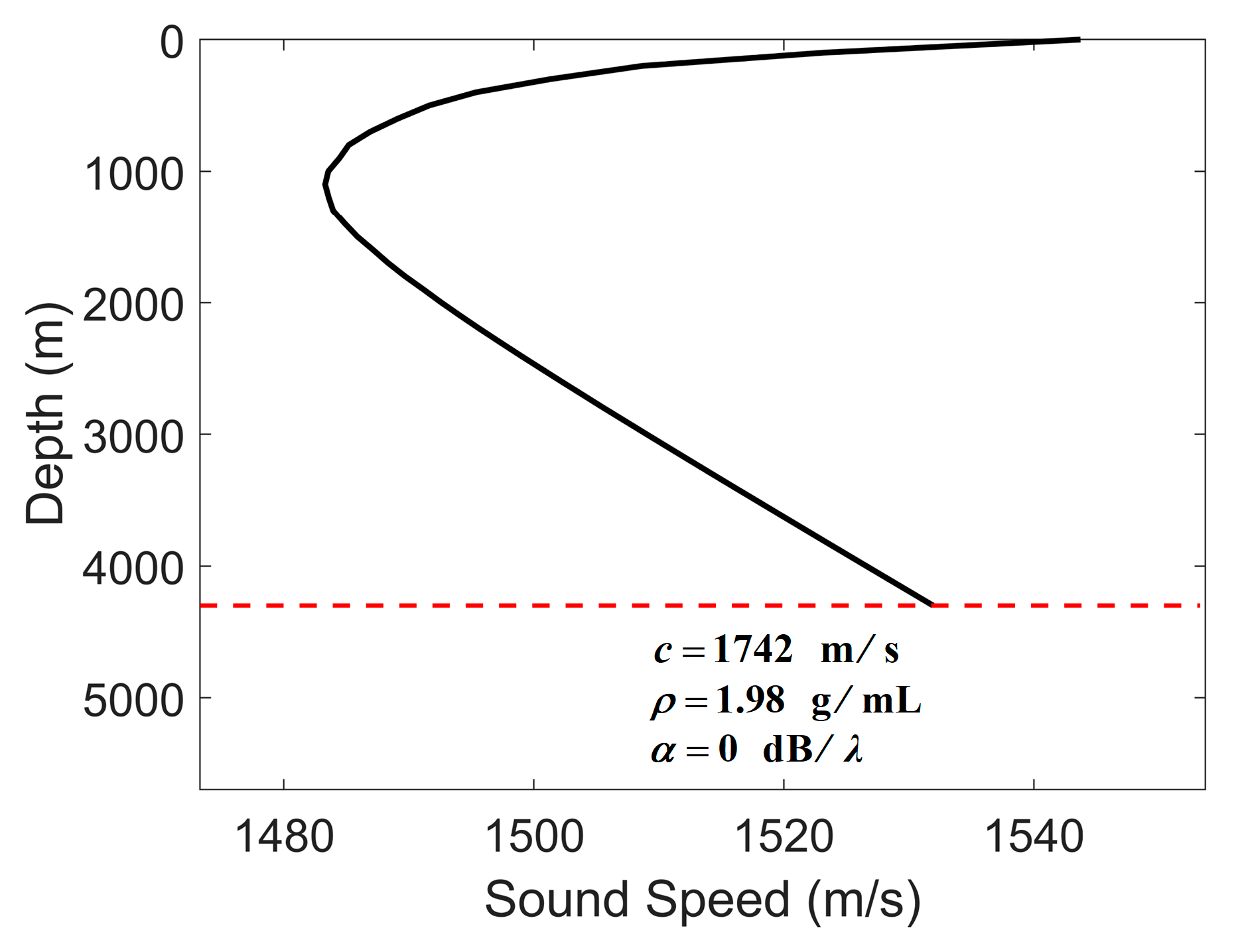
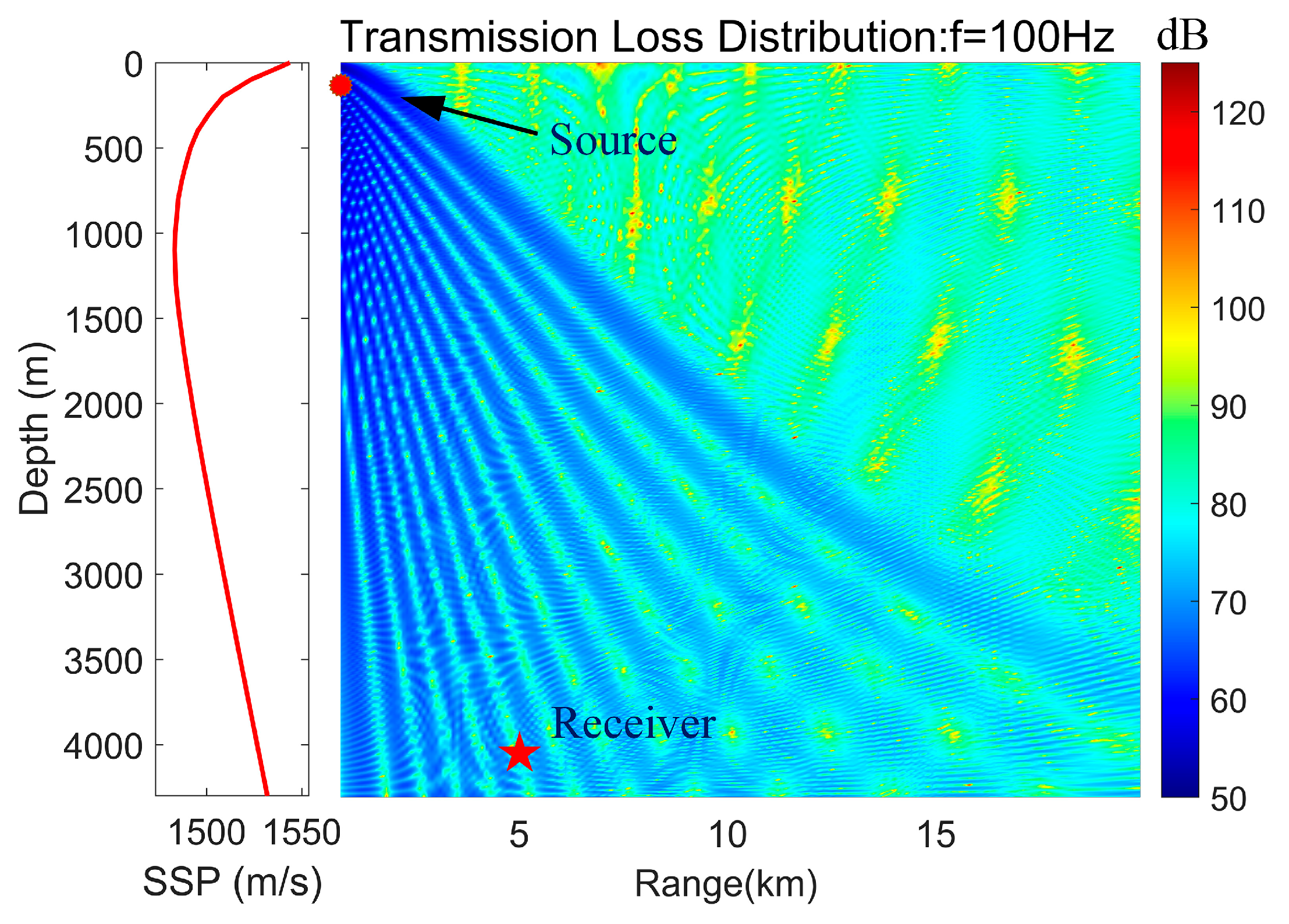


| Parameter | Value |
|---|---|
| Water depth | 4300 m |
| Source depth | 100 m |
| Source frequency (tonal) | 95 Hz, 132 Hz |
| Source frequency (broadband) | 1–512 Hz |
| Signal duration | 10 s |
| Sampling rate | 1024 Hz |
| Number of elements | 1 |
| Receiver depth | 4000 m |
| Horizontal range | 5000 m |
| SNR (dB) | ED | S-TriD | V-TriD-Single | V-TriD-Dual |
|---|---|---|---|---|
| −30 | 0.091 | 0.112 | 0.116 | 0.217 |
| −25 | 0.159 | 0.181 | 0.178 | 0.335 |
| −20 | 0.331 | 0.385 | 0.528 | 0.693 |
| −18 | 0.587 | 0.600 | 0.811 | 0.926 |
| −16 | 0.834 | 0.844 | 0.962 | 0.988 |
| −14 | 0.975 | 0.977 | 0.999 | 1 |
| −10 | 1 | 1 | 1 | 1 |
| SNR (dB) | ED | S-TriD | V-TriD-Single | V-TriD-Dual |
|---|---|---|---|---|
| −18 | 1 | 1 | 1 | 1 |
| −16 | 1 | 0. 997 | 0.995 | 0.997 |
| −14 | 0.998 | 0.955 | 0.868 | 0.858 |
| −12 | 0.983 | 0.754 | 0.376 | 0.365 |
| −10 | 0.901 | 0.279 | 0.039 | 0.040 |
| −5 | 0.246 | 0.001 | 0 | 0 |
| 0 | 0.011 | 0 | 0 | 0 |
| Parameter | Value |
|---|---|
| Programming Language | MATLAB 2024a |
| CPU | Intel(R) Core(TM) i5-10210U |
| Core Utilization Count | 1 |
| Memory | 32 GB |
| Operating System | Windows10 |
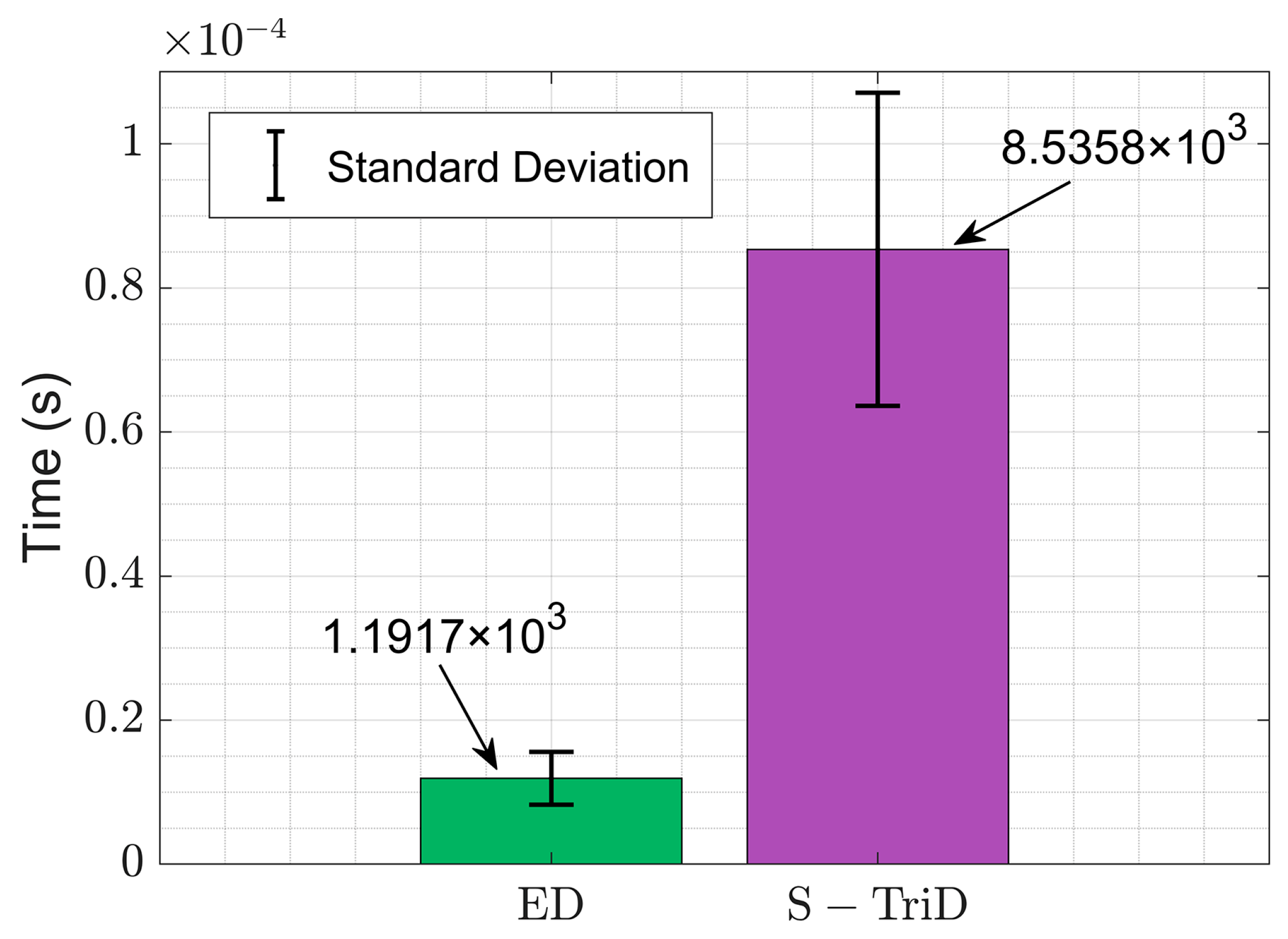
| Mean Computation Time (ED) | 1.1917 × 10−5 s |
| Mean Computation Time (S-TriD) | 8.5358 × 10−5 s |
| Variance of Computation Time (ED) | 1.3327 × 10−11 s2 |
| Variance of Computation Time (S-TriD) | 4.7248 × 10−10 s2 |
| Standard Deviation of Computation Time (ED) | 3.6506 × 10−6 s |
| Standard Deviation of Computation Time (S-TriD) | 2.1737 × 10−5 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Chen, Y.; Bian, Q.; Liu, Y.; Liang, Y.; Meng, Z. An Adaptive Dual-Channel Underwater Target Detection Method Based on a Vector Cross-Trispectrum Diagonal Slice. J. Mar. Sci. Eng. 2025, 13, 1628. https://doi.org/10.3390/jmse13091628
Zhang W, Chen Y, Bian Q, Liu Y, Liang Y, Meng Z. An Adaptive Dual-Channel Underwater Target Detection Method Based on a Vector Cross-Trispectrum Diagonal Slice. Journal of Marine Science and Engineering. 2025; 13(9):1628. https://doi.org/10.3390/jmse13091628
Chicago/Turabian StyleZhang, Weixuan, Yu Chen, Qiang Bian, Yuyao Liu, Yan Liang, and Zhou Meng. 2025. "An Adaptive Dual-Channel Underwater Target Detection Method Based on a Vector Cross-Trispectrum Diagonal Slice" Journal of Marine Science and Engineering 13, no. 9: 1628. https://doi.org/10.3390/jmse13091628
APA StyleZhang, W., Chen, Y., Bian, Q., Liu, Y., Liang, Y., & Meng, Z. (2025). An Adaptive Dual-Channel Underwater Target Detection Method Based on a Vector Cross-Trispectrum Diagonal Slice. Journal of Marine Science and Engineering, 13(9), 1628. https://doi.org/10.3390/jmse13091628








