Universal Screening Criteria for VIV of Free Spans, V*

Abstract

Vortex-induced vibrations (VIVs) pose significant risks to the structural integrity of subsea cables and pipelines under free-span conditions. It is extremely helpful to be able to screen for VIV and understand for a particular cable or pipeline what the minimum free-span threshold lengths are beyond which in-line and/or cross-flow VIV can be excited, causing fatigue problems. To date screening is a more complex and detailed task. This paper introduces a universal dimensionless velocity, V*, and one graph that can be used across all types of VIV free spans to quickly assess minimum free-span threshold lengths. Natural frequencies are not required to be calculated for screening each time, as they are implicit in the curve. The universal criteria are developed via non-dimensional analysis to establish the significant physical mechanisms, after which the relationships are populated, forming a single curve for in-line and for cross-flow VIV with a typical mass ratio and a conservative zero as-laid tension case.

1. Introduction

The VIV excitation of free spans poses an integrity concern for subsea power cables, umbilicals, flexible pipes and rigid pipelines.

An example power-cable VIV free-span problem is shown in Figure 1. Free spans can either be present from installation or can grow through seabed changes over time. A good overview of the issues and challenges of free spans is presented in [1], which also discusses advanced analysis techniques. Ref. [2] discusses model tests performed on cable spans with varying levels of tension and associated sag effects; this paper identifies the role of shifting modeshapes and natural frequencies when these effects are considered. The relatively complex techniques in [1] and ref. [2] are concerned with evaluating VIV response amplitudes and fatigue lives, whereas this current paper is only concerned with evaluating screening criteria to determine the necessary conditions for the onset of VIV.

In order to assess fatigue lives of free spans, one can turn to industry codes of practice [3] and analysis tools such as SHEAR7 [4] and FATFREE [5]. However, these can be relatively time-consuming exercises for a simple screening indication. These methods provide response predictions and can be used to compute estimated fatigue damage.

Prior to undertaking response predictions, it would be useful to have an expedient screening tool that identifies minimum critical free-span lengths or maximum onset velocities where VIV is predicted without resorting to these computationally intensive analysis tools. Up until now, there have not been universal screening criteria that allow a simple one-step check. Such a screening tool could be utilised during preliminary design stages or during operations where changes to seabed topology may require assessment of VIV predictions.

The Onset of VIV

A free span subject to a monotonically increasing current will generally experience the onset of in-line VIV prior to the onset of cross-flow VIV. This is because vortex shedding causes two in-line direction cycles of excitation for every one cross-flow cycle of excitation.

The onset of VIV is typically assessed by the coinciding of an excitation frequency with a natural frequency (including tolerance, or bandwidth). Typically, for fatigue-sensitive structures, an operating philosophy can involve avoiding in-line VIV altogether by keeping the excitation frequency always lower than the first response (natural) frequency. This can become challenging as the natural frequency gets lower with increasing span lengths.

To make the comparison of the natural frequencies and excitation frequencies from the current or wave-induced current action, existing pre-screening checks require calculation of the natural frequency each time a structure and different span lengths are measured. A more efficient and intuitive method for screening during design or operations would eliminate the need to compute the natural frequency altogether.

2. Non-Dimensional Analysis

2.1. Identification of Relevant Variables and Dimensions

We turn to a non-dimensional analysis to gain deeper insights into the free-span VIV problem and examine if the number of relevant parameters can be simplified. A non-dimensional analysis can reveal governing physics and highlight which physical effects dominate a system. A similar approach to dimensionless parameterisation has been implemented in analyzing the excitement of VIV [6]. The Buckingham Pi theorem [7] is utilised to perform a non-dimensional analysis on a typical VIV free-span problem.

Firstly, all physical variables influencing the problem are listed, along with their dimensions, which in this problem are confined to Mass [M], Length [L] and Time [T]. Viscosity is excluded from the list, in line with industry standard screening approaches [3]. In not considering Reynolds number effects, a constant high Strouhal number is maintained which will over-predict the onset of VIV [8]. The list of parameters considered is as follows:

• Characteristic outside diameter D [L];
• Current velocity, V [LT⁻¹];
• Fluid density ρ_f [ML⁻³];
• Mass density of structure (cable or pipe) ρ_S [ML⁻³];
• Characteristic free-span length, L [L];
• Cable or pipe bending stiffness, EI [MLT⁻²]. L² = [ML³T⁻²];
• Cable or pipe as-laid effective tension, T_eff [MLT⁻²].

Summarizing the list of physical variables: D, V, ρ_f, ρ_S, L, EI, T_eff.

The above list gives n = 7 parameters. Per the Buckingham Pi theorem, the independent dimensions are defined for this problem as being confined to M, L and T. Hence, the total independent dimensions, m, is m = 3.

The number of non-dimensional groups is calculated by the Buckingham Pi theorem as n − m = (7) − (3) = 4.

The non-dimensional groups are now constructed by choosing convenient repeating variables (any can be chosen, but the choices are made to gain greater physical interpretation of the remaining groups, which can then focus on stiffness, inertia and geometry system properties). The repeating variables chosen are:

• D, V and ρ_f.

These repeating variables are used to solve and represent each of the remaining group’s expressions.

The remaining groups, Π, are now solved, and physical interpretations are included in parentheses after each group:

For Mass density of cable or pipe, ρ_s,

Π₁ = ρ_s·D^a·(ρ_f)^b·V^c

Π₁ = (ML⁻³)·[L]^a E·(ML⁻³)^b·[LT⁻¹]^c

Π₁ = M^1+b L^{−3+a−3b+c} T^−c

Equating exponents,

1 + b = 0 -> b = −1

3 + a − 3b + c = 0 -> a = 0

−c = 0 -> c = 0

Π₁ = ρ_s·(ρ_f)⁻¹ or

$${\mathsf{\Pi }}_1={\displaystyle \frac{{\rho }_s}{{\rho }_f}}$$

(1)

The ratio expressed in Equation (1) is commonly called the specific gravity, or m*, the mass ratio. Although some historical definitions of mass ratio differ by a factor of ${\displaystyle \raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$4$}\right.}$ in the denominator [9], there is no impact on the dimensionless calculations put forth in this paper.

For span length L,

Π₂ = L·D^a·(ρ_f)^b·V^c

Π₂ = L·[L]^a·(ML⁻³)^b·[LT⁻¹]^c

Π₂ = M^b L^1+a−3b−c T^−c

Equating exponents,

−3b = 0 -> b = 0

−c = 0 -> c = 0

1 + a − 3b + c = 0 -> a = −1

Π₂ = L·(D)⁻¹ or

$${\mathsf{\Pi }}_2={\displaystyle \frac{L}{D}}$$

(2)

The ratio expressed in Equation (2), L/D, is commonly referred to as the aspect ratio.

For EI,

Π₃ = EI·D^a·(ρ_f)^b·V^c

Π₃ = ML³ T⁻²·D^a·(ρ_f)^b·V^c

Π₃ = (ML³ T⁻²)·[L]^a·(ML⁻³)^b·[LT⁻¹]^c

Π₃ = M^1+b L^3+a−3b+c T^−2−c

Equating exponents,

1 + b = 0 -> b = −1

−2 − c = 0 -> c = −2

3 + a – 3b + c = 0 -> 3 + a − 3(−1) + (−2)=0 -> a = −3 – 3 + 2 = −4

Π₃ = EI·D⁻⁴·(ρ_f)⁻¹·V⁻² or

$${\mathsf{\Pi }}_3={\displaystyle \frac{EI}{{\rho }_f{V}^2{D}^4}}$$

(3)

EI represents (flexural) bending stiffness. ${\rho }_f{V}^2{D}^2$ represents a fluid-induced forcing moment. The ratio represented in Equation (3), therefore, is a flexural stiffness ratio, comparing structural resistance to the fluid-induced forcing moment.

For convenience, it becomes easier to use ${\mathsf{\Pi }}_3$ as a velocity term, as engineers are often dealing with velocity as an input term for span analysis problems. Accordingly, the expression is changed by inversion, inclusion of a square root and multiplying by 1000 (the 1000 factor makes it a more user-friendly value) (none of these operations changes the fact that it is still a dimensionless expression). The resulting expression is chosen here to be named V*, a dimensionless velocity number as shown in Equation (4).

$${\mathsf{\Pi }}_3^{\prime }=V^{\ast }=1000.V.{\displaystyle \frac{D^2}{\sqrt{\raisebox{1ex}{$EI$}\!\left/ \!\raisebox{-1ex}{${\rho }_f$}\right.}}}$$

(4)

The physical explanation for V* is a fluid forcing to structural stiffness ratio, or a fluid-to-structure flexibility ratio. This can be expressed for either in-line or cross-flow, as non-dimensional onset velocities, V_IL* or V_CF* (with corresponding V_IL or V_CF—the dimensional onset velocities for VIV).

For T_eff,

Π₄ = T_eff·D^a·(ρ_f)^b·V^c

Π₄ = MLT⁻²·D^a·(ρ_f)^b·V^c

Π₄ = (MLT⁻²)·[L]^a·(ML⁻³)^b·[LT⁻¹]^c

Π₄ = M^1+b L^1+a−3b+c T^−2−c

Equating exponents,

1 + b = 0 -> b = −1

−2 – c = 0 -> c = −2

1 + a − 3b + c = 0 -> 1 + a − 3(−1) + (−2) = 0 -> 1 + a + 3 − 2 = 0 -> a = −2

Π₄ = T_eff·D⁻²·(ρ_f )⁻¹·V⁻² or

$${\Pi }_4={\displaystyle \frac{T}{{\rho }_f{D}^2{V}^2}}$$

(5)

${\rho }_f{V}^2$ represents a dynamic pressure, with the multiplication of D², it becomes a fluid-induced force. T is the axial tension (a force). The ratio expressed in Equation (5) represents the relative loading from tension versus fluid force. More relationships can be explored with ${\mathsf{\Pi }}_4$ if one is interested in non-zero as-laid tensions of cables and pipelines. For the purposes of screening, we can assume zero as-laid tension (not including the tension-stiffening effect). This will under-predict natural frequency values and therefore conservatively over-predict the minimum onset of VIV at lower velocities, or shorter span lengths than would occur with non-zero as-laid tension cases. Naturally, once the screening is complete, a full VIV analysis can be undertaken that includes tension effects to understand what, if any, VIV has been excited.

2.2. Simplified Governing Equations

The original system reduces to be described by Equation (6). Note that for completeness, the dimensionless parameter Strouhal number, St, is introduced here. Strouhal number defines the oscillating flow mechanisms [10].

$$f(St,{\mathsf{\Pi }}_1,{\mathsf{\Pi }}_2,{\mathsf{\Pi }}_3,{\mathsf{\Pi }}_4)=0$$

(6)

This expression can be simplified by ignoring tension effects in Equation (7):

$$f(St,m^{\ast },{\displaystyle \frac{L}{D}},V^{\ast })=0$$

(7)

The non-dimensional analysis revealed the commonly held knowledge that predicting VIV free spans is a function of the mass ratio and aspect ratio. Strouhal number varies with Reynolds number and surface roughness. Typical values range from 0.18 to 0.2 for VIV prediction applications [11]. In line with industry standard screening approaches [3], it can be assumed constant. Therefore, Equation (7) reduces to Equation (8) as a three-parameter simplification:

$$f(m^{\ast },{\displaystyle \frac{L}{D}},V^{\ast })=0$$

(8)

3. Simplified Response Curve

With only three parameters, two parameters can be plotted against one another for various values of the third parameter. Accordingly, L/D vs. V*, a normalised span length versus a dimensionless velocity, is chosen for various m* values.

We can now simplify the problem by assuming typical mass ratios to predict the onset of VIV to one universal curve for in-line VIV and one for cross-flow VIV.

Whilst various assumptions can be made to construct the curve, it is convenient to align the assumptions with DNV assumption for ease of agreement with the RP [3]. The curve is constructed using the following assumptions for in-line VIV:

• Clamped–clamped end condition (per DNV [3] single span recommendation);
• C_a = 1.0;
• Safety factor on onset value for in-line VIV, γ_onIL = 1.1 (cross-flow onset safety factor not applied in determining cross-flow VIV onset condition in [3]);
• Safety factor on in-line and cross-flow natural frequencies, γ _fIL = 1, γ _fCF = 1;
• Lowest natural frequencies in in-line and cross-flow directions for a given span are termed f_IL,1 and f_CF,1 and computed per Section 2.2 in [3];
• V_R onset for in-line VIV is 1/γ_onIL = 0.9 [3];
• V_R onset for cross-flow VIV is effectively 2.0 (Section 2.3.3 [3]);
• No multi-spans, interactions between spans or significant sagging are considered, except when a multi-span can be assumed as one span, which, under some circumstances, can be a very conservative assumption;
• This covers screening for fatigue (FLS), not local buckling of ultimate stress (ULS).

A clamped–clamped transverse pipe first natural frequency (from [3] and [12]) is shown in Equation (9), with rearrangement of this in terms of L (or L_eff from [3]) as shown in Equation (10).

$$f_n=3.56\sqrt{{\displaystyle \frac{EI}{m_e{L}^4}}}$$

(9)

$$L=\sqrt[4]{{{\displaystyle \frac{EI}{m_e}}\left({\displaystyle \frac{3.56}{f_n}}\right)}^2}$$

(10)

EI is the bending stiffness, m_e is the mass per unit length including structure, contents and added mass, and L is the length of the span in this scenario.

A plot of normalised span length (L/D) vs. dimensionless velocity V* for IL and CF, with a range of values for the mass ratio (m*), is shown in Figure 2 and Figure 3, respectively. Mass ratios from 1.5 to 4 are representative of the typical mass ratios for offshore assets where a mass ratio of 4 represents a very relatively heavy structure, such as a heavy-walled pipeline full of liquid contents. These plots represent universal free-span thresholds to predict the onset of VIV. Below each respective curve, no VIV is predicted; above each respective curve is the potential VIV excitation condition.

These plots demonstrate that a universal equation can represent the relationship, if m* is known, between the normalised span length (L/D) and the dimensionless velocity V*. The two sets of curves of Figure 2 and Figure 3 can be represented by the following power law regression equations, within the bounds of exploration, Equation (11), for in-line and Equation (12) for cross-flow:

$$V^{\ast }={\displaystyle \frac{3651}{\sqrt{m^{\ast }}({{(\frac{L}{D})}_{IL})}^2}} or {\left({\displaystyle \frac{L}{D}}\right)}_{IL}=\sqrt{{\displaystyle \frac{3651}{\sqrt{m^{\ast }}{V}^{\ast }}}}$$

(11)

$$V^{\ast }={\displaystyle \frac{8034}{\sqrt{m^{\ast }}({{(\frac{L}{D})}_{CF})}^2}} or {({\displaystyle \frac{L}{D}})}_{CF}=\sqrt{{\displaystyle \frac{8034}{\sqrt{m^{\ast }}{V}^{\ast }}}}$$

(12)

When a value for m* is selected, these equations represent universal free-span thresholds to predict the onset of VIV. For most practical purposes, it is reasonable to assume a mass ratio of 3; thus, a single plot of normalised span length (L/D) vs. dimensionless velocity V* for IL and CF, with a mass ratio of 3, is shown in Figure 4. The limits of 1.5 < m* < 4.0 are shown, but it is unlikely that practical structures will exceed these limits. One can easily assess the veracity of this m* = 3 assumption by inspection of Figure 2 and Figure 3.

The two curves of Figure 4, where m* = 3, can be represented by the following power law regression equations, within the bounds of exploration, Equation (13) for in-line and Equation (14) for cross-flow:

$$V^{\ast }={\displaystyle \frac{2108}{({{(\frac{L}{D})}_{IL})}^2}} or {\left({\displaystyle \frac{L}{D}}\right)}_{IL}=\sqrt{{\displaystyle \frac{2108}{V^{\ast }}}}$$

(13)

$$V^{\ast }={\displaystyle \frac{4638}{({{(\frac{L}{D})}_{CF})}^2}} or {({\displaystyle \frac{L}{D}})}_{CF}=\sqrt{{\displaystyle \frac{4638}{V^{\ast }}}}$$

(14)

4. Case Studies

4.1. Power-Cable Free-Span Screening—Critical Minimum Velocity

A power-cable free-span case study (as illustrated in Figure 1) with a known free-span length is assessed to determine the critical minimum velocities for the onset of in-line and cross-flow VIV. The cable properties are largely taken from Table 1 of [13]. The calculated critical minimum velocities, if smaller than the observed currents, either during operation or in metocean studies of the cable region, would flag the potential for VIV to result in fatigue of the power cable. Preventative or mitigative measures could then be put in place to avoid any unwanted fatigue effects.

Analysis Parameters

Inputs:

• Free-span length, L = 5 m;
• Diameter, D = 0.176 m;
• Bending Stiffness, EI = 12 kNm²;
• Mass/Length = 77.3 kg/m.

Outputs:

• L/D = 28.4;
• m* = 3.1 (from Equation (1));
• V_IL* = 2.57, V_CF* = 5.65 (from Equations (11) and (12));
• Onset velocities V_IL = 0.284 m/s, V_CF = 0.625 m/s (from Equation (4)).

Sensitivities:

• There is no difference in calculated onset velocities when compared to the methodology set out in DNV-GL-RP-F105 [3].
• If assuming m* = 3 (using Equation (13) and (14)), then V_IL = 0.289 m/s, and V_CF = 0.635 m/s.

  o

  The m* = 3 assumption is shown to only change the onset velocities by <2% in this example.

• If L = 6 m (+20%), then onset velocities are V_IL~0.20 m/s and V_CF~0.43 m/s.

  o

  A 20% increase in span length reduced the onset velocities by ~30%, noting that the relationship between these parameters has been established as non-linear.

4.2. Pipeline Free-Span Screening—Critical Minimum Span Length

A pipeline free-span case study (illustrated in Figure 5) is shown below to assess the inverse problem—determining what the critical minimum span length is for the onset of VIV with a known maximum velocity. The pipeline properties are hypothetical. The critical minimum span length, if known, may inform the designers/operators of the capacity of the cable along its route to handle dynamic seabed changes such as scouring.

Analysis Parameters

Inputs:

• Diameter, D = 0.483 m (~19 inch);
• Maximum V: 1.7 m/s;
• Bending Stiffness, EI: 4.68 × 10⁷ Nm²;
• Mass/Length = 518 kg/m.

Outputs:

• m* = 2.76 (from Equation (1));
• V* = 1.86 × 10⁻³ (from Equation (4));
• (L/D)_IL = 34.4, (L/D)_CF = 51.1 (from Equations (11) and (12));
• Critical minimum span lengths: L_IL = 16.6 m, L_CF = 24.7 m.

Sensitivities:

• There is no difference in calculated critical minimum span lengths when compared to the methodology set out in DNV-GL-RP-F105 [3].
• If assuming m* = 3 (using Equations (13) and (14)), then L_IL = 16.3 m, and L_CF = 24.2 m.

  o

  The m* = 3 assumption is shown to only change the onset velocities by ~2% in this example.

• If V = 2 m/s (+20%), then L_IL = 15.3 m, and L_CF = 22.7 m.

  o

  A 20% increase in maximum velocity reduced the span lengths by ~10%, noting the non-linear relationship of these parameters.

5. Discussion

The observations seen in this paper and the relationship between onset velocity for VIV and free-span length are limited to a single clamped–clamped end condition span with a constant Strouhal number. The following recommendations are provided to either over-predict the minimum onset VIV velocity or under-predict the minimum span length for complex scenarios:

• Multi-spans could be, for screening purposes, considered as one combined span length. Importantly, this approach does not account for the influence on VIV from interacting multi-spans. It is recommended that, if multi-spans are being considered, the reader seek further guidance on calculating these interactions per DNV [3].
• The free-span length of a curved pipeline can be estimated by using the arc length of the pipeline.
• Dynamic seabed conditions may be screened by assuming, if possible, that the end-of-life condition applies. For example, if scour of the seabed is anticipated, then the free-span length can be assumed as the largest length possible under those conditions.

However, in scenarios of free span where these limitations are present (i.e., multi-span interactions or variable axial tension), the reader should carefully consider if this screening approach is appropriate for their application.

If VIV is found to be potentially excited, then higher fidelity calculations are advisable, including fatigue predictions for the expected current profiles with their associated probabilities of exposures. Fatigue is generally assessed using industry codes such as DNV [3] or analysis tools such as SHEAR7 [4].

If predicted fatigue life is found to be less than project life, including the appropriate safety factors, there are many VIV treatment options widely used in industry. If the system is already in place, then post-installation of hydrodynamic shrouds can be performed. Such shrouds include Longitudinal Grooved Suppression (LGS) [14], or helical strakes [15] if clearance to seabed permits. These treatment options each have their own benefits and disadvantages. Where the LGS solution provides less reduction in VIV compared to helical strakes, it is less confined geometrically as a post-installed solution. The LGS treatment also has a significant decrease in drag of the free span when compared to a helical straked solution. An increase in drag can create issues if the cable/pipeline is adjacent to other subsea infrastructure where potential clashing is possible.

More expensive alternate options likely involve changes to the foundation via support additions [1] or even rock dumping. Although more expensive, this has the benefit of reducing or eliminating the free span entirely or significantly reducing the effective free-span length, thus preventing fatigue accumulation to undesirable levels. If the system is not already installed, additional options may be to investigate changing the routing of the pipeline/cable to avoid potential spanning scenarios where fatigue damage will be an issue. However, this may result in additional time and expense due to lengthening of the required pipeline/cable for both installation and manufacturing.

All of these factors underpin the value of this expedient screening tool, wherein the potential for VIV on free spans can be identified, and only the areas of potential are required to undergo higher fidelity fatigue calculations.

6. Conclusions

As a result of the non-dimensional assessment of VIV onset when applied to free spans outlined in this paper, the following conclusions can be drawn regarding creating universal screening criteria:

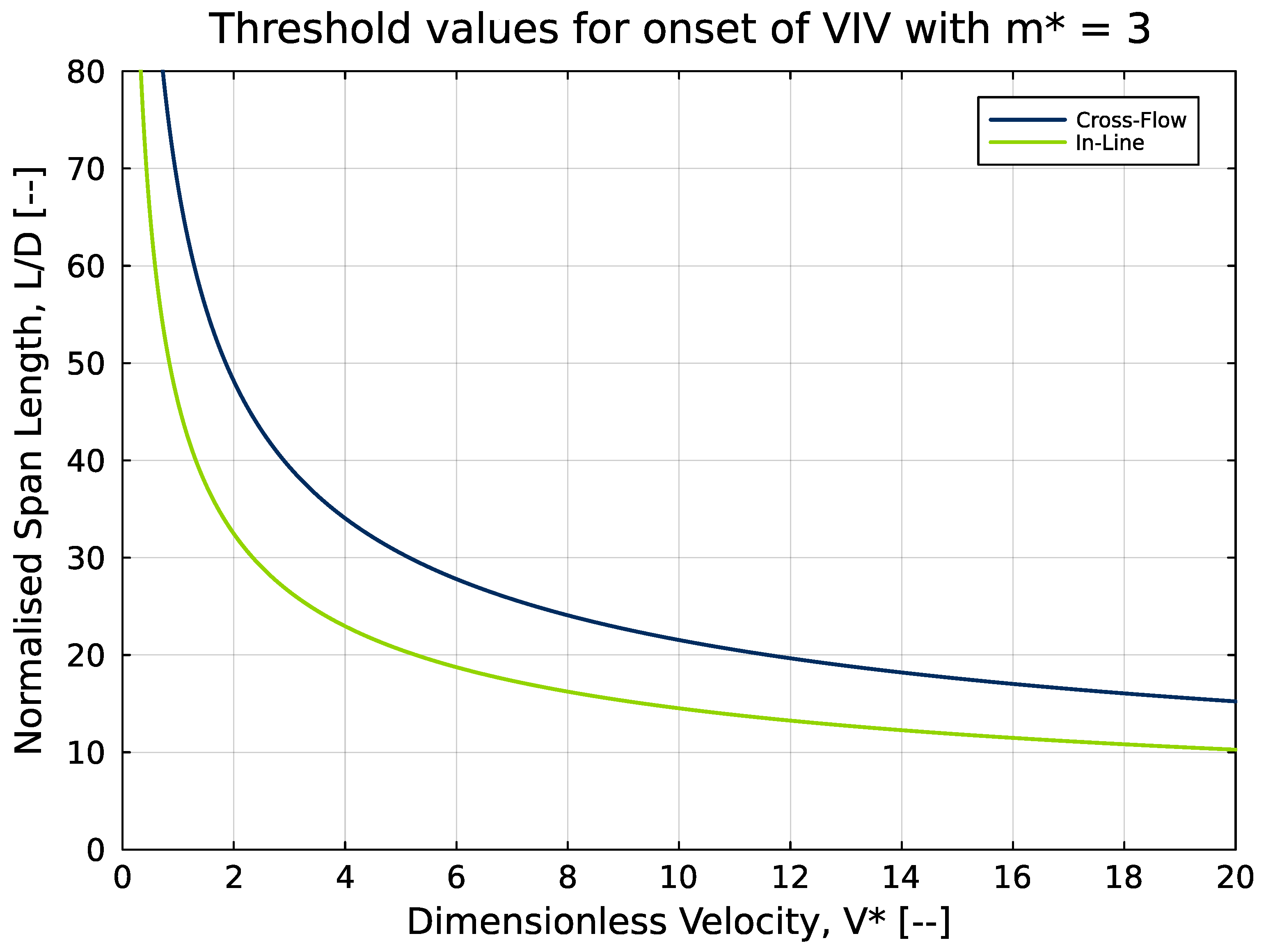
• The non-dimensionalisation of a free span under VIV revealed three dominant physical mechanisms: mass ratio, aspect ratio and bending stiffness curvature loading.
• A universal curve was established to conservatively assess the onset of VIV, where conservativism over-predicts VIV onset velocities or under-predicts threshold span lengths.
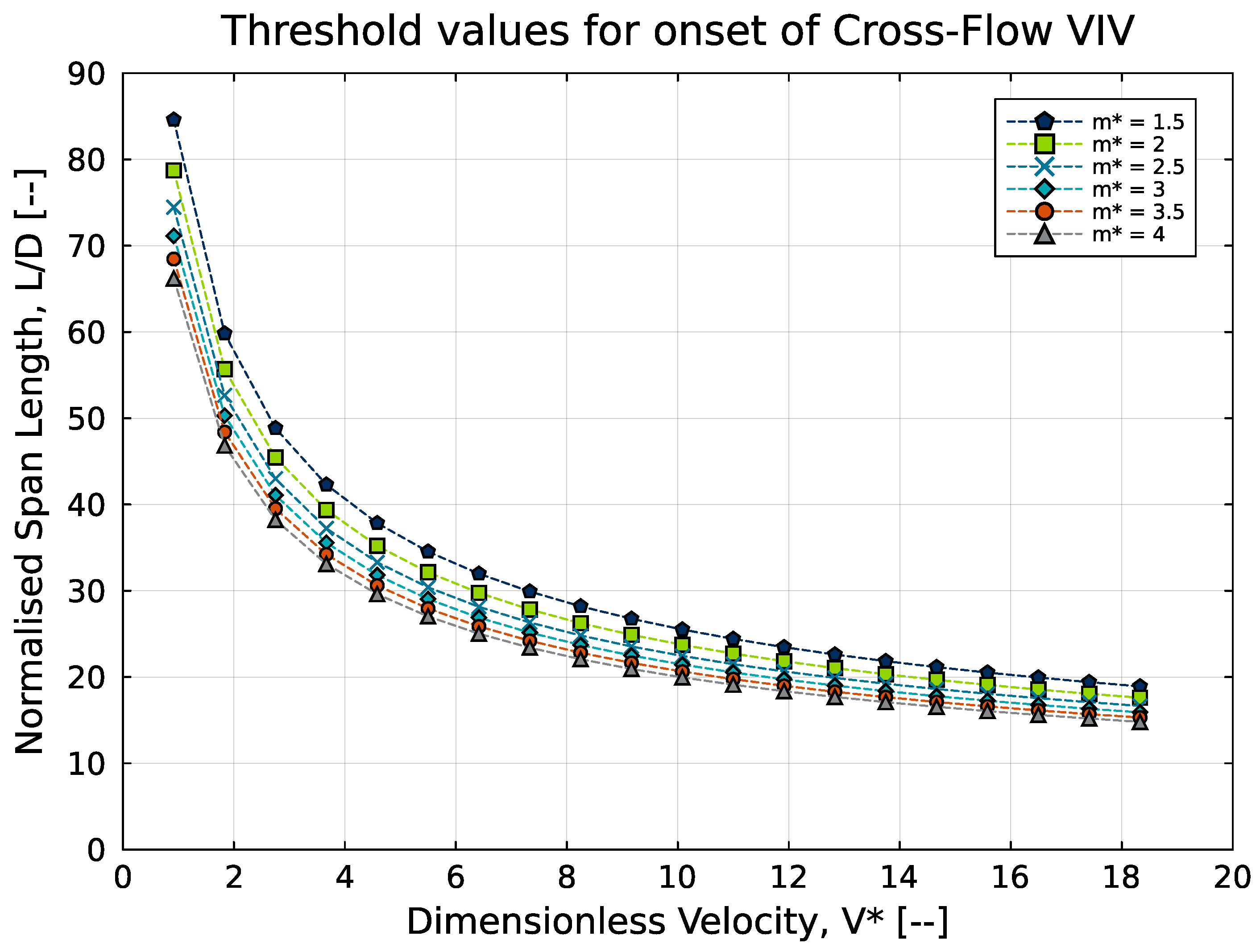
• Even though mass ratio is generally considered important in VIV predictions, the range of mass ratios considered in this investigation of VIV on free spans does not show a significant influence of mass ratio on the critical free-span length for a given non-dimensional flow velocity. Thus, a mass ratio of 3 is a reasonable approximation for screening free-span VIV on offshore cables and pipes.
• The methodology provided in this paper provides reduced complexity screening criteria for the determination of onset VIV and critical minimum span lengths. These screening criteria may be practically implemented during preliminary design or throughout the operational phases to determine the location and extent to which VIV high-fidelity fatigue assessments are required to be performed. In effect, this screening methodology will act as a precursor to select the instances where detailed analysis tools such as SHEAR7 and FATFREE can be implemented.
• This methodology may produce very conservative estimates if high as-laid tension is present in the system. However, it is important to note that the purpose of the method is for screening only.