Research on Underwater Laser Communication Channel Attenuation Model Analysis and Calibration Device
Abstract
1. Introduction
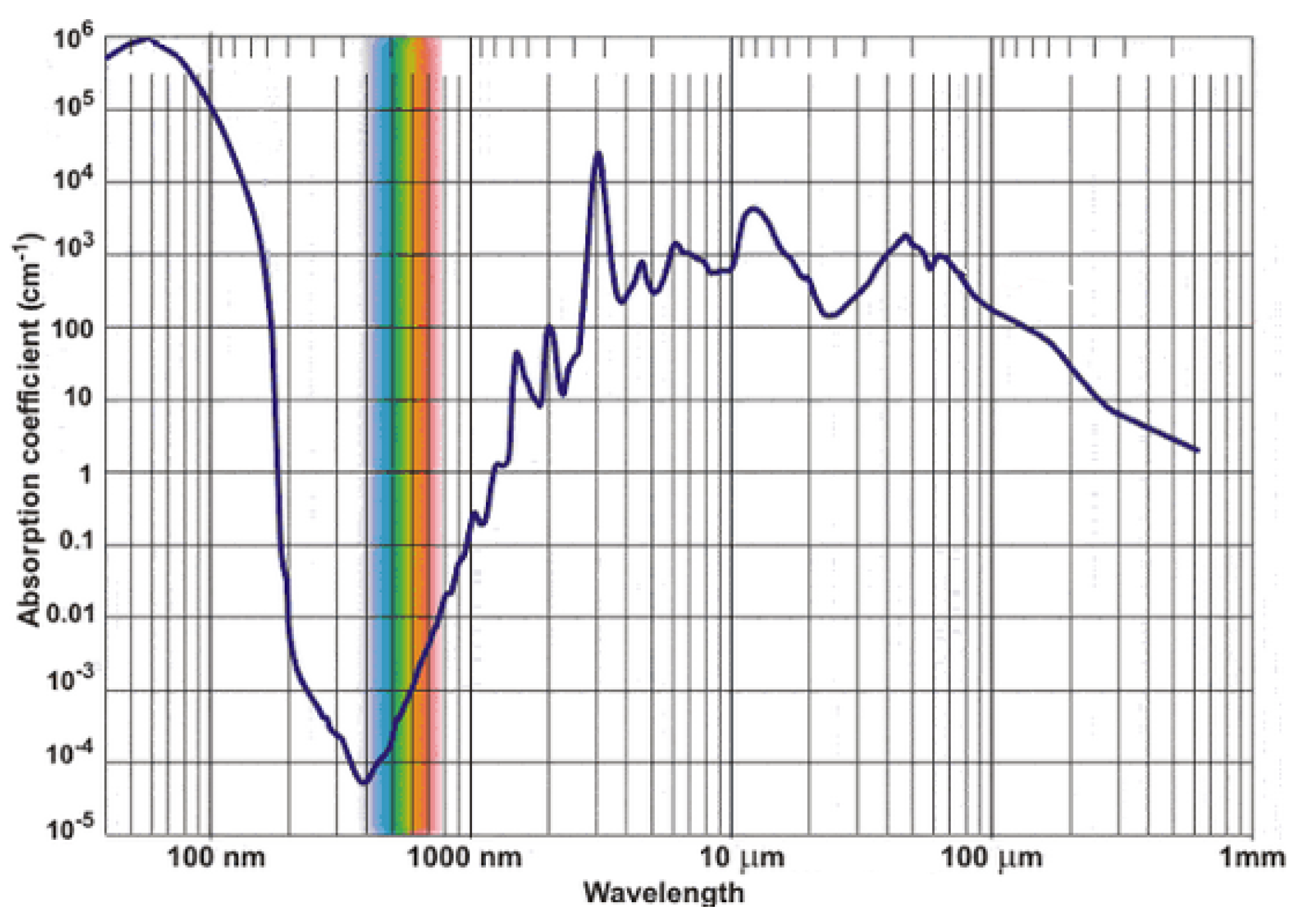
- Underwater laser communication channel modeling and loss analysis: The effects of various substances in the water body on the underwater laser communication channel are analyzed, and the corresponding computational model is established. The optical path loss and the attenuation characteristics of the light source in the underwater channel are calculated.
- Field measurement system design and experimental validation: A field measurement system is designed to measure the attenuation of underwater laser channels. The correctness of the computational model in the underwater laser communication channel is verified in different water quality environments. The calculation results are compared with underwater hyperspectral absorption coefficient spectrometer (ACS) measurements to verify the accuracy.
- Fusion filtering algorithms to optimize data quality: A fusion filtering algorithm based on wavelet analysis denoising and adaptive Kalman filtering is proposed to improve the reliability of collected data. Wavelet analysis denoising removes random noise and adaptive Kalman filtering removes systematic noise to enhance signal accuracy.
2. Related Works
3. Materials and Methods
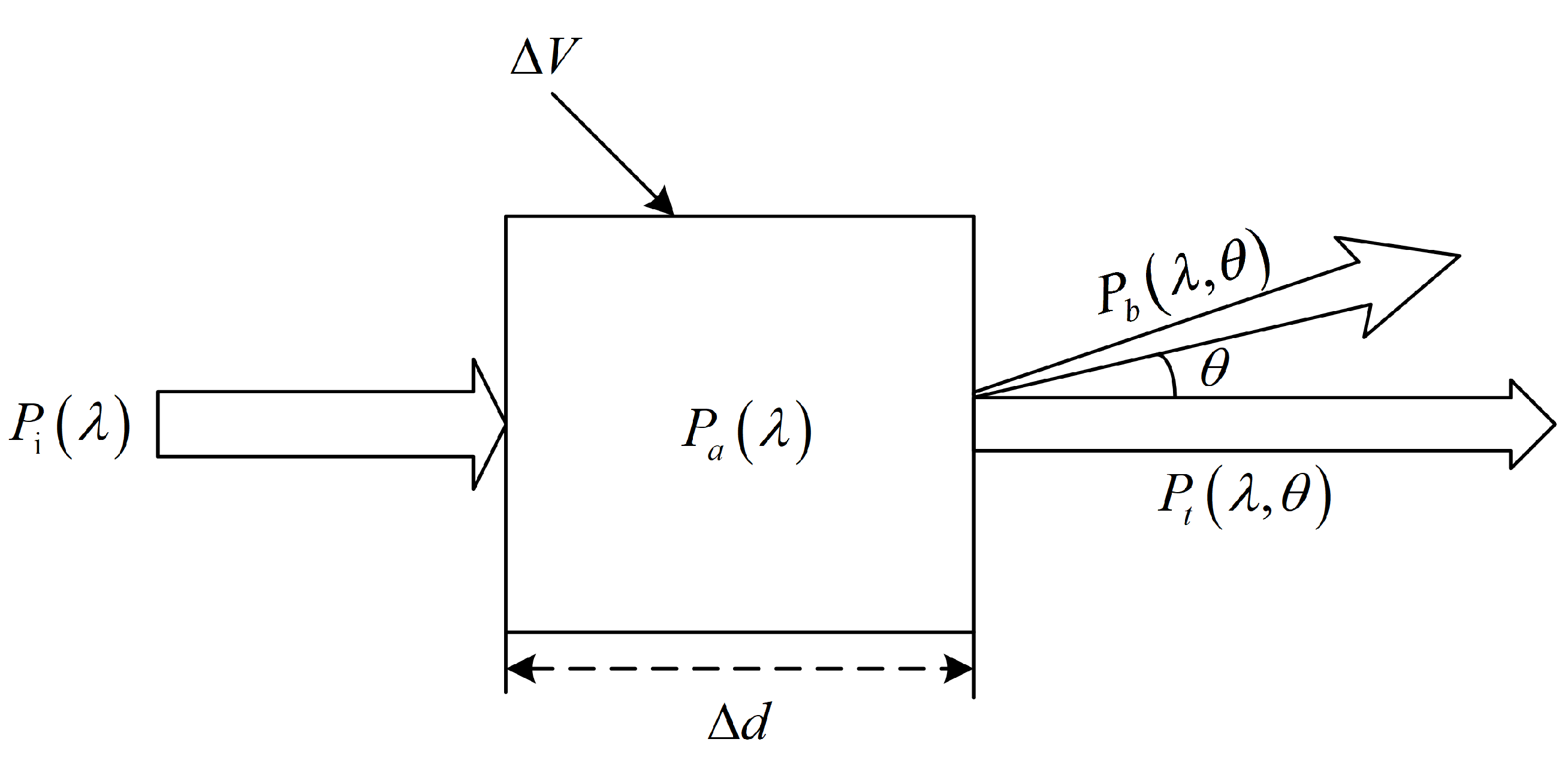
3.1. Modeling of Underwater Laser Transmission
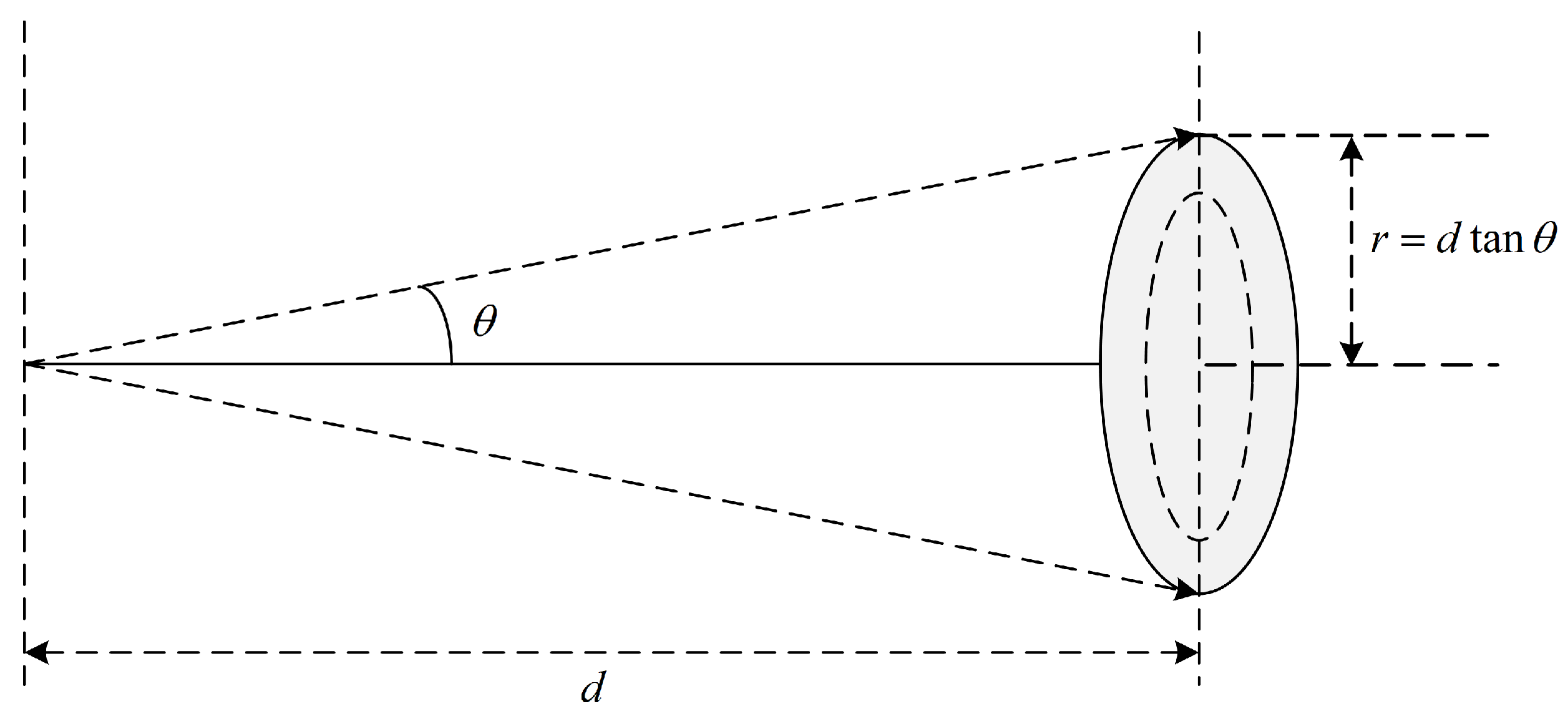
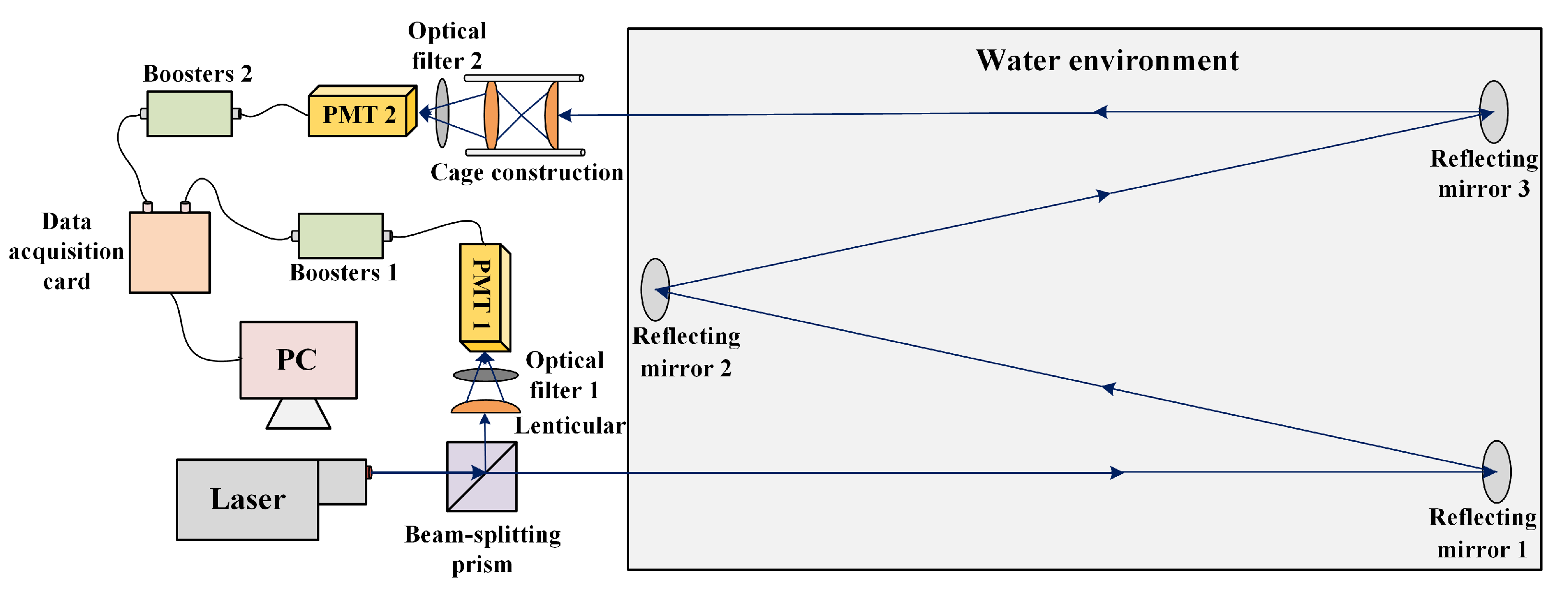
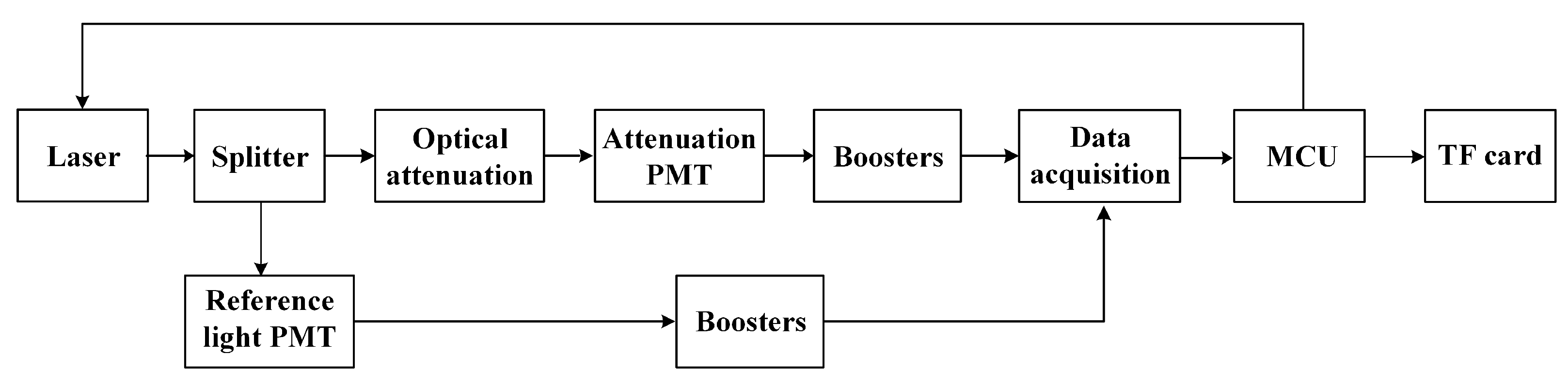
3.2. Underwater Laser Channel Attenuation Measurement System
3.2.1. System Design and Construction
3.2.2. Calculation of Optical Characterization Parameters of Water Bodies
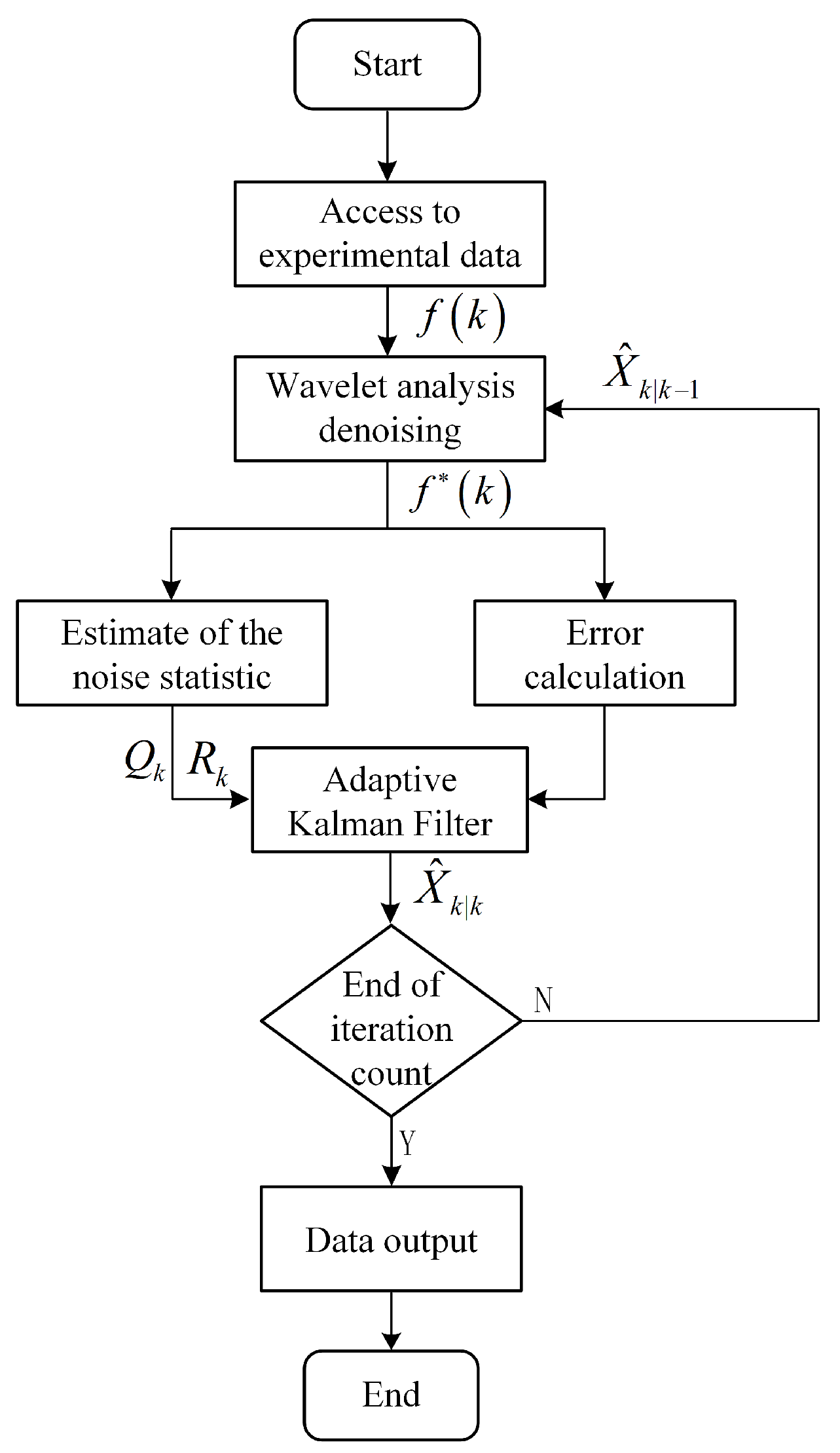
3.3. Post-Processing Denoising Algorithm
3.3.1. Data Correction and Calibration
- Reference light calibrationIn order to eliminate the effects of laser output power fluctuations or changes in laser source intensity on the measured results, in each measurement, the reference light intensity is measured through a reference optical path, and the measured signal is used to normalize with the reference signal.where is the corrected signal, is the measured signal, and is the reference signal.
- Dark current calibrationPhotodetectors still generate a weak current (dark current) when there is no input light signal, which can interfere with the actual light signal.where is the dark current signal, is the actual measured signal, and is the corrected signal.
- Ultrapure water calibrationUltrapure water is applied to set the calibration coefficients of attenuation coefficients, which can improve the accuracy and reliability of the measurement system.
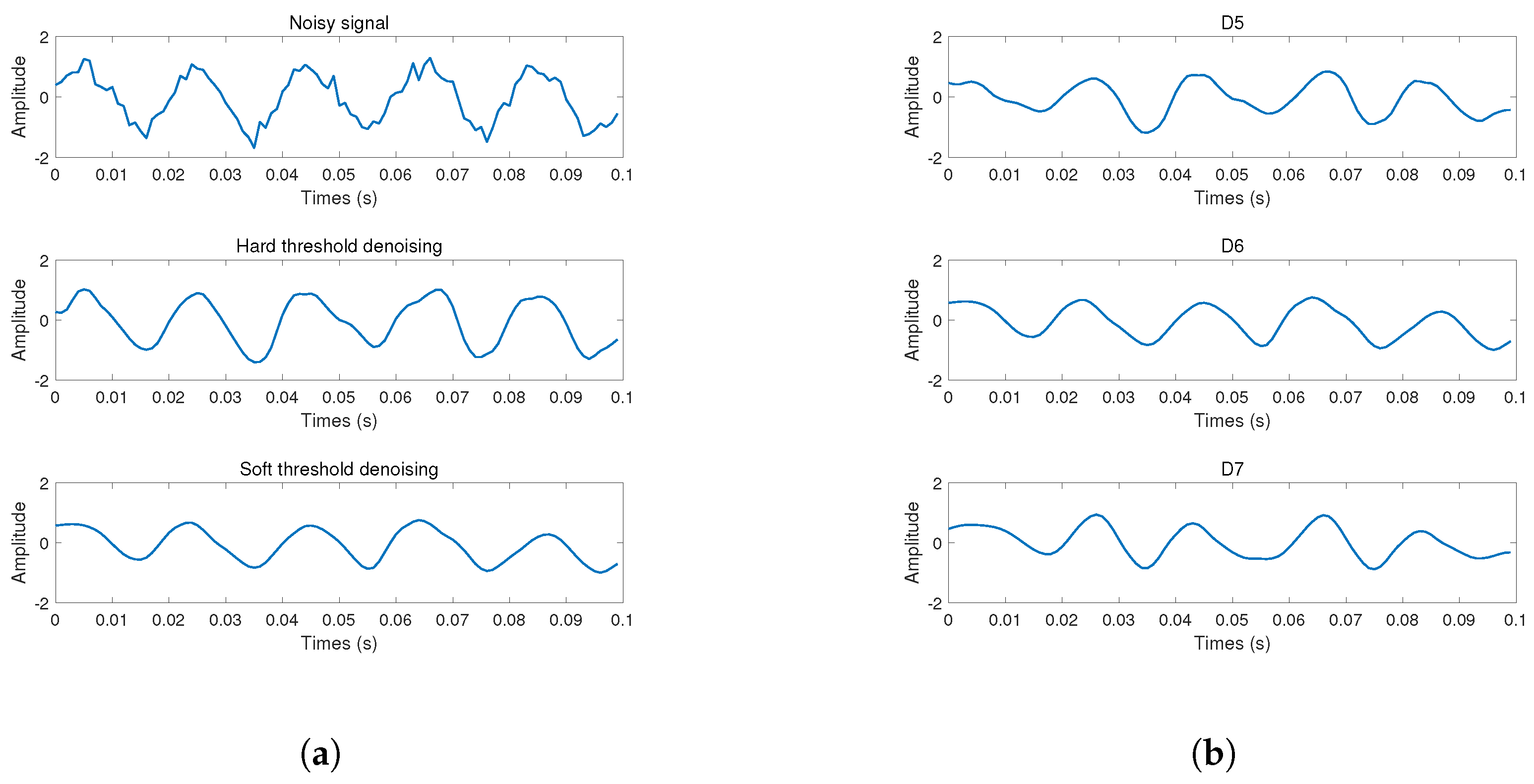
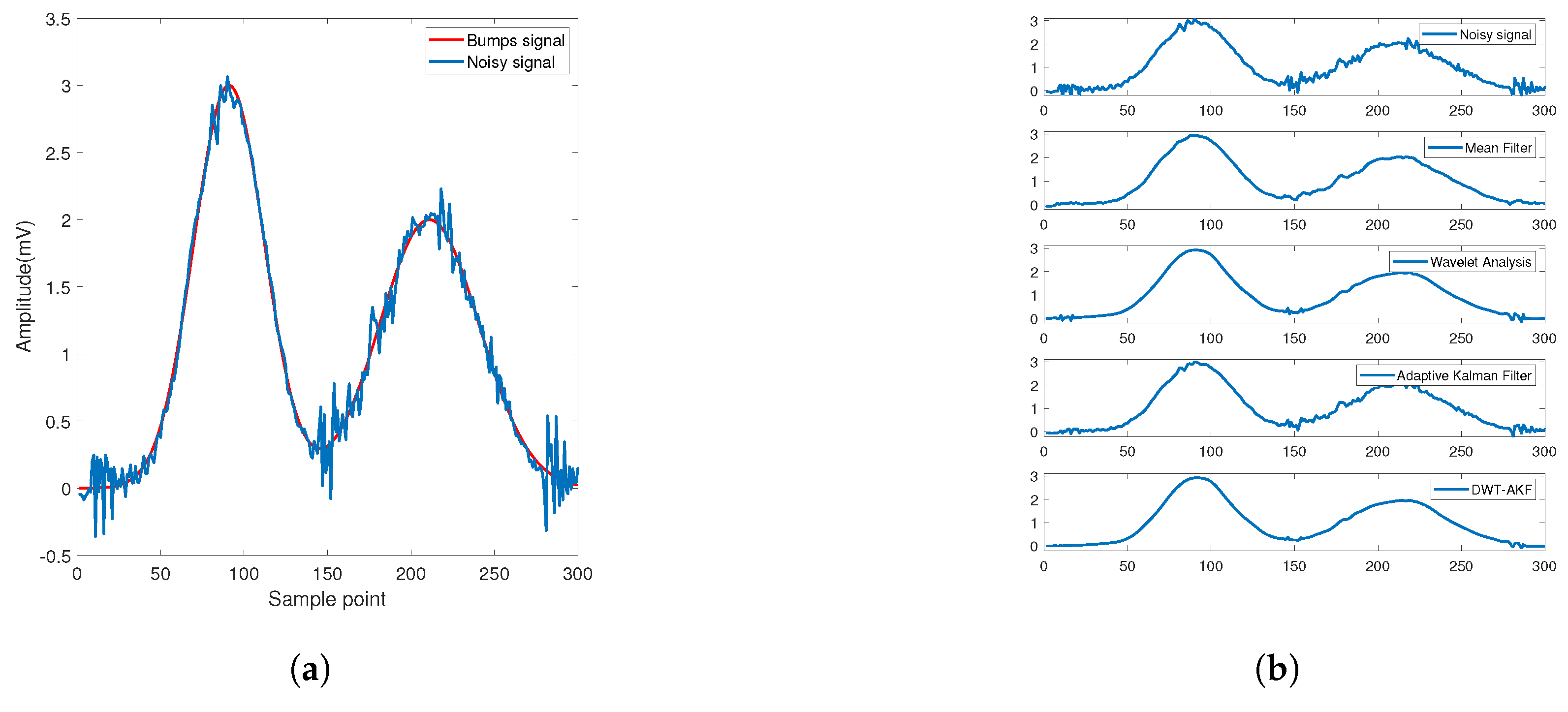
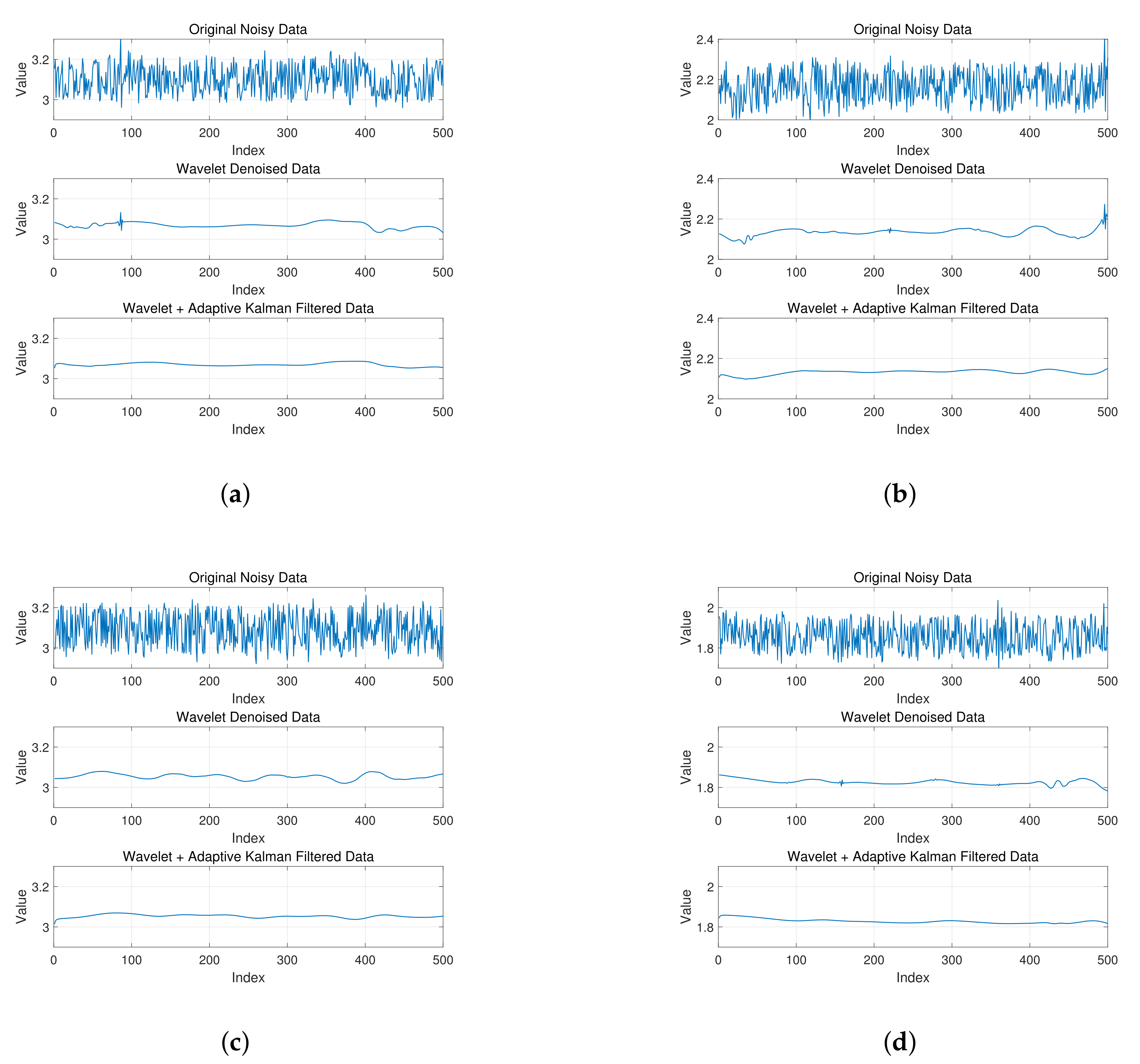
3.3.2. Multi-Scale Dynamic Denoising Method Based on DWT-AKF
- The wavelet decomposition of collected dataThis process can be expressed aswhere s denotes the collected data signal vector , , ⋯, , f is the real signal vector, and z is the Gaussian random vector.
- The threshold operation of the wavelet coefficientThe threshold functions include hard threshold functions and soft threshold functions. When the signal is processed by the hard threshold function, the signal is prone to oscillation. The soft threshold function can smooth the signal [33]. Hence, this paper uses the soft threshold function for threshold operation. Among them, the soft threshold expression [34] iswhereIn addition, the selection of isFurther, the estimated noise level is defined aswhere ) denotes the operation of taking the middle value; and are the wavelet coefficients before and after the denoising process, respectively.
- The signal reconstruction based on wavelet coefficientsAn inverse transformation is applied to the processed wavelet coefficients to reconstruct the signal, which can be expressed aswhere is the acquired signal after denoising and denotes the wavelet coefficients after the thresholding operation.
- Prediction phaseThe prediction equation of the system state can be expressed aswhere is the predicted value at moment for moment k, and is the optimal estimation of the previous state.In addition, the covariance prediction equation of this state can be calculated aswhere denotes the prediction of systematic error covariance at moment for moment k, denotes the estimate of covariance matrix corresponding to , denotes the transpose matrix of , and denotes the covariance matrix of the systematic process .The system state transfer matrix and the observation matrix are initialized as, respectively,
- Calibration phaseThe estimation equation of the system filter can be expressed aswhere denotes the optimal estimate at moment k; denotes the reconstructed signal value after wavelet analysis inverse transformation.In addition, the gain equation of the Kalman filter can be calculated aswhere denotes the transpose matrix of ; denotes the covariance matrix of system process .Therefore, the updated error covariance matrix can be expressed aswhere I is the unit matrix.
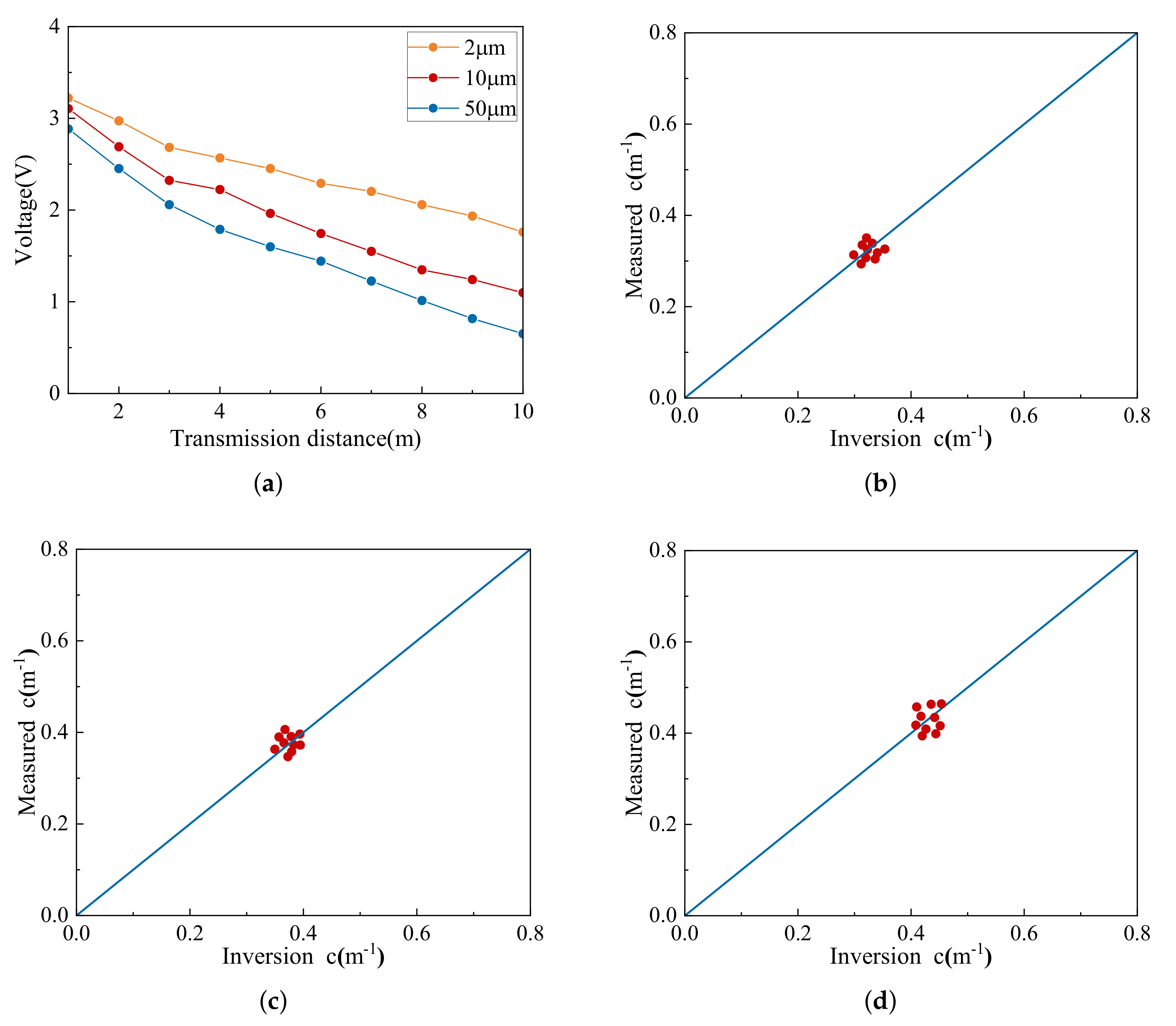
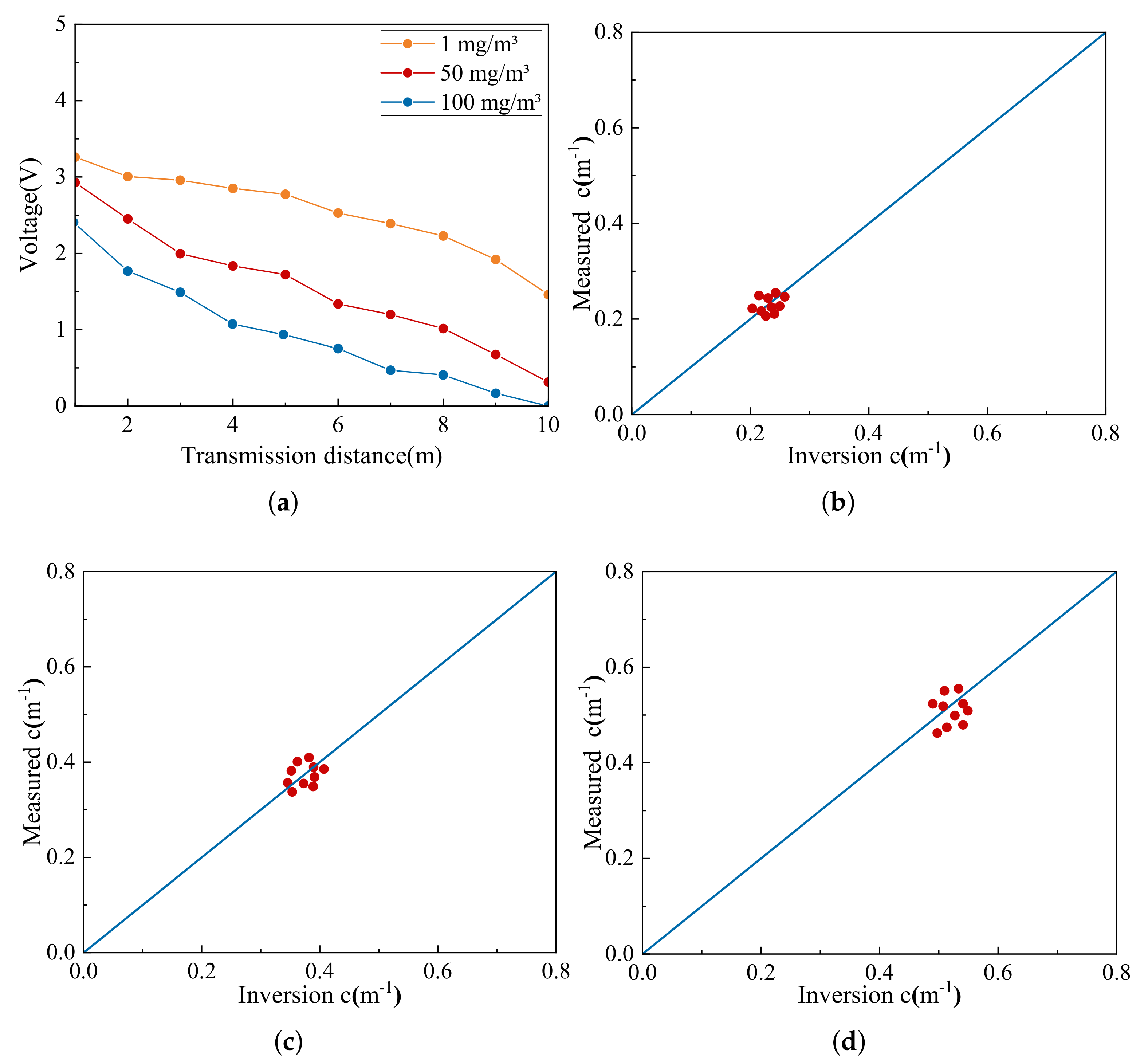
3.4. Validation of Attenuation Measurements
4. Experiment and Results
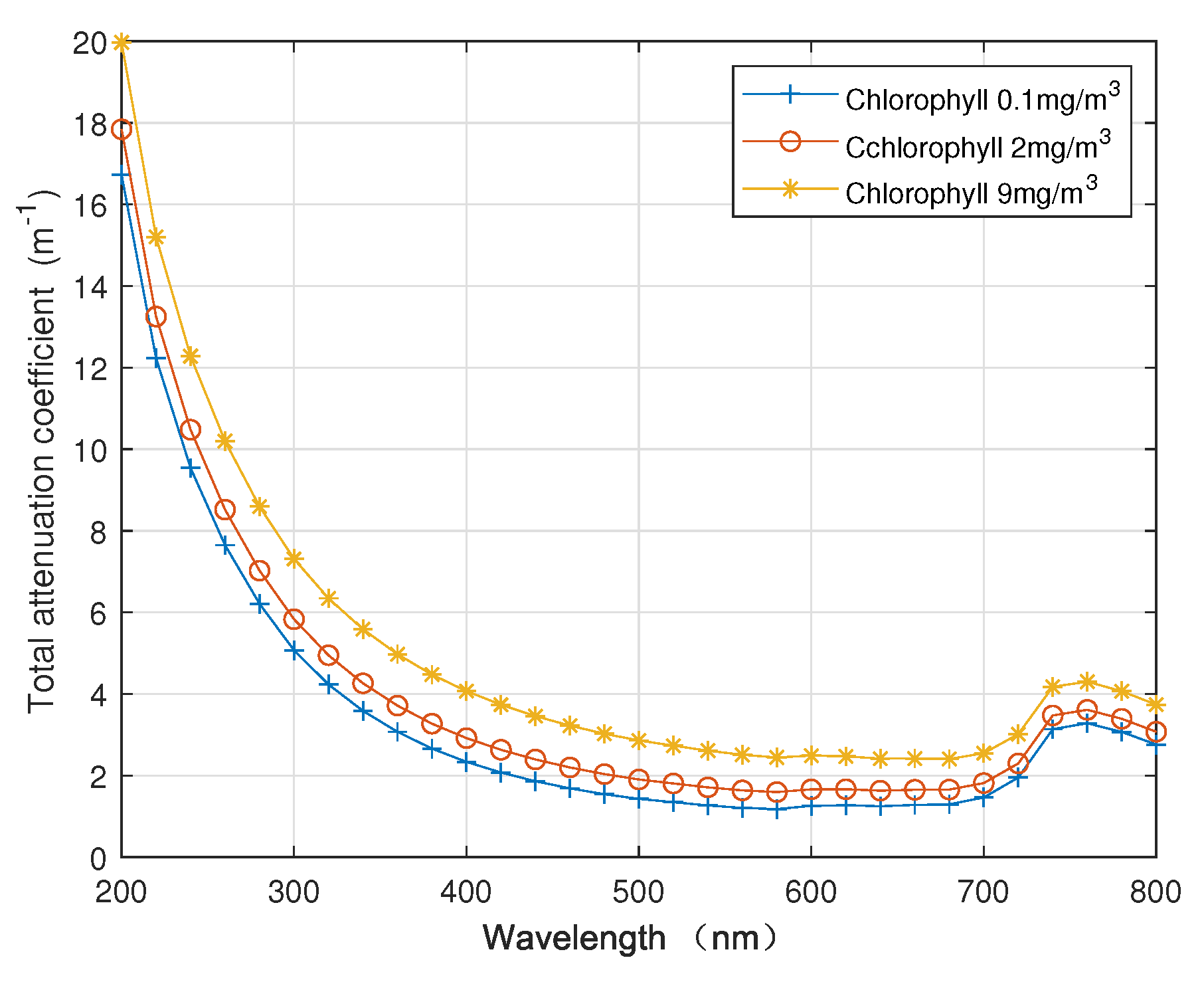
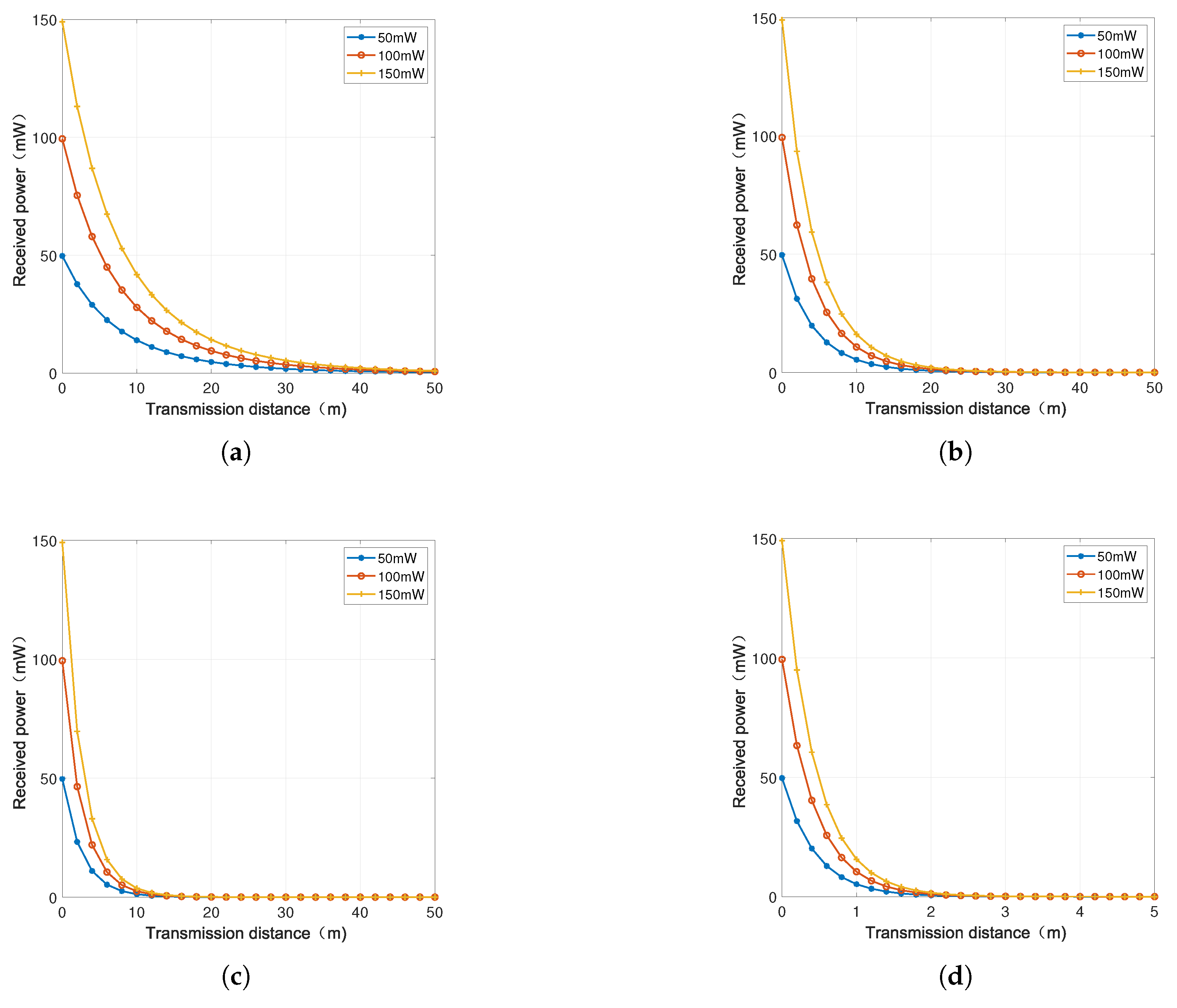
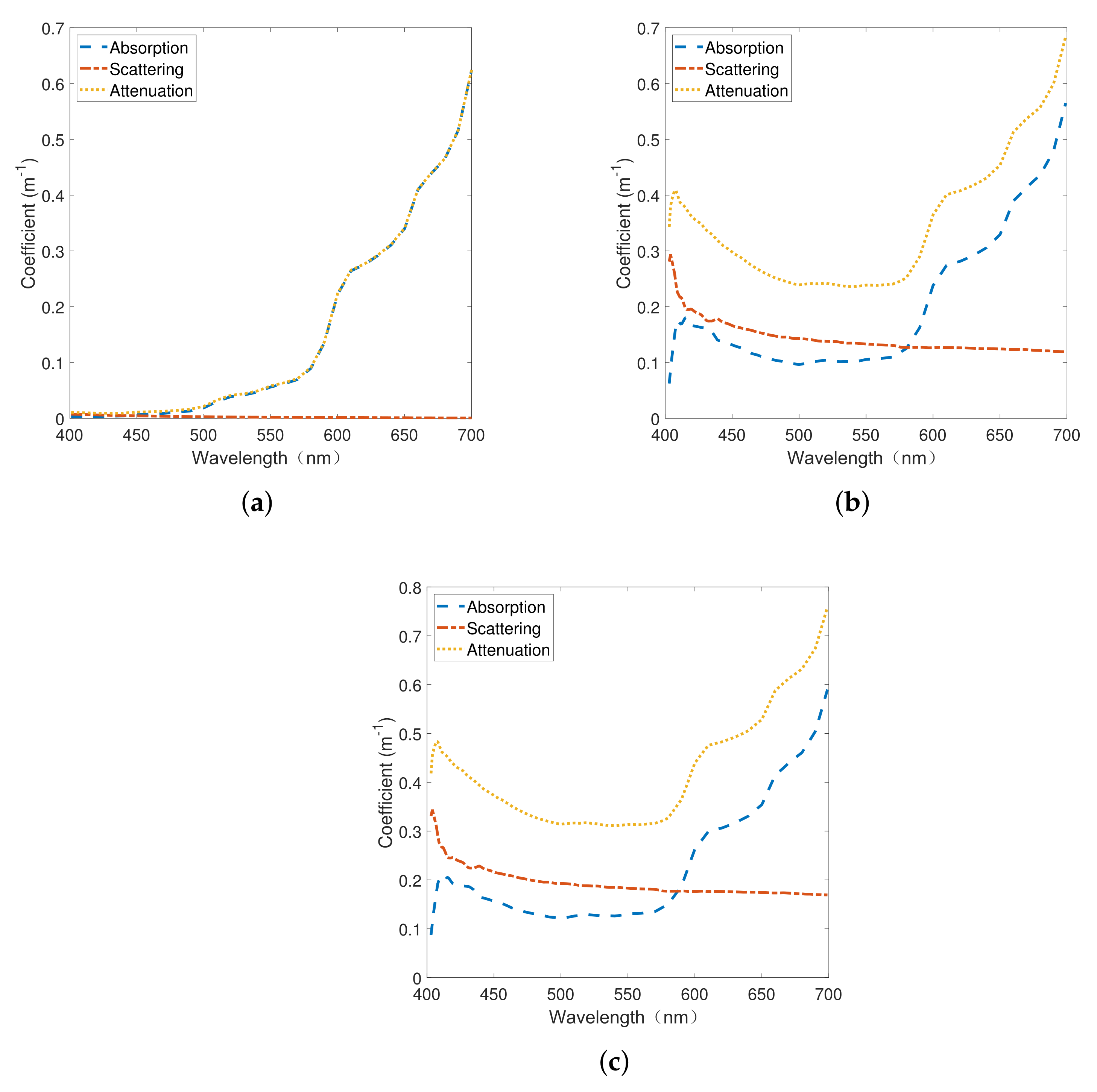
4.1. Underwater Laser Transmission Model Simulation and Analysis
4.2. Simulation Verification of DWT-AKF Denoising Algorithm
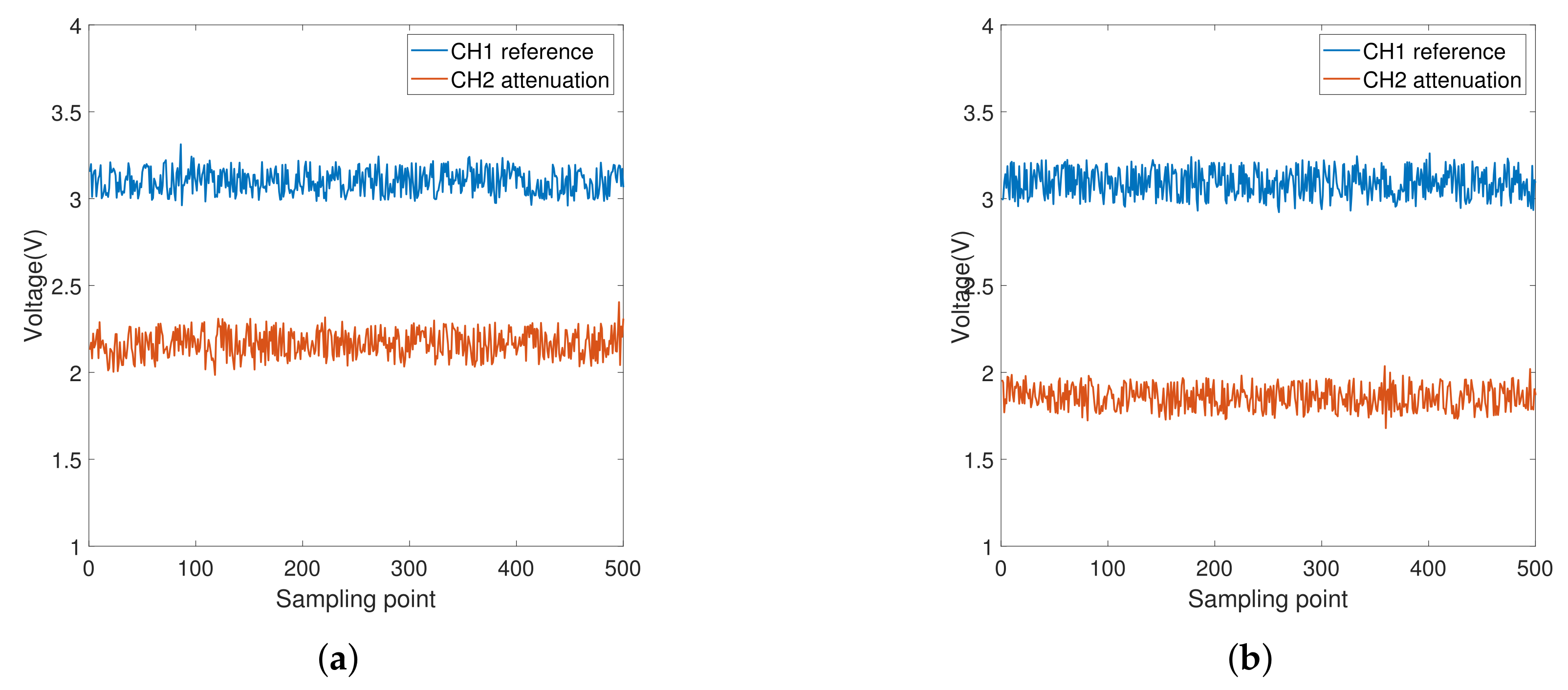
4.3. Analysis of Measured Data
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cossu, G. Recent achievements on underwater optical wireless communication. Chin. Opt. Lett. 2019, 17, 100009. [Google Scholar] [CrossRef]
- Smith, R.C.; Baker, K.S. Optical properties of the clearest natural waters (200–800 nm). Appl. Opt. 1981, 20, 177–184. [Google Scholar] [CrossRef]
- Shen, X.; Wang, T.; Wang, Z.; Zhu, R.; Jiang, L.; Tong, C.; Song, Y.; Zhang, P. Pulsed Laser Based Underwater Wireless Optical Communication: Smaller Channel Attenuation and Better Communication Performance. IEEE J. Ocean. Eng. 2025, 50, 1557–1568. [Google Scholar] [CrossRef]
- Miramirkhani, F.; Uysal, M. Visible light communication channel modeling for underwater environments with blocking and shadowing. IEEE Access 2017, 6, 1082–1090. [Google Scholar] [CrossRef]
- Gilbert, G.; Stoner, T.; Jernigan, J. Underwater experiments on the polarization, coherence, and scattering properties of a pulsed blue-green laser. Underw. Photo Opt. 1966, 7, 8–14. [Google Scholar]
- Zaneveld, J.R.V.; Kitchen, J.C. The variation in the inherent optical properties of phytoplankton near an absorption peak as determined by various models of cell structure. J. Geophys. Res. Ocean. 1995, 100, 13309–13320. [Google Scholar] [CrossRef]
- Li, J.; Ma, Y.; Zhou, Q.; Zhou, B.; Wang, H. Channel capacity study of underwater wireless optical communications links based on Monte Carlo simulation. J. Opt. 2011, 14, 015403. [Google Scholar] [CrossRef]
- Cox, W.; Muth, J. Simulating channel losses in an underwater optical communication system. J. Opt. Soc. Am. A 2014, 31, 920–934. [Google Scholar] [CrossRef]
- Qadar, R.; Kasi, M.K.; Ayub, S.; Kakar, F.A. Monte Carlo–based channel estimation and performance evaluation for UWOC links under geometric losses. Int. J. Commun. Syst. 2018, 31, e3527. [Google Scholar] [CrossRef]
- Fei, W.; Guan, Y. Channel simulation analysis of seawater laser communication. In Proceedings of the 2021 IEEE International Conference on Artificial Intelligence and Computer Applications (ICAICA), Dalian, China, 28–30 June 2021; pp. 1108–1109. [Google Scholar]
- Chami, M.; McKee, D.; Leymarie, E.; Khomenko, G. Influence of the angular shape of the volume-scattering function and multiple scattering on remote sensing reflectance. Appl. Opt. 2006, 45, 9210–9220. [Google Scholar] [CrossRef]
- Hameed, S.M.; Sabri, A.A.; Abdulsatar, S.M. Filtered OFDM for underwater wireless optical communication. Opt. Quantum Electron. 2023, 55, 77. [Google Scholar] [CrossRef]
- Mooradian, G.; Geller, M.; Stotts, L.; Stephens, D.; Krautwald, R. Blue-green pulsed propagation through fog. Appl. Opt. 1979, 18, 429–441. [Google Scholar] [CrossRef]
- Wei, W.; Zhang, X.; Rao, J.; Wang, W. Time domain dispersion of underwater optical wireless communication. Chin. Opt. Lett. 2011, 9, 030101. [Google Scholar] [CrossRef]
- Umar, A.A.B.; Leeson, M.S.; Abdullahi, I. Modelling impulse response for NLOS underwater optical wireless communications. In Proceedings of the 2019 15th International Conference on Electronics, Computer and Computation (ICECCO), Abuja, Nigeria, 10–12 December 2019; pp. 1–6. [Google Scholar]
- Shin, M.; Park, K.H.; Alouini, M.S. Statistical modeling of the impact of underwater bubbles on an optical wireless channel. IEEE Open J. Commun. Soc. 2020, 1, 808–818. [Google Scholar] [CrossRef]
- Zedini, E.; Kammoun, A.; Soury, H.; Hamdi, M.; Alouini, M.S. Performance analysis of dual-hop underwater wireless optical communication systems over mixture exponential-generalized gamma turbulence channels. IEEE Trans. Commun. 2020, 68, 5718–5731. [Google Scholar] [CrossRef]
- Cox, W.C., Jr. Simulation, Modeling, and Design of Underwater Optical Communication Systems; North Carolina State University: Raleigh, NC, USA, 2012. [Google Scholar]
- Yingluo, Z.; Yingmin, W.; Aiping, H. Analysis of underwater laser transmission characteristics under Monte Carlo simulation. In Proceedings of the 2018 OCEANS-MTS/IEEE Kobe Techno-Oceans (OTO), Kobe, Japan, 28–31 May 2018; pp. 1–5. [Google Scholar]
- Yuan, R.; Ma, J.; Su, P.; Dong, Y.; Cheng, J. Monte-Carlo integration models for multiple scattering based optical wireless communication. IEEE Trans. Commun. 2019, 68, 334–348. [Google Scholar] [CrossRef]
- Sahu, S.K.; Shanmugam, P. Improving the link availability of an underwater wireless optical communication system using chirped pulse compression technique. IEEE J. Ocean. Eng. 2020, 46, 687–703. [Google Scholar] [CrossRef]
- Ramley, I.; Alzayed, H.M.; Al-Hadeethi, Y.; Chen, M.; Barasheed, A.Z. An Overview of Underwater Optical Wireless Communication Channel Simulations with a Focus on the Monte Carlo Method. Mathematics 2024, 12, 3904. [Google Scholar] [CrossRef]
- Ramley, I.; Alzayed, H.M.; Al-Hadeethi, Y.; Barasheed, A.Z.; Chen, M. Novel optimization techniques for underwater wireless optical communication links: Using monte carlo simulation. Def. Technol. 2025, in press. [Google Scholar] [CrossRef]
- Jaruwatanadilok, S. Underwater wireless optical communication channel modeling and performance evaluation using vector radiative transfer theory. IEEE J. Sel. Areas Commun. 2008, 26, 1620–1627. [Google Scholar] [CrossRef]
- Sokoletsky, L.G.; Nikolaeva, O.V.; Budak, V.P.; Bass, L.P.; Lunetta, R.S.; Kuznetsov, V.S.; Kokhanovsky, A.A. A comparison of numerical and analytical radiative-transfer solutions for plane albedo of natural waters. J. Quant. Spectrosc. Radiat. Transf. 2009, 110, 1132–1146. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, A.; Zhu, L.; Lv, W.; Xu, J.; Li, S.; Wang, J. Performance evaluation of underwater optical communications using spatial modes subjected to bubbles and obstructions. Opt. Lett. 2017, 42, 4699–4702. [Google Scholar] [CrossRef] [PubMed]
- Shen, C.; Guo, Y.; Oubei, H.M.; Ng, T.K.; Liu, G.; Park, K.H.; Ho, K.T.; Alouini, M.S.; Ooi, B.S. 20-meter underwater wireless optical communication link with 1.5 Gbps data rate. Opt. Express 2016, 24, 25502–25509. [Google Scholar] [CrossRef] [PubMed]
- Lewis, M.R.; Cullen, J.J.; Platt, T. Phytoplankton and thermal structure in the upper ocean: Consequences of nonuniformity in chlorophyll profile. J. Geophys. Res. Ocean. 1983, 88, 2565–2570. [Google Scholar] [CrossRef]
- Morel, A.; Gentili, B.; Claustre, H.; Babin, M.; Bricaud, A.; Ras, J.; Tieche, F. Optical properties of the “clearest” natural waters. Limnol. Oceanogr. 2007, 52, 217–229. [Google Scholar] [CrossRef]
- Morel, A. Optical modeling of the upper ocean in relation to its biogenous matter content (case I waters). J. Geophys. Res. Ocean. 1988, 93, 10749–10768. [Google Scholar] [CrossRef]
- Buonassissi, C.; Dierssen, H. A regional comparison of particle size distributions and the power law approximation in oceanic and estuarine surface waters. J. Geophys. Res. Ocean. 2010, 115. [Google Scholar] [CrossRef]
- Li, M.; Wang, Z.; Luo, J.; Liu, Y.; Cai, S. Wavelet denoising of vehicle platform vibration signal based on threshold neural network. Shock Vib. 2017, 2017, 7962828. [Google Scholar] [CrossRef]
- Yan, B.; Pei, T.; Wang, X. Wavelet method for automatic detection of eye-movement behaviors. IEEE Sens. J. 2018, 19, 3085–3091. [Google Scholar] [CrossRef]
- Du, S.; Chen, S. Study on optical fiber gas-holdup meter signal denoising using improved threshold wavelet transform. IEEE Access 2023, 11, 18794–18804. [Google Scholar] [CrossRef]
- Hu, S.; Zhang, J.; Liu, Q.; Bai, L.; Yi, X.; Xu, B.; Qiu, K. Impacts of the measurement equation modification of the adaptive Kalman filter on joint polarization and laser phase noise tracking. Chin. Opt. Lett. 2022, 20, 020603. [Google Scholar] [CrossRef]
- Chen, P.; Ma, H.; Gao, S.; Huang, Y. Modified extended Kalman filtering for tracking with insufficient and intermittent observations. Math. Probl. Eng. 2015, 2015, 981727. [Google Scholar] [CrossRef]


| Parameters | ||||||
|---|---|---|---|---|---|---|
| Value | 0.97 | 0.91 | 3 mm | 8 mm | 1.12 mrad | A/W |
| Type of Seawater | a () | b () | c () |
|---|---|---|---|
| Pure seawater | 0.053 | 0.003 | 0.056 |
| Clear seawater | 0.114 | 0.037 | 0.151 |
| Coastal seawater | 0.179 | 0.219 | 0.298 |
| Turbid harbor water | 0.295 | 1.875 | 2.17 |
| Denoising Algorithm | SNR | RMSE |
|---|---|---|
| Noisy signal | 10 | 0.2236 |
| Hard threshold | 6.4905 | 0.3349 |
| Soft threshold | 10.2752 | 0.2116 |
| Denoising Algorithm | SNR | RMSE |
|---|---|---|
| Noisy signal | 21.4 | 0.18 |
| Mean filter | 25.13 | 0.145 |
| Wavelet analysis | 25.9 | 0.137 |
| Adaptive Kalman filter | 24.68 | 0.151 |
| DWT-AKF | 26.7 | 0.124 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, W.; Wang, H.; Zhang, M.; Wang, Y. Research on Underwater Laser Communication Channel Attenuation Model Analysis and Calibration Device. J. Mar. Sci. Eng. 2025, 13, 1483. https://doi.org/10.3390/jmse13081483
Cai W, Wang H, Zhang M, Wang Y. Research on Underwater Laser Communication Channel Attenuation Model Analysis and Calibration Device. Journal of Marine Science and Engineering. 2025; 13(8):1483. https://doi.org/10.3390/jmse13081483
Chicago/Turabian StyleCai, Wenyu, Hengmei Wang, Meiyan Zhang, and Yu Wang. 2025. "Research on Underwater Laser Communication Channel Attenuation Model Analysis and Calibration Device" Journal of Marine Science and Engineering 13, no. 8: 1483. https://doi.org/10.3390/jmse13081483
APA StyleCai, W., Wang, H., Zhang, M., & Wang, Y. (2025). Research on Underwater Laser Communication Channel Attenuation Model Analysis and Calibration Device. Journal of Marine Science and Engineering, 13(8), 1483. https://doi.org/10.3390/jmse13081483






