Precise Tracking Control of Unmanned Surface Vehicles for Maritime Sports Course Teaching Assistance

Abstract

With the rapid advancement of maritime sports, the integration of auxiliary unmanned surface vehicles (USVs) has emerged as a promising solution to enhance the efficiency and safety of maritime education, particularly in tasks such as buoy deployment and escort operations. This paper presents a novel high-precision trajectory tracking control algorithm designed to ensure stable navigation of the USVs along predefined competition boundaries, thereby facilitating the reliable execution of buoy placement and escort missions. First, the paper proposes an improved adaptive fractional-order nonsingular fast terminal sliding mode control (AFONFTSMC) algorithm to achieve precise trajectory tracking of the reference path. To address the challenges posed by unknown environmental disturbances and unmodeled dynamics in marine environments, a nonlinear lumped disturbance observer (NLDO) with exponential convergence properties is proposed, ensuring robust and continuous navigation performance. Additionally, an artificial potential field (APF) method is integrated to dynamically mitigate collision risks from both static and dynamic obstacles during trajectory tracking. The efficacy and practical applicability of the proposed control framework are rigorously validated through comprehensive numerical simulations. Experimental results demonstrate that the developed algorithm achieves superior trajectory tracking accuracy under complex sea conditions, thereby offering a reliable and efficient solution for maritime sports education and related applications.

1. Introduction

The rapid proliferation of maritime sports and teaching activities has substantially increased the need for reliable and high-performance auxiliary systems [1,2,3]. Unmanned surface vehicles (USVs) have emerged as pivotal platforms for improving maritime support operations, including precision buoy deployment [4,5] and athlete safeguarding [6,7], by enabling accurate path-following along designated competition perimeters. Nevertheless, attaining high-fidelity trajectory tracking in complex marine environments—characterized by stochastic disturbances, unmodeled hydrodynamic effects, and dynamic obstacles—constitutes a persistent technical hurdle [8,9]. Traditional tracking control strategies often struggle to maintain stability and accuracy in such environments, necessitating advanced control frameworks that integrate robustness, adaptability, and real-time disturbance rejection [10,11].

1.1. Related Works

Path tracking involves guiding the USV along a predefined trajectory from an initial position to a target destination, with relaxed temporal and velocity constraints. However, the inherently complex and dynamic marine environment introduces time-varying hydrodynamic forces and external disturbances, significantly complicating the control problem. Conventional control algorithms often fail to guarantee robust tracking performance under such conditions, necessitating the development of advanced nonlinear control strategies to address these challenges. Consequently, the design of high-performance path tracking controllers has emerged as a critical research focus in marine robotics [12,13].

Commonly used nonlinear control algorithms in the realm of the USV control include: the sliding mode control (SMC) algorithm [14,15,16], Backstepping control [11,17], line-of-sight (LOS) guidance algorithm [18], model prediction control (MPC) [19], and intelligent control approaches incorporating neural networks [20]. Among these, SMC exhibits distinct advantages for marine applications due to its finite-time convergence property and inherent robustness to matched disturbances (e.g., wave and current effects). By employing a well-designed sliding surface, SMC ensures system state convergence while maintaining complete disturbance rejection characteristics. These features make SMC particularly effective for handling abrupt wave disturbances and payload variations during maritime operations, thereby providing a reliable control framework for critical tasks such as competition boundary surveillance and precision buoy deployment. Experimental research demonstrates that conventional SMC maintains satisfactory tracking performance, with position errors constrained below 0.5 m under Beaufort scale 3 sea conditions [21]. To enhance control performance, the nonsingular fast terminal sliding mode control (NFTSMC) strategy has been developed, featuring a nonlinear sliding surface design that guarantees finite-time system state stabilization while significantly accelerating convergence rates. Comparative studies reveal that NFTSMC achieves a 40% reduction in settling time compared to conventional SMC approaches [22]. Furthermore, recent advances in [23] present a model-free higher-order SMC framework that incorporates temporal constraints in the control law synthesis, enabling both finite-time reference path tracking and a 50% reduction in energy consumption relative to baseline controllers. Study [18] designs an adaptive sliding mode controller combined with LOS guidance to realize USV motion control, and a nonlinear SMC algorithm is proposed to achieve the path tracking of underactuated USV in the presence of uncertain parameters and unknown external disturbances. Following up on this, study [24] proposes a fractional-order terminal sliding mode (FOTSM) control strategy based on dynamic neural fuzzy for rigid robot tracking control. All the aforementioned studies can effectively demonstrate the considerable advantage of SMC in the process of the USV path tracking. However, it still faces defects such as slow convergence speed, low robustness, and weak anti-disturbance ability.

During unmanned surface vehicle (USV) path tracking, actuator saturation, slow convergence rates, and time-varying model parameters—induced by environmental disturbances (e.g., wind, waves, and currents)—pose significant challenges to accurate dynamical modeling. These factors necessitate robust disturbance rejection strategies. Adaptive robust sliding mode control (ARSMC) addresses such uncertainties by synthesizing adaptive laws that compensate for bounded parameter perturbations, thereby enhancing trajectory tracking performance. Owing to its proven efficacy in handling nonlinearities and external disturbances, ARSMC has become a cornerstone technique for improving stability and robustness in unmanned systems [14,25]. In study [14], an adaptive robust sliding mode control method is proposed to compensate for the influence of uncertainties and nonlinear disturbances in the navigation process on the tracking performance. However, the effective premise of the adaptive robust sliding mode control method is that the parameter fluctuations and disturbance range are bounded, thus a relatively accurate evaluation model of system output error needs to be established. For systems where it is impossible to establish an accurate disturbance model or the disturbance numerical boundaries and action characteristics are not clear, a disturbance observer can be designed to estimate the disturbances and uncertainties in the system [26,27]. In literature [28], a nonlinear disturbance observer is first proposed and applied to the control links of a robotic arm to compensate for the disturbance of friction in the control force. Study [29] systematically summarizes disturbance estimation technology and compensation methods and provides the design steps for a nonlinear disturbance observer. In study [30,31], the disturbance observer is combined with sliding mode control and applied to USV tracking control and multi USVs formation control, respectively, fully demonstrating the feasibility of combining the nonlinear disturbance observer with the adaptive sliding mode control theory and applying it to the field of the USV control.

1.2. Contributions and Organization

To address these challenges, this paper proposes a novel tracking control framework combining an improved adaptive fractional-order nonsingular fast terminal sliding mode control (AFONFTSMC) algorithm with a nonlinear lumped disturbance observer (NLDO). The AFONFTSMC ensures finite-time convergence and high-precision trajectory tracking, while the NLDO compensates for environmental disturbances with exponential convergence, guaranteeing stable and continuous navigation. Furthermore, an improved artificial potential field (APF) method is integrated to dynamically avoid both static and dynamic obstacles, enhancing operational safety. Through rigorous numerical simulations, the proposed method is validated to achieve superior trajectory tracking performance under realistic sea conditions, demonstrating its potential to significantly improve the efficiency and reliability of maritime sports education. The present study makes the following significant contributions to the field of maritime robotics and sports education technology:

(1)

An adaptive fractional-order nonsingular fast terminal sliding mode control (AFONFTSMC) algorithm is proposed, which integrates fractional-order calculus with nonsingular fast terminal sliding mode control (NFTSMC). This approach eliminates the singularity problem inherent to conventional sliding mode control while leveraging fractional-order dynamics to enhance convergence speed and tracking accuracy. Additionally, an adaptive mechanism dynamically estimates the upper bounds of system uncertainties and disturbances, reducing the reliance on precise mathematical models and improving robustness in complex marine environments.

(2)

To address the challenges posed by internal unmodeled dynamics and external environmental disturbances, a nonlinear lumped disturbance observer (NLDO) with exponential convergence is designed. This observer effectively compensates for unknown disturbances in real time, ensuring global stability and high-precision trajectory tracking even under harsh sea conditions. The integration of NLDO with AFONFTSMC provides a comprehensive control framework that enhances the reliability of the USV operations in dynamic maritime scenarios.

(3)

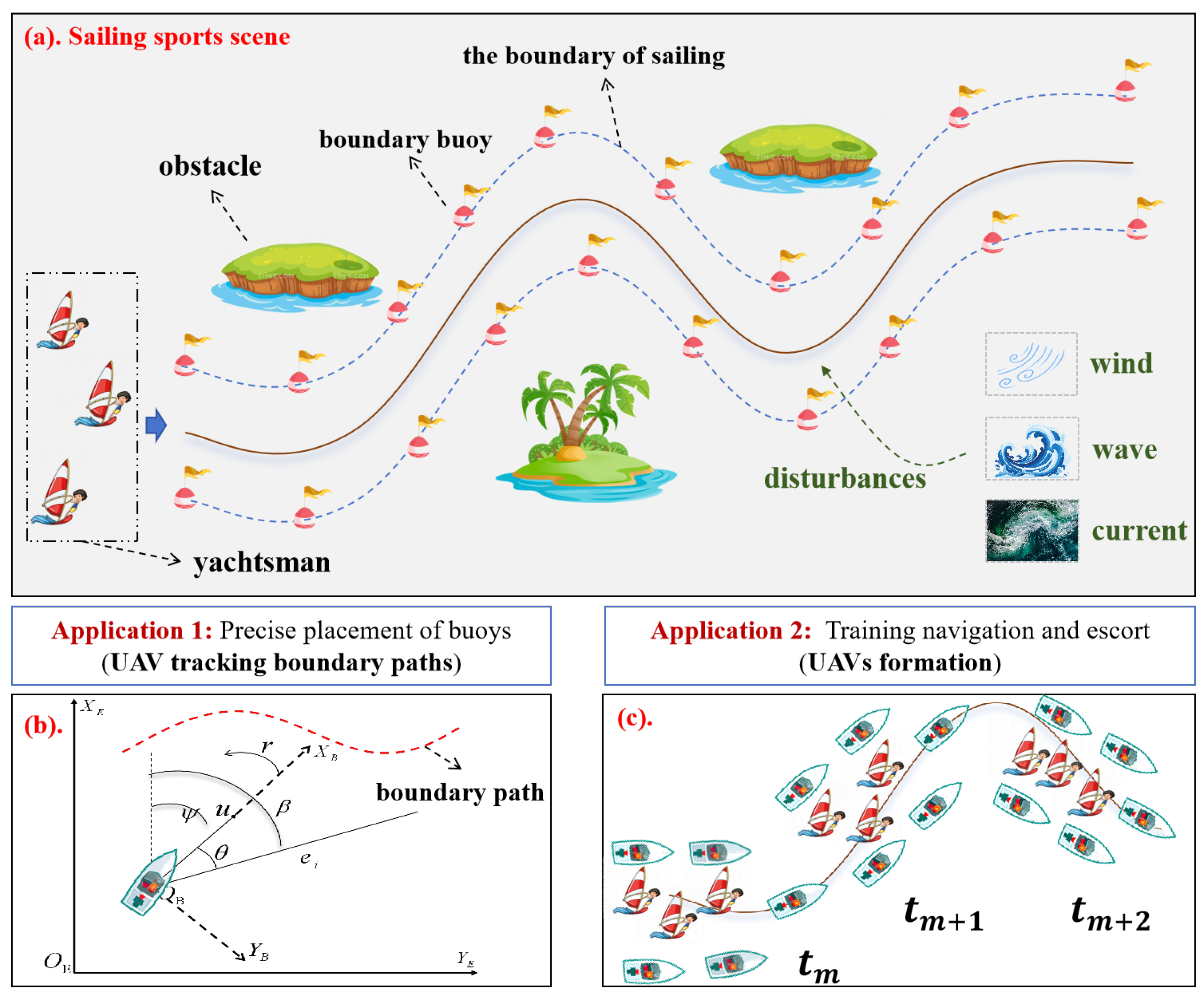
A realistic maritime sports scenario involving multiple static and dynamic obstacles is constructed to validate the proposed control strategy. Numerical simulations demonstrate the superior tracking performance and adaptability of the proposed algorithms in obstacle-rich environments, highlighting their potential for practical applications such as buoy deployment, athlete escort, and competition boundary patrolling. The proposed framework incorporates the APF approach to facilitate obstacle avoidance in complex maritime environments, which proves particularly essential for mission-critical operations, including athlete accompaniment and precision buoy deployment.

These contributions offer a robust, adaptive, and practically viable solution for enhancing safety and efficiency in maritime sports and educational applications.

The remainder of this paper is systematically structured as follows: Section 2 presents the fundamental mathematical modeling of the USV system along with essential theoretical preliminaries. In Section 3, a nonlinear lump disturbance observer is developed and subsequently integrated with the proposed AFONFTSMC trajectory tracking controller. Comprehensive numerical simulations and comparative analyses are conducted in Section 4 to validate the effectiveness of the proposed control framework under various operational scenarios. Finally, Section 5 concludes the paper by summarizing key findings.

2. Preliminaries

2.1. Basic Theories

This section provides the main introduction to the fractional-order control principle and some theorems and lemmas used in this study, and defines and assumes some parameters in the USV system.

Refer to the following system model [32]:

$$\begin{array}{c}\hfill \begin{array}{c}\dot{\pi }\left(t\right)=f\left(\pi \left(t\right)\right)\hfill \\ \pi \left(0\right)={\pi }_0,f\left(0\right)=0,\pi \in Z_0\subset R^n\hfill \end{array}\end{array}$$

(1)

where $\pi$ is the variable of system and $f\left(\pi \right(t\left)\right)$ is delineated as a continuous nonlinear function within the vicinity of the origin $Z_0$.

Definition 1

([33]). The main form of the Caputo-type definition of the fractional-order calculus is as follows:

$$\begin{array}{c}\hfill {}_{t_0}D_t^{\alpha }\pi \left(t\right)={\displaystyle \frac{1}{\Gamma \left(m-\alpha \right)}}{\int }_{\alpha }^t{\displaystyle \frac{{\pi }^{\left(m\right)}\left(\tau \right)}{{\left(x-\tau \right)}^{\alpha -m+1}}}d\tau \end{array}$$

(2)

where $m-1<a<m,m$ is a certificate, and $\Gamma \left(m-\alpha \right)$ is the gamma function with independent variables m-a.

Definition 2

([34]). The main form of the RL (Riemann–Liouville)-type definition of the fractional-order calculus on is as follows:

$$\begin{array}{c}\hfill {}_{\alpha }{}^{RL}D_t^{\alpha }\pi \left(t\right)={\displaystyle \frac{1}{\Gamma \left(m-\alpha \right)}}{\displaystyle \frac{d^m}{d{t}^m}}{\int }_{\alpha }^t{\displaystyle \frac{\pi \left(\tau \right)}{{\left(t-\tau \right)}^{\alpha -m+1}}}d\tau \end{array}$$

(3)

The RL-type definition combines Cauchy’s integral formula and ordinary derivatives to define m, which takes the same form as that of Definition 1 and mainly integrates m-a and then performs m-order differentiation.

Property 1.

Fractional-order calculus mainly satisfies three properties: exchange law, union law, and linear property [35].

Exchange law: ${}_{t_0}{}^{C}D_t^p\left({}_{t_0}{}^{C}D_t^{q}g\left(\pi \left(t\right)\right)\right)={}_{t_0}{}^{C}D_t^q\left({}_{t_0}{}^{C}D_t^{p}g\left(\pi \left(t\right)\right)\right)$

Union law: ${}_{t_0}{}^{C}D_t^p\left({}_{t_0}{}^{C}D_t^{\pm q}g\left(\pi \left(t\right)\right)\right)={}_{t_0}{}^{C}D_t^{p\pm q}g\left(\pi \left(t\right)\right)$

Linear property: ${}_{t_0}{}^{C}D_t^p\left(\ell f\left(\pi \left(t\right)\right)+ng\left(\pi \left(t\right)\right)\right)=\ell {}_{t_0}{}^{C}D_t^{p}f\left(\pi \left(t\right)\right)+{nD}_t^{p}g\left(\pi \left(t\right)\right)$

Lemma 1

([36]). Consider if the system is $\pi \left(t\right)$ and its Lyapunov function $\mathrm{I}\left(t\right)$ satisfies the following properties:

$$\begin{array}{c}\hfill \mathrm{I}\left(t\right)\le -{\mu }_a\mathrm{I}\left(t\right)-{\mu }_b{\mathrm{I}}^{\rho }\left(t\right),\forall \ge t_0,\mathrm{I}\left(t_0\right)\ge 0\end{array}$$

(4)

where ${\mu }_a>0$, ${\mu }_b>0$, $0<\rho <1$, and $t_0$ are the initial values of the system; then, the system stabilizes in a finite time, and the finite time is:

$$\begin{array}{c}\hfill t_d\le t_0+{\displaystyle \frac{1}{{\mu }_a\left(1-\rho \right)}}ln{\displaystyle \frac{{\mu }_a{\mathrm{I}}^{1-\rho }\left(t_0\right)+{\mu }_b}{{\mu }_b}}\end{array}$$

(5)

This lemma provides a theoretical basis for the stability proof of the precise trajectory tracking controller and disturbance observer designed in this paper.

Assumption 1

([37]). The matrices ${\mathrm{K}}_0^{-1}$ and ${\dot{\mathrm{K}}}_0$ are bounded, i.e., they satisfy ${\mathrm{K}}_0^{-1}\le \beta$ and $∥{\dot{\mathrm{K}}}_0∥\le \hslash$

Assumption 2

([38]). The full disturbance $d\left(t\right)$ of the system and its derivatives are bounded, i.e., satisfy $∥d\left(t\right)∥\le d_0$, $∥\dot{d}\left(t\right)∥\le d_1$.

2.2. USV Mathematical Model

As shown in Figure 1, where Figure 1a is typical maritime sports scene, USV and sailing athletes are similar; in the sailing process, they need to be based on fixed route sailing, and in the sailing process they are subject to wind, waves, currents, and other complex perturbations in the external environment. Figure 1b shows one of the applications of the USV in sailing, which is mainly used for the placement of buoys to guide the sailing route before sailing and mainly analyses the multi-dimensional force of the USV in the sailing process, while Figure 1c shows the USV further leading the players to navigate according to the routes in sailing. The USV model used in this study is based on the well-established Cybership II model, which has been widely adopted as a benchmark for the development and validation of trajectory tracking and control algorithms in marine applications. This model captures the essential nonlinear dynamics of underactuated surface vessels operating in the horizontal plane, including surge, sway, and yaw motions [39]. The model can be designed as:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\dot{\mathit{\eta }}=\mathit{R}\left(\mathit{\psi }\right)\mathit{\nu }\hfill \\ \mathit{M}\dot{\mathit{\nu }}+\mathit{C}\left(\mathit{\nu }\right)\mathit{\nu }+\mathit{D}\left(\mathit{\nu }\right)\mathit{\nu }=\mathit{\tau }+\mathit{d}\hfill \end{array}\right.\end{array}$$

(6)

where $X_E{O}_E{Y}_E$ is the geodetic coordinate system, $X_B{O}_B{Y}_B$ is the inertial coordinate system, $\mathit{\eta }$ = ${[x_e,y_e,\psi ]}^{\mathrm{T}}$ is the position of the USV, $\mathit{\nu }={[u,v,r]}^{\mathrm{T}}$ represents the velocity vector, and $\psi$ is the steering angle and r represents the angular velocity. $\mathit{\tau }$ is the control input vector of the USV, whose vector satisfies $\mathit{\tau }$ = ${[{\tau }_{\mathrm{k}1},0,{\tau }_{\mathrm{k}3}]}^{\mathrm{T}}$. $\mathit{d}$ represent the external disturbances to the USV. M, C, R and D are inertia matrix, Coriolis matrix, transformation matrix, and damping matrix, respectively, which characterized are as follows [40]:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}M=\left[\begin{array}{ccc}{m}_{11}& 0& 0\\ 0& m_{22}& m_{23}\\ 0& m_{32}& m_{33}\end{array}\right] C\left(v\right)=\left[\begin{array}{ccc}0& 0& c_{13}\left(v\right)\\ 0& 0& c_{23}\left(v\right)\\ -c_{13}\left(v\right)& -c_{23}\left(v\right)& 0\end{array}\right]\hfill \\ R\left(\psi \right)=\left[\begin{array}{ccc}cos\psi & -sin\psi & 0\\ sin\psi & cos\psi & 0\\ 0& 0& 1\end{array}\right] D\left(v\right)=\left[\begin{array}{ccc}{d}_{11}\left(v\right)& 0& 0\\ 0& d_{22}\left(v\right)& d_{23}\left(v\right)\\ 0& -d_{32}\left(v\right)& d_{33}\left(v\right)\end{array}\right]\hfill \end{array}\right.\end{array}$$

(7)

The parameters within the matrix are defined as shown in

Table 1. The matrix parameters’ definition.

Parameters	Values	Parameters	Values
$m_{11}$	${m-X}_{\dot{\mu }}$	$c_{23}\left(v\right)$	$m_{11}\mu$
$m_{22}$	${m-Y}_{\dot{v}}$	$d_{11}\left(v\right)$	$-X_{\mu }-X_{\left|\mu \right|\mu }\left|\mu \right|$
$m_{23}$	${m{x}_g-Y}_{\dot{r}}$	$d_{22}\left(v\right)$	$-X_u-X_{\left|u\right|u}\left|u\right|-X_{uuu}{u}^2$
$m_{32}$	${m{x}_g-N}_{\dot{v}}$	$d_{23}\left(v\right)$	$-Y_r-Y_{\left|v\right|r}\left|v\right|-Y_{\left|r\right|r}\left|r\right|$
$m_{33}$	${I_z-N}_{\dot{r}}$	$d_{32}\left(v\right)$	$-N_v-N_{\left|v\right|v}\left|v\right|-N_{\left|r\right|v}\left|r\right|$
$c_{13}\left(v\right)$	$-m_{11}-m_{23}r$	$d_{33}\left(v\right)$	$-N_r-N_{\left|v\right|r}\left|v\right|-N_{\left|r\right|r}\left|r\right|$

[41], where m represents the mass, $I_z$ is the moment of inertia, and $N_{\dot{v}}$ represents the hydrodynamic derivative. The desired trajectory is designed as ${\eta }_d$.

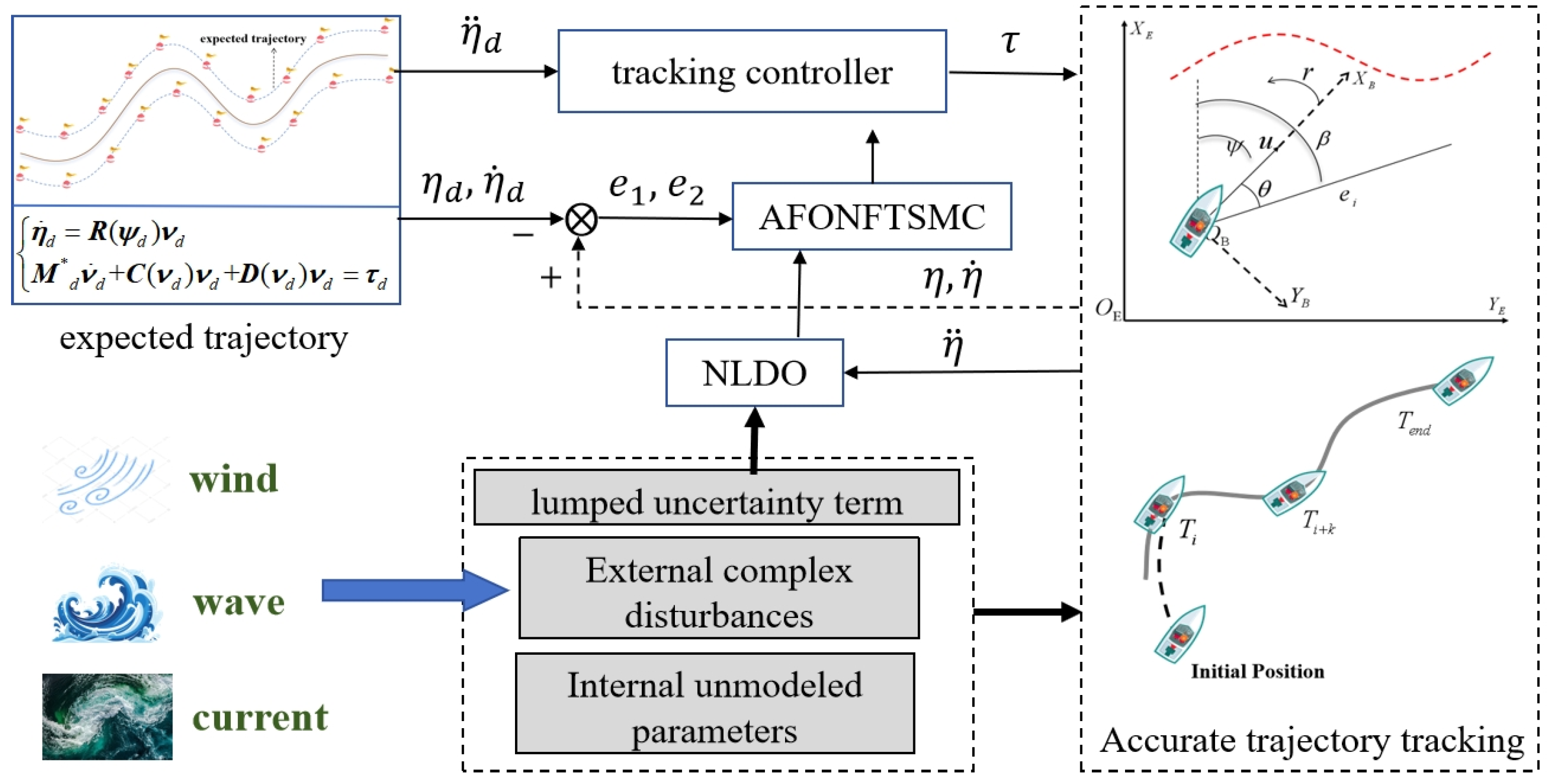
3. Design of the Trajectory Tracking Control Strategy

This section addresses the trajectory tracking problem for unmanned surface vehicle (USV) operating under complex environmental disturbances, including wind, waves, and ocean currents. To achieve robust tracking performance, a comprehensive control framework is proposed that integrates: (1) a nonlinear disturbance observer to estimate and compensate for external perturbations in real-time; (2) a fractional-order fast nonsingular terminal sliding mode control (FOFNTSMC) strategy, which combines the advantages of fractional-order calculus with nonsingular terminal sliding mode control. The proposed approach ensures finite time convergence to the desired trajectory while maintaining system stability against environmental disturbances. The specific algorithm flowchart is shown in Figure 2.

3.1. Design of Disturbance Observer

For the uncertainty of internal model parameters and unknown external disturbances, the exponentially convergent nonlinear lump disturbance observer (NLDO) is designed as:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\dot{\vartheta }=\Gamma \left(o\right)\left(C_0\dot{o}+G_0-\tau \right)-\Gamma \left(o\right)\widehat{d}\hfill \\ \widehat{d}=\vartheta +\zeta \left(\dot{o}\right)\hfill \\ \dot{\zeta }\left(\dot{o}\right)=\Gamma \left(o\right)M_0\ddot{o}\hfill \end{array}\right.\end{array}$$

(8)

where $\vartheta$ is the defined auxiliary variable, $\Gamma \left(o\right)$ is the observation gain matrix that determines the auxiliary vector $\zeta \left(\dot{o}\right)$, and $\widehat{d}$ is the observed value of the perturbation d. $\Gamma \left(o\right)$ and $\zeta \left(\dot{o}\right)$ are defined as:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\Gamma \left(o\right)=X^{-1}{\mathrm{K}}_0^{-1}\hfill \\ \zeta \left(\dot{o}\right)=X^{-1}o\hfill \end{array}\right.\end{array}$$

(9)

where X is an invertible matrix defining the perturbation observer error as:

$$\begin{array}{c}\hfill \tilde{d}=d-\widehat{d}\end{array}$$

(10)

Combined with Equation (8), this gives

$$\begin{array}{c}\hfill \dot{\tilde{d}}=\dot{d}-\Gamma \left(o\right)\tilde{d}\end{array}$$

(11)

Theorem 1

([42]). The USV system tracking the desired trajectory will be disturbed by the external complex environment, and the perturbation tracking is obtained by the observer (8), if the following is satisfied:

1. There exists a positive definite matrix $\Phi$ that satisfies $X+X^T-X^T{\dot{\mathrm{K}}}_{0}X\ge \Phi$;

2. The matrix X is invertible;

3. Assumption 2 holds.

Then, the perturbation error is globally and ultimately uniformly bounded, and the perturbation error converges at an exponential rate ${\displaystyle \frac{\left(1-\theta \right){\kappa }_{min}\left(\Phi \right)}{2{\zeta }_2{∥\mathrm{X}∥}^2}}$ in the spherical domain ${\displaystyle \frac{2{\rho }_1{\zeta }_2{∥\mathrm{X}∥}^2}{\theta {\kappa }_{min}\left(\Phi \right)}}$, where 0 < θ < 1.

Proof of Theorem 1.

Design the Lyapunov function as:

$$\begin{array}{c}\hfill V_d={\tilde{d}}^T{\mathrm{X}}^T{\Pi }_0\mathrm{X}\tilde{d}\end{array}$$

(12)

Solve the derivative as follows:

$$\begin{array}{c}\hfill {\dot{V}}_d=-\left(1-\theta \right){\kappa }_{min}\left(\Phi \right){∥\tilde{d}∥}^2,\forall ∥\tilde{d}∥\ge {\displaystyle \frac{2{\rho }_1{\zeta }_2{∥\mathrm{X}∥}^2}{\theta {\kappa }_{min}\left(\Phi \right)}}\end{array}$$

(13)

The disturbance observation error is bounded by:

$$\begin{array}{c}\hfill ∥\tilde{d}∥\le \sqrt{{\displaystyle \frac{V_d\left(t_0\right)}{{\zeta }_1{\kappa }_{min}\left({\mathrm{X}}^T\mathrm{X}\right)}}}{e}^{-\ell t}+{\displaystyle \frac{2{\rho }_1{\zeta }_2{∥\mathrm{X}∥}^2}{\theta {\kappa }_{min}\left(\Phi \right)}},\forall t\ge t_0,∥\tilde{d}∥\ge {\displaystyle \frac{2{\rho }_1{\zeta }_2{∥\mathrm{X}∥}^2}{\theta {\kappa }_{min}\left(\Phi \right)}},\ell ={\displaystyle \frac{\left(1-\theta \right){\kappa }_{min}\left(\Phi \right)}{2{\zeta }_2{∥\mathrm{X}∥}^2}}\end{array}$$

(14)

□

In summary, Theorem 1 effectively proves that the proposed NLDO can theoretically achieve the effective observation and approximation of lumped disturbances in complex marine environments, further supporting its potential application in practical maritime sports course teaching assistance.

3.2. Design of the USV Tracking Controller Under Ideal Conditions

From Formula (6), the following can be obtained:

$$\begin{array}{c}\hfill \ddot{\eta }=R{M}^{-1}\tau -R{M}^{-1}\left(C\left(\nu \right)+D\left(\nu \right)\right)R^T\dot{\eta }+S\dot{\eta }+R{M}^{-1}\widehat{d}\end{array}$$

(15)

The error between the actual position and the desired position of the USV system is defined as e:

$$\begin{array}{c}\hfill \mathit{e}=\mathit{\eta }-{\mathit{\eta }}_{\mathit{d}}\end{array}$$

(16)

The design of the adaptive fractional-order nonsingular fast terminal sliding mode surface (AFONFTSMS) is executed as delineated:

$$\begin{array}{c}\hfill s=\dot{e}+D^{{\lambda }_1-1}{c}_1{e}^{{\displaystyle \frac{p}{q}}}+I^{{\lambda }_2}{c}_2{e}^{\phi }sgn\left(e\right)\end{array}$$

(17)

where $c1$, $c2$, and $\psi$ are positive parameters; p and q satisfy $1<p/q<2$; and fractional-order derivative ${\lambda }_1$ and ${\lambda }_2$ satisfy $0<{\lambda }_1,{\lambda }_2<1$ where $sgn\left(x\right)=1$, $x>0$ or $sgn\left(x\right)=0$, $x\le 0$.

The derivative of AFONFTSMS (17) is as follows:

$$\begin{array}{c}\hfill \dot{\mathit{s}}=\ddot{\mathit{e}}+{\lambda }_1\mathit{e}+{\lambda }_2{\mathit{e}}^{q/\phantom{qp}p}\end{array}$$

(18)

Let $\dot{s}=0$; the following equation can be obtained:

$$\begin{array}{cc}\hfill \dot{s}=& \ddot{e}+D^{{\lambda }_1}{c}_1{e}^{p/q}+I^{{\lambda }_2}{c}_2\phi {\left|e\right|}^{\phi -1}\dot{e}\hfill \\ \hfill =& \ddot{\eta }-{\ddot{\eta }}_d+D^{{\lambda }_1}{c}_1{e}^{p/q}+I^{{\lambda }_2}{c}_2\phi {\left|e\right|}^{\phi -1}(\dot{\eta }-{\dot{\eta }}_d)\hfill \\ \hfill =& R{M}^{-1}\tau -R{M}^{-1}(C\left(\nu \right)+D\left(\nu \right))R^T\dot{\eta }+S\dot{\eta }\hfill \\ \hfill & +R{M}^{-1}\widehat{d}-{\ddot{\eta }}_d+D^{{\lambda }_1}{c}_1{e}^{p/q}+I^{{\lambda }_2}{c}_2\phi {\left|e\right|}^{\phi -1}\hfill \\ \hfill =& 0\hfill \end{array}$$

(19)

By rewriting Equation (19), the proposed AFONFTSMC tracking control strategy can be obtained:

$$\begin{array}{c}\hfill \tau =\left(C\left(\nu \right)+D\left(\nu \right)\right)R^T\dot{\eta }-M{R}^{-1}S\dot{\eta }+M{R}^{-1}{\ddot{\eta }}_d-\widehat{d}-M{R}^{-1}\left(D^{{\lambda }_1}{c}_1{e}^{{\displaystyle \frac{p}{q}}}+I^{{\lambda }_2}{c}_2\phi {\left|e\right|}^{\phi -1}\right)\end{array}$$

(20)

To achieve fast tracking of the sliding mode surface, the design of the arrival control strategy is:

$$\begin{array}{c}\hfill {\tau }_r=-m_{1}sgn\left(s\right)-m_{2}s-\left(n_1+n_{2}e+n_3\dot{e}+\chi \right)sgn\left(s\right)\end{array}$$

(21)

where $m_1$ and $m_2$ are the control parameters; $\chi$ is the small parameter; and $n_1$, $n_2$, and $n_3$ comprise the updated adaptive law:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{n}_1={\eta }_1\left|s\right|\hfill \\ n_2={\eta }_2\dot{e}\left|s\right|\hfill \\ n_3={\eta }_3\ddot{e}\left|s\right|\hfill \end{array}\right.\end{array}$$

(22)

where ${\eta }_1$, ${\eta }_2$, and ${\eta }_3$ are the design parameters, so the AFONFTSMC strategy for the USV system can be designed by combining the equivalent control law and arrival control law design as:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \tau =& \left(C\left(\nu \right)+D\left(\nu \right)\right)R\dot{\eta }-M{R}^{-1}S\dot{\eta }+M{R}^{-1}{\ddot{\eta }}_d-\widehat{d}-M{R}^{-1}\left(D^{{\lambda }_1}{c}_1{e}^{{\displaystyle \frac{p}{q}}}+I^{{\lambda }_2}{c}_2\phi {\left|e\right|}^{\phi -1}\right)\hfill \\ \hfill & -m_{1}sgn\left(s\right)-m_{2}s-\left(n_1+n_{2}e+n_3\dot{e}+\chi \right)sgn\left(s\right)\hfill \end{array}\end{array}$$

(23)

Theorem 2.

Consider the case where the USV is exposed to external perturbations such as complex external winds, waves, and currents and the external perturbations satisfy Assumption 2; the AFONFTSMC strategy (23) and its adaptive law can ensure that the system is stabilized in a finite amount of time.

Proof of Theorem 2.

The Lyapunov function is designed as:

$$\begin{array}{c}\hfill V={\displaystyle \frac{1}{2}}{s}^2\end{array}$$

(24)

Derivation of the above Equation (24) and further reasoning yields:

$$\begin{array}{cc}\hfill \dot{V}& =s\dot{s}\hfill \\ \hfill & =s\left(\ddot{e}+D^{{\lambda }_1}{c}_1{e}^{p/q}+I^{{\lambda }_2}{c}_2\phi {\left|e\right|}^{\phi -1}\dot{e}\right)\hfill \\ \hfill & =s\left[\ddot{\eta }-{\ddot{\eta }}_d+D^{{\lambda }_1}{c}_1{e}^{p/q}+I^{{\lambda }_2}{c}_2\phi {\left|e\right|}^{\phi -1}(\dot{\eta }-{\dot{\eta }}_d)\right]\hfill \\ \hfill & =s[R{M}^{-1}\tau -R{M}^{-1}(C\left(\nu \right)+D\left(\nu \right))R^T\dot{\eta }+S\dot{\eta }\hfill \\ \hfill & +R{M}^{-1}\widehat{d}-{\ddot{\eta }}_d+D^{{\lambda }_1}{c}_1{e}^{p/q}+I^{{\lambda }_2}{c}_2\phi {\left|e\right|}^{\phi -1}]\hfill \\ \hfill & =s\left[-m_1\mathrm{sgn}\left(s\right)-m_{2}s-(n_1+n_{2}e+n_3\dot{e}+\chi )\mathrm{sgn}\left(s\right)\right]\hfill \\ \hfill & \le -m_1\left|s\right|-m_2{s}^2-(n_1+n_{2}e+n_3\dot{e}+\chi )\left|s\right|\hfill \\ \hfill & \le -(m_1+\chi )\left|s\right|-m_2{s}^2\hfill \\ \hfill & \le -\sqrt{2}(m_1+\chi )V^{1/2}-2m_{2}V\hfill \end{array}$$

(25)

Combining Lemma 1, it can be obtained that the USV system is able to reach the sliding mode surface and stabilize in a finite time; the time is:

$$\begin{array}{c}\hfill t\le t_0+{\displaystyle \frac{2}{\sqrt{2}\left(m_1+\chi \right)}}ln{\displaystyle \frac{\sqrt{2}\left(m_1+\chi \right)V^{\frac{1}{2}}\left(t_0\right)+2m_2}{2m_2}}\end{array}$$

(26)

□

In summary, Theorem 2 rigorously proves that the AFONFTSMC tracking strategy proposed in this paper can theoretically achieve accurate tracking of the expected trajectory, providing preliminary support for the potential application of the algorithm in practical maritime sports course teaching assistance.

4. Numerical Simulation and Discussion Analysis

In this section, rigorous numerical simulations are conducted to validate the effectiveness of the precise trajectory tracking control algorithm proposed in this paper. Specifically, two sets of comparative simulations are conducted to verify the excellent tracking performance of the proposed AFONFTSMC algorithm and further validated that the proposed FLDO can stably handle lump disturbances during the tracking process. Secondly, a typical scenario for auxiliary USV in tracking maritime sports boundaries is constructed, and simulated multiple static and dynamic obstacles in this scenario to further verify the reliability of the proposed tracking control algorithm. To ensure that the numerical simulation results are more realistic, the Cybership II USV model is chosen for the experiment, and the specific parameters are shown in

Table 2. Detailed parameters of the Cybership II USV model [41].

Term	Value	Term	Value	Term	Value
$m_c$	23.8 kg	$Y_v$	$-0.8612$	$X_{\dot{u}}$	$-2.0$
$I_z$	1.76 kg·m2	$Y_{\left|v\right|v}$	$-36.2823$	$Y_{\dot{v}}$	$-10.0$
$X_g$	0.046 m	$Y_r$	$0.1079$	$N_{\dot{v}}$	$0.0$
$X_u$	$-0.7225$	$N_v$	$0.1052$	$N_{\dot{r}}$	$-1.0$
$X_{\left|u\right|u}$	$-1.3274$	$N_{\left|v\right|v}$	$5.0437$	$B_{\dot{I}}$	0.29 m
$X_{uuu}$	$-5.8664$	$Y_{\dot{r}}$	$0.0$	$L_{\dot{i}}$	1.225 m

.

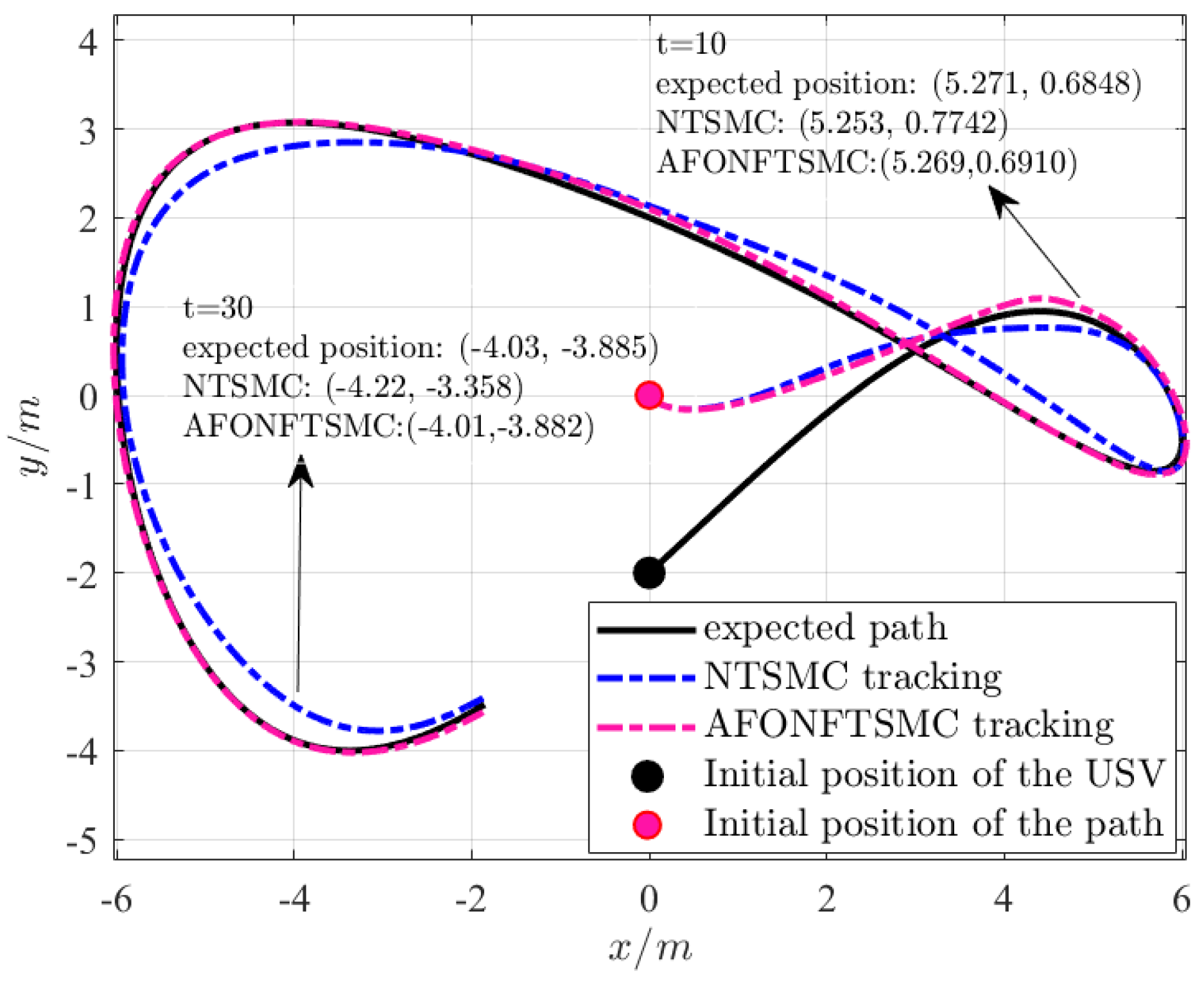
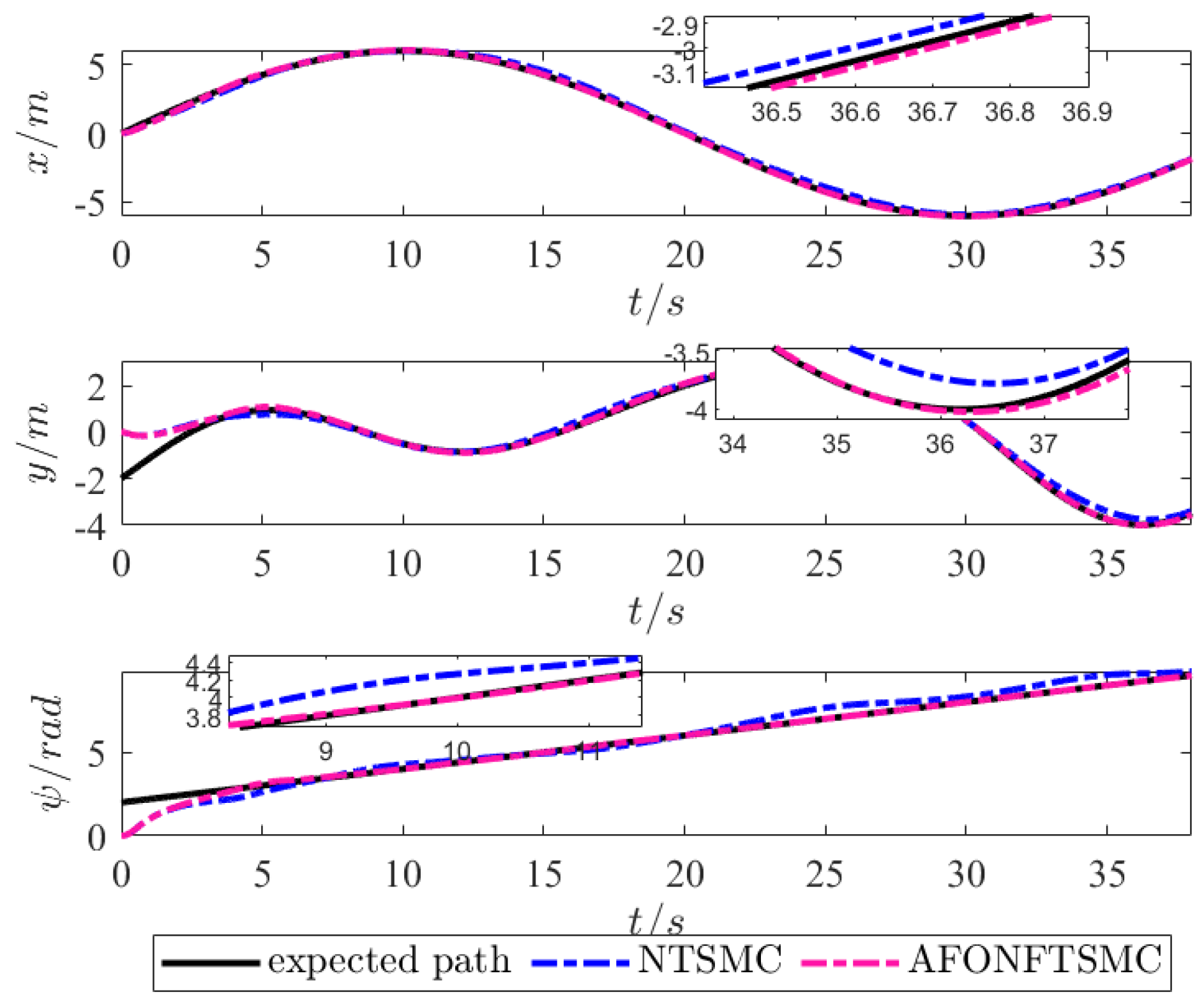
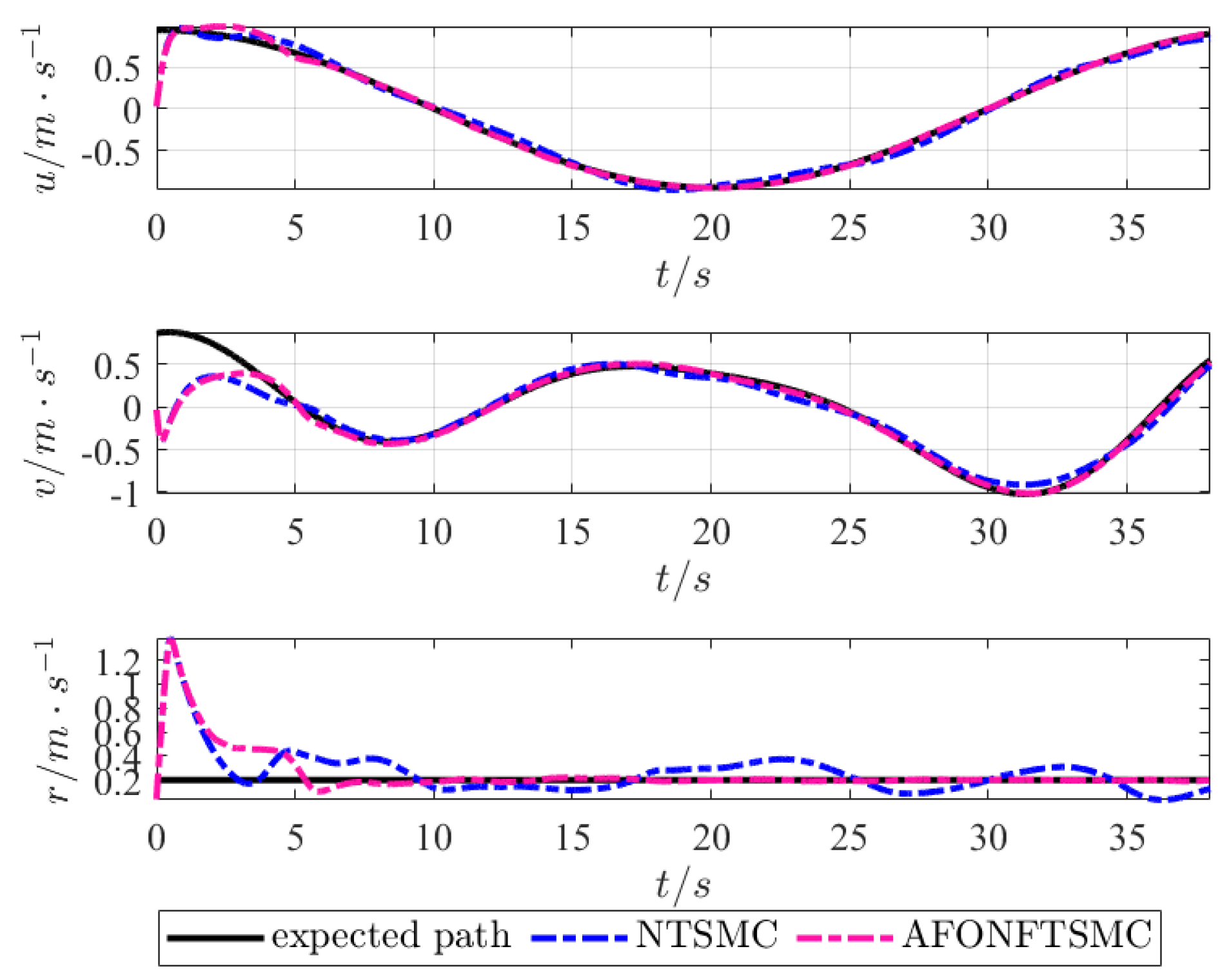
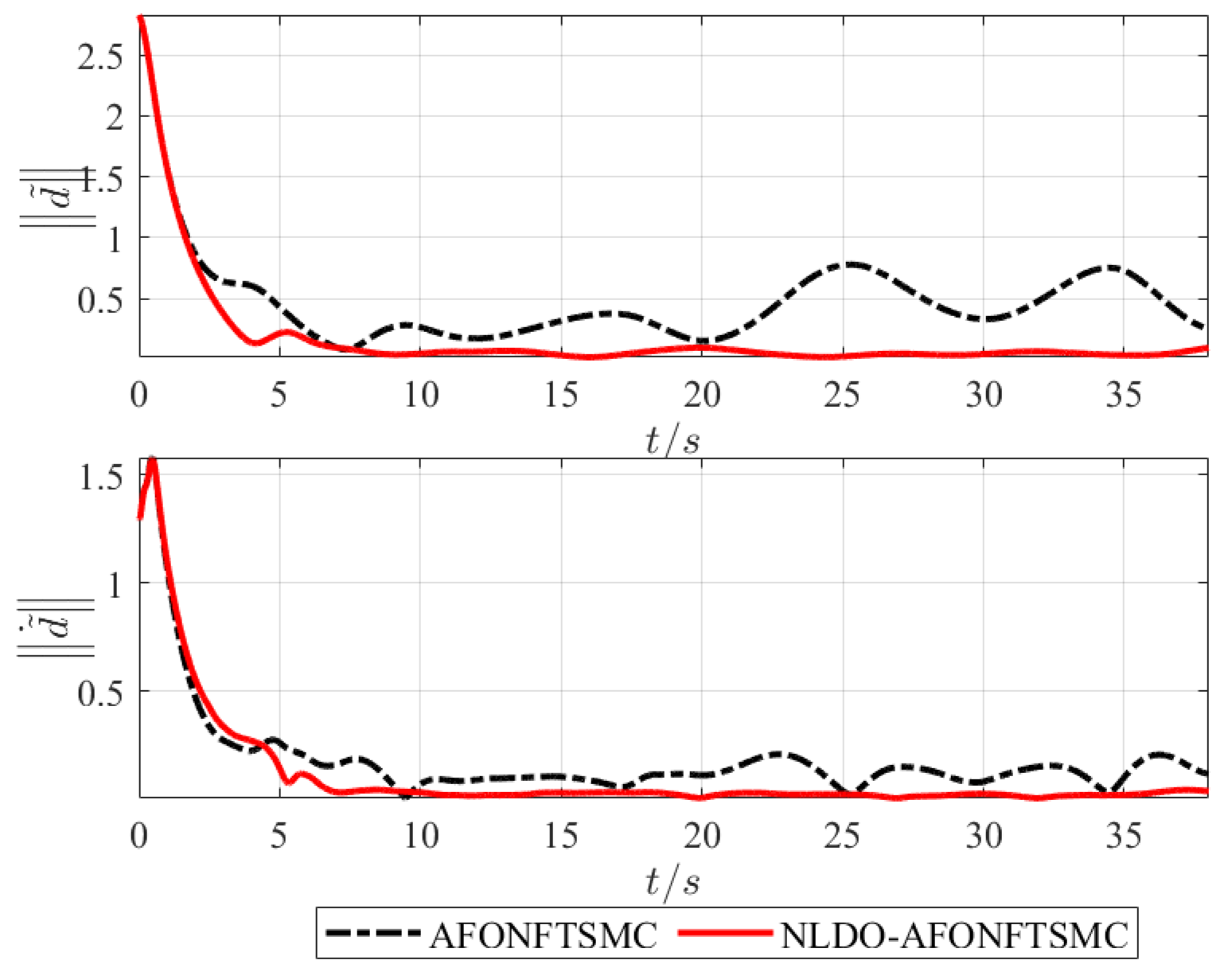
4.1. Comparison Simulation of Tracking Control Algorithms

In this part, two sets of comparative numerical simulations were designed. The first simulation scenario is shown in Figure 3, Figure 4 and Figure 5. The proposed AFONFTSMC tracking algorithm is compared with the NTSMC tracking algorithm [43]. To obtain relatively optimal parameters for the AFONFTSMC, multiple sets of parameters were tested and compared. A qualitative comparison was conducted under this control strategy using different trajectory profiles and parameter configurations, in order to ensure a balanced performance in terms of tracking speed, convergence accuracy, and robustness. The AFONFTSMC parameters after debugging are as follows: $c_1=[0.18,0.18,4{.4]}^T$, $c_2=[0.18,0.18,3{.7]}^T$, $m_1=[2.60,2.604,16.13{]}^T$, $m_2=[0.22,0.22,0.89{]}^T$, ${\lambda }_1={\lambda }_2=[0.99,0.99,0.01{]}^T$, $\chi$ = 3, and $n_1$ = $n_2$ = $n_3$ = 0.01; the lump disturbance term is set as follows: $[8\ast cos(0.1\ast pi\ast t-pi/3)$, $6\ast cos(0.2\ast pi\ast t+pi/2)$, ${2\ast cos(0.1\ast pi\ast t+pi/6)]}^T$; and the initial position of the USV is $(0,0)$. From Figure 3, it can clearly be seen that both algorithms can quickly track the set path, and the proposed AFONFTSMC can achieve global stable tracking control of the path and effectively reduce the chattering caused by controller parameters. However, the NSTMC fluctuates greatly in the actual tracking process and relies too much on precise mathematical models. From Figure 4 and Figure 5, it can be seen that the tracking performance of NTSMC is not as good as AFONFTSMC in different position and velocity dimensions. Especially when a significant adjustment of direction is required, the steering error and angular velocity error of the NTSMC are very obvious, further proving the global effectiveness of the proposed AFONFTSMC tracking algorithm.

The second simulation scenario is shown in Figure 6, Figure 7 and Figure 8. The proposed AFONFTSMC tracking algorithm is compared with the Backstepping tracking algorithm: [17]. In this scenario, a tracking path with a larger turning amplitude is designed to verify the robustness of the tracking algorithm proposed in this paper. From Figure 6, it can be seen that the AFONFTSMC tracking algorithm can still quickly converge to the set path and track stably, while the Backstepping tracking algorithm exhibits significant errors and fluctuations in different dimensions. Then, a set of comparative numerical simulations were conducted to verify the effectiveness of the designed NLDO in response to the lump disturbance term present during the tracking process. As shown in Figure 7, based on the proposed AFONFTSMC tracking algorithm, the tracking performance is significantly improved by observing and approximating the lump disturbance term through NLDO.

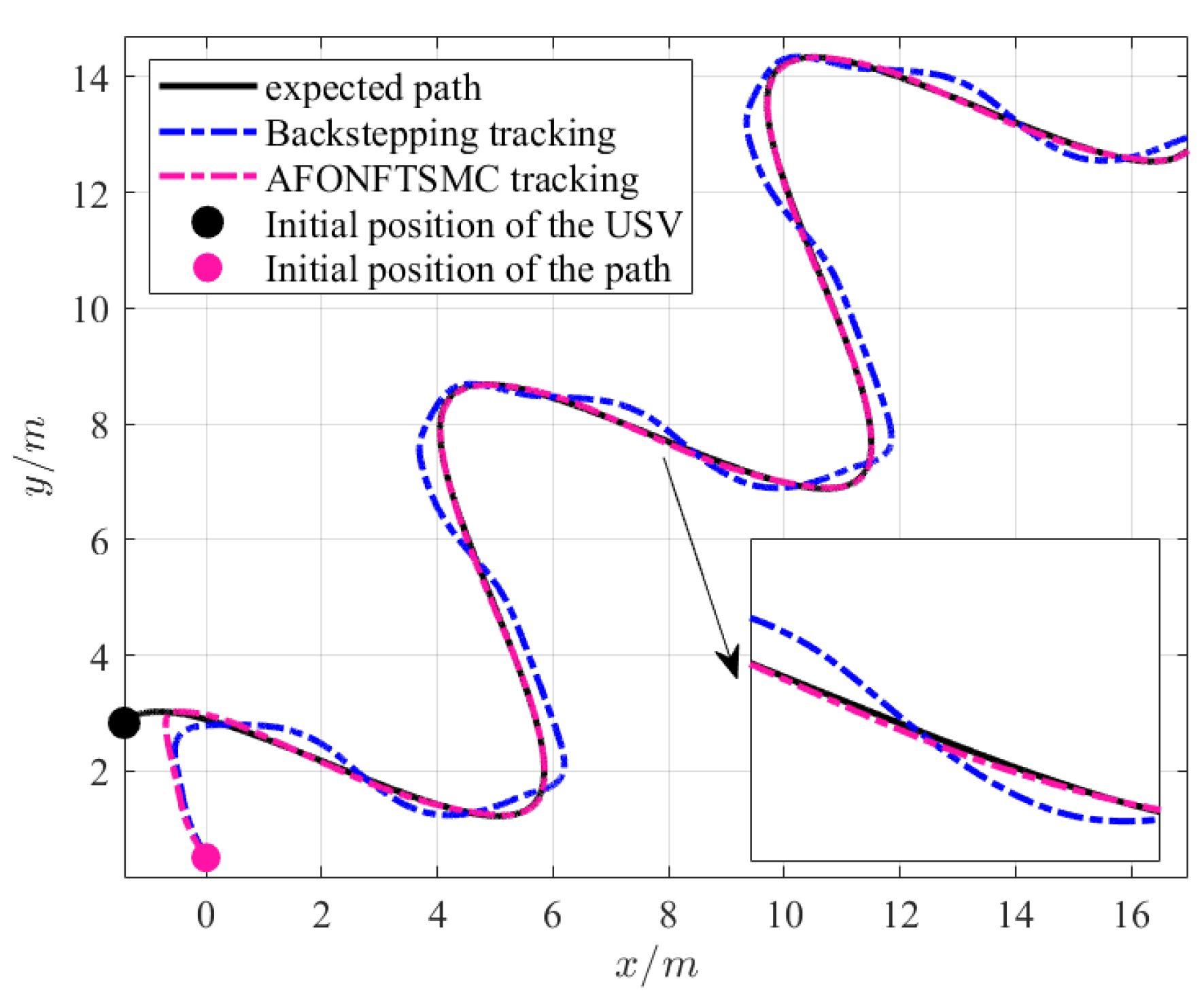
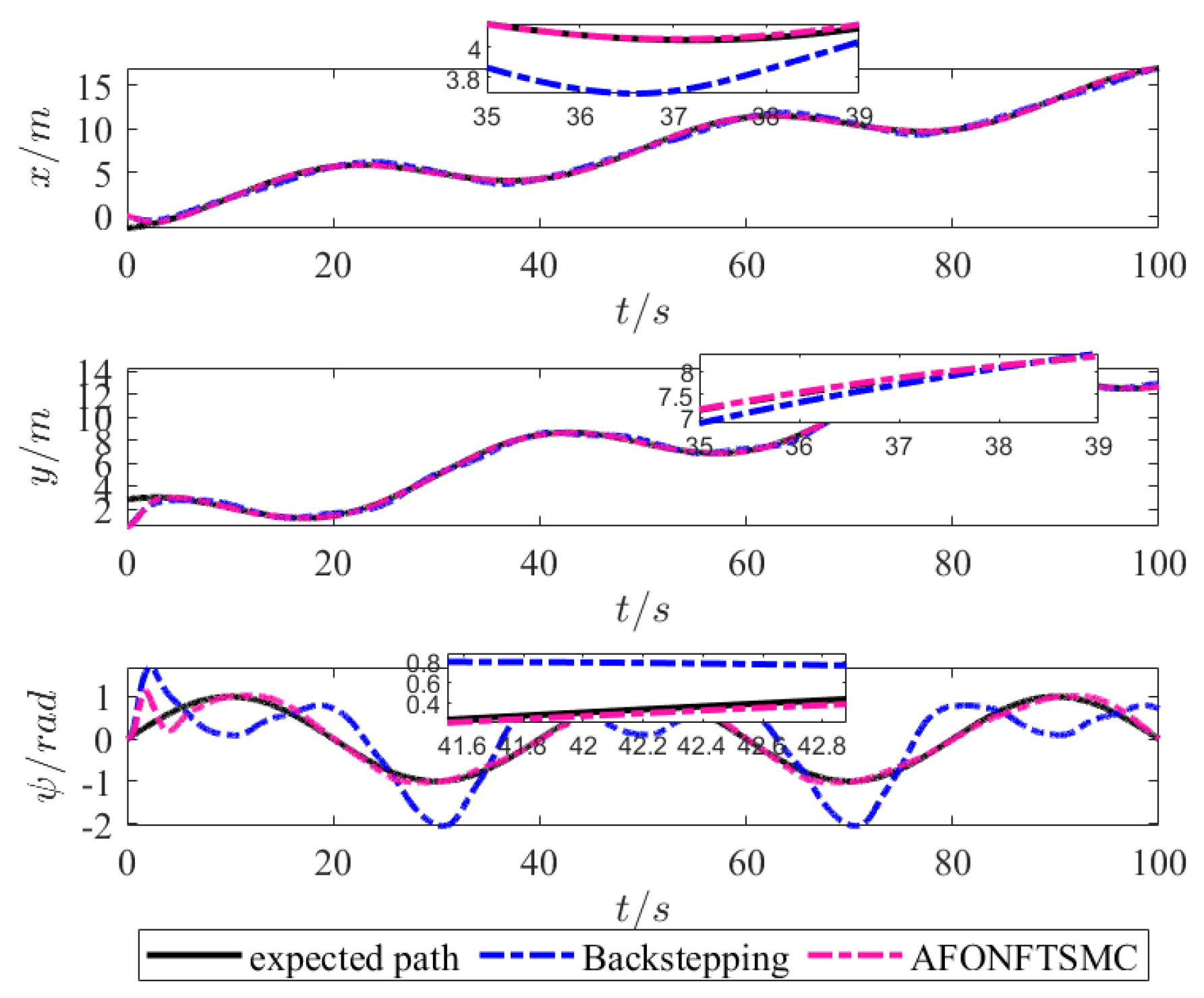
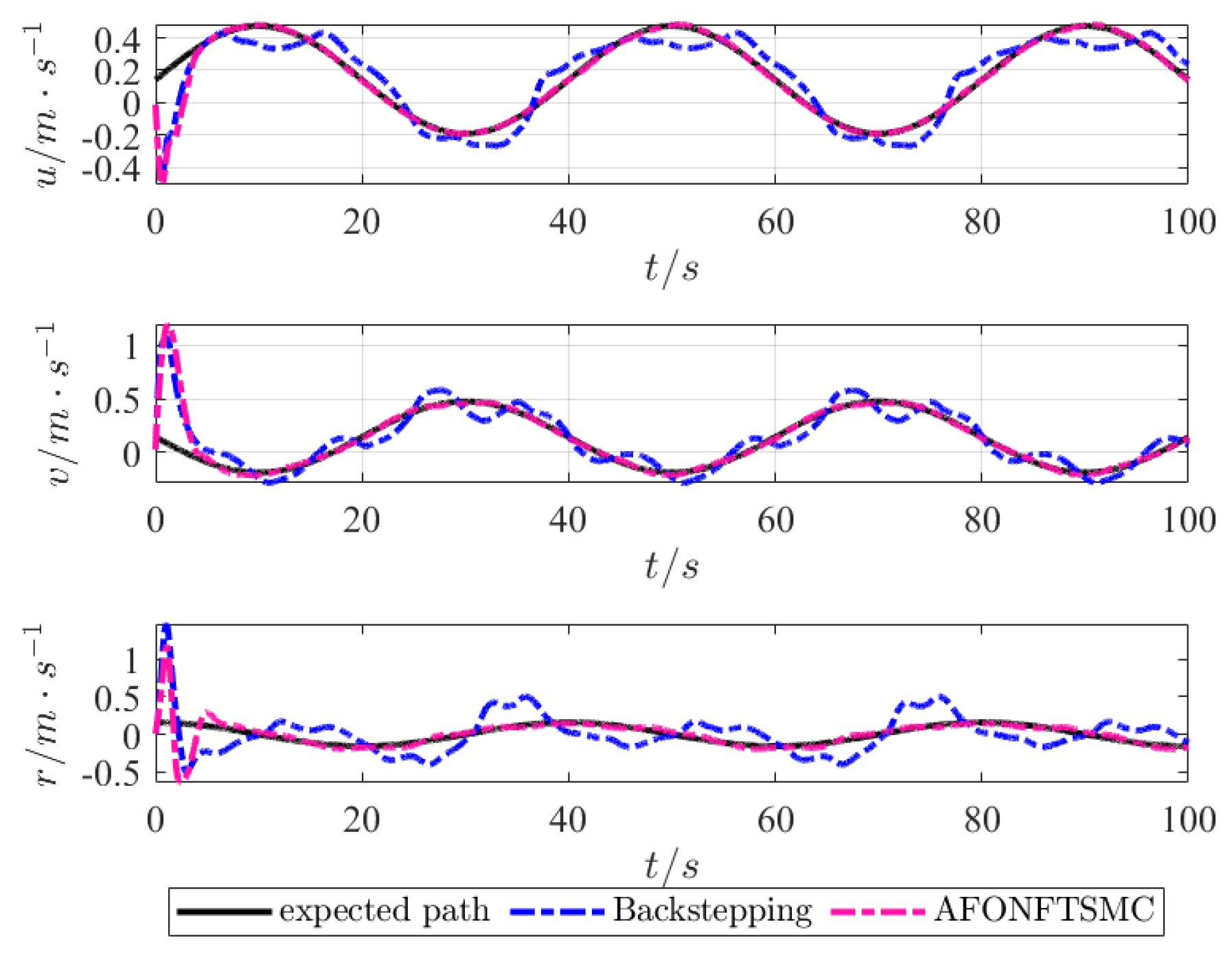
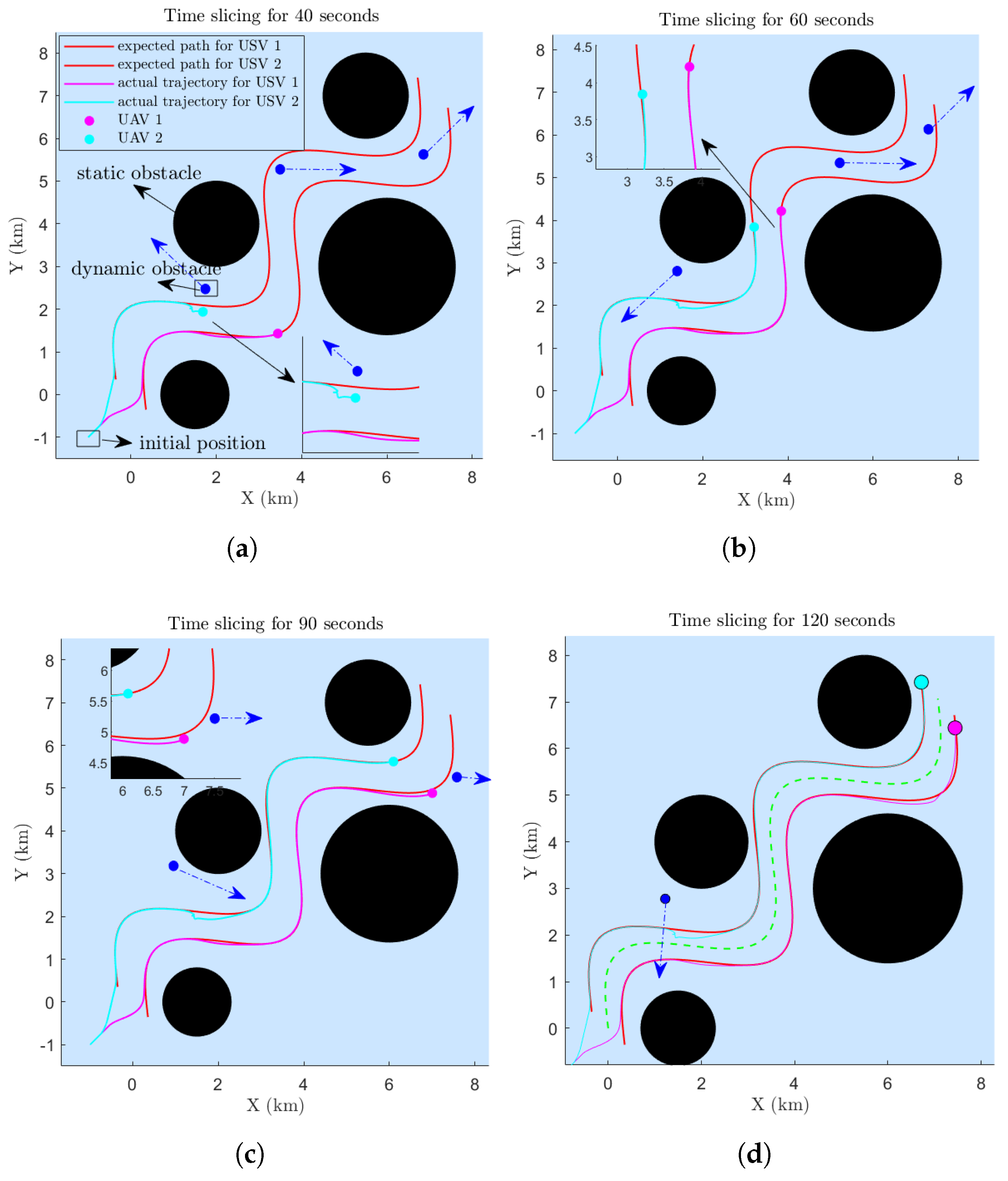
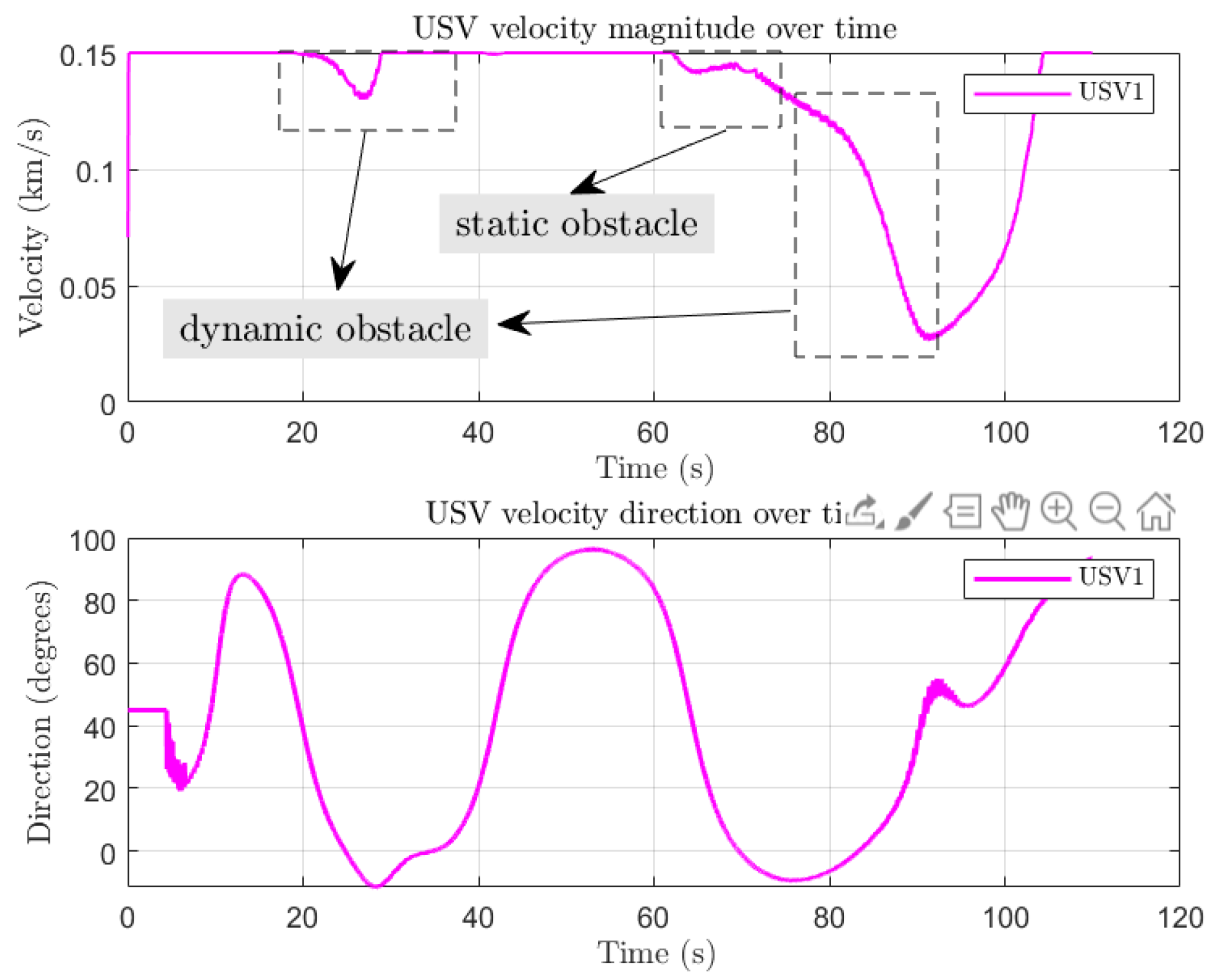
4.2. USVs Assisted Maritime Sports Scenarios: Tracking Boundary Paths

USVs play an important role in practical maritime sports teaching scenarios, such as assisting in the precise placement of indicator buoys and providing navigation and escort for athletes. In this part, a simulation environment containing multiple static and dynamic obstacles was built to verify the scalability of the proposed tracking control algorithm, as shown in Figure 9. The obstacles shown in Figure 10 were all designed based on real-world objects. The static obstacles simulate anchored buoys or floating barriers and are fixed at predetermined positions along the edges of the trajectory. The dynamic obstacles represent slowly moving vessels with limited maneuverability, including instructor boats and support craft, and follow deterministic paths. Specifically, based on the AFONFTSMC tracking algorithm and NLDO proposed in this paper, USVs are controlled to navigate along the boundary of the set maritime sports area while effectively avoiding the threats of dynamic and static obstacles using the artificial potential field method. Figure 10a shows the time slice at 40 s, where USV1 continues to track the path after smoothly avoiding dynamic obstacles, while USV2 actively avoids threats during precise tracking of the expected path. Similarly, Figure 10c shows the time slice at 90 s, further verifying the trajectory tracking performance and threat avoidance ability of the USVs, effectively supporting its potential application in precise placement of buoys and scout scenarios. Figure 11 further illustrates the tracking error; it can clearly be seen that the tracking error of the USVs is extremely small without threat avoidance, and it can quickly recover accurate tracking of the path after threat avoidance. Figure 12 and Figure 13 show the position and velocity tracking curves of the USV1, further verifying the effectiveness of the proposed AFONFTSMC tracking algorithm.

4.3. Discussion

In summary, the simulation results demonstrate the superior performance of the proposed Adaptive Fractional-Order Nonsingular Fast Terminal Sliding Mode Control (AFONFTSMC) algorithm in trajectory tracking for unmanned surface vehicles (USVs), particularly in scenarios involving rapid path adjustments, external disturbances, and dynamic obstacle avoidance. Specifically, the AFONFTSMC algorithm achieves global stable tracking with significantly reduced chattering compared to conventional NTSMC. While both methods initially converge quickly, NTSMC exhibits larger fluctuations during sharp turns, indicating its dependence on precise system modeling and susceptibility to disturbances. In contrast, the adaptive fractional order of AFONFTSMC ensures smoother transitions. Under large turning amplitudes, the Backstepping method suffers from persistent tracking errors and oscillations, whereas AFONFTSMC maintains rapid convergence and stability. This highlights the robustness of the proposed sliding mode strategy against nonlinearities and unmodeled dynamics. The Nonlinear Disturbance Observer (NLDO) further enhances the performance of AFONFTSMC by actively compensating for lumped disturbances. Through rigorous theoretical proof and numerical simulation, potential applications in maritime sports competitions and educational scenarios have been effectively demonstrated.

5. Conclusions

This study presents a novel control framework to enhance the precision and reliability of unmanned surface vehicles (USVs) in maritime sports education, addressing critical challenges in trajectory tracking, disturbance rejection, and obstacle avoidance. First, the proposed AFONFTSMC integrates fractional-order calculus with adaptive sliding mode control, resolving the singularity and chattering issues of traditional methods while achieving finite-time convergence. This advancement enables USVs to execute high-precision maneuvers, such as sharp turns during buoy deployment, a significant improvement over NTSMC and Backstepping. Then, the proposed NLDO compensates for lumped disturbances without requiring precise system models, ensuring stable performance under uncertainties, which directly addresses the limitations of model-dependent controllers. By integrating the APF method, the framework enables collision-free navigation in cluttered environments, critical for tasks like athlete escort and buoy placement. This work bridges a gap between theoretical control design and maritime education needs, offering a scalable solution for automating labor-intensive tasks. Future work will focus on hardware validation and adaptive learning for time-varying disturbances.