Abstract
The novel enhanced dynamic game method (EDGM) is proposed to advance game-based design approaches, with a focus on enhancing solution distribution, precision, and the ability to reveal the dynamic influence sensitivity of design variables on objective functions. An integrated mathematical model is developed by combining EDGM with PARSEC and CST parameterization methods, forming a systematic framework for offshore wind turbine airfoil optimization. Targeting airfoils with approximately 30% and 35% thickness, the study aims to improve annual energy production (AEP) and optimize the polar moment of inertia. Redesigned airfoils using the EDGM-integrated model exhibit significant enhancements in aerodynamic performance and anti-flutter capability compared to baseline airfoils DU97W300 and DU99W350. The methodology’s superiority is validated through analyses of pressure distributions, lift-to-drag ratios, and streamline patterns, as well as comparative evaluations using HV and Spacing metrics, demonstrating EDGM’s potential for broader engineering applications in complex multi-objective optimization scenarios.
1. Introduction
As fossil fuel reserves deplete and the environment deteriorates, countries worldwide are increasingly prioritizing clean energy to promote a low-carbon economy [1,2]. Among various renewable sources, wind energy stands out for its environmental benefits and high conversion efficiency, making it one of the fastest-growing sectors. The aerodynamic performance, structural design, and operational stability of wind turbine blades are all based on the aerodynamic characteristics, geometric parameters, and environmental adaptability of airfoils. They form a deep correlation through the logic of “local airfoil characteristics spanwise integrated to get blade performance” with airfoil performance being the core determinant of blade performance. Ali et al. [3] analyzed the impact of different airfoil shapes on stress distribution and fatigue resistance of wind turbines through numerical simulations, and the results showed that the NACA 0030 airfoil performed best, reducing strain by approximately 30% and fatigue damage by 25% compared to traditional structures. Lin et al. [4] calculated the lift–drag coefficients of multiple airfoils and found that airfoil design for offshore wind turbine blades was the basis for optimizing blade chord length, twist angle, and matching thrust performance. Su et al. [5] found that the performance of the airfoils was a key factor determining the overall effectiveness of the blade, and the performance of the airfoils directly affected the blade’s flutter boundary and torsional vibration. Chuang et al. [6] studied the impact of icing on the aerodynamic characteristics of airfoils, and the results indicated that changes in airfoil aerodynamic characteristics lead to significant variations in the power curve, directly related to the output power of wind turbines.
In offshore applications, where wind resources are more abundant and stable, turbines are designed with increasingly longer blades to maximize power output. However, the resulting increase in structural flexibility, combined with the harsh marine environment, significantly elevates the risk of blade flutter—a dynamic aeroelastic instability that can induce severe vibrations and compromise structural safety [7]. This study focuses on airfoil optimization to enhance not only power generation efficiency but also resistance to flutter. Airfoil shape construction is a prerequisite for optimization. Since an airfoil’s geometry is controlled by hundreds of discrete points, directly designing these coordinates would increase design variables and reduce optimization convergence speed. Therefore, airfoil parameterization methods are essential, including function-based approaches like the Hicks-Henne [8], PARSEC [9], and CST [10] methods, as well as spline-based methods like B-splines [11], Bezier curves [12], and NURBS [5].
Methods such as the particle swarm optimization algorithm [13], genetic algorithm [14], and evolutionary algorithm [5] have been applied to the optimization design of wind turbine blades or airfoils. However, the aforementioned methods have the following shortcomings: (1) They cannot reveal the dynamic influence relationships between design variables and objective functions. Different design variables have varying degrees of influence on the objective functions, and such influence relationships change with optimization iterations. Nevertheless, the above-mentioned methods fail to reveal such relationships. Yet, the influence relationships of design variables on objective functions are of great significance to designers, as they can provide valuable references. (2) When dealing with complex multi-dimensional optimization design problems (characterized by a large number of design variables, complex constraint conditions, and strong coupling of objective functions), these methods face issues such as high computational difficulty and may become trapped in local optimal solutions. Game theory, as a theory for resolving conflicts, seeks optimal decision-making solutions through mathematical modeling in the context of multiple participants’ confrontation and conflict. It is very suitable for solving such complex optimization problems. Compared to these multi-objective optimization methods [8,13,14], optimization methods based on game theory can convert a multi-objective problem into strategic interactions among multiple players. At the same time, high-dimensional and intricate issues are simplified into several lower-dimensional problems, making them easier to solve. Additionally, these methods help uncover how design variables affect sub-objectives by assigning them to specific strategy spaces for each player, which supports engineers in achieving an optimal design [15,16]. Game theory has also found widespread application in multi-objective optimization problems across a variety of engineering fields. Hati and Panda [17] evaluated the best strategies for improving the residual life of aging structures based on Nash non-cooperative and super standard cooperative games. Multi-objective robust design based on game theory was carried out by Saeedi et al. [18] and Ahmadi et al. [19], where cooperative and non-cooperative game models were applied. Tao and Feijóo [20] proposed the potential game approach to search for the Nash equilibrium of the layout of the wind farms. Mo et al. [21] proposed a multi-objective collaborative game optimization method to solve the conflict of interest among multiple energy suppliers. In addition, game theory has also been applied to parallel manipulators design [22], wind turbine blade optimization [15], intelligent transportation [23], parameter optimization of thin-walled pressure vessel and twin hull ship [24], scheduling of parallel machine production and transportation [25], and aerodynamic shape design of a hypersonic air-breathing vehicle [26]. Although game theory-based optimization methods offer advantages, most of them only provide a single solution within a fixed game model. The Pareto optimal solution set is vital for multi-objective optimization. Meng et al. [27] proposed a full information cooperative game that generates solutions near the Pareto frontier. However, the static strategy space limits solution distribution and precision. To overcome this, this paper proposes an enhanced dynamic game method (EDGM), where the strategy space evolves dynamically, yielding better-distributed and more accurate solutions.
To verify the feasibility of EDGM, it is combined with the PARSEC and CST parameterization methods to optimize offshore wind turbine airfoil design. The chapter structure is as follows: Section 2 introduces the theory behind generating airfoil geometry using PARSEC and CST methods. Section 3 details the airfoil optimization model, including objective functions, design variables, and constraints. Section 4 elaborates on the theoretical foundations and solution process of EDGM. Section 5 applies EDGM with CST and PARSEC methods to regenerate airfoils with thicknesses of approximately 30% and 35%, comparing them with DU97W300 and DU99W350. Section 6 presents the conclusions.
2. Airfoil Parameterization Model
2.1. PARSEC Parametric Method
The PARSEC parameterization method primarily employs 12 parameters to describe the original airfoil [9], as illustrated in Figure 1. The meaning of the parameters highlighted in Figure 1 is reported in Table 1.
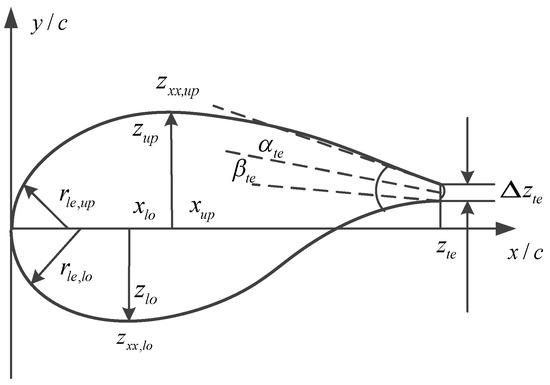
Figure 1.
Schematic diagram of PARSEC parameter method.

Table 1.
Physical meanings of PARSEC parameter method.
The PARSEC parametric method divides the airfoil into upper and lower airfoil surfaces, which are fitted to the upper and lower surfaces of the airfoil, respectively, with the following expressions:
is the required coordinate for the upper surface, is the required coordinate for the lower surface, and , are the coefficients to be solved from the twelve control variables.
The coefficients and are determined based on the following formulas derived from the twelve control variables:
where represents the horizontal coordinate at the trailing edge of the airfoil, refers to the coefficients in the equations for the upper surface, and similarly, denotes the coefficients in the equations for the lower surface.
2.2. CST Parametric Method
The CST method involves category and shape functions. The category function defines the base airfoil type, while the shape function refines it for precise geometric adjustments. As outlined by Akram and Kim [28], the CST parametric method is expressed as follows:
where let and represent the horizontal and vertical coordinates of the airfoil, respectively. c denotes the chord length of the airfoil, while refers to the shape function. represents the Bernstein polynomial, and n stands for the order of the Bernstein polynomial. serves as the parameter for controlling the shape, and represents the thickness of the airfoil’s trailing edge. is defined as the category function. N1 and N2 are the geometric shape-control coefficients of the category function. In this paper, N1 = 0.5, N2 = 1, n = 3.
3. Multi-Objective Optimization Design Model
3.1. Design Variables
When using the PARSEC parameterization method to construct the airfoil, the twelve parameters can be treated as design variables for airfoil optimization and can be expressed as: , the specific meanings of each design variable are detailed in Table 1. The upper and lower limits of design variables of PARSEC parameterization method are shown in Table 2.

Table 2.
Upper and lower limits of design variables of PARSEC parameterization method.
When using the CST parametric method to fit the geometric shape of the airfoil, the design variables of the airfoil can be expressed as: , where, and denote the design variables for the upper and lower surfaces of the airfoil, respectively. The range of values for the design variables in the CST parametric method is presented in Table 3.

Table 3.
Upper and lower limit of design variables of CST parameterization method.
3.2. Objective Functions
3.2.1. Anti-Flutter Performance
In the study conducted by Gao et al. [29], key factors influencing the anti-flutter performance of offshore wind turbine airfoils were thoroughly investigated. These factors include torsional stiffness, the position of the center of gravity, air density, and the location of the elastic axis. Among these, torsional stiffness, which is directly related to the polar moment of inertia I, plays a critical role in enhancing anti-flutter performance. Therefore, the optimization objective is defined as . Figure 2 presents the schematic of the airfoil and its associated parameters.

Figure 2.
Illustration of the airfoil used for determining the polar moment of inertia.
The calculation method for the polar moment of inertia I follows the approaches outlined by Gao et al. [29] and Gustavsson et al. [30].
The process of calculating the polar moment of inertia starts with the determination of the area of airfoil, denoted as A, which is given by:
where x and y represent the transverse and longitudinal coordinates of the airfoil, respectively. The chord length is denoted by c, and represent the functions of the lower and upper airfoil curves, respectively.
The coordinates of the airfoil’s centroid are calculated as follows:
For an airfoil of homogeneous material with uniform density, the above equations simplify to:
The moments of inertia, about the -axis and about the -axis, are calculated as follows:
When shifting the axis to the centroid, the adjusted moments of inertia are:
Ultimately, the polar moment of inertia is computed as follows:
3.2.2. Annual Energy Production
The output power of the airfoil was calculated using the improved fixed-point iteration method, which is an improvement on the blade element momentum (BEM) and addresses convergence failures in traditional numerical algorithms [31]. It is described in the form of pseudocode in Algorithm 1.
Assuming that the annual operation time of the wind turbine is 8700 h, which is a commonly used simplification and adjustments for real-world hours are feasible according to scheduled maintenance. The annual energy production (AEP) per unit length at the spanwise is calculated by the output power of the airfoil. The objective function is defined as . The AEP can be expressed as:
where is the power per unit span of the airfoil when the wind speed is . denotes the probability that the wind speed is greater than and less than , obtained from the Weibull distribution: , where A and k represent the scale factor and shape factor, respectively. In this study, A = 6.8 and k = 1.9. It is notable that A and k can be adjusted by airfoil designers according to local actual wind speed conditions, and wind speed statistics beyond the Weibull Distribution can refer to [32].
| Algorithm 1: Improved fixed-point iteration method |
| Input: Air density , number of blades B, wind speed V, blade rotation angular velocity , tip speed ratio , rotor radius R, chord length c, twist angle . |
| Output: Output power of airfoil dP(V) |
|
3.3. Design Constraints
To ensure the optimized airfoil satisfies geometric integrity, aerodynamic performance, and structural reliability, the design process need to satisfy the following constraints:
where represents the limits of design variables to ensure geometric integrity and prevent unreasonable shape, ensures that the optimized airfoil achieves higher AEP compared to the original airfoil, represents the airfoil thickness constraints, and thickness deviation range is ±0.6%. The specific meanings and ranges of the parameters are provided in Section 2 and Section 3.1.
4. Enhanced Dynamic Game Method
The formulation of the multi-objective optimization problem, which involves m objectives and n design variables, is given by:
The enhanced dynamic game method (EDGM) applies game theory to transform multi-objective optimization problems into game model. m optimization objectives are treated as m game players, and each objective function is mapped to the cost function according to the cooperative mode with different cooperation coefficient. The design variables are assigned to each game player to form their respective strategy spaces according to partition method of strategy space, where, and ; . Notably, the strategy space is dynamically updated in each game round, with the multi-objective optimization constraints aligning with those of the game model. Strategies for each player are determined through iterative repetition and convergence evaluation under different weight cooperation coefficients. The final solution, closely approximating the Pareto front, is derived from the strategy combinations across varying weight coefficients and game rounds.
4.1. Strategy Space Partition
In this paper, based on the concepts of spatial distance and moment [34], as well as the partitioning of strategy space [15], the design variables are allocated to each player’s strategy space accordingly. The algorithm is as follows:
- (1)
- The influence of design variables on the objective functions is represented as follows:
- (2)
- The spatial distance between the design variable and the objective function indicates the degree of influence, with a negative correlation between the distance and the variable’s impact. The formula is as follows:
- (3)
- Considering the overall effect of the design variables on all objective functions, the moment of the design variable is calculated as:The moment threshold is defined as:
- (4)
- In the actual allocation, design variables are ranked according to spatial distance and , and those with smaller distances and higher are prioritized for allocation. All design variables are assigned to the corresponding game players according to the corresponding instructions [15].
4.2. Construction of the Game Cost Function
The enhanced dynamic game establishes a cooperative model by combining the individual players’ cost functions with those of other participants [27]. The final cost function of the i-th game player is expressed as follows:
where is the relative cost of the i-th player when adopting a specific strategy, calculated as , where is the objective function, denotes the initial strategy set of the i-th player, and represents the complementary strategy set associated with the initial strategy of the i-th game player. denotes the cooperation coefficient matrix, which indicates the level of collaboration between players, with higher values indicating stronger cooperation. The symbol “*” represents the Hadamard product, “min” indicates that a smaller value of corresponds to a more optimal solution.
4.3. Solution Process of Enhanced Dynamic Game Method
Consider that there are Q groups, each characterized by distinct weight coefficients, and let the total number of game rounds be represented by M. Each player provides N strategies per round. By transforming the multi-objective optimization problem into a game, the enhanced dynamic game method is applied to find a solution. The weight settings of q are as follows [27]:
The flowchart of the enhanced dynamic game method is shown in Figure 3.
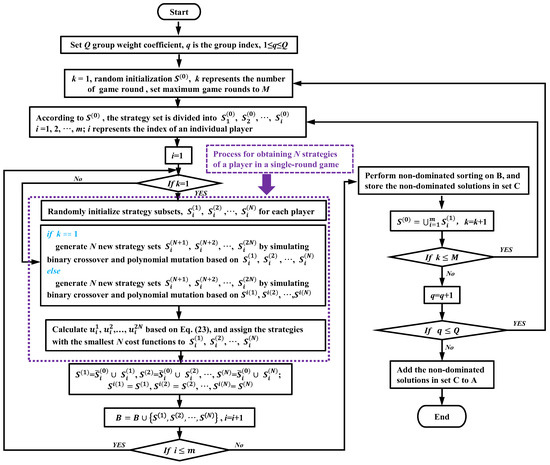
Figure 3.
Flowchart of the enhanced dynamic game method.
5. Airfoil Optimization Design Using Enhanced Dynamic Game Method
5.1. Airfoil Optimization Design Setup
Based on the 5MW wind turbine blade model [35], two typical airfoils, DU97W300 and DU99W350, are chosen as references, as detailed in Table 4.

Table 4.
Airfoil parameters at selected spanwise positions.
Based on the settings of Reynolds number and Mach number for different spanwise positions of a 5 MW wind turbine blade described in the book by Chen and Wang [36], the Reynolds and Mach numbers for the DU97W300 airfoil are set to and , while those for the DU99W350 airfoil are set to and .
Section 3 provides a detailed introduction to the optimization design variables, objective functions, and constraints. The optimization is carried out using the EDGM presented in Section 4, where the strategy space for each player is divided according to the method outlined in Section 4.1.
Set the values of Q, M, and N to 10, 10, and 100, respectively. The strategy sets for each player are randomly generated within the design space, serving as the initial optimization starting point. After each round of the game, the strategy space for each player is dynamically updated according to the method in Section 4.1, and the players submit their new strategies to start the next round of the game. The process of airfoil optimization is given by Figure 4.

Figure 4.
Three constituent modules.
Three constituent modules of offshore wind turbine airfoil optimization design based on enhanced dynamic game method are shown in Figure 4.
5.2. Computation Results
Figure 5 illustrates the solution sets optimized using the EDGM methodology in conjunction with two parameterization techniques, alongside the -AEP and 1/I result derived from fitting the coordinates of the DU97W300 and DU99W350 airfoils. FP300 and FP350 represent the objective functions for airfoils with approximately 30% and 35% thicknesses, respectively, using EDGM and PARSEC, while FC300 and FC350 correspond to the objective functions for airfoils derived from EDGM and CST. The results show that the objective function values for the EDGM and PARSEC have a broader distribution compared to those from EDGM and CST.
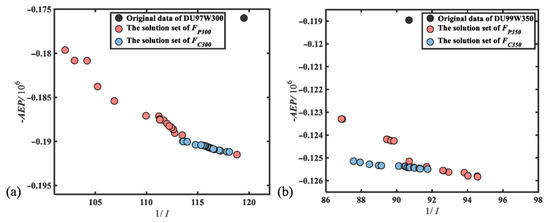
Figure 5.
Optimization solutions distribution and original solution. (a) optimization results compared with DU97W300; (b) optimization results compared with DU99W350.
Figure 6a shows new airfoils derived from EDGM and PARSEC, with thicknesses ranging from 29.41% to 30.24%, while Figure 6b displays airfoils derived from EDGM and CST, with thicknesses from 29.47% to 30.38%. In Figure 6c, airfoils from EDGM and PARSEC are shown, with thicknesses from 34.61% to 35.45%, while Figure 6d presents airfoils from EDGM and CST, with thicknesses from 34.51% to 35.47%. These variations are constrained by strict thickness requirements, with a deviation range of ±0.6%.
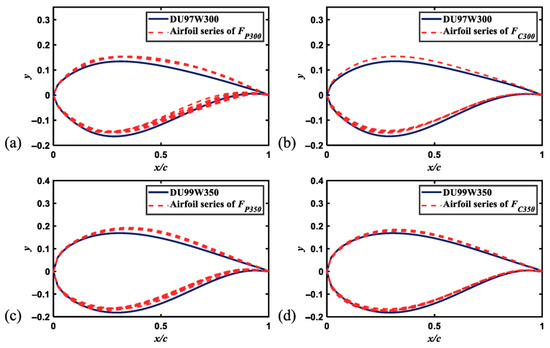
Figure 6.
Comparison of the new and original airfoils. (a) DU97W300 and airfoil series of FP300; (b) DU97W300 and airfoil series of Fc300; (c) DU99W350 and airfoil series of FP350; (d) DU99W350 and airfoil series of FC350.
As described in Section 4.1, the strategy space of each player is dynamically partitioned in each game round. Table 5 illustrates the dynamic partition of strategy space, S1 and S2, over a ten-round game process, where XP300, XC300, XP350, and XC350 refer to the design variables of FP300, FC300, FP350, and FC350, respectively. The results clearly demonstrate the dynamic evolution of each player’s strategy space across the game rounds. For instance, for airfoils with a thickness of approximately 30% generated using the EDGM and PARSEC, the design variables x2 to x7 predominantly fall within the strategy space S1 in most game rounds, significantly influencing the anti-flutter performance. In contrast, x9 to x11 have a greater impact on AEP. Similarly, for airfoils with a thickness of approximately 30% generated using the EDGM and CST, the design variables x1 to x4 and x6 to x8 are primarily located in strategy space S1 in most game rounds, playing a critical role in anti-flutter performance. Meanwhile, x9 mainly belongs to the strategy space S2, contributing more significantly to AEP.

Table 5.
Dynamic partition of strategy space over a ten-round game process of EDGM.
Table 5.
Dynamic partition of strategy space over a ten-round game process of EDGM.
| Strategy Space (S1 and S2) | ||||
|---|---|---|---|---|
| Game Rounds | By XP300 | By XC300 | By XP350 | By XC350 |
| 1 | {1,2,3,4,5,6,7,8,12} {9,10,11} | {1,2,3,4,7,8,9} {5,6} | {2,3,4,5,7,8,9,12} {1,6,10,11} | {1,2,3,4,5,6,7,8} {9} |
| 2 | {2,3,4,6,7,8} {1,5,9,10,11,12} | {1,2,3,4,5,6,7,8} {9} | {1,2,3,4,5,6,7,8,9} {10,11,12} | {1,3,5,6,8,9} {2,4,7} |
| 3 | {2,3,4,5,6,7,8,9,12} {1,10,11} | {5,8,9} {1,2,3,4,6,7} | {1,2,4,6,7,8,9,10,12} {3,5,11} | {3,4,6,7,8,9} {1,2,5} |
| 4 | {1,2,3,4,6,7,8} {5,9,10,11,12} | {1,2,3,4,6,7,9} {5,8} | {1,2,3,4,5,6,7,8,9,12} {10,11} | {1,2,3,4,5,6,7,8} {9} |
| 5 | {2,4,5,6,7,8} {1,3,9,10,11,12} | {1,2,3,4,5,6,7,8} {9} | {1,2,3,4,7,9} {5,6,8,10,11,12} | {2,4,5,7} {1,3,6,8,9} |
| 6 | {1,2,3,4,5,6,7,8,11,12} {9,10} | {1,2,3,4,5,6,7,8} {9} | {1,2,3,4,6,7,8} {5,9,10,11,12} | {1,2,3,4,5,6,7,8} {9} |
| 7 | {1,2,3,4,6,7,8,9} {5,10,11,12} | {1,2,3,4,5,6,7,8} {9} | {1,2,3,4,5,6,7,9} {8,10,11,12} | {1,3,4,6,7,8} {2,5,9} |
| 8 | {1,2,3,4,5,6,7,8,12} {9,10,11} | {2,3,4,6,7,9} {1,5,8} | {1,2,3,4,5,6,7,8,9,11,12} {10} | {2,4,5,6,7,8} {1,3,9} |
| 9 | {1,2,3,4,5,6,7,8,9} {10,11,12} | {1,2,3,4,6,7,8} {5,9} | {1,2,3,4,5,6,7,8,9} {10,11,12} | {1,3,5,7} {2,4,6,8,9} |
| 10 | {1,2,4,5,6,7,12} {3,8,9,10,11} | {1,2,3,4,5,6,7,8} {9} | {3,4,7,8,10} {1,2,5,6,9,11,12} | {1,2,3,4,5,6,7,8} {9} |
5.3. Analysis and Discussion
To further validate the effectiveness of the proposed method, the full information cooperative game (FICG) [27] is used for comparison. The solution sets are compared using two metrics: hypervolume (HV) [37] and Spacing [38]. The HV metric measures the coverage of the objective space by the non-dominated solution set, with a larger HV value indicating better convergence and diversity of the algorithm. The Spacing metric measures the uniformity of the distribution of solutions in the set. It calculates the standard deviation of the minimum distances from each solution in the set to the other solutions. A smaller Spacing value indicates a more uniform distribution of the solution set. The specific values of these metrics are shown in Table 6, and the comparison of solution set distributions is displayed in Figure 7. EDGM outperforms FICG in three of the Spacing metrics, indicating that the solution sets generated by EDGM have a more even distribution. Furthermore, EDGM surpasses FICG in three of the HV metrics, highlighting the superior convergence and diversity of the EDGM solution sets. Based on these two metrics, the overall performance of the solution sets obtained by EDGM is superior to that of FICG. This advantage stems from the new method’s capability to dynamically regulate the strategy space of each player in every round of the game. This dynamic adjustment not only enables more in-depth game computation but also enhances the diversity and convergence of game solutions.

Table 6.
Comparison of performance indicators between EDGM and FICG.

Figure 7.
Comparison of solution set distributions obtained by EDGM and FICG. (a) FP300 solution set distributions; (b) FC300 solution set distributions; (c) FP350 solution set distributions; (d) FC350 solution set distributions.
Four solutions with relatively balanced AEP and anti-flutter performance are selected from the non-dominated solutions by EDGM. They are located near the middle of non-dominated solutions, with relatively balanced improvement trends in the two objective performances. The core selection criterion is “balancing AEP and anti-flutter performance”. The specific locations of four selected solutions are shown in Figure 8.

Figure 8.
Four selected solutions from the solution set. (a) FP300 solution set distributions and selected solution I; (b) FC300 solution set distributions and selected solution II; (c) FP350 solution set distributions and selected solution III; (d) FC350 solution set distributions and selected solution IV.
Compared to the DU97W300, solution I achieves improvements of 6.31% in AEP and 8.69% in anti-flutter performance, while solution II results in improvements of 8.22% in AEP and 3.47% in anti-flutter performance. Compared to the DU99W350, solution III brings about improvements of 4.45% in AEP and 1.14% in anti-flutter performance, whereas solution IV gains improvements of 5.38% in AEP and 0.63% in anti-flutter performance. The strict constraint on thickness deviation (±0.6%) and the well-inherent aeroelastic stability of DU99W350 lead to a relatively low improvement in anti-flutter performance. The corresponding airfoils generated by these solutions are shown in Figure 9.
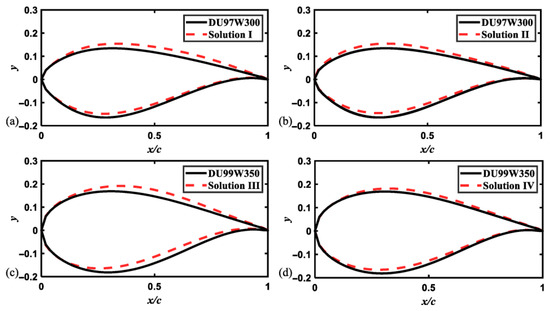
Figure 9.
Airfoils generated by four selected solutions. (a) DU97W300 and solution I; (b) DU97W300 and solution II; (c) DU99W350 and solution III; (d) DU99W350 and solution IV.
Figure 10a illustrates that the newly designed airfoils exhibit a superior lift-to-drag ratio compared to the DU97W300 within the angle of attack range of [−5°, 9°]. The lift-to-drag ratio only begins to show a slight decline, falling below that of DU97W300, when the angle of attack exceeds 10°, but this occurs beyond the optimal operational range. Similarly, Figure 10b reveals that the newly generated airfoils outperform the DU99W350 in terms of lift-to-drag ratio across the angle of attack range of [−5°, 7°]. The lift-to-drag ratio drops below that of DU99W350 only when the angle exceeds 8° that the lift-to-drag ratio falls below that of DU99W350, again beyond the optimal range. The optimized airfoils, when evaluated at the optimal power coefficient, demonstrate higher annual energy generation compared to the original airfoils. Therefore, the aerodynamic performance of the newly generated airfoils surpasses that of the original airfoils.

Figure 10.
Lift–drag ratio of airfoil generated by the four solutions. (a) DU97W300 and solution I, II; (b) DU99W350 and solution III, IV.
When analyzing the pressure coefficient distribution at angles of attack of 7° and 10°, corresponding to conditions where the lift-to-drag ratio is higher than the original airfoil and slightly lower, respectively, Figure 11 presents the pressure distributions for six airfoils.

Figure 11.
Pressure distribution of airfoils generated by the selected solutions. (a) DU97W300 and solution I, II at ; (b) DU97W300 and solution I, II at ; (c) DU99W350 and solution III, IV at ; (d) DU99W350 and solution III, IV at .
The results indicate that at an angle of attack of 7°, a notable increase in pressure difference across the upper and lower surfaces is observed for the four newly designed airfoils compared to the DU97W300 and DU99W350, which leads to a significant enhancement in lift. A similar trend is observed at an angle of attack of 10°, where the pressure difference also increases for the new airfoils.
The wind turbine blade functions under the influence of a multitude of factors, with the local angle of attack at each airfoil section varying along the span. Leveraging the parameters of the airfoils at different positions along the blade, along with key factors such as tip speed ratio, Mach number, and Reynolds number discussed in Section 5.1, the local angles of attack for both the optimized and original airfoils can be calculated, employing the methodologies detailed in the work of Schaffarczyk [39]. Table 7 presents the local angles of attack and the corresponding lift-to-drag ratios for each airfoil along the blade. The results demonstrate that the newly designed airfoils exhibit superior lift-to-drag ratios under local angles of attack when compared to the original airfoils. The streamline diagrams for each airfoil at their respective local angles of attack are presented in Figure 12. The study reveals that the streamline patterns for both the reference and newly generated airfoils remain relatively smooth, with no notable vortices or flow separations detected across all six airfoils. When comparing the DU97W300 airfoil with the newly generated designs, the vortices in the latter are notably smaller. Similarly, when comparing the DU99W350 airfoil to the new designs, the airfoil generated using the EDGM and PARSEC methods exhibits slightly larger vortices, whereas the airfoil derived using the CST method shows smaller vortices. The new airfoils exhibit no flow separation and outperform the original ones in terms of lift-to-drag ratio, thereby indicating an enhancement in aerodynamic efficiency. Furthermore, they demonstrate improvements in the uniformity of pressure distribution, the stability of lift–drag ratio, and the smoothness of flow field, which collectively confer potential adaptability to environmental disturbances. For instance, the more stable surface pressure distribution could mitigate turbulence-induced load fluctuations, while the optimized aerodynamic configuration might reduce sensitivity to aerodynamic efficiency degradation caused by sea spray.

Table 7.
Lift–drag ratio of the airfoil at the local angle of attack.

Figure 12.
Streamlines for each airfoil at the local angles of attack.
6. Conclusions
To address the shortcomings of current multi-objective game optimization approaches, a novel enhanced dynamic game method (EDGM) is proposed. This method is then utilized to redesign airfoils to enhance both AEP and anti-flutter performance.
- (1)
- The results of comparison between four optimized airfoils and two reference airfoils show that the EDGM and PARSEC-based airfoil (approximately 30% thickness) improves AEP by 6.31% and anti-flutter performance by 8.69%, while the EDGM and CST-based airfoil achieves 8.22% and 3.47% improvements, respectively. For the approximately 35% thickness airfoil, the EDGM and PARSEC-based airfoil improves AEP by 4.45% and anti-flutter performance by 1.14%, whereas the EDGM and CST-based airfoil shows gains of 5.38% in AEP and steady anti-flutter improvements. Enhanced pressure distributions and lift-to-drag ratios further confirmed the methodology’s effectiveness.
- (2)
- By comparing the HV and Spacing metrics with the full information cooperative game method, it is demonstrated that a series of solutions generated by EDGM outperforms the full information cooperative game in terms of distribution, diversity, and convergence. This advantage is due to the ability of the new method to dynamically update the strategy space of each player in every round of the game, which facilitates deeper computation and improves the multiplicity of game solutions.
- (3)
- The method demonstrates good generality and scalability. Although the optimization objectives for the airfoils listed in this paper are annual energy production and polar moment of inertia, designers can set different objective functions based on their specific design needs and apply this method to obtain airfoils with improved performance. Also, the method can be applied to a broader range of engineering optimization problems.
- (4)
- EDGM exhibits good performance in airfoil optimization (2D parameterized models), but in scenarios involving high-dimensional objectives (e.g., simultaneously considering aerodynamic performance, structural strength, fatigue life, etc.) or multi-player game scenarios (with more than 3 objective functions), the dynamically updated strategy space may lead to increased computational complexity. It is therefore necessary to further integrate dimensionality reduction techniques to improve efficiency.
- (5)
- Future research plans will extend EDGM to full-machine multi-objective optimization incorporating environmental parameters, which encompasses blade twist distribution, pitch control systems, and marine environmental load coupling, to realize progressive full-chain performance enhancement from components to systems. Further refinement of quantitative analysis on the mapping between airfoil optimization and overall performance will be conducted to ensure the research retains methodological innovation while demonstrating practical value in offshore wind engineering, thereby enhancing real-world relevance and balancing the integration of methodology and applications.
Author Contributions
Conceptualization, R.M.; methodology, R.M.; software, R.M. and X.C.; validation, R.M. and X.C.; formal analysis, J.S. and X.R.; data curation, J.S.; writing—original draft preparation, X.R. and J.S.; writing—review and editing, R.M.; visualization, X.R. and J.S.; funding acquisition, R.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the University Natural Science Research Key Project of Anhui Province (Grant No. KJ2020A0244).
Data Availability Statement
Data will be made available on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Li, J.F.; Zhang, T.M.; Du, X.Y.; Li, Y.P. How can the digital economy drive low-carbon city performance in China to achieve sustainable development goals? A multiple-output perspective. J. Clean. Prod. 2024, 454, 142316. [Google Scholar] [CrossRef]
- Agyeman, S.D.; Lin, B.Q. Nonrenewable and renewable energy substitution, and lowecarbon energy transition: Evidence from North African countries. Renew. Energy 2022, 194, 378–395. [Google Scholar] [CrossRef]
- Ali, S.; Park, H.; Lee, D. Structural Optimization of Vertical Axis Wind Turbine (VAWT): A Multi-Variable Study for Enhanced Deflection and Fatigue Performance. J. Mar. Sci. Eng. 2025, 13, 19. [Google Scholar] [CrossRef]
- Lin, J.; Duan, H.; Xu, B.; Wang, Y.; Zhang, J. Equivalent Aerodynamic Design of Blade for Offshore Floating Wind Turbine Model. J. Mar. Sci. Eng. 2022, 10, 132. [Google Scholar] [CrossRef]
- Su, H.; Ma, J.; Wang, J.; Gao, Z.; Li, Q.; Pan, W.; Yang, L. Cooperative Optimization Algorithm for Wind Turbine Airfoil Design and Numerical Validation of Blade Aerodynamic and Flutter Performance. Energy Convers. Manag. 2025, 333, 119818. [Google Scholar] [CrossRef]
- Chuang, Z.; Yi, H.; Chang, X.; Liu, H.; Zhang, H.; Xia, L. Comprehensive Analysis of the Impact of the Icing of Wind Turbine Blades on Power Loss in Cold Regions. J. Mar. Sci. Eng. 2023, 11, 1125. [Google Scholar] [CrossRef]
- Ageze, M.B.; Hu, Y.; Wu, H. Comparative study on uni-and bi-directional fluid structure coupling of wind turbine blades. Energies 2017, 10, 1499. [Google Scholar] [CrossRef]
- Zhou, S.Q.; Zhou, H.X.; Yang, K.; Dong, H.B.; Gao, Z.L. Research on blade design method of multi-blade centrifugal fan for building efficient ventilation based on Hicks-Henne function. Sustain. Energy Technol. 2021, 43, 100971. [Google Scholar] [CrossRef]
- Belda, M.; Hyhlik, T. Interactive Airfoil Optimization Using Parsec Parametrization and Adjoint Method. Appl. Sci. 2024, 14, 3495. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, W.W.; Peng, X.H.; Wang, Z.Y. Benchmark aerodynamic shape optimization with the POD-based CST airfoil parametric method. Aerosp. Sci. Technol. 2019, 84, 632–640. [Google Scholar] [CrossRef]
- Zhao, Y.C.; Zhang, M.Z.; Ni, Q.; Wang, X.H. Adaptive Nonparametric Density Estimation with B-Spline Bases. Mathematics 2023, 11, 291. [Google Scholar] [CrossRef]
- Zain, S.; Misro, M.Y.; Miura, K.T. Enhancing flexibility and control in k-curve using fractional Bézier curves. Alex. Eng. J. 2024, 89, 71–82. [Google Scholar] [CrossRef]
- Li, Z.; Wang, W.; Xie, Y.; Li, D. Optimization Design of Blades Based on Multi-Objective Particle Swarm Optimization Algorithm. J. Mar. Sci. Eng. 2025, 13, 486. [Google Scholar] [CrossRef]
- Saleem, A.; Kim, M.-H. Aerodynamic performance optimization of an airfoil-based airborne wind turbine using genetic algorithm. Energy 2020, 203, 117841. [Google Scholar] [CrossRef]
- Meng, R.; Wang, L.; Cai, X.; Xie, N.G. Multi-objective aerodynamic and structural optimization of a wind turbine blade using a novel adaptive game method. Eng. Optim. 2019, 52, 1441–1460. [Google Scholar] [CrossRef]
- Xie, N.G.; Meng, R.; Ye, Y.; Wang, L.; Cen, Y.W. Multi-objective design method based on evolution game and its application for suspension. Struct. Mul. Tidiscip Optim. 2013, 47, 207–220. [Google Scholar] [CrossRef]
- Hati, S.; Panda, S.K. Game theory approach for optimum design of an aged structure with multiple objectives. Structures 2021, 31, 205–215. [Google Scholar] [CrossRef]
- Saeedi, M.S.; Jamali, A.; Nariman-Zadeh, N.; Ahmadi, B. A novel bi-level decision-making approach based on game theory for mechanism design. Trans. Inst. Meas. Control. 2024, 47, 2050–2062. [Google Scholar] [CrossRef]
- Ahmadi, B.; Jamali, A.; Mallipeddi, R.; Nariman-zadeh, N.; Ahmadi, B.; Khayyam, H. Bi-level game theoretic approach for robust design: A case study of path-generating four-bar. Swarm Evol. Comput. 2024, 89, 101636. [Google Scholar] [CrossRef]
- Tao, S.Y.; Feijóo-Lorenzo, A.E. Multi-objective optimization of clustered wind farms based on potential game approach. Ocean Eng. 2024, 300, 117291. [Google Scholar] [CrossRef]
- Mo, L.; Deng, Z.; Chen, H.; Lan, J. Multi-Objective Co-Operative Game-Based Optimization for Park-Level Integrated Energy System Based on Exergy-Economic Analysis. Energies 2023, 16, 7945. [Google Scholar] [CrossRef]
- Yang, C.; Li, Q.; Chen, Q. Multi-Objective Optimization of Parallel Manipulators Using a Game Algorithm. Appl. Math. Model. 2019, 74, 217–243. [Google Scholar] [CrossRef]
- Tang, J.H.; Wu, Q.; Wang, K. Evolutionary game analysis on cross-border cooperative R&D of intelligent new energy vehicle industry. Kybernetes 2024. [Google Scholar] [CrossRef]
- Xiao, M.; Shao, X.; Gao, L.; Luo, Z. A new methodology for multi-objective multidisciplinary design optimization problems based on game theory. Expert. Syst. Appl. 2015, 42, 1602–1612. [Google Scholar] [CrossRef]
- Liu, P.; Xu, K.; Gong, H. Non-Cooperative Game of Coordinated Scheduling of Parallel Machine Production and Transportation in Shared Manufacturing. Comput. Mater. Contin. 2023, 76, 239–258. [Google Scholar] [CrossRef]
- Tang, Z.; Luo, S.; Chen, Y.; Zhao, X.; Wu, P. Hierarchical variable fidelity evolutionary optimization methods and their applications in aerodynamic shape design. Appl. Soft Comput. 2022, 114, 108135. [Google Scholar] [CrossRef]
- Meng, R.; Chen, L.L.; Zhao, R.X.; Cai, X.; Xie, N.G. Integrated design of aerodynamic and anti-flutter performance of offshore wind turbine airfoil based on full information cooperative game method. Ocean Eng. 2023, 281, 114967. [Google Scholar] [CrossRef]
- Akram, M.T.; Kim, M.-H. Aerodynamic Shape Optimization of NREL S809 Airfoil for Wind Turbine Blades Using Reynolds-Averaged Navier Stokes Model-Part II. Appl. Sci. 2021, 11, 2211. [Google Scholar] [CrossRef]
- Gao, Q.; Cai, X.; Meng, R.; Zhu, R. Anti-flutter optimization design of airfoil for wind turbine blade. J. Renew. Sustain. Ener. 2018, 10, 013307. [Google Scholar] [CrossRef]
- Gustavsson, R.; Ahlsén, D.; Fagerberg, L.; Högström, C.M. Effects of added mass and moments of inertia on hydroelectric turbines for dynamic applications using structural acoustic simulation. J. Fluid. Struct. 2022, 115, 103757. [Google Scholar] [CrossRef]
- Meng, R.; Chen, X.H.; Chen, L.L.; Xie, N.G.; Wang, L.; Xu, B.F. Aerodynamic and structural co-optimization of offshore wind turbine blades using a novel adaptive surrogate-based optimization method. Ocean. Eng. 2025, in press. [Google Scholar]
- Lencastre, P.; Yazidi, A.; Lind, P.G. Modeling Wind-Speed Statistics beyond the Weibull Distribution. Energies 2024, 17, 2621. [Google Scholar] [CrossRef]
- Montgomerie, B. Methods for root effects, tip effects and extending the angle of attack range to +− 180°, with application to aerodynamics for blades on wind turbines and propellers. Smart Grid Renew. Energy 2004. [Google Scholar]
- Wong, K.K.L. Bridging game theory and the knapsack problem: A theoretical formulation. J. Eng. Math. 2015, 91, 177–192. [Google Scholar] [CrossRef]
- Jonkman, J. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2009. [Google Scholar] [CrossRef]
- Chen, J.; Wang, Q. Wind Turbine Airfoils and Blades: Optimization Design Theory; Walter de Gruyter GmbH & Co KG.: Berlin, Germany, 2017; Volume 3. [Google Scholar] [CrossRef]
- Guerreiro, A.P.; Fonseca, C.M.; Paquete, L. The Hypervolume Indicator: Computational Problems and Algorithms. ACM Comput. Surv. 2021, 54, 1–42. [Google Scholar] [CrossRef]
- Premkumar, M.; Jangir, P.; Sowmya, R.; Alhelou, H.H.; Heidari, A.A.; Chen, H.L. MOSMA: Multi-Objective Slime Mould Algorithm Based on Elitist Non-Dominated Sorting. IEEE Access 2021, 9, 3229–3248. [Google Scholar] [CrossRef]
- Schaffarczyk, A.P. Introduction to Wind Turbine Aerodynamics; Springer: Cham, Switzerland, 2024. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).