Abstract
Reliable prediction of tunnel thruster performance under reverse, or off-design, reverse operating direction (ROD) conditions, is crucial for modern vessels that require bidirectional thrust from a single unit—such as yachts and offshore support vessels. Despite the increasing demand for such a capability, there remains limited understanding of the unsteady hydrodynamic behavior and performance implications of ROD operation. This study addresses this gap through a scale-resolving computational fluid dynamics (CFD) investigation of a full-scale, fixed-pitch propeller with a diameter of 0.62, installed in a tunnel geometry representative of yacht-class side thrusters. Using advanced turbulence modeling, we compare the thruster’s performance under both the normal operating direction (NOD) and ROD. The results reveal notable differences: in ROD, the upstream separation zone was more compact and elongated, average thrust increases by approximately 3–4%, and torque and pressure fluctuations rise by 15–30%. These findings demonstrate that a single tunnel thruster can meet bidirectional manoeuvring requirements. However, the significantly elevated unsteady loads during ROD operation offer a plausible explanation for the increased noise and vibration frequently observed in practice.
1. Introduction
The accurate numerical modeling of bow thruster hydrodynamics remains a challenging task due to the complex and highly unsteady nature of the flow field within the tunnel. This complexity arises from multiple interacting phenomena, including flow separations near the tunnel entrance, cavitation, and the aerodynamic interplay between the propeller, nacelle, tunnel walls, and the ship hull. These factors create difficulties in both modeling and experimental validation, especially given the limited availability of experimental data on bow thruster performance [1]. Despite this, numerous practical parameters—such as propeller position, tunnel geometry, and the impact of protective devices—can be effectively analyzed using computational fluid dynamics (CFD) techniques [1].
Previous studies using conventional RANS-based turbulence models (e.g., k– SST and realizable k–) have contributed significantly to understanding steady-state behaviors and performance metrics of bow thrusters. For instance, refs. [2,3,4] investigated the influence of blade pitch, tunnel geometry, and ship speed on performance, while [5] proposed a new tunnel design enabling the use of smaller propellers without compromising efficiency. Another study [6] extended these approaches to include spatially and temporally resolved simulations. The significance of the tunnel entrance shape was also demonstrated in [7], where it was shown that flow separation can be eliminated when the radius of the tunnel inlet edge exceeds , with being the tunnel diameter.
While most of the aforementioned studies focused on steady effects, the significance of unsteady hydrodynamics—including pressure pulsations, noise generation, and vibrations—has increasingly come into focus. An overview of these phenomena and potential mitigation strategies is given in [8], which discusses traditional design solutions such as blade pitch and number optimization, as well as novel methods like air injection and specially designed protection grilles. These concerns are particularly relevant for offshore support vessels (OSVs), where bow thrusters are now operated continuously under demanding environmental conditions, leading to increased levels of acoustic emission and structural vibration.
Quantitative insights into unsteady pressure loads were provided in [9], where the authors studied the influence of ship speed on thrust and torque. It was shown that pressure pulsation peaks occur primarily at the lower tunnel wall, between angular positions and , where they are nearly three times greater than on the upper wall. Moreover, thrust and torque coefficients were observed to decrease gradually—by approximately 3% to 4%—as ship speed increased to three knots.
To mitigate these unsteady effects, passive flow control strategies have gained attention. Two particularly effective methods are rounding the lower tunnel entrance and incorporating a specially profiled protection grille. As proposed in the earlier literature [8,10], the use of a guide vane or wing-like surface can deflect incoming flow and suppress separation. However, those works did not include quantitative assessments of the resulting reduction in unsteady loads or pressure pulsations.
To fill this gap, ref. [11] numerically evaluated the combined impact of tunnel entrance rounding and protection grille optimization. A two-step methodology is used: first, steady Reynolds-averaged Navier–Stokes (RANS) simulations (k– SST) with an actuator disk model are used in combination with response surface analysis and genetic optimization to identify optimal geometries. Then, these configurations are tested under unsteady conditions using a hybrid SLH (Shielded LeMoS Hybrid) turbulence model. The results demonstrate that these passive geometric modifications can significantly reduce the separation zone and pressure pulsations, ultimately improving thruster efficiency while reducing vibration and noise emissions.
More recent studies have broadened the scope of bow thruster research. Guo et al. [12] introduced a non-penetrating tunnel thruster (NPT) concept and achieved a 21.79% increase in mooring thrust via optimized tunnel design using CFD and response surface methodology. McNeill et al. [13] addressed drag reduction in Autonomous Underwater Vehicles (AUVs) by proposing a retractable thruster cover, reducing overall drag by 9.51%. In the context of manned vessels, Okuda et al. [14] validated the Oblique Sailing Navigation (OSN) method using model-scale experiments and simulations, highlighting the critical role of flap rudders and bow thruster coordination in shallow-water berthing scenarios.
Additional work by Li et al. [15] quantified the decay of near-bed velocities induced by bow thrusters, a finding of particular importance for harbor sediment stability and scour analysis. Meanwhile, Tan et al. [16] analyzed the directional dependency of pressure fluctuations under varied thrusting scenarios, reinforcing the importance of inflow symmetry in tunnel design and operation.
Due to the need for redundancy as a safety factor, it is common practice to install at least two side thrusters in the bow or stern [17]. Since each side thruster is optimized for a single design direction, its off-design operation must be evaluated to assess whether it can effectively produce thrust in both directions without requiring an additional pair of thrusters.
Bui [18] has studied the influence of propeller pitch angle using steady-state CFD simulations with both k– and k– SST turbulence models. The results indicated that the reverse operation direction (ROD, pitch angle °) yields marginally higher thrust and torque. However, to better understand the unsteady hydrodynamic behavior in ROD (i.e., off-design conditions), a full-scale transient analysis is needed. This investigation builds upon previous work to address the unresolved unsteady dynamics under ROD conditions.
Although Reynolds-averaged Navier–Stokes (RANS) simulations are widely used in marine hydrodynamics due to their efficiency and reliability in predicting time-averaged quantities such as thrust and torque, their steady-state formulation inherently limits their ability to resolve transient flow phenomena. These include vortex interactions, pressure pulsations, and cavitation dynamics, which are particularly important under off-design conditions. In bow thrusters, the flow becomes inherently unsteady and asymmetric, characterized by extended separation zones and intensified vortex–structure interactions. Moreover, due to the presence of flow separation and cavitation in the tunnel thruster geometry, the flow field exhibits significant temporal variability that cannot be captured by steady-state models. As a result, RANS methods are inadequate for resolving the detailed unsteady flow behavior that directly influences noise generation, vibration, and structural fatigue.
To overcome these limitations, transient computational methods must be employed. Unsteady RANS (URANS) models offer a compromise between computational cost and fidelity by accounting for time-dependent effects. However, previous studies [1,11] have shown that URANS lacks the resolution needed to capture the full range of unsteady dynamics, especially in scenarios involving complex turbulence and cavitation. Hybrid methods that combine Large Eddy Simulation (LES) with RANS, such as the Shielded LeMoS Hybrid (SLH) approach used in this work, provide a higher-fidelity alternative. These models resolve large-scale eddies directly while modeling smaller turbulent structures, enabling more accurate predictions of unsteady pressure loads, thrust oscillations, and cavitation behavior.
Therefore, to fully understand the unsteady hydrodynamic behavior of bow thrusters—especially under ROD (i.e., off-design) conditions—a detailed transient analysis is essential. The specific research gap addressed in this study is the lack of high-resolution, time-accurate simulation data capturing the differences in vortex dynamics, pressure fluctuations, and performance metrics between NOD and ROD. Accordingly, the main objectives of this study are as follows: (1) to characterize and compare the unsteady flow structures present in both operating directions, (2) to quantify the resulting differences in thrust, torque, and pressure pulsations, and (3) to evaluate the implications of these unsteady effects on vibration and acoustic emissions. This study aims to provide new insights that can inform design improvements and operational strategies for bow thrusters used in bidirectional applications.
2. Object of Investigations
CFD analyses were carried out on a full-scale bow thruster—featuring a fixed-pitch propeller of diameter —manufactured by Jastram GmbH & Co. KG for yacht use (Figure 1). The thruster was mounted in a 1.65 m-high mock ship section with both vertical and inclined side panels; its footprint measures m at the base and m at the top. Its axis was aligned with the towing tank’s longitudinal direction. With the carriage held stationary, the centrally positioned thruster produced a steady, unidirectional jet; measurements confirmed that secondary reverse flows were negligible and that the generous span of the ship section eliminated any wall-induced disturbances. The baseline geometry consists of a conical inlet with sharp edges and a simple protective grille (see [1,11] for validation and verification).
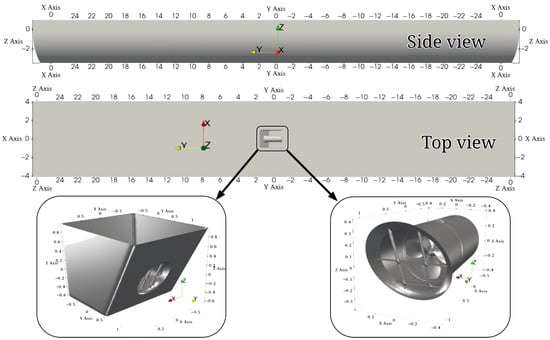
Figure 1.
Geometry of the computational domain for bow thruster CFD simulations.
3. Mathematical Model of Hybrid Simulations
CFD analysis was carried out using both steady RANS and scale-resolving hybrid URANS–LES approaches to capture the unsteady hydrodynamics of the full-scale bow thruster. Specifically, the Menter k– SST model and the Shielded LeMoS Hybrid (SLH) framework were utilized. A URANS–LES method was applied without modification from Kazemi et al. [1]. All simulations were performed in OpenFOAM [19] on body-fitted meshes generated by Numeca Hexpress (Figure 2). The tunnel geometry was discretized with nearly 21 million cells. Wall-adjacent cells were sized to achieve average on the tunnel walls, pod and strut, on the propeller blades, and on the protection grille, allowing the use of standard wall-function treatments.
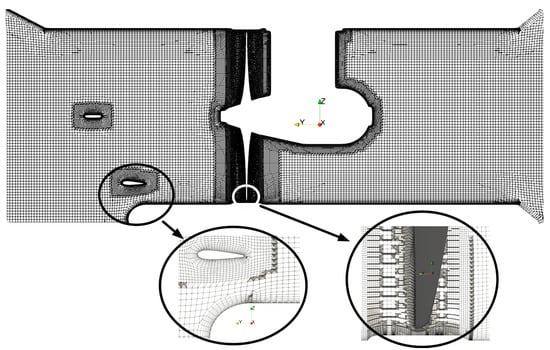
Figure 2.
Visualization of the computational grid at a mid-span cross-sectional slice of the tunnel.
The incompressible flow was governed by the continuity equation
and the unsteady momentum equation
where is the modified pressure, and and are the laminar and turbulent stress tensors, respectively. In the RANS regions, overbars denote Reynolds averages, while in LES zones they indicate spatial filtering. Turbulent stresses were computed via the Boussinesq approximation in URANS regions using the k– SST closures and in LES regions via a localized dynamic Smagorinsky model, with subgrid viscosity identified as the turbulent viscosity. Cavitation was modeled with the Schnerr–Sauer algorithm [20], and a volume-of-fluid (VOF) formulation tracked vapor fraction using a source term derived from the Rayleigh–Plesset equation.
A sliding-mesh technique with Arbitrary Mesh Interface (AMI) simulated propeller rotation, using a time step corresponding to a one-degree blade advance. Convective fluxes were discretized with OpenFOAM’s filteredLinear scheme—a blend of central differencing and upwind differencing limited to 20% upwind—to suppress numerical noise while minimizing dissipation. Diffusion terms employed non-orthogonal-aware linear schemes, pressure gradients were reconstructed via a Green–Gauss approach, and time advancement used the Crank–Nicolson method. Symmetry was enforced on the undisturbed free surface; zero-gradient conditions were applied on inlets and outlets for velocity, turbulence quantities, and vapor fraction, with total pressure specified at the outlet. The solver interPhaseChangeDyMFoam was used. Steady RANS solutions provided initialization, and simulations were continued until semi-periodic residuals settled at average levels of (velocity), (pressure), (), (k), and (vapor fraction), with global continuity error below .
4. Results
4.1. Flow Physics
Figure 3 presents two slices extracted at mid-span and mid-height of the domain for the ROD (reverse operation direction) configuration. The mid-span slice displays vorticity component , while the mid-height slice shows vorticity component . Only the SLH model results are shown, as this model exhibits the highest level of resolved turbulence. Additionally, it was observed that the delayed detached eddy simulation (DDES) model implementation in OpenFOAM does not activate the LES branch in the absence of significant upstream flow separation, consistent with previous findings [1,21].
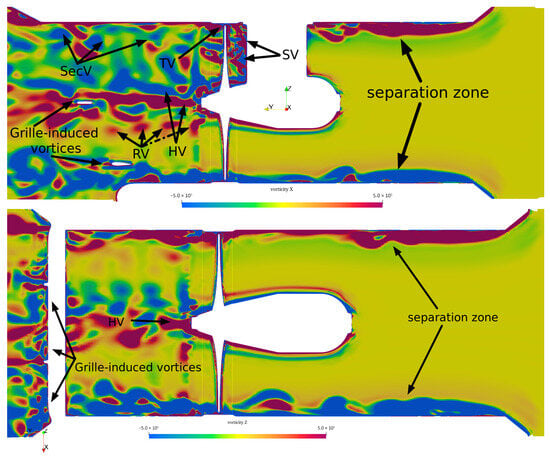
Figure 3.
Vorticity structures in ROD. Top: Vorticity-X at mid-span, bottom: Vorticity-Z at mid-height of tunnel. Results were obtained using SLH turbulence model for optimized geometry.
Several vortex structures are identified in Figure 3, including the tip vortex (TV), hub vortex (HV), strut vortex (SV), root vortex (RV), secondary vortex (SecV), and grille-induced vortex. Furthermore, the formation of a separation zone along the tunnel wall is evident near the entrance for ROD cases. While the NOD (nominal operation direction) configuration shows a single large separation zone mostly near the bottom of the tunnel entrance, the ROD cases display separation zones stretched along the entire tunnel wall at the entrance.
In the bow thruster geometry under NOD conditions, a strong interaction between the tip vortex (TV) and the wall is observed, giving rise to a prominent secondary vortex (SecV) [1]. A similar interaction is evident for the ROD cases.
Figure 4 shows the tip vortex (TV) for NOD (left) and ROD (middle). Both cases exhibit three rings of TV before breakdown. For NOD, this breakdown can be attributed to the strut position and its effect on the fluid flow. In contrast, for ROD, the TV breakdown appears to result from interactions with other vortex structures, particularly boundary vortices. An increased pitch of the helical vortices TV is clearly observed in the ROD mode. This was explained by the higher flow velocity behind the propeller blades in ROD mode. In contrast, in NOD mode, the flow behind the propeller was decelerated due to the braking effect caused by the strut and pod. The Q-criterion visualization on the right side of Figure 4 depicts the root vortex (RV) and hub vortex (HV) downstream of the propeller. In ROD, the RV remains coherent until it reaches the protective grille at the tunnel outlet.
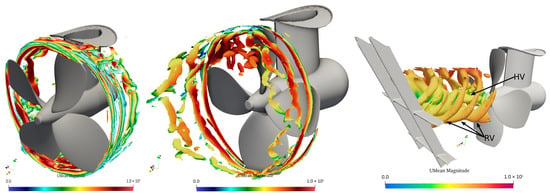
Figure 4.
Q-criteria presenting tip vortices in NOD (left) and ROD (middle), root and hub vortices in ROD (right).
Cavitation volumes predicted by CFD simulations using the Schnerr–Sauer model [20] are presented in Figure 5. Two images on the right show the ROD configuration, while the two images on the left correspond to the NOD case. All images are viewed from the propeller’s suction side, relative to its rotational direction. Several key observations emerge:
- In the NOD case, an accumulative cavitation region appears in front of the propeller at the bottom of the tunnel. This feature is absent in the ROD configuration.
- In ROD, cavitation accumulates (cavitation sheet has the largest extension) at a radius of approximately near the top of the tunnel (), which can be attributed to flow stagnation behind the strut.
- There are notable differences in cavitation volume between angular position in the ranges and in ROD and NOD. In NOD, the maximum cavitation volume occurs at the tunnel bottom (). The cavitation sheet does not collapse but instead follows the blade rotation, resulting in increased cavitation for compared to ROD. Conversely, in ROD, the peak cavitation volume occurs at the top (), leading to a greater cavitation sheet for .
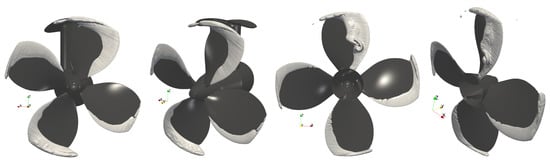
Figure 5.
Cavitation volume predicted by CFD and SLH for the optimized geometry: NOD (left), ROD (right).
4.2. Pressure Study
The circumferential distribution of the mean pressure at the tunnel wall is displayed in Slice 1 and Slice 2 located at a radial offset of 20% D from the propeller disk (Figure 6). The mean pressure (excluding the hydrostatic component) obtained from different models for the NOD and ROD cases is shown in the left and middle panels of Figure 6, respectively. The first notable observation is the smoother circumferential distribution of mean pressure in ROD compared to NOD. This smoothness can be attributed, in part, to the absence of a large separation zone at the tunnel bottom in front of the propeller, and the absence of a security grille at the ROD tunnel entrance.
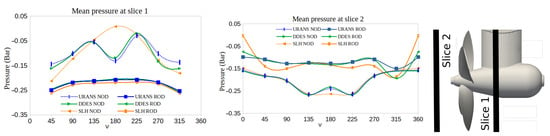
Figure 6.
Circumferential distribution of the mean pressure at the tunnel wall.
Reduction in the non-uniformity of the pressure pulsation distribution is evident in Figure 7, which displays the pressure pulsation (standard deviation, in bar) at slices near the tunnel inlet and outlet. Two main observations emerge from Figure 7: first, the variation in pressure pulsation is more uniform in ROD than in NOD; second, despite this smoothness, the amplitude of pressure pulsations in ROD is noticeably higher than in NOD, confirming that off-design thruster operation leads to increased noise and vibration. Based on these findings, it is reasonable to assume that positioning the thruster propeller closer to the end of the tunnel could yield smoother inflow and outflow, accordingly, a reduction in noise and vibration.
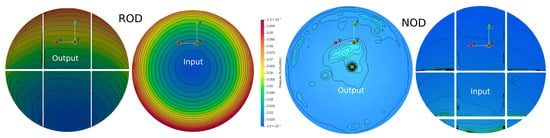
Figure 7.
Pressure pulsations (standard deviation in bar) at slices located at the tunnel inlet and outlet.
Polar diagrams of mean pressure (including the hydrostatic component) and mean pressure fluctuation, illustrating the circumferential distribution of pressure parameters along the tunnel wall, are presented in Figure 8. It should be noted that, for the ROD cases, Slice 1 and Slice 2 correspond to the propeller inflow and outflow, respectively; in the NOD cases, this assignment is reversed. In NOD, the maximum mean pressure occurs at the tunnel bottom, whereas in ROD it is observed at the tunnel top. The mean pressure fluctuation exhibits higher amplitudes in ROD compared to NOD at both slices, as expected.
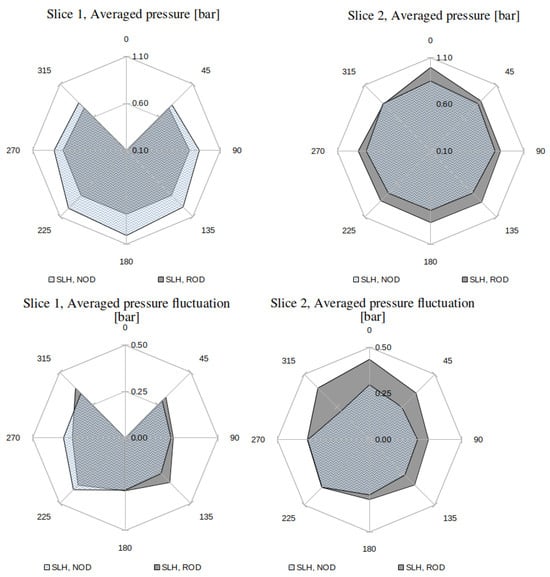
Figure 8.
Mean pressure and mean pressure fluctuation polar diagram.
4.3. Forces and Moments
Table 1 presents the mean thrust generated by the propeller for different turbulence models (URANS, DDES, and SLH) for both operational directions. The ROD configuration demonstrates a modest increase in thrust across all models—specifically, URANS, DDES, and SLH predict increases of 3.55%, 4.46%, and 5.88%, respectively, compared to NOD. These results are consistent with the findings reported in [22], where experimental analysis of pulling and pushing propeller modes demonstrated that positioning a nacelle (pod) upstream of the propeller can enhance thrust without significantly affecting the critical cavitation number.

Table 1.
Comparison of mean thrust generated by propeller [N].
Figure 9 shows the angular dependence of the averaged torque coefficient, , for both ROD and NOD configurations. In this figure, is computed by first dividing the total simulation time into individual propeller revolutions. For each revolution, the instantaneous torque coefficient is calculated as
where Q is the torque, T is the thrust, n is the rotational speed, and D is the propeller diameter. The quantities and represent the torque and thrust coefficients, respectively, at a given blade angle . These coefficients are computed for each revolution and then averaged over multiple revolutions for every angular position . In the figures, the solid line represents the ROD case, while the dotted line corresponds to the NOD case.
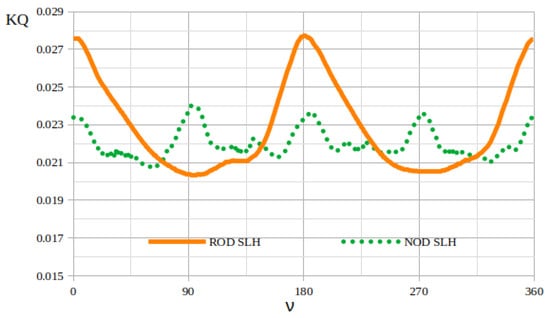
Figure 9.
Angular averaged torque coefficient .
Several noteworthy features emerge:
- In the ROD curve, the torque coefficient exhibits two pronounced peaks near and , reaching values around . Between these peaks, deep troughs appear at approximately and , with minima near . This “double-hump” pattern indicates a strong twice-per-revolution fluctuation in the loading on each blade when operating in the reverse-direction (ROD) configuration.
- By contrast, the NOD curve is much flatter: the torque coefficient oscillates gently between and , with only minor local peaks at and . This indicates a comparatively uniform torque distribution throughout each rotation under the normal operation (NOD) condition.
- Overall, the ROD configuration yields a larger mean and significantly larger amplitude of cyclic variation compared to NOD. In other words, ROD operation introduces stronger periodic torque fluctuations, whereas NOD operation maintains a more constant torque loading over the full sweep.
The averaged torque coefficient and thrust coefficient are presented in Table 2. The coefficients and were calculated using Equations (3) and (4), respectively. By performing a time-averaging of these values over multiple propeller revolutions, the results shown in Table 2 were obtained.
Hydrodynamic efficiency () is calculated using where T is thrust, is averaged velocity at a slice at tunnel entrance with respect to operational direction, n is rotational speed, and Q is torque. Table 2 presents a comparison of the averaged thrust coefficient (), torque coefficient (), and hydrodynamic efficiency () for both operation directions, using three different turbulence models: URANS, DDES, and SLH. These non-dimensional coefficients provide insight into the overall propulsive performance and the model sensitivity of the numerical predictions.

Table 2.
Comparison of , , and .
Across all models, the ROD cases exhibit slightly higher values compared to their NOD counterparts, indicating a modest increase in thrust during reverse operation. This observation is consistent with earlier findings from the CFD study by [18] and the experimental investigation by [22], and supports the physical interpretation that, in ROD mode, flow acceleration around the upstream nacelle contributes to increased thrust generation. In contrast, the torque coefficient remains relatively stable between NOD and ROD across all models, suggesting comparable levels of rotational resistance under both operating conditions.
Hydrodynamic efficiency () shows only minor variations across models and operating directions, with values ranging from 0.2113 to 0.2158.
These results underscore that, despite similar mean thrust in both configurations, the reverse-direction (ROD) case experiences more severe unsteady loading—an outcome that has important implications for noise, vibration, and structural fatigue in bow thruster applications.
Figure 10 compares the angular variation of thrust generated by the propeller—predicted via CFD—for each turbulence model under both NOD and ROD conditions.
where is the angularly averaged thrust at azimuthal position , is the instantaneous thrust at angle during the i-th revolution, and N is the total number of revolutions used for averaging.
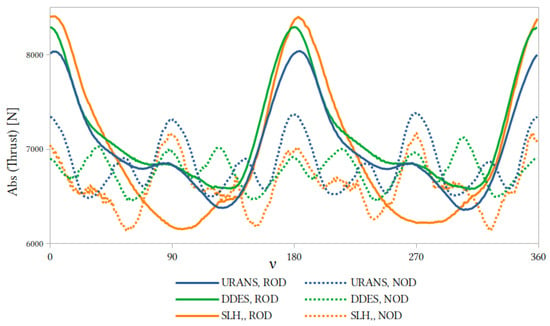
Figure 10.
Angular variation of averaged thrust over one propeller revolution for NOD and ROD.
In this plot, solid lines correspond to ROD cases and dashed lines correspond to NOD cases. Each curve exhibits four distinct thrust peaks over the – rotation, corresponding to the four blades passing through regions of highest loading.
However, in the ROD curves, two of these four peaks have noticeably lower magnitudes than the other two. By contrast, the NOD curves display all four thrust peaks at approximately the same intensity. In other words, under ROD operation, two of the thrust-generation peaks become “overpowered”, an effect likely caused by flow stagnation induced by the strut. This selective amplification of two peaks in ROD leads to an overall increase in the mean thrust, as observed in Table 1.
Figure 11 presents the power spectral density (PSD) of the thrust signal, obtained over 16 complete revolutions of the propeller. From this time series, the first four blade-passing frequencies (BPFs) were identified using
where m is the harmonic index (), and n is the rotational speed in revolutions per minute. The PSD amplitudes at these four BPFs are plotted for each turbulence model (URANS, DDES, and SLH) under both NOD and ROD conditions.
where is the power spectral density at frequency f, is the time domain thrust signal, is the total time duration of the signal, f is the frequency, and is the complex exponential from the Fourier Transform.
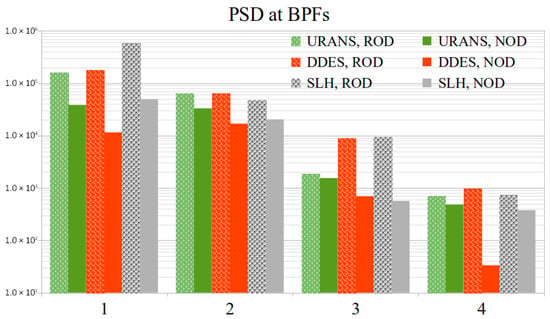
Figure 11.
Thrust power spectral density at the first four blade-passing frequencies.
Across all turbulence models and at the first four BPFs, ROD consistently exhibits higher power spectral density (PSD) values compared to the NOD, as shown in Figure 11. This elevated spectral energy reflects stronger unsteady hydrodynamic phenomena in ROD, such as intensified pressure pulsations and torque oscillations. Furthermore, cavitation dynamics in ROD—particularly the accumulation and collapse of vapor sheets near the tunnel top—introduce additional high-frequency fluctuations that reinforce the PSD peaks at harmonic frequencies.
A notable feature observed in both ROD and NOD configurations is the dominance of the fundamental frequency (BPF1) over its higher harmonics (BPF2 to BPF4), consistent with findings in previous studies. This predominance arises due to the primary pressure disturbances occurring once per blade passage, which are strongly tied to blade–inflow interaction and rotor–tunnel geometry alignment. While the higher harmonics emerge from nonlinear interactions and cavitation effects, they remain secondary in energy contribution. The sharp contrast in amplitude between ROD and NOD at all BPFs, however, underscores the critical importance of addressing off-design operation not only from a thrust efficiency standpoint but also from a vibration and acoustic signature perspective.
These observations suggest that, although ROD operation can yield slightly higher mean thrust, it does so at the expense of significantly increased unsteady loads. Designers should therefore consider additional damping strategies, improved tunnel symmetry, or blade geometry optimization if bidirectional thruster use is intended.
5. Conclusions
The comparative analysis of the ROD (reverse operation direction) and NOD (normal operation direction) thruster configurations reveals that, despite similarities in the fundamental flow physics and vortex systems—including tip vortices, hub vortex, strut vortices, root vortices, secondary vortices, and grille-induced vortices—key differences emerge in their hydrodynamic behavior and performance characteristics.
In the ROD mode, the tip vortex exhibits a noticeably increased helical pitch, attributed to the higher axial velocity of the wake which is not decelerated by the strut and pod elements present in the NOD configuration. This led to a more dynamic and spatially extended vortex field downstream. Additionally, while the NOD setup shows a concentrated separation zone near the bottom of the tunnel entrance, the ROD configuration was marked by more widespread separation zones distributed along the entire entrance tunnel wall.
Most significantly, the ROD mode induces substantially higher pressure pulsation amplitudes within the thruster domain. This is directly correlated with the more pronounced unsteadiness in thrust and torque delivery, indicating that operation in ROD mode leads to elevated levels of acoustic emission and mechanical vibration. Such findings confirmed that off-design operation—in this case, the ROD mode—could adversely affect the noise signature and structural loading of the propulsion system, thus demanding careful consideration in design and operational planning.
In summary, while both configurations generate similar types of vortical structures, the ROD mode amplifies unsteady phenomena and introduces greater hydrodynamic complexity, which manifests as higher fluctuations in thrust, torque, and pressure—key indicators of degraded performance and potential noise and vibration issues.
Author Contributions
M.K. performed the computations. N.K. supervised and coordinated the project; both authors analyzed the data and wrote the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This center is jointly supported by the Federal Ministry of Education and Research and the Ministry of Science, Research and the Arts of Baden-Württemberg, as part of the National High-Performance Computing (NHR) joint funding program. HoreKa is partly funded by the German Research Foundation (DFG).
Data Availability Statement
The datasets presented in this article are not publicly available because the geometry is proprietary to Jastram GmbH and protected by industrial secrecy. Requests for access should be directed to Jastram GmbH.
Acknowledgments
The authors acknowledge gratefully the support of the German Federal Ministry for Economic Affairs and Climate Action within the framework of the projects 03SX530E and 03SX530A monitored by J. Turnow. The authors also thank Jastram GmbH & Co. KG for providing geometric data of their bow thruster. The authors gratefully acknowledge the computing time provided on the high-performance computer HoreKa by the National High-Performance Computing Center at KIT (NHR@KIT).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kazemi, M.; Kornev, N.; Hinnenthal, J. Scale resolving simulation of unsteady bow thruster hydrodynamics. Ocean Eng. 2024, 298, 117212. [Google Scholar] [CrossRef]
- Ozdemir, Y.; Bayraktar, S.; Yilmaz, T.; Guner, M. Determining Optimum Geometry for a Bow Thruster Propeller. Ph.D. Thesis, Yildiz Technical University, Istanbul, Türkiye, 2008. Available online: https://www.researchgate.net/publication/288705948 (accessed on 3 July 2025).
- Yao, Z.; Yan, Z. Hydrodynamic performance analysis and verification of transverse thrusters. J. Ship Mech. 2012, 16, 236–245. [Google Scholar]
- Yu, C.; Yang, C. Study of Tunnel Thruster Performance and Flow by Quasi-Steady Reynolds-Averaged Navier-Stokes Simulation. J. Shanghai Jiaotong Univ. (Sci.) 2016, 21, 662–671. [Google Scholar] [CrossRef]
- Brizzolara, S.; Brizzolara, E. Long Tunnel Configurations for High Efficiency Thrusters. In Proceedings of the 5th International Symposium on Marine Propulsors SMP’17, Espoo, Finland, 12–15 June 2017. [Google Scholar]
- Mohan, A. Numerical Analysis of Bow Tunnel Thruster Performance. Master Thesis, TU Delft, Delft, The Netherlands, 2017. [Google Scholar]
- Ermolaev, A.; Saifullin, T.; Shevtsov, S. Effect of the thruster inlet configuration upon the force arising on the side. Trans. Krylov State Res. Cent. 2015, 88, 109–116. [Google Scholar]
- Ermolaev, A.; Shevtsov, S. Vibration of thrusters and ways to combat it. Trans. Krylov State Res. Cent. 2018, 67–74. [Google Scholar] [CrossRef]
- He, C.; Ma, X.; Wen, T.; Sun, Y.; Yang, Z.; Tan, Y.; Zhuo, J. Numerical simulation investigation on hydrodynamic performance of bow thruster under different velocity conditions. J. Mar. Sci. Eng. 2024. submitted. [Google Scholar]
- Dubensky, L.; Krikalo, T.T.V.; Pustoshny, A. Reduction of periodic forces arising on the propeller by artificial redistribution of the velocity field in the propeller disk using passive devices. Mater. Exch. Exp. Sci. Res. Inst. Named After Acad. A.N. Krylov L. Shipbuild. 1976, 241, 91–94. [Google Scholar]
- Kazemi, M.; Dause, M.; Hinnenthal, J.; Kornev, N. Numerical study of reduction of unsteady effects in bow thruster. Ocean Eng. 2025, 324, 120660. [Google Scholar] [CrossRef]
- Guo, W.; Yan, Z.; Han, Y.; Liu, M.; Sun, D.; Zhu, M. Design and Optimization of Non-Penetrating Tunnel Thruster for Small Vessels Using CFD. J. Mar. Sci. Eng. 2024, 12, 1960. [Google Scholar] [CrossRef]
- McNeill, D.; Wang, K.; Ning, Y.; Xu, L. Study on the Influence of Bow Thrusters on AUV Hydrodynamic Performance and a Novel Retractable Design. J. Mar. Sci. Eng. 2024, 12, 2021. [Google Scholar]
- Okuda, R.; Yasukawa, H.; Hirata, N.; Matsuda, A. A Study on Berthing and Unberthing of a Single-Shaft Ship with a Bow Thruster. J. Mar. Sci. Technol. 2024, 29, 53–74. [Google Scholar] [CrossRef]
- Li, B.; Zhang, J.; Chen, F.; Zhang, Z. Decay of Bow Thruster-Induced Near-Bed Flow Velocities. J. Coast. Harb. Struct. 2024, 11, 41–55. [Google Scholar]
- Tan, Y.; Sun, Y.; Cai, H.; Zhuo, J. Analysis of Pressure Fluctuations Caused by Bow Thrusters in Different Operating Directions. J. Mar. Sci. Eng. 2024, 12, 2054. [Google Scholar] [CrossRef]
- Hodge, R. Design Issues and Failure Modes in OSV Propulsion Systems. In Proceedings of the Dynamic Positioning Conference, Houston, TX, USA, 13–14 October 2009. [Google Scholar]
- Bui, T. Numerical simulation of the performance of bow thruster taking into account turbulence model influence using RANS method. In Proceedings of the Seventh International Symposium of Marine Propulsors (SMP’22), Wuxi, China, 17–21 October 2022; pp. 109–114. [Google Scholar]
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Schnerr, G.H.; Sauer, J. Physical and numerical modeling of unsteady cavitation dynamics. In Proceedings of the Fourth International Conference on Multiphase Flow, ICMF, New Orleans, LO, USA, 27 May–1 June 2001; Volume 1. [Google Scholar]
- Anschau, P.; Kornev, N.; Samarbakhsh, S. Unsteady hydrodynamic loads on energy saving ducts. Ocean Eng. 2023, 269, 113431. [Google Scholar] [CrossRef]
- Shevtsov, S. Investigation of Hydrodynamic Characteristics of Thrusters of the “Screw in the Pipe” Type. Clarification of the Design Methodology of These Devices, Including High Power Installations. Ph.D. Thesis, Krylov Research Centre, St. Petersburg, Russia, 2014. (In Russian). [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).