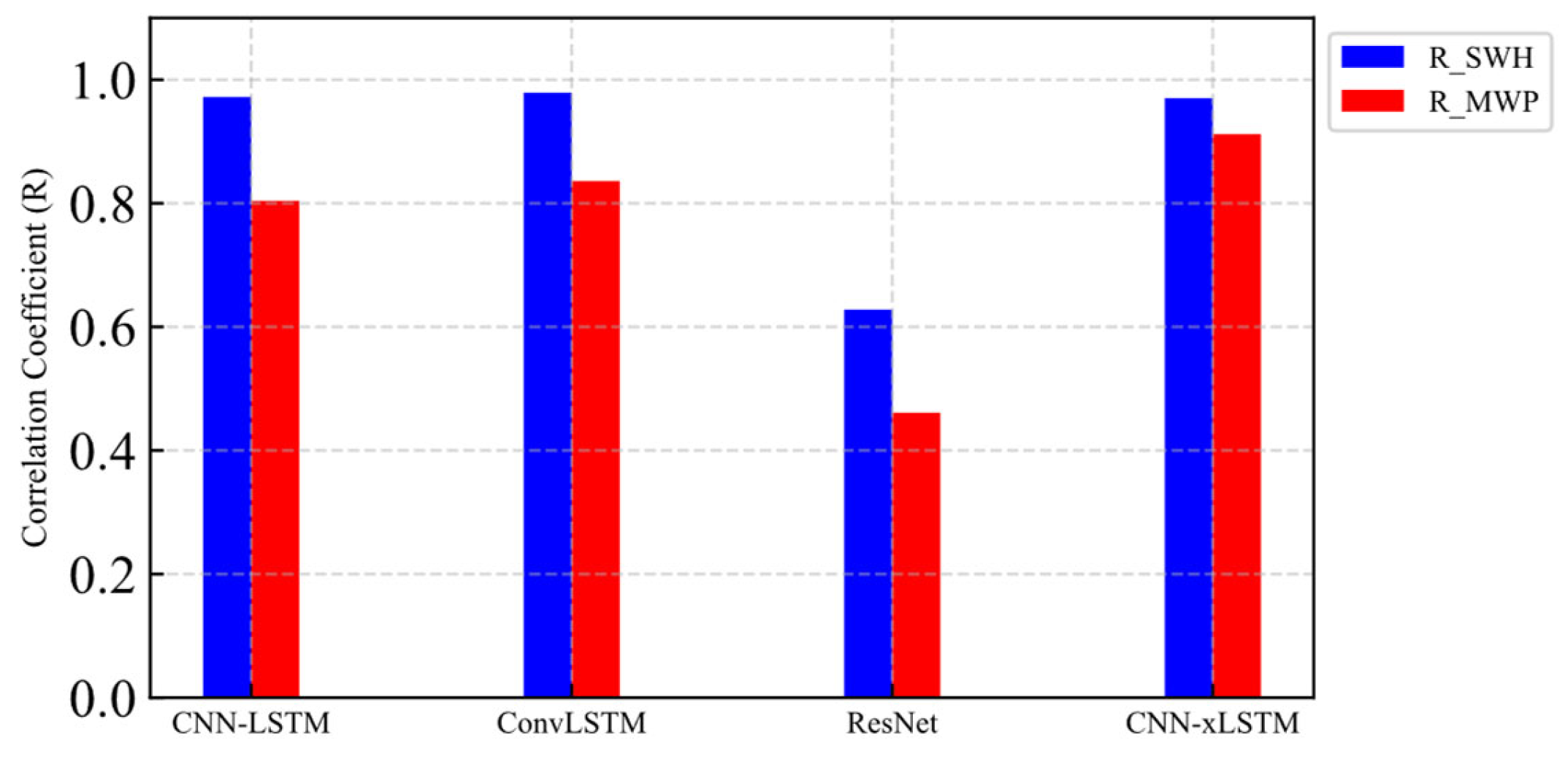
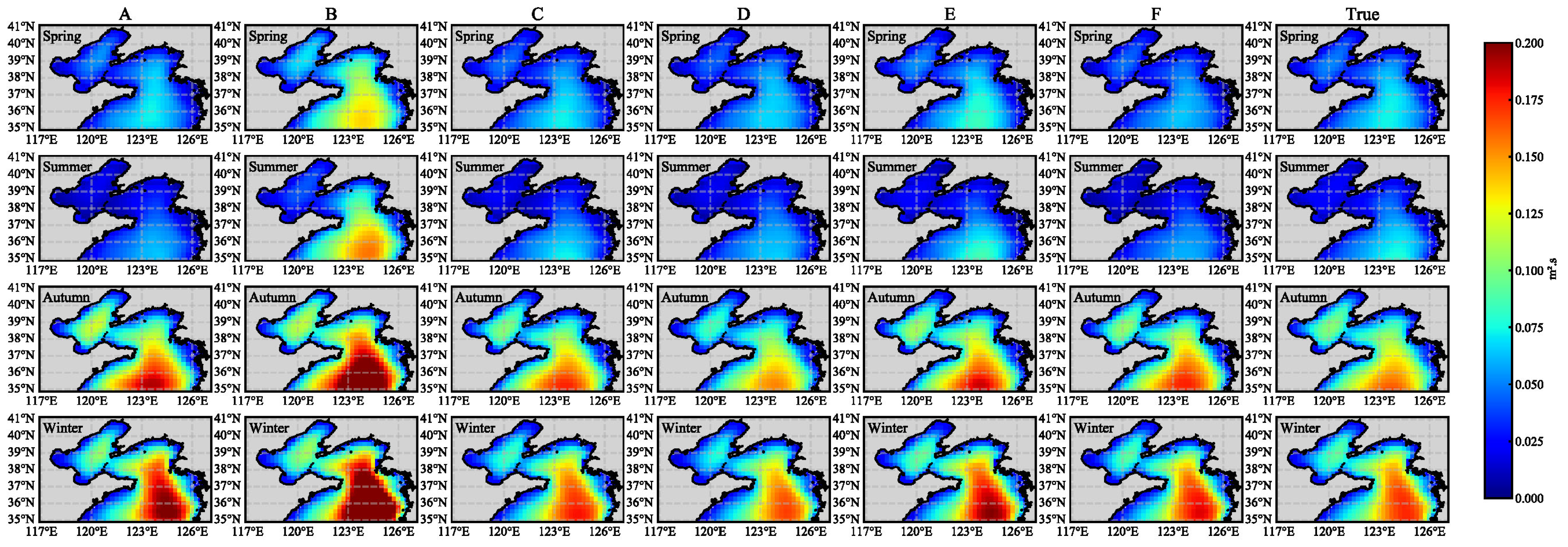
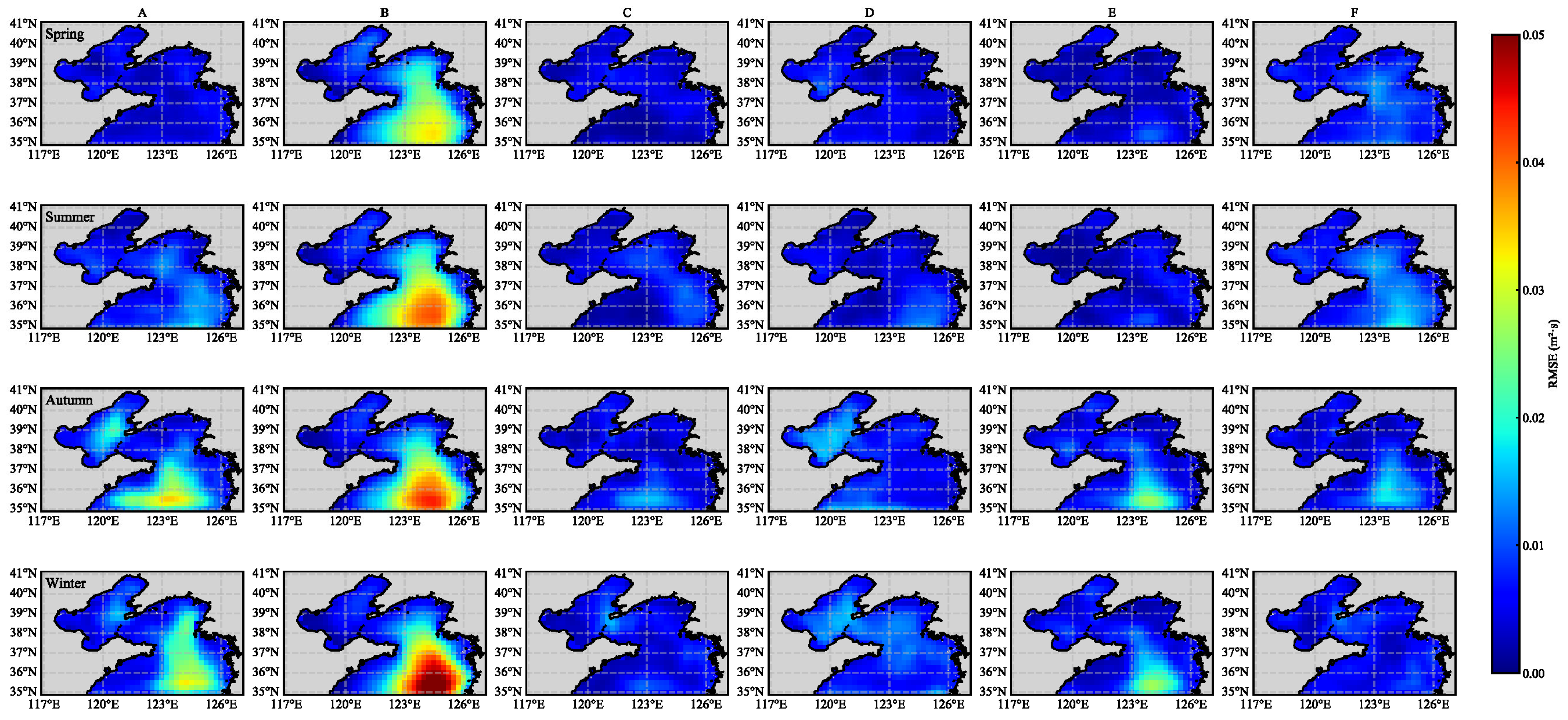
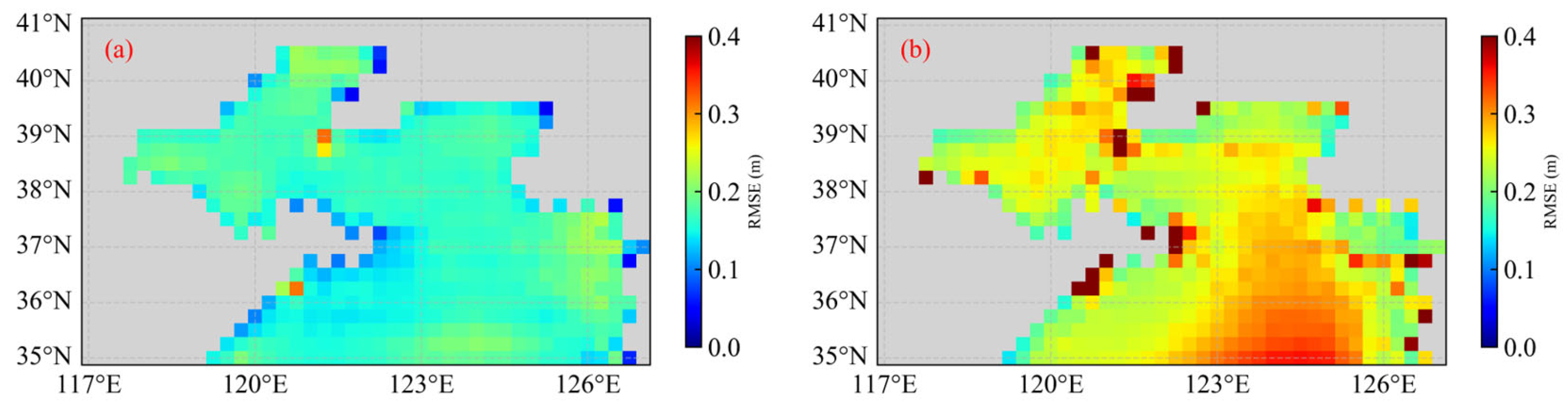
4.2. Single-Point Wave Spectrum Characterization
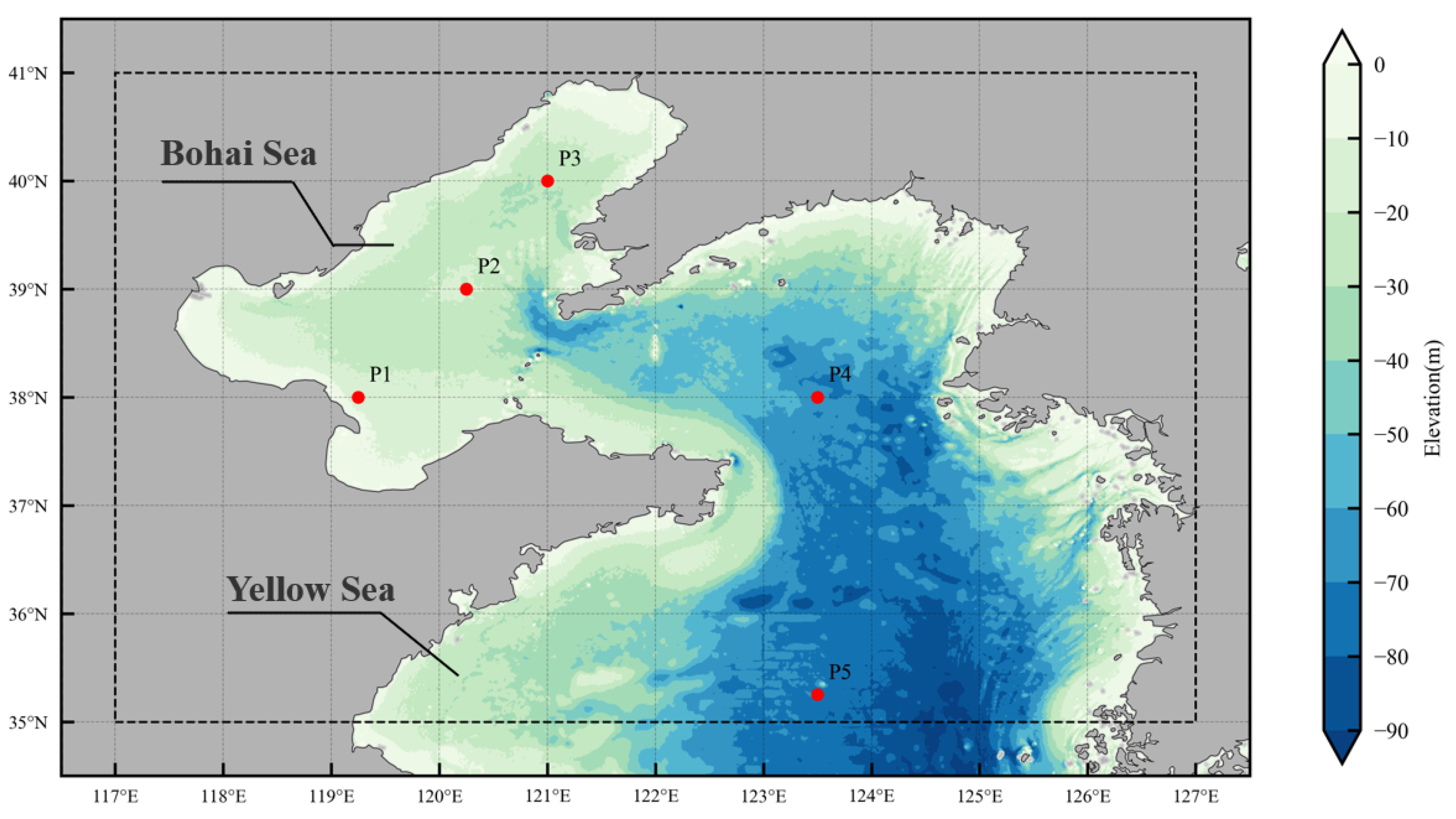
To validate the model’s performance in different regions, we select five points from
Figure 1 as representatives. Point P1 is located in the nearshore area of the Bohai Sea, where the water depth is relatively shallow. This point is influenced by the land topography, and the wave propagation path is relatively long. Points P2 and P3 are located between the Bohai Sea and Liaodong Bay. These two points are controlled by the southward movement of cold air, where the wind direction and speed vary greatly, and they are often accompanied by atmospheric disturbance processes. Selecting these points helps to investigate the model’s ability to capture the response mechanisms under wind region variations. Point P4 is located in the northern Yellow Sea, and its selection aims to test the model’s predictive ability in semi-enclosed sea areas. Point P5 is located in the central Yellow Sea, close to the boundary of the study area, which is easily influenced by typhoons, remote swell waves, and other events. This point is chosen to evaluate the model’s ability in deep-water areas near the boundary and its response to remote wind field influences.
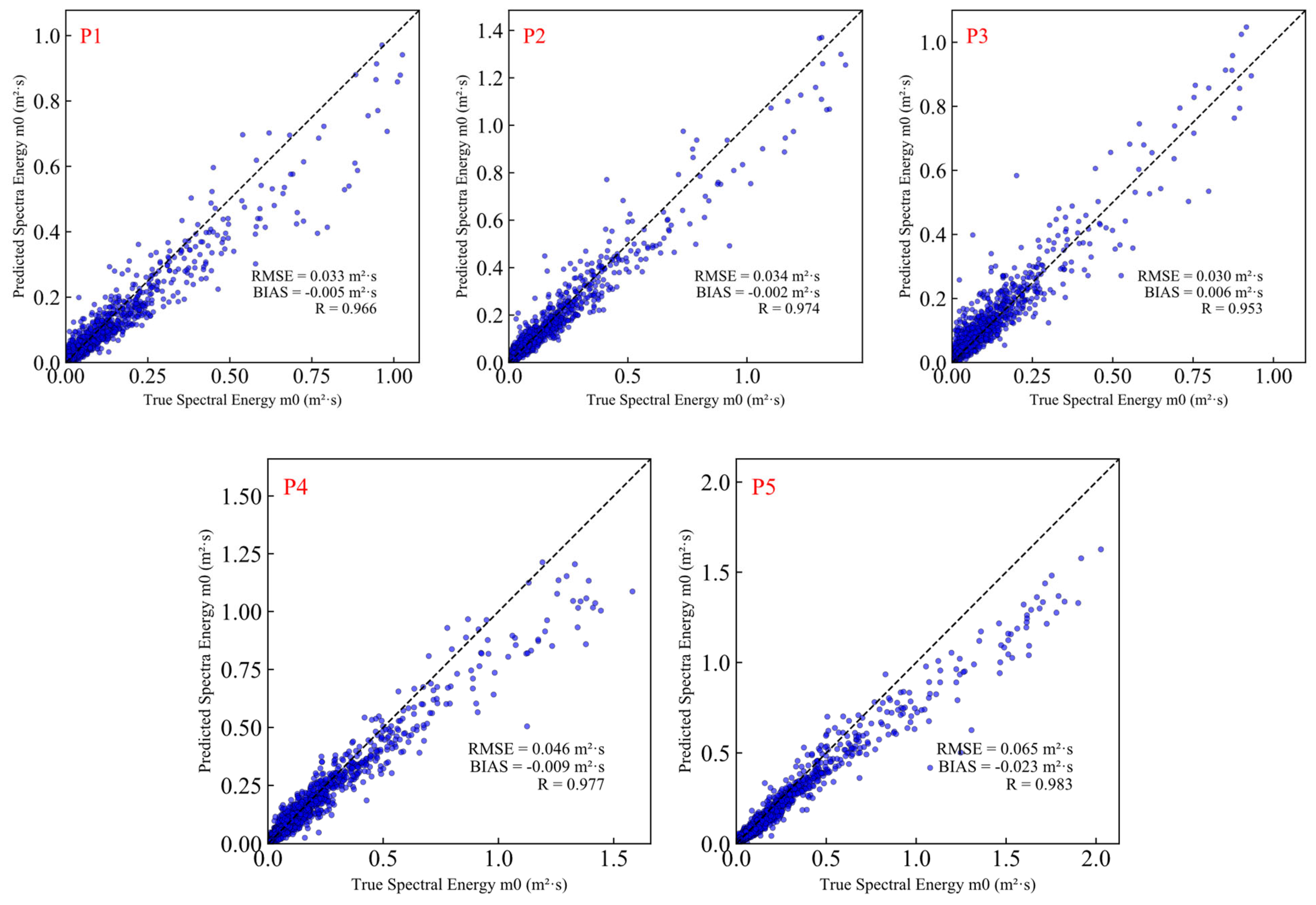
The scatter plots of the spectral energy M0 between the true values and predicted values at the five points are shown in
Figure 11. The deviations are close to zero with the correlation coefficient (CC) ranging from the lowest (0.95) to the highest (0.98). The RMSE at point P5 is higher than at the other four points because it is located at the boundary of the study area and is influenced by remote swell waves from the southern region. Additionally, wave breaking and dissipation occur as the waves propagate northward. As indicated [
40], closed and nearshore regions are more difficult to model compared to open sea areas. From the model’s perspective, the boundary area has fewer data, and the model is unable to access information outside the boundary. This leads to an insufficient understanding of the boundary extraction, and the evaluation metrics at the boundary area are more prone to error, which amplifies the overall mean error.
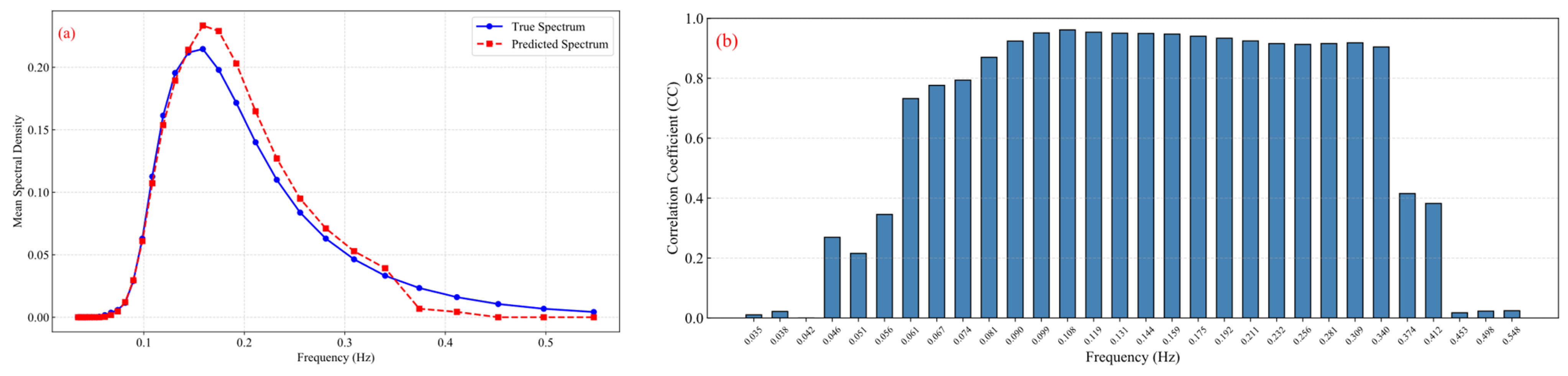
Figure 12a shows the average spectral energy density distribution with frequency across the entire study area, where the measured values are represented by the blue line and the model predictions are represented by the red line. From the figure, it can be observed that the model’s predicted spectral frequency is generally higher than the true values, and the high-frequency energy is underestimated and decays faster. In deep-sea areas, nonlinear interactions between waves can transfer energy from the spectral peak to the low-frequency range, which is an important characteristic of spectral evolution [
41]. In the main frequency range of 0.1 Hz to 0.3 Hz, the model’s predicted energy is slightly higher than the true values, indicating that the model has some fitting ability. However, when the spectral peak shifts to the high-frequency range, the model fails to fully capture this nonlinear transfer, which could be the reason for the high-frequency bias in the predicted spectral peak. Moreover, in the energy transfer process, high-frequency components quickly dissipate, while long-wave energy supports wave growth [
42], leading to a faster decay of the actual spectrum in the high-frequency tail. At the same time, neural networks tend to have spectral bias, favoring the fitting of low-frequency signals, and high-frequency components are often harder to learn [
43]. Therefore, insufficient energy fitting in the high-frequency range is one of the errors in the current model’s prediction.
Figure 12b shows the CC of the model across different frequencies on the validation set. In the main frequency range from 0.1 Hz to 0.35 Hz, the CC is greater than 0.90, but the correlation is lower at both low and high frequencies. This is consistent with the average spectral density distribution shown in
Figure 12a. Unlike the method in JIANG (2023), where the spectral prediction at a single point is trained from high to low frequencies on a per-band basis, we train the model as a whole. This approach works well in the main frequency range, but due to insufficient data in the low and high-frequency ranges, the model’s generalization ability is poor, and performance declines in the edge frequency bands. This is another reason for the errors observed.
This bias is also reflected in
Table 9 and
Table 10. In
Table 9, the peak frequency, as the most representative and easily measurable variable in the one-dimensional frequency spectrum, changes slowly and can reflect the development stage of the waves. The RMSE for the five representative points is between 0.03 and 0.04, with the lowest peak frequency errors at P4 and P5, indicating strong temporal consistency in the dominant wave periods. However, combining with the spectral peak value errors in
Table 10, it is evident that P4 and P5 have larger energy fluctuations with higher deviations in the predicted spectral peak values. This further indicates that while the model can predict the main frequency location well, it still has shortcomings in fitting high-frequency energy amplitudes.
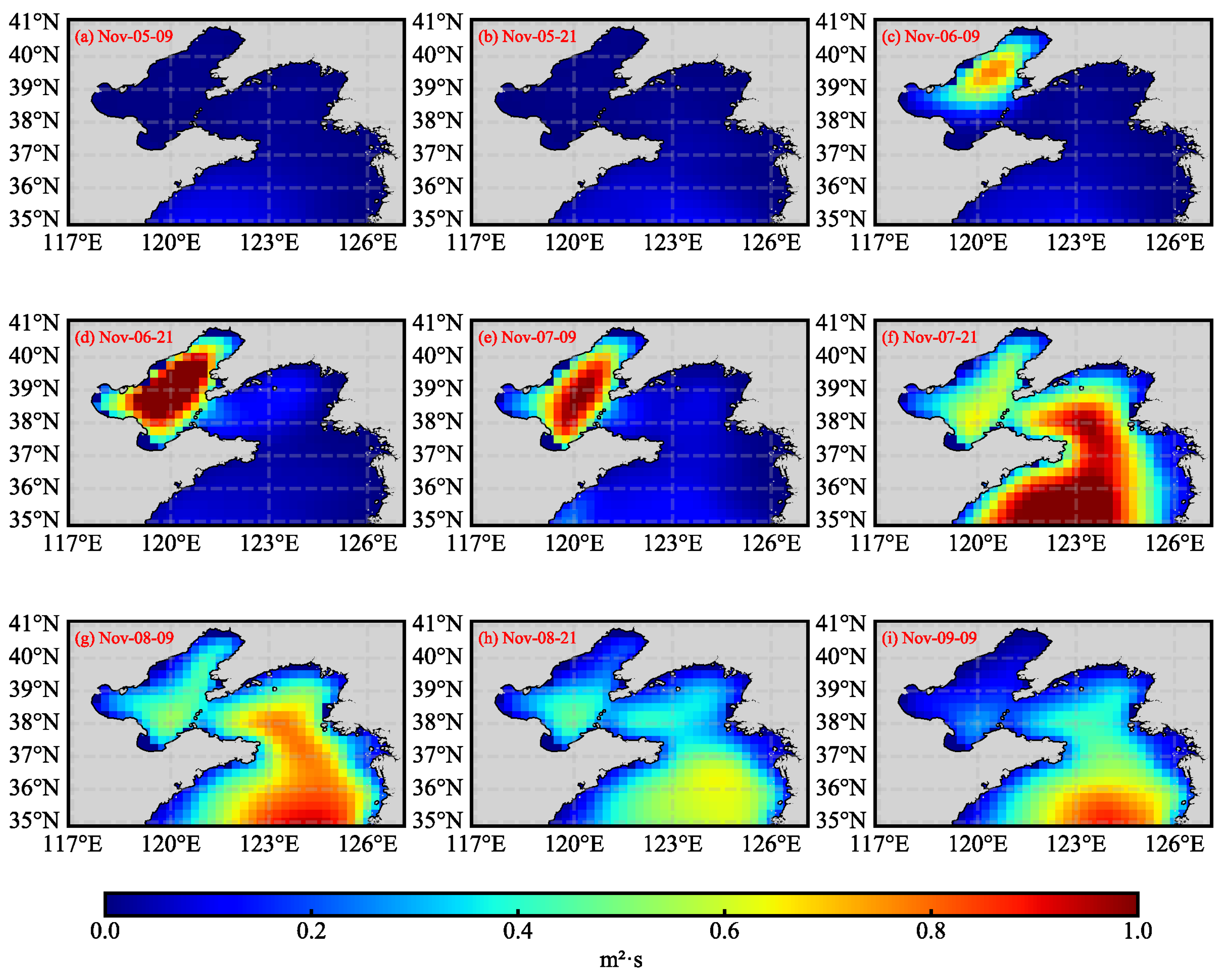
We select the wave characteristics of the Bohai Sea and its surrounding areas during the strong northern cold wave in early November 2021 as the research subject [
44]. We combine the spatiotemporal variation characteristics of M0 during the cold wave (
Figure 13) with the time-series wave spectrum at single points P1, P2, and P3 during the cold wave (
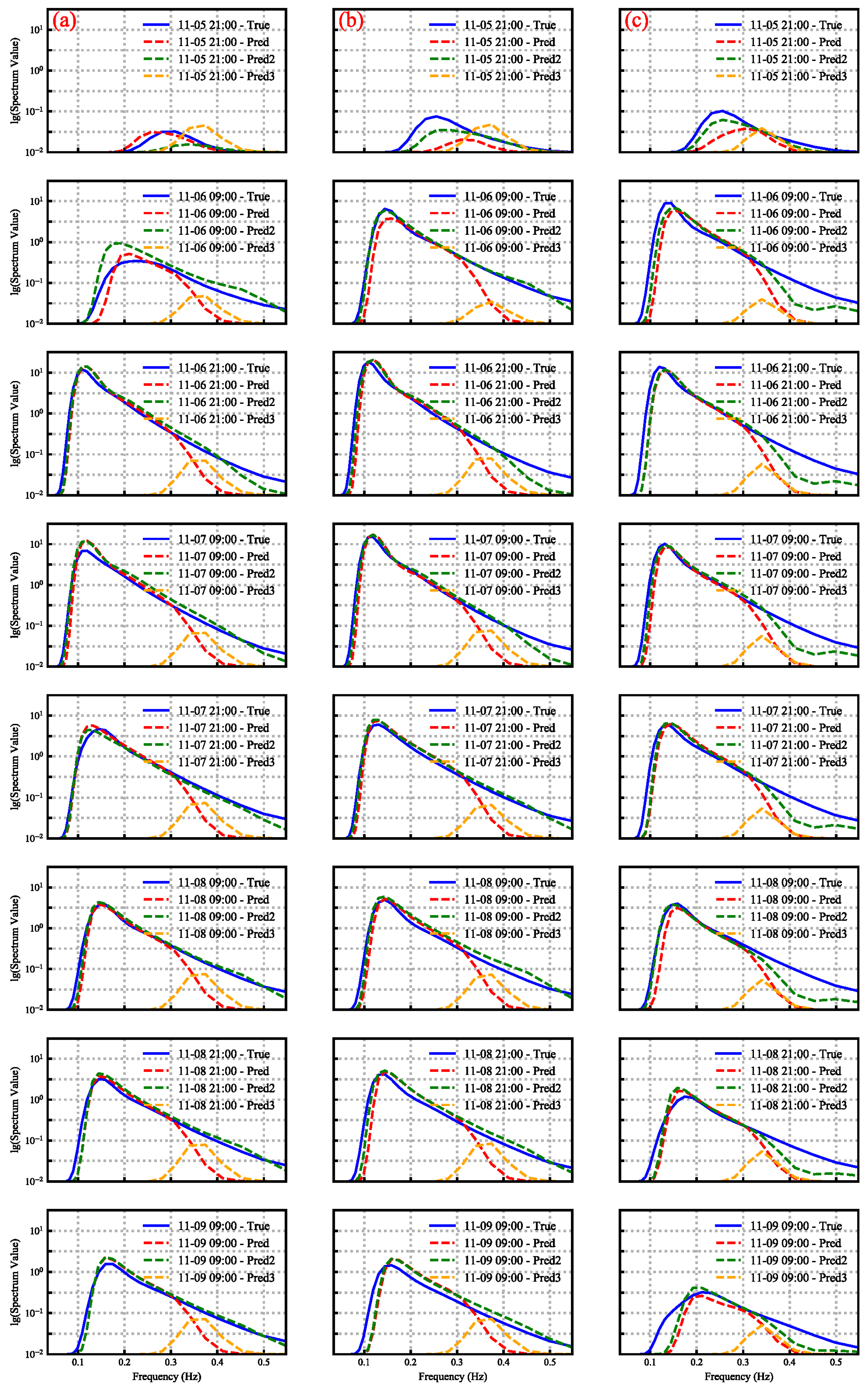
Figure 14) for analysis. In
Figure 14, the blue curve represents the ERA5 real data, and the red curve represents the predicted values. To clearly reflect the spectral variation, the
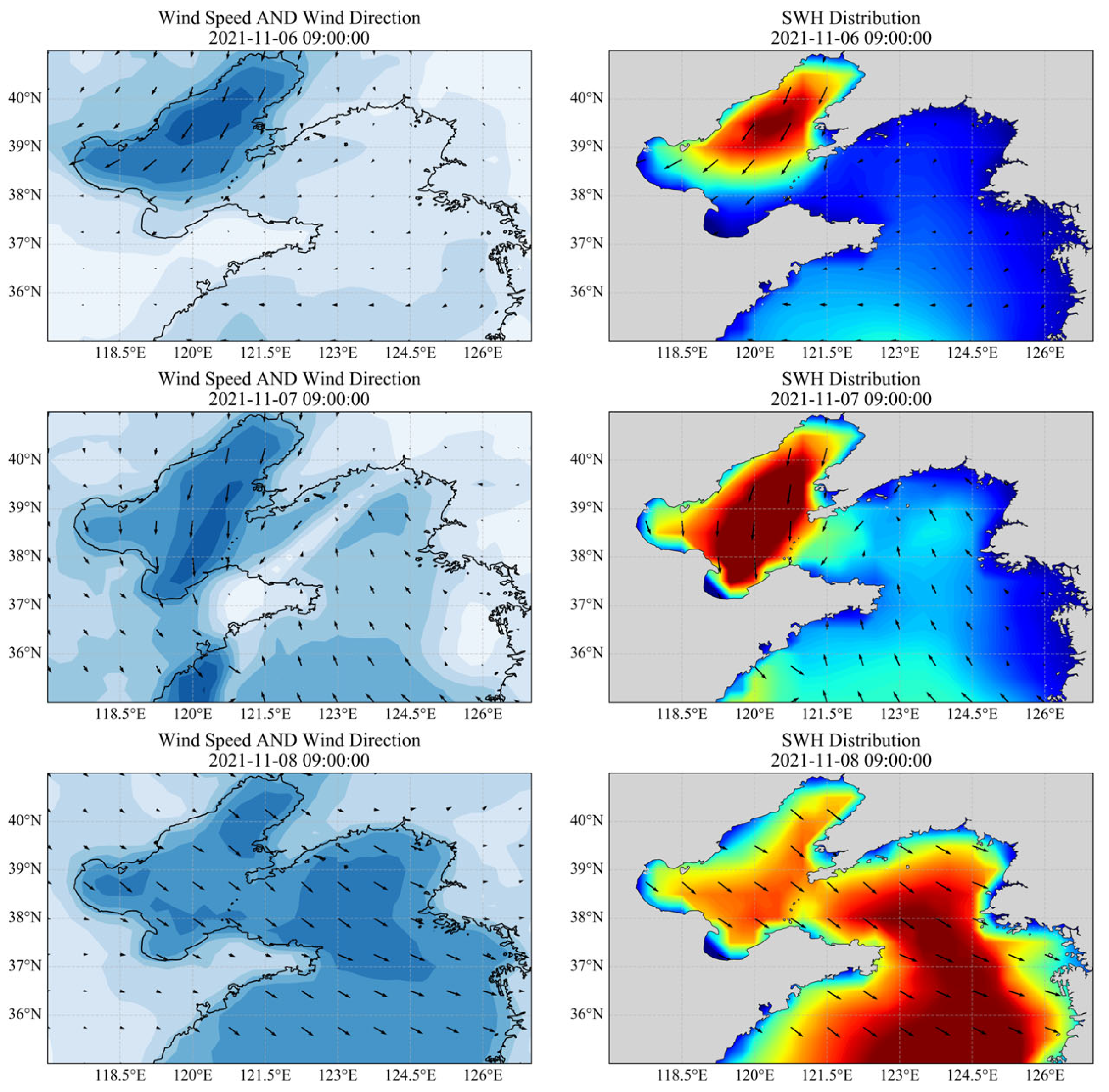
y-axis is plotted using a logarithmic scale (log10). For comparison, the spatial distribution of wind speed, wind direction, and SWH is also shown in
Figure 15.
Figure 14 shows that the wind-wave spectrum during the cold wave is unimodal with the main energy provided by the wave components corresponding to the narrow band frequencies. Starting from 09:00 on November 5th, the spectral energy at all three points is relatively low. From the 5th to the 6th, as the cold advection moves in, the wind speed strengthens, and the waves rapidly intensify. During the propagation of the spectrum from P3 to P1, processes such as wave breaking dissipation, nonlinear wave–wave interactions, and swell diffusion occur. Point P1, located near the coast, has a longer wave propagation path, so the growth of spectral energy is relatively delayed. The wave response at P2 and P3 is influenced by the lag of the wind field, resulting in overall lower energy levels. As the cold wave develops, the wind field gradually covers the entire Bohai Sea. Between the 6th and 7th, nonlinear interactions between wave components of different frequencies continuously transfer energy to lower frequencies, triggering the development of a low-frequency spectral peak. The spectral shape gradually changes from a broad peak to a narrow peak. The M0 first appears in Liaodong Bay and the central Bohai Sea, and by the 7th, it completely covers the Bohai Sea. Due to the transition from northeast winds to south winds, the wave propagation path also changes, with energy gradually transferring from the deep water region to the nearshore area. The model performs steadily during this phase and can capture the trend of the main frequency variation well. Between the 7th and 8th, the wave energy spreads to the Yellow Sea. As the wind field changes, the energy decreases, and the predicted values at the three points remain consistent with the real values. On the 8th and 9th, as the cold wave weakens and the wind direction shifts to northwest winds, the spectral energy generally decays. The offshore point P3 responds first with the spectral value decreasing. The energy dissipation curve from P3 to P2 to P1 is observed, but the spectral tail is still underestimated, which remains a key issue that needs to be addressed.
Therefore, we propose two methods to improve the predictive performance of the high-frequency part. One method is to strengthen the loss constraint on spectral values between 0.232 Hz and 0.548 Hz, guiding the model to pay more attention to high-frequency errors during the training process. The calculation method of the composite loss function is shown in Equation (29):
From
Figure 14, it can be seen that the introduction of the high-frequency weighted loss function in the green curve significantly improves the spectral prediction performance of the model in the high-frequency frequency band. Most high-frequency spectral values are closer to the true values, indicating that this method can effectively guide the model to focus on the errors in the high-frequency part. However, there is still a certain deviation at point P3, which may be related to the short duration of the wind field at that point. Short-term wind drive is difficult to fully reflect the wave growth process, thereby affecting performance.
Table 11 shows the comparison of prediction accuracy under different parameter settings. The results indicate that appropriate weighting can optimize the prediction performance, but parameters that are too large or too small can lead to an increase in error, indicating that a reasonable weighting amplitude is the key to improving model performance.
Throughout the entire process, as shown in
Figure 15, the spatial distributions of wind speed and SWH demonstrate strong temporal and spatial consistency between the wind field and the wave field. The transformation of the spectral shape from a broad to a narrow peak, and the wave propagation path shifting from deep water to nearshore areas, both align with the advancing direction of the cold wave. The unique geographic structure of the Bohai Sea and surrounding areas restricts the full development of waves, resulting in the dominance of locally generated wind waves during the cold wave event. Changes in water depth and topography also influence wave propagation: waves intensify along the wind direction in deeper waters but attenuate as they approach the nearshore region due to increased bottom friction caused by shallower depths. This process reflects the physical characteristic that high-frequency components dissipate more easily, while low-frequency waves can propagate farther. Overall, the model successfully simulates the full process of wave generation, propagation, and attenuation, and it also verifies its ability to capture the spatial energy transfer patterns under a typical synoptic weather event.
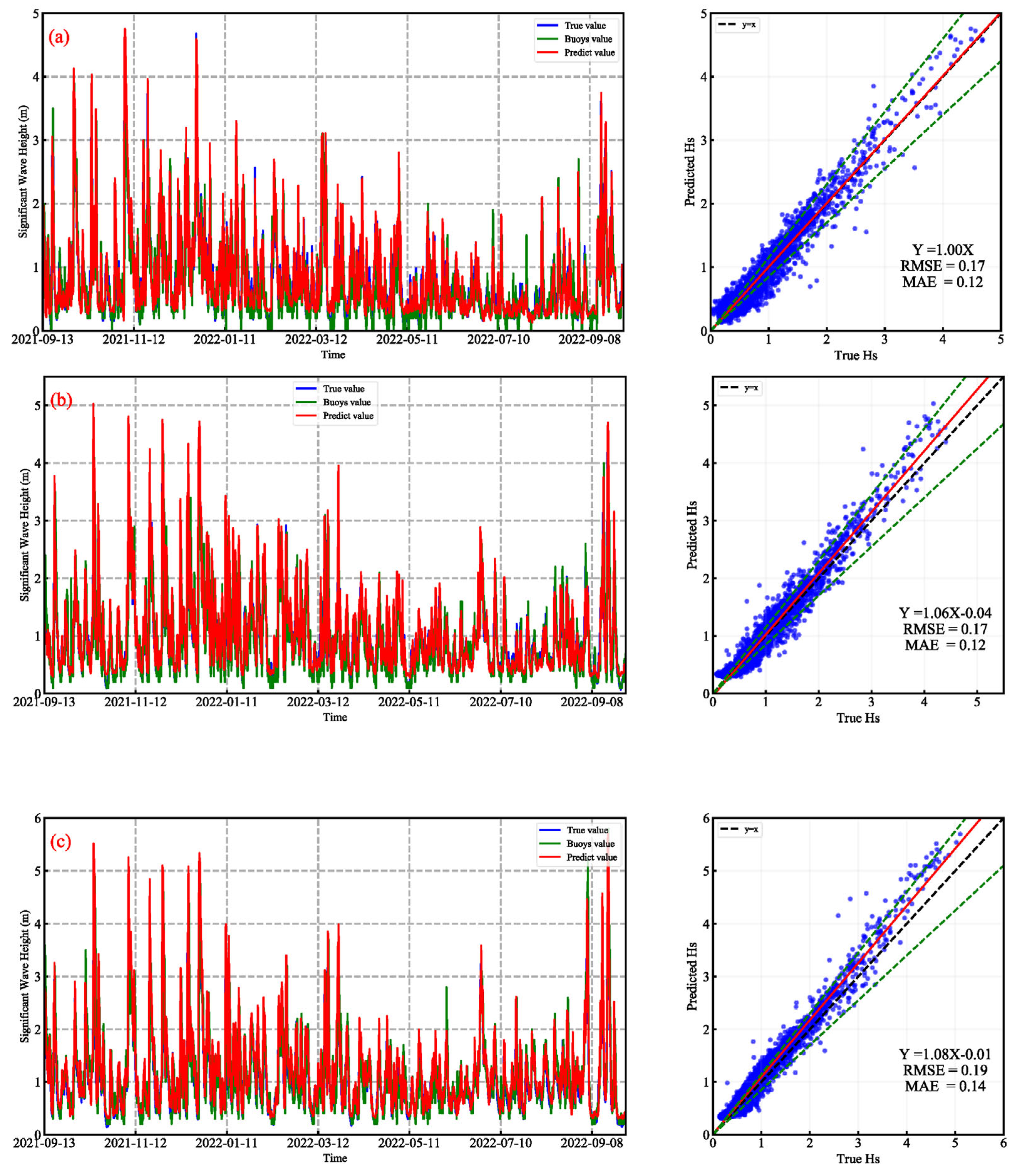
To further validate the model’s applicability under real observation conditions, buoy measurement data were introduced to compare the model’s predictions with ERA5 reanalysis data. In
Figure 16, the blue line represents ERA5 reference values, the green line shows buoy observations, and the red line indicates model predictions. Subplots (a), (b), and (c) present the comparison of SWH predictions at representative points P2, P4, and P5. At point P2, the model predictions closely follow the overall trend of both ERA5 and buoy data, especially under regular wave conditions (SWH < 2.5 m), where the predicted curves closely align with the observed data. The scatter plot shows a high linear correlation between predictions and reference values with the regression line having a slope close to 1. At point P4, which is located in a semi-enclosed sea area, the linear regression equation is y = 1.06x − 0.04. Even for SWH between 2 m and 4 m, the model maintains good performance. At point P5, the model accurately captures SWH variations during most periods, remaining consistent with both ERA5 and buoy data. The overall error remains within an acceptable range, indicating the model’s ability to adapt to complex boundary conditions. In summary, the predictions at all three points are stable. Combined with the comparison against buoy observations, this further confirms the practical value and reliability of the proposed model.
4.3. Discussion
The results of this study demonstrate that the proposed method can effectively utilize deep learning models to achieve regional one-dimensional frequency spectrum prediction, showing strong practical applicability. In the spectrum regression task, one-dimensional spectra combined with various meteorological and oceanographic factors were used to reflect the spatiotemporal trends of spectral energy, thereby overcoming the limitations of traditional buoy observations in terms of spatial coverage and real-time capability. During the prediction process, we found that the model performed well in the dominant frequency band but showed systematic underestimation in the high-frequency range. This bias may stem from two main causes: first, deep learning models are generally biased toward fitting low-frequency signals while neglecting high-frequency components; second, in deep-sea regions, nonlinear interactions among waves transfer energy from the spectral peak to lower frequencies, which is a mechanism that the current model does not adequately capture. We attempted to improve the model’s ability to fit high-frequency spectral values by adding a high-frequency weighted loss function, and the results indicate that appropriate weighting can optimize the prediction performance. We also introduced Toba’s 3/2 exponential law [
45,
46] as a physical constraint, attempting to further standardize the model’s prediction results through the physical relationship of wind and wave growth. The calculation method of the loss function is shown in Equations (30) and (31):
In the equations,
,
, and
. Considering that the value of
is too small, it will affect the convergence speed of the model. Therefore, we set the condition that when
is less than 0.1,
will be set to 0, so that the overall loss function of the model only corresponds to the Smooth L1 loss function. At the same time, in order to ensure that the loss function is of the same magnitude,
is 0.0001. From the orange curve in
Figure 14, it can be seen that the results are very poor, possibly because the Toba 3/2 index rate may not be applicable to all sea conditions, especially in the presence of swells. In fact, the delayed response of wave fields to wind forcing plays a significant role in wave evolution, particularly during wind onset or under strong wind conditions. Improving the model’s ability to capture energy fluctuations during these periods will be our next focus. Compared to existing studies in the field, which mostly address either two-dimensional spectrum reconstruction or pointwise spectral prediction, our study achieves one-dimensional spectrum prediction at a regional scale, offering a distinct advantage.
Improvements made to the model during the deep learning training process have enhanced its overall stability, providing potential directions for future performance optimization. From a practical application perspective, although one-dimensional spectra can capture the evolution of wave energy in the frequency domain, they are limited in describing energy propagation and the directional dimension. Consequently, the model cannot capture critical processes such as directional spreading and energy focusing. Future research should consider using regional two-dimensional directional spectra to provide a more comprehensive representation of wave dynamics. These limitations highlight important directions for subsequent work.