Design and Performance Study of a Magnetic Flux Leakage Pig for Subsea Pipeline Defect Detection
Abstract
1. Introduction
2. Theoretical Basis of Magnetic Flux Leakage Detection
2.1. Principles of In-Line Magnetic Flux Leakage Detection
2.2. Theoretical Calculation Methods for Magnetic Flux Leakage Fields
3. Numerical Model Development
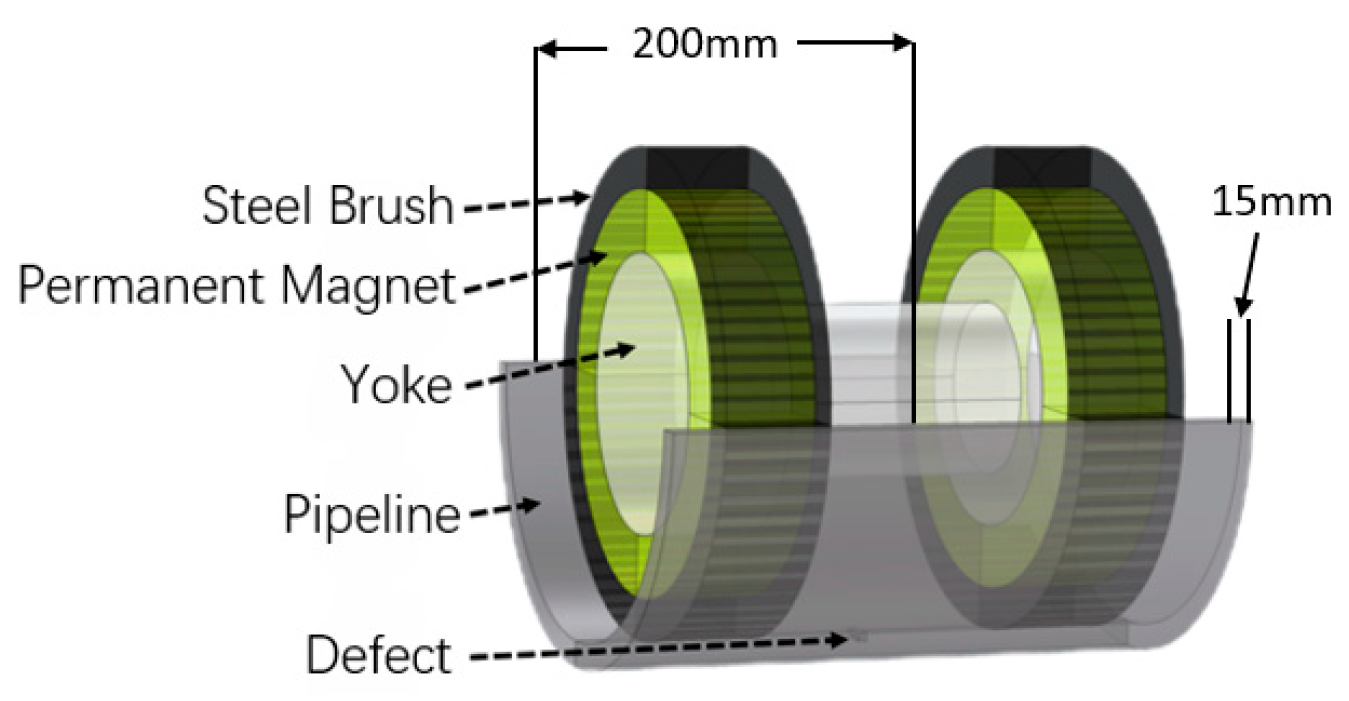
3.1. Establishment of the Geometric Model
3.2. Material Property Definition
3.3. Mesh Generation
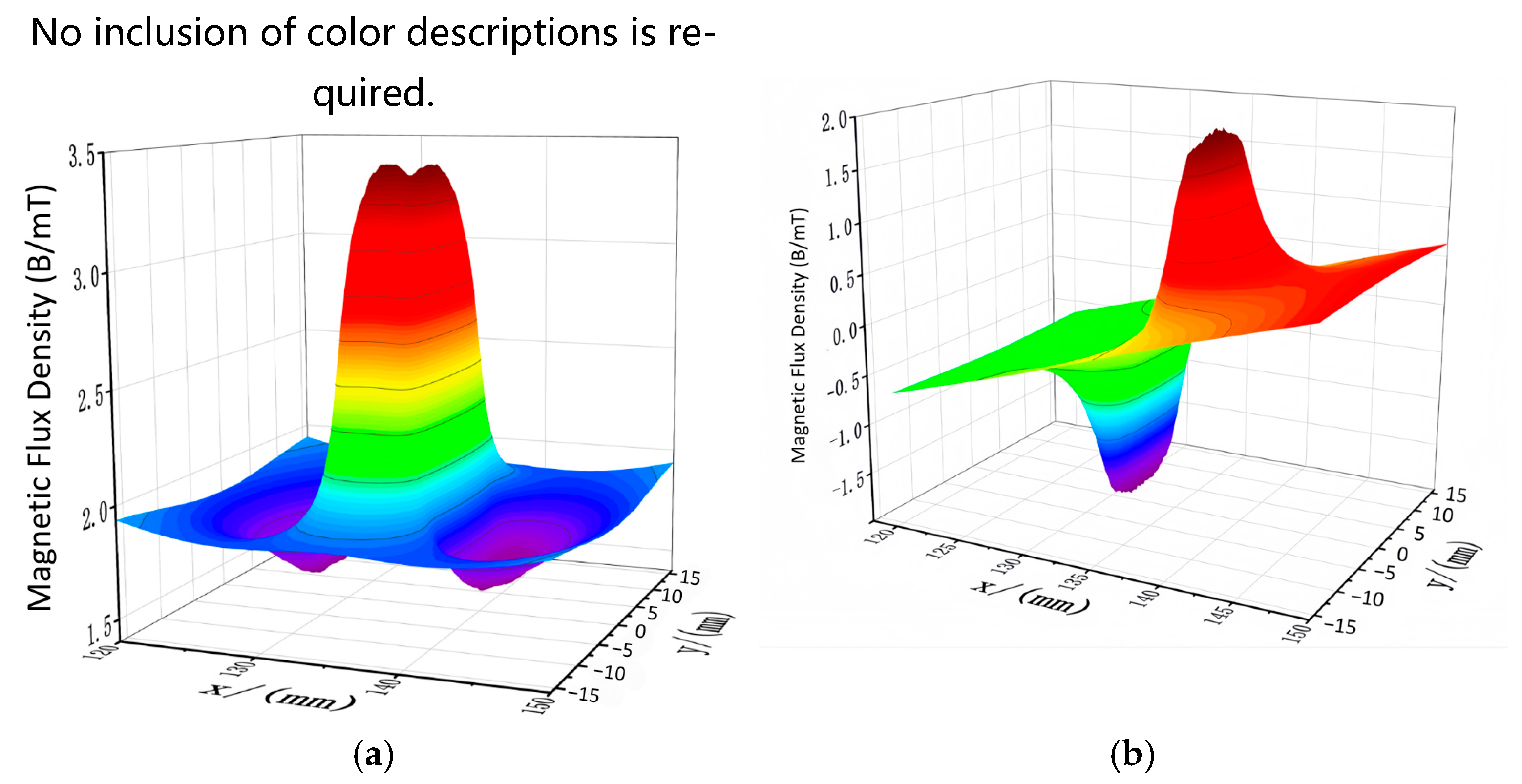
4. Analysis of Defect-Induced Magnetic Flux Leakage Field Distribution Characteristics
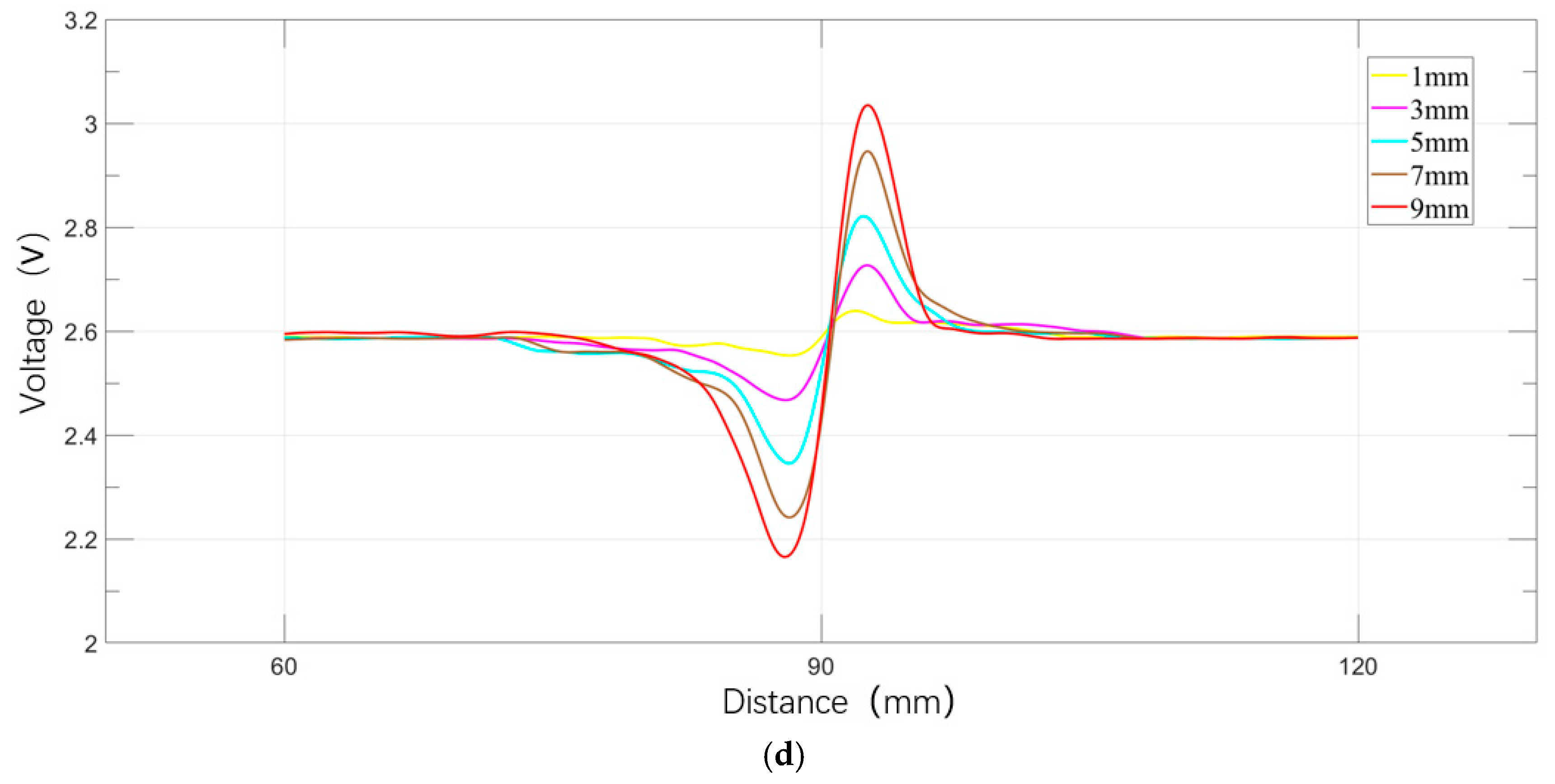
4.1. Influence of Defect Geometry on Magnetic Flux Leakage Signals
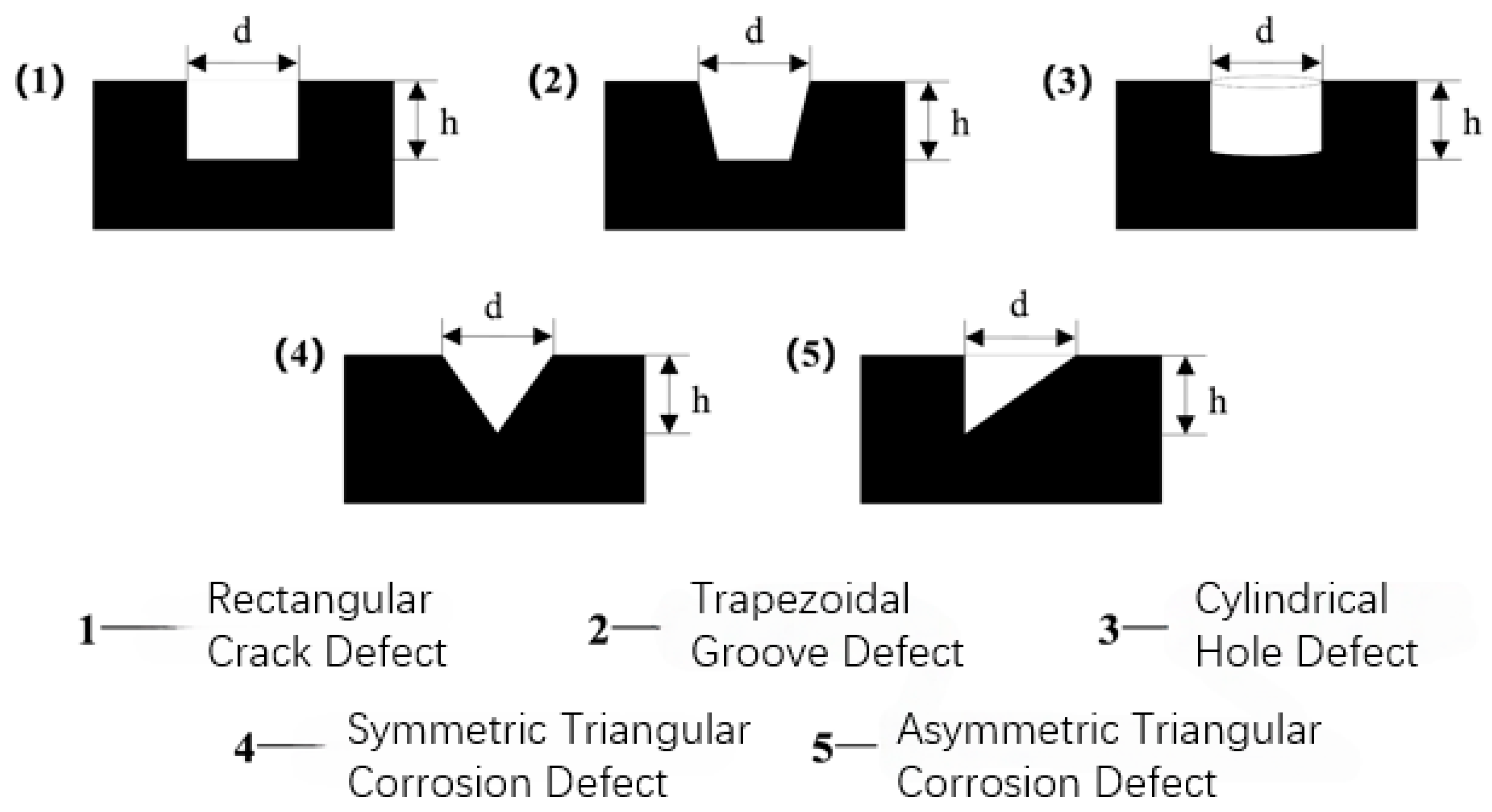
4.1.1. Defect Shape
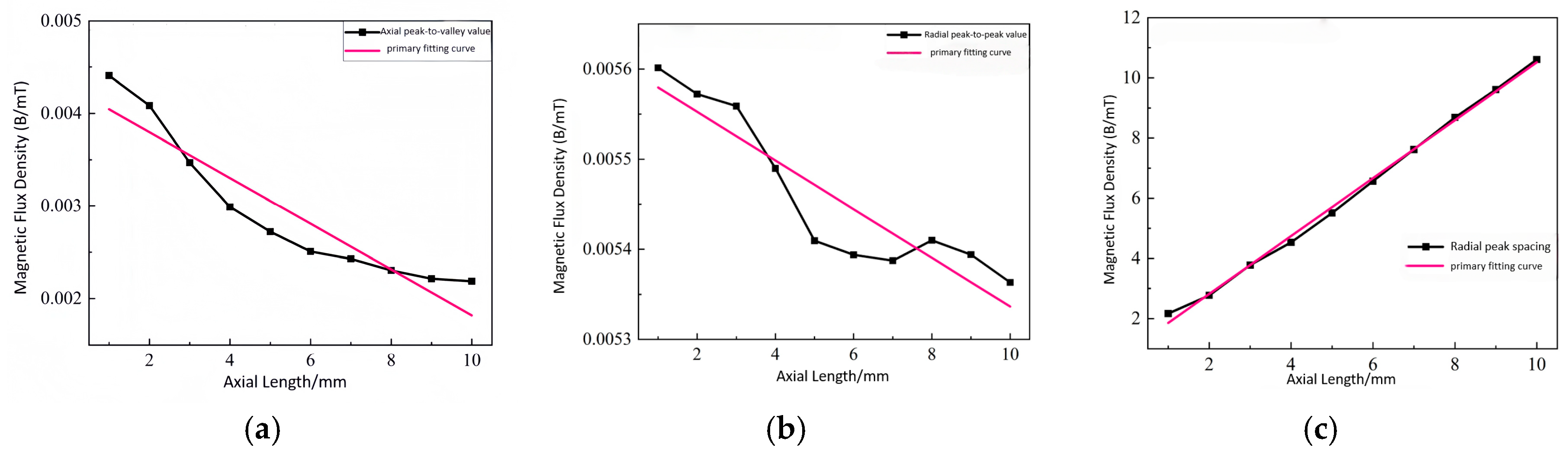
4.1.2. Defect Longitudinal Length
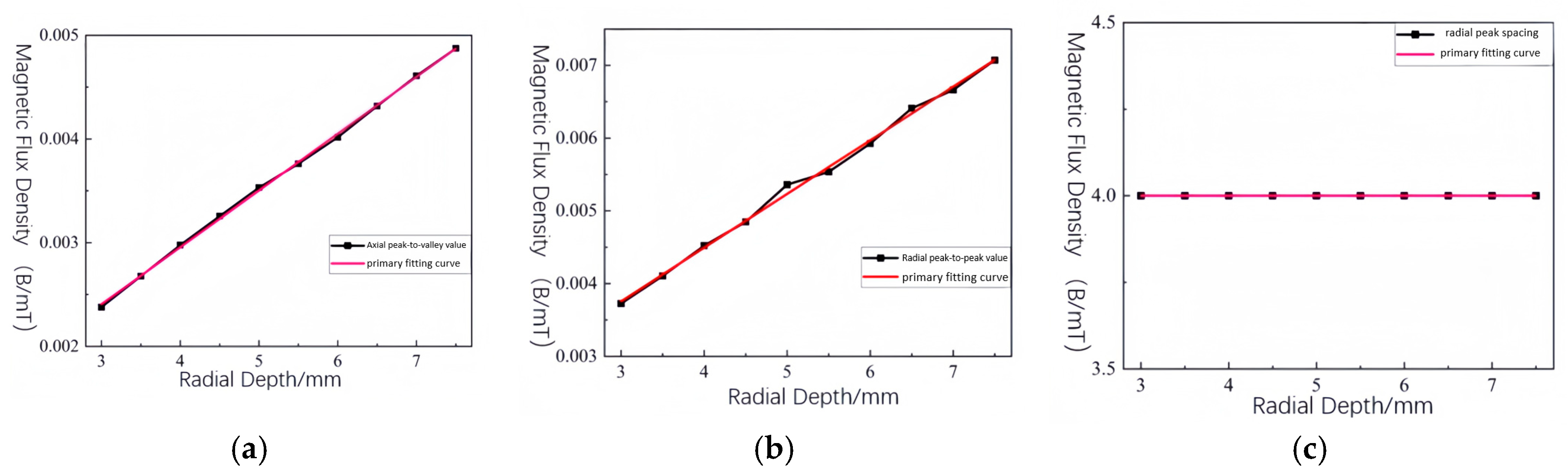
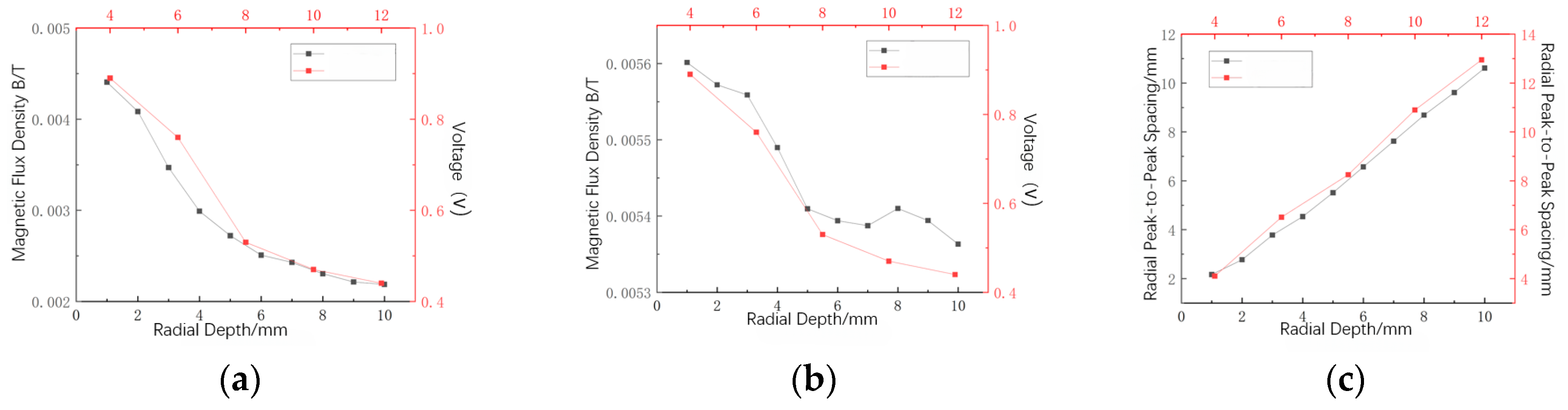
4.1.3. Defect Radial Depth
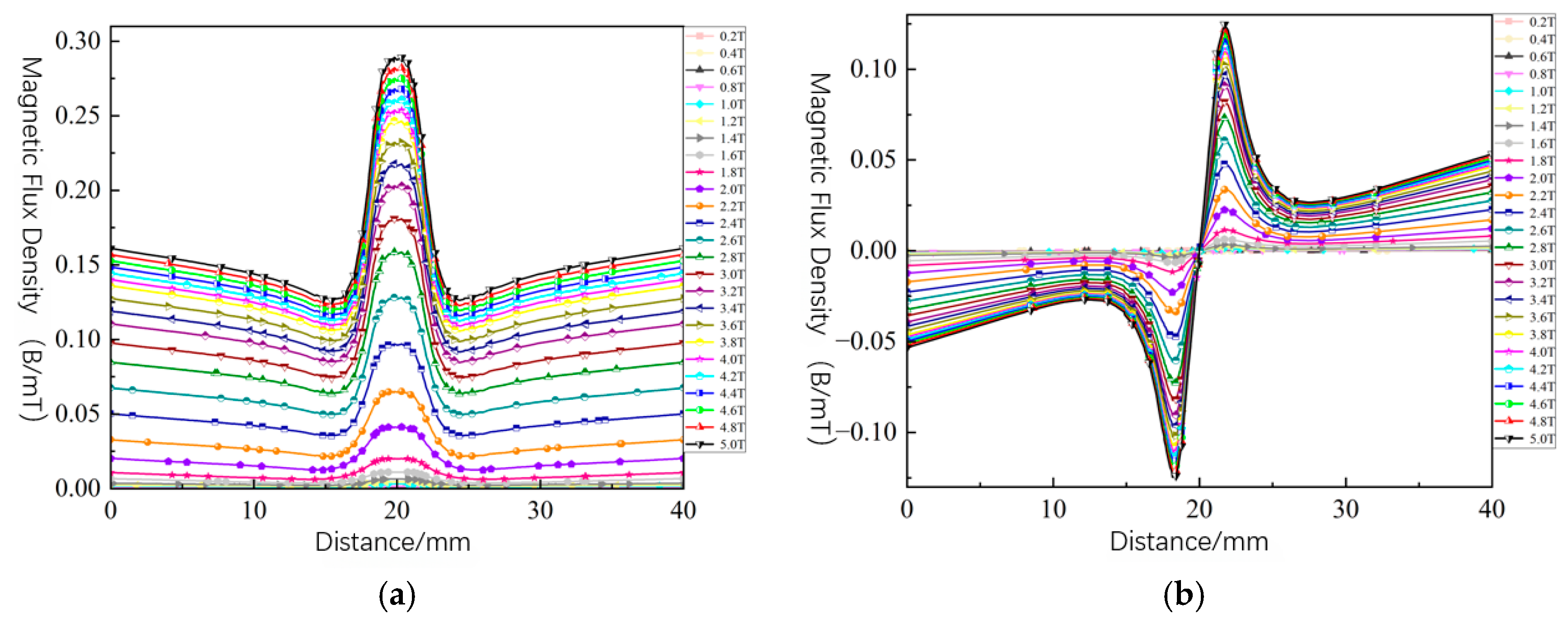
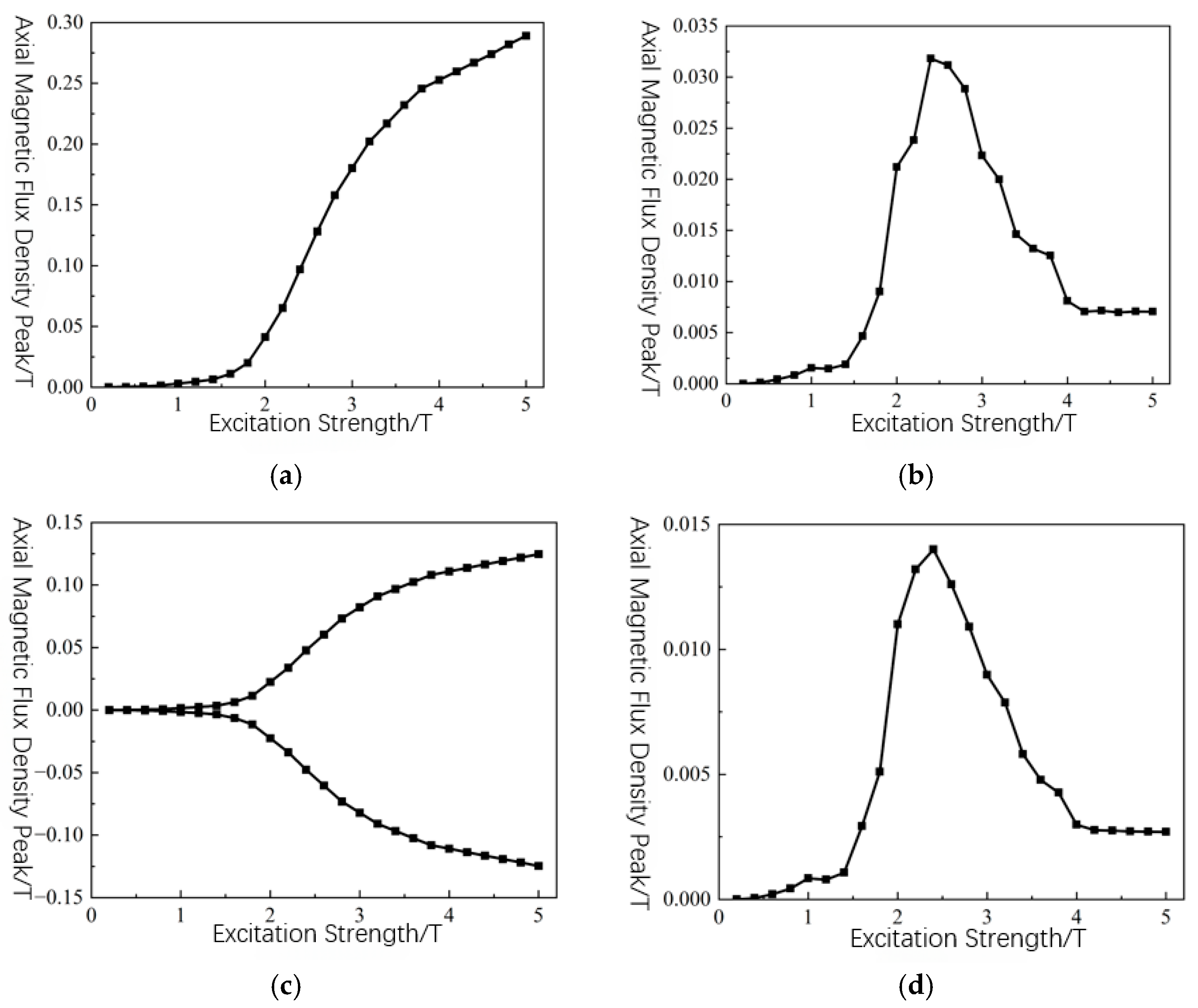
4.2. Regulation of Magnetic Leakage Signals by Excitation Intensity
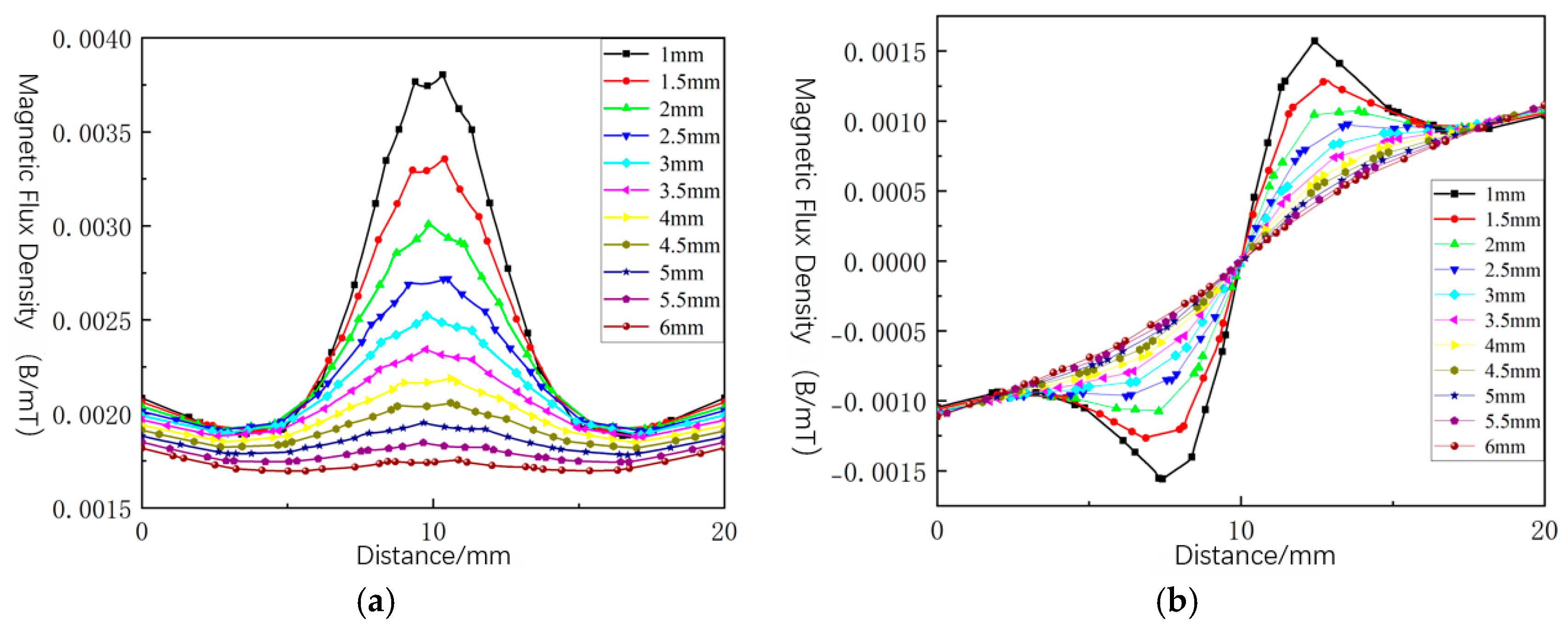
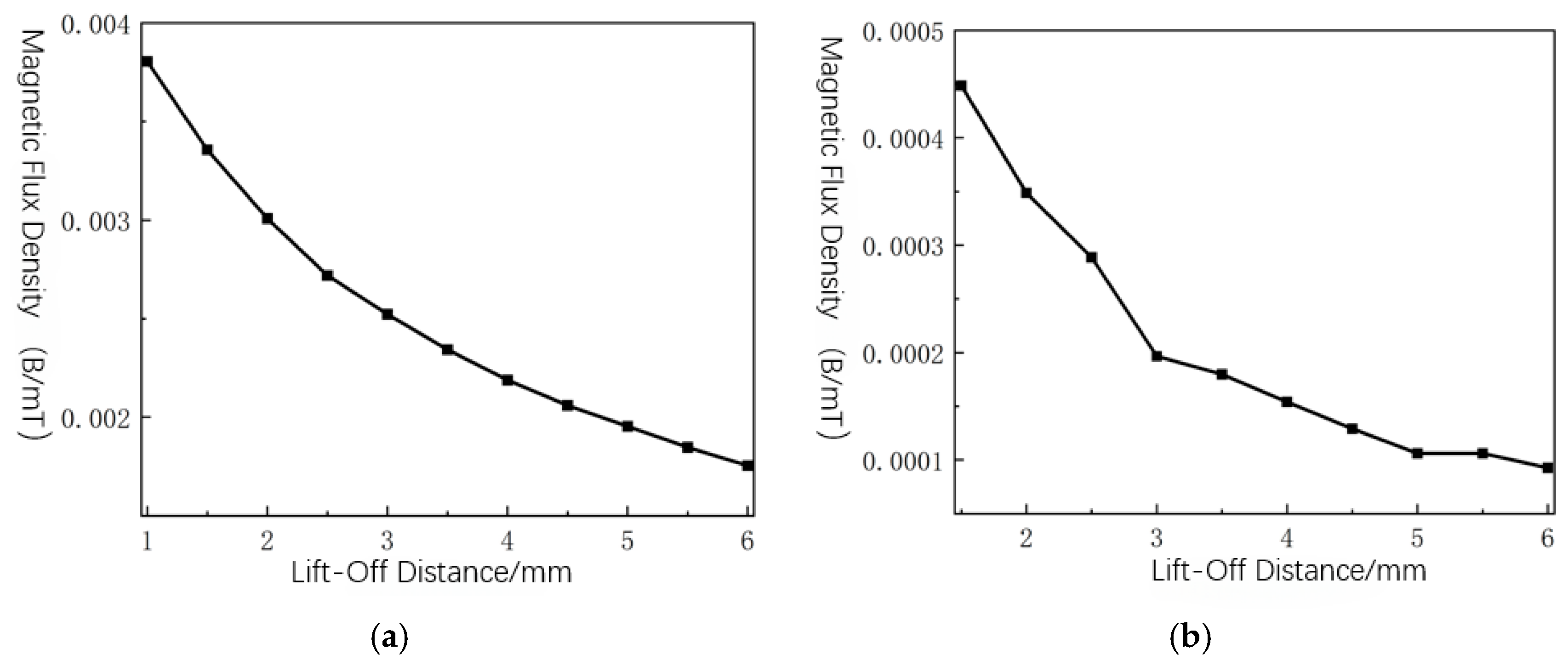
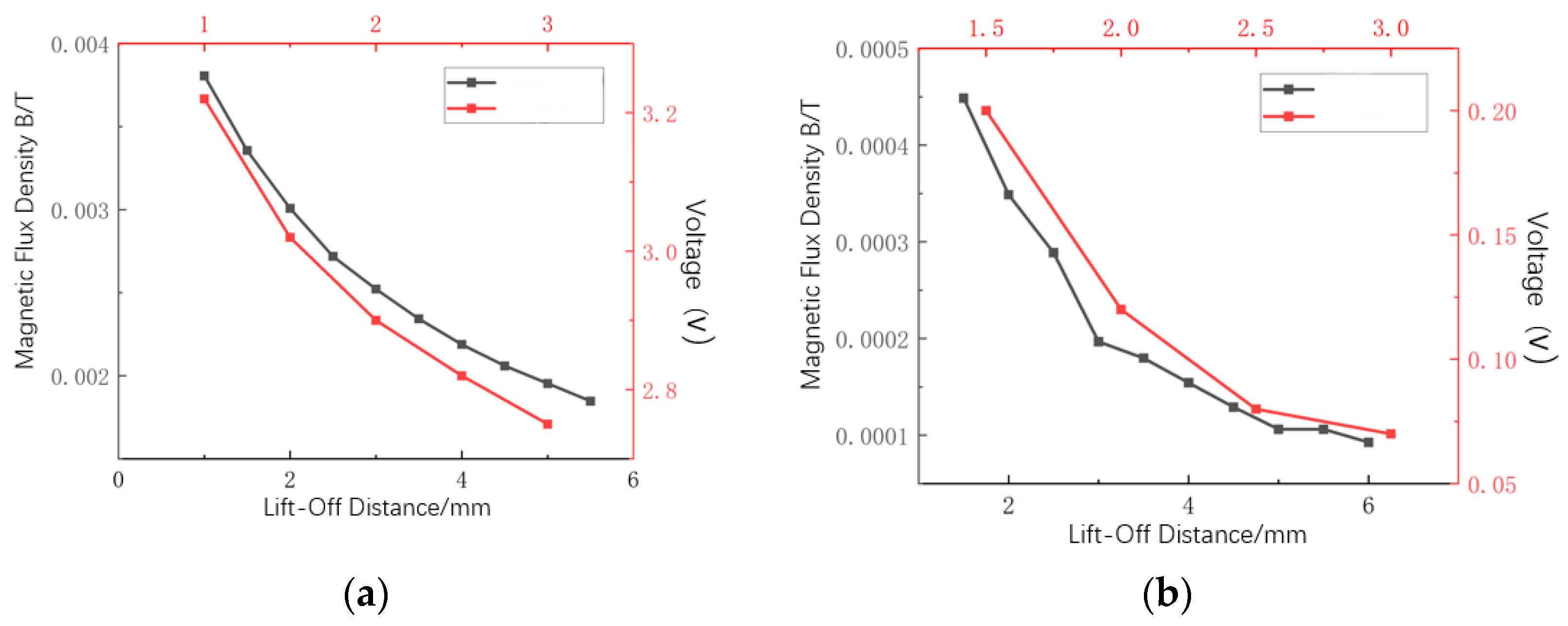
4.3. Sensitivity of Magnetic Leakage Signals to Sensor Lift-Off Value
4.4. Dynamic Influence of Operating Speed on Magnetic Leakage Signals
5. Design of the Magnetic Leakage Detection System
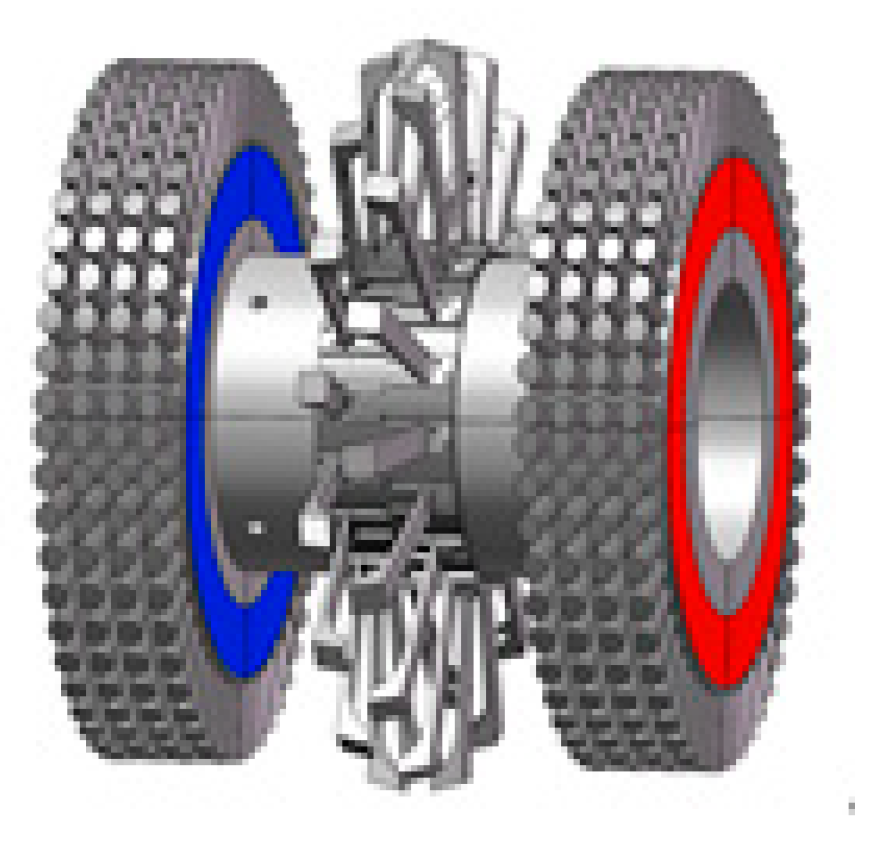
5.1. Design of the Magnetization Module
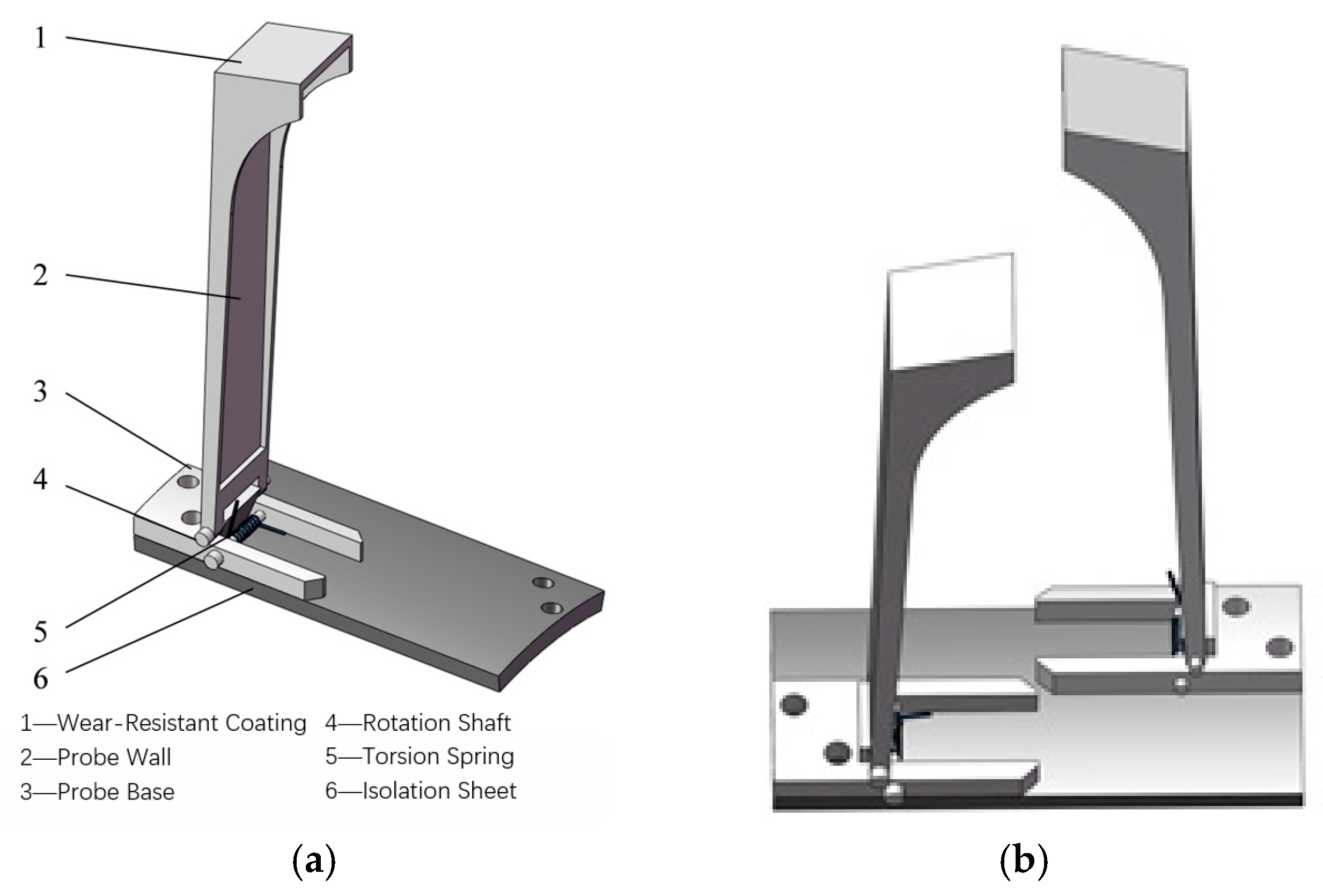
5.1.1. Structural Design
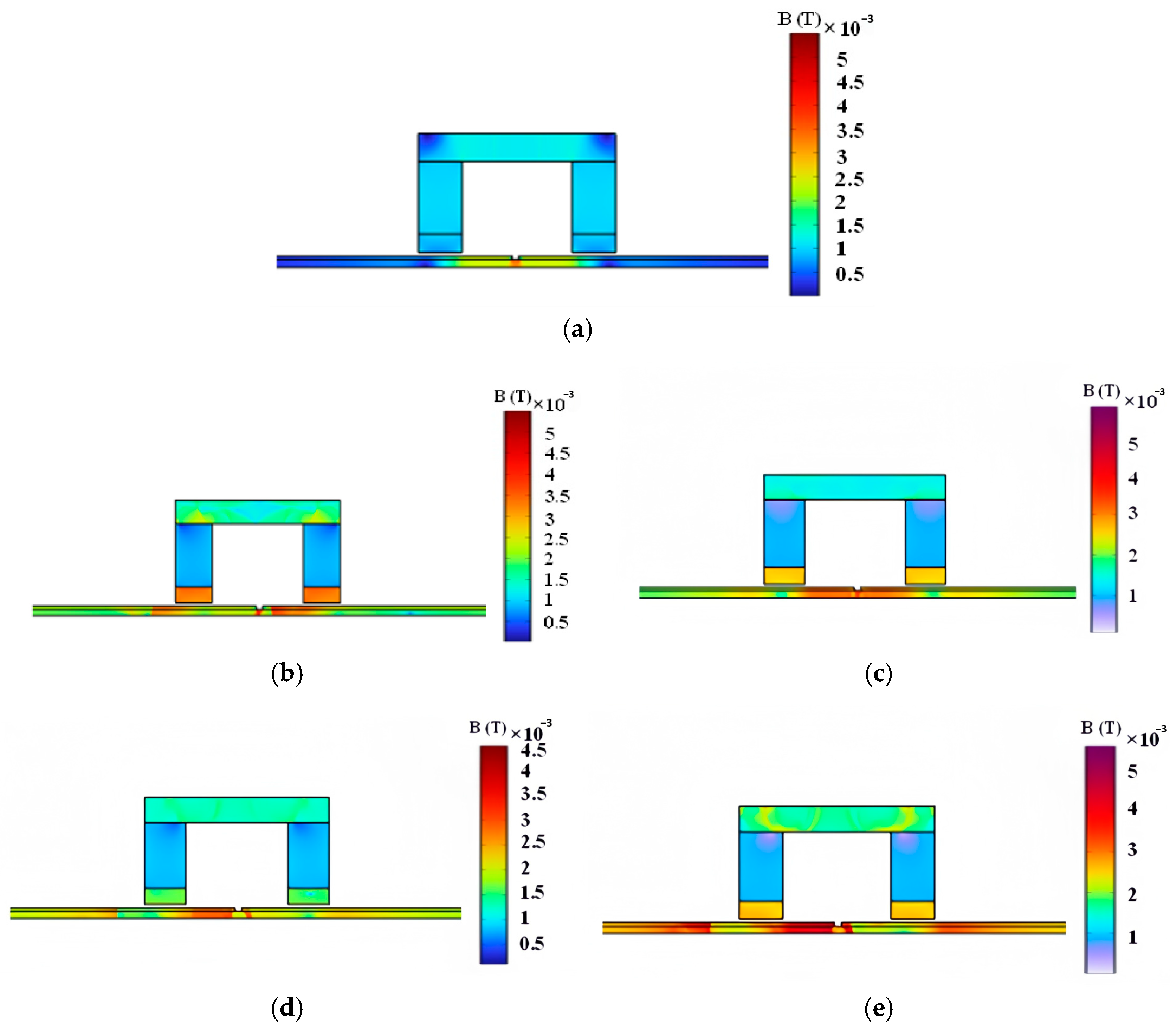
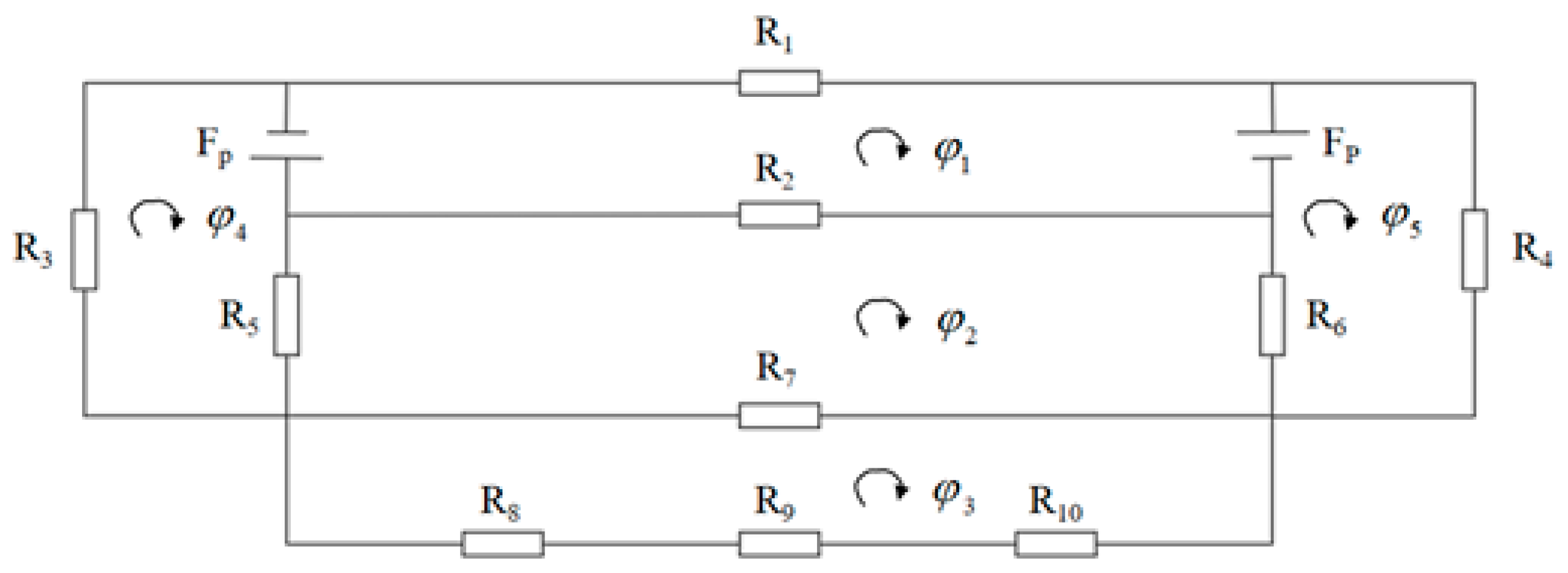
5.1.2. Magnetic Circuit Design
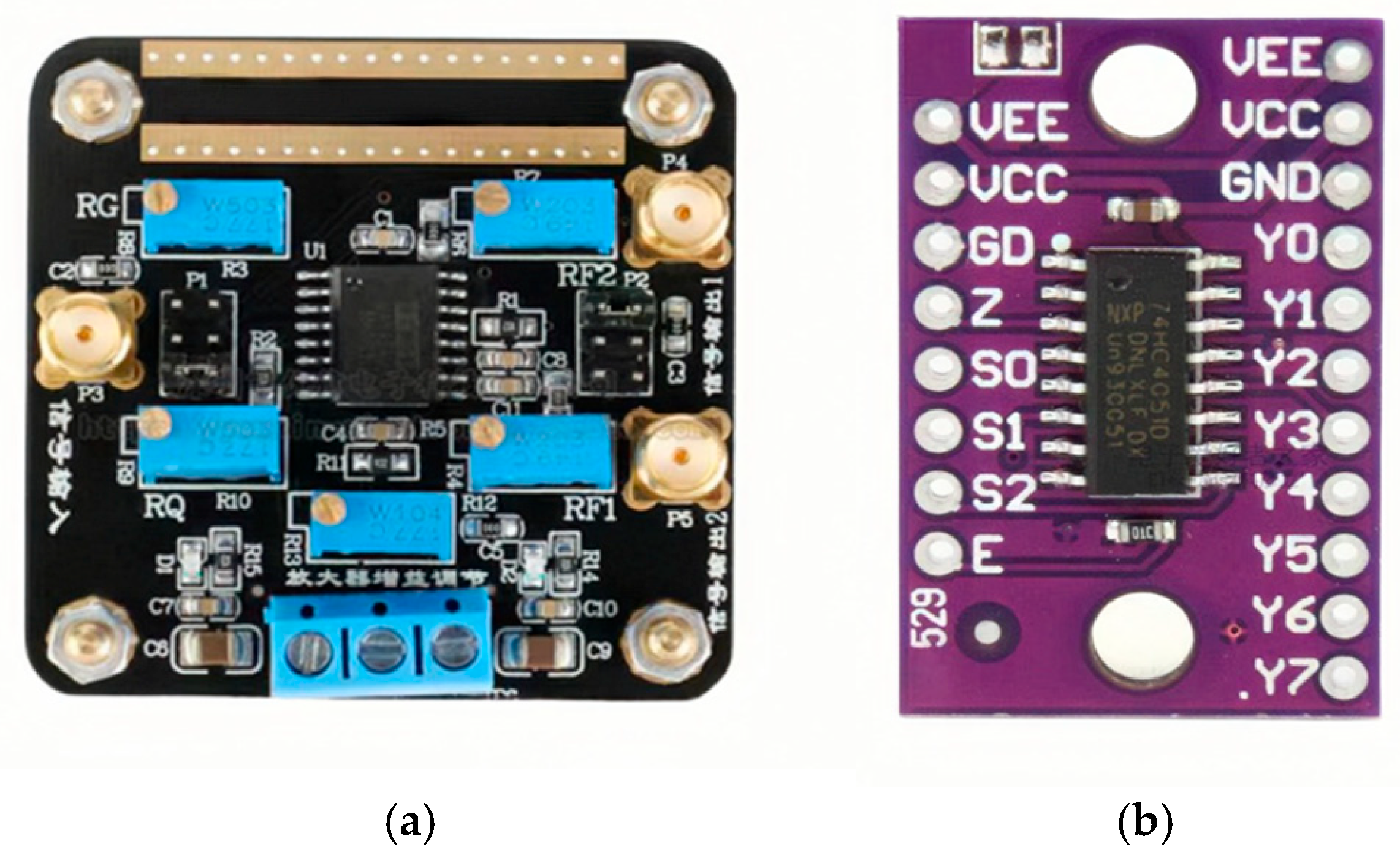
5.2. Development of the Signal Acquisition Module
5.3. Integration of the Control System
5.3.1. Main Control Chip
5.3.2. Signal Processing Module
5.3.3. Positioning Information Acquisition Module
5.3.4. Data Storage Module
5.3.5. Control System Circuit Design
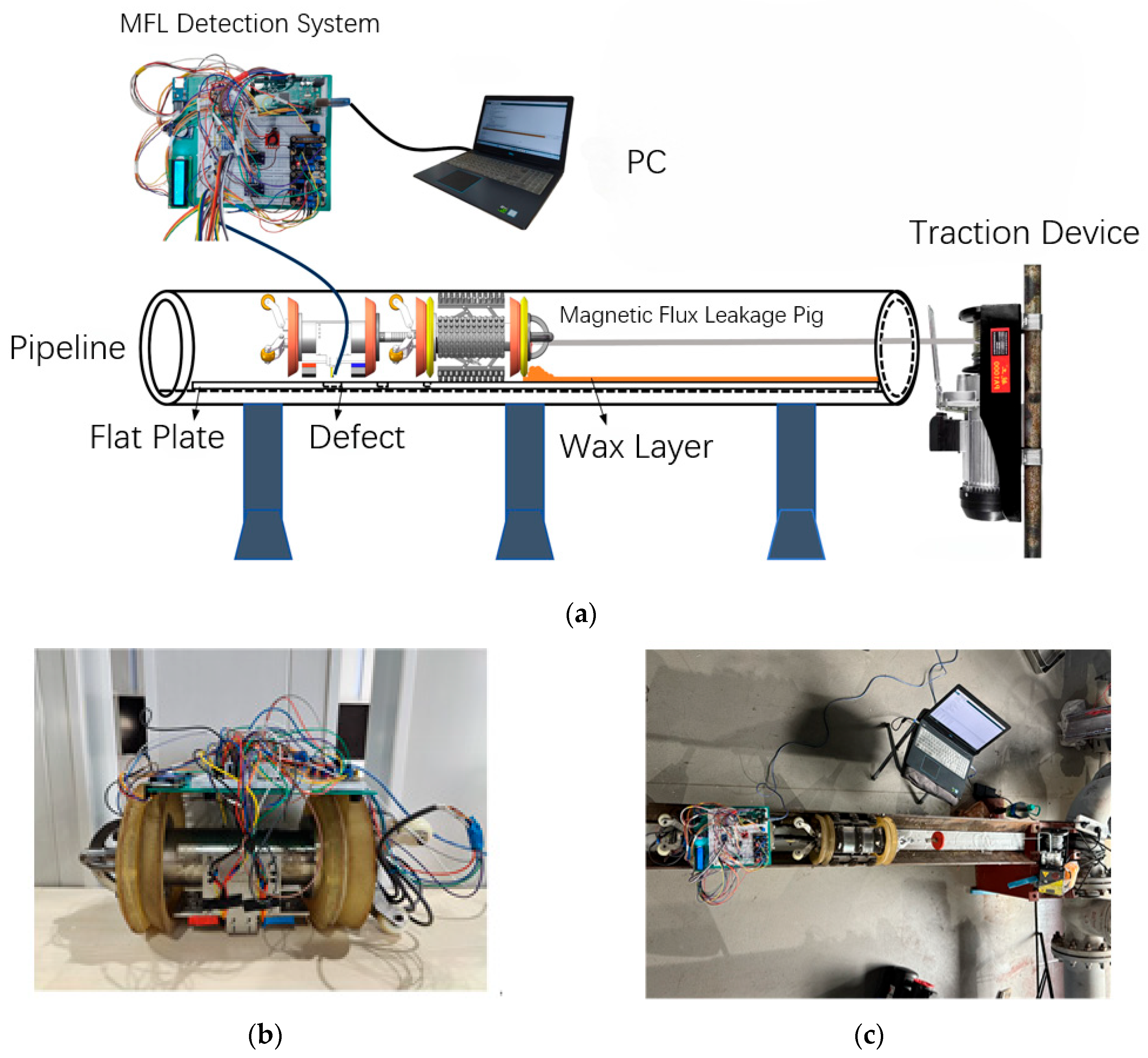
6. Experimental Validation
6.1. Simulation Setup
6.2. Defect Sample Preparation
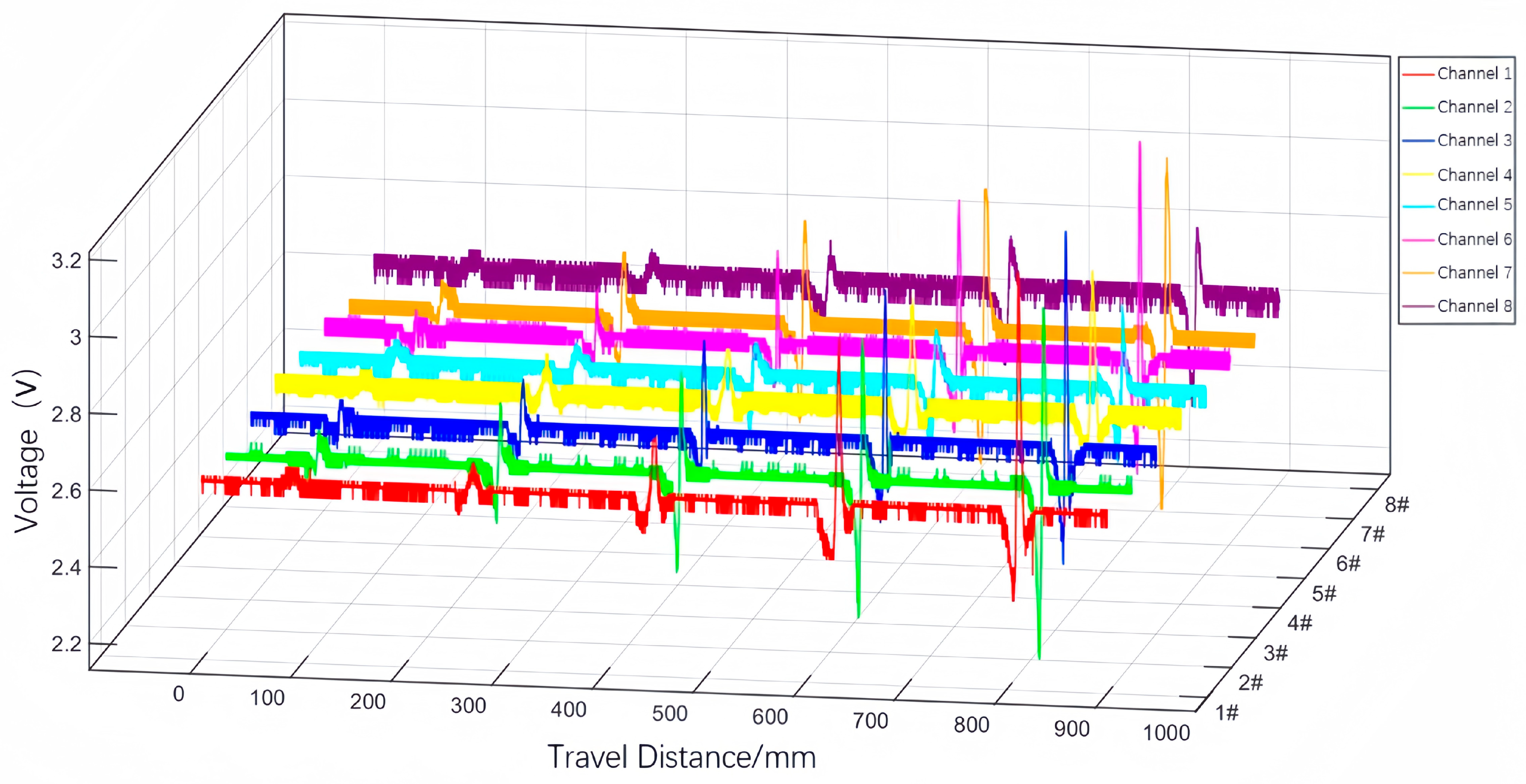
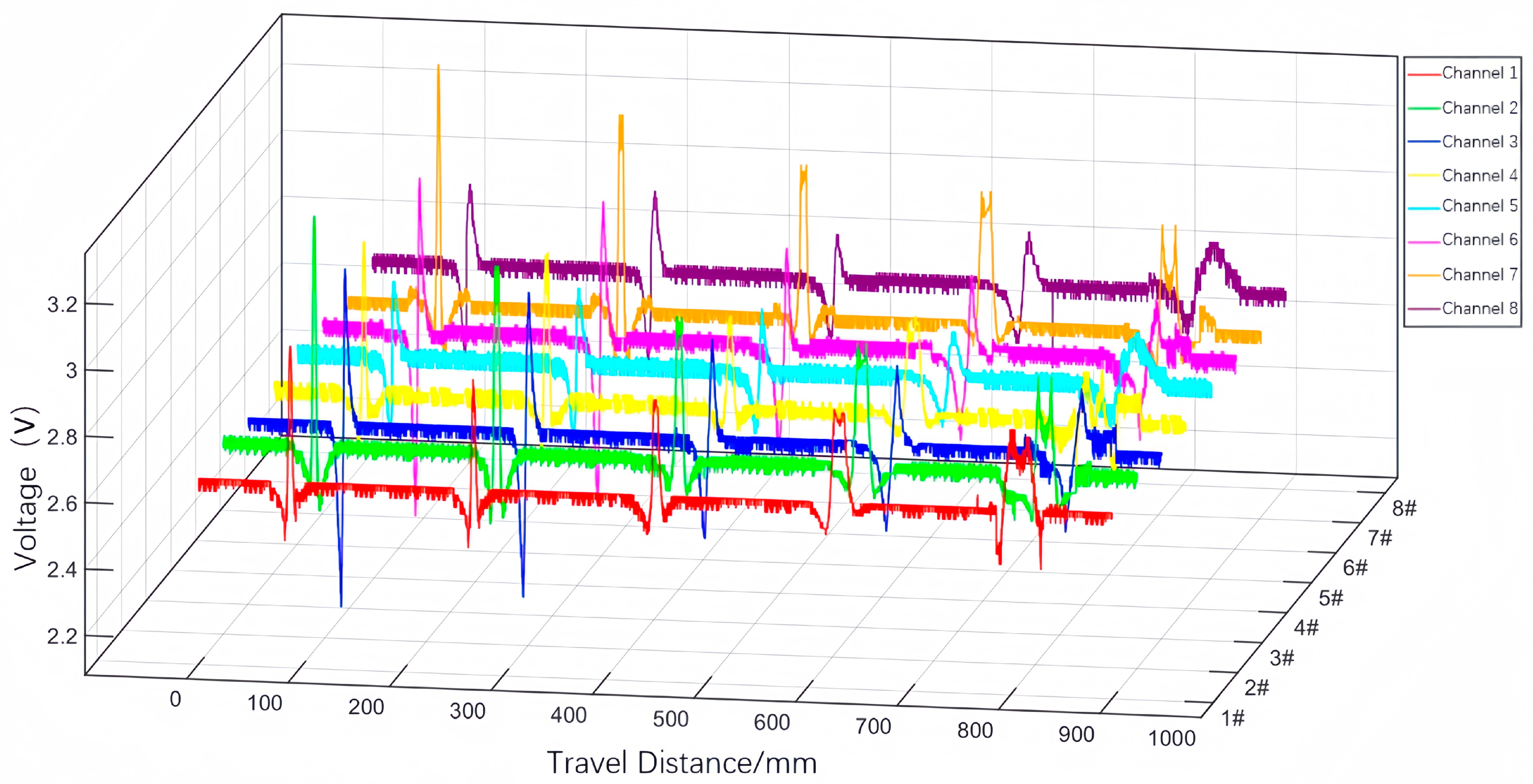
6.3. Experimental Results and Analysis
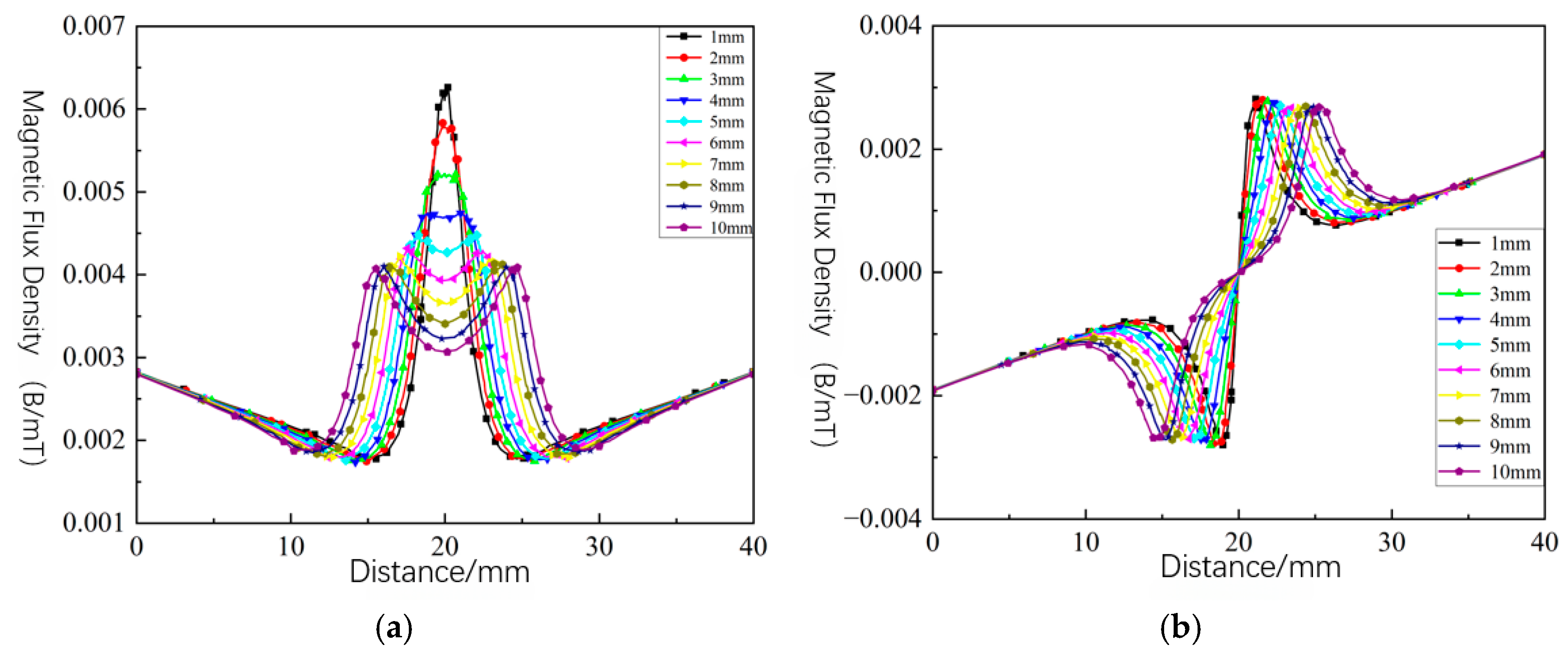
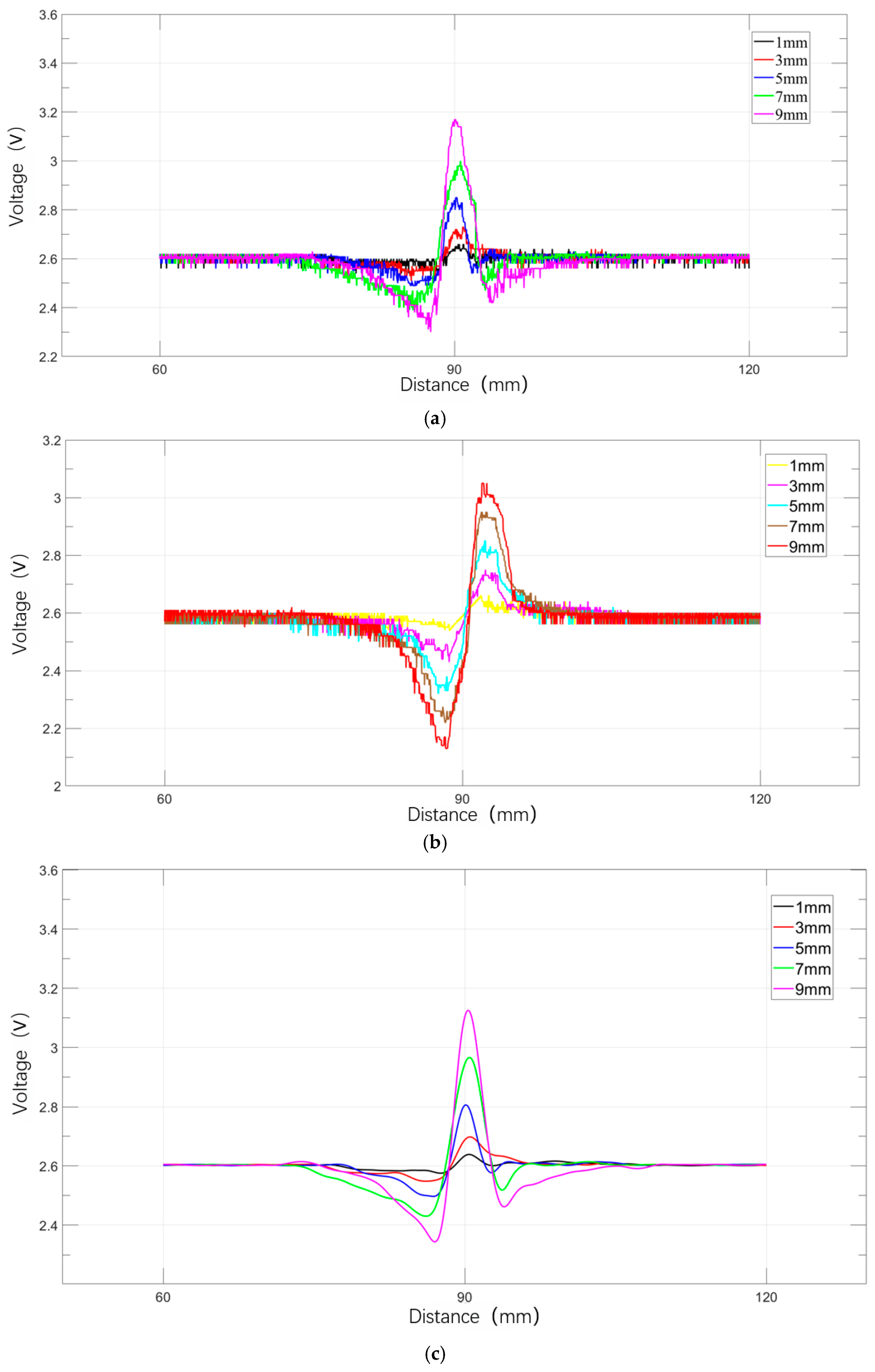
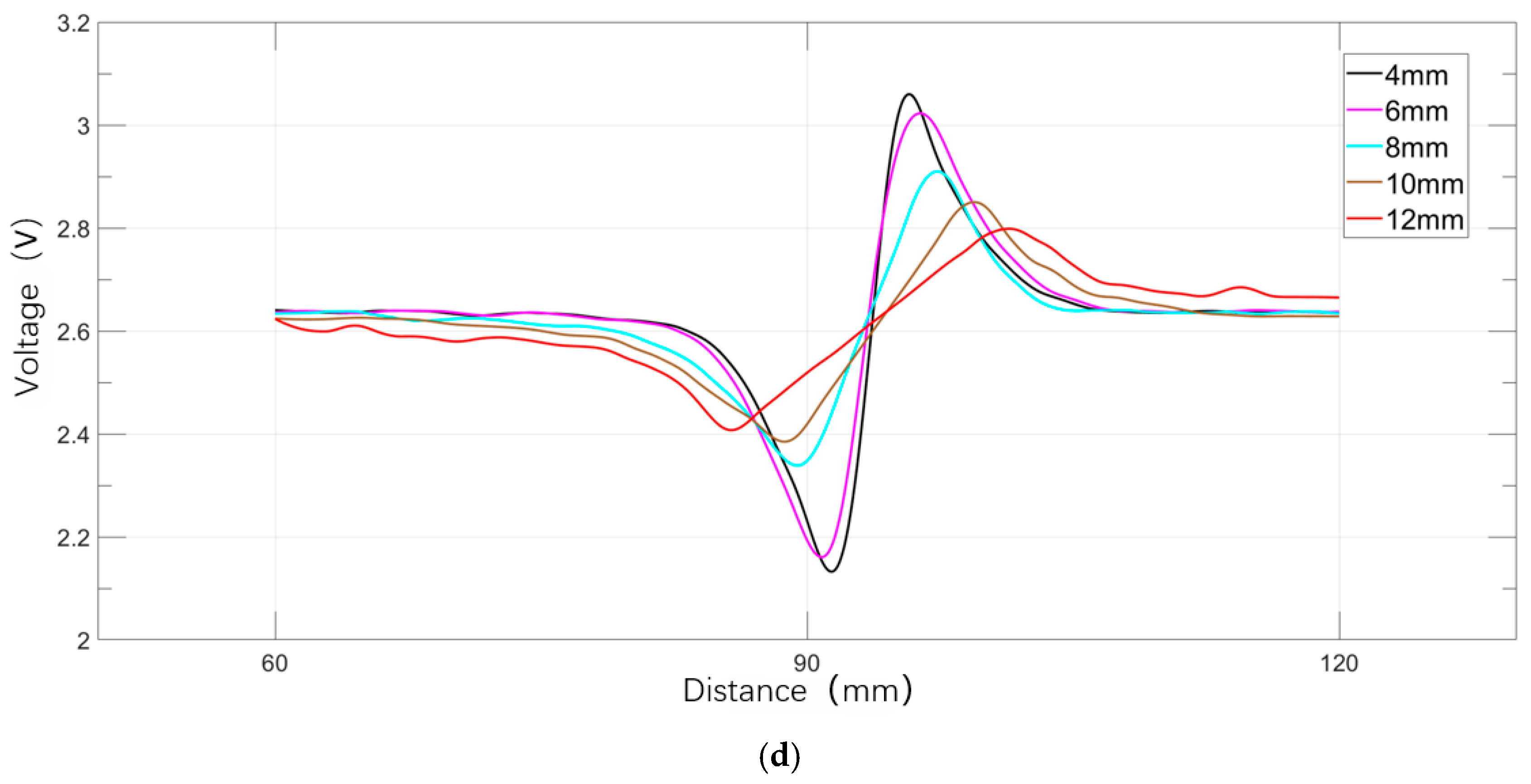
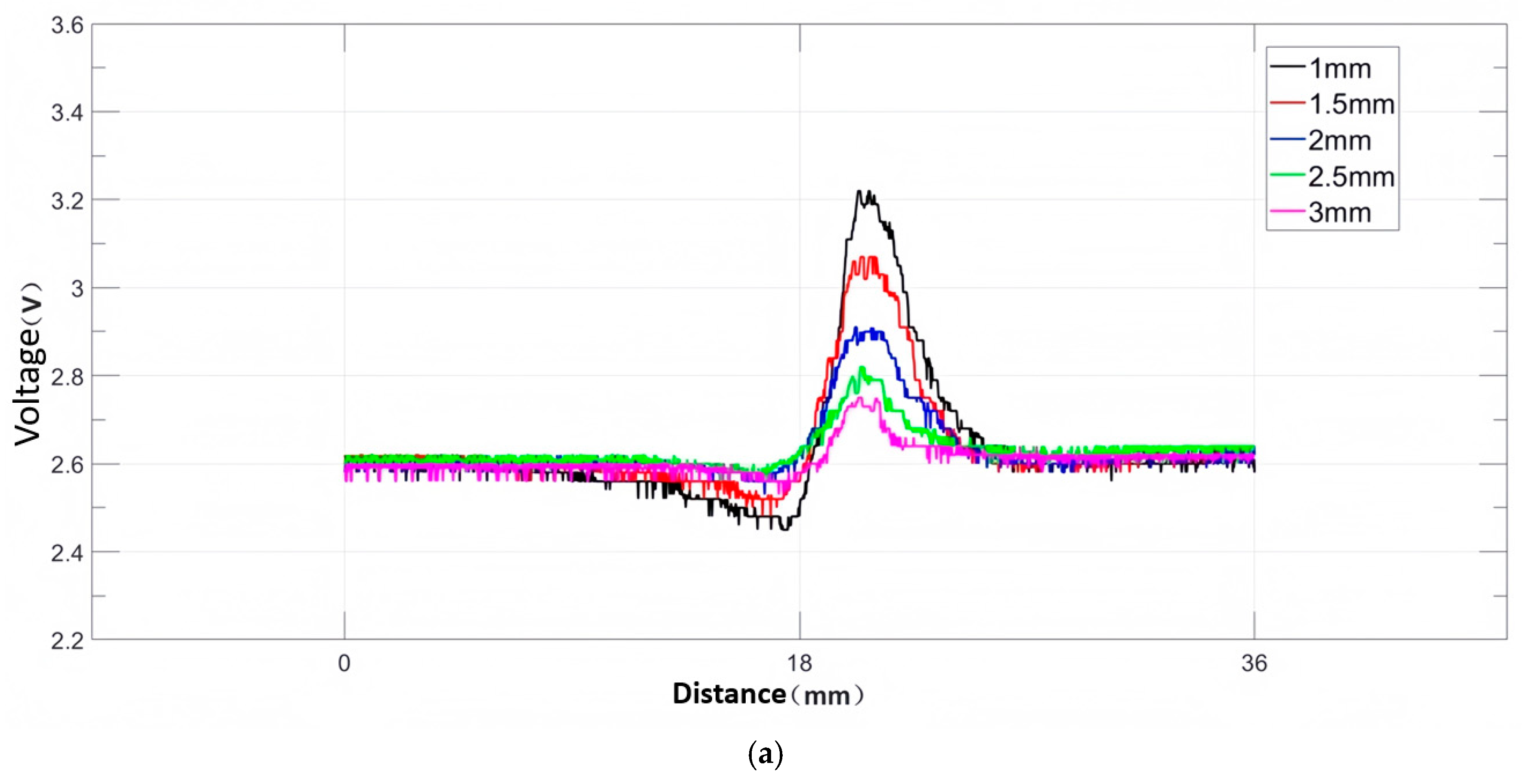
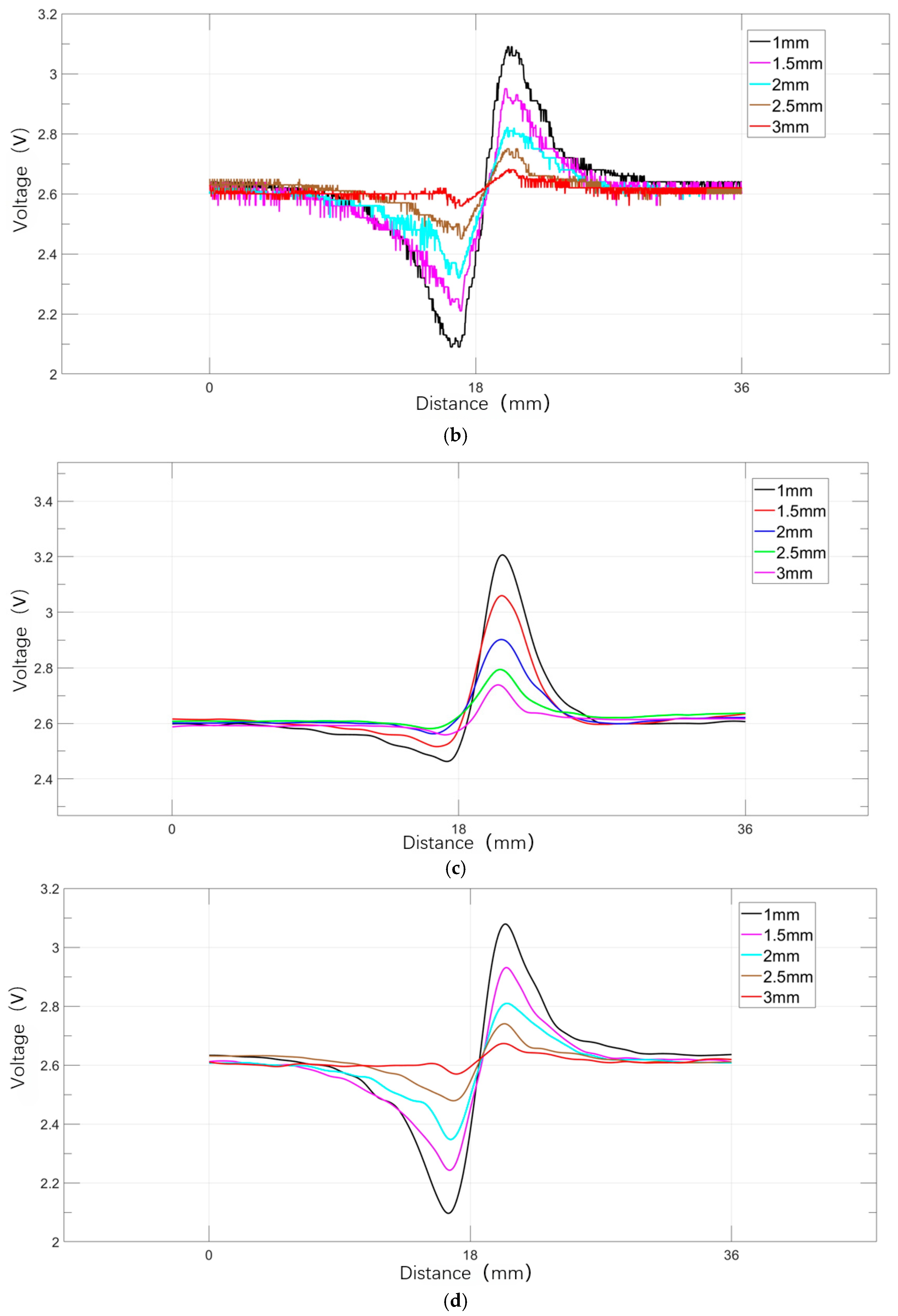
6.3.1. Effect of Rectangular Defect Radial Depth on Magnetic Leakage Signals
6.3.2. Effect of Axial Length of Rectangular Defects on Magnetic Leakage Signals
6.3.3. Effect of Rectangular Defect Lift-Off Value Variations on Magnetic Leakage Signals
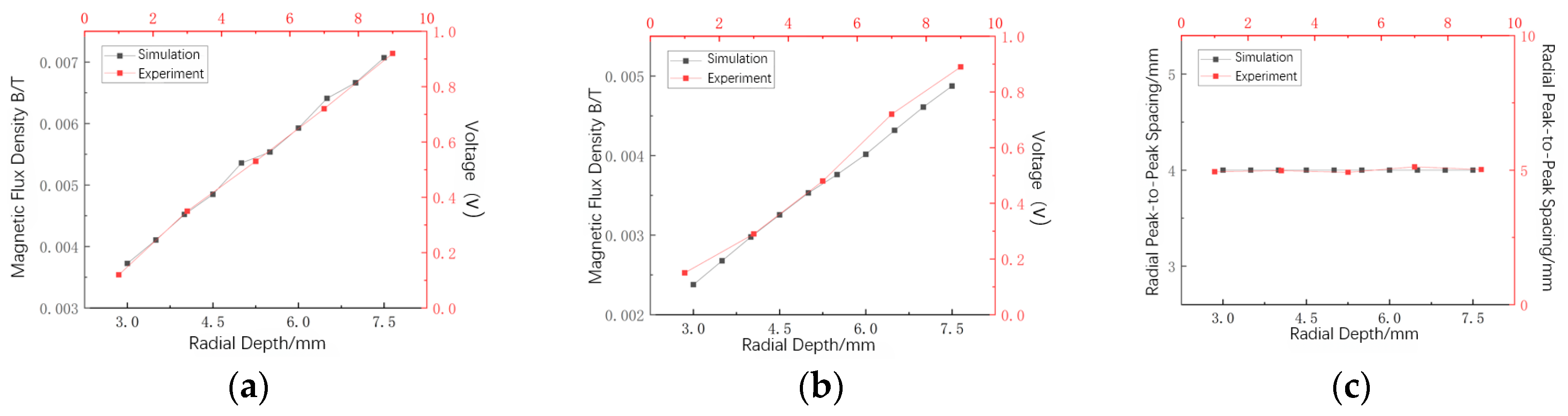
6.4. Comparative Validation of Experimental and Simulation Results
7. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bejinaru, C.; Burduhos-Nergis, D.; Cimpoesu, N. Immersion behavior of carbon steel, phosphate carbon steel and phosphate and painted carbon steel in saltwater. Materials 2021, 14, 188. [Google Scholar] [CrossRef]
- Salgar-Chaparro, S.J.; Lepkova, K.; Pojtanabuntoeng, T.; Darwin, A.; Machuca, L.L. Nutrient level determines biofilm characteristics and subsequent impact on microbial corrosion and biocide effectiveness. Appl. Environ. Microbiol. 2020, 86, e02885-19. [Google Scholar] [CrossRef]
- Vanaei, H.R.; Eslami, A.; Egbewande, A. A review on pipeline corrosion, in-line inspection (ILI), and corrosion growth rate models. Int. J. Press. Vessels Pip. 2017, 149, 43–54. [Google Scholar] [CrossRef]
- Chen, J.; Jia, G.; Fu, K.; Zhang, H. Integrity Assessment of Moda Crude Oil Pipeline Based on Multi In-Line Inspection Datasets. In Proceedings of the 12th International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering (QR2MSE 2022), Emeishan, China, 27 July 2022; pp. 1482–1486. [Google Scholar]
- Verma, A.; Kaiwart, A.; Dubey, N.D. A review on various types of in-pipe inspection robot. Mater. Today Proc. 2022, 50, 1425–1434. [Google Scholar] [CrossRef]
- Peng, X.; Anyaoha, U.; Liu, Z.; Tsukada, K. Analysis of magnetic-flux leakage (MFL) data for pipeline corrosion assessment. IEEE Trans. Magn. 2020, 56, 6200315. [Google Scholar] [CrossRef]
- Liu, B.; Luo, N.; Feng, G. Quantitative study on MFL signal of pipeline composite defect based on improved magnetic charge model. Sensors 2021, 21, 3412. [Google Scholar] [CrossRef] [PubMed]
- Yee, K.J. Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media. IEEE Trans. Antennas Propag. 1966, 14, 302–307. [Google Scholar]
- Zatsepin, N.J. Calculation of the magnetostatic field of surface defects. I Field Topogr. Defect Models Defectoscopy 1966, 5, 50–59. [Google Scholar]
- Shcherbinin, V.J. Calculation of the magnetostatic field of surface defects. II Exp. Verif. Princ. Theor. Relatsh. Defectoscopy 1966, 5, 59–65. [Google Scholar]
- Hwang, J.; Lord, W. Finite element modeling of magnetic field defect interactions. J. Test. Eval. 1975, 3, 21–25. [Google Scholar] [CrossRef]
- Coramik, M.; Citak, H.; Ege, Y.; Bicakci, S.; Gunes, H. Determining the effect of velocity on sensor selection and position in non-destructive testing with magnetic flux leakage method: A pipe inspection gauge design study with ANSYS Maxwell. IEEE Trans. Instrum. Meas. 2023, 72, 1–12. [Google Scholar] [CrossRef]
- Keshwani, R. Analysis of magnetic flux leakage signals of instrumented pipeline inspection gauge using finite element method. IETE J. Res. 2009, 55, 73–82. [Google Scholar] [CrossRef]
- Piotrowski, C.M. Analysis of the magnetic flux leakage signal detected by a pipeline inspection gauge with the help of the continuous wavelet transform. J. Electr. Eng. 2015, 66, 182–185. [Google Scholar]
- Adegboye, M.A.; Fung, W.-K.; Karnik, A. Recent Advances in Pipeline Monitoring and Oil Leakage Detection Technologies: Principles and Approaches. Sensors 2019, 19, 2548. [Google Scholar] [CrossRef]
- Meniconi, S.; Brunone, B.; Tirello, L.; Rubin, A.; Cifrodelli, M.; Capponi, C. Transient tests for checking the Trieste subsea pipeline: Towards the field tests. J. Mar. Sci. Eng. 2024, 12, 374. [Google Scholar] [CrossRef]
- Meniconi, S.; Brunone, B.; Tirello, L.; Rubin, A.; Cifrodelli, M.; Capponi, C. Transient tests for checking the Trieste subsea pipeline: Diving into fault detection. J. Mar. Sci. Eng. 2024, 12, 391. [Google Scholar] [CrossRef]
- Mukherjee, D.; Saha, S.; Mukhopadhyay, S. An adaptive channel equalization algorithm for MFL signal. NDT E Int. 2012, 45, 111–119. [Google Scholar] [CrossRef]
- Kim, Y.; Shin, J.; Lim, J. Design of spider-type non-destructive testing device using magnetic flux leakage. In Proceedings of the 2019 IEEE Student Conference on Electric Machines and Systems, Busan, Republic of Korea, 1–3 November 2019; pp. 1–4. [Google Scholar]
- Xin, J.; Li, R.; Chen, J. A crack characterization model for subsea pipeline based on spatial magnetic signals features. Ocean Eng. 2023, 274, 114112. [Google Scholar] [CrossRef]
- Guo, X.T.; Yang, L.; Song, Y.P. Design and validation of a triaxial high-definition magnetic flux leakage in-pipe inspection robot for oil and gas pipelines. Instrum. Tech. Sens. 2020, 12, 53–57. [Google Scholar]
- Piao, G.; Guo, J.; Hu, T. Fast reconstruction of 3-D defect profile from MFL signals using key physics-based parameters and SVM. NDT E Int. 2019, 103, 26–38. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, H.; Li, C.; Du, F.; Chen, J.; Feng, Q.; Cai, M. In-line inspection (ILI) techniques for subsea pipelines: State-of-the-art. J. Mar. Sci. Eng. 2024, 12, 417. [Google Scholar] [CrossRef]
- Wang, G.; Xia, Q.; Yan, H.; Bei, S.; Zhang, H.; Geng, H.; Zhao, Y. Research on pipeline stress detection method based on double magnetic coupling technology. Sensors 2024, 24, 6463. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.W.; Park, S. Magnetic flux leakage sensing and artificial neural network pattern recognition-based automated damage detection and quantification for wire rope non-destructive evaluation. Sensors 2018, 18, 109. [Google Scholar] [CrossRef] [PubMed]
- Xiong, Y.; Liu, S.; Hou, L.; Zhou, T. Magnetic flux leakage defect size estimation method based on physics-informed neural network. Philos. Trans. R. Soc. A 2024, 382, 20220387. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Sun, C. Research on magnetic flux leakage testing of pipelines by finite element simulation combined with artificial neural network. Int. J. Press. Vessels Pip. 2024, 212 Pt A, 105338. [Google Scholar] [CrossRef]
- Parlak, B.O.; Yavasoglu, H.A. A Comprehensive Analysis of In-Line Inspection Tools and Technologies for Steel Oil and Gas Pipelines. Sustainability 2023, 15, 2783. [Google Scholar] [CrossRef]
- Zhang, B.; Tang, J.; Zhang, S.; Kang, Y.; Zhang, Y.; Sun, Y. Study on the impact of pole spacing on magnetic flux leakage detection under oversaturated magnetization. Sensors 2024, 24, 5195. [Google Scholar] [CrossRef]
- Aulin, A.; Shahzad, K.; MacKenzie, R.; Bott, S. Comparison of Non-Destructive Examination Techniques for Crack Inspection; American Society of Mechanical Engineers: Lawrence, KS, USA, 2021. [Google Scholar]





















| Remanent Magnetic Induction Intensity | HcB (Normal Coercivity) | HcJ (Intrinsic Coercivity) | Intrinsic Coercivity | Maximum Magnetic Energy Product | |||||
|---|---|---|---|---|---|---|---|---|---|
| Max | Min | Min (kA/m) | Min (kOe) | Min (kA/m) | Min (kOe) | kOe | kA/m | Max | Min |
| 14.8 kGs | 14.6 kGs | 950 | 11.5 | 900 | 9.6 | ≥9.6 | ≥900 | 52 MGOe | 50 MGOe |
| 1.48 T | 1.46 T | 400 kJ/m3 | 380 kJ/m3 | ||||||
| Parameter Name | Symbol |
|---|---|
| Permanent Magnet Length | ly |
| Permanent Magnet Width | wy |
| Permanent Magnet Thickness | hy |
| Steel Brush Thickness | hg |
| Yoke Thickness | he |
| Distance Between the Steel Brush on One Side and the Pipeline at the Defect | Lgg |
| Defect Length | Lq |
| Defect Width | Wq |
| Defect Height | Hq |
| Pipeline Thickness | Hp |
| Magnetic Sensor | Advantages | Disadvantages |
|---|---|---|
| Induction Coil | Adjustable measurement sensitivity, sensitive to high-frequency magnetic signals | Highly susceptible to operating speed, complex signal processing |
| Fluxgate Sensor | Extremely high detection sensitivity | Large space requirement, suitable only for weak magnetic fields |
| Hall Element | Small space requirement, directly reflects magnetic field strength, unaffected by operating speed | Requires a power supply circuit, relatively high detection sensitivity |
| Magnetic Diode | Extremely high detection sensitivity | Significantly affected by temperature |
| Magnetoresistive Sensor | Extremely high detection sensitivity | Suitable only for weak magnetic fields |
| Model | SS495A |
|---|---|
| Dimensions | 4 × 3 × 2.5 mm |
| Operating Voltage | 5 V |
| Linear Range | −67~+67 mT |
| Sensitivity | 3.125 ± 0.125 mV/G |
| Linearity Error | 1.0% |
| Temperature Error | ±0.06% °C |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, F.; Chen, S.; Zhang, M.; Zhang, K.; Gong, Y. Design and Performance Study of a Magnetic Flux Leakage Pig for Subsea Pipeline Defect Detection. J. Mar. Sci. Eng. 2025, 13, 1462. https://doi.org/10.3390/jmse13081462
Qu F, Chen S, Zhang M, Zhang K, Gong Y. Design and Performance Study of a Magnetic Flux Leakage Pig for Subsea Pipeline Defect Detection. Journal of Marine Science and Engineering. 2025; 13(8):1462. https://doi.org/10.3390/jmse13081462
Chicago/Turabian StyleQu, Fei, Shengtao Chen, Meiyu Zhang, Kang Zhang, and Yongjun Gong. 2025. "Design and Performance Study of a Magnetic Flux Leakage Pig for Subsea Pipeline Defect Detection" Journal of Marine Science and Engineering 13, no. 8: 1462. https://doi.org/10.3390/jmse13081462
APA StyleQu, F., Chen, S., Zhang, M., Zhang, K., & Gong, Y. (2025). Design and Performance Study of a Magnetic Flux Leakage Pig for Subsea Pipeline Defect Detection. Journal of Marine Science and Engineering, 13(8), 1462. https://doi.org/10.3390/jmse13081462







