Research on Path Optimization for Underwater Target Search Under the Constraint of Sea Surface Wind Field
Abstract
1. Introduction
2. Methods
2.1. Overall Technical Roadmap
2.2. Sonar Search Performance Modeling Considering Wind Fields
2.2.1. Noise Level
2.2.2. Transmission Loss
2.3. Sixteen-Azimuth Path Planning Model
2.3.1. Discretized Azimuths
2.3.2. Inverse Distance Weighting (IDW) Interpolation
2.4. Path Optimization Based on QPSO-TS
2.4.1. Objective Function and Constraints
2.4.2. Initial Population and Encoding
2.4.3. Fitness Calculation
2.4.4. Particle Position Update
2.4.5. Tabu Search
2.4.6. Termination Condition Judgment
3. Results
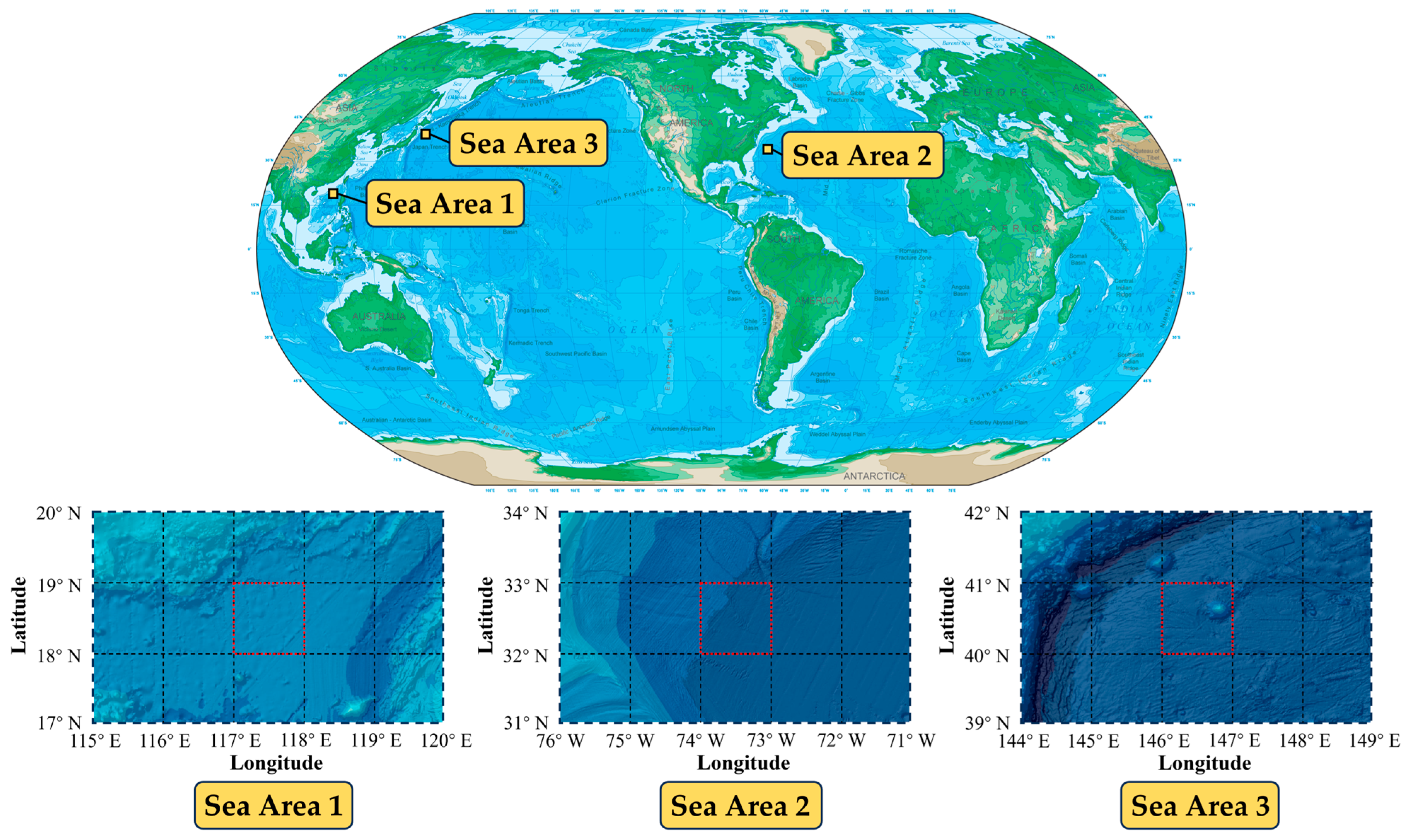
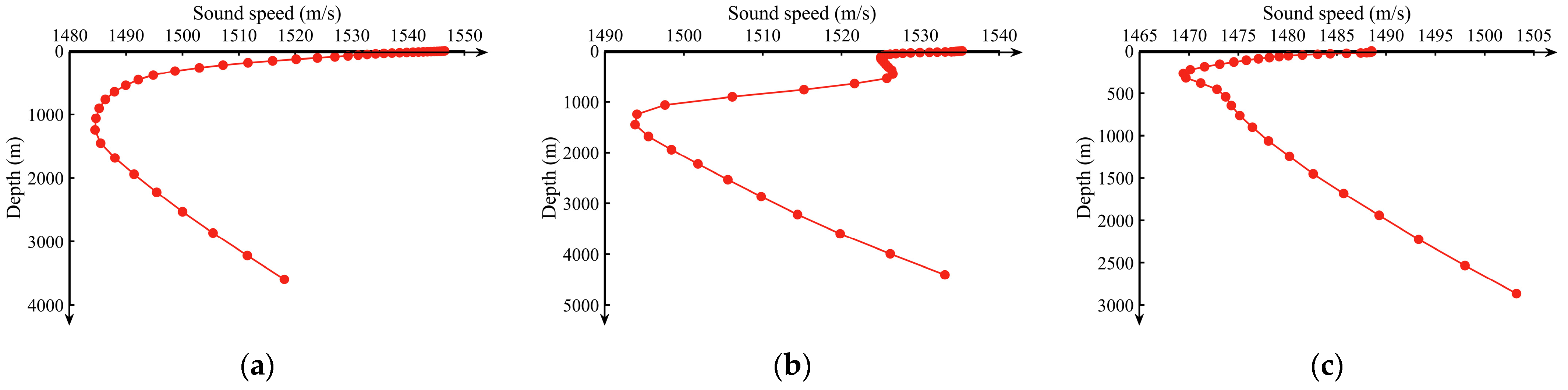
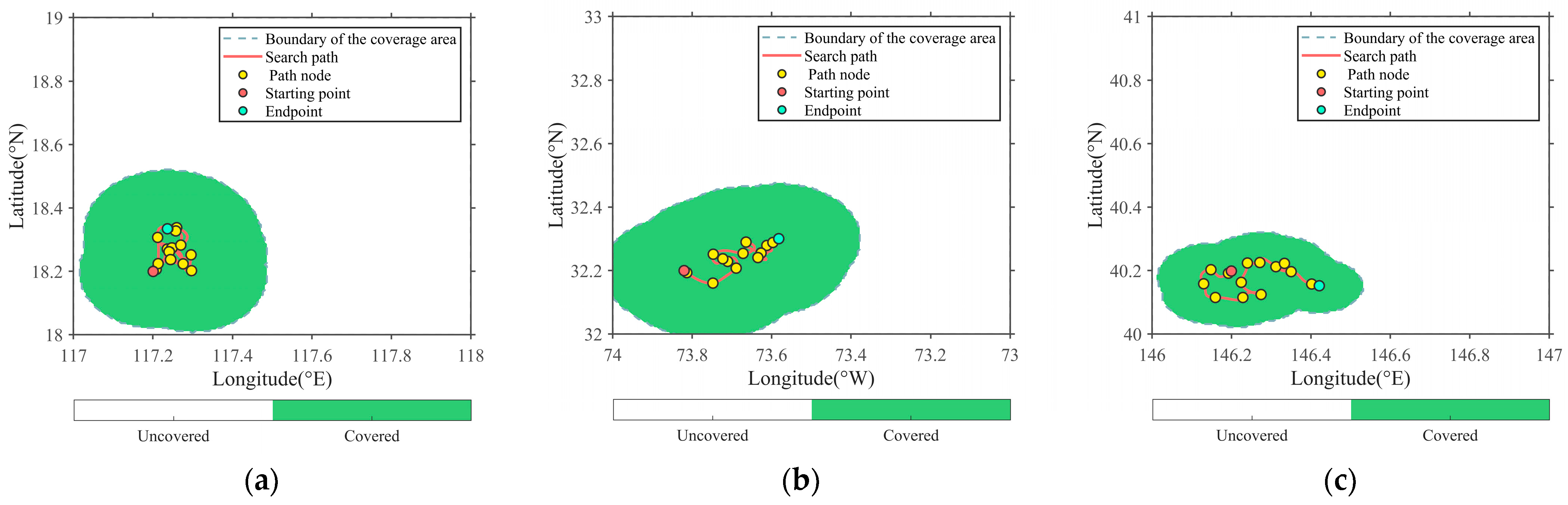
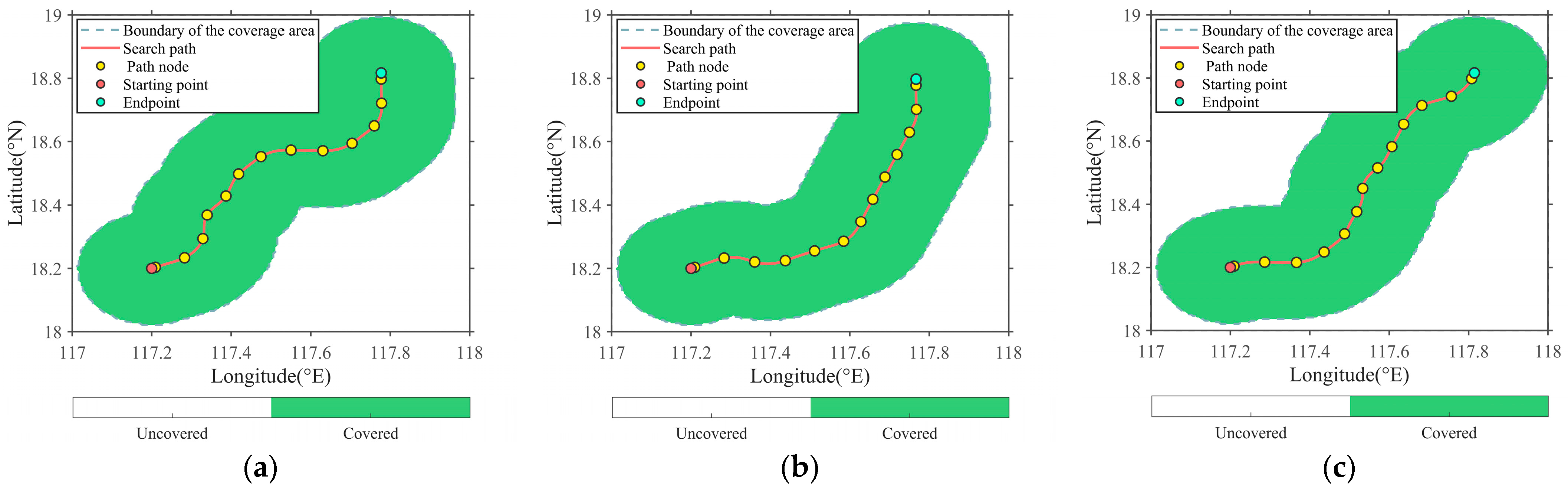
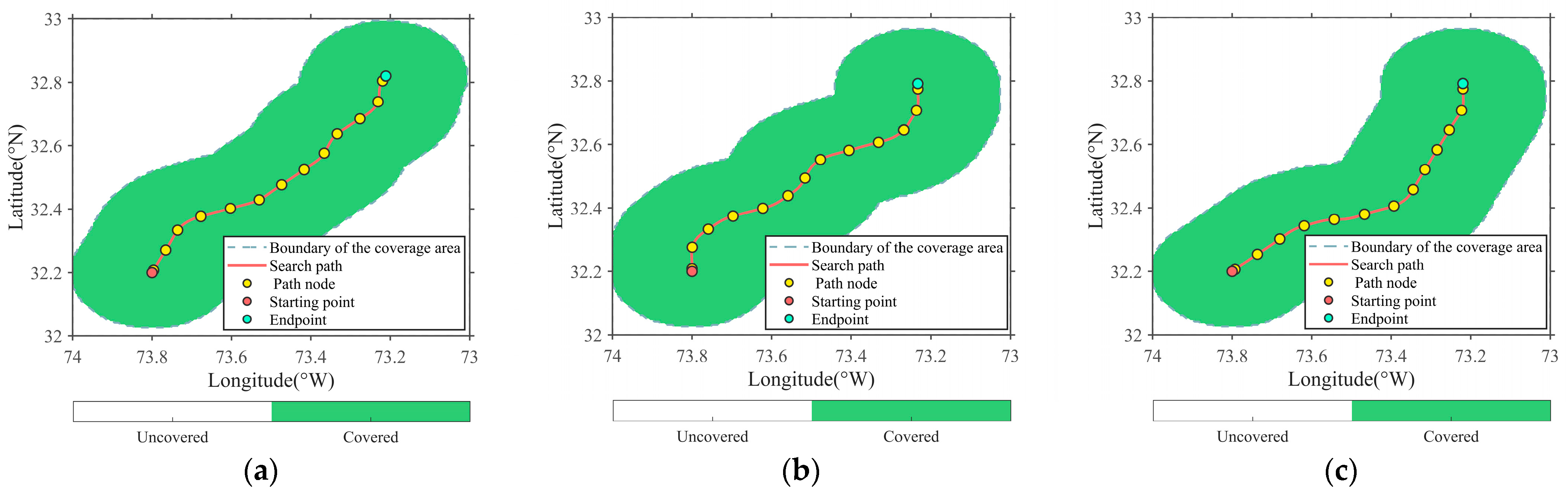
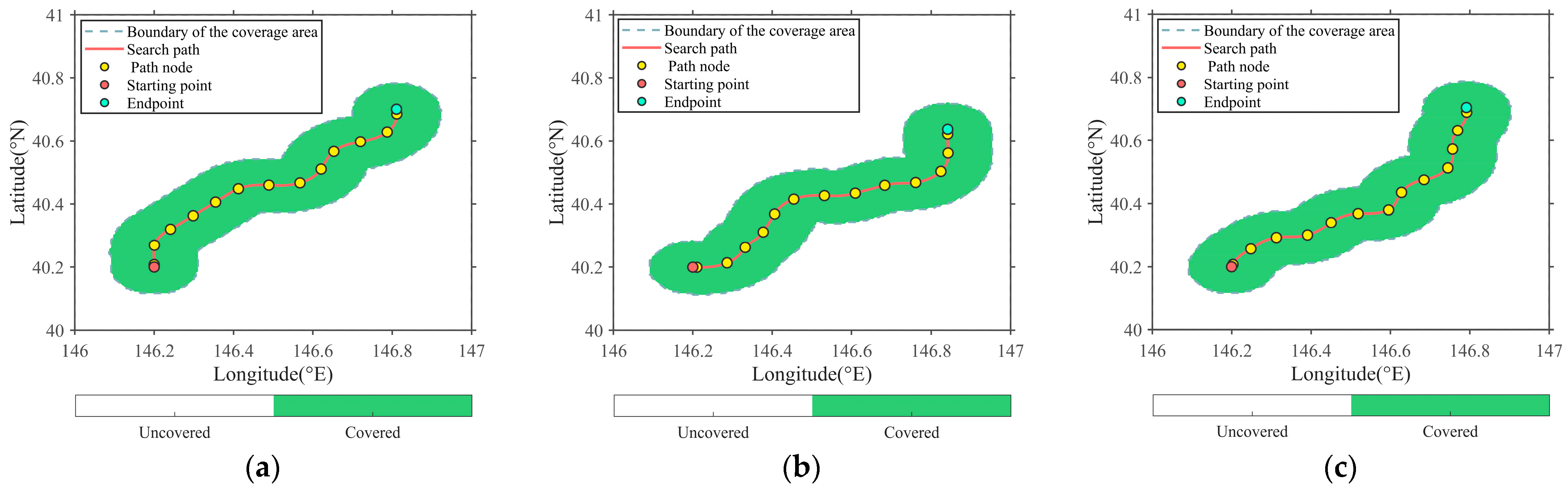
3.1. Experimental Data and Areas
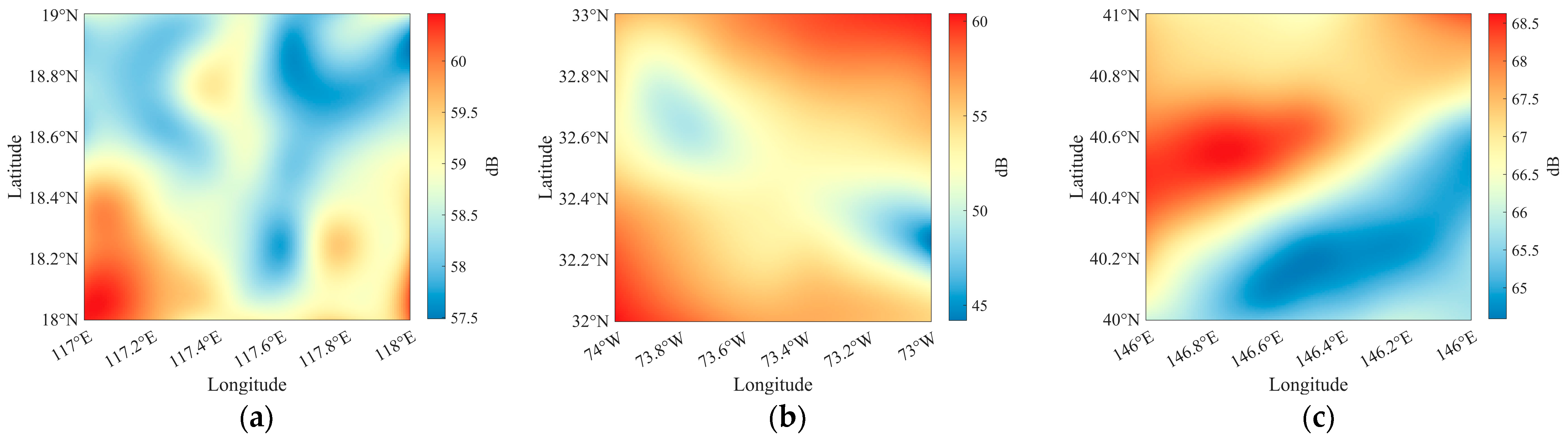
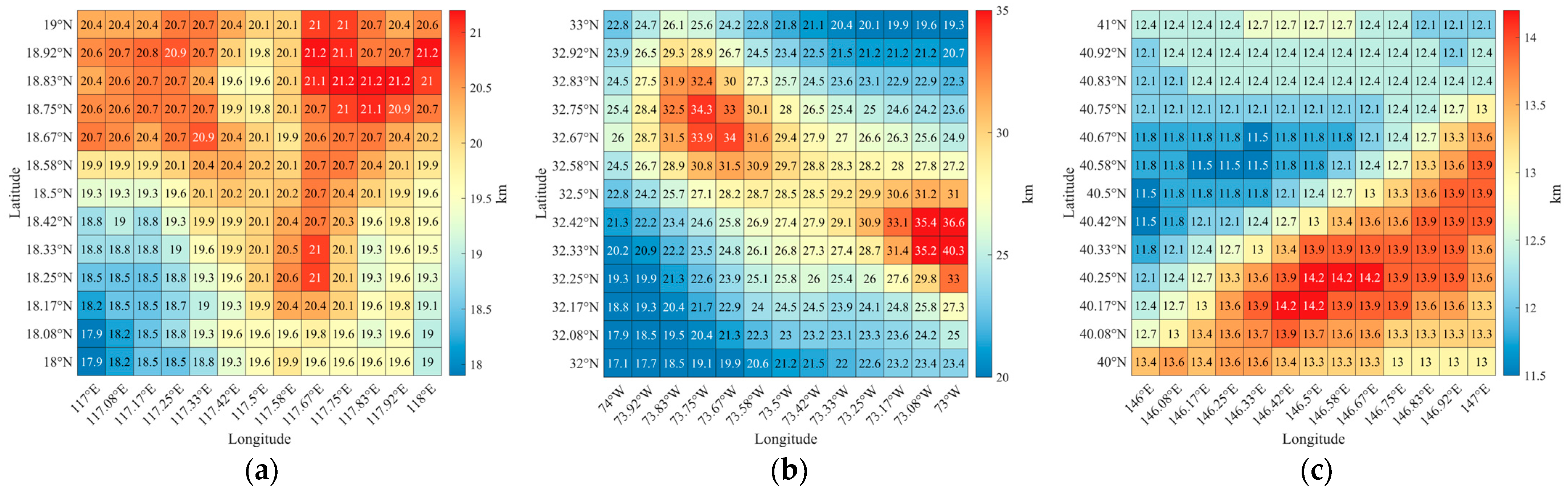
3.2. Sonar Search Performance
3.3. Path Planning Results
4. Discussion
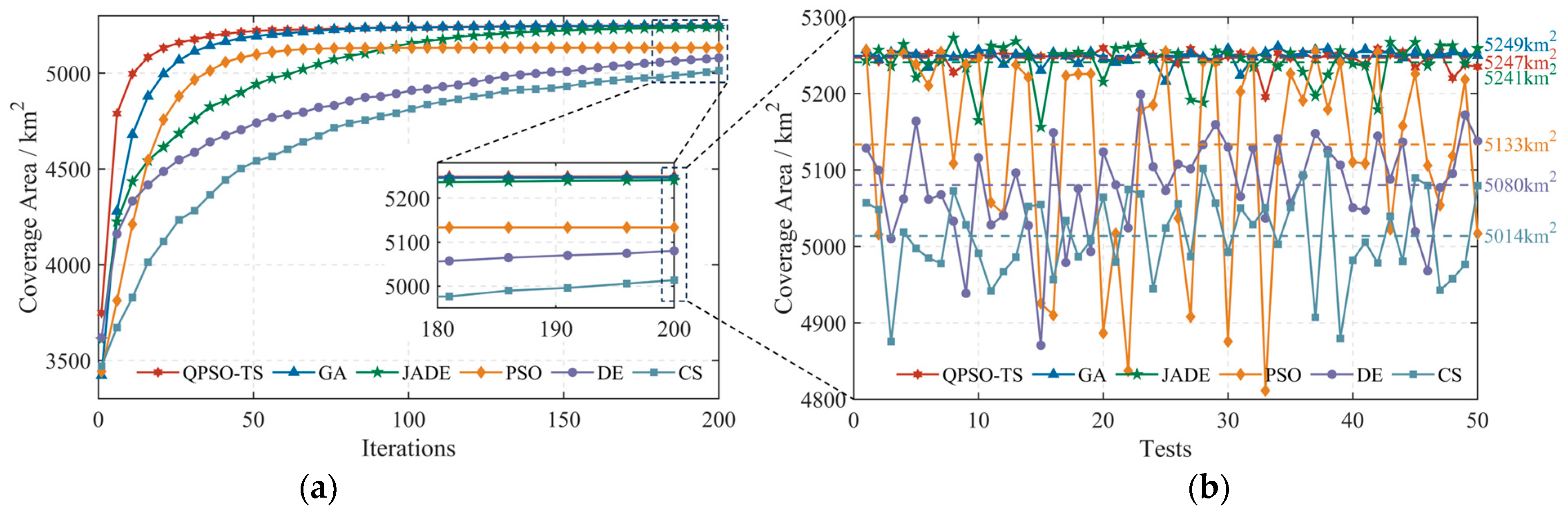
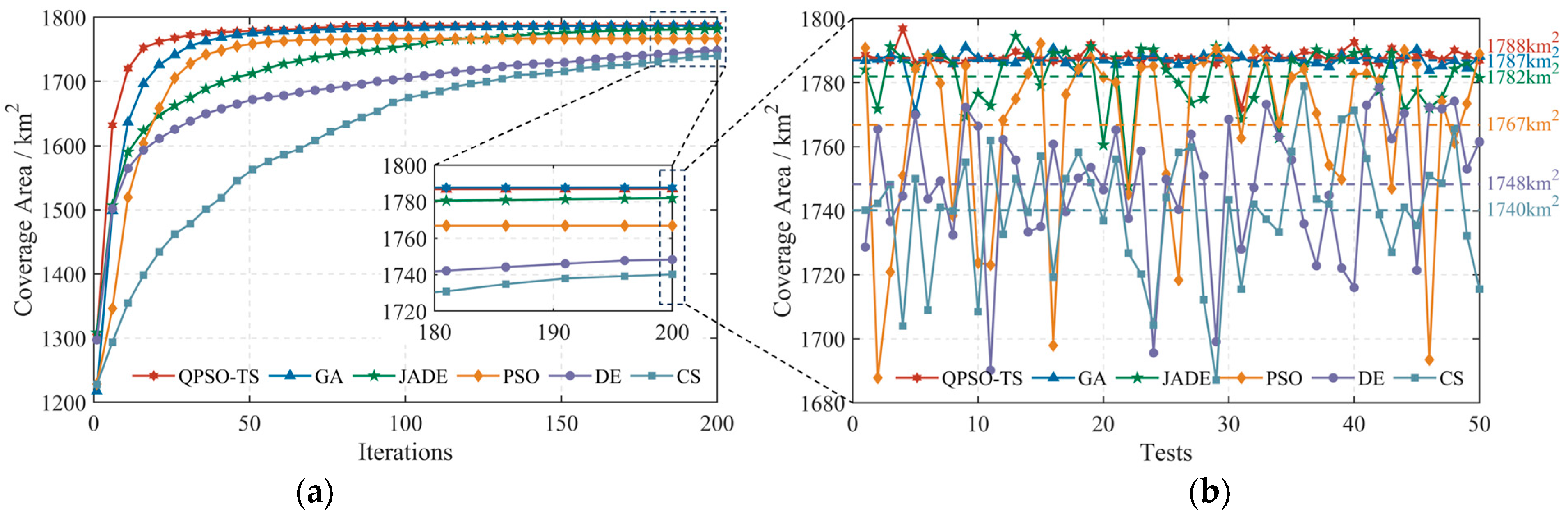
4.1. Convergence Curves and Optimization Effects
4.2. Significance Test
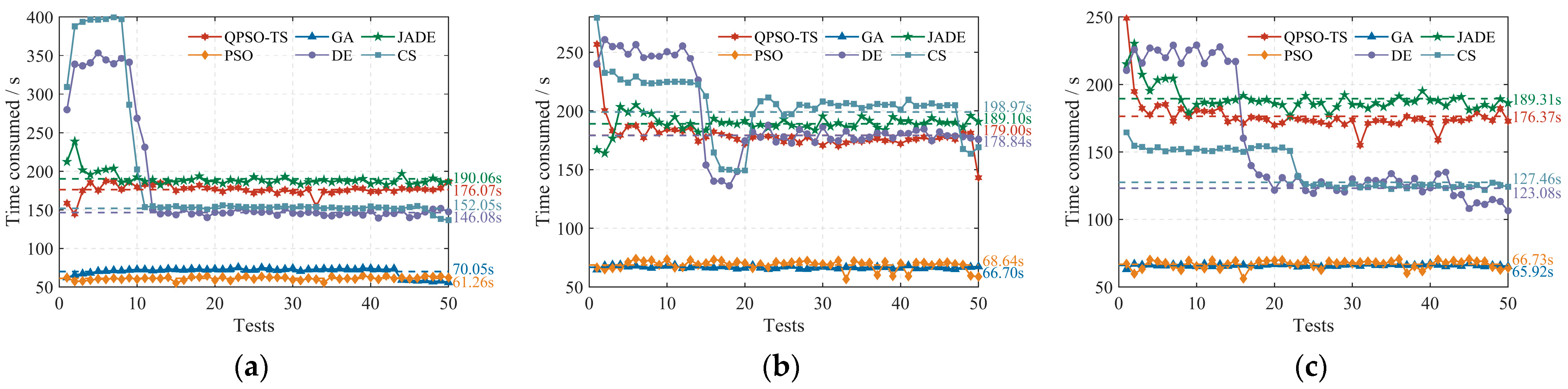
4.3. Optimization Time
4.4. Performance Analysis
5. Conclusions
- The dynamic changes of the acoustic environment driven by sea surface wind fields are first incorporated into the underwater target search path planning model, revealing the quantitative influence mechanism of wind-generated noise on the active sonar search distance;
- A sixteen-azimuth path planning model is proposed and optimized by GA, addressing the problem of maximizing the search range of surface search vessels in complex marine environments;
- Path planning based on in-situ marine data provides a highly adaptive path planning tool for underwater target search tasks, which is of engineering significance for improving underwater target search efficiency.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Y.; Liu, W.; Liu, J. Cooperative USV-UAV marine search and rescue with visual navigation and reinforcement learning-based control. ISA Trans. 2023, 137, 222–235. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Low, K.H.; Lv, C. Cooperative Path Planning for Heterogeneous Unmanned Vehicles in a Search-and-Track Mission Aiming at an Underwater Target. IEEE Trans. Veh. Technol. 2020, 69, 6782–6787. [Google Scholar] [CrossRef]
- Niu, Y.L.; Mu, Y.; Zhang, K.; Zhang, J.J.; Yang, H.H.; Wang, Y.M. Path planning and search effectiveness of USV based on underwater target scattering model. J. Phys. Conf. Ser. 2023, 2478, 102035. [Google Scholar] [CrossRef]
- Li, Y.; Huang, Y.; Zou, Z.; Yu, Q.; Zhang, Z.; Sun, Q. Multi-AUV underwater static target search method based on consensus-based bundle algorithm and improved Glasius bio-inspired neural network. Inf. Sci. 2024, 673, 120684. [Google Scholar] [CrossRef]
- Bai, Z.; Pang, H.; He, Z.; Zhao, B.; Wang, T. Path Planning of Autonomous Mobile Robot in Comprehensive Unknown Environment Using Deep Reinforcement Learning. IEEE Internet Things J. 2024, 11, 22153–22166. [Google Scholar] [CrossRef]
- Qian, L.; Li, H.; Wang, H.; Hong, M.; Han, J. Underwater target search and placement strategies based on an improved hidden Markov model. Sci. Sin. Technol. 2025, 55, 520–539. [Google Scholar] [CrossRef]
- Cao, Z.; Fan, H.; Hu, X.; Chen, Y.; Kang, S. Complete Coverage Search for Multiple Autonomous Underwater Vehicles Based on Neuronal Activity Reassignment. IEEE Trans. Intell. Transp. Syst. 2025, 26, 9693–9710. [Google Scholar] [CrossRef]
- Qi, B.; Li, Y.; Miao, H.; Chen, J.; Li, C. Research on Path Planning Method for Autonomous Underwater Vehicles Based on Improved Informed RRT. J. Syst. Simul. 2025, 37, 245–256. [Google Scholar] [CrossRef]
- Yu, F.; Shang, H.; Zhu, Q.; Zhang, H.; Chen, Y. An efficient RRT-based motion planning algorithm for autonomous underwater vehicles under cylindrical sampling constraints. Auton. Robots 2023, 47, 281–297. [Google Scholar] [CrossRef]
- Gao, F.; Xu, F.; Li, Z.; Qin, J.; Zhang, Q. Acoustic propagation uncertainty in internal wave environments using an ocean-acoustic joint model. Chin. Phys. B 2023, 32, 34302. [Google Scholar] [CrossRef]
- Dumont, P.-A.; Auclair, F.; Stéphan, Y.; Dumas, F. Modelling acoustic propagation in realistic ocean through a time-domain environment-resolving ocean model. J. Acoust. Soc. Am. 2024, 156, 4099–4115. [Google Scholar] [CrossRef] [PubMed]
- Zheng, L.; Hu, T.; Zhu, J. Underwater Sonar Target Detection Based on Improved ScEMA-YOLOv8. IEEE Geosci. Remote Sens. Lett. 2024, 21, 1503505. [Google Scholar] [CrossRef]
- Liao, S.; Xiao, W.; Wang, Y. Optimization of route planning based on active towed array sonar for underwater search and rescue. Ocean. Eng. 2025, 330, 121249. [Google Scholar] [CrossRef]
- Liu, B.; Huang, Y.; Chen, W. Principles of Underwater Acoustic, 3rd ed.; Science Press: Beijing, China, 2019; pp. 268–272. ISBN 978-7-03-063011-7. [Google Scholar]
- Wenz, G.M. Acoustic ambient noise in the ocean: Speactra and source. J. Acoust. Soc. Am. 1962, 34, 1936–1956. [Google Scholar] [CrossRef]
- Hildebrand, J.A.; Frasier, K.E.; Baumann-Pickering, S.; Wiggins, S.M. An empirical model for wind-generated ocean noise. J. Acoust. Soc. Am. 2021, 149, 4516–4533. [Google Scholar] [CrossRef] [PubMed]
- Stockhausen, J.H. Measurement and modeling of the vertical directionality of wind-generated ocean ambient noise. J. Acoust. Soc. Am. 1981, 70, S65. [Google Scholar] [CrossRef]
- Wang, Y.; Jiang, D.; Li, Z.; Peng, C.; Liu, Q. Characterization and source level modeling revision of thewind-generated ambient noise in South China Sea. Chin. J. Acoust. 2020, 45, 655–663. [Google Scholar] [CrossRef]
- Yang, J.; Nystuen, J.A.; Riser, S.C.; Thorsos, E.I. Open ocean ambient noise data in the frequency band of 100 Hz-50 kHz from the Pacific Ocean. JASA Express Lett. 2023, 3, 036001. [Google Scholar] [CrossRef] [PubMed]
- Derakhti, M.; Thomson, J.; Bassett, C.; Malila, M.; Kirby, J.T. Statistics of Bubble Plumes Generated by Breaking Surface Waves. J. Geophys. Res. Oceans 2024, 129, e2023JC019753. [Google Scholar] [CrossRef]
- Sun, J.; Feng, B.; Xu, W. Particle swarm optimization with particles having quantum behavior. In Proceedings of the 2004 Congress on Evolutionary Computation, Portland, OR, USA, 19–23 June 2004; Volume 1, pp. 325–331. [Google Scholar] [CrossRef]
- Glover, F. Tabu Search—Part I. ORSA J. Comput. 1989, 1, 190. [Google Scholar] [CrossRef]
- Glover, F. Tabu Search—Part II. ORSA J. Comput. 1990, 2, 1. [Google Scholar] [CrossRef]
- Sampson, J.R. Adaptation in Natural and Artificial Systems (John H. Holland). SIAM Rev. 1976, 18, 529–530. [Google Scholar] [CrossRef]
- Zhang, J.; Sanderson, A.C. JADE: Adaptive Differential Evolution with Optional External Archive. IEEE Trans. Evol. Comput. 2009, 13, 945–958. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution–A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Yang, X.; Deb, S. Cuckoo Search via Lévy flights. In Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing, Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar] [CrossRef]
- Abbas, A.A.M.; Mohideen, K.M.S.; Narayanaswamy, V. A passive sonar based underwater acoustic channel model for improved search and rescue operations in deep sea. Int. J. Electr. Comput. Eng. 2024, 14, 6148–6159. [Google Scholar] [CrossRef]
- Yu, C.; Gao, W.; Li, S.; Ge, Q. Detection model construction and performance analysis for target search and rescue via autonomous underwater vehicles. Kongzhi Yu Juece/Control Decis. 2025, 40, 170–179. [Google Scholar] [CrossRef]
- Freitas, E.B.A.; Albergamo, A.; Leite, M.; Leston, S.; Di Bella, G. Proceedings of the 1st International Conference-BeSafeBeeHoney (BEekeeping Products Valorization and Biomonitoring for the SAFEty of BEEs and HONEY). Bee World 2024, 101, 82–108. [Google Scholar] [CrossRef]
- Walkinshaw, H.M. Low-Frequency Spectrum of Deep Ocean Ambient Noise. J. Acoust. Soc. Am. 1960, 32, 1497. [Google Scholar] [CrossRef]
- Brown, M.G. A directional spectrum evolution model for wind-generated ocean noise. J. Acoust. Soc. Am. 2025, 157, 3245–3255. [Google Scholar] [CrossRef] [PubMed]
- Liao, S.; Xiao, W.; Wang, Y. Dynamic hybrid parallel computing of the Ray Model for solving underwater acoustic fields in vast sea. Sci. Rep. 2024, 14, 25385. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, T.C.A.; Lin, Y.; Porter, M.B. Underwater Sound Propagation Modeling in a Complex Shallow Water Environment. Front. Mar. Sci. 2021, 8, 751327. [Google Scholar] [CrossRef]
- Frye, H.W.; Pugh, J.D. A New Equation for the Speed of Sound in Seawater. J. Acoust. Soc. Am. 1971, 50, 384–386. [Google Scholar] [CrossRef]
- Zhang, H.; Lin, W.; Chen, A. Path Planning for the Mobile Robot: A Review. Symmetry 2018, 10, 450. [Google Scholar] [CrossRef]
- Ren, Y.; Zhang, L. An adaptive evolutionary multi-objective estimation of distribution algorithm and its application to Multi-UAV path planning. IEEE Access 2023, 11, 1. [Google Scholar] [CrossRef]
- Harman, B.I.; Koseoglu, H.; Yigit, C.O. Performance evaluation of IDW, Kriging and multiquadric interpolation methods in producing noise mapping: A case study at the city of Isparta, Turkey. Appl. Acoust. 2016, 112, 147–157. [Google Scholar] [CrossRef]
- Nuo, L.; Xuanzhen, C.; Wei, L. Research on the Best Working Depth for Active Sonar in Shallow Sea. Audio Eng. 2023, 47, 38–41. [Google Scholar] [CrossRef]
- Lan, T.; Wang, Y.; Qiu, L.; Liu, G. Array shape estimation based on tug vehicle noise for towed linear array sonar during turning. Ocean Eng. 2024, 303, 117554. [Google Scholar] [CrossRef]
- Yu, S.; Li, X.; Tian, X.; Pang, M. Protein structure prediction based on particle swarm optimization and tabu search strategy. BMC Bioinform. 2022, 23, 352. [Google Scholar] [CrossRef] [PubMed]
- Smairi, N.; Siarry, P.; Ghedira, K. A hybrid particle swarm approach based on Tribes and tabu search for multi-objective optimization. Optim. Method Softw. 2016, 31, 204–231. [Google Scholar] [CrossRef]



| Algorithm | M | Parameter Settings |
|---|---|---|
| GA | 30 | Crossover probability: 0.5; Mutation probability: 1/N; Tournament selection size: 3; Elite retention ratio: 0.15 |
| JADE | 30 | Adaptive rate: 0.1; Elite individual ratio: 0.05; Initial crossover probability mean: 0.5; Initial scaling factor mean: 0.5 |
| PSO | 30 | Inertia weight: 0.72; Learning factors c1: 1.49, c2: 1.49; Maximum velocity: 4 |
| DE | 30 | Mutation type: DE/rand/1; Crossover type: Binomial crossover; Crossover probability: 0.9; Scaling factor: 0.85 |
| CS | 30 | Discovery probability: 0.25; Step size scaling factor: 0.5; Lévy flight exponent: 1.5 |
| Mission Sea Areas | Statistical Index | GA | JADE | PSO | DE | CS |
|---|---|---|---|---|---|---|
| Sea area 1 | Rank sum | 2304.5 | 2501.5 | 3353.5 | 3774.0 | 3775.0 |
| p-value | 0.1293 | 0.8740 | 1.1358 × 10−8 | 7.4787 × 10−18 | 7.0422 × 10−18 | |
| Sea area 2 | Rank sum | 2610.0 | 3132.5 | 3539.0 | 3775.0 | 3775.0 |
| p-value | 0.5600 | 2.8472 × 10−5 | 2.7921 × 10−12 | 7.0200 × 10−18 | 7.0200 × 10−18 | |
| Sea area 3 | Rank sum | 2719.0 | 2934.5 | 3377.0 | 3768.5 | 3774.0 |
| p-value | 0.1817 | 0.0048 | 4.2918 × 10−9 | 1.0239 × 10−17 | 7.3518 × 10−18 |
| Mission Sea Areas | QPSO-TS | GA | JADE | PSO | DE | CS |
|---|---|---|---|---|---|---|
| Sea area 1 | 176.07 | 70.05 | 190.06 | 61.26 | 146.08 | 152.05 |
| Sea area 2 | 179.00 | 66.70 | 189.10 | 68.64 | 178.84 | 198.97 |
| Sea area 3 | 176.37 | 65.92 | 189.31 | 66.73 | 123.08 | 127.46 |
| Mission Sea Areas | g | QPSO-TS | GA | JADE | PSO | DE | CS |
|---|---|---|---|---|---|---|---|
| Sea area 1 | 65% | 0.622 | 0.381 | 0.780 | 0.332 | 0.791 | 0.923 |
| 70% | 0.622 | 1.011 | 1.544 | 0.717 | 1.596 | 6.463 | |
| 75% | 1.249 | 1.341 | 2.332 | 1.063 | 3.192 | 12.948 | |
| 80% | 1.249 | 2.020 | 4.736 | 1.496 | 5.606 | 23.211 | |
| 85% | 2.573 | 3.042 | 10.442 | 2.196 | 16.401 | 40.134 | |
| 90% | 4.032 | 4.066 | 25.139 | 3.506 | 42.791 | 73.360 | |
| 95% | 7.787 | 7.177 | 52.352 | 6.817 | 118.733 | 178.301 | |
| Sea area 2 | 65% | 0.630 | 0.663 | 0.783 | 0.709 | 0.834 | 0.978 |
| 70% | 0.630 | 0.971 | 1.555 | 0.957 | 1.686 | 6.791 | |
| 75% | 1.263 | 1.290 | 2.342 | 1.409 | 3.394 | 16.549 | |
| 80% | 1.263 | 1.933 | 4.710 | 1.941 | 6.844 | 28.172 | |
| 85% | 1.922 | 2.916 | 11.333 | 2.786 | 22.163 | 46.098 | |
| 90% | 4.091 | 4.222 | 26.196 | 4.375 | 57.741 | 82.462 | |
| 95% | 7.130 | 7.517 | 55.661 | 9.172 | 146.598 | 154.811 | |
| Sea area 3 | 65% | 0.616 | 0.359 | 0.785 | 0.364 | 0.639 | 0.658 |
| 70% | 0.616 | 0.663 | 0.785 | 0.689 | 0.639 | 2.606 | |
| 75% | 1.236 | 0.969 | 1.565 | 0.812 | 1.287 | 6.529 | |
| 80% | 1.892 | 1.599 | 3.166 | 1.377 | 2.572 | 13.767 | |
| 85% | 2.549 | 2.234 | 5.577 | 1.713 | 4.550 | 27.078 | |
| 90% | 3.992 | 3.216 | 11.401 | 2.953 | 14.247 | 48.200 | |
| 95% | 6.946 | 5.507 | 35.060 | 5.374 | 65.999 | 84.462 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Xiao, W.; Liu, Y. Research on Path Optimization for Underwater Target Search Under the Constraint of Sea Surface Wind Field. J. Mar. Sci. Eng. 2025, 13, 1393. https://doi.org/10.3390/jmse13081393
Wang W, Xiao W, Liu Y. Research on Path Optimization for Underwater Target Search Under the Constraint of Sea Surface Wind Field. Journal of Marine Science and Engineering. 2025; 13(8):1393. https://doi.org/10.3390/jmse13081393
Chicago/Turabian StyleWang, Wenjun, Wenbin Xiao, and Yuhao Liu. 2025. "Research on Path Optimization for Underwater Target Search Under the Constraint of Sea Surface Wind Field" Journal of Marine Science and Engineering 13, no. 8: 1393. https://doi.org/10.3390/jmse13081393
APA StyleWang, W., Xiao, W., & Liu, Y. (2025). Research on Path Optimization for Underwater Target Search Under the Constraint of Sea Surface Wind Field. Journal of Marine Science and Engineering, 13(8), 1393. https://doi.org/10.3390/jmse13081393







