Ancient Ship Structures: Ultimate Strength Analysis of Wooden Joints
Abstract
1. Introduction
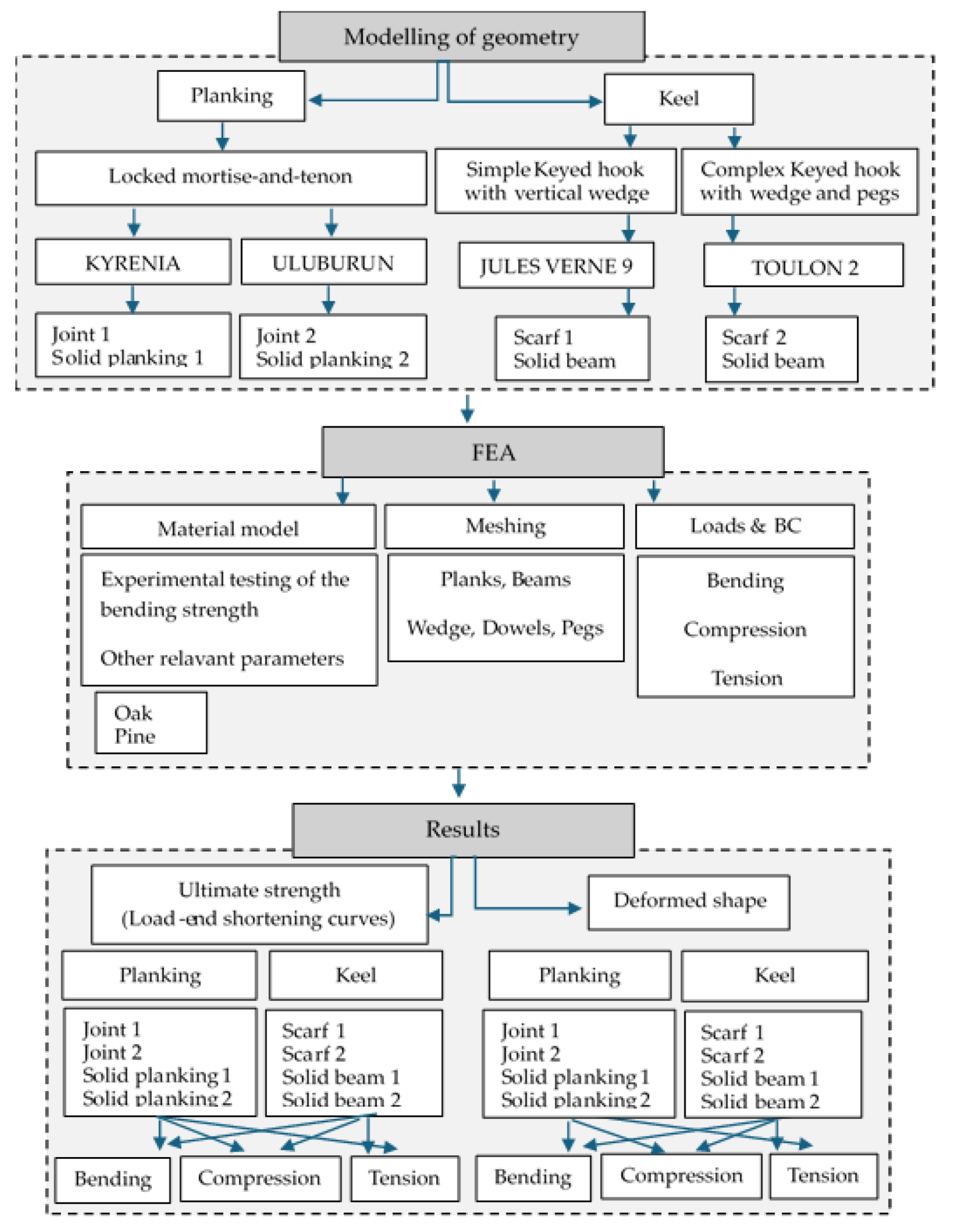
2. Methodology
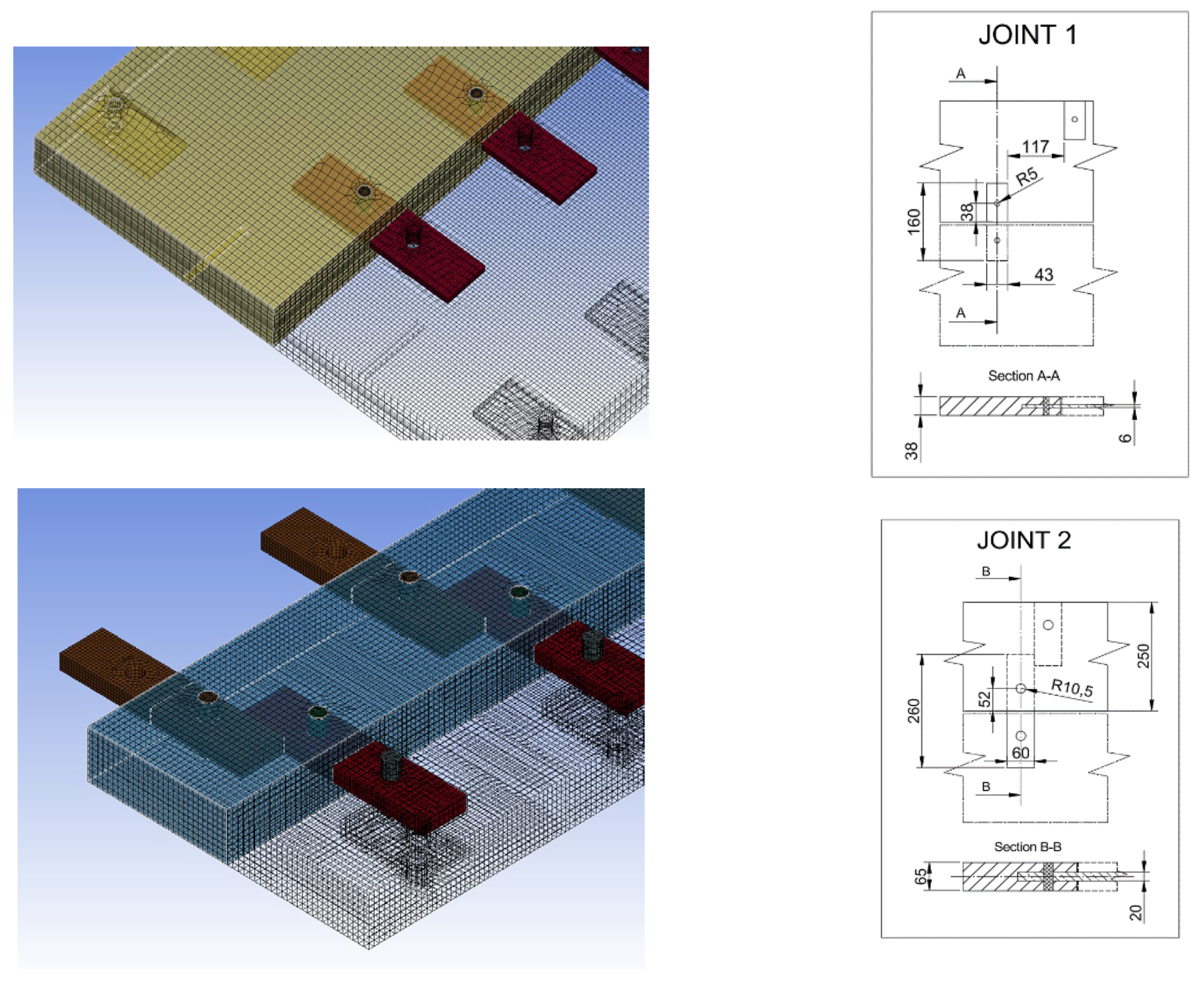
2.1. Structural Modelling and Geometry of Joints
2.2. Experimental Testing of Bending Strength
2.3. Numerical Model
2.3.1. Loads and Boundary Condition
2.3.2. Material Model
3. Results and Discussion
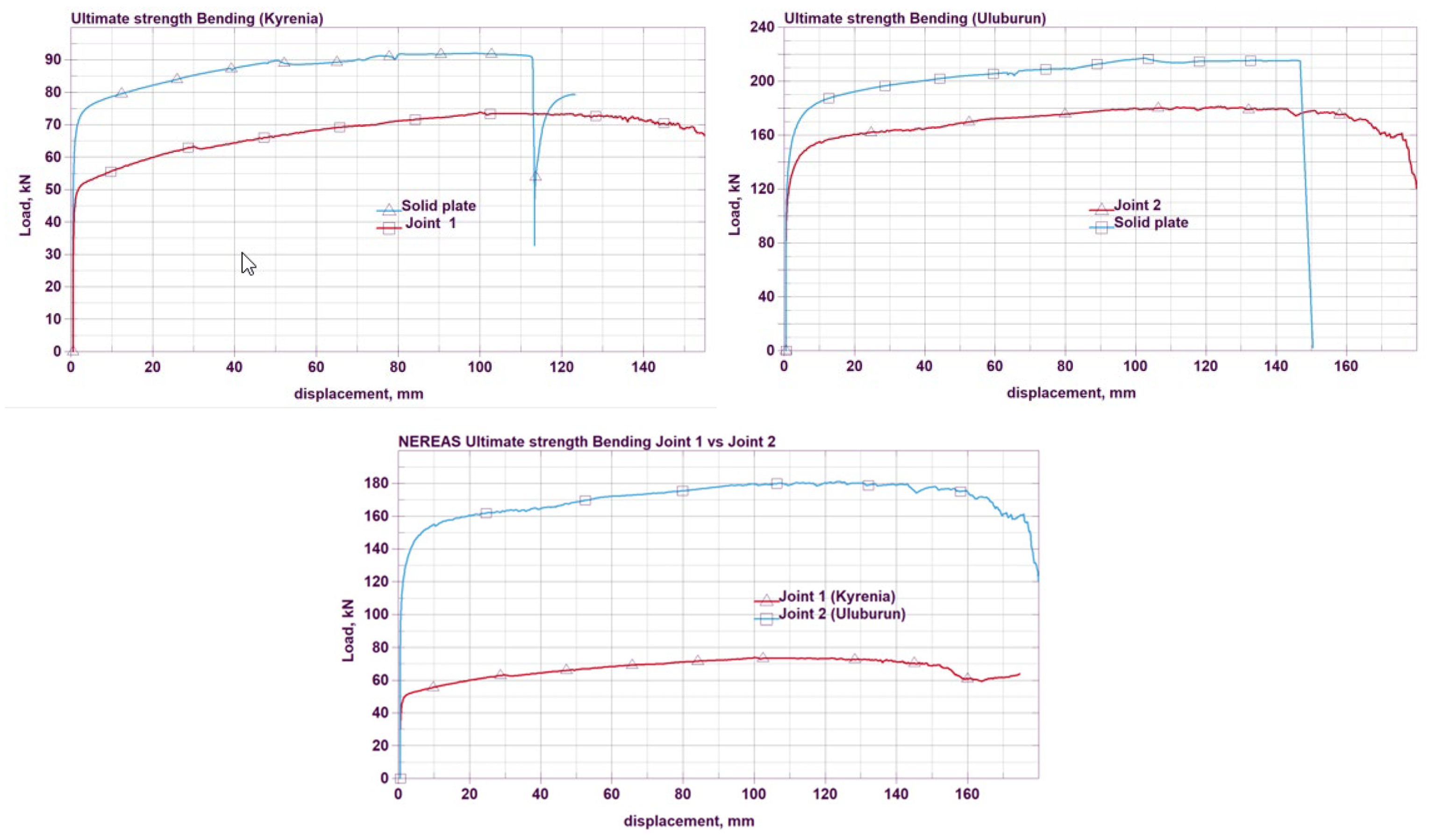
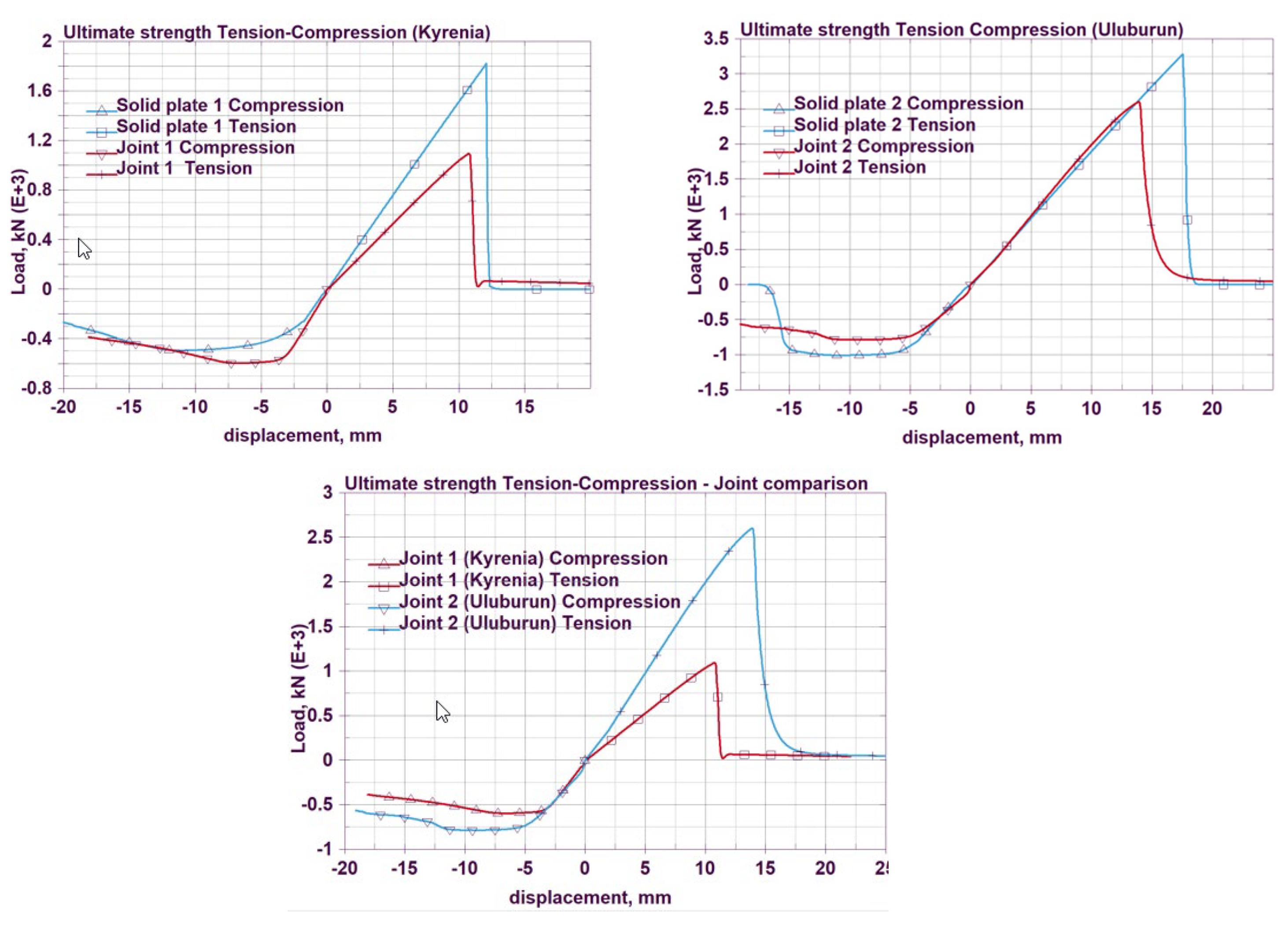
3.1. Planking Joints
3.2. Keel Joints

| Model | Max. Load, [kN] | Displacement, [mm] at Max. Load | ||||
|---|---|---|---|---|---|---|
| Bending | Compression | Tension | Bending | Compression | Tension | |
| Solid beam 1 (Jules-Verne 9) | 31.0 | 270 | 480 | 43 | 7.5 | 12.5 |
| Solid beam 2 (Toulon 2) | 18.1 | 110 | 180 | 38 | 3.7 | 5.6 |
| Scarf 1 (Jules-Verne 9) | 2.1 | 18 | 10 | 17 | 2.0 | 1.5 |
| Scarf 2 (Toulon 2) | 8.1 | 25 | 41 | 34 | 4.0 | 2.8 |
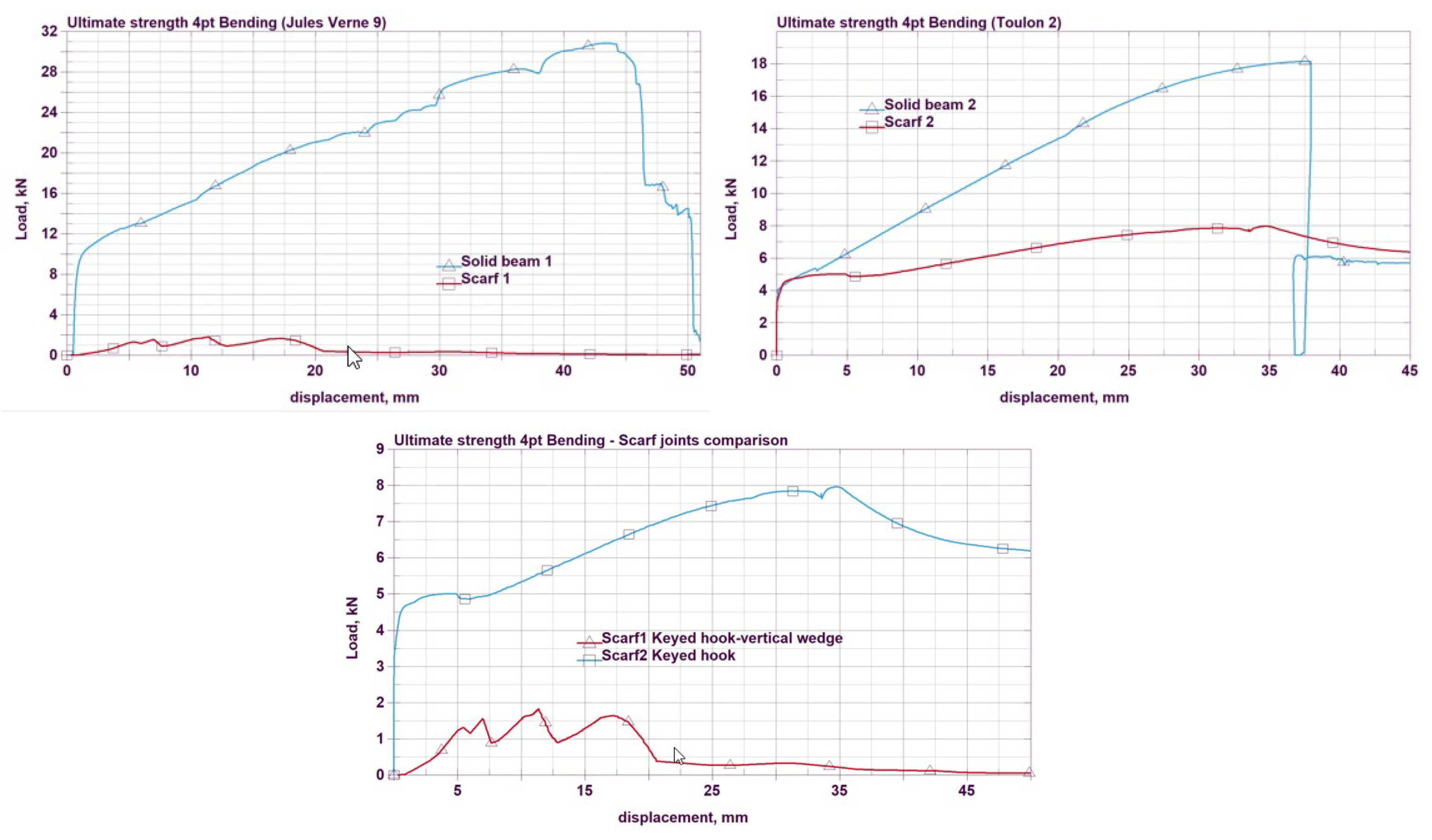

3.3. Discussion
4. Conclusions
- -
- Based on load-end shortening curves, it cannot be concluded that Joint 1 (Kyrenia) is stronger than Joint 2 (Uluburun) compared to the solid plankings. In fact, the relative difference for Joint 2 is smaller (16% compared to the planking versus 20% for Joint 1), despite Joint 2 belonging to a much earlier historical period of shipbuilding. A similar conclusion can be drawn for tension, again favouring Joint 2. In compression, Joint 1 exhibits a higher maximum load in the 2–8 mm shortening range than the solid planking.
- -
- When comparing the two scarfs, it is evident that the keyed hook scarf (Scarf 2—Toulon 2) performs significantly better, showing four to six times greater strength than the keyed hook scarf with a vertical wedge (Scarf 1—Jules-Verne 9) across all three stress states. The differences observed in joint performance between the Jules-Verne 9 and Toulon 2 vessels may also be linked to the evolving need to manage longitudinal stress in a boat that is no longer constructed using the sewn-plank technique.
- -
- However, when looking at the presented analysis of mortise-and-tenon joints, it becomes evident that ‘more recent’ does not necessarily imply ‘more efficient’. This opens the possibility that the transition towards different joint configurations over time was not driven solely by structural performance. Other factors, such as construction efficiency, material availability, or ease of replacement, may also have played a significant role.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jia, S.; Fan, C.; Li, C. Research on the Performance of New-Type Mortise and Tenon Joints, Proceedings of CIBv 2024. In Lecture Notes in Civil Engineering; Tuns, I., Muntean, R., Gălățanu, T., Cazacu, C., Conțiu, M., Eds.; Springer: Cham, Germany, 2025; Volume 665, pp. 466–483. [Google Scholar] [CrossRef]
- Liu, K.; Zhang, H.; Du, Y.; Hu, X.; Wang, L.; Li, L. Fatigue and damage evolution in wood T-shaped mortise and tenon joints. Sci. Rep. 2024, 14, 21515. [Google Scholar] [CrossRef]
- Karolak, A.; Jasieńko, J.; Raszczuk, K. Historical scarf and splice carpentry joints: State of the art. Herit. Sci. 2020, 8, 105. [Google Scholar] [CrossRef]
- Afshar, R.; van Dijka, N.P.; Bjurhager, I.; Gamstedt, E.K. Comparison of Experimental testing and finite element modelling of a replica of a section of the Vasa warshipto identify the behaviour of structural joints. Eng. Struct. 2017, 147, 62–76. [Google Scholar] [CrossRef]
- Afshar, R.; Alavyoon, N.; Ahlgren, A.; Gamstedt, E.K. Full scale finite element modelling and analysis of the 17th-century warship Vasa: A methodological approach and preliminary results. Eng. Struct. 2021, 231, 111765. [Google Scholar] [CrossRef]
- Pulak, C. The Uluburun Shipwreck and Late Bronze Age Trade. In Beyond Babylon: Art, Trade, and Diplomacy in the Second Millennium BC.; Aruz, J., Graff, S.B., Rakic, Y., Eds.; Metropolitan Museum of Art: New York, NY, USA, 2008; pp. 289–310. [Google Scholar]
- Steffy, J.R. Wooden Ship Building and the Interpretation of Shipwrecks; Texas A&M University Press: College Station, TX, USA, 1994; pp. 42–59. [Google Scholar]
- Cvikel, D. The Kyrenia Ship Final Excavation Report, Volume I: History of the Excavation, Amphoras, Ceramics, Coins and Evidence for Dating; Katzev, S.W., Swiny, H.W., Eds.; Oxbow Books: Oxford, UK, 2023; p. 464. ISBN 978-1-7857-0752-0. [Google Scholar]
- Pomey, P.; Poveda, P. Gyptis: Sailing Replica of a 6th-century-BC Archaic Greek Sewn Boat. Int. J. Naut. Archaeol. 2018, 47, 45–56. [Google Scholar] [CrossRef]
- Brun, J.-P.; Pasqualini, M. Toulon, Telo Martius: Une Agglomération Portuaire Romaine de la Cité d’Arles. Les Fouilles, le Mobilier, les Épaves (Recherches 1978–1988); Brun, J.-P., Pasqualini, M., Boetto, G., Botte, E., Eds.; Presses Universitaires de Provence (BiAMA 31): Aix-en-Provence, France, 2022; pp. 19–32. [Google Scholar]
- Poveda, P. Una nouvelle hypothèse de restitution de l’épave Toulon 2. In Toulon, Telo Martius: Une Agglomération Portuaire Romaine de la Cité d’Arles. Les fouilles, le Mobilier, les Épaves (Recherches 1978–1988); Brun, J.-P., Pasqualini, M., Boetto, G., Botte, E., Eds.; Presses Universitaires de Provence (BiAMA 31): Aix-en-Provence, France, 2022; pp. 389–395. [Google Scholar]
- Beltrame, C.; Bondioli, M. A hypothesis on the development of Mediterranean ship construction from Antiquity to the Late Middle Ages. In Connected by the Sea: Proceedings of the Tenth International Symposium on Boat and Ship Archaeology; Blue, L., Englert, H., Eds.; Oxford Books: Oxford, UK, 2016; pp. 89–94. [Google Scholar]
- Helfman, N.; Nishri, B.; Cvikel, D. A comparative structural analysis of shell-first and frame-based ship hulls of the 1st millennium AD. Int. J. Naut. Archaeol. 2018, 47, 299–312. [Google Scholar] [CrossRef]
- Arciszewska-Kedzior, A.; Kunecky, J.; Hasníková, H.; Sebera, V. Lapped scarf joint with inclined faces and wooden dowels: Experimental and numerical analysis. Eng. Struct. 2015, 94, 1–8. [Google Scholar] [CrossRef]
- Chen, C.; Qiu, H.; Lu, Y. Flexural behaviour of timber dovetail mortise–tenon joints. Constr. Build. Mater. 2016, 112, 366–377. [Google Scholar] [CrossRef]
- Fajman, P.; Máca, J. Stiffness of scarf joints with dowels. Comput. Struct. 2017, 207, 194–199. [Google Scholar] [CrossRef]
- Koch, H.; Eisenhut, L.; Seim, W. Multi-mode failure of form-fitting timber connections—Experimental and numerical studies on the tapered tenon joint. Eng. Struct. 2013, 48, 727–738. [Google Scholar] [CrossRef]
- del Coz Díaz, J.J.; García Nieto, P.J.; Lozano Martínez-Luengas, A.; Suarez Domínguez, F.J.; Domínguez Hernández, J. Non-linear numerical analysis of plywood board timber connections by DOE-FEM and full-scale experimental validation. Eng. Struct. 2013, 49, 76–90. [Google Scholar] [CrossRef]
- Akbar, J.M.; Aksa, R.A. Finite Element Analysis of Wood Structural Joints on Traditional Wooden Ship. J. Ocean. Mech. Aerosp.-Sci. Eng. 2016, 30, 14–20. [Google Scholar]
- Dubokovic, M. Finite Element Method Analysis of a Wooden Structure. Master’s Thesis, University of Zagreb, Zagreb, Croatia, 2015. [Google Scholar]
- Pomey, P. Les épaves grecques du VIe siècle av. J.-C. de la place Jules-Verne à Marseille. In Construction Navale Maritime et Fluviale. Approches Archéologiques, Historiques et Ethnologiques; Pomey, P., Rieth, É., Eds.; CNRS Éditions (Archaeonautica 14): Paris, France, 1998; pp. 147–154. [Google Scholar]
- Domìnguez, A.; Boetto, G. Le bois employé dans la construction des embarcations de Toulon. In Toulon, Telo Martius: Une Agglomération Portuaire Romaine de la Cité d’Arles. Les Fouilles, le Mobilier, les Épaves (Recherches 1978–1988); Brun, J.-P., Pasqualini, M., Boetto, G., Botte, E., Eds.; Presses Universitaires de Provence (BiAMA 31): Aix-en-Provence, France, 2022; pp. 372–386. [Google Scholar]
- ISO 13061-4 2014; Physical and Mechanical Properties of Wood—Test Methods for Small Clear Wood Specimens Part 4: Determination of Modulus of Elasticity in Static Bending. International Organization for Standardization: Geneva, Switzerland, 2014.
- ASTM D3043-17. 2022; Standard Test Methods for Structural Panels in Flexure. ASTM International: West Conshohocken, PA, USA, 2022.
- ASTM D198-21a. 2022; Standard Test Methods of Static Tests of Lumber in Structural Sizes. ASTM International: West Conshohocken, PA, USA, 2022.
- Hallquist, J.O. LS-DYNA KEYWORD USER’S MANUAL Vol. II Material Models. LSTC 2016. Available online: https://ftp.lstc.com/anonymous/outgoing/jday/manuals/LS-DYNA_Manual_Volume_II_R9.0.pdf (accessed on 18 June 2025).
- US Department of Transportation, Federal Highway Administration. USA Federal Highway Administration Report 2007, Manual for LS-DYNA Wood Material Model 143. FHWA-HRT-04-097; US Department of Transportation, Federal Highway Administration: Washington, DC, USA, 2007.
- Baumann, G. Comparison of the two material models for modelling solid birch wood. In Proceedings of the 12th European LSDYNA Conference, Koblenz, Germany, 14–16 May 2019. [Google Scholar]
- Branco, J.M.; Descamps, T. Analysis and strengthening of carpentry joints. Constr. Build. Mater. 2015, 97, 34–47. [Google Scholar] [CrossRef]
- Okamoto, S.; Nakatani, M.; Akiyama, N.; Tanaka, K.; Mori, T. Verification of the shear performance of mortise and tenon joints with top and bottom notches at the beam end. J. Wood Sci. 2021, 67, 47. [Google Scholar] [CrossRef]
- Gamerro, J.; Bocquet, J.F.; Weinand, Y. Experimental investigations on the load-carrying capacity of digitally produced wood-wood connections. Eng. Struct. 2020, 213, 110576. [Google Scholar] [CrossRef]
- Jenssen, K. Documentation and Analysis of Ancient Ships. Ph.D. Thesis, DTU, Center for Maritime Archeology, Department of Naval Architecture and Offshore Engineering, Lyngby, Denmark, 1999. [Google Scholar]





| Item | Title | Variable | Type of Wood | Units | |
|---|---|---|---|---|---|
| Pine | Oak | ||||
| Density | ρ | 673 | 770 | kg/m3 | |
| Moduli | Parallel Normal Modulus | EL | 11.35 | 11.138 | GPa |
| Perpendicular Normal Modulus | ET | 246.8 | 801.9 | GPa | |
| Parallel Shear Modulus | GLT | 715.2 | 902.2 | GPa | |
| Perpendicular Shear Modulus | GTR | 87.5 | 211.6 | GPa | |
| Parallel Major Poisson’s Ratio | υLT | 0.157 | 0.448 | ||
| Strengths | Parallel Tensile Strength | XT | 68.3 | 118.4 | MPa |
| Parallel Compressive Strength | XC | 19.67 | 59.3 | MPa | |
| Parallel Shear Strength | S|| | 7.27 | 13.8 | MPa | |
| Perpendicular Compressive Strength | YC | 3.80 | 8.2 | MPa | |
| Perpendicular Tensile Strength | YT | 1.64 | 5.7 | MPa | |
| Perpendicular Shear Strength | S⊥ | 10.20 | 12.3 | MPa | |
| Type of Wood | Deflection, mm | |
|---|---|---|
| Experiment | Numerical Simulation | |
| Pine | 6.78 | 7.0 |
| Oak | 9.2 | 9.0 |
| Structural Element | Planking | ||
|---|---|---|---|
| Type of planking joint/ Planking thickness, mm | Joint 1—Kyrenia 38 mm | Joint 2—Uluburun 65 mm | Solid planking (no joint) Planking 1—38 mm; Planking 2—65 mm |
| Model length and breadth, mm |  |  |  |
| Loads and boundary conditions: tension | 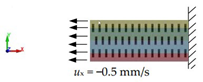 |  |  |
| compression | 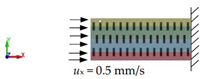 |  |  |
| bending | 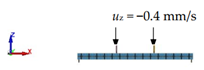 | 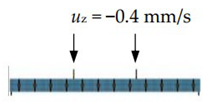 | 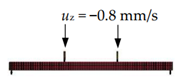 |
| Material/ Material model | PINE: planking OAK: wedges, dowels, pegs LS-Dyna Mat-143, transversally isotropic with erosion | ||
| Mesh size, mm Beams Wedges, Dowels and Pegs | 5 × 5 × 5 2 × 2 × 2 | ||
| Finite element type | Solid, 8-point hexahedron intended for elements with poor aspect ratios, efficient formulation | ||
| Solver | Dynamic, explicit, nonlinear | ||
| Structural Element | Keel | ||
|---|---|---|---|
| Type of scarf joint/ | Scarf 1—Keyed hook with vertical wedge | Scarf 2—Keyed hook | Solid beam (no joint) |
| Beam cross-section | Beam 1 | Beam 2 | Beam 1 and Beam 2 |
| Model length, mm |  |  |  |
| Loads and boundary conditions (top to bottom: tension, compression, and bending) | 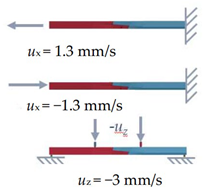 | 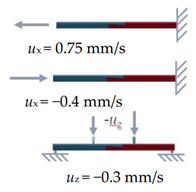 |  |
| Material/ Material model | OAK LS-Dyna Mat-143, transversally isotropic with erosion | ||
| Mesh size, mm Beams Wedges, Dowels, and Pegs | 5 × 5 × 5 2 × 2 × 2 | ||
| Finite element type | Solid, 8-point hexahedron intended for elements with poor aspect ratios, efficient formulation | ||
| Solver | Dynamic, explicit, nonlinear | ||
| Item | Title | Variable | Type of Wood | Units | |
|---|---|---|---|---|---|
| Oak | Pine | ||||
| Hardening | Parallel Hardening Initiation | N|| | 0.2 | 0.2 | |
| Parallel Hardening Rate | c|| | 600 | 600 | ms | |
| Perpendicular Hardening Initiation | N⊥ | 0.2 | 0.2 | ||
| Perpendicular Hardening Rate | c⊥ | 300 | 200 | ms | |
| Softening | Parallel Mode I Fracture Energy | Gf I || | 0.0225 | 0.03413 | MPa m |
| Parallel Mode II Fracture Energy | Gf II || | 0.0440 | 0.07061 | MPa m | |
| Parallel Softening | B | 20 | 20 | ||
| Parallel Maximum Damage | dmax|| | 0.99 | 0.99 | ||
| Perpendicular Mode I Fracture Energy | Gf I ⊥ | 0.000441 | 0.000401 | MPa m | |
| Perpendicular Mode II Fracture Energy | Gf II ⊥ | 0.000880 | 0.000830 | MPa m | |
| Perpendicular Softening | D | 20 | 20 | ||
| Perpendicular Maximum Damage | dmax⊥ | 0.99 | 0.999 | ||
| Model | Max. Load, [kN] | Displacement, [mm] at Max. Load | ||||
|---|---|---|---|---|---|---|
| Bending | Compression | Tension | Bending | Compression | Tension | |
| Solid planking 1 (Kyrenia) | 92 | 490 | 1820 | 90.0 | 11.0 | 12.5 |
| Solid planking 2 (Uluburun) | 216 | 1010 | 3300 | 102.0 | 11.2 | 17.5 |
| Joint 1 (Kyrenia) | 73 | 590 | 1100 | 99.0 | 6.6 | 10.8 |
| Joint 2 (Uluburun) | 180 | 790 | 2650 | 105.0 | 10.0 | 14.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zamarin, A.; Rudan, S.; Bolf, D.; Lucchini, A.; Rossi, I.R. Ancient Ship Structures: Ultimate Strength Analysis of Wooden Joints. J. Mar. Sci. Eng. 2025, 13, 1392. https://doi.org/10.3390/jmse13081392
Zamarin A, Rudan S, Bolf D, Lucchini A, Rossi IR. Ancient Ship Structures: Ultimate Strength Analysis of Wooden Joints. Journal of Marine Science and Engineering. 2025; 13(8):1392. https://doi.org/10.3390/jmse13081392
Chicago/Turabian StyleZamarin, Albert, Smiljko Rudan, Davor Bolf, Alice Lucchini, and Irena Radić Rossi. 2025. "Ancient Ship Structures: Ultimate Strength Analysis of Wooden Joints" Journal of Marine Science and Engineering 13, no. 8: 1392. https://doi.org/10.3390/jmse13081392
APA StyleZamarin, A., Rudan, S., Bolf, D., Lucchini, A., & Rossi, I. R. (2025). Ancient Ship Structures: Ultimate Strength Analysis of Wooden Joints. Journal of Marine Science and Engineering, 13(8), 1392. https://doi.org/10.3390/jmse13081392








