A Novel Transfer Learning-Based OFDM Receiver Design for Enhanced Underwater Acoustic Communication
Abstract
1. Introduction
1.1. Conventional OFDM Channel-Estimation Methods
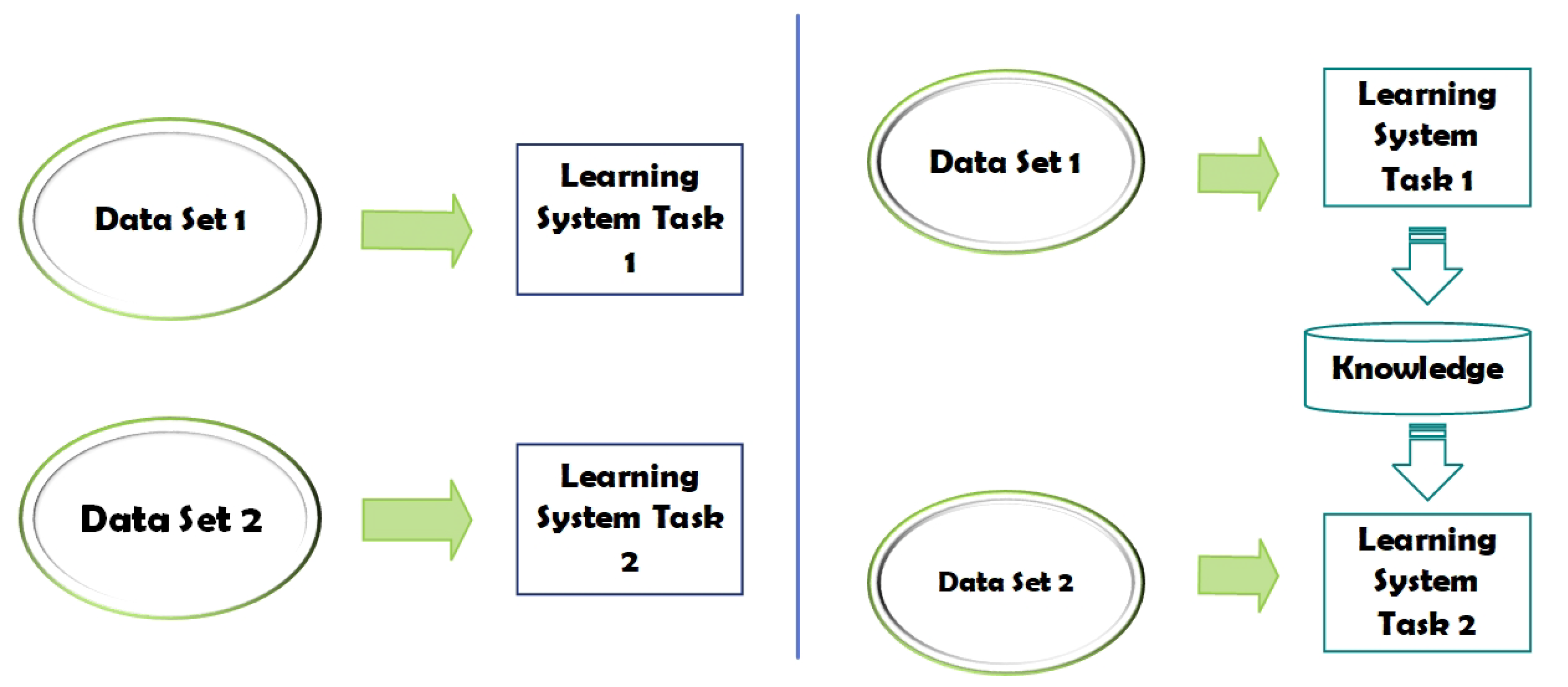
1.2. Existing Work in DNN Based OFDM Receiver
1.3. Problem Statement
1.4. Main Research Contributions
- We propose the first TL-based pre-trained model for UWA communication, trained on five distinct watermark channels to enable effective generalization across varying underwater environments.
- Development of a novel TL-based model that specifically addresses the channel mismatch problem in UWA systems and can efficiently adapt to new underwater conditions.
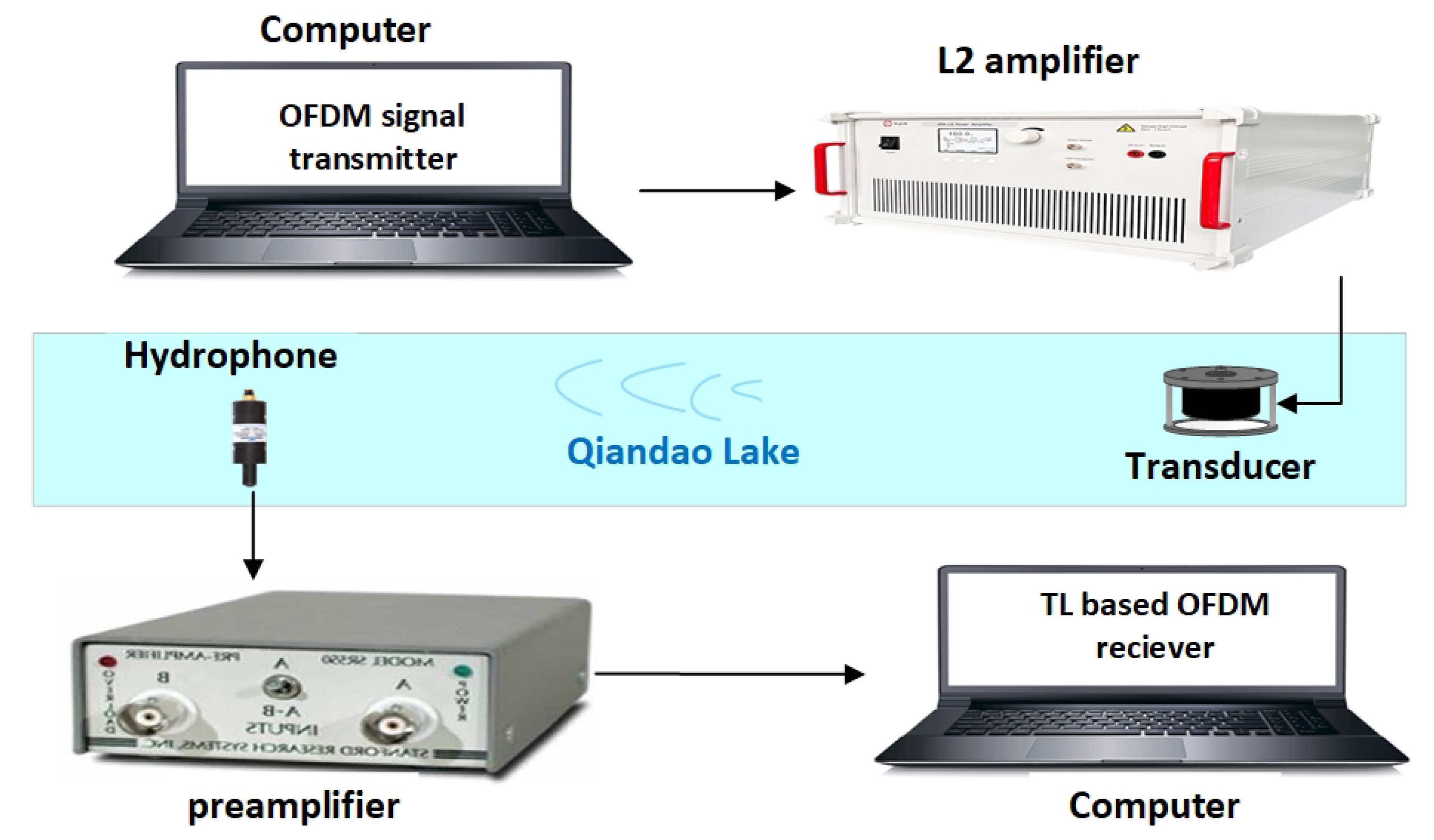
- We validate the robustness of the proposed model by conducting real-world experiments in Qingdao Lake, which show that our proposed TL-based OFDM receiver can generalize well to new environments, addressing challenges of model retraining and computational complexity.
- Compare our TL-based OFDM receiver against traditional channel-estimation methods in multiple aspects, including improved BER and adaptability to fluctuating channel conditions.
2. Overview of the UWA OFDM Communication System
2.1. Conventional UWA OFDM Communication System
- is the frequency-domain representation of the OFDM symbol
- is the time-domain signal obtained after IFFT,
- N is the total number of subcarriers,
- k is the subcarrier index, ranging from 0 to ,
- n is the time-domain sample index, ranging from 0 to .
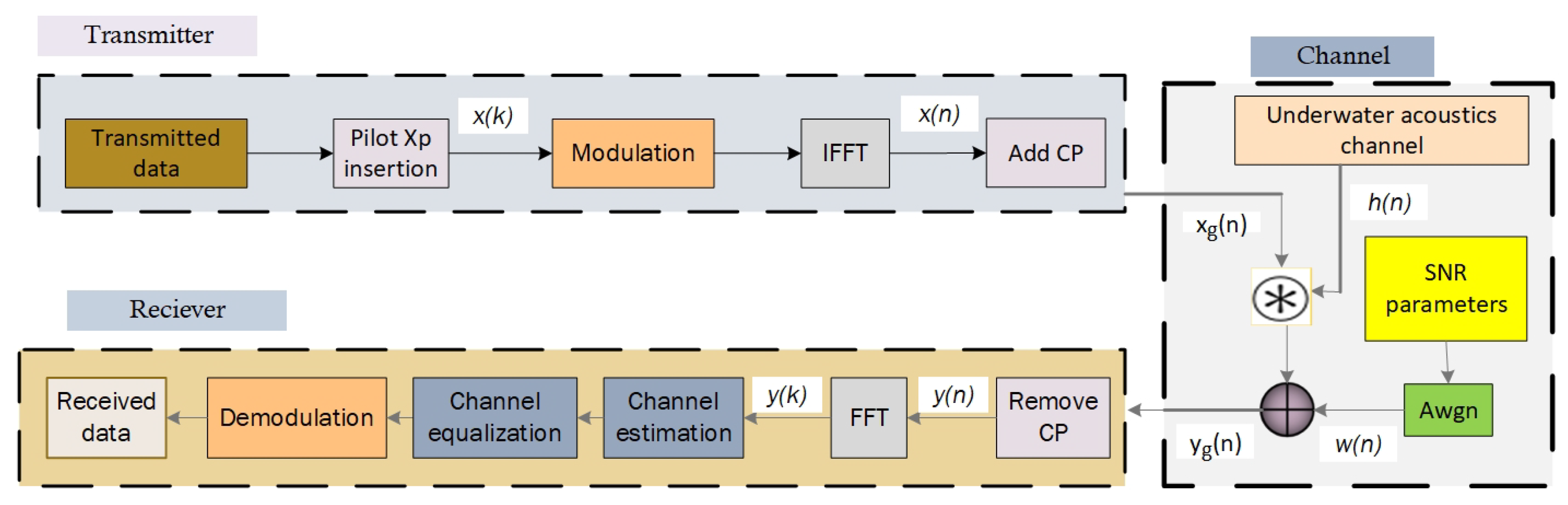
2.2. Deep Learning UWA OFDM Communication System Methods
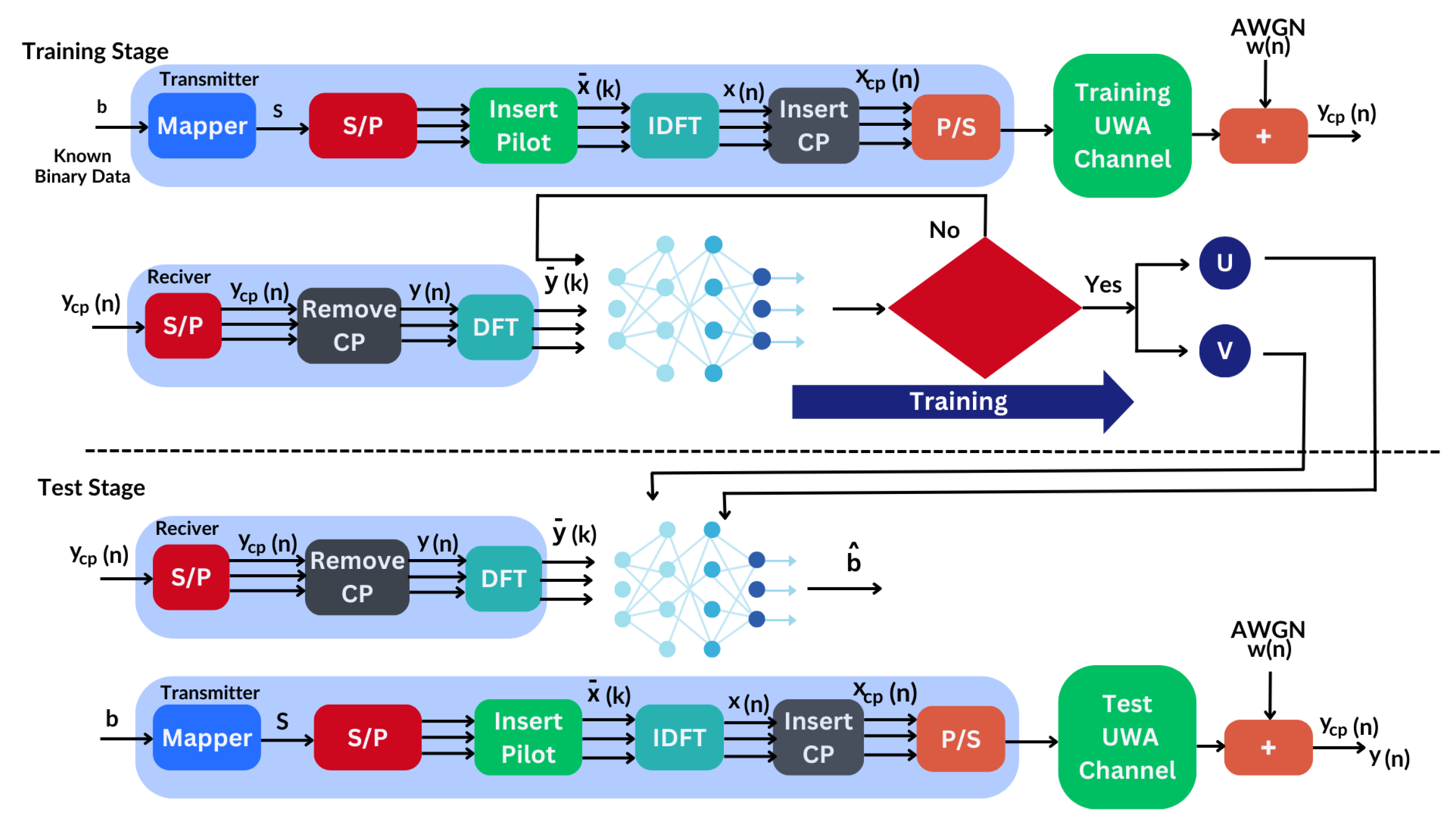
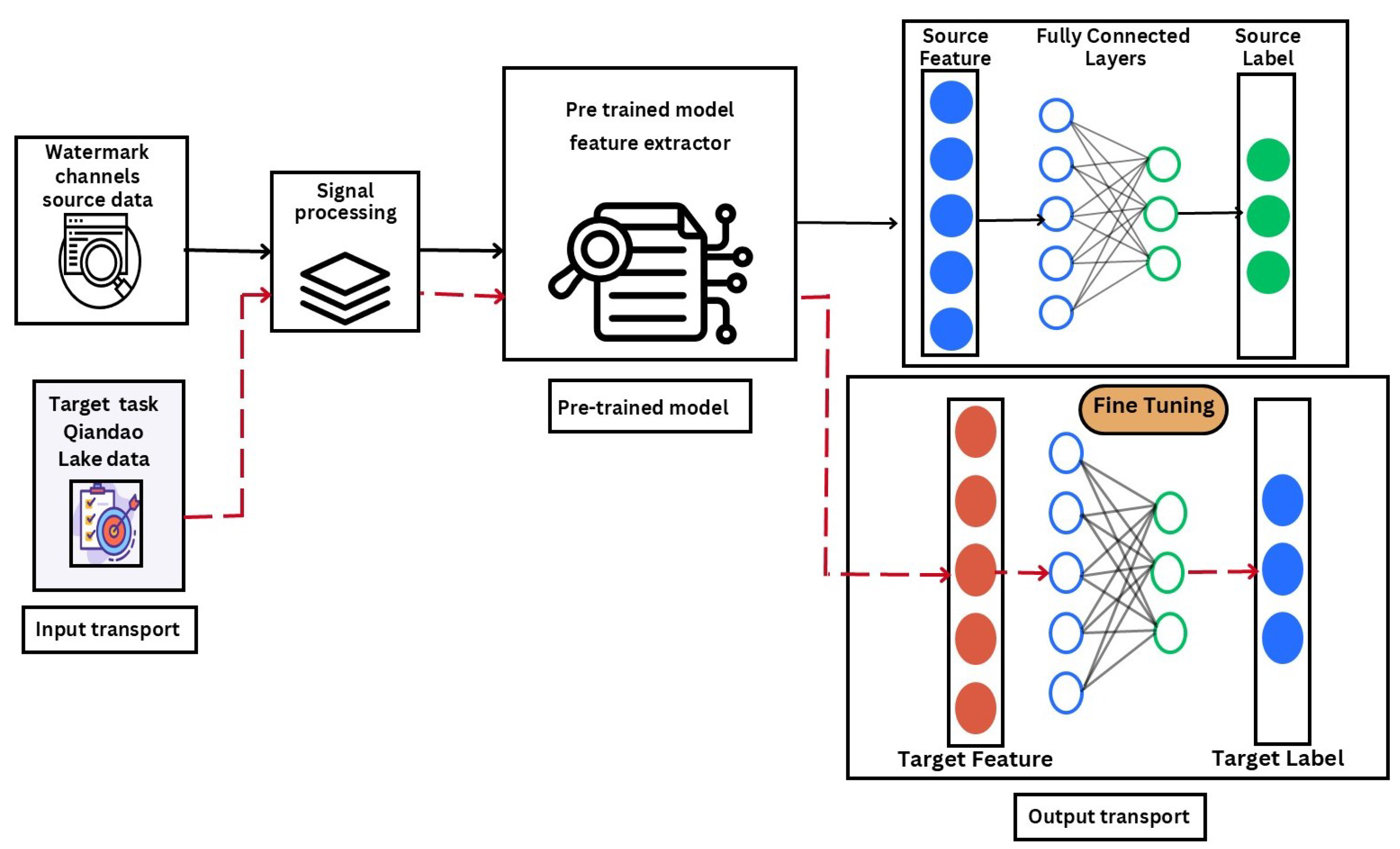
3. Proposed TL-Based UWA OFDM Receiver
3.1. Pre-Trained Model
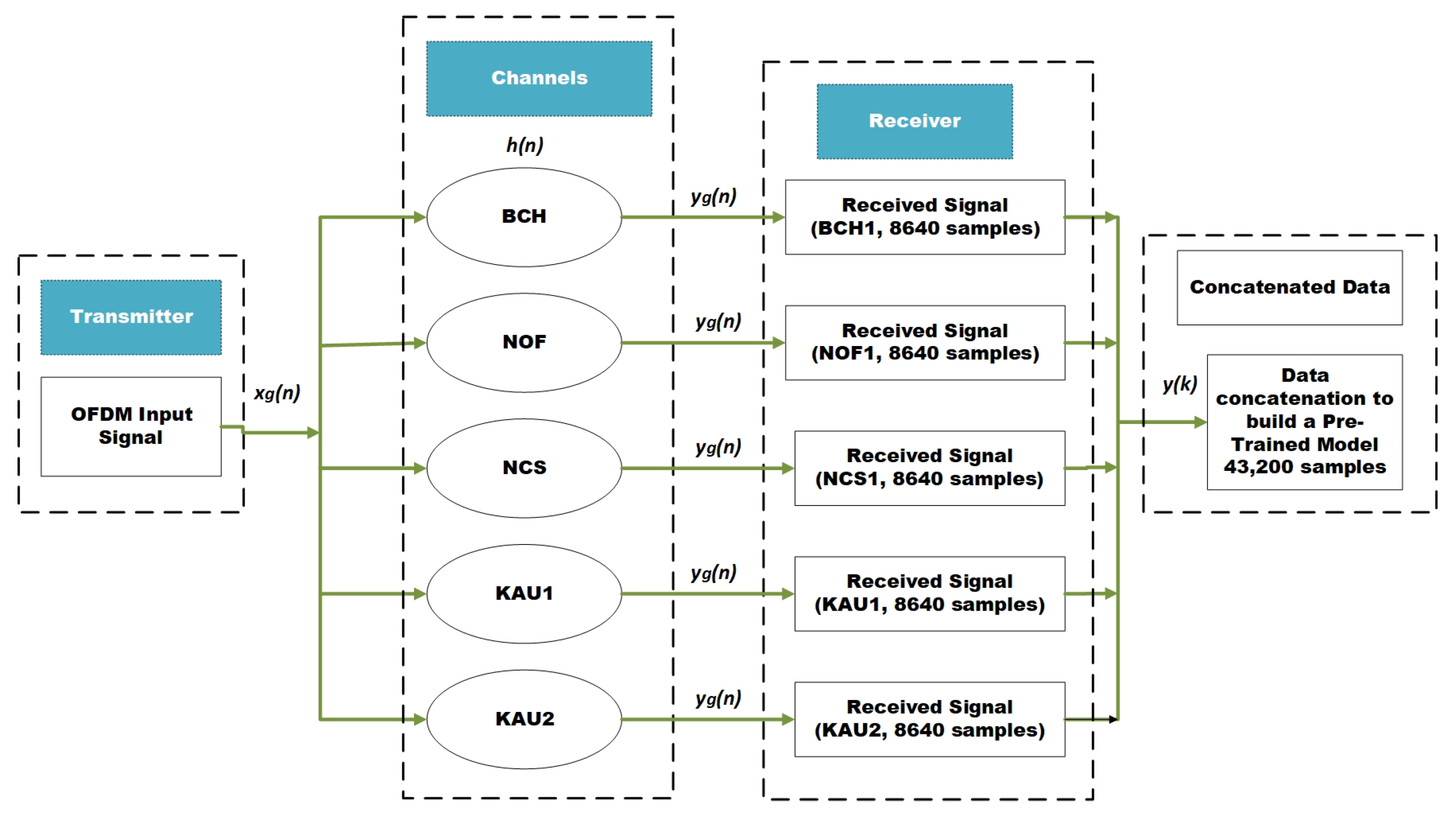
3.1.1. Data Collection and Training
3.1.2. Pre-Trained Model Architecture
3.2. Transfer Learning and Fine-Tuning
| Algorithm 1 Transfer Learning-based Channel OFDM receiver for UWA Communication |
|
- Dataset preparation: The dataset is split into training and testing sets.
- Freezing convolutional layers: The feature extraction layers, initialized with , remain fixed, while only the fully connected layers are updated.
4. Experimental Setup
4.1. OFDM Setup
4.2. Channel Setup
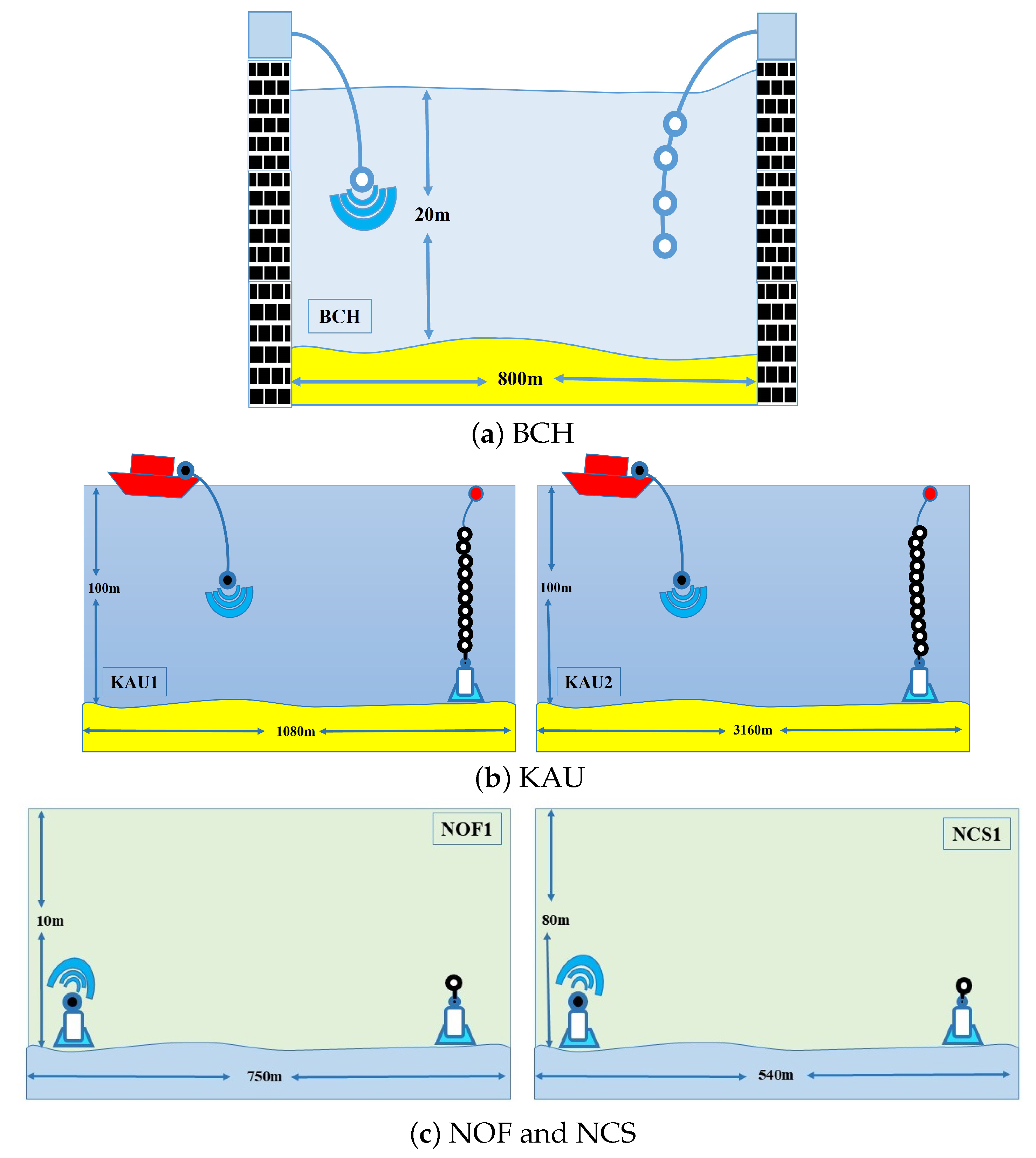
4.2.1. Watermark Channel Setup
4.2.2. Target Channel Setup
4.3. Hardware Implementation of Proposed Scheme
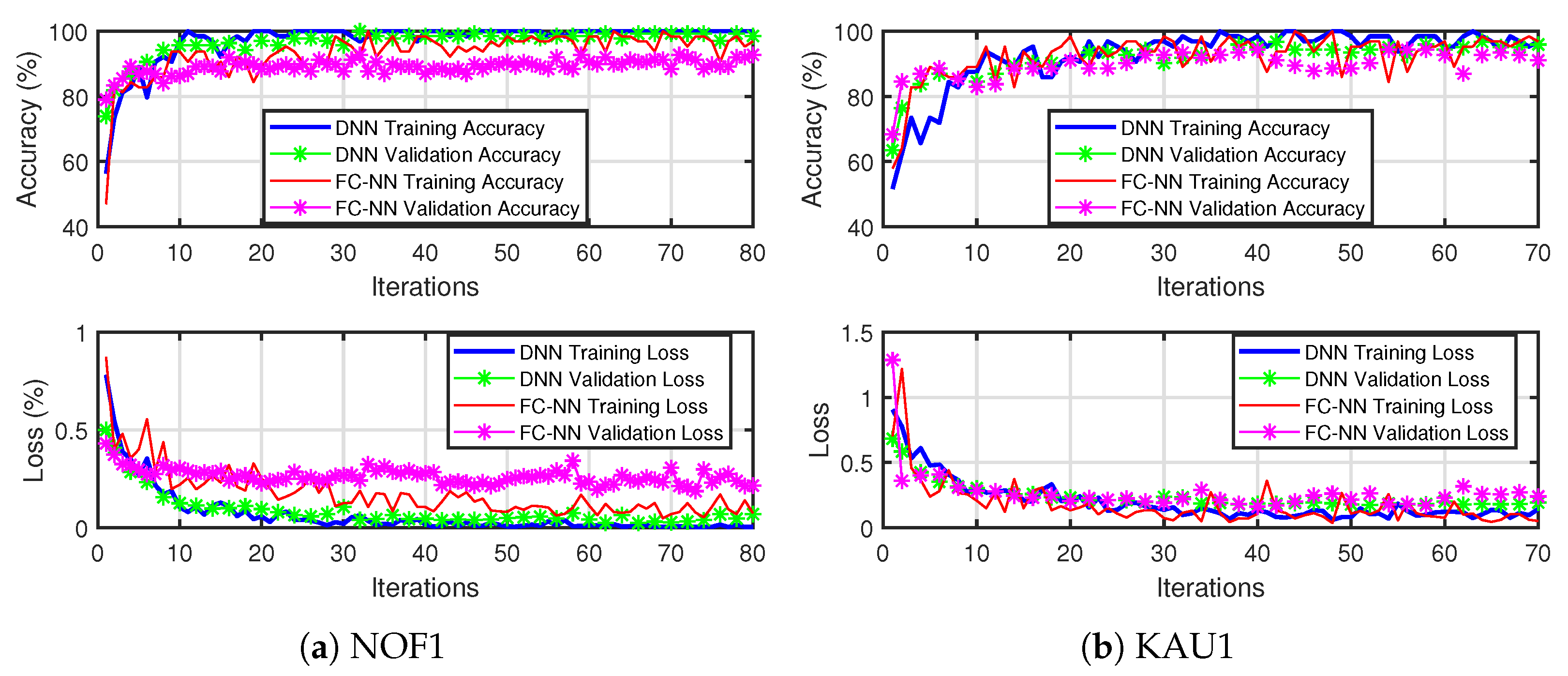
4.4. Proposed Model Training Setup
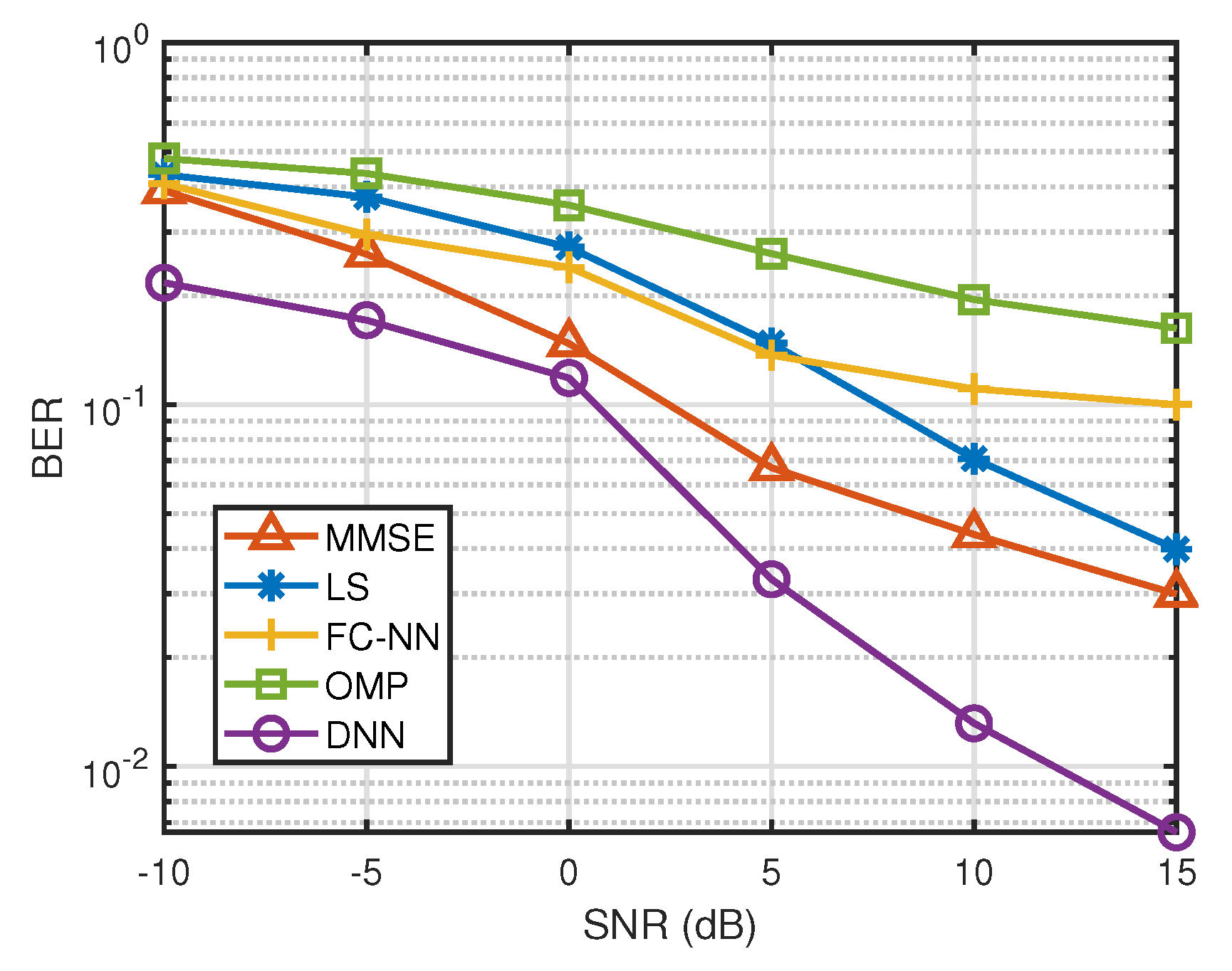
4.5. Benchmark Methods
4.5.1. Least Square
4.5.2. MMSE Estimator
4.5.3. FC-NN
4.5.4. OMP
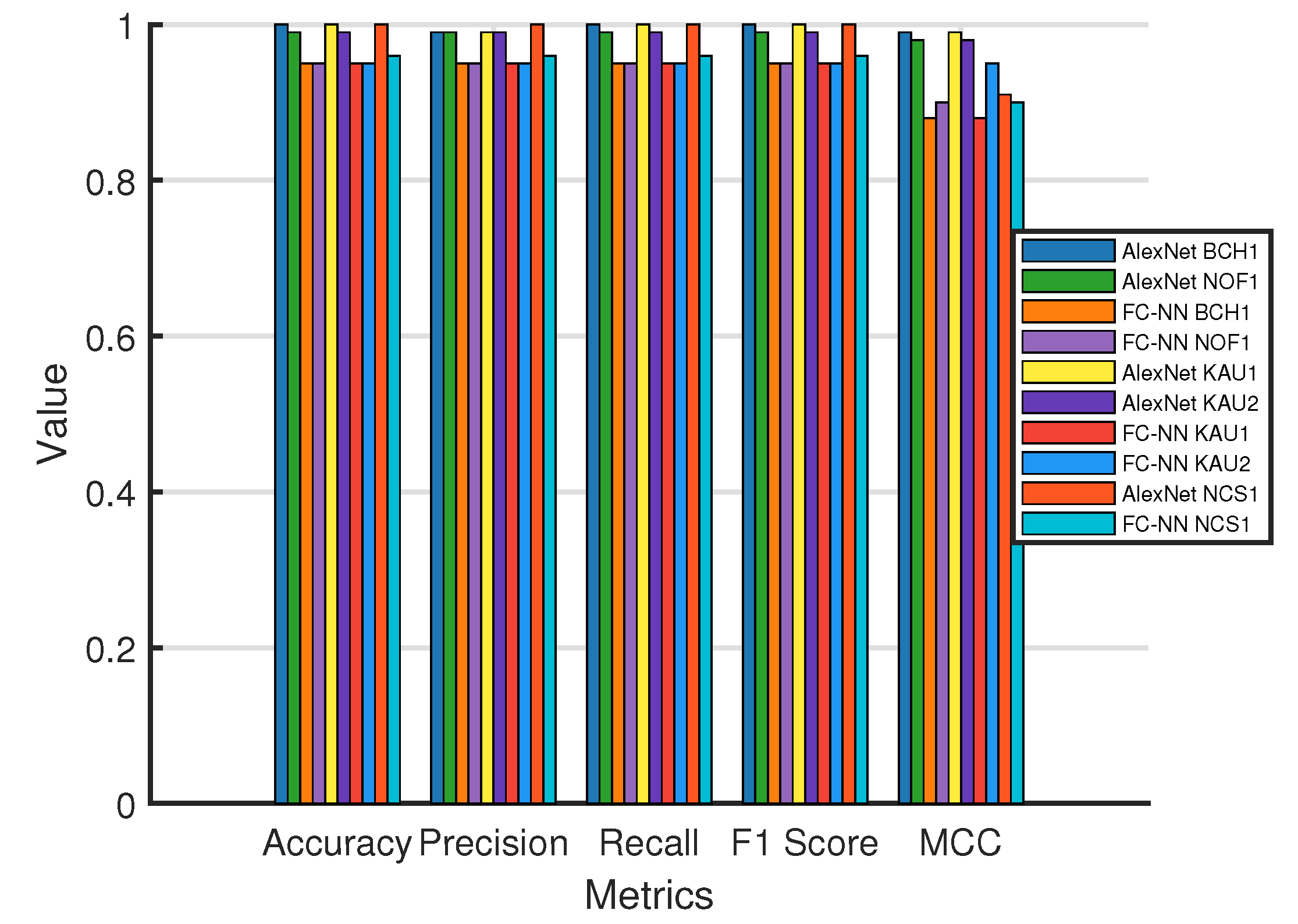
4.6. Performance Validation Metrics
5. Simulation and Experimental Results
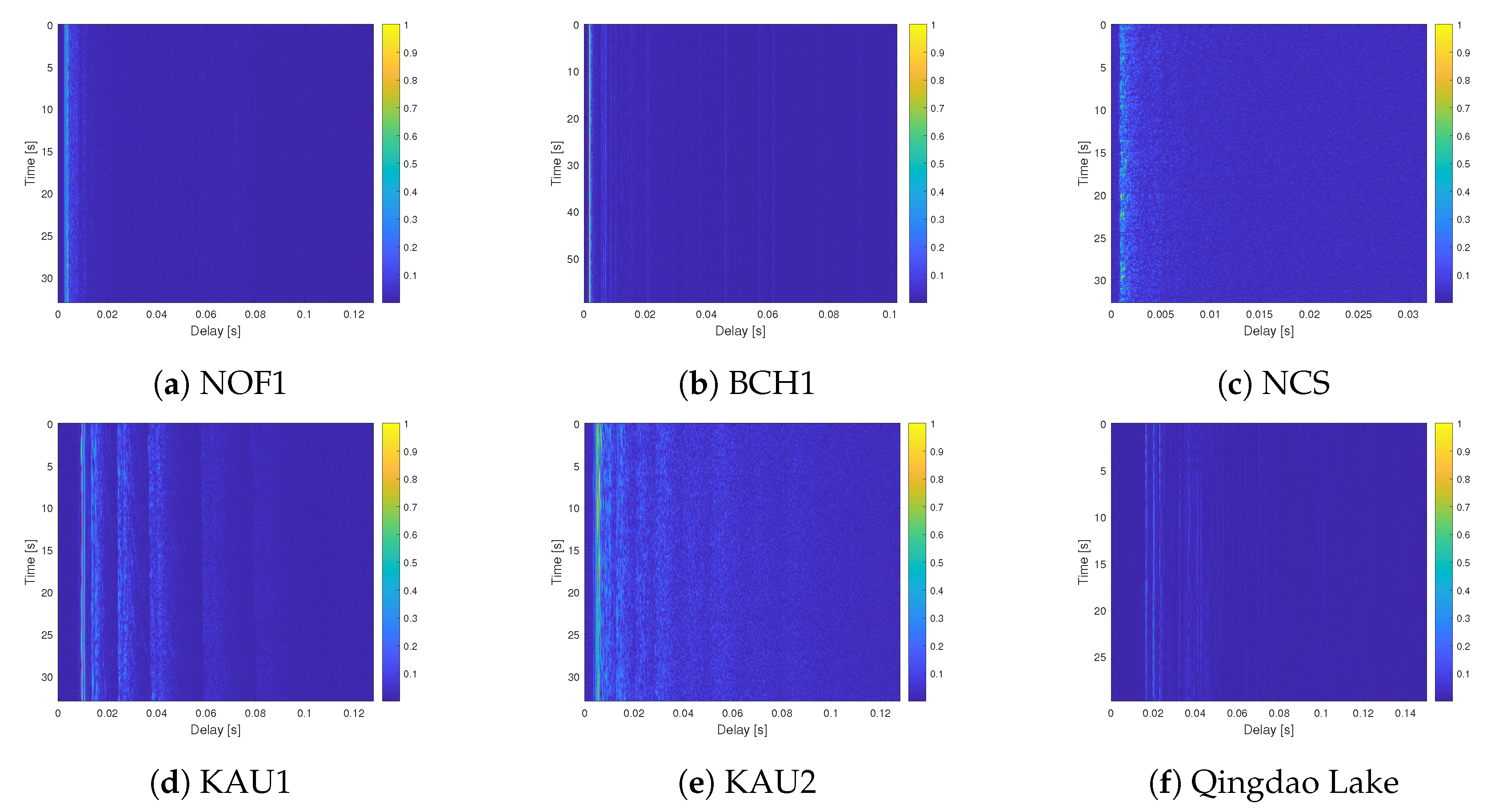
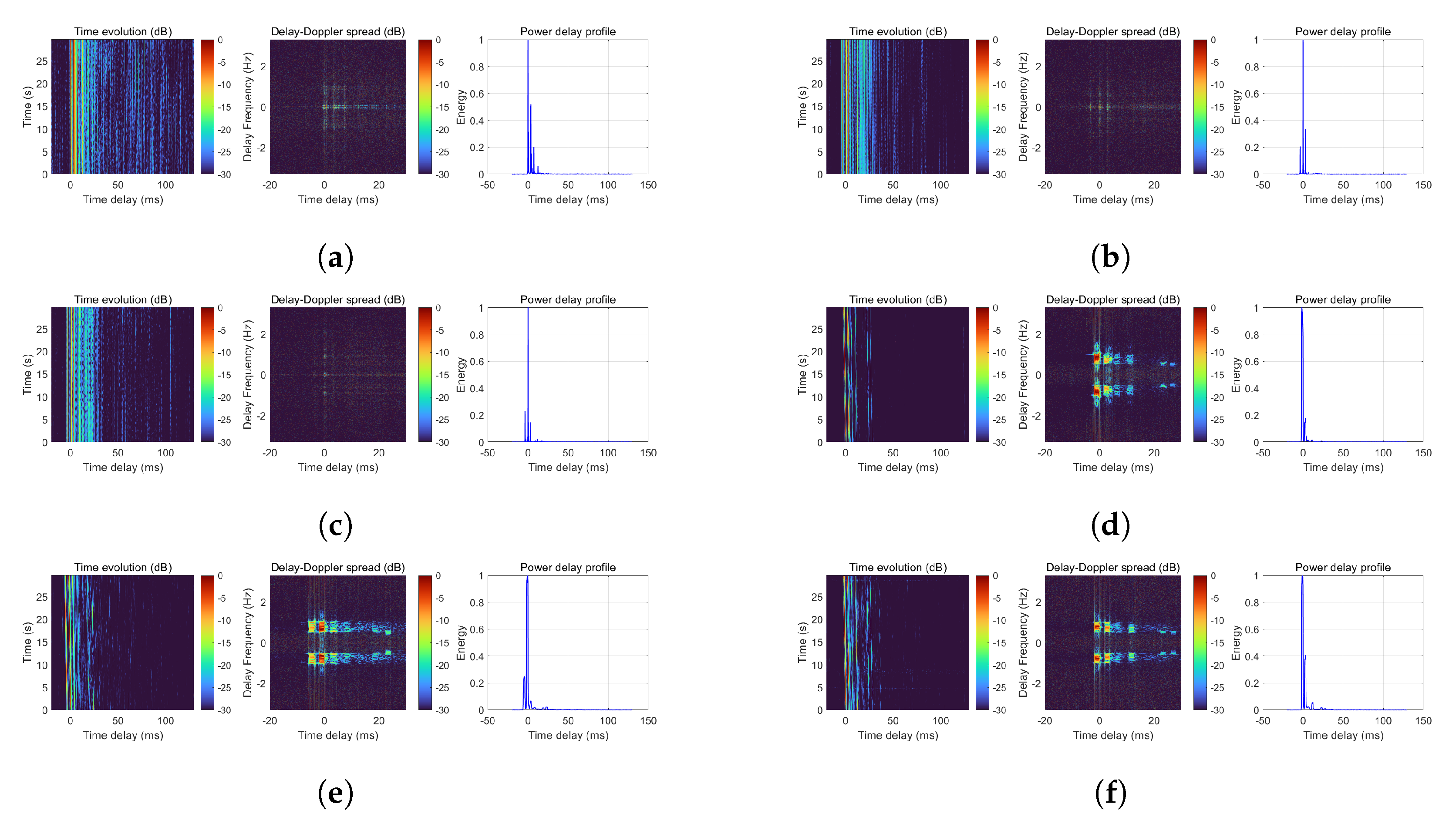
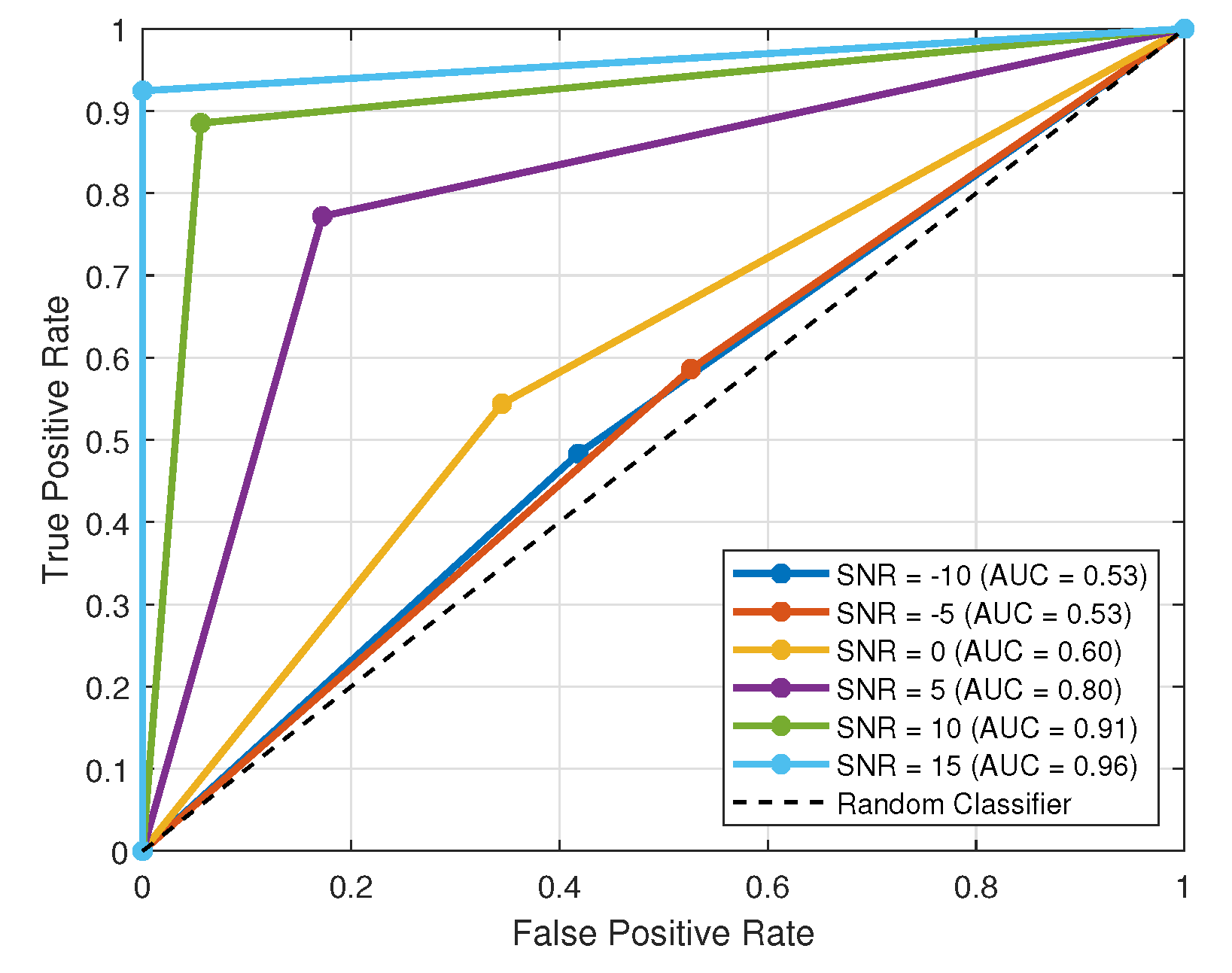
5.1. Average Fade Rating Analysis of Watermark Channels and Impact on OFDM Receiver
- is the power of the random component .
- is the power of the total channel .
- is the power deterministic or trend component . Since the channel tap is modeled as the sum of the trend component and the random component , the total power of the channel tap can be approximately decomposed as: ≈ + .
- N is the total number of samples.
- I is the number of channel taps.
5.2. Deep Learning-Based OFDM Receiver, When Trained and Tested on the Same Channel (Where Each Channel Is Split into Training and Testing Sets)
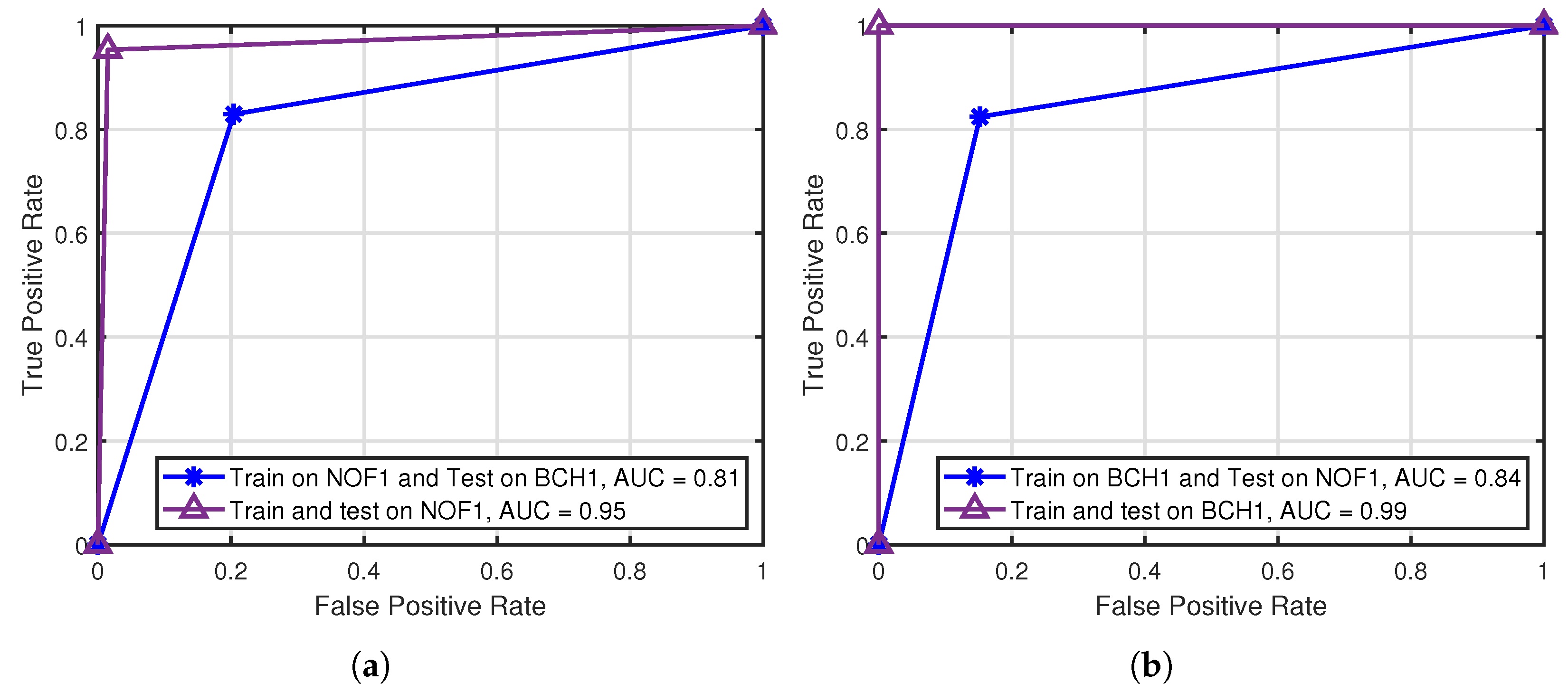
5.3. Robustness Analysis Under UWA Environment Mismatches
5.4. Pre-Trained Model Analysis
5.5. Transfer Learning Model Performance on Qingdao Lake Data
5.5.1. Comparative Study with and Without Transfer Learning
5.5.2. Comparative Study of Transfer Learning on Target Data
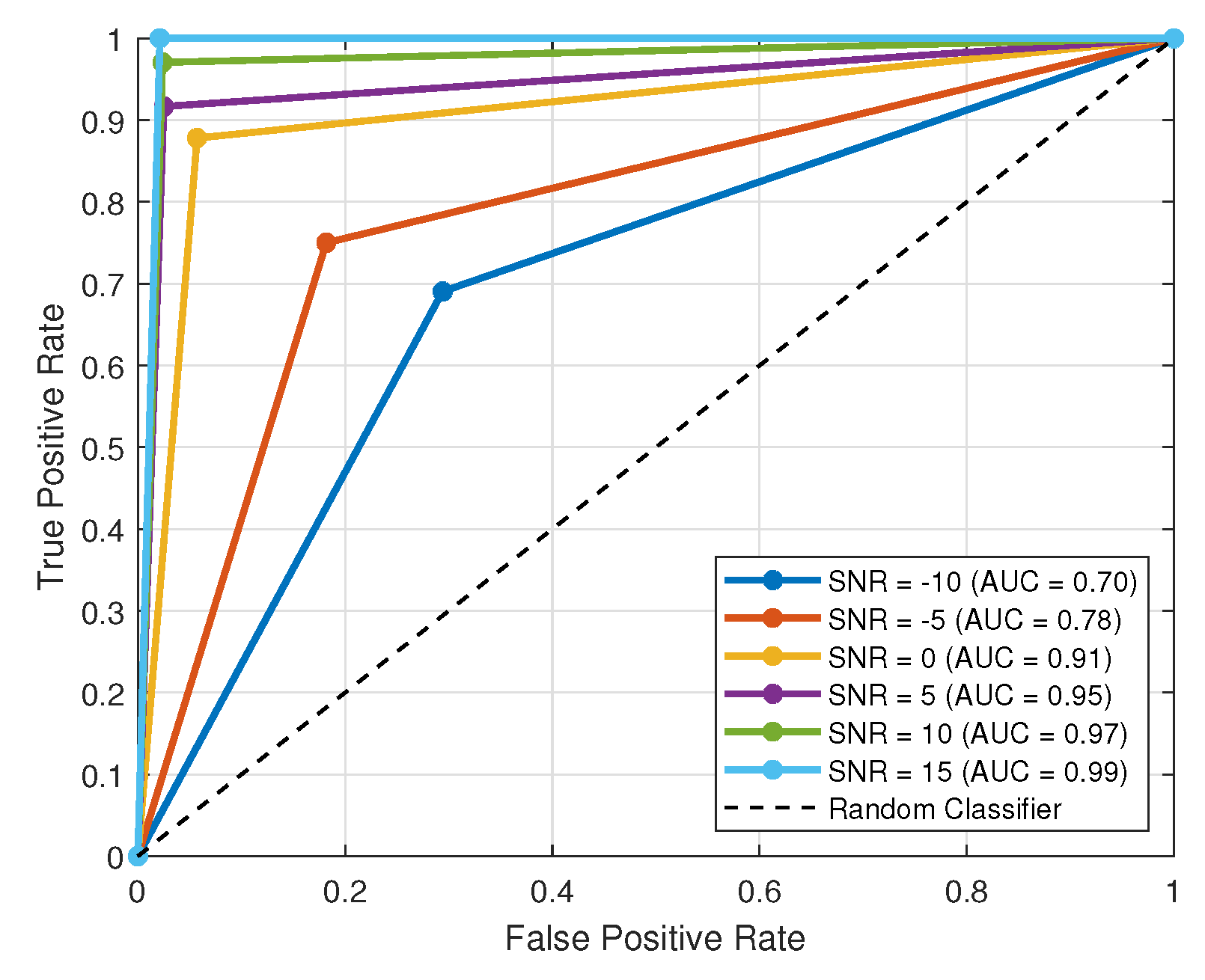
5.5.3. Evaluation of the Proposed Transfer Learning Model with BER Performance in an Extended Range of SNR
5.6. Computational Complexity Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, Z.; Chitre, M.; Stojanovic, M. Underwater acoustic communications. Nat. Rev. Electr. Eng. 2024, 2, 83–95. [Google Scholar] [CrossRef]
- Men, W.; Wang, J.; Dong, B.; Hou, X.; Jiang, C.; Ren, Y. OFDM-Based Underwater Integrated Sensing and Communication: Receiver Design for Doubly Spread Acoustic Channels. IEEE Trans. Commun. 2025. [Google Scholar] [CrossRef]
- Wan, L.; Deng, S.; Chen, Y.; Cheng, E. Sparse channel estimation for underwater acoustic OFDM systems with super-nested pilot design. Signal Process. 2025, 227, 109709. [Google Scholar] [CrossRef]
- Zhou, M.; Sun, H.; Wang, J.; Xie, Z.; Feng, X. Channel Estimation for Underwater Acoustic OFDM Communications: Recent Advances. Recent Patents Eng. 2025, 19, E050723218434. [Google Scholar] [CrossRef]
- Feng, X.; Wang, J.; Sun, H.; Qi, J.; Qasem, Z.A.H.; Cui, Y. Channel estimation for underwater acoustic OFDM communications via temporal sparse Bayesian learning. Signal Process. 2023, 207, 108951. [Google Scholar] [CrossRef]
- Tian, T.; Yang, K.; Wu, F.-Y.; Zhang, Y. Channel estimation for underwater acoustic communications in impulsive noise environments: A sparse, robust, and efficient alternating direction method of multipliers-based approach. Remote Sens. 2024, 16, 1380. [Google Scholar] [CrossRef]
- Manasa, B.M.R.; Venugopal, P. A systematic literature review on channel estimation in MIMO-OFDM system: Performance analysis and future direction. J. Opt. Commun. 2024, 45, 589–614. [Google Scholar] [CrossRef]
- Junejo, N.U.R.; Sattar, M.; Adnan, S.; Sun, H.; Adam, A.B.M.; Hassan, A.; Esmaiel, H. A survey on physical layer techniques and challenges in underwater communication systems. J. Mar. Sci. Eng. 2023, 11, 885. [Google Scholar] [CrossRef]
- Farzamnia, A.; Hlaing, N.W.; Haldar, M.K.; Rahebi, J. Channel estimation for sparse channel OFDM systems using least square and minimum mean square error techniques. In Proceedings of the International Conference on Engineering and Technology (ICET), Antalya, Turkey, 21–23 August 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Kumar, A. A new optimized least-square sparse channel estimation scheme for underwater acoustic communication. Int. J. Commun. Syst. 2023, 36, e5436. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, P. An improved sparsity-aware normalized least-mean-square scheme for underwater communication. Etri J. 2023, 45, 379–393. [Google Scholar] [CrossRef]
- Alraie, H.; Ishii, K. Channel estimation using pilot-assisted OFDM for underwater acoustic communication. J. Robot. Netw. Artif. Life 2023, 10, 160–165. [Google Scholar] [CrossRef]
- Chen, P.; Rong, Y.; Nordholm, S.; He, Z. Joint channel and impulsive noise estimation in underwater acoustic OFDM systems. IEEE Trans. Veh. Technol. 2017, 66, 10567–10571. [Google Scholar] [CrossRef]
- Liu, D.N.; Yerramalli, S.; Mitra, U. On efficient channel estimation for underwater acoustic OFDM systems. In Proceedings of the 4th International Workshop Underwater Acoustic Digital Signal Processing, Berkeley, CA, USA, 3 November 2009; Volume 16, no. 1, pp. 4–10. [Google Scholar] [CrossRef]
- Jiang, W.; Diamant, R. Long-range underwater acoustic channel estimation. IEEE Trans. Wirel. Commun. 2023, 22, 6267–6282. [Google Scholar] [CrossRef]
- Murad, M.; Tasadduq, I.A.; Otero, P. Pilots based LSE channel estimation for underwater acoustic OFDM communication. In Proceedings of the 2020 Global Conference on Wireless and Optical Technologies (GCWOT), Malaga, Spain, 6–8 October 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Tian, T.; Wu, F.-Y.; Yang, K. Estimation of underwater acoustic channel via block-sparse recursive least-squares algorithm. In Proceedings of the 2019 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Dalian, China, 20–22 September 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Junejo, N.U.R.; Esmaiel, H.; Sun, H.; Qasem, Z.A.H.; Wang, J. Pilot-based adaptive channel estimation for underwater spatial modulation technologies. Symmetry 2019, 11, 711. [Google Scholar] [CrossRef]
- Song, S.; Lim, J.-S.; Baek, S.J.; Sung, K.M. Variable forgetting factor linear least squares algorithm for frequency selective fading channel estimation. IEEE Trans. Veh. Technol. 2002, 51, 613–616. [Google Scholar] [CrossRef]
- Qiao, G.; Babar, Z.; Ma, L.; Liu, S.; Wu, J. MIMO-OFDM underwater acoustic communication systems—A review. Phys. Commun. 2017, 23, 56–64. [Google Scholar] [CrossRef]
- Ma, X.-F.; Zhao, C.-H.; Qiao, G. The underwater acoustic OFDM channel estimation based on wavelet and MMSE. In Proceedings of the 2009 WRI International Conference on Communications and Mobile Computing, Kunming, China, 6–8 January 2009; IEEE: Piscataway, NJ, USA, 2009; Volume 2, pp. 573–577. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, J.; Zakharov, Y.; Li, X.; Li, J. Deep learning-based underwater acoustic OFDM communications. Appl. Acoust. 2019, 154, 53–58. [Google Scholar] [CrossRef]
- Jiang, R.; Wang, X.; Cao, S.; Zhao, J.; Li, X. Deep neural networks for channel estimation in underwater acoustic OFDM systems. IEEE Access 2019, 7, 23579–23594. [Google Scholar] [CrossRef]
- Liu, S.; Adil, M.; Ma, L.; Mazhar, S.; Qiao, G. DenseNet-Based Robust Channel Estimation in OFDM for Improving Underwater Acoustic Communication. IEEE J. Ocean. Eng. 2025, 50, 1518–1537. [Google Scholar] [CrossRef]
- Xu, W.; Zhong, Z.; Be’ery, Y.; You, X.; Zhang, C. Joint neural network equalizer and decoder. In Proceedings of the 2018 15th International Symposium on Wireless Communication Systems (ISWCS), Lisbon, Portugal, 28–31 August 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–5. [Google Scholar]
- Zhang, Y.; Li, C.; Wang, H.; Wang, J.; Yang, F.; Meriaudeau, F. Deep learning aided OFDM receiver for underwater acoustic communications. Appl. Acoust. 2022, 187, 108515. [Google Scholar] [CrossRef]
- Liu, S.; Yan, H.; Ma, L.; Liu, Y.; Han, X. UACC-GAN: A Stochastic Channel Simulator for Underwater Acoustic Communication. IEEE J. Ocean. Eng. 2024, 49, 1605–1621. [Google Scholar] [CrossRef]
- Zhang, Y.; Chang, J.; Liu, Y.; Xing, L.; Shen, X. Deep learning and expert knowledge-based underwater acoustic OFDM receiver. Phys. Commun. 2023, 58, 102041. [Google Scholar] [CrossRef]
- Zhang, J.; Cao, Y.; Han, G.; Fu, X. Deep neural network-based underwater OFDM receiver. IET Commun. 2019, 13, 1998–2002. [Google Scholar] [CrossRef]
- Hassan, S.; Chen, P.; Rong, Y.; Chan, K.Y. Underwater acoustic OFDM receiver using a regression-based deep neural network. In Proceedings of the OCEANS 2022, Hampton Roads, VA, USA, 17–20 October 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar]
- Wang, Z.; Liu, L.; Cheng, Z.; Wang, J. Intelligent Receiver Design for Underwater Acoustic OFDM Communication Based on LSTM Networks. In Proceedings of the 2023 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Zhengzhou, China, 14–17 November 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar]
- Guo, J.; Guo, T.; Li, M.; Wu, T.; Lin, H. Underwater-Acoustic-OFDM Channel Estimation Based on Deep Learning and Data Augmentation. Electronics 2024, 13, 689. [Google Scholar] [CrossRef]
- Jiang, P.; Wang, T.; Han, B.; Gao, X.; Zhang, J.; Wen, C.-K.; Jin, S.; Li, G.Y. AI-aided online adaptive OFDM receiver: Design and experimental results. IEEE Trans. Wirel. Commun. 2021, 20, 7655–7668. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, J.; Zakharov, Y.; Sun, D.; Li, J. Underwater Acoustic OFDM Communications Using Deep Learning. 2018. Available online: https://eprints.soton.ac.uk/426097/1/FCAC_Deeplearning_OFDM_finally.pdf (accessed on 20 May 2025).
- Alves, W.; Correa, I.; González-Prelcic, N.; Klautau, A. Deep transfer learning for site-specific channel estimation in low-resolution mmWave MIMO. IEEE Wirel. Commun. Lett. 2021, 10, 1424–1428. [Google Scholar] [CrossRef]
- Hong, J.; Cheng, H.; Zhang, Y.D.; Liu, J. Detecting cerebral microbleeds with transfer learning. Mach. Vis. Appl. 2019, 30, 1123–1133. [Google Scholar] [CrossRef]
- Das, A.K.; Pramanik, A. A Survey Report on Underwater Acoustic Channel Estimation of MIMO-OFDM System. In Proceedings of the International Conference on Frontiers in Computing and Systems: COMSYS 2020, Jalpaiguri, India, 13–15 January 2020; Springer: Singapore, 2021; pp. 745–753. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, Y.; Zhang, P.; Zhou, L.; Li, J.; Jin, J.; Zhang, J.; Lv, Z. PN sequence based doppler and channel estimation for underwater acoustic OFDM communication. In Proceedings of the 2016 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Hong Kong, China, 5–8 August 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Jan, M.; Mazhar, S.; Adil, M.; Muhammad, A.; Gang, Q. Integration of Deep Neural Networks and Local mean decomposition for accurate underwater acoustic channel estimation. In Proceedings of the 2023 20th International Bhurban Conference on Applied Sciences and Technology (IBCAST), Bhurban, Murree, Pakistan, 22–25 August 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 866–871. [Google Scholar]
- Liu, H.; Ma, L.; Wang, Z.; Qiao, G. Channel prediction for underwater acoustic communication: A review and performance evaluation of algorithms. Remote Sens. 2024, 16, 1546. [Google Scholar] [CrossRef]
- Adil, M.; Liu, S.; Mazhar, S.; Jan, M.; Khan, A.Y.; Bilal, M. A Fully Connected Neural Network Driven UWA Channel Estimation for Reliable Communication. In Proceedings of the 2023 International Conference on Frontiers of Information Technology (FIT), Islamabad, Pakistan, 11–12 December 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 310–315. [Google Scholar]
- van Walree, P.A.; Socheleau, F.-X.; Otnes, R.; Jenserud, T. The watermark benchmark for underwater acoustic modulation schemes. IEEE J. Ocean. Eng. 2017, 42, 1007–1018. [Google Scholar] [CrossRef]
- Cho, Y.S.; Kim, J.; Yang, W.Y.; Kang, C.G. MIMO-OFDM Wireless Communications with MATLAB; John Wiley and Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Zhang, Y.; Wang, H.; Li, C.; Meriaudeau, F. Data augmentation aided complex-valued network for channel estimation in underwater acoustic orthogonal frequency division multiplexing system. J. Acoust. Soc. Am. 2022, 151, 4150–4164. [Google Scholar] [CrossRef]
- Hossin, M.; Sulaiman, M.N. A review on evaluation metrics for data classification evaluations. Data Min. Knowl. Manag. Process 2015, 5, 1–13. [Google Scholar] [CrossRef]
- Miao, J.; Zhu, W. Precision–recall curve (PRC) classification trees. Evol. Intell. 2022, 15, 1545–1569. [Google Scholar] [CrossRef]
- Yacouby, R.; Axman, D. Probabilistic extension of precision, recall, and F1 score for more thorough evaluation of classification models. In Proceedings of the First Workshop on Evaluation and Comparison of NLP Systems, Online, 20 November 2020; pp. 79–91. [Google Scholar] [CrossRef]
- Powers, D.M. Evaluation: From precision, recall and F-measure to ROC, informedness, markedness and correlation. arXiv 2020, arXiv:2010.16061. [Google Scholar] [CrossRef]
- Chicco, D.; Jurman, G. The Matthews correlation coefficient (MCC) should replace the ROC AUC as the standard metric for assessing binary classification. BioData Min. 2023, 16, 4–10. [Google Scholar] [CrossRef] [PubMed]
- Cao, C.; Chicco, D.; Hoffman, M.M. The MCC-F1 curve: A performance evaluation technique for binary classification. arXiv 2020, arXiv:2006.11278. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, H.; Li, C.; Chen, X.; Meriaudeau, F. On the performance of deep neural network aided channel estimation for underwater acoustic OFDM communications. Ocean Eng. 2022, 259, 111518. [Google Scholar] [CrossRef]






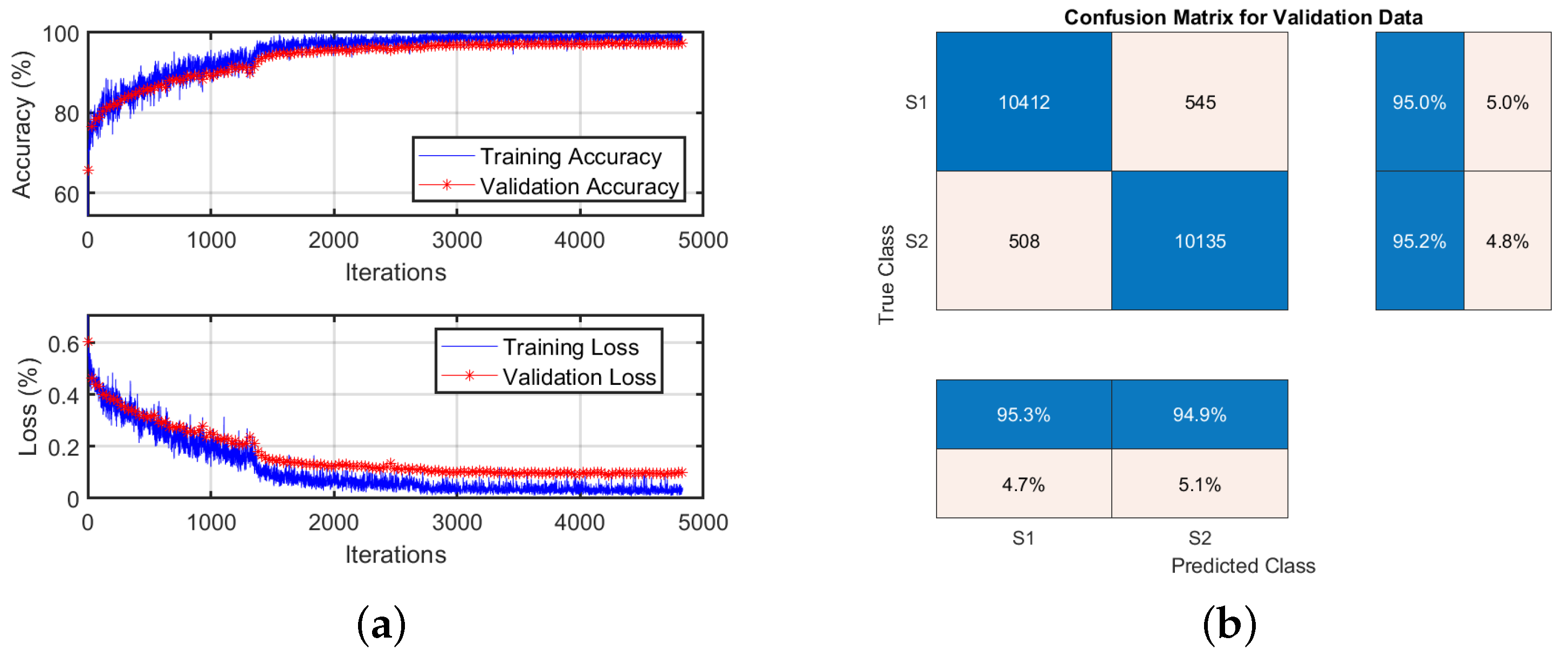


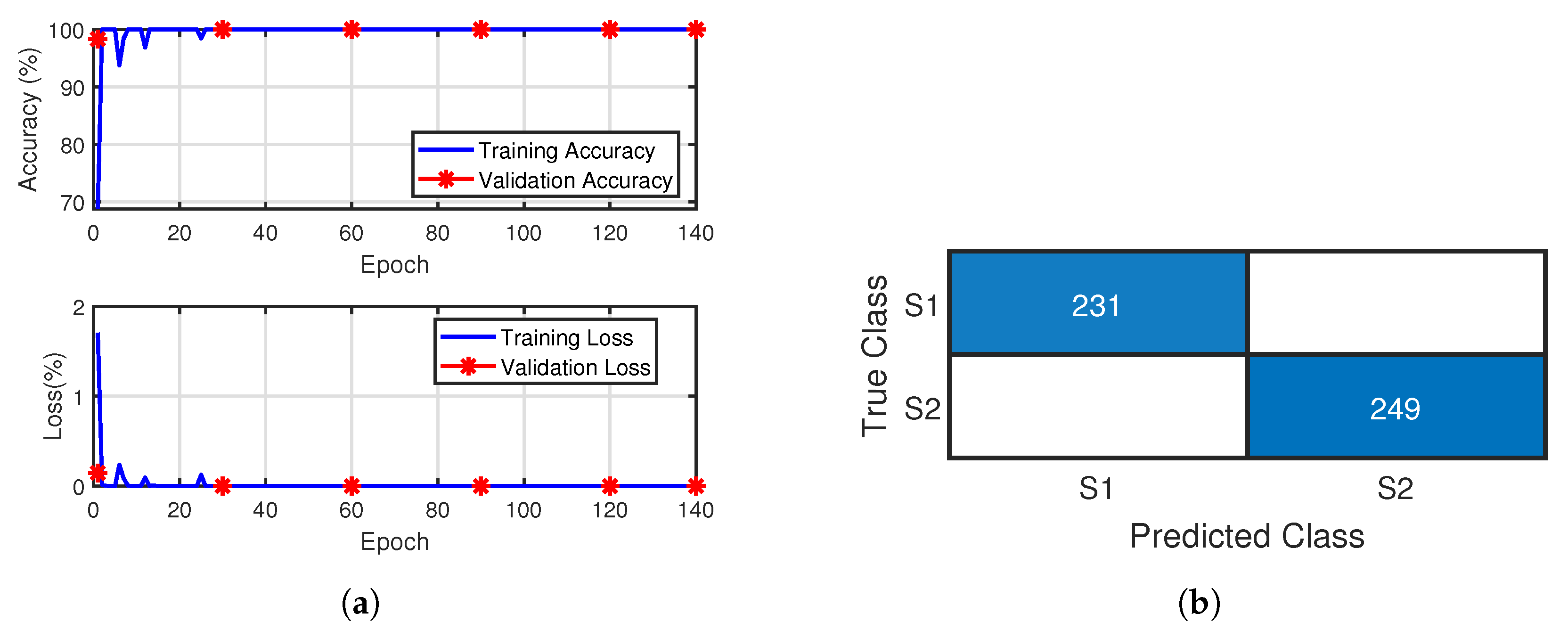
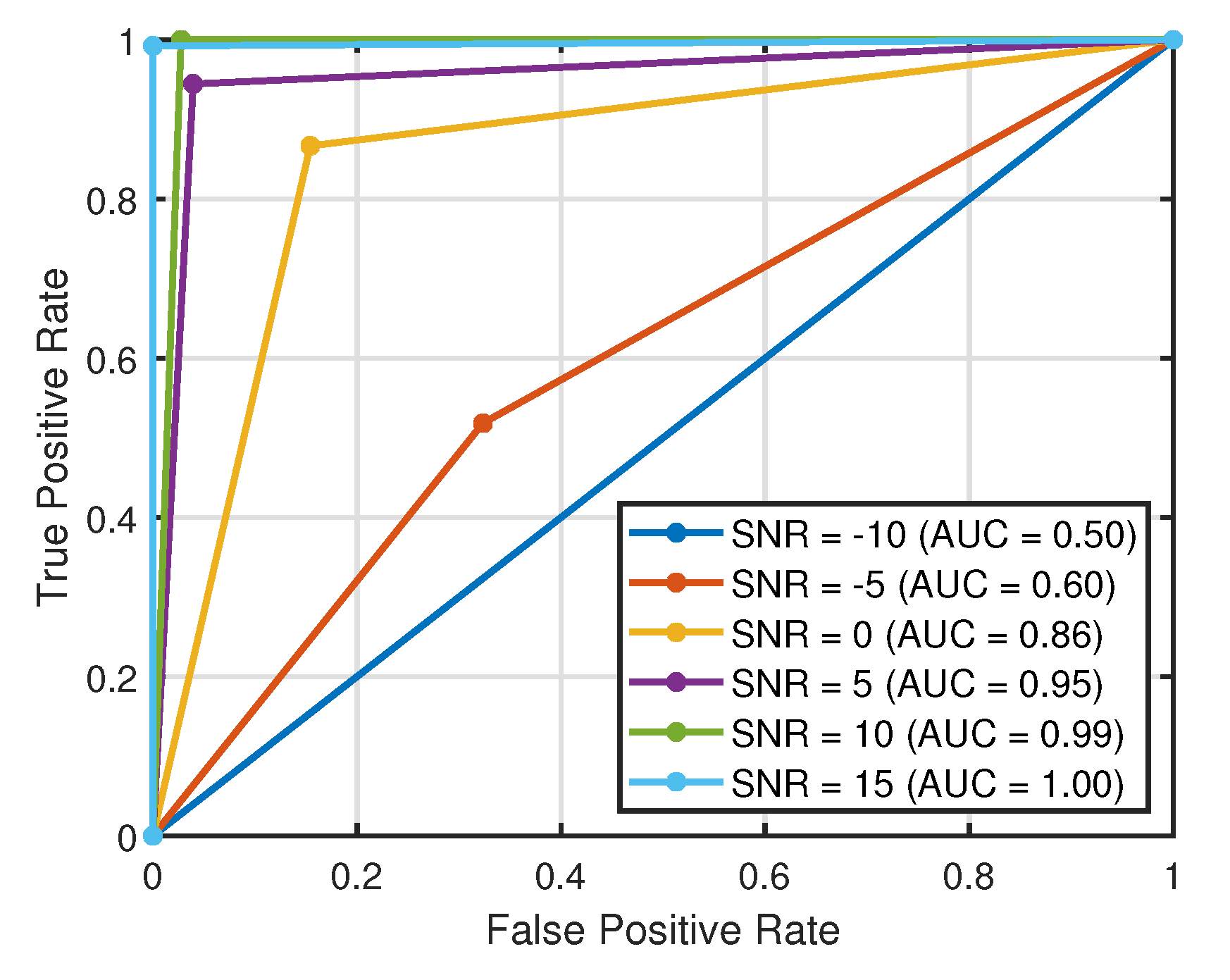
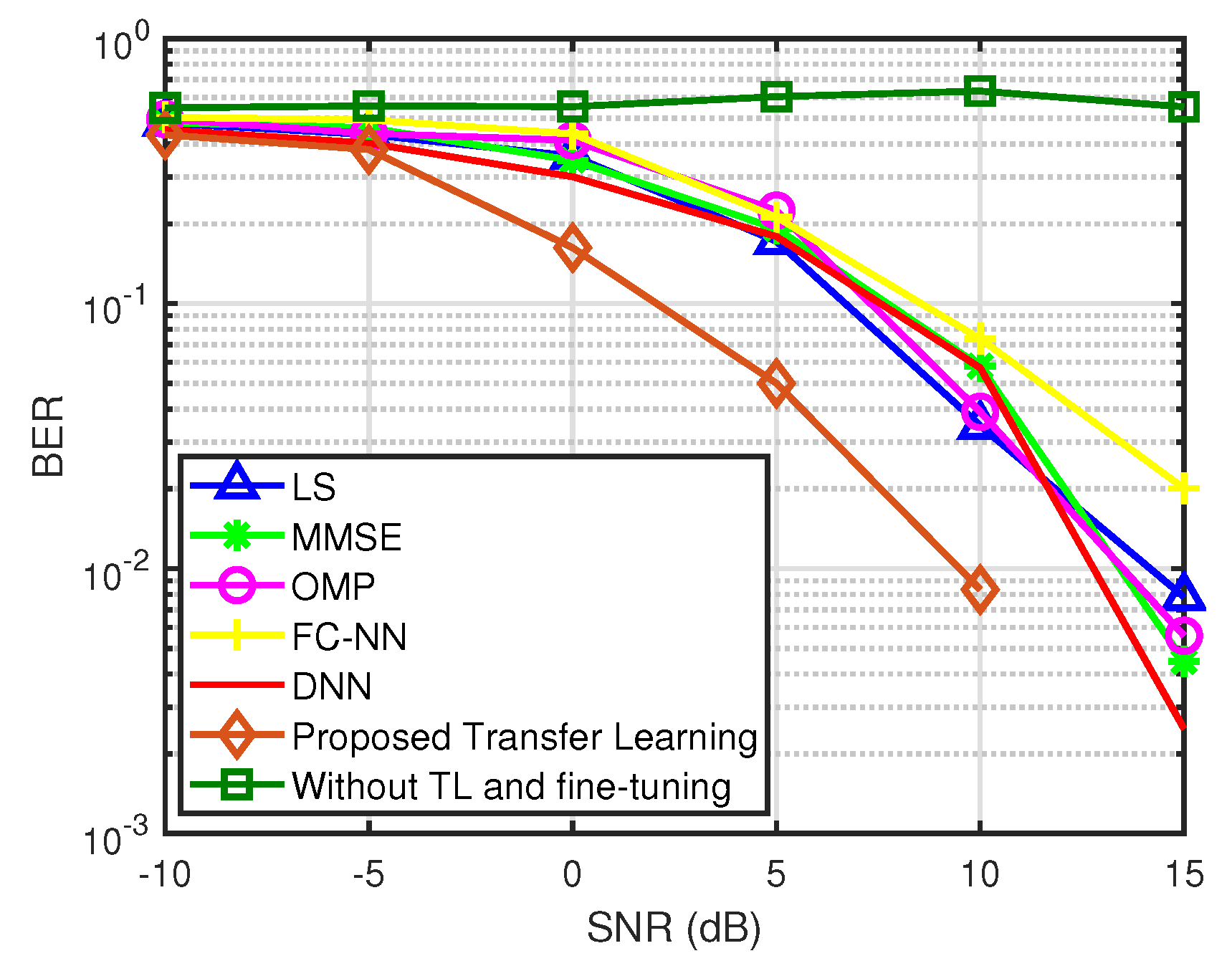
| Layer Type | Layer Name | Details |
|---|---|---|
| Input Layer | input | Input size: [1, Nt × 2, 1] where Nt = 46. |
| Convolutional Layer 1 | conv1 | Kernel: , Filters: 8, Stride: 10. |
| Activation Layer | relu1.1 | ReLU activation after conv1. |
| Convolutional Layer 2 | conv2 | Kernel: , Filters: 16. |
| Activation Layer | relu2.1 | ReLU activation after conv2. |
| Convolutional Layer 3 | conv3 | Kernel: , Filters: 16. |
| Activation Layer | relu3.1 | ReLU activation after conv3. |
| Convolutional Layer 4 | conv4 | Kernel: , Filters: 32. |
| Activation Layer | relu4.1 | ReLU activation after conv4. |
| Convolutional Layer 5 | conv5 | Kernel: , Filters: 32. |
| Activation Layer | relu5.1 | ReLU activation after conv5. |
| Fully Connected Layer 1 | fc1 | Units: 64, L2 regularization applied. |
| Batch Normalization Layer | bn1.1 | Batch normalization for fc1. |
| Activation Layer | relu1.2 | ReLU activation after fc1. |
| Dropout Layer | dropout1 | Dropout rate: 0.2. |
| Fully Connected Layer 2 | fc2 | Units: 32, L2 regularization applied. |
| Batch Normalization Layer | bn2.1 | Batch normalization for fc2. |
| Activation Layer | relu2.2 | ReLU activation after fc2. |
| Dropout Layer | dropout2 | Dropout rate: 0.2. |
| Fully Connected Layer 3 | fc3 | Units: 32, L2 regularization applied. |
| Activation Layer | relu3.2 | ReLU activation after fc3. |
| Dropout Layer | dropout3 | Dropout rate: 0.2. |
| Fully Connected Layer 4 | fc4 | Units: 2 (output classes). |
| Softmax Layer | softmax | Softmax activation for classification output. |
| Classification Layer | output | Categorical classification layer. |
| Layer Type | Layer Names | Freezing Details |
|---|---|---|
| Convolutional Layers | conv1 to conv5 | Weights and biases frozen during fine-tuning |
| Fully Connected Layers | fc1 to fc4 | Trainable for adaptation to the target dataset |
| Training Type | Dataset Used | Max Epochs | Initial Learning Rate | Updated Layers | Frozen Layers |
|---|---|---|---|---|---|
| Pre-training | Watermark channel datasets () | 20 | All layers | None | |
| Fine-tuning | Qingdao Lake dataset () | 150 | Fully connected layers | Conv. layers |
| Parameter | Value |
|---|---|
| UWA modulation scheme | OFDM |
| Sub-carriers, N | 1024 |
| Pilots | N/4 |
| Pilot insertion | Comb |
| Guard interval | CP |
| CP size | N/4 |
| Noise model | AWGN |
| SNR | −10:5:15 dB |
| Sampling frequency | 48–96 kHz |
| Carrier frequency | 14 kHz |
| Frequency spacing | 4.88 Hz |
| OFDM symbol period | 0.204 s |
| Modulation scheme | BPSK |
| UWA channel | Watermark |
| Name | NOF1 | BCH | KAU1 | KAU2 | NCS1 |
| Environment | Fjord | Harbour | Shelf | Shelf | Shelf |
| Time of year | June | June | July | July | June |
| Range | 750 m | 800 m | 1080 m | 3160 m | 540 m |
| Water depth | 10 m | 20 m | 100 m | 100 m | 80 m |
| Transmitter depl. | Bottom | Suspended | Towed | Towed | Bottom |
| Receiver depl. | Bottom | Suspended | Suspended | Suspended | Bottom |
| Frequency range | 10–18 kHz | 32.5–37.5 kHz | 4–8 kHz | 4–8 kHz | 10–18 kHz |
| Sounding duration | 32.9 s | 59.4 s | 32.9 s | 32.9 s | 32.9 s |
| Delay coverage | 128 ms | 102 ms | 128 ms | 128 ms | 32 ms |
| Doppler coverage | 7.8 Hz | 9.8 Hz | 7.8 Hz | 7.8 Hz | 31.4 Hz |
| Type | SISO | SIMO | SIMO | SIMO | SISO |
| Element spacing | - | 1 m | 3.75 m | 3.75 m | - |
| Cycles | 60 | 1 | 1 | 1 | - |
| Total play time | 33 min | 1 min | 33 s | 33 s | 33 min |
| Parameter | Morning | Noon | Evening |
|---|---|---|---|
| Water Temperature (°C) | 9.2 | 12.5 | 10.1 |
| Salinity (ppt) | 0.12 | 0.14 | 0.13 |
| Pressure (Pa) | 32.5 | 32.2 | 32.9 |
| Wind Speed (m/s) | 3.1 | 4.2 | 3.8 |
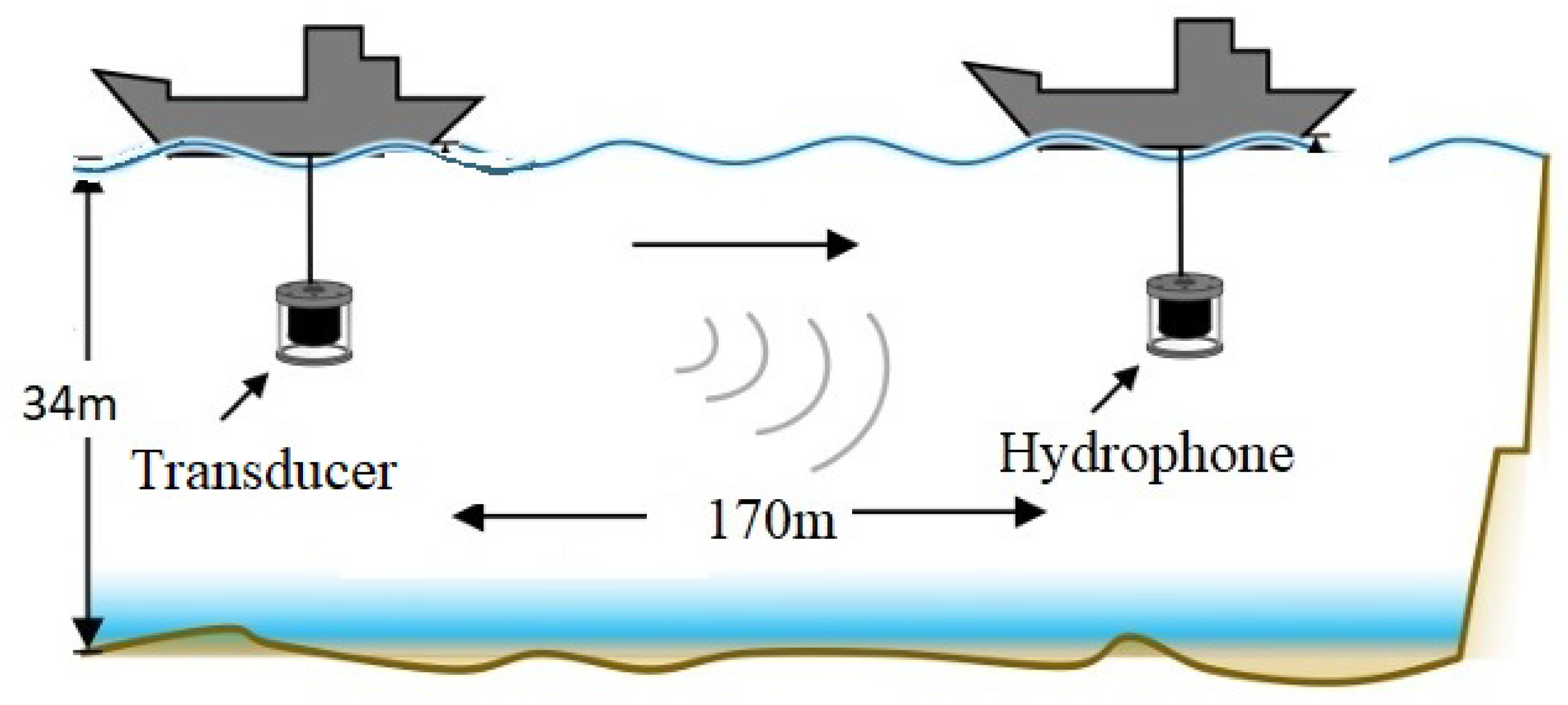
| Parameter | Value/Observation | Unit/Description |
|---|---|---|
| Distance (Range) | 170 | meters (m) |
| Transmitter Depth | 34 | meters (m) |
| Receiver Depth | 34 | meters (m) |
| Sound Speed Profile (SSP) | 1480–1495 | m/s (dependent on depth) |
| Maximum Multipath Spread () | 0.0275 | seconds (s) |
| RMS Multipath Spread () | 0.0293 | seconds (s) |
| Maximum Doppler Spread () | 2.3396 | Hz |
| RMS Doppler Spread () | 3.1487 | Hz |
| Environmental Temperature Range | 9–12 | °C |
| Salinity | Low (Freshwater) | Qingdao Lake is a freshwater lake |
| Probe Signal Type | LFM | Frequency: 8000–16,000 Hz |
| Number of Sounding Signals per Group | 272 | Each group lasts 30 s |
| Testing Frequency | 3 times per day | Interval ≈ 3 min between groups |
| Number of Data Samples Collected | 34 | Effective measured channel |
| Step | Details |
|---|---|
| Datasets Used | Watermark channels data for pre-training |
| Label Data | Concatenated categorical labels from the corresponding datasets |
| Data Concatenation | Training features of each watermark channel are concatenated |
| Training/Validation Split | 80% training, 20% validation |
| Fine-tuning Data | 50% of data Qingdao data used for fine-tuning, split further into 80% training and 20% validation |
| Testing Data | Remaining 50% of input data Qingdao Lake data used exclusively for testing |
| Channels | P(d) | P(r) | P(h) | AFR |
|---|---|---|---|---|
| KAU | 0.0011 | 0.0063 | 0.0074 | 0.8521 |
| BCH1 | 0.0016 | 0.0010 | 0.0026 | 0.3868 |
| NOF1 | 0.0018 | 0.0006 | 0.0024 | 0.2581 |
| NCS1 | 0.0002 | 0.0043 | 0.0045 | 0.9636 |
| Algorithm | Complexity |
|---|---|
| LS | |
| MMSE | |
| FC-NN | |
| DNN | |
| Proposed Transfer Learning | |
| Fine-Tuned Transfer Learning | (Frozen Conv. Layers) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adil, M.; Liu, S.; Mazhar, S.; Alharbi, A.; Yan, H.; Muzzammil, M. A Novel Transfer Learning-Based OFDM Receiver Design for Enhanced Underwater Acoustic Communication. J. Mar. Sci. Eng. 2025, 13, 1284. https://doi.org/10.3390/jmse13071284
Adil M, Liu S, Mazhar S, Alharbi A, Yan H, Muzzammil M. A Novel Transfer Learning-Based OFDM Receiver Design for Enhanced Underwater Acoustic Communication. Journal of Marine Science and Engineering. 2025; 13(7):1284. https://doi.org/10.3390/jmse13071284
Chicago/Turabian StyleAdil, Muhammad, Songzuo Liu, Suleman Mazhar, Ayman Alharbi, Honglu Yan, and Muhammad Muzzammil. 2025. "A Novel Transfer Learning-Based OFDM Receiver Design for Enhanced Underwater Acoustic Communication" Journal of Marine Science and Engineering 13, no. 7: 1284. https://doi.org/10.3390/jmse13071284
APA StyleAdil, M., Liu, S., Mazhar, S., Alharbi, A., Yan, H., & Muzzammil, M. (2025). A Novel Transfer Learning-Based OFDM Receiver Design for Enhanced Underwater Acoustic Communication. Journal of Marine Science and Engineering, 13(7), 1284. https://doi.org/10.3390/jmse13071284







