Improved Model Predictive Control Algorithm for the Path Tracking Control of Ship Autonomous Berthing

Abstract

To address the issues of path tracking accuracy and control stability in autonomous ship berthing, an improved algorithm combining nonlinear model predictive control (NMPC) and convolutional neural networks (CNNs) is proposed in this paper. A CNN is employed to train on a large dataset of ship berthing trajectories, combined with the rolling optimization mechanism of NMPC. A high-precision path tracking control method is designed, which accounts for ship motion constraints and environmental disturbances. Simulation results show an 88.24% improvement in tracking precision over traditional MPC. This paper proposes an improved nonlinear model predictive control (NMPC) strategy for autonomous ship berthing. By integrating convolutional neural networks (CNNs) and moving horizon estimation (MHE), the method enhances robustness and path-tracking accuracy under environmental disturbances. The amount of system overshoot is reduced, and the anti-interference capability is notably improved. The effectiveness, generalization, and applicability of the proposed algorithm are verified.

1. Introduction

With the advancement of intelligent shipping and autonomous navigation, autonomous ship berthing has become the final and critical operation in the navigation process. Its control accuracy and system robustness directly determine the safety and efficiency of the berthing process. Path tracking control is a key technology in autonomous berthing systems and is crucial for ensuring a ship approaches the berth smoothly and safely along the planned trajectory, serving as a fundamental prerequisite for realizing intelligent berthing [1]. Compared to open-water navigation, path tracking during berthing is significantly more complex. It involves tighter path curvatures and confined spaces while being subject to external disturbances such as wind, waves, and currents, as well as internal constraints, including actuator hysteresis and input saturation. These factors impose stricter demands on the accuracy and robustness of path tracking control methods.

Ship tracking control is mainly divided into two categories—heading-keeping control and track-keeping control—which are the core links to realize high-precision navigation and autonomous berthing of ships. Common control methods include closed-loop gain shaping control, backstepping, and model predictive control (MPC). Min [2] proposed a closed-loop gain shaping algorithm for ship heading tracking and utilized the mirror mapping theory [3,4] to realize unstable system control, which improved the response characteristics of large-inertia ships by adjusting the scaling term. Yuan [5,6] introduced the nonlinear feedback technique, which significantly improved the control performance while ensuring the control stability. Building on this approach, Song [7] addressed the issue of excessive control effort by introducing an enhanced extended Kalman filter (EKF) algorithm. Han [8] further improved the dynamic response by extending the heading control using the line of sight (LOS) method. Godhavn [9] was the first to introduce the backstepping method to the field of ship control. Building on this, Fossen [10] conducted in-depth investigations into its application for nonlinear system control and later enhanced steady-state accuracy by incorporating integral action [11]. Zhang [12,13] designed a robust adaptive controller for waypoint path tracking by integrating neural networks with dynamic surface control (DSC). However, these methods rely heavily on model accuracy, making them less effective in handling parameter uncertainties and external disturbances commonly encountered in practice. For this reason, Li [14] incorporated neural networks into the backstepping method to enhance adaptability. However, the approach did not fully account for rudder actuator load or steering frequency, which may lead to increased wear of the physical control components.

In terms of MPC, existing studies [15,16] have designed high-performance controllers based on linear and nonlinear models, incorporating the LOS method or Lyapunov theory to address path tracking challenges in dynamic environments. Despite improvements in control accuracy, these approaches still exhibit limitations in dealing with model uncertainty and external disturbances. The online update mechanism proposed by Lin [17] enhances the adaptive capability of MPC, but its high computational demand imposes limitations on real-time performance. Meanwhile, MPC approaches incorporating collision avoidance strategies [18,19] have focused on safety, enabling collision-free control in path planning and tracking. Song [20] fused ship collision risk assessment to propose an improved A* algorithm aimed at improving the safety and reducing the planning time of ship navigation in complex seas while achieving optimal path planning. Li [21,22] proposed a robust adaptive event-triggered path planning and control strategy for intelligent maritime search missions. It is worth noting that conventional MPC approaches generally fail to adequately address the impact of marine environmental disturbances, such as wind and waves, on path tracking accuracy and control smoothness. To address this problem, the MHE method was gradually introduced [23] and fused with MPC for real-time state estimation and control optimization [24], which improves the anti-interference ability and stability of the control system to a certain extent.

Although significant progress has been made in ship motion control, effective methods that ensure both high-precision path tracking and environmental robustness during autonomous berthing are still lacking. In dynamic and complex sea conditions, where wind, waves, and currents frequently change and interact, achieving a balance between control accuracy, real-time response, and robustness remains a major challenge. Therefore, this paper proposes a control method that integrates CNN with NMPC, utilizing CNN to extract features and assist in trajectory prediction based on historical path data. Additionally, moving horizon estimation (MHE) is incorporated for state estimation to enhance the accuracy and stability of path tracking. The main contributions are as follows:

(1)

A four-degree-of-freedom (4-DOF) ship motion model is developed, incorporating low-speed berthing, shallow water effects, and external disturbances such as wind and waves, to more accurately simulate ship dynamics in complex sea conditions.

(2)

A cooperative control framework based on CNN and NMPC is constructed to achieve high-precision path prediction and optimal control.

(3)

A high-precision path tracking control method is designed that accounts for ship motion constraints and environmental disturbances, effectively reducing overshoot and oscillations while enhancing system stability and robustness.

2. Mathematical Model of Ship Motion

For autonomous berthing, a 4-DOF ship motion mathematical model is established, which is enhanced to account for low-speed maneuvering, shallow water effects, and wind–wave disturbances. Ships are idealized as rigid bodies, moving in three dimensions. The motion of the ship includes the following 4-DOF: surge velocity ($u$), sway velocity ($v$), yaw rate ($r$) and roll rate ($p$). Joint modeling is carried out with a geodetic coordinate system ($O-xyz$) and an attachment coordinate system ($G-x_0{y}_0{z}_0$). As shown in Figure 1, $O-xyz$ is a geodetic coordinate system whose origin $O$ coincides with the center of gravity $G$ of the ship at the initial moment. The $x_0{y}_0$-plane lies in the horizontal plane, and the $z_0$-axis points downward. $G-x_0{y}_0{z}_0$ is the attached body coordinate system, with its origin also located at the ship’s center of gravity ($G$). In this coordinate system, the $G{x}_0$-axis oriented towards the bow, while the $G{y}_0$-axis points toward the starboard side, and the $G{z}_0$-axis is vertically downward, pointing to underwater. These two coordinate systems clearly describe both the ship’s overall motion and its local motion status.

The attitude and trajectory equations of the ship can be formulated as presented below:

$$\dot{\eta }=\mathrm{R}(\psi ,\phi )v$$

(1)

where $\eta ={\left[x,y,\phi ,\psi \right]}^{\mathrm{T}}$ denotes the position and attitude of the ship. $v={\left[u,v,\mathrm{r},p\right]}^{\mathrm{T}}$ is the velocity vector of the ship in the attached body coordinate system. $\mathrm{R}(\psi ,\phi )$ is the conversion matrix associated with the heading angle:

$$R(\psi ,\phi )=\left(\begin{array}{cccc}\cos \psi & -\sin \psi \cos \phi & 0& 0\\ \sin \psi & \cos \psi \cos \phi & 0& 0\\ 0& 0& \cos \phi & 0\\ 0& 0& 0& 1\end{array}\right)$$

(2)

The ship dynamics equations are constructed based on the modified Fossen model and are expressed as

$$M\dot{v}+C(v)v+D(v)v=\tau +{\tau }_w+{\tau }_h$$

(3)

where $M$ represents the inertia matrix of the ship, describing the effect of inertia on acceleration. The matrix $C(v)$ represents the coriolis and centrifugal forces, and $D$ denotes the damping matrix, representing the system’s damping forces. $\tau ={\left[{\tau }_u,0,{\tau }_r,0\right]}^{\mathrm{T}}$ is the matrix of control forces and moments, with ${\tau }_u$ as the propulsive force and ${\tau }_r$ as the yaw moment. The matrix ${\tau }_w={\left[{\tau }_{uw},{\tau }_{vw},{\tau }_{rw},{\tau }_{pw}\right]}^{\mathrm{T}}$ captures the wind–wave interference effects, characterizing the influence of wind–wave interference on surge velocity, sway velocity of the ship, roll rate, and yaw rate of the ship. ${\tau }_h={[{\tau }_{uh},{\tau }_{vh},{\tau }_{rh},{\tau }_{ph}]}^{\mathrm{T}}$ denotes the shallow water effect disturbance matrix. The additional mass and damping coefficients vary significantly with speed and water depth in low-speed navigation and shallow water environments, and are further modeled as

$$C(v)=\left(\begin{array}{cccc}0& 0& 0& m_{33}u\\ 0& 0& 0& -m_{22}v\\ 0& 0& 0& m_{11}u\\ -m_{33}u& m_{22}v& -m_{11}u& 0\end{array}\right)$$

(4)

$$M=\left(\begin{array}{cccc}{m}_{11}& 0& 0& 0\\ 0& m_{22}& 0& 0\\ 0& 0& m_{33}& 0\\ 0& 0& 0& m_{44}\end{array}\right)$$

(5)

$$D=\left(\begin{array}{cccc}{d}_{11}& 0& 0& 0\\ 0& d_{22}& 0& 0\\ 0& 0& d_{33}& 0\\ 0& 0& 0& d_{44}\end{array}\right)$$

(6)

The 4-DOF nonlinear Fossen model of a ship can be expressed in the following form:

$$\left\{\begin{array}{l}\stackrel{·}{x}=u\cos \psi -v\sin \psi \cos \phi \\ \stackrel{·}{y}=u\sin \psi +v\cos \psi \cos \phi \\ \stackrel{·}{\psi }=r\cos \phi \\ \stackrel{·}{\phi }=p\\ \stackrel{·}{u}=[(-m_{33}p-d_{11})u+{\tau }_u+{\tau }_{uw}+{\tau }_{uh}]m_{11}^{-1}\\ \stackrel{·}{v}=[(m_{22}p-d_{22})v+{\tau }_{vw}+{\tau }_{vh}]m_{22}^{-1}\\ \stackrel{·}{r}=[(-m_{11}u-d_{33})r+{\tau }_r+{\tau }_{rw}+{\tau }_{rh}]m_{33}^{-1}\\ \stackrel{·}{p}=[(m_{33}+m_{11})u^2-m_{22}{v}^2-d_{44}p+{\tau }_{pw}+{\tau }_{ph}]m_{44}^{-1}\end{array}\right.$$

(7)

Remark 1.

The model incorporates low-speed conditions, shallow water effects, and wind–wave disturbances to more accurately capture the complex dynamics encountered during actual navigation. It provides a more accurate representation of ship motion characteristics.

3. Path Tracking Control Method Design

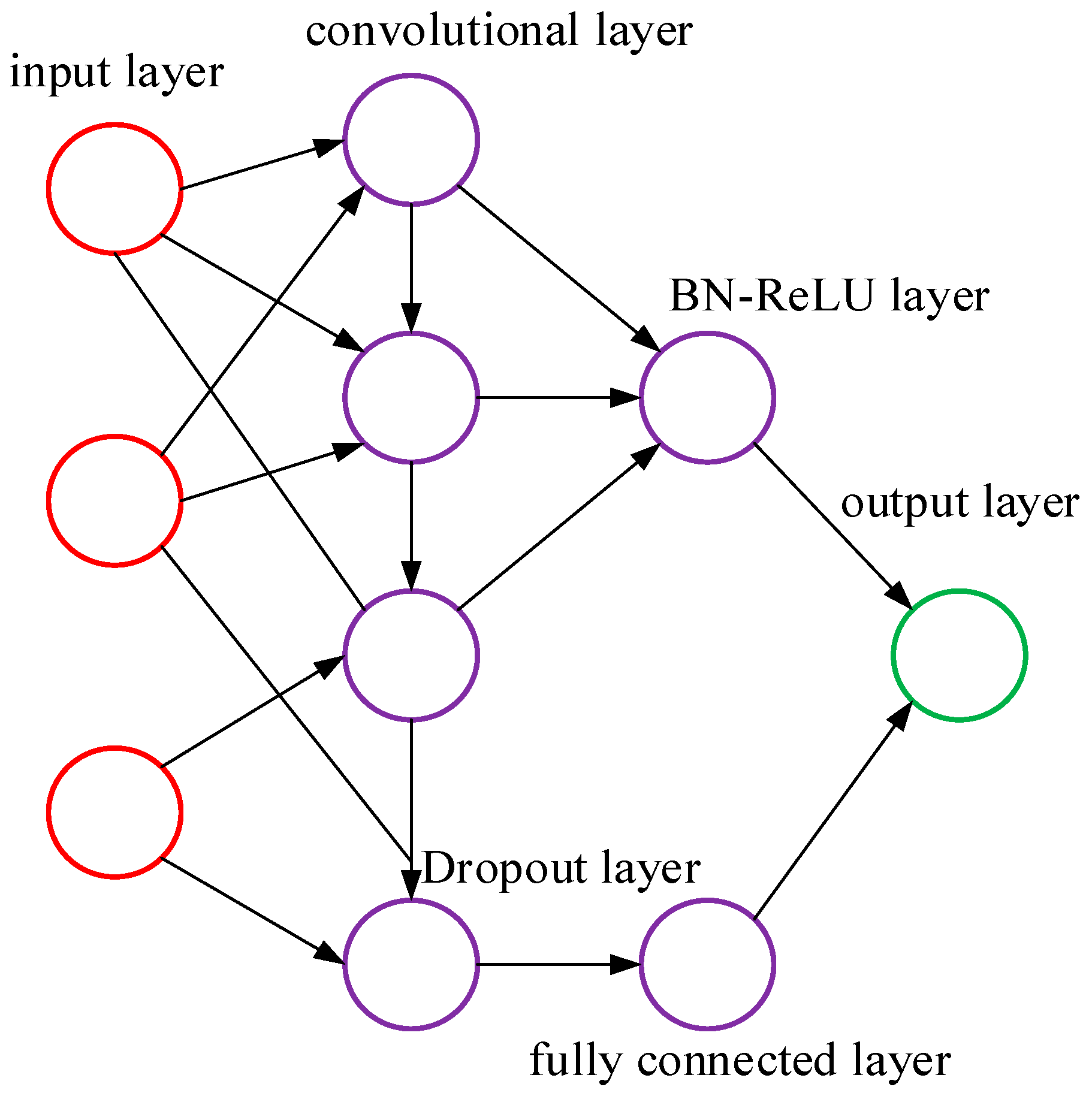
3.1. CNN

To enhance the path tracking performance of model predictive control, CNN is introduced to extract and learn features from predefined path data. CNN automatically identifies key features related to ship motion and environmental disturbances from large path datasets, reducing the complexity of manual feature design and improving the adaptability of the control method. A sliding window approach is used to construct training samples from the simulation-generated path dataset. Each sequence of consecutive data points serves as input to predict the $k+z$ data point. The input–output pairs are constructed as

$$P_i=[x_i,x_{i+1},\dots ,x_{i+k+1}],t_i=x_{i+k+z-1}$$

(8)

where $k$ is the input step and $z$ is the prediction step, $k=15,z=1$.

As shown in Figure 2, the CNN topological structure consists of input layers, convolutional layers, nonlinear transformation layers combining Batch Normalization (BN) and the ReLU activation function, dropout layers, fully connected layers, and an output layer. The input layer receives the path data. Convolutional layers apply multiple one-dimensional kernels to extract local patterns along the temporal dimension. The BN-ReLU activation layers reduce internal covariate shift during training, improving model stability. Used alongside dropout layers, which effectively mitigate overfitting and enhance generalization to unseen path scenarios. The output layer employs a linear activation function to produce the predicted path feature representation.

The structure captures both local detailed features and global trend information of the path, thus improving adaptability to complex path variations and environmental disturbances. The first convolutional layer employs 64 kernels with a size of 3 and a stride of 1 to capture local temporal features from the input sequence. The second convolutional layer uses 128 kernels to extract higher-level temporal dependencies, enhancing feature representation capability. The convolutional layer output is calculated as follows:

$$y_{ij}^n=f({\displaystyle \sum _{m=1}^{M^{(n-1)}}{\displaystyle \sum _{p=0}^{h-1}{\displaystyle \sum _{q=0}^{w-1}{W}_{m,p,q}^n}}}·x_{m,i+p,j+q}^{(n-1)}+b^{(n)})$$

(9)

where $n$ is the number of network layers, $W$ is the convolution kernel weights, $b$ is the bias, $f$ is the activation function, and $h,w$ denotes the convolution kernel size. Trained on large volumes of path data, the network can rapidly generate high-quality feature representations for new path scenarios and external disturbances, providing dynamic guidance and accurate reference inputs for the control strategy.

Remark 2.

By extracting common patterns from diverse historical data, the CNN enhances the disturbance resilience of path prediction and automatically learns the effects of external disturbances on the path.

Remark 3.

CNN reduces reliance on manual modeling, simplifies the path planning process, and improves system scalability and transferability.

3.2. NMPC

Given the nonlinear nature of ship dynamics, which becomes more pronounced in complex sea conditions, traditional linear control strategies struggle to maintain satisfactory performance. This paper employs an NMPC algorithm based on Fossen’s nonlinear dynamics model, combined with CNN-generated dynamic reference trajectories, to achieve high-precision path tracking control. The future state of the ship is given by the following nonlinear prediction model:

$$x_{k+1}=f(x_k,u_k)$$

(10)

where $x_k$ is the current state, $u_k$ is the control input, and $f(\cdot )$ denotes the nonlinear dynamics equation of the system. CNN generates reference trajectories in real time as targets of NMPC, which addresses delays in response to environmental changes in traditional path methods and improves adaptability to dynamic conditions. NMPC targets CNN-predicted paths and optimizes control inputs online in real time to ensure the smooth and efficient movement of the ship along the preset paths.

The controller aims to guide the ship to berth smoothly and stably along a predefined double-S trajectory plan. The optimization problem is formulated as follows:

$$\begin{array}{l}{\overline{y}}_{k+i|k}=y_{k+i|k}+e_{k+i|k}\\ e_{k+i|k}=E(e_k,\dots ,e_{k-j})\\ e_k=y_k-y_{k|k-1}\end{array}$$

(11)

where $E$ denotes the error estimation function, $j$ denotes the number of past errors in the error estimate, ${\overline{Y}}_{k+i|k}$ denotes the corrected predicted output, and $e_k$ denotes the error in the output estimate at moment $k-1$ for moment $k$. Assume that the tracking objective at step $k$ is ${\underset{\rightharpoondown }{\omega }}_k={\left[{\omega }_{k+1},\dots {\omega }_{k+q}\right]}^{\mathrm{T}}$, and the predicted output is ${\underrightarrow{\overline{y}}}_k={\left[{\overline{y}}_{k+1|k},\dots {\overline{y}}_{k+q|k}\right]}^{\mathrm{T}}$, where $q$ is the predicted time domain and $H$ is the constraints, thus, the optimization problem can be expressed as

$$\begin{array}{l}\underset{u_k}{\min }{J}_k=F(x_k,{\underrightarrow{u}}_k,{\omega }_k)\\ s.t.:x_{k+1}=f(x_k.u_k),k\ge 0\\ { h(x}_{k,}{u}_k,{\omega }_k)\in H\end{array}$$

(12)

Further considering the wind–wave and measurement noise disturbances, MHE is introduced for real-time state estimation and correction. MHE uses historical observation sequences to identify disturbance patterns and adjust the predicted trajectory accordingly. The external error terms are assumed to be bounded, ${\tau }_{uw}\le {\overline{\tau }}_{uw},{\tau }_{vw}\le {\overline{\tau }}_{vw},{\tau }_{rw}\le {\overline{\tau }}_{rw},{\tau }_{pw}\le {\overline{\tau }}_{pw}$, where ${\overline{\tau }}_{uw},{\overline{\tau }}_{vw},{\overline{\tau }}_{rw},{\overline{\tau }}_{pw}$ is an unknown constant, and these error terms are assumed to be bounded. At zero ship speed, the measurement error $V$ and disturbance $W$ are Gaussian-distributed with a specific measurement error matrix: $W={\left[0,0,0,0,{\displaystyle \frac{{\tau }_{uw}}{m_{11}}},{\displaystyle \frac{{\tau }_{vw}}{m_{22}}},{\displaystyle \frac{{\tau }_{rw}}{m_{33}}},{\displaystyle \frac{{\tau }_{pw}}{m_{44}}}\right]}^{\mathrm{T}}\in R^8$. In this model, the ship position information is obtained from the observation system $\stackrel{·}{X}=f(X,T)+W$ and measurement model $Y_m=h(x)={\left[x_m,y_m,{\theta }_m,l_m\right]}^{\mathrm{T}}\in R^4$. Then, the MHE problem is established:

$$\begin{array}{c}\underset{X,T_{\tau }}{\min }{J}_{n_{\mathrm{MHE}}}(X,T_{\tau })={\displaystyle \sum _{i=k-n_{\mathrm{MHE}}}^k\left|\right|Y(i)-Y_m(i)|{|}_{w_1}^2+{\displaystyle \sum _{i=k-n_{\mathrm{MHE}}}^{k-1}\left|\right|{\tilde{T}}_{\tau }(i)-T_{\tau }(i)|{|}_{w_2}^2}}\\ s.t. X(i+1)=f(X(i),T_{\tau }(i))\\ T_{\tau }\left(i\right)\in {\overline{T}}_{\tau },\forall i\in \left[k-n_{\mathrm{MHE}},k-1\right]\\ X(i)\in \overline{X},\forall i\in \left[k-n_{\mathrm{MHE}},k\right]\end{array}$$

(13)

The control system flow block diagram is shown in Figure 3.

Remark 4.

NMPC performs real-time adjustment of control inputs through nonlinear optimization, ensuring control accuracy. This approach also enhances system responsiveness, making it suitable for real-time ship path control tasks.

4. Stability Analysis

To verify the stability of the proposed control method under complex perturbation conditions, it is analyzed using Lyapunov stability theory [25]. Consider a control system operating in the following nonlinear state space model:

$$x_{t+1}=f(x_t,u_t)+d_t$$

(14)

where $x_t\in R^n$ is the system state, $u_t\in R^m$ is the control input, and $d_t$ is an external perturbation assumed to be bounded $\left|\right|d_t\left|\right|\le \overline{d}$. The stability of the controlled system is ensured by terminal constraints that need to be satisfied by the system state:

$$\widehat{X}(t_k | t)-X_{t+k}^r=0$$

(15)

The Lyapunov equation is established as

$$V(k)={\displaystyle \sum _{i=1}^N\mathrm{\iota }(\widehat{X}(k+1 | k),\widehat{T_{\tau }}(k+i-1 | k)})$$

(16)

It is required to satisfy the following inequality in the presence of perturbation:

$$\begin{array}{l}{V}^{*}(k+1)=\underset{T_{\tau }}{\min }\left[{\displaystyle \sum _{i=1}^N\mathrm{\iota }(X(k+i),T_{\tau }(k+i-1))-\mathrm{\iota }(X(k+1+N),T_{\tau }(k+N))}\right]\\ =-\mathrm{\iota }(X(k+i),T_{\tau }(k))+\underset{T_{\tau }}{\min }\left[{\displaystyle \sum _{i=1}^N\mathrm{\iota }(X(k+i),T_{\tau }(k+i-1))+\mathrm{\iota }(X(k+1+N),T_{\tau }(k+N))}\right]\\ \le -\mathrm{\iota }(X(k+i),T_{\tau }^{*}(k))+V^{*}(k)+\underset{T_{\tau }}{\min }\mathrm{\iota }(X(k+1+N),T_{\tau }(k+N))\end{array}$$

(17)

The control inputs are generated by NMPC, and the optimization objective function has the following form:

$$J={\displaystyle \sum _{k=0}^{\mathrm{N}}(||x_{t+k|t}-x_{t+k}^r||Q^2+||ut+k|t|{|}_R^2})$$

(18)

And fulfills the following conditions:

(1)

The reference trajectory $x^r$ is continuously bounded.

(2)

Control inputs meet system controllability requirements.

(3)

The CNN prediction module has a finite error bound $\left|\right|{\tilde{x}}_t^r-x_t^r\left|\right|\le ϵ$, where $ϵ$ is adjustable.

Under these conditions, it can be proven that the optimization problem is feasible at every moment, and the Lyapunov function decreases monotonically along the closed-loop trajectory. From that,

$$\underset{t\to \infty }{\lim \sup }\Vert x_t-x_t^r\Vert \le \beta (\overline{d},ϵ)$$

(19)

where $\beta$ is a positive function indicating that the final state of the system will converge to asymptotic stability within a bounded neighborhood of the reference trajectory. From Equation (15), $\underset{T_{\tau }}{\min }\mathrm{\iota }(X(k+1+N),T_{\mathrm{\tau }}(k+N)=0$, and $0\le V^{*}(k+1)\le V^{*}(k)$, the Lyapunov function is non-increasing and hence the controlled system is stable.

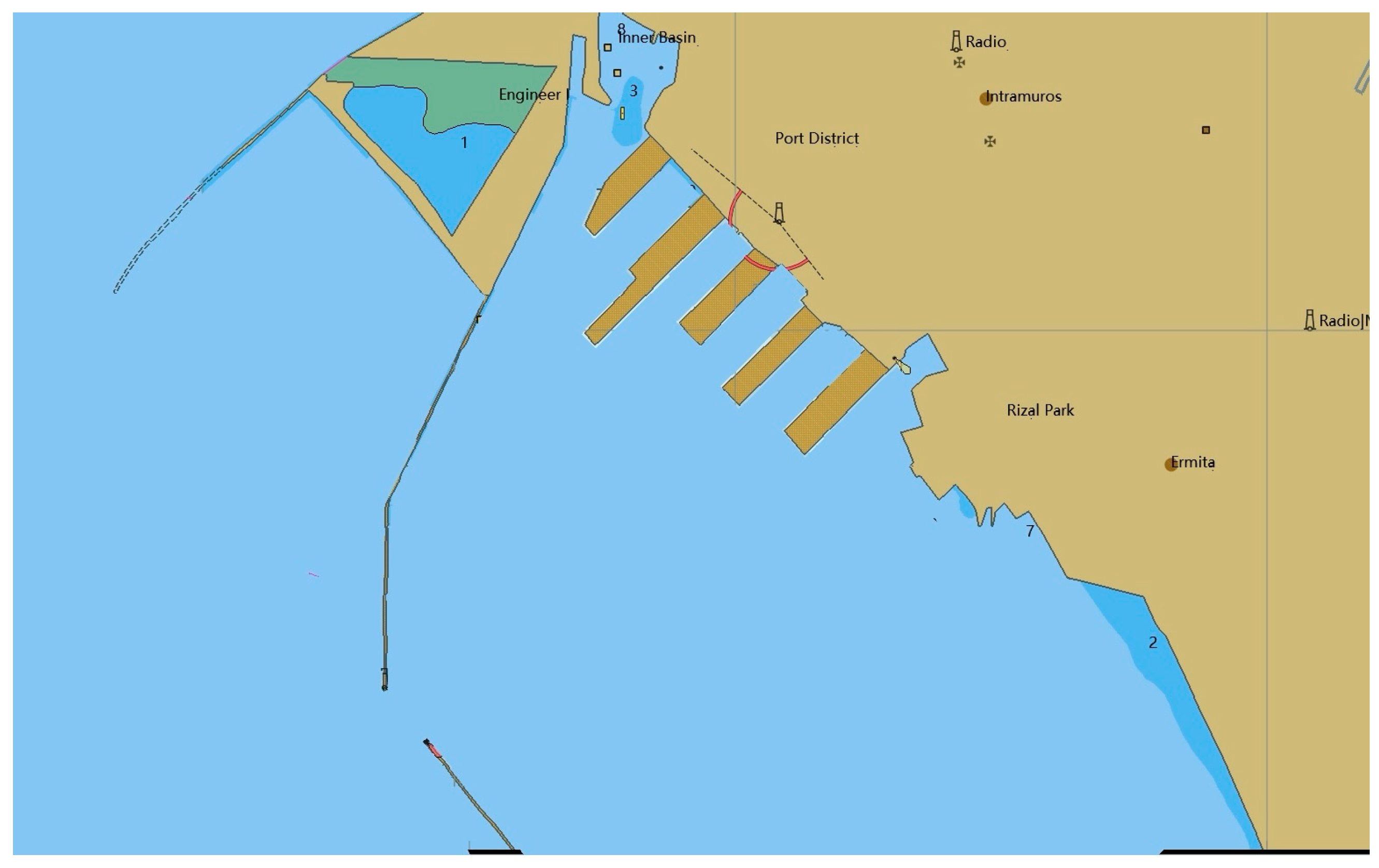
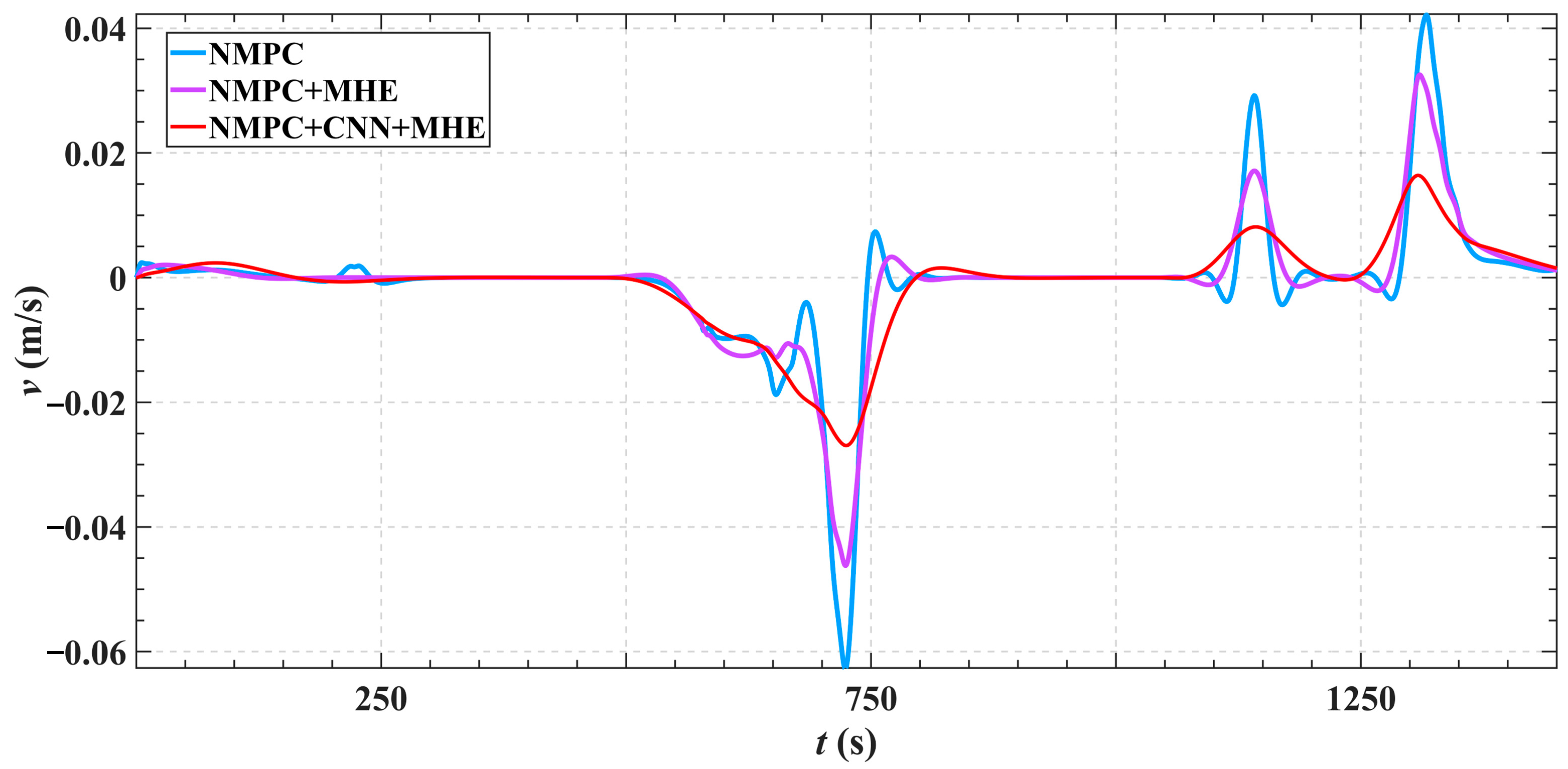
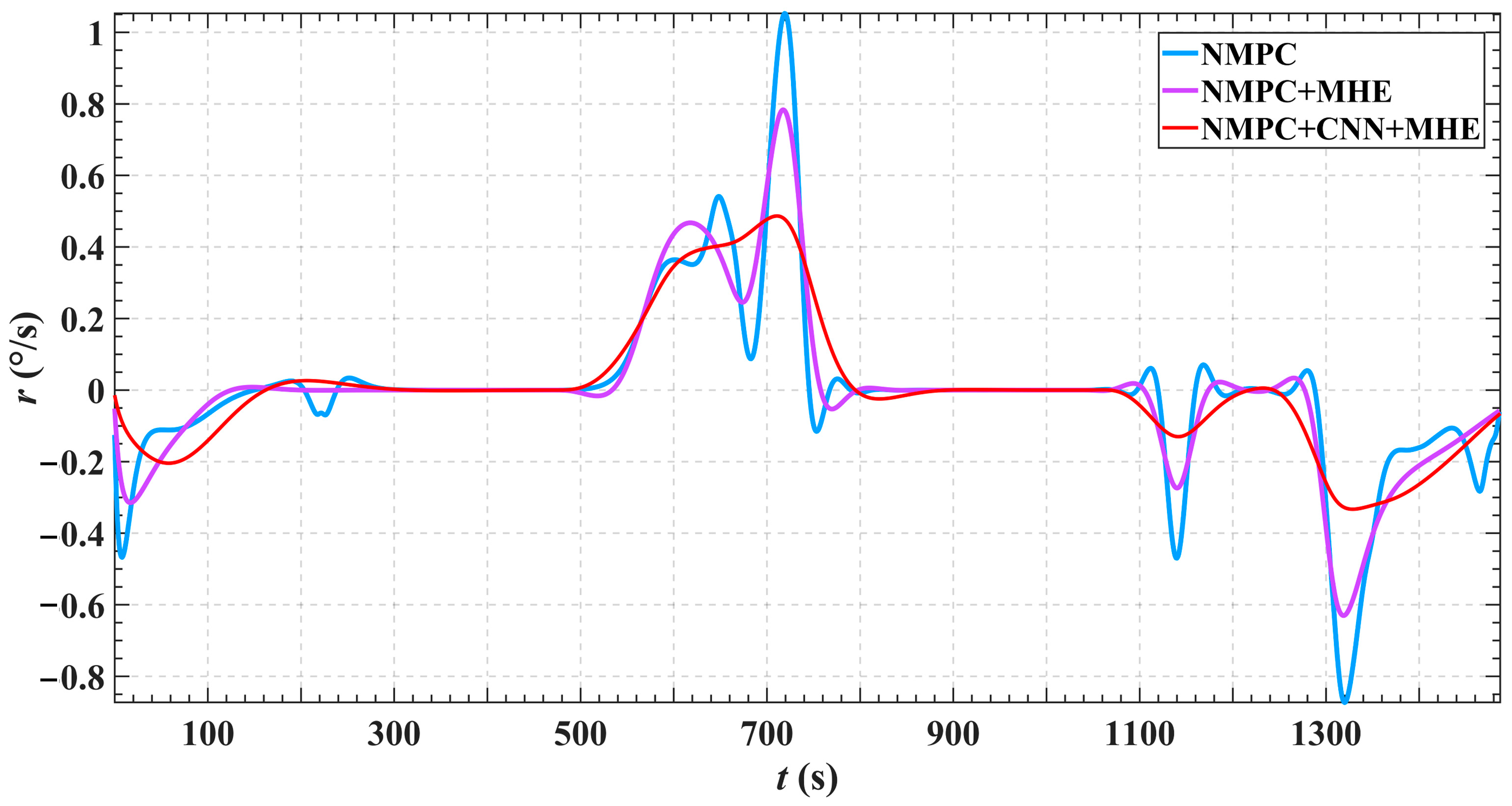
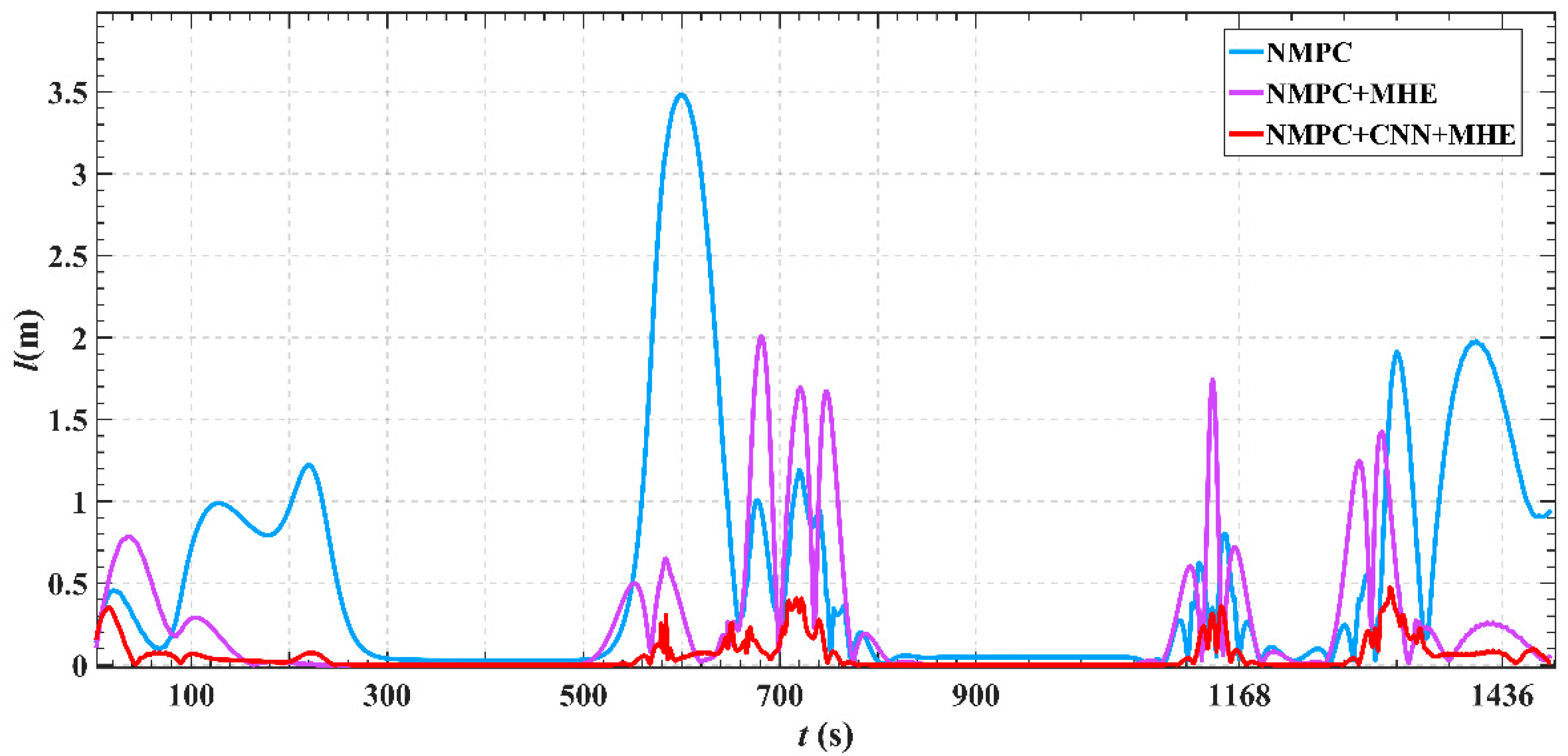
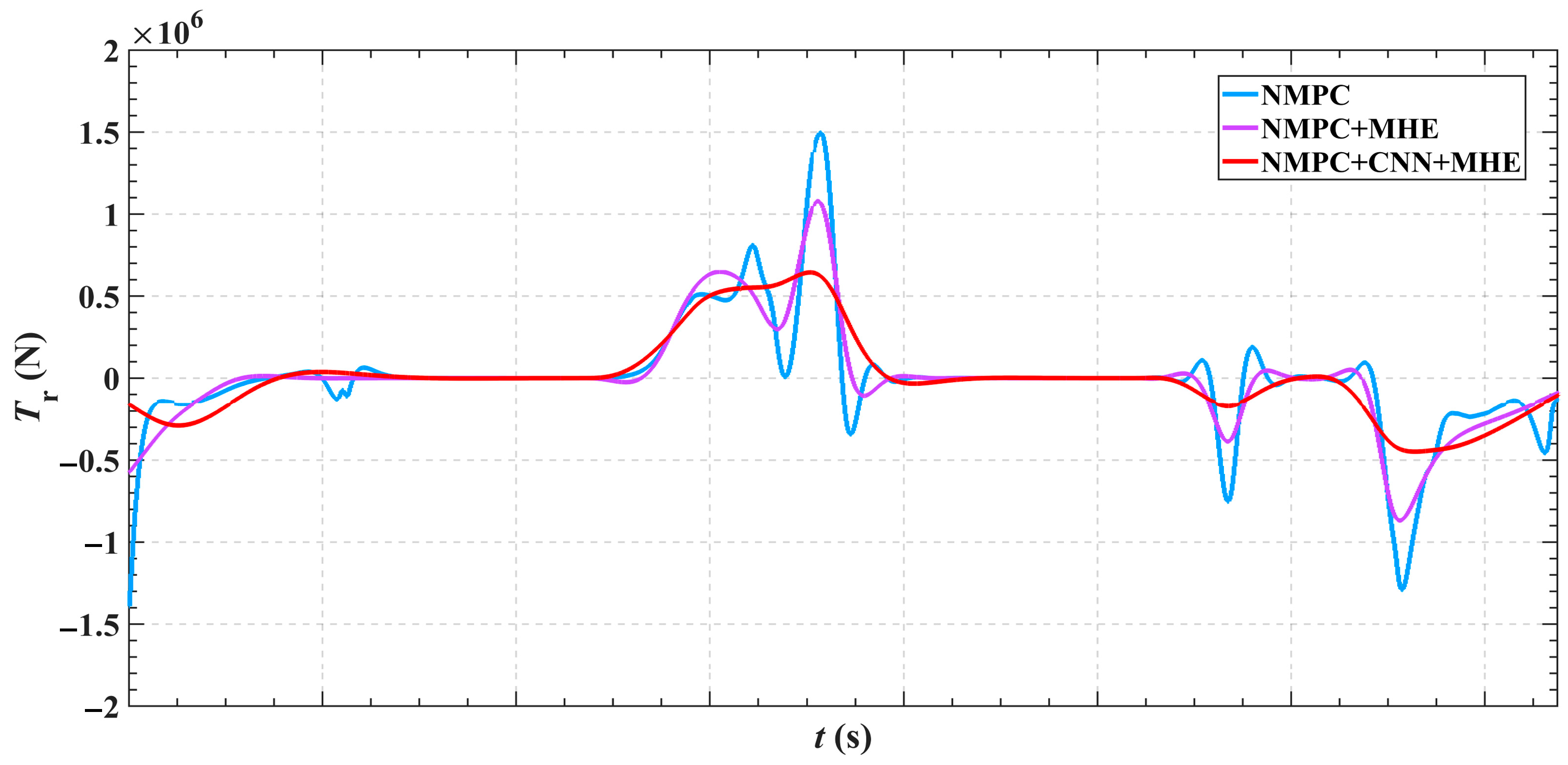
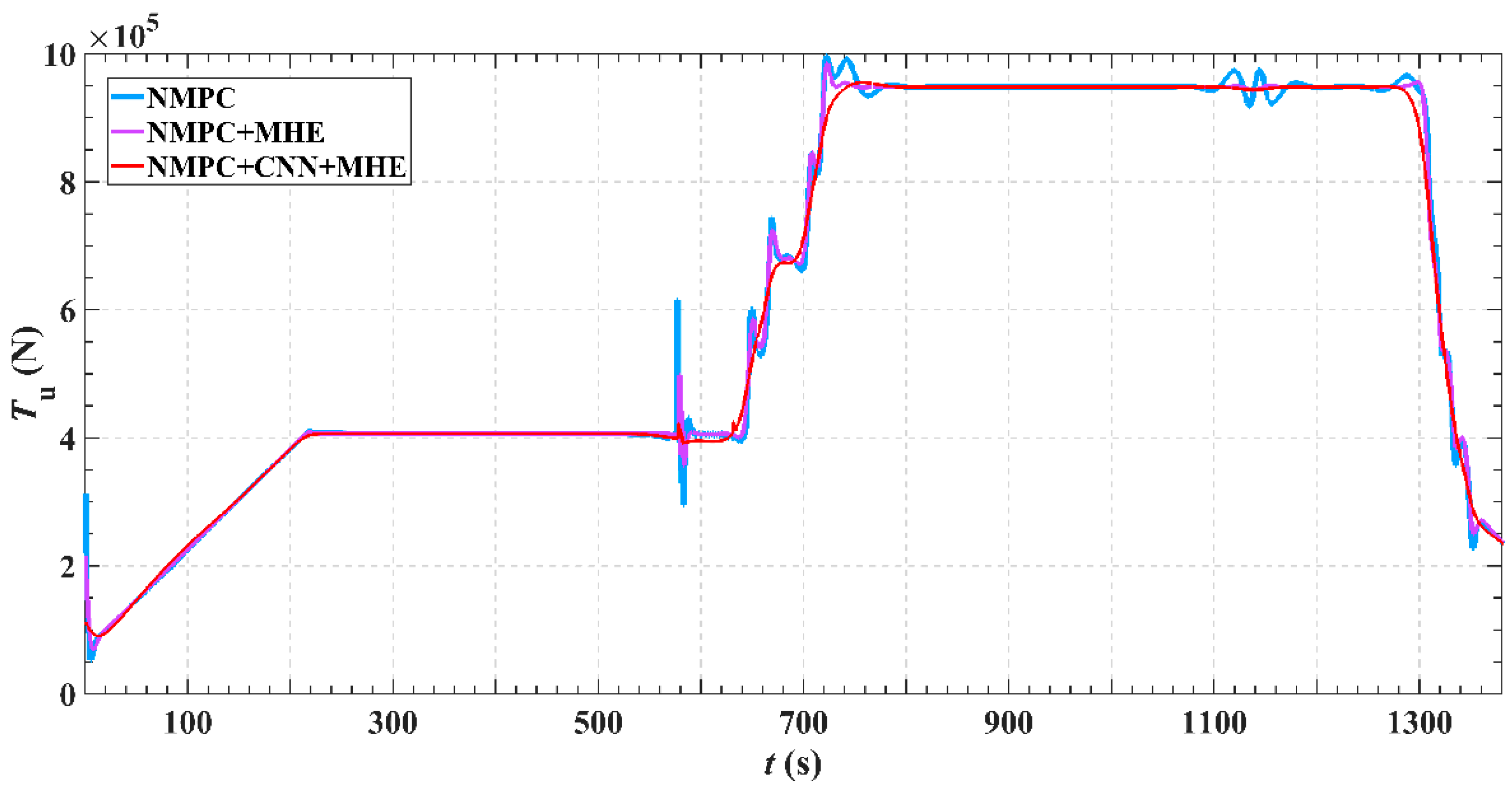
5. Simulation Experiments

To validate the effectiveness and superiority of the proposed control method, simulation experiments of ship berthing path tracking control were conducted at Manila International Port, as shown in Figure 4.

The control strategy setup prediction step is set to 80, and the discrete system sampling period is 1 s. The simulation is based on a Gulf-class utility ship [26], which has a length of 38 m and a mass of $m=118\times {10}^3\mathrm{kg}$. The Fossen model parameters can be configured based on the physical and dynamic characteristics of the ship, as shown in

Table 1. Simulation model parameters.

Notation	Numerical Value (kg)	Notation	Numerical Value (kg)
$m_{11}$	$1.2\times {10}^5$	$d_{11}$	$2.15\times {10}^4$
$m_{22}$	$1.779\times {10}^5$	$d_{22}$	$1.47\times {10}^5$
$m_{33}$	$6.36\times {10}^7$	$d_{33}$	$8.02\times {10}^6$
$m_{44}$	$9.865\times {10}^7$	$d_{44}$	$11.71\times {10}^6$

below:

In traditional algorithms, the path tracking accuracy and attitude control of the ship exhibit noticeable deviations under complex sea conditions. The control performance is particularly limited under dynamically changing sea conditions and nonlinear constraints. The improved control scheme is compared with the model predictive control algorithm by introducing the improved control scheme. As shown in Figure 5 and Figure 6, the ship berthing path tracking effect of the algorithm before and after the improvement is demonstrated in a dynamically disturbed harbor environment.

The tracking effect shows that before the improvement, the ship responded slowly to path changes. This led to delays in heading or speed adjustments and caused deviation from the planned trajectory. In contrast, the improved algorithm increases the response speed of the control strategy, allowing the ship to adjust its heading and speed more rapidly in response to path changes.

The simulation results are shown in Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13. A comparison of the control performance before and after the improvement demonstrates that the proposed control method successfully achieves effective ship path tracking and attitude regulation. During the control process, the variations of the relevant state variables are effectively controlled, including surge and sway velocity ($u$, $v$), yaw rate ($r$), roll rate ($p$) and track error ($l$). In addition, the changes in longitudinal thrust (${\tau }_u$) and yaw moment (${\tau }_r$) are shown.

Analyzing the figure, it can be seen that in terms of the response of surge and sway velocities, the improved control strategy exhibits stronger dynamic stability and disturbance resistance. In particular, the response of surge velocity shows a smooth rise with almost no overshoot. The sway velocity response exhibits minimal disturbance amplitude and faster oscillation decay, significantly enhancing the system’s ability to suppress lateral and yaw disturbances.

Simulation results show that the proposed method exhibits good no-overshoot characteristics around key turning points. The control curves transition smoothly, effectively avoiding attitude instability caused by excessive responses. In contrast, NMPC (blue line) and NMPC with MHE (green line) show noticeable overshoot during certain periods. Meanwhile, the control accuracy is significantly improved. The enhanced algorithm exhibits the smallest fluctuations in yaw and roll velocities throughout the process, resulting in more convergent and controllable system responses and effectively reducing attitude disturbances during berthing.

The improved algorithm also has a significant advantage in track error. Experimental results show that the method maintains low error levels over extended periods. Especially during abrupt path changes or strong external disturbances, the error curve remains smooth and continuous without significant spikes. This demonstrates strong robustness and high-precision tracking capability.

In terms of control inputs, the responses of longitudinal thrust and yaw moment also highlight differences between control strategies. Compared to previous algorithms, the improved method exhibits smoother and more continuous control actions, without high-frequency oscillations or abrupt changes. Especially during sudden heading changes, the control method maintains stable adjustments, demonstrating improved real-time responsiveness and continuity of the control system.

As shown in

Table 2. Comparison of tracking effects of control methods.

Control Variable	NMPC	NMPC + MHE	CNN + NMPC + MHE	Percentage Increase
surge and sway velocity deviation	3.0 m	2.0 m	1.0 m	66.67%
yaw rate	4.5 rad/s	3.3 rad/s	2.3 rad/s	48.89%
roll rate	0.04 rad/s	0.03 rad/s	0.01 rad/s	75.00%
track error	3.4 m	1.3 m	0.4 m	88.24%
longitudinal thrust	8.0 × 105 N	7.2 × 105 N	4.4 × 105 N	45.50%
yaw moment	1.5 × 106 N	1.3 × 106 N	0.3 × 106 N	80.67%

, the three control methods exhibit significant differences in path tracking performance and attitude control.

The traditional NMPC method exhibits considerable position errors and noticeable state oscillations, with overshoot particularly evident during turning, indicating limited stability. With the introduction of MHE, system response is optimized to a certain extent, reducing position errors and attenuating fluctuations in velocity and attitude variables. However, oscillations remain during periods of significant lateral disturbance. Further integration of CNN enhances the overall control performance of the system. The method exhibits very high stability and accuracy on all control variables. For example, in terms of track error, the traditional NMPC method results in an error of 3.4 m, while the integrated CNN and MHE approach reduces the error to just 0.4 m. For example, in terms of track error, the traditional NMPC method results in an error of 3.4 m, while the integrated CNN and MHE approach reduces the error to just 0.4 m, with an error reduction of 88.24%, demonstrating a significant improvement in path-tracking accuracy. The sway velocity error is reduced by up to 75%, further confirming the robustness and stability of the proposed method in dynamic response control. It basically achieves overshoot-free control in terms of position error. It also shows minimal fluctuations and optimal tracking in dynamic responses such as speed and heading.

In summary, the improved algorithm effectively integrates the advantages of observation accuracy and predictive control. It substantially improves control precision and response speed while mitigating system oscillations and overshoot. These improvements highlight its evident advantages and robustness, rendering it particularly suitable for autonomous berthing scenarios requiring high levels of accuracy and stability.

6. Conclusions

This paper introduces a convolutional neural network trained on extensive historical path data in a sequential manner. Combined with nonlinear model predictive control, it enables high-precision regulation of ship states under multiple disturbances and constraints. Simulation results show that the proposed method improves path tracking accuracy by 88.24% compared to traditional MPC in dynamic and disturbed port environments, demonstrating its superior performance. The main conclusions are as follows:

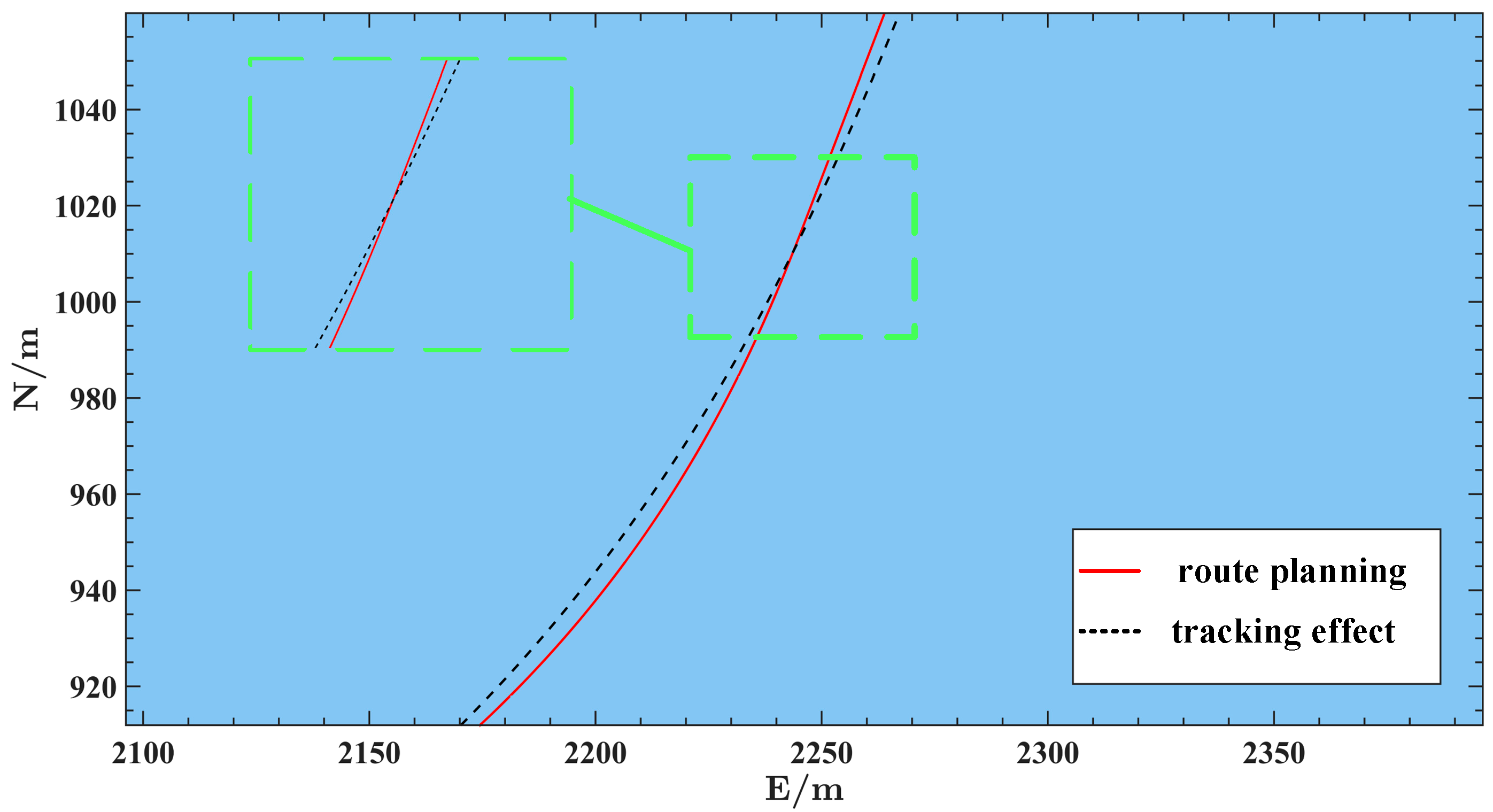
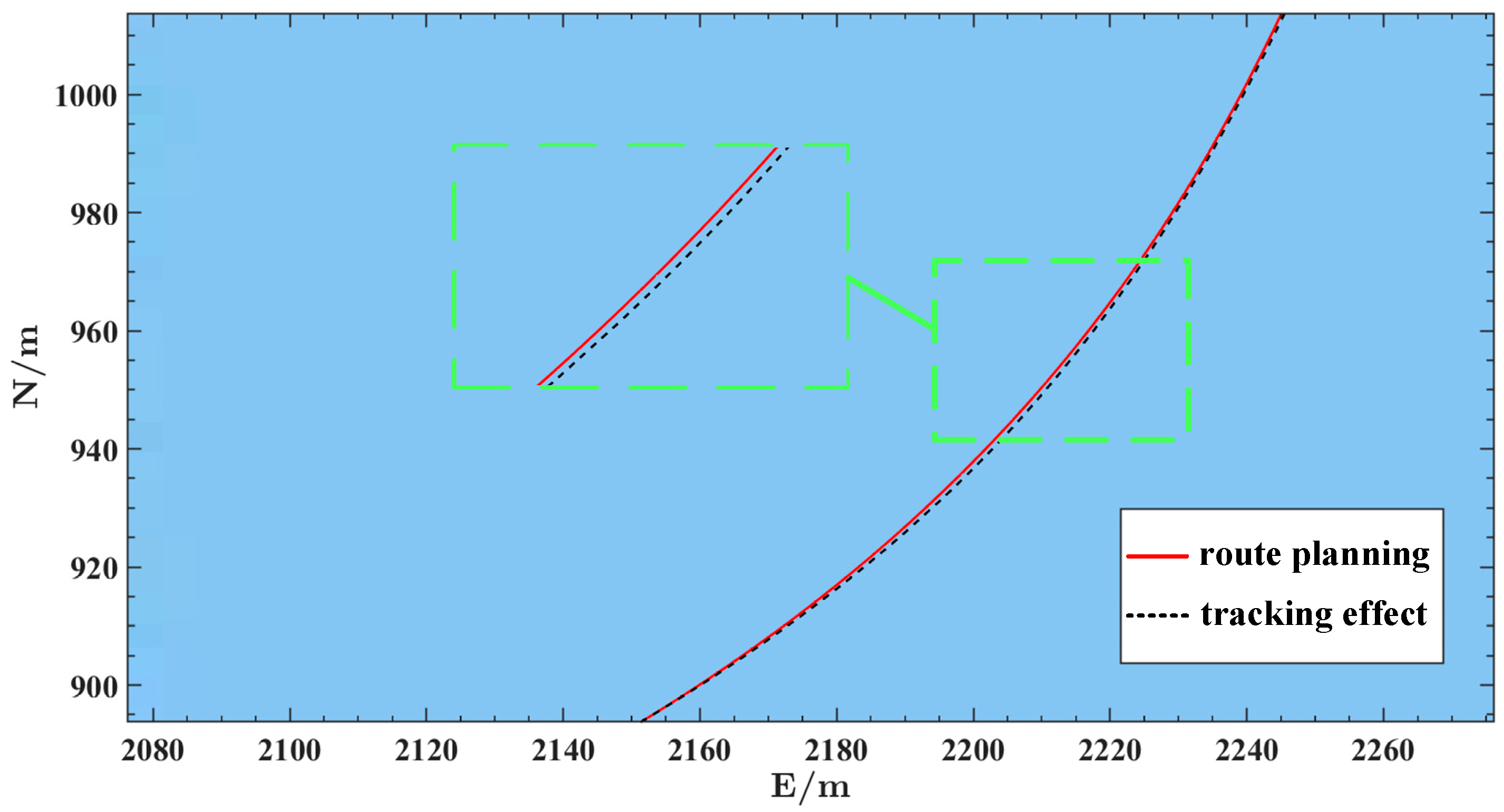
(1)

The dynamic responses of each velocity component remain smooth with minimal fluctuations, reducing speed deviations caused by environmental disturbances. This ensures the ship maintains effective motion during berthing. The path tracking error is significantly reduced to improve the control accuracy.

(2)

By integrating a CNN and a moving optimization mechanism, the system demonstrates enhanced robustness and stability under complex conditions such as wind and wave disturbances. Control commands remain smooth with no significant overshoot, reflecting superior dynamic response performance.

(3)

The control inputs exhibit smooth, continuous variations without abrupt changes, enhancing both system stability and energy efficiency. This indicates that the control method can effectively handle various disturbances and path variations, demonstrating strong environmental adaptability and control robustness.