Abstract
This study proposes an improved super-twisting sliding mode (STSM) control method for a brushless doubly fed induction generator (BDFIG) used in standalone ship shaft power generation systems. Focusing on the problem of the low tracking accuracy of the power winding (PW) voltages caused by the parameter perturbation of BDFIG systems, a mismatched uncertain model of the BDFIG is constructed. Additionally, an improved STSM control method is proposed to address the power load variation and compensate for the mismatched uncertainty through virtual control technology. Based on the direct vector control of the control winding (CW), the proposed method ensured that the voltage amplitude error of the power winding could converge to the equilibrium point rather than the neighborhood. Finally, in the experimental investigation of the BDFIG-based ship shaft independent power system, the dynamic performance in the startup and power load changing conditions were analyzed. The experimental results show that the proposed improved STSM controller has a faster dynamic response and higher steady-state accuracy than the proportional integral control and the linear sliding mode control, with strong robustness to the mismatched uncertainties caused by parameter perturbations.
1. Introduction
Increasing the efficiency of energy utilization has been emphasized with the diminishing availability of traditional fossil energy reserves. Within the maritime industry, there has been a growing adoption of shaft power generation technology to optimize energy efficiency while minimizing operational costs. The brushless doubly fed induction generator (BDFIG) has been found to increase utilization in constant-voltage constant-frequency variable-speed generation systems, particularly due to its brushless design, which eliminates the need for slip rings [1,2]. This feature significantly enhances the reliability and safety of the system, making it a promising solution for energy conversion in maritime applications. Consequently, integrating BDFIGs into ship propulsion systems has caused widespread concern [3,4].
The complex structure and the severe coupling of BDFIG lead to its control difficulties [5]. Due to the variability of the marine environment and climate, the temperature and frequency of BDFIG change [6]. The motor parameters are disturbed, affecting the control accuracy. At the same time, in some cold areas, the ship breaking the ice barrier will also make the motor suffer from load disturbance [7]. Therefore, the control strategy of the BDFIG requires strong robustness.
Much attention is paid to novel control strategies for the application of BDFIG. The vector control (VC) system possesses better dynamic performance by controlling the active and reactive powers of BDFIG [8,9,10]. However, the VC-based controller requires the appropriate decoupling of the system and is therefore sensitive to the presence of the inner parameters perturbations. The direct torque control [11] and direct power control [12,13] methods enhance the robustness of the control system. In contrast, the control is not optimal in real-time when selecting a predefined voltage vector. Moreover, this method may cause torque/power ripples and current waveform distortion.
The controller oriented with the CW-side current is proposed to reduce the influence of voltage fluctuation on the PW-side and has stronger robustness than traditional PW-oriented controllers [5]. Furthermore, by taking the Taylor expansion at the equilibrium point of PW-side voltage, the outer loop is transformed into a linear subsystem, and the control complexity is simplified. However, the uncertainties from model simplification and the mismatched parameter perturbations still exist, which could affect the dynamic response and precision of the controls.
Traditional control methods, such as PI or PID control, achieve the asymptotical convergence of the system by adjusting the proportional, integral and differential gains; they struggle to ensure the high accuracy of the uncertain systems with complex disturbances [14]. Adaptive disturbance rejection control (ADRC) and the disturbance-observer-based (DOB) control methods are proposed to compensate disturbances by using observers, while these methods are sensitive to parameter perturbations [15]. Due to the significant advantages of robustness and parameter insensitivity, SMC methods are used widely for uncertain nonlinear systems [16].
Integral sliding mode control (ISMC) can enhance the control accuracy, and terminal sliding mode control (TSMC) is capable of guaranteeing finite-time convergence while maintaining high precision [17,18]. Meanwhile, these traditional SMC methods suffer from the chattering problem. The chattering leads to the high-frequency switching of control signals because of the sign term in the traditional SMC law [19]. To eliminate the chattering, standard super-twisting sliding mode control (STSM) was designed [20,21,22]. The STSM control methods are widely used in practical applications, with strong robustness against perturbations and chattering-free characteristic [23]. However, the standard STSMs fail to compensate for the mismatched uncertainties, which limits their application in industrial control systems, such as BDFIG control systems.
This article proposes an improved STSM control algorithm combined with the virtual control law to compensate for the mismatched uncertainties caused by parameter perturbations, which guarantee the robustness and quick dynamic response of the controller. The innovation of the study can be outlined as follows:
- (1)
- Compared with traditional controllers, the improved STSM control method avoids the low-pass filter and improves the transient response of the terminal voltage.
- (2)
- The matched and mismatched uncertainties in BDFIG-based ship shaft power generation systems are considered and compensated.
The study is organized as follows. Section 2 describes the BDFIG mathematical model with parameter perturbation uncertainties. The main contribution of this research is presented in Section 3, which comprises the design of the super-twisting sliding mode controller (STSMC) and the stability analysis based on Lyapunov theory. Section 4 shows the experimental results and the rapidness and robustness of the uncertainties of the BDFIG control system. Finally, Section 5 presents the conclusions.
2. BDFIG Mathematical Model with Perturbations
2.1. Traditional BDFIG Model
While BDFIG operates for an independent power generation system, the PW is connected to a load rather than a power grid. The traditional PW-side voltage orientation control method ignores the fluctuation of PW-side voltage. In this article, the rotation frequency of the d–q coordinates is set as the angle frequency of CW to enhance the effectiveness of the control system.
The stator voltage function of the PW is given as follows:
where usd and usq, respectively, represent the stator voltage of PW in the d- and q-axes, isd and isq are the stator current of the PW, Rsd and Rsq are the stator resistance of the PW, ψsd and ψsq the stator flux of the PW, and ωs1 is the angular frequency of the CW.
The stator flux function of the PW is presented as:
where ird and irq, respectively, represent the rotor current in the d- and q-axes, Ls is the self-inductance of PW, and Lsr the mutual inductance between the PW and the rotor.
The stator voltage function of the CW is:
where us1d and us1q, respectively, represent the stator voltage of CW in the d- and q-axes, is1d and is1q are the stator current of CW, Rs1d and Rs1q correspond to the stator resistance of CW, ψs1d and ψs1q represent the stator flux of CW, ps and ps1, respectively, represent the number of pole pairs in PW side and the CW side, and ωr is the angular frequency of the rotor.
The stator flux of CW can be presented as:
where Ls1 represents the self-inductances of CW, and Ls1r represents the mutual inductance between the CW and the rotor.
The voltage function of the rotor can be expressed as:
where urd and urq, respectively, represent the rotor voltage in the d- and q-axes, Rrd and Rrq correspond to the rotor resistance, ψrd and ψrq are the rotor flux, and ωs is the angular frequency of PW.
The rotor flux function is:
where Lr represents the self-inductances of the rotor.
Under a stable doubly fed operation mode, the shaft speed is satisfied as follows:
The rotor voltage is satisfied with urd = urq = 0 when the load is a three-phase symmetric load. Combined with (5) and (6), the rotor current can be expressed as:
where s represents the differential operator. Compared to the self-induction of rotor winding, the rotor resistance is small enough to be neglected. Thus, the pole is approximately equal to zero for the first part in (8), which can be simplified as −(Lsrisd + Ls1ris1d)/Lr. In the rest, the term (Rr + Lrs)2 is small enough to be neglected as well. Finally, the rotor d-axis current (8) is simplified as:
Similarly, the rotor q-axis current (9) can be simplified as:
Substituting Equations (4), (7), (10) and (11) into Equation (3), the voltage of CW can be obtained as:
where σs1 = 1 − L2s1r/(Ls1 Lr) is defined by the leakage inductance of CW, and Ds1d = α1is1q + α2isd + α3i1q and Ds1q = α4is1d + α5isd + α6isq represent the cross disturbance of the d and q components, where:
α1, α2, α3, α4, α5 and α6 represent the cross-perturbation parameters, α1is1q and α4is1d can decouple the current loop of d-q axis, and the rest of the terms compensate for the disturbance in the PW current caused by load fluctuation. If we set is1q = 0, then is1d is equal to the amplitude of the CW current Is1. At this point, the current decoupling vector control of CW is completed.
To simplify the voltage outer loop, we analyze the system under steady-state conditions. The flux linkage ψsd and ψsq can be assumed as constant in this case. Substituting (2) and (12), is1q = 0 and is1d = Is1 into (1), the PW-side voltage can be obtained as follows:
where Is1 is the amplitude of the CW current, and the amplitude of the PW is expressed as:
where subscript character E represents the state of equilibrium. Us (Is1E) can be regarded as a given value of the output phase voltage amplitude at the PW side. Then, the tracking error of the output phase voltage amplitude at the PW side can be expressed as follows:
where subscript character E represents the state of equilibrium.
Combining (14) and (15) gives:
where Ku = ωs1LsrLs1r[ωs1LsrLs1rIs1E + ωs1(LsLr)isd − RsLrisq] is a linear proportional term.
From (14), the CW current amplitude Is1E at the equilibrium point is as follows:
where β1 = ωs1Ls − ωs1/Lr, β2 = ωs1LsrLs1r/Lr.
2.2. Parameter Perturbation Analysis
Defining the tracking error of the PW-side voltage as eU, according to the mathematical model of the BDFIG, eU can be expressed as:
where Usref represents the reference value of the PW output voltage.
Taking the parameter perturbation into consideration, the resistance and inductance can be rewritten as:
where Ri0 and Lj0 are the nominal values of stator and rotor resistance and inductance, respectively, and ΔRi and ΔLj are the parameter perturbations of stator and rotor resistance and inductance, respectively. The custom motor parameters in BDFIG also vary with the stator and rotor resistance and inductance of the motor:
where are the nominal values of the custom motor parameters. The motor perturbation parameters are as follows:
If we suppose that all the uncertainties have definite upper bounds, they are satisfied as:
Considering the variations in the motor parameters, the following parameter perturbations are defined as:
where , B10 = L1r0L2r0, , B30 = Rs0Lr0 are the nominal value of the custom motor parameters. Then the perturbation of the motor parameters are as follows:
We suppose that all the uncertainties have definite upper bounds, satisfied as:
We design the virtual control law as ΔIs1 to compensate the uncertainties in the PW-side voltage loop. Then, the reference CW-side current and tracking error are expressed as:
Thus, considering the uncertainties, the voltage tracking error in (18) can be rewritten as:
Defininf the virtual control law , the above can be further simplified to:
where gain uncertainty ΔKu0/Ku0 is satisfied with |ΔKu0/Ku0| < Mδs < 1.
The matrix expression of (12) can be obtained as:
where isdq = [isd,isq]T, is1dq = [is1d,is1q]T, us1dq = [us1d,us1q]T. Considering uncertainties, the coefficient matrices are satisfied with: F0 = F00 + ΔF0, F1 = F10 + ΔF1, G = G0 + ΔG, F2 = F20 + ΔF2: . We assume that all the uncertainties have an upper bound and are expressed by:
where us1e is the rated voltage of the CW, ise is the rated current of PW, and is1e is the rated current of the CW. Uncertainties (30) are transformed into:
where the uncertainty δ = ΔGudq+ ΔF0is1dq + (G + ΔG)(F10is1dq +F20is1dq), and udq= us1dq + F10is1dq + F20isdq.
The control block diagram of the system is shown in Figure 1.
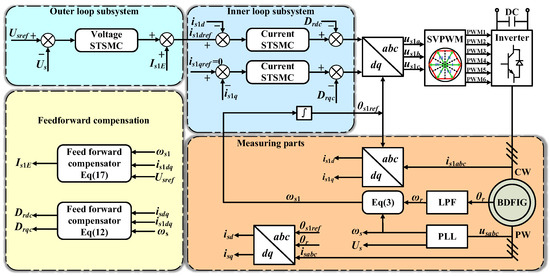
Figure 1.
The control block diagram of the BDFIG-based independent power generation system.
3. STSM Controller Design
The objective of the above system is to design a controller to compensate for the matched and mismatched uncertainties in the BDFIG system, so that the tracking error of the power winding voltage amplitude converges to zero rather than in the neighborhood. A virtual control law is designed to compensate for the unmatched uncertainties and force the state eU to converge to zero. After that, the actual control law udq is designed to compensate for the matched uncertainty in the system and make is1dq achieve the accurate tracking of its reference signal is1dqref.
To guarantee that the tracking error of the PW-side voltage eU converges to zero, the STSM controller can guarantee the condition for the control objective Us = Usref, and eU = Uref − Us is defined in (18).
Lemma 1
(see [19]). Consider a system = f(x), f(0) = 0, x ∈ , if there exists a positive definite continuous function V (x): U → R, real numbers c > 0 and 0 < α < 1, and an open neighborhood U0 ⊂ U of the origin such that + c(x) ≤ 0, x
∈ U0{0}, and then V (x) can approach zero in a finite time.
Proposition 1.
With the virtual control law, the outer-loop voltage tracking error dynamics can be regulated to converge to the equilibrium point in finite time:
where k1 and k2 are positive real numbers.
Proof of Proposition 1.
According to (29) and (34), the derivative is expressed by:
where ε = , which represents the uncertainties and the derivative of ε, is bounded by Mdε.
We define:
Thus, (35) is rewritten as:
We define:
The derivative of ζ1 can be expressed as:
The above can be simplified to:
where .
The characteristic equation of A is expressed by:
Considering that k1 and k2 are positive numbers, guaranteeing k2 > Mdε, then the characteristic root of (41) is guaranteed to be negative, which is proof that A is a Hurwitz matrix. For any positive definite matrix Q1, the solution P1 of ATP1 + P1A = −Q1 is a unique and positive definite. Thus, we propose the Lyapunov function V as follows:
Combined with the PW error equation, the derivative of V is expressed as:
Considering that V is a positive definite quadratic form, P is satisfied as:
where:
From (44), we can obtain:
Similarly, Q1 is a positive definite and is satisfied with the conclusion in (44). Then, we have:
Finally:
V, P1 and Q1 are positive definite and the derivative of V is negative definite. According to Lemma 1, the virtual control law satisfies the Lyapunov stability proof conditions and can converge in finite time. The mismatched uncertainties caused by the parameter perturbations are fully compensated by the virtual control law, and the PW voltage value can track the ideal value. The proof under the virtual control law is completed. □
Let and , where is1ref is the given value of the current on the CW side. is1ref is a matrix composed of is1dref = u0 and is1qref = 0. For (33), the error dynamics can be expressed as:
Theorem 1.
Based on the virtual control law (34) and the actual control law below, the inner-loop current tracking error dynamics ei and its derivatives can be adjusted to converge to zero in a finite time:
Proof of Theorem 1.
Substituting (51) into (49) gives:
We define:
Thus, (49) can be rewritten as:
We define:
The derivative of ζ is:
The above can be simplified to:
where .
The characteristic equation of B is given by:
Given that k3 and k4 are positive numbers with the condition that k4 > Mdδ, it is ensured that the characteristic roots of (59) are negative, which proves that B is a Hurwitz matrix. For all positive definite matrix Q2, the equation BTP2 + P2B = −Q2 has a unique and positive definite solution P2. Based on this, we can define the Lyapunov function V as follows:
Combined with the CW error equation, the derivative of V can be expressed as:
Given that V is a positive definite quadratic form, P2 meets the following:
where:
By combining Equations (62) and (63), we can obtain:
Similarly, if Q2 is a positive definite and satisfied with the conclusion in (62), then we have:
Finally:
Since V, P2, Q2 are positive definite and the derivative of V is negative definite, it is probable (according to Lemma 1) that the dynamic error converges to zero in a finite time. The actual control law can guarantee the virtual control law to track the ideal PW current value, which fully compensates the matched uncertainties and achieves finite-time convergence. The stability proof of the system under the actual control law is completed. □
4. Experimental Results
To verify the effectiveness of the controller design method proposed in this study, the control performance of the controller in the actual system is verified. The experiment is based on the BDFIG-based ship shaft independent power system shown in Figure 2. The BDFIG experimental platform includes a 5 kVA brushless doubly-fed motor (Tianjin Tongyu Jiahe Energy Saving Technology Co., Ltd., Tianjin, China) and a 10 kW induction motor (Zhong Dalide Intelligent Transmission Equipment Co., Ltd., Ningbo, China) as the prime mover to drive the BDFIG, as well as a set of four-quadrant inverters based on a TMS320F28335 chip (Texas instruments, Dalas, TX, USA), voltage and current sensors (Precision Electronics (Shenzhen) Co., Ltd., Shenzhen, China), and a host computer built by LabView. The communication protocol selects the CAN communication protocol, and the motor sampling frequency is set as 5 kHz. The parameters of the brushless doubly-fed machine on the experimental platform are shown in Table 1 below.
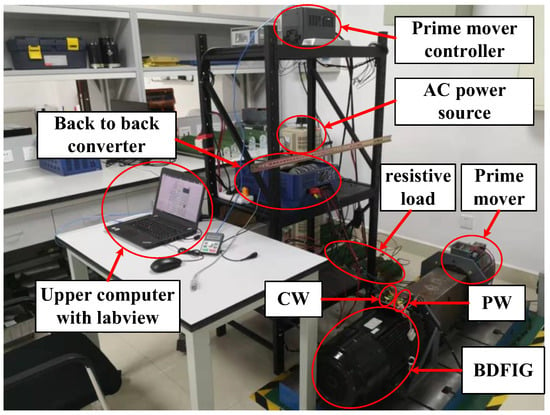
Figure 2.
Laboratory equipment of the BDFIG ship shaft independent power system.

Table 1.
Experiment parameters.
The startup and loading change conditions were investigated in an experiment. In the experiment, the reference voltage was set at 150 V. To account for uncertainties stemming from aging and temperature variations, the values of Ri and Li in the control algorithm were adjusted to 120% of their nominal values. The startup experiment results are shown in Figure 3 and Figure 4. The CW d-axis current rising response time with proportional-integral (PI), linear sliding mode (LSM), and STSM controllers are 0.366 s, 0.297 s, and 0.116 s, respectively. STSM exhibits a quicker dynamic response. The same conclusion can be drawn from experimental data on the current of the q-axis.
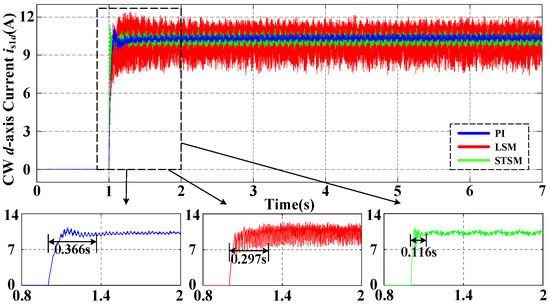
Figure 3.
Experimental results of the CW d-axis current with PI, LSM, and STSM under startup conditions.
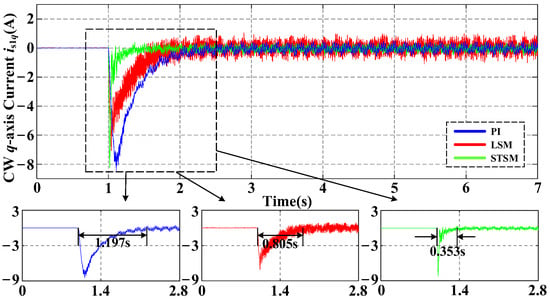
Figure 4.
Experimental results of the CW q-axis current with PI, LSM, and STSM under startup conditions.
Figure 5 and Figure 6 show the CW phase current and the effective values of PW line voltage under the starting experiment. In Figure 5 and Figure 6, the proposed STSM has smaller steady-state fluctuations compared to LSM and PI, but it has a faster dynamic response. These experimental results demonstrate that the proposed STSM controller exhibits a quick dynamic response and strong robustness against the uncertainties caused by parameter perturbation.
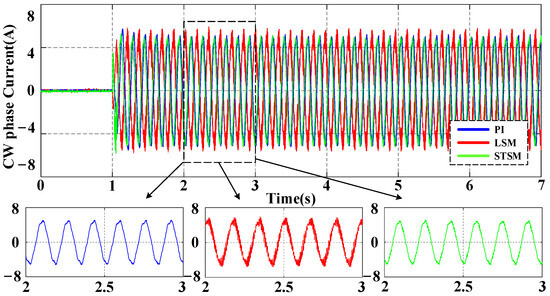
Figure 5.
Experimental results of the CW phase current with PI, LSM and STSM under startup conditions.
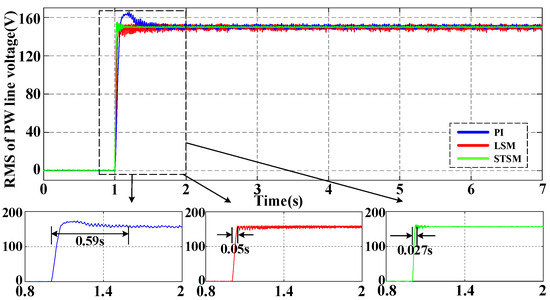
Figure 6.
Experimental results of the RMS of the PW line voltage with PI, LSM and STSM under startup conditions.
The experiment results under loading condition are shown in Figure 7 and Figure 8. In Figure 7 and Figure 8, the stability time of the d-axis current and the recovery time of the q-axis current with STSMC are both smaller than PI controller. The robustness against the uncertainties with proposed STSM is proven by the results of the loading experiment.
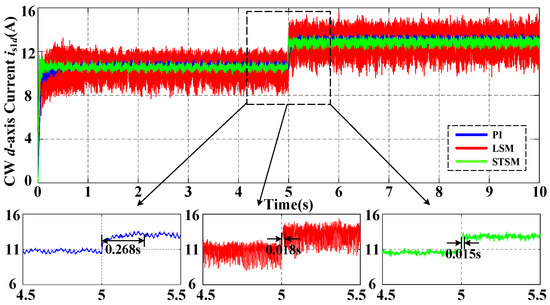
Figure 7.
Experimental results of the CW d-axis current with PI, LSM, and STSM under loading conditions.
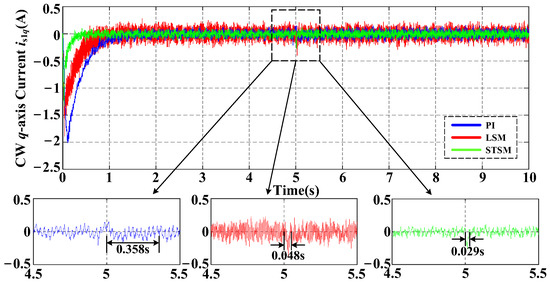
Figure 8.
Experimental results of the CW q-axis current with PI, LSM and STSM under loading conditions.
To verify the robustness of the proposed method under parameter perturbation. The values of Ri and Li in the control algorithm are adjusted to 160% of the nominal value, and the experimental results are shown in Figure 9 and Figure 10. The d-axis current response and q-axis current response of the CW side under the three control methods all show that the CW current response under the STSM control method have smaller ripples.
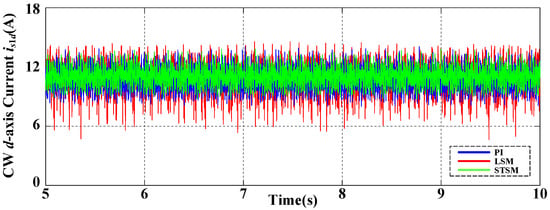
Figure 9.
Experimental results of the CW d-axis current with PI, LSM, and STSM under 150% parameter perturbation.
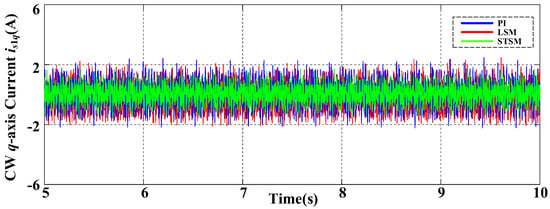
Figure 10.
Experimental results of the CW q-axis current with PI, LSM and STSM under 150% parameter perturbation.
Compared with the existing methods [12,15,24,25], the steady-state time and accuracy are shown in Table 2.

Table 2.
Comparison of existing methods.
It can be seen in Table 2 that the mismatched uncertainties lead to a reduction in the steady-state accuracy of active disturbance rejection control (ADRC), ISMC, TSMC, and standard STSM control. The improved STSM control method can overcome the mismatched uncertainties, thus achieving the highest accuracy among the methods. For the dynamic performance, the proposed method has the fastest dynamic response, while other methods compromise their response speed to guarantee the steady-state accuracy. The control of ISMC and TSMC has chattering, while the control signals using standard STSM and improved STSM are smooth without chattering. In summary, the proposed improved STSM control represent better control performance than the other methods in terms of chattering suppression, dynamic response, and especially steady-state accuracy under mismatched uncertainties.
5. Conclusions
In this study, an improved STSM controller of the BDFIG for standalone ship shaft power generation systems is designed. The mechanism of parameter perturbations is analyzed, and the mismatched uncertain model of BDFIG is established to improve the modelling accuracy. The proposed improved STSM method uses virtual control technology to compensate for the mismatched uncertainties, so that the PW voltage error can converge to the equilibrium point rather than the neighborhood, and the steady-state accuracy of the system is enhanced. Meanwhile, the improved STSM method brings excellent dynamic performance and eliminates chattering, which improves the rapidity and robustness of the standalone ship shaft power generation systems. The excellent performance of the proposed method in voltage control is verified by experiments. However, this study has the following two limitations:
- (1)
- Real-world component selection and constraints: idealized components are assumed in the theoretical controller design and experimental validation. However, practical applications face challenges related to the component’s selection, bandwidth limitations, noise sensitivity, the cost-effectiveness of high-bandwidth sensors, and marine operating conditions (vibration, high temperature, high humidity).
- (2)
- Computational complexity: the improved STSM method, while effective, has high computational requirements, especially for the existing control chip of the ships.
Future research will focus on addressing these limitations:
- (1)
- Hardware implementation: to verify the controller’s effectiveness, rigorous tests simulating real marine environments and using commercial chip will be conducted in our future studies.
- (2)
- Algorithm optimization: methods reducing the computational burden of the proposed improved STSM will be explored in our future research.
Author Contributions
X.F.: data curation, visualization, software, validation, writing—original draft; M.Z.: conceptualization, methodology, supervision; Y.J.: conceptualization, formal analysis, visualization; L.J.: formal analysis, methodology, project administration, resources, supervision; Y.L.: writing—review and editing, validation, investigation; Y.Y.: formal analysis, supervision, validation. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China under grant 52477041 and in part by the Natural Science Foundation for Excellent Young Scholars of Heilongjiang Province under grant YQ2024E043.
Data Availability Statement
The datasets generated during or analyzed during the current study are available from the corresponding author on reasonable request.
Acknowledgments
This research was funded by the New Energy Motor System and Key Materials Innovation Center in Harbin University of Science and Technology.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyzes, or interpretation of data; in the writing of the manuscript; nor in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| STSM | super-twisting sliding mode |
| BDFIG | brushless doubly fed induction generator |
| CW | control winding |
| PW | power winding |
| SMC | sliding mode control |
| ISMC | integral SMC |
| VC | vector control |
| TSMC | terminal sliding mode control |
| STSMC | super-twisting sliding mode controller |
| PI | Proportional integral |
| LSM | linear sliding mode |
| ADRC | active disturbance rejection control |
References
- Liu, Y.; Hussien, M.G.; Xu, W.; Shao, S.; Rashad, E.M. Recent Advances of Control Technologies for Brushless Doubly-Fed Generators. IEEE Access 2021, 9, 123324–123347. [Google Scholar] [CrossRef]
- Knight, A.M.; Betz, R.E.; Dorrell, D.G. Design and Analysis of Brushless Doubly Fed Reluctance Machines. IEEE Trans. Ind. Appl. 2021, 49, 50–58. [Google Scholar] [CrossRef]
- Abad, G.; Lopez, J.; Rodriguez, M.; Marroyo, L.; Iwanski, G. Doubly Fed Induction Machine: Modeling and Control for Wind Energy Generation; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Boldea, I.; Tutelea, L.N.; Wu, C.; Blaabjerg, F.; Liu, Y.; Hussien, M.G.; Xu, W. Fractional kVA Rating PWM Converter Doubly Fed Variable Speed Electric Generator Systems: An Overview in 2020. IEEE Access 2021, 9, 117957–117968. [Google Scholar] [CrossRef]
- Xu, W.; Dong, D.; Liu, Y.; Yu, K.; Gao, J. Improved sensorless phase control of stand-alone brushless doubly-fed machine under unbalanced loads for ship shaft power generation. IEEE Trans. Energy Convers. 2018, 33, 2229–2239. [Google Scholar] [CrossRef]
- Vadim, K.; Goncharov, N. Problem statement on the vessel braking within ice channel, Transportation Safety and Environment. Transp. Saf. Environ. 2021, 3, 50–56. [Google Scholar]
- Chen, X.; Wei, C.; Xin, Z.; Zhao, J.; Xian, J. Ship Detection under Low-Visibility Weather Interference via an Ensemble Generative Adversarial Network. J. Mar. Sci. Eng. 2023, 11, 2065. [Google Scholar] [CrossRef]
- Shao, S.; Abdi, E.; Barati, F.; McMahon, R. Stator-flux-oriented vector control for brushless doubly fed induction generator. IEEE Trans. Ind. Electron. 2009, 56, 4220–4228. [Google Scholar] [CrossRef]
- Hussien, M.G.; Liu, Y.; Xu, W.; Junejo, A.K.; Allam, S.M. Improved MRAS Rotor Position Observer Based on Control Winding Power Factor for Stand-Alone Brushless Doubly-Fed Induction Generators. IEEE Trans. Energy Convers. 2022, 37, 707–717. [Google Scholar] [CrossRef]
- Poza, J.; Oyarbide, E.; Sarasola, I.; Rodriguez, M. Vector control design and experimental evaluation for the brushless doubly fed machine. IET Electr. Power Appl. 2009, 3, 247–256. [Google Scholar] [CrossRef]
- Boudjema, Z.; Taleb, R.; Djeriri, Y.; Yahdou, A. A novel direct torque control using second order continuous sliding mode of a doubly fed induction generator for a wind energy conversion system. Turk. J. Electr. Eng. Comput. Sci. 2017, 25, 965–975. [Google Scholar] [CrossRef]
- Sadeghi, R.; Madani, S.M.; Ataei, M.; Kashkooli, M.R.A.; Ademi, S. Super-twisting sliding mode direct power control of a brushless doubly fed induction generator. IEEE Trans. Ind. Electron. 2018, 65, 9147–9156. [Google Scholar] [CrossRef]
- Yan, X.; Cheng, M. A robustness-improved control method based on ST-SMC for cascaded brushless doubly fed induction generator. IEEE Trans. Ind. Electron. 2020, 68, 7061–7071. [Google Scholar] [CrossRef]
- Sankhwar, P. Application of Permanent Magnet Synchronous Motor for Electric Vehicle. Indian J. Des. Eng. 2024, 4, 1–6. [Google Scholar] [CrossRef]
- Guo, H.; Zhang, X. Extended State Observer (ESO) Based Control Strategy with Parameter Optimization for Brushless Doubly-fed Machine. In Proceedings of the 2017 2nd International Conference on Automatic Control and Information Engineering (ICACIE 2017), Hong Kong, China, 26–28 August 2017. [Google Scholar]
- Utkin, V.; Poznyak, A.; Orlov, Y.; Polyakov, A. Conventional and high order sliding mode control. J. Frankl. Inst. 2020, 357, 10244–10261. [Google Scholar] [CrossRef]
- Pan, Y.; Yang, C.; Pan, L.; Yu, H. Integral sliding mode control: Performance, modification, and improvement. IEEE Trans. Ind. Inform. 2017, 14, 3087–3096. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, X.; Han, F. On nonsingular terminal sliding-mode control of nonlinear systems. Automatica 2013, 49, 1715–1722. [Google Scholar] [CrossRef]
- Feng, Y.; Han, F.; Yu, X. Chattering free full-order sliding-mode control. Automatica 2014, 50, 1310–1314. [Google Scholar] [CrossRef]
- Levant, A. Sliding order and sliding accuracy in sliding mode control. Int. J. Control. 1993, 58, 1247–1263. [Google Scholar] [CrossRef]
- Levant, A. Chattering analysis. IEEE Trans. Autom. Control. 2010, 55, 1380–1389. [Google Scholar] [CrossRef]
- Moreno, J.A.; Osorio, M. Strict Lyapunov functions for the super-twisting algorithm. IEEE Trans. Autom. Control. 2012, 57, 1035–1040. [Google Scholar] [CrossRef]
- Manzanilla, A.; Ibarra, E.; Salazar, S.; Zamora, Á.E.; Lozano, R.; Muñoz, F. Super-twisting integral sliding mode control for trajectory tracking of an Unmanned Underwater Vehicle. Ocean. Eng. 2021, 234, 109164. [Google Scholar] [CrossRef]
- Yang, X.; Qin, Y.; Zhan, J.; Li, Y.; Hao, S.; Fu, Z. Direct Power Control of BDFRG Based on Novel Integral Sliding Mode Control. Recent Adv. Electr. Electron. Eng. 2024, 17, 1–16. [Google Scholar] [CrossRef]
- Zhan, Y.; Guo, Y.; Zhu, J. Terminal sliding mode speed controller based on vector control for brushless doubly fed machine. In Proceedings of the 2011 International Conference on Applied Superconductivity and Electromagnetic Devices, Sydney, Australia, 14–16 December 2011. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).