Abstract
Autonomous ship navigation systems must ensure safe and efficient route planning while complying with the International Regulations for Preventing Collisions at Sea (COLREGs). This paper presents an integrated navigation framework that combines chart-based global path planning with a Model Predictive Control (MPC) approach for local trajectory tracking and COLREG-compliant collision avoidance. The method generates feasible reference routes using maritime charts and predefined waypoints, while the MPC controller ensures precise path following and dynamic re-planning in response to nearby vessels and coastal obstacles. Coastal features and shorelines are modeled using Global Self-consistent, Hierarchical, High-resolution Geography data, enabling MPC to treat landmasses as static obstacles. Other vessels are represented as dynamic obstacles with varying speeds and headings, and COLREG rules are embedded within the MPC framework to enable rule-compliant maneuvering during encounters. To address real-time computational constraints, a simplified MPC formulation is introduced, balancing predictive accuracy with computational efficiency, making the approach suitable for embedded implementations. The navigation framework is implemented in a MATLAB-based simulation with real-time visualization supporting multi-vessel scenarios and COLREG-aware vessel interactions. Simulation results demonstrate robust performance across diverse maritime scenarios—including complex multi-ship encounters and constrained coastal navigation—while maintaining the shortest safe routes. By seamlessly integrating chart-aware path planning with COLREG-compliant, MPC-based collision avoidance, the proposed framework offers an effective, scalable, and robust solution for autonomous maritime navigation.
1. Introduction
The development of Maritime Autonomous Surface Ships (MASSs) has the potential to significantly enhance the safety, efficiency, and sustainability of maritime transport. The Maritime Safety Committee (MSC) of the International Maritime Organization (IMO) is currently preparing the MASS Code, which is expected to be adopted as non-mandatory in 2026 and mandatory in 2030 [1].
Recent advancements in autonomous ship navigation have focused on compliance with the International Regulations for Preventing Collisions at Sea (COLREGs), dynamic obstacle avoidance, and path planning under environmental constraints. Since adherence to the COLREGs is fundamental for safe autonomous operation, considerable research has been devoted to rule-embedding techniques. Zhang et al. provide a comprehensive survey of collision avoidance systems and emphasize the persistent challenges in achieving fully autonomous navigation in complex maritime environments [2]. The authors also conclude that collision-free navigation would significantly benefit the integration of MASS autonomy in various maritime scenarios. García Maza critically analyzes COLREG ambiguities, emphasizing the need for homogeneous criteria for the regulation of navigable areas to reduce the possibility of problematic encounters, especially with the emergence of MASSs [3].
Rule-based systems, such as Constapel’s operationalized COLREG assessment framework, demonstrate how situation statements can formalize encounter scenarios [4]. However, as Chang notes, inconsistencies persist in translating COLREGs into machine-interpretable constraints, particularly for multi-ship encounters, and while academic research has focused on developing autonomous collision avoidance (CA), it is producing inconsistent results compared to conventional navigation practices [5]. Also, Kim and Park provided insights into the notable disparity between the understanding of COLREG rules by navigators and automated collision avoidance algorithms [6]. As a possible solution approach, Lyu addressed these challenges by classifying multi-vessel scenarios using the velocity obstacles algorithm and coupling risk assessment with COLREG responsibilities [7].
In terms of dynamic obstacle avoidance and path planning under environmental constraints, Model Predictive Control (MPC) provides a promising method for balancing trajectory optimization with dynamic constraints. Codesseira validates MPC’s robustness for underactuated ships in path following [8], while Zhang integrates spatial reformulation for time-optimal obstacle avoidance in a hierarchical MPC framework [9]. Tsolakis extends MPC to long-horizon trajectory optimization, incorporating COLREGs as traffic constraints [10]. Xue introduces human-like MPC with adaptive risk boundaries using control barrier functions, bridging safety and computational efficiency [11]. For coastal navigation, Fagerhaug proposes “Oceanscape”, a graph-based MPC framework that encodes maritime charts into geometric learning structures, enabling COLREG-aware pathfinding in complex environments [12].
Various hybrid and learning-based approaches have been investigated for handling COLREG compliance in dynamic environments. Wen proposed deep reinforcement learning (DRL)-based path planning for MASSs to address collision avoidance path planning while adhering to the COLREGs, though its reliance on pre-recorded data limits adaptability [13]. Shen proposed a novel differential evolution deep reinforcement learning algorithm to address problems of local and global path planning [14]. He combined MPC with artificial potential fields to address local optima in complex encounters [15], while Wang applied MPC to underwater vehicle-manipulator systems, demonstrating scalability to dynamic obstacles [16].
Namgung and Kim proposed a neuro-fuzzy inference system for collision risk assessment, enabling early and COLREG-consistent alerts based on an enlarged ship domain model [17]. In a follow-up study, Namgung combined fuzzy logic with velocity obstacle methods to design a local route planner that explicitly detected encounter types and applied corresponding avoidance maneuvers [18]. Both studies rely on rule-based logic to enforce COLREG compliance.
Despite considerable progress in autonomous ship navigation, several key limitations remain. Öztürk identifies insufficient COLREG relevance in velocity obstacle and artificial potential field methods [19], while Lyu highlights the underutilization of coupled speed–course adjustments in decision-making processes [20]. Fu emphasizes the trade-off between real-time performance and optimality in multi-objective planners [21]. Liu tackles this by integrating digital twins and an enhanced velocity obstacle algorithm to develop an autonomous collision avoidance framework for the ships’ routing waters [22]. Recent research trends focus on embedding COLREG rules by formalizing them as optimization constraints (e.g., [3,10]), improving environmental awareness through the integration of nautical chart data (e.g., [12]), and modeling dynamic obstacles (e.g., [9]), and enhancing real-time adaptability by combining MPC with machine learning (e.g., [11]) or DRL methods (e.g., [14]).
This study advances these directions by unifying chart-aware path planning and COLREG-constrained MPC for collision avoidance in a single framework, addressing gaps in dynamic coastal navigation identified in [2,5,19]. MPC is particularly well-suited for autonomous maritime applications, as it naturally accommodates motion constraints, predicts future trajectories, and supports multi-objective optimization. Compared to other MPC-related research works [10,11], this study integrates Model Predictive Control with global route planning based on nautical charts, and proposes a novel, simplified, and computationally efficient MPC formulation.
The proposed approach incorporates high-resolution coastline data (GSHHG) to model static obstacles such as land masses and coastal structures. These are treated within the MPC optimization in addition to the dynamic targets, enabling the simultaneous avoidance of both ships and shorelines. Global path planning algorithms are applied to generate a sequence of route waypoints based on chart data, and the MPC controller ensures accurate trajectory tracking and continuous adaptation to environmental changes.
The proposed framework is implemented in MATLAB (R2024b) as a real-time simulation environment with graphical visualization. The system supports multi-vessel scenarios and demonstrates robust performance in diverse navigation conditions, including restricted waters and open seas. The simulation environment is open-source and publicly available on GitHub [23], providing a valuable tool for the research community to test and develop autonomous navigation strategies.
The main contributions of this paper are as follows:
- The integration of GSHHG cartographic data for shoreline-aware navigation.
- A two-level navigation system combining global path planning with local MPC-based collision avoidance.
- A novel, simplified, and computationally efficient MPC formulation.
- A unified MPC navigation framework for autonomous ships integrating COLREG-compliant collision avoidance and trajectory tracking.
- An open-source, MATLAB-based multi-vessel simulation environment for the development and testing of autonomous navigation strategies.
The rest of the paper is organized as follows: Section 2 presents the methodology, with descriptions of the ship model, navigation framework, route following, and MPC-based navigation. Section 3 discusses the simulation results, and Section 4 and Section 5 provide a discussion and summarize the conclusions and future research directions.
2. Methodology
2.1. Navigation Levels
The methodology presented in this paper addresses autonomous ship navigation by combining chart-aware path planning and collision-avoidant navigation across two complementary navigation levels:
- Global path planning;
- Local collision avoidance and trajectory planning.
Global path planning optimizes a ship’s route from its departure point to its destination, resulting in a sequence of waypoints. A ship’s route optimization is performed in the early stages of navigation using its Electronic Chart Display and Information System (ECDIS) and aims to generate the shortest collision-free route from the starting point to the destination point by considering static obstacles and environmental constraints. The global planner operates using pre-existing cartographic data and defines the high-level route structure for the voyage.
Local collision avoidance and trajectory planning, in contrast, are responsible for dynamic decision-making during navigation. This level operates in real-time and ensures that the vessel adheres to COLREG rules while safely avoiding both static (e.g., landmasses, buoys) and dynamic obstacles (e.g., nearby vessels). The local planner must continuously adapt to unpredictable elements in the environment, such as sudden course or speed changes from other ships. To achieve this, the proposed framework utilizes a Model Predictive Control (MPC) approach, which incorporates the vessel’s basic parameters, prediction of future motion, and multi-objective optimization.
The local planner receives input from sensors and environmental models—such as AIS-based vessel tracking and the ECDIS—to construct a dynamic situational map of the environment. This information is then used in MPC to predict the trajectories of surrounding vessels over a finite time horizon and determine the optimal control actions for the own ship. This allows the ship to make context-aware navigation decisions that balance safety, rule compliance, and trajectory efficiency. The local planner also follows a series of pre-planned waypoints from the global planner and adjusts the ship’s heading accordingly, ensuring smooth and continuous operation even in dense traffic or restricted waters.
This study considers two levels (global path planning and local collision avoidance and trajectory planning) and does not take into account the layer of motion control, which refers to ship steering and closed-loop control. The motion control is considered as a physical implementation of navigation commands, issued at the higher navigation levels, which is not relevant within the scope of this study.
2.2. Global Path Planning
The global path planner operates on electronic nautical charts that include coastline geometry, restricted zones, shallow areas, and other navigational constraints. In this study, the Global Self-consistent Hierarchical High-resolution Geography (GSHHG) dataset was used to construct the situational map of the maritime environment [24]. Based on GSHHG data, the marine space was segmented into three regions: open sea, land, and coastal areas. Route planning was restricted to the open sea region and needed to avoid land masses while maintaining safe distances from shallow coastal zones.
The global planner computes a sequence of waypoints that form the reference trajectory from the departure location to the intended destination while avoiding non-navigable zones such as land and restricted coastal waters. The planned route can be updated during the voyage in response to mission changes or updated environmental information.
Commonly used algorithms for global route planning include dynamic programming, A*, Theta*, Dijkstra, trajectory point guidance, and others [25,26,27,28,29,30]. Table 1 summarizes and compares the considered path planning algorithms. In this study, the Theta* algorithm was selected to implement the global route planner due to its efficient and smooth pathfinding in complex coastal conditions. The resulting route is a piecewise linear path composed of feasible waypoints that satisfy chart-based constraints and provide a structured input for the local trajectory planner.

Table 1.
Comparison of route planning algorithms for maritime navigation.
To mathematically define the waypoint sequence, let W = [w0, w1, …, wN] denote the ordered set of waypoints, where each waypoint wi ∈ ℝ2 represents a position in a two-dimensional navigational space (latitude and longitude). The waypoint sequence must satisfy the following conditions:
- Start and goal constraints, where pstart and pgoal are the given departure and destination positions, respectively:
w0 = pstart, wN = pgoal
- 2.
- The feasibility of route segments, where F ⊆ ℝ2 denotes the set of feasible (navigable) points defined by the chart data and line(·,·) represents the straight-line path between two consecutive waypoints:
∀ i ∈ {0, …, N − 1}, line(wi, wi+1) ⊆ F
- 3.
- The path optimality criterion, which corresponds to minimizing the total path length (although other cost functions may be considered depending on mission requirements and environmental factors):
This formulation ensures that the global path is safe, feasible, and structured in a way that supports local trajectory optimization and control.
2.3. Ship Model
The ship model in this study was simplified within the relevance of the upper two navigation levels (global path planning and local collision avoidance and trajectory planning) and was defined by the following parameters:
- -
- Ship current location, expressed as latitude and longitude (lat, lon);
- -
- Ship direction (θ) and speed over the ground (S);
- -
- Max turning angle (∆θmax) (in one iteration of the simulation).
Besides the basic ship parameters, the following zones around the ship, referred to as COLREG application zones in [31], are defined for collision avoidance assessment:
- -
- Collision zone (defined by radius dCollision): objects appearing within radius dCollision from the ship are considered collision cases;
- -
- COLREG zone (defined by radius dCOLREG): objects appearing within radius dCOLREG from the ship are visible in the scope of the ship’s situational awareness, and considered potentially hazardous and therefore require attention and appropriate response.
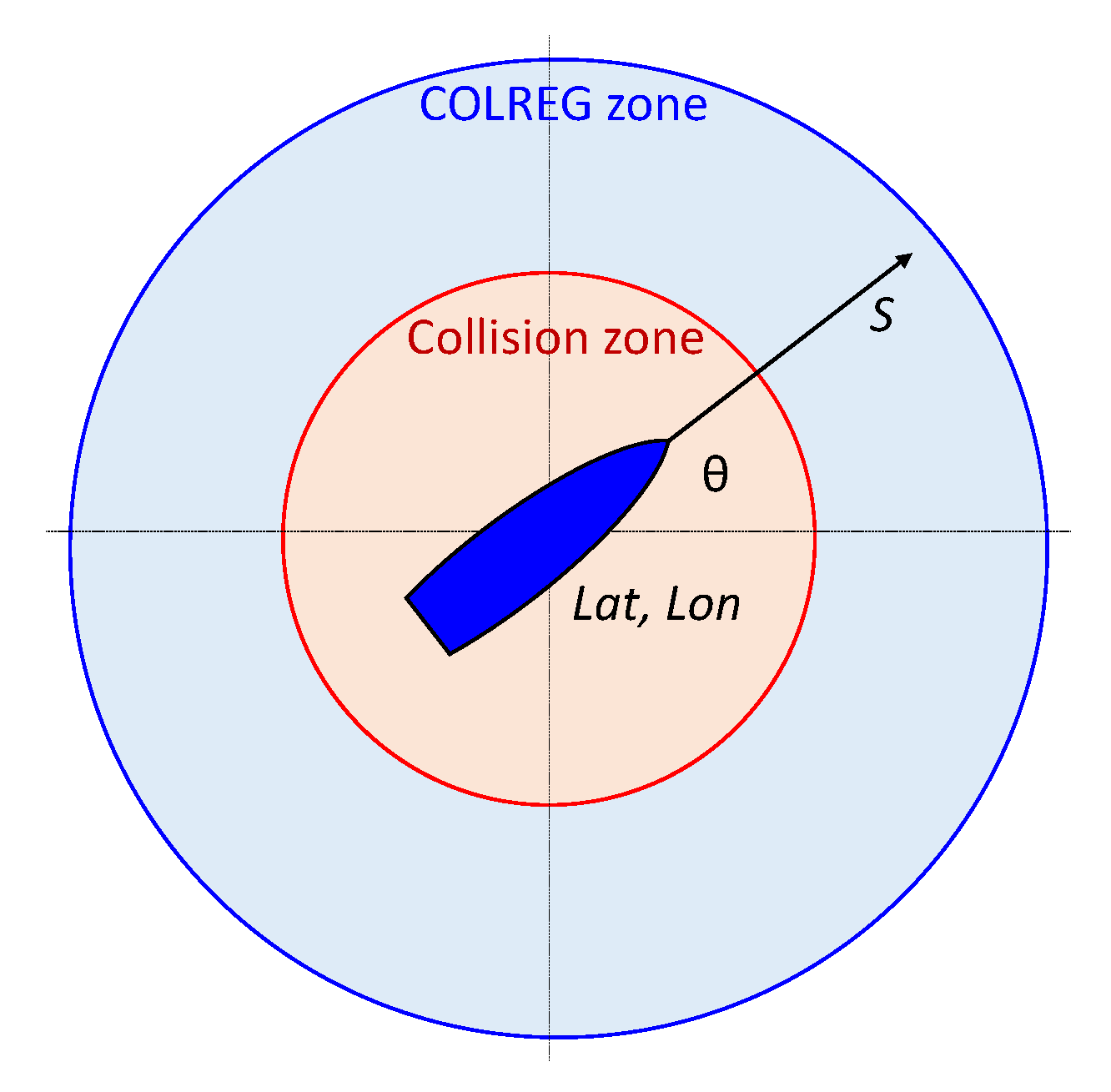
As noted in the review study by Szlapczynski and Szlapczynska [32], the concept of a ship domain is complex and asymmetric, with safe distances varying in different directions and depending on many factors. These include the own ship’s length, speed, and maneuverability, as well as the target ship’s size and speed, encounter angle, environmental conditions, and traffic density. While there is no single IMO-mandated standard for ship safety domain size, the values of the collision zone radius dCollision = 0.5 nm and the COLREG zone radius dCOLREG = 3 nm were chosen in this study as a balance between established ship domain models and practical implementation constraints in multi-ship encounter scenarios. Figure 1 presents the ship model and the COLREG application zones.
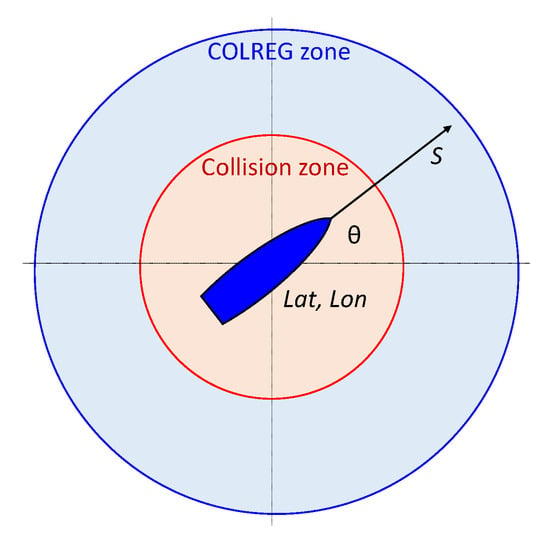
Figure 1.
Ship model defined by latitude and longitude (lat, lon), ship direction (θ), and speed over ground (S); COLREG application zones (COLREG zone, Collision zone).
2.4. Navigation Framework
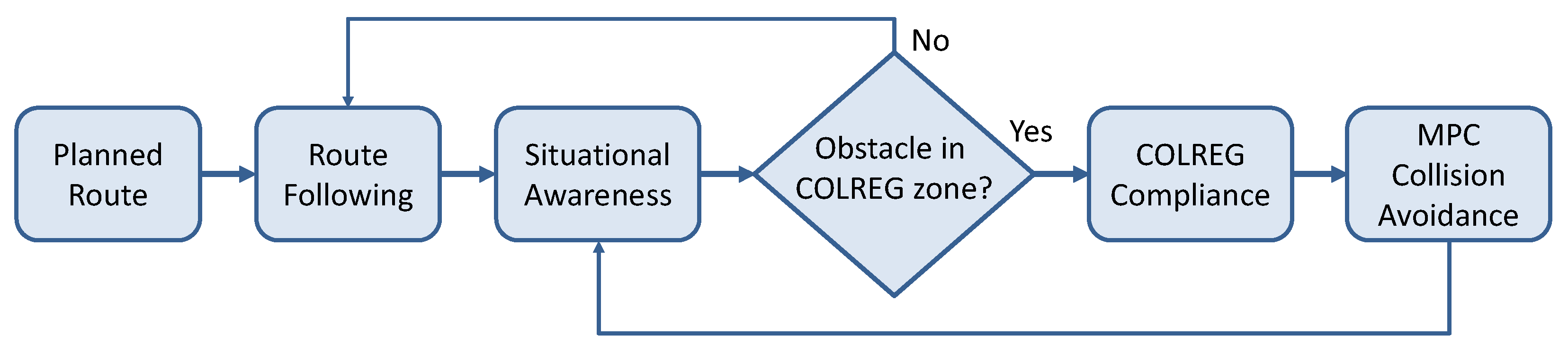
The proposed navigation framework consists of a hierarchically organized structure integrating global path planning and local collision avoidance into a coherent decision-making system. The core concept is that the ship continuously follows a planned route (route following) generated by the global planner, but switches to a collision avoidance mode when potential hazards are detected within the COLREG zone. During normal operation in the open sea without immediate hazards, the ship follows the pre-computed global trajectory defined by a sequence of waypoints. This process, referred to as route following, involves adjusting the vessel’s heading to remain on course while maintaining navigational efficiency. Route following assumes no immediate threat and allows for energy-efficient and direct transit.
However, when an obstacle (another vessel or landmass) is detected within the COLREG zone (defined as 3 nm in this study), the system transitions to MPC-based collision avoidance. In this regime, the local planner overrides simple waypoint following and takes full control of navigation by computing control actions using Model Predictive Control. The MPC module uses dynamic models and situational awareness data to predict the behavior of surrounding vessels, assess potential collision risks, and generate collision avoidance maneuvers that comply with COLREG rules.
Situational awareness and hazard detection are not addressed by this study; namely, modern autonomous navigation architectures rely on a dedicated module to provide real-time perception and interpretation of the maritime environment. The situational awareness module typically fuses data from multiple sources—such as AIS, radar, optical and infrared cameras, and LiDAR—to construct a reliable and up-to-date situational map. Recent studies demonstrate the effectiveness of multimodal sensor fusion using deep learning and probabilistic models for robust perception in complex maritime environments.
For example, Thombre et al. review key sensing modalities and AI techniques for autonomous ships, including abnormality detection and vessel classification [33]. Dagdilelis et al. present a deep fusion architecture that integrates RGB, infrared, radar, and LiDAR data into a unified birds-eye view for enhanced decision-making [34]. To improve the real-time detection and classification of maritime obstacles, Ponzini et al. propose a hybrid learning framework combining unsupervised LiDAR detection with supervised target classification [35], and Qiao et al. summarize the use of deep learning in situational awareness of the ocean surface in their review [36].
Furthermore, Liu et al. propose a dynamic risk assessment model to solve the problem of uncertainty and realize the fusion of multi-source information for the navigational safety evaluation of inland waterway ships under uncertain environmental conditions [37]. And Chen et al. present an advanced ship detection framework based on ensemble generative adversarial networks to enhance perception robustness in low-visibility weather conditions [38].
These studies provide insight into the autonomous perception layer that allows decision-making and control modules to focus on trajectory planning and collision avoidance.
The transition between route following and MPC-based collision avoidance is continuous and adaptive. The decision logic operates as a supervisory layer that monitors the environment in real time and switches between control modes depending on the proximity and type of obstacles:
- If no vessel or obstacle is present within the COLREG zone, the ship remains in the route-following mode.
- If an object enters the COLREG zone, the MPC-based local planner becomes active in assessing the situation and preparing corrective actions to prevent the object (or multiple objects) from entering the collision zone.
After the conflict is resolved and the environment is clear again, the system reverts to the route-following mode, resuming navigation along the global trajectory. This switching mechanism, presented in Figure 2, ensures a safe, COLREG-compliant, and efficient autonomous navigation process that dynamically adapts to environmental changes and traffic density, particularly in constrained or high-traffic maritime areas.
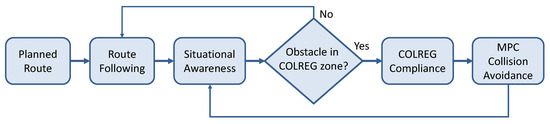
Figure 2.
Navigation framework with continuous situation awareness monitoring and switching between route following and MPC-based collision avoidance modes.
2.5. Route Following
Route following represents the baseline navigation behavior in the absence of imminent collision threats. During this mode, the vessel is guided along the pre-computed global path defined by the ordered set of waypoints W = [w0, w1, …, wN], as introduced in Section 2.2. The primary objective is to reach each waypoint sequentially while maintaining heading alignment, minimizing deviations from the nominal route and ensuring efficient transit.
At each time step t, the ship determines the next waypoint target wi+1 based on its current position p(t) ∈ ℝ2. A guidance law computes the target heading angle θTarget(t), which points toward the current target waypoint:
θTarget(t) = atan(wi+1,lat − plat(t), wi+1,lon − plon(t))
To avoid rapid oscillation near waypoint transitions and to ensure smooth path progression, a transition radius rtran is defined around each waypoint. The ship switches its active target from wi to wi+1 once it enters the circular region:
‖p(t) − wi‖ ≤ rtran
This simple logic enables robust and efficient waypoint tracking in open waters. The switching radius is, in this study, set to the collision zone radius dCollision. The motion control system adjusts the actual heading θ(t) toward θTarget(t) using proportional control (or more-advanced heading controllers). The heading error is defined as
and the rudder or propulsion system responds accordingly to minimize eθ over time, subject to the vessel’s dynamic constraints (maximum turning rate ∆θmax).
eθ(t) = θTarget(t) − θ(t),
Route following remains active as long as no obstacles are detected within the COLREG zone. In such conditions, the system focuses on energy-efficient and accurate progression along the planned trajectory. Once a potential hazard is detected, the supervisory navigation module suspends the route-following mode and activates the MPC-based local planner for collision avoidance.
2.6. MPC-Based Collision Avoidance
The collision avoidance mechanism within the navigation framework is activated when potential hazards are detected within the COLREG zone. This mechanism operates in two sequential steps. First, COLREG rules are applied to assess the type of encounter and ensure regulatory compliance, and the behavior of surrounding vessels in the simulation environment is adjusted based on rule-based logic. Second, the MPC-based controller computes optimal collision avoidance maneuvers for the own ship based on predicted trajectories. Rather than explicitly coding COLREG rules, the navigation logic for the own ship relies on real-time optimization to implicitly enforce collision-avoidant behavior. This approach reflects the growing trend in autonomous systems toward integrated, model-based control architectures.
2.6.1. COLREG Compliance
It is expected that the maneuverability of MASSs will far exceed that of manned ships, and the avoidance priority should be lower than manned ships under the “unmanned–manned” encounter situation. Therefore, Gao et al. proposed updating the maritime navigation regulations for MASSs as follows [39]: “Under the maritime encounter situation of unmanned-manned, the avoidance priority of MASS is lower than manned. A MASS underway shall keep out of the way of manned ship and a MASS shall not impede the passage of any other manned navigating vessels”. In accordance with this principle, the navigation framework assumes a conservative behavior for MASSs: it always prioritizes avoiding any other vessel, manned or unmanned. As such, MPC-based collision avoidance is used as the default navigation mode.
To ensure formal compliance with COLREGs, a rule-based COLREG layer was implemented. This layer operates independently of the MPC-based navigation and modifies the behavior of surrounding vessels in the simulation environment based on rule-based logic. When another ship enters the defined COLREG zone, the rule-based layer evaluates the situation and classifies the encounter into one of the standard types defined by COLREG: head-on, overtaking, or crossing. Encounter classification is based on the relative bearing M°, relative speed SR, and own and target ship heading (θO, θT) and courses (CO, CT), along with their respective speeds (SO, ST). Table 2 summarizes the rule formalization adapted from [3].

Table 2.
Formalization of COLREG rules for numerical application.
These rules are enforced on the simulated behavior of other ships in the environment. When the own ship has the right of way (e.g., when being overtaken or approached from the port side), the heading of the target ship θT is adjusted to simulate compliant behavior: θT(t + 1) = θT(t) + ∆θ(t), where ∆θ = ∆θmax is chosen to gradually steer the ship away from a potential collision course.
However, to ensure safety and robustness, even when own ship has the right of way, the MPC controller continues to generate avoidance maneuvers if the predicted trajectories over the horizon show an imminent risk of collision (e.g., distance less than a safety threshold. While explicit COLREG rule classification is not implemented in the proposed system for the own ship (MASS), compliance is achieved implicitly through conservative navigation and continuous conflict resolution. The MPC-based control prioritizes safety in complex multi-ship scenarios, where traditional pairwise rule logic may become ambiguous or conflicting.
2.6.2. General MPC Formulation
Following the COLREG assessment, the MPC-based collision avoidance strategy is executed for the own ship. At each control step, the MPC module solves an optimization problem over a finite prediction horizon H, where the objective is to determine the optimal control inputs (ship headings) that minimize a cost function while satisfying dynamic constraints. The MPC formulation is based on a general MPC algorithm [40] and was adapted to the ship navigation in this study by appropriately defining the state vector, control, objective function, and constraints.
The state vector x and control u in this study are defined as
where t denotes the discrete time step, (lat, lon) position coordinates, θ heading, S speed over ground, and Δθ the change in heading. The vessel’s motion is described by a simplified kinematic model:
x(t) = {lat(t), lon(t), θ(t), S(t)}
u(t) = Δθ(t)
lon(t + 1) = lon(t) + S(t) cos(θ(t)) Δt
lat(t + 1) = lat(t) + S(t) sin(θ(t)) Δt
θ(t + 1) = θ(t) + Δθ(t)
In a general MPC formulation, objective function J is defined over a finite prediction horizon H, and can be represented by terms describing adherence to the reference trajectory (i.e., route following toward the next waypoint wi+1), minimizing control effort, and avoiding collisions with static obstacles and nearby vessels :
where
- -
- xh is the predicted state of the own ship at prediction step h;
- -
- uh = Δθh is the control input (change in heading);
- -
- wi+1 is the position of the next waypoint;
- -
- is the predicted state of vessel i ∈ at step h;
- -
- PObstacle is a penalty function for proximity to a static obstacle;
- -
- PCollision is a penalty function for proximity to another vessel,
- -
- λu, λo, and λc are weighting parameters that determine the relative importance of control effort, obstacle avoidance, and collision avoidance.
The cost function is minimized at each control step, subject to the following constraints:
- -
- Ship dynamics: As defined above (Equations (9)–(11));
- -
- Control limits: |Δθh| ≤ Δθmax;
- -
- Collision avoidance (static): ∀j ∈ , dCollision;
- -
- Collision avoidance (dynamic): ∀i ∈ , dCollision.
By solving this constrained optimization problem at each time step using updated situational data, the MPC framework provides adaptive, rule-compliant navigation that accounts for both static and dynamic obstacles. This enables the ship to adapt in real-time to dynamic environmental changes, such as course or speed variations from nearby vessels, and ensures that the ship remains compliant with COLREG rules throughout the navigation.
The predicted trajectories of nearby vessels can be calculated based on situational awareness data (AIS, radar, etc.) and extrapolated using a constant velocity model, though more advanced motion prediction models can be integrated. At each control step, the optimal control sequence {Δθ1, Δθ2, …, ΔθH} is computed, and only the first control input Δθ1 is applied to the ship model. The process is then repeated at the next time step using updated environmental data (receding horizon approach).
2.6.3. Simplified MPC Formulation
While the general MPC formulation provides a powerful framework for collision avoidance, it may be computationally demanding for real-time applications in resource-constrained systems. Therefore, this study proposes a simplified, heuristic-based version that preserves the predictive control approach and safety guarantees while reducing the computational burden. The proposed simplified MPC strategy consists of the following steps, executed at each control interval:
- Generation of candidate trajectories:A discrete set of M fan-shaped trajectories is generated from the current ship state x(t), each corresponding to a fixed heading increment Δθm ∈ [−Δθmax, Δθmax], where m = 1, …, M. Each trajectory τm is simulated over the prediction horizon H using the kinematic model (Equations (9)–(11)):
- Feasibility filtering:Each trajectory τm is evaluated for potential collisions with
- -
- Static obstacles ;
- -
- The predicted positions of nearby vessels .
A binary feasibility function F(τm) is defined asOnly trajectories with F(τm) = 1 are retained for further evaluation. - Selection of optimal trajectory:Let wi+1 be the next waypoint and θTarget (Equation (4)) be the bearing to the waypoint. If the vessel’s current heading θ(t) is within [−90, 90°] of the direction to the next waypoint (the ship is approaching the waypoint), the trajectory whose initial segment most closely aligns with the bearing to the waypoint is selected. Otherwise, the trajectory that ends closest to the next waypoint is chosen. This selection rule is expressed as follows:
- If the current ship heading θ(t) satisfiesthen select|θ(t) − θTtarget| ≤ 90°
- Otherwise, select
This rule-based trajectory filtering and selection strategy significantly reduces the number of candidate solutions to be evaluated, allowing real-time operation even on low-power systems. Despite its simplicity, the approach preserves key features of MPC, such as receding horizon control and predictive situational awareness. This simplified controller is particularly suitable for near-shore navigation or congested traffic areas, where computational efficiency and rapid response are essential.
To ensure COLREG-compliant behavior, the collision avoidance formulation was designed to favor conservative maneuvers that prioritize yielding to surrounding vessels. This strategy aligns with current regulatory recommendations for MASSs and is embedded in the feasibility filtering of the MPC optimization.
An illustrative example of the proposed simplified MPC-based formulation is presented in Figure 3. The own ship is depicted in blue, along with its current set of candidate trajectories. Infeasible trajectories (F(τm) = 0), which are discarded, are shown in red, while feasible ones (F(τm) = 1), retained for further evaluation, are shown in green. The optimal trajectory τ*, selected according to Equation (16), is highlighted in blue. The magenta line indicates the reference direction toward the next waypoint. Surrounding vessels are shown in red, with their headings and velocities represented as forward-pointing vectors.
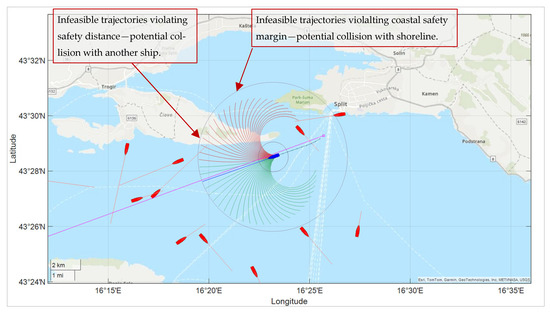
Figure 3.
Illustration of simplified MPC implementation, with candidate trajectories color-coded as infeasible (red) or feasible (green). Selected optimal trajectory τ* shown in blue.
2.7. Simulation Setup
To evaluate the performance of the proposed MPC-based navigation strategy, a multi-vessel simulation environment was implemented in MATLAB (R2024b) and Mapping Toolbox (Version 24.2). The simulation framework modeled vessel dynamics, environmental constraints, rule-based interactions in accordance with COLREGs, and the proposed route following and MCP-based collision avoidance methods. It supported the real-time visualization of vessel motion, including heading vectors, the safety zone of the own ship, and predicted trajectories. The simulation environment entitled “MPC-Autonomous-Ship-Navigation” is provided as open source on GitHub [23].
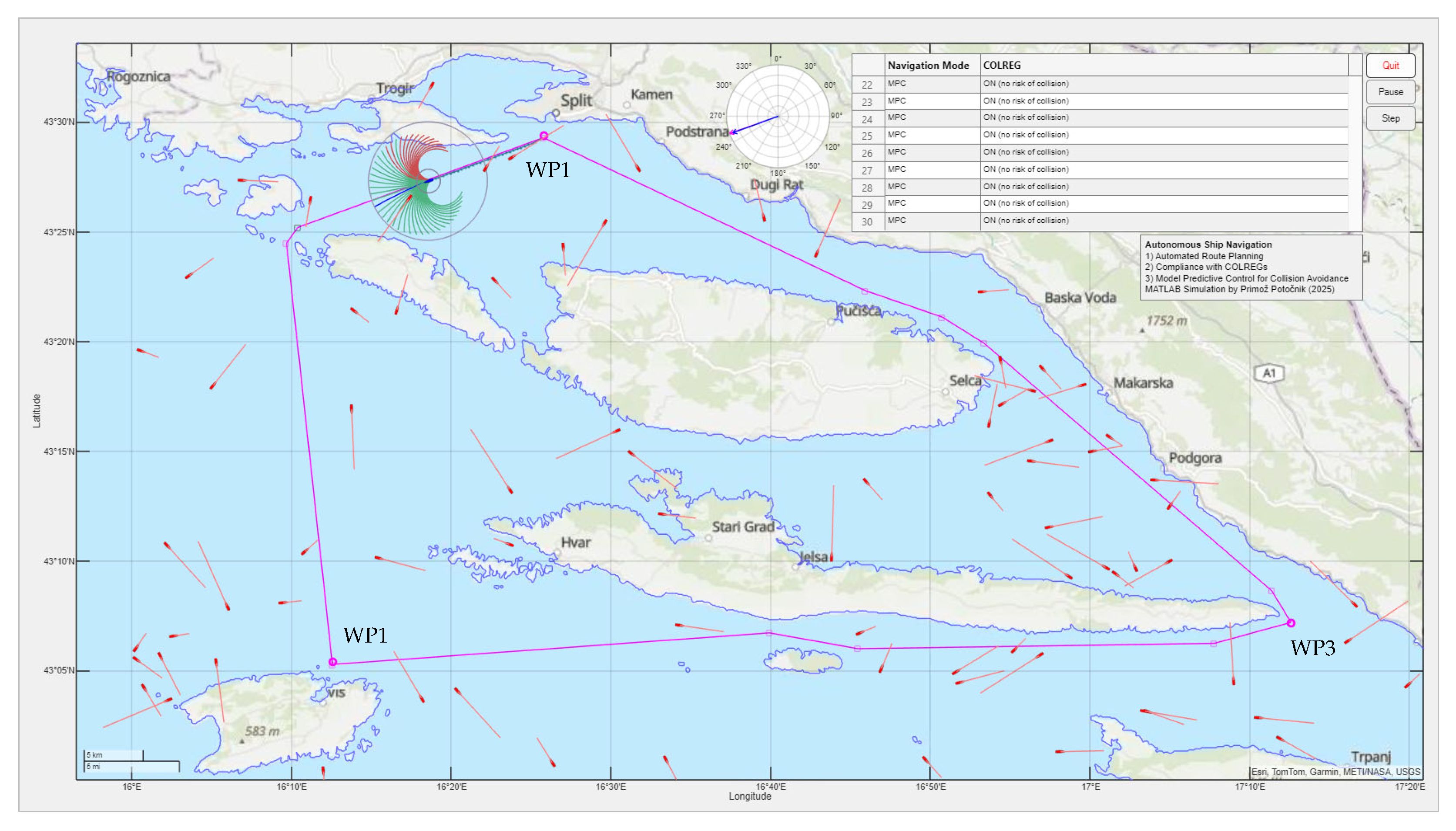
The simulation area was geographically defined in the Adriatic Sea and included the port of Split and the surrounding islands (Šolta, Vis, Brač, Hvar). Within this area, three initial waypoints (WP1, WP2, WP3) were set to define required stopovers, and a circular route—starting from the port of Split, passing Vis Island, continuing around Hvar Island, and returning to Split—was computed using the Theta* path planner (see Section 2.2). All vessels in the simulation were modeled as point masses with discrete-time kinematic updates.
The own ship was controlled using the simplified MPC formulation described in Section 2.6.3, while the other ships (target ships) follow predefined trajectories with constant velocities and headings and are subject to COLREG compliance as described in Section 2.6.1. When a target ship encountered the coastline, its heading was reversed to maintain motion within the simulation bounds. This resulted in a highly dynamic and challenging marine environment, well suited for evaluating the proposed method. The key parameters of the simulation are summarized in Table 3.

Table 3.
Key parameters of the simulation.
Ship speed was adjusted in the simulation proportionally so that the path traveled within the specified prediction horizon H matched the borders of the COLREG zone. To achieve this, the prediction horizon H = 16 was selected so that the total predicted travel distance within the MPC time window corresponded to the 3 nm radius of the COLREG zone. This design ensured that the controller anticipated all relevant encounters within the active COLREG zone. The choice of prediction horizon length is an open simulation parameter and can be adjusted for different simulation scenarios. The computation cost of the algorithm increases linearly with the length of H, allowing scalability depending on the required foresight range.
The initial positions and headings of the surrounding vessels were randomized for each simulation run, yielding diverse and unpredictable encounter scenarios. All scenarios were executed until the ship reached the final waypoint or until a violation of safety constraints (e.g., collision) was detected. The simulation area, along with the route of the own ship and the positions and headings of the surrounding vessels, is illustrated in Figure 4.
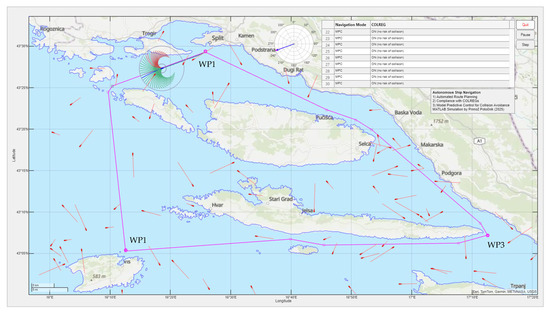
Figure 4.
The simulation area in the Adriatic Sea with a circular route between waypoints (WP1, WP2, WP3), calculated using the Theta* algorithm. The ships are represented by small icons with heading vectors. The own ship is shown along with its collision and COLREG zones. A set of candidate MPC trajectories is displayed, color-coded as infeasible (red) or feasible (green).
3. Results
This section presents simulation results for various COLREG scenarios (summarized in Table 2) which were executed using the simulation environment described in Section 2.7. The examples include coastal navigation, ship-to-ship encounters, and multi-ship interactions, illustrating the performance and adaptability of the proposed navigation framework.
3.1. Coastal Navigation
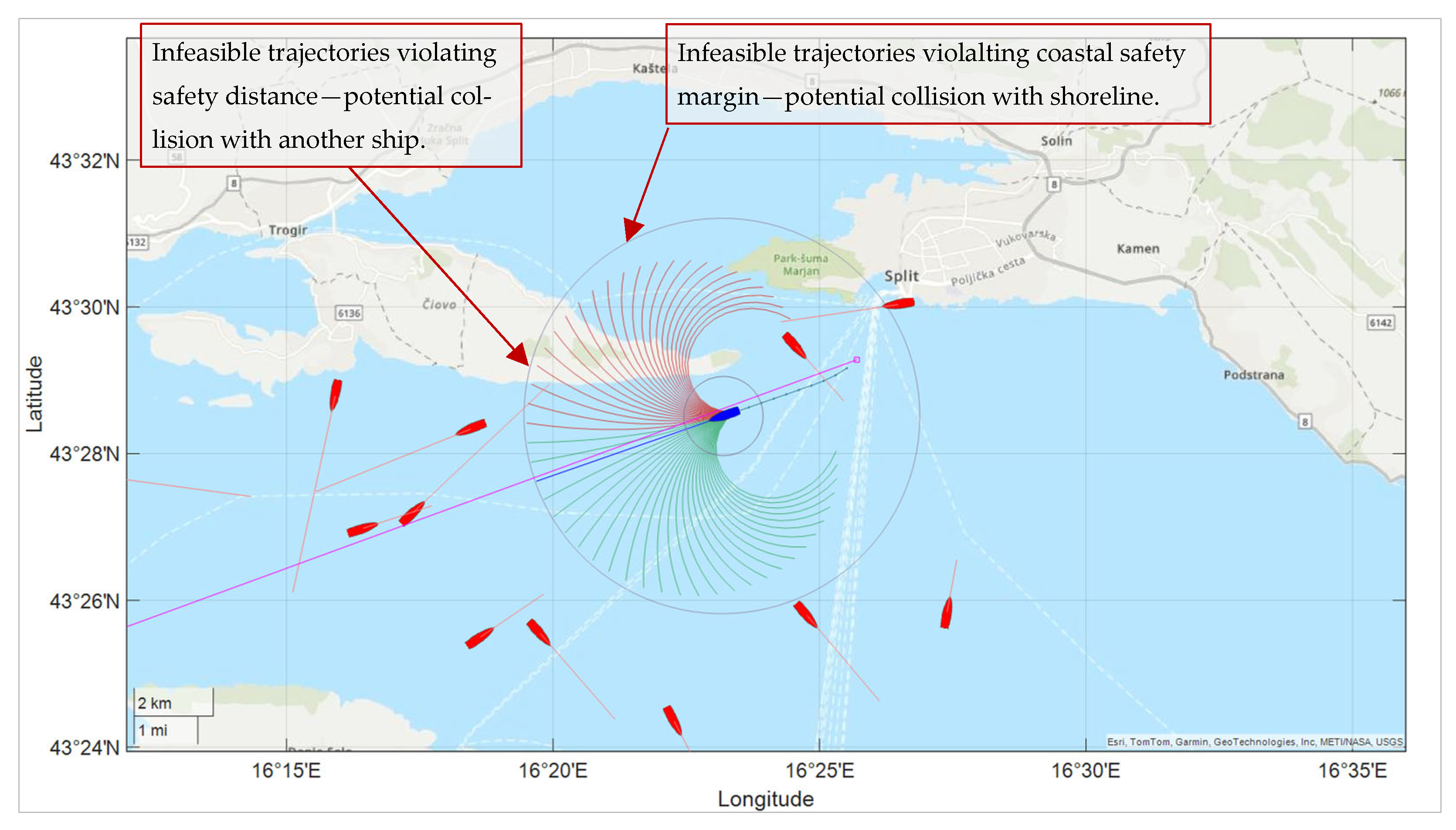
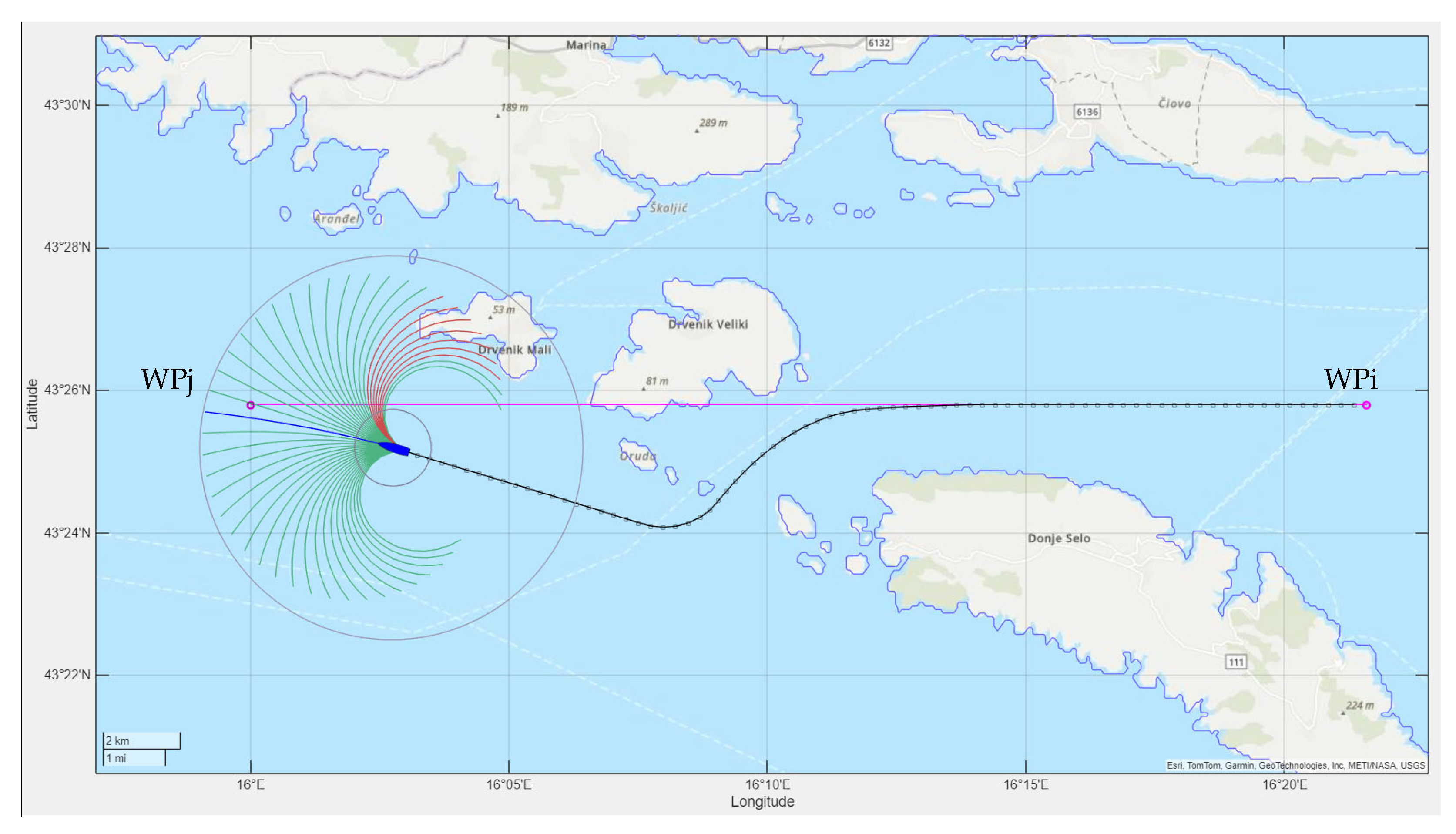
The first example demonstrates the effectiveness of MPC-based navigation in a coastal environment, where a direct route to the next waypoint would violate safe navigation constraints. Such a situation may arise due to the dynamic presence of other ships in the area, resulting in positions that are no longer collision-free if the ship continues directly toward the next waypoint. In these cases, MPC-based navigation is employed for local path planning and collision avoidance.
Figure 5 illustrates a scenario in which the direct path from WPi to the next waypoint WPj—obscured by static obstacles (islands)—would lead to a collision. The resulting trajectory (shown as black segments), generated by the MPC-based local planner, avoids the obstacles while guiding the ship toward its next waypoint, demonstrating the system’s capability for safe and efficient coastal navigation. However, it should be noted that the local MPC-based planner only addresses the path planning problem within its limited predictive horizon and may fail in more complex or long-range scenarios, where the use of a global path planner becomes necessary.
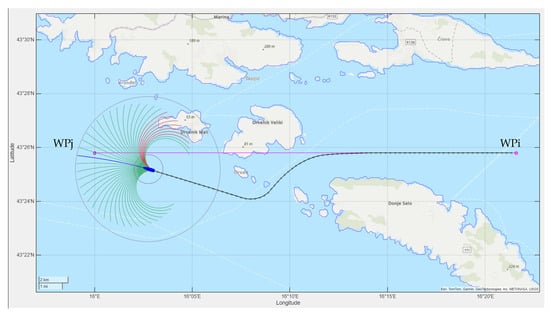
Figure 5.
Local MPC-based path planning in the case of static collision objects. The candidate trajectories are color-coded as infeasible (red) or feasible (green).
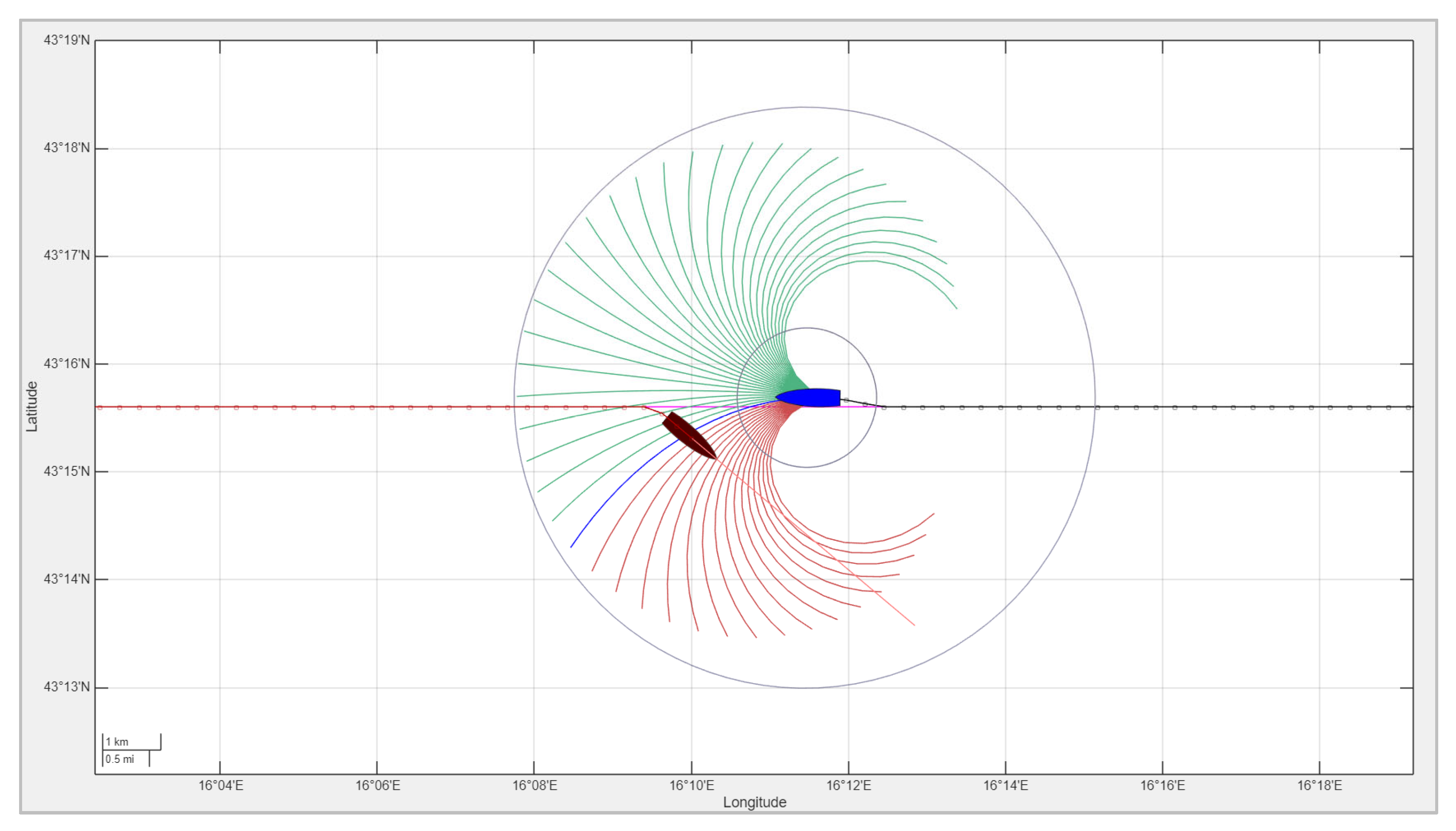
3.2. Head-On Encounter
In a head-on scenario, two vessels approach each other on reciprocal or nearly reciprocal courses. According to COLREG Rule 14, both vessels are required to alter their course to starboard to avoid a collision. Figure 6 illustrates such a situation: the other vessel initiates a starboard turn following a predefined maneuver, constrained by its maximum permissible turning angle ∆θmax, while the own ship, governed by an MPC-based navigation system, computes the optimal avoidance trajectory in real time. Unlike the other vessel, which executes a fixed maneuver, the own ship’s MPC controller determines the minimal course adjustment necessary to avoid a collision based on the predicted future positions of both ships.
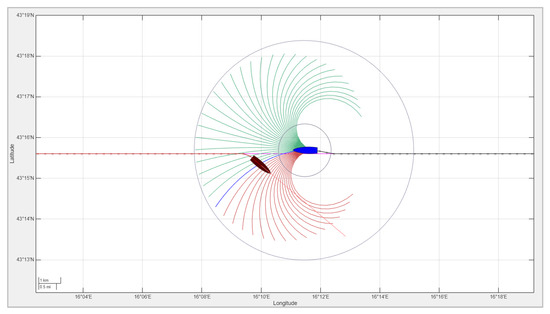
Figure 6.
Head-on encounter between two vessels. Both turn to starboard to avoid collision. Own ship (blue) adapts its maneuver using MPC, while other ship (dark red) follows fixed rule-based response. The candidate trajectories are color-coded as infeasible (red) or feasible (green), and the chosen trajectory is shown in blue.
The resulting trajectories are shown in Figure 6, with the own ship’s track in black and the other ship’s track in red. As illustrated, both vessels correctly turn to starboard, and the MPC-based decision-making allows the own ship to avoid the collision while minimizing deviation from its intended path. Note: The ship icons in Figure 6 (and in the following figures) are exaggerated in size for illustrative purposes only and do not represent actual vessel dimensions or separation distances.
3.3. Crossing Encounter
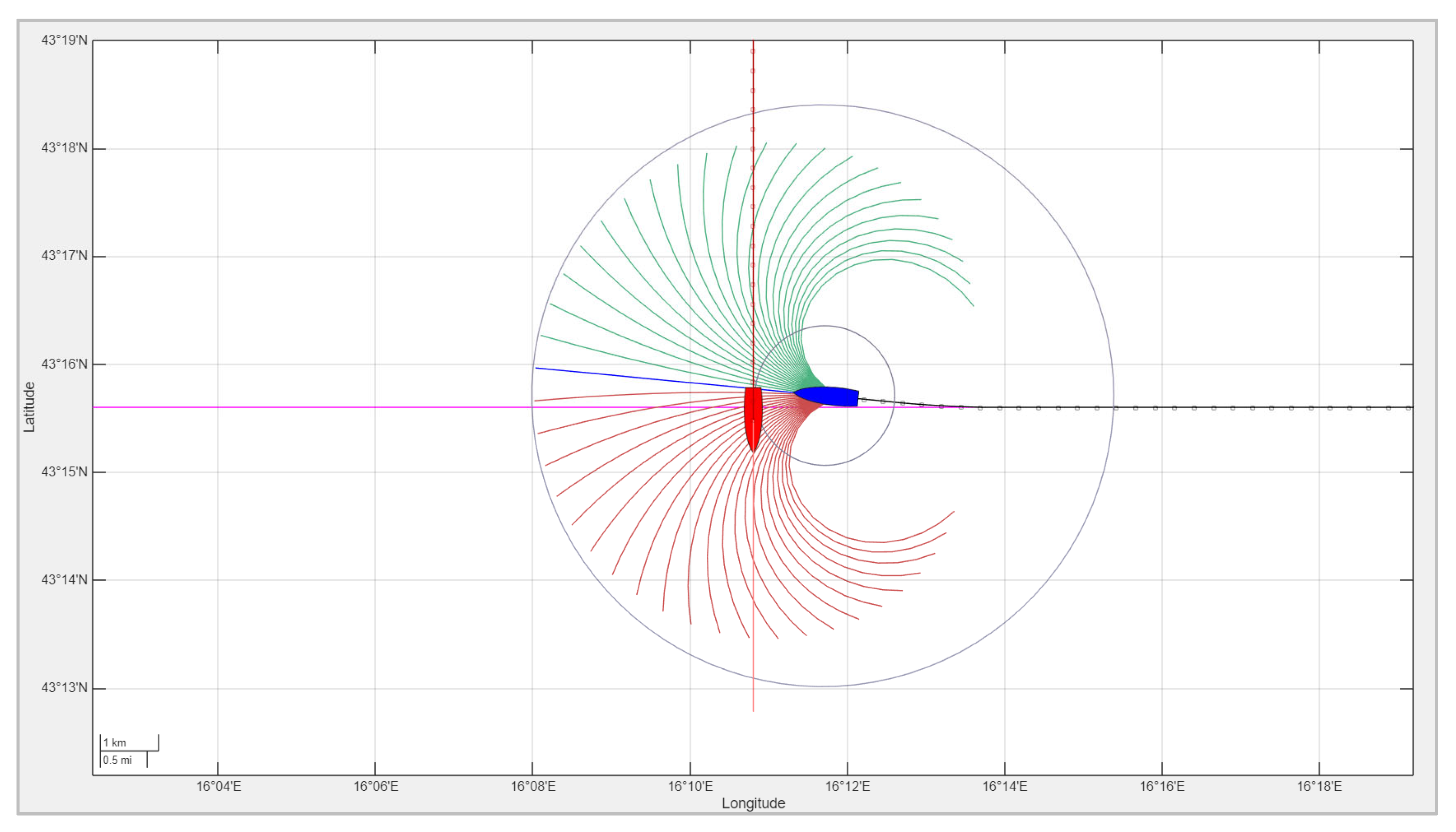
In crossing encounters, the required maneuver depends on whether the other vessel is approaching from the starboard or port side. According to COLREG Rule 15, when two power-driven vessels are crossing paths in such a manner that involves a risk of collision, the vessel that has the other on its starboard side must give way.
If the other vessel approaches from the port side, it is designated as the give-way vessel and is obliged to take action to avoid a collision. However, if the give-way vessel fails to comply with COLREG obligations, the own ship, controlled by the MPC-based autonomous navigation system, will still initiate a collision avoidance maneuver to maintain navigational safety. The MPC controller continuously predicts the future trajectories of both vessels and computes avoidance maneuvers when a collision risk is identified within a predictive horizon.
If the other vessel approaches from the starboard side, then the own ship is the give-way vessel and must take action to avoid crossing ahead. Figure 7 illustrates such a scenario, where the other vessel maintains a constant course and speed while the own ship adjusts its trajectory, computed in real time by the MPC system, to safely give way and pass behind the other vessel. The avoidance maneuver is optimized to be as efficient as possible: the deviation from the original path is minimized, and the own ship returns to its intended course toward the next waypoint as soon as it is safe to do so. This ensures compliance with COLREG rules while maintaining energy- and time-efficient navigation.
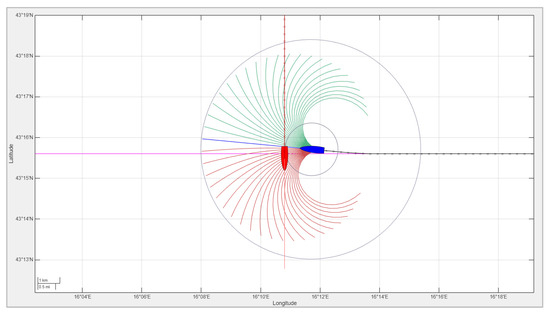
Figure 7.
A crossing encounter: The other ship (red) approaches from the starboard side and maintains course, while the own ship (blue) gives way using MPC-based navigation. The candidate trajectories are color-coded as infeasible (red) or feasible (green), and the chosen trajectory is shown in blue.
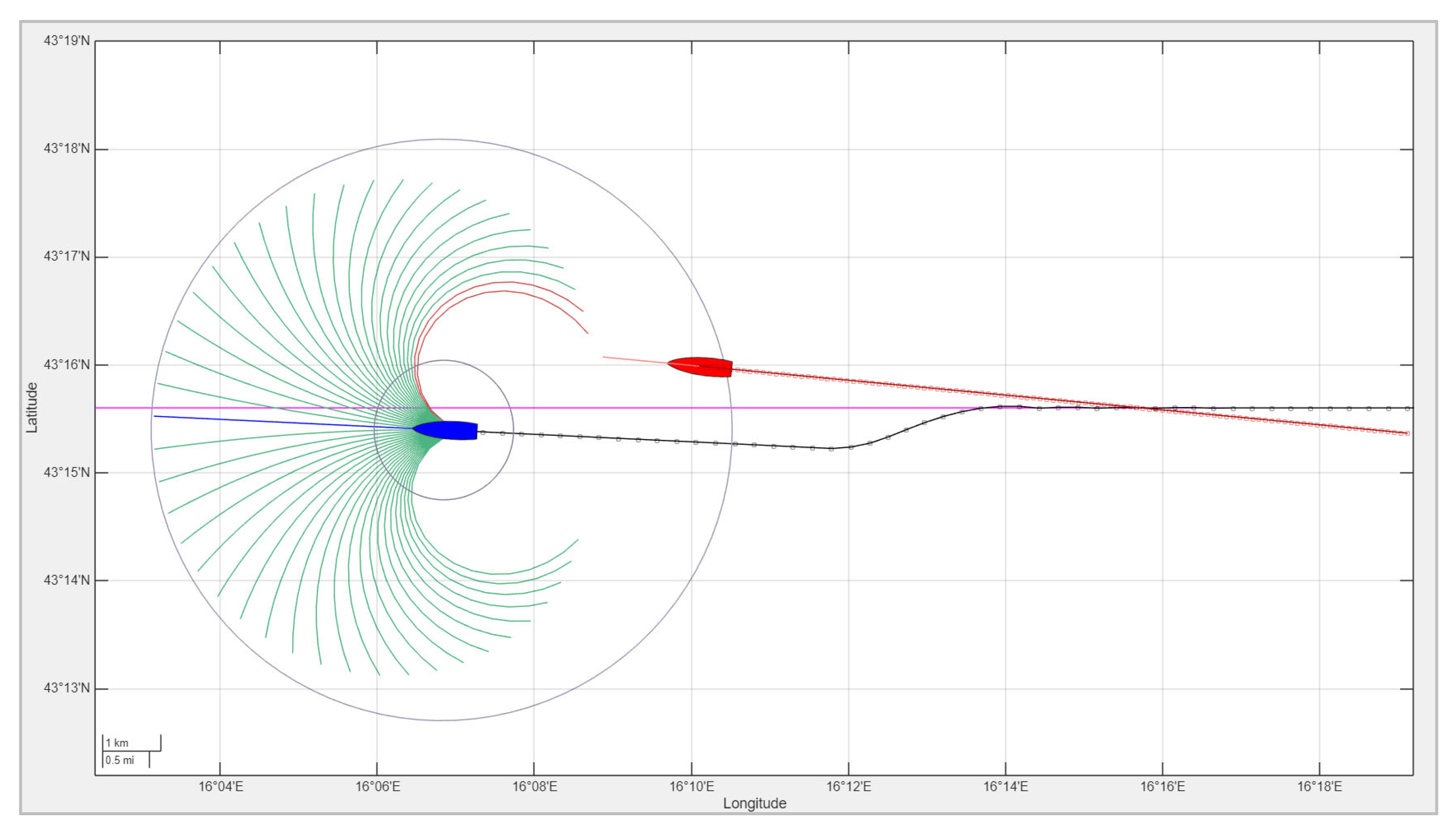
3.4. Overtaking Scenario
When overtaking a slower vessel, special care must be taken to ensure compliance with COLREG Rule 13, which states that any vessel overtaking another shall keep out of the way of the vessel being overtaken, regardless of its relative position. In this scenario, shown in Figure 8, the own ship—navigated by the MPC-based control system—approaches a slower vessel from astern. The other vessel maintains a constant course and speed, without performing any evasive maneuvers. The MPC controller identifies the overtaking condition and autonomously plans a safe overtaking trajectory, in accordance with COLREG recommendations, unless otherwise dictated by traffic or environmental constraints. The maneuver is optimized to avoid collision while minimizing deviation from the intended path. After passing the other vessel at a safe distance, the own ship directs itself toward the next waypoint.
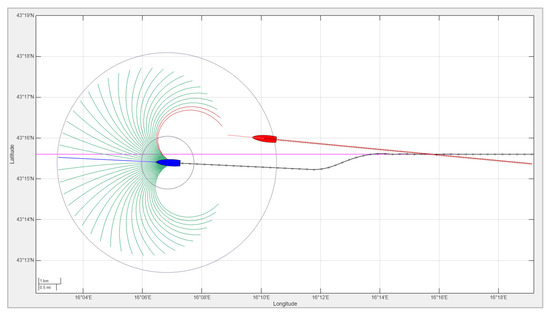
Figure 8.
An overtaking encounter: The own ship (blue) safely overtakes a slower vessel (red) using a trajectory computed by the MPC-based navigation system. The candidate trajectories are color-coded as infeasible (red) or feasible (green), and the chosen trajectory is shown in blue.
3.5. Multi-Ship Encounters
Multi-ship encounters represent more complex and realistic navigation scenarios in which the own ship must simultaneously consider multiple nearby vessels with potentially conflicting trajectories. In such situations, the application of COLREGs becomes less straightforward and significantly more challenging, as pairwise interaction rules (e.g., head-on, crossing, overtaking) must be applied in a coordinated and consistent manner. Consequently, multi-ship encounters are currently regarded as an open and challenging research topic, identified in several recent references as a direction for future investigation [7,41,42].
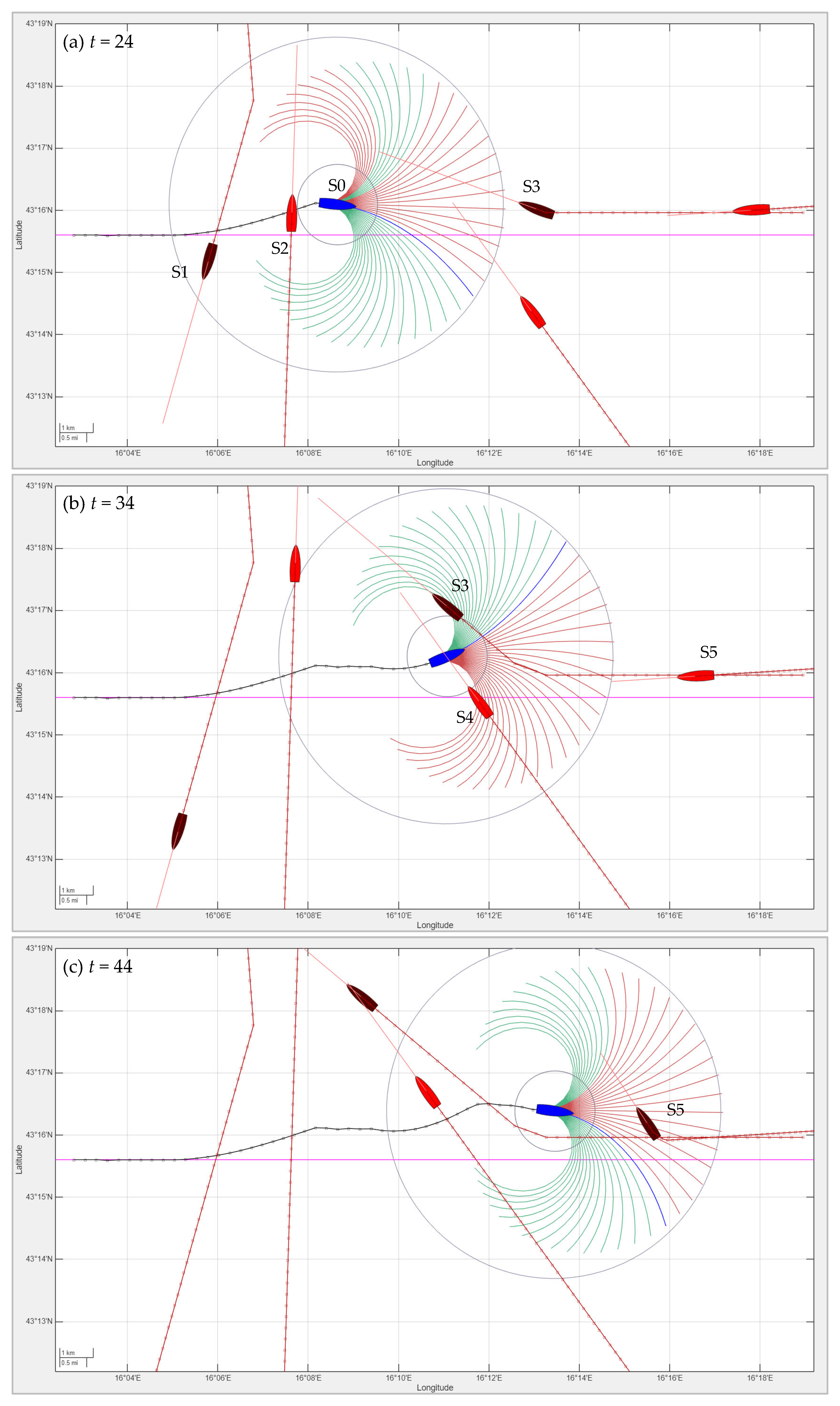
The proposed MPC-based navigation system is designed to address such scenarios by continuously predicting the motion of all surrounding vessels and resolving conflicts using a predictive control approach. The optimization framework prioritizes safety while minimizing deviations from the planned route and maintaining steady progress toward the next waypoint. Figure 9 illustrates an example of a multi-ship encounter involving five vessels approaching from various directions. The subfigures (a, b, c) depict the maritime situation at time steps t = (24, 34, 44), showing the following developments:
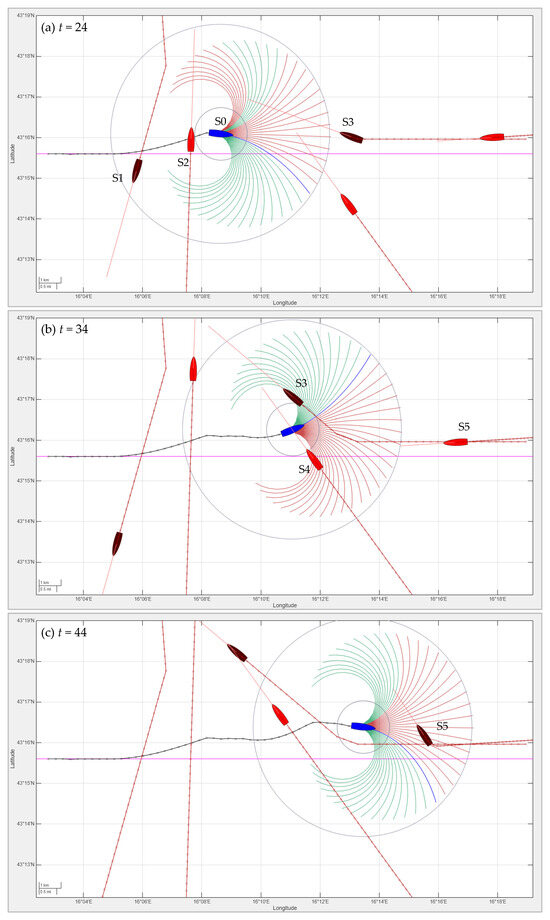
Figure 9.
A multi-ship encounter scenario at time steps t = (24, 34, 44): The own ship (blue, with a black track) avoids multiple surrounding vessels (red) using MPC-based navigation. The candidate trajectories are color-coded as infeasible (red) or feasible (green), and the chosen trajectory is shown in blue. The vessels that alter their heading in accordance with the COLREGs are highlighted in dark red.
- (a)
- t = 24: The own ship (S0) navigates between ships S1 and S2. While S1 is obligated to give way, S0 proactively avoids a potential collision with S2.
- (b)
- t = 34: S0 negotiates a narrow passage between ships S3 and S4. Although S3 alters its heading in accordance with the COLREGs, S0 changes course to give way to S4, which is approaching from the starboard side.
- (c)
- t = 44: S0 encounters a head-on situation with S5, in which both ships begin to alter their headings to avoid a collision.
The own ship (depicted with a black trajectory) dynamically adapts its path to safely navigate through the congested area. In such scenarios, the advantages of Model Predictive Control become apparent: the system evaluates multiple avoidance strategies over a finite prediction horizon and, at each step, selects the option that ensures safe navigation with minimal maneuvering effort. Furthermore, the controller avoids oscillatory or overly conservative behavior by continuously updating the predicted trajectories based on real-time observations. More illustrative examples of dynamic multi-ship navigation are available as video files in the open-source repository associated with this paper [23].
4. Discussion
The simulation results demonstrate that the proposed MPC-based navigation framework effectively handles a broad range of maritime scenarios, ranging from simple rule-based encounters (e.g., head-on, crossing, overtaking) to more complex multi-ship interactions in coastal environments. The system demonstrates real-time decision-making and adaptability to dynamic conditions by continuously optimizing the ship’s trajectory within a predictive horizon. A link to the simulation example video is provided in the Supplementary Materials.
Although rule classification is not explicitly performed, the resulting behavior remains conservative and compliant with COLREG principles. One of the key advantages of the MPC approach lies in its ability to resolve conflicting objectives—such as safety, rule compliance, and navigation efficiency—within a unified framework. For example, in both head-on and crossing scenarios, the own ship adjusts its course only as much as is necessary, minimizing deviation from the intended path while still achieving collision avoidance. Similarly, in overtaking situations, the controller ensures that the maneuver is not only safe but also efficient in terms of path length and energy expenditure.
The MPC-based navigation becomes especially relevant in multi-ship scenarios, where the complexity of applying COLREG rules increases significantly. Traditional rule-based systems may fail to coordinate interactions involving more than two vessels or may generate overly conservative behavior. In contrast, the MPC controller evaluates the future trajectories of all surrounding vessels and selects efficient avoidance strategies that are both collision-free and optimal with respect to route following.
It should be noted that increasing the number of ships in the simulation only partially increases the computational load of the local MPC-based guidance system for the own ship, since only vessels within the COLREG zone are considered potentially hazardous and included in the MPC optimization. Furthermore, the computational time related to feasibility checking, as expressed in Equation (14), increases linearly with the number of ships present within the COLREG zone.
The proposed framework provides a promising foundation for further development toward safe, autonomous maritime operations in both constrained and unconstrained environments.
However, some limitations of the proposed approach can be noted. First, the MPC-based controller operates within a finite prediction horizon H, which does not take into account long-term interactions or global obstacles (e.g., long coastlines or traffic separation schemes). As discussed in Section 3.1, local planning alone may fail in complex environments, underscoring the need for integration with a global route planner. In this simulation study, a predictive horizon of H = 16 was used; however, its length can be adjusted to match the complexity of the navigation context.
Second, this approach assumes that the motion of surrounding vessels can be reasonably predicted over the control horizon. In real-world conditions, where ships may behave unpredictably or violate COLREGs, additional mechanisms—such as intent inference or probabilistic modeling—may be required to ensure safety.
Finally, while the simulations rely on predefined ship dynamics and perfect state estimation, real-world deployment would necessitate robustness to sensor noise, environmental disturbances (e.g., wind, current), and communication delays. Future work may focus on incorporating environmental uncertainty, validating the approach in hardware-in-the-loop simulations, and extending the framework to mixed-traffic scenarios involving human-operated and autonomous vessels.
5. Conclusions
A Model Predictive Control-based approach for autonomous ship navigation, combined with chart-based route planning, is proposed in this paper. The framework integrates dynamic trajectory tracking with COLREG-compliant MPC-based collision avoidance, enabling Maritime Autonomous Surface Ships (MASSs) to navigate safely and efficiently in complex maritime environments. Using predefined waypoints and maritime charts, the system generates feasible reference paths, while the MPC controller ensures accurate path following and reactive maneuvering in response to dynamic vessels and coastal obstacles. Landmasses are modeled using GSHHG data, and other ships are treated as COLREG-compliant dynamic agents. Simulations demonstrate successful and robust collision avoidance and regulatory compliance across multi-vessel scenarios. The main novelties of the proposed approach include the following:
- The seamless integration of MPC, chart-based planning, and COLREG rules in a unified framework.
- A simplified MPC formulation that retains a predictive control approach while reducing computational demands, making it suitable for real-world implementation.
- The implementation of an open-source simulation environment for demonstrating and testing the proposed autonomous ship navigation, supporting multi-ship scenarios, real-time visualization, and decision-making analysis.
These contributions highlight the potential of the proposed system in addressing the challenges of autonomous navigation for MASSs. The simplified MPC formulation reduces the computational burden while maintaining the integrity of the control approach, thus making it suitable for practical deployment in a variety of autonomous vessels. Additionally, the open-source simulation platform developed in this study [23] provides valuable insights into the performance of the navigation system, allowing for further testing and refinement in different operational settings.
Future work will focus on expanding the simulation framework to include more realistic environmental factors, as well as enhancing the adaptability of the system to more complex, real-time decision-making scenarios. Furthermore, future research will address multi-MASS scenarios, where multiple autonomous ships utilize the same MPC-based navigation approach, requiring detailed analysis of their interactions. The current implementation operates under assumptions about the predictability of surrounding traffic and ideal sensing, and is limited by the finite prediction horizon. Therefore, these limitations also point to additional directions for future work, including integration with global route planners that incorporate environmental uncertainty and validation in real-world or hardware-in-the-loop settings.
The presented MPC framework provides a promising foundation for the development of intelligent, autonomous navigation systems capable of operating safely and efficiently in complex maritime environments. Extending the framework to support heterogeneous traffic—combining global planning, data-driven prediction models, and vessel-to-vessel communication—will be crucial for the practical deployment of autonomous maritime operations.
Supplementary Materials
The simulation example video is available at: https://www.mdpi.com/article/10.3390/jmse13071246/s1, Video S1: Simulation example.
Funding
This research was funded by ARIS—Slovenian Research and Innovation Agency—Research program P2-0241.
Data Availability Statement
The MATLAB simulation code is available at: https://github.com/ppotoc/MPC-Autonomous-Ship-Navigation (accessed on 19 May 2025).
Conflicts of Interest
The author declares no conflicts of interest.
References
- Maritime Safety Committee of the International Maritime Organization. 109th Session (MSC 109). Available online: https://www.imo.org/en/MediaCentre/MeetingSummaries/Pages/MSC-109th-session.aspx (accessed on 15 April 2025).
- Zhang, X.; Wang, C.; Jiang, L.; An, L.; Yang, R. Collision-Avoidance Navigation Systems for Maritime Autonomous Surface Ships: A State of the Art Survey. Ocean Eng. 2021, 235, 109380. [Google Scholar] [CrossRef]
- García Maza, J.A.; Argüelles, R.P. COLREGs and Their Application in Collision Avoidance Algorithms: A Critical Analysis. Ocean Eng. 2022, 261, 112029. [Google Scholar] [CrossRef]
- Constapel, M.; Koch, P.; Burmeister, H.C. On the Implementation of a Rule-Based System to Perform Assessment of COLREGs Onboard Maritime Autonomous Surface Ships. J. Phys. Conf. Ser. 2022, 2311, 012033. [Google Scholar] [CrossRef]
- Chang, C.H.; Wijeratne, I.B.; Kontovas, C.; Yang, Z. COLREG and MASS: Analytical Review to Identify Research Trends and Gaps in the Development of Autonomous Collision Avoidance. Ocean Eng. 2024, 302, 117652. [Google Scholar] [CrossRef]
- Kim, J.K.; Park, D.J. Understanding of Sailing Rule Based on COLREGs: Comparison of Navigator Survey and Automated Collision-Avoidance Algorithm. Mar. Policy 2024, 159, 105894. [Google Scholar] [CrossRef]
- Lyu, H.; Ma, X.; Tan, G.; Yin, Y.; Sun, X.; Zhang, L.; Kang, X.; Song, J. Identification of Complex Multi-Vessel Encounter Scenarios and Collision Avoidance Decision Modeling for MASSs. J. Mar. Sci. Eng. 2024, 12, 1289. [Google Scholar] [CrossRef]
- Codesseira, V.C.; Tannuri, E.A. Path Following Control for Autonomous Ship Using Model Predictive Control. IFAC-PapersOnLine 2021, 54, 57–62. [Google Scholar] [CrossRef]
- Zhang, M.; Hao, S.; Wu, D.; Chen, M.L.; Yuan, Z.M. Time-Optimal Obstacle Avoidance of Autonomous Ship Based on Nonlinear Model Predictive Control. Ocean Eng. 2022, 266, 112591. [Google Scholar] [CrossRef]
- Tsolakis, A.; Negenborn, R.R.; Reppa, V.; Ferranti, L. Model Predictive Trajectory Optimization and Control for Autonomous Surface Vessels Considering Traffic Rules. IEEE Trans. Intell. Transp. Syst. 2024, 25, 9895–9908. [Google Scholar] [CrossRef]
- Xue, H.; Lai, Y.H.; Sun, K. Human-like Constraint-Adaptive Model Predictive Control with Risk-Tunable Control Barrier Functions for Autonomous Ships. Ocean Eng. 2024, 308, 118219. [Google Scholar] [CrossRef]
- Fagerhaug, E.S.; Bye, R.T.; Osen, O.L.; Hatledal, L.I. Oceanscape: A Graph-Based Framework for Autonomous Coastal Navigation. Ocean Eng. 2025, 320, 120230. [Google Scholar] [CrossRef]
- Wen, N.; Long, Y.; Zhang, R.; Liu, G.; Wan, W.; Jiao, D. COLREGs-Based Path Planning for USVs Using the Deep Reinforcement Learning Strategy. J. Mar. Sci. Eng. 2023, 11, 2334. [Google Scholar] [CrossRef]
- Shen, Y.; Liao, Z.; Chen, D. Differential Evolution Deep Reinforcement Learning Algorithm for Dynamic Multiship Collision Avoidance with COLREGs Compliance. J. Mar. Sci. Eng. 2025, 13, 596. [Google Scholar] [CrossRef]
- He, Z.; Chu, X.; Liu, C.; Wu, W. A Novel Model Predictive Artificial Potential Field Based Ship Motion Planning Method Considering COLREGs for Complex Encounter Scenarios. ISA Trans. 2023, 134, 58–73. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Gao, J. Model Predictive Collision Avoidance Control for Object Transport of Unmanned Underwater Vehicle-Dual-Manipulator Systems. J. Mar. Sci. Eng. 2024, 12, 926. [Google Scholar] [CrossRef]
- Namgung, H.; Kim, J.S. Collision Risk Inference System for Maritime Autonomous Surface Ships Using COLREGs Rules Compliant Collision Avoidance. IEEE Access 2021, 9, 7823–7835. [Google Scholar] [CrossRef]
- Namgung, H. Local Route Planning for Collision Avoidance of Maritime Autonomous Surface Ships in Compliance with Colregs Rules. Sustainability 2022, 14, 198. [Google Scholar] [CrossRef]
- Öztürk, Ü.; Akdağ, M.; Ayabakan, T. A Review of Path Planning Algorithms in Maritime Autonomous Surface Ships: Navigation Safety Perspective. Ocean Eng. 2022, 251, 111010. [Google Scholar] [CrossRef]
- Lyu, H.; Hao, Z.; Li, J.; Li, G.; Sun, X.; Zhang, G.; Yin, Y.; Zhao, Y.; Zhang, L. Ship Autonomous Collision-Avoidance Strategies—A Comprehensive Review. J. Mar. Sci. Eng. 2023, 11, 830. [Google Scholar] [CrossRef]
- Fu, X.; Qian, D. Research on Automatic Trajectory Planning Method of Unmanned Ships Based on Multi-Objective Optimization. IEEE Access 2023, 11, 129829–129839. [Google Scholar] [CrossRef]
- Liu, X.; He, Y.; Zhang, K.; Mou, J.; Zhang, K.; Zhao, X. Research on the Decision-Making Method for Autonomous Navigation for the Ocean-Going Ship in the Ships’ Routeing Waters. Ocean Eng. 2025, 323, 120641. [Google Scholar] [CrossRef]
- Potočnik, P. MPC-Autonomous-Ship-Navigation. GitHub Repository. Available online: https://github.com/ppotoc/MPC-Autonomous-Ship-Navigation (accessed on 19 May 2025).
- Wessel, P.; Smith, W.H.F.; Global Self-Consistent, Hierarchical, High-Resolution Geography Database (GSHHG). NOAA National Centers for Environmental Information. Available online: https://www.soest.hawaii.edu/pwessel/gshhg/ (accessed on 15 April 2025).
- Zaccone, R.; Figari, M. Energy Efficient Ship Voyage Planning by 3D Dynamic Programming. J. Ocean Technol. 2017, 12, 49–71. [Google Scholar]
- Zaccone, R.; Martelli, M. A Random Sampling Based Algorithm for Ship Path Planning with Obstacles. Proc. Int. Sh. Control Syst. Symp. 2018, 1, 2–4. [Google Scholar] [CrossRef]
- Daniel, K.; Nash, A.; Koenig, S.; Felner, A. Theta*: Any-Angle Path Planning on Grids. J. Artif. Intell. Res. 2010, 39, 533–579. [Google Scholar] [CrossRef]
- Lee, S.M.; Roh, M.L.; Kim, K.S.; Jung, H.; Park, J.J. Method for a Simultaneous Determination of the Path and the Speed for Ship Route Planning Problems. Ocean Eng. 2018, 157, 301–312. [Google Scholar] [CrossRef]
- Biyela, P.; Rawatlal, R. Development of an Optimal State Transition Graph for Trajectory Optimisation of Dynamic Systems by Application of Dijkstra’s Algorithm. Comput. Chem. Eng. 2019, 125, 569–586. [Google Scholar] [CrossRef]
- Liu, C.; Mao, Q.; Chu, X.; Xie, S. An Improved A-Star Algorithm Considering Water Current, Traffic Separation and Berthing for Vessel Path Planning. Appl. Sci. 2019, 9, 1057. [Google Scholar] [CrossRef]
- Zaccone, R. COLREG-Compliant Optimal Path Planning for Real-Time Guidance and Control of Autonomous Ships. J. Mar. Sci. Eng. 2021, 9, 405. [Google Scholar] [CrossRef]
- Szlapczynski, R.; Szlapczynska, J. Review of Ship Safety Domains: Models and Applications. Ocean Eng. 2017, 145, 277–289. [Google Scholar] [CrossRef]
- Thombre, S.; Zhao, Z.; Ramm-Schmidt, H.; Vallet Garcia, J.M.; Malkamaki, T.; Nikolskiy, S.; Hammarberg, T.; Nuortie, H.; Bhuiyan, M.Z.H.; Särkkä, S.; et al. Sensors and AI Techniques for Situational Awareness in Autonomous Ships: A Review. IEEE Trans. Intell. Transp. Syst. 2022, 23, 64–83. [Google Scholar] [CrossRef]
- Dagdilelis, D.; Grigoriadis, P.; Galeazzi, R. Multimodal and Multiview Deep Fusion for Autonomous Marine Navigation. arXiv 2025, arXiv:2505.01615. [Google Scholar]
- Ponzini, F.; Zaccone, R.; Martelli, M. LiDAR Target Detection and Classification for Ship Situational Awareness: A Hybrid Learning Approach. Appl. Ocean Res. 2025, 158, 104552. [Google Scholar] [CrossRef]
- Qiao, D.; Liu, G.; Lv, T.; Li, W.; Zhang, J. Marine Vision-Based Situational Awareness Using Discriminative Deep Learning: A Survey. J. Mar. Sci. Eng. 2021, 9, 397. [Google Scholar] [CrossRef]
- Liu, J.; Jiang, X.; Huang, W.; He, Y.; Yang, Z. A Novel Approach for Navigational Safety Evaluation of Inland Waterway Ships under Uncertain Environment. Transp. Saf. Environ. 2022, 4, tdab029. [Google Scholar] [CrossRef]
- Chen, X.; Wei, C.; Xin, Z.; Zhao, J.; Xian, J. Ship Detection under Low-Visibility Weather Interference via an Ensemble Generative Adversarial Network. J. Mar. Sci. Eng. 2023, 11, 2065. [Google Scholar] [CrossRef]
- Gao, M.; Kang, Z.; Zhang, A.; Liu, J.; Zhao, F. MASS Autonomous Navigation System Based on AIS Big Data with Dueling Deep Q Networks Prioritized Replay Reinforcement Learning. Ocean Eng. 2022, 249, 110834. [Google Scholar] [CrossRef]
- Camacho, E.F.; Bordons, C. Model predictive controllers. In Advanced Textbooks in Control and Signal Processing; Springer: London, UK, 2007; pp. 13–30. [Google Scholar] [CrossRef]
- Liu, K.; Ding, S.; Yan, L.; Sun, J.; Wu, S.; Han, S.; Li, F.; Zhou, L. COLREGs-Compliant Autonomous Collision Avoidance and Improved Adaptive LOS-Based Motion Control for USVs in Complex Waters. Ocean Eng. 2025, 318, 120127. [Google Scholar] [CrossRef]
- Sonntag, V.; Perrusquía, A.; Tsourdos, A.; Guo, W. A COLREGs Compliance Reinforcement Learning Approach for USV Manoeuvring in Track-Following and Collision Avoidance Problems. Ocean Eng. 2025, 316, 119907. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).