Storm-Induced Evolution on an Artificial Pocket Gravel Beach: A Numerical Study with XBeach-Gravel
Abstract
1. Introduction
2. Materials and Methods
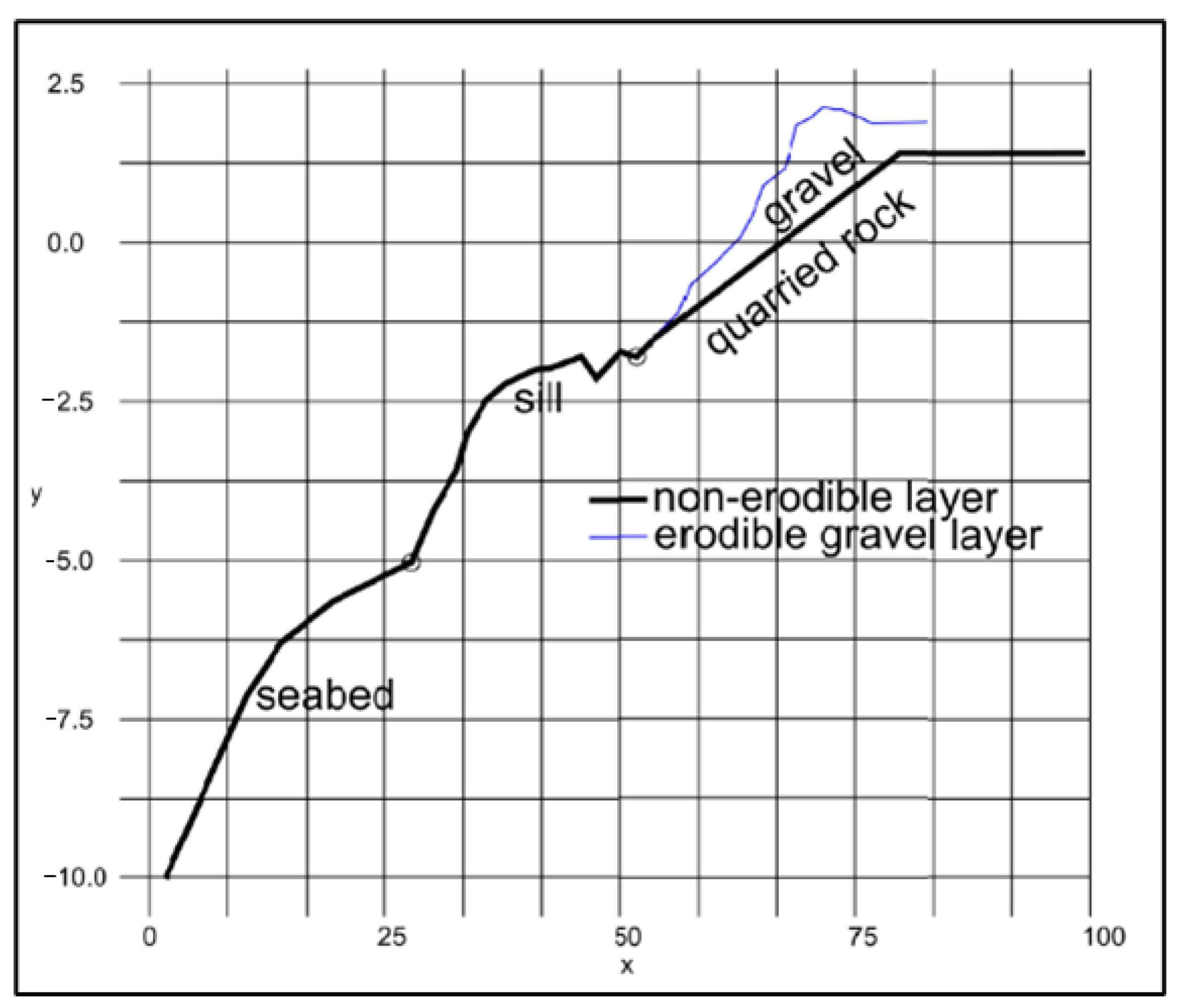
2.1. Conditions on the Artificial Beach Ploče
2.2. Numerical Model XBeach-Gravel and Model Setup
2.3. Brier Skill Score
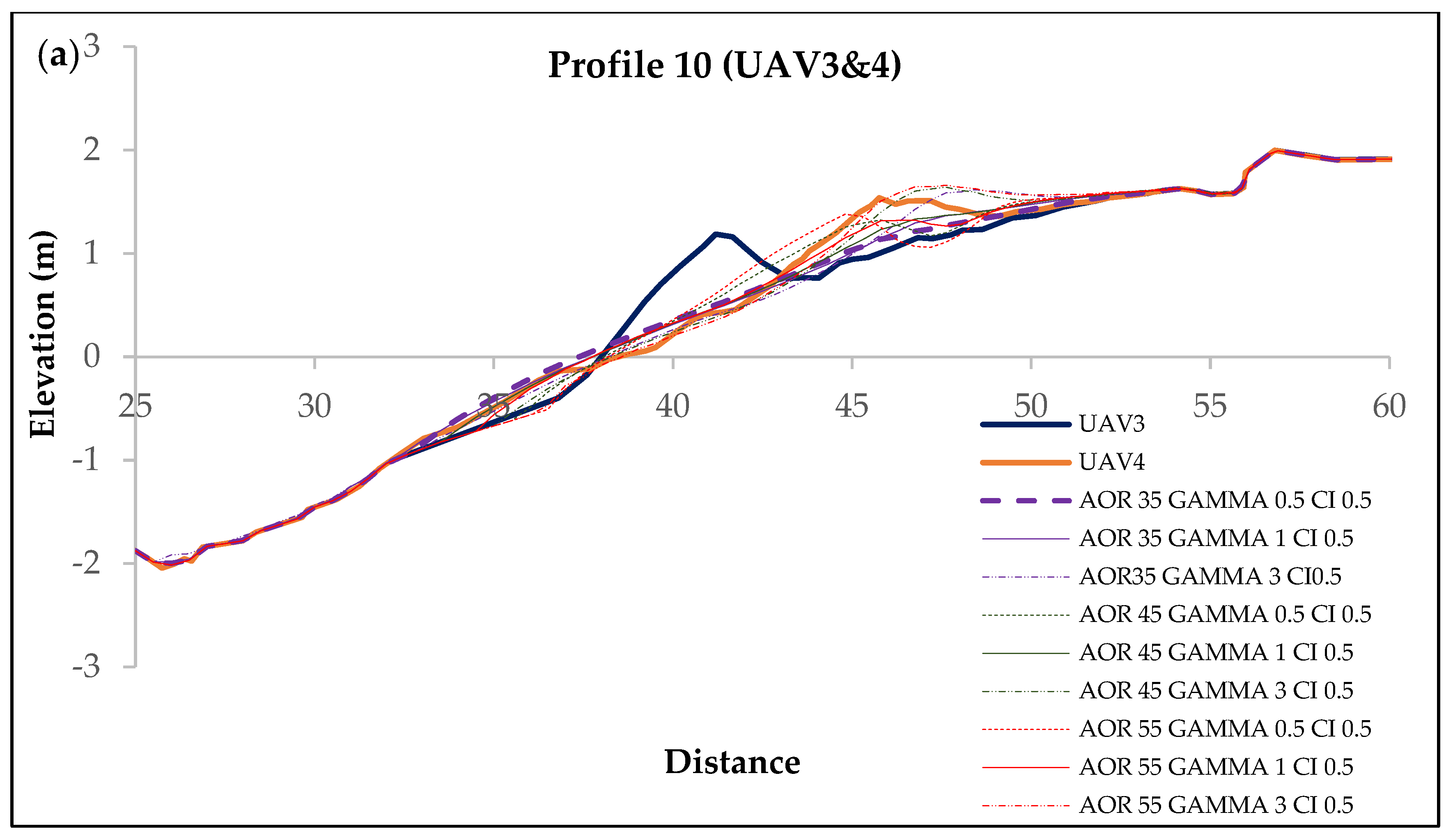
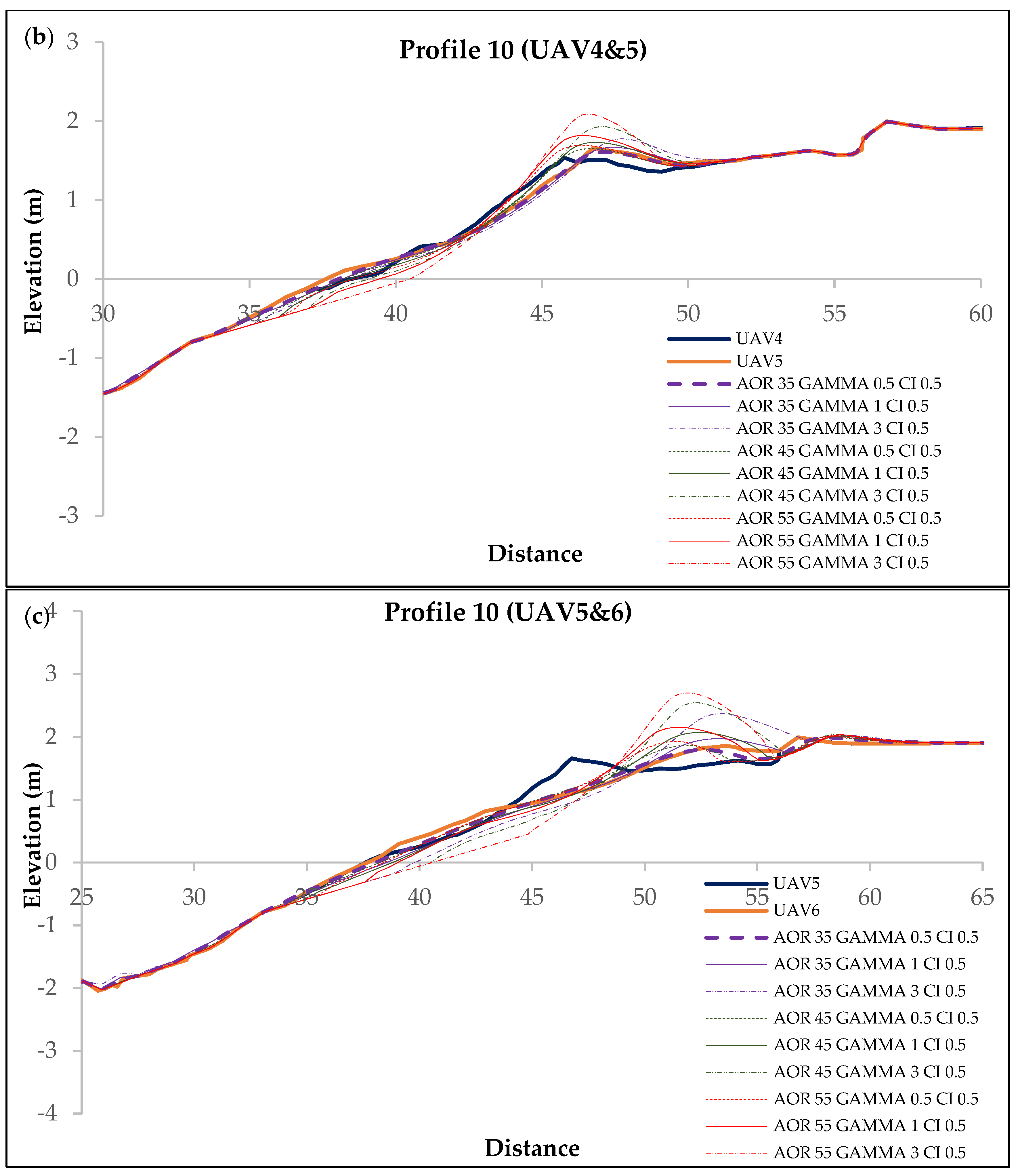
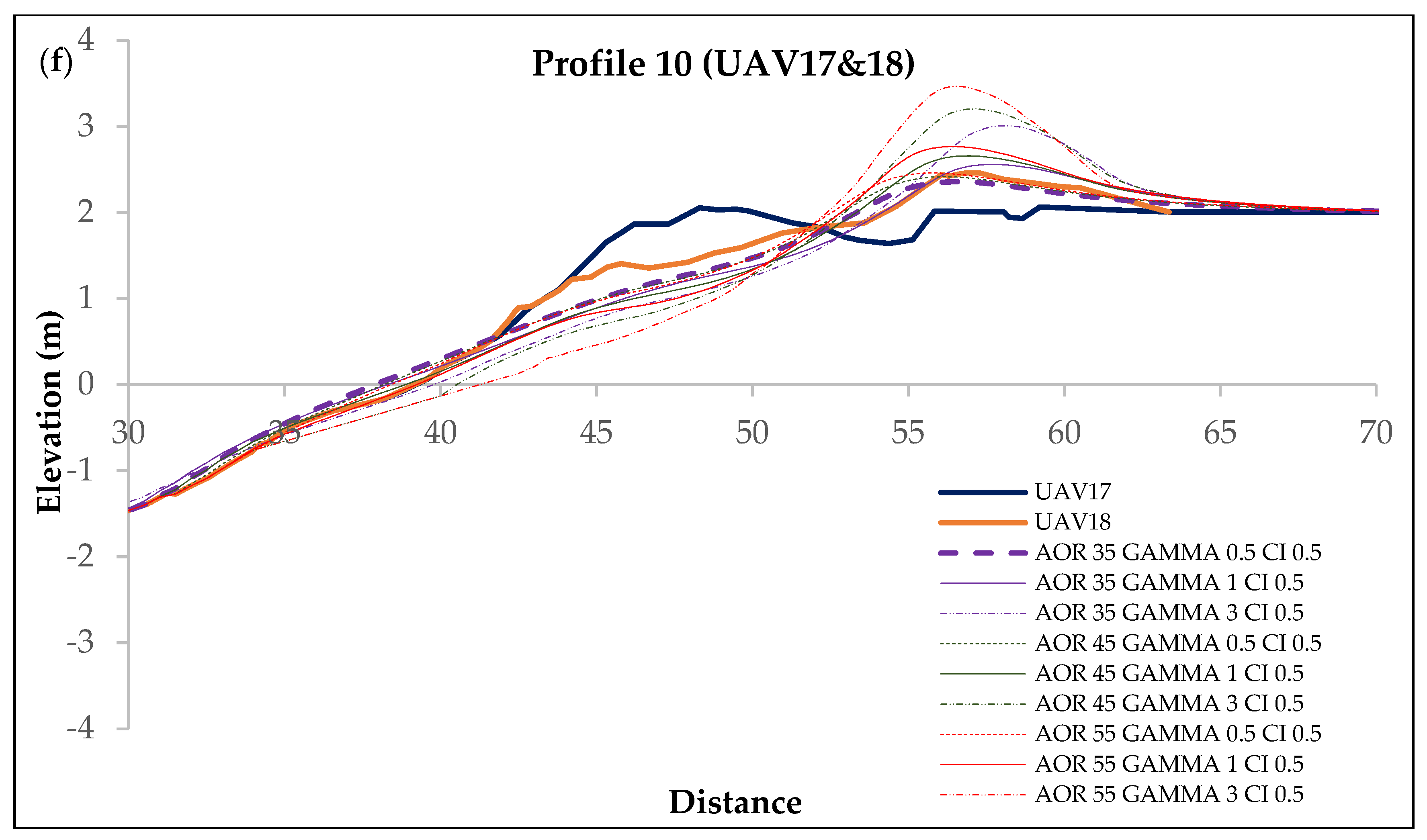
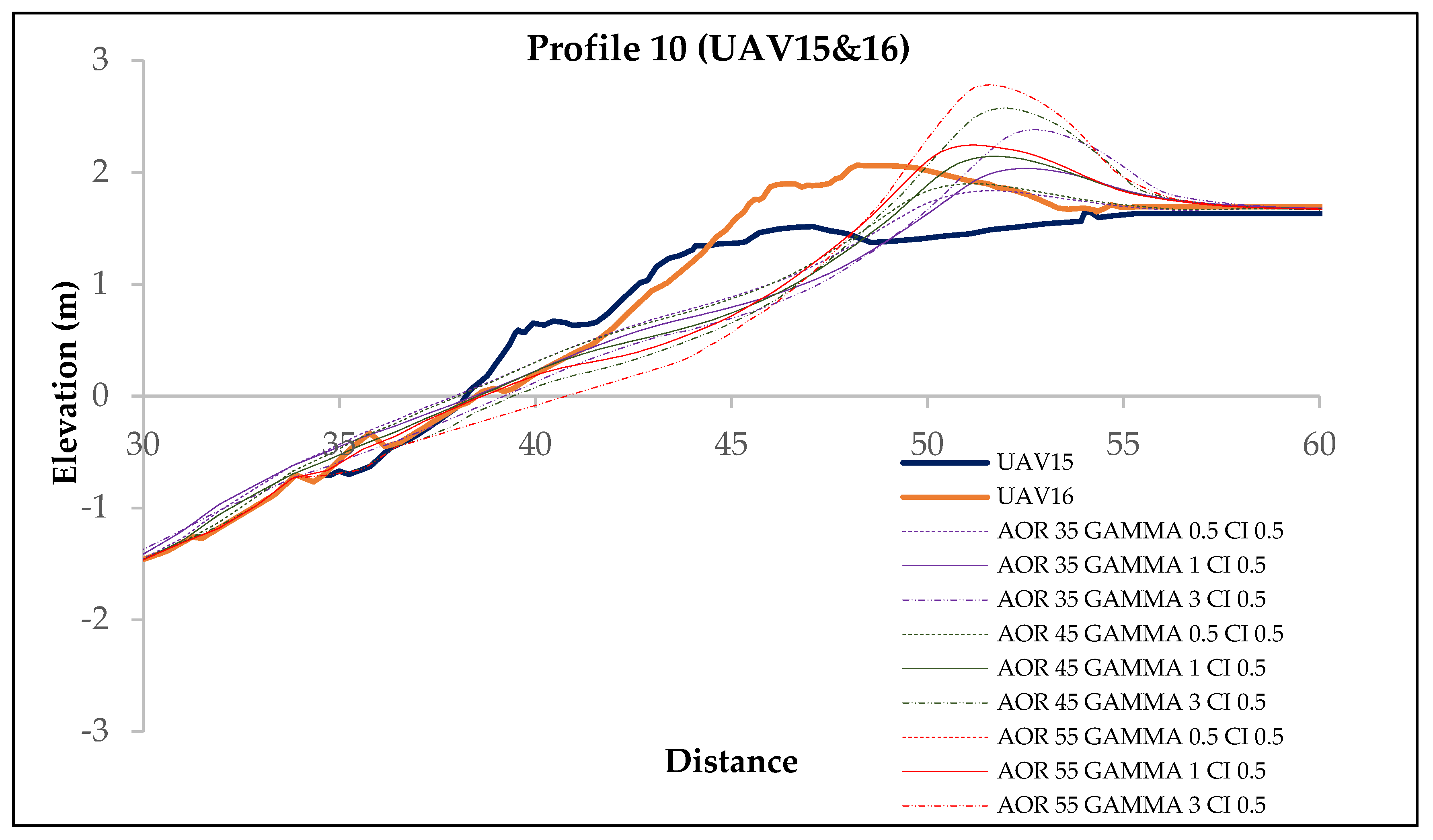
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Bujak, D.; Ilic, S.; Miličević, H.; Carević, D. Wave Runup Prediction and Alongshore Variability on a Pocket Gravel Beach under Fetch-Limited Wave Conditions. J. Mar. Sci. Eng. 2023, 11, 614. [Google Scholar] [CrossRef]
- Anthony, E.J.; Marriner, N.; Morhange, C. Human Influence and the Changing Geomorphology of Mediterranean Deltas and Coasts over the Last 6000 Years: From Progradation to Destruction Phase? Earth Sci. Rev. 2014, 139, 336–361. [Google Scholar] [CrossRef]
- Bogovac, T.; Carević, D.; Bujak, D.; Miličević, H. Application of the XBeach-Gravel Model for the Case of East Adriatic Sea-Wave Conditions. J. Mar. Sci. Eng. 2023, 11, 680. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Prediction of Dune Erosion Due to Storms. Coast. Eng. 2009, 56, 441–457. [Google Scholar] [CrossRef]
- Tadić, A.; Ružić, I.; Krvavica, N.; Ilić, S. Post-Nourishment Changes of an Artificial Gravel Pocket Beach 2 Using UAV Imagery. J. Mar. Sci. Eng. 2021, 10, 358. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S. Straightforward Reconstruction of 3D Surfaces and Topography with a Camera: Accuracy and Geoscience Application. J. Geophys. Res. Earth Surf. 2012, 117, F03017. [Google Scholar] [CrossRef]
- Westoby, M.J.; Brasington, J.; Glasser, N.F.; Hambrey, M.J.; Reynolds, J.M. “Structure-from-Motion” Photogrammetry: A Low-Cost, Effective Tool for Geoscience Applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef]
- Tuan, T.Q.; Verhagen, H.J.; Visser, P.; Stive, M. Numerical Modeling of Wave Overwash on Low-Crested Sand Barriers; World Scientific Pub Co Pte Ltd.: Singapore, 2007; pp. 2831–2843. [Google Scholar]
- Roelvink, D.; Reniers, A.; van Dongeren, A.; van Thiel de Vries, J.; McCall, R.; Lescinski, J. Modelling Storm Impacts on Beaches, Dunes and Barrier Islands. Coast. Eng. 2009, 56, 1133–1152. [Google Scholar] [CrossRef]
- Van Thiel de Vries, J.S.M. Dune Erosion During Storm Surges; Delft University of Technology: Delft, The Netherlands, 2009. [Google Scholar]
- Johnson, B.; Grzegorzewski, A. Modeling Nearshore Morphologic Evolution of Ship Island During Hurricane Katrina. In Proceedings of the Coastal Sediments; World Scientific: Singapore, 2011; pp. 1797–1810. [Google Scholar]
- Van Gent, M.R.A. Wave Interaction with Berm Breakwaters. J. Waterw. Port. Coast. Ocean. Eng. 1995, 121, 229–238. [Google Scholar] [CrossRef]
- Van Gent, M.R.A. Numerical Modelling of Wave Interaction with Dynamically Stable Structures. In Coastal Engineering 1996; ASCE Library: Reston, VA, USA, 2015. [Google Scholar]
- Roelvink, D.; Costas, S. Coupling nearshore and aeolian processes: XBeach and Duna process-based models. Environ. Model. Softw. 2019, 115, 98–112. [Google Scholar] [CrossRef]
- De Beer, A.F.; McCall, R.T.; Long, J.W.; Tissier, M.F.S.; Reniers, A.J.H.M. Simulating wave runup on an intermediate–reflective beach using a wave-resolving and a wave-averaged version of XBeach. Coast. Eng. 2021, 163, 103788. [Google Scholar] [CrossRef]
- Marino, M.; Nasca, S.; Alkharoubi, A.I.; Cavallaro, L.; Foti, E.; Musumeci, R.E. Efficacy of Nature-based Solutions for coastal protection under a changing climate: A modelling approach. Coast. Eng. 2025, 198, 104700. [Google Scholar] [CrossRef]
- Pedrozo-Acuña, A.; Simmonds, D.J.; Otta, A.K.; Chadwick, A.J. On the Cross-Shore Profile Change of Gravel Beaches. Coast. Eng. 2006, 53, 335–347. [Google Scholar] [CrossRef]
- Williams, J.J.; Buscombe, D.; Masselink, G.; Turner, I.L.; Swinkels, C. Barrier Dynamics Experiment (BARDEX): Aims, Design and Procedures. Coast. Eng. 2012, 63, 3–12. [Google Scholar] [CrossRef]
- Jamal, M.H.; Simmonds, D.J.; Magar, V. Modelling Gravel Beach Dynamics with XBeach. Coast. Eng. 2014, 89, 20–29. [Google Scholar] [CrossRef]
- McCall, R.T.; Masselink, G.; Poate, T.G.; Roelvink, J.A.; Almeida, L.P. Modelling the Morphodynamics of Gravel Beaches during Storms with XBeach-G. Coast. Eng. 2015, 103, 52–66. [Google Scholar] [CrossRef]
- McCall, R.T.; Masselink, G.; Poate, T.G.; Roelvink, J.A.; Almeida, L.P.; Davidson, M.; Russell, P.E. Modelling Storm Hydrodynamics on Gravel Beaches with XBeach-G. Coast. Eng. 2014, 91, 231–250. [Google Scholar] [CrossRef]
- López de San Román-Blanco, B.; Coates, T.T.; Holmes, P.; Chadwick, A.J.; Bradbury, A.; Baldock, T.E.; Pedrozo-Acuña, A.; Lawrence, J.; Grüne, J. Large Scale Experiments on Gravel and Mixed Beaches: Experimental Procedure, Data Documentation and Initial Results. Coast. Eng. 2006, 53, 349–362. [Google Scholar] [CrossRef]
- Powell, K.A. Predicting Short Term Profile Response for Shingle Beaches; Hydraulics Research Wallingford: Oxfordshire, UK, 1990. [Google Scholar]
- Goda, Y. Random Seas and Design of Maritime Structures; Advanced Series on Ocean Engineering 15; World Scientific: Singapore, 2000. [Google Scholar]
- Poulos, S.E.; Plomaritis, T.A.; Ghionis, G.; Collins, M.B.; Angelopoulos, C. The Role of Coastal Morphology in Influencing Sea Level Variations Induced by Meteorological Forcing in Microtidal Waters: Examples from the Island of Crete (Aegean Sea, Greece). J. Coast. Res. 2013, 29, 272–282. [Google Scholar] [CrossRef]
- Van Rijn, L.C.; Walstra, D.J.R.; Grasmeijer, B.; Sutherland, J.; Pan, S.; Sierra, J.P. The Predictability of Cross-Shore Bed Evolution of Sandy Beaches at the Time Scale of Storms and Seasons Using Process-Based Profile Models. Coast. Eng. 2003, 47, 295–327. [Google Scholar] [CrossRef]
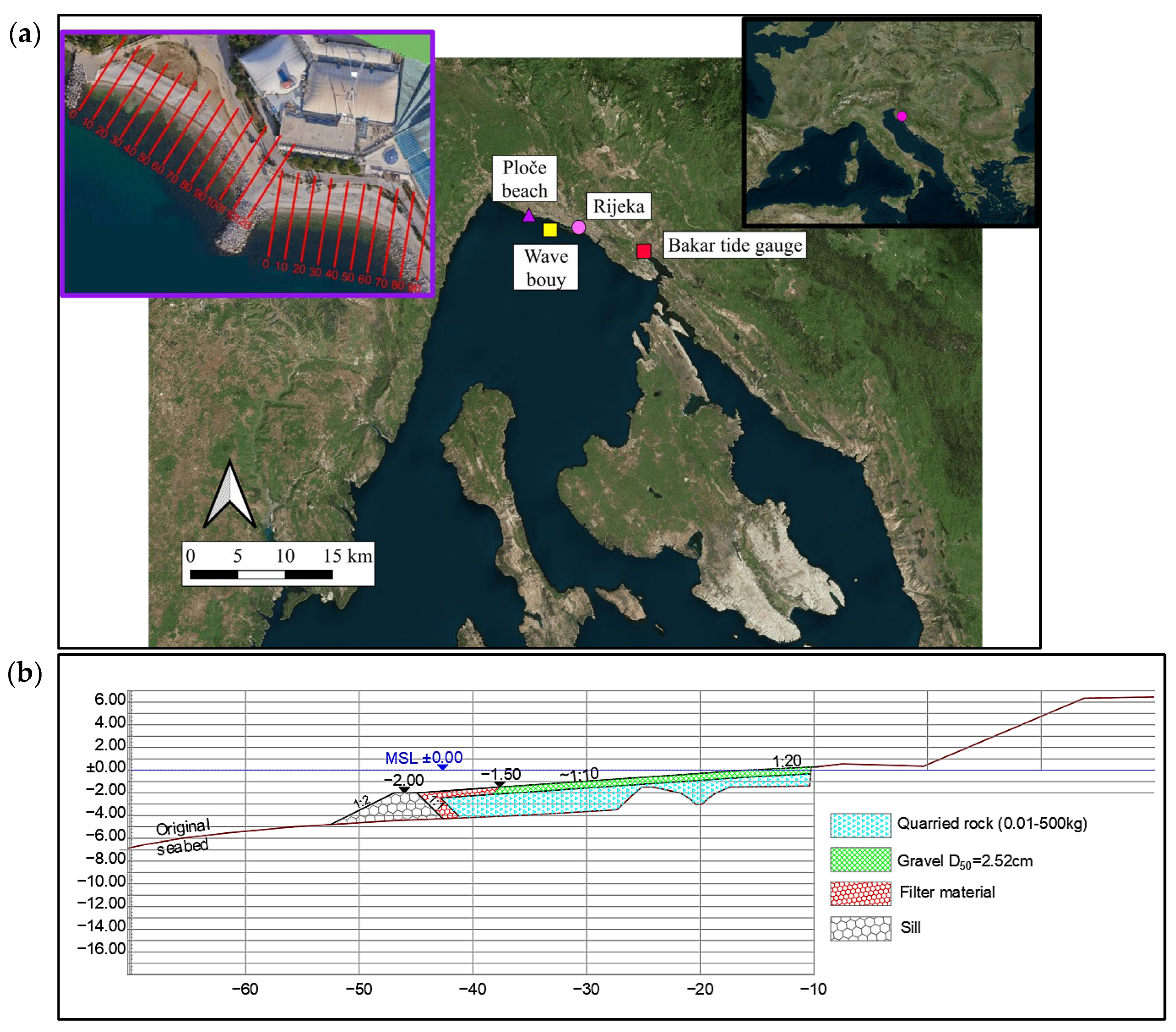
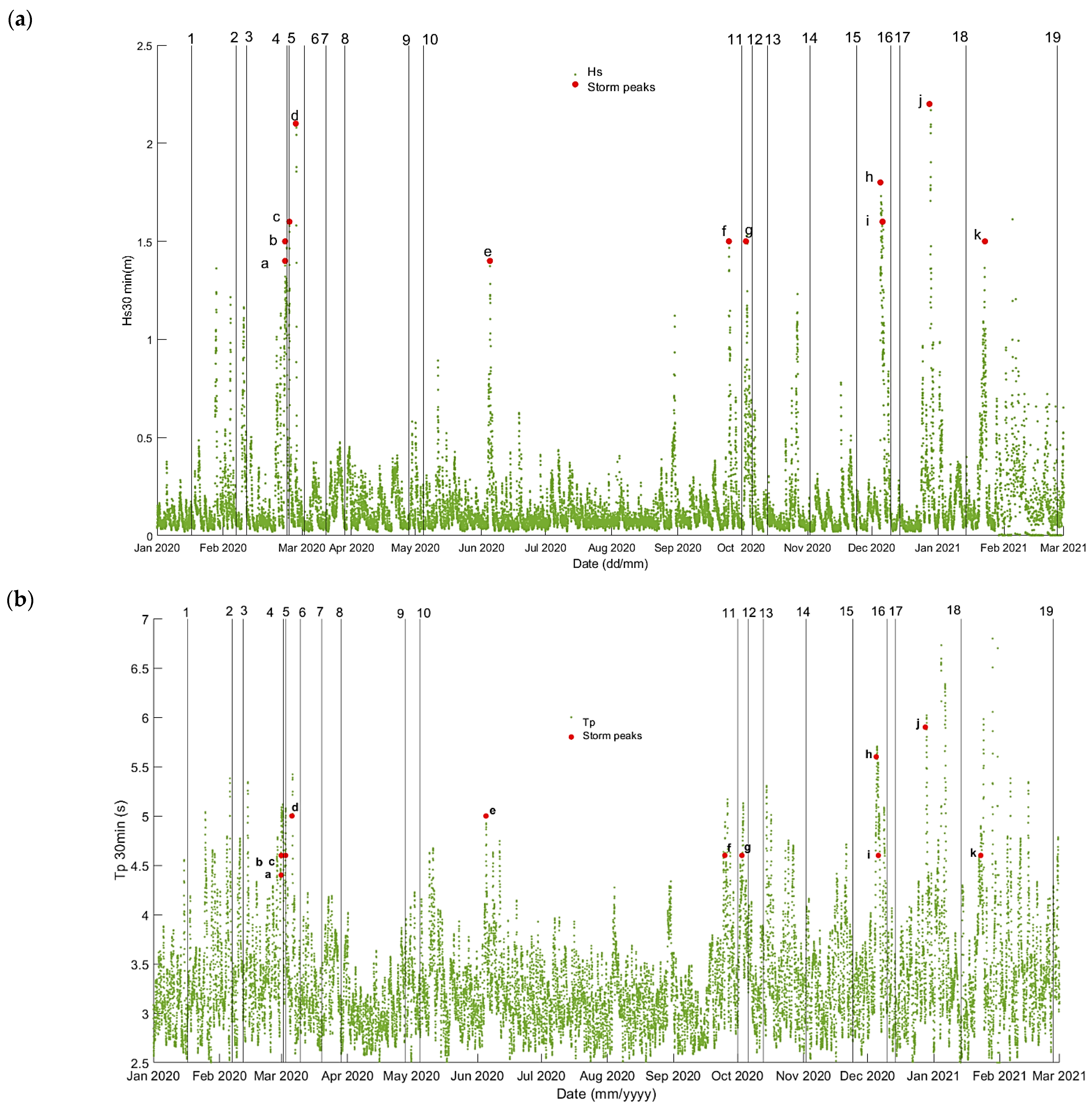
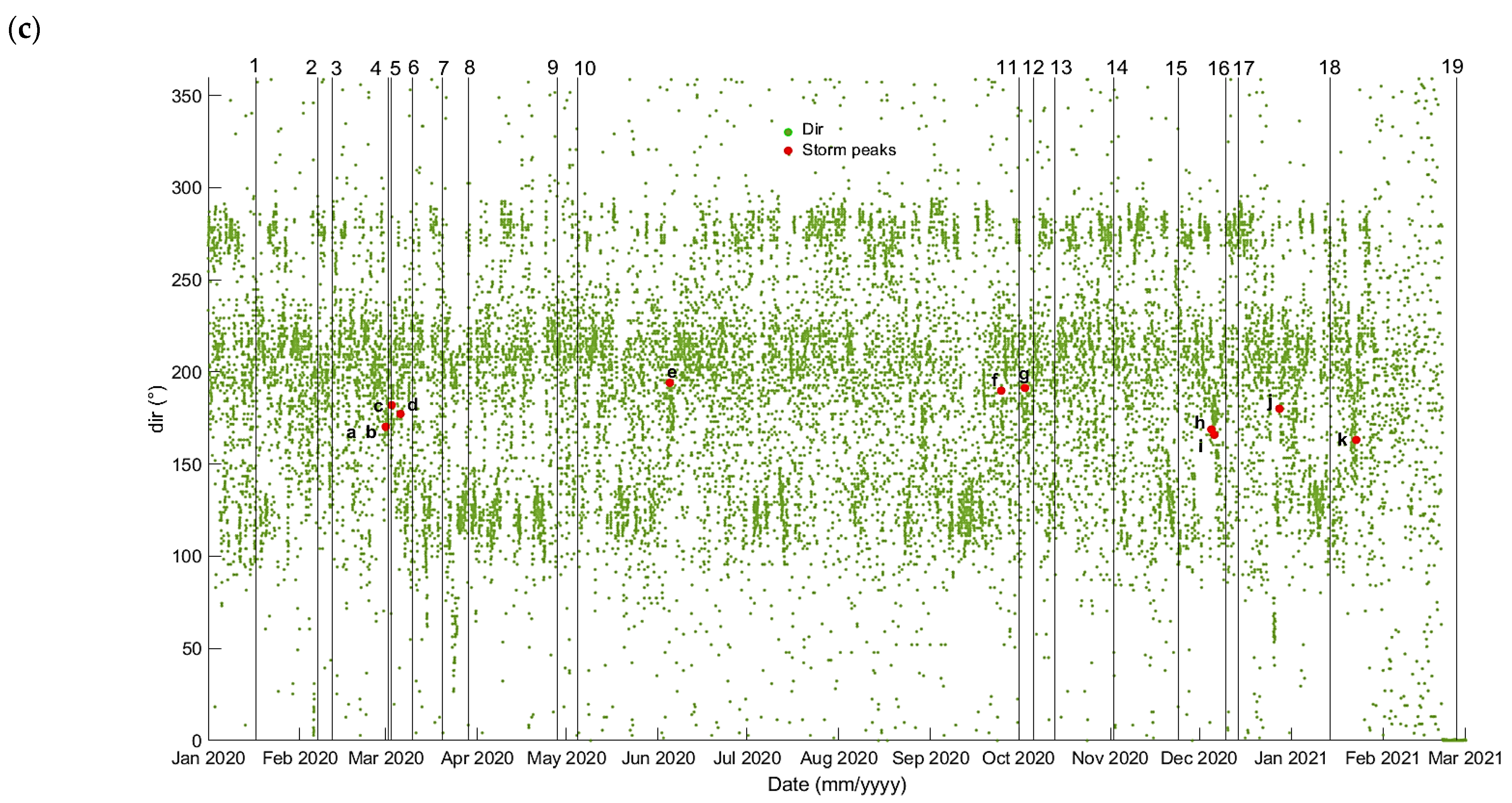


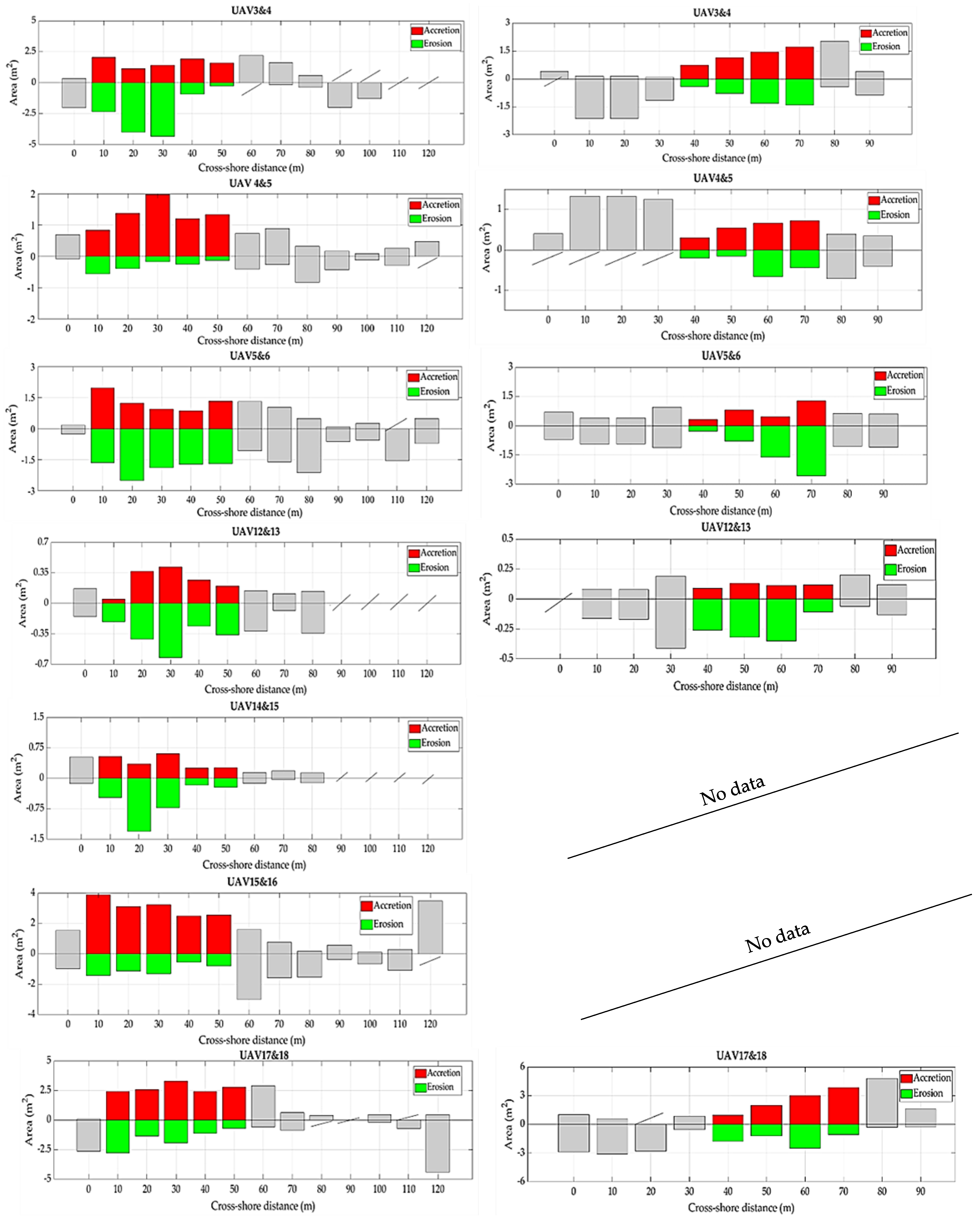

| Survey | Storm Event | Start of Storm | End of Storm | Hs,max [m] | Tp [s] | Dir [°] | Tide max [m] | Rc/Hmo | Morphodynamic Response | Selected Profiles for XBG Calibration in Western Cell [m] | Selected Profiles for XBG Validation in Eastern Cell [m] | Estimated Wave Setup in Western and Eastern Cell Wsadded [m] |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| UAV3&4 | a & b | 1 March 2020 00:34 | 1 March 2020 04:09 | 1.4 | 4.4 | 170.2 | 0.40 | 1.18 | Berm formation | 10 | 70 | 0.44 |
| 1 March 2020 14:29 | 1 March 2020 20:32 | 1.5 | 4.6 | 170.2 | 0.32 | 1.10 | ||||||
| UAV4&5 | c | 3 March 2020 00:15 | 3 March 2020 02:28 | 1.6 | 4.6 | 182.8 | 0.57 | 1.03 | Berm formation | 10 | 70 | 0.16 |
| UAV5&6 | d | 6 March 2020 05:46 | 6 March 2020 08:41 | 2.1 | 5 | 177.2 | 0.57 | 0.79 | Crest build-up | 10 | 70 | 0.53 |
| UAV10&11 | e & f | 5 June 2020 00:21 | 5 June 2020 01:53 | 1.4 | 5 | 194.1 | 0.00 | 1.18 | / | No profile selection due to intervention on the beach | / | |
| 25 September 2020 01:18 | 25 September 2020 03:41 | 1.5 | 4.6 | 189.8 | 0.29 | 1.10 | / | / | ||||
| UAV11&12 | g | 3 October 2020 15:01 | 3 October 2020 16:18 | 1.5 | 4.6 | 191.3 | 0.46 | 1.10 | / | No profile selection due to large tidal variations | / | |
| UAV12&13 | / | below storm conditions | 0.64 | 3.52 | 203.9 | 0.49 | 2.58 | Berm formation | 20 | 70 | 0.1 | |
| UAV14&15 | / | below storm conditions | 0.8 | 3.68 | 183.4 | 0.071 | 2.06 | Berm formation | 10 | missing UAV15 | 0.1 | |
| UAV15&16 | h & i | 5 December 2020 00:53 | 5 December 2020 22:58 | 1.8 | 5.6 | 168.8 | 0.61 | 0.92 | Crest build-up | 10 | missing UAV15 | 0.45 |
| 6 December 2020 08:31 | 6 December 2020 09:43 | 1.6 | 4.6 | 165.9 | 0.71 | 1.03 | / | |||||
| UAV17&18 | j | 28 December 2020 10:43 | 28 December 2020 20:08 | 2.2 | 5.9 | 180 | 0.69 | 0.75 | Crest build-up | 10 | intervention on the beach | 0.81 |
| UAV18&19 | k | 23 January 2021 00:03 | 23 January 2021 01:35 | 1.5 | 4.6 | 163.1 | 0.53 | 1.10 | / | No profile selection due to the measurement error | / | |
| Brier Skill Score | Interpretation |
|---|---|
| 0.8–1 | Excellent |
| 0.6–0.8 | Good |
| 0.3–0.6 | Fair |
| 0–0.3 | Poor |
| <0 | Bad |
| (a) | |||||||||
| BSS | ϕ 35°, γ 0.5 | ϕ 35°, γ 1 | ϕ 35°, γ 3 | ϕ 45°, γ 0.5 | ϕ 45°, γ 1 | ϕ 45°, γ 3 | ϕ 55°, γ 0.5 | ϕ 55°, γ 1 | ϕ 55°, γ 3 |
| UAV3&4 | 0.86 | 0.89 | 0.87 | 0.91 | 0.93 | 0.95 | 0.81 | 0.95 | 0.94 |
| UAV4&5 | 0.84 | 0.83 | 0.51 | 0.66 | 0.42 | −0.77 | −0.06 | −1.34 | −4.68 |
| UAV5&6 | 0.92 | 0.83 | −0.83 | 0.80 | 0.58 | −2.32 | 0.60 | −0.02 | −4.60 |
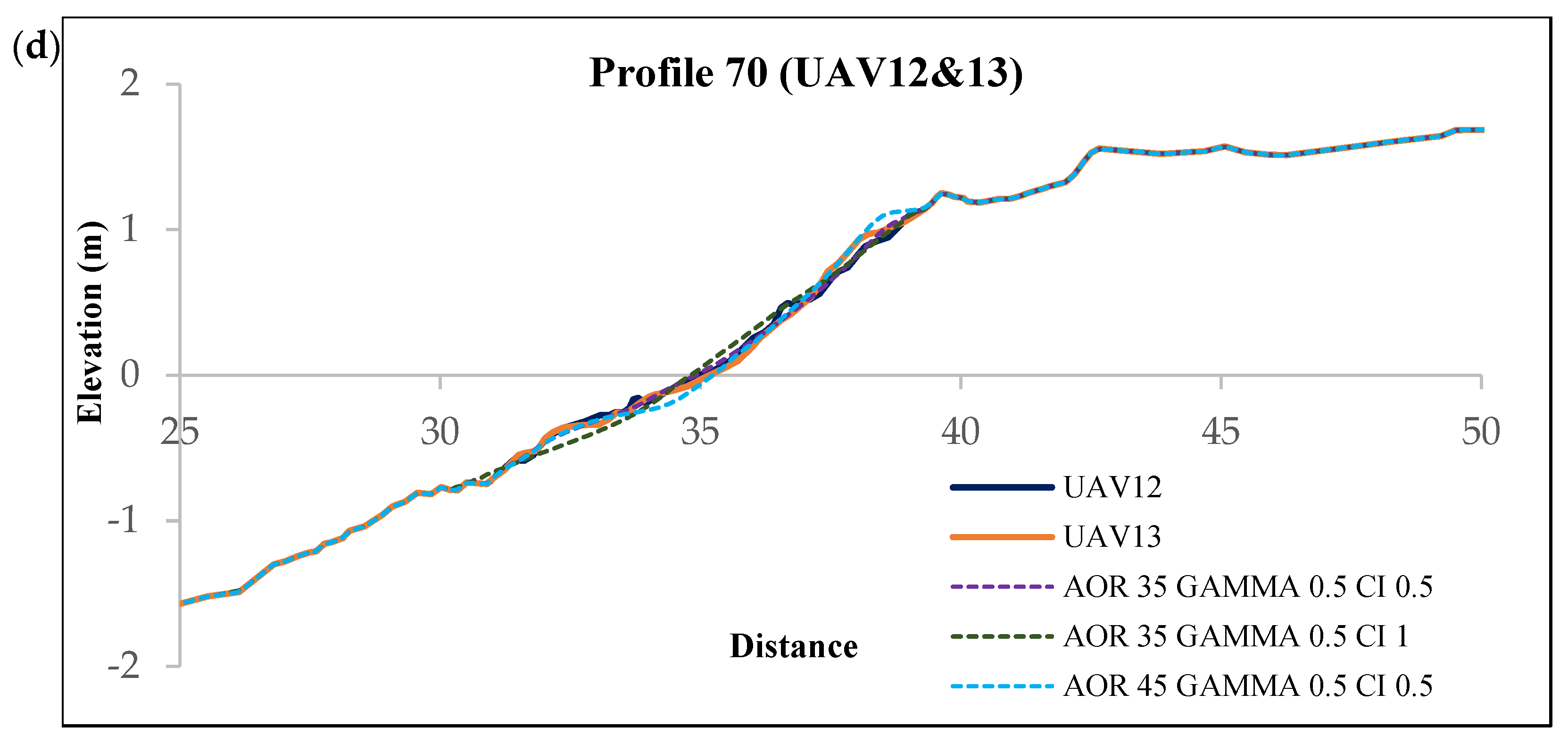
| UAV12&13 | 0.93 | 0.96 | 0.95 | 0.85 | 0.73 | 0.32 | 0.63 | 0.20 | −0.58 |
| UAV14&15 | 0.61 | 0.65 | 0.65 | 0.87 | 0.92 | 0.79 | 0.96 | 0.88 | 0.60 |
| UAV15&16 | −0.64 | −1.32 | −2.01 | −0.54 | −1.18 | −1.97 | −1.70 | −1.04 | −2.60 |
| UAV17&18 | 0.76 | 0.54 | −0.39 | 0.75 | 0.45 | −1.47 | 0.70 | 0.15 | −3.67 |
| Average BSS | 0.82 | 0.76 | 0.29 | 0.81 | 0.67 | −0.42 | 0.61 | 0.14 | −2.00 |
| (b) | |||||||||
| BSS | ϕ 35°, γ 0.5 | ϕ 35°, γ 1 | ϕ 35°, γ 3 | ϕ 45°, γ 0.5 | ϕ 45°, γ 1 | ϕ 45°, γ 3 | ϕ 55°, γ 0.5 | ϕ 55°, γ | ϕ 55°, γ 3 |
| UAV3&4 | 0.95 | 0.95 | 0.89 | 0.96 | 0.93 | 0.81 | 0.93 | 0.86 | 0.62 |
| UAV4&5 | 0.60 | 0.51 | 0.16 | −0.13 | −0.45 | −1.49 | −1.26 | −1.96 | −4.75 |
| UAV5&6 | 0.38 | −0.08 | −1.48 | −0.20 | −0.95 | −2.93 | −0.72 | −2.03 | −5.13 |
| UAV12&13 | 0.91 | 0.85 | 0.82 | 0.74 | 0.48 | 0.28 | 0.36 | −0.08 | −0.58 |
| UAV14&15 | 0.79 | 0.78 | 0.73 | 0.91 | 0.90 | 0.85 | 0.95 | 0.88 | 0.73 |
| UAV15&16 | −0.14 | −0.60 | −1.21 | 0.00 | −0.62 | −1.56 | 0.05 | −0.68 | −2.55 |
| UAV17&18 | 0.63 | 0.28 | −1.03 | 0.54 | −0.26 | −2.61 | 0.28 | −1.21 | −4.60 |
| Average BSS | 0.77 | 0.67 | 0.32 | 0.60 | 0.32 | −0.43 | 0.25 | −0.30 | −1.72 |
| (c) | |||||||||
| BSS | ϕ 35°, γ 0.5 | ϕ 35°, γ 1 | ϕ 35°, γ 3 | ϕ 45°, γ 0.5 | ϕ 45°, γ 1 | ϕ 45°, γ 3 | ϕ 55°, γ 0.5 | ϕ 55°, γ 1 | ϕ 55°, γ 3 |
| UAV3&4 | 0.95 | 0.94 | 0.90 | 0.90 | 0.91 | 0.85 | 0.79 | 0.83 | 0.73 |
| UAV4&5 | −0.25 | −0.28 | −0.47 | 0.66 | −1.11 | −1.90 | −2.05 | −2.77 | −4.14 |
| UAV5&6 | −0.52 | −1.01 | −1.56 | −1.42 | −2.02 | −3.10 | −2.05 | −2.90 | −4.56 |
| UAV12&13 | 0.78 | 0.78 | 0.88 | 0.34 | 0.34 | 0.34 | −0.08 | −0.15 | −0.35 |
| UAV14&15 | 0.85 | 0.86 | 0.78 | 0.92 | 0.92 | 0.90 | 0.93 | 0.92 | 0.78 |
| UAV15&16 | 0.17 | −0.34 | −0.38 | 0.01 | −0.55 | −1.05 | −0.17 | −0.94 | −0.60 |
| UAV17&18 | 0.02 | −0.90 | −1.37 | −0.93 | −0.93 | −1.79 | −1.63 | −2.67 | −3.86 |
| Average BSS | 0.31 | 0.07 | −0.14 | 0.08 | −0.32 | −0.78 | −0.68 | −1.12 | −1.90 |
| BSS | ϕ 35° γ 0.5 ci 0.5 | ϕ 35° γ 0.5 ci 1 | ϕ 45° γ 0.5 ci 0.5 |
|---|---|---|---|
| UAV3&4 | 0.69 | 0.89 | 0.87 |
| UAV4&5 | −0.33 | 0.63 | −0.08 |
| UAV5&6 | 0.93 | 0.79 | 0.85 |
| UAV12&13 | 0.93 | 0.48 | 0.86 |
| Average | 0.56 | 0.70 | 0.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miličević, H.; Carević, D.; Bujak, D.; Lončar, G.; Tadić, A. Storm-Induced Evolution on an Artificial Pocket Gravel Beach: A Numerical Study with XBeach-Gravel. J. Mar. Sci. Eng. 2025, 13, 1209. https://doi.org/10.3390/jmse13071209
Miličević H, Carević D, Bujak D, Lončar G, Tadić A. Storm-Induced Evolution on an Artificial Pocket Gravel Beach: A Numerical Study with XBeach-Gravel. Journal of Marine Science and Engineering. 2025; 13(7):1209. https://doi.org/10.3390/jmse13071209
Chicago/Turabian StyleMiličević, Hanna, Dalibor Carević, Damjan Bujak, Goran Lončar, and Andrea Tadić. 2025. "Storm-Induced Evolution on an Artificial Pocket Gravel Beach: A Numerical Study with XBeach-Gravel" Journal of Marine Science and Engineering 13, no. 7: 1209. https://doi.org/10.3390/jmse13071209
APA StyleMiličević, H., Carević, D., Bujak, D., Lončar, G., & Tadić, A. (2025). Storm-Induced Evolution on an Artificial Pocket Gravel Beach: A Numerical Study with XBeach-Gravel. Journal of Marine Science and Engineering, 13(7), 1209. https://doi.org/10.3390/jmse13071209





