Performance Analysis of Poppet Valves in Deep-Sea Hydraulic Systems: Considering Viscosity–Pressure Characteristics
Abstract
1. Introduction
2. Methodology
2.1. Governing Equation
2.2. Turbulence Model
2.3. Dynamic Mesh Method
2.4. Reynolds Number
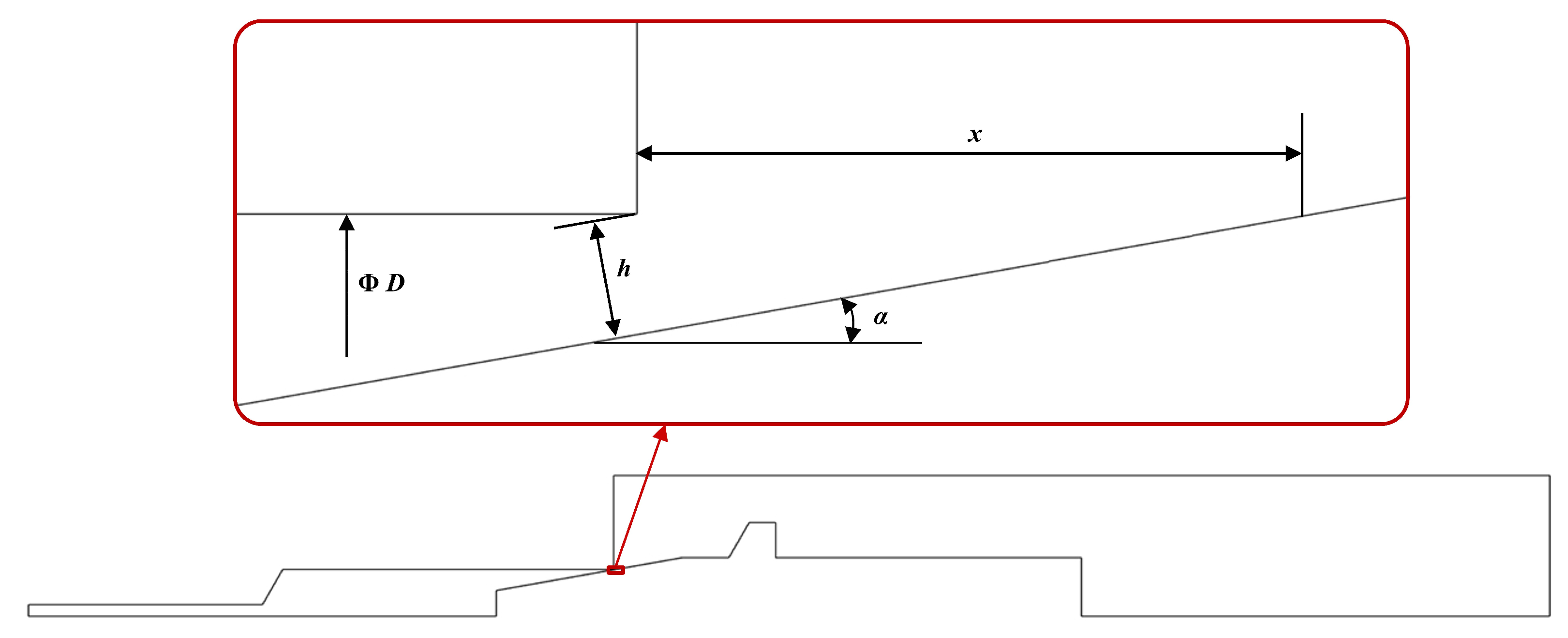
3. Model
3.1. Boundary Conditions
3.2. Mesh Independence Study
3.3. Timestep Independence Study
3.4. Turbulence Model Independence Study
3.5. Validation
4. Results and Discussions
4.1. Effect of Viscosity Variation During Flow Process
4.2. Dynamic Performance of the Poppet Valve at Different Flow Rates
4.3. Dynamic Performance of the Poppet Valve at Different Underwater Depths
- (1)
- The total pressure drop, , increases with depth;
- (2)
- The steady-state displacement, , increases with depth;
- (3)
- The rise time of the dynamic process, , increases with depth;
- (4)
- The overshoot of the dynamic process increases and then decreases with depth.
4.4. Dynamic Performance of the Poppet Valve at Different Cracking Pressures
4.5. Dynamic Performance of the Poppet Valve at Different Viscosity Characteristics
5. Conclusions
- 1.
- The poppet valve has nonlinearity, and the larger the displacement of the valve core is, i.e., the larger the opening of the valve port is, the larger the overshoot of the response process is.
- 2.
- As the underwater depth increases, the steady-state displacement, pressure loss, and rise time of the response process all increase dramatically, which will have a great influence on the response speed, load capacity, and energy consumption of the deep-sea hydraulic system. In particular, at 11 km underwater, the total pressure drop increases by 7 MPa compared with the preset cracking pressure of 10 MPa, and the rise time doubles compared with the land case. The overshoot of the response process first increases and then decreases with depth, with little overall change.
- 3.
- At the same depth, the larger the preset cracking pressure, the smaller the displacement of the valve core, i.e., the smaller the opening of the valve port. In particular, at 11 km depth, the steady-state displacement is only 0.29496 mm when the cracking pressure is 12 MPa, and it is 0.40827 mm at 6 MPa. At the same time, a larger cracking pressure results in a smaller rise time, meaning a faster response.
- 4.
- Selecting a hydraulic oil with a lower initial viscosity and a slower increase in viscosity with pressure can significantly slow the performance deterioration of the poppet valves in deep-sea conditions.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khadhraoui, A.; Beji, L.; Otmane, S.; Abichou, A. Stabilizing control and human scale simulation of a submarine ROV navigation. Ocean Eng. 2016, 114, 66–78. [Google Scholar] [CrossRef]
- Zhang, T.; Tang, J.; Qin, S.; Wang, X. Review of Navigation and Positioning of Deep-sea Manned Submersibles. J. Navig. 2019, 72, 1021–1034. [Google Scholar] [CrossRef]
- Wang, C.; Mei, D.; Wang, Y.; Yu, X.; Sun, W.; Wang, D.; Chen, J. Task allocation for Multi-AUV system: A review. Ocean Eng. 2022, 266, 112911. [Google Scholar] [CrossRef]
- Leng, D.; Shao, S.; Xie, Y.; Wang, H.; Liu, G. A brief review of recent progress on deep sea mining vehicle. Ocean Eng. 2021, 228, 108565. [Google Scholar] [CrossRef]
- Vu, M.T.; Jeong, S.K.; Choi, H.S.; Oh, J.Y.; Ji, D.H. Study on down-cutting ladder trencher of an underwater construction robot for seabed application. Appl. Ocean Res. 2018, 71, 90–104. [Google Scholar] [CrossRef]
- Sivčev, S.; Coleman, J.; Omerdić, E.; Dooly, G.; Toal, D. Underwater manipulators: A review. Ocean Eng. 2018, 163, 431–450. [Google Scholar] [CrossRef]
- Wang, F.; Chen, Y. Design and experimental study of oil-based pressure-compensated underwater hydraulic system. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2014, 228, 221–232. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, D.; Li, D.; Deng, Y. Applications and Research Progress of Hydraulic Technology in Deep Sea. J. Mech. Eng. 2018, 54, 14–23. [Google Scholar] [CrossRef]
- Cui, W. Development of the Jiaolong Deep Manned Submersible. Mar. Technol. Soc. J. 2013, 47, 37–54. [Google Scholar] [CrossRef]
- NDSF. Systems and Sensors of HOV Alvin. Available online: https://ndsf.whoi.edu/alvin/systems/ (accessed on 12 June 2025).
- Zhou, F.; Gu, L.; Luo, G.; Chen, J.; Zheng, M.; Shao, Z.; Dong, C. Development of a hydraulic propulsion system controlled by proportional pressure valves for the 4500 m work-class ROV. In Proceedings of the 2013 OCEANS, San Diego, CA, USA, 23–27 September 2013; pp. 1–6. [Google Scholar]
- Sathianarayanan, D.; Pranesh, S.B.; Chowdhury, T.; Chandrasekar, E.; Murugesan, M.; Radhakrishnan, M.; Subramanian, A.N.; Ramadass, G.A.; Atmanand, M.A. Mechanical engineering challenges in the development of deepwater ROV (ROSUB 6000). In Proceedings of the 2017 IEEE Underwater Technology (UT), Busan, Republic of Korea, 21–24 February 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Oceaneering International, Inc. ROV Systems of Oceaneering International, Inc. Available online: https://www.oceaneering.com/rov-services/rov-systems/ (accessed on 12 June 2025).
- Forum Energy Technologies, Inc. Work Class ROVs of Forum Energy Technologies, Inc. Available online: https://f-e-t.com/subsea/vehicles/work-class-rovs/ (accessed on 12 June 2025).
- TechnipFMC. ROV Systems of TechnipFMC plc. Available online: https://www.technipfmc.com/en/what-we-do/subsea/robotics/rov-systems/ (accessed on 12 June 2025).
- Jia, W.; Yin, C.; Hao, F.; Li, G.; Fan, X. Dynamic Characteristics and Stability Analysis of Conical Relief Valve. Mechanics 2019, 25, 25–31. [Google Scholar] [CrossRef]
- Min, W.; Wang, H.; Zheng, Z.; Wang, D.; Ji, H.; Wang, Y. Visual experimental investigation on the stability of pressure regulating poppet valve. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 2329–2348. [Google Scholar] [CrossRef]
- Yuan, C.; Song, J.; Liu, M. Coherent structure of paired vortex and transition in flow pattern in cavitating jet through a poppet valve. Int. J. Mech. Sci. 2019, 152, 19–33. [Google Scholar] [CrossRef]
- Yuan, C.; Song, J.; Liu, M. Investigation of flow dynamics and governing mechanism of choked flow for cavitating jet in a poppet valve. Int. J. Heat Mass Transf. 2019, 129, 113–131. [Google Scholar] [CrossRef]
- Yuan, C.; Song, J.; Zhu, L.; Liu, M. Numerical investigation on cavitating jet inside a poppet valve with special emphasis on cavitation-vortex interaction. Int. J. Heat Mass Transf. 2019, 141, 1009–1024. [Google Scholar] [CrossRef]
- Sang, Y.; Wang, X.; Sun, W. The Dynamic Characteristics of a Small Hydraulic Poppet Safety Relief Valve. Int. J. Fluid Mach. Syst. 2020, 13, 233–240. [Google Scholar] [CrossRef]
- Burhani, M.G.; Hos, C. An Experimental Study on the Force Coefficient and the Discharge Coefficient of a Safety Valve in Air-water Mixture Flow. Period. Polytech.-Mech. Eng. 2021, 65, 326–336. [Google Scholar] [CrossRef]
- Upadhyay, K.; Yu, R.; Zhou, H.; Yang, H. The CFD Analysis of Cavitation Erosion and Structural Optimization for an Unloading Valve. In Proceedings of the ASME 2021 Fluids Engineering Division Summer Meeting, Online, 10–12 August 2021; Volume 1: Aerospace Engineering Division Joint Track, Computational Fluid Dynamics. p. V001T02A043. [Google Scholar] [CrossRef]
- Min, W.; Li, C.; Wang, H.; Zheng, Z.; Zhao, J.; Ji, H. Discharge coefficient of pilot poppet valve at low Reynolds number. Flow Meas. Instrum. 2022, 85, 102141. [Google Scholar] [CrossRef]
- Hirose, N.; Masuda, S.; Shimizu, F.; Fuchiwaki, M.; Tanaka, K. Flow Patterns and Hysteresis Characteristic of a Poppet Valve. JFPS Int. J. Fluid Power Syst. 2022, 15, 53–61. [Google Scholar] [CrossRef]
- Hao, Q.; Wu, W.; Tian, G. Study on reducing both flow force and cavitation in poppet valves. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 11160–11179. [Google Scholar] [CrossRef]
- Sang, Y.; Liu, P.; Wang, X. CFD analysis of direct-operated poppet relief valve under different parameters and its structure optimisation. Int. J. Eng. Syst. Model. Simul. 2023, 14, 197–205. [Google Scholar] [CrossRef]
- Wang, F.; Chen, Y. Dynamic characteristics of pressure compensator in underwater hydraulic system. IEEE-Asme Trans. Mechatronics 2014, 19, 777–787. [Google Scholar] [CrossRef]
- Wu, J.B.; Li, L.; Wei, W. Research on dynamic characteristics of pressure compensator for deep-sea hydraulic system. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2022, 256, 19–33. [Google Scholar] [CrossRef]
- Barus, C. Isothermals, isopiestics, and isometrics relative to viscosity. Am. J. Sci. 1893, 45, 87–96. [Google Scholar] [CrossRef]
- Jiwei, W. Hydraulic Transmission, 2nd ed.; China Machine Press: Beijing, China, 2007. (In Chinese) [Google Scholar]
- En, M.; Sumin, L. Hydraulic and Fluid Power Transmission; Tsinghua University Press: Beijing, China, 2015. (In Chinese) [Google Scholar]
- Vacca, A.; Germano, F. Hydraulic Fluid Power: Fundamentals, Applications, and Circuit Design; John Wiley & Sons, Inc: Hoboken, NJ, USA, 2021. [Google Scholar]
- Ferziger, J.H.; Perić, M.; Street, R.L. Computational Methods for Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2002; Volume 3. [Google Scholar]
- ANSYS. Ansys Fluent Theory Guide, Release 2020R1; ANSYS Inc.: Canonsburg, PA, USA, 2020. [Google Scholar]
- Mawignon, F.J.; Liu, J.; Qin, L.; Kouediatouka, A.N.; Ma, Z.; Lv, B.; Dong, G. The optimization of biomimetic sharkskin riblet for the adaptation of drag reduction. Ocean Eng. 2023, 275, 114135. [Google Scholar] [CrossRef]
- Fan, S.; Shi, D.; Ma, G.; Zhang, W.; Chen, Y.; Sun, L.; Yuan, K.; Yang, Z.; Zhang, M. Research on similarity of water entry load for scaled-down underwater vehicle based on different model test environments. Ocean Eng. 2023, 286, 115697. [Google Scholar] [CrossRef]
- Liu, S.; Ong, M.C.; Obhrai, C.; Gatin, I.; Vukčević, V. Influences of free surface jump conditions and different k-ω SST turbulence models on breaking wave modelling. Ocean Eng. 2020, 217, 107746. [Google Scholar] [CrossRef]
- Hu, J.; Ye, X.; Wu, Y.; Li, C. On lift enhancement and noise reduction in serrated gurney flap airfoil of wind turbines using proper orthogonal decomposition. Ocean Eng. 2023, 287, 115706. [Google Scholar] [CrossRef]
- Sandoval, P.; Cornejo, P.; Tinapp, F. Evaluating the longitudinal stability of an UAV using a CFD-6DOF model. Aerosp. Sci. Technol. 2015, 43, 463–470. [Google Scholar] [CrossRef]
- Jinchun, S. Practical Handbook of Hydraulic Technology; China Electric Power Press: Beijing, China, 2010. (In Chinese) [Google Scholar]
- Wu, J.B.; Li, L. Pressure–flow rate relationship and its polynomial expansion for laminar flow in a circular pipe based on exponential viscosity-pressure characteristics: An extension of classical Poiseuille’s law. Phys. Fluids 2023, 35, 103613. [Google Scholar] [CrossRef]
- Guoling, N.; Caihua, L.; Xiaoping, H. Hydraulic and Pneumatic Transmission; Peking University Press: Beijing, China, 2019. (In Chinese) [Google Scholar]
- Bazsó, C.; Hős, C. An experimental study on the stability of a direct spring loaded poppet relief valve. J. Fluids Struct. 2013, 42, 456–465. [Google Scholar] [CrossRef]
- Tian, Q.; Zhang, Q.; Chen, Y.; Huo, L.; Li, S.; Wang, C.; Bai, Y.; Du, L. Influence of Ambient Pressure on Performance of a Deep-sea Hydraulic Manipulator. In Proceedings of the OCEANS 2019, Marseille, France, 17–20 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
























| Author (Year) | Research Focus | Main Findings |
|---|---|---|
| Yuan et al. (2019) [18] | Flow pattern | Different pressure drops in the poppet valve result in different evolutions of the coherent structure and variations in the flow pattern. |
| Yuan et al. (2019) [19] | Choked flow | Cavitation occurrence diminishes the pressure influence on flow performance and results in choked flow, with disintegration potentially serving as the governing mechanism. |
| Yuan et al. (2019) [20] | Cavitation–vortex interaction | Vortical cavitation elongation arises from the vortex shearing effect, while vorticity suppression is driven by cavitation growth in transitional cavitating jet flows. |
| Jia et al. (2019) [16] | Dynamic characteristics | A higher length-to-diameter ratio of the pre-valve core cylindrical fluid enhances poppet valve stability, with diameter having the most significant influence. |
| Min et al. (2020) [17] | Unstable vibration and cavitation | Significant cavitation emerges at the valve port as the poppet strikes the valve seat, and it is influenced by the pressure difference and the vibrational amplitude. |
| Sang et al. (2020) [21] | Dynamic characteristics | Despite an increase in the volume flow rate with increasing set pressure, there is no significant change in the displacement of the poppet due to the sum of the preset spring force and forces caused by back pressure being nearly equal to the lift force. |
| Burhani and Hos (2021) [22] | Coefficients of force and discharge | Fluid force in the poppet valve diminishes as valve lift increases, while discharge coefficients follow a quadratic relationship, declining with rising lift. |
| Upadhyay et al. (2021) [23] | Cavitation and structural optimization | Optimizing valve spool structure and streamline direction can reduce cavitation erosion and improve poppet valve performance, enhancing reliability at high pressure differences. |
| Min et al. (2022) [24] | Discharge coefficient | In low Reynolds number conditions, the pilot poppet valve’s discharge coefficient can still be defined as , but the coefficient m is notably lesser than the main stage poppet valve. |
| HIROSE et al. (2022) [25] | Flow pattern | Five types of flow patterns can be identified in poppet valves, and the relationship between these flow patterns, hysteresis characteristics, and flow forces has been clarified. |
| Hao et al. (2022) [26] | Flow force and cavitation | A comparative study of three poppet configurations was carried out, one of which achieved up to 44.2% reduction in flow force and 100% reduction in relative vapor volume. |
| Sang et al. (2023) [27] | Structural optimization | The effects of parameters such as annular clearances, spring stiffnesses and pressure jumps were studied, while the introducing of annular clearances can substantially improve the dynamic performance. |
| Symbol | Definition | Value |
|---|---|---|
| D | Valve seat diameter | 4 mm |
| Orifice diameter | 1 mm | |
| Valve core diameter | 5 mm | |
| Rear chamber diameter | 12 mm | |
| Orifice length | 10 mm | |
| Front chamber length | 15 mm | |
| Rear chamber length | 40 mm | |
| Cone length | 25 mm | |
| Valve core length | 8 mm | |
| Half-cone angle | 10° |
| Inlet Volumn Flow Rate (L/min) | (N) | (mm) | (N) |
|---|---|---|---|
| 0.6 | 127.93584 | 0.07587 | 125.65975 |
| 0.8 | 128.37820 | 0.09060 | 125.66029 |
| 1 | 128.79845 | 0.10460 | 125.66059 |
| 1.2 | 129.20781 | 0.11825 | 125.66037 |
| 1.4 | 129.60358 | 0.13145 | 125.66012 |
| 1.6 | 129.99474 | 0.14447 | 125.66059 |
| 1.8 | 130.37712 | 0.15723 | 125.66017 |
| 2 | 130.75685 | 0.16986 | 125.66116 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, P.-J.; Wu, J.-B. Performance Analysis of Poppet Valves in Deep-Sea Hydraulic Systems: Considering Viscosity–Pressure Characteristics. J. Mar. Sci. Eng. 2025, 13, 1177. https://doi.org/10.3390/jmse13061177
Wang P-J, Wu J-B. Performance Analysis of Poppet Valves in Deep-Sea Hydraulic Systems: Considering Viscosity–Pressure Characteristics. Journal of Marine Science and Engineering. 2025; 13(6):1177. https://doi.org/10.3390/jmse13061177
Chicago/Turabian StyleWang, Pin-Jian, and Jia-Bin Wu. 2025. "Performance Analysis of Poppet Valves in Deep-Sea Hydraulic Systems: Considering Viscosity–Pressure Characteristics" Journal of Marine Science and Engineering 13, no. 6: 1177. https://doi.org/10.3390/jmse13061177
APA StyleWang, P.-J., & Wu, J.-B. (2025). Performance Analysis of Poppet Valves in Deep-Sea Hydraulic Systems: Considering Viscosity–Pressure Characteristics. Journal of Marine Science and Engineering, 13(6), 1177. https://doi.org/10.3390/jmse13061177







