Analysis of Wind–Wave Relationship in Taiwan Waters
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
2.2.1. Distinguishing Between Wind Waves and Swells
2.2.2. Regression
2.2.3. Calculation of Wind Speed at 10 m Height
2.2.4. Machine Learning Methods
3. Results
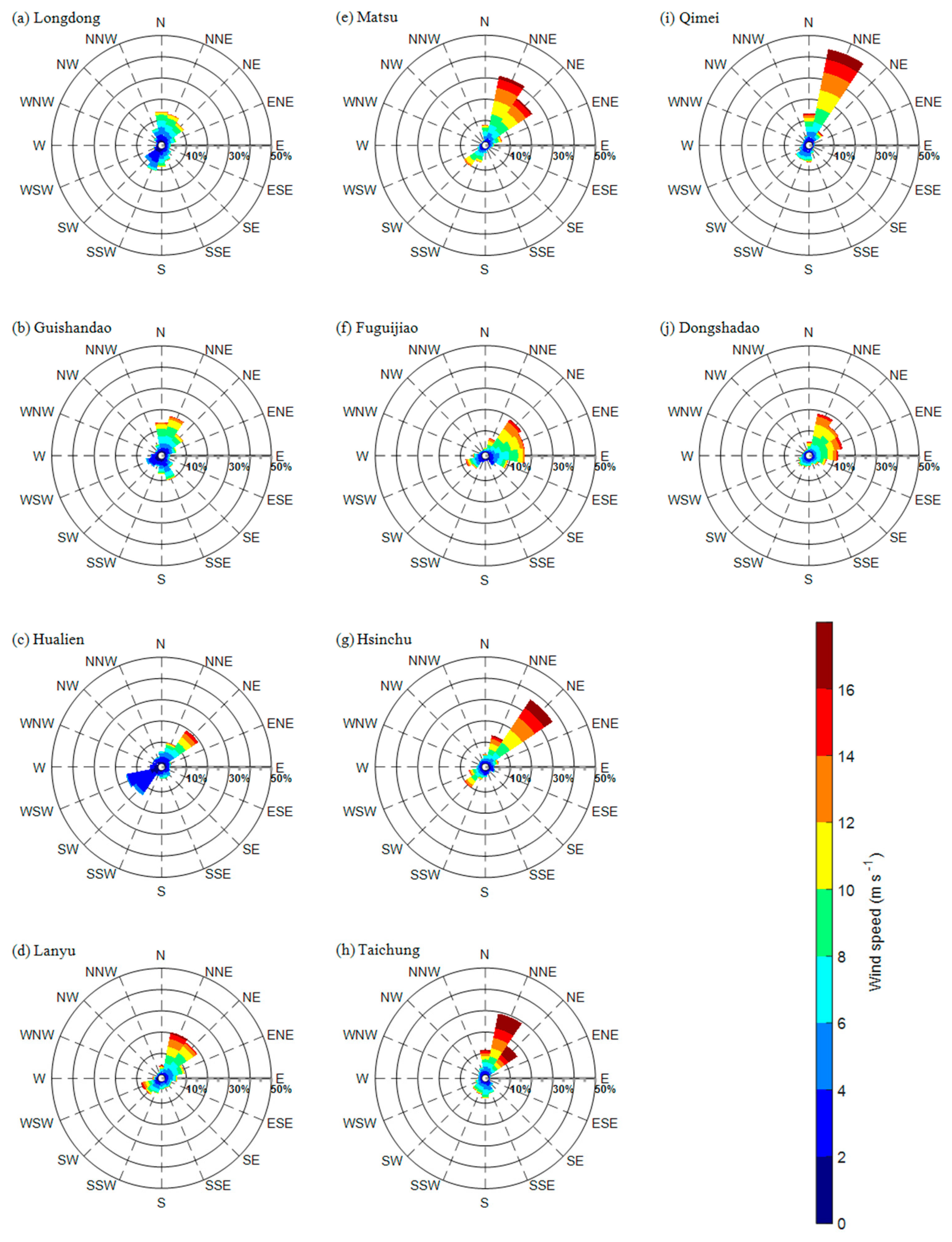
3.1. Wind Distribution
3.2. Significant Wave Height
3.3. Wind–Wave Relationship
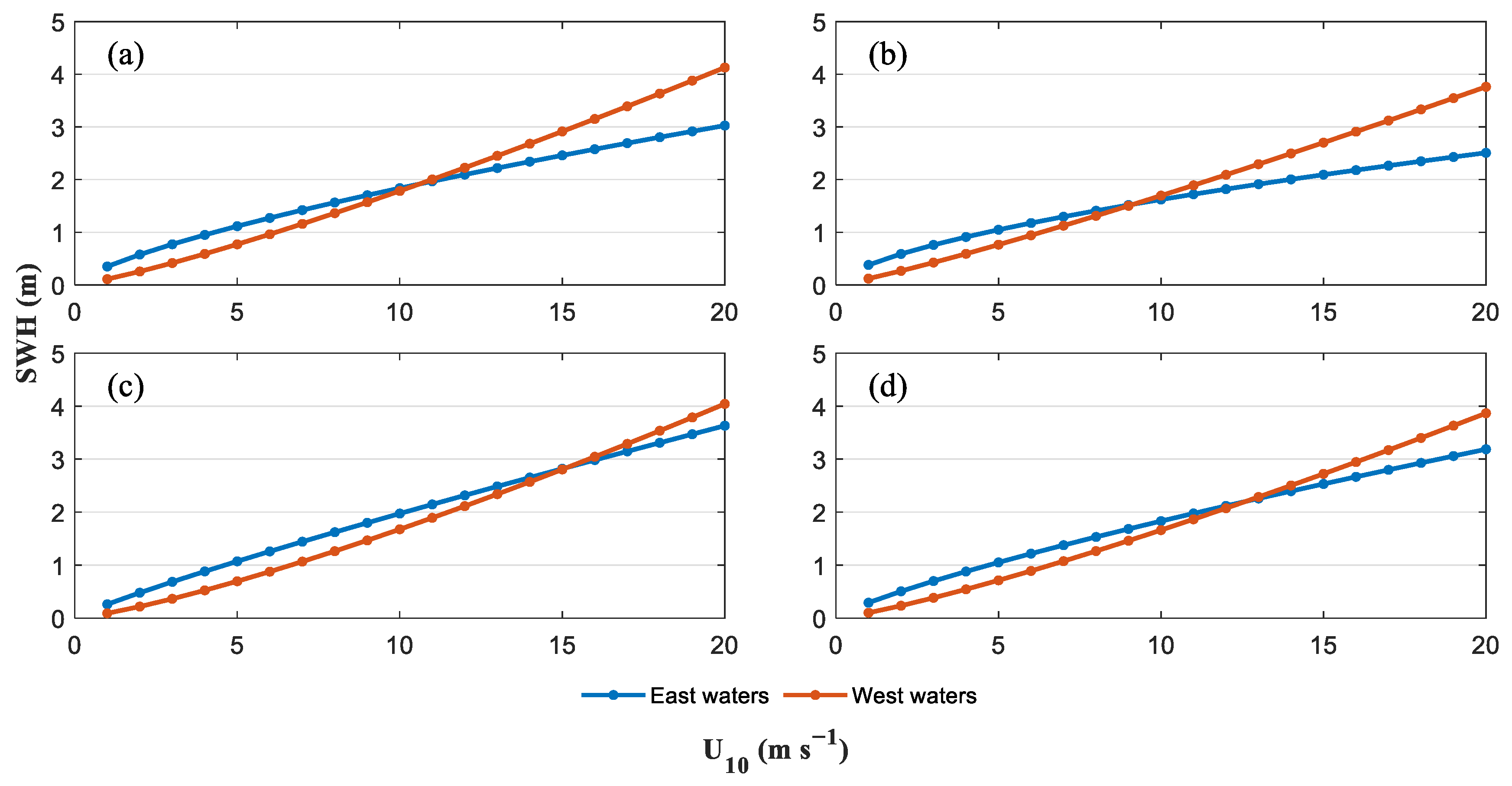
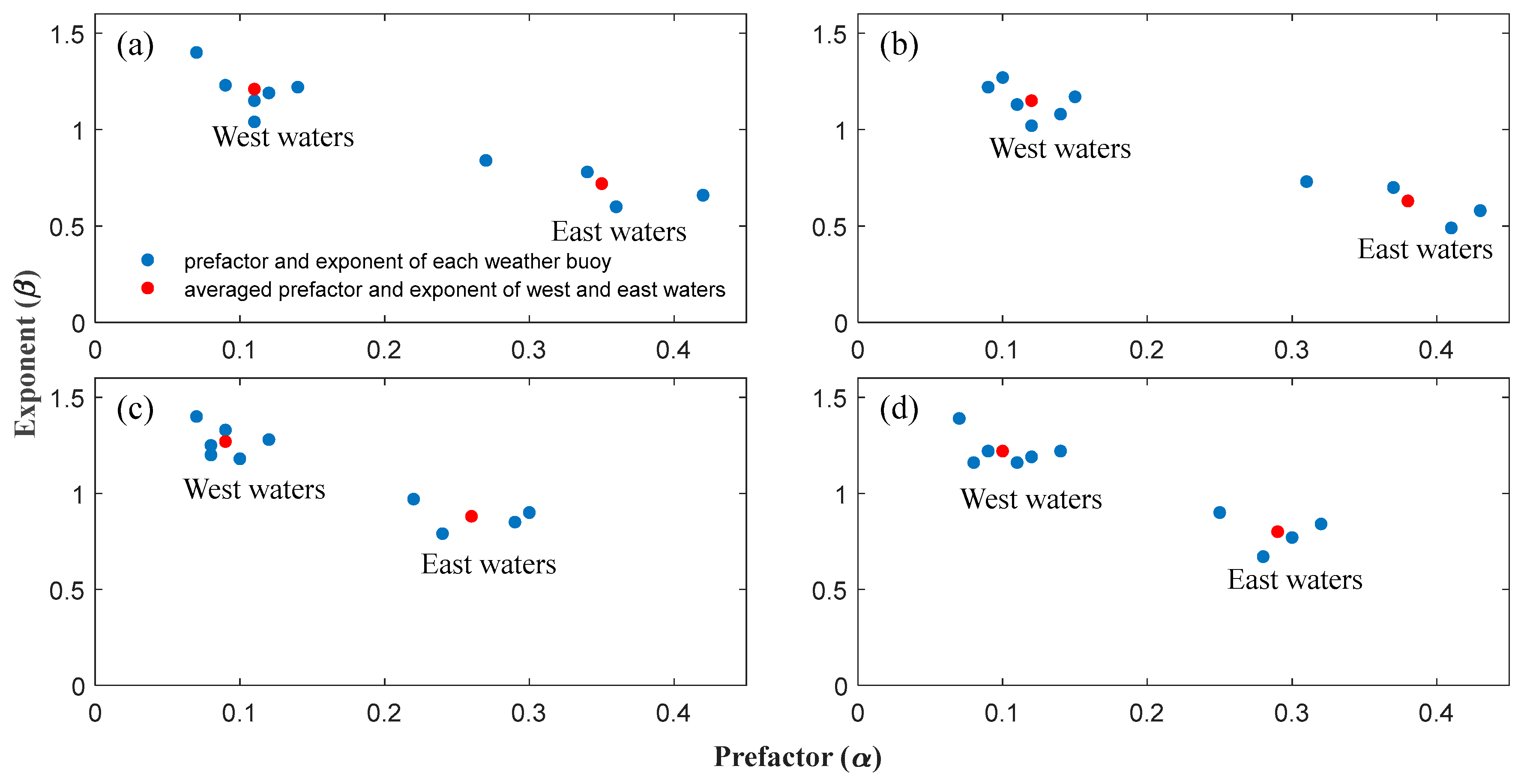
3.3.1. Regression Results
- When the wind speed is below the critical wind speed at the intersection point, the wind–wave relationship curve for the eastern waters lies above that of the western waters. This indicates that under relatively low wind speed conditions, the eastern waters generate a higher SWH for the same wind speed than the western waters. This phenomenon suggests that wave generation in the east of waters is more sensitive to wind in low-wind scenarios or that wave growth efficiency is higher.
- Conversely, the trend reverses when the wind speed exceeds the critical threshold. The wind–wave relationship curve for the western waters rises above that of the eastern waters. This means that the western waters produce a greater SWH under higher wind speed conditions than the eastern waters for the same wind speed. This may reflect specific geographical or oceanographic conditions in the western waters, such as fetch, bathymetry, or unique mechanisms of wind–wave interaction, all of which facilitate enhanced wave development at high wind speeds.
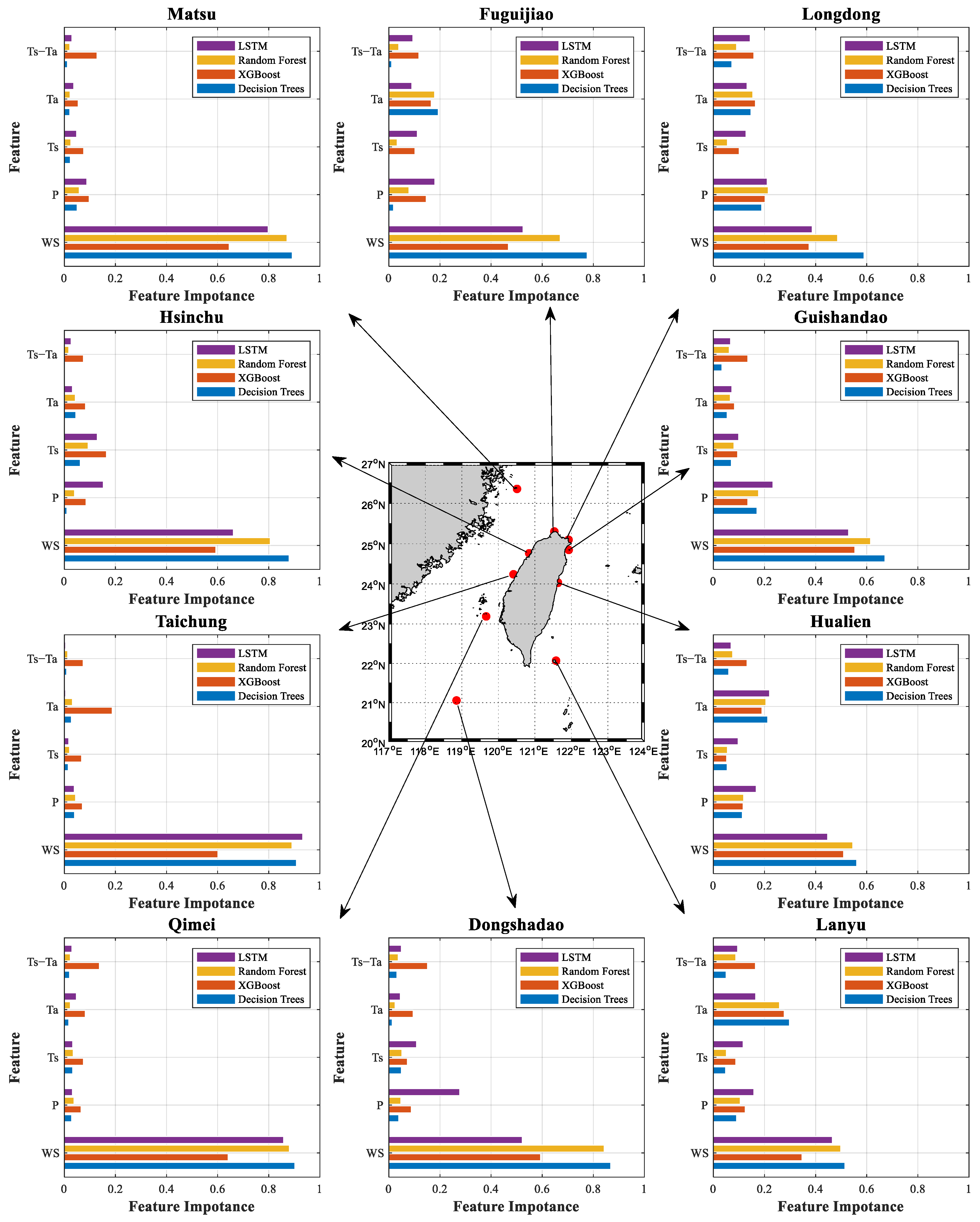
3.3.2. Regression Machine Learning Algorithms
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cimarelli, A.; Romoli, F.; Stalio, E. On wind–wave interaction phenomena at low Reynolds numbers. J. Fluid Mech. 2023, 956, A13. [Google Scholar] [CrossRef]
- Hou, B.; Fu, H.; Li, X.; Song, T.; Zhang, Z. Predicting significant wave height in the South China Sea using the SAC-ConvLSTM model. Front. Mar. Sci. 2024, 11, 1424714. [Google Scholar] [CrossRef]
- Zhan, Y.; Zhang, H.; Li, J.; Li, G. Prediction method for ocean wave height based on stacking ensemble learning model. J. Mar. Sci. Eng. 2022, 10, 1150. [Google Scholar] [CrossRef]
- Bujak, D.; Bogovac, T.; Carević, D.; Miličević, H. Filling Missing and Extending Significant Wave Height Measurements Using Neural Networks and an Integrated Surface Database. Wind 2023, 3, 151–169. [Google Scholar] [CrossRef]
- Carrasco, R.; Horstmann, J.; Seemann, J. Significant wave height measured by coherent X-band radar. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5355–5365. [Google Scholar] [CrossRef]
- Woo, H.J.; Park, K.A. Estimation of extreme significant wave height in the northwest pacific using satellite altimeter data focused on typhoons (1992–2016). Remote Sens. 2021, 13, 1063. [Google Scholar] [CrossRef]
- Ouyang, L.; Ling, F.; Li, Y.; Bai, L.; Luo, J.J. Wave forecast in the Atlantic Ocean using a double-stage ConvLSTM network. Atmos. Ocean. Sci. Lett. 2023, 16, 100347. [Google Scholar] [CrossRef]
- Song, T.; Han, R.; Meng, F.; Wang, J.; Wei, W.; Peng, S. A significant wave height prediction method based on deep learning combining the correlation between wind and wind waves. Front. Mar. Sci. 2022, 9, 983007. [Google Scholar] [CrossRef]
- Medina-Manuel, A.; Molina Sánchez, R.; Souto-Iglesias, A. AI-Driven Model Prediction of Motions and Mooring Loads of a Spar Floating Wind Turbine in Waves and Wind. J. Mar. Sci. Eng. 2024, 12, 1464. [Google Scholar] [CrossRef]
- Wang, X.; Jiang, H. Physics-guided deep learning for skillful wind-wave modeling. Sci. Adv. 2024, 10, eadr3559. [Google Scholar] [CrossRef]
- Shen, J.; Zhang, J.; Qiu, Y.; Li, L.; Zhang, S.; Pan, A.; Huang, J.; Guo, X.; Jing, C. Winter counter-wind current in western Taiwan Strait: Characteristics and mechanisms. Cont. Shelf Res. 2019, 172, 1–11. [Google Scholar] [CrossRef]
- Cheng, K.S.; Ho, C.Y.; Teng, J.H. Wind characteristics in the Taiwan strait: A case study of the first offshore wind farm in Taiwan. Energies 2020, 13, 6492. [Google Scholar] [CrossRef]
- Dong, S.; Gong, Y.; Wang, Z. Long-term variations of wind and wave conditions in the Taiwan Strait. Reg. Stud. Mar. Sci. 2020, 36, 101256. [Google Scholar] [CrossRef]
- Lu, W.S.; Tseng, C.H.; Hsiao, S.C.; Chiang, W.S.; Hu, K.C. Future Projection for Wave Climate around Taiwan Using Weather-Type Statistical Downscaling Method. J. Mar. Sci. Eng. 2022, 10, 1823. [Google Scholar] [CrossRef]
- Doong, D.J.; Fan, Y.M.; Chen, J.Y.; Kao, C.C. Analysis of Long-Period Hazardous Waves in the Taiwan Marine Environment Monitoring Service. Front. Mar. Sci. 2021, 8, 657569. [Google Scholar] [CrossRef]
- Doong, D.J.; Tsai, C.H.; Chen, Y.C.; Peng, J.P.; Huang, C.J. Statistical analysis on the long-term observations of typhoon waves in the Taiwan sea. J. Mar. Sci. Tech. 2015, 23, 893–900. [Google Scholar] [CrossRef]
- Ou, Y.; Zhai, F.; Li, P. Interannual wave climate variability in the Taiwan Strait and its relationship to ENSO events. J. Oceanol. Limnol. 2018, 36, 2110–2129. [Google Scholar] [CrossRef]
- Chien, H.; Cheng, H.Y.; Chiou, M.D. Wave climate variability of Taiwan waters. J. Oceanogr. 2014, 70, 133–152. [Google Scholar] [CrossRef]
- Doong, D.J.; Chen, S.H.; Kao, C.C.; Lee, B.C.; Yeh, S.P. Data quality check procedures of an operational coastal ocean monitoring network. Ocean Eng. 2007, 34, 234–246. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S.; Cartwright, D.E.; Smith, N.D. Observations of the directional spectrum of sea waves using the motions of a floating buoy. In Ocean Wave Spectra; Prentice-Hall: Saddle River, NJ, USA, 1963; pp. 111–136. [Google Scholar]
- Lygre, A.; Krogstad, H.E. Maximum entropy estimation of the directional distribution in ocean wave spectra. J. Phys. Oceanogr. 1986, 16, 2052–2060. [Google Scholar] [CrossRef]
- Capon, J. Maximum-likelihood spectral estimation. In Nonlinear Methods in Spectral Analysis; Heykin, S., Ed.; Springer: New York, NY, USA, 1979; pp. 155–179. [Google Scholar] [CrossRef]
- Hashimoto, N.; Kobune, K. Directional spectrum estimation from a Bayesian approach. In Proceedings of the American Society of Civil Engineers 21st International Conference on Coastal Engineering, Costa del SoL-MaLaga, Spain, 20–25 June 1988; pp. 62–76. [Google Scholar] [CrossRef]
- Falnes, J. A review of wave-energy extraction. Mar. Struct. 2007, 20, 185–201. [Google Scholar] [CrossRef]
- World Meteorological Organization. Guide to Wave Analysis and Forecasting, 2018th ed.; World Meteorological Organization: Geneva, Switzerland, 2018; pp. 1–189. [CrossRef]
- Gao, Y.; Schmitt, F.G.; Hu, J.; Huang, Y. Probability-based wind-wave relation. Front. Mar. Sci. 2023, 9, 1085340. [Google Scholar] [CrossRef]
- Lee, Y.C.; Doong, D.J. Duration-limited growth method for wind sea and swell separation of directional wave spectrum. Ocean Eng. 2025, 329, 121182. [Google Scholar] [CrossRef]
- Kinsman, B. Wind Waves: Their Generation and Propagation on the Ocean Surface; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1984; pp. 1–676. [Google Scholar]
- Hanson, J.L.; Phillips, O.M. Wind sea growth and dissipation in the open ocean. J. Phys. Oceanogr. 1999, 29, 1633–1648. [Google Scholar] [CrossRef]
- Vettor, R.; Soares, C.G. A global view on bimodal wave spectra and crossing seas from ERA-interim. Ocean Eng. 2020, 210, 107439. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, K.; Shi, J. The Effect of Different Swell and Wind-Sea Proportions on the Transformation of Bimodal Spectral Waves over Slopes. Water 2024, 16, 296. [Google Scholar] [CrossRef]
- Snodgrass, F.E.; Hasselmann, K.F.; Miller, G.R.; Munk, W.H.; Powers, W.H. Propagation of ocean swell across the Pacific. Philos. Trans. A Math. Phys. Eng. Sci. 1966, 259, 431–497. [Google Scholar] [CrossRef]
- Yan, Y.; Hu, M.; Ni, Y.; Qiu, C. Simulated Directional Wave Spectra of the Wind Sea and Swell under Typhoon Mangkhut. Atmosphere 2024, 15, 1174. [Google Scholar] [CrossRef]
- Davis, J.R.; Thomson, J.; Houghton, I.A.; Fairall, C.W.; Butterworth, B.J.; Thompson, E.J.; de Boer, G.; Doyle, J.D.; Moskaitis, J.R. Ocean surface wave slopes and wind-wave alignment observed in Hurricane Idalia. J. Geophys. Res. Oceans 2025, 130, e2024JC021814. [Google Scholar] [CrossRef]
- Wyatt, L.R.; Green, J.J. Swell and wind-sea partitioning of HF radar directional spectra. J. Oper. Oceanogr. 2024, 17, 28–39. [Google Scholar] [CrossRef]
- Pierson Jr, W.J.; Moskowitz, L. A proposed spectral form for fully developed wind seas based on the similarity theory of SA Kitaigorodskii. J. Geophys. Res. 1964, 69, 5181–5190. [Google Scholar] [CrossRef]
- Liu, P.L.F.; Losada, I.J. Wave propagation modeling in coastal engineering. J. Hydraul. Res. 2002, 40, 229–240. [Google Scholar] [CrossRef]
- Ribal, A.; Young, I.R. 33 years of globally calibrated wave height and wind speed data based on altimeter observations. Sci. Data 2019, 6, 77. [Google Scholar] [CrossRef]
- Guan, C.; Xie, L. On the linear parameterization of drag coefficient over sea surface. J. Phys. Oceanogr. 2004, 34, 2847–2851. [Google Scholar] [CrossRef]
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Patel, H.H.; Prajapati, P. Study and analysis of decision tree based classification algorithms. Int. J. Comput. Sci. Eng. 2018, 6, 74–78. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Biau, G. Analysis of a random forests model. J. Mach. Learn. Res. 2012, 13, 1063–1095. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Greff, K.; Srivastava, R.K.; Koutník, J.; Steunebrink, B.R.; Schmidhuber, J. LSTM: A search space odyssey. IEEE Trans. Neural Netw. Learn. Syst. 2015, 28, 2222–2232. [Google Scholar] [CrossRef] [PubMed]
- Noh, S.-H. Analysis of gradient vanishing of RNNs and performance comparison. Information 2021, 12, 442. [Google Scholar] [CrossRef]
- Sahoo, B.B.; Jha, R.; Singh, A.; Kumar, D. Long short-term memory (LSTM) recurrent neural network for low-flow hydrological time series forecasting. Acta Geophys. 2019, 67, 1471–1481. [Google Scholar] [CrossRef]
- Fairall, C.W.; Bradley, E.F.; Hare, J.E.; Grachev, A.A.; Edson, J.B. Bulk parameterization of air–sea fluxes: Updates and verification for the COARE algorithm. J. Clim. 2003, 16, 571–591. [Google Scholar] [CrossRef]
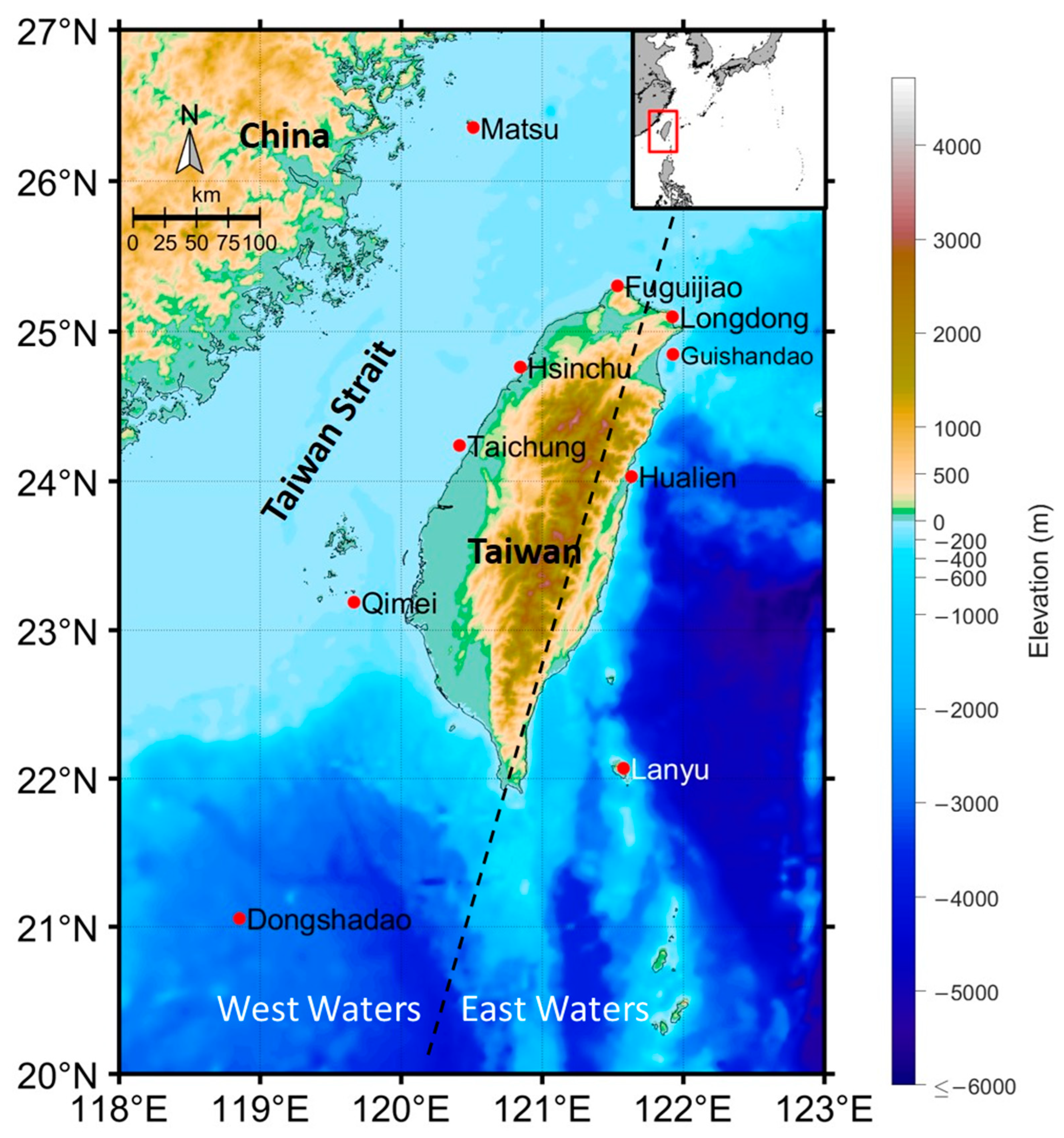

| Buoy | Latitude (°N) | Longitude (°E) | Water Depth (m) | Distance to Coast (Km) | Date of Data Available |
|---|---|---|---|---|---|
| Longdong | 25.098610 | 121.922770 | 27 | 0.5 | 1998–2025 |
| Guishandao | 24.848300 | 121.926100 | 19 | 0.8 | 2002–2024 |
| Hualien | 24.031500 | 121.632300 | 24 | 0.4 | 1997–2025 |
| Lanyu | 22.069720 | 121.579160 | 50 | 1 | 2017–2024 |
| Matsu | 26.354440 | 120.510830 | 52 | 2.7 | 2010–2025 |
| Fuguijiao | 25.303880 | 121.532770 | 30 | 0.8 | 2015–2025 |
| Hsinchu | 24.763300 | 120.844100 | 24.5 | 6.4 | 1997–2025 |
| Qimei | 23.188880 | 119.665000 | 50 | 22.8 | 2015–2025 |
| Taichung | 24.239400 | 120.413300 | 18.5 | 11 | 2019–2025 |
| Dongshadao | 21.055600 | 118.853300 | 2550 | 224 | 2010–2024 |
| Location | All | Spring | Summer | Autumn | Winter |
|---|---|---|---|---|---|
| Longdong | 5.30 ± 2.86 | 4.76 ± 2.45 | 4.37 ± 2.74 | 5.54 ± 2.92 | 6.47 ± 2.86 |
| Guishandao | 5.70 ± 3.26 | 5.15 ± 2.94 | 4.54 ± 2.99 | 6.01 ± 3.26 | 6.99 ± 3.31 |
| Hualien | 4.49 ± 3.17 | 4.23 ± 2.81 | 3.33 ± 1.74 | 4.82 ± 3.40 | 5.54 ± 3.85 |
| Lanyu | 7.53 ± 3.75 | 7.00 ± 3.14 | 6.14 ± 3.53 | 8.07 ± 3.93 | 9.40 ± 3.48 |
| Matsu | 8.82 ± 3.88 | 7.35 ± 3.30 | 7.17 ± 3.20 | 9.97 ± 4.04 | 10.59 ± 3.61 |
| Fuguijiao | 7.50 ± 3.71 | 6.54 ± 3.27 | 5.66 ± 3.55 | 8.68 ± 3.53 | 8.83 ± 3.42 |
| Hsinchu | 8.42 ± 4.61 | 7.50 ± 4.02 | 6.82 ± 3.63 | 9.24 ± 5.14 | 9.95 ± 4.63 |
| Taichung | 9.09 ± 5.30 | 8.38 ± 4.64 | 5.92 ± 2.83 | 9.94 ± 5.78 | 13.03 ± 4.89 |
| Qimei | 8.30 ± 4.53 | 7.00 ± 3.76 | 5.20 ± 2.67 | 9.49 ± 4.77 | 11.38 ± 3.91 |
| Dongshadao | 8.39 ± 3.56 | 7.23 ± 3.14 | 6.23 ± 3.29 | 9.01 ± 3.53 | 10.52 ± 2.65 |
| Location | All | Spring | Summer | Autumn | Winter |
|---|---|---|---|---|---|
| Longdong | 1.25 ± 0.84 | 1.11 ± 0.62 | 0.64 ± 0.63 | 1.47 ± 0.82 | 1.71 ± 0.83 |
| Guishandao | 0.99 ± 0.55 | 0.88 ± 0.40 | 0.73 ± 0.53 | 1.08 ± 0.61 | 1.24 ± 0.50 |
| Hualien | 1.10 ± 0.73 | 1.00 ± 0.56 | 0.58 ± 0.44 | 1.25 ± 0.72 | 1.54 ± 0.76 |
| Lanyu | 1.44 ± 0.92 | 1.25 ± 0.68 | 0.78 ± 0.56 | 1.75 ± 0.94 | 2.17 ± 0.79 |
| Matsu | 1.67 ± 0.93 | 1.35 ± 0.64 | 1.21 ± 0.74 | 1.99 ± 1.01 | 2.09 ± 0.93 |
| Fuguijiao | 1.36 ± 0.98 | 1.14 ± 0.72 | 0.64 ± 0.47 | 1.64 ± 1.02 | 1.96 ± 1.01 |
| Hsinchu | 1.09 ± 0.68 | 0.91 ± 0.50 | 0.60 ± 0.34 | 1.33 ± 0.74 | 1.47 ± 0.65 |
| Taichung | 1.42 ± 1.04 | 1.23 ± 0.82 | 0.59 ± 0.40 | 1.83 ± 1.07 | 2.22 ± 0.88 |
| Qimei | 1.33 ± 0.87 | 1.01 ± 0.63 | 0.90 ± 0.67 | 1.61 ± 0.99 | 1.75 ± 0.80 |
| Dongshadao | 1.97 ± 1.13 | 1.51 ± 0.84 | 1.30 ± 0.90 | 2.29 ± 1.20 | 2.61 ± 0.97 |
| All | T < 10 s | dir_diff < 45° | T < 10 s and dir_diff < 45° | |||||
|---|---|---|---|---|---|---|---|---|
| Location | α | β | α | β | α | β | α | β |
| Longdong | 0.34 | 0.78 | 0.37 | 0.70 | 0.30 | 0.90 | 0.32 | 0.84 |
| Guishandao | 0.36 | 0.60 | 0.41 | 0.49 | 0.24 | 0.79 | 0.28 | 0.67 |
| Hualien | 0.42 | 0.66 | 0.43 | 0.58 | 0.29 | 0.85 | 0.30 | 0.77 |
| Lanyu | 0.27 | 0.84 | 0.31 | 0.73 | 0.22 | 0.97 | 0.25 | 0.90 |
| Matsu | 0.07 | 1.40 | 0.10 | 1.27 | 0.07 | 1.40 | 0.07 | 1.39 |
| Fuguijiao | 0.12 | 1.19 | 0.14 | 1.08 | 0.09 | 1.33 | 0.12 | 1.19 |
| Hsinchu | 0.11 | 1.04 | 0.12 | 1.02 | 0.08 | 1.20 | 0.08 | 1.16 |
| Taichung | 0.09 | 1.23 | 0.09 | 1.22 | 0.10 | 1.18 | 0.11 | 1.16 |
| Qimei | 0.11 | 1.15 | 0.11 | 1.13 | 0.08 | 1.25 | 0.09 | 1.22 |
| Dongshadao | 0.14 | 1.22 | 0.15 | 1.17 | 0.12 | 1.28 | 0.14 | 1.22 |
| East waters mean | 0.35 | 0.72 | 0.38 | 0.63 | 0.26 | 0.88 | 0.29 | 0.80 |
| West waters mean | 0.11 | 1.21 | 0.12 | 1.15 | 0.09 | 1.27 | 0.10 | 1.22 |
| All | T < 10 s | dir_diff < 45° | T < 10 s and dir_diff < 45° | |||||
|---|---|---|---|---|---|---|---|---|
| Location | R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE |
| Longdong | 0.35 | 0.67 | 0.31 | 0.60 | 0.50 | 0.63 | 0.47 | 0.51 |
| Guishandao | 0.35 | 0.44 | 0.33 | 0.35 | 0.44 | 0.42 | 0.40 | 0.37 |
| Hualien | 0.37 | 0.58 | 0.32 | 0.46 | 0.57 | 0.57 | 0.56 | 0.46 |
| Lanyu | 0.36 | 0.73 | 0.34 | 0.62 | 0.66 | 0.53 | 0.66 | 0.44 |
| Matsu | 0.67 | 0.54 | 0.72 | 0.48 | 0.73 | 0.49 | 0.73 | 0.47 |
| Fuguijiao | 0.50 | 0.69 | 0.48 | 0.63 | 0.51 | 0.74 | 0.47 | 0.68 |
| Hsinchu | 0.62 | 0.42 | 0.61 | 0.41 | 0.65 | 0.41 | 0.64 | 0.40 |
| Taichung | 0.79 | 0.48 | 0.78 | 0.47 | 0.80 | 0.47 | 0.79 | 0.46 |
| Qimei | 0.70 | 0.48 | 0.72 | 0.43 | 0.74 | 0.45 | 0.75 | 0.42 |
| Dongshadao | 0.68 | 0.64 | 0.66 | 0.58 | 0.65 | 0.64 | 0.64 | 0.60 |
| East waters mean | 0.36 | 0.61 | 0.33 | 0.51 | 0.54 | 0.54 | 0.52 | 0.45 |
| West waters mean | 0.66 | 0.54 | 0.66 | 0.50 | 0.68 | 0.53 | 0.67 | 0.51 |
| Location | DT | XGBT | RF | LSTM | ||||
|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | |
| Longdong | 0.58 | 0.52 | 0.64 | 0.48 | 0.63 | 0.49 | 0.62 | 0.50 |
| Guishandao | 0.52 | 0.39 | 0.57 | 0.35 | 0.59 | 0.36 | 0.51 | 0.36 |
| Hualien | 0.58 | 0.44 | 0.62 | 0.40 | 0.61 | 0.40 | 0.61 | 0.40 |
| Lanyu | 0.65 | 0.53 | 0.75 | 0.45 | 0.72 | 0.48 | 0.70 | 0.49 |
| Matsu | 0.77 | 0.45 | 0.83 | 0.38 | 0.80 | 0.42 | 0.81 | 0.41 |
| Fuguijiao | 0.70 | 0.54 | 0.75 | 0.48 | 0.73 | 0.50 | 0.73 | 0.50 |
| Hsinchu | 0.76 | 0.33 | 0.82 | 0.28 | 0.79 | 0.31 | 0.79 | 0.31 |
| Taichung | 0.85 | 0.39 | 0.90 | 0.33 | 0.88 | 0.36 | 0.87 | 0.37 |
| Qimei | 0.76 | 0.42 | 0.81 | 0.38 | 0.79 | 0.39 | 0.79 | 0.39 |
| Dongshadao | 0.71 | 0.58 | 0.64 | 0.49 | 0.75 | 0.45 | 0.76 | 0.52 |
| East waters mean | 0.59 | 0.47 | 0.65 | 0.42 | 0.64 | 0.43 | 0.61 | 0.44 |
| West waters mean | 0.76 | 0.45 | 0.81 | 0.39 | 0.79 | 0.40 | 0.79 | 0.41 |
| Waters | DT | XGBT | RF | LSTM | ||||
|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | |
| East | 0.53 | 0.52 | 0.64 | 0.46 | 0.61 | 0.48 | 0.60 | 0.48 |
| West | 0.63 | 0.60 | 0.71 | 0.53 | 0.69 | 0.56 | 0.69 | 0.56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, K.-H.; Chang, C.-H.; Yang, Y.-C.; Tseng, Y.-H.; Ho, C.-R.; Hsu, T.-W.; Doong, D.-J. Analysis of Wind–Wave Relationship in Taiwan Waters. J. Mar. Sci. Eng. 2025, 13, 1047. https://doi.org/10.3390/jmse13061047
Cheng K-H, Chang C-H, Yang Y-C, Tseng Y-H, Ho C-R, Hsu T-W, Doong D-J. Analysis of Wind–Wave Relationship in Taiwan Waters. Journal of Marine Science and Engineering. 2025; 13(6):1047. https://doi.org/10.3390/jmse13061047
Chicago/Turabian StyleCheng, Kai-Ho, Chih-Hsun Chang, Yi-Chung Yang, Yu-Hao Tseng, Chung-Ru Ho, Tai-Wen Hsu, and Dong-Jiing Doong. 2025. "Analysis of Wind–Wave Relationship in Taiwan Waters" Journal of Marine Science and Engineering 13, no. 6: 1047. https://doi.org/10.3390/jmse13061047
APA StyleCheng, K.-H., Chang, C.-H., Yang, Y.-C., Tseng, Y.-H., Ho, C.-R., Hsu, T.-W., & Doong, D.-J. (2025). Analysis of Wind–Wave Relationship in Taiwan Waters. Journal of Marine Science and Engineering, 13(6), 1047. https://doi.org/10.3390/jmse13061047









