Review on Sensitivity and Uncertainty Analysis of Hydrodynamic and Hydroelastic Responses of Floating Offshore Structures

Abstract

This review comprehensively overviews of theoretical and numerical methods used to assess the sensitivity and uncertainty in the hydrodynamic and hydroelastic behavior of floating offshore structures. The different methodologies associated with basic governing equations for floating offshore structure systems on the sensitivity and uncertainty assessments are discussed. Then, a brief overview of a comparative analysis of the methodologies, highlighting their key features, applications, and findings are provided in a table form. In addition, a technical comparative analysis of different numerical models and a comparative analysis of the sensitivity of different mooring parameters are also provided in a table form. Further, the uncertainty and sensitivity analysis for floating structure systems are presented by providing detailed discussions. In conclusion, this review highlights the revisions arising from the present analysis and outlines future research directions.

1. Introduction

The design, optimization, operation, and safety of floating offshore structures play a very important role in ocean infrastructure and energy conversion, both of which are complicated activities due to the dynamic and uncertain marine environment. Sensitivity and uncertainty assessment have emerged as a critical tool to manage this complexity, providing vital information on how to input variability and parametric uncertainties propagate in numerical models and influence structural performance [1,2]. Recent advances in methodology for floating offshore structures prioritize accuracy, computational efficiency, and the capability to address highly nonlinear and probabilistic behaviors. The objective of this review is to discuss the development of sensitivity and uncertainty methods, their increasing importance in optimizing design processes, enhancing reliability, and reducing risks of these sophisticated engineering systems, and point out the direction towards robust and data-driven methodologies [3,4,5].

By systematically evaluating the sensitivity assessment of different mooring line types and configurations and various connection types between different structural arrangements within multi-module structures, uncertain environmental conditions, structural materials, and boundary conditions, designers can ascertain critical parameters that influence hydrodynamic behavior. This comprehensive analysis facilitates enhancing computational models, improving analytical and numerical accuracy, and guiding decision-making for an optimum design of floating offshore structures [6,7,8,9,10,11,12].

To investigate the hydroelastic analysis of floating flexible perforated system structures, different analytical models are developed in 2D, 3D, and oblique wave cases based on BIEM and solution techniques [13,14,15,16,17,18]. On the other hand, a couple of theoretical models associated with wave interaction with a Timoshenko-Mindlin Beam theory subjected to current loads [19,20], investigate the influence of current speed on the bending moment, shear force, and deflection on the structural responses and transmission coefficients.

To date, sensitivity and uncertainty analysis in floating offshore structures and wave-structure interactions have been well-documented in various literature review articles. For example, an extensive review of the uncertainty models within the structures, hydrodynamics, environmental loads, and those materials degrade gradually as a result of fatigue, corrosion, and climate-related risks for the proper structural design and reliability prediction of FOWTs was provided [21]. It was concluded that large uncertainties are connected in the hydrodynamic computations of FOWTs, which are intrinsically related to the composition and behavior of the structures and materials. A comprehensive review of recent developments in floating multi-body hydrodynamics and gap resonance was conducted [22], including theoretical, numerical, and experimental research works for various applications. The optimization of mooring line parameters and the transition from classical to EAs for floating offshore structures, was reviewed, considering the dynamic interaction of the platform, risers, and moorings [23]. The different numerical approaches to the hydroelastic response of VLFSs were reviewed [24].

Saltelli et al. [25] reviewed sensitivity analysis and uncertainty analysis practices in various scientific fields, emphasizing the importance of global sensitivity analysis methods for nonlinear models and calling for better standards and guidelines in sensitivity analysis to improve the reliability of model-based conclusions. The advances in modeling for coupled hydrodynamic and hydroelastic VLFS analyses, including classifying their shapes and various applications based on theories and methods, were reviewed [26]. A comprehensive literature review was provided [27] to explore the developments and performance of various FB designs and associated wave attenuation devices.

The above literature confirmed that to date no review has been presented to the public on the hydrodynamic and hydroelastic of especially offshore floating structures; therefore, this review seeks to present a comprehensive review on the theoretical, numerical, and experimental methodologies of the sensitivity and uncertainty of the hydrodynamic and hydroelastic responses of offshore floating structures models. A brief overview of the methodologies for offshore floating structure systems is outlined in Section 2. Further, the influence of boundary conditions and nonlinearities within different methodologies is highlighted. Section 3 is dedicated to providing a detailed analysis of different components of the offshore structure systems by presenting the basic equations and their numerical result discussions. Further, a comparative discussion of sensitivity and uncertainty analysis is provided. Section 4 presents the review’s final conclusions and points out avenues for future improvements in model development.

2. Different Methods for Sensitivity Analysis and Uncertainty

VLFSs are complex engineering systems that need precise analysis to ensure their safety, efficiency, and reliability. Sensitivity and uncertainty analysis are critical components of this process, as they provide insights into the principal factors affecting the structure’s response and assess the effects of uncertainties in design parameters. This paper addresses the current research and methodologies related to these analyses.

2.1. Neural-Network-Driven Sensitivity Analysis

A novel methodology combining ANN and sparse polynomial chaos expansion (SPCE) is proposed for sensitivity analysis in high-dimensional systems, as are common in VLFS design. This method employs ANN to create a model that accurately represents the complex interplay between input variables and system responses [28]. The integration of SPCE refines computational efficiency by reducing the number of Monte Carlo samples needed for GSA [29]. A probe variable is introduced to track the convergence of variable importance to ensure the accurate determination of sensitive parameters. This method is validated by ship motion analysis and is a promising tool to use in VLFS applications. The primary benefits of this method include the possibility to run high-dimensional data and its computational efficiency compared to Monte Carlo-based methods. However, the computational cost and data requirements associated with ANN training may constrain its applicability in scenarios characterized by limited computational resources.

The model input is $\mathit{X}=\left(x_1,\dots ,x_M\right)$, with $M$ parameters while according [30], the following expression result from [29], as

$$\begin{array}{rr}f(\mathit{X})=& f_0+{\displaystyle \sum _{i=1}^M} f_i\left(x_i\right)+{\displaystyle \sum _{1\le i\le j\le M}} f_{ij}\left(x_i,x_j\right)+\dots +f_{\mathrm{1,2},\dots ,M}\left(x_1,x_2,\dots ,x_M\right)\\ & \end{array}$$

(1)

Considering [28]. Equation (1) can be read as

$$\int f^2(\mathit{X})d\mathit{X}-f_0^2=\sum _{i=1}^M \int f_i^2\left(x_i\right)+\sum _{1\le i\le j\le M} \int f_{ij}^2\left(x_i,x_j\right)$$

(2)

The left-hand side in Equation (2) leads to

$$V=\int f^2(\mathit{X})d\mathit{X}-f_0^2$$

(3)

where the total variance denoted by $V$.

$$\begin{array}{l}{V}_i={\displaystyle \sum _{i=1}^M} \int f_i^2\left(x_i\right)\\ V_{ij}={\displaystyle \sum _{1\le i\le j\le M}} \int f_{ij}^2\left(x_i,x_j\right)\end{array}$$

(4)

In essence, the main effect sensitivity index is determined as

$$S_i={\displaystyle \frac{V_i}{V}}$$

(5)

The total order is defined as

$$S_{Ti}=1-{\displaystyle \frac{V_{\sim i}}{V}}$$

(6)

The high computational cost associated with Sobol’s method, which relies on Monte Carlo simulations to analyze the sensitivity index, can be reduced by utilizing polynomial chaos expansion (PCE). It should also be noted that PCE offers a much faster computational approach than the Monte Carlo method, but this efficiency is primarily seen when the number of uncertain parameters is limited.

Once formulated the truncation strategy [28], the weights $b_i$ is obtained by reducing the expression below:

$$\underset{b}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}\left(\sum _{i=1}^{N^{\prime }} {\left[f\left({\mathit{x}}_i\right)-{\mathit{b}}^T\mathit{K}\left({\mathit{x}}_i\right)\right]}^2+\eta \sum _{i=1}^{N^{\prime }} b_i\right)$$

(7)

where the symbols used in Equation (7) can be found from [28].

Proceeding similarly as in [28], one can determine as

$$S_{i1,\dots ,iq}={\displaystyle \frac{\sum _{k\in R_{i1},\dots ,iq} b_k^2{\Psi }_k^2\left({\mathit{X}}_{i1},\dots ,{\mathit{X}}_{iq}\right)}{\sum _{i=0}^d b_i^{2}E\left[{\Psi }_i^2(\mathit{X})\right]}}$$

(8)

Since the summands in (8) are derived from the coefficients defined from (7), the solutions of Sobol index are estimated to have insignificant computation cost.

Nonlinearity Limitations:

While ANNs can approximate nonlinear functions, their accuracy depends heavily on the training data. For highly nonlinear wave-structure interactions (e.g., breaking waves), a very large and diverse training dataset would be needed, which might be difficult and computationally expensive to obtain.

FSI Complexity:

Integrating ANNs directly into a fully coupled FSI framework is challenging. Typically, ANNs are used as surrogate models for either the fluid or structural response, but capturing the dynamic interplay between the two remains a complex task.

General Role of Boundary Conditions: In using ANNs for sensitivity analysis of floating structures, boundary conditions are crucial inputs to the numerical model that generates the training data for the ANN. These boundary conditions define the physical environment and constraints under which the structure responses.

Boundary Conditions:

ANNs do not explicitly handle boundary conditions in their mathematical formulation. Instead, the training data fed into the ANN must adequately represent the range of relevant boundary conditions. The ANN learns the relationship between these input boundary conditions and the structural response.

Sensitivity analysis using ANNs then reveals how variations in these input boundary conditions affect the output responses.

Limitations:

ANNs are limited by the data they are trained on. If the training data does not sufficiently cover the range of possible boundary condition uncertainties, the ANN’s predictions and sensitivity analysis may be inaccurate.

2.2. Gaussian Process Models for Sensitivity and Uncertainty Analysis

Gaussian process (GP) surrogate models were employed for uncertainty quantification in large-scale structures, under seismic conditions, such as pile-supported wharf structures. The approach is particularly useful in nonlinear systems where direct simulation is computationally prohibitive [31]. Through the advancement of a surrogate model of the system response, GP delivers computationally efficient uncertainty propagation and sensitivity analysis. The method is most applicable for scenario-based seismic analyses, in which the ground motion and material property uncertainty must be carefully quantified. The primary advantage of GP surrogate models is their potential to deal with nonlinear relations and make probabilistic predictions with quantified uncertainty. However, the method can be computationally intensive and require optimal hyperparameter tuning, and it becomes inefficient for extremely high-dimensional problems. The Gaussian process metamodeling techniques were applied to estimate the dynamic motions of floating offshore wind turbine platforms [32]. Several experimental and numerical methods are explored to investigate the sensitivity analysis of the metamodels to more accurate dynamic load predictions. The standard GP determines the results, ${\left\{y_n\right\}}_{n=1}^N$, as

$$y_n=f\left(x_n\right)+{\epsilon }_n$$

(9)

$$\mathrm{where}f(x)\sim \mathcal{G}\mathcal{P}\left(0,k_{\theta }\left(x,x^{\prime }\right)\right);{\epsilon }_n\sim \mathcal{N}\left(0,{\sigma }^2\right)$$

(10)

with the definition of $k_{\theta }\left(x,x^{\mathrm{\text{'}}}\right)$ and ${\sigma }^2$ are being the same as in [32].

Nonlinearity Limitations:

GPs, like ANNs, can model nonlinear relationships, but their computational cost increases significantly with the amount of data. For highly nonlinear FSI problems with complex free surface flows, GPs might become computationally prohibitive.

FSI Challenges:

Similar to ANNs, GPs are often used as surrogate models within FSI. Accurately representing the FSI with a GP model requires careful selection of input parameters and training data to capture the essential coupling mechanisms.

General Role of Boundary Conditions: Similar to ANNs, boundary conditions are inputs to the numerical model used to generate training data for the GP model.

Boundary Conditions:

GP models can incorporate boundary conditions as input parameters. The GP learns a probabilistic relationship between these input boundary conditions and the output responses. Uncertainty in the boundary conditions can be propagated through the GP model to quantify its effect on the uncertainty of the predictions.

Limitations:

GP models can become computationally expensive for high-dimensional input spaces. If the boundary conditions are described by many parameters, this can be a limitation.

2.3. Robust Uncertainty and Sensitivity Assessment

An efficient technique for sensitivity analysis is developed to address model uncertainty in stochastic optimization problems [33]. The approach employs Wasserstein balls to characterize the uncertainty of a suggested model, providing explicit corrections for both the value function and the optimizer. The approach is non-parametric and, hence, flexible for various applications. For VLFS, the method would be employed to estimate the sensitivity of structural responses concerning design parameter uncertainty, environmental conditions, and material property uncertainty. The primary advantage of this method is that it can provide first-order approximations to the sensitivity measures in a manner that enables computationally efficient calculation even for complex systems. However, the approach assumes the form of uncertainty (Wasserstein balls), which may not be suitable for all forms of model uncertainty. Étienne and Pelletier [34] proposed a monolithic framework for sensitivity analysis for FSI problems, employing a CSE method derived from the pseudo-solid method to deal with deformations within the fluid domain, thereby guaranteeing full coupling. Using FEM, the work examines an elastic cylinder subjected to uniform flow, addressing the method’s capability for uncertainty estimation and solution predictions.

Following a general method [35], the sensitivities are determined as the partial derivatives ${\mathit{s}}_u=\mathcal{\partial }\mathit{u}/\mathcal{\partial }a,s_p=\mathcal{\partial }p/\mathcal{\partial }a$ and ${\mathit{s}}_{\chi }=\mathcal{\partial }\mathit{\chi }/\mathcal{\partial }a$.

The fluid and structural sensitivity equations are defined as follows:

$${\rho }_f^{\prime }{\mathit{u}}_f·\mathcal{\nabla }{\mathit{u}}_f+{\rho }_f{\mathit{s}}_{u_f}·\mathcal{\nabla }{\mathit{u}}_f+{\rho }_f{\mathit{u}}_f·\mathcal{\nabla }{\mathit{s}}_{u_f}=\mathcal{\nabla }·{\mathit{\sigma }}_f^{\prime }+{\mathit{f}}^{\prime }$$

(11)

$$\mathcal{\nabla }·{\mathit{s}}_{u_f}=0$$

(12)

$$\mathcal{\nabla }·{\mathit{\sigma }}_l^{\prime }+{\mathit{f}}_s^{\prime }=0$$

(13)

$${\mathit{h}}^{\prime }=\mathcal{\nabla }{\mathit{s}}_{{\chi }_s}$$

(14)

$${\mathit{F}}^{\prime }={\mathit{h}}^{\prime }$$

(15)

where the equilibrium condition results in

$${\displaystyle \frac{D}{Da}}\left[{\mathit{\sigma }}_c·{\mathit{n}}_s\right]+{\displaystyle \frac{D}{Da}}\left[{\mathit{\sigma }}_f·{\mathit{n}}_f\right]=0\mathrm{on}{\Gamma }_{I_1}$$

(16)

Considering an infinitesimal surface $\delta \Gamma$ are constant and the Nanson formula is used as ${\mathit{n}}_{s1}\delta {\Gamma }_1=J{\mathit{F}}_{ps}^{-T}·{\mathit{n}}_{s0}\delta {\Gamma }_0$, which yields

$${\mathit{\sigma }}_l^{\prime }·{\mathit{n}}_0^s\delta {\Gamma }_0+\left[\left({\mathit{\sigma }}_f^{\prime }+\mathcal{\nabla }{\mathit{\sigma }}_f·{\mathit{s}}_z\right)·J{\mathit{F}}_{ps}^{-T}+{\mathit{\sigma }}_f·{\left(J{\mathit{F}}_{ps}^{-T}\right)}^{\prime }\right]·{\mathit{n}}_0^s\delta {\Gamma }_0=0$$

(17)

In this case, the symbol $n_0^s\delta {\Gamma }_0$ is the same as defined in [35].

Using the Nanson equation results in

$${\mathit{\sigma }}_l^{\prime }·{\mathit{n}}_0^s\delta {\Gamma }_0+\left[\left({\mathit{\sigma }}_f^{\prime }+\mathcal{\nabla }{\mathit{\sigma }}_f·{\mathit{s}}_{\chi }\right)+{\mathit{\sigma }}_f·{\left(J{\mathit{F}}_{ps}^{-T}\right)}^{\prime }·J^{-1}{\mathit{F}}_{ps}^T\right]·{\mathit{n}}_1^s\delta {\Gamma }_1=0$$

(18)

Uncertainty Characterization:

Methods using Wasserstein balls or other robust optimization techniques make assumptions about the nature of uncertainty. If the actual uncertainties in wave loads or structural behavior deviate significantly from these assumptions, the results may be inaccurate.

Nonlinearity Complexity:

While these methods can handle some level of nonlinearity, highly nonlinear wave-structure interactions can violate the assumptions of the models or make the optimization problem very difficult to solve.

General Role of Boundary Conditions:

Robust methods are specifically designed to handle cases where boundary conditions are uncertain. Instead of treating them as fixed values, they are treated as sets of possible values.

Boundary Conditions:

Methods like using Wasserstein balls explicitly define sets of possible boundary conditions. The analysis then seeks solutions that are “robust”—meaning they perform well across the entire range of possible boundary conditions.

Limitations:

These methods rely on how accurately the uncertainty in the boundary conditions can be characterized. If the assumed uncertainty sets are incorrect, the results may not be reliable.

2.4. Polynomial Chaos Expansions

Polynomial Chaos Expansion (PCE) is an important tool for sensitivity analysis to facilitate efficient uncertainty propagation. The approach employs a surrogate model to estimate Sobol indices, which estimate the influence of input uncertainties on output responses, specifically in six-DOF vessel motions [36]. The approach minimizes computational costs through enhanced probabilistic collocation techniques to minimize sampling points without sacrificing accuracy [37]. PCEs have been applied to uncertainty quantification in mooring systems, which are critical components of VLFS [38]. The non-intrusive surrogate-based approach based on gPC computes how input parameter uncertainties, such as drag coefficients and anchor position, propagate through the system and affect significant responses like cable tension and floater dynamics. The technique has been utilized to identify the most dominant parameters, like the average drag coefficient, and examine their effect on system performance. The advantages of PCEs are highlighted by their ability to deal with uncertainties and their computational efficiency compared to Monte Carlo simulations. However, this approach may face challenges in highly nonlinear systems.

As in [38], the surrogate model is written as

$$f_{gPC}(\mathit{x},Z)=\sum _{k=0}^{\infty } {\hat{f}}_k(\mathit{x}){\varphi }_k(Z)$$

(19)

where ${\hat{f}}_k(\mathit{x})$, gPC, and ${\left\{{\varphi }_k(Z)\right\}}_{k=0}^{\infty }$ can be found from [38].

With $d$ input stochastic variables, $d\in \mathbb{N},\varphi (Z)$ in Equation (25) is substituted by a tensor product of polynomials referring to individual variable as

$$f_{gPC}(\mathit{x},\mathit{Z})\approx \sum _{\left|\mathit{k}\right|=0}^p {\hat{f}}_{\mathit{k}}(\mathit{x}){\Phi }_{\mathit{k}}(\mathit{Z})=\sum _{\left|\mathit{k}\right|=0}^p {\hat{f}}_{\mathit{k}}(\mathit{x}){\varphi }_{k_1}\left(Z_1\right){\varphi }_{k_2}\left(Z_2\right)\dots {\varphi }_{k_d}\left(Z_d\right)$$

(20)

Nonlinearity Limitations:

PCEs rely on representing the system response as a polynomial expansion. For highly nonlinear systems, many terms are required in the expansion to achieve accuracy, which increases the computational cost and can lead to convergence issues.

FSI Coupling:

Applying PCEs to fully coupled FSI problems is challenging because it requires propagating uncertainties through both the fluid and structural domains simultaneously, which can be computationally very demanding.

General Role of Boundary Conditions: Boundary conditions are represented as input random variables in the PCE framework.

Boundary Conditions:

PCE expands the model output as a series of polynomials of the input random variables (representing the boundary conditions). This allows for efficient propagation of the uncertainty in the boundary conditions to the model output.

Limitations:

PCE’s efficiency is best when the input random variables have well-defined probability distributions and when the model is not highly nonlinear. Complex or ill-defined boundary condition uncertainties can pose challenges.

2.5. Matrix Decomposition Approach for Sensitivity Assessment

An effective and accurate method of sensitivity analysis using matrix decomposition was given for structural optimization [39]. The approach utilizes the decomposition matrix using FDP to derive direct formulas for structural displacement sensitivities. The method applies to various modifications to structural parameters, making it effective for different engineering demands. The main benefits of this method are its computational efficiency and accuracy. However, its application may be limited to systems where the flexibility matrix can be decomposed effectively and may involve significant computational resources for very large structures.

Further, the equations of FDP are determined. Based on FEM, structural stiffness matrix $K$ is the result of sum of all stiffness matrices $K_i(i=1\sim N)$ as

$$K=\sum _{i=1}^N{K}_i$$

(21)

where $N$ and $K_i$ are the same as defined in [39].

The spectral decomposition on a beam element yields [40]

$$\left[p_i\right]=\left[\begin{array}{ccc}{\displaystyle \frac{2EA}{L}}& 0& 0\\ 0& {\displaystyle \frac{2EI}{L}}& 0\\ 0& 0& {\displaystyle \frac{6EI\left(L^2+4\right)}{L^3}}\end{array}\right]$$

(22)

$$\left[c_i\right]=\left[\begin{array}{ccc}{\displaystyle \frac{1}{\sqrt{2}}}& 0& 0\\ 0& 0& {\displaystyle \frac{\sqrt{2}}{\sqrt{L^2+4}}}\\ 0& {\displaystyle \frac{-1}{\sqrt{2}}}& {\displaystyle \frac{L}{\sqrt{2}\sqrt{L^2+4}}}\\ {\displaystyle \frac{-1}{\sqrt{2}}}& 0& 0\\ 0& 0& {\displaystyle \frac{-\sqrt{2}}{\sqrt{L^2+4}}}\\ 0& {\displaystyle \frac{1}{\sqrt{2}}}& {\displaystyle \frac{L}{\sqrt{2}\sqrt{L^2+4}}}\end{array}\right]$$

(23)

From Equations (22) and (23), the stiffness disassembly procedure reads as

$$K=CP{C}^T$$

(24)

where $C$ is similar as in [40].

$$P=\left[\begin{array}{lllll}{p}_1^1& & & & \\ & \ddots & & & \\ & & p_1^r& & \\ & & & \ddots & \\ & & & & p_N^r\end{array}\right]$$

(25)

The $K_d$, the stiffness matrix is defined as

$$K_d=C{P}_d{C}^T$$

(26)

$$P_d=\left[\begin{array}{lllll}{p}_1^1\left(1+{\alpha }_1^1\right)& & & & \\ & \ddots & & & \\ & & p_1^r\left(1+{\alpha }_1^r\right)& & \\ & & & \ddots & \\ & & & & p_N^r\left(1+{\alpha }_N^r\right)\end{array}\right]$$

(27)

Equation (26) can be expressed as

$$K_d=C{P}_d{C}^T=C^{\prime }{P}_d^{\prime }{\left(C^{\prime }\right)}^T+C^{\prime \prime }{P}_d^{\prime \prime }{\left(C^{\prime \prime }\right)}^T$$

(28)

Further, in Equation (28), the flexibility disassembly can be obtained by $F_d=K_d^{-1}$, where $F_d$ and the explanations of each symbol can be found in [40].

In addition, regarding the displacement, the 2nd-order sensitivity $\left({\displaystyle \frac{{\mathcal{\partial }}^2{x}_d}{\mathcal{\partial }{p}_i^2}}\right)$ is defined as (see for detail [39])

$${\displaystyle \frac{{\mathcal{\partial }}^2{x}_d}{\mathcal{\partial }{p}_i^2}}=-F_d{\displaystyle \frac{{\mathcal{\partial }}^2{K}_d}{\mathcal{\partial }{p}_i^2}}{F}_{d}y-2F_d{\displaystyle \frac{\mathcal{\partial }{K}_d}{\mathcal{\partial }{p}_i}}·{\displaystyle \frac{\mathcal{\partial }{x}_d}{\mathcal{\partial }{p}_i}}$$

(29)

Linearity Assumptions:

This method is based on decomposing the flexibility matrix, which is most suitable for linear structural analysis. Nonlinear material behavior or geometric nonlinearities in large deformations can limit its applicability.

Hydrodynamic Nonlinearities:

This method primarily focuses on the structural side and does not directly address the nonlinearities inherent in wave-structure interactions, such as those caused by breaking waves or complex free surface phenomena.

Boundary Conditions:

This method primarily focuses on the sensitivity of structural behavior to changes in structural parameters (e.g., stiffness). Hydrodynamic boundary conditions are generally assumed to be known inputs to the structural analysis.

Limitations:

This method is less suited for directly incorporating uncertainties in wave loading or other hydrodynamic boundary conditions. It typically requires a separate hydrodynamic analysis to determine the loads on the structure.

2.6. Comparative Analysis of Methodologies

Table 1. Comparative analysis of different mentioned methodologies.

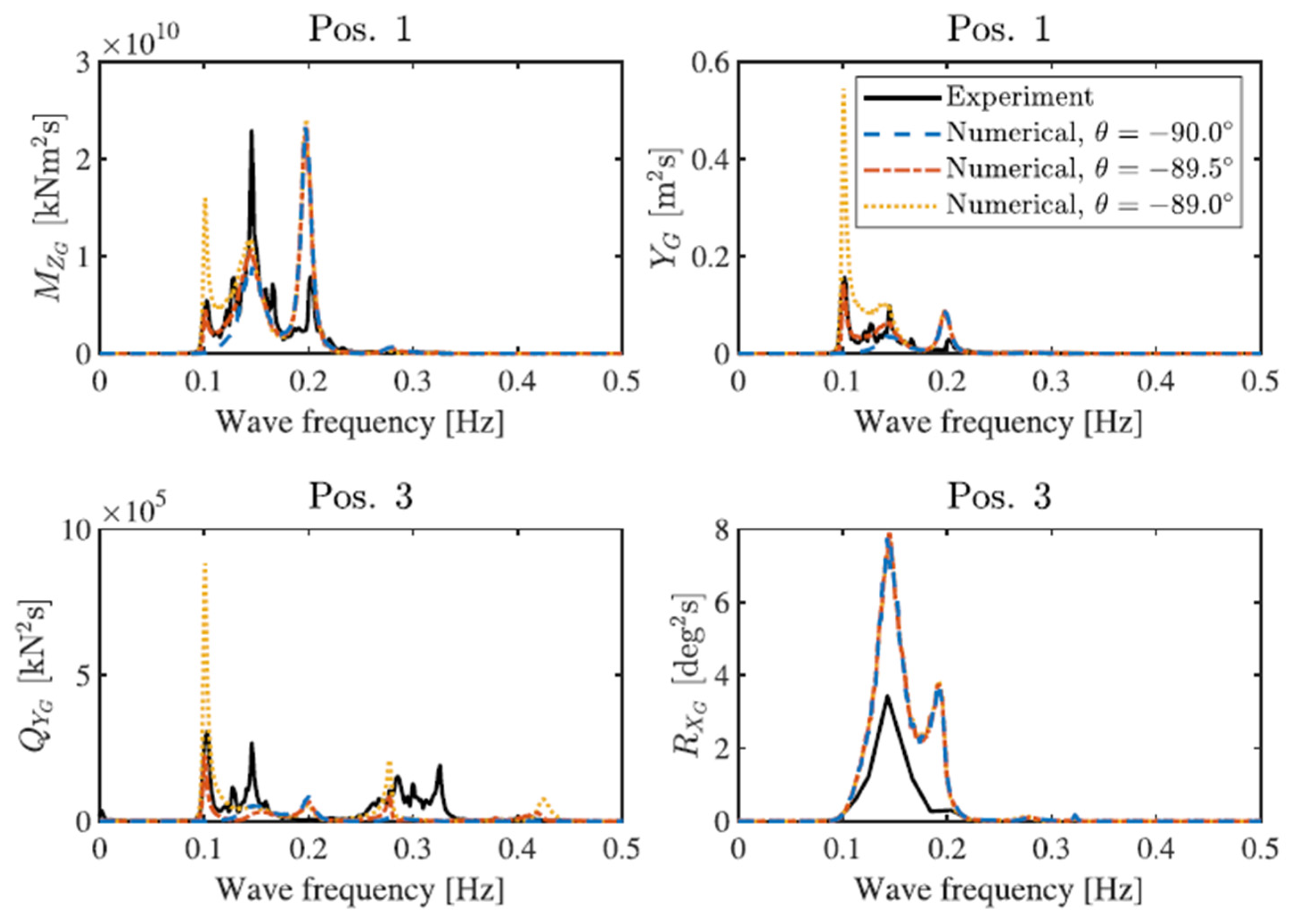
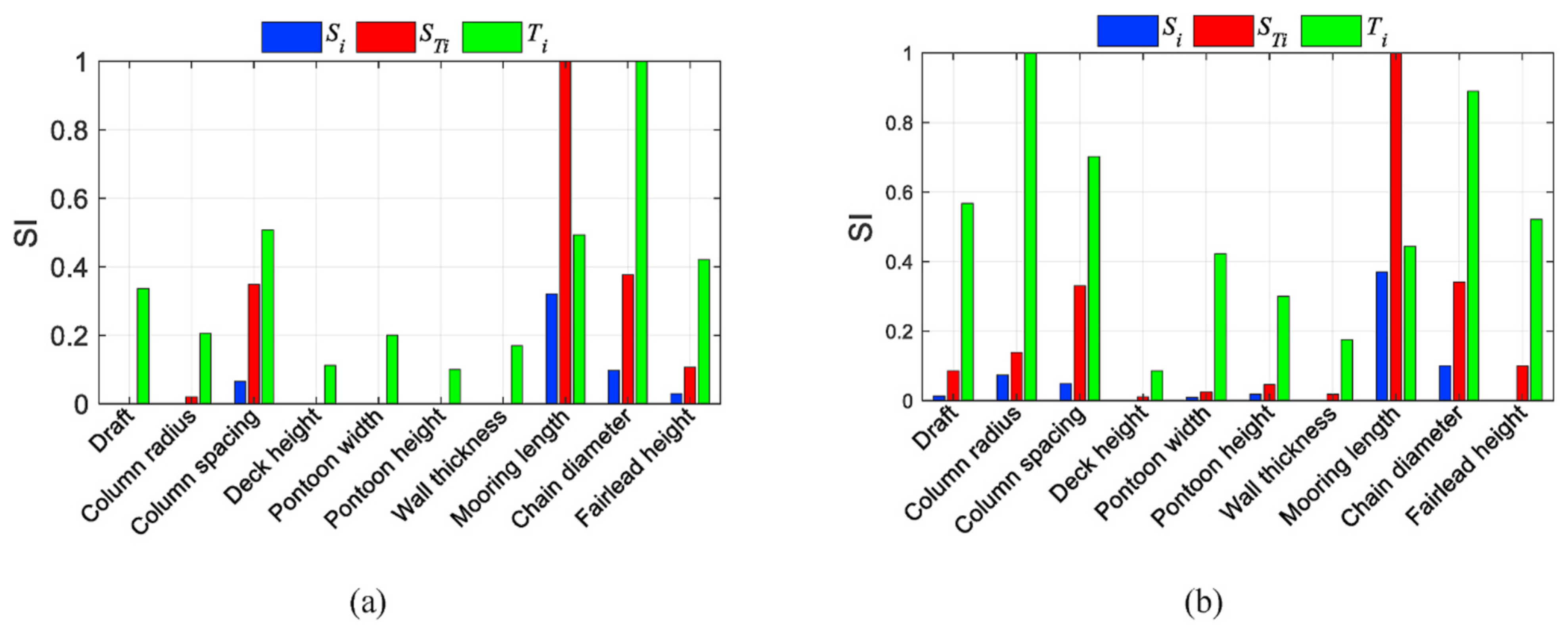
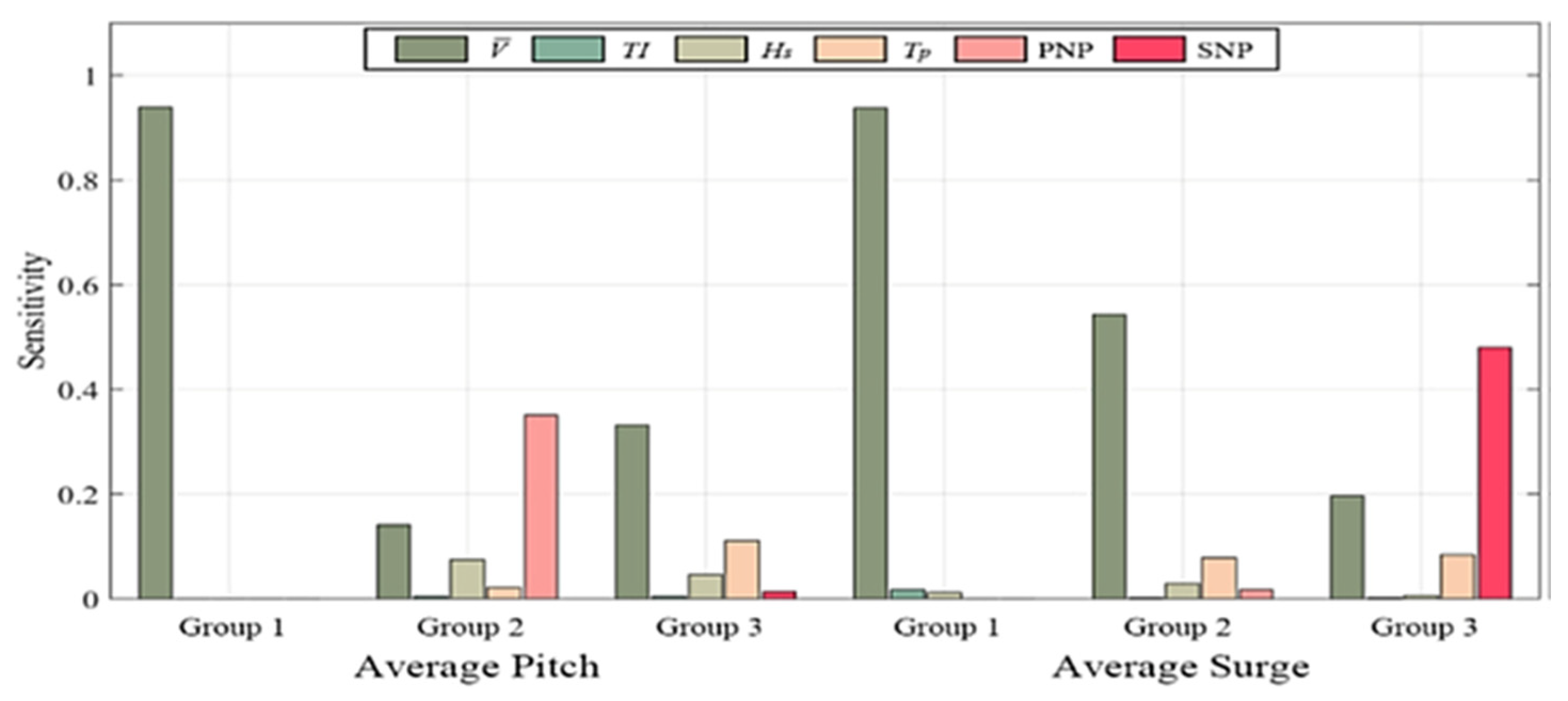
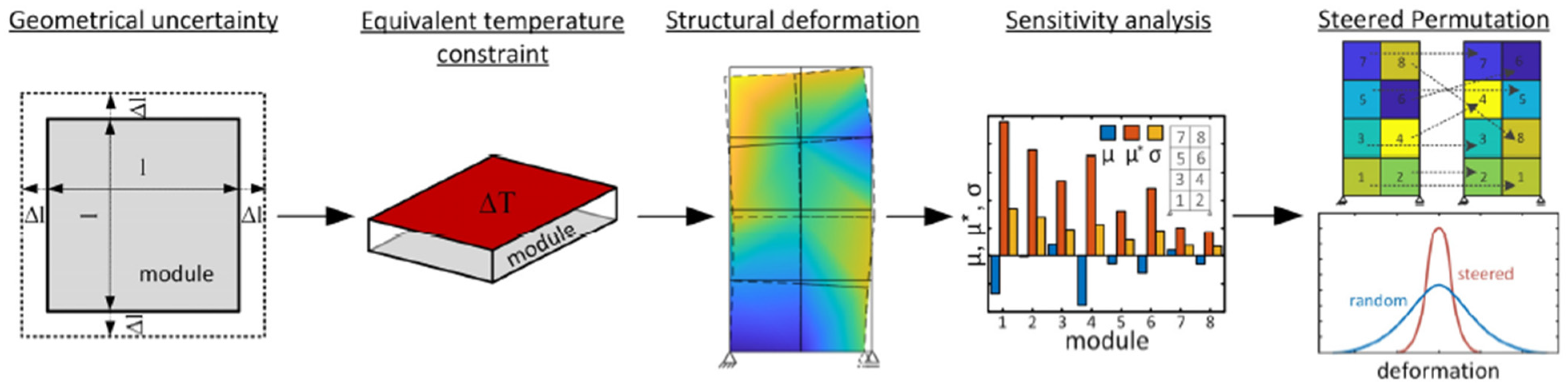
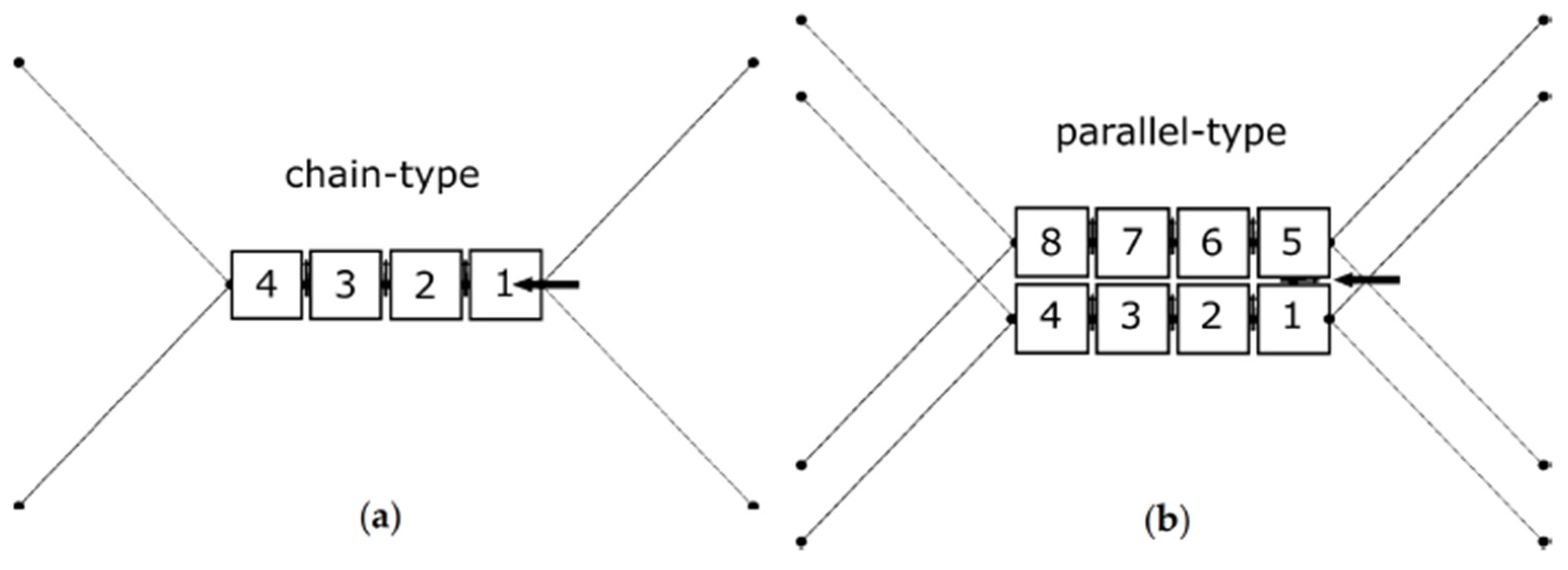
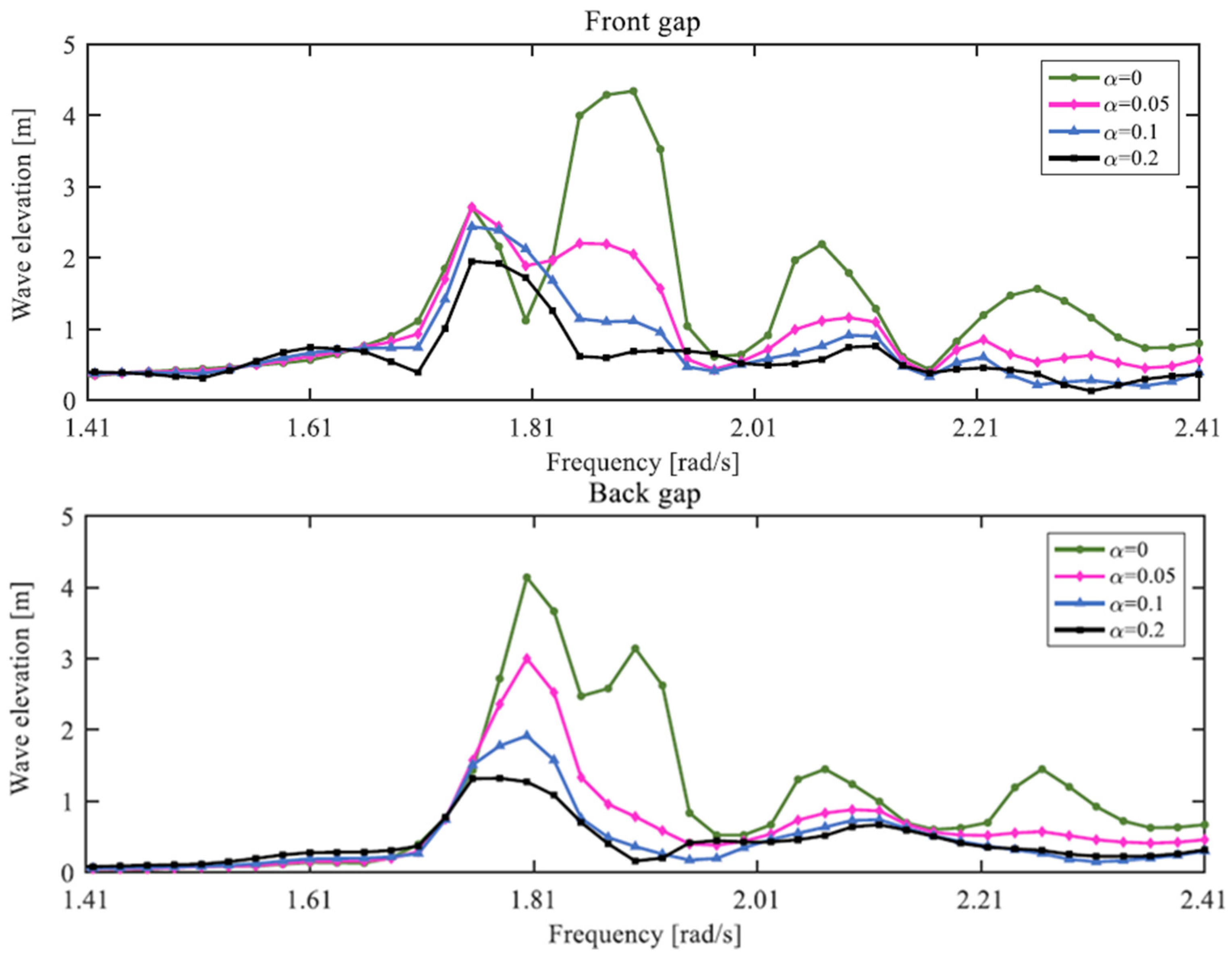
Methodology	Key Features	Application Examples	Key Findings
Neural-Network-Based Sensitivity	Combines ANN and SPCE for high-dimensional data; probe variable for convergence [28,29,30].	Ship motion analysis; potentially applicable to VLFS	Efficient and accurate identification of sensitive factors; handles high-dimensional data effectively.
Gaussian Process Surrogate Models	Surrogate modeling for nonlinear systems; uncertainty propagation [31,32].	Predict the dynamic responses of floating platforms-seismic assessment of pile-supported wharf structures.	Efficient handling of nonlinear relationships; provides probabilistic predictions with uncertainty quantification.
Robust Uncertainty Sensitivity	Non-parametric approach using Wasserstein balls; first-order corrections [33,34,35].	Stochastic optimization; applicable to VLFS design and analysis	Provides explicit sensitivity metrics; flexible for various applications.
Polynomial Chaos Expansions	Non-intrusive surrogate-based UQ; handles aleatory and epistemic uncertainties [36,37,38].	Mooring systems; applicable to VLFS mooring cable dynamics	Identifies influential parameters; computationally efficient compared to Monte Carlo simulations.
Matrix Decomposition Technique	Fast and exact sensitivity reanalysis; applicable to various modifications [39,40].	Structural optimization; applicable to VLFS design and analysis	High computational efficiency and accuracy; versatile for different types of modifications.

provides a comparative overview of the above-mentioned methodologies, highlighting their key features, applications, and findings.

In the next section, the sensitivity and uncertainty analysis of different floating structures using the numerical approaches are analyzed based on suitable numerical approaches mentioned in

Table 2. Comparative analysis of CFD with BEM and FEM.

	BEM	FEM	CFD
Primary Use	Linear Hydrodynamics [18,41]	Structural Analysis, Coupled FSI [41,42,43]	Nonlinear Hydrodynamics, Viscous Flow, Turbulence [9,42,43]
Accuracy	High for linear problems	High (structural), Variable (fluid)	High (most detailed)
Computational Cost	Low to Medium (for linear hydrodynamics)	Medium to High (structure), High (fluid)	High to Very High
Nonlinearities	Limited	Can handle nonlinearities (structure)	Captures nonlinearities
Viscous Effects	Not included	Not included	Included
Free Surface	Efficient for linear waves	Less efficient for the free surface	Accurate for complex free surface flows (e.g., breaking waves)
Complexity	Relatively simple for linear problems	Complex	Very complex

. It may be mentioned that Table 2 provides a technical comparative overview of CFD, BEM, and FEM models, highlighting their complexity, computational cost, and accuracy.

Figure 1 is provided as a flow chart to guide practitioners in selecting the most appropriate sensitivity and uncertainty methodology.

Here is an outline of limitations in nonlinearity, computational complexity and how boundary conditions and nonlinearities typically come into play with each methodology mentioned in Table 1. It is important to emphasize that this is a general overview. The specific way boundary conditions and nonlinearities are handled will vary depending on the particular implementation and the complexity of the problem being analyzed.

In summary, while the methods discussed offer valuable tools for sensitivity and uncertainty analysis, they all face limitations in fully capturing the complexities of nonlinear wave-structure interactions. The optimal method selection hinges on the particular problem at hand, the required precision, and the computational power accessible. The computational cost and modeling concepts in handling nonlinearity and FSI are outlined below:

Computational Cost: Accurately modeling nonlinear wave-structure interactions and FSI often requires high-fidelity methods like CFD, which are computationally very expensive.

Modeling Complexity: Developing accurate models for these phenomena is challenging due to the complex physics involved, including turbulence, multiphase flow, and large deformations.

Validation: Validating these models requires high-quality experimental data, which can be difficult and expensive to obtain, especially for large-scale offshore structures.

3. Sensitivity and Uncertainty Assessment for Floating Structure Systems

3.1. Floating Structures Systems

Floating structures are now extensively used to enable various offshore applications, including wind energy, aquaculture, etc. The dynamic analysis of floating docks under accidental loading focused on stability problems and mitigation measures was examined [44]. The numerical and model tests response for a floating pontoon to measure the essential uncertainties associated with both types of models and to enhance the grasping of hydroelastic modeling was provided [45]. Hence, a numerical model was developed and subsequently, the results were validated against model tests under wave–current induced responses. The findings demonstrate a clear directional dependence in the response spectra associated with horizontal response that significantly affected along the pontoon with $R_{X_G}$ (Figure 2).

A study comparing coupling methods for semi-submersible floating wind turbines found that fully coupled analyses yield the most accurate predictions of dynamic behavior [1]. A CFD-FEA coupling approach was introduced to compute hydrodynamic interactions in flexible floating bodies and demonstrated improved accuracy over traditional potential-flow models [9]. CFD and BEM are used to simulate the fluid flow around the floating structure and determine the hydrodynamic loads acting on its wet surface, while FEM is used to model the structural behavior of the floating body to model its displacements under the wave loads [41,42,43].

Long-term observations of an SRDP close to islands and reefs in the South China Sea validated the key technologies developed to address design challenges and predict the behavior of floating structures [46]. The relative differences between the measured and predicted results of platform stress responses, expressed as absolute values, were generally found to be in good agreement with marginally high strain in the connection zone at S15 (Figure 3).

A systematic methodology was provided for the optimizing of connection parameters within modular floating structures, effectively balancing operational efficacy with economic considerations [4]. The influence of the connector’s stiffness and the grid type on the hydroelastic behavior and the internal loads on the connectors was analyzed [6]. Furthermore, the study identified the optimum design arrangement of the PFS under different wave situations based on a genetic algorithms-based optimization process in terms of performance specification related to the hydroelastic heave response and the internal loads of the connectors with varying the connectors’ rotational stiffness. A novel connection for super-scale modularized floating platforms was presented to suppress the oscillation of the platform [5] and the short-term responses of the floating platform adjusted to its ideal configuration of the connection stiffness were analyzed.

3.2. Mooring Systems

Stability for offshore floating platforms is achieved through the use of mooring systems, and some potential works related to the sensitivity analysis of mooring systems are demonstrated. For example, a sensitivity analysis of semi-submersible FOWT was conducted to determine the critical design parameters influencing hydrodynamic performance and manufacturing cost [3]. The mooring length is predicted to be the key factor, and platform configuration parameters contribute very little (Figure 4).

Amaechi et al. [12] investigated the hydrodynamic characteristics of submarine hoses connected to a CALM buoy, considering the effects of wave-current interactions. A comparative sensitivity analysis reveals that various mooring systems, such as SALM and CALM configurations, demonstrate substantial differences in load distribution and dynamic behavior [47]. The study in [48] evaluated how changes in mooring parameters affected the dynamic behavior and mooring tension of a grid mooring system used for gravity cages. An impact of the sensitivity analysis of air gap concerning the parameters of the length, elasticity, and type of the mooring line for a semi-submersible platform based on the results of the tunnel test and wave tank and validated by ANSYS AQWA under wave, wind, and current loads [49].

Furthermore, a sensitivity analysis was performed on the air gap motion, considering the influence of the mooring system under wind loads, for the analysis of the semi-submersible platform using the numerical simulation, which was presented based on model test results [50]. It is concluded that the influence of the mooring system on air gap motion and the impact of various mooring systems on platform heave is near the natural heave period.

A novel technique was introduced on the mooring system, integrating DNN with the NSGA-III [51] and a DNN surrogate model was employed to assess the dynamic behavior of the FOWT, utilizing Bayesian methods to optimize the system components and enhance general design performance. The research in [52] explored the ideal design parameters for moorings employing catenary lines, specifically for FOWTs with a tri-floater structure in offshore regions, assessing operational and extreme environmental loads subjected to wind, wave, and current velocity. An extensive series of sensitivity analyses regarding the fatigue of mooring chains, examining various environmental loads and mooring design parameters through multiple fatigue analysis methodologies are carried out [53], which encompassed the stress and strain fatigue analysis approach, the fracture and damage mechanics analysis approach.

A holistic optimization approach was developed for designing mooring systems for vessel-shaped offshore fish farms [54], combining the design of numerical and experiments along with optimization process. A sensitivity analysis of mooring parameters on the dynamic behavior of a truss spar platform was conducted [55], and the workflow is shown in Figure 5. The platform is modeled as a rigid body with three DOGs whose motions are analyzed in the time domain using the implicit NBT by establishing a relationship of the mooring restoring force under quasi-static technique.

A comparative analysis on the influence of different mooring parameters, e.g., lengths, types, arrangements, etc., based on their applications are provided in

Table 3. Comparative analysis on the effect of different mooring parameters based on their applications.

Mooring Parameter	Application	Quantitative Comparison/Influence
Mooring Length	Floating platform/FOWT	Longer mooring lines generally lead to a greater impact of mooring length on the air gap [49,50]/It is a key factor influencing hydrodynamic performance and manufacturing cost [3,46,52].
Mooring Type	Floating platform	Due to its greater stiffness, chain mooring has demonstrated superior performance in minimizing air gap motion response [49].
Mooring Configuration	Net cage/Multibody floating structure	Enlarging the frame line length can equalize tension distribution within the mooring system and minimize peak tension under wave-load conditions [48,54]. The parallel combination of modules may reduce the hydrodynamic motions on the multibody structure [11].
SALM/CALM System	Buoy	Comparative sensitivity analysis reveals that various mooring systems, such as SALM and CALM configurations, demonstrate substantial differences in load distribution and dynamic behavior [12,47].
Mooring Diameter/Pretension	Truss spar platform	Thicker mooring lines generally increase stiffness and can reduce motions but increase cost while higher pretension can improve stability but also increase the risk of line breakage [55].

.

3.3. Fluid–Structure Interactions

Understanding the FSI is essential for forecasting wave-induced forces and how structures will respond. The efficiency of floating wind turbines was assessed using a neural network-based global sensitivity analysis framework, with a special focus on the impact of platform natural periods and metocean conditions [2]. It was indicated that the wind load and platform natural period are significantly influenced by the motion (Figure 6).

Additionally, the hydrodynamic characteristics of floating photovoltaic systems and how rigid connectors can enhance stability were examined [10]. The sensitivity analysis techniques for the optimization of flexible multi-body systems and the effects of parameter variations on system behavior and performance were focused on [56] using finite element analysis and gradient-based optimization. The study identified the most influential design parameters to maximize efficiency and stability for multi-body system applications. The effects of various numerical modeling input parameters on FOWT loads were analyzed [57], and the research uses the elementary effects approach to examine which parameters contribute most significantly to turbine loads. The key results determine that wind turbulence, the center of mass position, and current velocity are the most influential parameters on FOWT operation. The potential of sensitivity-based permutation techniques in managing geometric inaccuracy in modular structures was examined by employing the elementary effects technique in identifying the influences of inaccuracy on the deformation of structures [58]. The study shows that the conscious positioning of modules according to their influence can be used to mitigate overall deformations by a substantial amount, thus promoting sustainable and effective modular design. Figure 7 illustrates the general approach of the sensitivity-based permutation method.

The hydrodynamic efficiency of articulated floating structures under various configurations and environmental loads was studied [11] through a numerical model based on AQWA. The study analyzed the sensitivity of the number of modules, module and mooring arrangements (Figure 8), and incident wave angle on hydrodynamic behavior.

Ren et al. [7] analyzed the hydrodynamic efficiency of an MMFS with different configurations of its outermost connector. The study analyzes the impacts of hydrodynamic interactions and the mechanical coupling effect, and the outputs suggested that applying the hinged connector greatly impacts reducing the utmost bending moment and shear force responses. The motions and external loads under the influence of inner water resonance on a VLTFS was investigated, providing an assurance for the platform design and safety analysis using a three-dimensional frequency-domain hydroelasticity method [59].

Developing a local derivative form of the CSE method, specifically leveraging the boundary velocity method, was applied to fluid–structure shape design problems. while addressing the discontinuity issue in local sensitivity variables at the joints of built-up structures [60]. A frequency-domain model to efficiently compute the sensitivity of wave-induced fatigue loads on FOWT monopile foundations subjected to various conditions was developed [61]. It was found that the accuracy and computational efficiency of the model make it ideal for preliminary design and sensitivity analysis.

The application of DoE was introduced [62], which is an effective alternative to high computational cost optimization techniques for the structural analysis of platform supply vessels. The study explains how RSM can be employed to facilitate multi-objective optimization and, hence, minimizing computational costs while maintaining structural integrity. The sensitivity analysis of the effects of gap width and damping ratio on free surface elevation (Figure 9) and the impact of hydrodynamic forces on the behavior of floating structures composed of multiple interconnected modules with small gaps between them was studied [8].

The influence of the sensitivity of structural parameters of the floater on the platform’s motion and deformation was examined [63] under the conditions of regular waves. It is found that the platform’s hydroelastic behavior is affected by the floater’s stiffness and membrane (Figure 10). Further, the floater and membrane follow the wave’s shape when frequencies are low, but at high frequencies, the stiffness of the floater acts as a dominant factor.

The sensitivity analysis of hydroelastic behavior of many-module floating structures to various connector stiffness or flexibility is studied [64], implying that uncertainties in connector properties can significantly affect system behavior. The experimental validation of the reliability of the network modeling method highlights discrepancies between different modeling approaches [65], suggesting that uncertainties in model assumptions and connector characteristics can lead to variations in predicted responses on the dynamic behavior of multi-module floating platforms. A nonlinear network model is proposed to analyze multi-module floating structures joined by arbitrarily flexible connections [66]. The developed model accounts for the impact of parameter uncertainties on dynamic stability under varying environmental conditions and different connector stiffness, emphasizing the need for careful consideration of these factors [67].

4. Conclusions

This review presents an overview of the theoretical and numerical methods used to assess sensitivity and uncertainty in the hydrodynamic and hydroelastic behavior of floating offshore structures, comparing and contrasting different likely methodologies associated with the basic governing equations, evaluating their strengths and weaknesses, and examining their applications in various scenarios related to offshore structures, while a comparative analysis of these methodologies has been provided. Most methods are based on numerical ANN, SPCE, PCE, CSE, and FDP for the sensitivity analysis, and GP and FD-FEA are used for the uncertainty.

The review highlights the importance of sensitivity and uncertainty analysis in the design, optimization, operation, and safety of floating offshore structures, emphasizing the influence of boundary conditions and nonlinearities within different methodologies. The review identifies the following key remarks to be considered for future research:

The analysis of various sensitivity and uncertainty studies reveals that factors such as mooring system and parameters, connectors and structural parameters significantly influence the hydrodynamic and hydroelastic responses of floating systems.

The findings underscore the necessity of employing robust and data-driven methodologies to enhance the accuracy, reduce computational complexity and guide decision-making for the optimal design of floating offshore structures.

Developing more advanced and accurate models for predicting the hydrodynamic and hydroelastic behavior of offshore floating structures. amplifying the performance and reliability of sensitivity and uncertainty analysis methods. Further, exploring and addressing the challenges of nonlinearity and probabilistic behavior in offshore structure systems.

Accurately modeling nonlinear wave-structure interactions often requires high-fidelity methods like CFD, which are computationally very expensive. Hence, developing accurate models for these phenomena is challenging while studying the sensitivity and uncertainty analysis of the floating offshore structures.

Additionally, the hydrodynamics of flexible offshore floating platforms with various types of mooring parameters subjected to wave-current loads are recommended to be performed to predict the sensitivity analysis.

Future research should conduct a more thorough sensitivity analysis of the different connection types between the modules for a multi-module floating platform under different environmental conditions.

This review offers a valuable resource for researchers seeking information on sensitivity and uncertainty analysis. It summarizes the current state of knowledge, providing insights into potential directions for future research and developments in the field of hydrodynamic and hydroelastic modeling of offshore floating structures.