Feasibility and Limitations of Solar Energy Integration in Merchant Ships: A Case Study on Fire Detection Systems

Abstract

The electrical installation of a ship includes the generation, transport and distribution of the generated electrical energy to the electrical consumers on board. In recent years, there have been many attempts to replace traditional auxiliary generators with renewable energy sources, in particular solar panels, as this is a highly developed technology on land. Accordingly, this paper analyzes the different energy requirements on board a merchant vessel and carries out a feasibility analysis. The feasibility analysis considers technical, economic and legal aspects. Sustainable aspects are analyzed too, due to their importance nowadays. It is verified that the use of solar panels is only technically feasible for a small part of the ship’s total consumption, as the area required by the panels to cover the total demand would exceed the available area of the ship. Therefore, the possibility of installing solar panels for the fire detection system only was analyzed. This is a technically and legally feasible solution, but not an economically viable one. However, from a sustainability point of view, which takes into account economic, social and environmental aspects, this proposal is appropriate. This study concludes that, while solar panels are not a viable solution for covering all energy needs on merchant ships, they can be used for specific systems such as the fire detection network or similar small consumers, albeit with economic limitations. These findings provide valuable insights for future research and practical implementations of renewable energy solutions in the maritime sector.

1. Introduction

According to SOLAS [1], merchant ships must have at least two independent sources of electrical power:

-

A main source of sufficient capacity to supply all the consumers necessary for navigation conditions without the need to use the emergency source. This system must be redundant, both in terms of generation and in terms of transformers and converters and other elements of the main network so that, at least in the event of a failure of one item of equipment, all the consumers necessary for navigation, operation and propulsion can be supplied with power and the comfort of the crew can be maintained [2].

-

An autonomous emergency source of sufficient capacity to supply the emergency consumers. This source, which may be an electrical generator or a battery system, is connected to the main emergency switchboard in the event of a main power failure. The services supplied by the emergency source on a cargo vessel are the firefighting system, steering gear, watertight doors and hatch covers, emergency lighting for muster and embarkation stations and similar, the rest of the emergency lighting, navigations lights, fire pumps, VHF radio, GMDSS communication system, internal communication system, navigation equipment, fire detection system, and the alarm system. It is not compulsory for all vessels to have an emergency source installed, but it is always recommendable. It is mandatory on all merchant vessels, with the exception of those under 500 GT, fishing vessels under 24 m and those with the following navigation restrictions in nautical miles: R2 (50 miles winter and 100 miles summer), R3 (20 miles winter and 50 miles summer) and R4 (50 miles winter and 10 miles summer) [3].

These main and emergency networks can be AC (alternating current) or DC (direct current). The use of one or the other depends mainly on the power to be supplied and the installation costs, as well as the final consumers. At the beginning of the 20th century, most ships were powered by DC but, over the years, AC has largely replaced DC for power generation and transport on cargo and passenger ships [4,5], as well as in civil engineering throughout the world. Nowadays, AC is used almost exclusively on merchant ships [6,7], with independent DC networks for small electronical consumers [8,9].

AC is divided into two groups: high voltage (rated voltages greater than 1 kV and up to and including 15 kV with rated frequencies of 50 Hz or 60 Hz) and low voltage (rated voltages greater than 50 V and up to and including 1 kV with rated frequencies of 50 Hz or 60 Hz), with the most common networks on ships being 400 V, 440 V and 690 V [10,11]. For power requirements of less than 5 MW, low voltage is generally used [12,13]. On the other hand, for higher power requirements, it is practically essential to use high voltage in order to reduce the weight of the generators, the cross-sections of the cables and the short-circuit level of the network [9,13]. For lighting, both for normal and emergency networks, a maximum of 250 V can be used, according to the rules of the various classification societies [3].

Each ship has its own particular characteristics, and the power installed on board depends on several variables such as the tonnage of the ship, its expected cargo, the experience and expectations of the shipowner and so on [14,15,16,17]. What can be roughly stated is that it is common for merchant ships to require several MW during navigation [18]. Today, there is a global need to improve the sustainability of ships [19], and solar energy constitutes a very interesting additional source to improve sustainability in the naval sector. Solar photovoltaic (PV) energy can significantly reduce a ship’s fuel consumption and emissions, making it a viable alternative to conventional energy sources [20,21]. Of particular interest are hybrid systems that combine solar panels with batteries and diesel generators to ensure a reliable power supply, even under varying operational conditions [5,22]. Several researchers investigated the optimization of efficiency from the configuration of the solar panels, batteries and electric drives. For example, a study on a fishing vessel showed that the integration of solar panels with a DC electric power system could effectively replace traditional fuel sources, thereby improving the sustainability of the vessel [23]. In addition, the use of lithium-ion batteries for energy storage allows for the temporary storage of solar energy, to be used when sunlight is not available, thus ensuring a continuous power supply for critical applications [24]. Recent advancements in solar technology have also contributed to the feasibility of solar-powered ships [25,26]. In recent years, the integration of intelligent energy management systems, such as those based on fuzzy logic or particle swarm optimization, has shown how to optimize the distribution of power generated from solar energy and other sources, further improving the operational efficiency of hybrid ships [27].

The integration of solar energy into maritime vessels presents significant challenges, particularly due to limited installation space and the variable output of solar power. Recent advancements and strategies have emerged to address these challenges, focusing on maximizing space utilization and enhancing the reliability of integration with traditional power systems. Several studies indicate strategies for enhancing solar panel area maximization, such as retractable or adjustable mechanisms that allow panels to be positioned for optimal sun exposure regardless of the vessel’s position or movement [28]. Another challenge lies in the variable nature of solar power generation, which can lead to synchronization issues when integrated with existing diesel systems. Accordingly, research has been carried out to develop smoother transitions in the power supply in hybrid systems, adapting to fluctuations in solar generation while ensuring a reliable power supply to the ship [29,30]. Furthermore, advanced battery storage systems and deploying energy management systems that intelligently balance load requirements can enhance the efficiency of these hybrid systems, enabling vessels to adaptively manage varying energy demands while integrating renewable sources [31,32].

Despite growing interest in renewable energy integration within maritime applications, a significant research gap remains in assessing the practical feasibility, economic viability and sustainability of PV systems specifically tailored for merchant ships. This study addresses that gap by conducting a comprehensive, real-world case study on the integration of solar panels aboard a multipurpose oceanographic fishery research vessel. Unlike prior research that often focuses on large-scale hybrid systems or theoretical simulations, this work provides a grounded, multidisciplinary analysis that encompasses technical, economic, legal and sustainability dimensions. The novelty of this study lies in its targeted application of solar energy to a mission-critical, low-demand subsystem—the fire detection network—which operates independently from the main electrical grid during emergencies. This is the first known study to propose and evaluate the use of solar PV specifically for such a safety-critical system under real operational constraints, including limited deck space, SOLAS regulatory compliance and synchronization challenges with onboard diesel generators. Furthermore, this study introduces a multi-criteria sustainability assessment framework that balances economic, environmental and social factors, offering a holistic lens for evaluating renewable energy adoption in maritime contexts. The originality of this work is reflected in its detailed modeling of real-world conditions, its focus on a subsystem often overlooked in energy studies and its practical insights for ship design, policy development and future research in sustainable maritime energy systems.

The remainder of this paper is structured as follows: Section 2 presents the materials and methods used in the study, detailing the case study of the ship analyzed and the technical feasibility analysis of solar energy integration. Section 3 provides an economic analysis of different alternatives for powering the fire detection system, including a comparison of investment costs and fuel consumption. A sustainability analysis is also developed in this section. Section 4 presents the conclusions and directions for future research. Finally, Appendix A describes the details of the fire detection system network.

2. Materials and Methods

The present work adopts a mixed-methods case study approach to evaluate the feasibility of integrating solar PV systems into merchant ships, with a specific focus on powering the fire detection system. The research design integrates the following:

-

Technical modeling of energy generation and consumption;

-

Economic evaluation using lifecycle cost analysis and investment metrics;

-

Sustainability assessment based on a multi-criteria decision-making framework.

The following sub-sections describe both the ship under analysis and the details of the methodology employed.

2.1. Materials

The ship analyzed is the multipurpose oceanographic fishery research vessel NB730 Jaywun (Freire shipyard, Vigo, Spain). It is shown in Figure 1, and the main characteristics are summarized in

Table 1. Main characteristics of the ship analyzed.

Characteristic	Value
Length overall (m)	47.1
Beam (m)	12
Depth to main deck (m)	5.95
Speed (knots)	13
Endurance	25 days at 11 knots
Propulsion	Twin screw with 2 controllable pitch propellers Main engines: 2 × 1840 kW @ 1800 rpm
Electrical plant	Main generator sets: 2 × 650 kWe @ 1500 rpm
	Emergency generator: 1 × 248 kWe @ 1500 rpm
	Shaft alternators (PTI): 2 × 200 kWe @ 1485 rpm
Maneuvering thrusters	Bow: 1 × 95 kW @ 1500 rpm
	Stern: 1 × 265 kW @ 1500 rpm

. Jaywun is a 47.1 m-long oceanographic fishery research vessel operated by the Environment Agency—Abu Dhabi (EAD) and launched in 2022 as the most advanced marine research vessel in the Middle East. Designed for oceanic fishery assessments, blue carbon evaluations, climate change research and marine water quality studies, it is equipped with cutting-edge technology, including an ROV, underwater drones, seabed mapping systems, DNA analysis tools and six onboard laboratories. Powered by twin MTU 16V4000M53 engines, it has a top speed of 13 knots, an endurance of 25 days at 11 knots and can accommodate up to 30 personnel.

NB730 Jaywun was chosen due to its representative size, operational profile and advanced onboard systems, making it a suitable model for assessing renewable energy integration in modern merchant vessels.

2.2. Methods

2.2.1. Technical Feasibility of Solar Energy in the Main and Emergency Networks

As shown in Table 1, the vessel has two 650 kW auxiliary generators, in addition to the two shaft generators which help to reduce the consumption of the vessel during navigation. The electrical energy generated for different load percentages of the generators, considering only one auxiliary generator connected to the busbars, is sufficient to supply all the electrical consumers in the most unfavorable conditions (the starting peak of the heavy consumers has not been considered). Several possible replacement percentages (the percentage of energy that is replaced by solar energy) are shown in Table 2. This table is based on the following assumptions:

-

Solar panel specification: 550 Wp;

-

Panel inclination: 0° and 30° scenarios were considered;

-

Inverter efficiency: 95% [33,34].

Table 2. Electrical energy generated by the generators and corresponding solar panels.

Load Replacement Percentage (%)	Power (kW)	Solar Panels 550 Wp
		Number of Solar Panels	Horizontal Surface (m2) with 0° Solar Panel Inclination	Horizontal Surface (m2) with 30° Solar Panel Inclination
50%	325	616	1590	1377
60%	390	739	1908	1652
70%	455	862	2226	1928
80%	520	985	2544	2203
90%	585	1108	2862	2479
100%	650	1231	3180	2754

Table 2. Electrical energy generated by the generators and corresponding solar panels.

Load Replacement Percentage (%)	Power (kW)	Solar Panels 550 Wp
		Number of Solar Panels	Horizontal Surface (m2) with 0° Solar Panel Inclination	Horizontal Surface (m2) with 30° Solar Panel Inclination
50%	325	616	1590	1377
60%	390	739	1908	1652
70%	455	862	2226	1928
80%	520	985	2544	2203
90%	585	1108	2862	2479
100%	650	1231	3180	2754

It is worth noting that the 550 W value was chosen to represent an approximate average estimate, which can vary significantly depending on weather conditions and geographical location. On cloudy days, the actual power output is lower while, on sunny days, it may exceed this value. The mobility of a ship further complicates the determination of solar radiation, as it is not fixed to a specific geographic point, resulting in fluctuations in the amount of sunlight received. This variability underscores the challenge of accurately predicting the energy yield from solar panels on ships, which requires the consideration of a range of conditions and the integration of advanced energy management systems to optimize performance.

As can be seen from Table 2, the minimum electrical power considered (50% of a generator) would be around 325 kW. This results in a surface area of more than 1350 m². Estimating the available deck area from ship dimensions (length × width), it corresponds to 565 m². This result relates to the fact that the area required for the panels is much larger than the area available on the ship, which makes it impossible to install enough solar panels to cover the ship’s energy needs. Techniques to increase the available area would be necessary to mitigate this limitation.

Regarding the emergency network, the same conclusions can be drawn as for the normal (main) network, in addition to the disadvantages that would arise when complying with the conditions of the classification society and SOLAS [1]:

• A self-contained emergency source of electrical power shall be provided, which would be difficult to provide with solar panels.
• The emergency source of power, associated transforming equipment, emergency switchboard, emergency lighting switchboard and transitional source of emergency power shall be located above the uppermost continuous deck and be readily accessible from the open deck. It shall not be located forward of the collision bulkhead.

For the reasons given above, it is not possible to supply either all the consumers of the normal network or the emergency network of this ship, and this conclusion can be extrapolated to any other similar cargo ship. The next section analyzes the supply of a single critical emergency load, such as a fire detection system, on a ship operating in isolated emergency mode.

2.2.2. Technical Feasibility of Solar Energy in the Fire Detection System Network

Given the limitations of full-scale integration, a focused analysis was conducted on powering the fire detection system using solar energy. The fire control plan proposed for the present work follows the specifications described in SOLAS [1], particularly Regulation 15 of Chapter II-2, Fire Protection, Fire Detection and Fire Extinction. The fire detection system on a ship, as in any land-based installation, is based on a series of automatic smoke, heat, flame and other detectors, as well as a number of manual call points, installed in the different areas and vertical zones of the ship and connected to one or more fire detection control panels. The basic function of the fire detection system is to automatically, quickly and safely detect the presence of fire in all main spaces of the ship.

The most important consideration with this system is that an isolated power network can be used to power the system via internal batteries, so no inverter or other equipment needs to be installed. This system must be powered 24 h a day and its own batteries must always be fully charged. The fire detection system network does not need to be connected to the onboard networks (in emergency mode it works isolated by its own batteries) and it needs to be powered 24 h per day. It is always powered by the main and emergency network in normal conditions and by its own battery network (24 Vdc) in emergency mode. More details about the fire detection system of the analyzed ship are given in Appendix A, and the consumption balance is indicated in

Table 3. Consumption balance of the fire detection network.

Qty.	Equipment Description	Max. Current	Max. Installed
			Current (A)	Power (W)
1	Central panel with four addressable loops	1.2 A	1.2	28.80
1	Alarm repeater unit	500 µA	0.0005	0.01
41	Addressable smoke detector for dry spaces	450 µA	0.01845	0.44
20	Addressable smoke detector for wet spaces	450 µA	0.009	0.22
2	IS addressable smoke and heat detector	450 µA	0.0009	0.02
5	Addressable smoke and heat detector for dry spaces	450 µA	0.00225	0.05
11	Addressable smoke and heat detector for wet spaces	450 µA	0.00495	0.12
5	Addressable heat detector (57 °C)	450 µA	0.00225	0.05
2	Addressable heat detector (90 °C)	450 µA	0.0009	0.02
4	Addressable 3IR flame detector	800 µA	0.0032	0.08
13	Addressable manual call point with isolator for accommodation spaces	300 µA	0.0039	0.09
12	Addressable manual call point with isolator for machinery and/or wet spaces.	300 µA	0.0036	0.09
2	Zener barrier for IS devices	50 µA	0.0001	0.00
1	Timer unit for workshop	300 µA	0.0003	0.01
	TOTAL		1.2503	30.00

. In this table, the maximum current for each component of the fire detection system was identified based on the manufacturer’s specifications for each device.

According to the class rules [4], the duration of the emergency power supply of the fire detection system is 18 h, so the capacity of the emergency power supply is 18 × 1.3503 = 24.3054 Ah and so a set of 2 × 12 Vdc batteries of 26 Ah is required. In Table 3, the daily energy consumption of the fire alarm system is 30 W × 24 h/day = 0.72 kWh/day. This contribution can be made by a single PV panel, which confirms its technical feasibility.

3. Results and Discussion

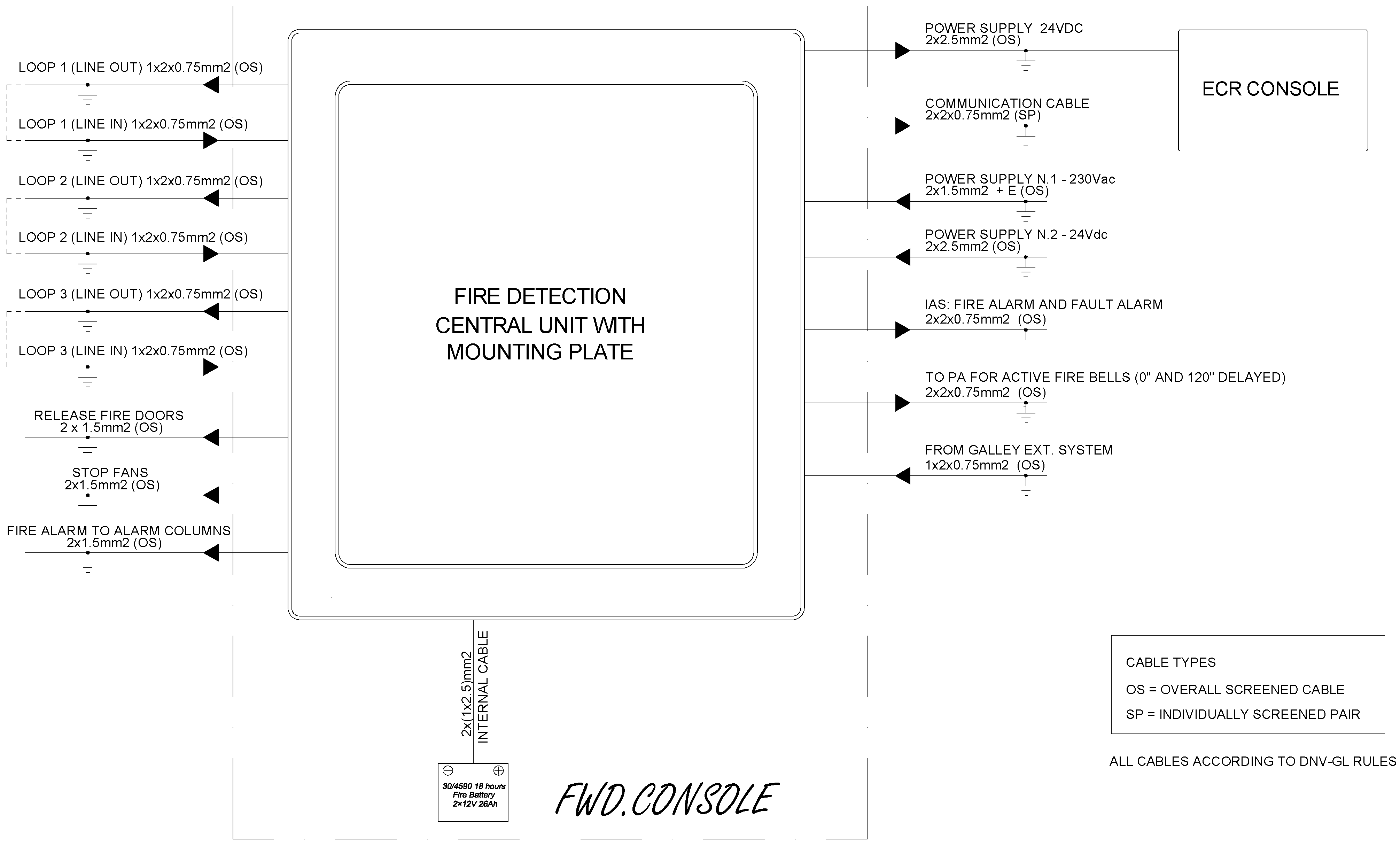
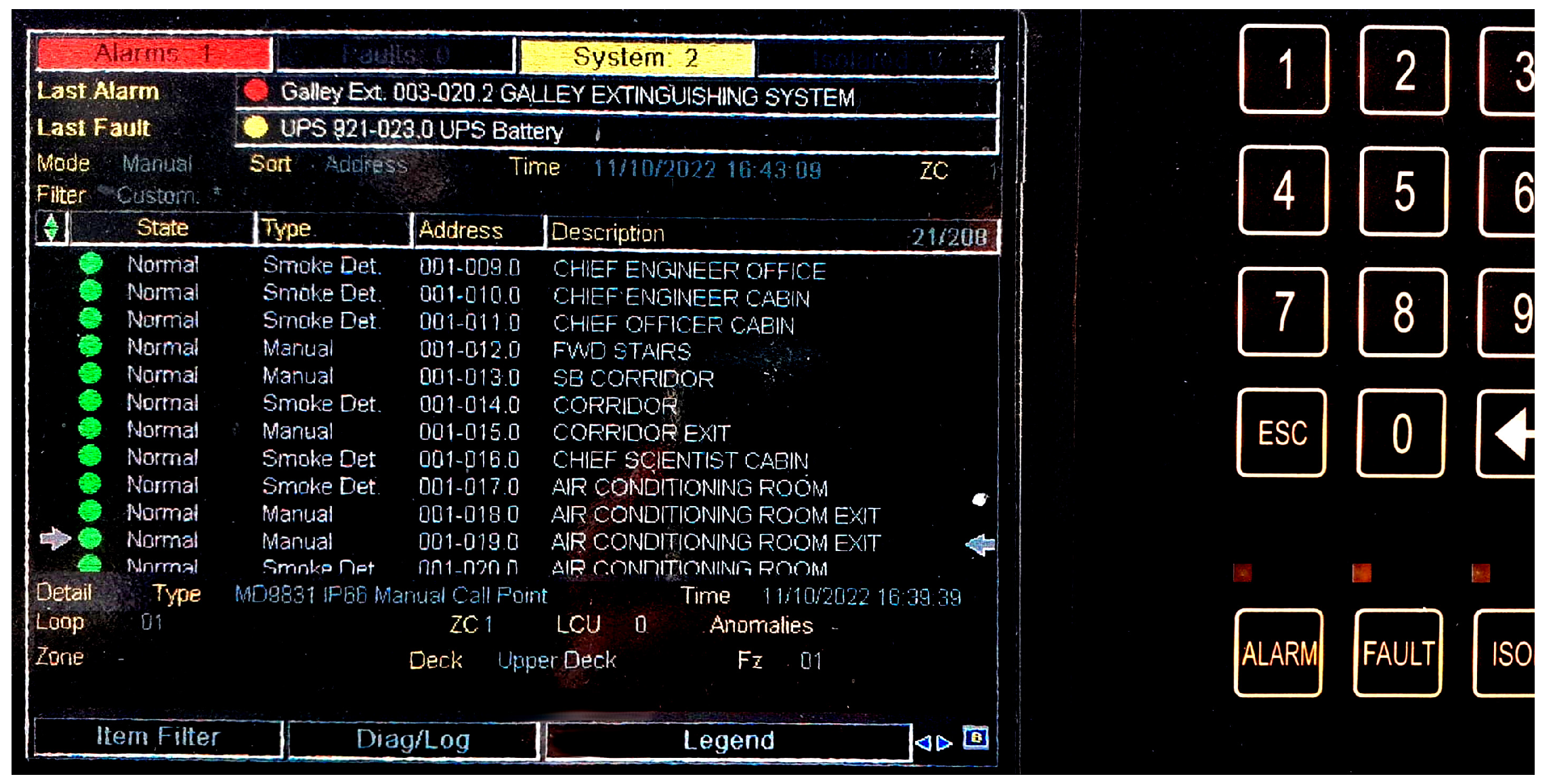
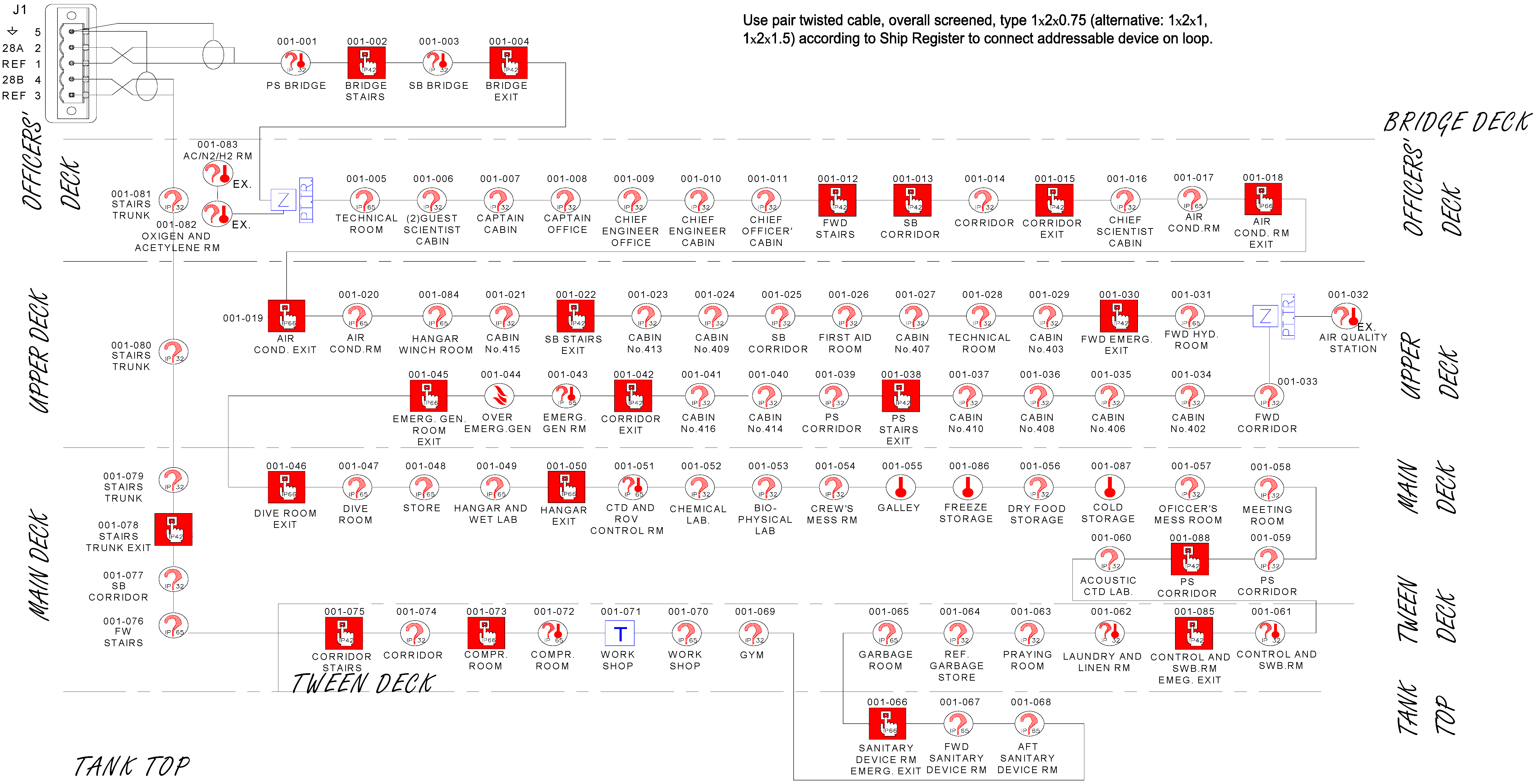
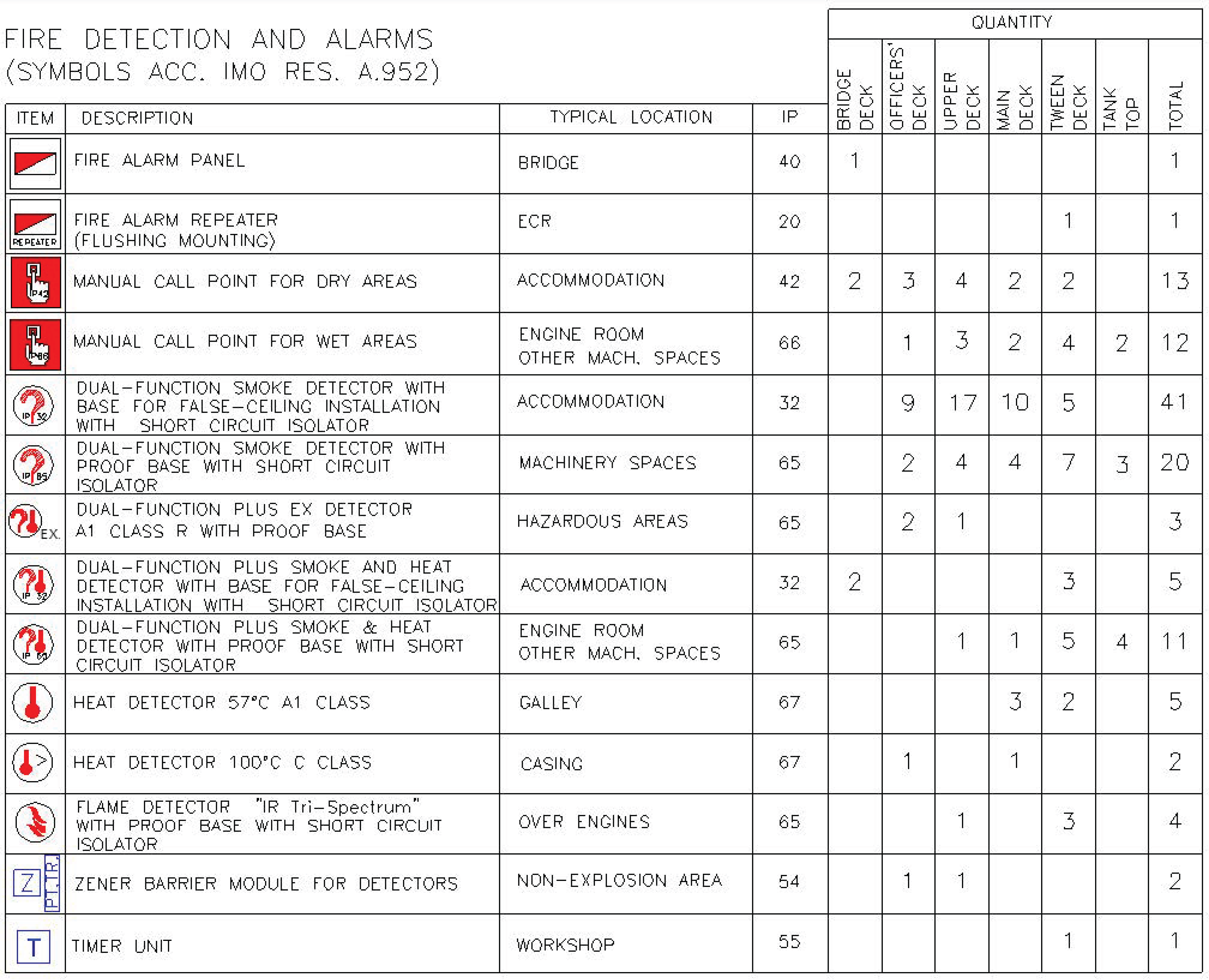
Once the installation of PV panels for the fire detection system network had been verified from a technical point of view, an analysis was carried out taking into account economic, legal and sustainable aspects. The results are presented in the following sections.

3.1. Economic Analysis

This section analyzes both the investment required and the consumption in tons of marine diesel oil (MDO) for several alternatives to power the fire detection system for one year. It has been taken into account that the ship is out of port for 200 days per year while, the rest of the time, it is in port and powered by the harbor network on the shore (this part is outside the scope of this work). Three alternatives were evaluated:

-

Alternative 1, based on a diesel-powered system (baseline);

-

Alternative 2, based on a solar-only system;

-

Alternative 3, based on a hybrid solar and emergency backup system.

More details of these alternatives are described below.

Alternative 1

The detection system is powered only by the ship’s 230 Vac emergency mains (via interconnection to the 230 Vac main switchboard), where an AC/DC converter is installed to supply the fire detection system with 24 Vdc in addition to the emergency mains. Under these conditions, the planned investment is shown in

Table 4. Investment corresponding to alternative 1.

Description	Quantity	Unit Cost (EUR)	Total Investment (EUR)
Circuit breaker in the ship’s 230 Vac main emergency switchboard dedicated exclusively to the fire detection system	1	15.9	15.9
30 m cable 2 × 1.5 mm2 + E from the 230 V ESB to the fire alarm control panel	15	2.54	38.1
Converter 230 Vac/24 Vdc-output 10 A for console installation next to the panel	1	168.43	168.43
Auxiliary material and labor	6	35	210
TOTAL			432.43

. The unit costs shown in this table were obtained from the manufacturers’ websites and directly from the manufacturers themselves.

In addition to this initial investment, the consumption of MDO that must be consumed in the generator set to power the system must be taken into account. An average consumption of the generators of 180 g/kWh is considered, which corresponds to 180 g/kWh × 0.72 kWh/day × 200 days = 25.92 kg of fuel per year. Taking into account the current price of MDO, which is around 761 USD/t (700 EUR/t), this is equivalent to 18.14 EUR/year, which would amount to EUR 453.6 considering a service life of 25 years.

Alternative 2

The normal power supply relies solely on solar panels installed on the decks with sufficient capacity to keep both the fire detection battery charged and the operating system running when the sun is shining. The remainder of the power generated by the panels is used for charged a battery system 2 × 100 Ah—2 × 12 Vdc, in order to supply power to the system at night (10 h of sun per day). The investment is shown in

Table 5. Investment corresponding to alternative 2.

Description	Quantity	Unit Cost (EUR)	Total Investment (EUR)
Supply, installation and connection of a monocrystalline PV panel 550 Wp with the following technical characteristics:	1	131.11	131.11
Rated power: 550 Wp
Efficiency: 21.29%
VImp: 41.48 V
Impp: 13.26 A
Battery set (2 batteries 100 Ah × 12 Vdc)	1	299.72	299.72
30° inclined support 60 kg or similar	1	142.08	142.08
Fuse type G 20 A Icc: 100 kA	2	22.73	45.46
Watertight junction box IP54 RAL 7035 89.4 × 89.4	1	11.46	11.46
Cu conductor line 2 × 4 mm2 Z2Z2, 1.5/1.5 kV 1T DN25	50	3.74	187
Circuit breaker, 2P, 10C	1	50	50
Auxiliary material and labor	16	35	560
TOTAL			1426.83

.

Although this solution is technically feasible, it is forbidden by SOLAS. Also, its implementation would mean that, during long periods where there the sun is not shining, the system would go into emergency mode and would be powered by its own batteries, which would quickly reduce the life of the batteries and the system would not be prepared for a real emergency on the ship. It would be necessary to have power supplied from the emergency network for at least eight hours a day, as is shown in alternative 3.

Alternative 3

A solar panel of sufficient capacity to keep the system operational and the fire detection batteries charged is proposed, with solar batteries to maintain the rest of the generated power supply and to supply the fire detection system with power at night, and an auxiliary power supply so that, in the event of insufficient voltage being generated by the solar panels or their solar batteries, it could switch to the ship’s emergency 230 Vac network, thus keeping the system always operational from the ship’s networks and also keeping the battery always charged. This solution would be a combination of the above situations together with an automatic switching system so that the power supply to the solar panels would be prioritized. The investment is shown in

Table 6. Investment corresponding to alternative 3.

Description	Quantity	Unit Cost (EUR)	Total Investment (EUR)
Supply, installation and connection of monocrystalline PV panel 550 Wp with the following technical characteristics:	1	131.11	131.11
Nominal power: 550 Wp
Efficiency: 21.29%.
VImp: 41.48 V
Impp: 13.26 A
Battery set (2 batteries 100 Ah × 12 Vdc)	1	299.72	299.72
Support inclined 30° 60 kg	1	142.08	142.08
Fuse type G 20 A Icc.: 100 kA	2	22.73	45.46
Watertight junction box IP54 RAL 7035 89.4 × 89.4	1	11.46	11.46
Cu conductor line 2 × 4 mm2 Z2Z2, 1.5/1.5 kV 1T DN25	50	3.74	187
Circuit breaker, 2P, 10C	1	50	50
Circuit breaker on the ship’s main 230 Vac emergency main switchboard dedicated exclusively to the fire detection system	1	15.9	15.9
30 m cable 2 × 1.5 mm2 + E from the 230 V ESB to the fire alarm control panel	15	2.54	38.1
Converter 230 Vac/24 Vdc-output 10 A for console installation next to the panel	1	168.43	168.43
Power supply switching and paralleling system	1	325	325
Auxiliary material and labor	23	35	805
TOTAL			2219.26

.

In addition to this investment, fuel consumption does not need to be taken into account, as the supply of the fire detection system from the onboard emergency network would be an exceptional situation.

In order to quantify the savings achieved by alternative 3 compared to alternative 1, the following economic parameters were estimated: NPV (net present value), IRR (internal rate of return) and DPBP (discounted pay-back period)—Equations (1)–(3), respectively [35].

The NPV is the present value of the cash flow at the required rate of return of the economic savings generated by the consumption of MDO compared to the investment of alternative 3

$$NPV=\Sigma {\displaystyle \frac{\mathrm{Cash} \mathrm{flow}}{(1+\mathrm{t}{)}^i}}-\mathrm{Initial} \mathrm{investment}$$

(1)

where t is the required return or discount rate, i the number of time periods and the cash flow considered was the revenue between the yearly cost of the MDO consumption of alternative 1 (18.15 EUR/year).

The IRR is calculated by solving the previous NPV expression for the discount rate required to make the NPV equal to zero.

$$0=\Sigma {\displaystyle \frac{\mathrm{Cash} \mathrm{flow}}{(1+\mathrm{IRR}{)}^i}}-\mathrm{Initial} \mathrm{investment}$$

(2)

The DPBP refers to the amount of time it takes to break even from undertaking the initial expenditure.

$$0 \ge \Sigma {\displaystyle \frac{\mathrm{Cash} \mathrm{flow}}{(1+\mathrm{t}{)}^i}}-\mathrm{Initial} \mathrm{investment}$$

(3)

A service life of 25 years [36,37,38,39], 3% of the inversion for maintenance [40,41] and a discount rate of 12% were considered. The initial investment is the subtraction of the total cost shown in Table 6 minus the total cost shown in Table 4, i.e, 2219.26 – 432.43 = EUR 1743.83. The annual saving is EUR 18.15. Using these data, the NPV results EUR –1746.32. Given that this value is negative, the installation of the solar panel is not economically viable. IRR: Considering the previous values, the IIR is −14.58%. As this value is negative, the sum of the post-investment cash flow is less than the initial investment.

These results show that, from an economic point of view, the installation of solar panels is not worthwhile for supplying energy to small consumers, as the installation costs are too high compared to those of supplying energy using a diesel generator. While the technical feasibility of powering a ship’s fire detection system using a single 550 Wp solar panel was clearly demonstrated, the economic justification remains weak. The system’s low energy demand—approximately 0.72 kWh/day—means that the cost savings in fuel consumption are minimal when compared to the high upfront investment in solar infrastructure, including batteries, converters and installation. This highlights a critical insight: for low-consumption systems, the fixed costs of renewable integration are disproportionately high relative to the marginal savings. Consequently, the economic viability of solar energy on ships improves only when scaled to serve larger loads or when integrated into broader hybrid systems that can amortize costs across multiple consumers.

In view of the previous negative result, the main conclusion is that it is advisable to install as many panels as possible. Taking into account the different layouts of merchant vessels, it would normally be possible to install around 20 solar panels (550 Wp per panel) on a typical bridge deck covering an area of around 45 m² (panels inclined at 30°), which is possible on most merchant vessels. The total power generated by the 20 solar panels should be approximately 10 kW. An inverter (DC/AC 3-phase) would be required to supply this solar energy to any consumer whose power consumption is less than 10 kW. The investment corresponding to this proposal is shown in

Table 7. Investment corresponding to the installation of 20 solar panels.

Description	Quantity	Unit Cost (EUR)	Total Investment (EUR)
Supply, installation and connection of monocrystalline PV panel 550 Wp with the following technical characteristics:	20	131.11	2622.2
Nominal power: 550 Wp
Efficiency: 21.29%
VImp: 41.48 V
Impp: 13.26 A
Inverter 17.5 kW/400 Vac	1	2587.77	2587.77
Support inclined 30° 60 kg structure for 10 panels	2	1601.71	3203.42
Fuse type G 20 A Icc.: 100 kA	2	22.73	45.46
Electrical installation up to inverter (junction boxes, cables, cable trays and others)	1	3850	3850
TOTAL			12,308.85

. As can be seen, the total investment amounts to EUR 12,308.85.

Table 8. Breakdown of investment year by year over the service life.

Year (i)	Maintenance (EUR)	Saving (EUR)	Cash Flow (EUR)	Cash Flow/(1 + t)i (EUR)
1	369.26	2016	1646.73	1470.30
2	369.26	2016	1646.73	1312.77
3	369.26	2016	1646.73	1172.11
4	369.26	2016	1646.73	1046.53
5	369.26	2016	1646.73	934.40
6	369.26	2016	1646.73	834.29
7	369.26	2016	1646.73	744.90
8	369.26	2016	1646.73	665.09
9	369.26	2016	1646.73	593.83
10	369.26	2016	1646.73	530.20
11	369.26	2016	1646.73	473.40
12	369.26	2016	1646.73	422.68
13	369.26	2016	1646.73	377.39
14	369.26	2016	1646.73	336.95
15	369.26	2016	1646.73	300.85
16	369.26	2016	1646.73	268.62
17	369.26	2016	1646.73	239.84
18	369.26	2016	1646.73	214.14
19	369.26	2016	1646.73	191.20
20	369.26	2016	1646.73	170.71
21	369.26	2016	1646.73	152.42
22	369.26	2016	1646.73	136.09
23	369.26	2016	1646.73	121.51
24	369.26	2016	1646.73	108.49
25	369.26	2016	1646.73	96.87
			$\Sigma {\displaystyle \frac{\mathrm{Cash} \mathrm{flow}}{(1+\mathrm{t}{)}^i}}$	12,915.57
			NPV (EUR)	606.7
			IRR (%)	12.7
			DPBP (years)	21

shows the breakdown of investments by year. This table assumes a life of 25 years and a discount rate of 12%. The maintenance costs shown in this table correspond to the assumed value of 3% of the inversion, which is 369.26 EUR/year. In order to calculate the savings in MDO consumption, it was assumed that the solar panels operate for 8 h/day, providing a load of about 10 kW, for 200 days/year, which (considering the engine consumption of 180 g/kWh) corresponds to a saving of 2.88 t/year of MDO, which in economic terms corresponds to 2016 EUR/year (considering an MDO price of 700 EUR/kg). As can be seen from the table, the NPV is EUR 606.7. This value indicates that the investment is profitable, but there are no major savings. The result for the IRR is 12.7%, which indicates that it is positive, but it is too similar to the initial rate of return, so it is not a very profitable project in economic terms. The result for the DPBP is 21 years.

The assumed value of 12% for the discount rate corresponds to the sum of the risk-free rate (such as the yield on Treasury bills) and the risk premium, representing the minimum return desired by the investor. Hernández-Moro et al. [42] discuss the wider economic implications of using discount rates for renewable technologies compared to traditional power plants. They mention that PV installations carry higher technological risks, which can justify applying higher discount rates. Although the assumption of a 12% discount rate for a PV inversion is reasonable, this value is obviously not universally accepted [43,44]. According to this, and taking into account that the discount rate is a critical parameter in economic calculations, a sensitivity analysis of this parameter was performed. Figure 2 shows the NPV as a function of the discount rate for values between 8 and 14%. As expected, the NPV decreases as the discount rate increases. In this particular case, it becomes 0 for discount rates from 12.71%, a value above which the investment is not economically viable.

In view of the results obtained, it can be stated that, from an economic point of view, the installation of solar panels on merchant ships is not profitable given the small number of panels that can be installed due to the limited surface area. It is worth noting that although approximately 20 solar panels (550 Wp each) could be installed on the deck of a typical merchant vessel—covering approximately 45 m² at a 30° tilt—this theoretical capacity does not take into account real operational constraints. In practice, shading from structural elements, equipment and safety routes significantly reduces the usable area and therefore the actual energy yield. Another important problem is that the electricity generated by solar panels is difficult to connect in parallel and synchronize with the auxiliary generators on board, given that the variation of their frequency goes, typically, at ±10% of the nominal value and is not stable. Also, the difference in the power supplies generated on both networks means that this coupling would be unbalanced.

3.2. Sustainability Analysis

The feasibility analysis carried out above considers technical, legal and economic factors to determine whether the proposal can be implemented. In contrast, a sustainability analysis considers whether a project can maintain its benefits over time without depleting resources or harming the environment [45,46].

A sustainability analysis includes environmental, social and economic factors [47]. Various methods for calculating what is known as the sustainability index (SI) can be found in the literature. One of the most commonly used methods is simple additive weighting (SAW), according to which the SI can be calculated using Equation (4) [48], where i is the alternative analyzed, c the criteria, w the weight assigned to each criterion j and n the number of criteria. The SI ranges between 0 (corresponding to the worst sustainability) and 1 (corresponding to the optimal sustainability).

$$S{I}_i={\displaystyle \underset{j=1}{\overset{n}{\Sigma }}{w}_j{c}_{ij}}$$

(4)

Three criteria are considered in the present analysis: economic, social and environmental. As far as the alternatives are concerned, since alternative 2 does not meet the SOLAS legal requirements, only alternatives 1 and 3 are compared. The numerical data are shown in

Table 9. Data for the sustainability analysis.

Alternative (i)	Criterion (j)
	j = 1	j = 2	j = 3
	Economic (EUR)	Environmental (-)	Social (-)
Alternative 1	896.03	0	0
Alternative 3	1426.83	1	1

. With regard to the economic criteria, the costs of alternative 1 and alternative 3 are considered. The cost of alternative 3 refers to the investment cost (EUR 1426.83), while the cost of alternative 1 refers to the investment cost plus the MDO consumption cost (EUR 432.43 + 463.6 = 896.03). These are measurable values obtained in the previous section. On the other hand, the environmental and social criteria were treated as discrete values, so that alternative 1 was given a value of 0 and alternative 3 a value of 1, given that the latter is more ecological and also more socially appropriate (in terms of community benefits, social equity, cultural impact and so on).

Once the data for the sustainability analysis are collected, the next step is to normalize them. The normalization process in a sustainability analysis is essential to ensure fair comparisons. In this case, the economic criterion is provided through continuous values in EUR while the other criteria are provided through discontinuous values as 0 (bad) and 1 (good). Normalization adjusts values to a common scale for consistency and comparability in the analysis. The linear max normalization was used, which follows the following Equations (5) and (6) [47] for beneficial and non-beneficial criteria, respectively. In these equations, X is the value and X_j,max the maximum value corresponding to that criterion. In this case, the economic criterion is a non-beneficial criterion since it is desirable that the cost is as low as possible, while environmental and social criteria are beneficial since an environmental and social solution is desirable.

$$S{I}_{ij}={\displaystyle \frac{X_{ij}}{X_{j,\max }}} \mathrm{For} \mathrm{beneficial} \mathrm{criteria}$$

(5)

$$S{I}_{ij}=1-{\displaystyle \frac{X_{ij}}{X_{j,\max }}} \mathrm{For} \mathrm{non}-\mathrm{beneficial} \mathrm{criteria}$$

(6)

The normalized data are shown in

Table 10. Normalized data for the sustainability analysis and sustainability index of each alternative.

Alternative (i)	Criterion (j)			SI
	j = 1	j = 2	j = 3
	Economic (EUR)	Environmental (-)	Social (-)
Alternative 1	0.37	0	0	0.185
Alternative 3	0	1	1	0.5

. This table includes the normalized values calculated using Equations (5) and (6), as well as the SI calculated using Equation (4). In order to calculate the SI, a weight must be given to each alternative. In a sustainability analysis, weights represent the relative importance assigned to different environmental, social and economic criteria to prioritize key factors in decision-making. For example, Table 10 shows the results of the SI corresponding to 50% economic weight (0.5 on a per-unit basis), 25% environmental weight (0.25 on a per-unit basis) and 25% social weight (0.25 on a per-unit basis). These weights correspond to economic factors, given half of the possible importance (50%); the remaining importance has been equally distributed between the other two factors (25% and 25%). Logically, the sum of the assigned weights must be 100, or 1 on a per-unit basis. This weighting distribution reflects a decision-making approach where economic sustainability is considered twice as important as environmental and social aspects, influencing how the project’s overall sustainability performance is assessed. It is worth mentioning that choosing weights in a sustainability analysis depends on several factors such as stakeholder priorities, industry standards, regulatory requirements, project goals and so on. Common methods include expert judgment, stakeholder surveys, historical data analysis and even statistical analyses. For example, a government policy might prioritize environmental factors, while a business-driven project may emphasize profitability. According to this, a sensitivity analysis of the weights was carried out. The results are shown in Figure 3, which shows the SI for alternative 1 and for alternative 3, with the weight of the economic criterion ranging from 0 (lowest possible) to 100 (highest possible). As can be seen, the solution of installing solar panels is recommendable from a sustainability point of view, unless the economic issue is of high relevance in the decision-making process.

4. Conclusions

The present work presents an analysis of the different energy requirements on an oceanographic fishery research vessel and the possibility of installing solar energy. In addition to a techno-economic study, a sustainability analysis was carried out, taking into account economic, social and environmental criteria. This work addresses three main issues: the technical feasibility, economic viability and sustainability of integrating PV panels on an oceanographic research vessel. The main outcome of the research is that, while solar panels can technically meet a small portion of the ship’s energy needs, the area required for sufficient panels exceeds the available space, making it impractical to rely solely on solar energy. Specifically, using solar panels to power the fire detection system is technically and legally feasible but not economically viable due to the high initial investment and low return on investment.

This study is justified as it provides a comprehensive and detailed analysis of the feasibility of integrating PV panels on an oceanographic research vessel, addressing technical, economic and sustainability aspects. Despite the expected conclusions, this work offers valuable insights into the practical challenges and limitations of solar energy integration in maritime applications, such as space constraints and regulatory issues. By focusing on a specific case study, this study contributes unique data and perspectives that can guide future research and practical implementations, promoting sustainable development and encouraging innovation in renewable energy solutions for the maritime sector.

This study faced several limitations, including regulatory constraints and the variability of solar energy availability, which posed significant challenges in assessing the feasibility of solar energy integration. While this study confirms the expected limitations of solar energy integration on merchant ships—such as limited deck space, high investment costs and synchronization challenges with existing generators—it also opens the door to more innovative strategies that merit further exploration. One such insight is the potential for modular hybrid systems that combine solar with other renewable energy sources, such as wind turbines, particularly during docked operations where drag is not an issue. Another is the integration of intelligent energy management systems. As a result, it is recommended that future studies explore hybrid energy systems that combine solar with other renewable energy sources, as well as pilot projects and real-world trials. While the current study focuses on the feasibility of PV generators, it would be beneficial to analyze the potential of installing small wind turbines on ships, especially given the typically windy conditions at sea. The commercial ONMIFLOW system, which combines wind and solar PV with integrated energy storage, is an example of this option. Although the installation of wind turbines may increase drag and affect propulsion, their use when the ship is docked could significantly improve energy efficiency and sustainability. It is also recommended that future studies investigate the feasibility, economic viability and environmental impact of hybrid systems combining wind and solar energy, considering both operational and docked scenarios, in order to optimize energy use and reduce dependence on fossil fuels.