Adaptive Kalman Filter Under Minimum Error Entropy with Fiducial Points for Strap-Down Inertial Navigation System/Ultra-Short Baseline Integrated Navigation Systems

Abstract

The integration of strap-down inertial navigation systems (SINSs) and ultra-short baseline (USBL) systems has become a mainstream navigation approach for unmanned underwater vehicles (UUVs). In shallow-sea environments, USBL measurements are frequently affected by complex non-Gaussian disturbances. Under such challenging conditions, traditional Kalman filters often exhibit limited performance in maintaining navigation accuracy. A novel adaptive Kalman filter is proposed to address this issue. The proposed method demonstrates significant robustness to complex non-Gaussian noise through the construction of an advanced regression model, the development of an adaptive free-parameter optimization scheme, and the implementation of a recursive filtering architecture incorporating entropy-based error correction. Comprehensive validation via numerical simulations and field experiments in offshore SINS/USBL integrated navigation scenarios demonstrates the superior robustness of the proposed method in complex underwater non-Gaussian noise environments.

1. Introduction

Recently, the integration of strap-down inertial navigation systems (SINSs) with ultra-short baseline (USBL) systems has garnered significant attention in the field of underwater positioning and navigation [1,2,3]. At present, SINS/USBL integrated navigation is predominantly implemented using the Kalman filters (KFs) and their variants, such as the extended Kalman filter (EKF) and the unscented Kalman filter (UKF) [4,5]. The aforementioned filtering methods, including the KF, are constructed based on the recognized minimum mean square error (MMSE) principle and provide optimal efficacy under the presumption of noise following a Gaussian distribution.

In shallow marine environments, USBL measurements are often disrupted by multipath effects and underwater interference, which significantly reduces the navigation accuracy of the SINS/USBL integration system in non-Gaussian noise environments. To tackle this problem, numerous robust filters have been proposed for handling outliers in sensor measurements. The H-infinity filter is an earlier technique that is commonly utilized to tackle problems related to inaccuracies in the system model and uncertainties in the noise characteristics present in the measurements [6]. The particle filter (PF), grounded in the principles of sequential importance resampling, has the ability to effectively manage any non-Gaussian noise [7,8]. However, it suffers from issues related to high computational complexity and particle degradation. The Gaussian sum filter (GSF) approximates the state probability density function using a Gaussian mixture model (GMM) to refine non-Gaussian noise stochastic models [9,10]. However, the heavy computational demands hinder its use in systems that rely on real-time navigation. The Huber-based Kalman filter (Huber-KF), obtained by optimizing the piecewise Huber objective, exhibits good robustness [11,12,13]. However, its performance may degrade in dynamic situations owing to the limitation of static parameters. The robust Student’s t-based Kalman filter (RSTKF) employs a Student’s t distribution to effectively model heavy-tailed non-Gaussian disturbances, providing a robust posterior estimate [14,15,16]. Nevertheless, the RSTKF suffers from a deficiency in high-order statistics resulting from both moment-matching challenges and the selection of incorrect parameters. Additionally, its performance may deteriorate when the noise follows a light-tailed or multi-modal distribution.

In addition to the aforementioned robust Kalman filters, the application of entropy-based criteria from information theory learning (ITL) also provides effective approaches for managing heavy-tailed noise. The maximum correntropy criterion (MCC) and the minimum error entropy (MEE) criterion have been incorporated into the KF, resulting in new robust KF variants, namely the MCC-based KF (MCCKF) and MEE-based KF (MEEKF) [17,18,19,20,21]. Based on existing research findings, these approaches exhibit superior performance compared to the conventional MMSE criterion when handling non-Gaussian noise environments. Although the MCCKF is proficient at improving estimation accuracy in instances of heavy-tailed noise, it may struggle with performance issues when faced with more complex noise types, like those arising from multi-modal distributions. To tackle this challenge, a new approach known as the MEEKF has been introduced. Within the framework of the MEEKF, kernel density estimation (KDE) is employed to approximate the probability density function (PDF) of the error, thereby constructing a flexible functional framework that can effectively accommodate a broad spectrum of diverse signals representing various statistical distributions. Although the MEEKF possesses the capacity to deal with complex non-Gaussian disturbances, the MEE retains the intrinsic property of translation invariance, which can be automatically ensured by the Gaussian kernel function in the MEE via differential operations. This implies that it cannot guarantee the convergence of the estimation error to zero. And the MCC can fix the peak value of the PDF to zero. Accordingly, the criterion known as the minimum error entropy criterion with fiducial points (MEEF), also referred to as the centered error entropy (CEE), was proposed by the weighted combining of the MCC and MEE [22]. Recently, the stochastic information gradient (SIG) method combined with a fixed-point iterative approach gave rise to the introduction of the CEE-based KF (CEEKF) [23]. The fixed-point CEE approach’s convergence is illustrated in [24]. Nevertheless, the CEEKF typically determines fixed free parameters empirically, which might lead to the reduced performance of real-time navigation systems in complex non-Gaussian noise environments.

In this paper, we propose a novel filter termed the adaptive minimum error entropy Kalman filter with fiducial points (AMEEF-KF) to address the issue at hand. First, the AMEEF-KF is constructed by integrating the MEEF into the KF framework. Specifically, the MEEF is devised to automatically align the peak of the error PDF at zero, thereby substantially improving robustness against non-Gaussian noise. Subsequently, a new free-parameter optimization scheme is introduced, enabling real-time updates of the free parameters based on the state error vector. Finally, this scheme is incorporated into the recursive filtering architecture with entropy-based error correction, enhancing the overall effectiveness of the filter.

The rest of this article is organized as follows: The related error entropy criterion and traditional KF are briefly introduced in Section 2. A novel adaptive Kalman Filter named AMEEF-KF is derived in Section 3. Section 4 covers the simulation and marine experiment results of SINS/USBL integration, and Section 5 provides a concise discussion of this study.

2. Related Work

In this section, we review the criteria of the MEE and MCC, the principle of the MEEF, and the traditional KF to facilitate subsequent algorithmic derivation.

2.1. Minimum Error Entropy Criterion

Entropy is an effective tool for quantifying the uncertainty of random variables in ITL [25]. The mathematical expression for Renyi’s quadratic entropy is formulated as follows:

$$H_2\left(e\right)=-log\left(\int p^2\left(e\right)de\right)$$

(1)

where $p(·)$ represents the PDF of the error variable $\mathit{e}$.

The information potential (IP) is denoted by

$$IP\left(e\right)=\int p^2\left(e\right)de$$

(2)

By minimizing Equation (1), the MEE is formulated, which is equivalent to maximizing the IP.

In practice, since the PDF of the variables remains unspecified, the KDE is typically employed to estimate density, which is also referred to as the Parzen windowing approach. By employing the KDE method, a nonparametric estimation of the error’s PDF is obtained by [25,26]

$${\widehat{p}}_{X;\sigma }\left(x\right)={\displaystyle \frac{1}{N}}\sum _{i=1}^N{\kappa }_{\sigma }\left(x-e_i\right)$$

(3)

where ${\left\{e_i\right\}}_{i=1}^N$ denotes the error samples, $N$ represents the length of the sliding data window, and ${\kappa }_{\sigma }(·)$ is the Gaussian kernel function with a specified kernel size $\sigma$.

Therefore, by substituting Equation (3) into Equation (2), the MEE can be obtained by maximizing

$$\widehat{IP}\left(e\right)={\displaystyle \frac{1}{N^2}}\sum _{i=1}^N\sum _{j=1}^N{\kappa }_{\sqrt{2}\sigma }\left(e_i-e_j\right)$$

(4)

2.2. Maximum Correntropy Criterion

The correntropy between two random variables $A,B\in \mathbb{R}$ can be defined by [27,28]

$$V_{\sigma }\left(A,B\right)=E\left[{\kappa }_{\sigma }\left(A,B\right)\right]=\iint {\kappa }_{\sigma }\left(a,b\right)p_{AB}\left(a,b\right)dadb$$

(5)

where $E\left[·\right]$ represents the expectation operator, ${\kappa }_{\sigma }(·,·)$ denotes the continuous kernel function, $p_{AB}\left(a,b\right),a\in A,b\in B$ is the joint PDF, and $\sigma$ represents the specified kernel bandwidth. The Gaussian kernel function, which is widely regarded as the most frequently employed kernel function in various applications due to its excellent mathematical properties and versatility, is represented as

$${\kappa }_{\sigma }\left(a,b\right)=G_{\sigma }\left(e\right)=\exp \left(-{\displaystyle \frac{e^2}{{2\sigma }^2}}\right)$$

(6)

where $e=a-b$.

However, most real-time applications can only use a limited amount of data, and the joint PDF remains unknown. A sample mean estimator can be utilized to estimate the correntropy, which can be represented as

$${\widehat{C}}_{\sigma }\left(A,B\right)={\displaystyle \frac{1}{N}}\sum _{i=1}^N{\kappa }_{\sigma }\left(e_i\right)={\displaystyle \frac{1}{N}}\sum _{i=1}^N{\kappa }_{\sigma }\left(a_i-b_i\right)$$

(7)

A cost function derived from the MCC can be formally defined as [29]

$$J_{MCC}={\displaystyle \frac{1}{N}}\sum _{i=1}^N{G}_{\sigma }\left(e_i\right)$$

(8)

The correntropy is capable of capturing more abundant information compared to traditional second-order statistics and has a probabilistic interpretation related to maximizing the probability density of errors around the origin [27,28,30].

2.3. Minimum Error Entropy Criterion with Fiducial Points

The MEE approach concentrates on diminishing the disparities among errors, thereby efficiently reducing the error entropy in estimation problems; however, it is possible that the errors cannot be located at zero even after optimization. To address this issue, an extended error vector denoted as $E_A[e_0,E]$ can be formulated, where $e_0=0$ is used as a reference point, or a fiducial point, and $E=[e_1,e_2,\dots ,e_N]$ represents the error samples [31]. Then, the error IP is established by taking the fiducial point into consideration, which can be represented as

$$\begin{gathered} \widehat{IP}(e)={\displaystyle \frac{1}{{(N+1)}^2}}\sum _{i=0}^N\sum _{j=0}^N{\kappa }_{\sigma }(e_i-e_j) \\ ={\displaystyle \frac{1}{{\left(N+1\right)}^2}}\left[2\sum _{j=1}^N{\kappa }_{\sigma }\left(e_j\right)+\sum _{i=1}^N\sum _{j=1}^N{\kappa }_{\sigma }\left(e_i-e_j\right)+{\kappa }_{\sigma }\left(0\right)\right] \end{gathered}$$

(9)

By disregarding the constants ${\kappa }_{\sigma }\left(0\right)$ and $1/{(N+1)}^2$, the aforementioned cost function represents a unified and weighted integration of the MCC and MEE, which can be described as

$$\widehat{IP}\left(e\right)=\lambda \sum _{j=1}^L{\kappa }_{{\sigma }_1}\left(e_j\right)+\left(1-\lambda \right)\sum _{i=1}^L\sum _{j=1}^L{\kappa }_{{\sigma }_2}\left(e_j-e_i\right)$$

(10)

where $\lambda$ denotes a scaling factor between 0 and 1, and ${\sigma }_1$ and ${\sigma }_2$ are the kernel bandwidths of the MCC and MEE, respectively. When $\lambda =0$, the above criterion is reduced to the MEE; when $\lambda =1$, it degenerates into the MCC. The MEEF integrates the advantageous features of both the MCC and MEE, with the MEE term minimizing error entropy and the MCC ensuring that the peak of the error PDF is anchored at zero. Therefore, the MEEF can work in a more elegant and robust way than the MCC and MEE.

2.4. Traditional Kalman Filter

Consider this discrete-time linear system model

$$x_k=F_{k|k-1}{x}_{k-1}+w_{k-1}$$

(11)

$$z_k=H_k{x}_k+v_k$$

(12)

where $x_k \in {\mathbb{R}}^n$ is the n-dimensional process state vector, $z_k \in {\mathbb{R}}^m$ is the m-dimensional measurement vector, $F_{k|k-1}$ denotes the state transition matrix from k − 1 to k, and $w_k$ and $v_k$ are mutually uncorrelated process noise and measurement noise, respectively, characterized by zero mean and prescribed covariance matrices

$$E\left[w_k{w}_k^T\right]=Q_k,E\left[v_k{v}_k^T\right]=R_k$$

(13)

The traditional Kalman filter comprises two steps [32,33]:

• Time updating:

$${\widehat{x}}_{k|k-1}=F_{k-1}{\widehat{x}}_{k-1}$$

(14)

$$P_{k|k-1}=F_{k-1}{P}_{k-1}{F}_{k-1}^T+Q_{k-1}$$

(15)

2.

Measurement updating:

$$K_k={P_{k|k-1}{H}^T\left(H{P}_{k|k-1}{H}^T+R_k\right)}^{-1}$$

(16)

$${\widehat{x}}_{k|k}={\widehat{x}}_{k|k-1}+K_k\left(z_k-H{\widehat{x}}_{k|k-1}\right)$$

(17)

$$P_{k|k}=P_{k|k-1}-K_k\left(H{P}_{k|k-1}{H}^T+R_k\right)K_k^T$$

(18)

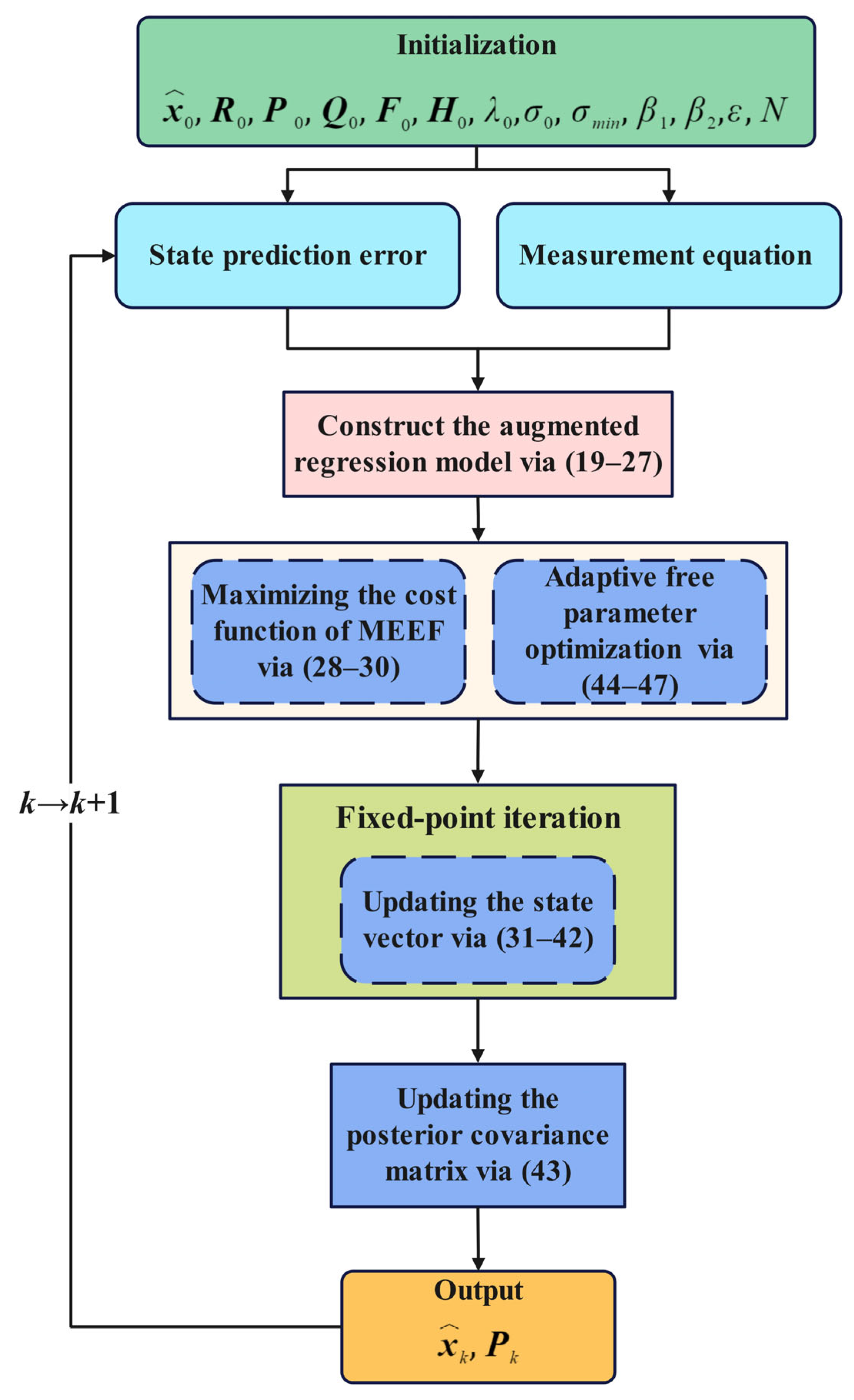
3. Methodology

In this section, a novel adaptive Kalman filter under minimum error entropy with fiducial points is derived by constructing an augmented regression model and formulating a free-parameter optimization scheme. Additionally, in this article, the algorithm is designed based on an error-state approach.

3.1. Augmented Regression Model

The augmented regression model can be constructed by

$$\left[\begin{array}{c}{\widehat{x}}_{k|k-1}\\ z_k\end{array}\right]=\left[\begin{array}{c}{I}_n\\ H_k\end{array}\right]x_k+\left[\begin{array}{c}-{ϵ}_{k|k-1}\\ v_k\end{array}\right]$$

(19)

where ${\mathit{ϵ}}_{k|k-1}={\mathit{x}}_k-{\widehat{\mathit{x}}}_{k|k-1}$ denotes the state prediction error, and $I_n$ represents an n × n identity matrix. The augmented noise vector, which is composed of state prediction error ${\mathit{ϵ}}_{k|k-1}$ and measurement noise ${\mathit{v}}_k$, can be abbreviated as

$${\mu }_k=\left[\begin{array}{c}-{ϵ}_{k|k-1}\\ v_k\end{array}\right]$$

(20)

The covariance matrix of the augmented noise vector $E\left[{\mu }_k{\mu }_k^T\right]$ is set to be positive definite; by performing Cholesky decomposition on its components, we can obtain

$$E\left[{\mu }_k{\mu }_k^T\right]=\left[\begin{array}{cc}{P}_{k|k-1}& 0\\ 0& R_k\end{array}\right]=S_k{S}_k^T=\left[\begin{array}{cc}{S}_{P_{k|k-1}}{S}_{P_{k|k-1}}^T& 0\\ 0& S_{R_k}{S}_{R_k}^T\end{array}\right]$$

(21)

with

$$S_k=\left[\begin{array}{cc}{S}_{P_{k|k-1}}& 0\\ 0& S_{R_k}\end{array}\right]$$

(22)

Multiplying both sides of the augmented model by $S_k^{-1}$ gives

$$d_k=W_k{x}_k+e_k$$

(23)

where

$$d_k=S_k^{-1}\left[\begin{array}{c}{\widehat{x}}_{k|k-1}\\ z_k\end{array}\right]$$

(24)

$$W_k=S_k^{-1}\left[\begin{array}{c}{I}_n\\ H_k\end{array}\right]$$

(25)

$$e_k=S_k^{-1}{\mu }_k$$

(26)

with $d_k={\left[d_{1,k},\cdots ,d_{L,k}\right]}^T$, $W_k={\left[w_{1,k},\cdots ,w_{L,k}\right]}^T$, $e_k={\left[e_{1,k},\cdots ,e_{L,k}\right]}^T$, $L=m+n$.

Consequently, the batch-mode regression form can be expressed as

$$e_k=d_k-W_k{x}_k$$

(27)

The cost function of the MEEF is [31]

$$J_L\left(x_k\right)=\lambda \sum _{j=1}^L{\kappa }_{{\sigma }_1}\left(e_{j,k}\right)+\left(1-\lambda \right)\sum _{i=1}^L\sum _{j=1}^L{\kappa }_{{\sigma }_2}\left(e_{j,k}-e_{i,k}\right)$$

(28)

where $\lambda \in [0,1]$ denotes a weighting factor, which can be construed as the number of fiducial points placed at the origin.

Then, the optimal solution for ${\widehat{x}}_k$ is obtained by maximizing the cost function, which can be expressed as

$${\widehat{x}}_k=\mathrm{a}\mathrm{r}\mathrm{g} \underset{x_k}{\max }{J}_L\left(x_k\right)$$

(29)

Taking the derivative of $J_L\left(x_k\right)$ with respect to $x_k$ results in

$$\begin{gathered} {\displaystyle \frac{\partial J_L\left(x_k\right)}{\partial x_k}}={\lambda }_1\sum _{j=1}^L{e}_{j,k}{\kappa }_{{\sigma }_1}\left(e_{j,k}\right)w_{j,k}+{\mathrm{T}}_1-{\mathrm{T}}_2-{\mathrm{T}}_3+{\mathrm{T}}_4 \\ ={\lambda }_1{W}_k^T{\mathsf{{\rm Y}}}_k{e}_k+2{\lambda }_2{W}_k^T\left({\mathsf{\Psi }}_k-{\mathsf{\Phi }}_k\right)e_k \end{gathered}$$

(30)

where ${\lambda }_1=\lambda /{\sigma }_1^2$, ${\lambda }_2=(1-\lambda )/{\sigma }_2^2$, and ${\left\{{\mathsf{\Phi }}_k\right\}}_{\mathcal{l}\overline{\mathcal{l}}}={\kappa }_{\sigma }(e_{\overline{\mathcal{l}},k}-e_{\mathcal{l},k})$; here, ${\left\{{\mathsf{\Phi }}_k\right\}}_{\mathcal{l}\overline{\mathcal{l}}}$ represents the element in row $\mathcal{l}$ and column $\overline{\mathcal{l}}$ of ${\mathsf{\Phi }}_k$. ${\mathsf{{\rm Y}}}_k$ and ${\mathsf{\Psi }}_k$ are diagonal matrices with the $\mathcal{l}$-th diagonal entry ${\mathsf{{\rm Y}}}_{\mathcal{l}\mathcal{l},k}={\kappa }_{\sigma }\left(e_{\mathcal{l},k}\right)$ and ${\mathsf{\Psi }}_{\mathcal{l}\mathcal{l},k}={\sum }_{i=1}^L{\kappa }_{\sigma }(e_{\mathcal{l},k}-e_{i,k})$, respectively. Let ${\tilde{\mathrm{T}}}_{ab}={\lambda }_2{\sum }_{i=1}^L{\sum }_{j=1}^L{e}_{a,k}{\kappa }_{{\sigma }_2}[e_{j,k}-e_{i,k}]w_{b,k}$. Scalars ${\mathrm{T}}_1$, ${\mathrm{T}}_2$, ${\mathrm{T}}_3$, and ${\mathrm{T}}_4$ in Equation (30) are set as ${\mathrm{T}}_1={\tilde{\mathrm{T}}}_{jj}$, ${\mathrm{T}}_2={\tilde{\mathrm{T}}}_{ij}$, ${\mathrm{T}}_3={\tilde{\mathrm{T}}}_{ji}$, and ${\mathrm{T}}_4={\tilde{\mathrm{T}}}_{ii}$, respectively.

From Equation (30), $x_k$ can be estimated by a fixed-point iterative algorithm:

$$\begin{gathered} {\widehat{x}}_{k,\tau +1}=\mathrm{g}\left({\widehat{x}}_{k,\tau }\right) \\ ={\left[{\lambda }_1\sum _{j=1}^L{\kappa }_{{\sigma }_1}\left(e_{j,k}\right)w_{j,k}{w}_{j,k}^T+{\lambda }_2\sum _{i=1}^L\sum _{j=1}^L{\kappa }_{{\sigma }_2}\left[e_{j,k}-e_{i,k}\right]{\mathsf{\Xi }}_1\right]}^{-1} \\ \times \left[{\lambda }_1\sum _{j=1}^L{\kappa }_{{\sigma }_1}\left(e_{j,k}\right)w_{j,k}{d}_{j,k}+{\lambda }_2\sum _{i=1}^L\sum _{j=1}^L{\kappa }_{{\sigma }_2}\left[e_{j,k}-e_{i,k}\right]{\mathsf{\Xi }}_2\right] \\ ={\left({\mathrm{W}}_k^T{\Lambda }_k{\mathrm{W}}_k\right)}^{-1}\left({\mathrm{W}}_k^T{\Lambda }_k{\mathrm{d}}_k\right) \end{gathered}$$

(31)

where ${\widehat{x}}_{k,\tau }$ denotes the solution of $x_k$ obtained during the $\tau$-th fixed-point iteration step; ${\mathsf{\Xi }}_1=\left[w_{i,k}-w_{j,k}\right]{\left[w_{i,k}-w_{j,k}\right]}^T$; ${\mathsf{\Xi }}_2=\left[d_{i,k}-d_{j,k}\right]\left[w_{i,k}-w_{j,k}\right]$;

$${\Lambda }_k=2{\lambda }_2\left({\mathsf{\Psi }}_k-{\mathsf{\Phi }}_k\right)+{\lambda }_1{\mathsf{{\rm Y}}}_k=\left[\begin{array}{cc}{\Gamma }_{xx,k}& {\Gamma }_{yx,k}\\ {\Gamma }_{xy,k}& {\Gamma }_{yy,k}\end{array}\right]$$

(32)

with ${\Lambda }_k\in {\mathbb{R}}^{L\times L}$ and ${\Gamma }_{xx,k}\in {\mathbb{R}}^{n\times n}$, ${\Gamma }_{xy,k}\in {\mathbb{R}}^{m\times n}$, ${\Gamma }_{yx,k}\in {\mathbb{R}}^{n\times m}$, and ${\Gamma }_{yy,k}\in {\mathbb{R}}^{m\times m}$.

From Equations (24), (25) and (32), Equation (31) can be rewritten as

$${\widehat{x}}_k={\left({\mathsf{\Omega }}_1+{\mathsf{\Omega }}_2{\mathsf{\Omega }}_3\right)}^{-1}{\mathsf{\Omega }}_1{\widehat{x}}_{k|k-1}+{\left({\mathsf{\Omega }}_1+{\mathsf{\Omega }}_2{\mathsf{\Omega }}_3\right)}^{-1}{\mathsf{\Omega }}_2{z}_k$$

(33)

where

$${\mathsf{\Omega }}_1=\left[{\left(S_{P_{k|k-1}}^T\right)}^{-1}{\Gamma }_{xx}+H_k^T{\left(S_{R_k}^T\right)}^{-1}{\Gamma }_{xy}\right]{\left(S_{P_{k|k-1}}^T\right)}^{-1}$$

(34)

$${\mathsf{\Omega }}_2=\left[{\left(S_{P_{k|k-1}}^T\right)}^{-1}{\Gamma }_{yx}+H_k^T{\left(S_{R_k}^T\right)}^{-1}{\Gamma }_{yy}\right]{\left(S_{R_k}^T\right)}^{-1}$$

(35)

$${\mathsf{\Omega }}_3=H_k$$

(36)

Based on the matrix inversion lemma, Equation (33) can be rewritten as [34]

$${\widehat{x}}_k={\widehat{x}}_{k|k-1}+{\overline{K}}_k\left(z_k-{\widehat{z}}_{k|k-1}\right)$$

(37)

where

$${\overline{K}}_k={\left[{\overline{P}}_{k|k-1}+H_k^T{\overline{P}}_{xy,k|k-1}+\left({\overline{P}}_{yx,k|k-1}+H_k^T{\overline{R}}_k\right)H_k\right]}^{-1}$$

(38)

$${\overline{P}}_{k|k-1}={\left(S_{P_{k|k-1}}^T\right)}^{-1}{\Gamma }_{xx,k}{S}_{P_{k|k-1}}^{-1}$$

(39)

$${\overline{P}}_{xy,k|k-1}={\left(S_{R_k}^T\right)}^{-1}{\Gamma }_{xy,k}{S}_{P_{k|k-1}}^{-1}$$

(40)

$${\overline{P}}_{yx,k|k-1}={\left(S_{P_{k|k-1}}^T\right)}^{-1}{\Gamma }_{yx,k}{S}_{R_k}^{-1}$$

(41)

$${\overline{R}}_k={\left(S_{R_k}^T\right)}^{-1}{\Gamma }_{yy,k}{S}_{R_k}^{-1}$$

(42)

Then, the posterior covariance is

$$P_k=\left[I-{\overline{K}}_k{H}_k\right]P_{k|k-1}{\left[I-{\overline{K}}_k{H}_k\right]}^T+{\overline{K}}_k{R}_k{\overline{K}}_k^T$$

(43)

The procedure of the MEEF-KF is summarized in Algorithm 1.

Algorithm 1: MEEF-KF

Step 1: Initialize the state a priori estimate ${\widehat{x}}_{1|0}$ and the corresponding state prediction error covariance matrix $P_{1|0}$; select two kernel bandwidths ${\sigma }_1$ and ${\sigma }_2$, choose a proper weight factor $\lambda$ and a specified small positive value $\epsilon$; Step 2: Utilize Equations (14) and (15) to calculate ${\widehat{x}}_{k|k-1}$ and $P_{k|k-1}$, use Cholesky decomposition to get $S_{P_{k|k-1}}$ and $S_{R_k}$; calculate the $d_k$ and $W_k$; Step 3: Let $\tau =1$ and ${\widehat{x}}_{k,0}={\widehat{x}}_{k|k-1}$, where ${\widehat{x}}_{k,\tau }$ is the estimated state at the fixed-point iteration $\tau$:

${\widehat{x}}_{k,\tau }={\widehat{x}}_{k|k-1}+{\tilde{K}}_k(z_k-{\widehat{z}}_{k|k-1})$

with:

${\tilde{K}}_k={\tilde{P}}_{k|k-1}{H}_k^T{(H_k{\tilde{P}}_{k|k-1}{H}_k^T+{\tilde{R}}_k)}^{-1}$ ${\tilde{P}}_{k|k-1}={\left(S_{P_{k|k-1}}^T\right)}^{-1}{\tilde{\Gamma }}_{xx,k}{S}_{P_{k|k-1}}^{-1}$ ${\tilde{P}}_{xy,k|k-1}={\left(S_{R_k}^T\right)}^{-1}{\tilde{\Gamma }}_{xy,k}{S}_{P_{k|k-1}}^{-1}$ ${\tilde{P}}_{yx,k|k-1}={\left(S_{P_{k|k-1}}^T\right)}^{-1}{\tilde{\Gamma }}_{yx,k}{S}_{R_k}^{-1}$ ${\tilde{R}}_k={\left(S_{R_k}^T\right)}^{-1}{\tilde{\Gamma }}_{yy,k}{S}_{R_k}^{-1}$ ${\tilde{e}}_{i,k}=d_{i,k}-w_k^T{\widehat{x}}_{k,\tau -1}$

Step 4: if ${\displaystyle \frac{‖{\widehat{x}}_{k,\tau }-{\widehat{x}}_{k,\tau -1}‖}{‖{\widehat{x}}_{k,\tau -1}‖}} \le \epsilon$ then go to Step 5. else $\tau =\tau +1$, and return to Step 3. Step 5: Update $k+1\to k$ and compute the posterior error covariance matrix by:

$P_k=\left[I-{\tilde{K}}_k{H}_k\right]P_{k|k-1}{\left[I-{\tilde{K}}_k{H}_k\right]}^T+{\tilde{K}}_k{R}_k{\tilde{K}}_k^T$

and return to Step 2.

It should be pointed out that the MEEF-KF algorithm may encounter numerical instability issues, as extremely large measurement errors could potentially render the matrix ${\Lambda }_k$ singular. Consequently, formulating an adaptive free-parameter optimization scheme suitable for the MEEF-KF is of particular significance.

3.2. Free-Parameter Optimization Scheme

The accuracy of the MEEF-KF estimation is significantly impacted by the parameters $\lambda$, ${\sigma }_1$, and ${\sigma }_2$. The weight factor $\lambda$ is utilized to achieve an optimal balance between correntropy and error entropy. ${\sigma }_1$ and ${\sigma }_2$ are the kernel bandwidth for the MCC and MEE part of the MEEF, respectively. When $\lambda =1$, the MEEF-KF will reduce to the MCCKF, when $\lambda =0$, the MEEF-KF will reduce to the MEEKF. In addition, when $\lambda =1$, ${\sigma }_1 \to \infty$, the MEEF-KF will reduce to the classical KF algorithm. The MEE term serves to minimize the error entropy, while the MCC term functions to anchor the error peak around the origin. As a result, the MEEF is capable of outperforming both the MEE and MCC in a variety of scenarios. However, the aforementioned parameters are typically pre-selected and remain invariant while running the algorithm, thereby restricting the performance of the algorithm. In this section, we propose an adaptive free-parameter optimization scheme aimed at enhancing the robustness of the filtering algorithm.

For the kernel bandwidth ${\sigma }_1$, theoretically, both too small and too large kernel bandwidth parameters are detrimental to filter state estimation. An excessively small kernel bandwidth can lead to severe numerical stability issues, while a larger kernel bandwidth can weaken the robustness of the filtering algorithm. To address these issues, we introduce a kernel bandwidth adjustment strategy based on the variable kernel width adaptive maximum correlation entropy algorithm.

This study uses the Mahalanobis Distance (MD) to identify outliers in the data by comparing the measurement at time $k$ with its previous estimate. The MD is calculated as follows [35]:

$$M{D}_k=\sqrt{{\left(z_k-H_k{\widehat{x}}_{k|k-1}\right)}^T{\left(H_k{P}_{k|k-1}{H}_k^T+{ R}_k\right)}^{-1}\left(z_k-{ H}_k{\widehat{x}}_{k|k-1}\right)}$$

(44)

Subsequently, we define ${\mu }_k={MD}_k^2$ and perform the Chi-square test to identify potential outliers. Specifically, if ${\mu }_k>{\chi }_{n,\alpha }^2$, the corresponding observations are classified as outliers, and the kernel bandwidth is adjusted to a smaller value to enhance the robustness of the filtering process. Conversely, if ${\mu }_k\le {\chi }_{n,\alpha }^2$, the corresponding data points are classified as normal data points, and the kernel bandwidth is increased to enhance the filtering precision. Nevertheless, employing an excessively small kernel bandwidth may result in numerical instability, potentially causing program interruptions. Therefore, a predefined minimum kernel bandwidth ${\sigma }_{min}$ is necessary. The initial kernel bandwidth ${\sigma }_0$ is determined according to the nominal measurement noise. Subsequently, the adaptive kernel bandwidth is calculated as

$${\sigma }_{1,k}=\left\{\begin{array}{cc}{\sigma }_0+{ \beta }_1\times {MD}_k,& {\mu }_k\le {\chi }_{n,\alpha }^2\\ {\sigma }_0\times \mathrm{e}\mathrm{x}\mathrm{p}\left(-{\beta }_2\times {MD}_k\right),& {\mu }_{k }>{\chi }_{n,\alpha }^2\end{array}\right.$$

(45)

$${\sigma }_k=\max \left({\sigma }_{1,k},{\sigma }_{min}\right)$$

(46)

where ${\beta }_1$ and ${\beta }_2$ are scaling factors used to regulate the variations in the kernel bandwidth. These factors should be carefully selected based on specific environmental conditions. The parameter $n$ represents the degree of freedom, and the parameter $\alpha$ indicates the confidence level.

For the weight factor $\lambda$, we have formulated a real-time adjustment strategy to achieve a lower steady-state deviation:

$${\lambda }_k=\mathrm{m}\mathrm{a}\mathrm{x}\left(\mathrm{e}\mathrm{x}\mathrm{p}\left(-\rho \times {MD}_k\right),{\lambda }_0\right)$$

(47)

where $\rho$ represents a scale factor, and ${\lambda }_0$ is the nominal weight factor.

By incorporating the real-time-adjusted parameters into the MEEF-KF, we derive the AMEEF-KF, as summarized in Algorithm 2. To further facilitate the comprehension of the algorithm, Figure 1 depicts the fundamental procedure of the AMEEF-KF.

Algorithm 2: AMEEF-KF

Step 1: Initialize the state a priori estimate ${\widehat{x}}_{1|0}$ and the corresponding state prediction error covariance matrix $P_{1|0}$; choose a specified small positive value $\epsilon$; set a nominal weight factor ${\lambda }_0$; Step 2: Utilize Equations (14) and (15) to get ${\widehat{x}}_{k|k-1}$ and $P_{k|k-1}$, use Cholesky decomposition to get $S_{P_{k|k-1}}$ and $S_{R_k}$; calculate the $d_k$ and $W_k$; Step 3: Construct the error discrimination statistic ${\mu }_k$ by Equation (44), calculate the variable kernel bandwidth ${\sigma }_1$ by Equations (45) and (46), and determine the weight factor $\lambda$ by Equation (47); Step 4: Let $\tau =1$ and ${\widehat{x}}_{k,0}={\widehat{x}}_{k|k-1}$, where ${\widehat{x}}_{k,\tau }$ represents the estimated state at the fixed-point iteration $\tau$:

${\widehat{x}}_{k,\tau }={\widehat{x}}_{k|k-1}+{\tilde{K}}_k(z_k-{\widehat{z}}_{k|k-1})$

with:

${\tilde{K}}_k={\tilde{P}}_{k|k-1}{H}_k^T{(H_k{\tilde{P}}_{k|k-1}{H}_k^T+{\tilde{R}}_k)}^{-1}$ ${\tilde{P}}_{k|k-1}={\left(S_{P_{k|k-1}}^T\right)}^{-1}{\tilde{\Gamma }}_{xx,k}{S}_{P_{k|k-1}}^{-1}$ ${\tilde{P}}_{xy,k|k-1}={\left(S_{R_k}^T\right)}^{-1}{\tilde{\Gamma }}_{xy,k}{S}_{P_{k|k-1}}^{-1}$ ${\tilde{P}}_{yx,k|k-1}={\left(S_{P_{k|k-1}}^T\right)}^{-1}{\tilde{\Gamma }}_{yx,k}{S}_{R_k}^{-1}$ ${\tilde{R}}_k={\left(S_{R_k}^T\right)}^{-1}{\tilde{\Gamma }}_{yy,k}{S}_{R_k}^{-1}$ ${\tilde{e}}_{i,k}=d_{i,k}-w_k^T{\widehat{x}}_{k,\tau -1}$

Step 5: if ${\displaystyle \frac{‖{\widehat{x}}_{k,\tau }-{\widehat{x}}_{k,\tau -1}‖}{‖{\widehat{x}}_{k,\tau -1}‖}} \le \epsilon$ then go to Step 6. else $\tau =\tau +1$, and return to Step 4. Step 6: Update $k$ to $k+1$ and compute the posterior error covariance matrix by:

$P_k=\left[I-{\tilde{K}}_k{H}_k\right]P_{k|k-1}{\left[I-{\tilde{K}}_k{H}_k\right]}^T+{\tilde{K}}_k{R}_k{\tilde{K}}_k^T$

and return to Step 2.

The AMEEF-KF improves the accuracy of robust filtering estimation based on the MEEF by dynamically adjusting two critical parameters in real time according to the specific application scenario. Notably, the adjustment of the kernel bandwidth in the MEE term is omitted since an improperly selected kernel bandwidth, whether too small or too large, may result in instability in the MEEKF. Additionally, another reason is to prevent the non-convergence of estimation errors, which could arise due to the inherent translation invariance property of the MEE.

In terms of the computational complexity of the AMEEF-KF, according to [18], the MEEKF introduces an additional computational load due to the incorporation of error entropy functions, leading to higher computational complexity compared to the KF and slightly greater complexity than the MCCKF. However, from the perspective of the order of magnitude, the computational complexities of the MEEKF, MCCKF, and KF remain comparable. The computational complexity of the MEEF-KF can be expressed as $C=O\left(n^3\right)$, which is analyzed by counting floating-point operands, indicating that the above four filtering algorithms share the same order of magnitude. Since the AMEEF-KF does not incorporate any additional iterative steps, its computational complexity should remain close to that of the MEEF-KF. This also implies that the computational complexity of the proposed AMEEF-KF is of the same order of magnitude as the KF, making it suitable for real-time navigation applications.

4. Experiments and Analysis

In order to verify the effectiveness and reliability of the proposed AMEEF-KF for underwater SINS/USBL integration, comprehensive numerical simulations and offshore experiments were conducted.

4.1. Simulation Test

To validate the proposed algorithm presented in this article, a SINS/USBL integrated navigation simulation test was designed. Specifically, the trajectory of the UUV is depicted in Figure 2. The UUV’s initial position was 115.3° E, 14.8° N, with an initial velocity of 0 m/s. The entire simulation lasted for 1500 s. The red asterisk indicates the precise location of the USBL transponder.

By utilizing the spatial geometric relationships among various sensors and establishing appropriate coordinate systems, such as the inertial coordinate frame, Earth-centered rectangular coordinate frame, body-fixed coordinate frame, inverted USBL coordinate frame, and navigation frame, the state equation and measurement equation for the SINS/USBL integrated system were constructed. The specific form of the equations can be found in [36]. Here, the sampling frequency of the inertial measurement unit (IMU) was set to 100 Hz, while that of the USBL system was set to 1 Hz. The simulation parameters of the IMU and USBL are shown in

Table 1. The parameters of the IMU and USBL.

Sensors	Parameter	Value
IMU	Random noise in gyro	0.01°/h1/2
	Constant drift of gyro	0.05°/h
	Random noise in accelerometer	100 μg/h1/2
	Constant bias of accelerometer	0.1 mg
USBL	Constant drift of USBL	0.5% × Slant range
	Random noise of USBL	3 m
Initial error	Initial position error	9 m
	Initial velocity error	0.1 m/s
	Initial horizontal attitude error	30′′

.

To verify the effectiveness of the proposed method, the KF, MCCKF, MEEKF, and MEEF-KF were compared with the AMEEF-KF. Additionally, crucial parameters such as ${\sigma }_1$ and $\lambda$ are essential for enhancing filtering accuracy. Consequently, the parameters of the AMEEF-CKF undergo adaptive updates, as illustrated in Algorithm 2, whereas the MEEF-KF employs fixed nominal parameters. The specific parameter settings for each filtering method are listed in

Table 2. The free parameters of different filters.

KF	MCCKF	MEEKF	MEEF-KF			AMEEF-KF
-	σ	σ	λ	σ1	σ2	λ0	σ0	σmin
-	30	30	0.9	30	30	0.9	30	15

.

Three performance evaluation indices—the position error (PE), root mean square error (RMSE), and averaged root mean square error (ARMSE)—are utilized to assess the filtering accuracy in complex non-Gaussian noise environments. Among these, the PE evaluates positional deviations, RMSE quantifies the magnitude of errors, and ARMSE provides an averaged assessment over multiple simulations, thereby offering comprehensive insights into the filter’s performance in challenging noise environments.

The PE for the horizontal position can be expressed as

$$\Delta P_E={\widehat{P}}_E-P_E$$

(48)

$$\Delta P_N={\widehat{P}}_N-P_N$$

(49)

where ${\widehat{P}}_{·}$ and $P_{·}$ denote the desired and estimated positions in different directions, respectively.

The RMSE in the horizontal direction is defined as

$${\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}}_{\Delta P_E}=\sqrt{{\displaystyle \frac{1}{T}}\sum _{i=1}^T{\left({\widehat{P}}_{i,E}-P_{i,E}\right)}^2}$$

(50)

$${\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}}_{\Delta P_N}=\sqrt{{\displaystyle \frac{1}{T}}\sum _{i=1}^T{\left({\widehat{P}}_{i,N}-P_{i,N}\right)}^2}$$

(51)

where ${\widehat{P}}_{i,·}$ and $P_{i,·}$ represent the desired and estimated positions at epoch $i$, respectively, and T denotes the total duration of the UUV’s navigation.

The value of the ARMSE can be expressed as

$${\mathrm{A}\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}}_{\Delta P_E}=\sqrt{{\displaystyle \frac{1}{NT}}\sum _{j=1}^N\sum _{i=1}^T{\left({\widehat{P}}_{i,E}^j-P_{i,E}^j\right)}^2}$$

(52)

$${\mathrm{A}\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}}_{\Delta P_N}=\sqrt{{\displaystyle \frac{1}{NT}}\sum _{j=1}^N\sum _{i=1}^T{\left({\widehat{P}}_{i,N}^j-P_{i,N}^j\right)}^2}$$

(53)

where ${\widehat{P}}_{i,·}^j$ and $P_{i,·}^j$ represent the desired and estimated positions at epoch $i$ in the $j$-th Monte Carlo, respectively, and N denotes the number of Monte Carlo simulations. To further assess the reliability of the proposed method, a total of 50 independent Monte Carlo simulations were conducted. Two cases of the distribution of measurement noise were considered:

• Gaussian Noise

The measurement noise is assumed to have a Gaussian distribution, which is presented as follows:

$$v_k~N\left(0,R_m\right)$$

(54)

where $R_m$ is the nominal measurement noise covariance of the USBL. In this simulation, we set $R_m=diag(3^2,3^2,3^2) \left(m^2\right)$. Additionally, the constant drift noise of the USBL is characterized as slow time-varying noise.

The simulation PEs in the eastern and northern directions are presented in Figure 3 and Figure 4, respectively. To quantitatively compare the filter results, the ARMSEs of different filtering algorithms in the horizontal direction are shown in

Table 3. ARMSE of different filtering algorithms.

Filtering Algorithm	East ARMSE (m)	North ARMSE (m)
KF	3.7453	3.5440
MCCKF	3.7456	3.5448
MEEKF	11.2364	11.7799
MEEF-KF	3.7454	3.5441
AMEEF-KF	3.7454	3.5441

.

As depicted in Figure 3 and Figure 4, the MEEKF exhibits inferior performance compared to other algorithms because its superiority is generally observed only in complex non-Gaussian noise environments, such as multi-modal distributions. Furthermore, the performance of other filtering methods is comparable. As shown by Table 3, the traditional KF achieves the best estimate performance among all filtering methods. Notably, the proposed AMEEF-KF achieves performance comparable to that of the KF under Gaussian noise, primarily due to the adaptively adjusted parameter strategy, which makes it nearly equivalent to the KF.

2.

Bimodal Gaussian Mixture Noises with Outliers

Apart from the aforementioned Gaussian noise, the noise in measurements is additionally modeled as a bimodal Gaussian mixture distribution that incorporates outliers, which can be represented by the following:

$$v_k~0.48N\left({10}^{-4},{\left(3m\right)}^2\right)+0.04N\left(0,{\left(30m\right)}^2\right)+0.48N\left(-{10}^{-4},{\left(3m\right)}^2\right)$$

(55)

The simulated PEs in the eastern and northern directions are systematically illustrated in Figure 5 and Figure 6, respectively. Comparative analyses of the ARMSEs across distinct estimation algorithms for horizontal position estimation are comprehensively summarized in

Table 4. ARMSE of different filtering algorithms.

Filtering Algorithm	East ARMSE (m)	North ARMSE (m)
KF	20.6289	21.4342
MCCKF	11.6084	11.0833
MEEKF	11.2552	10.7322
MEEF-KF	10.6727	10.1434
AMEEF-KF	8.2994	7.7308

.

As illustrated in Figure 5 and Figure 6, the PE of the classical KF demonstrates significantly higher statistical dispersion relative to contemporary estimation techniques. This phenomenon fundamentally arises from the inherent limitations of the MMSE criterion in dynamic systems characterized by non-Gaussian noise distributions. The MCCKF and MEEKF have significantly enhanced navigation accuracy by leveraging their superior robustness in complex noise environments. The estimation accuracy of the MEEF-KF algorithm shows statistically significant superiority over the KF in two aspects. This improvement is predominantly due to its innovative integration of the MEEF criterion for robust covariance matrix estimation. Furthermore, the AMEEF-KF achieves enhanced positioning performance through an adaptive free-parameter optimization mechanism.

From the analysis of the ARMSE numerical results presented in Table 4, it can be observed that in the eastern direction, the AMEEF-KF achieves improvements of 59.77%, 28.51%, 26.26%, and 22.24% in accuracy compared to the KF, MCCKF, MEEKF, and MEEF-KF, respectively. In the northern direction, the ARMSE values are 63.93%, 30.25%, 27.97%, and 23.78% lower than those of the KF, MCCKF, MEEKF, and MEEF-KF, respectively. The simulation results confirm that the proposed filtering algorithm demonstrates superior performance relative to existing methods when processing measurements corrupted by mixed non-Gaussian noise.

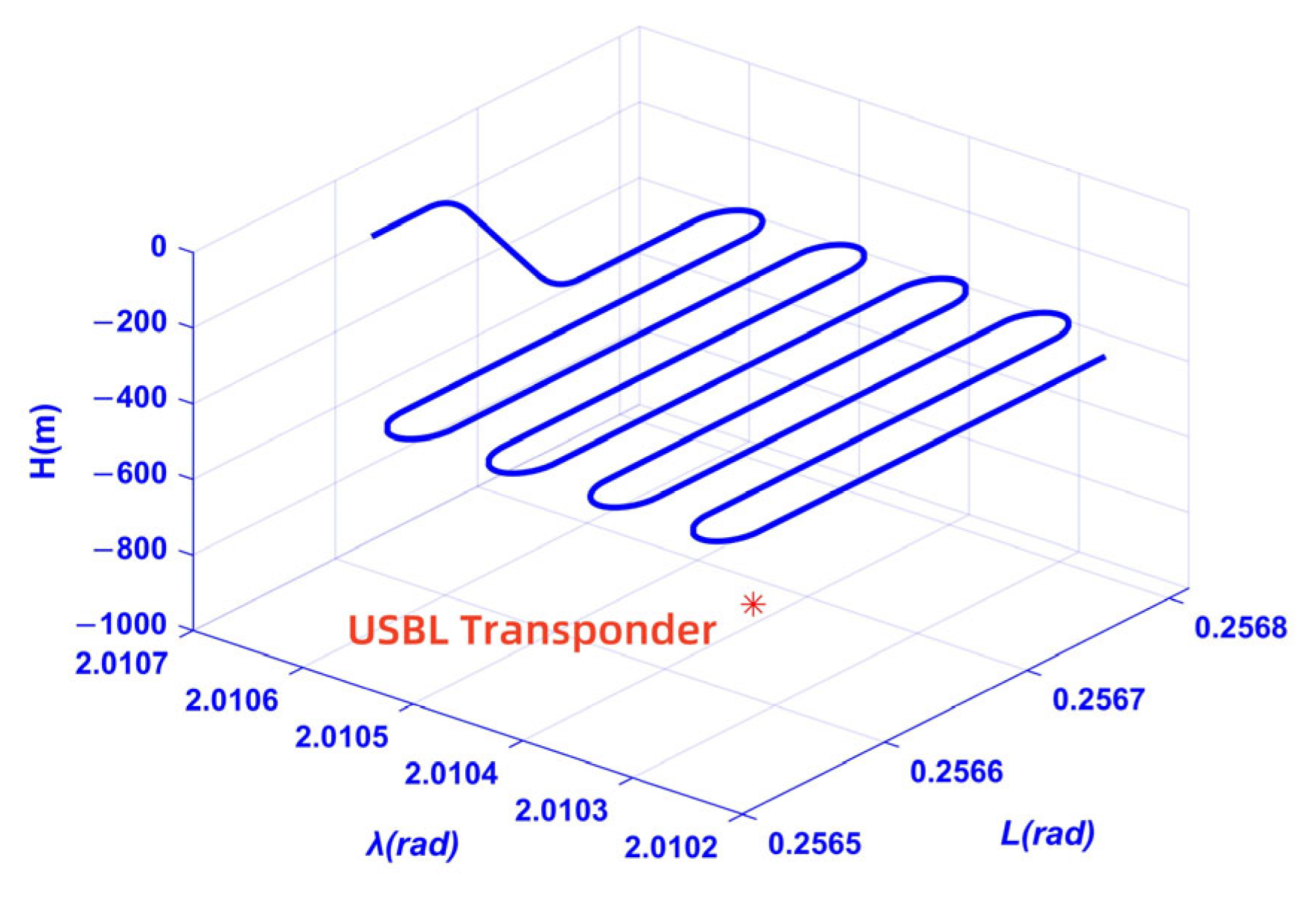
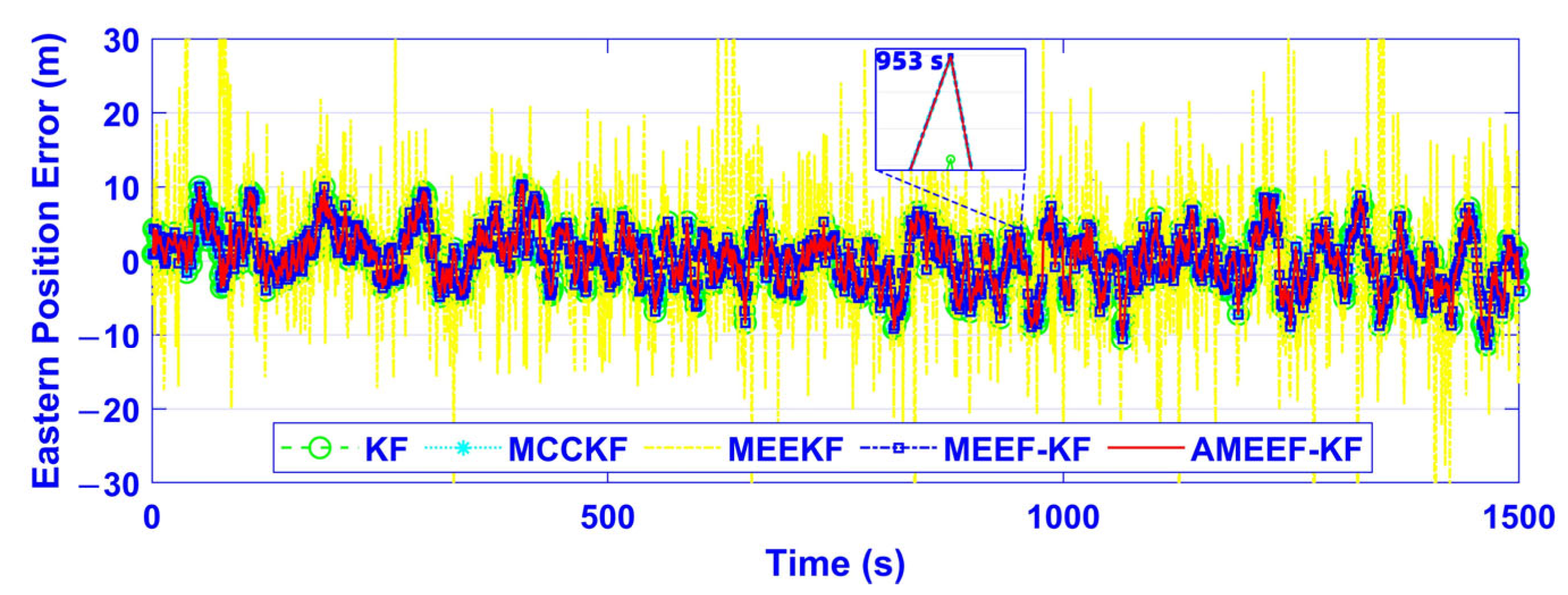
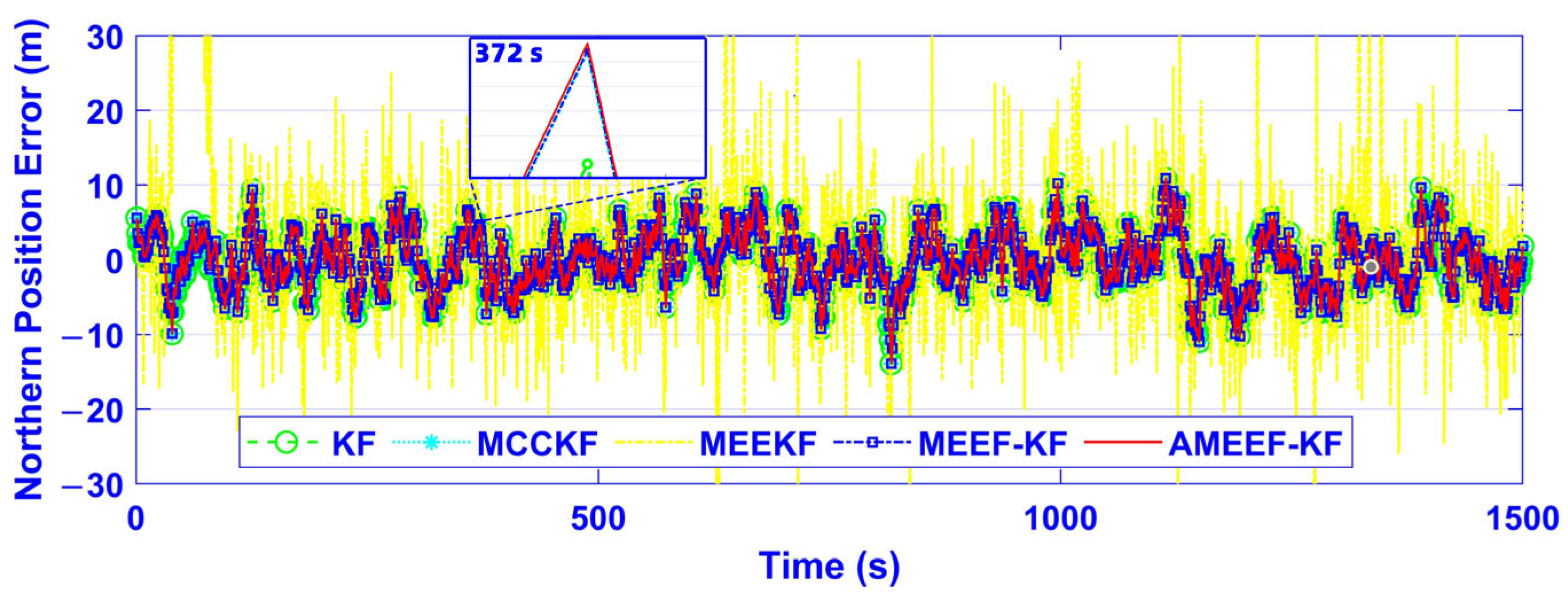
4.2. Experimental Verification

To rigorously validate the operational effectiveness of the AMEEF-KF algorithm, comprehensive field trials were conducted in the Jiaozhou Bay maritime environment. The architectural configuration of the multi-sensor integrated navigation platform is shown in Figure 7, while Figure 8 depicts the vessel’s trajectory under dynamic maritime conditions. The multi-sensor integrated navigation platform incorporates three principal subsystems:

(1)

An IMU providing 6-DOF motion perception with a sampling rate of 200 Hz;

(2)

A USBL acoustic positioning system (Kongsberg Maritime Inc., Kongsberg, Norway) comprising a surface transceiver and a submerged transponder;

(3)

A SPAN-ISA-100C GNSS/INS integrated system (NovAtel Inc., Calgary, AB, Canada) delivering RTK-level positioning accuracy.

Notably, the seabed-mounted USBL transponder was pre-deployed and attained centimeter-level absolute positioning accuracy, which was achieved through the GNSS–acoustic joint calibration method [37]. Furthermore, the IMU and high-precision SPAN-ISA-100C navigation system were collocated on the same mobile platform, and the tightly coupled GNSS/INS navigation solutions of SPAN-ISA-100C served as the trajectory reference standard.

In this experiment, the SINS and USBL both accomplished the procedure of alignment. The 1500 s circular track was intercepted, and the position of the transponder was 36.089° N, 120.254° E, and −18.240 m. The parameters of the IMU and USBL are listed in

Table 5. The parameters of the IMU and USBL.

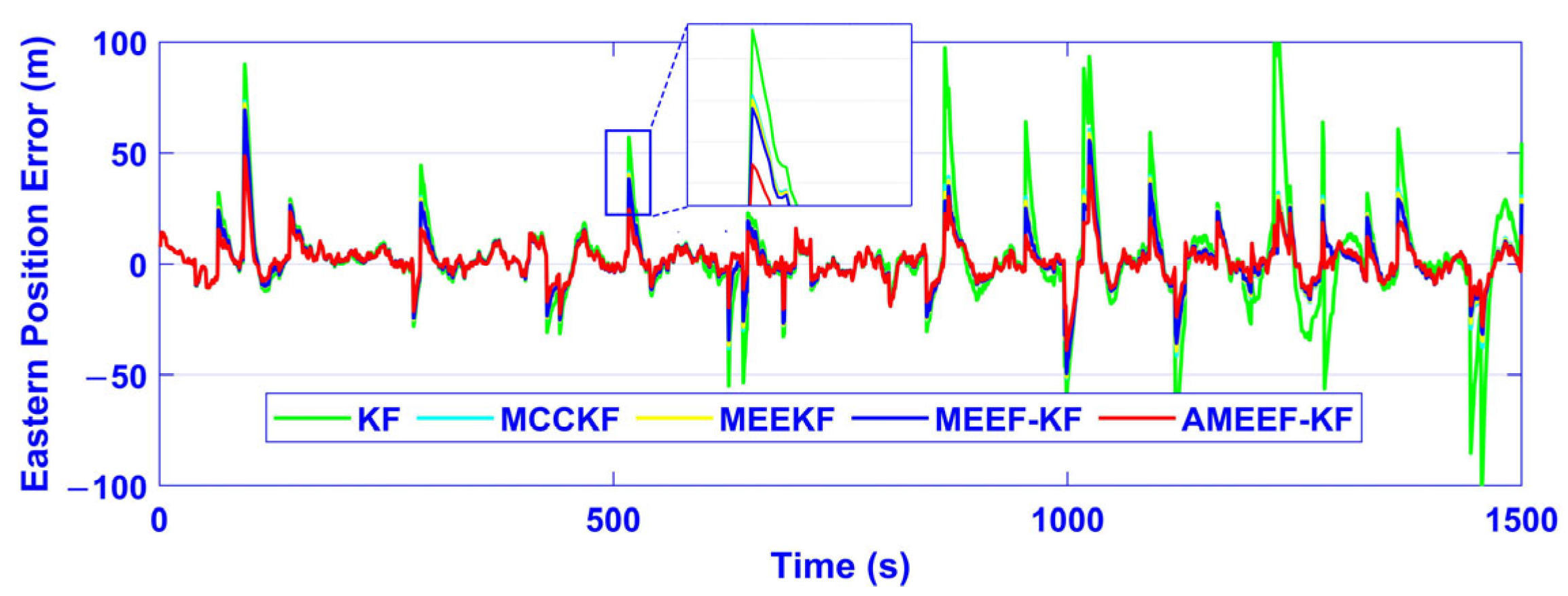
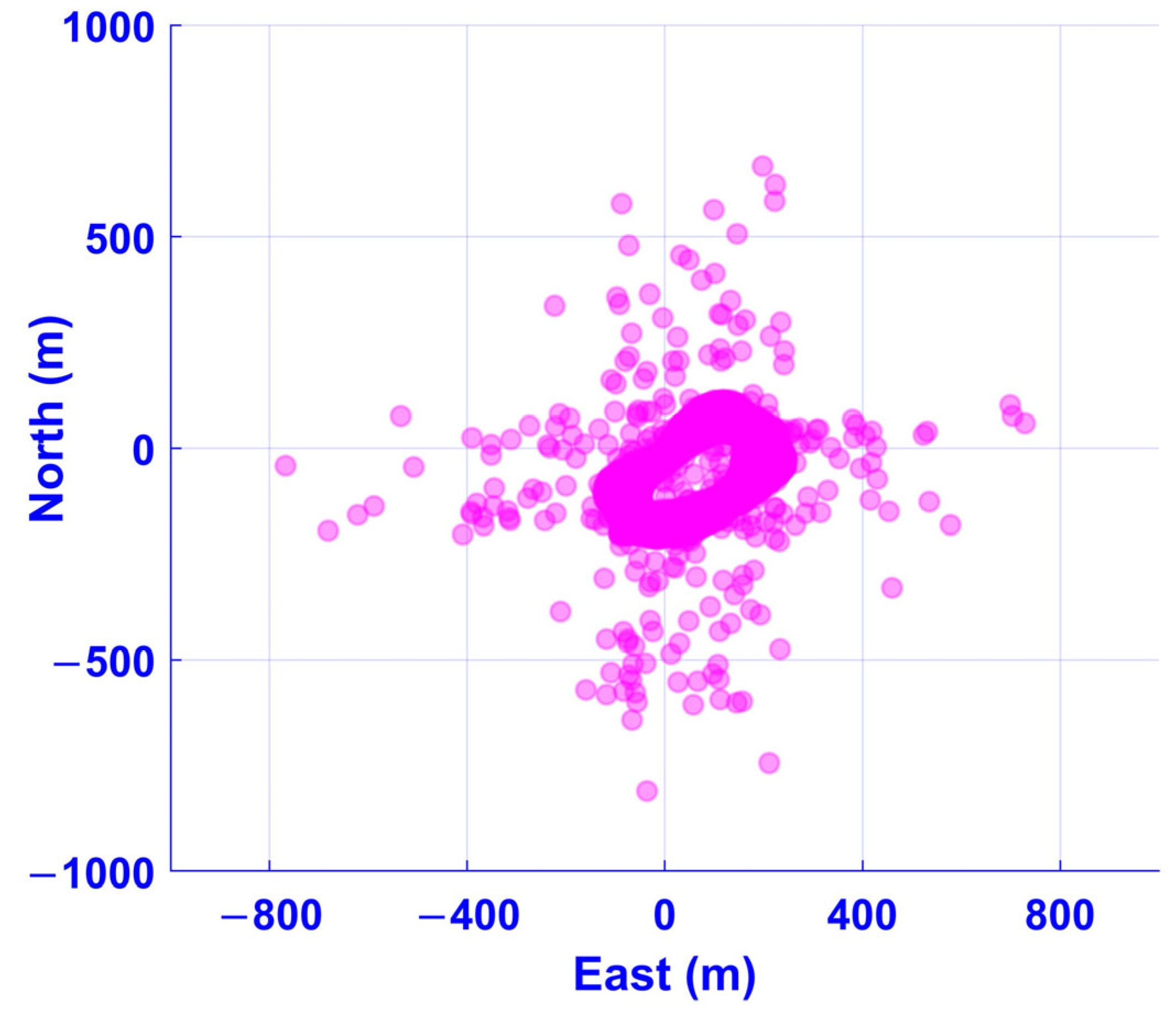
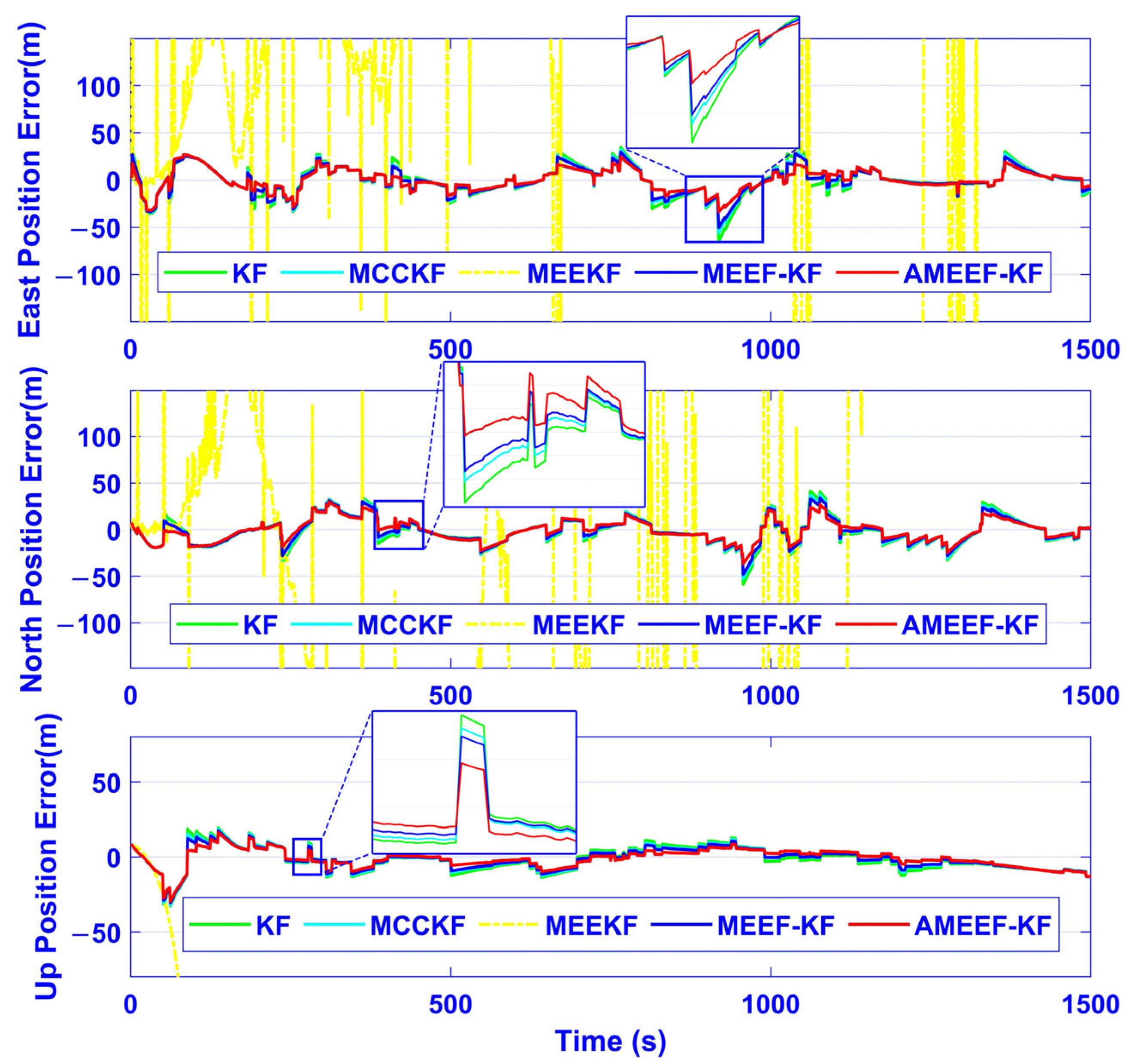
Sensors	Parameter	Value
IMU	Random noise in gyro	0.01°/h1/2
	Constant drift of gyro	0.05°/h
	Random noise in accelerometer	100 μg/h1/2
	Constant bias of accelerometer	0.1 mg
	Sampling frequency of IMU	200 Hz
USBL (Kongsberg μPAP)	Constant drift of USBL	0.5% × Slant range
	Random noise of USBL	3 m
	Sampling frequency of USBL	1 Hz
Initial error	Initial position error	9 m
	Initial velocity error	0.1 m/s
	Initial horizontal attitude error	30″
	Initial heading error	30′

. Furthermore, artificial outliers were intentionally introduced into the observations to facilitate a more effective comparison of the performance of the proposed AMEEF-KF against the KF, MCCKF, MEEKF, and MEEF-KF. The output horizontal USBL position data are shown in Figure 9. The kernel bandwidths of the MCCKF and MEEKF were set to 10 and 30, respectively. Additionally, the parameters σ₁ and σ₂ for the MEEF-KF were also configured as 10 and 30, respectively. The weighted factor λ of the MEEF-KF was set to 0.9.

The comparison of the PE is presented in Figure 10, while

Table 6. RMSE of position.

Filter Schemes	East RMSE (m)	North RMSE (m)	Up RMSE (m)
KF	13.3726	13.7601	10.4809
MCCKF	11.8538	12.8465	10.2193
MEEKF	1.6855 × 104	1.3108 × 104	5.9684 × 104
MEEF-KF	11.0102	11.8840	9.9075
AMEEF-KF	8.9214	10.4060	9.5613

provides the RMSE values of the PE for a quantitative evaluation of different filtering algorithms. As can be clearly observed from Figure 10, the proposed AMEEF-KF demonstrates superior performance compared to the four other filtering algorithms. The traditional KF exhibits significant fluctuations due to its sensitivity to non-Gaussian noise. The MEEKF fails to achieve satisfactory convergence as a result of inherent numerical instability issues. As shown in Table 6, the RMSE value of the east PE for the AMEEF-KF is 8.9214 m, representing reductions of 33.29%, 24.74%, and 18.97% compared to the KF, MCCKF, and MEEF-KF, respectively. For the north direction, the accuracy of the AMEEF-KF improves by 24.38%, 19.00%, and 14.20% relative to the KF, MCCKF, and MEEF-KF, respectively. In the up direction, the RMSE value for the AMEEF-KF is 9.5613 m, which reflects reductions of 8.77%, 6.43%, and 3.49% compared to the KF, MCCKF, and MEEF-KF, respectively.

With the results of the simulation and offshore experiment, it can be concluded that the proposed AMEEF-KF method performs better than other algorithms in non-Gaussian environments with outliers.

5. Discussion

Presently, the operation of UUVs in shallow-sea scenarios faces significant challenges in terms of navigation accuracy. The noise influencing navigation accuracy is typically simply modeled as symmetric heavy-tailed non-Gaussian noise. Nevertheless, the noise in practical application environments cannot fully comply with this modeling. From a more comprehensive perspective, it is essential to develop an adaptive Kalman filter to address the challenges posed by complex non-Gaussian noise in the navigation mathematical model.

Aiming at the complex non-Gaussian noise characteristics caused by USBL acoustic observations in complex underwater environments, an adaptive Kalman filter method is proposed to enhance the robustness against measurement outliers. Notably, the proposed approach is theoretically capable of mitigating abnormal process noise. Therefore, when outliers occur in the IMU data of the integrated navigation system, their effects can be effectively suppressed by the proposed algorithm. The simulation and offshore experimental results demonstrate the superiority of the proposed method over existing filters in terms of positioning estimation accuracy under complex non-Gaussian noise conditions. However, the proposed algorithm still exhibits certain limitations owing to its mathematical modeling based on error states. Its performance may degrade under strongly nonlinear conditions in marine environments. Furthermore, the theoretical implications of some free parameters warrant deeper investigation.

As a direction for future endeavors, the proposed algorithm holds the potential to be expanded into a broader spectrum of nonlinear Kalman filters, such as the unscented Kalman filter and Cubature Kalman filter, thereby finding application in an even wider array of sophisticated underwater integrated navigation systems.