Performance Study of Spark-Ignited Methanol–Hydrogen Engine by Using a Fractal Turbulent Combustion Model Coupled with Chemical Reaction Kinetics
Abstract
1. Introduction
2. Materials and Methods
2.1. Simulation Model
2.1.1. Fractal Turbulent Combustion Model
2.1.2. Early Flame Development Model
2.1.3. Combustion Completion Model
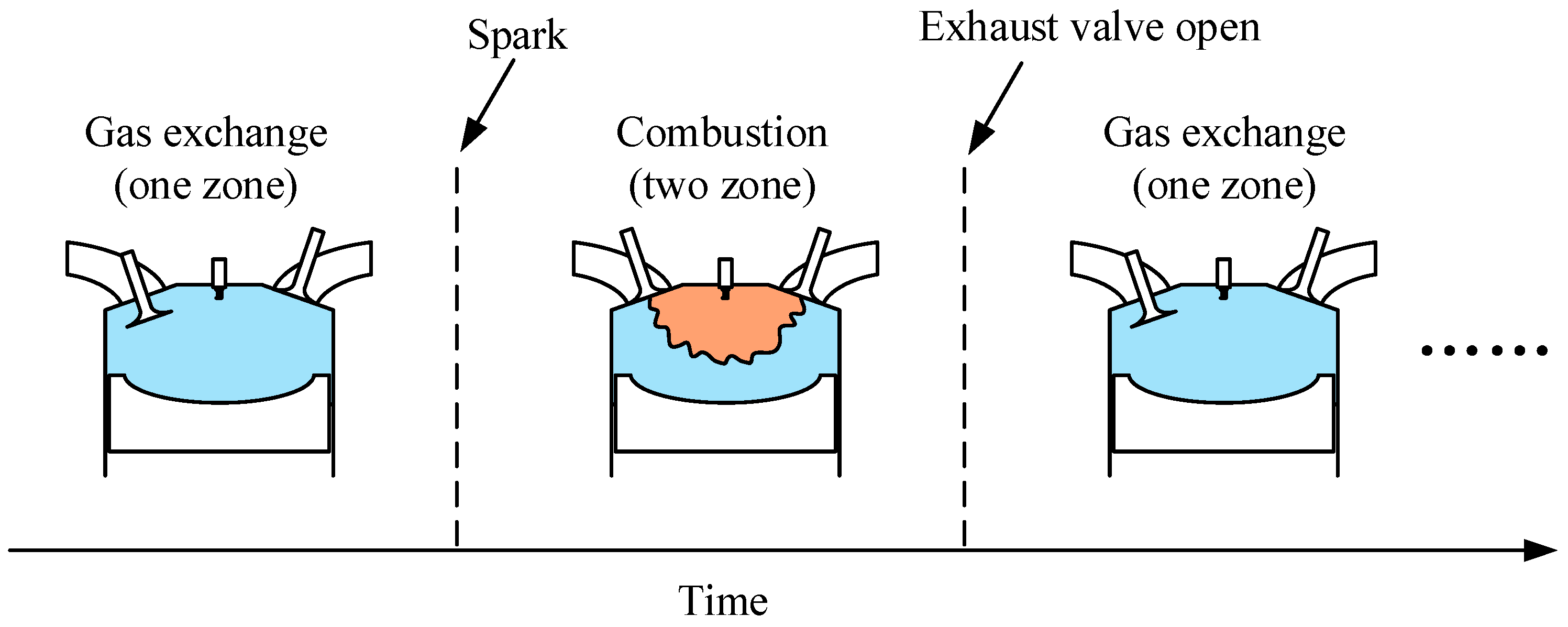
2.1.4. Model Framework
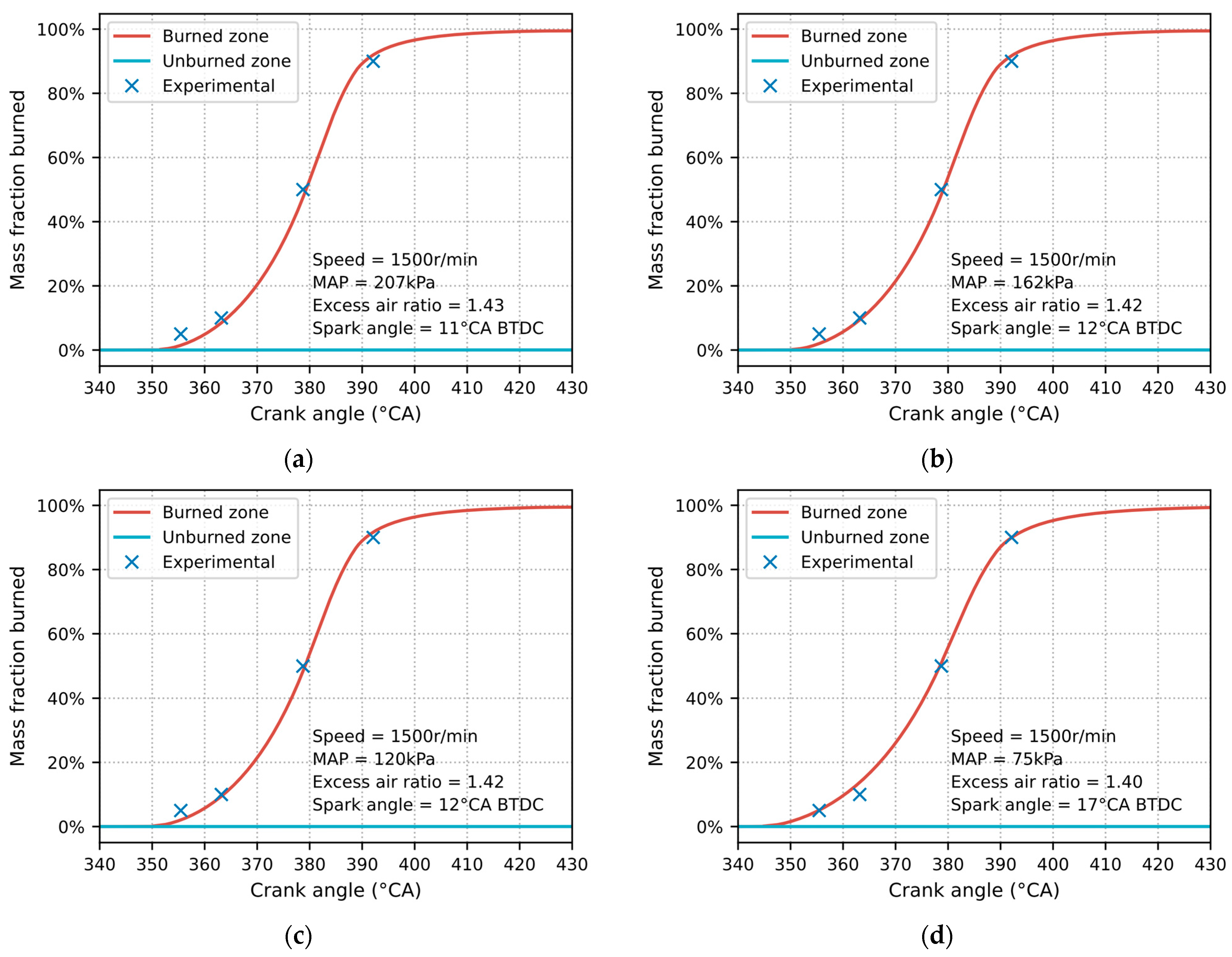
2.2. Model Validation
2.3. Setup of the Hydrogen–Methanol Simulation Model
3. Results and Discussion
3.1. Engine Performance Under High Operation Load
3.2. Engine Performance Under Low Operation Load
3.3. Knocking Limit of HER Under Different MAPs
4. Conclusions
- (1)
- The simulation model was validated using experimental data from a spark-ignited methanol engine. Under four operating conditions (100%, 75%, 50%, and 25% load), the root mean square errors (RMSE) for the mass fraction burned were 2.50%, 1.93%, 1.90%, and 1.94%, respectively, while the relative errors for Indicated Mean Effective Pressure (IMEP) were 0.18%, 0%, 0.37%, and 0.36%, respectively, demonstrating the model’s high prediction accuracy.
- (2)
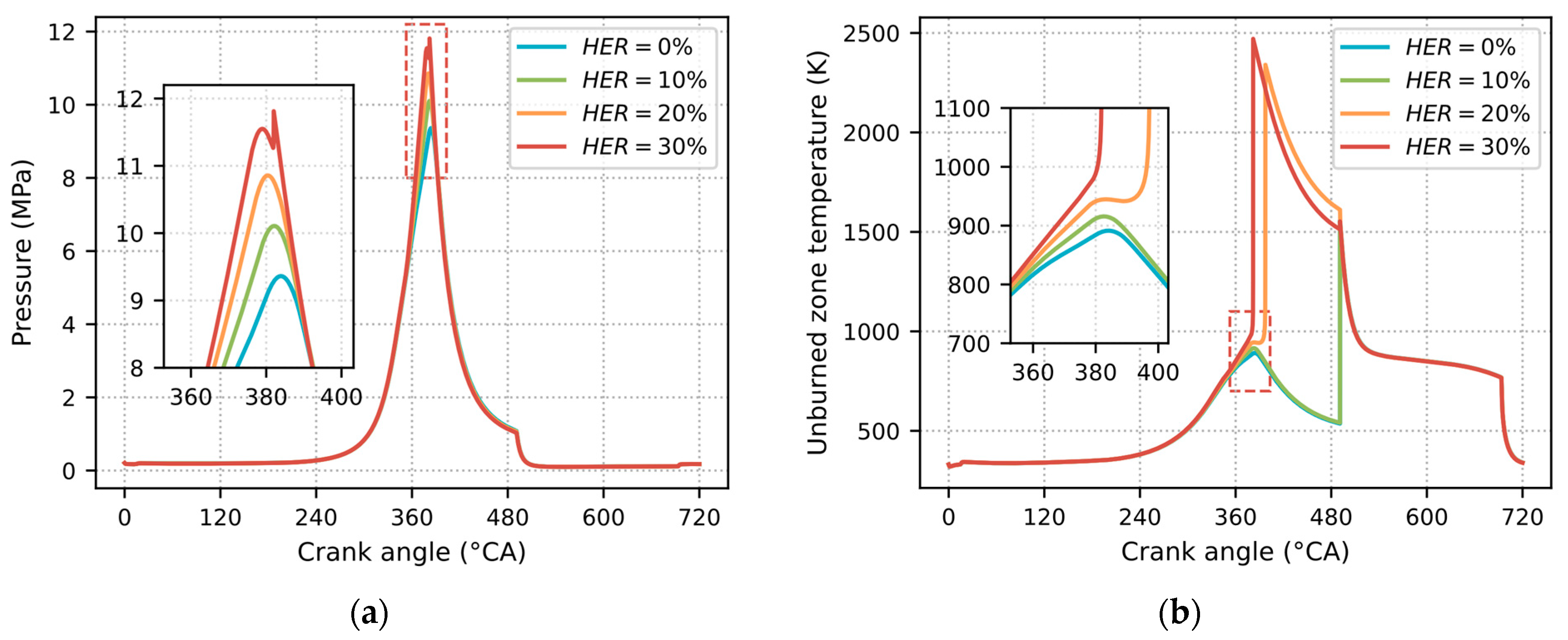
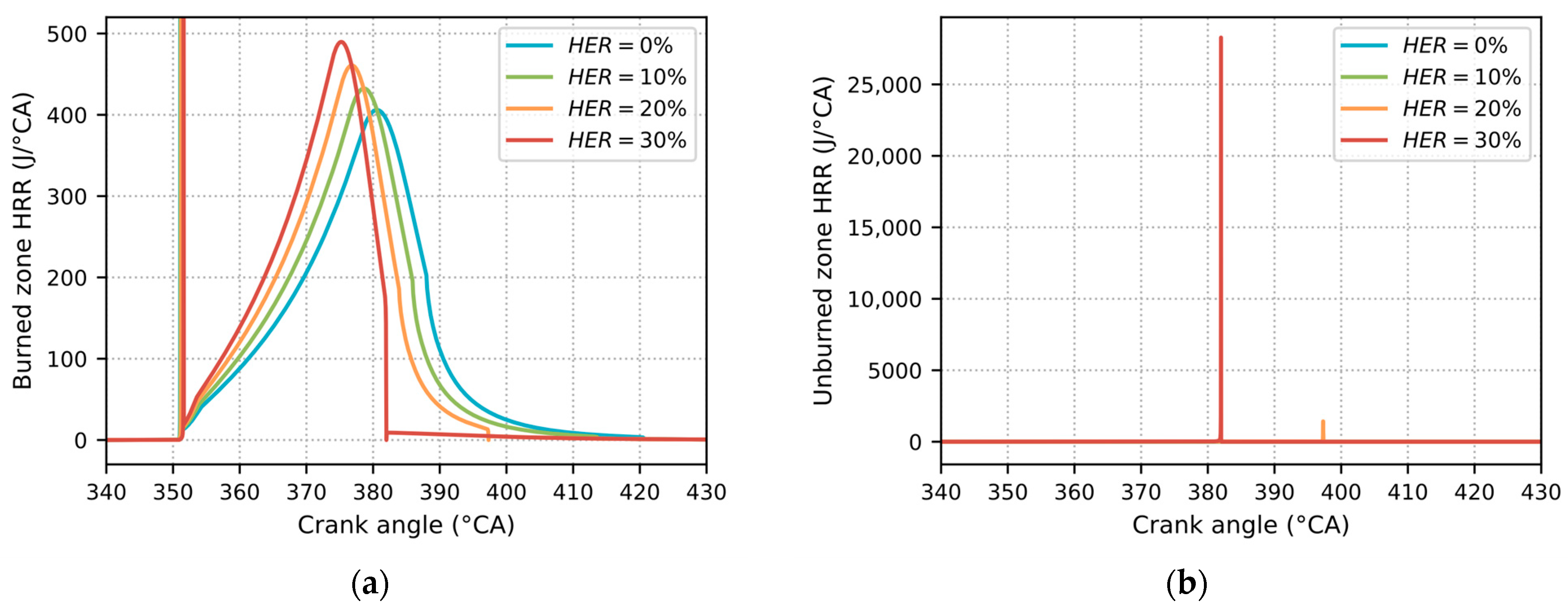
- Under high-load conditions, as HER increased from 0% to 30%, the peak in-cylinder pressure rose from 9.3 MPa to 11.8 MPa, with the peak pressure angle advancing from 384 °CA to 379 °CA, and the peak heat release rate escalated from 406 J/°CA to 490 J/°CA. The heat release peak angle shifted forward from 381 °CA to 375 °CA, with a shorter duration and more concentrated heat release.
- (3)
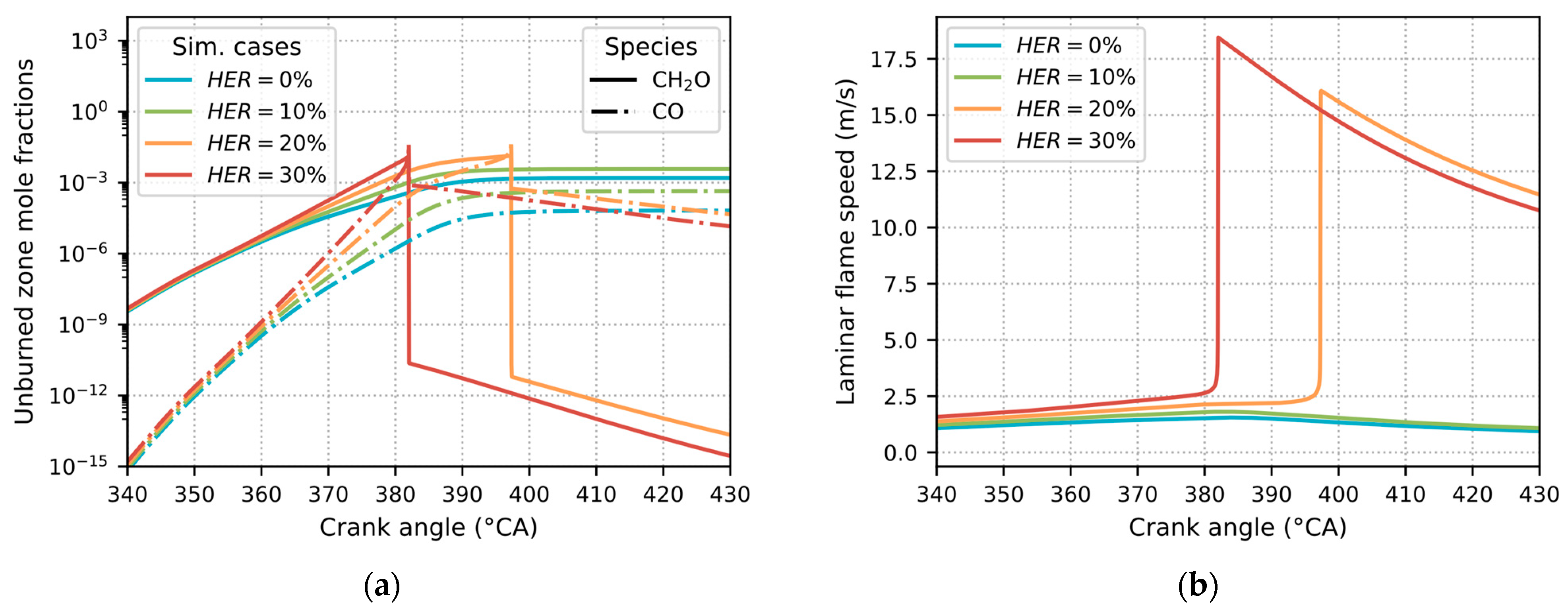
- At high load, spontaneous ignition occurred in the unburned zone at HER values of 20% and 30%, indicating the onset of knocking. The unburned zone temperature reached approximately 2400 K during these events. Concurrently, elevated formaldehyde () levels—an intermediate of methanol combustion—coincided with rapid heat release in the unburned zone and a laminar flame speed of approximately 16 m/s, suggesting rapid compression of the unburned zone by the flame front. Analysis revealed that this rapid flame front compression and temperature surge in the unburned zone triggered spontaneous ignition, resulting in knocking.
- (4)
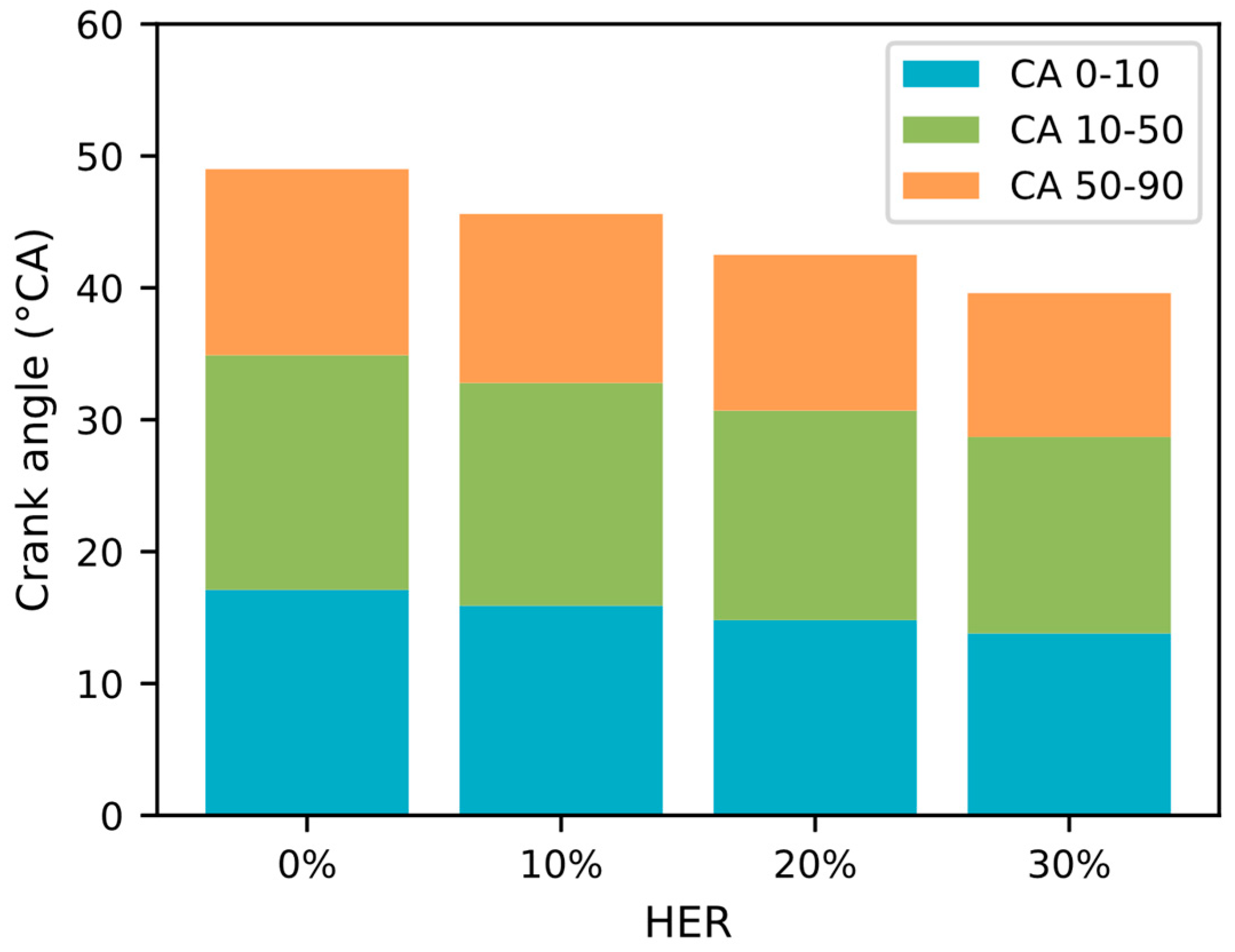
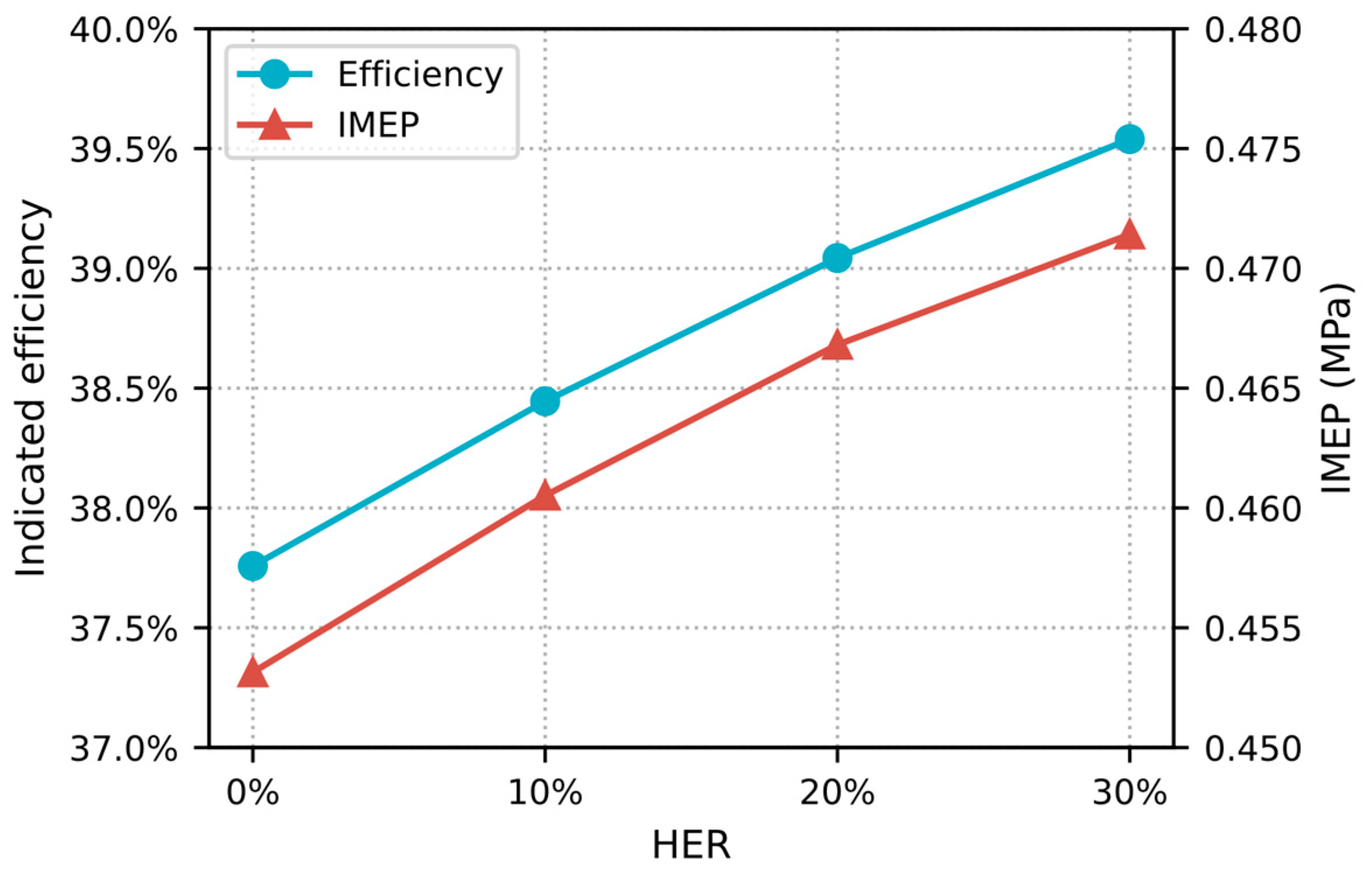
- Under low-load conditions, as HER rose from 0% to 30%, peak pressure increased, heat release became more concentrated, and post-combustion mole fractions of and decreased. Additionally, IMEP rose from 0.453 MPa to 0.471 MPa. This indicated that thermal efficiency improved from 37.76% to 39.54%, underscoring that higher HER enhanced power performance.
- (5)
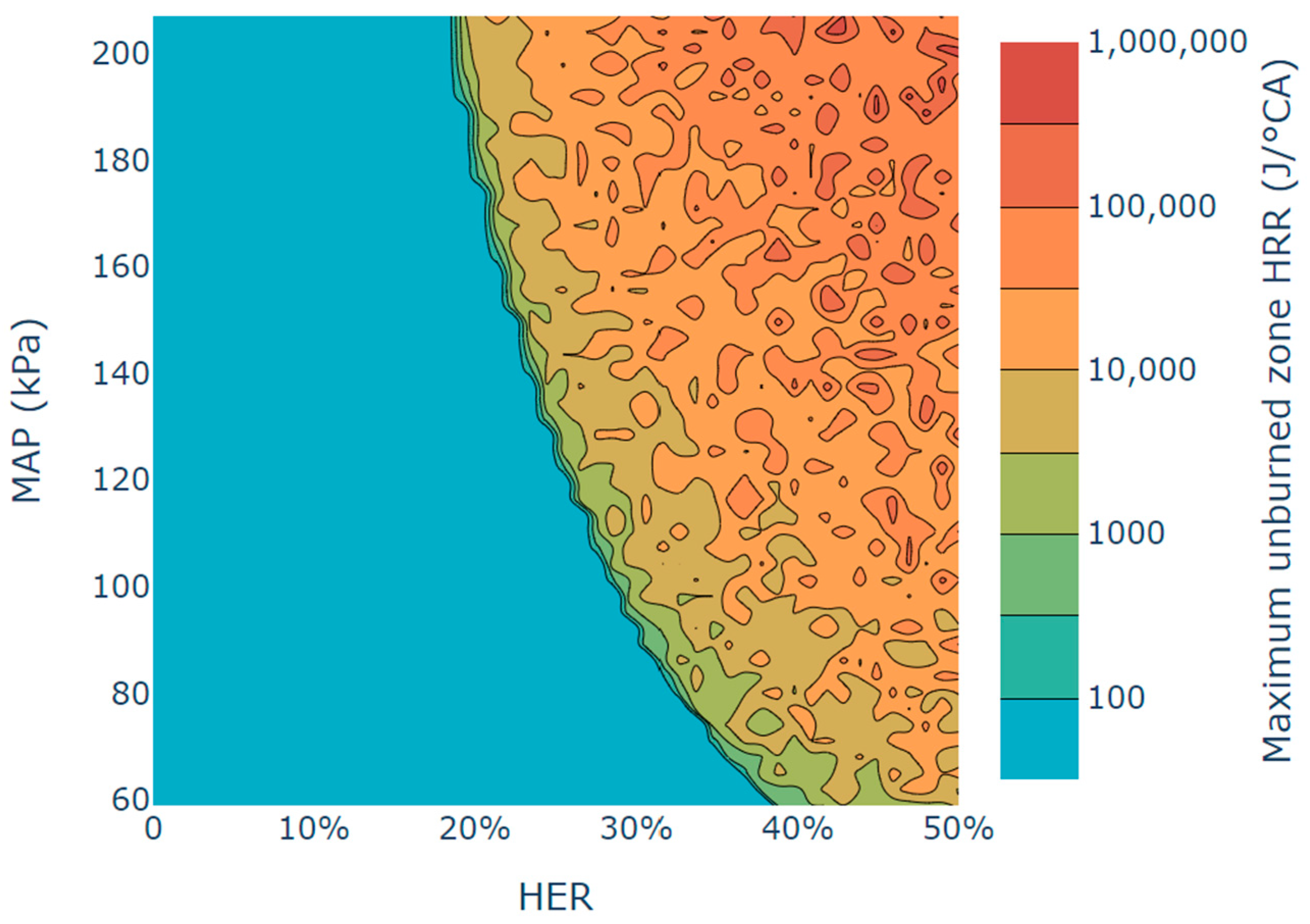
- A total of 2500 operating conditions, spanning MAP from 59 to 207 kPa and HER from 0% to 50%, were simulated. The maximum heat release rate in the unburned zone served as the criterion for identifying knocking, enabling delineation of the unburned zone limit line. Higher MAP increased knocking propensity, reducing the maximum hydrogen energy replacement rate from 40% at MAP = 59 kPa to 20% at MAP = 207 kPa; within the knocking zone, elevated MAP and HER intensified knocking.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ATDC | After Top Dead Center |
| BTDC | Before Top Dead Center |
| CA | Crank Angle |
| CFD | Computational Fluid Dynamics |
| CII | Carbon Intensity Index |
| EEXI | Existing Energy Efficiency Index |
| EGR | Exhaust Gas Recirculation |
| GHG | Greenhouse Gas |
| HER | Hydrogen Energy Rate |
| HRR | Heat Release Rate |
| IMEP | Indicated Mean Effective Pressure |
| IMO | International Maritime Organization |
| KI | Knock Intensity |
| LHV | Lower Heating Value |
| MAP | Manifold Absolute Pressure |
| MEPC | Maritime Environment Protection Committee |
| MFB | Mass Fraction Burned |
| PFI | Port Fuel Injection |
| RMSE | Root Mean Squared Error |
| SEEMP | Ship Energy Efficiency Management Plan |
| SI | Spark Ignition |
Appendix A
Appendix A.1
- (a)
- Laminar flame area

- (b)
- Stretched laminar flame speed
- (c)
- Flame wrinkling scale ratio
- (d)
- Fractal dimension
Appendix A.2
References
- Miola, A.; Ciuffo, B. Estimating air emissions from ships: Meta-analysis of modelling approaches and available data sources. Atmos. Environ. 2011, 45, 2242–2251. [Google Scholar] [CrossRef]
- Balcombe, P.; Brierley, J.; Lewis, C.; Skatvedt, L.; Speirs, J.; Hawkes, A.; Staffell, I. How to decarbonise international shipping: Options for fuels, technologies and policies. Energy Convers. Manag. 2019, 182, 72–88. [Google Scholar] [CrossRef]
- IMO. Greenhouse Gas Study 2014, Executive Summary and Final Report; International Maritime Organization: London, UK, 2014; p. 480. [Google Scholar]
- IMO. Adoption of the initial IMO strategy on reduction of GHG emissions from ships and existing IMO activity related to reducing GHG emissions in the shipping sector. In Note by the International Maritime Organization to the UNFCCC Talanoa Dialogue; International Maritime Organization: London, UK, 2018. [Google Scholar]
- IMO. 2023 IMO strategy on reduction of GHG emissions from ships. In Resolution MEPC. 377 (80); International Maritime Organization: London, UK, 2023. [Google Scholar]
- Psaraftis, H.N. Shipping decarbonization in the aftermath of MEPC 76. Clean. Logist. Supply Chain 2021, 1, 100008. [Google Scholar] [CrossRef]
- Čampara, L.; Hasanspahić, N.; Vujičić, S. Overview of MARPOL ANNEX VI regulations for prevention of air pollution from marine diesel engines. SHS Web Conf. 2018, 58, 01004. [Google Scholar] [CrossRef]
- Zhou, F.; Yu, J.; Wu, C.; Fu, J.; Liu, J.; Duan, X. The application prospect and challenge of the alternative methanol fuel in the internal combustion engine. Sci. Total Environ. 2024, 913, 169708. [Google Scholar] [CrossRef]
- Reddy, V.J.; Hariram, N.; Maity, R.; Ghazali, M.F.; Kumarasamy, S. Sustainable e-fuels: Green hydrogen, methanol and ammonia for carbon-neutral transportation. World Electr. Veh. J. 2023, 14, 349. [Google Scholar] [CrossRef]
- Kumarasamy, S.; Selvanathan, S.P.; Ghazali, M.F. From offshore renewable energy to green hydrogen: Addressing critical questions. Clean Energy 2025, 9, 108–122. [Google Scholar] [CrossRef]
- Reddy, V.J.; Hariram, N.; Maity, R.; Ghazali, M.F.; Kumarasamy, S. Sustainable vehicles for decarbonizing the transport sector: A comparison of biofuel, electric, fuel cell and solar-powered vehicles. World Electr. Veh. J. 2024, 15, 93. [Google Scholar] [CrossRef]
- Celik, M.B.; Özdalyan, B.; Alkan, F. The use of pure methanol as fuel at high compression ratio in a single cylinder gasoline engine. Fuel 2011, 90, 1591–1598. [Google Scholar] [CrossRef]
- Balki, M.K.; Sayin, C.; Canakci, M. The effect of different alcohol fuels on the performance, emission and combustion characteristics of a gasoline engine. Fuel 2014, 115, 901–906. [Google Scholar] [CrossRef]
- Zhang, Y.; Mu, Z.; Wei, Y.; Zhu, Z.; Du, R.; Liu, S. Comprehensive study on unregulated emissions of heavy-duty SI pure methanol engine with EGR. Fuel 2022, 320, 123974. [Google Scholar] [CrossRef]
- Xu, C.; Zhuang, Y.; Qian, Y.; Cho, H. Effect on the performance and emissions of methanol/diesel dual-fuel engine with different methanol injection positions. Fuel 2022, 307, 121868. [Google Scholar] [CrossRef]
- Güdden, A.; Pischinger, S.; Geiger, J.; Heuser, B.; Müther, M. An experimental study on methanol as a fuel in large bore high speed engine applications–Port fuel injected spark ignited combustion. Fuel 2021, 303, 121292. [Google Scholar] [CrossRef]
- MEPC. Amendments to the Annex of the Protocol of 1997 to Amend the International Convention for the Prevention of Pollution From Ships, 1973, as Modified by the Protocol of 1978 Relating Thereto. Amendments to MARPOL Annex VI. In RESOLUTION MEPC.328(76); Marine Environment Protection Committee (MEPC): London, UK, 2011. [Google Scholar]
- Gong, C.; Peng, L.; Chen, Y.; Liu, J.; Liu, F.; Han, Y. Computational study of intake temperature effects on mixture formation, combustion and unregulated emissions of a DISI methanol engine during cold start. Fuel 2018, 234, 1269–1277. [Google Scholar] [CrossRef]
- Gong, C.; Liu, J.; Peng, L.; Liu, F. Numerical study of effect of injection and ignition timings on combustion and unregulated emissions of DISI methanol engine during cold start. Renew. Energy 2017, 112, 457–465. [Google Scholar] [CrossRef]
- Liu, J.; Gong, C.; Peng, L.; Liu, F.; Yu, X.; Li, Y. Numerical study of formaldehyde and unburned methanol emissions of direct injection spark ignition methanol engine under cold start and steady state operating conditions. Fuel 2017, 202, 405–413. [Google Scholar] [CrossRef]
- Yuan, B.; Zhao, H.; Huang, Y.; Zhang, M.; Song, Z.; Shen, Y.; Cheng, X.; Wang, Z. Investigation on cold start issues of methanol engines and its improvement from the perspective of droplet evaporation. Fuel 2025, 380, 133249. [Google Scholar] [CrossRef]
- Purayil, S.; Hamdan, M.O.; Al-Omari, S.; Selim, M.; Elnajjar, E. Influence of ethanol–gasoline–hydrogen and methanol–gasoline–hydrogen blends on the performance and hydrogen knock limit of a lean-burn spark ignition engine. Fuel 2024, 377, 132825. [Google Scholar] [CrossRef]
- Duan, X.; Chu, X.; Wang, R.; Chen, Z.; Zhou, F.; Abdellatief, T.M. The performance and emissions characteristics of the gasoline spark ignition engine fuelled with green and renewable methanol and hydrogen. Renew. Energy 2025, 240, 122184. [Google Scholar] [CrossRef]
- Gong, C.; Li, D.; Liu, J.; Liu, F. Numerical evaluation of ignition timing influences on performance of a stratified-charge H2/methanol dual-injection automobile engine under lean-burn condition. Energy 2024, 290, 130209. [Google Scholar] [CrossRef]
- Gong, C.; Li, Z.; Huang, K.; Liu, F. Research on the performance of a hydrogen/methanol dual-injection assisted spark-ignition engine using late-injection strategy for methanol. Fuel 2020, 260, 116403. [Google Scholar] [CrossRef]
- Prasad, B.N.; Pandey, J.K.; Kumar, G. Effect of hydrogen enrichment on performance, combustion, and emission of a methanol fueled SI engine. Int. J. Hydrogen Energy 2021, 46, 25294–25307. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, Y.; Li, C.; Li, Q.; Liu, H.; Huang, Z. Investigation on a combined system with methanol on-board hydrogen production and internal combustion engine. Fuel 2024, 375, 132586. [Google Scholar] [CrossRef]
- Abbas, A.H.M.; Cheralathan, K.K.; Porpatham, E.; Arumugam, S.K. Hydrogen generation using methanol steam reforming–catalysts, reactors, and thermo-chemical recuperation. Renew. Sustain. Energy Rev. 2024, 191, 114147. [Google Scholar] [CrossRef]
- Tang, Y.; Long, W.; Wang, Y.; Xiao, G.; Wang, Y.; Lu, M. Multi-objective optimization of methanol reforming reactor performance based on response surface methodology and multi-objective particle swarm optimization coupling algorithm for on-line hydrogen production. Energy Convers. Manag. 2024, 307, 118377. [Google Scholar] [CrossRef]
- Wang, Y.; Long, W.; Tian, H.; Dong, P.; Lu, M.; Tang, Y.; Wang, Y.; Zhang, W. Research on oxidation mechanism of hydrogen/syngas-methanol and its application on engine performance prediction. Fuel 2024, 365, 131211. [Google Scholar] [CrossRef]
- Ji, C.; Yang, J.; Liu, X.; Zhang, B.; Wang, S.; Gao, B. A quasi-dimensional model for combustion performance prediction of an SI hydrogen-enriched methanol engine. Int. J. Hydrogen Energy 2016, 41, 17676–17686. [Google Scholar] [CrossRef]
- Liu, X.; Ji, C.; Gao, B.; Wang, S.; Liang, C.; Yang, J. A laminar flame speed correlation of hydrogen–methanol blends valid at engine-like conditions. Int. J. Hydrogen Energy 2013, 38, 15500–15509. [Google Scholar] [CrossRef]
- Matthews, R.D.; Chin, Y.-W. A fractal-based SI engine model: Comparisons of predictions with experimental data. SAE Trans. 1991, 100, 99–117. [Google Scholar]
- Santavicca, D.A.; Liou, D.; North, G.L. A fractal model of turbulent flame kernel growth. SAE Trans. 1990, 99, 90–98. [Google Scholar]
- Bozza, F.; Gimelli, A.; Merola, S.S.; Vaglieco, B. Validation of a fractal combustion model through flame imaging. SAE Trans. 2005, 114, 973–987. [Google Scholar]
- Li, J.; Zhao, Z.; Kazakov, A.; Chaos, M.; Dryer, F.L.; Scire Jr, J.J. A comprehensive kinetic mechanism for CO, CH2O, and CH3OH combustion. Int. J. Chem. Kinet. 2007, 39, 109–136. [Google Scholar] [CrossRef]
- Gouldin, F.C. An application of fractals to modeling premixed turbulent flames. Combust. Flame 1987, 68, 249–266. [Google Scholar] [CrossRef]
- Verhelst, S.; Sheppard, C. Multi-zone thermodynamic modelling of spark-ignition engine combustion—An overview. Energy Convers. Manag. 2009, 50, 1326–1335. [Google Scholar] [CrossRef]
- Saliba, A.T.; Agius, E.; Scerri, K.; Farrugia, M. Simulation of operation and control of LNG and diesel dual fuel engine for marine application. In Proceedings of the 7th Offshore Energy & Storage Symposium (OSES 2023), St. Julian’s, Malta, 12–14 July 2023; pp. 349–356. [Google Scholar]
- Zhen, X.; Wang, Y.; Xu, S.; Zhu, Y.; Tao, C.; Xu, T.; Song, M. The engine knock analysis—An overview. Appl. Energy 2012, 92, 628–636. [Google Scholar] [CrossRef]
- Chung, S.; Law, C. An integral analysis of the structure and propagation of stretched premixed flames. Combust. Flame 1988, 72, 325–336. [Google Scholar] [CrossRef]
- Chung, S.H.; Law, C. An invariant derivation of flame stretch. Combust. Flame 1984, 55, 123–125. [Google Scholar] [CrossRef]
- Law, C. Dynamics of stretched flames. In Symposium (International) on Combustion; Elsevier: Amsterdam, The Netherlands, 1989; pp. 1381–1402. [Google Scholar]
- Wu, C.; Roberts, C.; Matthews, R.D.; Hall, M. Effects of engine speed on combustion in SI engines: Comparisons of predictions of a fractal burning model with experimental data. SAE Trans. 1993, 102, 2277–2291. [Google Scholar]





| Model | Sub-Model | Method or Proposed Scholar |
|---|---|---|
| Fractal turbulent combustion model | Flame front geometry | Ideal cylinder |
| Laminar flame speed | Methanol–hydrogen flame speed [32] | |
| Flame wrinkling scale | Proposed by Matthews [33] | |
| Fractal dimension | Proposed by Santavicca [34] | |
| Early flame development and combustion completion | Early flame development | Proposed by F. Bozza [35] |
| Combustion completion | Proposed by F. Bozza [35] | |
| Chemical reaction kinetics | Chemical reaction mechanism | Li [36] |
| Reactor | Cantera IdealGasReactor | |
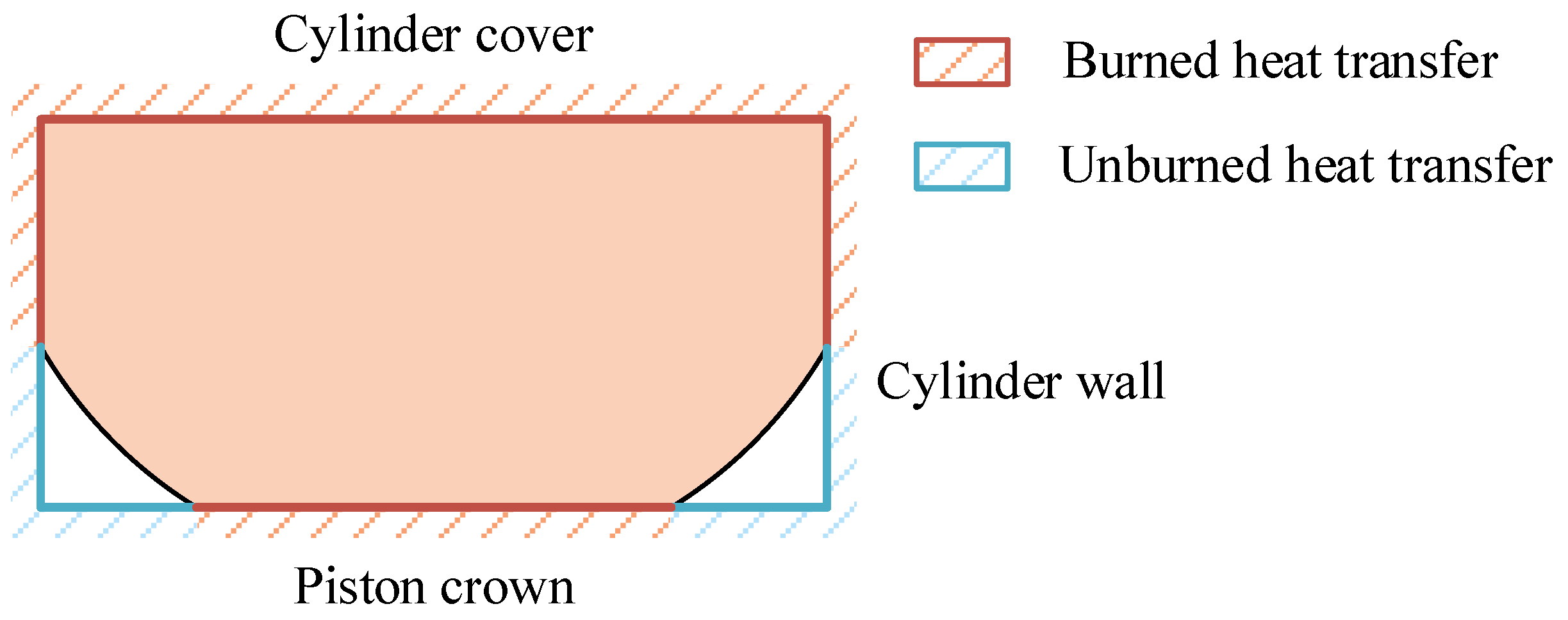
| Wall heat transfer | - | Woschni |
| Engine Type | SI Engine, V-Type 8-Cylinder, Turbo Charging, 4-Stroke |
|---|---|
| Rated Speed | 1500 r/min |
| Rated power | 320 kW |
| Bore | 128 mm |
| Stroke | 140 mm |
| Compression ratio | 12 |
| Connecting rod length | 255 mm |
| Inlet valve opening/closure | 26.5 °CA BTDC/133.5 °CA BTDC |
| Exhaust valve opening/closure | 131 °CA ATDC/15 °CA ATDC |
| Fuel type |
| Load | 100% | 75% | 50% | 25% |
|---|---|---|---|---|
| Speed (r/min) | 1500 | 1500 | 1500 | 1500 |
| Torque (N·m) | 2040.07 | 1568.30 | 1019.64 | 520.81 |
| Power (kW) | 320.06 | 246.07 | 160.11 | 81.74 |
| Fuel flow rate (kg/h) | 140.8323 | 110.2674 | 77.33882 | 45.08454 |
| Air flow rate (kg/h) | 1474.042 | 1134.464 | 787.1 | 447.614 |
| MAP (kPa) | 207 | 162 | 120 | 75 |
| Inlet air relative humidity (%) | 28.34291 | 25.47025 | 23.84762 | 24.03501 |
| Post-intercooler charge air temperature (°C) | 57.61 | 53.29 | 50.43 | 50.35 |
| Excess air coefficient | 1.43 | 1.42 | 1.42 | 1.40 |
| Spark timing (°CA BTDC) | 11 | 12 | 12 | 17 |
| Operating Conditions | 100% Load | 75% Load | 50% Load | 25% Load |
|---|---|---|---|---|
| Experimental IMEP | 2.057 MPa | 1.588 MPa | 1.151 MPa | 0.640 MPa |
| Calculation IMEP | 2.054 MPa | 1.588 MPa | 1.155 MPa | 0.637 MPa |
| Relative error | 0.18% | 0% | 0.37% | 0.36% |
| Power | Speed | MAP | Spark Angle | Excess Air Ratio | HER |
|---|---|---|---|---|---|
| 100% | 1500 r/min | 207 kPa | 11 °CA BTDC | 1.4 | 0~30% |
| 15% | 1500 r/min | 59 kPa | 15 °CA BTDC | 1.4 | 0~30% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Ding, Y.; Ren, X.; Xiang, L. Performance Study of Spark-Ignited Methanol–Hydrogen Engine by Using a Fractal Turbulent Combustion Model Coupled with Chemical Reaction Kinetics. J. Mar. Sci. Eng. 2025, 13, 959. https://doi.org/10.3390/jmse13050959
Zhang Y, Ding Y, Ren X, Xiang L. Performance Study of Spark-Ignited Methanol–Hydrogen Engine by Using a Fractal Turbulent Combustion Model Coupled with Chemical Reaction Kinetics. Journal of Marine Science and Engineering. 2025; 13(5):959. https://doi.org/10.3390/jmse13050959
Chicago/Turabian StyleZhang, Yingting, Yu Ding, Xiaohui Ren, and La Xiang. 2025. "Performance Study of Spark-Ignited Methanol–Hydrogen Engine by Using a Fractal Turbulent Combustion Model Coupled with Chemical Reaction Kinetics" Journal of Marine Science and Engineering 13, no. 5: 959. https://doi.org/10.3390/jmse13050959
APA StyleZhang, Y., Ding, Y., Ren, X., & Xiang, L. (2025). Performance Study of Spark-Ignited Methanol–Hydrogen Engine by Using a Fractal Turbulent Combustion Model Coupled with Chemical Reaction Kinetics. Journal of Marine Science and Engineering, 13(5), 959. https://doi.org/10.3390/jmse13050959






