Synergistic Effects of Ocean Background and Tropical Cyclone Characteristics on Tropical Cyclone-Induced Sea Surface Cooling in the Western North Pacific
Abstract
1. Introduction
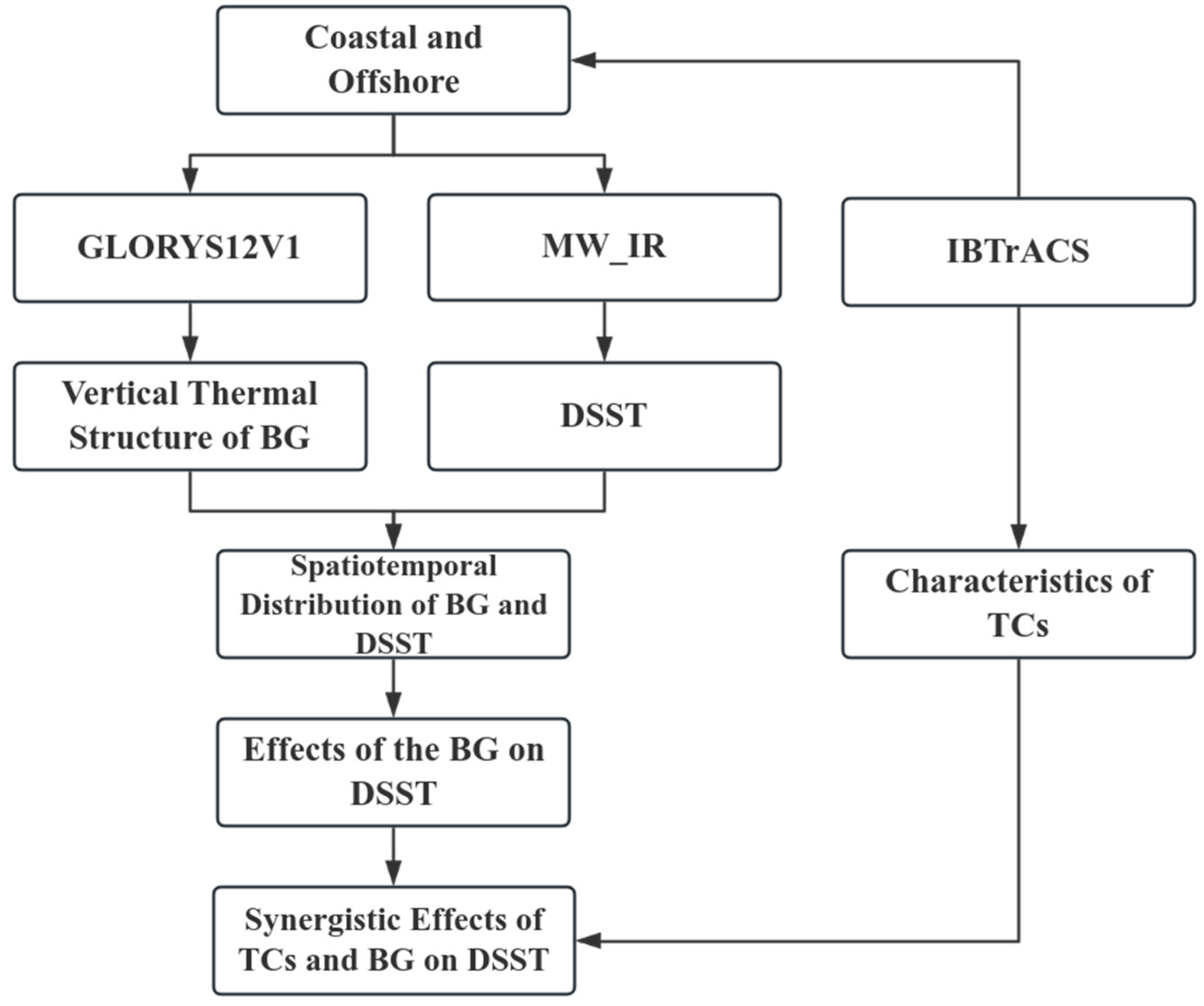
2. Materials and Methods
2.1. Data
2.2. Methods
3. Results
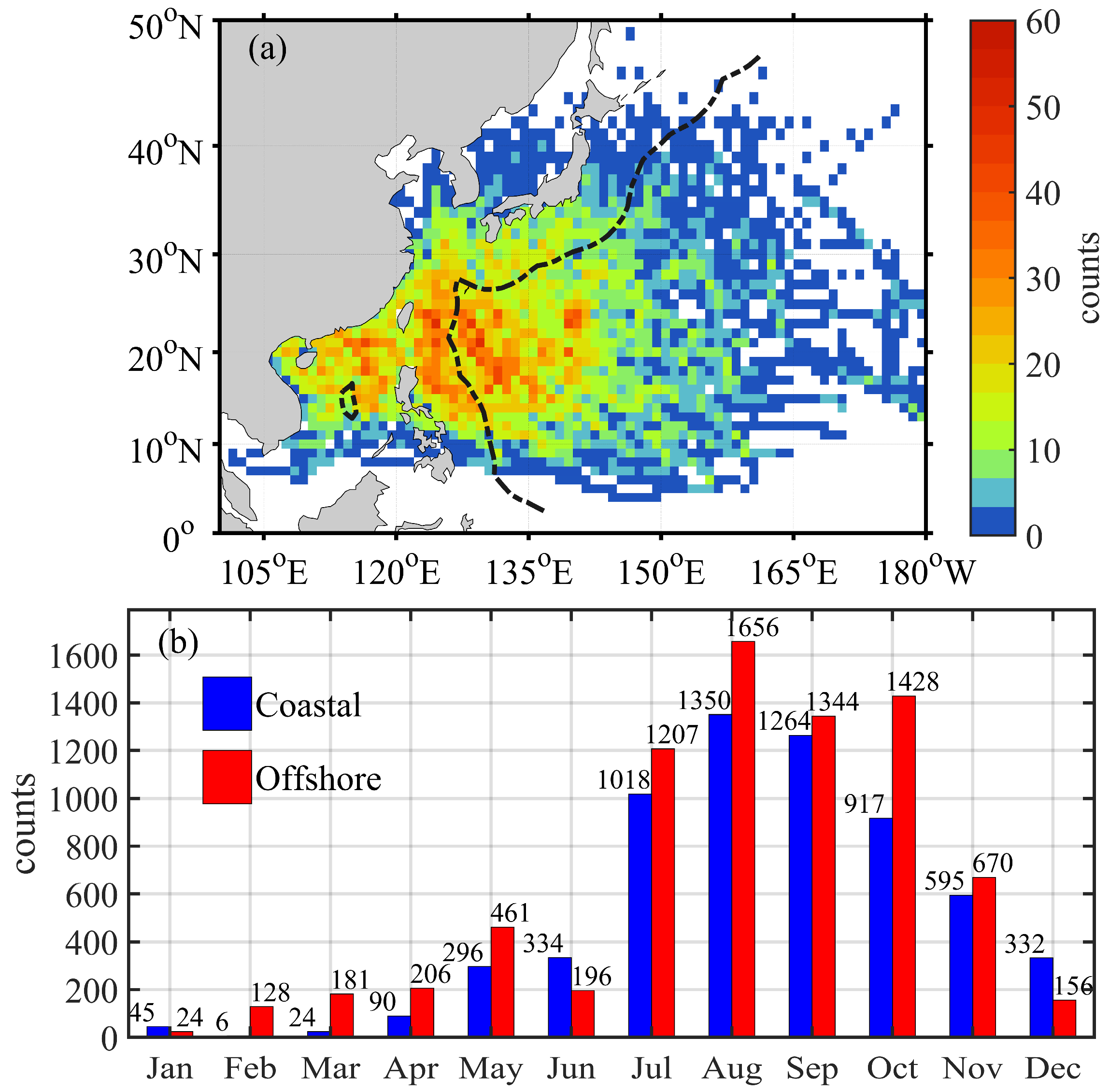
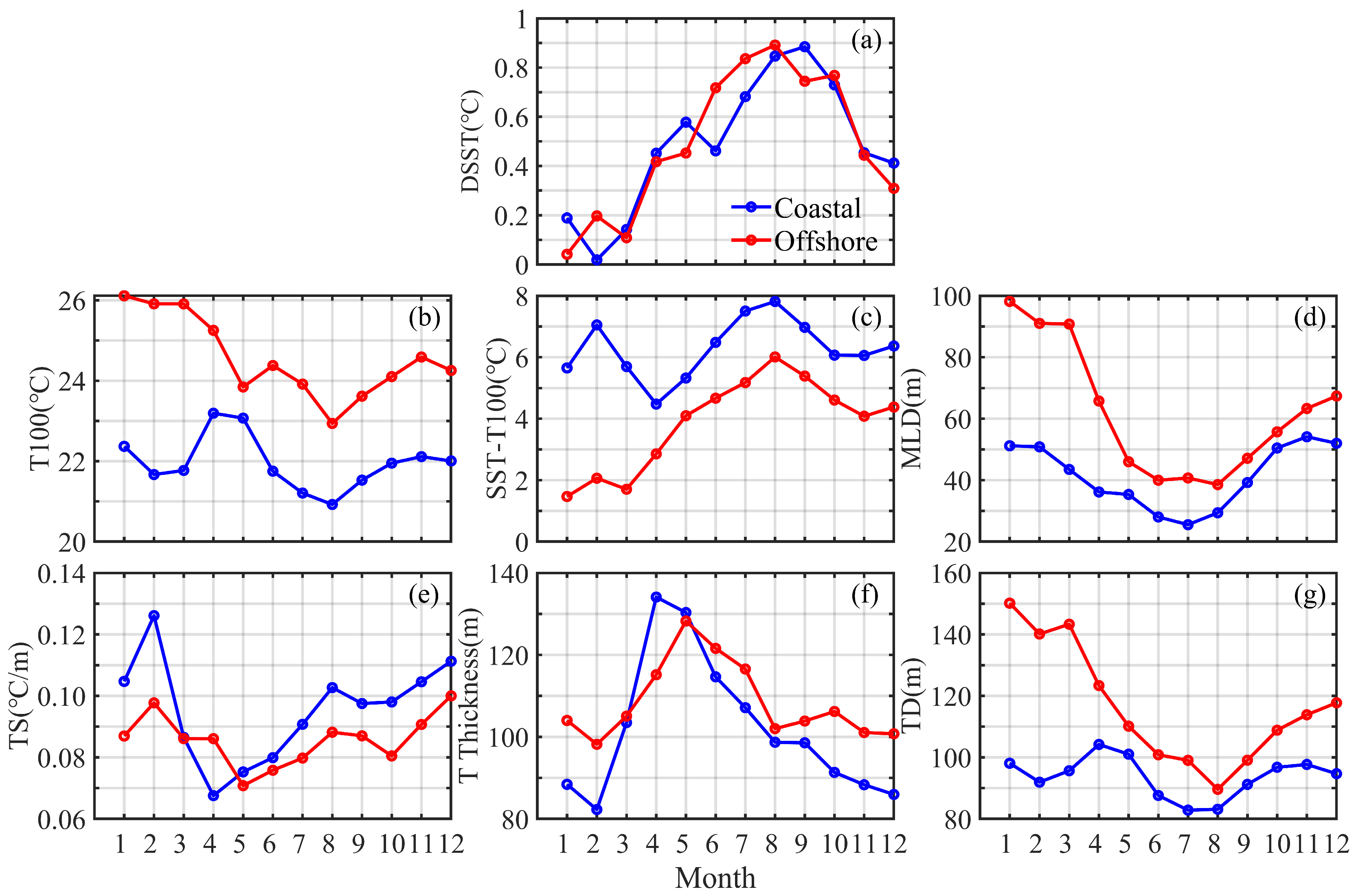
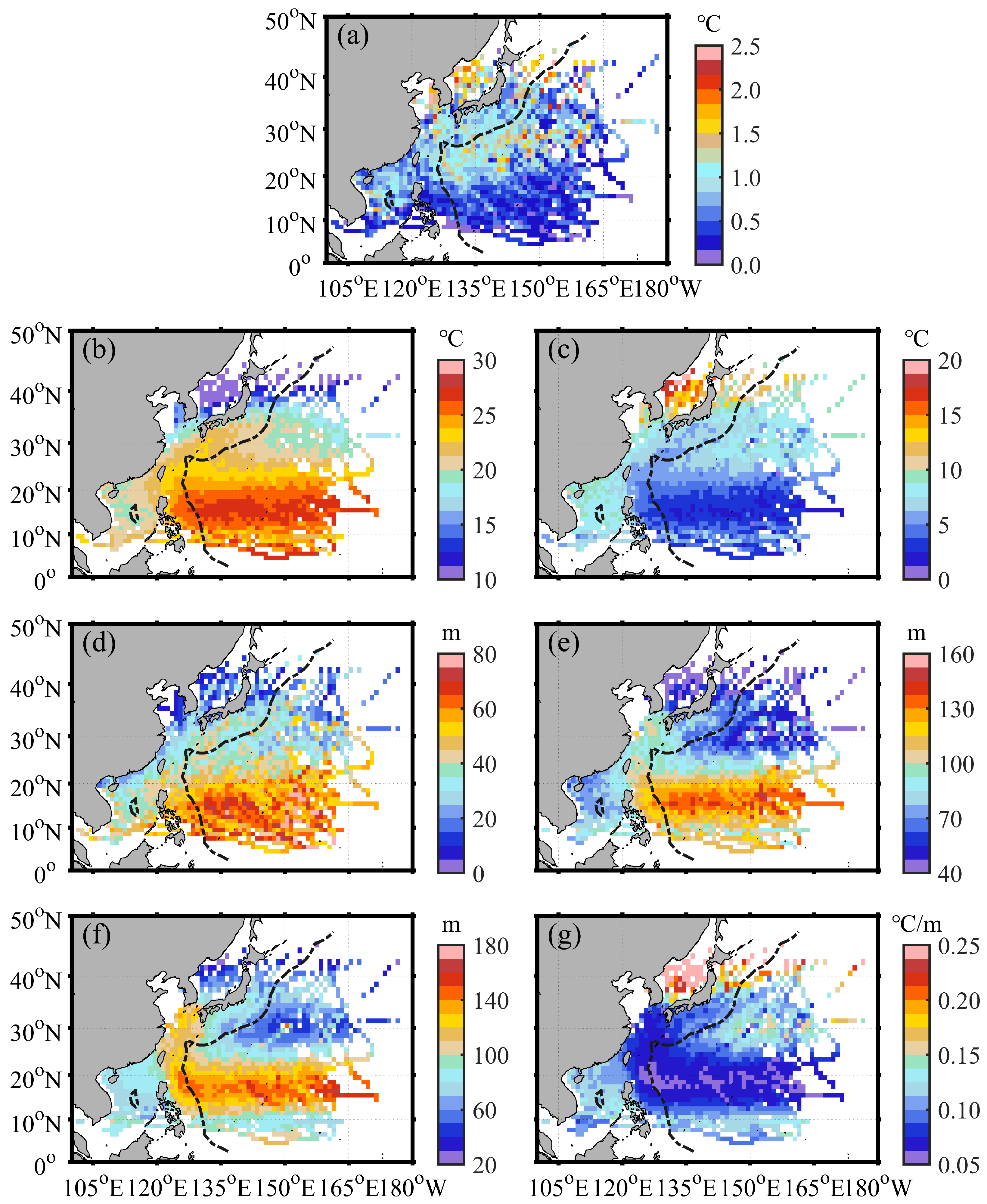
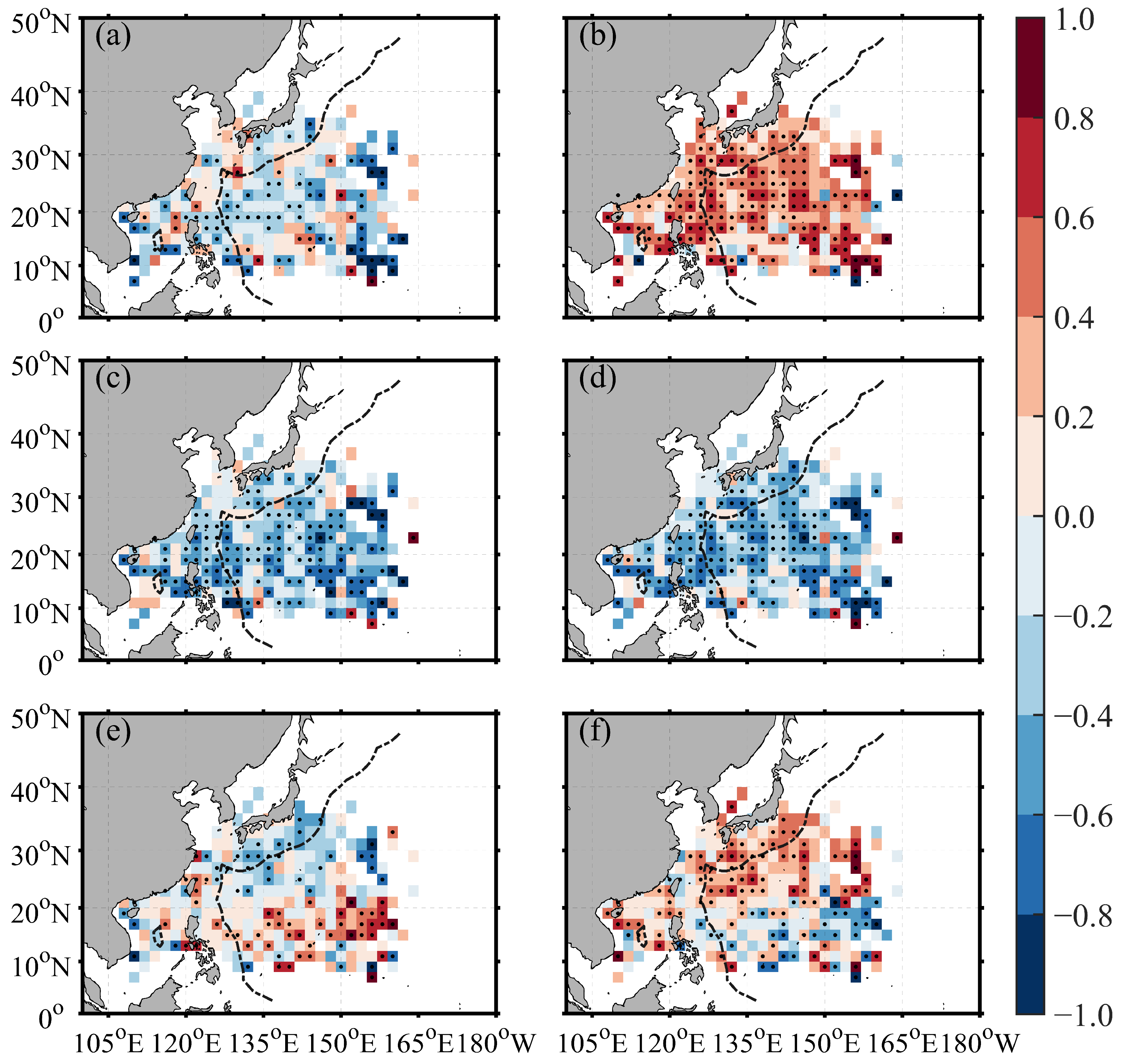
3.1. Spatial and Temporal Distribution of BG and DSST in the WNP
3.2. Effects of the BG on DSST
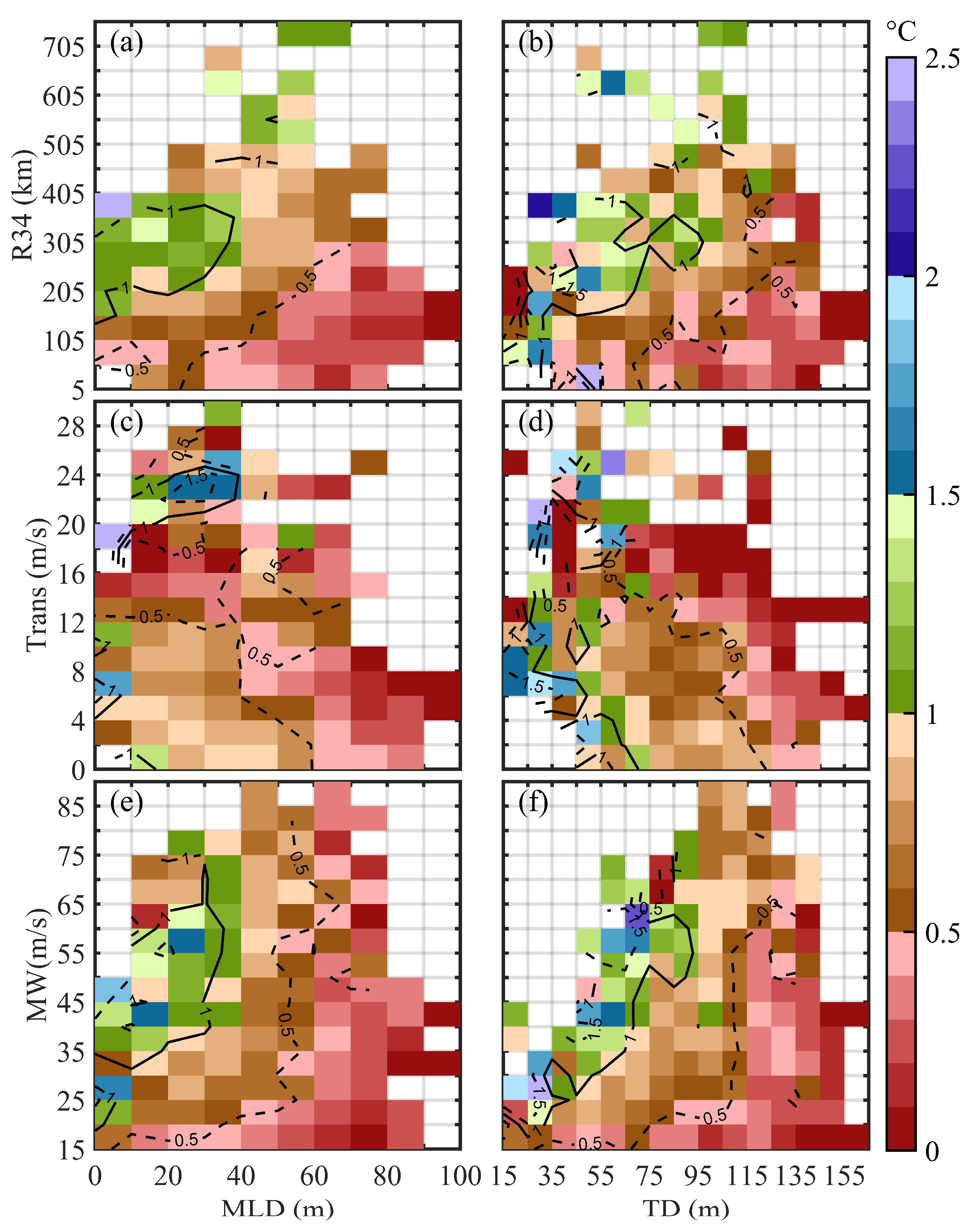
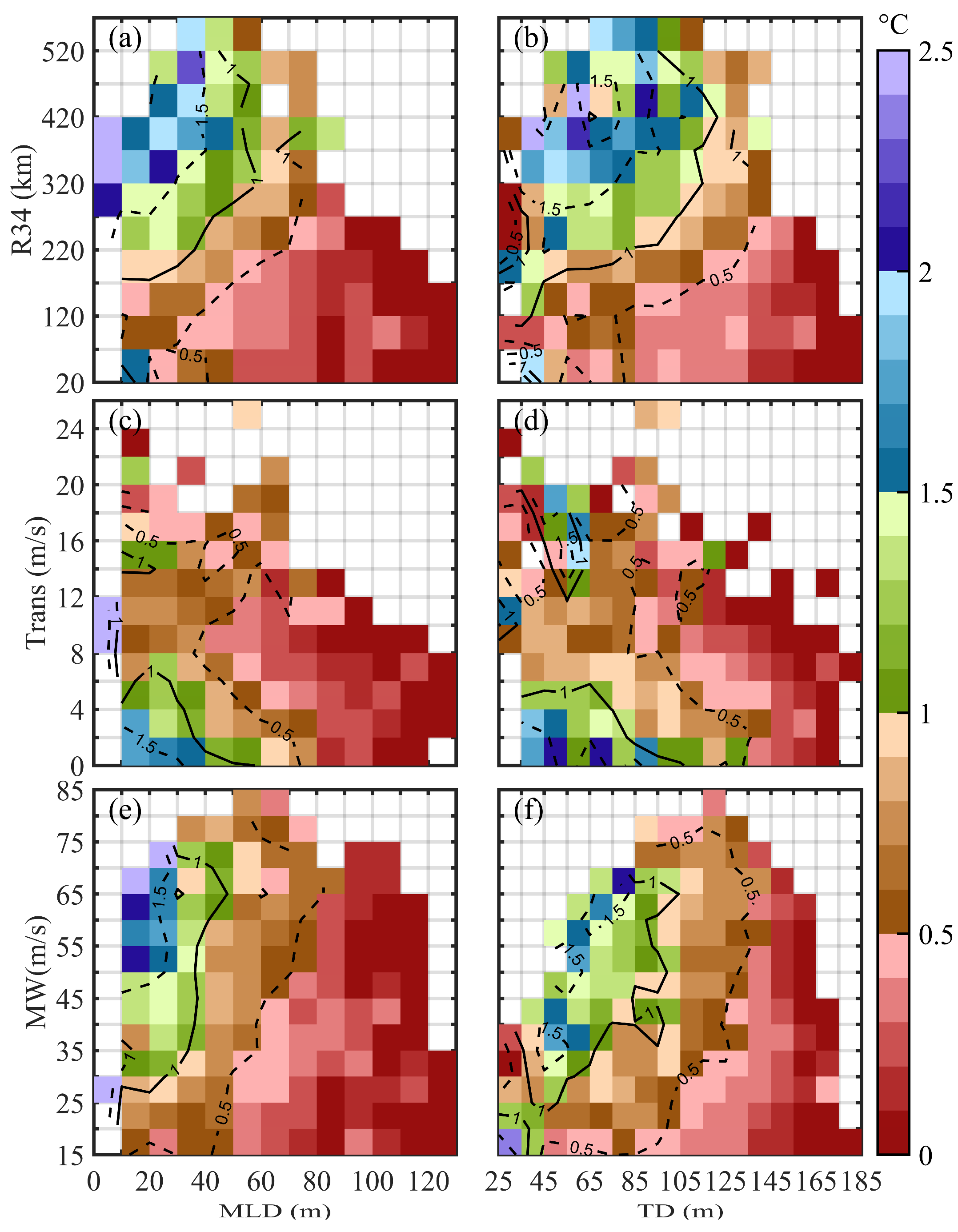
3.3. Synergistic Effects of the BG and TC on DSST
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Emanuel, K. Tropical Cyclones. Annu. Rev. Earth Planet. Sci. 2003, 31, 75–104. [Google Scholar] [CrossRef]
- Li, A.; Guan, S.; Mo, D.; Hou, Y.; Hong, X.; Liu, Z. Modeling Wave Effects on Storm Surge from Different Typhoon Intensities and Sizes in the South China Sea. Estuar. Coast. Shelf Sci. 2020, 235, 106551. [Google Scholar] [CrossRef]
- Emanuel, K.A. Thermodynamic Control of Hurricane Intensity. Nature 1999, 401, 665–669. [Google Scholar] [CrossRef]
- Jin, F.-F.; Boucharel, J.; Lin, I.-I. Eastern Pacific Tropical Cyclones Intensified by El Niño Delivery of Subsurface Ocean Heat. Nature 2014, 516, 82–85. [Google Scholar] [CrossRef]
- Lin, I.-I.; Black, P.; Price, J.F.; Yang, C.-Y.; Chen, S.S.; Lien, C.-C.; Harr, P.; Chi, N.-H.; Wu, C.-C.; D’Asaro, E.A. An Ocean Coupling Potential Intensity Index for Tropical Cyclones. Geophys. Res. Lett. 2013, 40, 1878–1882. [Google Scholar] [CrossRef]
- Mei, W.; Xie, S.-P.; Primeau, F.; McWilliams, J.C.; Pasquero, C. Northwestern Pacific Typhoon Intensity Controlled by Changes in Ocean Temperatures. Sci. Adv. 2015, 1, e1500014. [Google Scholar] [CrossRef] [PubMed]
- Bracken, W.E.; Bosart, L.F. The Role of Synoptic-Scale Flow during Tropical Cyclogenesis over the North Atlantic Ocean. Mon. Weather. Rev. 2000, 128, 353–376. [Google Scholar] [CrossRef]
- Dare, R.A.; McBride, J.L. Sea Surface Temperature Response to Tropical Cyclones. Mon. Weather Rev. 2011, 139, 3798–3808. [Google Scholar] [CrossRef]
- Gray, W. Global View of the Origin of Tropical Disturbances and Storms. Mon. Weather Rev. 1968, 96, 669–700. [Google Scholar] [CrossRef]
- Cione, J.J.; Uhlhorn, E.W. Sea Surface Temperature Variability in Hurricanes: Implications with Respect to Intensity Change. Mon. Weather Rev. 2003, 131, 1783–1796. [Google Scholar] [CrossRef]
- Price, J.F. Upper Ocean Response to a Hurricane. J. Phys. Oceanogr. 1981, 11, 153–175. [Google Scholar] [CrossRef]
- Vincent, E.M.; Lengaigne, M.; Madec, G.; Vialard, J.; Samson, G.; Jourdain, N.C.; Menkes, C.E.; Jullien, S. Processes Setting the Characteristics of Sea Surface Cooling Induced by Tropical Cyclones. J. Geophys. Res. Oceans 2012, 117, C02020. [Google Scholar] [CrossRef]
- Lin, I.-I.; Pun, I.-F.; Wu, C.-C. Upper-Ocean Thermal Structure and the Western North Pacific Category 5 Typhoons. Part II: Dependence on Translation Speed. Mon. Weather Rev. 2009, 137, 3744–3757. [Google Scholar] [CrossRef]
- Shay, L.K.; Brewster, J.K. Oceanic Heat Content Variability in the Eastern Pacific Ocean for Hurricane Intensity Forecasting. Mon. Weather Rev. 2010, 138, 2110–2131. [Google Scholar] [CrossRef]
- Glenn, S.M.; Miles, T.N.; Seroka, G.N.; Xu, Y.; Forney, R.K.; Yu, F.; Roarty, H.; Schofield, O.; Kohut, J. Stratified Coastal Ocean Interactions with Tropical Cyclones. Nat. Commun. 2016, 7, 10887. [Google Scholar] [CrossRef]
- Guan, S.; Zhao, W.; Sun, L.; Zhou, C.; Liu, Z.; Hong, X.; Zhang, Y.; Tian, J.; Hou, Y. Tropical Cyclone-Induced Sea Surface Cooling over the Yellow Sea and Bohai Sea in the 2019 Pacific Typhoon Season. J. Mar. Syst. 2021, 217, 103509. [Google Scholar] [CrossRef]
- Mahapatra, D.K.; Rao, A.D.; Babu, S.V.; Srinivas, C. Influence of Coast Line on Upper Ocean’s Response to the Tropical Cyclone. Geophys. Res. Lett. 2007, 34, L17603. [Google Scholar] [CrossRef]
- Shen, W.; Ginis, I. Effects of Surface Heat Flux-Induced Sea Surface Temperature Changes on Tropical Cyclone Intensity. Geophys. Res. Lett. 2003, 30, 1933. [Google Scholar] [CrossRef]
- Greatbatch, R.J. On the Response of the Ocean to a Moving Storm: Parameters and Scales. J. Phys. Oceanogr. 1984, 14, 59–78. [Google Scholar] [CrossRef]
- Jacob, S.D.; Shay, L.K.; Mariano, A.J.; Black, P.G. The 3D Oceanic Mixed Layer Response to Hurricane Gilbert. J. Phys. Oceanogr. 2000, 30, 1407–1429. [Google Scholar] [CrossRef]
- Lin, S.; Zhang, W.-Z.; Shang, S.-P.; Hong, H.-S. Ocean Response to Typhoons in the Western North Pacific: Composite Results from Argo Data. Deep Sea Res. Part Oceanogr. Res. Pap. 2017, 123, 62–74. [Google Scholar] [CrossRef]
- Peng, Y.; Tian, D.; Zhou, F.; Zhang, H.; Ma, X.; Zeng, D.; Meng, Q.; Zhou, B.; Ye, R.; Chen, Y.; et al. Observed Oceanic Response to Tropical Cyclone Amphan (2020) from a Subsurface Mooring in the Bay of Bengal. Prog. Oceanogr. 2023, 219, 103148. [Google Scholar] [CrossRef]
- Shay, L.K.; Black, P.G.; Mariano, A.J.; Hawkins, J.D.; Elsberry, R.L. Upper Ocean Response to Hurricane Gilbert. J. Geophys. Res. Oceans 1992, 97, 20227–20248. [Google Scholar] [CrossRef]
- Da, N.D.; Foltz, G.R.; Balaguru, K.; Fernald, E. Stronger Tropical Cyclone–Induced Ocean Cooling in Near-Coastal Regions Compared to the Open Ocean. J. Clim. 2023, 36, 6447–6463. [Google Scholar] [CrossRef]
- Zheng, Y.; Ma, Z.; Tang, J.; Zhang, Z. The Coastal Effect on Ahead-of-Eye-Center Cooling Induced by Tropical Cyclones. J. Phys. Oceanogr. 2023, 53, 1519–1534. [Google Scholar] [CrossRef]
- Chiang, T.-L.; Wu, C.-R.; Oey, L.-Y. Typhoon Kai-Tak: An Ocean’s Perfect Storm. J. Phys. Oceanogr. 2011, 41, 221–233. [Google Scholar] [CrossRef]
- Guan, S.; Zhao, W.; Huthnance, J.; Tian, J.; Wang, J. Observed Upper Ocean Response to Typhoon Megi (2010) in the Northern South China Sea. J. Geophys. Res. Oceans 2014, 119, 3134–3157. [Google Scholar] [CrossRef]
- Ren, D.; Han, S.; Wang, S. Upper Ocean Responses to Tropical Cyclone Mekunu (2018) in the Arabian Sea. J. Mar. Sci. Eng. 2024, 12, 1177. [Google Scholar] [CrossRef]
- Bender, M.A.; Ginis, I.; Kurihara, Y. Numerical Simulations of Tropical Cyclone-Ocean Interaction with a High-Resolution Coupled Model. J. Geophys. Res. Atmos. 1993, 98, 23245–23263. [Google Scholar] [CrossRef]
- Lin, I.-I.; Wu, C.-C.; Emanuel, K.A.; Lee, I.-H.; Wu, C.-R.; Pun, I.-F. The Interaction of Supertyphoon Maemi (2003) with a Warm Ocean Eddy. Mon. Weather Rev. 2005, 133, 2635. [Google Scholar] [CrossRef]
- Price, J.F. Internal Wave Wake of a Moving Storm. Part I. Scales, Energy Budget and Observations. J. Phys. Oceanogr. 1983, 13, 949–965. [Google Scholar] [CrossRef]
- Pun, I.-F.; Lin, I.-I.; Lien, C.-C.; Wu, C.-C. Influence of the Size of Supertyphoon Megi (2010) on SST Cooling. Mon. Weather Rev. 2018, 146, 661–677. [Google Scholar] [CrossRef]
- Pun, I.-F.; Chan, J.C.L.; Lin, I.-I.; Chan, K.T.F.; Price, J.F.; Ko, D.S.; Lien, C.-C.; Wu, Y.-L.; Huang, H.-C. Rapid Intensification of Typhoon Hato (2017) over Shallow Water. Sustainability 2019, 11, 3709. [Google Scholar] [CrossRef]
- Wang, H.; Li, J.; Song, J.; Leng, H.; Wang, H.; Zhang, Z.; Zhang, H.; Zheng, M.; Yang, X.; Wang, C. The Abnormal Track of Super Typhoon Hinnamnor (2022) and Its Interaction with the Upper Ocean. Deep. Sea Res. Part Oceanogr. Res. Pap. 2023, 201, 104160. [Google Scholar] [CrossRef]
- Pun, I.-F.; Knaff, J.A.; Sampson, C.R. Uncertainty of Tropical Cyclone Wind Radii on Sea Surface Temperature Cooling. J. Geophys. Res. Atmos. 2021, 126, e2021JD034857. [Google Scholar] [CrossRef]
- Cui, H.; Tang, D.; Mei, W.; Liu, H.; Sui, Y.; Gu, X. Predicting Tropical Cyclone-Induced Sea Surface Temperature Responses Using Machine Learning. Geophys. Res. Lett. 2023, 50, e2023GL104171. [Google Scholar] [CrossRef]
- Moon, I.-J.; Kwon, S.J. Impact of Upper-Ocean Thermal Structure on the Intensity of Korean Peninsular Landfall Typhoons. Prog. Oceanogr. 2012, 105, 61–66. [Google Scholar] [CrossRef]
- Balaguru, K.; Foltz, G.R.; Leung, L.R.; Hagos, S.M. Impact of Rainfall on Tropical Cyclone-Induced Sea Surface Cooling. Geophys. Res. Lett. 2022, 49, e2022GL098187. [Google Scholar] [CrossRef]
- D’Asaro, E.A.; Black, P.G.; Centurioni, L.R.; Chang, Y.-T.; Chen, S.S.; Foster, R.C.; Graber, H.C.; Harr, P.; Hormann, V.; Lien, R.-C.; et al. Impact of Typhoons on the Ocean in the Pacific. Bull. Am. Meteorol. Soc. 2014, 95, 1405–1418. [Google Scholar] [CrossRef]
- Knaff, J.A.; DeMaria, M.; Sampson, C.R.; Peak, J.E.; Cummings, J.; Schubert, W.H. Upper Oceanic Energy Response to Tropical Cyclone Passage. J. Clim. 2013, 26, 2631–2650. [Google Scholar] [CrossRef]
- Lin, I.-I.; Rogers, R.F.; Huang, H.-C.; Liao, Y.-C.; Herndon, D.; Yu, J.-Y.; Chang, Y.-T.; Zhang, J.A.; Patricola, C.M.; Pun, I.-F.; et al. A Tale of Two Rapidly Intensifying Supertyphoons: Hagibis (2019) and Haiyan (2013). Bull. Am. Meteorol. Soc. 2021, 102, E1645–E1664. [Google Scholar] [CrossRef]
- Mei, W.; Lien, C.-C.; Lin, I.-I.; Xie, S.-P. Tropical Cyclone–Induced Ocean Response: A Comparative Study of the South China Sea and Tropical Northwest Pacific. J. Clim. 2015, 28, 5952–5968. [Google Scholar] [CrossRef]
- Potter, H.; DiMarco, S.F.; Knap, A.H. Tropical Cyclone Heat Potential and the Rapid Intensification of Hurricane Harvey in the Texas Bight. J. Geophys. Res. Oceans 2019, 124, 2440–2451. [Google Scholar] [CrossRef]
- Zhuang, Z.; Yang, Y.; Shu, Q.; Song, Z.; Zhao, B.; Yuan, Y. Variability of Non-Breaking Surface-Wave Induced Mixing and Its Effects on Ocean Thermodynamical Structure in the Northwest Pacific during Typhoon Lekima (2019). Deep. Sea Res. Part Oceanogr. Res. Pap. 2023, 202, 104178. [Google Scholar] [CrossRef]
- Chan, J.C.L.; Duan, Y.; Shay, L.K. Tropical Cyclone Intensity Change from a Simple Ocean–Atmosphere Coupled Model. J. Atmos. Sci. 2001, 58, 154–172. [Google Scholar] [CrossRef]
- Maneesha, K.; Murty, V.S.N.; Ravichandran, M.; Lee, T.; Yu, W.; McPhaden, M.J. Upper Ocean Variability in the Bay of Bengal during the Tropical Cyclones Nargis and Laila. Prog. Oceanogr. 2012, 106, 49–61. [Google Scholar] [CrossRef]
- Mei, W.; Pasquero, C. Restratification of the Upper Ocean after the Passage of a Tropical Cyclone: A Numerical Study. J. Phys. Oceanogr. 2012, 42, 1377–1401. [Google Scholar] [CrossRef]
- Wang, G.; Wu, L.; Johnson, N.C.; Ling, Z. Observed Three-Dimensional Structure of Ocean Cooling Induced by Pacific Tropical Cyclones. Geophys. Res. Lett. 2016, 43, 7632–7638. [Google Scholar] [CrossRef]
- Wu, C.-R.; Chang, Y.-L.; Oey, L.-Y.; Chang, C.-W.J.; Hsin, Y.-C. Air-Sea Interaction between Tropical Cyclone Nari and Kuroshio. Geophys. Res. Lett. 2008, 35, L12605. [Google Scholar] [CrossRef]
- Yu, J.; Zhang, H.; Wang, H.; Tian, D.; Li, J. Upper-Ocean Structure Variability in the Northwest Pacific Ocean in Response to Tropical Cyclones. Front. Mar. Sci. 2023, 10, 1245348. [Google Scholar] [CrossRef]
- Balaguru, K.; Chang, P.; Saravanan, R.; Leung, L.R.; Xu, Z.; Li, M.; Hsieh, J.-S. Ocean Barrier Layers’ Effect on Tropical Cyclone Intensification. Proc. Natl. Acad. Sci. USA 2012, 109, 14343–14347. [Google Scholar] [CrossRef] [PubMed]
- Balaguru, K.; Foltz, G.R.; Leung, L.R.; Asaro, E.D.; Emanuel, K.A.; Liu, H.; Zedler, S.E. Dynamic Potential Intensity: An Improved Representation of the Ocean’s Impact on Tropical Cyclones. Geophys. Res. Lett. 2015, 42, 6739–6746. [Google Scholar] [CrossRef]
- Balaguru, K.; Foltz, G.R.; Leung, L.-Y.; Kaplan, J.; Xu, W.; Reul, N.; Chapron, B. Pronounced Impact of Salinity on Rapidly Intensifying Tropical Cyclones. Bull. Am. Meteorol. Soc. 2020, 101, E1497–E1511. [Google Scholar] [CrossRef]
- Miles, T.N.; Coakley, S.J.; Engdahl, J.M.; Rudzin, J.E.; Tsei, S.; Glenn, S.M. Ocean Mixing during Hurricane Ida (2021): The Impact of a Freshwater Barrier Layer. Front. Mar. Sci. 2023, 10, 1224609. [Google Scholar] [CrossRef]
- Neetu, S.; Lengaigne, M.; Vincent, E.M.; Vialard, J.; Madec, G.; Samson, G.; Ramesh Kumar, M.R.; Durand, F. Influence of Upper-Ocean Stratification on Tropical Cyclone-Induced Surface Cooling in the Bay of Bengal. J. Geophys. Res. Oceans 2012, 117, C12020. [Google Scholar] [CrossRef]
- Vincent, E.M.; Lengaigne, M.; Vialard, J.; Madec, G.; Jourdain, N.C.; Masson, S. Assessing the Oceanic Control on the Amplitude of Sea Surface Cooling Induced by Tropical Cyclones. J. Geophys. Res. Oceans 2012, 117, C05023. [Google Scholar] [CrossRef]
- Oey, L. A Simple Model of Sea-Surface Cooling under a Tropical Cyclone. J. Mar. Sci. Eng. 2023, 11, 397. [Google Scholar] [CrossRef]
- Doong, D.-J.; Peng, J.-P.; Babanin, A.V. Field Investigations of Coastal Sea Surface Temperature Drop after Typhoon Passages. Earth Syst. Sci. Data 2019, 11, 323–340. [Google Scholar] [CrossRef]
- Knapp, K.R.; Kruk, M.C.; Levinson, D.H.; Diamond, H.J.; Neumann, C.J. The International Best Track Archive for Climate Stewardship (IBTrACS): Unifying Tropical Cyclone Data. Bull. Am. Meteorol. Soc. 2010, 91, 363–376. [Google Scholar] [CrossRef]
- Da, N.D.; Foltz, G.R.; Balaguru, K. A Satellite-Derived Upper-Ocean Stratification Data Set for the Tropical North Atlantic with Potential Applications for Hurricane Intensity Prediction. J. Geophys. Res. Oceans 2020, 125, e2019JC015980. [Google Scholar] [CrossRef]
- Jean-Michel, L.; Eric, G.; Romain, B.-B.; Gilles, G.; Angélique, M.; Marie, D.; Clément, B.; Mathieu, H.; Olivier, L.G.; Charly, R.; et al. The Copernicus Global 1/12° Oceanic and Sea Ice GLORYS12 Reanalysis. Front. Earth Sci. 2021, 9, 698876. [Google Scholar] [CrossRef]
- He, Y.; Lin, X.; Han, G.; Liu, Y.; Zhang, H. The Different Dynamic Influences of Typhoon Kalmaegi on Two Pre-Existing Anticyclonic Ocean Eddies. Ocean Sci. 2024, 20, 621–637. [Google Scholar] [CrossRef]
- Yu, J.; Lv, H.; Tan, S.; Wang, Y. Tropical Cyclone-Induced Sea Surface Temperature Responses in the Northern Indian Ocean. J. Mar. Sci. Eng. 2023, 11, 2196. [Google Scholar] [CrossRef]
- Kara, A.B.; Rochford, P.A.; Hurlburt, H.E. An Optimal Definition for Ocean Mixed Layer Depth. J. Geophys. Res. Oceans 2000, 105, 16803–16821. [Google Scholar] [CrossRef]
- Fiedler, P.C. Comparison of Objective Descriptions of the Thermocline. Limnol. Oceanogr. Methods 2010, 8, 313–325. [Google Scholar] [CrossRef]
- Jin, M.; Zhao, Z.; Wu, R.; Zhu, P. Latitudinal and Seasonal Variations in Tropical Cyclone-Induced Ocean Surface Cooling in the Tropical Western North Pacific. J. Meteorol. Res. 2023, 37, 790–801. [Google Scholar] [CrossRef]
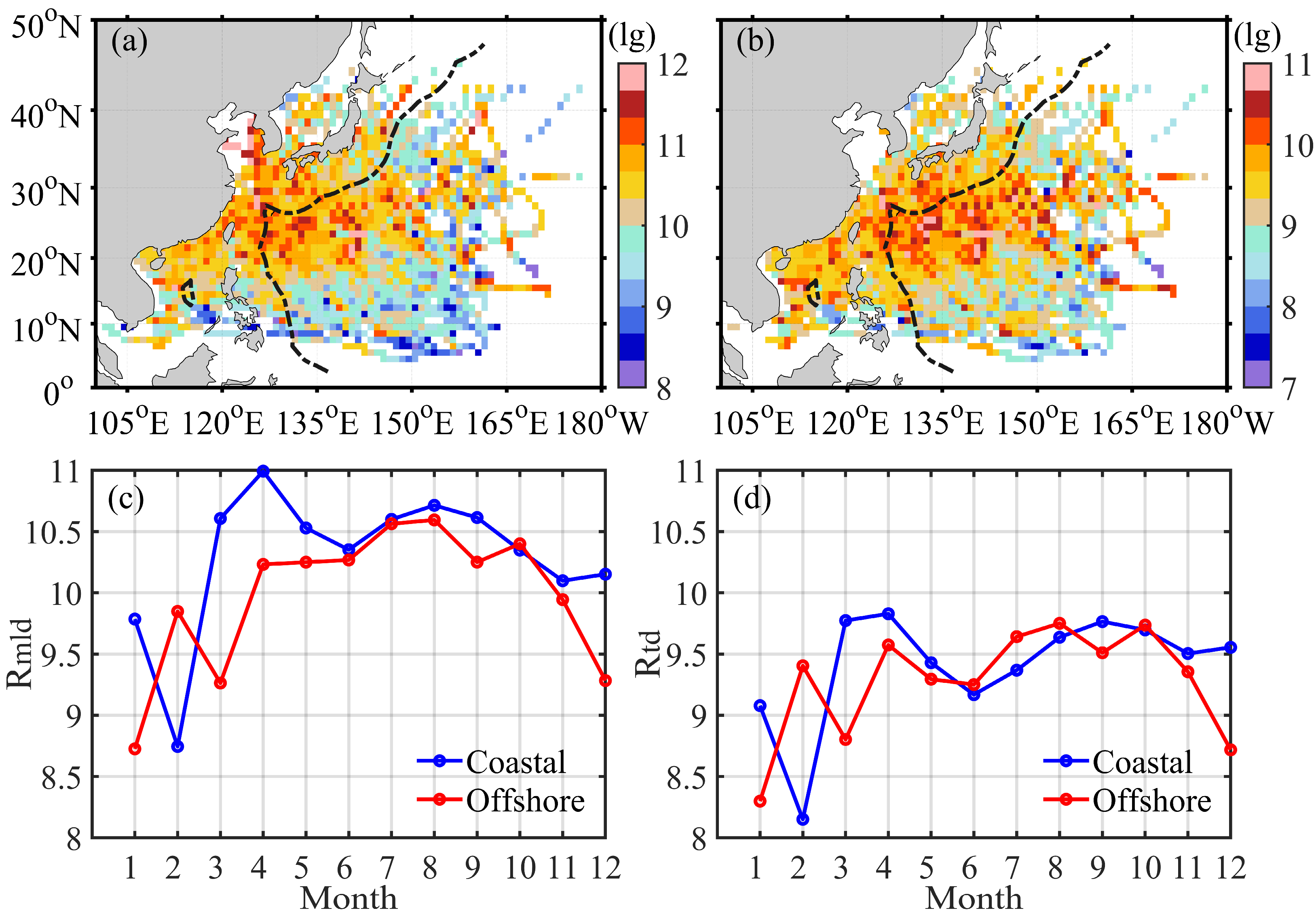
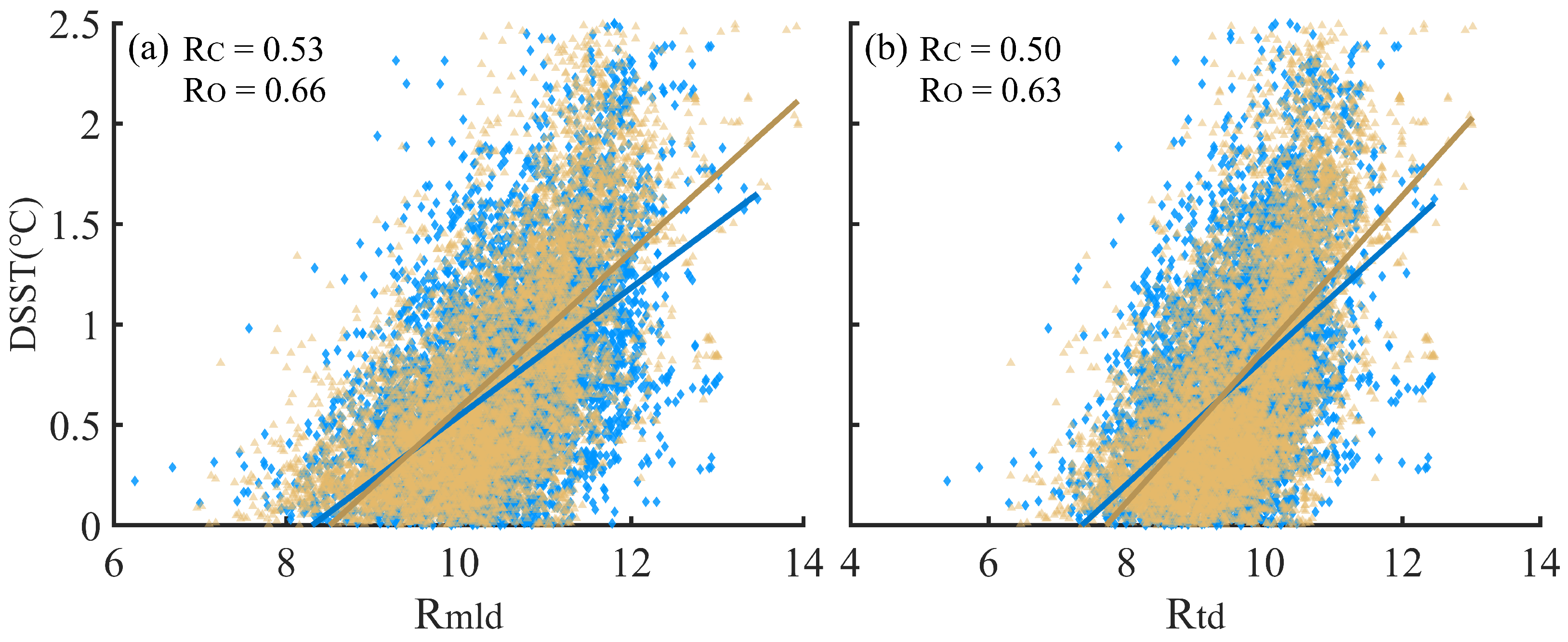
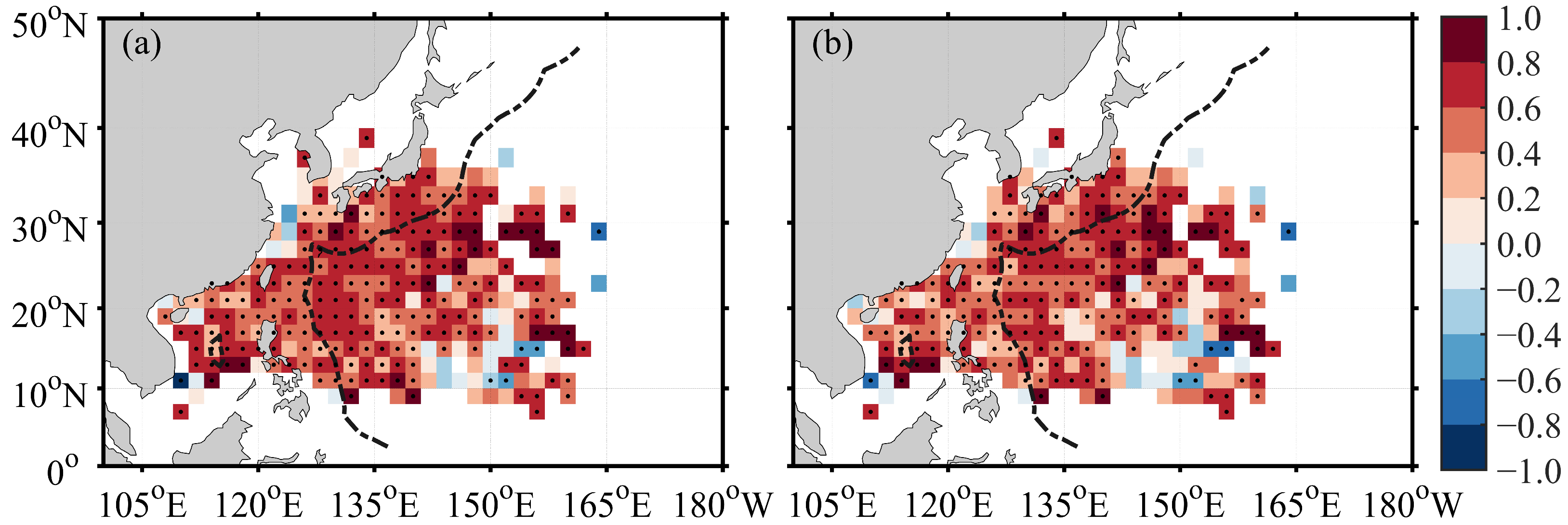
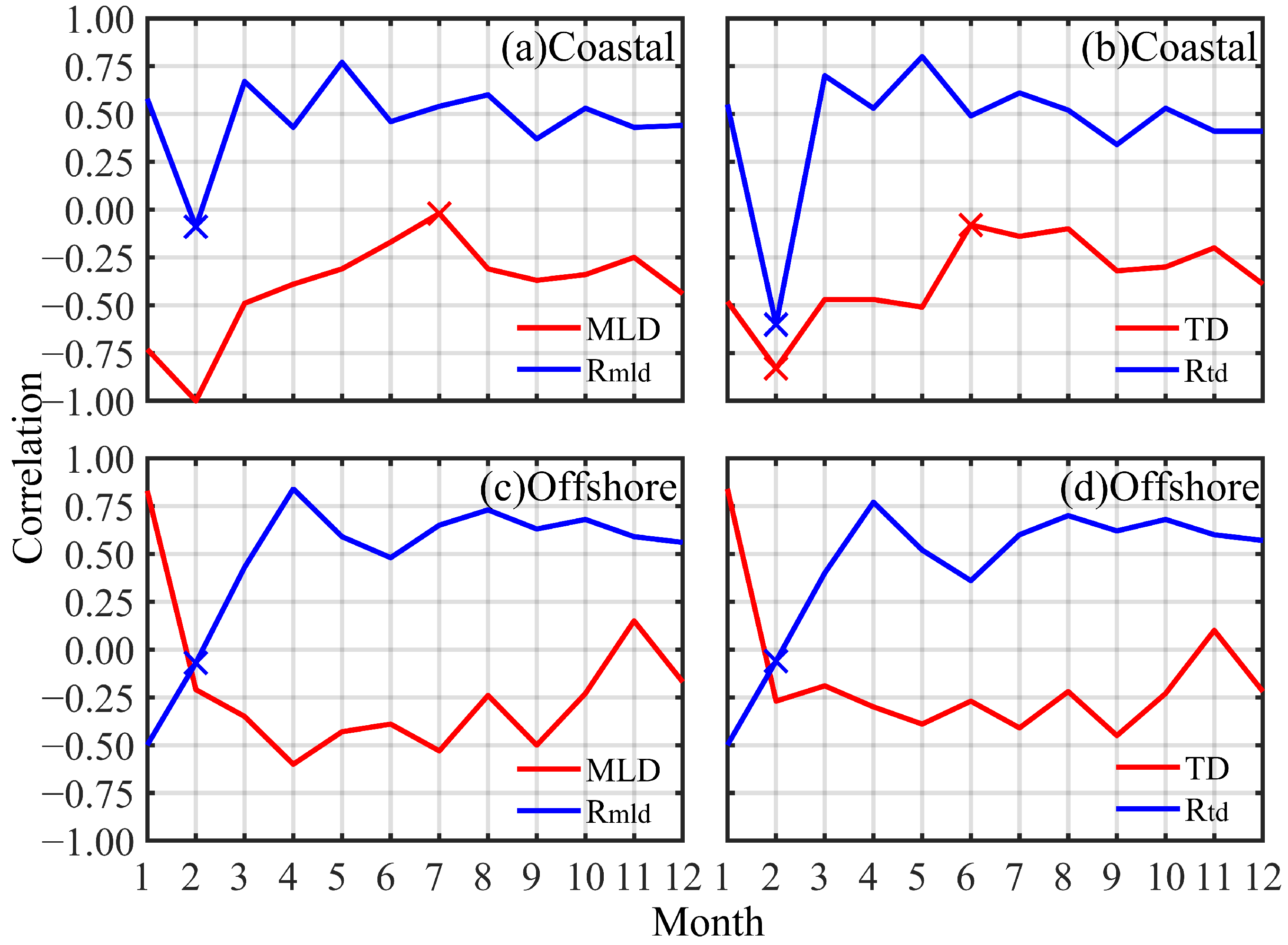
| Abbreviation | Full Term | Abbreviation | Full Term |
|---|---|---|---|
| BG | Ocean Background State | TB | Thermocline Bottom |
| DSST | Decrease in Sea Surface Temperature | TC | Tropical Cyclone |
| MLD | Mixed Layer Depth | TD | Thermocline Depth |
| MLT | Mix Layer Temperature | Trans | Translation Speed of TC |
| MW | Maximum Sustained Wind Speed | TS | Thermocline Strength |
| R34 | Radius of 34-knot Winds | TT | Thermocline Temperature |
| SST | Sea Surface Temperature | T Thickness | Thermocline Thickness |
| T100 | Temperature at 100 m | WNP | Western North Pacific |
| Month | T100 | SST−T100 | MLD | T Thickness | TD | TS | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C | O | C | O | C | O | C | O | C | O | C | O | |
| 1 | −0.31 * | 0.63 | 0.33 | −0.83 | −0.73 | 0.83 | −0.50 | 0.70 | −0.48 | 0.84 | 0.34 * | −0.83 |
| 2 | −0.94 | 0.06 * | 0.94 | 0.16 * | −1.00 | −0.21 | 0.94 | −0.34 | −0.83 * | −0.27 | −0.83 * | 0.42 |
| 3 | −0.35 * | −0.18 | 0.92 | 0.18 | −0.49 | −0.35 | −0.88 | 0.42 | −0.47 | −0.19 | 0.92 | −0.44 |
| 4 | −0.38 | −0.46 | 0.42 | 0.40 | −0.39 | −0.60 | −0.21 | 0.20 | −0.47 | −0.30 | 0.31 | −0.14 |
| 5 | −0.13 | −0.19 | 0.57 | 0.31 | −0.31 | −0.43 | −0.38 | −0.06 * | −0.51 | −0.39 | 0.46 | −0.05 * |
| 6 | 0.35 | −0.09 * | 0.16 | 0.43 | −0.17 | −0.39 | 0.05 * | 0.16 | −0.08 * | −0.27 | 0.11 | −0.23 |
| 7 | 0.08 | −0.32 | 0.13 | 0.48 | −0.02 * | −0.53 | −0.12 | −0.22 | −0.14 | −0.41 | 0.11 | 0.15 |
| 8 | −0.07 | −0.16 | 0.13 | 0.23 | −0.31 | −0.24 | 0.04 * | −0.18 | −0.10 | −0.22 | −0.08 | 0.15 |
| 9 | −0.25 | −0.39 | 0.30 | 0.47 | −0.37 | −0.50 | −0.18 | −0.35 | −0.32 | −0.45 | 0.16 | 0.22 |
| 10 | −0.18 | −0.23 | 0.27 | 0.24 | −0.34 | −0.23 | −0.19 | −0.19 | −0.30 | −0.23 | 0.12 | 0.03 * |
| 11 | −0.08 | −0.01 * | 0.20 | −0.14 | −0.25 | 0.15 | −0.08 | 0.05 * | −0.20 | 0.10 | 0.16 | −0.26 |
| 12 | −0.45 | −0.31 | 0.40 | 0.21 | −0.44 | −0.17 | −0.20 | −0.11 * | −0.39 | −0.22 | 0.02 * | 0.09 * |
| All | −0.13 | −0.27 | 0.28 | 0.37 | −0.27 | −0.40 | −0.11 | −0.18 | −0.25 | −0.35 | 0.08 | 0.06 |
| Month | ||||
|---|---|---|---|---|
| C | O | C | O | |
| 1 | 0.58 | −0.50 | 0.55 | −0.50 |
| 2 | −0.09 * | −0.07 * | −0.60 * | −0.06 * |
| 3 | 0.67 | 0.43 | 0.70 | 0.40 |
| 4 | 0.43 | 0.84 | 0.53 | 0.77 |
| 5 | 0.77 | 0.59 | 0.80 | 0.52 |
| 6 | 0.46 | 0.48 | 0.49 | 0.36 |
| 7 | 0.54 | 0.65 | 0.61 | 0.60 |
| 8 | 0.60 | 0.73 | 0.52 | 0.70 |
| 9 | 0.37 | 0.63 | 0.34 | 0.62 |
| 10 | 0.53 | 0.68 | 0.53 | 0.68 |
| 11 | 0.43 | 0.59 | 0.41 | 0.60 |
| 12 | 0.44 | 0.56 | 0.41 | 0.57 |
| All | 0.53 | 0.66 | 0.50 | 0.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rao, R.; Yu, C.; Bai, P.; Li, B. Synergistic Effects of Ocean Background and Tropical Cyclone Characteristics on Tropical Cyclone-Induced Sea Surface Cooling in the Western North Pacific. J. Mar. Sci. Eng. 2025, 13, 955. https://doi.org/10.3390/jmse13050955
Rao R, Yu C, Bai P, Li B. Synergistic Effects of Ocean Background and Tropical Cyclone Characteristics on Tropical Cyclone-Induced Sea Surface Cooling in the Western North Pacific. Journal of Marine Science and Engineering. 2025; 13(5):955. https://doi.org/10.3390/jmse13050955
Chicago/Turabian StyleRao, Rao, Chengcheng Yu, Peng Bai, and Bo Li. 2025. "Synergistic Effects of Ocean Background and Tropical Cyclone Characteristics on Tropical Cyclone-Induced Sea Surface Cooling in the Western North Pacific" Journal of Marine Science and Engineering 13, no. 5: 955. https://doi.org/10.3390/jmse13050955
APA StyleRao, R., Yu, C., Bai, P., & Li, B. (2025). Synergistic Effects of Ocean Background and Tropical Cyclone Characteristics on Tropical Cyclone-Induced Sea Surface Cooling in the Western North Pacific. Journal of Marine Science and Engineering, 13(5), 955. https://doi.org/10.3390/jmse13050955






