Scenario-Based Economic Analysis of Underwater Biofouling Using Artificial Intelligence
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Setup
2.2. Model Theory
2.2.1. ANN
2.2.2. Curve-Fitting Algorithm
2.3. Methodology
2.3.1. Analysis of Sea Trial Data
2.3.2. Acquisition of Voyage Data
2.3.3. Data Cleaning
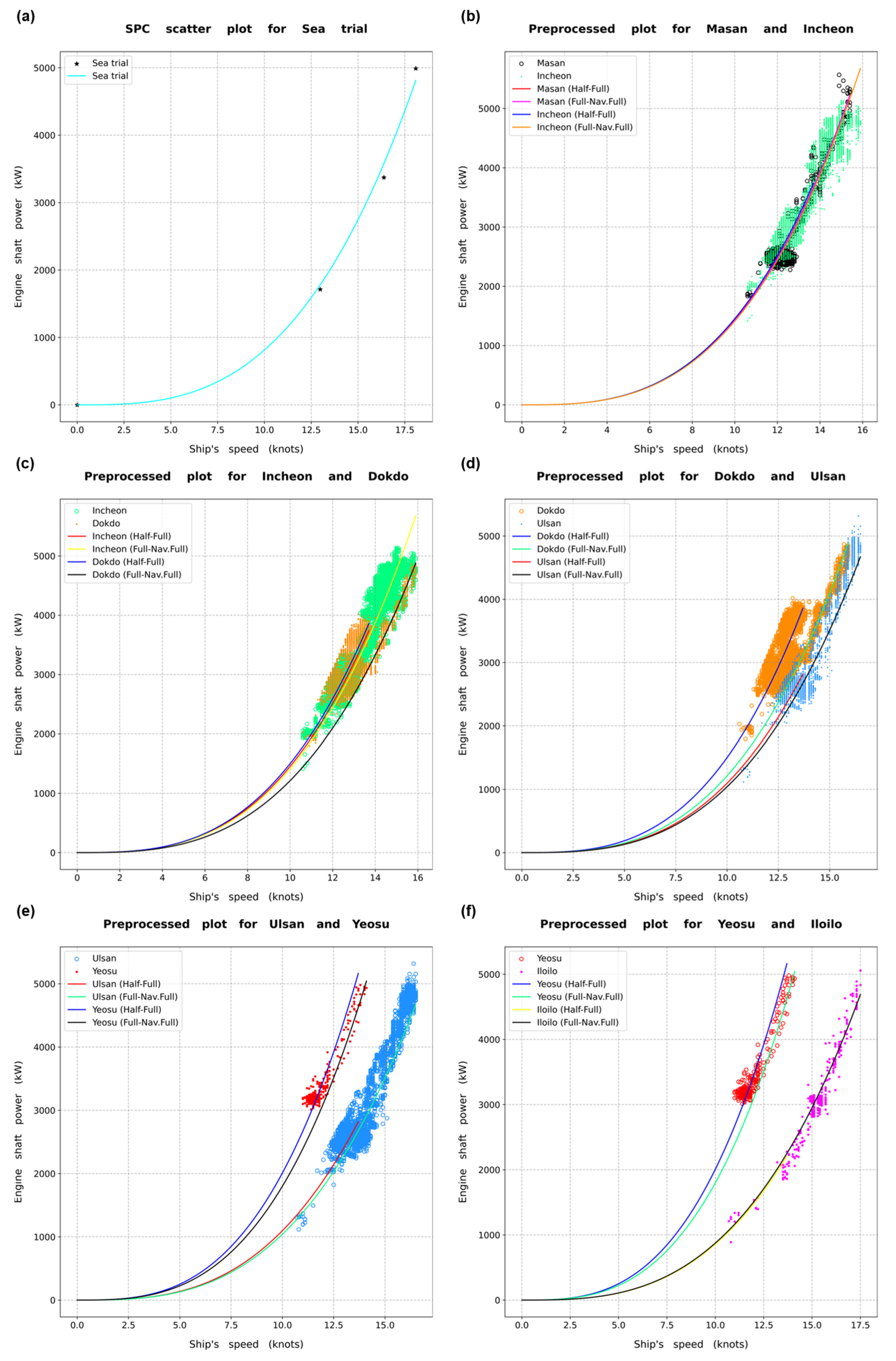
2.3.4. Curve Fitting
2.3.5. Feature Engineering
2.3.6. Performance Metrics
2.3.7. ANN Modeling Process
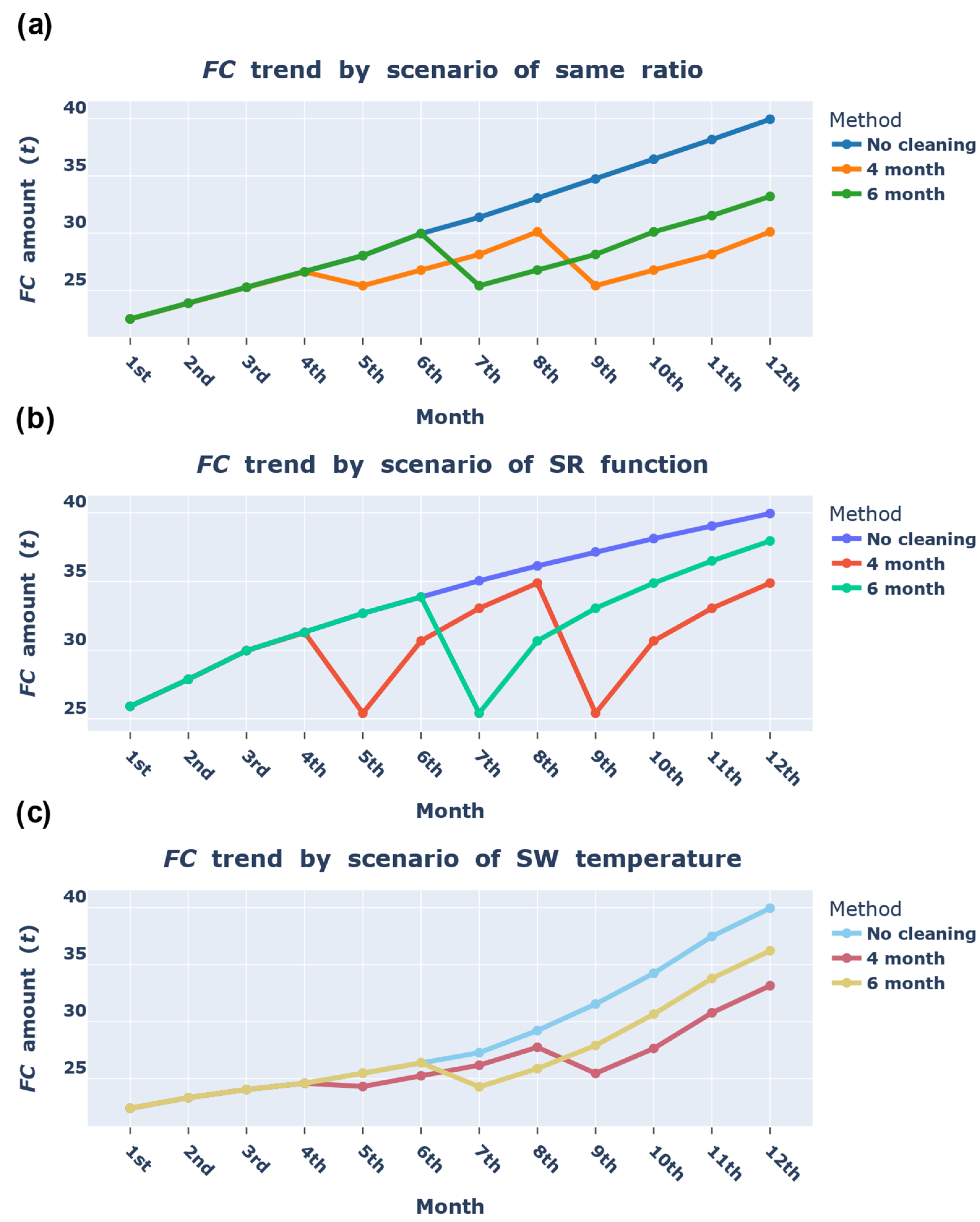
2.3.8. Scenarios for Calculation of Monthly k
2.3.9. Scenarios for Ship Operation
| Departure | Run/Up Engine Date (Time) | Arrival | Stand by Engine Date (Time) | Total Sailing Time (h) | |
|---|---|---|---|---|---|
| Ulsan voyage | Busan | 31 October 2022 (10:36) | Ulsan | 1 Noveber 2022 (08:00) | 21.4 |
| Ulsan | 2 Noveber 2022 (09:30) | Busan | 3 Noveber 2022 (07:30) | 22 | |
| Jeju voyage | Busan | 21 Noveber 2022 (14:24) | Jeju | 22 Noveber 2022 (12:00) | 21.6 |
| Jeju | 24 Noveber 2022 (08:48) | Busan | 25 Noveber 2022 (07:30) | 22.7 | |
| Masan voyage | Busan | 5 December 2022 (10:00) | Masan | 6 December 2022 (07:00) | 21 |
| Masan | 7 December 2022 (10:18) | Busan | 8 December 2022 (07:30) | 21.2 | |
| Jeju voyage | Busan | 13 March 2023 (11:30) | Jeju | 14 March 2023 (09:30) | 22 |
| Jeju | 15 March 2023 (16:12) | Busan | 16 March 2023 (13:00) | 20.8 | |
| Yeosu voyage | Busan | 27 March 2023 (11:30) | Yeosu | 28 March 2023 (08:48) | 21.3 |
| Yeosu | 29 March 2023 (11:30) | Busan | 30 March 2023 (09:30) | 22 | |
| Donghae voyage | Busan | 10 April 2023 (11:36) | Donghae | 11 April 2023 (06:36) | 19 |
| Donghae | 12 April 2023 (11:42) | Busan | 13 April 2023 (09:18) | 21.6 | |
| Busan voyage | Busan | 24 April 2023 (11:06) | Busan | 26 April 2023 (10:00) | 46.9 |
| Japan voyage | Busan | 17 May 2023 (11:06) | Naha | 20 May 2023 (08:00) | 68.9 |
| Naha | 22 May 2023 (13:06) | Tokyo | 25 May 2023 (07:36) | 66.5 | |
| Tokyo | 29 May 2023 (09:42) | Busan | 31 May 2023 (19:36) | 57.9 | |
| Mokpo voyage | Busan | 7 August 2023 (19:36) | Mokpo | 8 August 2023 (11:48) | 16.2 |
| Mokpo | 10 August 2023 (22:12) | Busan | 11 August 2023 (14:12) | 16 | |
| Jeju voyage | Busan | 18 September 2023 (11:30) | Jeju | 19 September 2023 (09:30) | 22 |
| Jeju | 21 September 2023 (10:12) | Busan | 22 September 2023 (08:00) | 21.8 | |
| Yeosu voyage | Busan | 15 October 2023 (11:12) | Yeosu | 17 October 2023 (07:12) | 44 |
| Yeosu | 29 October 2023 (16:24) | Busan | 30 October 2023 (13:24) | 21 | |
| Total sum of sailing time (h) from 31 October 2022 to 30 October 2023 | 637.8 | ||||
| Total time (h) in a year | 8760 | ||||
| Sailing rate (%) in one year | 7.2808 | ||||
| Sailing time in a month based on the sailing rate in one year | 2 days and 5 h | ||||
2.3.10. Calculation of FC Based on Scenarios
3. Results
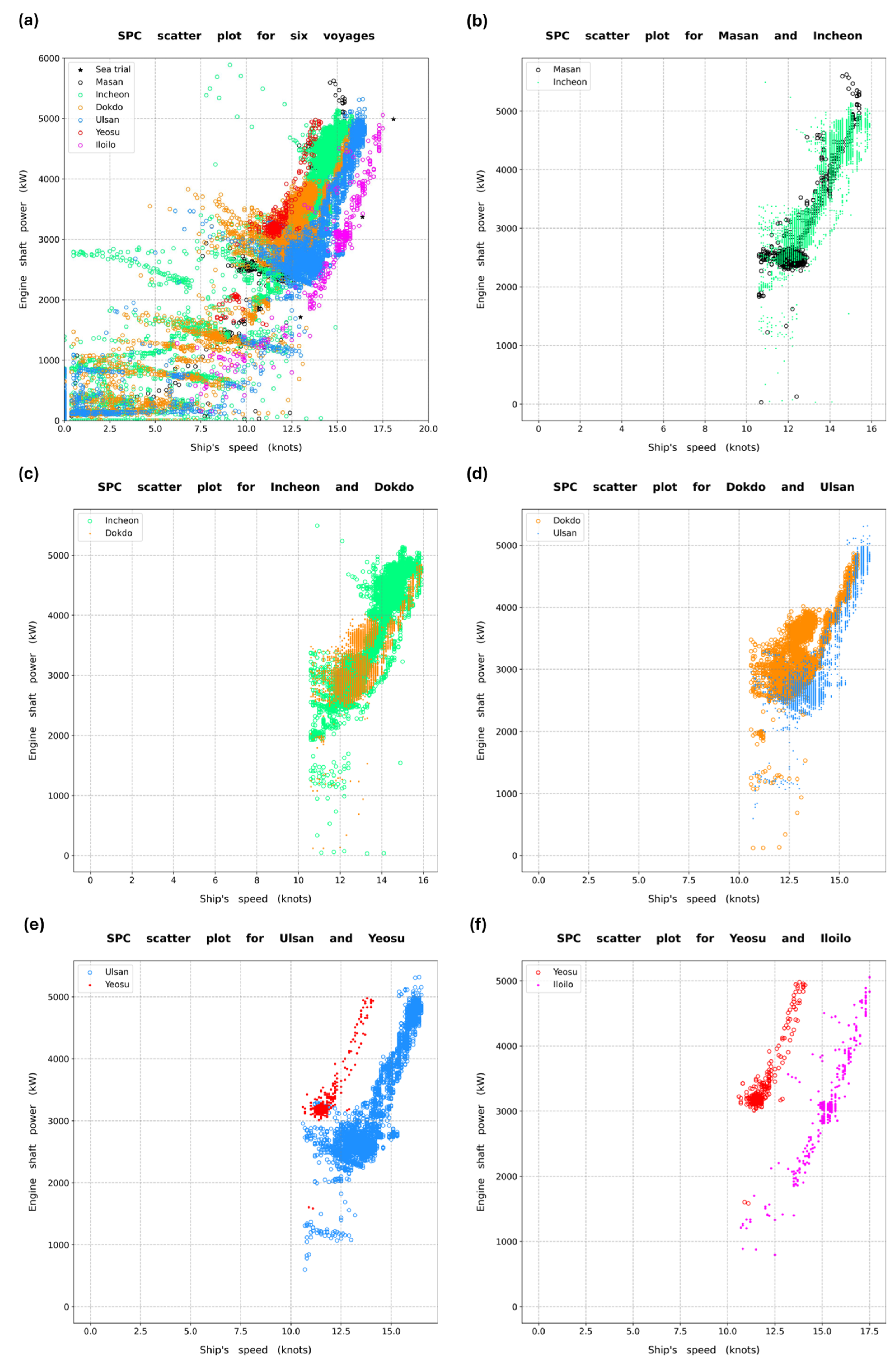
3.1. Analysis of SPC Scatter Plot for Six Voyages
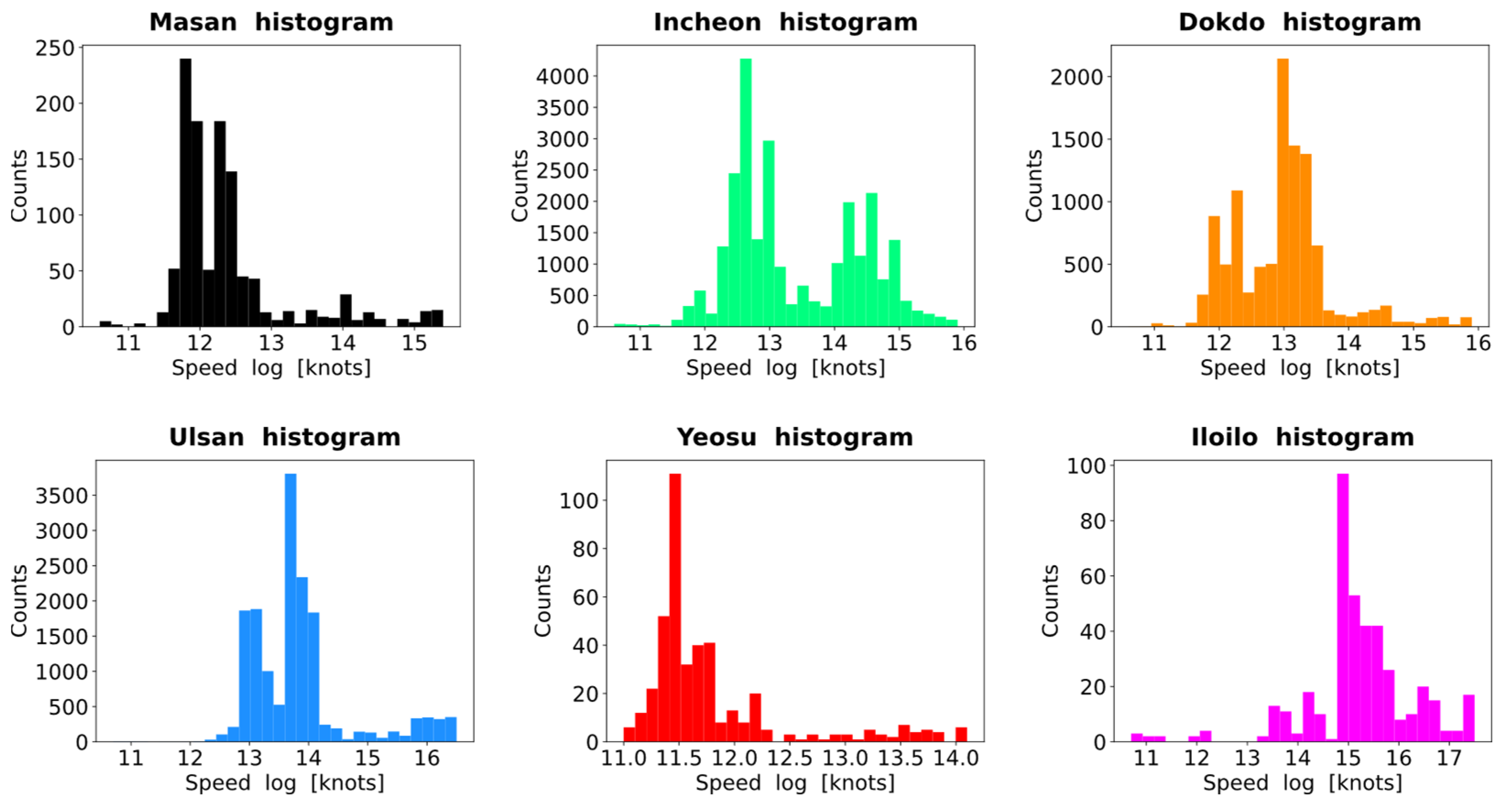
3.2. Outlier Removal and Normalization
3.3. Hyperparameter Optimization for ANN
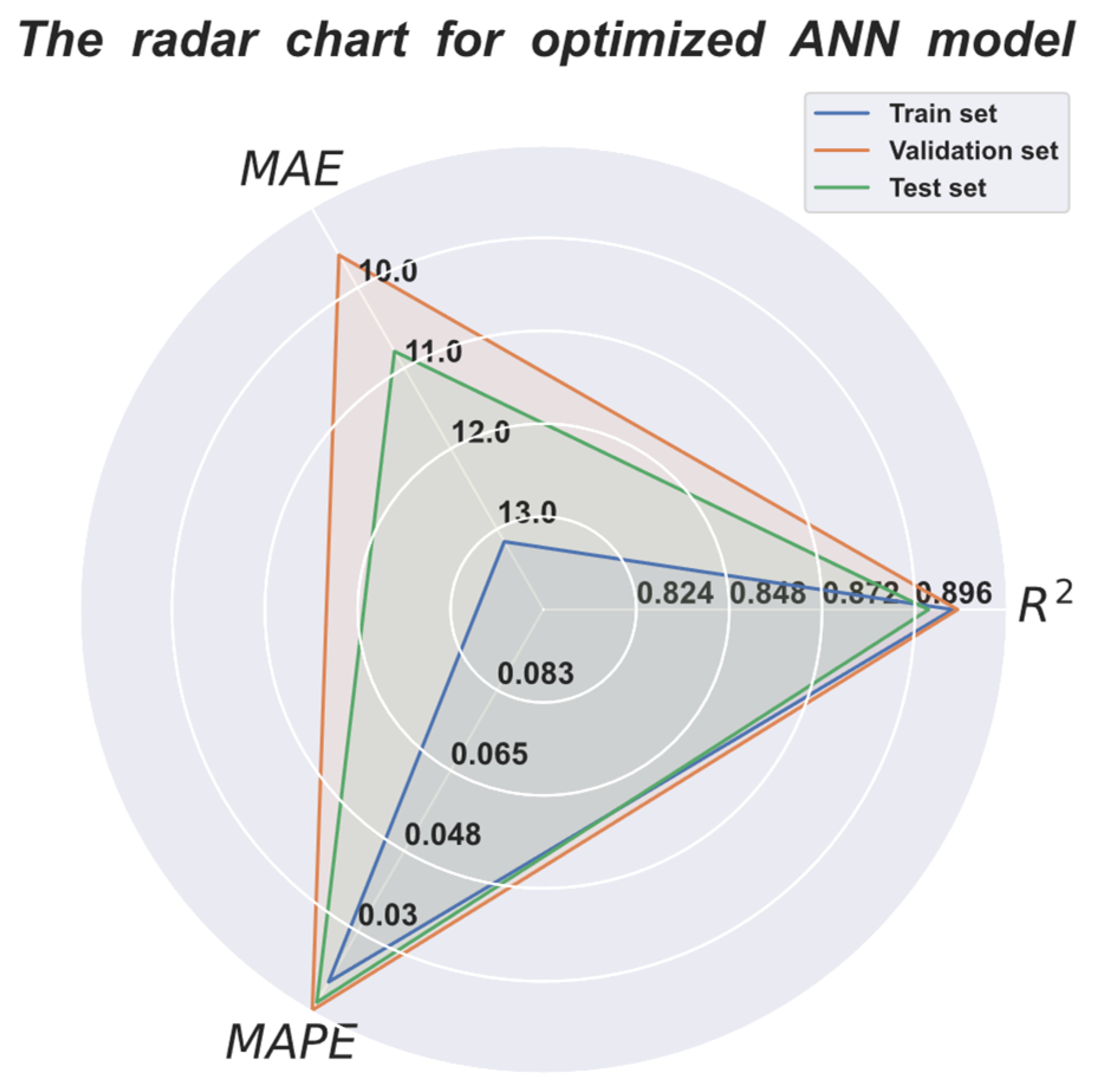
3.4. Evaluation of ANN Model Based on Performance Metrics
4. Scenario-Based Economic Analysis
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| AI | Artificial intelligence |
| ANN | Artificial neural network |
| FC | Fuel consumption |
| IMO | International Maritime Organization |
| ISO | International Organization for Standardization |
| KHOA | Korea Hydrographic and Oceanographic Agency |
| KRISO | Korea Research Institute of Ships and Ocean Engineering |
| LM | Levenberg–Marquardt |
| LSMGO | Low-sulfur marine gas oil |
| MAE | Mean absolute error |
| MAPE | Mean absolute percentage error |
| M/E | Main engine |
| ReLU | Rectified linear unit |
| RMSE | Root mean square error |
| RPM | Revolutions per minute |
| SPC | Speed–power curve |
| SR | Square root |
| SW | Sea water |
| UHPC | Underwater hull and propeller cleaning |
| UK | United Kingdom |
| W&B | Weights and biases |
References
- Lindholdt, A.; Dam-Johansen, K.; Olsen, S.M.; Yebra, D.M.; Kiil, S. Effects of Biofouling Development on Drag Forces of Hull Coatings for Ocean-Going Ships: A Review. J. Coat. Technol. Res. 2015, 12, 415–444. [Google Scholar] [CrossRef]
- Adland, R.; Cariou, P.; Jia, H.; Wolff, F.C. The Energy Efficiency Effects of Periodic Ship Hull Cleaning. J. Clean. Prod. 2018, 178, 1–13. [Google Scholar] [CrossRef]
- Oliveira, D.R.; Granhag, L. Ship Hull In-Water Cleaning and Its Effects on Fouling-Control Coatings. Biofouling 2020, 36, 332–350. [Google Scholar] [CrossRef]
- Demirel, Y.K.; Turan, O.; Incecik, A. Predicting the Effect of Biofouling on Ship Resistance Using CFD. Appl. Ocean Res. 2017, 62, 100–118. [Google Scholar] [CrossRef]
- Oliveira, D.; Larsson, A.I.; Granhag, L.; Ralston, E.; Gardner, H.; Hunsucker, K.Z.; Swain, G.; Schultz, M.P.; Tian, L.; Yin, Y.; et al. Factors That Influence Vessel Biofouling and Its Prevention and Management; Final Report for CEBRA Project 190803; Cebra: Parkville, Australia, 2021; p. 34. [Google Scholar]
- Hakim, M.L.; Nugroho, B.; Nurrohman, M.N.; Suastika, I.K.; Utama, I.K.A.P. Investigation of Fuel Consumption on an Operating Ship Due to Biofouling Growth and Quality of Anti-Fouling Coating. IOP Conf. Ser. Earth Environ. Sci. 2019, 339, 012037. [Google Scholar] [CrossRef]
- Valchev, I.; Coraddu, A.; Kalikatzarakis, M.; Geertsma, R.; Oneto, L. Numerical Methods for Monitoring and Evaluating the Biofouling State and Effects on Vessels’ Hull and Propeller Performance: A Review. Ocean Eng. 2022, 251, 110883. [Google Scholar] [CrossRef]
- Liu, S.; Kee, Y.H.; Shang, B.; Papanikolaou, A. Assessment of the Economic, Environmental and Safety Impact of Biofouling on a Ship’s Hull and Propeller. Ocean Eng. 2023, 285, 115481. [Google Scholar] [CrossRef]
- Swain, G.; Erdogan, C.; Foy, L.; Gardner, H.; Harper, M.; Hearin, J.; Hunsucker, K.Z.; Hunsucker, J.T.; Lieberman, K.; Nanney, M.; et al. Proactive In-Water Ship Hull Grooming as a Method to Reduce the Environmental Footprint of Ships. Front. Mar. Sci. 2022, 8, 808549. [Google Scholar] [CrossRef]
- Song, C.; Cui, W. Review of Underwater Ship Hull Cleaning Technologies. J. Mar. Sci. Appl. 2020, 19, 415–429. [Google Scholar] [CrossRef]
- Oliveira, D.R.; Lagerström, M.; Granhag, L.; Werner, S.; Larsson, A.I.; Ytreberg, E. A Novel Tool for Cost and Emission Reduction Related to Ship Underwater Hull Maintenance. J. Clean. Prod. 2022, 356, 131882. [Google Scholar] [CrossRef]
- Coraddu, A.; Lim, S.; Oneto, L.; Pazouki, K.; Norman, R.; Murphy, A.J. A Novelty Detection Approach to Diagnosing Hull and Propeller Fouling. Ocean Eng. 2019, 176, 65–73. [Google Scholar] [CrossRef]
- Coraddu, A.; Oneto, L.; Baldi, F.; Cipollini, F.; Atlar, M.; Savio, S. Data-Driven Ship Digital Twin for Estimating the Speed Loss Caused by the Marine Fouling. Ocean Eng. 2019, 186, 106063. [Google Scholar] [CrossRef]
- Farkas, A.; Degiuli, N.; Martić, I.; Ančić, I. Energy Savings Potential of Hull Cleaning in a Shipping Industry. J. Clean. Prod. 2022, 374, 134000. [Google Scholar] [CrossRef]
- Laurie, A.; Anderlini, E.; Dietz, J.; Thomas, G. Machine Learning for Shaft Power Prediction and Analysis of Fouling Related Performance Deterioration. Ocean Eng. 2021, 234, 108886. [Google Scholar] [CrossRef]
- Cesium The Platform for 3D Geospatial. Available online: https://cesium.com/ (accessed on 1 April 2025).
- Archnuri Completion of Basic Design for Construction of New Training Ship Hannara. Available online: http://www.archnuri.com/new/sub01.asp?mode=list&page=33&s_type=&s_value=&n_code=ARCHNURI-201201&c_code=02&c_sort=0201 (accessed on 1 April 2025).
- Amato, F.; López, A.; Peña-Méndez, E.M.; Vaňhara, P.; Hampl, A.; Havel, J. Artificial Neural Networks in Medical Diagnosis. J. Appl. Biomed. 2013, 11, 47–58. [Google Scholar] [CrossRef]
- Villarrubia, G.; De Paz, J.F.; Chamoso, P.; De la Prieta, F. Artificial Neural Networks Used in Optimization Problems. Neurocomputing 2018, 272, 10–16. [Google Scholar] [CrossRef]
- Park, M.-H.; Hur, J.-J.; Lee, W.-J. Prediction of Diesel Generator Performance and Emissions Using Minimal Sensor Data and Analysis of Advanced Machine Learning Techniques. J. Ocean Eng. Sci. 2023, 10, 150–168. [Google Scholar] [CrossRef]
- Park, M.H.; Lee, C.M.; Nyongesa, A.J.; Jang, H.J.; Choi, J.H.; Hur, J.J.; Lee, W.J. Prediction of Emission Characteristics of Generator Engine with Selective Catalytic Reduction Using Artificial Intelligence. J. Mar. Sci. Eng. 2022, 10, 1118. [Google Scholar] [CrossRef]
- Jiang, J.; Trundle, P.; Ren, J. Medical Image Analysis with Artificial Neural Networks. Comput. Med. Imaging Graph. 2010, 34, 617–631. [Google Scholar] [CrossRef]
- Park, M.H.; Hur, J.J.; Lee, W.J. Prediction of Oil-Fired Boiler Emissions with Ensemble Methods Considering Variable Combustion Air Conditions. J. Clean. Prod. 2022, 375, 134094. [Google Scholar] [CrossRef]
- SciPy v1.12.0 Manual Scipy.Optimize.Curve_fit. Available online: https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.curve_fit.html (accessed on 1 April 2025).
- Chen, K.; Zhang, M.; Fu, S.; Zhao, B.; Luo, C. A Numerical Model for Stress Relaxation Analysis of Sealing Systems in Nonbonded Pipe End Fittings. J. Ocean Eng. Sci. 2023, 2, 43. [Google Scholar] [CrossRef]
- Shan, S. A Levenberg-Marquardt Method for Large-Scale Bound-Constrained Nonlinear Least-Squares. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 2008. [Google Scholar]
- Wang, M.; Xu, X.; Yan, Z.; Wang, H. An Online Optimization Method for Extracting Parameters of Multi-Parameter PV Module Model Based on Adaptive Levenberg-Marquardt Algorithm. Energy Convers. Manag. 2021, 245, 114611. [Google Scholar] [CrossRef]
- Gavin, H.P. The Levenberg-Marquardt Algorithm for Nonlinear Least Squares Curve-Fitting Problems; Duke University: Durham, NC, USA, 2019. [Google Scholar]
- Dkhichi, F.; Oukarfi, B.; Fakkar, A.; Belbounaguia, N. Parameter Identification of Solar Cell Model Using Levenberg-Marquardt Algorithm Combined with Simulated Annealing. Sol. Energy 2014, 110, 781–788. [Google Scholar] [CrossRef]
- Furuno Electric. Finished Plan—Speed Log (DS-60); Furuno Electric: Nishinomiya, Hyogo, Japan, 2019. [Google Scholar]
- Aquametro. Final Drawing—Flowmeter for M/E F.O (10K-40A); Aquametro: Therwil, Switzerland, 2018. [Google Scholar]
- Specs. Final Drawing for Shaft Torque Power Meter; Specs: Austin, TX, USA, 2018. [Google Scholar]
- Psaraftis, H.N.; Lagouvardou, S. Ship Speed vs Power or Fuel Consumption: Are Laws of Physics Still Valid? Regression Analysis Pitfalls and Misguided Policy Implications. Clean. Logist. Supply Chain 2023, 7, 100111. [Google Scholar] [CrossRef]
- Park, M.H.; Yeo, S.; Yang, S.K.; Shin, D.; Kim, J.H.; Choi, J.H.; Lee, W.J. Analysis and Forecasting of National Marine Litter Based on Coastal Data in South Korea from 2009 to 2021. Mar. Pollut. Bull. 2023, 189, 114803. [Google Scholar] [CrossRef]
- Renaud, O.; Victoria-Feser, M.P. A Robust Coefficient of Determination for Regression. J. Stat. Plan. Inference 2010, 140, 1852–1862. [Google Scholar] [CrossRef]
- Aydın, B.; Yağuzluk, S.; Açıkkar, M. Prediction of Landslide Tsunami Run-up on a Plane Beach through Feature Selected MLP-Based Model. J. Ocean Eng. Sci. 2024, 9, 222–231. [Google Scholar] [CrossRef]
- Keras. Keras 3 API Documentation. Available online: https://keras.io/api/ (accessed on 1 April 2025).
- Weights & Biases. The AI Developer Platform. Available online: https://wandb.ai/site (accessed on 1 April 2025).
- Wu, J.; Chen, X.Y.; Zhang, H.; Xiong, L.D.; Lei, H.; Deng, S.H. Hyperparameter Optimization for Machine Learning Models Based on Bayesian Optimization. J. Electron. Sci. Technol. 2019, 17, 26–40. [Google Scholar] [CrossRef]
- Visscher, J.P. Nature and Extent of Fouling of Ships’ Bottoms. Bull. Bur. Fish. Part II 1927, 43, 193–252. [Google Scholar]
- Hadžić, N.; Gatin, I.; Uroić, T.; Ložar, V. Biofouling Dynamic and Its Impact on Ship Powering and Dry-Docking. Ocean Eng. 2022, 245, 110522. [Google Scholar] [CrossRef]
- Munk, T.; Kane, D.; Yebra, D.M. The Effects of Corrosion and Fouling on the Performance of Ocean-Going Vessels: A Naval Architectural Perspective. In Advances in Marine Antifouling Coatings and Technologies; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Graham, H.W.; Gay, H. Season of Attachment and Growth of Sedentary Marine Organisms at Oakland, California. Ecology 1945, 26, 375–386. [Google Scholar] [CrossRef]
- Lord, J.P.; Calini, J.M.; Whitlatch, R.B. Influence of Seawater Temperature and Shipping on the Spread and Establishment of Marine Fouling Species. Mar. Biol. 2015, 162, 2481–2492. [Google Scholar] [CrossRef]
- UK Defence Club. Hull Fouling: The Legal and the Practical. Available online: https://www.ukdefence.com/fileadmin/uploads/uk-defence/Documents/Soundings/2020/1411-UKDC-Hull-Fouling-web.pdf (accessed on 1 April 2025).
- Crisp, D.J. The Effects of the Severe Winter of 1962–63 on Marine Life in Britain. J. Anim. Ecol. 1964, 33, 165. [Google Scholar] [CrossRef]
- Lord, J.P. Impact of Seawater Temperature on Growth and Recruitment of Invasive Fouling Species at the Global Scale. Mar. Ecol. 2017, 38, e12404. [Google Scholar] [CrossRef]
- KHOA. Ocean Data in Grid Framework. Available online: http://www.khoa.go.kr/oceangrid/khoa/intro.do (accessed on 1 April 2025).
- Ship & Bunker. World Bunker Prices. Available online: https://shipandbunker.com/prices#MGO (accessed on 1 April 2025).
- Bayraktar, M.; Yuksel, O.; Pamik, M. An Evaluation of Methanol Engine Utilization Regarding Economic and Upcoming Regulatory Requirements for a Container Ship. Sustain. Prod. Consum. 2023, 39, 345–356. [Google Scholar] [CrossRef]
- Korean Register Rules for the Classification of Steel Ships Part 1 Classification and Surveys. Available online: https://www.krs.co.kr/KRRules/KRRules2022/KRRulesE.html (accessed on 1 April 2025).
- Akinfiev, T.; Janushevskis, A.; Lavendelis, E. A Brief Survey of Ship Hull Cleaning Devices. Transp. Eng. 2007, 24, 133–146. [Google Scholar]
- GloMEEP. Hull Cleaning. Available online: https://glomeep.imo.org/technology/hull-cleaning/ (accessed on 1 April 2025).
- FAO. Estimate of the Global Fleet and Its Regional Distribution. Available online: https://www.fao.org/3/cc0461en/online/sofia/2022/fishing-fleet.html (accessed on 1 April 2025).
- UNCTAD. Review of Maritime Transport 2023. Available online: https://unctad.org/system/files/official-document/rmt2023_en.pdf (accessed on 1 April 2025).
- Nassiraei, A.A.F.; Sonoda, T.; Ishii, K. Development of Ship Hull Cleaning Underwater Robot. In Proceedings of the International Conference on Emerging Trends in Engineering and Technology, ICETET, Himeji, Japan, 5–7 November 2012. [Google Scholar]
- Soon, Z.Y.; Jung, J.H.; Yoon, C.; Kang, J.H.; Kim, M. Characterization of Hazards and Environmental Risks of Wastewater Effluents from Ship Hull Cleaning by Hydroblasting. J. Hazard. Mater. 2021, 403, 123708. [Google Scholar] [CrossRef]






| Parameter | Value | Parameter | Value |
|---|---|---|---|
| IMO number | 9,807,279 | Length between perpendiculars (m) | 120 |
| Name | HANNARA | Breadth (m) | 19.4 |
| Type | Training ship | Wetted surface area (m2) | 2694.8 |
| Flag | South Korea | Year built | 2019 |
| Gross tonnage (t) | 9196 | Engine type | MAN 6S40ME-B9.5 |
| Summer deadweight (t) | 3671 | Engine power | 6618 kW at 146 rpm |
| Displacement at maximum draught (t) | 9122.2 | No. of propeller blades | 4 |
| Length overall (m) | 133 | Propeller diameter (m) | 4 |
| Voyage Destination | Date of Data Collection | Description |
|---|---|---|
| Masan | 25–26 April 2022 | Two months before bow/stern thrusters’ cleaning and propeller polishing. |
| Incheon | 25–30 May 2022 | One month before bow/stern thrusters’ cleaning and propeller polishing. |
| Dokdo | 25–27 June 2022 | After bow/stern thrusters’ cleaning and propeller polishing (23 June 2022). |
| Ulsan | 31 October–3 November 2022 | (1) Two months after stern thruster cleaning (24 August 2022). (2) One month after underwater hull and propeller cleaning (30 September 2022). |
| Yeosu | 16 October 2023 | Before drydocking. |
| Iloilo | 11 November 2023 | After drydocking. |
| Painting Area | Paint Name | Paint Maker | Paint Type | Dry Film Thickness (µm) | Thinner Number | Order of Painting |
|---|---|---|---|---|---|---|
| Upper part for the waterline of hull | EH2350-2260 | KCC Corporation | Epoxy anti-abrasion | 100 | 024 | 1st |
| EH2350-1128 | Epoxy anti-abrasion | 100 | 024 | 2nd | ||
| UT6581(K1)-1000 | Polyurethane finish | 100 | 0624 | 3rd | ||
| Lower part for the waterline of hull | EH2350-2260 | Epoxy anti-abrasion | 100 | 024 | 1st | |
| EH2560-Y/LIGHT | Modified vinyl epoxy | 100 | 024 | 2nd | ||
| A/F795-RED BROWN | Tin-free SPC antifouling paint | 100 | 002 | 3rd | ||
| Propeller | EH2350-2260 | Epoxy anti-abrasion | 125 | 024 | 1st | |
| MetaCruise Primer | Epoxy primer | 125 | 024 | 2nd | ||
| MetaCruise Tie | Tie coat | 100 | 002 | 3rd | ||
| MetaCruise NS | Silicone AF | 150 | Not recommended | 4th |
| Fuel Oil Flowmeter | Shaft Torque Power Meter | Doppler Sonar | |||
|---|---|---|---|---|---|
| Item | Description | Item | Description | Item | Description |
| Manufacturer | Aquametro | Manufacturer | Specs | Manufacturer | Furuno Electric |
| Type | VZFA II 40 FL 130/25 | Rotor
|
|
|
|
| Nominal diameter | DN 40 mm | Stator
|
| Transducer
|
|
| Nominal pressure | PN 25 bar | RPM sensing unit and power head
|
| Ship’s speed range
|
|
| Maximum temperature | 130 °C | Working depth
|
| ||
| Measuring range | 225–9000 l/h | Accuracy
|
| ||
| Maximum permissible error | ±0.5% of actual value |
|
| ||
| Repeatability | ±0.1% | ||||
| Nominal voltage | 24 V DC | ||||
| Power supply via 4~20 mA | 6–30 V DC | ||||
| Protection degree (IEC60529) | IP66/IP68/IP69 | ||||
| Ambient temperature | –25 to +70 °C | ||||
| Voyage | Original Data (Rows/Columns) | Preprocessed Data (Rows/Columns) | Half–Full Data (Rows/Columns) | Full–Nav. Full Data (Rows/Columns) |
|---|---|---|---|---|
| Masan | (1440/3) | (1194/3) | (1089/3) | (105/3) |
| Incheon | (42,996/3) | (26,552/3) | (16,527/3) | (10,025/3) |
| Dokdo | (25,709/3) | (11,751/3) | (10,795/3) | (956/3) |
| Ulsan | (34,331/3) | (16,456/3) | (9803/3) | (6653/3) |
| Yeosu | (467/3) | (433/3) | (423/3) | (10/3) |
| Iloilo | (475/3) | (432/3) | (45/3) | (387/3) |
| Voyage | Half–Full | Full–Nav. Full | Half–Nav. Full |
|---|---|---|---|
| Sea trial | – | – | 0.8139 |
| Masan | 1.4212 | 1.4300 | 1.4231 |
| Incheon | 1.4546 | 1.4120 | 1.4298 |
| Dokdo | 1.5008 | 1.2137 | 1.4517 |
| Ulsan | 1.0961 | 1.0401 | 1.0654 |
| Yeosu | 2.0078 | 1.7988 | 1.9954 |
| Iloilo | 0.8581 | 0.8750 | 0.8744 |
| Model | Hyperparameter | Range/Values |
|---|---|---|
| ANN | Batch size | min: 8, max: 128 |
| Activation function | relu, selu, elu, leaky relu, gelu, swish | |
| Dropout rate | min: 0.1, max: 0.3 | |
| Number of hidden layers | min: 1, max: 3 | |
| Initial mode | random normal, random uniform, glorot normal, glorot uniform, he normal, he uniform | |
| Learning rate | min: 10−4, max: 0.1 | |
| Number of neurons | min: 3, max: 15 | |
| Optimizer | sgd, rmsprop, adam, adagrad, nadam |
| Difference in | Description | |||
|---|---|---|---|---|
| Half–Full | Full–Nav. Full | Half–Nav. Full | ||
| Change in values over a year | 0.9117 | 0.7587 | 0.93 | Difference in the values between Ulsan and Yeosu voyages. |
| Monthly increase in | Description | |||
| Half–Full | Full–Nav. Full | Half–Nav. Full | ||
| (1) Same ratio () | 0.076 | 0.0632 | 0.0775 | value change over a year divided by 12. |
| (2) SR function | Monthly difference in the calculated SR function. | |||
| (3) SW temperature | Percent cover value for each month calculated based on research and data [47,48]. | |||
| ANN | Training set | 13.1560 | 0.9057 | 0.0195 |
| Validation set | 9.5960 | 0.9070 | 0.0134 | |
| Test set | 10.7925 | 0.8995 | 0.0151 |
| Range | Price (USD/MT) | Date | |
|---|---|---|---|
| Rotterdam | Maximum | 995.5 | 15 September 2023 |
| Minimum | 643.5 | 3 May 2023 | |
| Average | 819.5 | ||
| Singapore | Maximum | 981 | 15 September 2023 |
| Minimum | 656 | 4 May 2023 | |
| Average | 818.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, M.-H.; Hur, J.-J.; Yun, G.-H.; Lee, W.-J. Scenario-Based Economic Analysis of Underwater Biofouling Using Artificial Intelligence. J. Mar. Sci. Eng. 2025, 13, 952. https://doi.org/10.3390/jmse13050952
Park M-H, Hur J-J, Yun G-H, Lee W-J. Scenario-Based Economic Analysis of Underwater Biofouling Using Artificial Intelligence. Journal of Marine Science and Engineering. 2025; 13(5):952. https://doi.org/10.3390/jmse13050952
Chicago/Turabian StylePark, Min-Ho, Jae-Jung Hur, Gwi-Ho Yun, and Won-Ju Lee. 2025. "Scenario-Based Economic Analysis of Underwater Biofouling Using Artificial Intelligence" Journal of Marine Science and Engineering 13, no. 5: 952. https://doi.org/10.3390/jmse13050952
APA StylePark, M.-H., Hur, J.-J., Yun, G.-H., & Lee, W.-J. (2025). Scenario-Based Economic Analysis of Underwater Biofouling Using Artificial Intelligence. Journal of Marine Science and Engineering, 13(5), 952. https://doi.org/10.3390/jmse13050952






