Underwater Time Delay Estimation Based on Meta-DnCNN with Frequency-Sliding Generalized Cross-Correlation
Abstract
1. Introduction
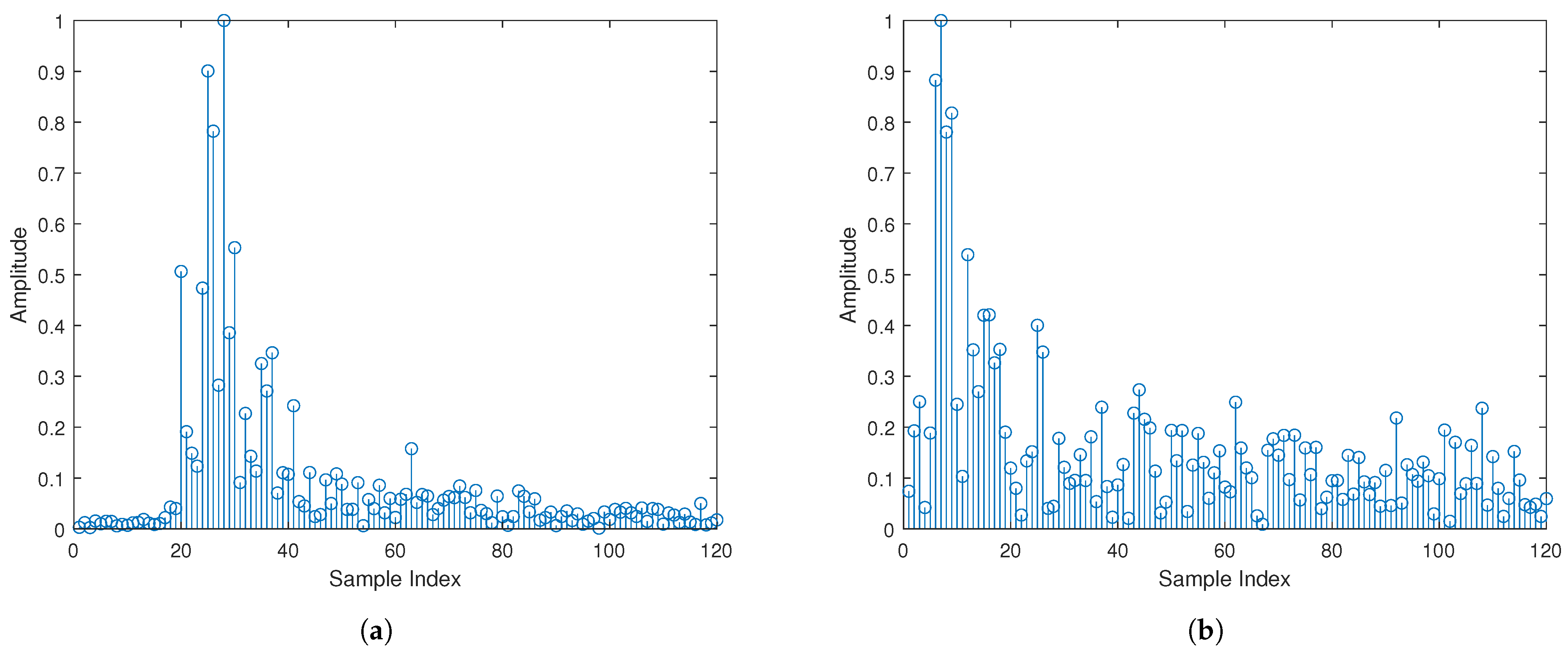
- Reconstruct FS-GCC matricies for multiple subwindow groups. Each subwindow captures time delay-related signal features from different frequency band perspectives, thereby enriching the information dimension of the FS-GCC matricies and enhancing the key feature vectors. Compared with traditional FS-GCC procedure, this reconstruction operation can more fully extract the time delay information in the signals, improve the accuracy of TDE, and reduce the probability of abnormal estimation.
- Recognizing the effectiveness of the DnCNN in image denoising and feature extraction, this paper introduces it into the field of underwater TDE. The FS-GCC matrix is transformed into a grayscale image, and the DnCNN architecture is utilized to strengthen time delay features reconstructed from the FS-GCC. The network automatically learns and extracts refined time delay features through multi-layer convolution operations, effectively suppressing noise interference and significantly improving estimation accuracy. Compared with other deep learning methods, DnCNN has stronger noise extraction capabilities and can better adapt to the complex underwater noise environment.
- Considering the variable SNR in underwater acoustic environments and the scarcity of high-quality training samples due to equipment limitations, we train the DnCNN model using a model-agnostic meta-learning (MAML) framework [21,22,23]. MAML simulates training tasks under diverse SNR conditions, enabling the model to adapt swiftly to new environments. This approach facilitates efficient learning with limited samples and promotes knowledge sharing across tasks, consequently increasing the model’s generalization ability in varying SNR scenarios and improving its practicality and robustness in complex underwater environments.
2. Basic Theory
2.1. Signal Model
2.2. Generalized Cross-Correlation
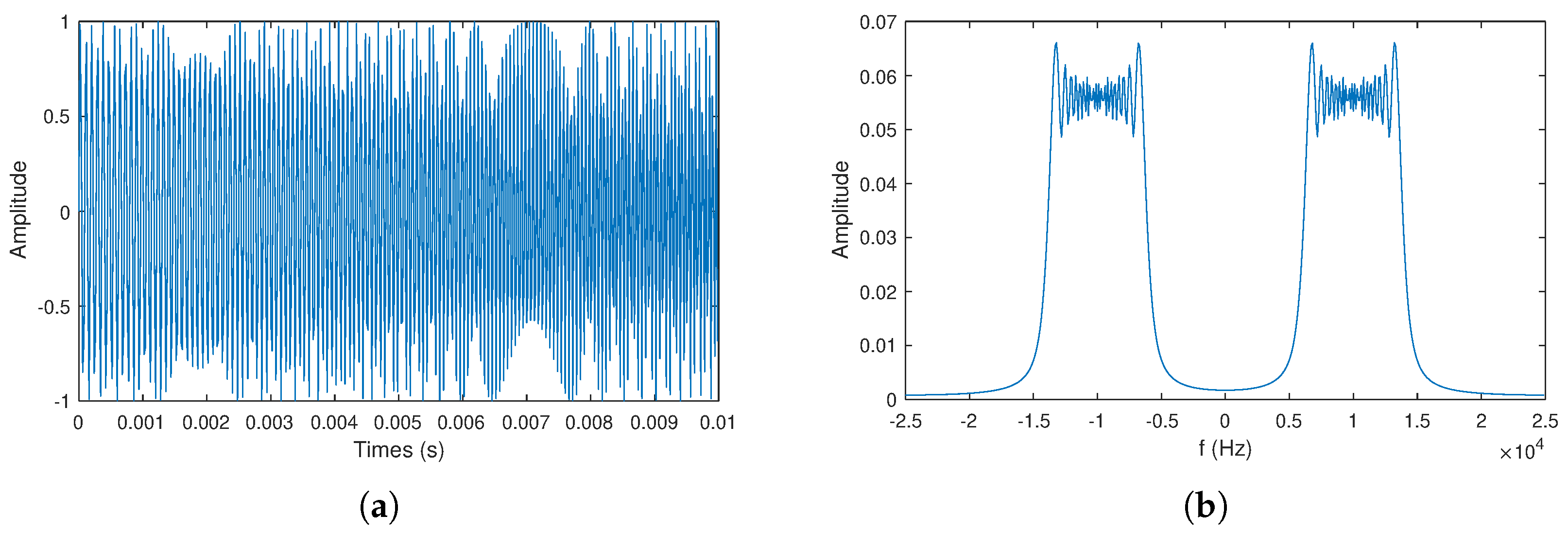
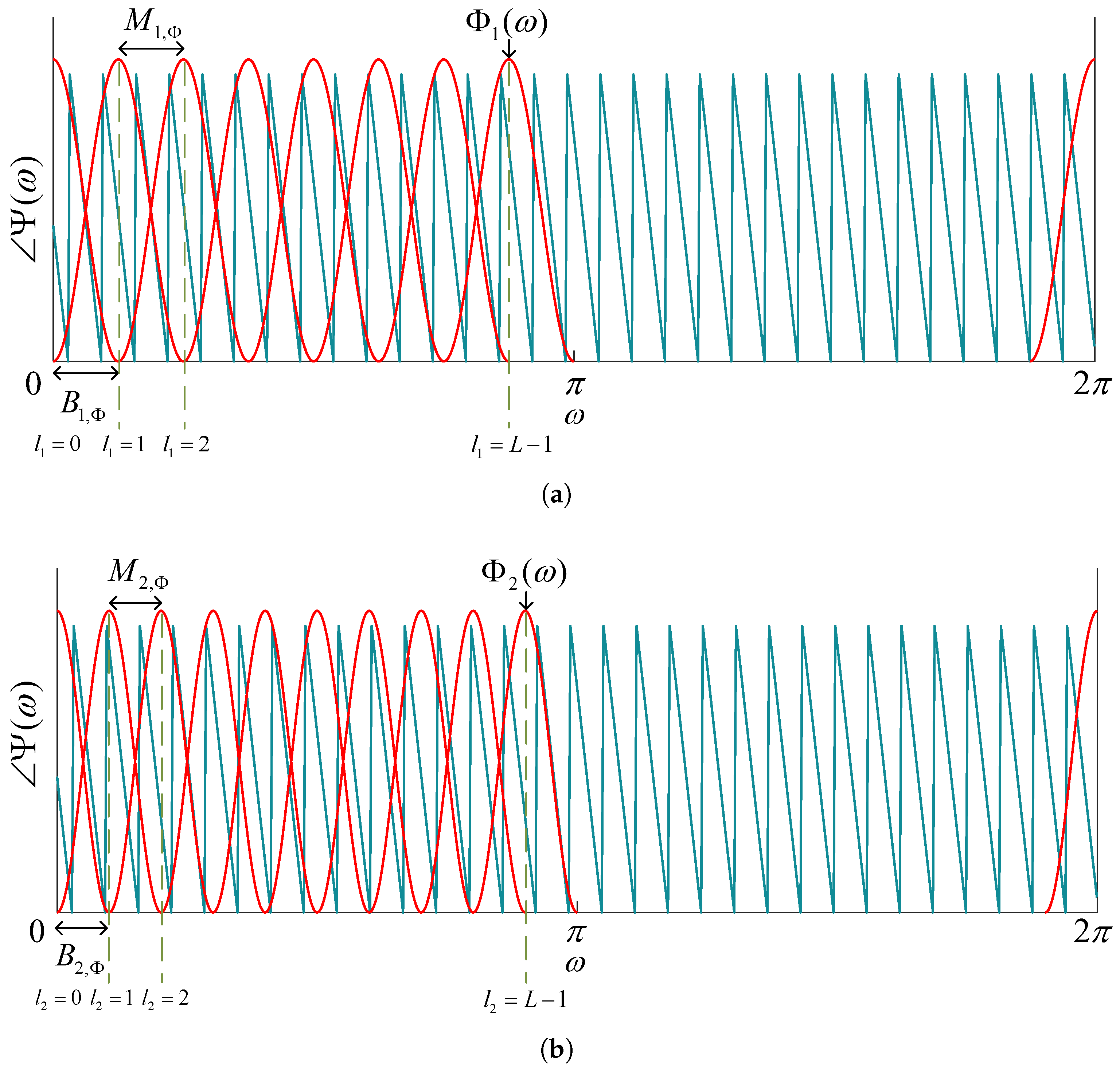
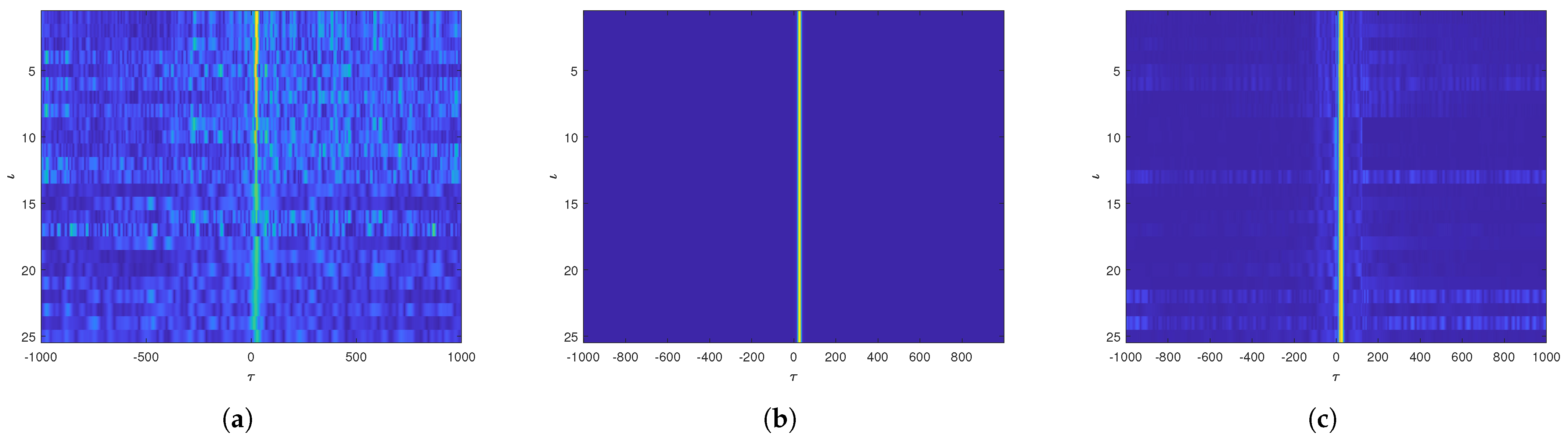
2.3. Frequency-Sliding Generalized Cross-Correlation
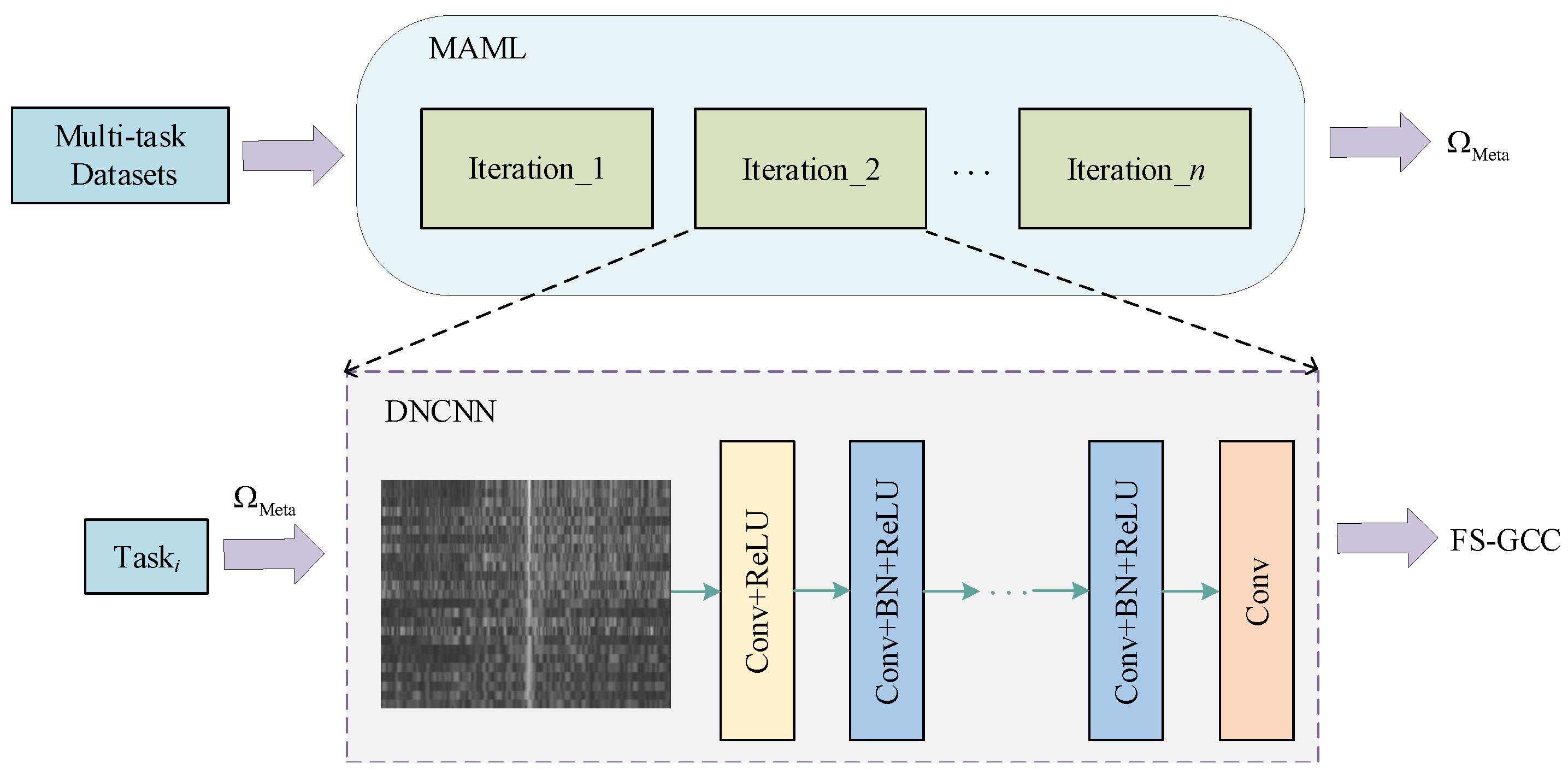
3. Proposed Method
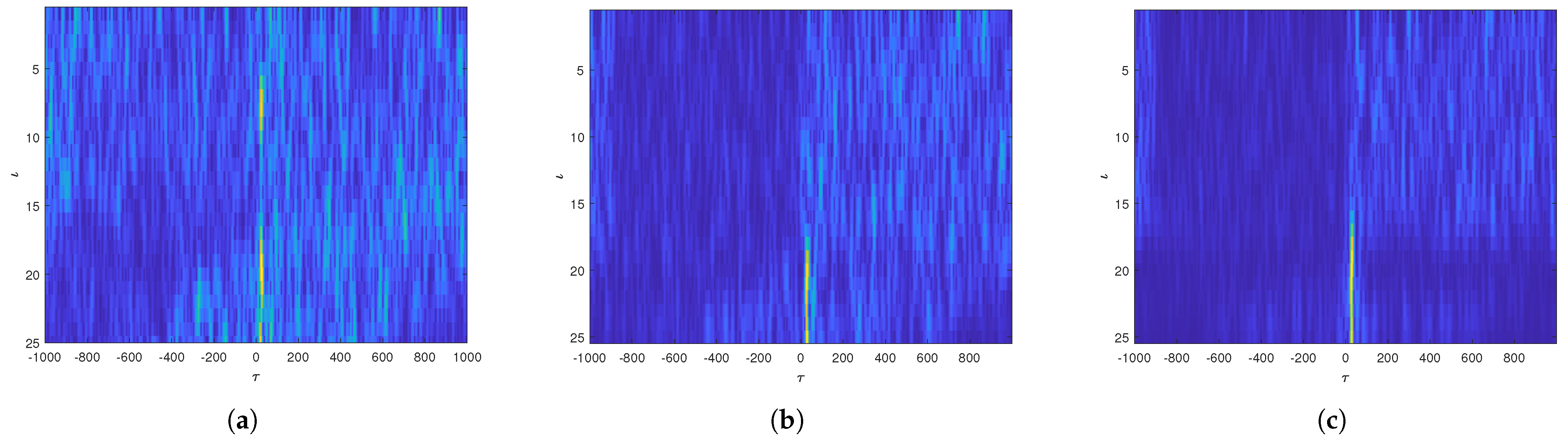
- FS-GCC matrix Feature Enhancement: This step focuses on reconstructing multiple subwindow groups of the FS-GCC matrix to capture time delay-related signal features from various frequency band perspectives, enriching the information dimension and strengthening the key feature vectors.
- MAML-based DnCNN Network Optimization Training: The FS-GCC matrix is first converted into a grayscale image, and DnCNN’s multi-layer convolution is applied to automatically learn and extract the time delay features reconstructed from the FS-GCC, effectively suppressing noise interference. Then, we incorporate the MAML framework to facilitate training under various SNR conditions. This integration allows the model to rapidly adapt to new environments and learn efficiently with a limited number of samples, thereby improving its generalization capabilities and robustness across different SNR scenarios.
3.1. FS-GCC Matrix Feature Enhancement
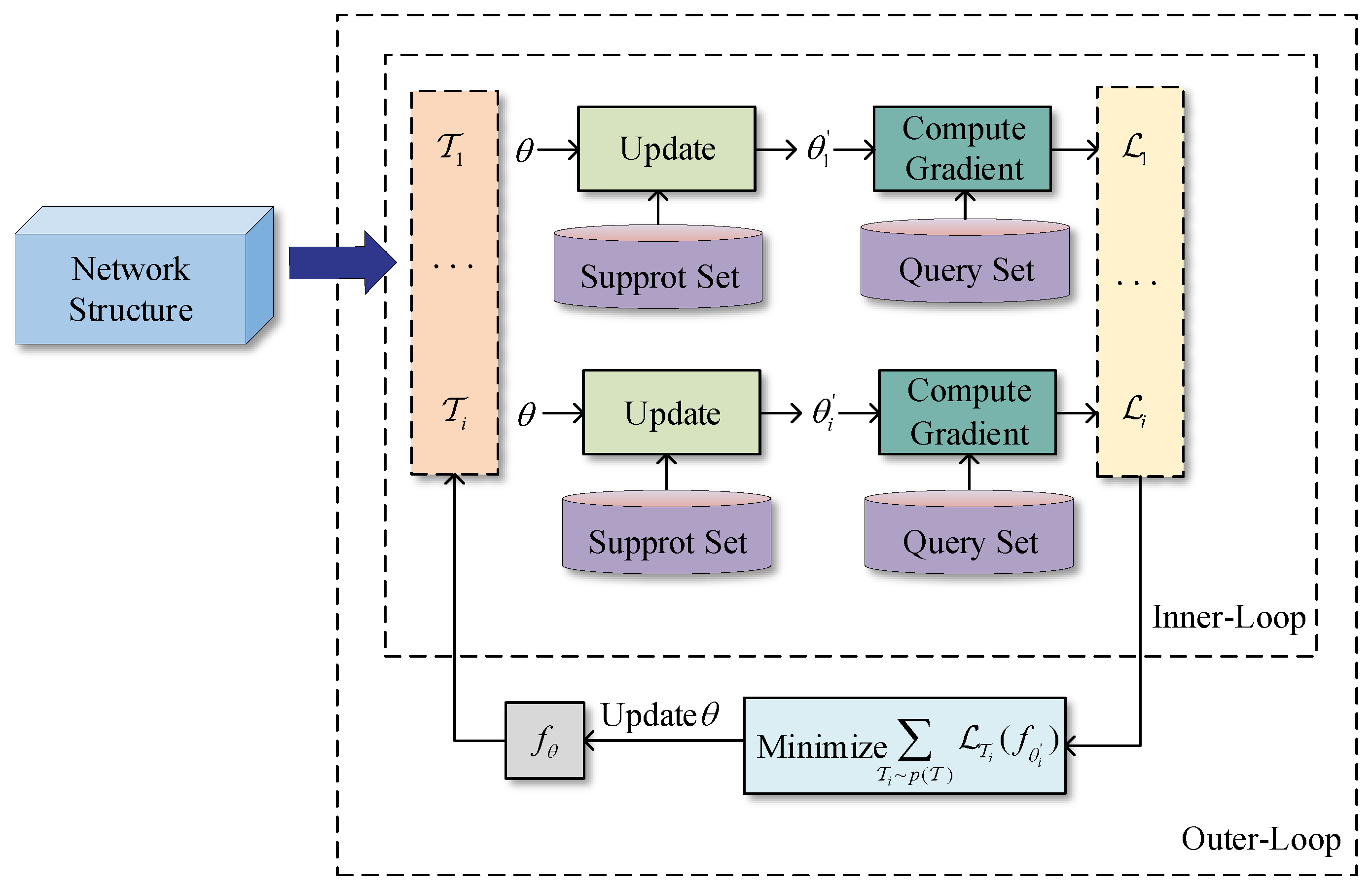
3.2. Meta-DnCNN Network Optimization Training
3.2.1. MAML Framework
| Algorithm 1 The training stage of MAML |
3.2.2. Meta-DnCNN Model
4. Simulation Results and Discussion
4.1. Evaluation Metrics
4.2. Simulation Settings
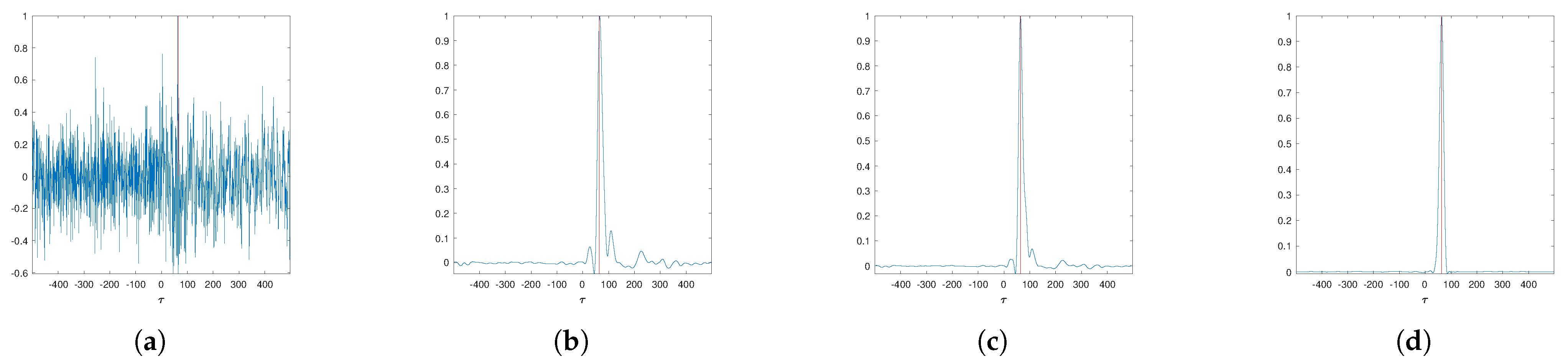
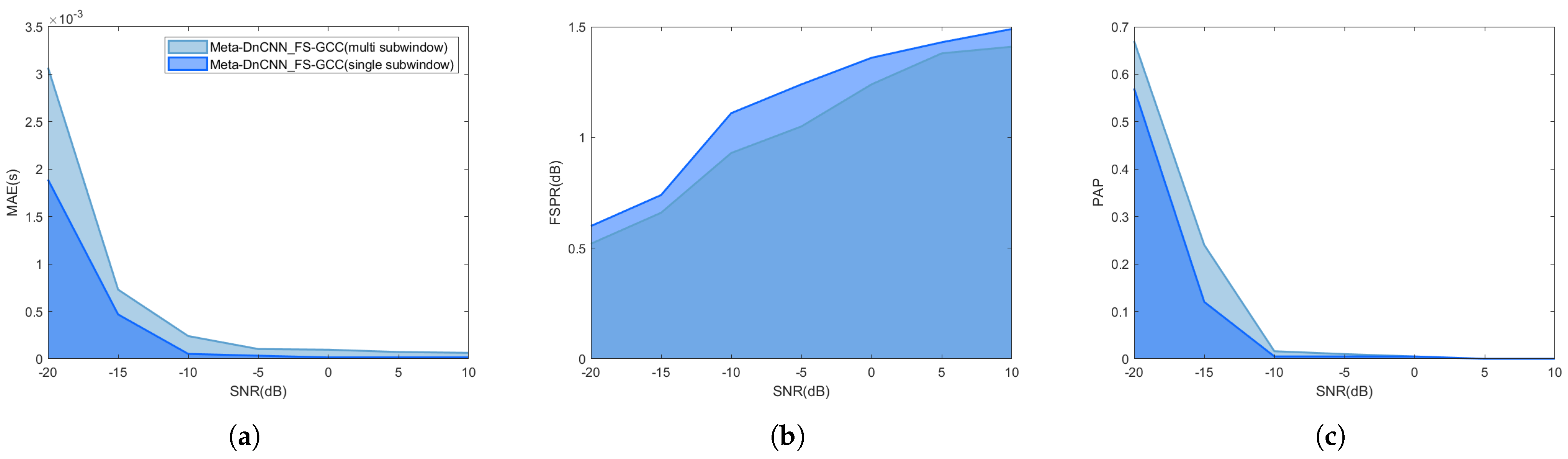
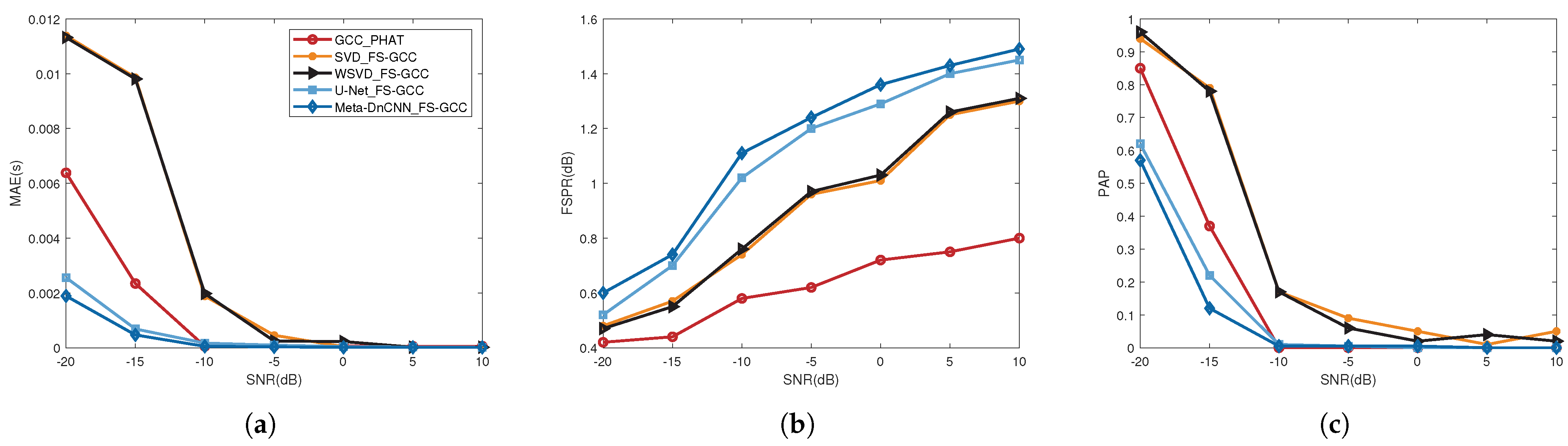
4.3. TDE Results and Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Luo, J.; Yang, Y.; Wang, Z.; Chen, Y. Localization algorithm for underwater sensor network: A review. IEEE Internet Things J. 2021, 8, 13126–13144. [Google Scholar] [CrossRef]
- Li, S.; Qu, W.; Liu, C.; Qiu, T.; Zhao, Z. Survey on high reliability wireless communication for underwater sensor networks. J. Netw. Comput. Appl. 2019, 148, 102446. [Google Scholar] [CrossRef]
- Fan, H.; Nie, W.; Yao, S.; An, L.; Yu, F.; Zhang, Y.; Wu, Q. A high-order time-delay difference estimation method for signal enhancement in the distorted towed hydrophone array. J. Acoust. Soc. Am. 2024, 156, 1996–2008. [Google Scholar] [CrossRef]
- Wang, X.; Xu, B.; Guo, Y. Minimum error entropy robust delay filter for multi-auv cooperative localization. IEEE/ASME Trans. Mechatronics 2024, 30, 1567–1577. [Google Scholar] [CrossRef]
- Xia, Z.; Li, X.; Meng, X. High resolution time-delay estimation of underwater target geometric scattering. Appl. Acoust. 2016, 114, 111–117. [Google Scholar] [CrossRef]
- Lowes, G.J.; Neasham, J. PADAL—Passive acoustic detection and localisation: Low energy underwater wireless vessel tracking network. Comput. Netw. 2024, 241, 110216. [Google Scholar] [CrossRef]
- Jo, M.J.; Choi, J.W.; Han, D.G. Estimation of Source Range and Location Using Ship-Radiated Noise Measured by Two Vertical Line Arrays with a Feed-Forward Neural Network. J. Mar. Sci. Eng. 2024, 12, 1665. [Google Scholar] [CrossRef]
- Hu, X.; Zhang, L.; Hu, B.; Wang, J.; Guo, L.; Zhang, H. Position estimation of acoustic elements based on improved delay estimation algorithm. Appl. Acoust. 2025, 228, 110286. [Google Scholar] [CrossRef]
- Jang, J.; Meyer, F.; Snyder, E.R.; Wiggins, S.M.; Baumann-Pickering, S.; Hildebrand, J.A. Bayesian detection and tracking of odontocetes in 3-D from their echolocation clicks. J. Acoust. Soc. Am. 2023, 153, 2690. [Google Scholar] [CrossRef]
- Jia, L.; Zhang, G.; Liu, Y.; Bai, Z.; Geng, Y.; Wu, Y.; Zhang, J.; Zhang, W. Sonar buoy active detection and localization for underwater targets using high-level sound sources and MEMS hydrophone. Measurement 2025, 241, 115740. [Google Scholar] [CrossRef]
- Pang, X.; Jiang, F. Generalized quadratic correlation delay estimation algorithm based on Phase Transform weighting function. In Proceedings of the 2023 7th International Conference on Electronic Information Technology and Computer Engineering, Xiamen, China, 20–22 October 2023; pp. 1069–1074. [Google Scholar]
- Ferguson, E.L. Multitask convolutional neural network for acoustic localization of a transiting broadband source using a hydrophone array. J. Acoust. Soc. Am. 2021, 150, 248–256. [Google Scholar] [CrossRef]
- Whitaker, S.; Barnard, A.; Anderson, G.D.; Havens, T.C. Through-ice acoustic source tracking using vision transformers with ordinal classification. Sensors 2022, 22, 4703. [Google Scholar] [CrossRef]
- Yao, S.; Meng, Q.; Chen, C.; Tariq, I.; Zhou, C.; Liu, W. High-precision time delay estimation of narrowband radio signal by PHAT-LSTM. Meas. Sci. Technol. 2021, 32, 075001. [Google Scholar] [CrossRef]
- Salvati, D.; Drioli, C.; Foresti, G.L. Time delay estimation for speaker localization using CNN-based parametrized GCC-PHAT features. In Proceedings of the Interspeech, Brno, Czechia, 30 August–3 September 2021; pp. 1479–1483. [Google Scholar]
- Comanducci, L.; Borra, F.; Bestagini, P.; Antonacci, F.; Tubaro, S.; Sarti, A. Source localization using distributed microphones in reverberant environments based on deep learning and ray space transform. IEEE/ACM Trans. Audio Speech Lang Process. 2020, 28, 2238–2251. [Google Scholar] [CrossRef]
- Wang, S.; Zhou, Y.; Yang, X.; Liu, H. A robust blind source separation algorithm based on non-negative matrix factorization and frequency-sliding generalized cross-correlation. In Proceedings of the 2021 IEEE Statistical Signal Processing Workshop (SSP), Rio de Janeiro, Brazil, 11–14 July 2021; pp. 231–235. [Google Scholar]
- Cobos, M.; Antonacci, F.; Comanducci, L.; Sarti, A. Frequency-sliding generalized cross-correlation: A sub-band time delay estimation approach. IEEE/ACM Trans. Audio Speech Lang. Process. 2020, 28, 1270–1281. [Google Scholar] [CrossRef]
- Song, Q.; Ou, Z. Modified frequency-sliding generalized cross correlation for time delay difference estimation of microphone array. IEEE Sensors J. 2023, 23, 31038–31049. [Google Scholar] [CrossRef]
- Comanducci, L.; Cobos, M.; Antonacci, F.; Sarti, A. Time difference of arrival estimation from frequency-sliding generalized cross-correlations using convolutional neural networks. In Proceedings of the ICASSP 2020-2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 4945–4949. [Google Scholar]
- Yang, N.; Zhang, B.; Ding, G.; Wei, Y.; Wei, G.; Wang, J.; Guo, D. Specific emitter identification with limited samples: A model-agnostic meta-learning approach. IEEE Commun. Lett. 2021, 26, 345–349. [Google Scholar] [CrossRef]
- Lin, W.; Mak, M.W. Model-agnostic meta-learning for fast text-dependent speaker embedding adaptation. IEEE/ACM Trans. Audio Speech Lang. Process. 2023, 31, 1866–1876. [Google Scholar] [CrossRef]
- Yang, F.; Liu, J.; Hua, C.; Liu, W.; Dong, D. Early fault diagnosis strategy for high-speed train suspension systems based on model-agnostic meta-learning. Veh. Syst. Dyn. 2024, 62, 2510–2532. [Google Scholar] [CrossRef]
- Wu, J.; Li, M.; Fang, X.; Ramaccia, D.; Toscano, A.; Bilotti, F.; Ding, D. Anti-interference DoA estimation for LFM radar signals using space-time-modulated metasurfaces. IEEE Trans. Microw. Theory Tech. 2024, 73, 1460–1472. [Google Scholar] [CrossRef]
- Mehdizadeh, M.; MacNish, C.; Xiao, D.; Alonso-Caneiro, D.; Kugelman, J.; Bennamoun, M. Deep feature loss to denoise OCT images using deep neural networks. J. Biomed. Opt. 2021, 26, 046003. [Google Scholar] [CrossRef] [PubMed]
- Van Walree, P.A.; Socheleau, F.X.; Otnes, R.; Jenserud, T. The watermark benchmark for underwater acoustic modulation schemes. IEEE J. Ocean. Eng. 2017, 42, 1007–1018. [Google Scholar] [CrossRef]



| Parameters | Value |
|---|---|
| Number of Tasks | 6 |
| SNR of Training Tasks | −15∼10 dB |
| Number of Training Data of Each Task | 150 |
| Number of Test Data of Each Task | 20 |
| Outer-Loop Learning Rate | 0.001 |
| Inner-Loop Learning Rate | 0.001 |
| Epoch | 200 |
| Optimizer | Adam |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, M.; Cui, X.; Li, J.; Li, L.; Jiang, B. Underwater Time Delay Estimation Based on Meta-DnCNN with Frequency-Sliding Generalized Cross-Correlation. J. Mar. Sci. Eng. 2025, 13, 919. https://doi.org/10.3390/jmse13050919
Ji M, Cui X, Li J, Li L, Jiang B. Underwater Time Delay Estimation Based on Meta-DnCNN with Frequency-Sliding Generalized Cross-Correlation. Journal of Marine Science and Engineering. 2025; 13(5):919. https://doi.org/10.3390/jmse13050919
Chicago/Turabian StyleJi, Meiqi, Xuerong Cui, Juan Li, Lei Li, and Bin Jiang. 2025. "Underwater Time Delay Estimation Based on Meta-DnCNN with Frequency-Sliding Generalized Cross-Correlation" Journal of Marine Science and Engineering 13, no. 5: 919. https://doi.org/10.3390/jmse13050919
APA StyleJi, M., Cui, X., Li, J., Li, L., & Jiang, B. (2025). Underwater Time Delay Estimation Based on Meta-DnCNN with Frequency-Sliding Generalized Cross-Correlation. Journal of Marine Science and Engineering, 13(5), 919. https://doi.org/10.3390/jmse13050919





