Next Article in Journal
NSMO-Based Adaptive Finite-Time Command-Filtered Backstepping Speed Controller for New Energy Hybrid Ship PMSM Propulsion System
Previous Article in Journal
Fast Non-Dominated Sorting Tuna Swarm Optimization Algorithm (FNS-TSO): Time-Energy-Impact Multi-Objective Optimization of Underwater Manipulator Trajectories
Previous Article in Special Issue
Investigating the Impact of Seafarer Training in the Autonomous Shipping Era
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
JMSE
Volume 13
Issue 5
10.3390/jmse13050917
jmse-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A Data Cleaning Method for the Identification of Outliers in Fishing Vessel Trajectories Based on a Geocoding Algorithm

by
Li Zhang
1,2,† and
Weifeng Zhou
1,*,†
1
East China Sea Fisheries Research Institute, Chinese Academy of Fishery Sciences, Shanghai 200090, China
2
College of Information Engineering, Zhejiang Ocean University, Zhoushan 316022, China
*
Author to whom correspondence should be addressed.
†
These authors contributed equally to this work.
J. Mar. Sci. Eng. 2025, 13(5), 917; https://doi.org/10.3390/jmse13050917
Submission received: 20 March 2025 / Revised: 1 May 2025 / Accepted: 3 May 2025 / Published: 6 May 2025
(This article belongs to the Special Issue Management and Control of Ship Traffic Behaviours)
Browse Figures
Versions Notes

Abstract

:
In modern fishery management, fishing vessel trajectory data are used to monitor and analyze fishing vessel activities. However, trajectory data are often of low quality, probably due to environmental factors, equipment failures, signal loss and operation errors, leading to numerous outliers in these data. These outliers not only undermine the credibility of the data but also negatively affect the subsequent data mining and decision-making. In this study, a data cleaning method for the identification of outlier points in fishing vessel trajectories based on the Geohash geocoding algorithm is given, which involves several key steps: obtaining and preprocessing the raw trajectory data; generating the corresponding Geohash codes for each ship position based on its latitude and longitude; calculating the reachable distance considering the time interval between the current point and the following points and their speeds; querying the neighborhood of the current point based on the reachable distance; and obtaining all Geohash codes of the reachable areas of the fishing vessels within the time interval as the reachable range grid set of the current position. The reachable range grid set of the current position is compared with the reachable range grid sets of the previous point identified as normal and the next point in the fishing vessel trajectory. If there is no intersection, it is determined that the current fishing vessel position is an outlier, and this point will be excluded. The method proposed in this study is able to effectively identify outliers in trajectory data, achieving efficient and effective trajectory data cleaning and improving the accuracy and reliability of the data.

1. Introduction

Fishing vessel trajectory data provide detailed information about the movement of a fishing vessel at sea, including the geographic location, time, and speed. Fishing vessel trajectory data can be used for a variety of analyses, with a wide range of applications. Data mining and application using fishing vessel trajectory data can not only enhance the efficiency and safety of fishery production but also provide important support for environmental protection, policy formulation, and economic benefit analysis. Through the comprehensive use of these data, the optimal allocation of resources can be achieved to promote the sustainable development of fisheries while protecting the marine environment [1].
Trajectory data usually consist of a series of temporal and spatial points (timestamped spatial points), reflecting the dynamic changes of objects or individuals in time and space. However, raw trajectory data are often characterized by high dimensionality and redundancy. Due to the many limitations of trajectory data in the process of acquisition and transmission, there is often a considerable portion of low-quality trajectory data in the collected trajectory data [2]. For example, due to factors such as the data collection accuracy, signal drift at sea, and the network transmission conditions, the trajectory data collected by the AIS system in practical scenarios may contain outliers. Variable quality, noise, missing values, etc., have been common problems in ship spatiotemporal trajectory data [3]. Therefore, there are so-called rubbish data in the real spatiotemporal trajectory data that do not match with the actual situation, and this type of low-quality trajectory data will affect the success of trajectory data mining from the source [4], so it is necessary to remove them, i.e., through data cleaning [5].
The current data cleaning methods for fishing vessel trajectory data mainly rely on statistical analysis techniques; they then use rules to identify outliers that deviate from regular patterns by setting statistical thresholds or constructing probabilistic models. Thresholds are set for single dimensions such as speed, acceleration, or heading (e.g., the 3σ rule), with values exceeding the threshold considered outliers [6,7,8]. Chen et al. [9], Alvares et al. [10], and Zheng et al. [11] employed constant threshold methods to detect outliers by removing trajectory points where the instantaneous speed exceeded the set threshold and then performed their respective trajectory data mining tasks. Ristic et al. [12] proposed a statistical non-parametric method to analyze fishing vessel movement patterns in ports and channels, using adaptive kernel density estimation to obtain the probability density functions of fishing vessel trajectories for outlier detection. Zhen Rong et al. [13] used the least squares curve fitting method in statistics to fit the fishing vessel trajectory points in the training set, obtaining a mathematical model of the vessel’s typical navigation trajectory. This model was used as a standard, and, after calculating the distance between the monitored vessel trajectory points and the typical trajectory, the fishing vessel was identified as having an outlier if this distance exceeded the 95% confidence interval of the typical trajectory. Mascaro et al. [14,15] used actual fishing vessel trajectory data to train a Bayesian network, forming dynamic and static Bayesian network models, expanding the coverage of the network, and enabling successful outlier detection in fishing vessel trajectories.
Distance-based methods: Knorr et al. [16] proposed the DB(p, D) algorithm, which states that, if at least p part of the data objects in the dataset have a distance greater than D from object o, then o is considered a distance-based outlier with respect to parameters p and D. This algorithm is based on a distance metric. This method requires an appropriate distance metric and cannot detect local outliers in fishing vessel trajectory data with different density distributions. Zhang et al. [17] proposed the TODMF algorithm, which improves on the distance-based outlier detection method by combining multiple factors, such as the velocity, acceleration, and heading angle, to detect outliers in fishing vessel trajectories.
Density-based method: This method assumes that the density around an outlier is significantly different from the density around its neighborhood. Breunig et al. [18] proposed the Local Anomaly Factor (LOF) algorithm, which calculates the LOF value of each point based on the locally reachable densities of all points in the neighborhood, and the points with a high LOF are identified as outliers in the fishing vessel trajectory.
Existing techniques for the identification of outliers in fishing vessel trajectory data are usually based on simple statistical analyses, with data cleaning typically relying on basic thresholding methods. However, the differences in the types and sizes of fishing vessels, as well as the fact that vessels may be moving at irregular speeds and in different directions, make the selection of appropriate thresholds particularly challenging [9]. Additionally, these techniques fail to effectively utilize the characteristics of the voyage data, resulting in outlier identification that is neither accurate nor efficient. Moreover, these methods do not account for the effects of the vessel speed and travel time intervals on the accuracy of trajectory analysis, which limits their effectiveness and reliability.
Therefore, this study presents a method for the identification of outliers and the data cleaning of fishing vessel trajectories using Geohash geographic grid encoding. Due to the variability in the speed and direction of fishing vessels according to the operational type and status, it is difficult to select appropriate thresholds, and the characteristics of the trajectory data are also not fully utilized. Our idea is to determine whether the subsequent point of a point in trajectory data is normal or constitutes an outlier or anomalous point. Outliers, or anomalous points, are points that exceed the reachable range, which is determined by the velocity and interval time corresponding to this specific point in the trajectory sequence. Outliers are identified through a neighborhood search and the comparison of encoded characters. The Geohash geocoding algorithm does not handle the irregularity of fishing vessels’ types, sizes, and speeds directly. Geohash transforms the spatial information contained by trajectory data into string-based representations. The spatial information contained in its built-in encoding rules can replace the distance calculation in the traditional trajectory data cleaning method. At the same time, the method proposed in this paper makes full use of the speed and time in the trajectory data. It addresses the fact that the previous data cleaning methods only focus on the distance or density of trajectory points for the identification and removal of outliers. This approach effectively identifies outliers in the trajectory data and removes them, enabling the efficient and reliable cleaning of the trajectory data, which in turn enhances the accuracy and reliability of subsequent analyses and applications.

2. Materials and Methods

In this study, a Geohash coding-based method for the identification of outlier trajectory points and data cleaning for fishing vessels is proposed. This method achieves the efficient identification and cleaning of outlier trajectory points in trajectory data by combining Geohash spatial coding and a neighborhood search, as well as dynamic time interval and vessel speed calculation. The technical flow chart is as follows (Figure 1).

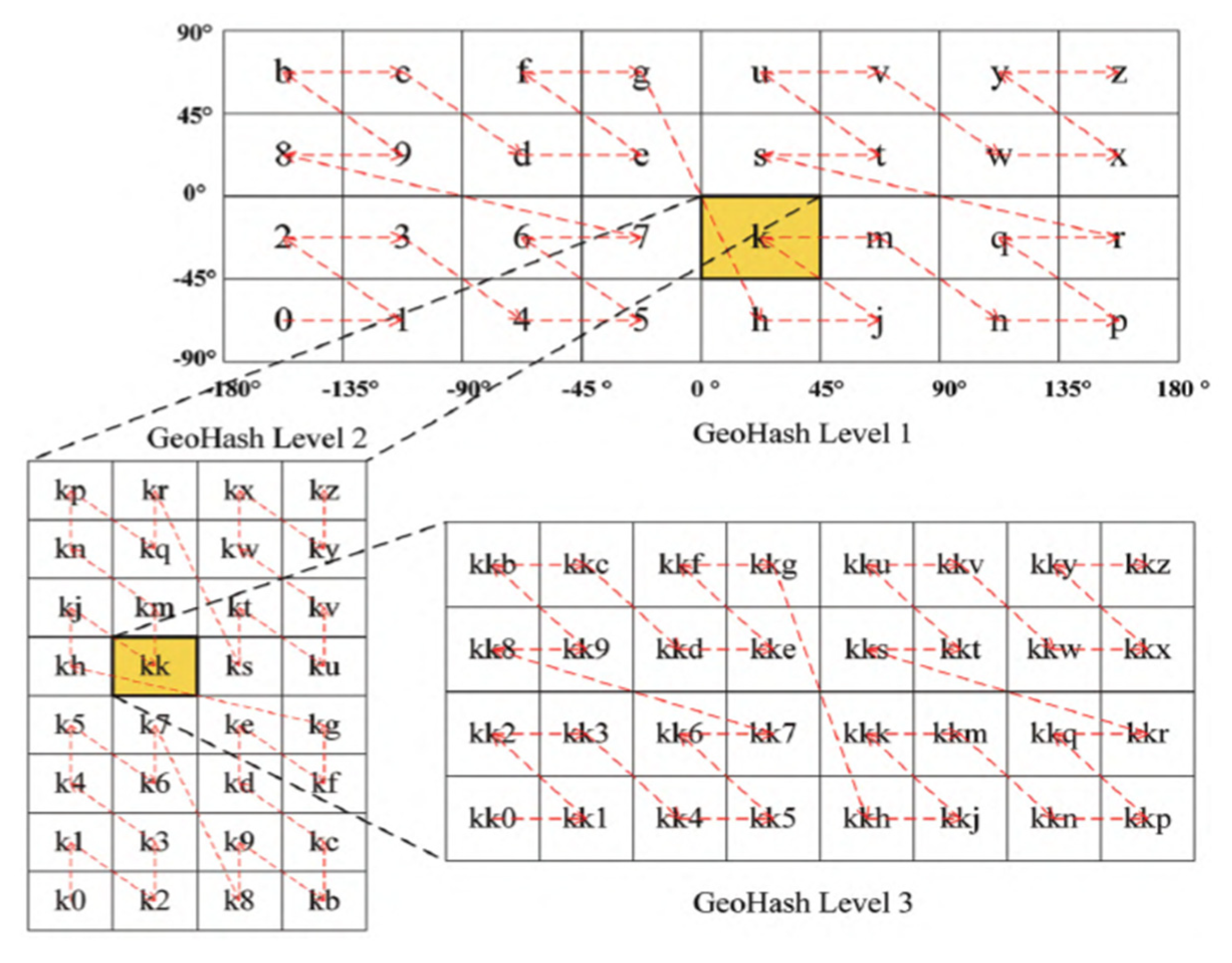
2.1. Geohash Principles

Geohash is an algorithm used to encode geographic coordinates (longitude and latitude) into a short string [19]. It was proposed by Gustavo Niemeyer in 2008 and is widely used in geographic information systems (GIS), location searching, and proximity searching. The principle of Geohash is to map longitude and latitude coordinates onto a hierarchical rectangular grid system, enabling the efficient partitioning and querying of the geographic space through a hierarchical encoding design. The core idea is to recursively divide the longitude and latitude regions alternately using binary division, combined with a Z-order curve, which transforms the spatial indexing problem into a string encoding problem [20].
Specifically, Geohash first divides the global longitude range (−180° to 180°) into 8 segments and the latitude range (−90° to 90°) into 4 segments, forming 32 regions at the first level, each corresponding to a unique Base32 character. In subsequent levels, subregions are alternately divided into 4 × 8 or 8 × 4 grids based on the parity bit, and a Z-order curve is used to encode adjacent regions, ensuring that geographically close areas also have continuous encoding [21] (Figure 2). In each level, the longitude and latitude are each divided using binary division. The left half of the longitude is represented by 0 and the right half by 1; the lower half of the latitude is represented by 0 and the upper half by 1. The binary encoding of longitude and latitude is then combined by alternately interleaving their bits to form a combined binary sequence. Finally, every 5 bits of binary are converted into decimals, and the decimal values are mapped to characters according to the Base32 encoding table [22] (Table 1), resulting in the final Geohash code.
Adjacent grid position encoding calculation utilizes the Geohash coding rules to decompose the latitude and longitude into binary. Combined with common sense geography, the central grid in the north–south (up and down) direction is reflected in the change in latitude: to the north is the dimension of the binary plus 1, and to the south is the dimension of the binary minus 1. The grid in the east–west (left and right) direction is reflected in the change in longitude: to the east is the dimension of the binary plus 1, and to the west is the dimension of the binary minus 1. We determine the binary encoding of the latitude and longitude for the four grids—top, bottom, left, and right—and then combine the latitude and longitude derived from addition and subtraction two by two. The binary encodings of the latitude and longitude for the four grids of top-left, bottom-left, top-right, and bottom-right are then computed; thus, the neighborhood strings of the surrounding eight grids are calculated according to the Geohash encoding rules [23].
This encoding exhibits uniqueness, recursion, and prefix matching properties, i.e., longer encodings correspond to smaller geographic ranges, and the hierarchical encodings in the same region share prefixes, thus supporting a fast neighborhood search and spatial retrieval based on string comparisons. In addition, Geohash has the feature of graded accuracy: the longer the encoding length, the smaller the geographical range and the higher the accuracy.

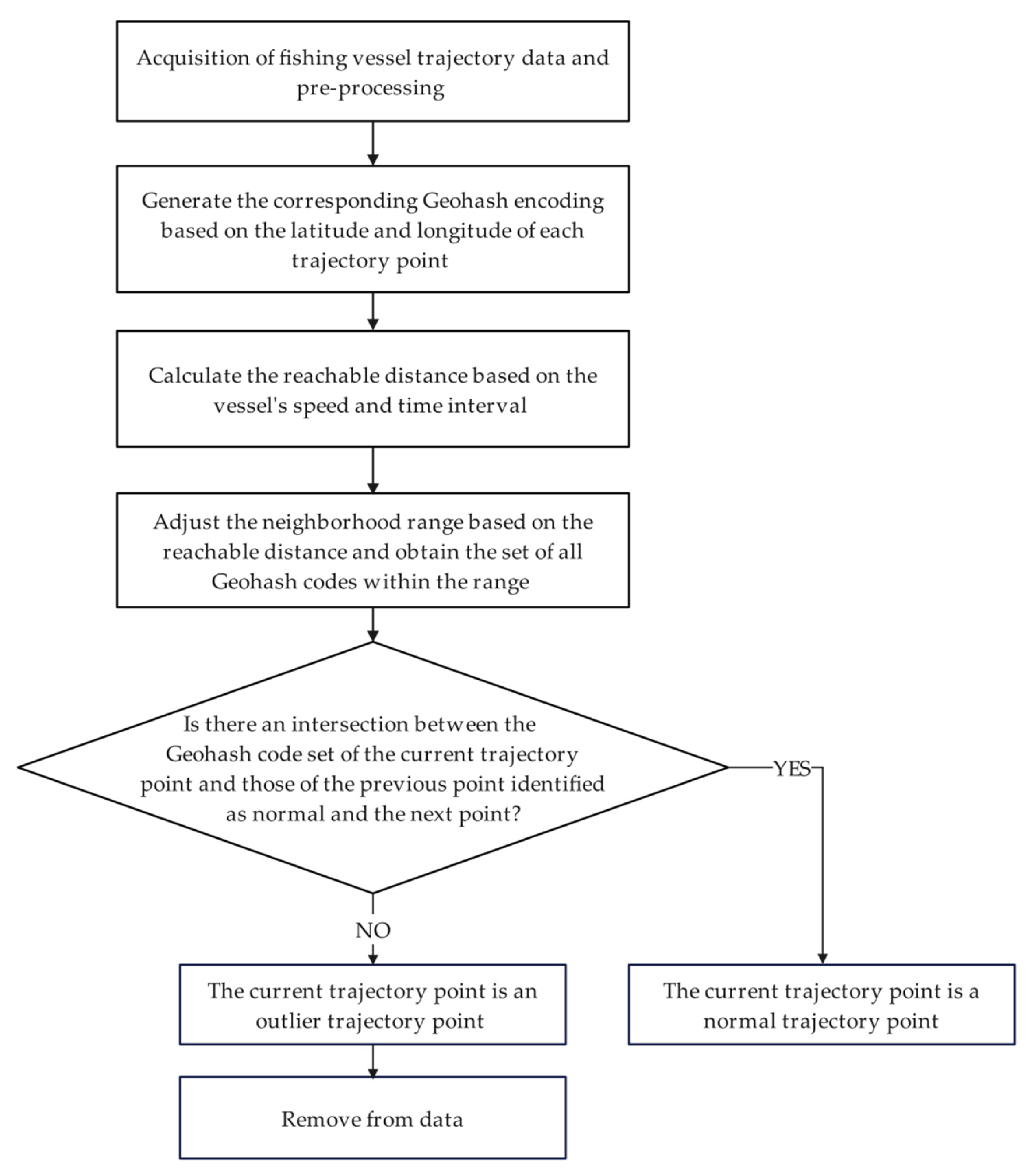
2.2. Identifying Outliers Based on the Filtered Code Set Derived from the Reachable Distance During Navigation

According to the flowchart, the specific steps of the method are described as follows, with the key step being the filtering of the reachable range grid set based on the reachable distance, enabling us to identify outliers.
(1) Acquire the Beidou ship position data of the fishing vessel, which include information such as timestamps, longitude, latitude, speed (in knots), etc., and preprocess the collected data to ensure a consistent time format. Remove missing values and duplicated data and delete the ship position point data where the speed exceeds the maximum speed of the fishing vessel, so as to ensure the accuracy of the subsequent analysis.
(2) Perform the Geohash encoding of the acquired current Beidou ship position data according to its latitude and longitude to generate the corresponding Geohash string, using 7-bit precision to obtain the appropriate spatial resolution. Perform 7-bit precision Geohash encoding in the vicinity of the latitude of 30° to form a range with a size of about 132.2 m wide by 152.7 m long. Geohash encoding can also be adjusted to achieve higher precision as needed.
(3) Based on the current vessel’s speed (in knots) and the time interval (in seconds) to the next point, the reachable distance that the vessel can travel within the time interval, with the current vessel position as the center, can be calculated as follows:
Reachable Distance = Speed × Time Interval × Conversion Factor
where the conversion factor converts knots to meters per second (1 knot ≈ 0.51444 m/second). For the last vessel position, the time interval is calculated using the time difference from the previous vessel position.
(4) According to the calculated reachable distance, dynamically adjust the Geohash neighborhood layer and the neighborhood range containing the central grid for each ship location. Divide the reachable distance by 132.2, and round up the result to obtain the number of Geohash layers. Layer 1 contains the 9-neighborhood range of the central grid, layer 2 contains the 25-neighborhood range of the central grid, layer 3 contains the 49-neighborhood range of the central grid, and so on. The maximum number of layers is 8, which contains 289 neighborhoods.
(5) Obtain the set of all Geohash codes of the multi-layer neighborhood range of the current position based on the Geohash code of the current position.
(6) Perform intersection detection between the set of Geohash codes of the multi-layer neighborhood range of the current position point and the set of Geohash codes of the multi-layer neighborhood ranges of the previous point identified as normal and the next position point to determine whether there is an intersection. In other words, determine whether a link is formed between the ship’s position points by determining whether the same Geohash code is present. If the same code is found, it is recognized as a normal track point. If the Geohash code of the multi-layer neighborhood range of a position point does not intersect with the multi-layer neighborhood ranges of the previous and subsequent position points, the point is identified as an outlier.
(7) Retain the position points with intersections as normal fishing vessel trajectories, and delete those that do not intersect with the previous or subsequent position points, which are identified as outliers. Position points that have already been identified as outliers are not included in subsequent intersection detection.

3. Results

We take the trajectory data of a fishing ship equipped with a Beidou device, named ZheLingYu 00028 and ZhePuYu 68823, as examples to conduct experiments examining the identification and cleaning of outliers in the fishing boat’s trajectory. The entire trajectory data of the two ships can be found in the Supplementary Materials.

3.1. Data Cleaning

3.1.1. Data and Preprocessing

This study takes the trajectory data on 7 January 2018 from the fishing boat named ZheLingYu 00028 and the trajectory data on 2 January 2018 from ZhePuYu 68823 as examples; these ships were equipped with a Beidou device. The data include information such as the timestamp, longitude, latitude, and speed (in knots). The collected data are preprocessed to ensure that the time format is consistent. The time format is ‘yyyy/m/d hh:mm:ss’ to ensure the accuracy of the subsequent analysis. Some of the pre-processed ZheLingYu 00028 data are shown in Table 2.
We observe that normal and abnormal trajectory points appear alternately between the times of 8:09 and 8:29 in the trajectory data of the fishing vessel named ZhePuYu 68823 on 2 January 2018, as shown in Table 3.

3.1.2. Geohash Code Generation

The latitude and longitude of the current position are encoded using Geohash, and the geographical coordinates are converted into a string. A Geohash encoding of 7 bits is selected to ensure accuracy. This accuracy is sufficient to balance the spatial resolution and processing efficiency, and it is suitable for the analysis needs of most fishing vessel trajectories. The Python Geohash library is used to perform the transformation, and the results are restored in the xls format in turn. The length of the Geohash encoding corresponds to the area size, as shown in Table 4.

3.1.3. Calculating the Reachable Distance Based on the Vessel’s Speed and Time Interval

The timestamp of the fishing boat’s Beidou data is accurate to the second, which facilitates the precise calculation of the time differences between ship positions. We multiply the time interval by the vessel’s speed to obtain the reachable travel distance of the vessel at this position within the given time interval. Since the time difference cannot be calculated for the last position, the time difference from the movement of the previous position is used to calculate the distance.

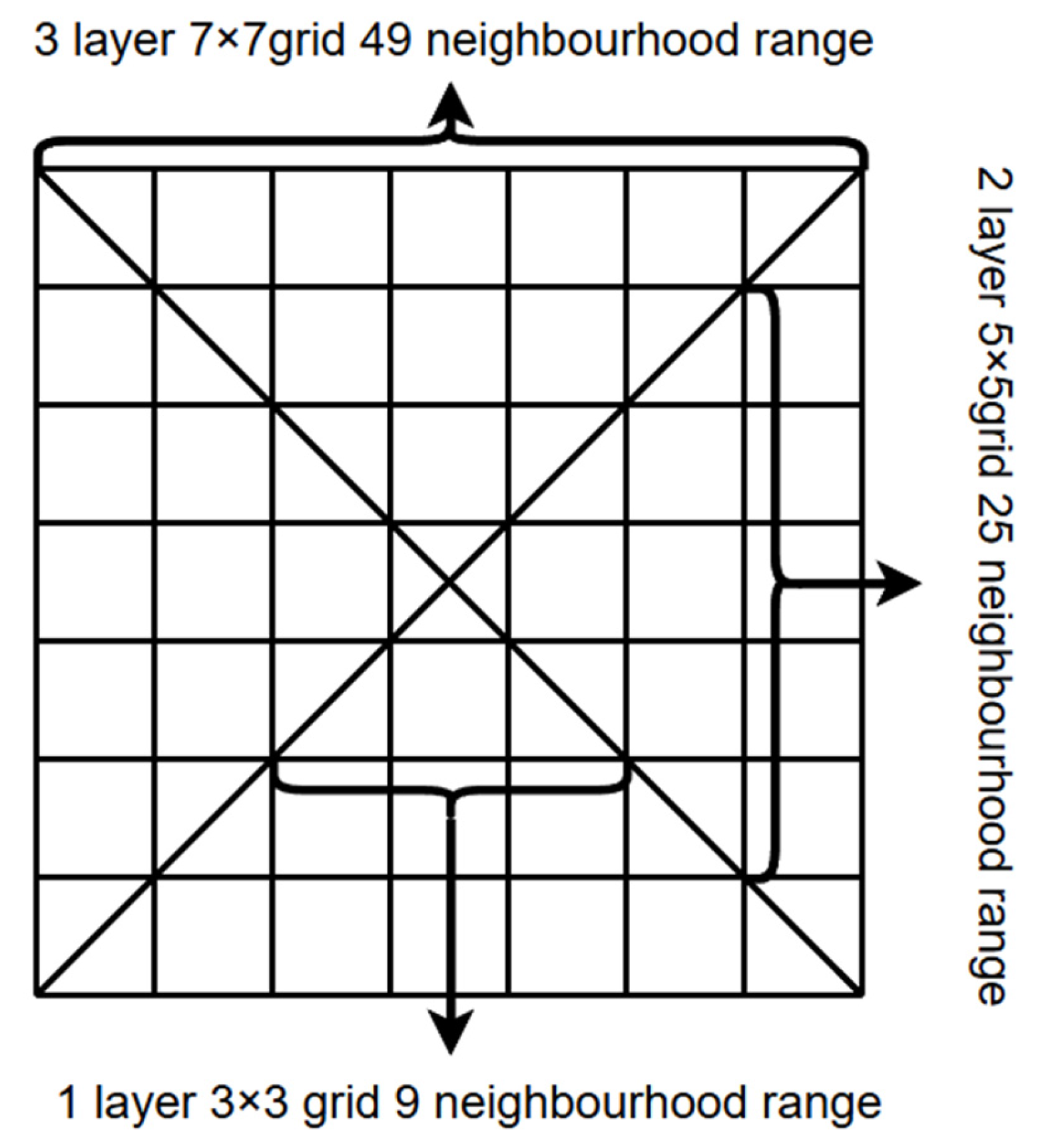
3.1.4. Geohash Layer and Neighborhood Range Adjustment

After obtaining the reachable travel distance of the vessel at a given position, it is necessary to determine the set of Geohash codes within this range. To accommodate the activity ranges of fishing vessels in China, a grid width of 132.2 m at a latitude of around 30° is used to calculate the Geohash layer. The reachable distance is divided by the grid width, and the result is rounded up to obtain the Geohash layer for the vessel’s position. The number of layers is then used to determine the reachable neighborhood range.
Neighborhood scope: 1 layer indicates 9 neighborhoods (3 × 3 grid), 2 layers indicate 25 neighborhoods (5 × 5 grid), 3 layers indicate 49 neighborhoods (7 × 7 grid), and so on, covering a larger spatial scope. The maximum number of layers is 8, covering 289 neighborhoods. Calculations beyond 8 layers are based on the maximum number of layers. The layers and neighborhood scopes are shown in Figure 3.

3.1.5. Obtaining a Collection of Geohash Encodings for a Multi-Layer Neighborhood Range

Based on the Geohash encoding of the current vessel position point, and the calculated neighborhood layer and neighborhood range of the point, the Geohash library of Python is used to obtain all of the neighborhood Geohash encodings within the multi-layer neighborhood range of the vessel position point. This enables us to form a set of Geohash encodings of the neighborhood range of the vessel position point, which represents all possible spatial locations to which the vessel position point may be travelling.

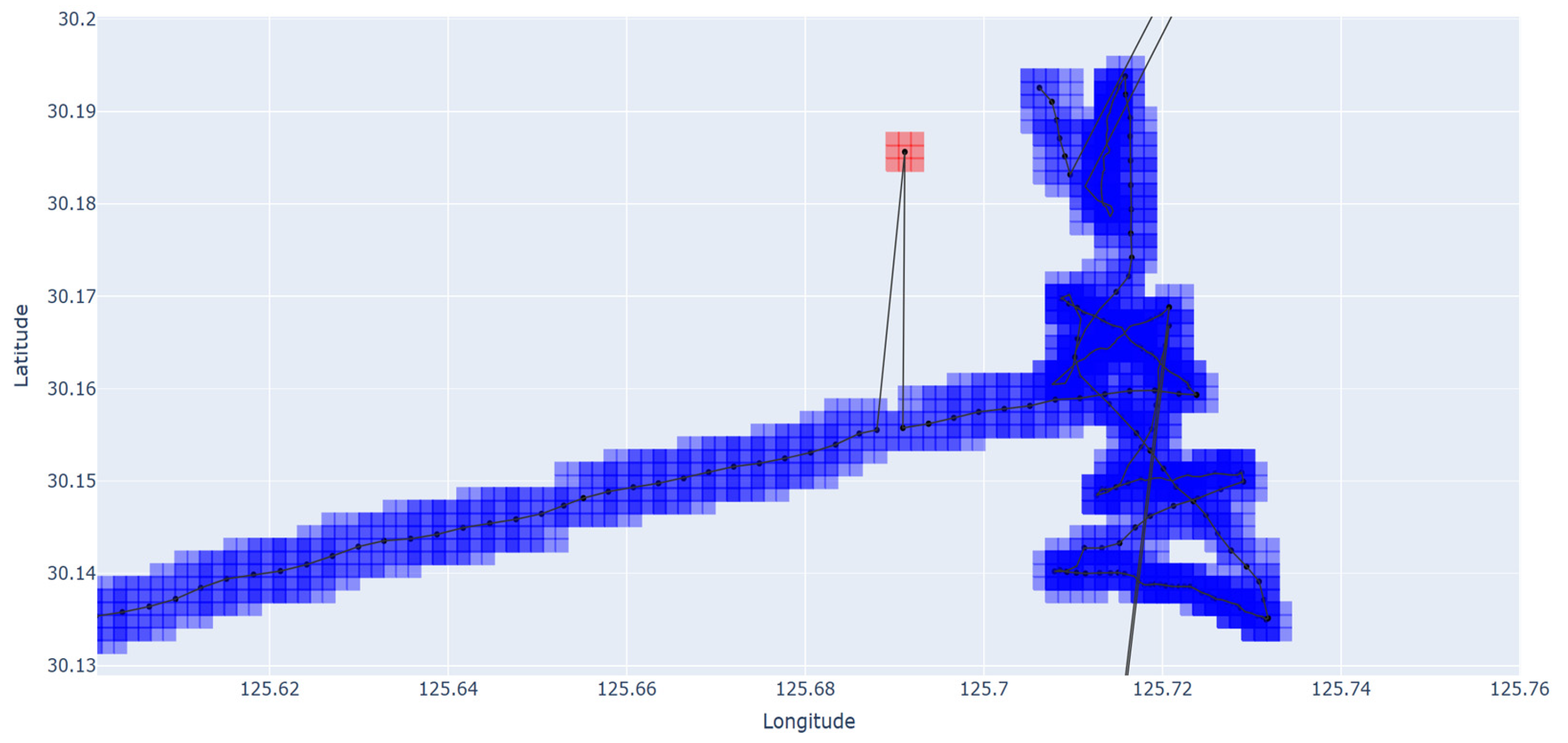
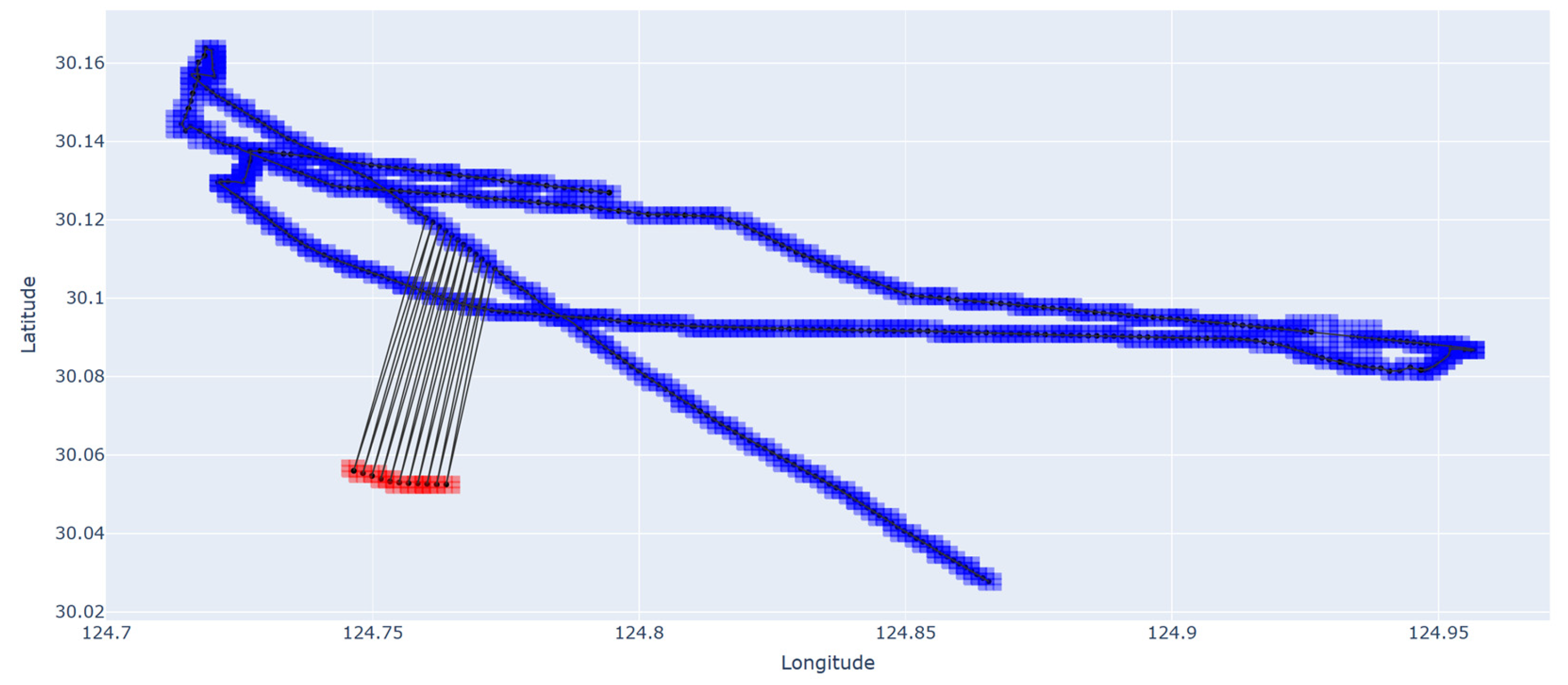
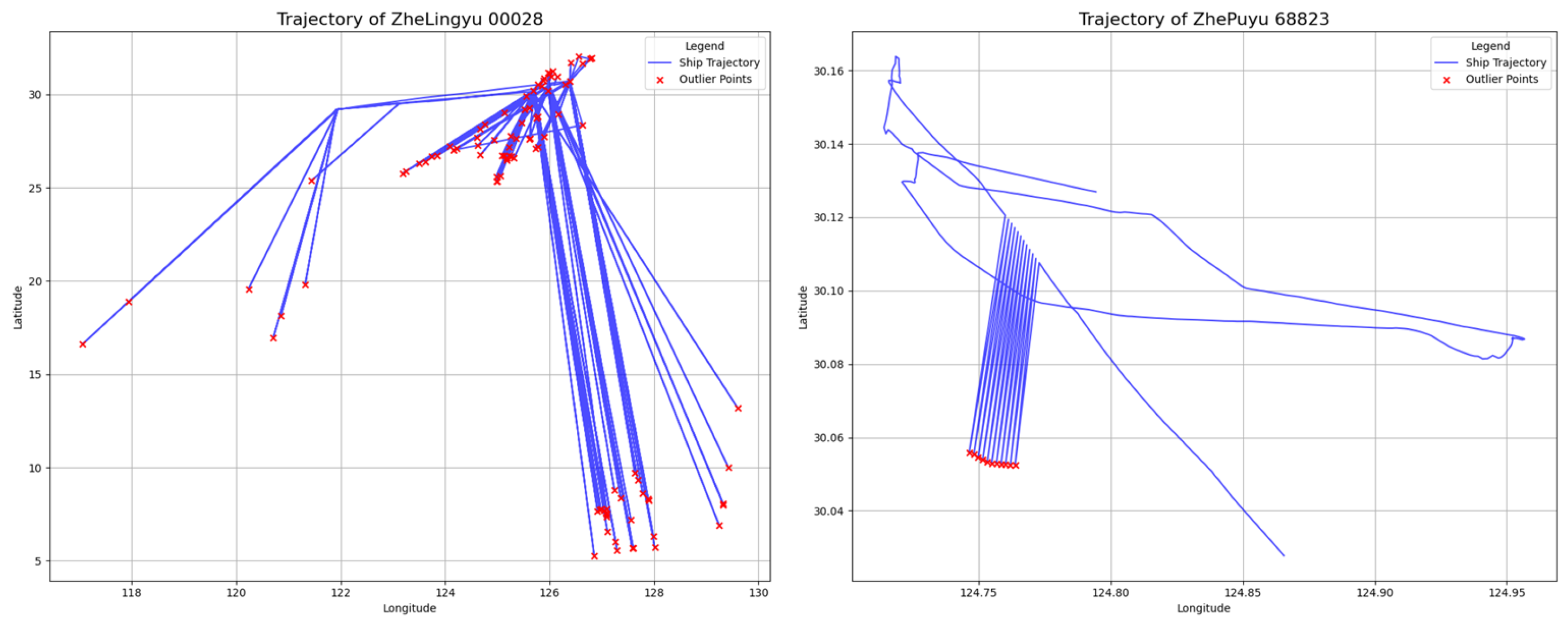
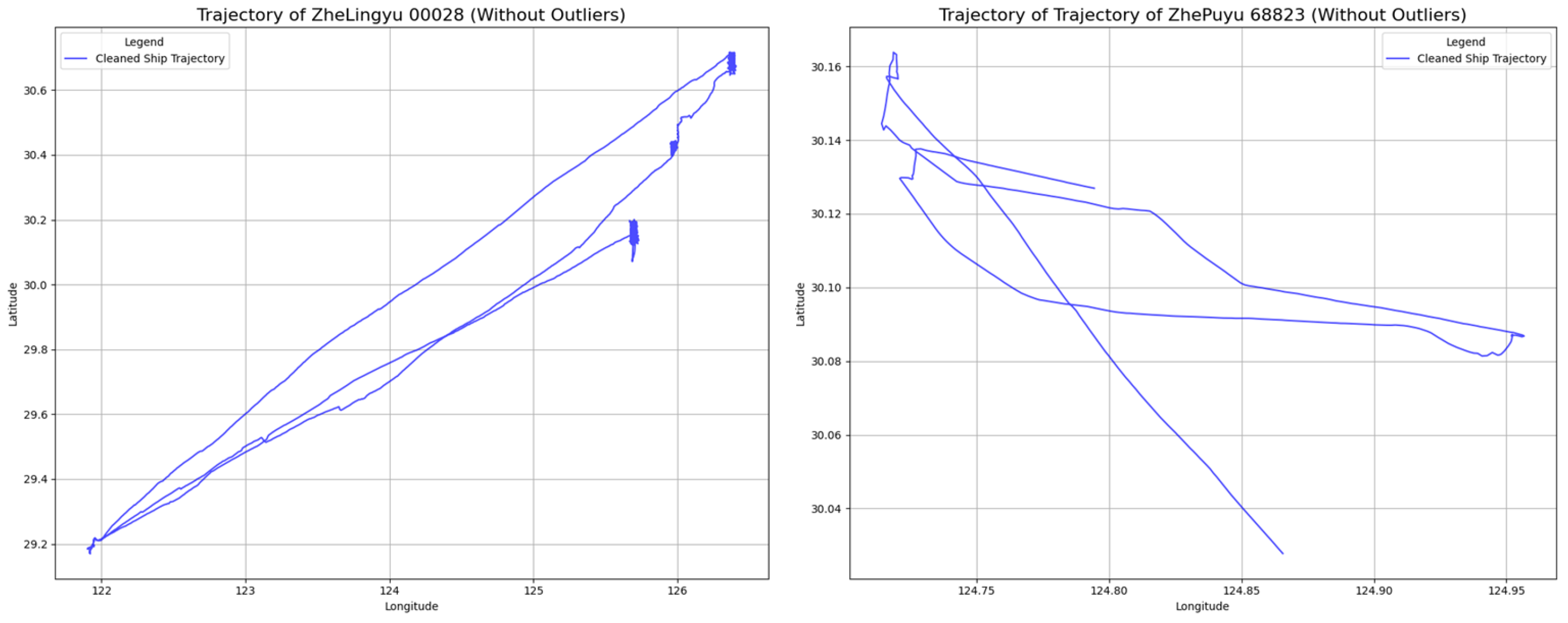
3.2. The Case of Single Outlier Identification

For each fishing vessel point, the set of encodings of its Geohash multi-layer neighborhood range is obtained, and the intersection detection of the Geohash encodings of the current fishing vessel point, the previously identified normal fishing vessel point, and the next fishing vessel point is performed using Python. If the same Geohash encoding exists (i.e., there is an overlap in the neighborhood range), the current point is considered to form a valid trajectory link with the neighboring points. The multi-layer neighborhood range of each fishing vessel point was visualized using Python, with the presence of neighborhood overlap marked in blue. If there was no intersection with either the preceding or following fishing vessel point, the point was identified as an outlier, marked in red. The visualization of the experimental results for ZheLingYu 00028 is shown in Figure 4. The grid in the figure is the set of all Geohash codes within the travelling distance range of the fishing vessel. The dark blue grid denotes the overlapping Geohash codes within the travelling distance range of each fishing vessel position point, and the intersection between the grids produces an intersection to form a trajectory link for the fishing vessel. Meanwhile, the red grid point in the figure has no intersection with the grid between the fishing vessel position points and is regarded as an outlier that is outside the normal route distance.

3.3. Outlier Identification with Alternating Normal and Abnormal Trajectory Points

Fishing vessel trajectory outliers may not only appear in isolation but can also result from equipment malfunctions, causing alternating normal and outlier points. For example, the fishing vessel ZhePuYu 68823 displayed alternating outliers between 08:09 and 08:29 on 2 January 2018, as shown in Table 3. These outliers formed a new abnormal trajectory segment. The experimental analysis and visualization of ZhePuYu 68823’s trajectory data (Figure 5) revealed that, although the outliers created a new trajectory segment, the absence of validated normal points allowed our method to distinguish alternating outliers from normal points individually, rather than labeling the entire segment as abnormal. This approach effectively resolves the identification and processing of abnormal trajectory segments.

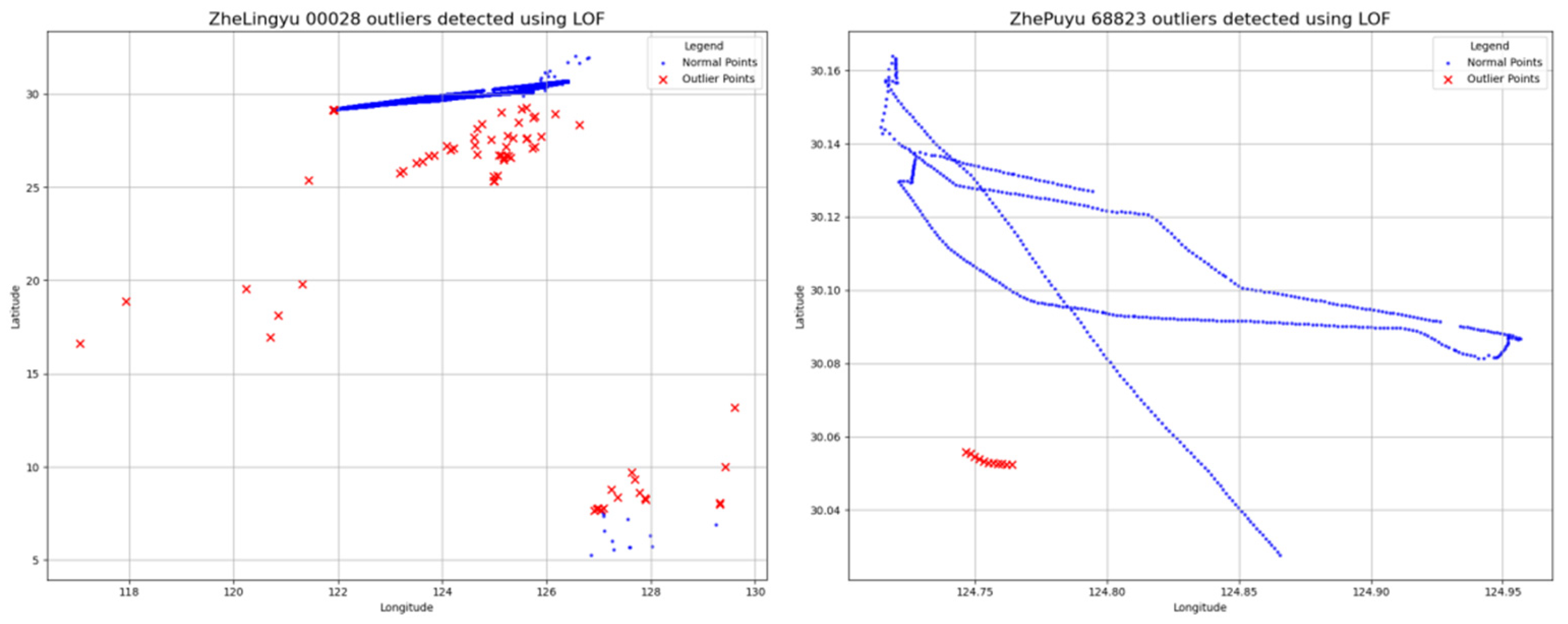
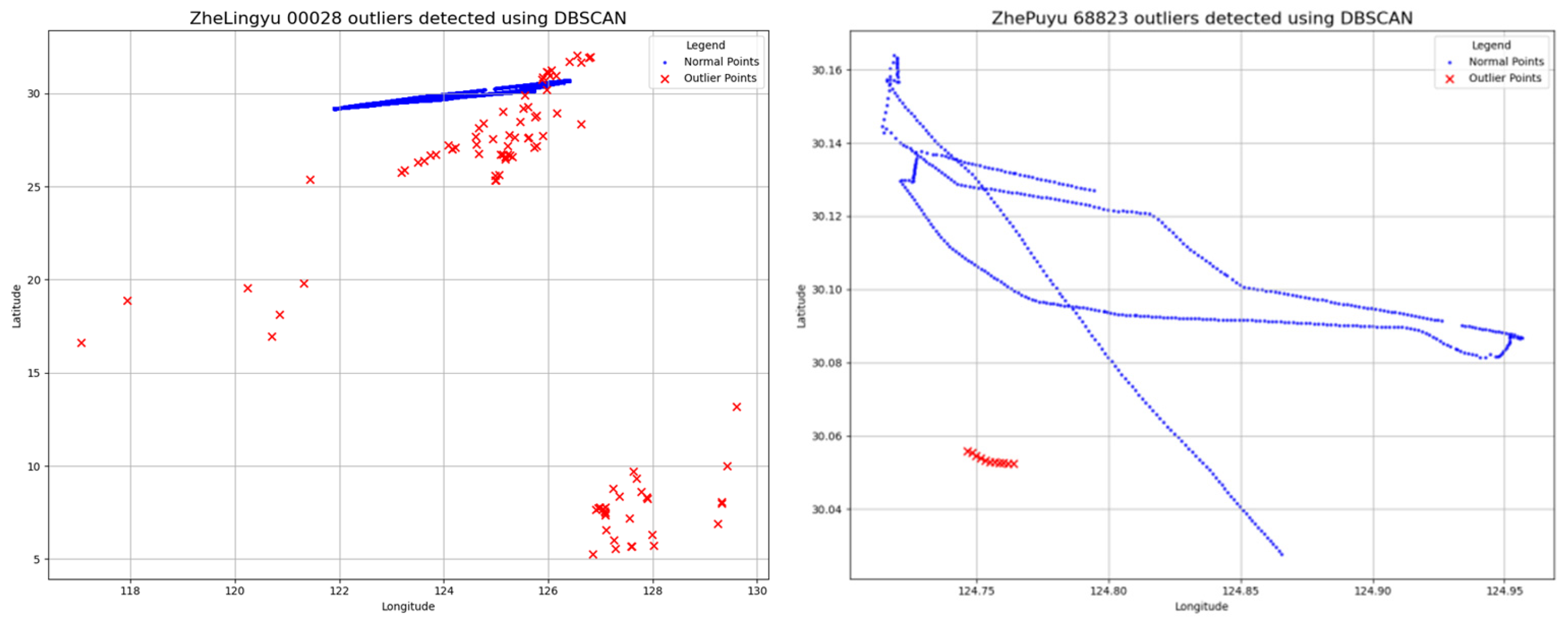
3.4. Comparative Analysis with Methods of LOF, DBSCAN, and Hampel Filter

This study selects three algorithms for a comparison experiment: LOF, DBSCAN, and Hampel filtering.
Local Outlier Factor (LOF): A density-based unsupervised anomaly detection method that determines whether a point is an outlier by calculating its local reachable density.
DBSCAN: A density-based clustering algorithm that divides data points into different clusters based on the distance between points and cluster centers.
Hampel Filter: A median-based anomaly detection method typically used in time-series data. It uses a sliding window approach to detect outliers by calculating the deviation of each data point from the median within the window.
For this experiment, the dataset included a total of 21,377 ship positions from ZheLingyu 00028 and ZhePuyu 68823. Different methods were used to conduct experiments on this dataset. During the experiments, the LOF, DBSCAN, and Hampel filtering methods required continuous parameter adjustment to achieve good recognition results. The outliers identified by each method were manually inspected and verified to obtain the actual outliers. Table 5 shows a comparison of the numbers of outliers identified by the different methods on the dataset. The results indicate that the Geohash-based method outperforms the other methods both in terms of the number of detected actual outliers and false detections.
First, this method is used to identify trajectory outliers, and the results are visualized, as shown in Figure 6. After cleaning the outliers, the results are as displayed in Figure 7.
The results of outlier detection using the LOF algorithm are shown in Figure 8. Due to the varying density of outlier distribution, only some of the outliers can be identified, and some normal trajectory points are also classified as outliers. Although the algorithm is effective in identifying alternating outliers, it requires different parameter settings for different fishing vessels. Therefore, it is necessary to estimate the proportion of outliers in advance, which leads to difficulties in parameter setting.
The outlier detection results using the DBSCAN algorithm are shown in Figure 9. The algorithm performs well for both individual outliers and trajectories formed by outliers, but it requires parameter adjustment for different fishing vessels and has cases of missed detection—for example, when outliers are located close to past or subsequent normal trajectories.
The outlier detection results using the Hampel filter are shown in Figure 10. Although it can identify outliers, there are difficulties in selecting the window size. Additionally, normal points may be misclassified as outliers, and, when there is a large change in the ship’s heading, turning points are likely to be identified as outliers.

4. Discussion

From Figure 6, it can be seen that trajectory data without data cleaning are of poor quality and cannot support reliable data mining work. The Geohash-based fishing vessel trajectory anomaly identification method proposed in this study can effectively improve the efficiency and accuracy of trajectory data cleaning. This method fully utilizes the spatial characteristics and dynamic computations of fishing vessel trajectories. The identified and cleared outliers in the trajectory can be considered as errors in the trajectory data, but not as abnormal states of the ship.
Compared with traditional methods based on statistical thresholds or distances, our method avoids the challenges associated with threshold selection and enables more accurate anomaly detection. Traditional threshold-based anomaly identification methods usually rely on single dimensions such as velocity or acceleration. For abnormal situations similar to those identified in the trajectory data of ZheLingYu 00028 considered in this study, the speed threshold method cannot eliminate outliers with seemingly normal speeds but abrupt coordinate jumps. The distance-based DB(p, D) algorithm has advantages when handling large-scale data, but it faces difficulties in parameter selection for different fishing vessel trajectories [16]. Additionally, the Local Outlier Factor (LOF) algorithm relies on density analysis [18]. When the data density varies significantly, it may miss some local anomalies. Lee [24] et al. proposed an outlier partitioning detection framework. They used the TRAOD algorithm to perform the coarse-grained and fine-grained partitioning of trajectories and then used a method based on a combination of the distance and density to detect outlier trajectory partitions. Luan [25] et al. proposed a trajectory outlier algorithm based on local density on the basis of the traditional TRAOD algorithm. However, the sparseness and density of fishing vessel trajectories will affect the results of this algorithm. Wang [26] proposed a method named Anomalous Trajectory Detection and Classification Based on Difference and Intersection Set Distance, but this only considers the distance and ignores factors such as the time and speed. Using smoothing filters such as mean or median filters for noise pre-processing in fishing vessel trajectories may cause the loss of local details for fishing vessel navigation. The sampling rate of fishing vessel trajectories also has an impact on filtering [27]. Although the Local Outlier Factor (LOF), DBSCAN, and the Hampel filter can achieve certain results in outlier detection, they require continuous parameter adjustment for different trajectory segments to perform effectively. Therefore, these three methods lack self-adaptability and are unsuitable for the cleaning of large-scale trajectory data. Manually tuning the parameters for each abnormal trajectory segment to remove outliers is infeasible in the context of big data mining, as it is impractical to manually adjust the parameters for every segment during large-scale data processing.
In contrast, our method discretizes spatial information using Geohash encoding. By combining spatial encoding with dynamic range verification, it significantly enhances the robustness and accuracy of anomaly detection and provides a more reliable solution for trajectory data cleaning.
In addition, the Geohash encoding method can also be used to compress fishing vessel trajectories. For example, only one position with the same Geohash encoding can be retained. It can also be used to detect the stopping points of fishing vessels. When there are multiple positions with the same Geohash encoding in the time series, it indicates that the fishing vessel has remained in the same area. By changing the length of the Geohash encoding, the fishing vessel trajectory can be downsampled. For example, if the length of the 7-bit encoding is reduced by 1 bit, the grid area will increase by 32 times, and only one of the same encodings will be retained.
Although this paper focuses on fishing vessel trajectory data, the method proposed can also be generalized to the identification of trajectory outliers in merchant vessels and other types of ships and can adapt to the vessel speed and transmission frequency. When the latitude and longitude of the trajectory data are normal but the vessel speed exceeds the limit, or the time interval of vessel position information transmission is too long, this method is still applicable.
In addition, the geohash geocoding algorithm used in this paper can also be replaced by the Google S2 geocoding method, but the encoding range in the method needs to be modified [28]. Therefore, this proposed method is still effective for trajectory-dependent analyses and applications, such as ship collision prevention [29] and route planning [30].

5. Conclusions

This study proposes a Geohash-based method for outlier detection and data cleaning in fishing vessel trajectories. Compared to traditional approaches, this method exhibits significant advantages in terms of algorithm performance and application scenarios. It involves dynamically calculating the reachable distance according to the fishing vessel’s speed and time interval and calculating the corresponding Geohash neighborhood hierarchy, followed by obtaining the neighborhood range of the fishing vessel position point by dynamically adjusting the Geohash hierarchy. Ultimately, the validity of the fishing vessel position point is verified in both directions by performing the intersection detection of the current point with the multi-layered Geohash encoding of the preceding and following points. This data cleaning process makes full use of the regional representation and spatial characteristics of Geohash coding, and the fishing vessel trajectory data can be cleaned without the need for a large amount of historical data. It primarily utilizes the neighborhood search characteristics of Geohash. Outlier identification mainly involves the relationships between the current point and its preceding and following trajectory points, thus requiring a relatively small amount of data for processing. It can be applied to the online anomaly detection of the trajectories of fishing vessels, and, in the context of intermittent trajectories due to irregular transmission frequencies, it is not necessary to clean the trajectory of the fishing vessel by segment processing. This approach can be adapted to the trajectory data of fishing vessels under different sailing conditions. Whether it is high-speed sailing or low-speed cruising, the algorithm can adjust the neighborhood range of the trajectory points according to the specific conditions, which improves the adaptability and applicability range of the algorithm. Thus, it effectively improves the accuracy in the detection of the outliers and the efficiency of data cleaning.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/jmse13050917/s1, The entire trajectory data of ZheLingYu 00028 and ZhePuYu 68823 can be found in the Supplementary Files. The Beidou fishing vessel position data come from the Beidou civil sub-processing service provider, and the data mainly include the Beidou card number, latitude and longitude positions, speed, heading, and transmission time of the fishing vessel. The temporal resolution of the data is 3 min.

Author Contributions

Conceptualization, W.Z.; methodology, W.Z. and L.Z.; software and validation, L.Z.; writing—original draft preparation, L.Z.; writing—review and revising, W.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This work was financially supported by the National Key R&D Program of China (No. 2023YFD2401303) and the Central Public-Interest Scientific Institution Basal Research Fund, ECSFR, CAFS (No. 2022ZD0402).

Data Availability Statement

Data are available upon request from the authors.

Acknowledgments

The authors would like to express their sincere gratitude to the reviewers and the academic editor of the journal, whose suggestions and opinions have greatly contributed to improving the quality of the paper.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Zhou, W.; Chen, X.; Fan, W.; He, Z.; Yu, L.; Dai, Y.; Wang, L. Application and prospect of location-based information service in marine fishery. World Sci. Technol. Res. Dev. 2015, 37, 611–617. [Google Scholar] [CrossRef]
  2. Li, C.; Feng, G.; Yao, H.; Liu, R.; Li, Y.; Xie, K.; Miao, Q.A. Survey on Trajectory Anomaly Detection. J. Softw. 2024, 35, 927–974. [Google Scholar] [CrossRef]
  3. Cao, H.; Tang, H.; Wang, F.; Xu, Y. Survey on Trajectory Representation Learning Techniques. J. Softw. 2021, 32, 1461–1479. [Google Scholar] [CrossRef]
  4. Hawkins, D. Identification of Outliers; Chapman and Hall: London, UK, 1980. [Google Scholar]
  5. Sun, S. Research on Ship Trajectory Anomaly Detection and Early Warning in Port Area Based on Spatio-Temporal Trajectory Mining. Ph.D. Thesis, Dalian Maritime University, Dalian, China, 2024. [Google Scholar] [CrossRef]
  6. Mei, L.; Zhang, F.; Gao, Q. Overview of outlier detection technology. Comput. Appl. Res. 2020, 37, 3521–3527. [Google Scholar] [CrossRef]
  7. Feng, Z.; Zhu, Y. A survey on trajectory data mining: Techniques and applications. IEEE Access 2016, 4, 2056–2067. [Google Scholar] [CrossRef]
  8. Han, Z.; Xu, G.; Huang, T.; Ren, W. Vessel Trajectory Outlier Detection Algorithm Based on Adaptive Threshold. Comput. Mod. 2018, 42–47+51. [Google Scholar] [CrossRef]
  9. Chen, L.; Lv, M.; Ye, Q.; Chen, G.; Woodward, J. A personal route prediction system based on trajectory data mining. Inf. Sci. 2011, 181, 1264–1284. [Google Scholar] [CrossRef]
  10. Alvares, L.O.; Oliveira, G.; Heuser, C.A.; Bogorny, V. A Framework for Trajectory Data Preprocessing for Data Mining. In Proceedings of the SEKE, Boston, MA, USA, 1–3 July 2009; pp. 698–702. [Google Scholar] [CrossRef]
  11. Zheng, Y.; Xie, X.; Ma, W.-Y. GeoLife: A collaborative social networking service among user, location and trajectory. IEEE Data Eng. Bull. 2010, 33, 32–39. [Google Scholar]
  12. Ristic, B.; La Scala, B.; Morelande, M.; Gordon, N. Statistical analysis of motion patterns in AIS data: Anomaly detection and motion prediction. In Proceedings of the 2008 11th International Conference on Information Fusion, Cologne, Germany, 30 June–3 July 2008; pp. 1–7. [Google Scholar]
  13. Zhen, R.; Shao, Z.; Pan, J.; Zhao, Q. A Study on the Identification of Abnormal Ship Trajectory Based on Statistic Theories. J. Jimei Univ. (Nat. Sci. Ed.) 2015, 20, 193–197. [Google Scholar] [CrossRef]
  14. Mascaro, S.; Nicholso, A.E.; Korb, K.B. Anomaly detection in vessel tracks using Bayesian networks. Int. J. Approx. Reason. 2014, 55, 84–98. [Google Scholar] [CrossRef]
  15. Castaldo, F.; Bastani, V.; Marcenaro, L.; Palmieri, F.A.N.; Regazzoni, C. Abnormal vessel behavior detection in port areas based on Dynamic Bayesian Networks. In Proceedings of the International Conference on Information Fusion, Salamanca, Spain, 7–10 July 2014. [Google Scholar]
  16. Knorr, E.M.; Ng, R.T. Algorithms for Mining Distance-Based Outliers in Large Datasets. In Proceedings of the 24th International Conference on Very Large Data Bases, New York, NY, USA, 24–27 August 1998; pp. 392–403. [Google Scholar]
  17. Zhang, L.; Hu, Z.; Yang, G. Trajectory Outlier Detection Based on Multi-Factors. IEICE Trans. Inf. Syst. 2014, E97.D, 2170–2173. [Google Scholar] [CrossRef]
  18. Breunig, M.M.; Kriegel, H.-P.; Ng, R.T.; Sander, J. LOF: Identifying density-based local outliers. ACM Sigmod Rec. 2000, 29, 93–104. [Google Scholar] [CrossRef]
  19. Liu, J.; Li, H.; Gao, Y.; Yu, H.; Jiang, D. A geohash-based index for spatial data management in distributed memory. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 1–4. [Google Scholar] [CrossRef]
  20. Hafez, I.; Mehedi, H.M.; Raed, H.; Seok, O.J. User Activity and Trip Recognition using Spatial Positioning System Data by Integrating the Geohash and GIS Approaches. Transp. Res. Rec. 2021, 2675, 391–405. [Google Scholar] [CrossRef]
  21. Jiang, B.; Zhou, W. Comparative Analysis of GeoHash, Google S2 and Uber H3 as Global Geographic Grid Coding Methods. Geomat. Inf. Sci. Wuhan Univ. 2024, 40. [Google Scholar] [CrossRef]
  22. Yuan, M.; Nara, A. Space-Time Analytics of Tracks for the Understanding of Patterns of Life. In Space-Time Integration in Geography and GIScience; Springer: Dordrecht, The Netherlands, 2015. [Google Scholar] [CrossRef]
  23. Zhou, W.F.; Sui, X.; Guo, X.T.; Jiang, Y.; Cheng, T. Searching method for marine ship rescue based on grid neighborhood query. J. Geo-Inf. Sci. 2021, 23, 1422–1432. [Google Scholar] [CrossRef]
  24. Lee, J.G.; Han, J.; Li, X. Trajectory Outlier Detection: A Partition-and-Detect Framework. In Proceedings of the IEEE International Conference on Data Engineering, Cancun, Mexico, 7–12 April 2008; IEEE: Piscataway, NJ, USA, 2008. [Google Scholar] [CrossRef]
  25. Luan, F.; Zhang, Y.; Cao, K.; Li, Q. Based local density trajectory outlier detection with partition-and-detect framework. In Proceedings of the 2017 13th International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery (ICNC-FSKD), Guilin, China, 29–31 July 2017; IEEE: Piscataway, NJ, USA; pp. 1708–1714. [Google Scholar]
  26. Wang, J.; Yuan, Y.; Ni, T.; Ma, Y.; Liu, M.; Xu, G.; Shen, W. Anomalous Trajectory Detection and Classification Based on Difference and Intersection Set Distance. IEEE Trans. Veh. Technol. 2020, 69, 2487–2500. [Google Scholar] [CrossRef]
  27. Zheng, Y. Trajectory Data Mining: An Overview. ACM Trans. Intell. Syst. Technol. 2015, 6, 1–41. [Google Scholar] [CrossRef]
  28. Jiang, B.; Zhou, W.; Han, H. Storage and Management of Ship Position Based on Geographic Grid Coding and Its Efficiency Analysis in Neighborhood Search—A Case Study of Shipwreck Rescue and Google S2. Appl. Sci. 2024, 14, 1115. [Google Scholar] [CrossRef]
  29. He, Y.; Li, Z.; Mou, J.; Chen, P.; Tang, Y. Collision-avoidance path planning for multi-ship encounters considering ship manoeuvrability and COLREGs. Transp. Saf. Environ. 2021, 3, 103–113. [Google Scholar] [CrossRef]
  30. Chen, X.; Hu, R.; Luo, K.; Wang, Y.; Zhang, L. Intelligent ship route planning via an A∗ search model enhanced double-deep Q-network. Ocean. Eng. 2025, 120956. [Google Scholar] [CrossRef]
Jmse 13 00917 g001
Figure 1. The technical flowchart of the proposed data cleaning method for trajectory data.
Figure 1. The technical flowchart of the proposed data cleaning method for trajectory data.
Jmse 13 00917 g001
Jmse 13 00917 g002
Figure 2. Geohash encoding of different levels of region division.
Figure 2. Geohash encoding of different levels of region division.
Jmse 13 00917 g002
Jmse 13 00917 g003
Figure 3. Geohash multi-layer neighborhood range.
Figure 3. Geohash multi-layer neighborhood range.
Jmse 13 00917 g003
Jmse 13 00917 g004
Figure 4. Single outlier of ZheLingYu 00028 (red point is identified as outlier).
Figure 4. Single outlier of ZheLingYu 00028 (red point is identified as outlier).
Jmse 13 00917 g004
Jmse 13 00917 g005
Figure 5. Abnormal trajectory segment of ZhePuYu 68823 (red point is identified as outlier).
Figure 5. Abnormal trajectory segment of ZhePuYu 68823 (red point is identified as outlier).
Jmse 13 00917 g005
Jmse 13 00917 g006
Figure 6. Outliers identified in ZheLingyu 00028 and ZhePuyu 68823 data by the proposed method.
Figure 6. Outliers identified in ZheLingyu 00028 and ZhePuyu 68823 data by the proposed method.
Jmse 13 00917 g006
Jmse 13 00917 g007
Figure 7. ZheLingyu 00028 and ZhePuyu 68823 trajectories after cleaning outliers.
Figure 7. ZheLingyu 00028 and ZhePuyu 68823 trajectories after cleaning outliers.
Jmse 13 00917 g007
Jmse 13 00917 g008
Figure 8. ZheLingyu 00028 and ZhePuyu 68823 outliers identified using LOF.
Figure 8. ZheLingyu 00028 and ZhePuyu 68823 outliers identified using LOF.
Jmse 13 00917 g008
Jmse 13 00917 g009
Figure 9. ZheLingyu 00028 and ZhePuyu 68823 outliers identified using DBSCAN.
Figure 9. ZheLingyu 00028 and ZhePuyu 68823 outliers identified using DBSCAN.
Jmse 13 00917 g009
Jmse 13 00917 g010
Figure 10. ZheLingyu 00028 and ZhePuyu 68823 outliers identified using the Hampel filter.
Figure 10. ZheLingyu 00028 and ZhePuyu 68823 outliers identified using the Hampel filter.
Jmse 13 00917 g010
Table 1. Base32 encoding table.
Table 1. Base32 encoding table.
Decimal0123456789101112131415
Base 320123456789bcdefg
Decimal16171819202122232425262728293031
Base 32hjkmnpqrstuvwxyz
Table 2. The pre-processed vessel position data of ZheLingYu 00028 as an example.
Table 2. The pre-processed vessel position data of ZheLingYu 00028 as an example.
Fishing Boat NameTimestampLongitudeLatitudeSpeedDirection
ZheLingYu 00028 2018/01/07 6:05:14125.70228830.15784.4133
ZheLingYu 000282018/01/07 6:06:16125.69942230.157484.6127
ZheLingYu 000282018/01/07 6:07:18125.69663330.1568274.5126
ZheLingYu 000282018/01/07 6:08:20125.69381130.15624.5128
ZheLingYu 000282018/01/07 6:09:22125.69093330.1557444.5131
ZheLingYu 000282018/01/07 6:09:50125.69114630.1856234.5131
ZheLingYu 000282018/01/07 6:10:24125.68802230.1555274.6131
ZheLingYu 000282018/01/07 6:11:06125.68604430.1551334.6124
ZheLingYu 000282018/01/07 6:12:08125.683430.1539444.6122
ZheLingYu 000282018/01/07 6:13:10125.68061130.1530834.6126
ZheLingYu 000282018/01/07 6:14:12125.67771130.1524444.6127
ZheLingYu 000282018/01/07 6:15:14125.67485530.1519114.5129
ZheLingYu 000282018/01/07 6:16:16125.67198830.1515524.4131
ZheLingYu 000282018/01/07 6:17:18125.66917730.150954.5127
ZheLingYu 000282018/01/07 6:18:20125.66637730.1502914.5127
ZheLingYu 000282018/01/07 6:19:22125.66355530.1497554.4129
ZheLingYu 000282018/01/07 6:20:24125.66074430.1493224.4129
ZheLingYu 000282018/01/07 6:21:26125.65794430.148854.5128
ZheLingYu 000282018/01/07 6:22:28125.65515530.1481494.3125
ZheLingYu 000282018/01/07 6:23:30125.65295530.1473443.5122
Table 3. Abnormal trajectory data segment of ZhePuYu 68823 on 2 January 2018.
Table 3. Abnormal trajectory data segment of ZhePuYu 68823 on 2 January 2018.
Fishing Boat NameTimestampLongitudeLatitudeSpeedDirection
ZhePuYu 68823 2018/01/02 8:09:53124.77167730.108781.4159
ZhePuYu 688232018/01/02 8:11:37124.76230.0524771.4137
ZhePuYu 688232018/01/02 8:11:53124.77048830.1099911.5160
ZhePuYu 688232018/01/02 8:13:37124.760230.0526021.5137
ZhePuYu 688232018/01/02 8:13:53124.76933330.1112161.4162
ZhePuYu 688232018/01/02 8:15:37124.75846630.052751.4137
ZhePuYu 688232018/01/02 8:15:53124.76817730.1124411.3158
ZhePuYu 688232018/01/02 8:17:37124.75671130.0528021.4134
ZhePuYu 688232018/01/02 8:17:53124.76704430.1136551.4160
ZhePuYu 688232018/01/02 8:19:37124.75496630.0529611.4139
ZhePuYu 688232018/01/02 8:19:53124.76597730.1148751.3161
ZhePuYu 688232018/01/02 8:21:37124.75325530.0532691.5146
ZhePuYu 688232018/01/02 8:21:53124.76484430.1160331.4157
ZhePuYu 688232018/01/02 8:23:37124.75154430.0539131.5145
ZhePuYu 688232018/01/02 8:23:54124.763730.1171881.4157
ZhePuYu 688232018/01/02 8:25:38124.74985530.0546581.5147
ZhePuYu 688232018/01/02 8:25:54124.762530.1183081.4160
ZhePuYu 688232018/01/02 8:27:38124.74815530.055351.4151
ZhePuYu 688232018/01/02 8:27:54124.76126630.1193941.4157
ZhePuYu 688232018/01/02 8:29:38124.74644430.0559581.4144
Table 4. Geohash code lengths corresponding to region sizes near 30° latitude.
Table 4. Geohash code lengths corresponding to region sizes near 30° latitude.
Geohash Encoding LengthWidthLength
14604.5 km5003.8 km
21072.5 km625.5 km
3135.1 km156.4 km
433.9 km19.5 km
54.2 km4.9 km
61.1 km610.8 m
7132.2 m152.7 m
833.1 m19.1 m
94.1 m4.8 m
101.0 m0.596 m
11129.1 mm149 mm
1232.3 mm18.6 mm
Table 5. The performance of different methods.
Table 5. The performance of different methods.
Detection MethodTotal Number of Detected OutliersVerified to be True Verified to be False
Geohash1101100
LOF1027824
DBSCAN1071070
Hampel filter988216
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Zhang, L.; Zhou, W. A Data Cleaning Method for the Identification of Outliers in Fishing Vessel Trajectories Based on a Geocoding Algorithm. J. Mar. Sci. Eng. 2025, 13, 917. https://doi.org/10.3390/jmse13050917

AMA Style

Zhang L, Zhou W. A Data Cleaning Method for the Identification of Outliers in Fishing Vessel Trajectories Based on a Geocoding Algorithm. Journal of Marine Science and Engineering. 2025; 13(5):917. https://doi.org/10.3390/jmse13050917

Chicago/Turabian Style

Zhang, Li, and Weifeng Zhou. 2025. "A Data Cleaning Method for the Identification of Outliers in Fishing Vessel Trajectories Based on a Geocoding Algorithm" Journal of Marine Science and Engineering 13, no. 5: 917. https://doi.org/10.3390/jmse13050917

APA Style

Zhang, L., & Zhou, W. (2025). A Data Cleaning Method for the Identification of Outliers in Fishing Vessel Trajectories Based on a Geocoding Algorithm. Journal of Marine Science and Engineering, 13(5), 917. https://doi.org/10.3390/jmse13050917

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop