Weak Underwater Signals’ Detection by the Unwrapped Instantaneous Phase
Abstract
1. Introduction
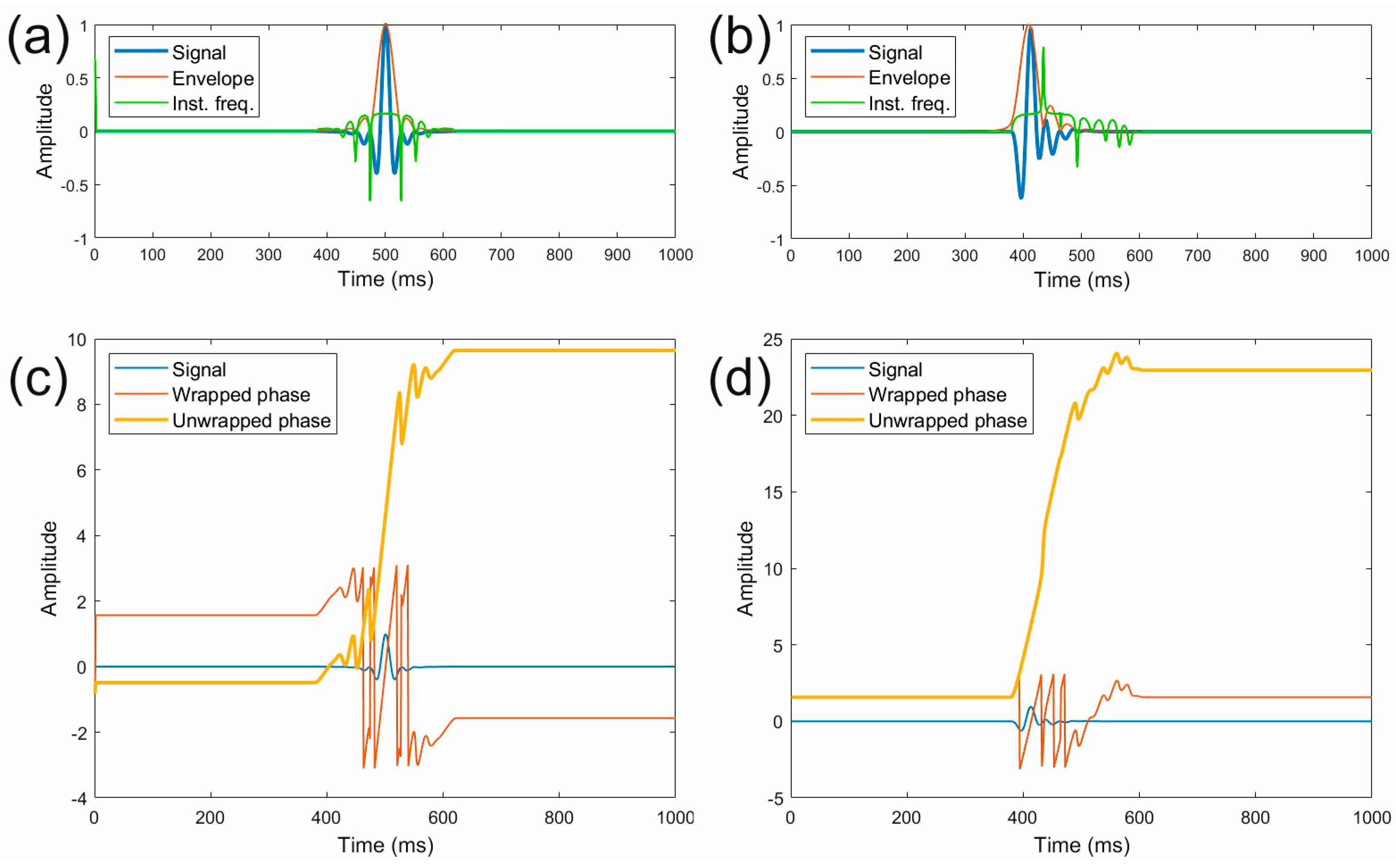
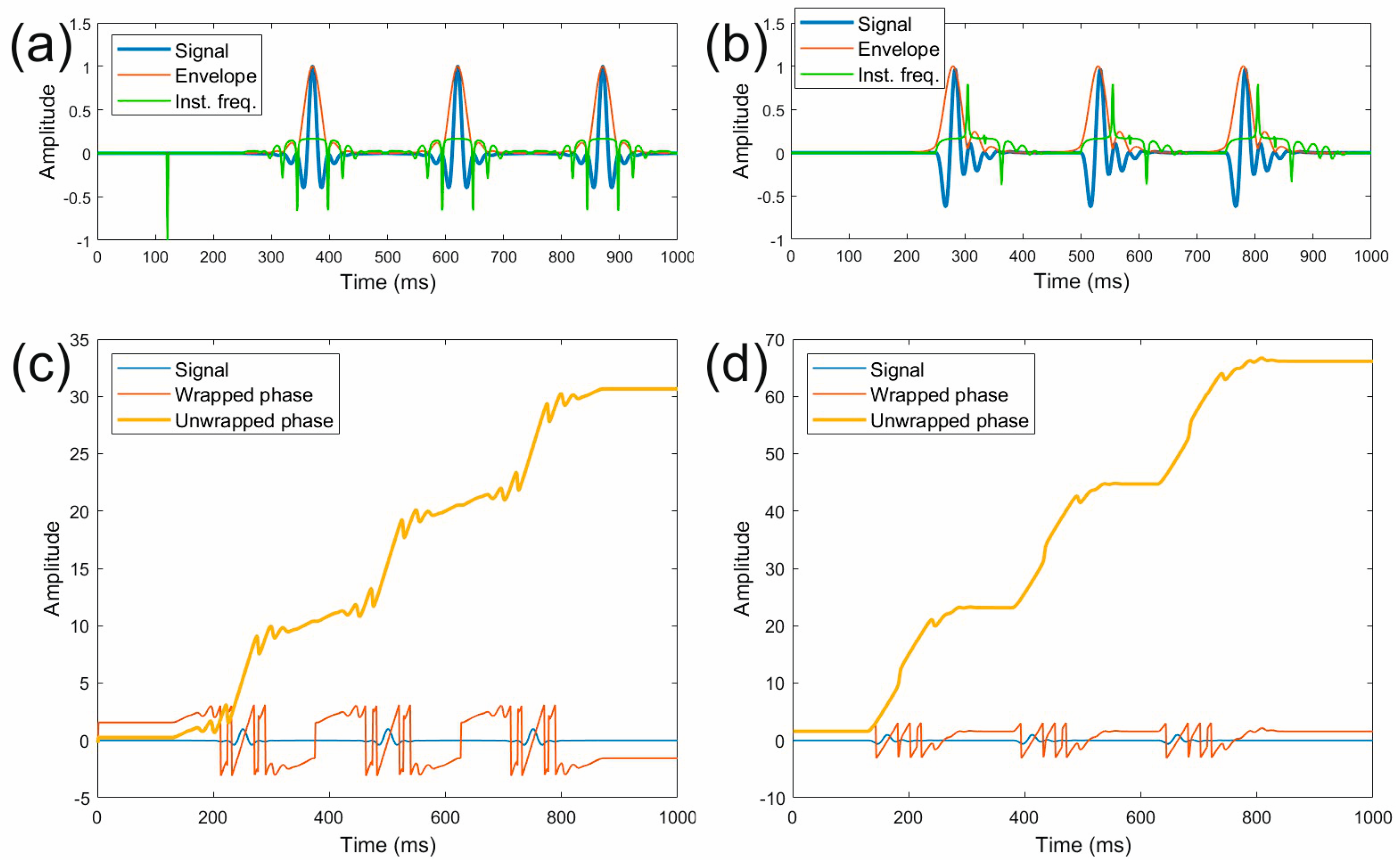
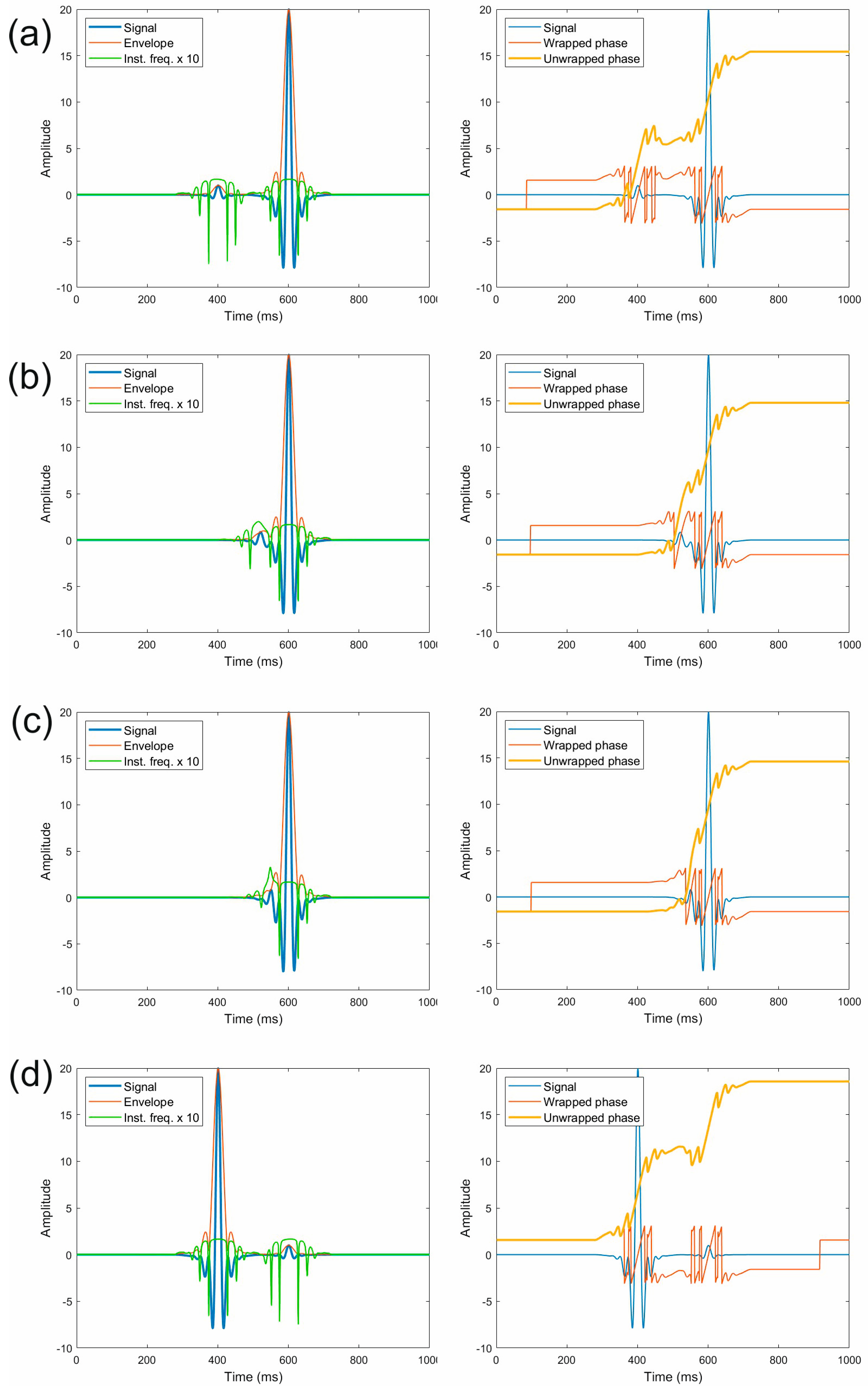
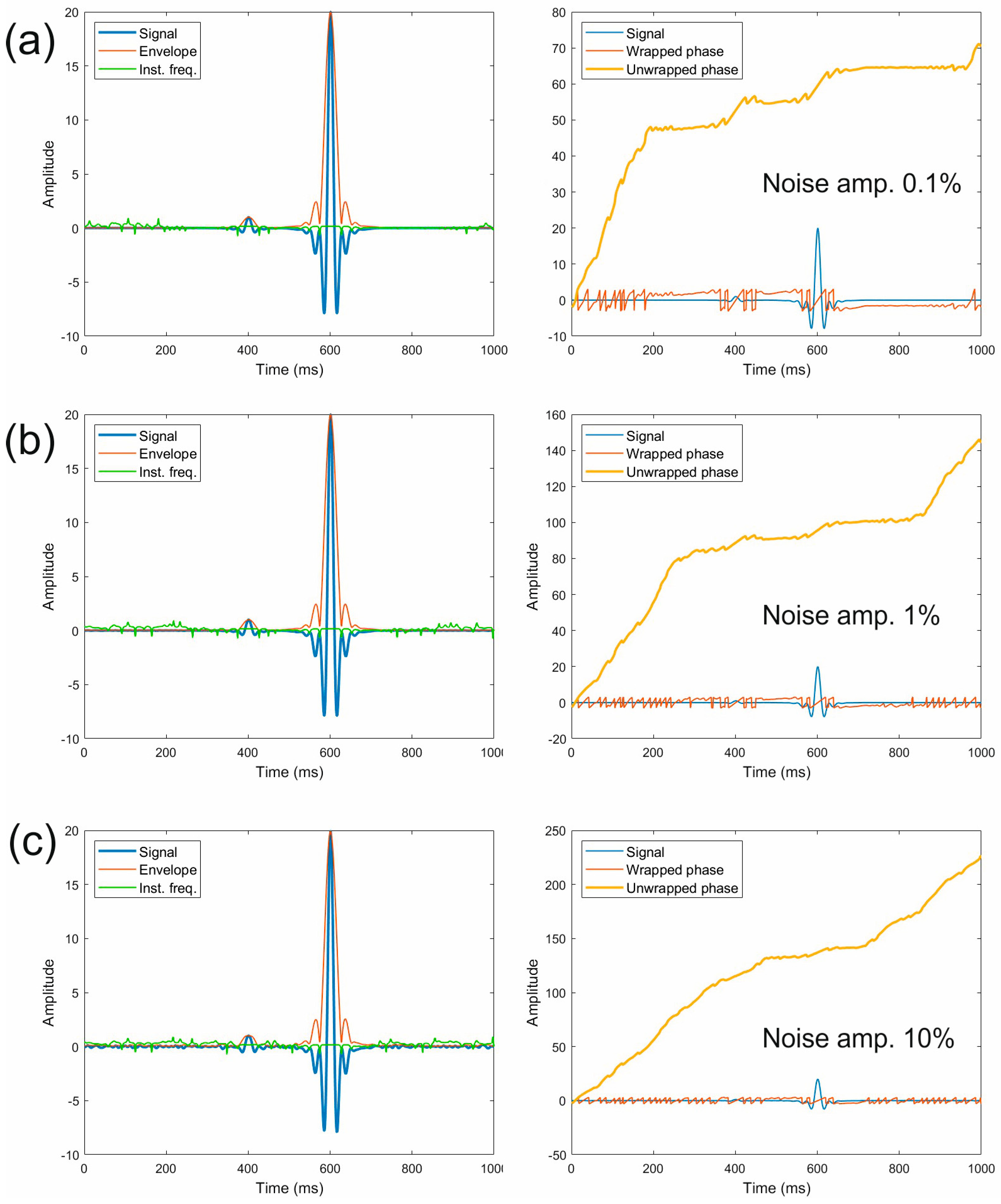
2. Materials and Methods
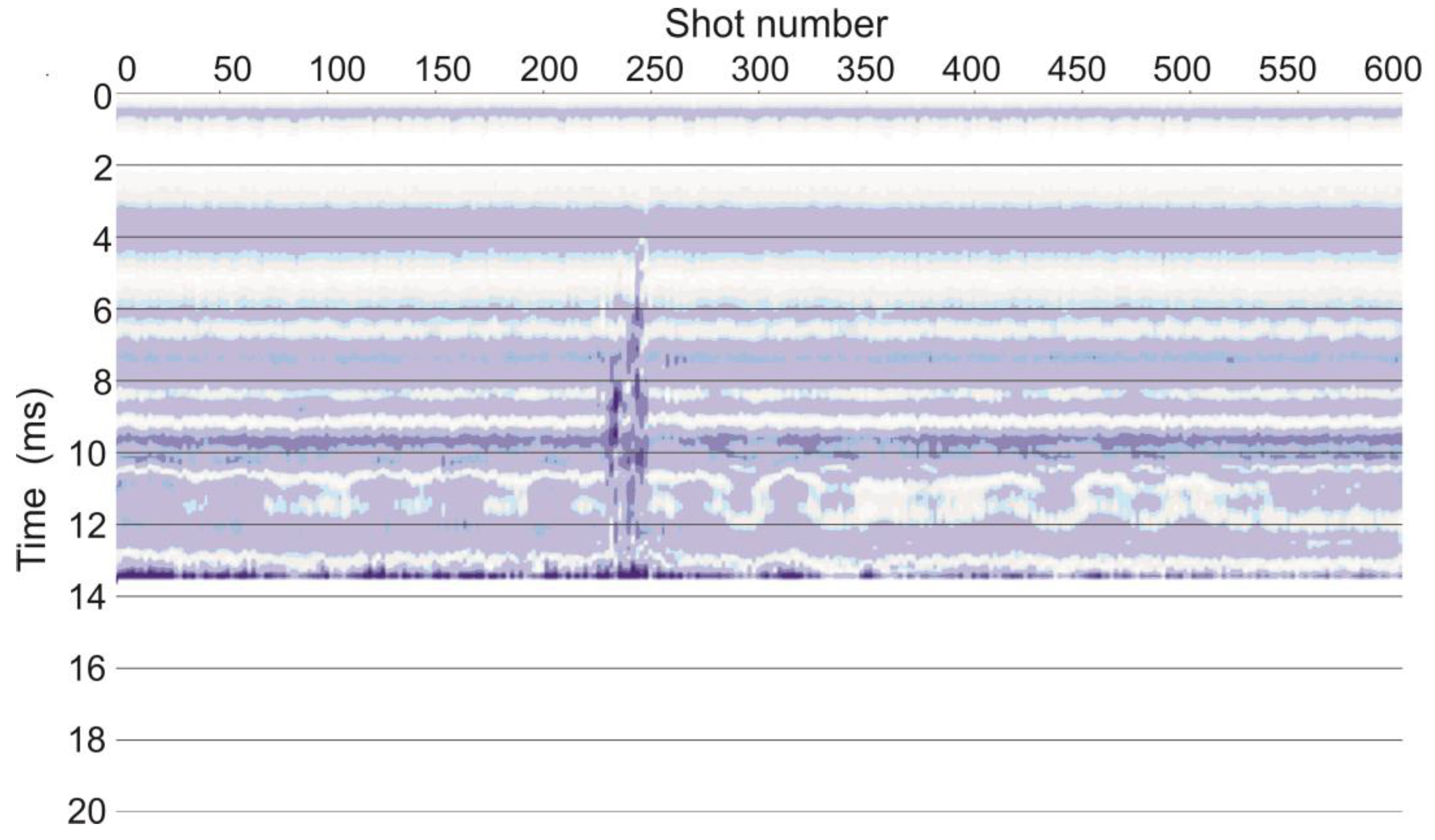
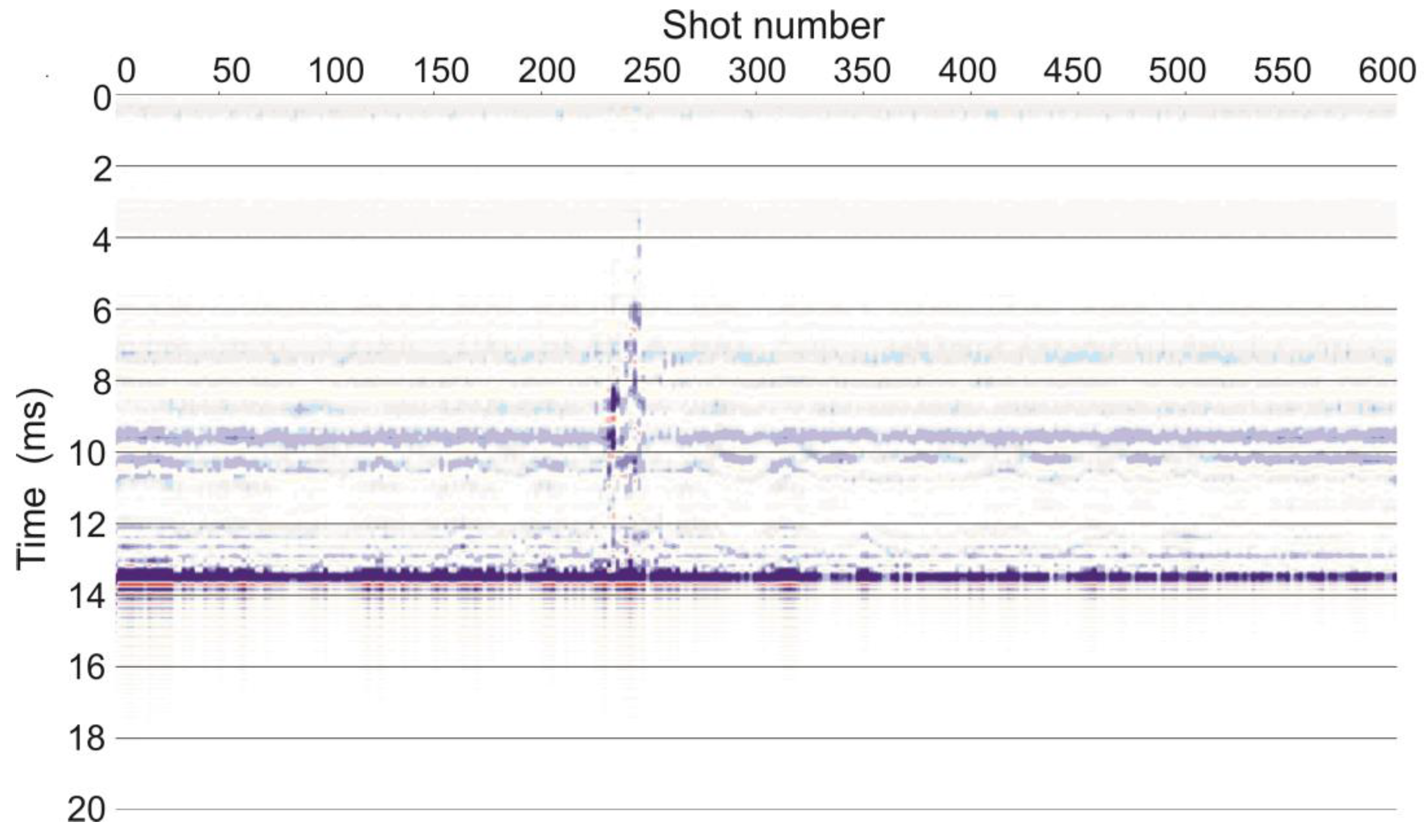
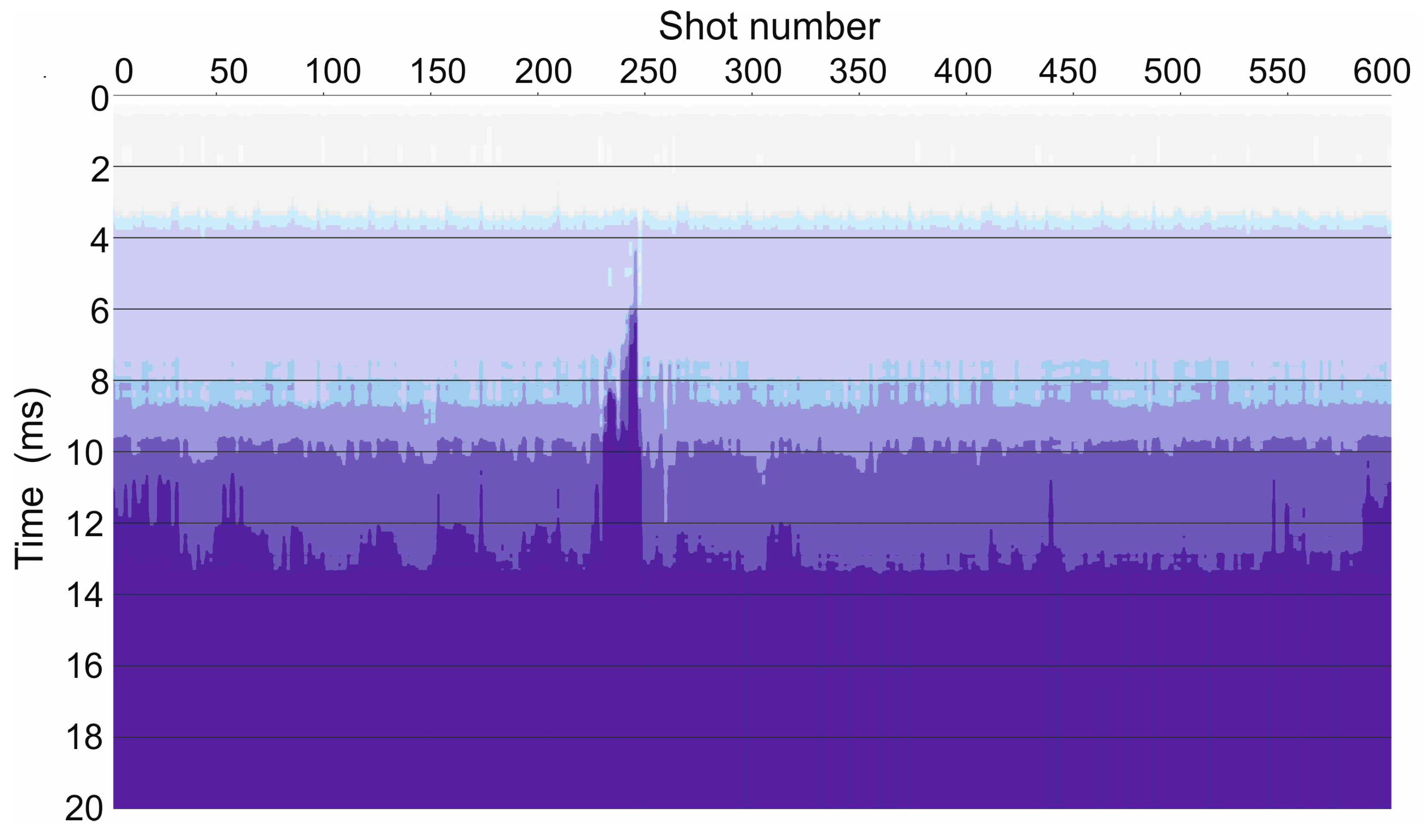
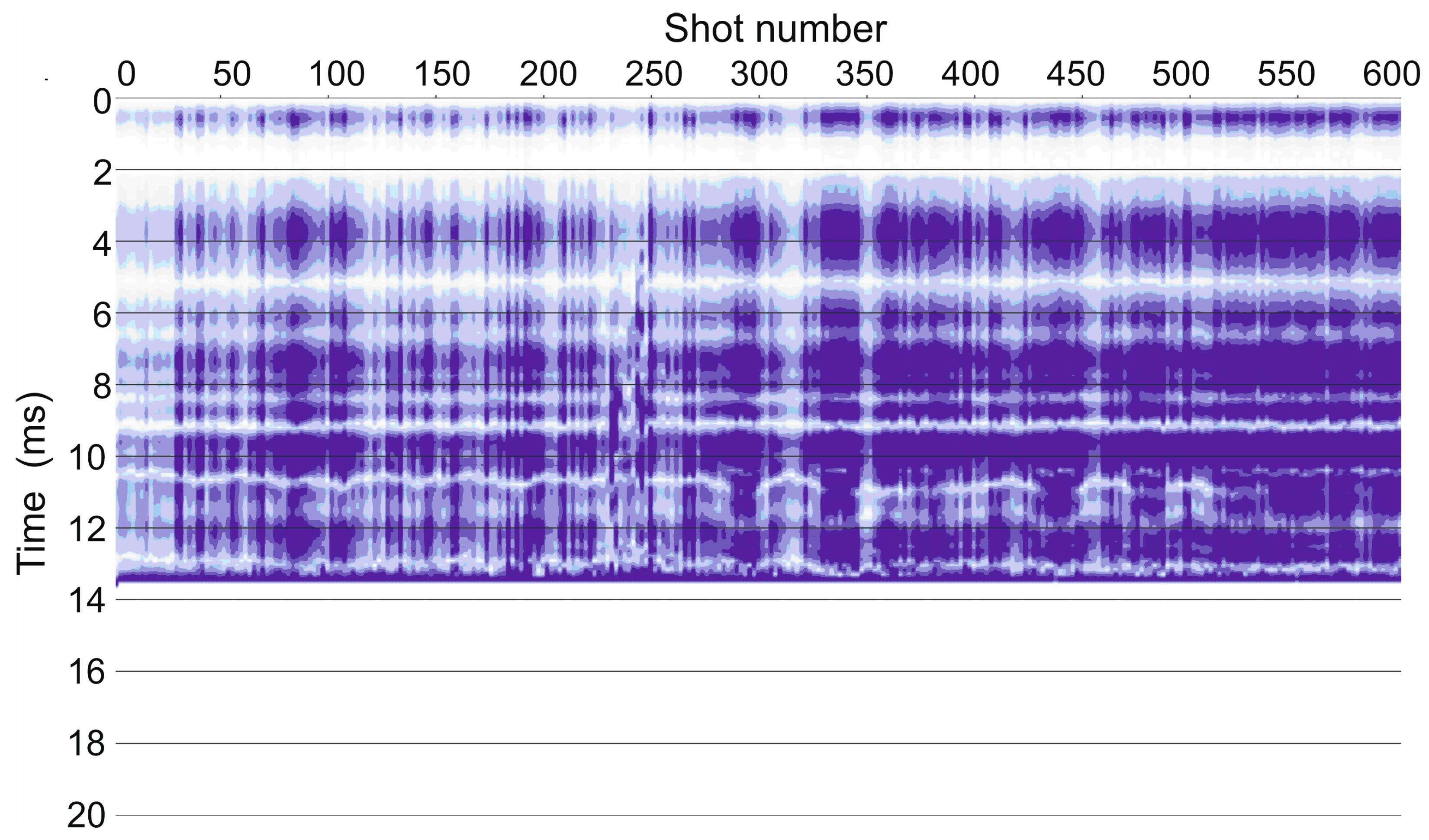
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Canales, L.L. Random Noise Reduction; SEG Annual Meeting 1984, Expanded Abstracts; SEG: Tulsa, OK, USA, 1984; pp. 525–527. [Google Scholar] [CrossRef]
- Gulunay, N. FXDECON and Complex Wiener Prediction Filter; SEG Annual Meeting 1986, Expanded Abstracts; SEG: Tulsa, OK, USA, 1986; pp. 279–281. [Google Scholar] [CrossRef]
- Gulunay, N. Signal leakage in f-x deconvolution algorithms. Geophysics 2017, 82, W31–W45. [Google Scholar] [CrossRef]
- Zhu, W.; Mousavi, S.M.; Beroza, G.C. Seismic signal denoising and decomposition using deep neural networks. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9476–9488. [Google Scholar] [CrossRef]
- Ji, G.; Wang, C. A Denoising Method for Seismic Data Based on SVD and Deep Learning. Appl. Sci. 2022, 12, 12840. [Google Scholar] [CrossRef]
- Li, J.; Trad, D.; Liu, D. Robust seismic data denoising via self-supervised deep learning. Geophysics 2024, 89, V437–V451. [Google Scholar] [CrossRef]
- Oppenheim, A.V.; Schafer, R.W. Digital Signal Processing; Prentice-Hall: Englewood Cliffs, NJ, USA, 1975; ISBN 0132146355. [Google Scholar]
- White, R.S. Applied high-resolution geophysical methods: Offshore geoengineering hazards. Geophys. J. Int. 1986, 86, 214–215. [Google Scholar] [CrossRef]
- Marsset, B.; Missiaen, T.; Noble, M.; Versteeg, W.; Henriet, J.-P. Very high resolution 3D marine seismic data processing for geotechnical applications. Geophys. Prospect. 1998, 46, 105–120. [Google Scholar] [CrossRef]
- Minh Hue Le, T.; Eiksund, R.G.; Strøm, P.J.; Saue, M. Geological and geotechnical characterization for offshore wind turbine foundations: A case study of the Sheringham Shoal wind farm. Eng. Geol. 2014, 177, 40–53. [Google Scholar] [CrossRef]
- Negro, V.; López-Gutierrez, J.-S.; Esteban, M.D.; Matutano, C. Uncertainties in the design of support structures and foundations for offshore wind turbines. Renewable Energy 2014, 63, 125–132. [Google Scholar] [CrossRef]
- Perveen, R.; Kishor, N.; Mohanty, S.R. Off-shore wind farm development: Present status and challenges. Renew. Sustain. Energy Rev. 2014, 29, 780–792. [Google Scholar] [CrossRef]
- Monrigal, O.; de Jong, I.; Duarte, H. An ultra-high-resolution 3D marine seismic system for detailed site investigation. Near Surf. Geophys. 2017, 15, 335–345. [Google Scholar] [CrossRef]
- Wei Min, P.; Yi Gen, W.; Song Chuan, X.; Hu, B.; Zhang, Y.; Li Zheng, S.; Xiao Li, J. Advancing offshore wind farm site assessments in Guangxi using single-channel seismic method. J. Phys. Conf. Ser. 2024, 2895, 012003. [Google Scholar] [CrossRef]
- Wang, R.; Hu, B.; Zhang, H.; Zhang, P.; Li, C.; Chen, F. Seismic interferometry for single-channel data: A promising approach for improved offshore wind farm evaluation. Remote Sens. 2025, 17, 325. [Google Scholar] [CrossRef]
- International Association of Oil & Gas Producers (IOGP). Guidelines for the Conduct of Offshore Drilling Hazard Site Surveys; IOGP Report 373-18-1; 2017; pp. 1–46. Available online: https://www.deparentis.com/wp-content/uploads/2020/04/IGOP-373-18-1-1.pdf (accessed on 7 April 2025).
- Gabor, D. Theory of communications. J. Inst. Electr. Eng.—Part III Radio Commun. 1946, 93, 429–457. [Google Scholar] [CrossRef]
- Ville, J.A. Theorie et application de la notion du signal analytique. Cable Transm. 1948, 2, 61–74. Available online: https://archive.org/details/VilleSigAnalytiqueCablesEtTrans1948Fr (accessed on 1 May 2025).
- Taner, M.T.; Koehler, F.; Sheriff, R.E. Complex seismic trace analysis. Geophysics 1979, 44, 1041–1063. [Google Scholar] [CrossRef]
- Tribolet, J. A new phase unwrapping algorithm. IEEE Trans. Acoust. Speech Signal Process. 1977, 25, 170–177. [Google Scholar] [CrossRef]
- Strand, J.; Taxt, T. Performance evaluation of two-dimensional phase unwrapping algorithms. Appl. Opt. 1999, 38, 4333–4344. [Google Scholar] [CrossRef]
- Egidi, N.; Maponi, P. A comparative study of two fast phase unwrapping algorithms. Appl. Math. Comput. 2004, 148, 599–629. [Google Scholar] [CrossRef]
- Wang, S. An Improved quality guided phase unwrapping method and its applications to MRI. Prog. Electromagn. Res. 2014, 145, 273–286. [Google Scholar] [CrossRef]
- Poggiagliolmi, E.; Vesnaver, A. Instantaneous phase and frequency derived without user-defined parameters. Geophys. J. Int. 2014, 199, 1544–1553. [Google Scholar] [CrossRef]
- Vesnaver, A. Instantaneous frequency and phase without unwrapping. Geophysics 2017, 82, F1–F7. [Google Scholar] [CrossRef]
- Ackroyd, M.H. Instantaneous spectra and instantaneous frequency. Proc. IEEE 1970, 58, 141. [Google Scholar] [CrossRef]
- Saha, J.G. Relationship Between Fourier and Instantaneous Frequency; Expanded Abstracts 1987, SEG Annual Meeting; SEG: Tulsa, OK, USA, 1987; pp. 591–594. [Google Scholar] [CrossRef]
- Quan, Y.; Harris, J. Seismic attenuation tomography using the frequency shift method. Geophysics 1997, 62, 895–905. [Google Scholar] [CrossRef]
- Lin, R.; Vesnaver, A.; Böhm, G.; Carcione, J.M. Broad-band visco-acoustic Q factor imaging by seismic tomography and instantaneous frequency. Geophys. J. Int. 2018, 214, 672–686, https://doi.org/10.1093/gji/ggy168. Erratum in Geophys. J. Int. 2022, 229, 898–899. [Google Scholar] [CrossRef]
- Caldwell, J.; Dragoset, W. A brief overview of seismic air-gun arrays. Lead. Edge 2000, 19, 898–902. [Google Scholar] [CrossRef]
- Dragoset, B. Introduction to air guns and air-gun arrays. Lead. Edge 2000, 19, 892–897. [Google Scholar] [CrossRef]
- Gutowski, M.; Bull, J.; Henstock, T.; Dix, J.K.; Hogarth, P.; Leighton, T.; White, P. Chirp sub-bottom profiler source signature design and field testing. Mar. Geophys. Res. 2002, 23, 481–492. [Google Scholar] [CrossRef]
- Schock, S.G.; LeBlanc, L.R. Chirp Sonar: New technology for sub-bottom profiling. Sea Technol. 1990, 31, 35–43. [Google Scholar]
- Schock, S.G.; LeBlanc, L.R.; Mayer, L.A. Chirp sub-bottom profiler for quantitative sediments analysis. Geophysics 1989, 54, 445–450. [Google Scholar] [CrossRef]
- Simpkin, P.G. The Boomer sound source as a tool for shallow water geophysical exploration. Mar. Geophys. Res. 2005, 26, 171–181. [Google Scholar] [CrossRef]
- Yilmaz, Ö. Seismic Data Analysis; SEG: Tulsa, OK, USA, 2001; p. 2065. [Google Scholar] [CrossRef]
- Vesnaver, A.; Busetti, M.; Baradello, L. Chirp data processing for fluid flow detection at the Gulf of Trieste (Adriatic Sea). Bull. Geophys. Oceanogr. 2021, 62, 365–386. [Google Scholar] [CrossRef]
- Millero, F.J.; Chen-Tung, C.; Bradshaw, A.; Schleicher, K. A new high-pressure equation of state for seawater. Deep Sea Res. Part A. Oceanogr. Res. Pap. 1980, 27, 255–264. [Google Scholar] [CrossRef]
- Vesnaver, A.; Baradello, L. A workflow for processing monochannel Chirp and Boomer surveys. Geophys. Prospect. 2023, 71, 1387–1403. [Google Scholar] [CrossRef]
- Lee, T.-G.; Hein, J.R.; Lee, K.; Moon, J.-W.; Ko, Y.-T. Sub-seafloor acoustic characterization of seamounts near the Ogasawara Fracture Zone in the western Pacific using Chirp (3–7 kHz) sub-bottom profiles. Deep Sea Res. Part I Oceanogr. Res. Pap. 2005, 52, 1932–1956. [Google Scholar] [CrossRef]
- Hamouda, A.Z.; El-Gendy, N.H.; El-Gharabawy, S.; Salah, M.; Barakat, M.K. Marine geophysical surveys and interpretations on the ancient Eunostos harbor area, Mediterranean coast, Egypt. Egypt. J. Pet. 2023, 32, 47–55. [Google Scholar] [CrossRef]
- Toker, M.; Tur, H. Structural patterns of the Lake Erçek Basin, eastern Anatolia (Turkey): Evidence from single-channel seismic interpretation. Mar. Geophys. Res. 2018, 39, 567–588. [Google Scholar] [CrossRef]
- Abramowitz, M. Handbook of Mathematical Functions, with Formulas, Graphs, and Mathematical Tables; Dover Publications Inc.: Mineola, NY, USA, 1974; ISBN 978-0-486-61272-0. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vesnaver, A.; Baradello, L.; Denich, E. Weak Underwater Signals’ Detection by the Unwrapped Instantaneous Phase. J. Mar. Sci. Eng. 2025, 13, 907. https://doi.org/10.3390/jmse13050907
Vesnaver A, Baradello L, Denich E. Weak Underwater Signals’ Detection by the Unwrapped Instantaneous Phase. Journal of Marine Science and Engineering. 2025; 13(5):907. https://doi.org/10.3390/jmse13050907
Chicago/Turabian StyleVesnaver, Aldo, Luca Baradello, and Eleonora Denich. 2025. "Weak Underwater Signals’ Detection by the Unwrapped Instantaneous Phase" Journal of Marine Science and Engineering 13, no. 5: 907. https://doi.org/10.3390/jmse13050907
APA StyleVesnaver, A., Baradello, L., & Denich, E. (2025). Weak Underwater Signals’ Detection by the Unwrapped Instantaneous Phase. Journal of Marine Science and Engineering, 13(5), 907. https://doi.org/10.3390/jmse13050907





