A New Characterization Method for Dynamic Connectivity Field Between Injection and Production Wells in Offshore Reservoir
Abstract
1. Introduction
2. Comprehensive Model for Three-Dimensional Dynamic Connectivity Field
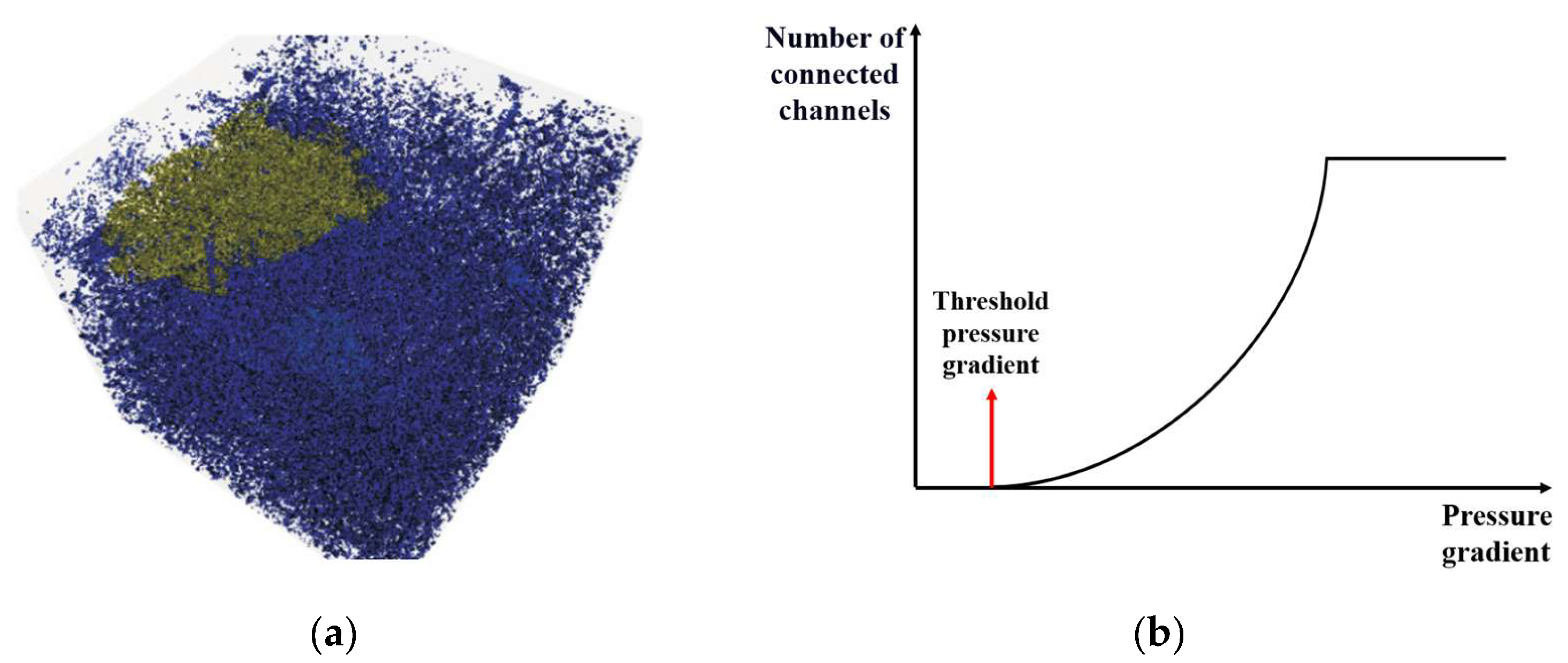
2.1. Analysis of Microscopic Connectivity from Digital Rock Analysis
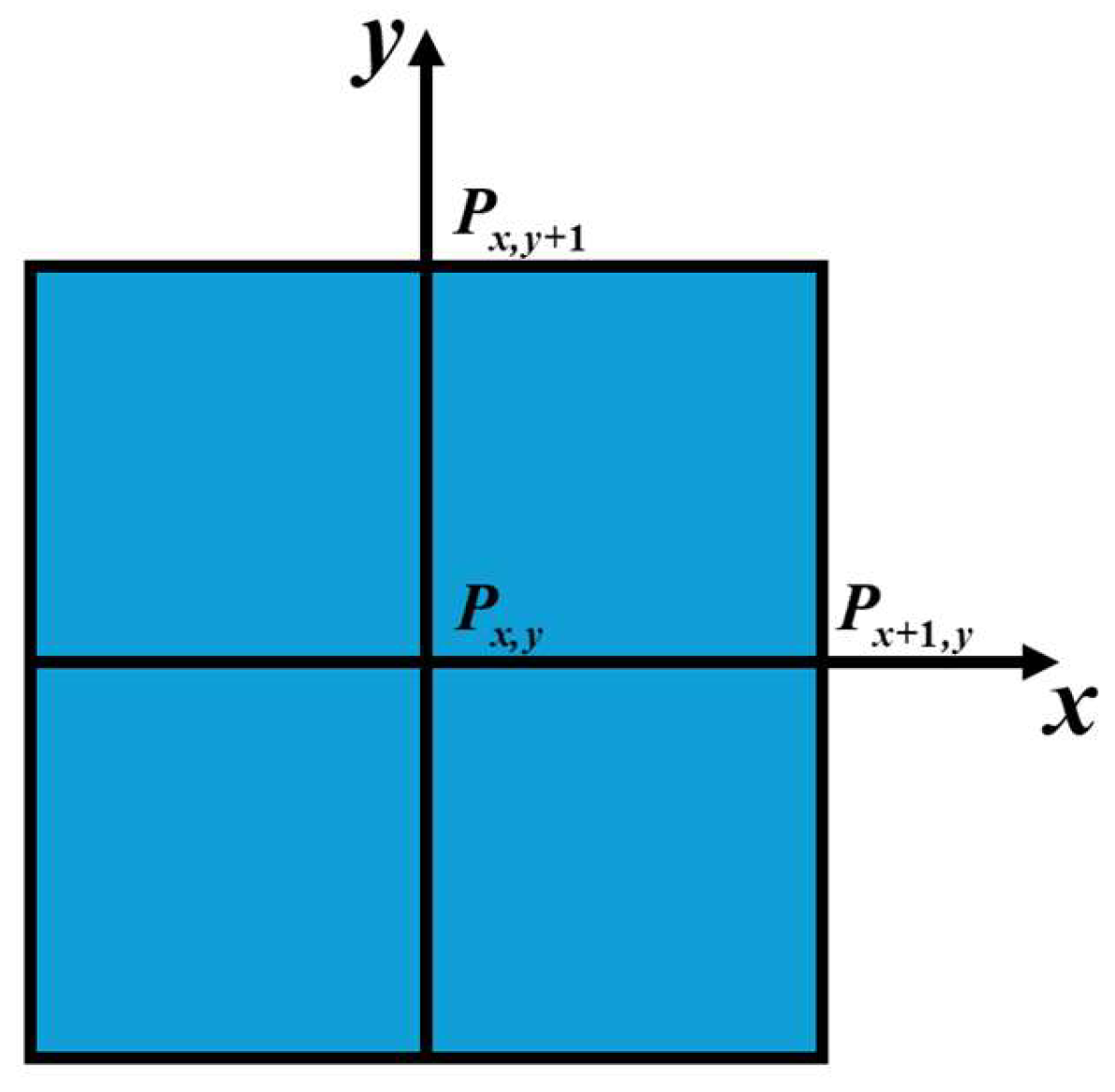
2.2. Establishment of Comprehensive Model for Macroscopic Connectivity Field
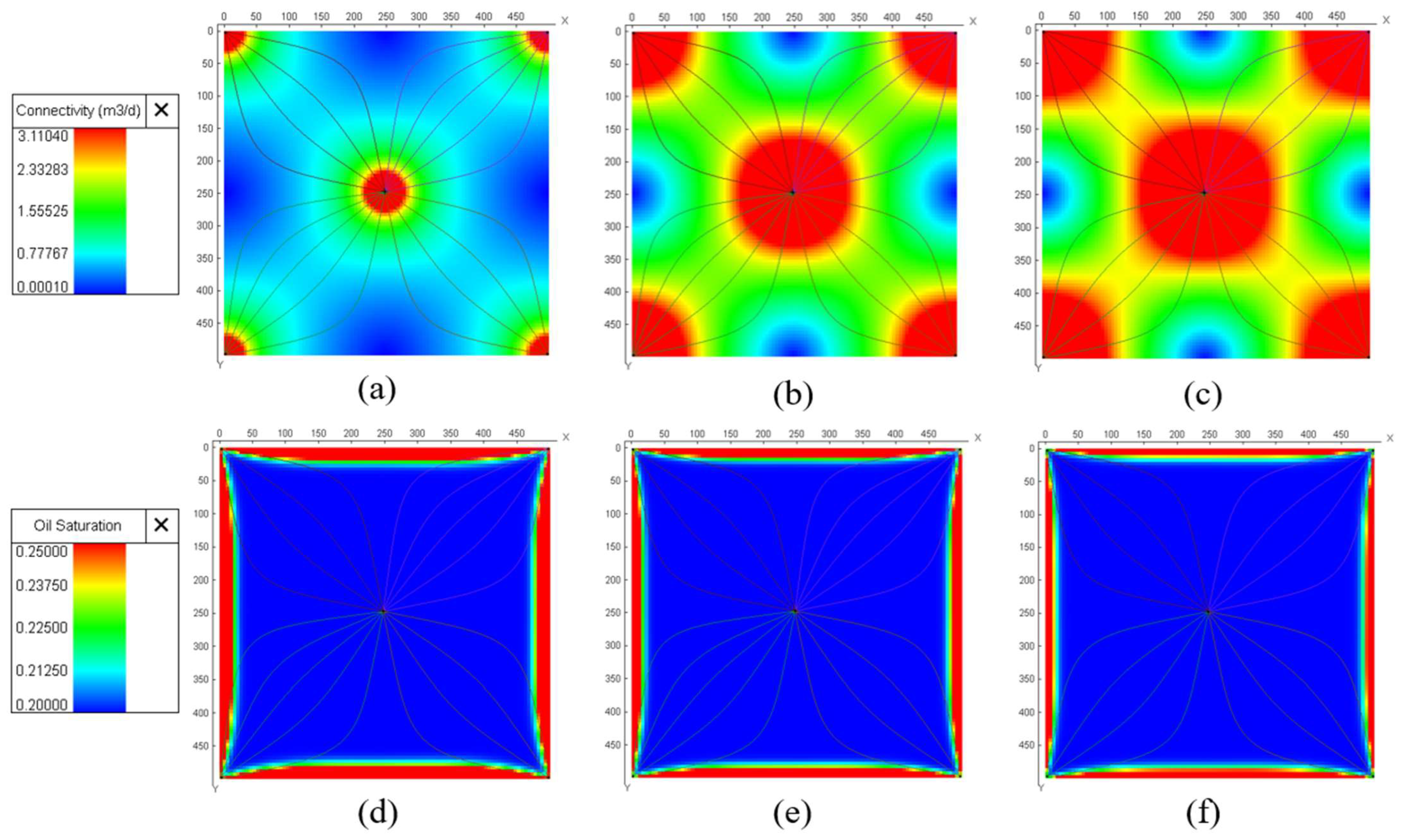
2.3. Validation of the Proposed Model for Connectivity Field
3. Analysis of Connectivity Field in an Offshore Reservoir Using Proposed Method
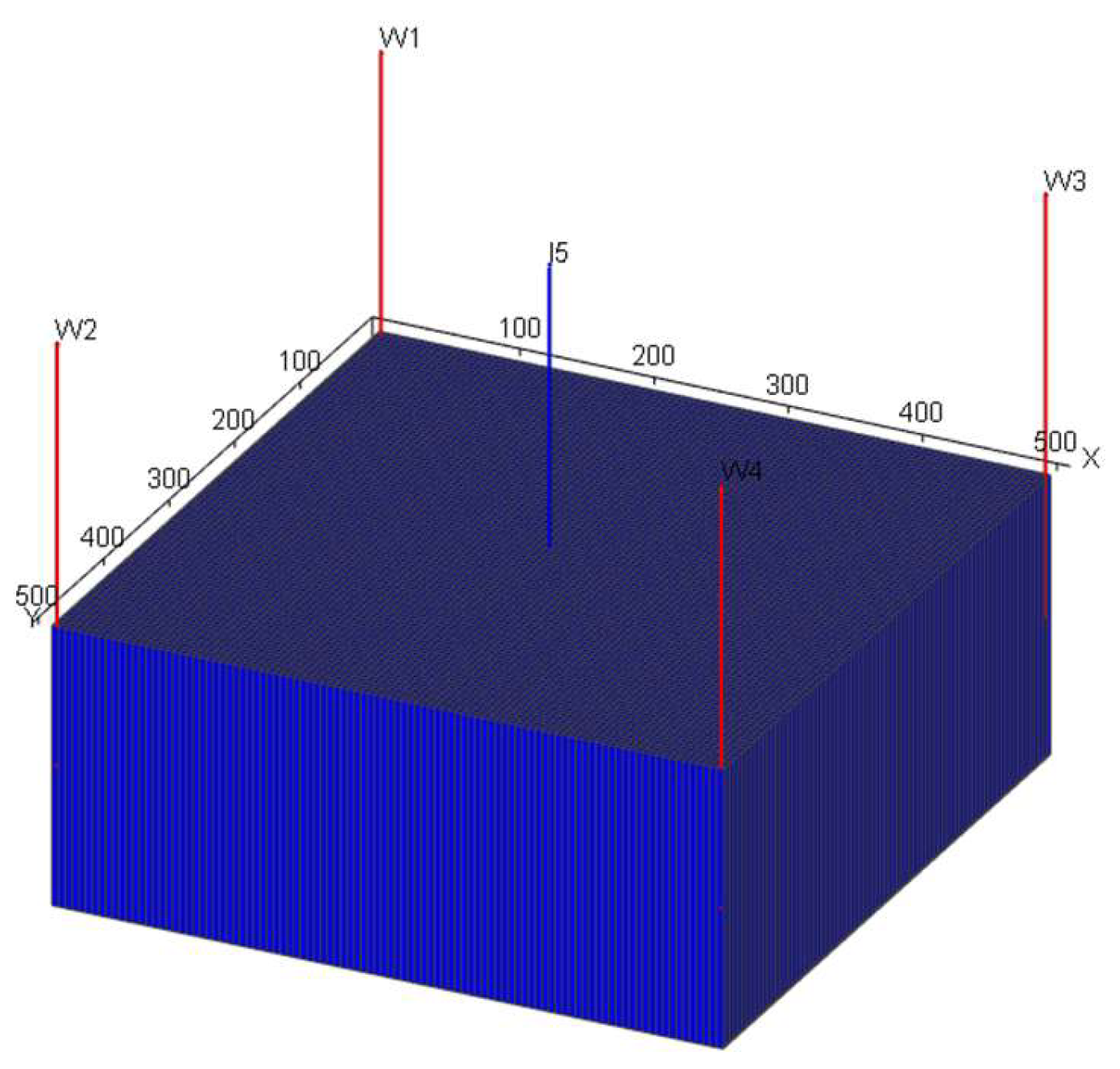
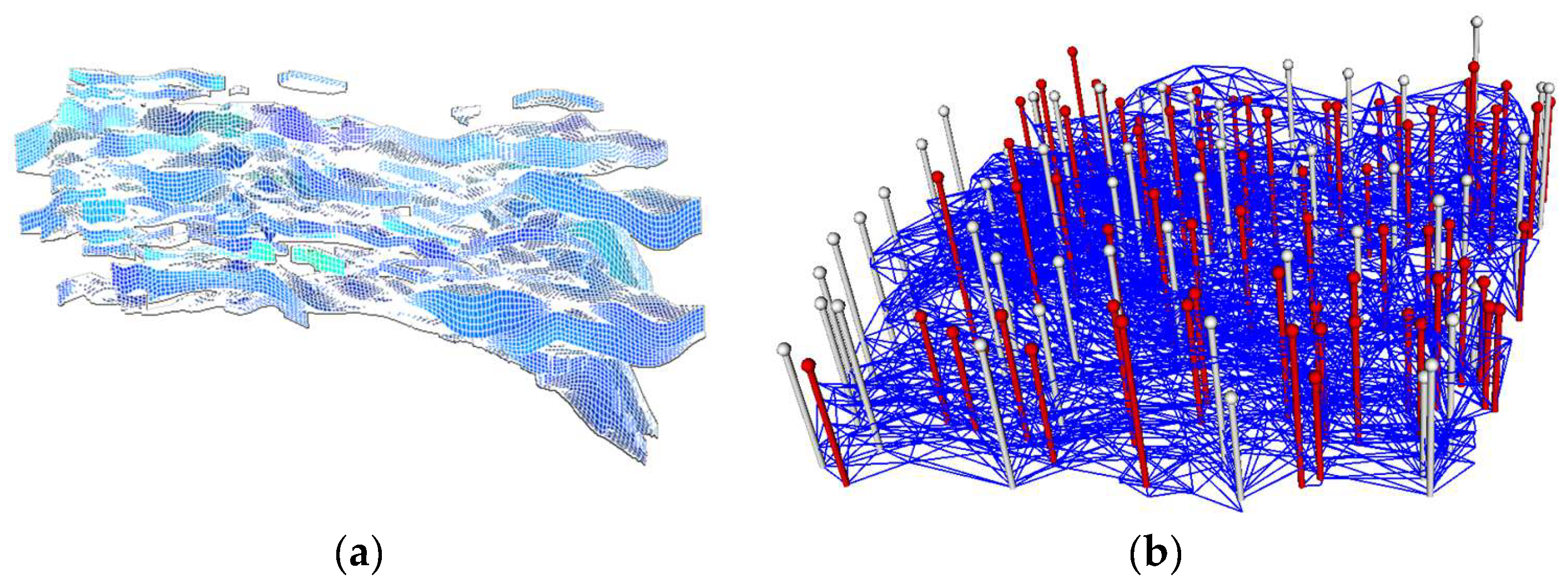
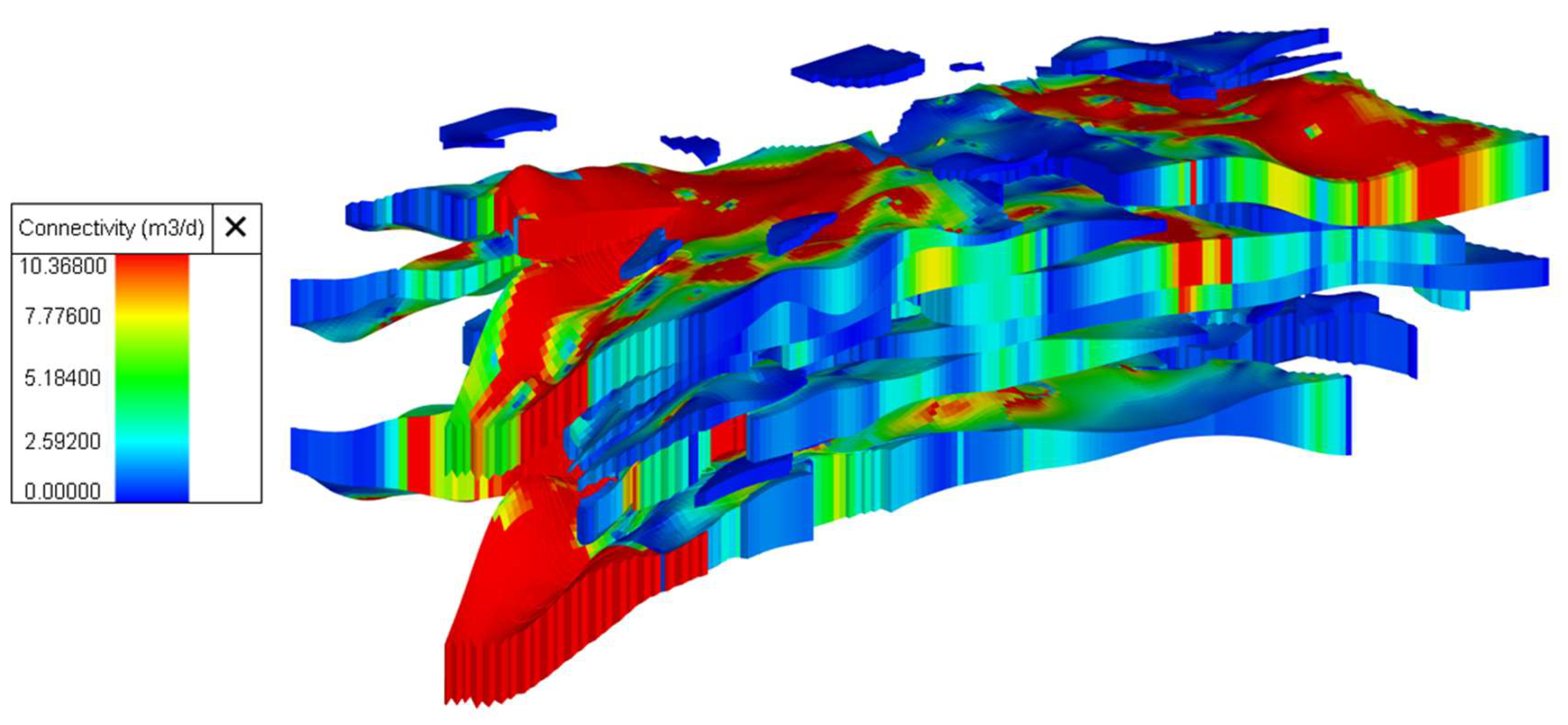
3.1. Establishment of a Three-Dimensional Dynamic Connectivity Field Model
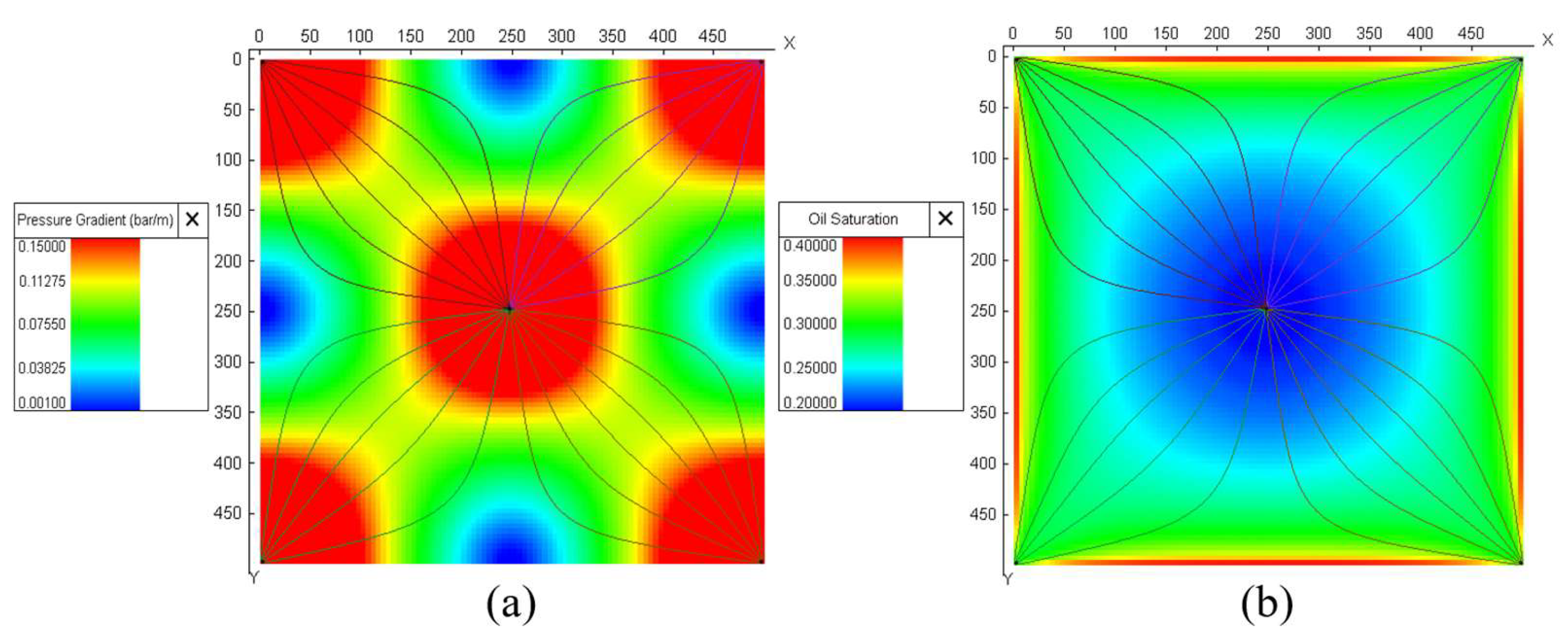
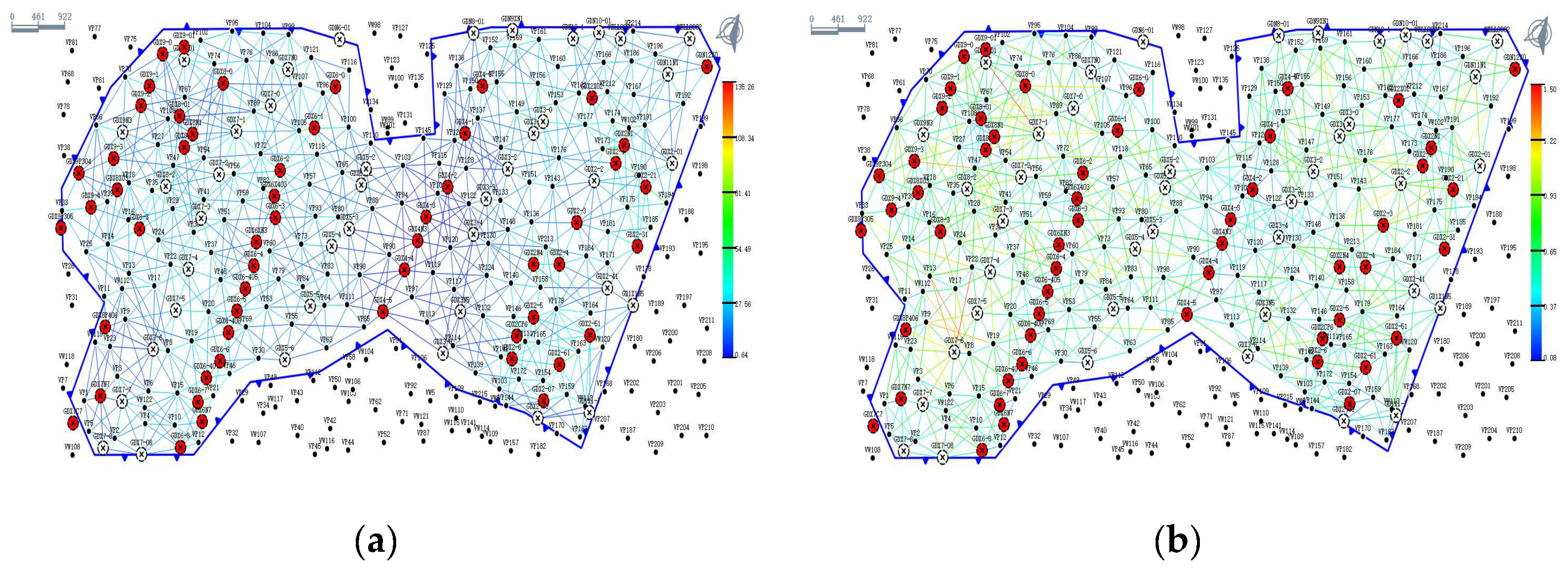
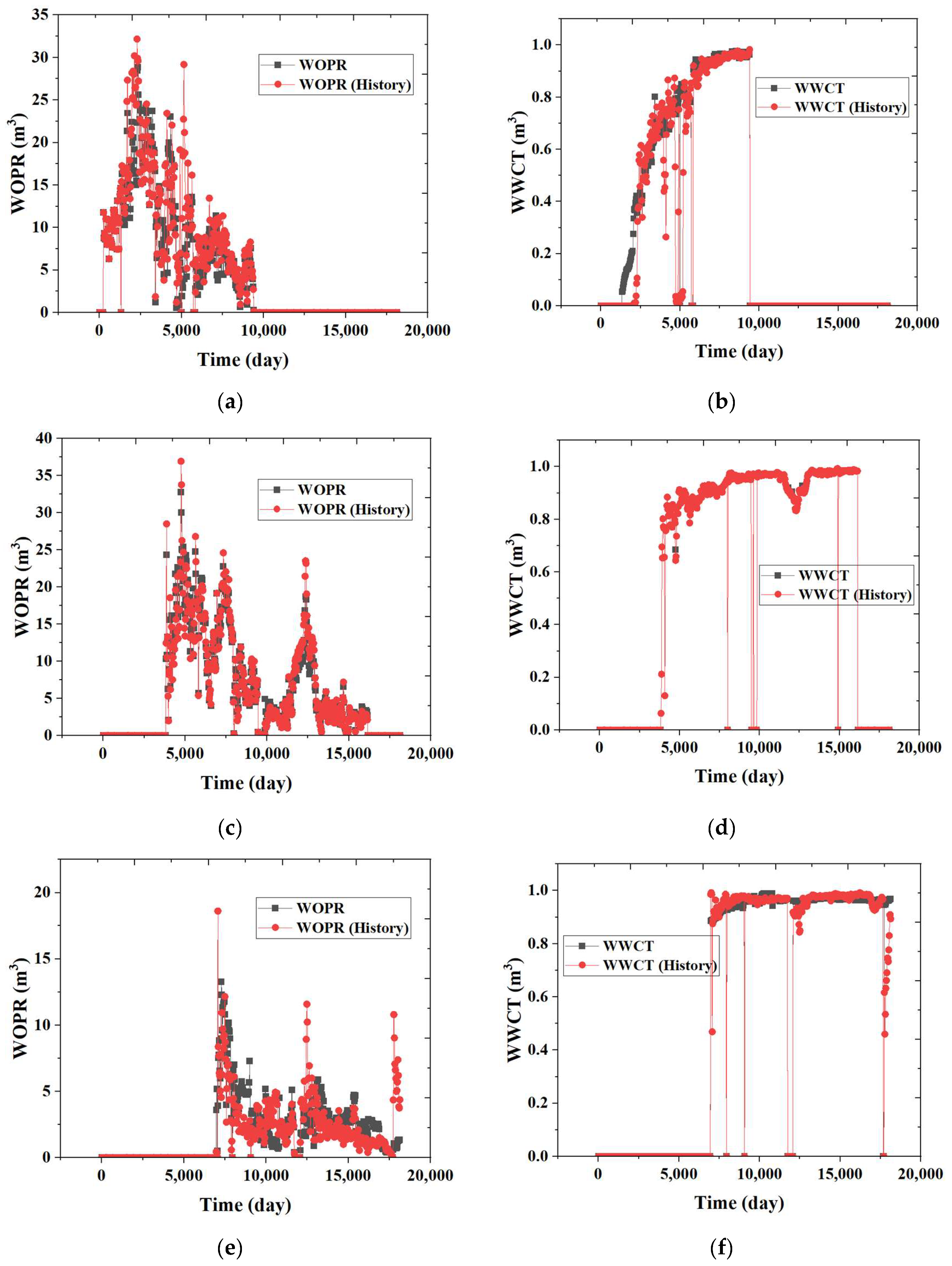
3.2. Comparisons Between Connectivity Field with On-Site Data
- A.
- Comparison with the Tracer Test
- B.
- Comparison with splitting coefficient of injected water
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Moyen, R.; Doyen, P.M. Reservoir connectivity uncertainty from stochastic seismic inversion. In SEG Technical Program Expanded Abstracts 2009; Society of Exploration Geophysicists: Tulsa, Ok, USA, 2009; pp. 2378–2382. [Google Scholar]
- Ragagnin, G.M.; Moraes, M.A.S. Seismic geomorphology and connectivity of deepwater reservoirs. SPE Reserv. Eval. Eng. 2008, 11, 686–695. [Google Scholar] [CrossRef]
- Riazi, N.; Clarkson, C.R. The importance of seismic attributes in reservoir characterization and inter-well connectivity studies of tight oil reservoirs. In Proceedings of the Geoconvention 2016, Calgary, AB, Canada, 7–11 March 2016. [Google Scholar]
- Van-Dunem, F.; Contreiras, K.D.; Weinheber, P.; Rueda, M. Evaluating Reservoir Connectivity and Compartmentalization Using a Combination of Formation Tester and NMR Data. In Proceedings of the SPWLA 49th Annual Logging Symposium, Austin, TX, USA, 25–28 May 2008. [Google Scholar]
- Azari, M.; Hadibeik, H.; Eyuboglu, S.; Jambunathan, V.; Khan, W.; Ramakrishna, S.; Haack, J.; Bargas, C.; Khan, M. Using Wireline Formation-Tester Data for Reservoir Characterization and Connectivity Determination in Ultradeepwater and High-Pressure Wilcox Formation in Gulf of Mexico. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 9–11 October 2017. [Google Scholar]
- Sanni, M.; Abbad, M.; Kokal, S.; Ali, R.; Zefzafy, I.; Hartvig, S.; Huseby, O. Reservoir description insights from an inter-well chemical tracer test. In Proceedings of the SPE Kingdom of Saudi Arabia Annual Technical Symposium and Exhibition, Dammam, Saudi Arabia, 24–27 April 2017. [Google Scholar]
- Sanni, M.L.; Al-Abbad, M.A.; Kokal, S.L.; Hartvig, S.; Olaf, H.; Jevanord, K. A field case study of inter-well chemical tracer test. In Proceedings of the SPE International Conference on Oilfield Chemistry, The Woodlands, TX, USA, 13–15 April 2015. [Google Scholar]
- Al-Qasim, A.; Kokal, S.; Hartvig, S.; Huseby, O. Reservoir description insights from inter-well gas tracer test. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, United Arab Emirates, 11–14 November 2019. [Google Scholar]
- Meister, M.; Lee, J.; Krueger, V.; Georgi, D.; Chemali, R. Formation pressure testing during drilling: Challenges and benefits. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 5–8 October 2003. [Google Scholar]
- Hahne, U.; Kaniappan, A.; Pragt, J.; Buysch, A. LWD formation pressure testing allows decision making while drilling. In Proceedings of the IADC/SPE Asia Pacific Drilling Technology Conference and Exhibition, Bangkok, Thailand, 13–15 November 2006. [Google Scholar]
- Almasoodi, M.; Andrews, T.; Johnston, C.; Singh, A.; McClure, M. A new method for interpreting well-to-well interference tests and quantifying the magnitude of production impact: Theory and applications in a multi-basin case study. Geomech. Geophys. Geo-Energy Geo-Resour. 2023, 9, 95. [Google Scholar] [CrossRef]
- Ohaeri, C.U.; Sankaran, S.; Fernandez, J. Evaluation of reservoir connectivity and hydrocarbon resource size in a deep water gas field using multi-well interference tests. In Proceedings of the SPE Annual Technical Conference and Exhibition, Amsterdam, The Netherlands, 27–29 October 2014. [Google Scholar]
- Aref, E.; Jahangiri, H.R. Data Driven Approach to Infer Inter-well Connectivity among Production Wells in an Oil Synthetic Reservoir. J. Pet. Res. 2021, 31, 40–53. [Google Scholar]
- Hird, K.B.; Dubrule, O. Quantification of reservoir connectivity for reservoir description applications. SPE Reserv. Eval. Eng. 1998, 1, 12–17. [Google Scholar] [CrossRef]
- Alabert, F.G.; Modot, V. Stochastic models of reservoir heterogeneity: Impact on connectivity and average permeabilities. In Proceedings of the SPE Annual Technical Conference and Exhibition, Washington, DC, USA, 4–7 October 1992. [Google Scholar]
- Malik, Z.A.; Silva, B.A.; Brimhall, R.M.; Wu, C.H. An integrated approach to characterize low-permeability reservoir connectivity for optimal waterflood infill drilling. In Proceedings of the SPE Rocky Mountain Petroleum Technology Conference/Low-Permeability Reservoirs Symposium, Denver, CO, USA, 26–28 April 1993. [Google Scholar]
- Canas, J.A.; Malik, Z.A.; Wu, C.H. Use of Hydraulic Interwell Connectivity Concepts in Reservoir Characterization. In Proceedings of the SPE Permian Basin Oil and Gas Recovery Conference, Midland, TX, USA, 16–18 March 1994. [Google Scholar]
- Heffer, K.J.; Fox, R.J.; McGill, C.A.; Koutsabeloulis, N.C. Novel techniques show links between reservoir flow directionality, earth stress, fault structure and geomechanical changes in mature waterfloods. SPE J. 1997, 2, 91–98. [Google Scholar] [CrossRef]
- Soeriawinata, T.; Kelkar, M. Reservoir management using production data. In Proceedings of the SPE Oklahoma City Oil and Gas Symposium/Production and Operations Symposium, Oklahoma City, OK, USA, 28–31 March 1999. [Google Scholar]
- Albertoni, A.; Lake, L.W. Inferring interwell connectivity only from well-rate fluctuations in waterfloods. SPE Reserv. Eval. Eng. 2003, 6, 6–16. [Google Scholar] [CrossRef]
- Yousef, A.A.; Gentil, P.; Jensen, J.L.; Lake, L.W. A capacitance model to infer interwell connectivity from production-and injection-rate fluctuations. SPE Reserv. Eval. Eng. 2006, 9, 630–646. [Google Scholar] [CrossRef]
- Yousef, A.A.; Lake, L.W.; Jensen, J.L. Analysis and interpretation of interwell connectivity from production and injection rate fluctuations using a capacitance model. In Proceedings of the SPE Improved Oil Recovery Conference, Tulsa, Ok, USA, 22–26 April 2006. [Google Scholar]
- Yousef, A.A.; Jensen, J.L.; Lake, L.W. Lake. Integrated interpretation of interwell connectivity using injection and production fluctuations. Math. Geosci. 2009, 41, 81–102. [Google Scholar] [CrossRef]
- Zhao, H.; Li, Y.; Gao, D.; Cao, L. Research on reservoir interwell dynamic connectivity using systematic analysis method Acta Pet. Sin. 2010, 31, 633–636. [Google Scholar]
- Li, F.; Lei, X.; Zhang, Q.; Cha, Y.; Sun, S. A new technique for characterization of reservoir connectivity based on CT scanning. Petrochem. Ind. Appl. 2019, 38, 74–81+88. [Google Scholar]
- Deng, Y.; Liu, S.; Ma, C. Integrated Analysis Methods for Inter-Well Connectivity. Fault-Block Oil Gas Field 2003, 10, 50–53. [Google Scholar]
- Tang, L.; Yin, Y.; Zhang, G. Study on Connectivity of Injection-Production Systems. J. Oil Gas Technol. 2008, 30, 134–136. [Google Scholar]
- Wang, H.; Wang, L.; Liu, H.; Liu, J.; Liu, W.; Shen, C. Analysis of Fluvial Sand Connectivity with Production and Seismic Data. Offshore Oil 2014, 34, 66–71. [Google Scholar]
- Zahm, C.K.; Zahm, L.C.; Bellian, J.A. Integrated fracture prediction using sequence stratigraphy within a carbonate fault damage zone, Texas, USA. J. Struct. Geol. 2010, 32, 1363–1374. [Google Scholar] [CrossRef]
- Fabuel-Perez, I.; Hodgetts, D.; Redfern, J. Integration of digital outcrop models (DOMs) and high resolution sedimentology–workflow and implications for geological modelling: Oukaimeden Sandstone Formation, High Atlas (Morocco). Pet. Geosci. 2010, 16, 133–154. [Google Scholar] [CrossRef]
- Yan, J.; Liang, Q.; Geng, B.; Lai, F.; Wen, D.; Wang, Z. Relationship between micro-pore characteristics and pore structure of lowpermeability sandstone: A case of the fourth member of ShahejieFormation in southern slope of Dongying Sag. Lithol. Pet. Reserv. 2017, 29, 18–26. [Google Scholar]
- Zhao, H.; Liu, W.; Rao, X.; Zhan, W.; Li, Y. Reservoir Numerical Simulation Using Connectivity Element Method. Sci. China Technol. Sci. 2022, 52, 1869–1886. [Google Scholar]



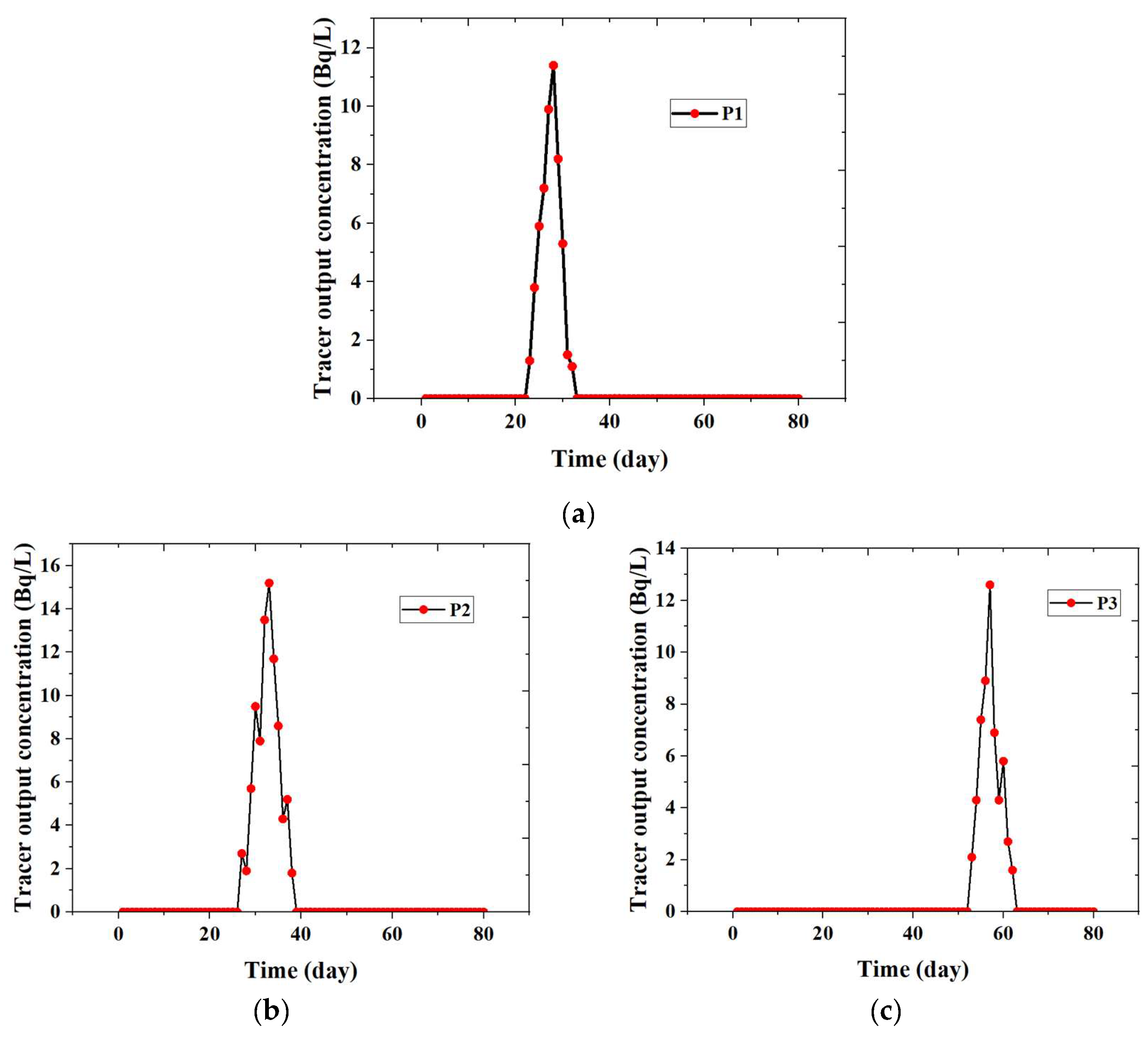

| Injection Well | Production Wells | Tracer Detection Situation | Whether It Corresponds | Accuracy |
|---|---|---|---|---|
| P | P1 | Preferential tracer detection (23 days) | Yes | 100% |
| P2 | Tracer detected after 27 days | Yes | ||
| P3 | Tracer detected after 53 days | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, C.; Hu, Y.; Tao, L.; Cheng, M.; Meng, F.; Zhao, H.; Du, F. A New Characterization Method for Dynamic Connectivity Field Between Injection and Production Wells in Offshore Reservoir. J. Mar. Sci. Eng. 2025, 13, 906. https://doi.org/10.3390/jmse13050906
Guo C, Hu Y, Tao L, Cheng M, Meng F, Zhao H, Du F. A New Characterization Method for Dynamic Connectivity Field Between Injection and Production Wells in Offshore Reservoir. Journal of Marine Science and Engineering. 2025; 13(5):906. https://doi.org/10.3390/jmse13050906
Chicago/Turabian StyleGuo, Changchun, Yuzhou Hu, Li Tao, Mengna Cheng, Fankun Meng, Hui Zhao, and Fengshuang Du. 2025. "A New Characterization Method for Dynamic Connectivity Field Between Injection and Production Wells in Offshore Reservoir" Journal of Marine Science and Engineering 13, no. 5: 906. https://doi.org/10.3390/jmse13050906
APA StyleGuo, C., Hu, Y., Tao, L., Cheng, M., Meng, F., Zhao, H., & Du, F. (2025). A New Characterization Method for Dynamic Connectivity Field Between Injection and Production Wells in Offshore Reservoir. Journal of Marine Science and Engineering, 13(5), 906. https://doi.org/10.3390/jmse13050906





