Enhancing Trajectory Tracking Performance of Underwater Gliders Using Finite-Time Sliding Mode Control Within a Reinforcement Learning Framework
Abstract
1. Introduction
- 1
- Precise hydrodynamic parameter identification and dynamic modeling: Hydrodynamic parameters are accurately identified using the Trust Region Reflective Algorithm, based on experimental data obtained from the South China Sea. A dynamic model is subsequently established, incorporating a depth correction term and nonlinear hydrodynamic effects. The model’s accuracy is validated by comparing the root-mean-square error (RMSE) between the proposed full-order model and experimental results.
- 2
- Critic–actor reinforcement learning framework with radial basis function neural networks: Radial Basis Function (RBF) neural networks are embedded within a critic–actor reinforcement learning framework to construct a unified perturbation estimation model, enabling the real-time approximation of unmodeled dynamics and external disturbances. Compared to conventional sliding mode control, the proposed SD-RLSMC approach reduces the RMSE by approximately 42% in disturbance rejection scenarios and substantially enhances trajectory tracking performance.
- 3
- Standard deviation adjustment: An adaptive standard deviation updating mechanism based on gradient descent is introduced to dynamically regulate the local approximation capability of RBF neural networks. This mechanism improves the approximation accuracy for complex nonlinear systems, enhances controller adaptability under varying environmental conditions, and reduces the required control effort.
2. Dynamic Modeling and Parameter Identification
2.1. Model Description
- 1
- The center of buoyancy is typically considered to be fixed, a condition supported by the glider’s structural symmetry and inherent hydrostatic stability. However, in practical scenarios, minor shifts in the center of buoyancy may occur due to fluid disturbances or structural deformations. These shifts are generally small in magnitude, evolve gradually, and can therefore be treated as bounded, unmodeled dynamic perturbations.
- 2
- The influence of actuator motion on mass distribution is negligible. The glider’s actuators, such as the buoyancy and attitude adjustment units, operate slowly and have a limited capacity for mass adjustments, resulting in minimal dynamic impact on the overall mass distribution. Any unmodeled perturbations can be incorporated into the bounded uncertainty analysis.
- 3
- The pitch angle is constrained between and to prevent the occurrence of inverted or runaway gliders in the vertical plane. In practice, the physical limitations of the actuators, such as the operational range of the hydraulic pump, along with stability requirements, ensure that the pitch angle remains within this range. Exceeding this range may lead to control failures or complicate the dynamic behavior.
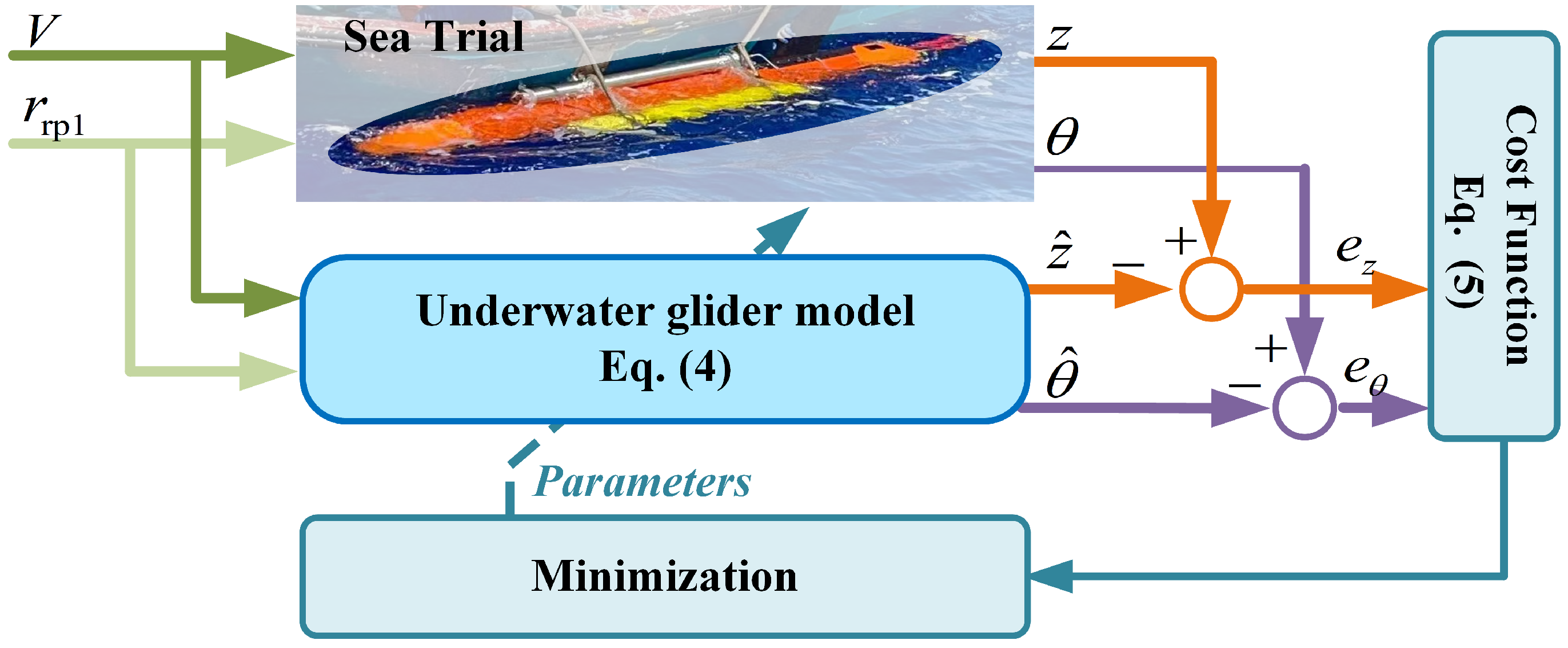
2.2. Parameter Identification
2.3. Model Validation
2.4. Standard Forms
3. Controller Design
3.1. Prior Knowledge
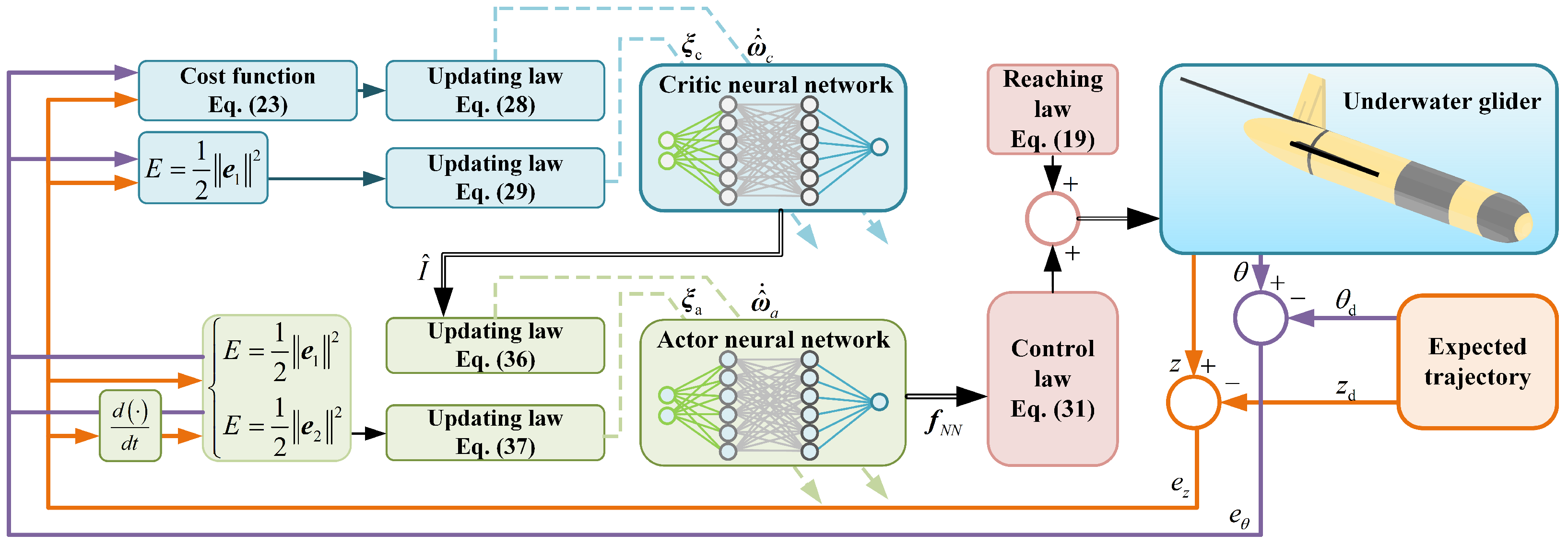
3.2. Sliding Mode Controller Design
3.3. Critic Neural Network Design
3.3.1. Weight Updates
3.3.2. Standard Deviation Update
3.4. Actor Neural Network Design
3.4.1. Weighs’ Update
3.4.2. Standard Deviation Update
4. Simulation Analysis
- 1
- Model uncertainty: This case examines the controller’s effectiveness in handling underwater glider dynamics with unmodeled components or time-varying hydrodynamic parameters, which introduce model uncertainty.
- 2
- External disturbance suppression: The controller’s ability to suppress external disturbances is evaluated by applying two typical disturbances to the angular velocity q.
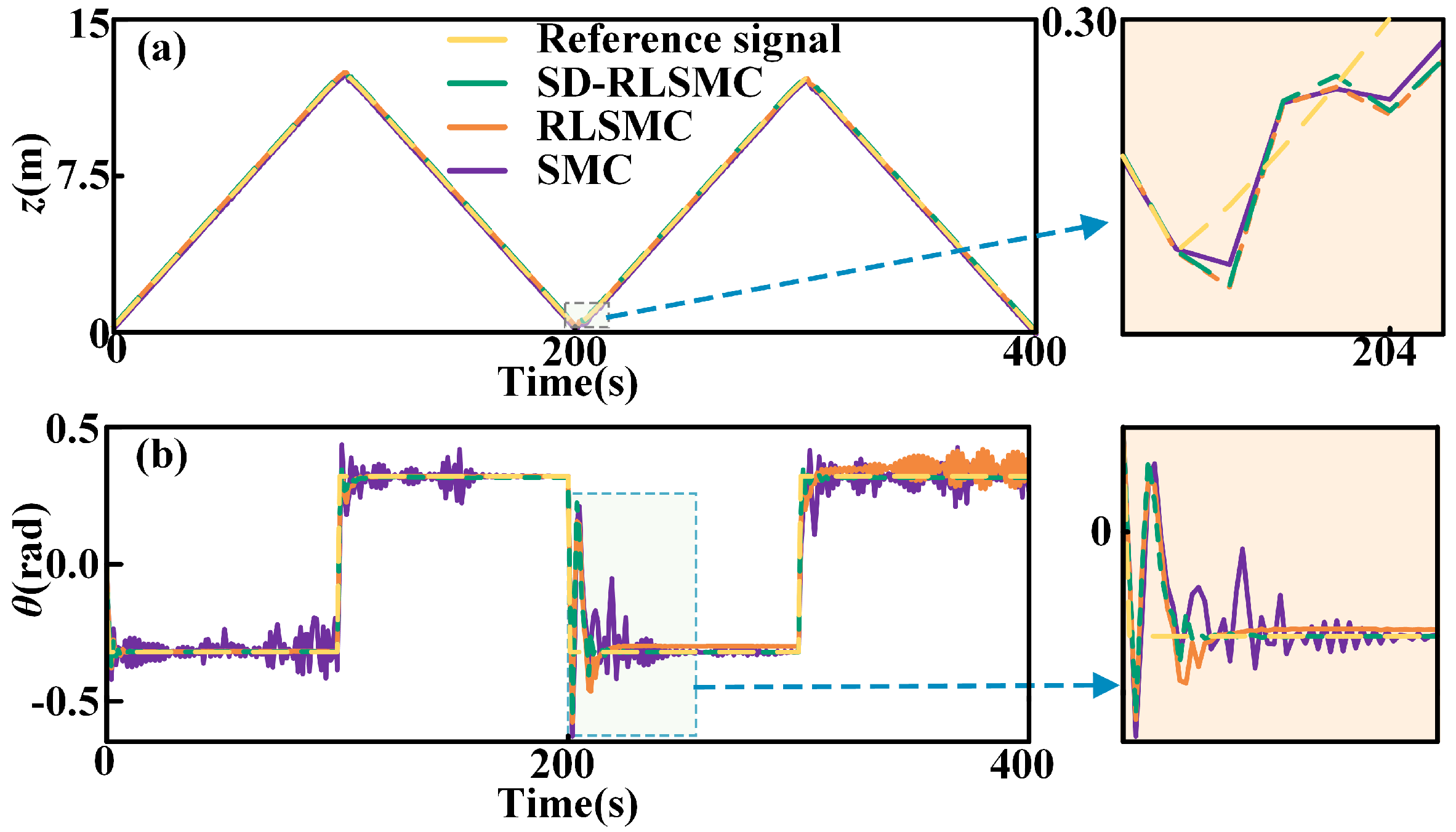
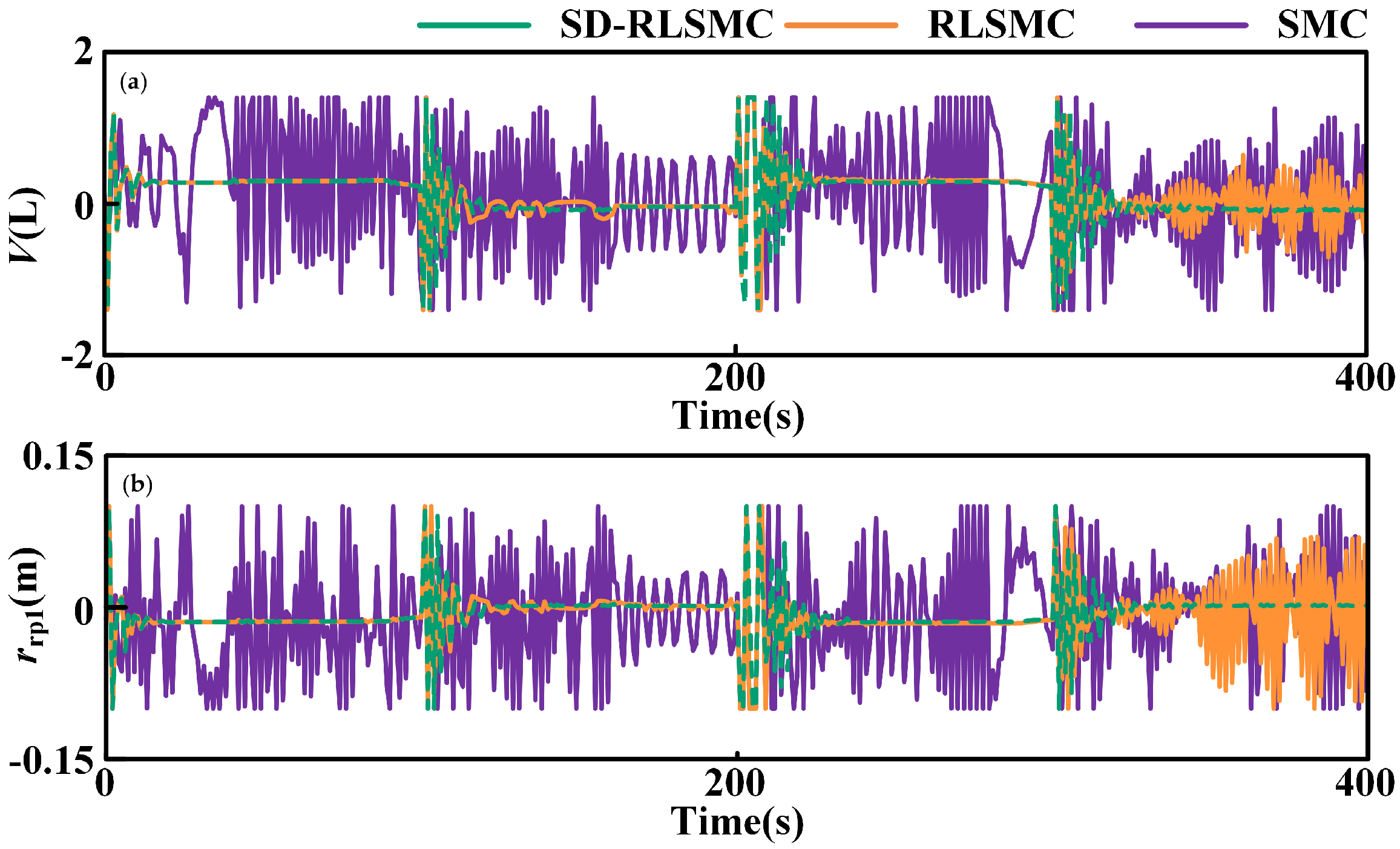
4.1. Case 1: Model Uncertainty
4.2. Case 2: External Disturbance Suppression
5. Conclusions and Prospects
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Stability Analysis
References
- Tian, B.; Guo, J.; Song, Y.; Zhou, Y.; Xu, Z.; Wang, L. Research progress and prospects of gliding robots applied in ocean observation. J. Ocean Eng. Mar. Energy 2023, 9, 113–124. [Google Scholar] [CrossRef]
- Yuan, S.; Li, Y.; Bao, F.; Xu, H.; Yang, Y.; Yan, Q.; Zhong, S.; Yin, H.; Xu, J.; Huang, Z.; et al. Marine environmental monitoring with unmanned vehicle platforms: Present applications and future prospects. Sci. Total Environ. 2023, 858, 159741. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Z.; Wu, H.; Wu, Q.; Yang, Y.; Tan, L.; Yan, S. Control parameter optimization based trajectory design of underwater gliders executing underwater fixed-point exploration missions. Ocean Eng. 2023, 279, 114127. [Google Scholar] [CrossRef]
- Joshi, B.; Xanthidis, M.; Roznere, M.; Burgdorfer, N.J.; Mordohai, P.; Li, A.Q.; Rekleitis, I. Underwater exploration and mapping. In Proceedings of the 2022 IEEE/OES Autonomous Underwater Vehicles Symposium (AUV), Singapore, 19–21 September 2022; pp. 1–7. [Google Scholar]
- Alexandris, C.; Papageorgas, P.; Piromalis, D. Positioning Systems for Unmanned Underwater Vehicles: A Comprehensive Review. Appl. Sci. 2024, 14, 9671. [Google Scholar] [CrossRef]
- Liang, Y.; Wang, Y.; Zhang, L.; Wang, Y.; Yang, M.; Niu, W.; Yang, S. Conceptual design and analysis of a two-stage underwater glider for ultra-long voyage. Appl. Ocean Res. 2023, 138, 103639. [Google Scholar] [CrossRef]
- Yang, H.; Mahmoudian, N. Gliding in extreme waters: Dynamic Modeling and Nonlinear Control of an Agile Underwater Glider. arXi 2024, arXiv:2402.06055. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, J.; Pan, G.; Huang, Q.; Guo, L. Vibration Analysis and Isolator Component Design of the Power System in an Autonomous Underwater Glider. Int. J. Acoust. Vib. 2022, 27, 112–121. [Google Scholar] [CrossRef]
- Leonard, N.E.; Graver, J.G. Model-based feedback control of autonomous underwater gliders. IEEE J. Ocean. Eng. 2001, 26, 633–645. [Google Scholar] [CrossRef]
- Liu, Y.; Su, Z.; Luan, X.; Song, D.; Han, L. Motion analysis and fuzzy-PID control algorithm designing for the pitch angle of an underwater glider. J. Math. Comput. Sci. 2017, 17, 133–147. [Google Scholar] [CrossRef]
- Landau, I.D.; Lozano, R.; M’Saad, M.; Karimi, A. Adaptive Control: Algorithms, Analysis and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Wan, L.; Zhang, D.; Sun, Y.; Qin, H.; Cao, Y.; Chen, G. Fast fixed-time vertical plane motion control of autonomous underwater gliders in shallow water. J. Frankl. Inst. 2022, 359, 10483–10509. [Google Scholar] [CrossRef]
- Sang, H.; Zhou, Y.; Sun, X.; Yang, S. Heading tracking control with an adaptive hybrid control for under actuated underwater glider. ISA Trans. 2018, 80, 554–563. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, N.D.; Choi, H.s.; Jin, H.S.; Huang, J.; Lee, J.H. Robust Adaptive Depth Control of hybrid underwater glider in vertical plane. Adv. Technol. Innov. 2020, 5, 135–146. [Google Scholar] [CrossRef]
- García-Valdovinos, L.G.; Salgado-Jiménez, T.; Bandala-Sánchez, M.; Nava-Balanzar, L.; Hernández-Alvarado, R.; Cruz-Ledesma, J.A. Modelling, design and robust control of a remotely operated underwater vehicle. Int. J. Adv. Robot. Syst. 2014, 11, 1. [Google Scholar] [CrossRef]
- Ding, W.; Wei, D.; Diao, Y.; Yang, C.; Zhang, X.; Zhang, X.; Huang, H. Research on trajectory tracking control of ocean unmanned aerial vehicles based on disturbance observer and nonlinear sliding mode. Ocean Eng. 2024, 293, 116682. [Google Scholar] [CrossRef]
- Zeng, Z.; Lyu, C.; Bi, Y.; Jin, Y.; Lu, D.; Lian, L. Review of hybrid aerial underwater vehicle: Cross-domain mobility and transitions control. Ocean Eng. 2022, 248, 110840. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, H.; Fu, J.; Wen, H.; Yao, B.; Lian, L. Adaptive integral terminal sliding mode based trajectory tracking control of underwater glider. Ocean Eng. 2023, 269, 113436. [Google Scholar] [CrossRef]
- Zhou, H.; Xu, H.; Cao, J.; Fu, J.; Mao, Z.; Zeng, Z.; Yao, B.; Lian, L. Robust adaptive control of underwater glider for bottom sitting-oriented soft landing. Ocean Eng. 2024, 293, 116725. [Google Scholar] [CrossRef]
- Zou, H.; Zhang, G.; Hao, J. Nonsingular fast terminal sliding mode tracking control for underwater glider with actuator physical constraints. ISA Trans. 2024, 146, 249–262. [Google Scholar] [CrossRef]
- Roy, R.G.; Ghoshal, D. A novel adaptive second-order sliding mode controller for autonomous underwater vehicles. Adapt. Behav. 2021, 29, 39–54. [Google Scholar] [CrossRef]
- Juan, R.; Wang, T.; Liu, S.; Zhou, Y.; Ma, W.; Niu, W.; Gao, Z. High-precision motion control of underwater gliders based on reinforcement learning. Ocean Eng. 2024, 310, 118603. [Google Scholar] [CrossRef]
- Wang, J.; Chen, Y.; Gao, J.; Min, B.; Pan, G. Adaptive fault tolerant control of unmanned underwater glider with predefined-time stability. J. Frankl. Inst. 2025, 362, 107364. [Google Scholar] [CrossRef]
- Lei, L.; Gang, Y.; Jing, G. Physics-guided neural network for underwater glider flight modeling. Appl. Ocean Res. 2022, 121, 103082. [Google Scholar] [CrossRef]
- Jeong, S.k.; Choi, H.S.; Ji, D.H.; Kim, J.Y.; Hong, S.M.; Cho, H.J. A study on an accurate underwater location of hybrid underwater gliders using machine learning. J. Mar. Sci. Technol. 2020, 28, 7. [Google Scholar]
- Gao, J.; Min, B.; Chen, Y.; Jing, A.; Wang, J.; Pan, G. Compound learning based event-triggered adaptive attitude control for underwater gliders with actuator saturation and faults. Ocean Eng. 2023, 280, 114651. [Google Scholar] [CrossRef]
- Emami, S.A.; Castaldi, P.; Banazadeh, A. Neural network-based flight control systems: Present and future. Annu. Rev. Control 2022, 53, 97–137. [Google Scholar] [CrossRef]
- Su, Z.q.; Zhou, M.; Han, F.f.; Zhu, Y.w.; Song, D.l.; Guo, T.t. Attitude control of underwater glider combined reinforcement learning with active disturbance rejection control. J. Mar. Sci. Technol. 2019, 24, 686–704. [Google Scholar] [CrossRef]
- Zang, W.; Yao, P.; Song, D. Standoff tracking control of underwater glider to moving target. Appl. Math. Model. 2022, 102, 1–20. [Google Scholar] [CrossRef]
- Mirza, J.; Kanwal, F.; Salaria, U.A.; Ghafoor, S.; Aziz, I.; Atieh, A.; Almogren, A.; Haq, A.U.; Kanwal, B. Underwater temperature and pressure monitoring for deep-sea SCUBA divers using optical techniques. Front. Phys. 2024, 12, 1417293. [Google Scholar] [CrossRef]
- Mirza, J.; Atieh, A.; Kanwal, B.; Ghafoor, S.; Almogren, A.; Kanwal, F.; Aziz, I. Relay aided UWOC-SMF-FSO based hybrid link for underwater wireless optical sensor network. Opt. Fiber Technol. 2025, 89, 104045. [Google Scholar] [CrossRef]
- Wang, Y.; Thanyamanta, W.; Bose, N. Cooperation and compressed data exchange between multiple gliders used to map oil spills in the ocean. Appl. Ocean Res. 2022, 118, 102999. [Google Scholar] [CrossRef]
- Shi, Y.; Dong, H.; He, C.R.; Chen, Y.; Song, Z. Mixed Vehicle Platoon Forming: A Multi-Agent Reinforcement Learning Approach. IEEE Internet Things J. 2025. [Google Scholar]
- Fossen, T.I. Marine Control Systems—Guidance: Navigation, and Control of Ships, Rigs and Underwater Vehicles; Marine Cybernetics, Trondheim, Norway, Org. Number NO 985 195 005 MVA; Springer: Berlin/Heidelberg, Germany, 2002; ISBN 82-92356-00-2. Available online: www.marinecybernetics.com (accessed on 1 April 2025).
- Wang, G.; Yang, Y.; Wang, S. Adaptive digital disturbance rejection controller design for underwater thermal vehicles. J. Mar. Sci. Eng. 2021, 9, 406. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, Y.; Wang, Y.; Zhang, H.; Zhang, L. Dynamic modeling and motion control strategy for deep-sea hybrid-driven underwater gliders considering hull deformation and seawater density variation. Ocean Eng. 2017, 143, 66–78. [Google Scholar] [CrossRef]
- Hussain, N.A.A.; Arshad, M.R.; Mohd-Mokhtar, R. Underwater glider modelling and analysis for net buoyancy, depth and pitch angle control. Ocean Eng. 2011, 38, 1782–1791. [Google Scholar]
- Liang, Y.; Zhang, L.; Yang, M.; Wang, Y.; Niu, W.; Yang, S. Dynamic behavior analysis and bio-inspired improvement of underwater glider with passive buoyancy compensation gas. Ocean Eng. 2022, 257, 111644. [Google Scholar]
- Miniguano, H.; Barrado, A.; Lázaro, A.; Zumel, P.; Fernández, C. General parameter identification procedure and comparative study of Li-Ion battery models. IEEE Trans. Veh. Technol. 2019, 69, 235–245. [Google Scholar] [CrossRef]
- Tekin, M.; Karamangil, M.I. Development of dual polarization battery model with high accuracy for a lithium-ion battery cell under dynamic driving cycle conditions. Heliyon 2024, 10, e28454. [Google Scholar] [CrossRef]
- Hodson, T.O. Root mean square error (RMSE) or mean absolute error (MAE): When to use them or not. Geosci. Model Dev. Discuss. 2022, 2022, 5481–5487. [Google Scholar] [CrossRef]
- Lee, T.H.; Harris, C.J. Adaptive Neural Network Control of Robotic Manipulators; World Scientific: Singapore, 1998; Volume 19. [Google Scholar]
- Guo, Q.; Li, X.; Zuo, Z.; Shi, Y.; Jiang, D. Quasi-synchronization control of multiple electrohydraulic actuators with load disturbance and uncertain parameters. IEEE/ASME Trans. Mechatronics 2020, 26, 2048–2058. [Google Scholar] [CrossRef]
- Jiang, B.; Hu, Q.; Friswell, M.I. Fixed-time attitude control for rigid spacecraft with actuator saturation and faults. IEEE Trans. Control Syst. Technol. 2016, 24, 1892–1898. [Google Scholar] [CrossRef]
- Saeki, S. The Lp-conjecture and Young’s inequality. Ill. J. Math. 1990, 34, 614–627. [Google Scholar]
- Ouyang, Y.; He, W.; Li, X. Reinforcement learning control of a single-link flexible robotic manipulator. IET Control Theory Appl. 2017, 11, 1426–1433. [Google Scholar] [CrossRef]
- Cao, S.; Sun, L.; Jiang, J.; Zuo, Z. Reinforcement learning-based fixed-time trajectory tracking control for uncertain robotic manipulators with input saturation. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 4584–4595. [Google Scholar] [CrossRef] [PubMed]
- Panda, S.; Panda, G. On the development and performance evaluation of improved radial basis function neural networks. IEEE Trans. Syst. Man Cybern. Syst. 2021, 52, 3873–3884. [Google Scholar] [CrossRef]
- Zhou, H.; Wei, Z.; Zeng, Z.; Yu, C.; Yao, B.; Lian, L. Adaptive robust sliding mode control of autonomous underwater glider with input constraints for persistent virtual mooring. Appl. Ocean Res. 2020, 95, 102027. [Google Scholar] [CrossRef]
- Steele, J.M. The Cauchy-Schwarz Master Class: An Introduction to the Art of Mathematical Inequalities; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]


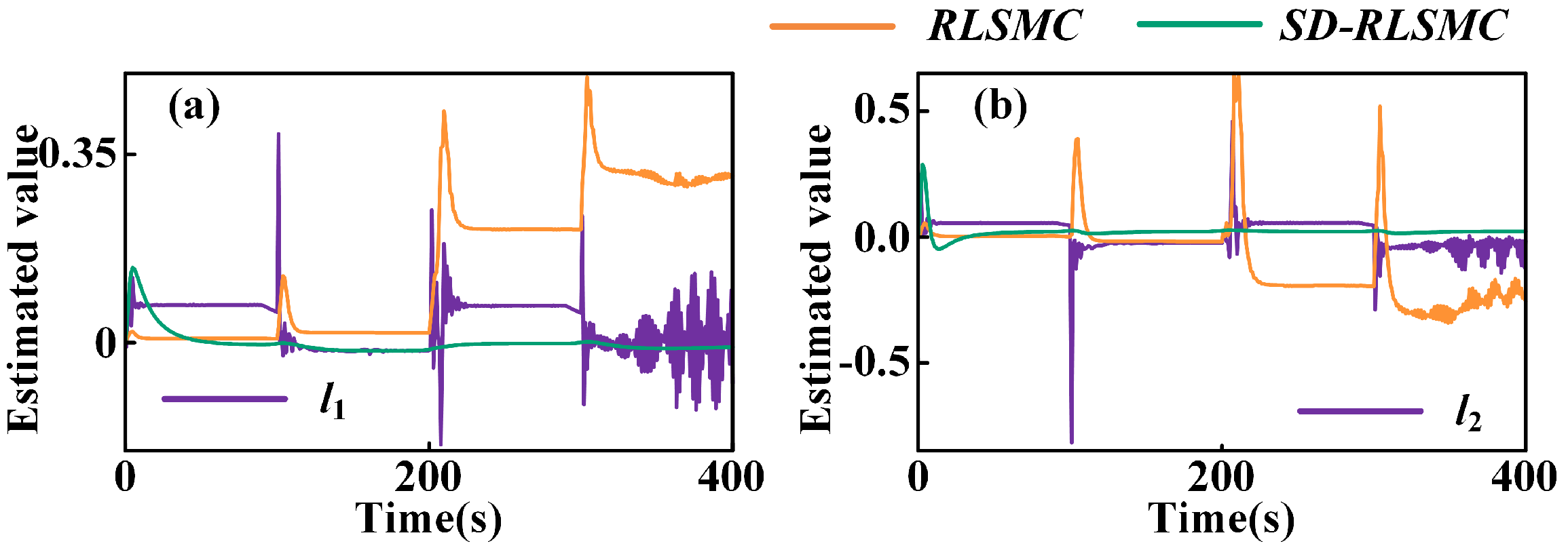

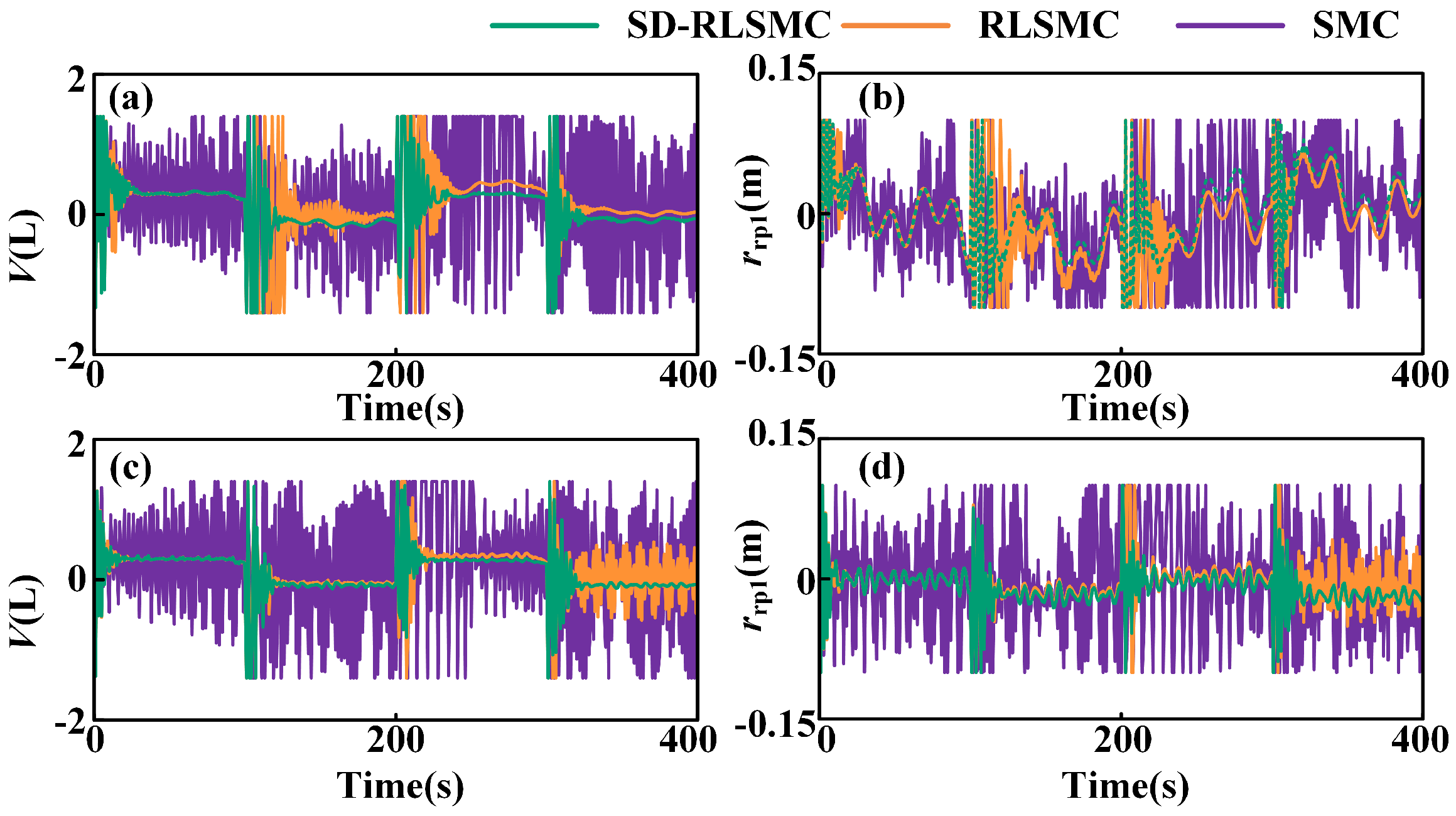
| Step | Procedure |
|---|---|
| Step 1 | Utilize Simulink software (v. 24.2) to construct a nonlinear simulation model of the underwater glider. |
| Step 2 | Import the sea trial data into the parameter identification toolbox in Simulink. |
| Step 3 | Choose the parameters to be estimated and define the upper and lower bounds for each parameter. |
| Step 4 | Configure the optimization and parallel computing settings. |
| Step 5 | Execute the estimation process, iterating as needed to determine the desired parameters and optimize the cost function. |
| Step 6 | Verify the accuracy of the model by assessing the simulated data against the estimated parameters. If significant discrepancies are found, iterate this process or adjust the model in Step 2, considering alternative identification methods if necessary. |
| Parameters | Identification Results | Parameters | Identification Results |
|---|---|---|---|
| −0.000257 | −124.60 kg/rad | ||
| 6.33 | −134.02 | ||
| 271.37 | −3.71 | ||
| 5.85 | −59.16 | ||
| 136.48 | 114.37 | ||
| 2.10 |
| Parameters | Full Model | Simplified Model |
|---|---|---|
| z | 33.8584 | 34.9584 |
| 0.9710 | 0.9730 |
| Controller Composition | Variable |
|---|---|
| Critic NN | , , |
| , | |
| , , . | |
| Active NN | , |
| , , , . | |
| SMC Controller | , , , , |
| , , , | |
| , | |
| , , |
| Parameter | Controllers | RMSE | Overshoot |
|---|---|---|---|
| z | SMC | 0.0228 | 0.21% |
| RLSMC | 0.0285 | 0.02% | |
| SD-RLSMC | 0.0154 | 0.01% | |
| SMC | 0.0659 | 36.13% | |
| RLSMC | 0.0514 | 30.74% | |
| SD-RLSMC | 0.0430 | 9.77% |
| Parameter | Controllers | Power |
|---|---|---|
| SMC | 0.7841 | |
| RLSMC | 0.1500 | |
| SD-RLSMC | 0.1573 | |
| SMC | 0.0036 | |
| RLSMC | 0.0011 | |
| SD-RLSMC | 0.0006 |
| Parameter | Controllers | ||||
|---|---|---|---|---|---|
| RMSE | Overshoot | RMSE | Overshoot | ||
| z | SMC | 0.0278 | 0.12% | 0.284 | 0.03% |
| RLSMC | 0.1480 | 0.03% | 0.0401 | 0.02% | |
| SD-RLSMC | 0.0159 | 0.05% | 0.0145 | 0.02% | |
| SMC | 0.1340 | 113.64% | 0.1082 | 89.82% | |
| RLSMC | 0.1161 | 63.04% | 0.0591 | 31.79% | |
| SD-RLSMC | 0.0722 | 20.39% | 0.0304 | 16.21% | |
| Parameter | Controllers | Power | |
|---|---|---|---|
| SMC | 0.9582 | 0.9582 | |
| RLSMC | 0.3234 | 0.1852 | |
| SD-RLSMC | 0.2038 | 0.1346 | |
| SMC | 0.0044 | 0.0044 | |
| RLSMC | 0.0021 | 0.0008 | |
| SD-RLSMC | 0.0016 | 0.0006 | |
| Reference | Performance Effect |
|---|---|
| Wang et al., 2025 [23] | Average integral absolute error: 0.29 |
| Zou et al., 2024 [20] | Trajectory tracking error between and |
| Juan et al., 2024 [22] | Average control errors in velocities along u, v, and w directions: 0.5195 ± 0.5452, 0.4703 ± 0.5859, and 0.2149 ± 0.3041 |
| Lei et al., 2024 [24] | Pitch angle steady-state error less than rad |
| This paper | For various disturbances: Z-direction RMSE between 0.0145 and 0.0159; RMSE in other directions between 0.003 and 0.007 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Yu, J.; Yang, Y. Enhancing Trajectory Tracking Performance of Underwater Gliders Using Finite-Time Sliding Mode Control Within a Reinforcement Learning Framework. J. Mar. Sci. Eng. 2025, 13, 884. https://doi.org/10.3390/jmse13050884
Wang G, Yu J, Yang Y. Enhancing Trajectory Tracking Performance of Underwater Gliders Using Finite-Time Sliding Mode Control Within a Reinforcement Learning Framework. Journal of Marine Science and Engineering. 2025; 13(5):884. https://doi.org/10.3390/jmse13050884
Chicago/Turabian StyleWang, Guohui, Jianing Yu, and Yanan Yang. 2025. "Enhancing Trajectory Tracking Performance of Underwater Gliders Using Finite-Time Sliding Mode Control Within a Reinforcement Learning Framework" Journal of Marine Science and Engineering 13, no. 5: 884. https://doi.org/10.3390/jmse13050884
APA StyleWang, G., Yu, J., & Yang, Y. (2025). Enhancing Trajectory Tracking Performance of Underwater Gliders Using Finite-Time Sliding Mode Control Within a Reinforcement Learning Framework. Journal of Marine Science and Engineering, 13(5), 884. https://doi.org/10.3390/jmse13050884






